The Economics of Agricultural Water Use and the Role of Prices
David Sunding
Agricultural production depends heavily on the nature of the local environment. Factors such as soil permeability, slope, and microclimate have a large effect on yield and water use. It is important to explicitly incorporate the influence of these “microparameters” when assessing agricultural water demand.
The farmer’s choice of irrigation technology can have a large influence on the demand for applied water, so it is sensible to begin with a description of how farmers select irrigation methods. Let
y = output / acre
e = effective input / acre
a = applied input /acre

a = land quality
p = output price
w = input price
ki = per acre cost of technology i, k1 > k0.
The crop production function is y = f(e) with ![]() and
and ![]() . The input efficiency function, hi(α), is the fraction of the applied input consumed by the crop under technology on land quality. The technologies are such that
. The input efficiency function, hi(α), is the fraction of the applied input consumed by the crop under technology on land quality. The technologies are such that
The farmer’s irrigation technology choice problem is as follows:
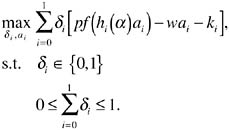
(1)
The search for a maximum consists of two stages. First, the optimal amount of applied water (a continuous choice) is determined conditional on each technology. Then, working backwards, the highest-profit technology is identified.
The applied input choice is determined by the following:
(2)
The Future Operating Capability (FOC) is
(3)
In words, this optimization condition implies that the Value of the Marginal Product (VMP) of effective water must equal the marginal price of effective water. Once the second-stage, continuous problem is solved, the discrete choice problem of technology selection must be addressed, choosing
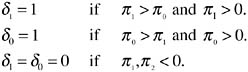
The model generates a number of testable hypotheses about the influence of environmental and market conditions on adoption of precision technology. Con-
sider first the role of land quality. The marginal impact on profits under technology i of a change in α is as follows:
(4)
where ηi = hi (α)α / hi (α). It follows that the difference in profits between the two technologies is equal to
(5)
Now, this expression can be signed by taking a Taylor’s series approximation of a as follows:
(6)
recognizing that adoption of the precision technology is equivalent to a shift in land quality from a to hi(α) Substituting the elasticity expressions above, it follows that
(7)
where ![]() . Substituting this equation into (5), it follows that
. Substituting this equation into (5), it follows that
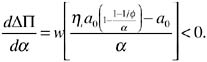
(8)
Thus, the profit gap between the modern and traditional technologies decreases as land quality improves. In this sense, the modern technology augments land quality. A further result helps in understanding the influence of land quality on adoption. At the highest possible level of land quality (i.e., α=1), the modern technology will not be adopted. To see this, simply note that at this land quality h1(1)=h0(1)=1, and ΔΠ(1)=k0−k1<0
At some level of land quality, all else being equal, the identity of the highest-profit technology will change. This level of land quality is called the switch point (αs). Modern technology is adopted for levels of land quality below α = αs and the traditional technology elsewhere. Note that the modern irrigation technology also has an extensive margin effect in that it enables profitable operation on lower levels of land quality than does the traditional technology (i.e., ![]() where
where ![]() is the shut-down level of land quality under technology i).
is the shut-down level of land quality under technology i).
Figure 1 shows that it is not profitable to operate on land of quality ![]() regardless of the type of irrigation technology chosen. On the other hand, with high quality land, either technology is profitable, although the traditional technology is more profitable. This is because on high quality land, the increase in yield with the modern technology is not worth the fixed cost of installing it. Where the modern technology makes a difference is on land of moderate quality, i.e., the land between
regardless of the type of irrigation technology chosen. On the other hand, with high quality land, either technology is profitable, although the traditional technology is more profitable. This is because on high quality land, the increase in yield with the modern technology is not worth the fixed cost of installing it. Where the modern technology makes a difference is on land of moderate quality, i.e., the land between ![]() and αs. The modern technology increases profits on land between
and αs. The modern technology increases profits on land between ![]() and αs, and enables production to be profitable on land between
and αs, and enables production to be profitable on land between ![]() and
and ![]() .
.
With respect to market parameters, total differentiation of the equation implicitly defining the switch point, αs, reveals that
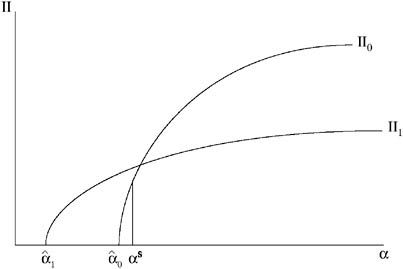
FIGURE 1 Adoption of precision technology.
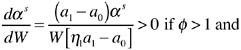
(9)
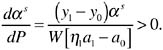
(10)
OTHER FARM-LEVEL EFFECTS OF PRECISION TECHNOLOGY ADOPTION
Recall that profit maximization requires
(11)
at the optimum. Since f' (e) > 0, it follows that
Thus, modern technology increases the optimal level of effective water use (e). But note that a higher level of effective water use does not imply a higher level of applied water use (a). This is because the ratio of applied to effective water is smaller with modern technology, so that greater effective water can be utilized with lower applied water. In most cases, modern technology reduces the optimal level of applied water use, and is therefore water-saving. If e0 < e1, then y0 < y1. Thus, use of the modern technology increases crop output.
If land quality is high, water quality is high, and the weather is mild, then h1 and h0 are not very different, and the adoption of modern irrigation technology will have only a small effect on the optimal levels of crop output and applied water.
If land quality is low, water quality is low, or the weather is hot, then adoption of modern irrigation technology may affect optimal crop output and applied water use significantly. When land quality is low and temperature is high, the effect of adopting new technology depends on water price.
EMPIRICAL ANALYSIS OF IRRIGATION TECHNOLOGY CHOICE
Despite the importance placed on micro-level variations in the theoretical literature, most empirical studies of irrigation technology adoption suffer from the use of regional average data on technology choices and resort to comparing
percentages of adoption among states or counties. Previous empirical studies have not been able to match technology choice on a one-to-one basis with micro-level variables, such as water-holding capacity, field gradient and size, water price, and water supply source. Averaging data on a regional basis has a homogenizing influence on both grower behavior and physical characteristics; it may obscure the effect of micro-variables, and, as a result, it may seriously bias statistical estimates of adoption behavior.
Empirical Model
The grower decides which irrigation technology to adopt on the jth field by calculating expected profits under each of the i technologies, while taking into account what type of crop is grown and the field’s physical characteristics. The grower chooses the technology that maximizes perceived profits, given that crop choice already has been made.1 In this study, crop and technology choice are modeled as sequential. An alternative assumption would be to model the crop and technology choice simultaneously, as suggested by Negri and Brooks (1990) and by Lichtenberg (1989). While this approach may be appropriate for grain crops, it does not appear to be appropriate for high-value fruits and vegetables. The distinction is that the production of high-value crops involves extremely specialized capital, where grains are not as highly specialized. Therefore, even though the actual investment in a new crop and technology physically may be made at the same time, the decision to invest is made sequentially. To test this, a model of simultaneous crop and technology choice was estimated. The model had inconsistent results, predicted poorly, and was statistically insignificant.
Given the assumption of sequential choice, the per acre profits are given by
(12)
where βi is a vector of estimable parameters, Xj is a vector of observed field characteristics (including crop choice), and εij is an unobserved scalar associated with unmeasured characteristics. Setting the index of the traditional technology to i=0, the grower selects the i, the modern technology if
(13)
To estimate the model parameters, it is necessary to choose a distribution for the εij’s and, thus, the distribution of the difference of the error terms. Two common assumptions are either the normal or the Weibull distributions (Domencich and McFadden, 1975). Normal random variables have the property that any linear combination of normal variants is normal. The difference between two Weibull random variables has a logistic distribution, which is similar to the normal, but with larger tails. Thus, the choice is somewhat arbitrary, especially with large sample sizes. We assume that the εij’s follow a low Weibull distribution. Given this assumption, the probability that the ith technology is adopted on the jth field is
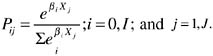
(14)
These give the estimation equations for the standard multinominal logit model that is based on the characteristics of the field, not the characteristics of the choice. In this model the parameters vary across technology choices, but not across field characteristics. Thus, the number of estimated parameters is equal to the number of characteristics times the number of choices.
The effect of each of these variables is captured in the estimated parameter vector β. The difference in characteristics across fields affects the technology choice via the perceived effect on the profitability of production on a specific field. This differs from previous studies that have looked at how regional differences affect profitability. While the previous results have given insight to regional differences, they do not correspond to individual grower choices given the field characteristics they face.
Data
The model is applied to the Arvin Edison Water Storage District (the District) located in the southern San Joaquin Valley in central California. Because of the regional climate and favorable soils, growers in the District benefit from an early harvest season that allows for diverse cropping patterns, as shown in Table 1. In addition, there has been a large degree of irrigation technology adoption: 30 percent furrow or flood, 37 percent high-pressure sprinkler, and 33 percent low-pressure drip and micro-sprinkler (Table 1). The distribution of crops and irrigation technologies makes the District ideal for analysis; yet, the area is relatively small, so the growers participate in many of the same markets and institutions.
TABLE 1 Irrigation and Acreage by Crop
|
|
Percentage of Acreage by Irrigation Technology |
|||
|
Crop |
Acreage |
Furrow |
Sprinkler |
Drip |
|
Citrus |
2,065 |
15 |
1 |
84 |
|
Deciduous |
11,700 |
27 |
33 |
40 |
|
Grapes |
23,665 |
61 |
2 |
37 |
|
Truck Crops |
27,283 |
11 |
86 |
3 |
|
Total |
74,713 |
30 |
37 |
33 |
The data on crop choice, irrigation technology, price of water, and water source were collected by the District. The study considers four crop categories: truck crops, citrus trees, deciduous trees, and grape vineyards. Taken together, these crops constitute 76 percent of the cultivated acreage in the District. The remaining acreage is distributed among grains, irrigated pasture, cotton, and dry land crops.
Irrigation technologies are consolidated into three groups based on the required level of pressurization. These groups are as follows: (1) furrow, flood, and border, which are considered the traditional or gravity technology and are used on all types of crops; (2) high-pressure sprinklers, which are used primarily on truck and deciduous crops; and (3) low-pressure systems like drip, micro-sprinklers, and fan jets, which are also used in each crop group.
There are several important points to be raised concerning low-pressure technologies and perennial crops in the District. First, low-pressure systems such as drip irrigation only wet a small area of soil. As a result, perennial crops under drip irrigation form a smaller root system than if a traditional irrigation system were used. Many growers feel that this makes the crop more susceptible to disease and the accumulation of salts, reducing the attractiveness of these systems. Second, many of the perennial crops were established prior to the introduction of low-pressure systems. Because different types of root systems are developed under the different types of technologies, growers are reluctant to switch technologies on an established crop for fear of damaging the crop. To combat these potential problems, growers have used multiple emitters for each tree to achieve a larger area of water dispersion.
The marginal price of groundwater is estimated by the District based on depth to groundwater and the energy cost for the size of pump needed to lift water from a given depth. The marginal price for surface water is the variable component of the District charge for each acre-foot that is actually delivered. In 1993, marginal water price ranged from $2 to $57 per acre-foot for surface water, and $40 to $88 per acre-foot for groundwater. Though the marginal price of groundwater is about $25 more per acre-foot than surface water, the fixed
component of the District charge for surface water is set so that the total price for ground and surface water is approximately the same, ranging from $50 to $110 per acre-foot.
The Kern County Natural Resource Conservation Service collected data on soil permeability and field slope to define land quality for each quarter section. To match the quarter sections (which are 160-acre plots) to the specific fields, District land maps were used to identify the exact location of each field. Permeability and slope were given in inches per hour and percentage, respectively. The data indicate that the distribution of irrigation technology varies by slope; when the slope increases so does the percentage of acreage under drip irrigation. This indicates that the grower’s irrigation technology choice is conditioned on land characteristics. The effect of soil permeability on technology choice is not as distinct.
Estimation
The econometric model explains the use of the different types of irrigation technologies as a function of the characteristics of the fields for which they are used. The estimation equations in (14) provide a set of probabilities for the I + 1 choices faced by the decision maker. However, to proceed it is necessary to remove an indeterminacy in the model. A convenient normalization is to assume that β0 is a vector of zeros. We can then take the log and estimate the log odds ratio of choosing the ith technology on the jth field. This is given by
(15)
The coefficients can be interpreted as the marginal impact of the variable on the log odds of selecting a modern technology relative to the benchmark (traditional) technology.
The data for the study are from the 1993 growing year, and there are 1,493 fields cultivated by approximately 350 growers. Though we are unable to identify which growers cultivated which fields, based on sample interviews we determined that most growers had fewer than four fields and grew at least two different crops. Growers that had a large number of fields grew at least five crops. There are eight independent variables, four continuous, and four binary. The four continuous variables are (a) field size, (b) field slope, (c) soil permeability, and (d) price of water. The four binary variables are (e) water source (i.e., groundwater or both ground and surface water), (f) citrus crop, (g) deciduous crop, and (h) grape vineyard. Without loss of generality, truck crops and gravitational technology are used as benchmarks for crops and technology choice.
Estimation Results
The Limdep statistical package is used to estimate the parameters of the model using maximum likelihood estimation and Newton’s method. We report the coefficients, asymptotic t-statistics, and three statistical tests to evaluate the performance of the model. To allow comparison of adoption rates among traditional, sprinkler, and drip technologies, we calculate the probability of adoption, the elasticity of the continuous variables, and the percent change in probability of the discrete variables if they were to change from 0 to 1. These are all reported in Table 2.
Of the coefficient estimates in Table 2, more than half were significant at the 0.0001 level, and all but two were significant at the 0.07 level. To measure the performance of the model, the McFadden R2, the log-likelihood ratio test, and the percentage of correct predictions are reported. The McFadden R2 is calculated as R2 = 1 − LΩ / Lω, where LΩ is the restricted maximum log-likelihood and Lω is the restricted maximum log-likelihood with all slope coefficients set equal to zero (Amemiya, 1981). The log-likelihood ratio test is given by 2(LΩ−Lω) and is asymptotically distributed as a chi-squared random variable. The percentage of correct predictions is calculated as the total number of correct predictions as a percentage of the number of observations. Each of these measures indicated that the model has strong explanatory power.
The statistical results indicate that the adoption of irrigation technologies is highly dependent on crop choice. The coefficients on the perennial crop variables in the sprinkler technology equation are all negative, large, and highly significant. This result implies that the probability of adopting sprinkler rather than the traditional technology is low for perennials and reflects the physical characteristics of perennial crops. For example, high-pressure sprinklers disperse water over a large area, saturating the tree and causing fruit decay, which is not a problem for many annual crops such as potatoes. Crop choice also strongly affects drip adoption, although in nearly the opposite way as for sprinklers. Perennial crops, especially citrus trees, are more likely to be grown under drip irrigation than annuals. The influence of crop type on technology choice is also reflected in the change in probability figures in Table 2. These results show that a grower producing perennial crops is much more likely to adopt drip than furrow or sprinkler irrigation. For example, growing citrus trees increases the probability of adopting drip by 58 percent, holding all other variables at their mean value. Previous studies that focused on a small number of crops (Lichtenberg, 1989; Shrestha and Gopalakrishnan, 1993) could not fully identify the importance of crop type on irrigation technology adoption.
Economic factors are also important in determining irrigation technology choices. The coefficient on the water price variable in the drip equation is positive and significant, confirming previous findings that water-saving technology will be adopted as water price increases. However, the coefficient on water price
TABLE 2 Estimation Results, Elasticities and Probabilities
|
|
Estimation Resultsa |
|
Elasticitiesb |
||
|
Variable |
Sprinkler |
Drip |
Furrow |
Sprinkler |
Drip |
|
Constant |
1.9855 (3.372) |
–4.5480 (–7.701) |
|
||
|
Water Price ($/acre-foot) |
–0.0130 (–1.333) |
0.0257 (3.151) |
–0.24 |
–0.84 |
0.96 |
|
Surface water (0/1) |
–0.5099 (–1.636) |
0.9706 (3930) |
[–0.11] |
[–0.12] |
[0.23] |
|
Soil permeability (in/hr) |
0.0002 |
0.0529 |
–0.04 |
–0.04 |
0.11 |
|
Field slope (%) |
0.2210 |
0.6277 |
–0.32 |
0.01 |
0.61 |
|
Field size (acres) |
0.0101 |
0.0065 |
–0.19 |
0.34 |
0.15 |
|
Crops |
|
||||
|
Citrus (0/1) |
–5.1537 (–8.380) |
2.1117 (6.095) |
[–0.21] |
[–0.37] |
[0.58] |
|
Deciduous (0/1) |
–2.3600 (–11.186) |
1.3872 (4.064) |
[–0.16] |
[–0.23] |
[0.39] |
|
Grapes (0/1) |
-6.3777 |
0.6760 |
[0.24] |
[-0.57] |
[0.33] |
|
Probability of adoption evaluated at variable means |
|
|
0.54 |
0.18 |
0.28 |
|
Observations |
1,493 |
|
|
|
|
|
McFadden R2 |
0.44 |
|
|
|
|
|
Likelihood ratio test |
1,441.16 |
|
|
|
|
|
Correct prediction |
74% |
|
|
|
|
|
aTerms in parenthesis are asymptomatic t-statistics. bTerms in brackets are not elasticities. They are the percent change in the probability of adoption as the discrete variable cha nges from 0 to 1. |
|||||
in the sprinkler equation is negative. Figure 2 shows the change in the probability of adoption as a function of the price of water, with all other variables set at their mean values. This figure demonstrates that, as the price of water increases, growers switch from both furrow and sprinkler irrigation technologies to drip.
The results in Table 2 and Figure 2 are in sharp contrast to the results of previous studies that have found similar adoption patterns for high- and low-pressure irrigation systems. For example, Caswell and Zilberman (1985) reported coefficients of 0.03 on marginal water price in equations explaining both drip and sprinkler adoption, and Cason and Uhlaner (1991) estimated water price coefficients between 0.02 and 0.07 for all technologies, depending on the region. The results differ from these studies for several reasons. Examining several technology choices simultaneously gives a more complete picture of grower decision-making behavior and allows for explicit estimation of marginal probabilities. Further, growers in this study farm in an arid, hot climate and pay more for water than irrigators in many other areas. As a result, the diffusion process for pressurized technologies is more advanced in the District than in other regions, and sprinkler technologies appear to be nearing the end of their product life cycle. Sprinkler irrigation has been employed in the District since the early 1960s and is widely utilized on crops that grow well with this technology. In particular, Table 1
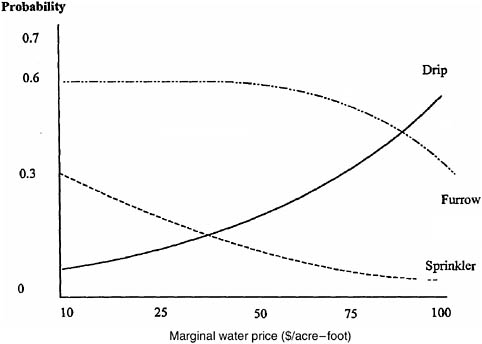
FIGURE 2 Probability of adoption by marginal water price.
shows that truck crops are grown largely under sprinkler irrigation. However, potato growers in the District are now beginning to convert to low-pressure systems (especially drip tape) in response to changes in water price. This observation is consistent with the findings of Dinar and Yaron (1992). In their model of technology adoption and abandonment, Dinar and Yaron estimate the technology cycle of hand-move sprinklers to range from 22 to 24 years.
The coefficients on the land quality variables, soil permeability and field slope, are of the expected sign and magnitude. Again, however, there are important differences between technologies in terms of the effect of land quality variables. Sprinkler adoption is not as sensitive to land quality as drip irrigation, which is especially dependent on field slope. Prior to the introduction of drip irrigation, it was difficult and costly to grow irrigated crops on lands with steep slopes. As a result, the introduction of drip has allowed cultivation of land that had previously been unproductive. This relationship is best seen in Figure 3, which shows that variations in slope have a dramatic effect on the probability of adopting furrow and drip irrigation.
Caswell and Zilberman (1986) show theoretically that modern irrigation
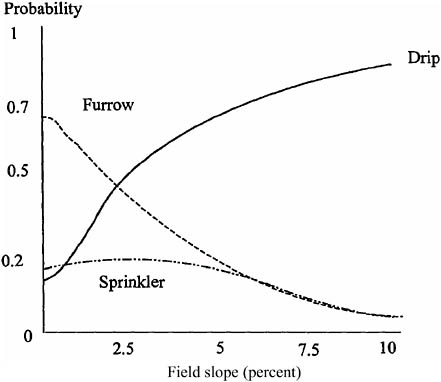
FIGURE 3 Probability of adoption by field slope.
technologies are less likely to be adopted on fields with surface water supplies rather than groundwater supplies on the assumption that surface water is supplied at lower pressure than groundwater. The statistical results show that sprinkler adoption is less likely in areas with surface water supplies, but that drip adoption is more likely with surface supplies. While the District is one of the few California districts supplying pressurized surface water to its growers, the pressure is not consistent and is only sufficient to run a low-pressure system such as drip.
Discussion and Implications
These empirical results point out that cross-section technology adoption coefficients must be interpreted with the dynamic diffusion process in mind and also show that the effect of economic factors such as price on adoption is path-dependent. For example, in the results, we obtained a negative coefficient on the water price variable for adoption of sprinkler irrigation, which would seem to refute the theoretical and empirical literature. However, high-pressure sprinklers are widely adopted in the study area, and because these technologies are far from the beginning of their life cycle in the District, abandonment of sprinkler technologies is more sensitive to water price increases than is adoption. In another area where growers rely more on gravitational systems, and hence sprinklers are at the beginning of their life cycle, the opposite should be true. This demonstrates that the coefficients cannot be interpreted at face value and that it is important to consider the underlying diffusion process when considering the policy implications of an analysis.
The results show that water price is not the most important factor governing irrigation technology adoption; physical and agronomic characteristics appear to matter more. As a result, the distributional impacts of irrigation water pricing reforms will be significant, with changes in producer welfare following the spatial distribution of environmental characteristics. To the extent that micro-level factors condition irrigation technology choice, policies that change the price of irrigation water to reflect its off-farm value will result in a pure loss for some producers while encouraging adoption of modern irrigation technologies for other producers. This demonstrates the importance for economists to bear in mind the equity implications of water pricing reform proposals when interacting with decision makers.
This type of empirical research has important implications for the design of water pricing and delivery policies. The statistical results above show that large increases in the price of water generally stimulate the adoption of drip irrigation systems; that adoption patterns are heavily influenced by crop type; and that the adoption decision is also strongly conditioned by slope, but is only slightly affected by variations in water-holding capacity. These results are a significant departure from previous studies, which have generally failed to account for differences in adoption behavior within the group of pressurized technologies and
for the influence of crop type on adoption behavior, and which have inadequately measured physical characteristics and water prices by relying on regional data.
WATER ALLOCATION MECHANISMS AND AGRICULTURAL WATER USE
In many regions of the United States, water allocation has been based on queuing systems rather than on markets. Queuing systems are sets of laws defining property rights regarding who has priority to use water, when water may be used, how water may be used, and how much water may be used. Although queuing systems are still the norm in many parts of the world, they are undergoing change. A typical queuing system is a use-it-or-lose-it system of water property rights based on the principle “first come, first served.”
Queuing systems for water were established in the western United States to encourage settlement of land and the economic use of water resources. In early periods, water was abundant, governments were poor, and they wanted to encourage people to develop water resources. As a result, government gave individuals the right to the water that they diverted, so long as they used it in a way that generated economic benefits. Note that markets are the best allocation mechanisms when there is scarcity, but queuing can be very effective when scarcity does not exist. The biggest problem with queuing is that demands for water can increase, and when that happens, scarcity suddenly can emerge. In this situation, water reforms are needed.
As water scarcity increases there is a tendency to allow trading in water. In California, for example, water trading was introduced during drought periods. The transition from queuing to markets may involve redesign of the water allocation system, building a system for the monitoring of water use, and protection against theft, and all this entails high transaction costs. If the gains from transition are smaller than these transaction costs, reform will not and should not occur.
The queuing system is not an efficient means of allocating water resources if scarcity exists, that is, if junior rights holders do not receive enough water. In particular, if a unit of water provided to junior rights holders has positive Marginal Value of Product (MVP), then we know queuing is inefficient since senior rights holders apply water to the point where their MVP = 0. Figure 4 illustrates this argument.
Because the prices facing senior and junior users are unequal, the corresponding marginal benefits of water use are unequal. Since the marginal cost to supply each type of user is essentially the same, social welfare may be increased by reallocating water from senior users to junior users. Thus, allocation by queuing is inefficient. Allowing water to be freely traded would lead to water transfers from senior rights holders to junior rights holders.
Notice also that the total level of water consumed is inefficiently high under
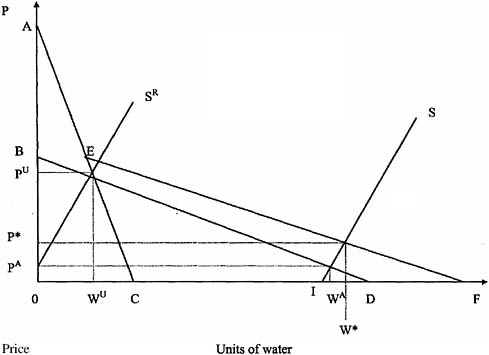
FIGURE 4 Queuing versus markets.
(a) Water supply projects (dams, canals, etc.) often have high initial fixed costs associated with construction and low marginal costs of supplying water up to the capacity of the project. At full capacity, the marginal cost of water supply rises steeply, because additional projects or procurement strategies are required in order to supply additional water. Thus, the marginal cost of water supply curve is 0IS.
(b) Assume that senior water demand is given by curve BD.
(c) Assume that junior water demand is given by curve AC.
(d) Aggregate demand for water is given by curve AEF, if water markets exist. Under water markets, the equilibrium level of water consumed is W* and the equilibrium price is P*.
(e) Water rights allocate water to different users at different times. Demand is not aggregated, but discriminated by time in the residual demand curves BD and AC. Senior rights holders purchase an amount of water equal to WA, which is where their water demand equals the marginal cost of water. The price of water used by senior rights holders is PA.
(f) Once the WA units of water have been consumed by senior users, junior users face residual water supply SR, and therefore consume WU units of water and pay a price of PU. The price of water in junior rights areas is higher than in senior rights regions.
a queuing system, or that ![]() . Thus, moving to a market oriented system of water allocation can lead to greater water conservation.
. Thus, moving to a market oriented system of water allocation can lead to greater water conservation.
Queuing System
We now return to the analysis in the first section of this paper and demonstrate some economic implications of the transition from queuing to markets. Water trading is disallowed under a queuing system. In this case, there is no incentive for senior rights holders to adopt modern technology since water has no price. Water is simply diverted, as needed, according to a farmer’s place in the queue.
Suppose that A is the total amount of water available in a region and that L is the total amount of land available for cultivation. Also, let ![]() denote maximum output per acre, where em is defined by
denote maximum output per acre, where em is defined by ![]() is the effective water associated with maximum yield.
is the effective water associated with maximum yield.
Senior rights owners use water until the Value of the Marginal product (VMP) of water = 0, which is the level that will maximize yields. Settlement occurs until water resources are exhausted, so water becomes the limiting factor on development. Applied water use is ![]() per acre, the amount of applied water associated with the maximum effective water absorbed by the crop.
per acre, the amount of applied water associated with the maximum effective water absorbed by the crop.
Under a queuing system of water rights, the water price is equal to 0, and the per-acre fee for water use μ. Settlement will occur until all water is appropriated and the total acres under cultivation is ![]() Total output under a water rights system is
Total output under a water rights system is ![]() and producer surplus is
and producer surplus is ![]()
Market System
When all land quality is the same, the efficient solution involves applying water uniformly across all land to equate the MVP. Thus, under a market system, all land is utilized, and each owner faces the choice of technology i.
Under a market system, water use per acre is A/L yield per acre under technology i is ![]() , and the price of water VMP of applied water = Pfehi.
, and the price of water VMP of applied water = Pfehi.
Producers’ annual profits per acre are
(16)
where t equals transaction costs so that
(17)
Technology 1 is selected if Π1 − Π0 > 0.
Both technologies require the same water per acre, because water is evenly distributed across all acres as a result of equating the MVP. When each farmer is a small unit, the farmer does not believe that her choice of technology will affect the market price of water, and the market price of water is considered as a constant in the problem. Then the choice of technology can be expressed as follows:
Select technology 1 when ![]() .
.
Both technologies result in the same water use per acre, but the modern technology increases the yield by raising the amount of effective water received by the crop. If the market value of the increase in yield is greater than the extra capital costs involved with investing in the new technology, then the farmer should invest.
COMPARING MARKET AND QUEUING OUTCOMES
Assume that, under market conditions, technology i is optimal and adopted by all farmers. Under a market system all arable land is utilized. The transition to market will increase irrigated land from Ah0 / em to L. Output will increase by
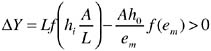
(18)
as water is shifted from low Marginal Product (MP) land to the high MP lands now under cultivation. Output per acre will decrease from ![]() . The reduction in water use per acre is from em·h0 to A / L.
. The reduction in water use per acre is from em·h0 to A / L.
In the transition to the market, ![]() units of water that were used to produce the output associated with area B in Figure 5 are allocated to irrigate new lands. Overall, output increases because the water that was used under queuing to produce output associated with region B of Figure 5 is used under markets to produce output in region A on new land that is brought into production. Obviously, the marginal productivity of this water increases.
units of water that were used to produce the output associated with area B in Figure 5 are allocated to irrigate new lands. Overall, output increases because the water that was used under queuing to produce output associated with region B of Figure 5 is used under markets to produce output in region A on new land that is brought into production. Obviously, the marginal productivity of this water increases.
If the senior rights owners who appropriated water under the queuing system have to buy water after the transition to a market, their profits will decrease. Under water markets, they now have lower yields, they now have to pay for
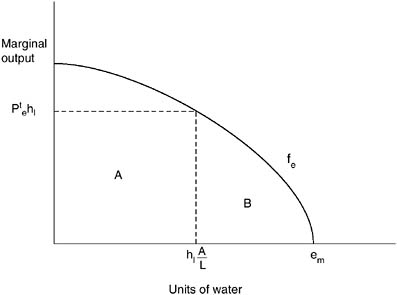
FIGURE 5 Output effect of transition to markets.
water, and they also must pay to adopt the new technology, since doing so is now optimal. Their loss per acre is
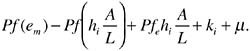
(19)
But if the senior rights holders are given the property rights to the water, they may gain. These users still have lower output than under queuing, but the gain from selling water may overcome this output loss. Their income per acre will be
(20)
If the transaction costs are high, there may be no reason to switch to a system of water markets. Namely, if
(21)
then transaction costs per acre exceed the per acre change in output plus the cost of adopting the optimal modern technology less the cost savings of senior owners not adopting the conventional technology. In this case, water markets are inefficient.
Because markets for final products have negatively sloped demand, the transition from queuing to markets will also reduce the market price of agricultural commodities. Senior rights owners may thus lose, even if they sell water because of the price decline of their output. Producers as a whole may actually lose, but consumer surplus will increase.
WATER PRICING IN A CONJUNCTIVE USE SYSTEM
The economics of agricultural water use and pricing become more complicated when the possibility of groundwater use is considered. Let yt = pumping in year t and xt = the level of the ground1water stock in year t. The level of the stock increases in year t by g(yt), where ∂g / ∂yt ≥ 0. For example, g(yt) = A + Θy, where A is rainfall plus imported surface water (which is influenced by the price of water charged by the government) and Θ is percent of irrigation water that is return flow. Thus, the growth equation for the stock of groundwater is
(22)
Let B(yt) = benefits from groundwater use and C(xt1 yt) = total cost of pumping, where ∂c / ∂xt = 0 and ∂c / ∂yt ≥ 0.
Groundwater is managed optimally when pumping and the stock are chosen each year to maximize
(23)
where r is the price of land, subject to ![]() To solve this problem, convert the constrained problem into an unconstrained one using Lagrange multipliers as follows:
To solve this problem, convert the constrained problem into an unconstrained one using Lagrange multipliers as follows:
(24)
The first order conditions are
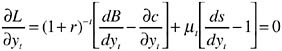
(25)
where s is units of surface water
(26)
(27)
(28)
λt is the value in period t of an extra unit of groundwater stock in period t. μt is the value in period 0 of an extra unit of groundwater in period t.
We can rewrite (25) as
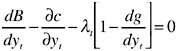
(29)
So optimal pumping equates the marginal benefit of pumping with its marginal cost plus user cost of pumping adjusted for return flows to the aquifer.
Now, from (28) it follows that
(30)
Substituting into (26) we get
(31)
Multiplying by (1+r)−1 and rearranging yields
(32)
This condition says that the optimal stock of groundwater occurs when the opportunity cost of keeping a unit of water in the ground (rλt) equals the capital gain when water is kept in the ground (λt−λt-1) minus the reduction in pumping cost from having more water in the ground.
In a steady-state,
(33, 34)
In this case, optimality conditions (22), (29), and (32) reduce to the following:
(22′)
(29′)

(32′)
I will consider the effect of changes in surface water prices in the context of a steady-state.
When ![]() and is influenced by the price of surface water, it is clear first of all that raising the price of surface water reduces A, reduces the amount of groundwater pumping, and reduces total water use. The shadow price of groundwater, λ*, decreases (from equation (32′), and the stock of groundwater decreases (from (29′)). All of these effects must be considered when evaluating the optimality of water price reforms in a conjunctive use setting.
and is influenced by the price of surface water, it is clear first of all that raising the price of surface water reduces A, reduces the amount of groundwater pumping, and reduces total water use. The shadow price of groundwater, λ*, decreases (from equation (32′), and the stock of groundwater decreases (from (29′)). All of these effects must be considered when evaluating the optimality of water price reforms in a conjunctive use setting.
AGRICULTURE AS A SUPPLIER OF LAST RESORT: AN EXAMPLE FROM CALIFORNIA
Agriculture in the western United States is highly dependent on the diversion of water resources for irrigation. At the same time, population growth, increased industrialization and, most importantly, heightened public awareness of environmental benefits from enhancing instream flows are all exerting tre-
mendous pressure on federal and state agencies to reduce these diversions. These forces are resulting in a large-scale reallocation of water from agriculture to urban and environmental uses. What is the effect of this reallocation on agriculture?
A Conceptual Model of the Economic Impacts of Water Supply Reduction
The modeling framework applied here is drawn from Sunding et al. (2001), and consists of a microeconomic model of resource allocation by the irrigated agricultural sector. Profit maximization in agriculture is conducted subject to water supply reductions and economic relationships.
Following on the discussion above, it is crucial to recognize heterogeneity among producers. In this conceptual framework, farming is carried out by J micro production units of various sizes. Such units may be interpreted as farms, water districts, or counties depending on the application and the data available. The micro production unit indicator is j, j = J; and the land base of each unit is denoted by Lj. It is assumed that there are no constraints on water movement within the micro production units, but there may be barriers to trade and transfer of water between micro production units. Indeed, water rights regimes, such as the prior appropriation system and riparian rights systems, restrict trading; one major feature of a policy reform is the extent to which water trading is allowed.
The analysis is conducted for N + I water policy scenarios, with n as a scenario indicator n = 0,1,2,…,N. The scenario n = 0 corresponds to the preregulation or base water allocation. Under each scenario, micro production units are aggregated into regions. Water trading is feasible within regions but not between regions. Let Kn be the number of regions under scenario n, and kn be the region indicator, so that kn = 1,…Kn. The set of micro production units in region kn is denoted by ![]() . For example, if we have eight micro production units divided into two regions under scenario n,
. For example, if we have eight micro production units divided into two regions under scenario n,
Each micro production unit has an initial “endowment” of surface or groundwater representing annual surface water rights and groundwater pumping capacity. Let ![]() be annual surface water available to district j in the base scenario and
be annual surface water available to district j in the base scenario and ![]() be annual groundwater available to district j. Alternative policy scenarios affect these water availability constraints.
be annual groundwater available to district j. Alternative policy scenarios affect these water availability constraints.
In the base scenario, total water available to kn region
However, surface water availability differs among alternative scenarios. Let ![]() be the reduction of water supply available to region kn. The overall surface water supply reduction in scenario n is
be the reduction of water supply available to region kn. The overall surface water supply reduction in scenario n is
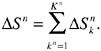
(35)
This change reflects the total amount of water reallocated from agriculture. Actual use levels of ground and surface water at region j are denoted by Gj and Sj respectively, with ![]() and
and ![]()
Following theory and empirical evidence, Sunding et al. (2001) suggest that California growers have responded to reductions in water supply by (i) changing land allocation among crops (including fallowing), (ii) increasing the amount of groundwater pumping, and (iii) modernizing their water application methods (on this point, see also Moreno and Sunding, 2001; Green and Sunding, 1997; Green et al., 1996; and Zilberman et al., 1995). The modeling of production relationships in Sunding et al. (2001) considers all of these possibilities. There are I crops and i is the crop indicator, i=1,I. Let the amount of water applied to crop i in micro production unit j be denoted by Aij, and let Lij be the amount of land allocated to the production of crop i at micro production unit j. Let Yij be the output of crop i at micro production unit j. For modeling convenience, total output is represented as the product of yield per acre, yij, and acreage of crop i in micro production unit j is ![]()
Output is produced by land, labor, irrigation equipment, and other inputs (e.g., chemicals), and is affected by local environmental conditions. The general specification of the per acre production function is
(36)
where
aij = Aij / Lij (applied water per acre),
zij = Zij / Lij (annual irrigation equipment cost per acre),
Zij = total irrigation equipment cost on crop i in micro production unit j,
and
θij = regional environmental quality parameters.
This specification is consistent with the observations of Dinar and Zilberman (1991). Specifically, they argue that increased annual irrigation equipment costs increase output by increasing irrigation efficiency, and that both land quality (in
particular, water-holding capacity) and water quality (especially salinity) affect the productivity of water. Specific applications may have special functional forms, but all specifications maintain concavity. Yield per acre may decline as land use increases (i.e., ![]() ) because of decreasing marginal productivity of land.
) because of decreasing marginal productivity of land.
Let the cost of surface water at micro production unit j be ![]() and cost of groundwater be
and cost of groundwater be ![]() .2 Generally,
.2 Generally, ![]() so that surface water is cheaper than groundwater. The cost of inputs other than water and irrigation technology is assumed to be a convex function of crop i acreage in micro production unit j and is denoted by the function Cij(Lij) with
so that surface water is cheaper than groundwater. The cost of inputs other than water and irrigation technology is assumed to be a convex function of crop i acreage in micro production unit j and is denoted by the function Cij(Lij) with
(37)
This cost function reflects the important empirical observation that land fertility is heterogeneous in California and that increases in acreage lead to increased expenditures on inputs, such as fertilizers, that augment land productivity.3
The most general specification of output markets would assume that producers face downward sloping demand curves and that output prices are determined endogenously. In this case, the optimization problem will maximize the sum of producer and consumer surplus subject to resource constraints. In our model, we assume price-taking behavior and denote the price of output i by Pi. This assumption is consistent with the high demand elasticity that California producers face.
Assuming profit-maximizing behavior by growers, the aggregate regional optimization problems under scenario n are
(38)
(39)
(40)
(41)
Constraint (39) states that total water used in crops is composed of either surface water or groundwater. Condition (40) is the most important constraint, as it sets a limit on the water available to each region under a given policy scenario. Availability is the sum of water available to districts under initial allocation minus the amount diverted under the specific scenario. Inequality (41) is the land availability constraint.
The solution of the regional optimization problem using Kuhn-Tucker conditions requires assigning shadow prices for each of the constraints. The shadow price of equation (39) is ![]() . This is the shadow cost of water delivery and is equal to
. This is the shadow cost of water delivery and is equal to ![]() if only surface water is used and
if only surface water is used and ![]() if groundwater is used in district j. The shadow price of the regional water constraint (40) is
if groundwater is used in district j. The shadow price of the regional water constraint (40) is ![]() . Thus, the marginal cost of a unit of water in district j that belongs to region k under scenario n is
. Thus, the marginal cost of a unit of water in district j that belongs to region k under scenario n is ![]()
If the production function is differentiable, optimal water use per acre with crop i at district j is at the level where the value of marginal product of water is equal to the shadow price of water.
(42)
Optimal irrigation cost per acre is determined similarly at the level where the value of marginal product of the expenditure is equal to its price. The next condition is
(43)
The shadow price of the land availability constraint in district j is rj, and under standard assumptions, land is allocated to crop i in district j so that the value of marginal product of land is equal to rj, i.e.,
(44)
Condition (44) states that the optimal acreage of crop i at district j is such that net marginal benefit of land is equal to its shadow price. Marginal net benefits of land are the difference between revenue added by marginal land and the extra cost of water, irrigation technology, and other inputs, as well as the extra cost associated with the decline of land productivity. The conditions are more elaborate if there are land availability constraints for individual crops.
In principle, conceptual and empirical analysis requires solving the model under scenario 0, the initial condition, and then under each alternative scenario. The net income effect of a policy under the scenario denoted by ΔΠn is the change in producer surplus between scenario 0 and scenario n, i.e.,
(45)
It is expected that, for most scenarios, ΔΠn, namely, reduction in water supply, reduces overall income. But different scenarios assume different partitions of the regions. Under the initial scenario (n = 0), the state is divided into K0 regions, where water trading is feasible within regions and where water trading is allowed between regions. Two types of scenarios are likely to be associated with a given reduction in overall surface water supply. Under water trade scenarios, trading is allowed throughout the state; under proportional cuts scenarios, the supply reductions to regions are proportional to initial allocations so that the reduction in surface water for regions under such scenarios, ![]() , is
, is
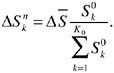
(46)
By the La Chatelier Principle, given total supply reduction, aggregate profit is higher under the free trade scenario, as there are fewer constraints. In some cases, a water reform that reduces surface water supply and allows trading may increase profit (ΔΠn > 0) if gains from trading are greater than losses from surface water supply reductions.
Standard welfare analysis considers impacts on consumer and producer surplus, but policy makers may be interested in changes in other variables.4 Other such variables are gross farm income, regional income, and employment.
The gross income effect of scenarion n,ΔRn is derived by subtracting gross revenues of scenario n from gross revenues of the initial scenario. As with net
income, it seems that gross revenues will decline as aggregate water levels decline. However, under some scenarios, the reduced water supply may lead producers to adopt modern irrigation technologies, which tend to increase per acre yields (Caswell and Zilberman, 1986) but also entail higher production costs. Under these scenarios, the higher yield will result in increased revenues in spite of the overall water supply reductions.
The impact of water policy changes on the nonagricultural economy is another useful policy indicator. Let ψi be a regional impact coefficient, denoting an increase in regional product (both direct and indirect effects) associated with a $1.00 increase in revenues of crop i. The reduction in regional impact associated with policy scenario n,ΔRnPn is
(47)
In most cases one expects regional product to decline as a result of reduction in water supply. However, if supply reduction is associated with increased water trading possibilities and higher water prices, regional income may increase because of adoption of conservation technologies that increase yield or increase water used for production of high value crops. These crops generate more revenue per acre-foot of water than low value crops and have stronger linkages to the nonagricultural regional economy due to their higher labor requirements.
The employment impact of a water policy change can also be calculated using standard multipliers. Typically, job loss is measured based on changes in gross revenues. Of course the scope of water trading should mitigate the total labor market impact of water policy changes, particularly if trading results in less high-value fruits and vegetables going out of production following a supply cut.
APPLICATION TO CALIFORNIA
This framework has been applied to study the impact on California agriculture of losing surface water supplies. In the problem considered here, farmers stand to lose between 800,000 and 1,300,000 acre-feet (AF) due to environmental restrictions.
To understand the economic impacts from such a cutback, it is also necessary to know how the cut is to be allocated among users. To a large extent, the final allocation of the supply reduction is an open question, depending on which state or federal agency takes responsibility for the decision. If the state of California makes the decision, then all water users in the state whose consumption affects bay/delta flows are potential targets for cutbacks. However, if the federal government implements the reduced diversions, then only Central Valley Project (CVP)
users are liable for the reductions. Thus, the allocation of the cuts is treated as a choice variable, and a variety of initial allocation schemes is considered.
The extent of water trading is currently a policy choice. Trading is highly active within small units such as water districts, and a large volume of water is traded between neighboring districts within the CVP system. There is, however, controversy about how much water can and should be traded among growers, between growers and urban areas, and between basins. Further, there are physical constraints on conveyance that are, at present, hard to define precisely due to hydrological uncertainties and constantly changing regulatory restrictions on pumping. Thus, the scope of the water market is treated here as a policy variable, and the impact models are used to examine a wide array of trading scenarios.
These policy choices are examined using three alternative impact models. These models vary in terms of the production functions, degree of detail, and time scale, as described in Sunding et al. (2001).
BENEFITS TO AGRICULTURE OF WATER TRADING
The incremental costs of removing water from the Central Valley increase sharply as the quantity reallocated increases. Increasing the amount of water devoted to environmental protection from 0.8 million acre-feet (MAF) to 1.3 MAF more than doubles the cost of the regulation to growers. Experimental runs with higher levels of water supply reduction show that this tendency continues and incremental costs of water supply reduction increase as water scarcity increases. This result is attributable to the fact that profit-maximizing farmers will first reduce or cease production of low-value crops in response to reductions in water supply, and will only cease producing high-value crops if the reductions are drastic.
The overall level of the water supply cut is not the most important factor affecting the social cost of protecting bay/delta water quality. Rather, the impacts depend more importantly on the extent of a water market and, when trading is limited, on how supply cuts are distributed among regions. If a market mechanism is used to allocate an annual reduction of 0.8 MAF among a large body of growers in the Central Valley, farm revenue decreases by $10 to $19 million. Using a proportional allocation for the same region, losses are from $45 to $85 million.
COMMENTS
There is increasing pressure in the western United States to protect natural resources by enhancing instream flows. Such policies inevitably mean reducing diversions to irrigated agriculture. This section presents a method for measuring the impacts on agriculture of such reductions. The fundamental tension to be addressed in constructing an agricultural impact model is between the detail
necessary to permit examination of the distributional consequences impacts, and the fact that growers have a multidimensional response to policy changes. Rather than constructing a highly complex model incorporating all growing regions and all responses, the results of existing, smaller models can be compared to accurately measure policy impacts in a cost-effective way.
SELECTED BIBLIOGRAPHY
Amemiya, T. 1981. Qualitative response models: A survey. Journal of Economic Literature 19(4):1483-1536.
Anderson, L.T., ed. 1983. Water Rights, Scarce Resource Allocation, Bureaucracy and the Environment. San Francisco, CA: Pacific Institute for Public Policy; Cambridge, MA: Ballinger Publishing Company.
Atkeson, A. and P.J. Kehoe. 1999. Models of energy use: Putty-putty versus putty-clay. American Economic Review 89(4):1028-1043.
Bellon, M.R. and J.E. Taylor. 1993. “Folk” soil taxonomy and the partial adoption of new seed varieties. Economic Development and Cultural Change 41(4):763-786.
Burness, H.S. and J.P. Quirk. 1979. Appropriative water rights and the efficient allocation of resources. The American Economic Review 69(l):25-37.
California Air Resources Board. 1987. Effects of ozone on vegetation and possible alternative ambient air quality standards. Technical Support Document, Sacramento, CA.
Cason, T. N. and R. T. Uhlaner. 1991. Agricultural production’s impact on water and energy demand: A choice modeling approach. Resource and Energy Economics 13(4):307-321.
Caswell, M.F. 1983. The diffusion of low-volume irrigation technology in California agriculture. Ph.D. Dissertation, University of California, Berkeley, CA.
Caswell, M.F. and D. Zilberman. 1985. The choices of irrigation technologies in California. American Journal of Agricultural Economics 67(2):223-234.
—————. 1986. The effects of well depth and land quality on the choice of irrigation technology. American Journal of Agricultural Economics 68(4):798-811.
Chakravorty, U., E. Hochman, and D. Zilberman. 1995. A spatial model of optimal water conveyance. Journal of Environmental Economics and Management 29(l):25-41.
Coase, R. 1992. The institutional structure of production. The American Economic Review 82(4):713-719.
County Supervisors Association of California (CSAC). 1990. California County Fact Book 1988-1989. Sacramento, CA.
Davies, S. 1979. The Diffusion of Process Innovations. Cambridge, UK: Cambridge University Press.
Dinar, A. and D. Yaron. 1992. Adoption and abandonment of irrigation technologies. Agricultural Economics 6(April):315-332.
Dinar, A. and D. Zilberman. 1991. Effects of input quality and environmental conditions on selection of irrigation technologies. In: A. Dinar and D. Zilberman, eds., The Economics and Management of Water and Drainage in Agriculture. Norwell, MA: Kluwer Academic Publishers.
—————-1991b. The economics of resource-conservation, pollution-reduction technology selection: The case of irrigation water. Resource and Energy Economics 13(4):328-348.
Dinar, A., S. Hatchett, and E. Loehman. 1991. Modeling regional irrigation decisions and drainage pollution control. Natural Resource Modeling 5(2):191-212.
Dixon, L., N. Moore, and S. Schechter. 1993. California’s 1991 drought water bank. RAND Corporation, Santa Monica, CA.
Domencich, T. and D. McFadden. 1975. Urban Travel Demand: Behavioral Analysis. Amsterdam: North-Holland Publishing.
Fudenberg, D. and J. Tirol. 1991. Game Theory. Cambridge, MA: MIT Press.
Gisser, M. and R.N. Johnson. 1983. Institutional restrictions on the transfer of water rights and the survival of an agency. In: T.L. Anderson, ed., Water Rights, Scarce Resource Allocation, Bureaucracy, and the Environment. San Francisco, CA: Pacific Institute for Public Policy; Cambridge, MA: Ballinger Publishing Co.
Gisser, M. and D.A. Sanchez. 1980. Competition versus optimal control in ground water pumping. Water Resources Research 16(4):638-642.
Goodman, C. and R.E. Howitt. 1986. The California agricultural resources model: Structure, calibration and applications under positive quadratic programming. Working Paper, Department of Agricultural Economics, University of California at Davis.
Green, G. and D. Sunding. 1997. Land allocation, soil quality and irrigation technology choices. Journal of Agricultural and Resource Economics 27(2):367-375.
—————. 2000. Designing environmental regulations with empirical microparameter distributions: The case of seawater intrusion. Resource and Energy Economics 22(1):63-78.
Green, G., D. Sunding, D. Zilberman, and D. Parker. 1996. Explaining irrigation technology choice: A microparameter approach. American Journal of Agricultural Economics 78(4): 1064-1072.
Greene, D.L., J.R. Kahn, and R.C. Gibson. 1999. Fuel economy rebound effect for U.S. household vehicles. Energy Journal 20(3):1-31.
Hall, D.C. and M.W. Hanemann. 1996. Urban water rate design based on marginal cost. In: D.C. Hall, ed., Advances in the Economics of Environmental Resources, Volume 1. Greenwich, CT: JAI Press, Inc., pp. 95-122.
Hausman, J.A. 1979. Individual discount rates and the purchase and utilization of energy using durables. Bell Journal of Economics 10(l): 33-54.
Hicks, J.R. 1939. Value and Capital. Oxford: Clarendon Press.
Hochman, E. and D. Zilberman. 1978. Examination of environmental policies using production and pollution microparameter distributions. Econometrica 46(4):739-760.
Houthakker, H. 1955-56. The Pareto distribution and the Cobb-Douglas production function in activity analysis. Review of Economic Studies 23(l):27-31.
Howe, W.C., D.R. Schurmeier, and W. Douglas. 1986. Innovative approaches to water allocation: The potential for water markets. Water Resources Research 22(4):439-445.
Howitt, R.E. 1989. The economic assessment of California field crop losses due to air pollution. Working Paper, Department of Agricultural Economics, University of California at Davis.
————.1992. Economic assessment of acid deposition and ozone damage on the San Joaquin valley agriculture. Working Paper, Department of Agricultural Economics, University of California at Davis.
————. 1995. Positive mathematical programming. American Journal of Agricultural Economics 77(2):329-342.
Johansen, L. 1959. Substitution versus fixed production coefficients in the theory of economic growth: A synthesis. Econometrica 27(April):157-176.
—————. 1972. Production Functions: An Integration of Micro and Macro, Short-Run and Long-Run Aspects. Amsterdam: North Holland.
Just, R., D. Hueth, and A. Schmitz. 1982. Applied Welfare Economics and Public Policy. Englewood Cliffs, NJ: Prentice Hall.
Knapp, K.C., A. Dinar, and J. Letey. 1986. On-farm management of agricultural drainage problems: An economic analysis. Hilgardia 54(4):1-31.
Letey, J. and A. Dinar. 1986. Simulated crop-water production functions for several crops when irrigated with saline waters. Hilgardia 54(l):1-32.
Letey, J., A. Dinar, and K. Knapp. 1985. A crop-water production function model for saline irrigation waters. Soil Science of America Journal 49(4):1005-1009.
Lichtenberg, E. 1989. Land quality, irrigation development, and cropping patterns in the northern high plains. American Journal of Agricultural Economics 71(l):187-194.
Moreno, G. and D. Sunding. 2001. Factor price risk and conservation technology adoption. Working Paper, Department of Agricultural and Resource Economics, University of California at Berkeley.
Moreno, G., D. Osgood, D. Sunding, and D. Zilberman. 1999. The economics of water supply reliability. Working Paper, Department of Agricultural and Resource Economics, University of California at Berkeley.
Moyle, P. and R. Yoshiyama. 1992. Fishes, aquatic diversity management areas, and endangered species: A plan to protect California’s native aquatic biota. California Policy Seminar, University of California at Berkeley.
Negri, D. and D. Brooks. 1990. Determinants of irrigation technology choice. Western Journal of Agricultural Economics 15(2):213-223.
Olmstead, J., D. Sunding, D. Parker, R. Howitt, and D. Zilberman. 1997. Water marketing in the ’90s: Entering the electronic age. Choices (Third Quarter):15-19.
Perrin, R.K. and D. Winkelmann. 1976. Impediments to technical progress on small versus large farms. American Journal of Agricultural Economics 58(5):888-894.
Rausser, G. and P. Zusman. 1991. Organizational failure and the political economy of water resources management. In: A. Dinar and D. Zilberman, eds, The Economics and Management of Water and Drainage in Agriculture. Norwell, MA: Kluwer Academic Publishers.
Rosen, D.M. 1989. Property rights and public choice in water districts: An application to water markets. Ph.D. Dissertation, University of California at Berkeley.
Rothschild, M. and J. Stiglitz. 1970. Increasing risk 1: A definition. Journal of Economic Theory 2(3):225-243.
Scheuring, A.F., ed. 1983. A Guidebook to California Agriculture by Faculty and Staff of the University of California. Berkeley: University of California Press.
Shrestha, R. and C. Gopalakrishnan. 1993. Adoption and diffusion of drip irrigation technology: An econometric analysis. Economic Development and Cultural Change 41(2):407-418.
Smith, T. Rodney. 1984. The economic determinants and consequences of private and public ownership of local irrigation facilities. In: T.L. Anderson, ed., Water Rights, Scarce Resource Allocation, Bureaucracy, and the Environment. San Francisco, CA: Pacific Institute for Public Policy; Cambridge, MA: Ballinger Publishing Co.
State of California, Department of Water Resources. 1980. Measuring Economic Impacts, the Application of Input-Output Analysis to California Water Resources Problems. State of California, The Resources Agency, Sacramento, CA.
————. 1985. CIMIS Final Report. State of California, The Resources Agency, Sacramento, CA.
————. 1989. Drought Contingency Planning Guidelines for 1989. State of California, The Resources Agency, Sacramento, CA.
————. 1991. California’s Continuing Drought 1987-1991. State of California, The Resources Agency, Sacramento, CA.
————. 1993. California Water Plan Update. State of California, The Resources Agency, Sacramento, CA.
Stoneman, P.L. and N. Ireland. 1986. Technological diffusion, expectations and welfare. Oxford Economic Papers 38(2):283-304.
Sunding, D., D. Zilberman, and N. MacDougall. 1995. Water markets and the cost of improving environmental quality in the San Francisco Bay/delta estuary. West-Northwest Journal of Environmental Law and Policy 2(3):159-165.
Sunding, D., D. Zilberman, R. Howitt, A. Dinar, and N. MacDougall. 2001. Measuring the costs of reallocating water from agriculture: A multi-model approach. Natural Resources Modeling: in press.
Tsur, Y. and A. Dinar. 1995. Efficiency and equity considerations in pricing and allocating irrigation water. World Bank, Policy Research Working Paper No. 1460, Washington, DC.
Wichelns, D. 1991a. Increasing block-rate prices for irrigation water motivates drain water reduction. In: A. Dinar and D. Zilberman, eds., The Economics and Management of Water and Drainage in Agriculture. Norwell, MA: Kluwer Academic Publishers.
—————. 1991b. Motivating reductions in drain water with block-rate prices for irrigation water. Water Resources Bulletin August.
Wirl, F. 2000. Lesson from utility conservation programs. Energy Journal 21(l):87-108.
Zilberman, D. and F. Shah. 1994. Queuing vs. markets in water resource allocation. Working Paper, Department of Agricultural and Resource Economics, University of California at Berkeley.
Zilberman, D., A. Dinar, N. MacDougall, M. Khanna, C. Brown, and F. Castillo. 1995. Individual and institutional responses to drought: The case of California agriculture. Working Paper, Department of Agricultural and Resource Economics, University of California at Berkeley.
Zusman, P. 1988. Individual Behavior and Social Choice in A Cooperative Settlement. Jerusalem: Hebrew University, Magnes Press.
—————. 1991. A conceptual framework for a regulatory policy of the Israeli water resources. Working Paper No. 9108, The Center For Agricultural Economic Research, Hebrew University, Jerusalem.

































