4
Transport and Fate
Spilled oil is transported, and its composition and character altered, by a variety of physical, chemical, and biological processes (Figure 4-1). Use of chemical dispersants changes the relative importance of these processes, affecting the fate of the oil, and altering subsequent ecological effects. Thus, it is important to understand the transport and fate of oil with and without dispersant use. A number of comprehensive studies have reviewed these mechanisms including Stolzenbach et al. (1977), Kerr and Barrientos (1979), Huang and Monastero (1982), Payne and McNabb (1984), Payne et al. (1984), Delvigne et al. (1986), Spaulding (1988), Lee et al. (1990), Payne et al. (1991a,b,c,d), Yapa and Shen (1994), ASCE (1996), Reed et al. (1999), Payne and French-McCay (2001), Payne and Driskell (2003), and NRC (1985, 1989, 2003). These mechanisms are reviewed briefly in the first two sections of this chapter, with a focus on how transport and fate influence the subsurface concentration of oil, and how the composition and concentration of surface and entrained oil droplets can be expected to vary with and without application of chemical dispersants. The latter portion of the chapter and Appendix E discuss how the mechanisms are integrated into computer oil spill models that simulate the fate of spilled oil, and how such models are used (or might be used) for purposes of pre-planning, emergency response, and natural resource damage assessment.
TRANSPORT PROCESSES
There are three major modes of transport for spilled oil or petroleum products discussed in the following subsections. The first deals with the
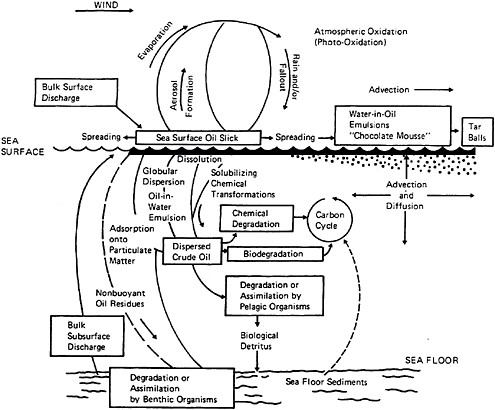
FIGURE 4-1 Major open-ocean oil fate and transport processes.
SOURCE: NRC, 1985.
surface transport of slicks, which is important because the shape, thickness, and location of a slick affect the ability to effectively apply dispersants. The second subsection deals with vertical transport, which is responsible for the initial dilution of dispersed oil. Finally, the last subsection deals with horizontal subsurface transport, which is responsible for the ultimate dilution of dispersed oil.
Surface Transport
Oil spilled directly on a calm water surface spreads radially by gravity and is resisted by inertia, viscosity, and surface tension until the slick reaches a thickness of ~0.1 mm. Fay (1969), Hoult (1972), and others have modeled this spreading under idealized conditions (e.g., instantaneous spill, no wind, no waves). Application of chemical dispersants can temporarily affect this spreading through the phenomenon of herding.
Additional spreading takes place because (1) oil is usually spilled over a period of time and into a moving current, (2) wind, waves, and non-uniform currents diffuse and break up the slick, and (3) droplets periodi-cally disperse and resurface, tending to stretch the plume. This last mechanism has been described by Johansen (1984) and Elliott et al. (1986) and may increase in significance when considering the fate of chemically dispersed oil.
Slick thicknesses were estimated during several well-documented oil spills, usually indirectly by dividing volume/area (Mackay and Chau, 1986; Lunel and Lewis, 1993a,b; Lewis et al., 1995a,b; Walker et al., 1995; Brandvik et al., 1996; Brown et al., 2000). These studies indicate that oil does not spread uniformly, but is irregular in shape and thickness—generally elongated in the direction of the wind and often composed of thick patches (>1 mm) and thinner sheens (<0.01 mm). S.L. Ross (1997) gives a general rule of thumb that 90 percent of an oil spill’s volume is contained in 10 percent of its area. Figure 2-5 (in Chapter 2) presents representative descriptions of the wide range of slick thicknesses typical of an oil slick along with an approximation of the estimated volume/unit area for the different thicknesses. The non-uniform characteristics of a slick can be included in models (e.g., Mackay et al., 1980a,b; Lehr et al., 1984), but such models are basically empirical.
Surface spreading has important implications for the operational effectiveness of dispersant application because dispersant delivery systems have finite encounter rates (area coated per unit time) and capacities (total volume of dispersant used; Gregory et al., 1999). As such, dispersants are most effective when they are applied as soon as possible (before the slick has had time to spread and break up), and with the benefit of airborne sensing to identify locations of maximum slick thickness. In particularly thick regions, it is not practical to treat the slicks with a single pass and lacking visual confirmation of dispersion, a multi-pass approach is often used (S.L. Ross, 1997; Lunel et al., 1997b).
Of additional concern is oil that is accidentally released from subsurface blowouts during offshore exploration or production. Here the oil will likely be mixed with substantial quantities of natural gas, which provides the major source of buoyancy. Masutani and Adams (2004) and Tang (2004) describe the spectrum of oil droplet sizes that can be expected as a function of dimensionless exit conditions. The combination of gas and oil forms a buoyant droplet/bubble plume that entrains seawater as it ascends toward the surface. A similar situation, but without the gas, would occur with the rupture of an underwater oil pipeline. Models to describe such plumes have been developed by Yapa and Zheng (1997; 1999) and Johansen (2000) among others. If the oil is released in shallow water (less than roughly 100 m), it will rise as a coherent plume, containing a mixture
of gas, oil, and water. Once the plume surfaces, the oil and water will spread radially in a surface layer (Fannelop and Sjoen, 1980). Because of the presence of water, the resulting oil slick will be significantly thinner than those produced by oil spilled directly on the surface. In deeper waters, ambient currents, and potentially density stratification, will cause the gas bubbles and larger oil droplets to separate from the remainder of the plume and ascend as individual (or small groups of) droplets and bubbles (Socolofsky and Adams, 2002). Because droplet rise velocity depends on diameter, the larger oil droplets will reach the surface sooner and closer to their source than the smaller droplets. This fractionation leads to a substantially longer (and thinner) plume than would be produced by a surface spill.
Work is being conducted both in the United States and abroad, to assess if and how to chemically disperse oil from a subsurface blowout. In many cases, it is impractical to apply dispersants at the surface because the slick is too thin. However, if the surface slick is subsequently concentrated by Langmuir circulation cells or other convergence mechanisms, dispersants can be applied to the thicker portions. In the absence of such surface convergence, the most effective method would be to apply dispersant within the well (down hole) before the oil can mix with seawater, but this may be difficult, so attention is being paid to schemes that dispense the dispersants directly into the plume. This should be done as close to the seafloor as possible to minimize dilution, and hence achieve the desired dispersant-to-oil ratio (DOR) without bearing the cost and potential environmental consequences of using excessive quantities of dispersant. Some initial concepts for dispersant application to blowouts can be found in Johansen and Carlsen (2002).
Slicks are advected downwind by a combination of wind and waves. Pure advection (without spreading) does not affect the concentration of oil or the effectiveness of dispersants, but it is important for understanding where an oil slick will end up. Many researchers have studied these processes from theoretical and empirical perspectives, and a rule of thumb is that slicks move at approximately 3 percent of the wind speed measured 10 m above the water surface (i.e., the “wind factor” is about 3 percent). For moderate to high sea states, approximately two-thirds of this transport can be attributed to Stokes drift (the fact that near-surface wave orbits in deep water waves do not follow exact circles, as linear theory would suggest, but exhibit a net transport in the direction of wave propagation). The remaining one-third represents the slick moving relative to the water directly underneath it (Lehr et al., 2002). Coriolis acceleration causes the slick to drift ~10–20 percent to the right of the wind in the northern hemisphere, but this effect is often omitted in transport models. Experimental observations support these conclusions, with some sugges-
tion that the wind factor and deflection angle decline with wind speed (Youssef and Spaulding, 1993).
Vertical Transport
Dispersion of a surface slick, whether caused naturally or through application of chemical dispersants, results in the formation of droplets that are entrained into the water column and transported with the subsurface currents. The importance of vertical transport is clearly seen by a simple calculation for illustrative purposes: a surface slick that is 0.1 mm thick and dispersed with an efficiency of 50 percent to an average depth of 5 m, will receive a dilution of 105, resulting in an immediate drop in concentration to ~10 ppm.
Dispersion results in a distribution of droplet sizes with the smaller droplets being transported deeper and longer. If Q is the mass of oil entrained per unit area of the slick, and d is a characteristic droplet diameter, it is clear that the goal of chemical dispersants is to increase Q and decrease d. And while it is obvious that use of chemical dispersants increases the mass of oil within the water column, it may or may not increase the concentration of oil, because the greater dilution achieved by smaller droplets may offset the increase in mass. This question will be revisited at the end of this subsection.
The initial depth of droplet penetration, hi, is proportional to the wave height, hw, with many studies showing that ![]() (Nilsen et al., 1985; Delvigne and Sweeney, 1988). [Variables used in this chapter are summarized in Table 4-1.] Subsequent vertical transport depends on a balance between vertical diffusion (characterized by a vertical diffusivity Ez, with dimensions of L2/T) and buoyant rise (characterized by a terminal velocity ws). Vertical diffusivity transports droplets deeper into the water column, while buoyancy makes them return to the surface.
(Nilsen et al., 1985; Delvigne and Sweeney, 1988). [Variables used in this chapter are summarized in Table 4-1.] Subsequent vertical transport depends on a balance between vertical diffusion (characterized by a vertical diffusivity Ez, with dimensions of L2/T) and buoyant rise (characterized by a terminal velocity ws). Vertical diffusivity transports droplets deeper into the water column, while buoyancy makes them return to the surface.
Vertical diffusivity generally ranges between 1 and 200 cm2/s depending on a number of environmental factors. Near the surface, diffusivity is a strong function of wave height, and a number of investigators report Ez ~ hw2 (Koh and Fan, 1970). Because wave energy decreases with depth, Ez decreases below the surface. For example, Ichiye (1967) suggests that, in the absence of density stratification,
(4-1)
where L is wave length, T is wave period, and hw is taken as the significant wave height. Other formulations suggest a stronger cut-off with depth, attributed to the depth of Langmuir circulation (windrows), which is caused by the interaction of wind and waves (Leibovich and Lumley, 1982;
TABLE 4-1 Variables Used in Scaling Arguments in Chapter 4
|
Variable |
Definition |
Dimension |
|
Cdiss |
Oil concentration in dissolved phase |
ML−3 |
|
Cdrop |
Oil concentration in droplet phase |
ML−3 |
|
d |
Droplet diameter |
L |
|
Ez |
Vertical diffusion coefficient |
L2T−1 |
|
Er |
Horizontal (radial) diffusion coefficient |
L2T−1 |
|
hchar |
Characteristic depth of oil droplets |
L |
|
hi |
Initial depth of oil droplets |
L |
|
hw |
Wave height |
L |
|
L |
Wave length |
L |
|
Q |
Mass of oil entrained per unit area of slick |
ML−2 |
|
T |
Wave period |
T |
|
ws |
Droplet slip (rise) velocity |
LT−1 |
|
λz |
Vertical velocity gradient |
T−1 |
|
σr |
Radial standard deviation of spreading patch |
L |
|
ν |
Kinematic viscosity |
L2T−1 |
|
P1 |
Water density |
ML−3 |
and references in Champ, 2000). Diffusivity also decreases under the influence of vertical density stratification, and a host of formulations suggest that Ez is inversely proportional to the vertical density gradient (Koh and Fan, 1970; Broecker and Peng, 1982). A thermocline is a region of maximum density gradient suggesting small Ez, and if stratification is strong enough, a “diffusion floor” may be assumed. Some models assume that the depth of this floor is simply proportional to wave height.
Unless there is significant interaction with suspended particulates, most oil droplets will be positively buoyant and will rise toward the surface. Those with a diameter less than about 300 mm will obey Stokes Law and rise with a velocity of:
(4-2)
where ν is the kinematic viscosity of water, Δρ/ρ is the normalized density difference between seawater and oil, g is gravitational acceleration, and d is droplet diameter. The quadratic dependence of rise velocity on droplet diameter suggests that the smallest droplets will rise very slowly, accentuating dispersion. For example, with Δρ/ρ = 0.13 (for an oil with a density of 0.89 mg/mL and seawater at 1.025 mg/mL), ν = 10−2 cm2/s and g = 981 cm/s2, droplets with a diameter of 300µm will rise with a velocity of 0.6 cm/s while droplets with a diameter of 30 µm will rise with a velocity of 0.006 cm/s. The former will take less than 8 minutes to rise a height
of 3 m, while the latter will take over 12 hours. And, because of vertical diffusion, the smaller droplets will most likely reside deeper in the water column, further prolonging their ascent.
The above discussion can be used to estimate how the concentration of droplet and dissolved phase oil might depend on dispersion efficiency and vertical transport mechanisms. The concentration of oil in the droplet phase is proportional to the mass of oil entrained per unit area, Q, divided by a characteristic depth of droplet penetration, hchar, or
(4-3a)
The rate of dissolution of dispersed oil per volume of seawater is proportional to the number of droplets per volume (~Q/hchard3) times the surface area of a drop (~d2). Hence the concentration of dissolved oil
(4-3b)
A simple model for the characteristic depth is hchar ~ Ez/ws, where Ez ~ hw2 (independent of depth), and ws ~ d2 (from Eq. 4-2). The wave flume experiments by Delvigne and Sweeney (1988) suggest that Q ~ hw1.14, while d is independent of hw. Thus, from Eq. (4-3a), cdrop ~ d2/hw0.86, and from Eq. (4-3b), cdiss ~ d/hw0.86. With this “model” both droplet and dissolved phase concentrations decrease with wave height and increase with droplet diameter. In reality, diffusivity is not likely to be constant with depth so an alternative model assumes a characteristic depth that is proportional to wave height, or hchar ~ hw. In this case, equations (4-3a) and (4-3b) give cdrop ~ hw1.14 and cdiss ~ hw1.14/d. Here both droplet and dissolved phase concentrations increase with wave height and either decrease with, or are independent of, droplet diameter, i.e., quite different from the conclusions of the first model.
These arguments are qualitative, and more precise information should come from computer models that integrate multiple mechanisms in a quantitative manner as later discussed. But computer models are no better than our understanding of the individual mechanisms upon which they are based, and the uncertainty in even the direction of change noted above suggests we need better understanding of dispersant effectiveness (i.e., the dependence of Q and d on oil properties and environmental parameters), as well as better models of the vertical distribution of Ez, in order to accurately predict the concentrations of dispersed oil.
Horizontal Subsurface Transport
Subsurface advection of dispersed and dissolved phase oil by a uniform current affects the location of the oil, but does not, in itself, cause
additional mixing. However, mixing is produced when the currents are non-uniform, and this mixing is responsible for the ultimate dilution of the oil. Without horizontal mixing, and under sufficiently calm weather conditions, vertically dispersed oil droplets could all ultimately resurface given enough time.
Horizontal mixing consists of two fundamental processes. The first process is called scale-dependent diffusion and represents the fact that large eddies will advect a patch of marked fluid if the patch is smaller than the scale of the eddies, but mix and dilute the patch if it is larger than the eddies (Csanady, 1973). The second process is termed shear dispersion and results from the combination of velocity gradient(s) in combination with mixing (or other transport mechanism) in the direction of the gradient(s) (Fischer et al., 1979). The latter effect is enhanced with the use of chemical dispersants, because the smaller droplets that are produced are transported deeper, where they experience greater differences in horizontal velocity. Unfortunately, field measurements cannot always distinguish the two processes, and frequently their effects are combined.
Horizontal mixing is determined best using site-specific measurements, but as these are often not available, literature values should be used. Okubo (1971) summarizes a number of coastal tracer studies and shows that
(4-4)
where σr is a characteristic radius (standard deviation) of an equivalent circular tracer patch (cm) and t is time (sec). Other investigators report similar trends. Okubo’s data apply to patch sizes ranging from ~30 m to ~100 km, and more recent data suggest the approximate relationship applies to even larger scales (Ledwell et al., 1998). Simple relationships such as this are useful because dilution resulting from horizontal mixing is proportional to patch variance, σr2, and hence Eq. (4-4) can be used to directly compute changes in concentration due to horizontal mixing. Also, predictive models make use of horizontal diffusion coefficients (Er, with dimensions of L2/T) defined by the time rate of change of patch variance. For example, using Eq. (4-4)
(4-5)
For σr = 100 m, Er = 0.3 m2/s, while for σr = 1,000 m, Er = 5 m2/s. Note that these values of horizontal diffusivity are orders of magnitude larger than the corresponding vertical values (Ez) suggesting that horizontal mixing is much stronger than vertical mixing. However, horizontal mixing is also much less effective, because horizontal plume dimensions are much larger
(and hence horizontal concentration gradients are much smaller) than in the vertical.
It should also be recognized that different investigators define horizontal diffusion coefficients differently. For example, as implied above, some data used to determine mixing coefficients include the effects of vertical shear, while others do not. Also some analyses separate Er into separate components in the longitudinal and lateral direction (i.e., an Ex and Ey), and some analyses define an apparent diffusivity based on a cumulative, rather than instantaneous, change in σr2 (i.e., Era = σr2/4Δt). In order for a predictive model not to over or under account for mixing, care should be taken to define Er in the same way in the model that it was defined in the analysis of field measurements used to determine its value.
Horizontal mixing can be considered important to the dilution process when it has caused the patch concentration to be diluted by a significant amount. Again using Eq. (4-4), the time required for patch size to increase from σr to ![]() σr (a two-fold increase in dilution) is
σr (a two-fold increase in dilution) is
(4-6)
where Δtdouble is in sec, and σr is in cm. For example, Δt = 12 hours for σr = 1,000 m, and only about 1.7 hours for σr = 100 m. The fact that this time increases with σr suggests that horizontal mixing is more important for small spills, and that dispersants can be used more effectively when applied before substantial spreading has occurred (i.e., small σr). Of course, other factors affecting dispersant effectiveness are also time dependent. Tank studies, or small-scale field experiments, cannot be used to directly simulate horizontal mixing because the spills in such tests are too small, and there are additional artifacts due to the presence of walls.
While horizontal mixing data such as those compiled by Okubo (1971) usually include the effects of shear dispersion, it is interesting to consider this component separately and evaluate how it varies with sea state and dispersant effectiveness. One type of shear dispersion that was discussed previously involves larger droplets that become vertically entrained into the water column and later rise to the surface. Because the slick generally travels faster than the underlying water, the droplets will re-enter the slick at the “back-of-the-pack,” leading to a long tail. This effect can be especially important nearshore, where vertical circulation is more pronounced. Indeed, this effect has been proposed as the reason oil from the Braer spill off the Shetland Islands was observed to travel in the opposite direction of the surface current (Proctor et al., 1994; Ritchie and O’Sullivan, 1994; Spaulding et al., 1994).
Smaller droplets that are (nearly) permanently dispersed, and hence behave like water, are also affected by conventional shear dispersion. Con-
sider a parcel of marked seawater occupying a depth hchar. If there is a vertical gradient in the near-surface velocity of magnitude λz (dimensions of velocity per depth, or T−1), the patch will experience a top-to-bottom velocity difference of Δu = λzhchar. Following Taylor’s analysis of longitudinal dispersion (see Fischer et al., 1979), a shear dispersion coefficient Esd (part of Er) ~ (Δu)2hchar2/Ez ~ λz 2hchar4/Ez. Based on the previous discussion of hchar, Esd is expected to increase strongly with increasing wave height and decreasing droplet diameter, suggesting an increase in shear-induced mixing, and hence dilution of dispersed oil, as sea state and dispersant effectiveness increase.
The above discussion clearly implies that the vertical dimension needs to be included in modeling the transport of dispersed oil—not just to represent the concentration field, but also to properly represent the velocity field (i.e., a model needs to realistically represent the vertical gradients in velocity). Normally this requires a 3-D model. In shallow water, dispersed oil may become distributed over the entire water depth. However, even in this case, vertical gradients in velocity are important for dispersing the oil and these gradients should be accounted for, either by explicitly simulating the vertical shear in a 3-D model, or by computing horizontal shear dispersion coefficients for use in a 2-D (depth-integrated) model. In deeper locations where the dispersed oil is not uniformly distributed over depth, the oil will tend to be concentrated in a relatively thin horizontal layer near the surface. As with models of thermal or salinity stratification, this horizontal layering can present numerical challenges associated with resolving strong near-surface gradients. Resolution can be enhanced by employing models with stretched coordinates, such as σ-coordinates (that use a constant number of vertical grid cells regardless of water depth) or γ-coordinates (that, in addition, provide unequal grid spacing, allowing greater resolution near the surface). However, care should be taken to minimize or counteract the spurious vertical mixing that may result with such models due to the fact that the “horizontal” grid lines are not parallel with the stratification (Huang and Spaulding, 1995).
FATE AND WEATHERING
In addition to spreading and drift as discussed earlier, there are numerous processes that affect the ultimate fate of spilled oil or petroleum products (Figure 4-1). These include evaporation, dissolution, dispersion of whole oil droplets into the water column (entrainment), interaction of dissolved and dispersed components with suspended particulate material (SPM), photooxidation, biodegradation, uptake by organisms, water-in-oil emulsification (mousse formation), and stranding on shorelines (NRC, 1985, 1989, 2003).
Chapter 3 summarized the changes in rheological properties (viscosity, interfacial tension, density, etc.) that begin to occur immediately after oil is spilled. The changes in physical properties caused by water-in-oil emulsification are particularly important because they affect how spilled oil is physically dispersed (entrained) into the water column (with and without dispersants), the ability of oil spill skimmers to recover oil from the sea surface, the ability of pumps to transfer the collected oil, and the volume of collected material that requires storage and disposal.
In the following sections, the chemical and physical changes to oil on the water surface (generally thought of as weathering) caused by evaporation, photooxidation, and water-in-oil emulsification are discussed, with particular emphasis given to the latter (including identification of the chemical constituents within oil that largely control emulsion behavior) because of its importance in controlling dispersant effectiveness. After that, the fate of physically and chemically entrained oil droplets in the water column is considered. In evaluating the fate of entrained oil droplets, the primary focus is on biodegradation of dispersant-treated oil and the interaction of both physically entrained and dispersant-treated oil droplets with suspended particulate material.
Surface Oil Evaporation Weathering
Evaporation of lower-molecular-weight volatile components from a surface slick is important for dispersant applications because it can indirectly affect the formation of stable water-in-oil emulsions through the precipitation of asphaltenes and resins that help to stabilize the emulsion (Fingas and Fieldhouse, 2003). As the solvent components are evaporated from the slick, these higher-molecular-weight components can precipitate to coat entrained water droplets in the emulsion and inhibit water-water droplet coalescence and phase separation (Sjoblom et al., 2003). In addition, the evaporative loss of mono-aromatic components (benzene, toluene, xylenes, etc.) and two- and three-ring polynuclear aromatic hydrocarbons (PAH) and their alkyl-substituted homologues can significantly reduce the toxicity of the oil and the concomitant water-soluble fractions generated after physical or chemically enhanced entrainment of oil droplets into the water column.
Evaporation is the single most important and rapid of all weathering processes (McAuliffe, 1989), and it can account for the loss of 20–50 percent of many crude oils, 75 percent or more of refined petroleum products, and 10 percent or less of residual fuel oils (Butler, 1975; Butler et al., 1976; NRC, 1985; 2003). Most of the early studies on evaporation focused on the loss of individual hydrocarbon components as a function of their vapor pressures and other factors such as temperature, wind speed, and
sea state. Traditionally, loss of lower-molecular-weight hydrocarbons as a function of time and weathering conditions was tracked by gas chromatographic (GC) analyses of the residual components in the oil. For example, Figure 4-2 shows time-series chromatograms from Prudhoe Bay crude oil weathered in subarctic summer conditions in the flow-through wave-tank systems described in Chapter 3. Note that all compounds with volatilities (vapor pressures) greater than n-C11 (b.p. < 400° F, roughly 204° C) were lost within the first twelve days. (In these and subsequent chromatographic profiles, individual peaks are identified by relative GC retention time indices (i.e., n-C11 = 1100, n-C12 = 1200, etc., with a peak eluting midway between n-C11 and n-C12 = 1150) as defined by Kovats (1958). Between the late spring and the following summer and fall period, there was little additional evaporative loss. There was, however, a significant change in the straight-chain/branched-chain hydrocarbon ratios due to selective bacterial degradation of the n-alkanes in preference to the isoprenoid components (Figure 4-2D).
While compound-specific and gravimetric pan-evaporation studies were useful in characterizing rates of evaporation processes and served as input for early model development (Mackay and Matsugu, 1973; Mackay and Leinonen, 1977; Mackay et al., 1980a,b; 1982; Payne et al., 1983), in the mid 1980s the concept of using True Boiling Point (TBP) distillation data (available for all crude oils and refined products) to generate “pseudocomponents” for modeling evaporation behavior was introduced by Payne et al. (1984). The pseudo-component approach allowed a mass balance to be calculated for the oil remaining after evaporation (something that couldn’t be done on a compound-specific basis), and it was validated for Alaska North Slope crude oil by National Oceanic and Atmospheric Administration (NOAA) and Minerals Management Service (MMS) sponsored laboratory and outdoor wave-tank studies and ultimately comparison of model predictions with measured oil weathering behavior after the T/V Exxon Valdez oil spill (Payne et al., 1991a).
Many oil weathering observations have been reported at accidental spills (Mackay, 1993; Thomas and Lunel, 1993; Harris, 1997; Law et al., 1997; Lunel et al., 1996, 1997b) and various controlled dispersant field trials in Canada and Europe (Green et al., 1982; Bocard et al., 1987; Humphrey et al., 1987; McDonagh and Colcomb-Heiliger, 1992; Lunel and Lewis, 1993a,b; Lunel, 1993, 1994a,b; Lunel et al., 1995b,c; Walker and Lunel, 1995; Lewis et al., 1995a,b; Strom-Kristiansen et al., 1995; Brandvik et al., 1995, 1996; Lunel and Davies, 1996), plus numerous shorter-term laboratory and wave-basin studies on a variety of different oils with and without dispersants (Mackay and Chau, 1986; Brown and Goodman, 1987; Cormack et al., 1987; Daling and Lichtenthaler, 1987; Bobra, 1990; Brandvik and Daling, 1990; Daling et al., 1990b; Brandvik et al., 1991, 1992; Ross and Belore,
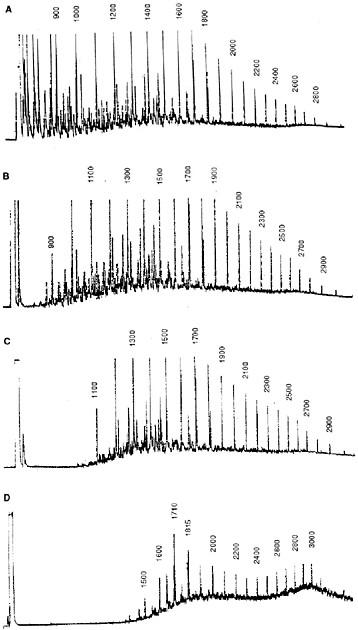
FIGURE 4-2 FID gas chromatograms of oil samples obtained from 2,800 L flow-through open-air summer wave-tank experiments using 16 liters of Prudhoe Bay crude oil. A) fresh oil; B) the oil slick after 48 hours of weathering, showing loss of the most volatile compounds; C) the oil slick after 12 days of weathering, showing the loss of all compounds with molecular weights less than n-C11 (Kovats Index 1100); and D) the slick after 12 months of weathering, showing significant biodegradation (Kovats Indices 1710 and 1815 represent the isoprenoids pristane and phytane, respectively).
SOURCE: Modified from Payne et al., 1984.
1993; Knudsen et al., 1994; Major et al., 1994; Strom-Kristiansen et al., 1994; Lunel et al., 1995a; Mackay, 1995; Hokstad et al., 1996; Venosa et al., 1999).
Many of these studies have been reviewed and recently summarized by S.L. Ross (1997) and in the proceedings of a two-day symposium held in Anchorage, Alaska, in March 1998 on oil spill dispersant applications in Alaskan waters (Trudel, 1998). The data from these studies have led to refinements in the overall ability to mathematically model oil spill behavior, and significantly more oil-specific data are now available on the magnitude and rates of change of density, viscosity, and water content for numerous oils and water-in-oil emulsions (Fingas and Fieldhouse, 2003; 2004a,b). No attempt will be made to duplicate or even briefly cover the findings presented in each of these most recent papers. Instead, several of the most significant observations specifically related to predicting evaporation and spilled oil behavior will be highlighted below.
A recent oil-weathering development has been the evaporation modeling approach proposed by Fingas (1996; 1997; 1999a) who has taken issue with the boundary layer regulation model based on earlier work by Mackay (Mackay and Matsugu, 1973; Mackay et al., 1980a,b; Stiver and Mackay, 1984; Berger and Mackay, 1994) that has been the basis for most evaporation algorithms used for predicting oil-weathering behavior. Fingas now proposes that evaporation rates are independent of oil film thickness and surface area and, instead, he has developed a set of empirical equations for estimating oil-specific evaporation rates as a function of exposure time (natural log or square root time-dependence) and the percentage of oil distilled at 180° C (roughly 356° F). Most of these experiments were conducted with a calculated film thickness (based on the cross-sectional area of the experimental evaporation dish and the volume of oil added) ranging from 0.8 to 10 mm. Tasaki and Ogawa (1999) have also reported that evaporation processes are not affected by oil film thicknesses in the range of 1 to 4 mm. A similar representation for evaporation from film thicknesses around 15 mm was also reported earlier by Bobra (1992). Additional discussions of the significance of Fingas’ approach and counter arguments based on modifications of more traditional pseudocomponent approaches are considered by Jones (1996,1997), who has proposed a simplified pseudo-component (SPC) model relating molar volume, vapor pressure, and molecular weight to the boiling point of the component. Thus, only the boiling points and initial volume fractions of the components need to be specified to implement the model.
Overprediction of evaporation rates can be a problem with oil-weathering models that assume a well-mixed oil phase (which is probably valid for very thin slicks) and also assume that resistance to mass transfer is entirely in the air phase (Berger and Mackay, 1994). Results from several studies suggest that evaporation rates may be controlled in the oil phase,
especially at low temperatures and for higher viscosity water-in-oil emulsions (Payne et al., 1984, 1987c; Ross and Buist, 1995) and for waxy oils where a skin may form on the oil surface inhibiting component loss from within the oil phase (Berger and Mackay, 1994). As a result, it may be inappropriate to always model oil as a well-mixed phase, and algorithms for both well-mixed and diffusion-controlled fluids may need to be sequentially utilized as a function of oil weathering-dependent viscosity changes to better approximate spilled oil evaporative behavior. The possibility of oil-phase diffusion-controlled evaporative weathering was discussed at length by Payne et al. (1984). Experimental evidence for the importance of liquid-phase resistance for lower molecular weight compounds (e.g., hexane, cyclohexane, toluene, p-xylene) was presented by Berger and Mackay (1994), and experimental confirmation of the phenomenon for intermediate molecular weight components (decane through tetradecane) was obtained by Payne et al. (1987c; 1991b) during cold-room experiments examining the evaporation behavior of oil spilled onto ice.
In a related study, Ross and Buist (1995) reported that hydrocarbon evaporation was reduced when oil is mixed with water to form a stable water-in-oil emulsion. The degree of evaporation inhibition appears to increase with increasing water content and increasing slick thickness, which again suggests internal resistance to mass transfer within an emulsified slick, in line with the observations of Payne et al. (1987c; 1991b).
Most research indicates that differences in evaporation rates due to different slick thicknesses should be considered in evaporation weathering algorithms. These observations are in direct contrast with the findings by Fingas (1996; 1997; 1999a), who concluded that evaporation was not a function of wind speed, turbulence level, slick area, or thickness. In the modeling approach used by S.L. Ross (1997), smaller slicks are emulsified faster, yielding higher viscosities because of faster evaporation caused by thinner films. This is a subtle effect, but it is worth noting in developing models to predict oil weathering and slick behavior. The S.L. Ross model also predicts that smaller slicks will dissipate faster, which is at variance with the viscosity prediction, because Payne et al. (1984), Lunel et al. (1997b), and others have observed that as viscosity increases, natural dispersion of oil droplets decreases and eventually becomes self-limiting.
Photooxidation
Numerous laboratory studies have been completed on photochemical oxidation of oil, and in general, increases in the water-soluble fraction of most crude oils are readily apparent. As discussed in greater detail below, the photochemical generation of additional polar products (resins, carboxylic acids, ketones, aldehydes, alcohols, and phenols) with low hydro-
philic-lipophilic balance (HLB) values that remain in the oil phase can also lead to the formation and stabilization of water-in-oil emulsions with greater water content (Payne and Phillips, 1985b; NRC, 1985; Daling and Brandvik, 1989; Daling et al., 1990b; Lewis et al., 1994). In addition, photooxidation of oil on the water surface can result in higher-molecular-weight products through the condensation of peroxide and other free-radical intermediates to yield intractable tar and gum residues (NRC, 1985; 2003). To the extent that chemical dispersion of surface oil can remove it from exposure to direct sunlight (or prevent it from stranding on shorelines where additional direct photo-transformations and tar/gum formation can occur), the effects of photooxidation as described below may be reduced.
Payne and Phillips (1985a) reviewed the earlier literature on the photooxidation of petroleum, and details on component-specific transformations, photooxidation products, viscosity changes, reaction mechanisms, the role of various sensitizers, reaction rates, etc., are summarized in that paper. An even more comprehensive treatise on organic photochemistry is available in Schwarzenbach et al. (1993) who review the basic principles of photochemistry, the roles of direct and indirect (sensitized) photolysis of numerous organic compounds in aqueous solutions, and the effects of particulates on photolytic transformations. While several PAH components are discussed, their treatment doesn’t focus specifically on petroleum, and additional details on oil-related compounds can be found in Kochany and Maguire (1994) who completed a critical review of the chemical and photooxidation of PAH and polynuclear aromatic nitrogen heterocycles (PANHs) in water. More recently, Garrett et al. (1998) studied photooxidation of PAH in a variety of crude oils, and a general overview is presented in NRC (2003).
In general, aliphatic hydrocarbons in oils are more resistant to photochemical oxidation whereas aromatic compounds are particularly sensitive, and alkyl substitution increases the sensitivity of the aromatic compounds. Aliphatic sulfur compounds were more easily oxidized compared to aromatic thiophene compounds, with the sulfur in the aliphatic components being oxidized to sulfoxides, sulfones, sulfonates, and sulfates in approximately equal amounts. PAH degrades to relatively stable quinones via reactions initiated by electron transfer from singlet state PAH to molecular oxygen (Sigman et al., 1998), and natural organic mater (humic and fulvic acids) in seawater may enhance indirect photolysis of PAH through the generation of triplet excited states (NRC, 2003).
The extent of photooxidation of dissolved petroleum constituents is controlled by the spectrum and intensity of incident light, and photooxidation occurs faster with shorter-wavelength light (<300 nm), which is rapidly absorbed by seawater and natural dissolved organic matter (which can both enhance and inhibit photochemical processes).
Another more recent finding with regard to photochemical processes is the apparent increase in toxicity to transparent oil-exposed organisms when they are subsequently exposed to sunlight. Phototoxicity may occur by two processes: photomodification and photosensitization. Photomodification (or photooxidation) is the structural modification of a chemical in the oil or water column to more toxic or reactive oxidation products as described in NRC (1985, 2003), Garrett, et al. (1998), Kochany and Maguire (1994), and Payne and Phillips (1985a). In photosensitization, the bioaccumulated chemical transfers light energy to other molecules within the organism causing tissue damage. Phototoxic components in oil are primarily three- to five-ring PAH and heterocycles. The importance of this phenomenon as it relates to the toxicological effects of dispersed oil is discussed in Chapter 5.
Water-in-Oil Emulsification
Significant progress has been made in the identification of factors affecting water-in-oil emulsification (Bridie et al., 1980a,b; Zagorski and Mackay, 1982; Payne and Phillips, 1985b; Mackay, 1987; Bobra,1990; 1991; Fingas and Fieldhouse, 1994; 2003; 2004a,b; Fingas et al., 1995a,b; 1996b; 2002a,b; 2003a; Walker et al., 1993a,b, 1995; McLean and Kilpatrick, 1997a,b; McLean et al., 1998; Sjoblom et al., 2003). It has long been recognized that the indigenous petroleum emulsifying agents are contained in the higher boiling fractions (boiling points >350–400° C [roughly >662–752° F]), and particularly in the non-distillable residuum (Lawrence and Killner, 1948). These higher boiling fractions contain the higher-molecular-weight asphaltenes and resins that are now recognized as the necessary emulsifying agents for stable water-in-oil emulsion formation. These higher-molecular-weight components are believed to orient within the continuous oil phase at the water-droplet/oil interface where they retard recoalescence of the water droplets to form separate water and oil phases.
It is now known that, to be effective, these emulsifying agents should be in the form of precipitated, finely divided, submicron particles (Bobra, 1990, 1991; McLean and Kilpatrick 1997a,b; McLean et al., 1998; Sjoblom et al., 2003). Secondly, it has been shown that the lower-molecular-weight alkane and aromatic components in fresh crude oils serve as solvents to control the in-situ solubility and precipitation behavior of these higher-molecular-weight constituents within the oil phase. The chemical composition of the oil also determines the amount and size of the precipitated asphaltene and resin particles, as well as the “wetting” properties of those particles.
Fingas et al. (2002a, 2003a) and Fingas and Fieldhouse (2003, 2004a,b) classified four “states” that describe how water can exist in combination
with oil. These include: stable emulsions, unstable water-in-oil mixtures, meso-stable emulsions, and (simply) entrained water. These states are differentiated by rheological properties as well as by differences in visual appearance, and very few emulsions were reported by these authors to have questionable stability. The viscosity of a stable emulsion can be as much as three orders of magnitude greater that the starting oil, and the product has significant elasticity. Stable emulsions are also usually reddish or red-brown in color. An unstable emulsion usually has a viscosity no more that about 20 times greater than the starting oil, and no elasticity is observed. Unstable or entrained-water mixtures are always the color of the starting oil (brown or black). Meso-stable emulsions are emulsions that have properties between stable and unstable emulsions, and can be either reddish or brown/black in color. Fingas et al. (1999) hypothesized that meso-stable emulsions lack sufficient asphaltenes to render them completely stable or that they still contained too many de-stabilizing materials such as the smaller aromatic solvent components that solubilize the asphaltenes. If the viscosity of the initial oil is high enough, it can stabilize some water droplets for a period of time in a meso-stable state. However, meso-stable emulsions may evolve to form either separate layers of oil and water or stable emulsions. Unstable emulsions are those that rapidly decompose to separate water and oil phases after mixing energy is removed, generally within a few hours. Some water (usually <10 percent) may be retained by the oil, especially if the oil is viscous.
The type of emulsion produced is determined primarily by the properties of the starting oil, and the most important of these are the asphaltene and resin content as noted above, and the initial viscosity of the oil (Fingas and Fieldhouse, 2003). At one time, waxes were thought to be important in the formation of water-in-oil emulsions, but Fingas et al. (2000a) have shown that they are not a factor in the formation of either stable or mesostable emulsions. They may, however, play a role in certain circumstances by temporarily stabilizing entrained water with highly viscous oils. Stable emulsions have more asphaltenes and fewer resins, and interestingly, a narrow initial viscosity window. Instability results when the parent oil has too high or too low an initial viscosity, and as a result, the formation of stable emulsions may not occur with highly viscous oils. While this may initially appear to be contrary to intuitive reasoning, it has been explained by diffusion-controlled migration of asphaltenes and resins being too slow in the highly viscous oils to permit water-water droplet stabilization. In line with these observations, Daling and Brandvik (1989) previously reported that the maximum water uptake versus initial parent oil viscosity actually decreases as higher initial oil viscosities increase (Figure 4-3).
Turbulent kinetic energy is the most important form of energy related to emulsion formation. Although they were unable to measure turbulent
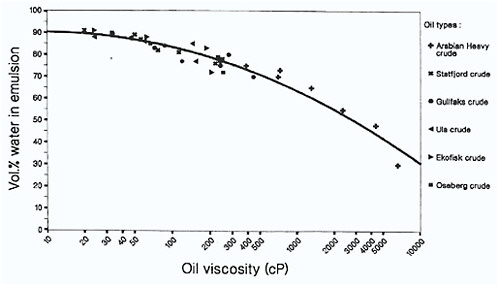
FIGURE 4-3 Maximum water uptake in water-in-oil emulsions versus initial parent oil viscosity. The mixing time is 24 hours at 6 and 13° C. Note that water uptake decreases as initial oil viscosity increases.
SOURCE: Daling and Brandvik, 1989.
energy directly in their laboratory experiments, Fingas et al. (1999) and Fingas and Fieldhouse (2003) correlated emulsion stability with total kinetic energy (proportional to the rotational speed of their rotary agitator and measured in ergs) and work (a measure of the power input to the agitator integrated over time, recorded in joules—same dimensions as energy—and proportional to time for a given energy). Neither of these metrics was normalized by the mass of oil, so results can only be interpreted in a relative sense. Oil that forms an entrained water state required relatively little threshold energy (200–300 ergs), and showed no increase in stability with increasing energy. Oil that forms a mesoscale emulsion required a relatively high level of energy (about 25,000 ergs) but also displayed no increase in stability with additional energy. Meanwhile oils that form stable emulsions showed increasing stability with increasing energy. Figure 4-4 displays the trend in emulsion state as a function of time (work) for oils displaying various final emulsion states. An implication is that formation of a given emulsion type at sea may require both a threshold energy level (corresponding to a given sea state) and a finite period of time. Because of the lack of higher-molecular-weight asphaltenes and resins, most light refined products (such as gasoline, kerosene, heating oil, and diesel fuels) do not easily form a stable water-in-oil emulsion.
In addition to the influence of indigenous asphaltenes and resins in
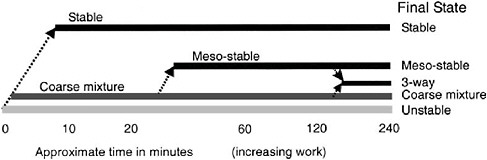
FIGURE 4-4 The overall concept of state and approximate kinetics in emulsion and water-in-oil state formation.
SOURCE: Fingas and Fieldhouse, 2003; courtesy of Elsevier.
the oils themselves, oxidation products from oil photolysis-weathering have also been suspected to play a significant role in water-in-oil emulsification behavior (Payne and Phillips, 1985a,b; NRC 1985). Daling and Brandvik (1989) correlated the increase in resin components in photolyzed oils with increased water contents and smaller-sized water droplets in the resultant water-in-oil emulsions. Specifically they found that photolysis results in:
-
the formation of polar compounds (resins)
-
significant reductions in oil-water interfacial tension
-
slightly increased rates of water-in-oil emulsion formation (not for waxy crudes)
-
slightly higher maximum water content in the water-in-oil emulsion
-
significantly higher stability in viscosity of the water-in-oil emulsion
-
a higher concentration of chemicals needed to break or inhibit water-in-oil emulsion formation, and
-
oil-specific changes in chemical dispersibility
In subsequent dispersant tests, Daling and Brandvik (1989) reported that naphthenic crudes were more highly dispersible after photolysis. Waxy crudes showed drastic reduction in dispersibility. Photolyzed components were believed to facilitate the accumulation of waxes at the oil-water interface, which were believed to “block” the access and penetration of the dispersant’s surfactant into the oil phase. Without such stabilizing agents the water droplets in a water-in-oil emulsion will tend to coalesce and separate from the oil phase.
In an attempt to generate a database of oil properties that might be useful in predicting water-in-oil emulsification and dispersibility behavior as a function of the degree to which oil weathering has occurred, Daling et al. (1990b) undertook the systematic study of emulsification behavior on three standard test oils that had been artificially weathered in the laboratory. The results demonstrated that the rate of weathering processes (water uptake, viscosity increases, etc.) was critically dependent on the type of oil studied and the different environmental conditions. Even when the variations in the physical-chemical parameters of the starting oils were relatively small, the weathering behavior of the oil and effectiveness of the different dispersants varied significantly. The authors suggested that this approach be considered by other laboratories and used in a similar way to generate a larger database of valuable information, which could be used in oil weathering modeling. Using experimental weathering data available for a wide range of oils, they hoped that correlations could be developed for model predictions of oil-weathering behavior based on only generally available crude oil assay data (e.g., true boiling point curves, density, pour point, wax, resin, and asphaltene content).
Lewis et al. (1994) expanded Daling et al.’s weathering approach and incorporated a mesoscale flume to investigate the chemical dispersion of oil and water-in-oil emulsions after different stages of weathering. In addition to the more common laboratory bench-scale methods used for assessing chemical dispersibility, the flume approach allowed testing of higher viscosity water-in-oil mixtures and more closely approximated conditions that might be encountered at sea.
This approach, or modifications of it, has now been successfully used to investigate the oil weathering properties and dispersibility of a wide variety of heavier and more viscous crude oils and emulsions (Guyomarch et al., 1999a,b,c; Fiocco et al., 1999), and the more recent data have significantly expanded the viscosity-limited range of dispersant effectiveness (and the concomitant time window available for responding to an oil spill at sea). In addition, the flume approach has allowed the rapid and cost-effective evaluation and testing of various emulsion breaking chemicals and the effectiveness of multiple dispersant applications and sequential emulsion breaker/dispersant combinations to disperse particularly recalcitrant slicks.
Without question, water-in-oil emulsification is a critically important process that affects oil droplet entrainment and dispersant effectiveness, and for many years it was believed to be the most difficult process to model or predict on a oil-specific basis (S.L. Ross, 1997). Except for the few oils that had been extensively tested, it was virtually impossible to predict when a particular oil would start to emulsify or how long it would take for the spilled oil to form a “stable” highly viscous emulsion. Like-
wise, it was not possible to predict the final water content that a water-in-oil emulsion might contain.
Nevertheless, oil spill models have to deal with the problem of emulsification because it is such an important process. Traditionally, many oil spill models used data from an older laboratory test, called the Mackay-Zagorski Test (Zagorski and Mackay, 1982) that was developed to measure: (1) an oil’s tendency to form an emulsion, and (2) the stability of the emulsion once formed. The test did not, however, predict the rate of emulsification under field conditions. Likewise, the conventional emulsification equation (Mackay and Matsugu, 1973) that had been generally used in oil-weathering modeling includes some inconsistencies. For example, it does not include the influence of initial oil thickness and the progress of evaporation on emulsification. Emulsified oil takes up water as evaporation progresses, thus maintaining a constant oil-to-water (OWR). Therefore, Tasaki and Ogawa (1999) developed a new equation and governing parameters for emulsification of crude oil. Through the differentiation of a formula defining the water content ratio, a water-in-oil emulsification equation for crude oil was derived to include the effects of evaporation loss and entrained water with time. The equation reveals that the emulsification is governed by two fixed parameters (related to the evaporation process) and four free constant parameters selected to fit the numerical solutions to the measured values obtained in flume tests on six types of Middle East crude oils.
Noting the requirement for the loss of lower-molecular-weight alkane and aromatic solvents to precipitate asphaltenes for the formation of stable mousse with Alaska North Slope (ANS) crude oil, S.L. Ross (1997) and NOAA (in their Automated Data Inquiry for Oil Spills [ADIOS] 2 oil weathering model) do not initiate the formation of a water-in-oil emulsion in their computer models until after a specified percent evaporation for the crude oil has occurred.
To further this research effort and develop an empirical database that can be used in a predictive sense, Fingas and Fieldhouse (2003) have examined the emulsion forming tendencies of over 200 oils. The resulting emulsified products were characterized as a function of time (day of formation and after one week) by viscosity, complex modulus, elasticity modulus, viscosity modulus, water content, and several other parameters, including visual appearance. These empirical data were then used to develop a numerical model that uses the density, viscosity, and the saturate, asphaltene, and resin contents to compute a class index, which in turn yields either an unstable or entrained water-in-oil state or a meso-stable or stable emulsion (Fingas and Fieldhouse, 2004a,b). This approach has been used to develop a prediction scheme to estimate the water content and viscosity of the resulting water-in-oil state and the time to formation
with input of wave-height. When compared to the laboratory data upon which the empirical approach was based, this model was reported to provide accurate predictions of stability class about 50 percent of the time, and 90 percent of the predictions were no more that one category off. Predictions could not be compared to field data because there are very few data available for the comparison; however, this empirical approach clearly advances the ability to make a priori predictions about how a particular oil might behave in a spill situation.
Fate of Physically and Chemically Entrained Oil Droplets in the Water Column
Physical Entrainment of Untreated Oil
Notwithstanding the fact that most oils will not readily sink (NRC, 1999), fresh oil can be temporarily entrained/driven into the water column by wind and wave turbulence as described previously. In such instances, however, droplets above a certain size range (generally greater than 60–80 µm or 0.06–0.08 mm) would be expected to quickly resurface after the turbulence regime subsides. Then, as the viscosity of the surface slick increases due to evaporation and water-in-oil emulsification (mousse formation), it becomes increasingly difficult for wind-driven waves to plunge discrete oil droplets into the water column.
In the wave-tank systems used by Payne et al. (1983; 1984; 1991a) for subarctic oil weathering studies with Prudhoe Bay crude oil, the total entrained oil droplet concentrations in the water column were over 9,000 µg/L immediately after the oil release, 2–3 µg/L after 4 hours, 0.5 µg/L after 2 days, and less than 0.1 µg/L after 12 days. Initial chromatograms of the entrained oil droplets appeared essentially identical to those from the simultaneously collected surface oil samples (Figure 4-2), but between 8 and 48 hours, there was evidence for slightly enhanced evaporation and/or dissolution loss of lighter molecular weight components in the physically entrained oil droplets compared to the surface oil slick. Presumably, this loss resulted from the increased surface-area-to-volume ratio of the smaller physically entrained oil droplets compared to the more continuous surface oil slick. After 12 days with continued constant turbulent mixing in the wave tank there was little evidence of physically dispersed oil droplets in the water column.
Energy dissipation rates and oil droplet-size distributions were not measured in the wave-tank studies by Payne et al., but these parameters have been measured in other studies (Delvigne and Sweeney, 1988; Sterling et al., 2004a). Delvigne and Sweeney (1988) measured droplet sizes in their turbulent grid and breaking-wave experiments with both Ekofisk
and Prudhoe Bay crude oils. These studies showed that droplet sizes between 60 and 200 µm were obtained with the non-dispersant-treated oils in their turbulent-grid column experiments at the highest turbulence regimes tested, and that droplet size diameters increased significantly as the oil viscosity increased and the turbulence regime decreased. In their breaking wave experiments, Delvigne and Sweeney (1988) measured droplet sizes from 6 to >800 µm with the highest number concentrations in the 6–50 µm size range with greater numbers of the smaller droplets driven deeper into the water column and greater numbers of larger droplets near the surface. Clearly, as oil viscosity increased, droplet dispersion was inhibited with a concomitant increase in the proportions of larger droplets with faster rising velocities being generated. Similar findings of inhibited oil droplet dispersion/entrainment from higher-viscosity water-in-oil emulsions have also been reported by Lewis et al. (1994).
Enhanced Entrainment of Smaller Droplets with Dispersants
Franklin and Lloyd (1986) presented various size distributions for oil:dispersant mixtures studied in the laboratory using a toxicity test developed by the United Kingdom’s Ministry of Agriculture, Fisheries and Food. All droplet sizes were reported as volume median diameter, which is the droplet diameter that divides the sample distribution into two equal parts by volume. The hydrocarbon solvent based dispersants yielded droplet histogram plots that peaked at 20 µm (the mode diameter). Water-dilutable concentrates yielded drops in the 25–65 µm range. Dispersants that were concentrates applied to the oil undiluted generated a flat bimodal distribution with a large proportion of droplets <5 µm.
More recently, Lunel (1993a,b; 1995b) reported the first successful field measurements of oil droplet-size distribution below experimental dispersant-treated oil slicks at sea from a premixed oil-dispersant combination (medium fuel oil and Slickgone NS) measured at sea using a Phase Doppler Particle Analyzer (see Figure 3-3 in Chapter 3). For a variety of test oils and dispersants, the range of mean diameters was between 15 and 25 µm (volume distribution 35 to 50 µm). Smaller droplet sizes (or increased number densities of smaller droplets) were observed in both instances.
Compound-Specific Dissolution Behavior
True dissolution of individual components from an oil slick is not generally significant in terms of the overall mass balance of an oil spill (NRC, 1985; 2003). As a result, many oil-weathering models generally do not include dissolution in their mass-balance calculations. Dissolution of
individual components is important, however, when considering the potential for biological impacts.
The dissolved concentrations of individual components from an oil slick are controlled by partition coefficients, rather than the solubilities of individual oil components. Payne et al. (1984) and Payne and McNabb (1984) presented data for Prudhoe Bay crude oil:seawater partitioning reporting that the truly dissolved components were almost exclusively alkyl-substituted lower-molecular-weight mono-aromatic hydrocarbons (MAH) and two-ring PAH. The water-soluble fraction contained no appreciable n-alkanes. Published octanol:water partition coefficients, Kow, for many parent (and fewer alkyl-substituted) PAH can be used to predict dissolution behavior (Nirmalakhandan and Speece, 1988; Hodson et al., 1988; Blum and Speece,1990; McCarty, 1986; McCarty et al., 1992; Mackay et al., 1992; McCarty and Mackay, 1993; Varhaar et al., 1992; Swartz et al., 1995; French-McCay et al., 1996; French-McCay, 1998; 2001; 2004). For modeling dissolution behavior, partition coefficients, not pure component solubility data, should be used.
In the case of an oil spill, true dissolution of individual components is controlled by the mole fraction of each component in the slick, the oil/water partition coefficient, the oil-water interfacial surface area (which significantly increases with successful dispersant application), and the interphase mass transfer coefficient. During a spill, however, a static equilibrium can never be established because the dissolved components are removed (diffused and advected) away from the surface oil source (and dispersed oil droplets), mixed with fresh uncontaminated water, and subjected to evaporation loss from the water column itself.
As a result of these processes, dissolution should not be modeled as an equilibrium process, but instead as a kinetics-controlled process where the driving force is determined by the distance of the system from equilibrium. The oil-water interfacial area should be a term in the rate equation, and the aqueous-phase concentration could be modeled as being arbitrarily low (e.g., zero) or through a mass balance on the water-soluble components. In a study related to this conceptual approach, Page et al. (2000b) reported on the importance of kinetics, thermodynamics, and colloidal phenomena in controlling the partitioning of naphthalenes from West Texas and Arabian medium crude oils into seawater. Under conditions of light turbulence, the alkyl-substituted naphthalenes showed an inverse correlation between both the dissolution rate coefficients and saturation concentrations and the degree of alkyl-substitution. At higher turbulence levels and variable oil loadings, there was a direct correlation between the measured total petroleum hydrocarbon concentrations in the water and the nominal oil loading; however, there was no such correla-
tion between the naphthalenes and oil loading. It was concluded that the first experiment was controlled by dissolution kinetics across the oil/water boundary and solubility phenomenon, while the second experiment also included a colloidal oil-phase contribution to the measured constituent concentrations.
Sterling et al. (2003) examined the partitioning of PAH components from oil droplets into the water column and the influence of the shear stresses used to generate those droplets. Their approach was based on Raoult’s Law using pure component solubilities and individual-component mole fractions in the oil phase. At low shear stresses generating relatively low dispersed oil droplet concentrations, the influence of PAH solubility dominated the observed PAH concentrations. At higher shear stresses and dispersed oil droplet loadings, the PAH concentrations in the water column were influenced primarily by the mole fraction of the individual PAH in the entrained oil droplets.
To assess the time-series water-column concentrations in the subarctic flow-through wave-tank studies discussed above, Payne et al. (1984) filtered 20-liter subsurface seawater samples through 0.7 µm pore-size 293 mm diameter glass-fiber filters for separate analyses of the dissolved components and dispersed- and/or particulate-bound oil droplets (Gordon et al., 1973). Chromatograms of dissolved components measured in time-series filtered seawater samples from the wave-tank systems are shown in Figure 4-5. These chromatograms are characterized only by the individual aromatic components, not the evenly repeating series of n-alkanes that predominate in the dispersed oil droplets and surface oil samples (Figure 4-2). As shown in Figure 4-5A, dissolution of lower-molecular-weight aromatic components began immediately, as little as five minutes after the spill. The major dissolved components measured over time include benzene, toluene, xylene(s), ethylbenzenes, C3-substituted benzenes, naphthalene, methylnaphthalenes, C2- and C3-substituted naphthalenes, phenanthrene, and C1- and C2-substituted phenanthrenes.
As shown in Figures 4-6 and 4-7, maximum dissolved-component concentrations were observed very early in the spill. Dissolved-phase total benzene, toluene, ethylbenzene, and xylenes (BTEX) concentrations reached a maximum of 250 µg/L during the first 2 hours of the spill and were less than 25 µg/L after 2 days. The maximum total PAH concentration was somewhat delayed, occurring between 4 and 12 hours (Figure 4-7). Subsequent water-column concentrations decreased from a combination of evaporative losses from the water surface and advective/diffusion processes (simulated by one tank-volume water exchange every 4 hours). Concomitant (and orders of magnitude greater) evaporative losses of these same components also occurred from the surface slick over the same time frame. However, the higher-molecular-weight PAH were persistent in the
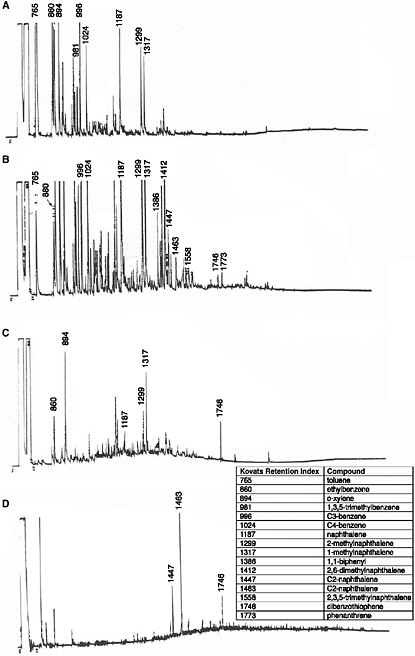
FIGURE 4-5 FID gas chromatograms of filtered water samples showing dissolved-phase components obtained from 2,800-liter flow-through open-air summer wave-tank experiments using 16 liters of Prudhoe Bay crude oil after: A) 5 minutes; B) 48 hours; C) 12 days and D) 12 months of weathering. Selected components are identified by Kovats Retention Index (see text and inset).
SOURCE: Modified from Payne et al., 1984.
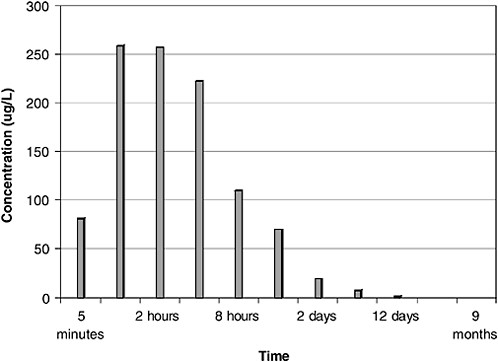
FIGURE 4-6 Total dissolved benzene, toluene, ethylbenzene, and xylenes (BTEX) concentrations in ppb over time from flow-through open wave-tank experiments using Prudhoe Bay crude oil. BTEX concentrations peaked at 1–2 hours.
SOURCE: Data from Payne et al., 1984.
oil, and continued dissolution of C2-substituted naphthalenes and alkyl-substituted phenanthrenes from the surface oil occurred for periods of up to 4 to 7 months (Figure 4-8) even though there was little or no physical dispersion of oil droplets occurring at that time. There was no evidence of significant aromatic hydrocarbon dissolution into the water column after 13 months in the wave-tank systems.
Clearly, the absolute concentrations of oil droplet- and dissolved-phase components presented in Figures 4-5 through 4-8 were influenced by the size of the wave tank systems (2,800 L), the water-column turnover rate or residence time (one tank volume every 4 hrs), and the volume of oil (16 L) used for the experiments. Slick spreading was also inhibited by the walls of the tanks, so extrapolating these data to actual open-ocean conditions must be done with caution. Nevertheless, it is worthy of note that excellent agreement was obtained between the wave-tank data and observed changes in oil rheology and oil chemistry after the T/V Exxon Valdez oil spill (Payne et al., 1991a). Both the wave-tank studies and the
EVOS observations are representative of ice-free Alaskan subarctic conditions, and the rates of evaporation, emulsification, (and possibly to a lesser extent, dissolution) would be different in warmer environments, but the processes themselves would still occur. Computer models can help define the anticipated changes in these rates for other environmental conditions and oil types. The data are included here to provide insight on the dynamic nature of the dissolved- and oil-phase component concentrations in the water column that ultimately drive toxicity considerations.
Although the use of chemical dispersants will clearly increase the upper water column concentration of entrained oil droplets, and theoretically should lead to enhanced dissolution of water-soluble PAH components (French-McCay and Payne, 2001), no field measurements of this phenomenon have been successfully completed to date. It is known that enhanced dissolved-phase concentrations occur with subsurface blowouts (Brooks et al., 1980; Payne et al., 1980a,b; Boehm and Fiest, 1980, 1982; Fiest and Boehm, 1980) and after extensive surface entrainment of fresh
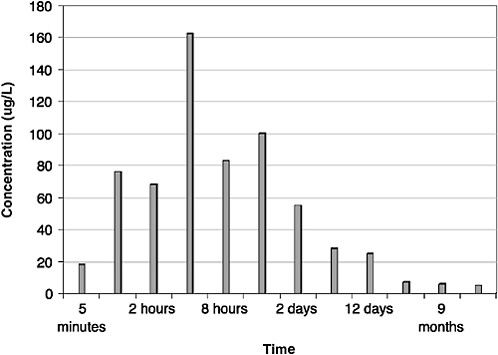
FIGURE 4-7 Total dissolved polynuclear aromatic hydrocarbons (PAH) concentrations in ppb over time from flow-through open wave-tank experiments using Prudhoe Bay crude oil. PAH concentrations peaked at 4 hours but continued to dissolve from the surface slicks for one year.
SOURCE: Data from Payne et al., 1984.
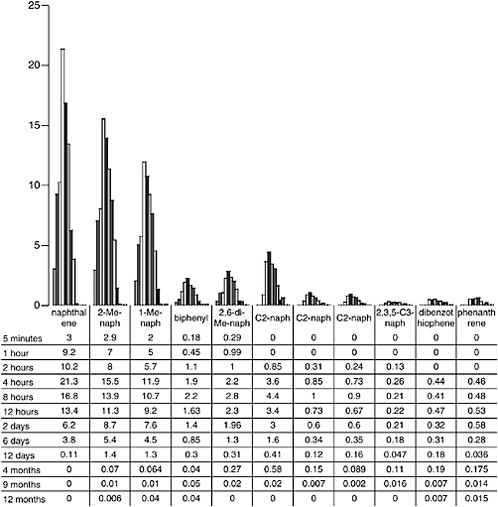
FIGURE 4-8 Dissolved individual PAH concentrations in ppb over time from flow-through open wave-tank experiments using Prudhoe Bay crude oil.
SOURCE: Data from Payne et al., 1984.
petroleum products, such as occurred with the North Cape (French-McCay, 2003). However, attempts to measure this during dispersant applications to accidental spills have not documented similar behavior.
Dispersants were used during the response to the Mega Borg spill of 3.9 million gallons (roughly 13,000 tonnes) of Angola Planca crude oil off Galveston, Texas, in 1990, and Payne et al. (1993) examined target and control areas of the treated slick to see if evidence of enhanced PAH dissolution could be observed. The measured concentrations of dispersed oil droplets were very heterogeneous and reflected the patchy distribution of oil on the water surface before dispersant application. Nevertheless, the
ratio data for aliphatic:aromatic concentrations showed no evidence of significantly enhanced dissolution of lower- and intermediate-molecular-weight aromatics as a result of the dispersant treatment.
Payne et al. (1991d) demonstrated that dissolved aromatic compounds from oil introduced into refreezing leads can be advected as conservative components in the brine generated during frazil ice formation to the benthic bottom boundary layer in field experiments completed in the Chukchi Sea. If dispersants were applied to oil released in open water during freezing conditions or to oil contained in open leads/broken sea ice during a refreezing event, it is conceivable that the enhanced dissolution process predicted by French-McCay and Payne (2001) could lead to transport of dissolved aromatic components to the benthos before significant evaporative weathering could otherwise occur. Clearly, any such enhanced transport would be spill or location specific, as it assumes only minor horizontal transfer.
Biodegradation
The effects of surfactants and commercial oil dispersant mixtures on the rate and extent of biodegradation of crude oil, petroleum products, and individual hydrocarbons have been intensively investigated for over thirty years with mixed results. In some studies, biodegradation is stimulated, others find evidence of inhibition, and others observe no effects attributable to the presence of surfactants or commercial dispersants. Experimental systems have used a wide variety of substrates (e.g., crude oil, individual hydrocarbons), surfactants (e.g., commercial dispersant mixtures, pure surfactants), and microbial communities (e.g., natural seawater microbiota, microbial communities enriched by growth on crude oil, pure cultures). None of these factors appear to systematically affect the outcome. Instead, the effects of surfactants or commercial dispersant mixtures on the biodegradation rates of crude oil and defined hydrocarbons appear to depend on the chemical characteristics of the surfactants, the hydrocarbons, and the composition of the microbial community. Other factors, such as nutrient concentrations, oil-water ratios, and mixing energy, can also be expected to affect the observed biodegradation rate of dispersed oil.
One source of confusion in the literature on dispersant effects on oil biodegradation is that conclusions are often based on indirect evidence. For example, Corexit 9527 (DOR = 1:10) was shown to increase the rate of oxygen uptake in suspensions of South Louisiana and Kuwait crude oils relative to suspensions of physically dispersed oil (Traxler and Bhattacharya, 1978), and several dispersants increased the rate or extent of microbial growth on Arabian (Mulkins-Phillips and Stewart, 1974) or For-
ties (Swannell and Daniel, 1999) crude oil. Unfortunately, this stimulation cannot be unambiguously attributed to growth on dispersed oil as opposed to growth on the dispersants themselves, which are usually readily biodegradable and support microbial growth (Mulkins-Phillips and Stewart, 1974; Bhosle and Row, 1983; Bhosle and Mavinkurve, 1984; Lindstrom and Braddock, 2002). Corexit 9500 (DOR = 1:10), however, had no effect on the growth rate of hydrocarbon degraders on Alaska North Slope crude oil, and it slightly decreased the gross rate of oil mineralization (Davies et al., 2001; Lindstrom and Braddock, 2002). Total extractable material (TEM), which is a gravimetric measurement of the concentration of hydrophobic (e.g., oil and grease) compounds, is a somewhat more direct measure of oil biodegradation than is oxygen consumption or microbial growth rate, but it is still subject to interference from surfactants or other dispersant components. Based on this metric, Dispolene 34 S (DOR = 1:5) decreased the rate of biodegradation of Kuwait crude oil by about two-thirds relative to physically dispersed oil when both were present at realistically low concentrations in natural seawater (Literathy et al., 1989).
More direct evidence for the effects of dispersants on oil biodegradation rates involve measurement of oil composition, usually by gas chromatographic-flame ionization detector (GC-FID) or gas chromatographic-mass spectroscopy (GC-MS), or measurement of the rate of biotransformation of specific hydrocarbons to carbon dioxide (e.g., mineralization). Based on changes in oil composition, Corexit 9527 was found to inhibit the biodegradation of normal and branched alkanes and sulfur heterocycles in Prudhoe Bay crude oil, but biodegradation of PAH was not affected (Foght and Westlake, 1982; Foght et al., 1983). Corexit 9500 had no effect on the rate of n-alkane biodegradation in Alaskan North Slope crude oil when compared to physically dispersed oil (Davies et al., 2001). The rate of biodegradation of naphthalene and phenanthrene in the water-accommodated fraction (WAF) of a heavy residual fuel oil was not affected by the presence of a dispersant (Taiho Self-Mixing S-7), but the biodegradation rates of the 4-ring PAH pyrene and chrysene were faster (Yamada et al., 2003). It should be noted, however, that the initial concentrations of pyrene and chrysene in the WAF that was prepared with chemically dispersed oil were sufficiently high that their final aqueous-phase concentrations were higher after biodegradation than the initial concentrations in the water-only WAF.
Although disappearance of target compounds from samples provides a very detailed and sensitive view of changes in oil composition that occur during incubation under specified experimental conditions, the mechanism that causes the observed compositional changes and the fate of the compounds that disappear often must be inferred. It is, for example, often difficult to determine whether specific compounds were lost from the
sample by physical, chemical, or biological processes, and even when biological transformation is indicated, the fate of the biotransformation products is not known (i.e., a single metabolic reaction, such as hydroxylation by a nonspecific oxygenase enzyme, is sufficient to cause a compound to disappear from a gas chromatogram, but it might not reduce the toxicity of the oil). Isotopically labeled substrates can provide more information on the ultimate products of biotransformation reactions, but these data are much more restricted in that they provide information only on the fate of specific compounds, which may or may not be representative of larger classes of petroleum hydrocarbons. Like other measures of dispersant effects on oil biodegradation, the effects on mineralization of specific hydrocarbons vary with target compound, dispersant, oil, and microbial community composition. For example, when n-[1-14C]-hexadecane, [1-14C]-pristane, or [9-14C]-phenanthrene were added to Norman Wells crude oil (Foght et al., 1987), mineralization of pristane was inhibited by all dispersants that were tested, whereas hexadecane mineralization was stimulated by Corexit 7664 and Corexit 9600 and inhibited by Dispersol SD and W-1911. Although phenanthrene mineralization by the oil-degrading enrichment culture was stimulated by Corexit 9600, this dispersant inhibited its mineralization by indigenous bacteria in natural river water. Note that the position of the radiolabel is important in these studies, because it determines the extent of metabolism that must occur before the labeled carbon atom can be released as 14CO2. In general, end-labeled substrates, such as n-[1-14C]-hexadecane and [1-14C]-pristane, will release 14CO2 following much more limited metabolic transformation than is required for a molecule that is internally labeled, like [9-14C]-phenanthrene. This distinction is probably relatively unimportant for n-alkanes, which are usually completely degraded following the initial oxygen-insertion reaction, but it can be somewhat more important for molecules for which partial metabolic transformations are more common (e.g., branched and cyclic alkanes, PAH).
The effect of dispersants on oil biodegradation rate is very sensitive to the chemical characteristics of the dispersant, even when all other factors (e.g., oil, microbial community) are kept constant. A survey of thirteen dispersants and two surfactants showed that none significantly stimulated the biodegradation rate of Norman Wells crude oil by an oil-degrading enrichment culture in an artificial freshwater medium (Foght et al., 1987). About half of the dispersants—and both of the surfactants—that were tested inhibited biodegradation of one or more classes of petroleum hydrocarbons (e.g., aliphatics, aromatics, sulfur heterocycles) as measured by GC-MS. The class of compounds whose degradation was inhibited and the degree of inhibition that was observed varied from dispersant to dispersant, even though the oil and the microbial culture were the same. A
systematic investigation of the relationship between surfactant chemical structure and oil biodegradation involved the use of a homologous series of nonylphenol ethoxylate surfactants that varied in the length of the polyethoxylate chain, which confers the hydrophilic character to the molecule. The hydrophilic-lipophilic balances (HLBs) of this homologous series ranged from 4.6 to 18.2, but only compounds with HLBs between about 12 and 14 stimulated the biodegradation rate of Bow River crude oil by a culture of oil-degrading bacteria enriched from refinery sludge (Van Hamme and Ward, 1999). The most effective surfactant in this series, Igepal CO-630, stimulated the biodegradation of both aliphatic and aromatic hydrocarbons. The degree of stimulation was strongly dependent on surfactant concentration; the optimal surfactant-to-oil ratio (SOR) was 1:32. Notably, HLB alone was not an adequate predictor of the ability to stimulate oil biodegradation: of seven surfactants with similar HLBs but which varied in chemical structure, two stimulated oil biodegradation by this enrichment culture, two inhibited it, and three had no effect. A similarly systematic, but conceptually distinct, approach was used in another investigation of the relationships between dispersant chemical composition and effect on oil biodegradation rate (Varadaraj et al., 1995). A series of model dispersant mixtures that differed in HLB was created by varying the relative proportions of two surfactants that are components of Corexit 9527 and 9500: Span 80 (sorbitan monooleate, HLB = 4.3) and Tween 80 (eicosethoxy sorbitan monooleate, HLB = 15). In this study, the maximum rate of biodegradation of Alaska North Slope crude oil by sludge from a refinery wastewater treatment system was obtained at a dispersant HLB of about 8, which is significantly lower than the HLB that was most efficient for the homologous series of Igepals (Van Hamme and Ward, 1999). The extent to which the effects of HLB and surfactant structure on biodegradation efficiency depend on the dispersion efficacy (i.e., do surfactants that stimulate biodegradation entrain higher concentrations of oil as very small droplets than those that do not?) is not known.
Further evidence that the effects of surfactants and dispersant mixtures on oil biodegradation involve complex interactions between the oil, the surfactants, and the composition of the microbial community was obtained through studies with pure cultures. The effect of surfactants on the biodegradation of Statfjord crude oil (topped at 210° C [roughly 410° F]) by Rhodococcus sp. O94, an alkane-degrading bacterium, varied with the physiological state of the cells (Bruheim et al., 1997). Oil biodegradation and hexadecane mineralization by exponentially growing cells, which were highly hydrophobic and adhered strongly at oil-water interfaces, were inhibited by all of the dispersants and surfactants that were tested, including Corexit 9527, Finasol OSR-5, Inipol IPF, and Tween 85 (a component of Corexit 9527). Stationary-phase cells, which were relatively hy-
drophilic and degraded the oil slowly relative to exponential-phase cells, were generally stimulated by the pure surfactants that were tested, but the dispersants either inhibited oil biodegradation and hexadecane mineralization or had no effect on these processes (Bruheim et al., 1997). Further research showed that the difference between the effects of Tween 85 and Corexit 9527 are probably due to synergistic interactions between the nonionic and anionic surfactants that are present in the dispersant mixture (Bruheim et al., 1999). The anionic surfactant in Corexit 9527 and 9500, sodium dioctyl sulfosuccinate, was highly inhibitory to Rhodococcus sp. O94 and Acinetobacter calcoaceticus ATCC 31012, another alkane-degrading bacterium. Corexit 9527 inhibited the rate of crude oil biodegradation by stationary-phase cells of A. calcoaceticus ATCC 31012 by about 40 percent relative to physically dispersed oil, but the nonionic surfactants stimulated the oil biodegradation rate under the same conditions when they were tested alone. These surfactants apparently acted directly at the cell surfaces, possibly interacting with proteins in the cytoplasmic membranes, because they also affected transport and/or oxidation of acetate, a completely water-miscible substrate (Bruheim et al., 1999). For Gram-negative bacteria, surfactants with chemical characteristics that stimulated the rate of n-alkane oxidation also stimulated the rate of penetration of fluorescein diacetate (FDA) through the outer membrane (Bruheim and Eimhjellen, 2000). Thus, these surfactants appeared to affect the permeability of the outer membrane. Although these surfactants also stimulated the rate of alkane oxidation by some Gram-positive bacteria (e.g., Rhodococcus sp. 094 and 015), they did not affect the rate of FDA hydrolysis, implying that surfactants interacted more strongly with the outer membrane than with the cytoplasmic membrane (Bruheim and Eimhjellen, 2000).
The variable effects of dispersants and surfactants on oil biodegradation rate are probably due to their effect on microbial uptake of hydrocarbons. Three main mechanisms are recognized by which microorganisms take up hydrocarbons as a prelude to metabolic transformation: transport of aqueous-phase substrates through a variety of well-characterized membrane transport mechanisms (e.g., passive diffusion, active transport); direct contact with nonaqueous-phase liquids or solids followed by poorly understood incorporation into cell membranes or intracellular vesicles; and uptake of water-accommodated hydrocarbons present in surfactant micelles (Singer and Finnerty, 1984; Watkinson and Morgan, 1990). There is good evidence for each of these mechanisms in specific cases. For example, microbial uptake of low-molecular-weight PAH, such as naphthalene and phenanthrene, has been shown to occur by transport of aqueous-phase (i.e., truly dissolved) molecules (Wodzinski and Bertolini, 1972; Wodzinski and Coyle, 1974), whereas direct attachment to nonaqueous-
phase liquid droplets is essential for growth of certain alkane degraders (Miura et al., 1977; Rosenberg and Rosenberg, 1981). Some hydrocarbon degraders produce biological emulsifying agents that appear to function in substrate transport (Rosenberg and Rosenberg, 1981; Reddy et al., 1983).
These different transport mechanisms for hydrocarbons will almost certainly be affected differently by dispersants; so, it is perhaps not surprising that the effects of dispersants on oil biodegradation rate vary from system to system. The mechanism that would be expected to be affected least, and possibly enhanced, by surfactant-mediated dispersion of oil is uptake of dissolved hydrocarbons. Dispersion of oil into small droplets will increase the oil-water interfacial area and, therefore, increase the transport rate of hydrocarbons from the nonaqueous to the aqueous phase. It may be significant that dispersants are often reported to have no effect on the degradation rate of low-molecular-weight PAH (Foght and Westlake, 1982; Lindstrom and Braddock, 2002; Yamada et al., 2003), which may reflect the fact that these PAH are more water soluble than other petroleum components. Conversely, direct attachment is the mechanism that should be affected most by chemical dispersion, because accumulation of surfactants at the oil-water interface will change its chemical characteristics and, perhaps, interfere with normal attachment mechanisms. For example, low concentrations of a rhamnolipid biosurfactant reduced the apparent hydrophobicity, measured by the efficiency of attachment to hexadecane, of four strains of Pseudomonas aeruginosa (Zhang and Miller, 1994), and a hydrophobic Rhodococcus sp. that adhered strongly to oil droplets suspended in water could be released by addition of a nonionic surfactant, Igepal CO-630 (Van Hamme and Ward, 2001). Interference with bacterial attachment to oil droplets may have been the mechanism by which several dispersants and surfactants inhibited oil biodegradation by the highly hydrophobic exponential-phase cells of Rhodococcus sp. O94 (Bruheim et al., 1997), and the biosurfactant emulsan strongly inhibited mineralization of n-[1-14C]-hexadecane and [1-14C]-pristane in crude oil by six pure cultures of alkane-degrading bacteria (Foght et al., 1989). Notably, emulsan had no effect on mineralization of [9-14C]-phenanthrene in oil by three pure cultures of PAH-degrading bacteria, which presumably accumulated the phenanthrene directly from the aqueous phase, in the same study.
Although it is clear that surfactants can interfere with attachment of hydrophobic bacteria to oil droplets, the overall effects of chemical dispersion of crude oil on its biodegradation rate are likely to be very complex. For example, although low concentrations of a rhamnolipid biosurfactant interfered with microbial attachment to hexadecane, higher concentrations (above the critical micelle concentration [CMC]) promoted attachment of two hydrophilic strains of P. aeruginosa but did not affect
the attachment efficiency of two hydrophobic strains (Zhang and Miller, 1994). Also, treatment of ANS crude oil with Corexit 9500 only marginally affected bacterial colonization of oil droplets, with 40 percent of chemically dispersed oil droplets being colonized by at least one bacterium after four days compared to colonization of 60 percent of physically dispersed oil droplets after about one week (Davies et al., 2001). Note, however, that chemical dispersion of ANS crude oil had no significant effect on the oil biodegradation rate in this study. Alternatively, although Igepal CO-630 decreased the biodegradation of the aliphatic fraction of Bow River crude oil by the hydrophobic bacterium Rhodococcus sp. F9-D79, which attaches to oil droplets, it did not affect the rate of biodegradation of the aromatic fraction (Van Hamme and Ward, 2001). In addition, the presence of the surfactant had no effect on the biodegradation rate of either hydrocarbon fraction by Pseudomonas sp. JA5-B45, which did not attach to oil droplets, and it significantly enhanced the oil biodegradation rate by a coculture of these two organisms (Van Hamme and Ward, 2001). In the long term, the effect of dispersants on bacterial attachment to oil droplets may be less important than is indicated by these studies, because the surfactants will partition out of the droplets into the aqueous phase as the dispersed-oil plume dilutes into a large volume of seawater. The ultimate result of this dilution and partitioning will be small isolated oil droplets lacking a surfactant coating that can interfere with microbial attachment. Thus far, no studies have specifically investigated the biodegradability of these surfactant-depleted droplets of dispersed oil.
The third mechanism of hydrocarbon uptake, transport of micelle-accommodated hydrocarbons, is probably relatively unimportant within the context of the fate of chemically dispersed oil. It is clear that this is an important transport mechanism in some cases (Miller and Bartha, 1989; Bury and Miller, 1993; Garcia et al., 2001), and it may be particularly important for hydrocarbon-degrading bacteria with relatively hydrophilic surfaces (Churchill and Churchill, 1997; Van Hamme and Ward, 2001). Nonetheless, surfactants must be present in the aqueous phase at concentrations greater than their CMC before micelles can form, and the micelle-accommodated hydrocarbon concentration is almost always less than the surfactant concentration (Miller and Bartha, 1989; Zhang and Miller, 1992; Bury and Miller, 1993; Churchill and Churchill, 1997; Schippers et al., 2000; Garcia et al., 2001). Given the large dilution potential of the surface mixed layer in the ocean and the relatively low treatment rate of oil slicks with dispersants (DOR usually less than 1:10), accommodation of a significant fraction of the oil slick in micelles is extremely unlikely.
Implications for the Fate of Dispersed Crude Oil No systematic and reproducible effects of chemical dispersion on the biodegradation rate of
crude oil have been demonstrated. In most cases, however, the experimental systems used to investigate these effects may have been inappropriate for extrapolation to behavior in the environment, because they generally applied high mixing energy in an enclosed, usually nutrient-sufficient, environment and allowed sufficient time for microbial growth to result in a substantial enhancement of the extent of physical dispersion of the oil. Microbial growth on open-ocean oil slicks is likely to be nutrient limited and may be slow relative to processes that lead to formation of water-in-oil emulsions, which tend to be extremely resistant to biodegradation. The only way to predict the contribution of biodegradation to the fate of dispersed crude oil is to incorporate this process as a term in a comprehensive fate and transport model. At a minimum, this term would be a function of dispersed oil-water interfacial area (L−1 or L2L−3), a heterogeneous rate coefficient (LT−1), and the oil density (MoilL−3) or the concentration of specific components or pseudocomponents in the oil (Mi). If specific components or pseudocomponents are considered, the rate coefficient should be specific for the target component or pseudocomponent. For example, the rate of change of the concentration of phenanthrene (MpheL−3T−1) in a dispersed oil plume would be given by:
(4-7)
The heterogeneous rate coefficient, k, is probably a function of the nutrient concentration and the concentration of hydrocarbon-degrading bacteria. A second equation that links oil degradation to microbial growth could be used to account for changes in the size of the microbial population over time.
Unfortunately, existing studies do not provide the type of data that is needed to estimate kinetic parameters for this simple model. The size of hydrocarbon-degrading microbial populations is often measured in oil-biodegradation studies (Mulkins-Phillips and Stewart, 1974; Bhosle and Row, 1983; Bhosle and Mavinkurve, 1984; Lindstrom et al., 1999; Swannell and Daniel, 1999; Van Hamme and Ward, 1999; Davies et al., 2001; Lindstrom and Braddock, 2002; MacNaughton et al., 2003; Yamada et al., 2003), but few studies have measured droplet size distributions in conjunction with biodegradation experiments (Varadaraj et al., 1995; Swannell et al., 1997; Swannell and Daniel, 1999; MacNaughton et al., 2003) and none attempted to estimate interfacial-area normalized biodegradation rates. Good quantitative degradation rates for specific components or pseudocomponents are also missing in many studies, especially if one is interested in components other than normal alkanes and pristane or phytane. In some cases, when information on changes in the oil composition is presented, it is qualitative (i.e., gas chromatograms; Foght and Westlake, 1982;
Foght et al., 1983, 1987, 1989) or given for only one incubation time, usually the endpoint (Swannell et al., 1997; Burns et al., 1999; Swannell and Daniel, 1999; Davies et al., 2001; MacNaughton et al., 2003). Other studies use radiolabeled tracers to monitor the biological mineralization of specific hydrocarbons (Foght et al., 1987, 1989; Bruheim et al., 1999; Davies et al., 2001; Lindstrom and Braddock, 2002), but the selected substrates were usually easily degradable hydrocarbons, such as hexadecane and phenanthrene, that do not provide any information regarding the biodegradation rates of compounds that may be of concern with regard to the long-term effects of dispersed oil (e.g., high-molecular-weight PAH). The use of tracer compounds to monitor the mineralization of high-molecular-weight PAH is important, because relatively minor structural modifications (e.g., hydroxylation by a nonspecific monooxygenase) will result in removal of the target compound when GC-MS is the primary analytical tool, but the biotransformation products may not be significantly less toxic than the parent substrate, and in fact could be much more toxic. For example, whereas some studies have demonstrated relatively rapid biodegradation of 4-ring PAH, such as pyrene and chrysene, in chemically dispersed crude oil when the process was monitored by GC-MS (Yamada et al., 2003), others have been unable to detect any mineralization when [4,5,9,10-14C]-pyrene was used to monitor the process (Lindstrom and Braddock, 2002). Only PAH mineralization can be confidently equated with toxicity reduction.
Interactions with Suspended Particulate Material
In its most recent review of oil in the sea, the NRC (2003) stated, “Understanding the distribution of petroleum hydrocarbons between the dissolved phase and the variety of aquatic particles is important for determining the fate of hydrocarbons in the sea and the bioavailability of these chemicals to marine biota.” For chemically dispersed oil, the formation and fate of whole oil/suspended particulate material (SPM) aggregations are of particular importance.
Several of the earlier and fundamental studies in this area included examination of sediments following oil spills (Hoffman and Quinn, 1978; 1979), controlled experimental ecosystems (Gearing et al., 1980; Gearing and Gearing, 1982a,b; Wade and Quinn, 1980), estimates of sedimentation rates in regions of petroleum activity (Malinky and Shaw, 1979), and more fundamental studies of adsorption (Bassin and Ichiye, 1977; Herbes 1977; Rogers et al., 1980; Karickhoff, 1981). Studies examining the direct interaction of physically (and chemically) dispersed oil droplets with suspended particulate material include those by Mackay and Hossain (1982), Boehm (1987), Payne et al. (1984, 1987a,b, 1989, 2003), Wood et al. (1998), Guyo-
march et al. (1999a,b,c; 2002), Hill et al. (2003), Le Floch et al. (2002), Muschenheim and Lee (2002), and Sterling et al. (2004a,b). Also, related studies have now demonstrated that removal and biodegradation of stranded oil in the intertidal zone can be enhanced by augmenting oil/mineral-particle interactions through berm relocation and so-called surf-washing (Bragg and Owens, 1994, 1995; Lee et al., 1997a,b, 2001; Hill et al., 2003; Owens and Lee, 2003). These studies are not considered in detail in this section except to the extent of how specific measured parameters such as salinity, mineral type, and oil type have been shown to affect oil/SPM binding, aggregation, and sedimentation as reviewed by Lee (2002) and Muschenheim and Lee (2002). Lee (2002) stated that the principal environmental parameters affecting oil/SPM interactions include: (1) quantity, type, and surface properties of associated minerals; (2) quantity, viscosity, and composition of the oil; (3) physical energy of the system; and (4) salinity.
Wood et al. (1998) reported that oil/SPM interactions drive the reversible process of oil droplet entrainment and surface slick recoalescence in favor of the dispersed oil phase. Specifically, as entrained oil droplets interacted with SPM and their density increased, the agglomerates were removed from the upper water column and were no longer able to recoalesce and rejoin the surface slick. Their studies also showed that oil/SPM aggregate formation occurs primarily with dispersed oil droplets in the water column interacting with SPM rather than SPM scavenging oil from the surface. The minerals used in their studies did not increase the rate of oil droplet formation from the surface slick, but they did prevent recoalescence and the effect was greatest with minerals with greater cation exchange capacities. The more readily entrained oils (which formed oil/SPM aggregates more easily) were characterized by relatively lower percentages of resins and asphaltenes relative to higher percentages of alkanes, which presumably limited the formation of water-in-oil emulsions.
Schlautman and Morgan (1993) examined the effects of aqueous chemistry on the binding of PAH by dissolved humic materials. Henrichs et al. (1997) and Braddock and Richter (1998) examined the partitioning of naphthalene and phenanthrene onto representative Alaskan sediments and SPM, and a recent special edition of Environmental Toxicology and Chemistry (Volume 18, No. 8, 1999) was devoted to causes and effects of resistant sorption and desorption of hydrophobic organic contaminants (including several PAH) onto natural particulate material.
Adsorption of oil droplets onto suspended particulates may provide a relatively efficient mechanism for sedimenting significant fractions of the oil mass. For example, following the Tsesis oil spill in the Baltic Sea, approximately 10–15 percent of the 300 tons of spilled oil were removed
by sedimentation of the SPM-adsorbed oil (Johansson et al., 1980). The high oil flux was due to the large SPM concentrations resulting from turbulent resuspension of bottom sediments. Likewise, as a result of the hurricane-force winds during the Braer oil spill in the Shetland Islands (as well as the influence of a local gyre) it was estimated that as much as 30 percent (30,000 tonnes) of the oil was deposited in the subtidal sediments around the Shetlands Islands, with hot spot concentrations of 2,000 to greater than 10,000 ppm total hydrocarbons (Ecological Steering Group on the Oil Spill in Shetland, 1994).
Payne et al. (1989, 2003) investigated the interaction of physically dispersed (entrained) oil droplets and individual dissolved constituents from fresh and weathered Alaska North Slope (ANS) crude oil and commercially available No. 1 fuel oil with nine SPM/sediment types collected from a variety of Alaskan coastal regions at high sediment loadings (200–1,000 mg/L). In these studies, entrainment of oil droplet-SPM interactions overwhelmed dissolved constituent-SPM adsorption by many orders of magnitude. Results of statistical analyses indicated that particle number density per unit mass showed the highest correlation (r = 0.902) with the values for the oil/SPM reaction rate. A slightly lower degree of correlation (r = 0.798) existed with the values for sediment fractions comprising the 0–2 µm particle-size range. The remaining three variables (total organic carbon [TOC], specific density, and background total GC resolved hydrocarbon content) showed no significant correlation with the oil/SPM reaction rate.
More recent studies on the fractal dimensions of oil/SPM agglomerates under differing turbulence conditions have been reported by Sterling et al. (2004a). Smaller and more compact aggregates were observed with increasing velocity gradients, and the authors concluded that colloidal oil and mixing shear were the more dominant factors (compared to salinity and mineral type) affecting aggregate morphology in nearshore waters. In a related study Sterling et al. (2004b) described a modeling approach to simulate changes in particle-size distribution and density as a result of aggregation with oil. Aggregation studies were reported for clay, colloidal silica, crude oil, clay-oil, and silica-crude oil systems. Clay and crude oil by themselves were characterized as cohesive particles while silica was classified as noncohesive. The introduction of crude oil increased the aggregation of the noncohesive silica. Apparent first-order aggregation rates for oil, clay, and silica and apparent second-order aggregation rates for oil and clay in clay-oil systems and oil and silica in silica-oil systems were obtained. For oil and clay systems alone, droplet coalescence and clay aggregation were observed to occur on the same time scales as oil resurfacing and clay settling, respectively. For the mixed oil-clay studies, the relative time scales for clay settling and clay-oil aggregation were within
an order of magnitude, and it was concluded that oil-clay aggregation should be considered when modeling crude oil transport in nearshore waters. In this regard, excellent agreement was obtained between observed and model-predicted behavior for the oil-clay systems. Conversely, the data for the silica and silica-oil systems suggested that the silica aggregation and oil-silica aggregation both occurred more slowly than aggregate settling. Because of the greater volume mean diameters and densities of the silica particles compared to the clay, it was concluded that the removal of oil by silica was less efficient than that by clay.
Additional modeling of the effects of sediment size on the size of subsequently generated oil/SPM agglomerates has been reported by Khelifa et al. (2004). Both model simulation and laboratory results showed negative effects of sediment size on oil/mineral/aggregate formation. Variations of the concentration of stabilized oil with sediment size showed a maximum when the ratio between the sediment and oil droplet sizes varied between 0.1 and 0.4. The highest concentration of stabilized oil was observed when sediment size varied between 0.3 and 1.2 µm. The model results showed that the sticking efficiency between oil droplets and sediment particles is a significant factor in oil/SPM aggregate formation.
Not as much is known about the longer-term fate of oil-SPM agglomerates while still in suspension in the water column; however, Wood et al. (1998) implied that an association of mineral particles and bacteria may be more efficient at biodegrading dispersed oil compared to bacteria alone. Based on what is known about weathering of free oil droplets, it can be inferred that oil-SPM agglomerates would still be subject to the same oil-phase diffusion-controlled weathering behavior (although possibly at an altered rate due to changes in the surface area-to-volume ratios for the agglomerates and the presence of bacteria associated with the SPM). It is known that bacteria are more likely to be associated with particulate surfaces in the water column (Subba-Rao and Alexander, 1982; van Loosdrecht et al., 1990), and introduction of clay-sized particles into oil trapped in sandy intertidal sedimentary regimes to form oil-SPM agglomerates has been shown to enhance bacterial utilization of the hydrocarbons by generating increased surface area (Lee et al., 1997a; Jezequel et al., 1998, 1999; Weise et al., 1999). Likewise, Jahns et al. (1991) demonstrated the enhanced removal and biodegradation of previously buried oil in low-energy cobble beaches due to the natural incorporation of clay-sized SPM over time following the T/V Exxon Valdez oil spill, and these mechanisms may also apply to oil SPM agglomerates while still suspended in the water column.
Once formed, oil-mineral aggregates appear to be very stable structures, and the buoyancy will ultimately depend on the ratio of oil to mineral in each individual aggregate (Stoffyn-Egli and Lee, 2002). Because
oil-mineral aggregates are typically less dense than mineral-only aggregates and in many cases buoyant (Stoffyn-Egli and Lee, 2002), associated residual oil is believed to be kept in suspension long enough to be dispersed over a wider area by physical processes.
Dispersant-Treated Oil Droplet/SPM Interactions
Mackay and Hossain (1982) completed one of the earliest exploratory studies of naturally and chemically dispersed oil in which several crude oils were dispersed with varying amounts of chemical dispersants in seawater in the presence of differing quantities of sedimenting mineral and organic matter. Mineral concentrations ranged from 40 to 160 mg/L and DOR ratios ranged from 1:5 to 1:20 with no dispersant added in some cases. Oil and dispersant were premixed and shaken with water to form the dispersion in the test apparatus.
Settling velocities in the test chamber were quite low, and it was concluded that little actual settling would occur in a turbulent ocean surface layer. Corexit 9527 consistently gave lower amounts of oil settled than BP 1100 WD. In generally all cases, more oil was settled to the bottom in the absence of any chemical dispersant, than when dispersants were used. Compared to kaolinite, higher settling values were obtained with higher organic content sediments such as humic acid and dead algae. Higher concentrations of oil and sediment tended to give higher fractions settled.
Dispersant dosage had a major effect in Mackay and Hossain’s study, as illustrated by the observation that at zero dosage, 30 percent of the oil settled, but at higher dispersant dosage this dropped to 10–15 percent at 1:10 (dispersant:oil) and to 6 percent at 1:5 (dispersant:oil). It appears that either smaller oil droplets are less able to associate with sedimenting particles than are larger droplets, or the association results in particles that do not settle. The higher the dispersant to oil ratio, the more the oil/SPM aggregate tends to return to the surface, and the less the oil/SPM aggregate tends to settle to the bottom.
Surprisingly, there have only been a few additional studies published over the last 22 years since Mackay and Hossain’s seminal work. Guyomarch et al. (1999c) used laboratory-scale experiments to demonstrate that very high suspended mineral loads (from 1,300 to 3,600 mg/L) were required to form aggregates with dispersant-treated oil, and the threshold mineral concentration value depended on the oil and clay type, their relative concentrations, and the water salinity (Guyomarch, et al., 1999c). Not surprisingly, the maximum amount of oil trapped on the mineral particles also depended on the dispersant (Inipol IP 90) efficiency, and Guyomarch et al. (1999c) observed that lower clay concentrations were required to sediment 40 percent of the oil as the polar fraction in the oil
phase increased. Conversely, as the salinity increased, higher clay concentrations were required to sediment 40 percent of the oil. In their larger-scale Polludrome tests, aggregates were formed at slightly lower SPM loads (750 mg/L). In all experiments, the oil concentrations were quite high (e.g., 120 ppm in the Polludrome tests), and the authors stated that additional tests should be conducted at lower oil and SPM concentrations such as those that might be encountered in outer estuaries or other coastal systems. It should be noted that keeping a steady-state SPM load in a wave tank is very difficult and depends on the turbulence regime utilized in the experiment and the SPM size range being studied.
In a subsequent laboratory study, Guyomarch et al. (2002) focused on the size distribution of oil-mineral aggregates when the oil was chemically dispersed with Inipol IP 90. Four oil types or blends were examined to provide a wide variety of initial oil viscosities (25 to 20,000 mPa-s) and asphaltene content (1 to 16 percent). Mixtures of oil, dispersant, and clay were stirred at 75 rpm for 2.5 min in a 250 mL beaker and allowed to settle for 1 hour. Clay concentrations were varied from 200 to 2,000 mg/L at a constant oil loading of 35 ppm.
Photo-microscopic observations (Figure 4-9) demonstrated that at low clay concentrations (<200 mg/L), small aggregates were mainly composed of clay with an occasional oil droplet (Figure 4-9A). At intermediate clay concentrations, much larger aggregates containing up to 15 oil droplets in a single cluster were observed (Figure 4-9B), and these higher oil-droplet density aggregates were reported to be much more common than in a previous study completed without dispersants (Lee et al., 1998). At higher clay concentrations (Figure 4-9C), the smaller agglomerates were explained by the hypothesis that all the oil droplets were completely covered by clay particles, which prevented interactions with each other and the concomitant formation of larger (multiple droplet) structures.
The effects of salinity examined by Guyomarch et al. (2002) confirmed their early findings that increased clay concentrations were needed to form aggregates as the salinities increased. Likewise, the influence of oil type (presence of asphaltenes) supported the hypothesis that interactions between polar compounds in the oil and the negatively charged clay particles by the intermediary action of a cation, as proposed by Bragg and Yang (1995), was important for stable aggregate formation. In a competitive sense, however, it is also known that as asphaltene content in the crude oil increases, its propensity to form higher viscosity water-in-oil emulsions also increases, and this inhibits dispersant effectiveness and oil droplet formation. Guyomarch et al. (2002) did not observe any significant difference in the maximum size of the oil-mineral aggregates for the different oils studied.
Taken in total, these studies might lead to the conclusion that because

FIGURE 4-9 Photomicrographs of: A) oil droplet aggregate formed at low clay concentrations. Oil appears as the darkest areas; B) multiple oil droplet aggregate formed at intermediate clay concentration; and C) oil droplet aggregate at high clay concentration.
SOURCE: Guyomarch et al., 2002; courtesy of Elsevier.
dispersant treatment results in the formation of greater numbers of oil droplets, the potential for their interaction with SPM will increase (i.e., because of higher oil droplet number densities as described and modeled by Payne et al., 2003), but the ultimate agglomerate size distribution will be controlled by the SPM loading in the water column as described by Guyomarch et al. (2002).
The size and composition of an oil/SPM aggregate will control the buoyancy of the agglomerate affecting its ultimate fate (transport vs. sedimentation), which in turn will vary with the local salinity and hydrodynamic regime. That is, the behavior of dispersant-enhanced oil droplets in the presence of SPM will be stochastic, depending on a number of variables that can complement or compete with one another to determine the ultimate disposition of the oil. As such, the transport of oil-mineral aggregates should be studied further to determine if it is beneficial to apply dispersants to oil on seawater that is loaded with SPM. This will be particularly important in estuaries and coastal zones where elevated SPM levels are often encountered. Likewise, additional studies on the biodegradation of dispersed oil/SPM agglomerates (both in the water column and after sedimentation) are warranted.
MODELS
Models of oil transport and fate integrate into one system the major physical, chemical, and biological processes discussed previously in this chapter (and some models also include the toxicological processes discussed in the following chapter). As such, models can provide decisionmakers with a more complete picture of what happens to spilled oil—and what effects it has on the environment—both with and without the use of chemical dispersants. Models of the trajectory of floating oil are regularly used, along with field measurements, in real time during a spill. To date in the United States, models of the transport and fate of dispersed oil have primarily been used in pre-planning exercises to simulate hypothetical spills in order that response measures, including use of chemical dispersants, can be evaluated before the fact, or to assist with natural resource damage assessment of real spills after the fact. So far models have not been used to evaluate the use of dispersants in real time, but we argue that this should be possible. The remainder of this chapter presents a brief overview of available models and their attributes (focusing on transport and fate only), summarizes a sensitivity study that is described in more detail in Appendix E, and provides recommendations on how models could be used more effectively.
The literature contains many reviews of oil transport and fate models (Yapa and Shen, 1994; ASCE, 1996; Reed et al., 1999; NRC, 1989, 1999,
2003). Computer codes are available for different water bodies—offshore open sea, nearshore water, semi-confined coastal water, estuaries, rivers, lakes, and reservoirs—and include ADIOS2 (Lehr et al., 2002), Spill Impact Model Application Package (SIMAP; French-McCay and Payne, 2001; French-McCay, 2003, 2004), Natural Resource Damage Assessment Model (NRDAM; Reed et al. 1991; French-McCay et al., 1996), Oil Spill Information System (OSIS; Leech et al. 1993), Oil Spill Contingency and Response (OSCAR; Aamo et al. 1997), OILMAP (Howlett et al. 1993), IMMSP (Institute of Mathematical Machines and Systems Problems; Brovchenko et al., 2003), Zhang (Zhang et al., 1997), General NOAA Oil Modeling Environment (GNOME; Simecek-Beatty et al., 2002), and River Oil Spill Simulation (ROSS) Model (Yapa et al., 1994). A few models, such as ROSS (Yapa et al., 1994), Water Planning and Management Branch (WPMB) model (Fingas and Sydor, 1980), and RiverSpill (Tsahalis, 1979) are specifically developed for rivers because major transport mechanisms and concerns in rivers are significantly different from those in open seas. Some models (e.g., ADIOS2) predict oil transport and fate on the water surface only; others (e.g., 3-D GNOME, IMMSP) simulate oil movements on the water surface, water column, and shorelines; some (e.g., SIMAP) predict oil on the water surface, in the water column and shorelines, and also quantify the biological impacts.
Most models simulate oil as a single substance, but a few treat oil as a composite of multiple hydrocarbons, usually sorted by distillation cut. Because various constituents weather at different rates, respond differently to chemical dispersants, and have different impacts on biota, the latter approach is superior (though often limited by toxicological data). It is recommended that models be formulated by constituent wherever this can be supported by available data.
Among their capabilities, one would like models to predict the effectiveness of chemical dispersants (i.e., the amount of oil entrained below the surface as droplets, and the resulting droplet size distribution) as a function of environmental conditions, type of oil and the extent of oil weathering, type and quantity of dispersant, etc. However, all models that purport to simulate the effect of chemical dispersants include such effectiveness measures as model inputs, rather than model outputs. Developing the ability to predict dispersant effectiveness, and integration of this predictive ability into models, is strongly recommended.
Sensitivity Study
In order to understand the effects of various processes on the transport and fate of spilled oil, a series of sensitivity tests was performed with the NOAA surface oil fate model ADIOS2 (Lehr et al., 2002), and the
NOAA oil transport code 3-D GNOME (Simecek-Beatty et al., 2002). Hypothetical spills were simulated off the coast of Florida using a range of oils, wind speeds (that in turn affect surface transport, wave height, and horizontal and vertical mixing), percentage effectiveness of dispersant application, and oil droplet-size distribution. These models were selected because they are three-dimensional, they treat oil as a composite of pseudocomponents, and they have limited computing requirements to operate the models. They are also used in real time during oil spills by NOAA to provide scientific support to the FOSC. This review was not intended as an endorsement of these particular models and indeed similar sensitivity analysis should be conducted using other models. Results of some sensitivity runs are presented below while the entire set is contained in Appendix E.
It is very difficult to predict where, when, and how much spilled oil moves. For example, the effect of wind on the movement of Alaskan North Slope crude oil is illustrated in Figure 4-10. This figure shows predicted changes in oil distributions 24 hours after oil is spilled on the water surface in the south Florida nearshore area under 2, 10 and 25m/s wind. As the wind becomes stronger, more oil is naturally entrained into the water column—from 0 volume percent at 2 m/s wind to 3 volume percent at 10
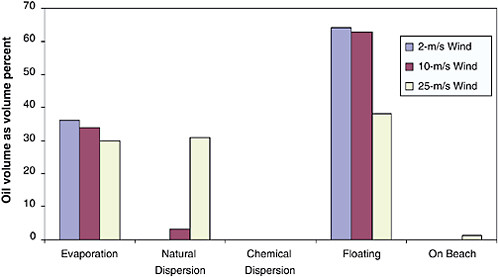
FIGURE 4-10 Predicted oil distributions 24 hours after the release of Alaskan North Slope crude oil (no dispersant applied) under 2-, 10-, and 25-m/s wind in nearshore off Florida Keys. There is no oil dispersed by a chemical dispersant for these three cases.
m/s, to 31 volume percent at 25 m/s. The greater entrainment means that less oil floats on the water surface, and hence less is available for evaporation, a result that might seem counterintuitive. Oil concentrations in the water column vary depending on the amount of oil naturally dispersed (entrained), but they also reflect the diffusivity (which increases at higher wind speed) in the water column. This example indicates some of the complexity involved with the way that currents and wind, and in turn waves and diffusion, affect the horizontal and vertical movement of oil.
When a dispersant is applied, more oil is entrained into the water column, and the droplets changes size distribution from the original size, further complicating oil transport and fate processes (see Figure 3-1). For example, assuming 50 percent effectiveness for a dispersant applied between 6 and 12 hours after the oil spill, 40 percent of the oil discussed previously was predicted to end up in the water column (37 percent by chemical entrainment and 3 percent by natural entrainment) under 10-m/s wind. Figure 4-11 shows the location of the predicted plume 24 hours after the spill. The oil spill location is marked by “+.” Black spots represent oil floating on the water surface, and the shaded areas show different ranges of oil concentrations in the top 1 m of the water column. The oil plume in the top 1 m of the water column is following a different trajectory at a different speed than the oil on the surface that is moved by the wind and the current. This figure also indicates that the area of the top 1 m of water column containing oil is about 64 km2, 2.5 times more than the contaminated top 1 m water area without dispersant application. Clearly such quantitative estimates would not be possible without a model.
Further complexity comes from the fact, mentioned previously, that oil consists of a wide ranges of hydrocarbons. Although oil toxicity comes from the cumulative impacts of multiple hydrocarbon components, low-and intermediate-molecular-weight components such as BTEX and PAH tend to cause more acute risks to aquatic biota, as is discussed in Chapter 5. These components usually evaporate faster and to a greater extent than large-molecular-weight components such as wax, resins, and asphaltenes. The latter are contributing components in the formation of mousse, which makes it more difficult for a dispersant to work effectively (see Chapter 3). Table 4-2 presents Alaska North Slope crude oil’s chemical components (Environment Canada, 2005), as indicated in their distillation cuts (built into the ADIOS2 code), together with those of intermediate fuel oil (IFO) 300 and marine diesel oil used in the sensitivity analysis. As shown in this table, the Alaska North Slope crude oil has more low molecular-weight components than the two refined oils. Oil composition changes and emulsification occurring during the transport of spilled oil significantly alter the physical properties of oil, especially viscosity and dispersant effectiveness, as previously discussed. Thus, it is important to
FIGURE 4-11 Predicted oil movement at 24 hours after the release of Alaskan North Slope crude at point + under 10-m/s wind with a dispersant application (additional details contained in the text of Chapter 4).
simulate the behavior and transport of the components of the various hydrocarbons rather than treating oil as one substance.
Figure 4-12 presents the predicted composition (a relative volume fraction of each distillation cut) of these three oils floating on the water surface 0 and 6 hours after the spill. Because of evaporation, the composi-
TABLE 4-2 Distillation Cuts of the Three Oils Used in the Modeling Sensitivity Analysis
|
Oil Cut Number |
Alaska North Slope Crude Oil |
Intermediate Fuel Oil 300 |
Diesel Fuel Oil |
|||
|
Weight Fraction, wt percent |
Temperature, °C |
Weight Fraction, wt percent |
Temperature, °C |
Weight Fraction, wt percent |
Temperature, °C |
|
|
1 |
1.0 |
42 |
1.1 |
180 |
1.1 |
120 |
|
2 |
4.0 |
98 |
1.1 |
200 |
1.1 |
140 |
|
3 |
5.0 |
127 |
6.4 |
250 |
1.1 |
160 |
|
4 |
5.0 |
147 |
9.4 |
300 |
3.2 |
180 |
|
5 |
5.0 |
172 |
7.2 |
350 |
5.2 |
200 |
|
6 |
10.0 |
216 |
8.1 |
400 |
20.4 |
250 |
|
7 |
10.0 |
238 |
6.0 |
450 |
31.9 |
300 |
|
8 |
5.0 |
247 |
3.0 |
500 |
25.5 |
350 |
|
9 |
5.0 |
258 |
4.9 |
550 |
9.7 |
400 |
|
10 |
5.0 |
265 |
9.8 |
600 |
1.0 |
450 |
|
11 |
5.0 |
272 |
14.7 |
650 |
— |
— |
|
12 |
10.0 |
282 |
10.7 |
700 |
— |
— |
|
13 |
30.0 |
>282 |
17.4 |
>700 |
— |
— |
|
SOURCE: Data from Environment Canada, 2005. |
||||||
tion of each oil changed significantly over time. Most of the cuts that distill at about 200° C [roughly 392° F] or lower, including alkanes with <10 carbons plus the monocyclic aromatics, benzene and toluene, ethylbenzene, o-, m-, and p-xylene, and most of the C2- and C3-substituted benzenes), evaporated within six hours. Thus, if a dispersant is applied six hours after the oil spill, it would not be expected to introduce these compounds into the water column. The IFO 300 does not naturally disperse into water due to its high viscosity (~15,000 cP), according to the modeling. On the other hand, diesel, with very low viscosity (~4 cP), disperses naturally (73 percent) without adding a chemical dispersant, and after 16 simulation hours, no diesel would be floating on the water surface. The combination of natural and chemical dispersal would disperse 78 percent of the diesel into the water, so there is no merit to applying a dispersant in this particular case. Because these refined oils have a low percentage of low-temperature distillation cuts, the IFO 300 and diesel evaporated only 10 and 18 volume percent, respectively, over 24 and 14 hours (much less than Alaska North Slope crude oil). This example clearly shows contrasting behavior of these three oils having different hydrocarbon composition.
FIGURE 4-12 Predicted compositions of floating oils initially and 6 hours after the releases of Alaskan North Slope crude oil, Intermediate Fuel Oil (IFO) 300, and Marine Diesel Oil (additional details contained in the text of Chapter 4).
These examples of the sensitivity analysis results illustrate very complex and sometimes competing interactions among oil types, environmental conditions, and dispersant use. Quantitative estimates of oil concentration distributions clearly require the use of computer models, especially those with oil pseudo-component modeling capabilities.
A final motivation for the sensitivity study was to assess whether models could be used in real time to help decide whether or not to use chemical dispersants during an actual spill. These questions are particularly important in nearshore areas where the impacts of using—and not using—dispersants are likely to be most significant. Unfortunately nearshore areas are also the most complicated hydrodynamically. Although 3-D GNOME can accept a three-dimensional flow field, it presently uses two-dimensional flows that are calculated based on a simplified force balance involving pressure, Coriolis, bottom friction, and variation in water density adjusted by tide and wind. This simplified approach is justified because of the need to make simulations very quickly for real-time model predictions, and because field observations can be used to update model output. Because chemical dispersants help transport oil into the water column, realistic simulation of subsurface transport becomes more important when evaluating the use of chemical dispersants, and the same formulation may not be sufficient. It is recommended that a range of 3-D
hydrodynamic formulations be evaluated with the goal of identifying approaches that are sufficiently accurate, yet still efficient, for real-time use.
APPLYING KNOWLEDGE ABOUT THE TRANSPORT AND FATE OF DISPERSED OIL TO SUPPORT DECISIONMAKING
As discussed in Chapters 2 and 3, many ultimate conclusions about the wise and effective use of dispersants in nearshore settings will need to be based on an accurate and adequate understanding of many processes controlling the transport and fate of dispersed oil. These processes may play a significant role from the instant the oil enters the environment, and they constrain a number of operational decisions and play a significant role in evaluating potential impacts of whole and dispersed oil on sensitive species or habitats.
Fate and Weathering of Oil
Oil on the Surface
Better information is still needed to determine the window of opportunity and percent effectiveness of dispersant application for different oil types and environmental conditions. Coordinated research should be undertaken at bench and wave-tank scales to define those parameters that control oil dispersability as the oil is allowed to weather under carefully controlled but realistic environmental conditions.
Overprediction of evaporation rates can be a problem with oil-weathering models that assume a well-mixed oil phase (which is probably only valid for very thin and relatively unweathered oil slicks) and also assume that resistance to mass transfer is entirely in the air phase. As a result, it may be inappropriate to always model oil as a well-mixed phase. Algorithms for both well-mixed and diffusion-controlled fluids may need to be sequentially utilized as a function of oil weathering-dependent viscosity changes to better approximate spilled oil evaporative behavior. Additional work is recommended to reconcile the differences between the empirical evaporation approach utilized by Fingas (1996, 1997, 1999a) and more traditional pseudo-component approaches as considered by Jones (1996, 1997), who has proposed a simplified pseudo-component (SPC) model relating molar volume, vapor pressure, and molecular weight to the boiling point of the components.
Sediment Particle Interactions
The ultimate fate of dispersed oil is poorly understood. Of particular
concern is the fate of dispersed oil in areas with high suspended solids and areas of low flushing rates. Although this has been an area of recent research, there is still insufficient information on which to determine how chemically dispersed oil interacts with a wide variety of suspended sediment types, both short- and long-term, compared to physically dispersed oil. In this regard, there appears to be more information on short-term comparisons versus the longer-term fate of oil/SPM agglomerates generated with and without dispersant addition. In particular, the longer-term biodegradation of oil/SPM agglomerates in the water column has not been adequately studied. Likewise, there are uncertainties in how dispersed oil might be consumed by plankton and deposited on the seafloor with fecal matter or passed through the food chain. Relevant state and federal agencies, industry, and appropriate international partners should develop and implement a focused series of studies to quantify the weathering rates and final fate of chemically dispersed oil droplets in high SPM-concentration regimes compared with non-dispersed oil.
Biodegradation
Past research on the effects of dispersants on the biodegradation of petroleum hydrocarbons cannot be used to predict the fate of chemically dispersed crude oil at sea. The results of many of these studies may be confounded by metabolism of the dispersant or short-term effects of dispersants on bacterial attachment to oil droplets. When dispersed oil plumes become diluted by the transport processes that act in the surface layer of the ocean, however, the surfactants present in the dispersant will partition out of the oil into the surrounding seawater. If this partitioning is fast relative to the kinetics of bacterial attachment to oil droplets, the dispersant may not interfere with microbial uptake of the petroleum hydrocarbons (i.e., the dispersed oil droplets will behave like physically dispersed oil except the oil-water interfacial area will be larger due to entrainment of a larger number of small droplets in the water column). Therefore, future research on the kinetics of dispersed oil biodegradation should be conducted at low oil-water ratios to simulate conditions that represent those that follow significant dilution of the dispersed oil plume. In addition, the experimental designs of laboratory studies that have been used are probably inappropriate for estimating the in-situ biodegradation rate of oil that is floating on the sea surface, because the mixing energies that are typically applied are usually sufficient to result in substantial physical dispersion (i.e., oil droplets continuously break away from the floating slick and are entrained into the aqueous phase due to vigorous mixing) and there is little opportunity for formation of water-in-
oil emulsions, which can dramatically reduce in-situ biodegradation rates. Therefore, the biodegradation rates for chemically dispersed and undispersed oil that have been compared in most laboratory studies are probably skewed in opposite directions relative to their in-situ rates: the biodegradation rates that have been measured in the laboratory for chemically dispersed oil are probably lower than what would prevail in a dispersed oil plume and those measured for undispersed oil are probably higher than could be realized in a floating oil slick that is not subject to a high degree of natural dispersion. Due to the difficulty of designing laboratory-scale experimental systems that adequately simulate the in-situ processes that are expected to affect the biodegradation rate of chemically dispersed oil, future biodegradation studies should be designed to support dispersed oil fate and transport modeling. Ideally, droplet-scale models of biodegradation kinetics should be developed and the appropriate kinetic parameters should be estimated. In general, existing oil biodegradation kinetics data cannot be used to support modeling of biodegradation in dispersed-oil fate and transport models, because one or more important variables (e.g., oil-water interfacial area, microbial population size, hydrocarbon concentrations as a function of time) were not monitored.
Another major limitation for predicting the fate (and effects) of chemically dispersed oil based on available laboratory studies is that few studies have quantitatively investigated the biodegradation rates and products of compounds that are of most long-term concern. These include the high-molecular-weight PAH (e.g., 4- and 5-ring compounds), which are degraded slowly if at all by microorganisms, have the potential to bioaccumulate, and can exert chronic toxic, mutagenic, or developmental effects. Most studies have focused on bulk measurements of oil degradation (e.g., carbon dioxide production or reductions in TPH) or degradation of major components, such as n-alkanes. Although these are important metrics, because they measure the extent of reduction in the total oil mass, they may not be the most important drivers of long-term effects, because normal and branched alkanes are well known to be easily biodegradable by bacteria that are ubiquitous. So, while the rate of degradation of these compounds is of interest from a model mass-balance perspective, their ultimate fate is not in doubt. High-molecular-weight PAH, on the other hand, are likely to persist in the residual oil droplets, which may be ingested by animals in the water column or benthos where they can exert chronic effects. Therefore, the biodegradation kinetics and ultimate biotransformation products of high-molecular-weight PAH should be investigated using indigenous microbial communities from seawater. The ecological impact of these persistent compounds will be determined
by their transport characteristics, which can best be predicted by accurate fate and transport models that include all relevant processes (including biodegradation) and robust estimates of the model parameters.
Present and Possible Role of Models
As discussed previously, various processes constrain a number of operational decisions and play a significant role in evaluating potential impacts of whole and dispersed oil on sensitive species or habitats. Models are, therefore, powerful and necessary tools to support decisionmakers during all phases of oil spill planning, response, and assessment. Currently trajectory analysis is a key component of contingency planning, real-time prediction of slick trajectory, size, and thickness, and in natural resource damage assessment. These models are not currently used in real time to support decisionmaking for dispersant use, but in principle they could be. The required sophistication of the models for these purposes varies, but their performance could be improved for all purposes. Specifically, they are incomplete in terms of their representation of the natural physical process involved, verification of the codes, and validation of the output from these models in an experimental setting or during an actual spill. Thus, their ability to predict the concentrations of dispersed oil and dissolved aromatic hydrocarbons in the water column with sufficient accuracy to aid in spill decisionmaking has yet to be fully determined.
The sensitivity analysis identified that dispersant effectiveness and oil droplet size change are the most important parameters for dispersant application modeling. Unfortunately, oil spill models currently available do not simulate physical mechanisms and chemical reactions in order to predict these parameters. Emulsification is also an important process that greatly influences dispersant effectiveness. Predicting emulsification requires accurate oil properties, as well as conducting a detailed mechanistic investigation on emulsification processes and their influence on dispersant effectiveness. It is also important to evaluate turbulence in the open sea and reflect it more accurately in the transport and fate modeling.
Models show significant progress for supporting real-time spill-response decisions regarding dispersants use, especially in complex nearshore regions; however, any improved models should be evaluated for their ability to satisfy this need. Oil trajectory and fate models used by relevant state and federal agencies to predict the behavior of dispersed oil should be improved, verified, and then validated in an appropriately designed experimental setting or during an actual spill. Specific steps that should be taken to improve the value of models for dispersant use decisionmaking include:
-
Improve the ability to model physical components of dispersed oil behavior (e.g., shear in vertical dimension, distribution of horizontal velocities as a function of depth, variations in the vertical diffusivity as a function of depth, sea-surface turbulence, etc.)
-
Improve the ability for models to predict concentrations of dissolved and dispersed oil, expressed as specific components or pseudocomponents, that can be used to support toxicity analysis
-
Validate how advective transport of entrained oil droplets is modeled through specifically designed flume/tank studies and open-ocean (spill of opportunity) tests.
-
Develop an ability to predict the formation of water-in-oil emulsions under a variety of conditions
-
Conduct a sensitivity analysis based on three-dimensional, oil-component, transport and fate models, and develop necessary databases (evaporation, dissolution, toxicity, etc.) for the oil-component based assessment approach
Once the models are improved, they will be valuable tools for transport and fate modeling and associated biological assessments with and without dispersants. They should be used as part of the overall effort to define operational guidelines for dispersant use, including what oils are dispersible and for how long, the predicted effectiveness of dispersant application (which will be a key input into predicting the dispersed oil concentrations in the water column), likely extent and duration of different oil concentrations of concern, and guidelines for buffers around sensitive resources.
Because this study did not explicitly evaluate the pseudo-components and their dissolved chemical components of the oil in the water column with and without dispersant application, additional sensitivity analyses should be conducted with three-dimensional oil-component transport and fate models. It is also important to develop the necessary database (evaporation, dissolution, toxicity, etc.) for the pseudo-component-based assessment approach. This evaluation focused more on nearshore water, and it is recommended to also conduct sensitivity modeling for offshore, semi-confined waters and rivers. A consensus regarding “how good is good enough” needs to be developed among decisionmakers and model developers, and used to guide the future development of models and to optimize their use in real time.
In discussions with NOAA modelers, it was noted that predicting the three-dimensional flow distribution as a part of the oil transport and fate modeling within several hours after an oil spill is difficult. A real-time model application uses actual environmental conditions and oil properties, but, because of time limitations, uses simple approaches for approxi-
mating hydrodynamic data. To reflect three-dimensional flow and mixing, NOAA is implementing simple schemes to handle vertically varying diffusion and horizontal velocity fields. There have been some attempts to incorporate surface flow measurements into real-time oil transport models (Hodgins et al., 1993; Ojo and Bonner, 2002). However, these require pre-installation of data acquisition (e.g., high frequency radar) and transmission systems, and are currently applicable only to horizontal surface current and diffusion with relatively coarse grid resolution—not for the three-dimensional distributions needed for the three-dimensional modeling (Ojo and Bonner, 2002). The growing availability of ocean observing systems in coastal waters will likely improve the availability of real-time data useful for improved modeling of physical processes. Unlike real-time model applications, a pre-planning assessment uses hypothetical environmental conditions and oil properties, but can use detailed models, including complex three-dimensional flow fields. Thus, real-time and pre-planning modeling efforts should complement each other to provide better information to a decisionmaker.
One of the greatest weaknesses in correlating laboratory-scale and mesoscale experiments with conditions in the open ocean derives from a lack of understanding the turbulence regime in all three systems. Likewise, one of the biggest uncertainties in computer modeling of oil spill behavior (with and without dispersant addition) comes from obtaining appropriate horizontal and vertical diffusivities. It is difficult to integrate all interacting transport and fate processes and oil properties to predict how much oil will be found in specific areas during an actual oil spill without the use of models. Relevant state and federal agencies, industry, and appropriate international partners should develop a coordinated program to obtain needed information about turbulence regimes at a variety of interrelated scales. This effort should include a field program to measure the upper sea-surface turbulence, under a variety of conditions with particular emphasis on quantifying horizontal and vertical diffusivities and the rate of energy dissipation, which can be compared to similar turbulent regimes in mesocosm systems.


























































