6
Atomic Bomb Survivor Studies
INTRODUCTION
The Life Span Study (LSS) cohort consists of about 120,000 survivors of the atomic bombings in Hiroshima and Nagasaki, Japan, in 1945 who have been studied by the Radiation Effects Research Foundation (RERF) and its predecessor, the Atomic Bomb Casualty Commission. The cohort includes both a large proportion of survivors who were within 2.5 km of the hypocenters at the time of the bombings and a similar-sized sample of survivors who were between 3 and 10 km from the hypocenters and whose radiation doses were negligible. The LSS cohort has several features that make it uniquely important as a source of data for developing quantitative estimates of risk from exposure to ionizing radiation. The population is large, not selected because of disease or occupation, has a long follow-up period (1950–2000), and includes both sexes and all ages at exposure, allowing a direct comparison of risks by these factors.
Doses are reasonably well characterized and cover a useful range. Doses are lower than those usually involved in medical therapeutic exposures, but many survivors were exposed at doses that are sufficiently large to estimate risks with reasonable statistical precision. In addition, the cohort includes a large number of survivors exposed at low doses, allowing some direct assessment of effects at these levels. The exposure is a whole-body exposure, which makes it possible to assess risks for specific cancer sites and to compare risks among sites. Because of the use of the Japanese family registration system, mortality data are virtually complete for survivors who remained in Japan. High-quality tumor registries in both Hiroshima and Nagasaki allow the study of site-specific cancer incidence with reasonably reliable diagnostic data. In addition, the LSS cohort is probably less subject to potential bias from confounding than many other exposed cohorts because a primary determinant of dose is distance from the hypocenter, with a steep gradient of dose as a function of distance. Finally, special studies involving subgroups of the LSS have provided clinical data, biological measurements, and information on potential confounders or effect modifiers.
The LSS also has limitations, which are important to consider in using and interpreting results based on this cohort. The subjects were Japanese and exposed under wartime conditions and, in this sense, differ from various populations for which risk estimates are desired. To be included in the study, subjects had to survive the initial effects of the bombings, including the acute effects of radiation exposure, and it is possible that this might have biased the findings. Dose estimates are subject to uncertainty, especially that due to survivor location and shielding. The cohort provides no information on dose-rate effects since all exposure is at high dose rates. Estimates of linear risk coefficients tend to be driven by doses that exceed 0.5 Gy; although estimates based only on survivors with lower doses can be made, their statistical uncertainty is considerably greater than those that include survivors with higher doses. Even at higher doses, data are often inadequate for evaluating risks of cancers at specific sites, especially those that are not common (although, for many site-specific cancers, the LSS provides more information than any other study).
Because of its many advantages, the LSS cohort of A-bomb survivors serves as the single most important source of data for evaluating risks of low-linear energy transfer radiation at low and moderate doses. This chapter describes the LSS cohort and presents findings for leukemia and for solid cancers as a group. The most recent major publications on cancer mortality (Preston and others 2003) and incidence (Preston and others 1994; Thompson and others 1994) are emphasized, but papers addressing special issues such as the shape of the dose-response function are also considered. Results for cancers of specific sites, including results from the three publications just noted, are discussed along with material from various special studies. Risks from in utero exposure are discussed separately. Although cancer is the main late effect that has been demonstrated in the A-bomb survivor studies, several studies have addressed the effects
of radiation exposure on other health outcomes including benign tumors and mortality from causes of death other than cancer. These are discussed at the end of the chapter. In general, the committee has summarized papers on cancer incidence, cancer mortality, and noncancer mortality in the LSS cohort that have been published since BEIR V (NRC 1990).
This chapter is based on published material and does not include results of analyses conducted by the committee, which are described in Chapter 12. At the time of this writing, detailed analyses of mortality data covering the period 1950–1997 and of incidence data covering the period 1958–1987 had been published. The committee’s analyses were based on the most recent DS02 dosimetry system, whereas most of the published analyses described in this chapter were based on the earlier DS86 dosimetry system (see discussion of dosimetry below for further comment). Preston and colleagues (2004) recently evaluated the impact of changes in dosimetry on cancer mortality risk estimates using mortality data through 2000; these results are summarized in the discussion of dosimetry.
DESCRIPTION OF THE COHORT
The full LSS cohort consists of approximately 120,000 persons who were identified at the time of the 1950 census. It includes 93,000 persons who were in Hiroshima or Nagasaki at the time of the bombings and 27,000 subjects who were in the cities at the time of the census but not at the time of the bombings. This latter group has been excluded from most analyses since the early 1970s because of inconsistencies between their mortality rates and those for the remainder of the cohort.
Health End Point Data
Data on health end points are obtained from several sources. Vital status is updated in 3-year cycles through the legally mandated Japanese family registration system in which deaths, births, marriages, and divorces are routinely recorded. This ensures virtually complete ascertainment of death regardless of where individual subjects reside in Japan. Death certificates provide data on the cause of death. The Leukemia Registry has served as a resource for leukemia and related hematological disease (Brill and others 1962; Ichimaru and others 1978). In the 1990s, it became possible to link data from both the Hiroshima and the Nagasaki tumor registries to the LSS cohort, which allows the evaluation of cancer incidence (Mabuchi and others 1994). An advantage of the registry data, in addition to the inclusion of nonfatal cancers, is that diagnostic information is of higher quality than that based on death certificates. Both tumor registries employ active approaches for case ascertainment and provide high-quality data from 1958 onward. Published analyses based on these data cover the period 1958–1987 (Thompson and others 1994). Limitations of the incidence data are that they are not available before 1958 and do not include subjects who have migrated from Hiroshima or Nagasaki.1
The Adult Health Study (AHS) is a resource for data on health end points that require clinical data. The AHS cohort is a 20% subsample of the LSS, oversampled to provide greater representation of subjects in high-dose categories. Since 1958, AHS subjects have been invited to participate in biennial comprehensive health examinations at RERF. The level of participation has been between 70 and 85% for those living in the Hiroshima and Nagasaki areas (Ron and others 1995a).
Dosimetry
Most results presented in this chapter were based on the dosimetry system adopted in 1986 (DS86). The committee’s analyses, described in Chapter 12, are based on the revised DS02 system, adopted in 2004. The DS02 system is the result of a major international effort to reassess and improve survivor dose estimates. This effort was initiated because reports in the early 1990s on thermal neutron activation measured in exposed material (e.g., Straume and others 1992; Shizuma and others 1993) were interpreted as suggesting that the then-current survivor dosimetry system (DS86) might systematically underestimate neutron doses for Hiroshima survivors who were more than about 1 km from the hypocenter. However, the revised estimates of neutron dose do not differ greatly from the DS86 estimates. The new dosimetry system also introduces improved methods for the computation of γ-radiation doses and better adjustments for the effects of external shielding by factory buildings and local terrain features.
Preston and colleagues (2004) analyzed mortality data on solid cancer and on leukemia using both DS86 and DS02 dose estimates. They found that both the risk per sievert for solid cancer and the curvilinear dose-response for leukemia were decreased by about 10% by the dosimetry revision. They also found that parameters quantifying the modifying effects of gender, age at exposure, attained age, and time since exposure were changed very little by the revision.
Table 6-1, based on Preston and colleagues (2003), shows the distribution of survivors in the LSS cohort by their estimated DS86 doses to the colon. The dose to the colon is taken to be the γ-ray absorbed dose to the colon plus the neutron absorbed dose to the colon times a weighting factor 10. This weighted dose is denoted by d, and its unit sieverts;2 such estimates were available for 86,572 survivors. The
TABLE 6-1 Number of Subjects, Solid Cancer Deaths, and Noncancer Disease Deaths by Radiation Dose
|
|
DS86 Weighted Colon Dose (Sv)a |
|||||||
|
Total |
0 (<0.005) |
0.005–0.1 |
0.1–0.2 |
0.2–0.5 |
0.5–1.0 |
1.0–2.0 |
2.0 |
|
|
Number of subjects |
86,572 |
37,458 |
31,650 |
5,732 |
6,332 |
3,299 |
1,613 |
488 |
|
Solid cancer deaths (1950–1997) |
9,335 |
3,833 |
3,277 |
668 |
763 |
438 |
274 |
82 |
|
Noncancer disease deaths (1950–1997) |
31,881 |
13,832 |
11,633 |
2163 |
2,423 |
1,161 |
506 |
163 |
|
aThese categories are defined using the estimated dose to the colon, obtained as the sum of the γ-ray dose to the colon plus 10 times the neutron dose to the colon. SOURCE: Based on data from Preston and others (2003). |
||||||||
37,458 survivors (43%) with doses less than 0.005 Sv were primarily survivors who were located more than 2.5 km from the hypocenter. Only 2101 (2.4%) had doses exceeding 1 Sv. Table 6-1 also shows the number of solid cancer deaths and noncancer disease deaths in the period 1950–1997.
STATISTICAL METHODS
The material in the sections that follow draws heavily on results presented by Thompson and colleagues (1994) and Preston and colleagues (1994, 2003). Here, features of the statistical methods that were used for most analyses in these papers are described. Readers should consult the source papers for details. In nearly all cases, analyses were based on Poisson regression using the AMFIT module of the computer software EPICURE (Preston and others 1991).
Most recent analyses have been based on either excess relative risk (ERR)3 models, in which the excess risk is expressed relative to the background risk, or excess absolute risk (EAR)4 models, in which the excess risk is expressed as the difference in the total risk and the background risk. The age-specific instantaneous risk is given either by
(6-1)
or
(6-2)
where λ denotes the background rate at zero dose and depends on city (c), sex (s), attained age (a), and birth year (b), and the excess may depend on sex (s), age at exposure (e), attained age (a), and time since exposure (t). Not all variables are included in all models; in fact, any two of the variables e, t, and a determine the third. Parametric models are used for the ERR and EAR. The most recent analyses of solid cancer mortality (Preston and others 2003) have been based on models of the form
(6-3)
Earlier analyses (Thompson and others 1994; Pierce and others 1996) were based primarily on ERR models of the form
(6-4)
The function ρ(d) is usually taken to be a linear or linear-quadratic function of dose, although threshold and categorical (nonparametric) models have also been evaluated. With the linear function, ρ(d)=βsd, and βs is the excess relative risk per sievert (ERR/Sv), which provides a convenient summary statistic. The parameters γ and η measure the dependence of the ERR/Sv on age at exposure and attained age.
Preston and colleagues (2003) and Thompson and colleagues (1994) used parametric models for the background risks. Some past analyses, such as those by Pierce and coworkers (1996) treated the background risk in ERR models by including a separate parameter for each category defined by city, sex, age at risk, and year. Thompson and colleagues did not fit EAR models; however, average EARs were estimated by dividing the estimated number of excess cancers by the total person-year-Sv.
Analyses of leukemia are based on bone marrow dose; analyses of the combined category of all solid cancers are based on colon dose; and analyses of site-specific cancers are based on specific organ doses. Dose is expressed in sieverts and is a weighted dose obtained as the sum of the dose of γ-radiation and 10 times the neutron dose. This approach is based on the assumption of a constant relative biological effectiveness (RBE) of 10 for neutrons. In most
analyses, the kerma5 doses are truncated at 4 Gy, equivalent to truncating organ doses at 3 Gy. Analyses by Preston and colleagues (2003) and by Pierce and colleagues (1996) were adjusted for random errors in doses using an approach described by Pierce and colleagues (1990) and based on the assumption of a coefficient of variation of 35% for the error in individual dose estimates. This adjustment generally increases estimated risk coefficients by about 10%. Earlier papers, such as analyses by Thompson and coworkers (1994) and by Preston and coworkers (1994), did not include this adjustment.
For analyses based on tumor registry data, adjustments were necessary to account for migration from the two cities. These are described briefly by Thompson and colleagues (1994) and Preston and colleagues (1994) and in more detail by Sposto and Preston (1992).
Leukemia
This section reviews analyses of mortality data for the period 1950–1990 (Pierce and others 1996) and of incidence data for the period 1958–1987 (Preston and others 1994). Leukemia mortality data for the period 1950–2000 were analyzed by Preston and colleagues (2004) and used to develop the committee’s models for estimating leukemia risks; these analyses are described in Chapter 12.
Leukemia was the first cancer to be linked with radiation exposure in A-bomb survivors (Folley and others 1952) and has the highest relative risk of any cancer. Pierce and colleagues estimated that 78 of 176 (44%) leukemia deaths among survivors with doses exceeding 0.005 Sv were due to radiation exposure. Leukemia risks increased with dose up to about 3 Sv, with evidence of upward curvature; that is, a linear-quadratic function fitted the data significantly better than a linear function. With this linear-quadratic function, the excess risk per unit of dose at 1 Sv was about three times that at 0.1 Sv.
For those exposed under about age 30, nearly all of the excess deaths occurred before 1975, but for those exposed at older ages, the excess risk appeared to persist throughout the follow-up period. The temporal trends also differed by sex, with evidence of a steeper decline in risk for males than for females. Both the nonlinear dose-response and the complex patterns by age and time since exposure mean that simple models cannot adequately summarize leukemia risks.
Preston and colleagues (1994) analyzed data from the leukemia registry. An important recent development in studies of leukemia is the reclassification of leukemia cases by new systems and criteria (Matsuo and others 1988; Tomonaga and others 1991), which allows meaningful analyses of specific types of leukemia. Preston and colleagues evaluated patterns of risk by sex, age at exposure, and time since exposure for four major subtypes of leukemia: acute lymphocytic leukemia (32 cases), acute myelogenous leukemia (103 cases), chronic myelogenous leukemia (57 cases), and adult T-cell leukemia (39 cases). Dose-response relationships were seen for the first three but not for adult T-cell leukemia. The estimated numbers of cases in excess of background were 17.1 for acute lymphocytic leukemia, 29.9 for acute myelogenous leukemia, and 25.9 for chronic myelogenous leukemia. The other major type of leukemia, chronic lymphocytic leukemia, showed no excess, but it is infrequent in Japan.
Results of analyses of all types of leukemia showed dependencies on sex, age at exposure, and time since exposure similar to those for the mortality data and led to a model similar to that based on mortality data. Preston and colleagues note that allowing overall modification by sex and age at exposure in an EAR model did not significantly improve the fit once time since exposure was included in the model, but that these factors significantly modified the time since exposure effects. Specifically, risks for those exposed early in life decreased more rapidly than for those exposed later, and the decrease was less rapid for women than for men. Analyses of specific leukemia types indicated that there were significant differences in the effects of age at exposure and sex and in the temporal pattern of risks. The shape of the dose-response did not show statistically significant differences among the subtypes.
ALL SOLID CANCERS
Analyses of cancers in this category, which excludes leukemia and other hematopoietic cancers, are useful for providing summary information and models based on larger numbers than are available for cancers of specific sites (discussed below). The discussion in this section is based on both mortality (Preston and others 2003) and incidence data (Thompson and others 1994). Mortality analyses were based on 9335 solid cancer deaths that occurred during 1950–1997, whereas incidence analyses included 8613 incidence cases occurring during 1958–1987.6 The incidence data do not include cases of subjects who migrated and were diagnosed with cancer outside of Hiroshima and Nagasaki; as noted above, analyses were adjusted for migration.
Preston and collegues estimate that 8% of the 5502 solid cancer deaths among those with doses exceeding 0.005 Sv were due to radiation, much lower than the corresponding percentage of 44% for leukemia. This percentage was
|
5 |
Kinetic energy released in material. A dosimetric quantity, expressed in grays, that equals the kinetic energy transferred to charged particles per unit mass of irradiated medium when indirectly ionizing (uncharged) particles, such as neutrons, traverse the medium. If all of the kinetic energy is absorbed “locally,” the kerma is equal to the absorbed dose. |
|
6 |
These numbers contrast with 10,127 solid cancer deaths occurring in 1950–2000 and 12,778 incident cases of solid cancer excluding thyroid and nonmelanoma skin cancer occurring in 1958–1998, the periods covered by analyses conducted by the committee and described in Chapter 12. |
slightly higher for the incidence data, where 11% of 4327 cancers in the exposed were estimated to result from radiation exposure (Thompson and others 1994). For both the mortality and the incidence data, risks of solid cancer increased with dose up to about 3 Sv, with little evidence of nonlinearity in the dose-response for doses in the 0–3Sv range. For mortality data, this is illustrated by Figure 6-1, taken from Preston and colleagues (2003). Estimates based on only the low-dose portion of the mortality data are similar to those based on the range from 0 to 2 Sv. For example, there was a statistically significant dose-response (p = .025) based on analyses restricted to the 0–0.125 Sv dose range, with the ERR/Sv estimated to be 0.74 (SE = 0.38). This estimate did not differ significantly (p > .5) from the estimate of 0.54 Sv−1 (SE = 0.07) based on the 0–2 Sv range (Preston and others 2003, Table 4).
Figure 6-2 shows plots of the ERR and EAR for solid cancer mortality by age at exposure and attained age. The ERR for females was about twice that for males, but the EARs were similar for the two sexes since baseline risks for females are about half those for males. Both the ERR and the EAR were found to decrease with increasing age at exposure. The EAR increased with increasing attained age within age-at-exposure groups, while the ERR decreased with increasing attained age, especially for those exposed in childhood. Preston and colleagues emphasize results based on a model that allows the ERR to vary with both age at exposure and attained age, but also pay attention to a model in which the ERR varies only with age at exposure since the evidence for this effect was stronger.
Similar plots based on the committee’s analyses of cancer incidence data are presented in Figures 12-1 and 12-2. These data show similar patterns to those for mortality except that the evidence for modification of the ERR by attained age was stronger with the updated incidence data than with the mortality data.
Preston and colleagues (2003) also present lifetime risk estimates for an LSS cohort member exposed to 1 Sv. These estimates were 18–22% for a person exposed at age 10, 9% for a person exposed at age 30, and 3% for a person exposed at age 50. These estimates did not differ greatly from those based on earlier mortality data (Pierce and others 1996).
Additional Analyses Addressing the Shape of the Dose-Response Function
Several additional papers address the shape of the dose-response function and evidence for risk at the lower end of the dose distribution; these include analyses by Kellerer and Nekolla (1997), Little and Muirhead (1997), Hoel and Li (1998), and Pierce and Preston (2000). These analyses take advantage of the large number of survivors with lower doses and investigate the possibility of a threshold, departures from linearity, and the degree to which effects might be overesti-
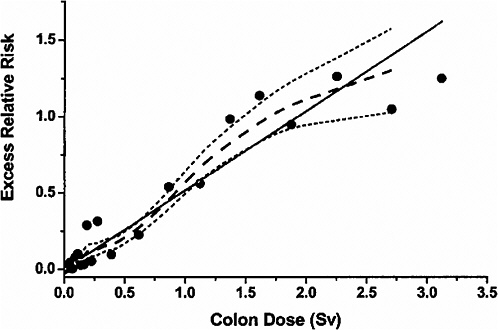
FIGURE 6-1 Solid cancer mortality dose-response function averaged over sex for attained age 70 after exposure at age 30. The solid straight line is the linear slope estimate, the points are dose-category-specific ERR estimates, the dashed curve is a smoothed estimate derived from the points. Dotted curves indicate upper and lower one-standard-error bounds on the smoothed estimate. SOURCE: Reproduced with permission from Preston and others (2003).
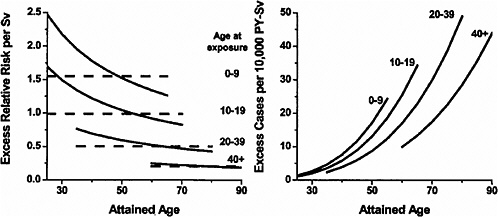
FIGURE 6-2 Primary descriptions of the excess risk of solid cancer mortality. Left panel: fitted sex-averaged ERR estimates using both attained-age-declining (solid black line) and attained-age-constant (dashed lines) forms, for age-at-exposure groups 0–9, 10–19, 20–39, and 40+. ERR estimates for women are about 25% greater, and ERR estimates for men 25% lower, than the values shown. Right panel: fitted EAR estimates for the same dose groups. There is no evidence of significant sex differences in the fitted EAR. SOURCE: Reproduced with permission from Preston and others (2003).
mated based on linear extrapolation from high to low doses. The committee discusses the analyses by Pierce and Preston (2000) because these are the only analyses that include updated cancer incidence data.
Pierce and Preston (2000) investigated solid cancer risks at low doses using cancer incidence data for 1958–1994, thus adding 7 years of data to that available in previously published incidence data analyses. Because experimental data have indicated that the RBE of neutrons decreases with increasing dose, the RBE was assumed to be a function of dose, with a value of 40 at very low doses that decreased to about 8 when the neutron dose reached 0.02 Gy (where the gamma dose was about 2 Gy). Because of evidence that survivors located more than 3000 m from the bombings had higher cancer rates than other survivors estimated to have zero doses, these distally located survivors were omitted from the analyses described below. This exclusion had little effect on analyses based on the full dose range, but did affect analyses directed specifically at low-dose effects.
In analyses based on the range 0–2 Sv, Pierce and Preston (2000) found little evidence of nonlinearity in the dose-response except for a small elevation in risk over linearity in the 0.15–0.3 Sv range. They estimated a curvature parameter θ, defined as the ratio of the quadratic and linear coefficients for gamma dose, and found that the upper 95% confidence limit for θ was 0.75 Gy−1. At this value, the linear coefficient was estimated to be a factor of 1.9 smaller than that obtained from a strictly linear model, and the factor 1.9 (i.e., the dose rate effectiveness factor, DREF) was termed the “overestimation factor.” This result might be interpreted as indicating that the maximum DREF that is reasonably compatible with the A-bomb survivor data is unlikely to be greater than 2. In addition, Pierce and Preston (2000) evaluated threshold models in which the risk was zero up to a given threshold and then increased linearly. They estimated the threshold to be 0 Sv with an upper confidence limit of 0.06 Sv. Evidence of a statistically significant dose-response was found in the dose range 0–0.10 Sv.
Pierce and Preston (2000) warn against overinterpretation of the minimum dose at which evidence of a significant dose-response is found, indicating that “in the presence of available data, it is neither sound statistical interpretation nor prudent risk evaluation to take the view that the risk should be considered as zero in some low-dose range due to lack of statistical significance when restricting attention to that range.” They further call attention to the large potential for bias due to confounding in analyses based on low doses, noting particularly that A-bomb survivor results in the low-dose range are influenced by whether or not distally located survivors are included.
Other Analyses
The A-bomb survivor data have been combined with data from cohorts of persons exposed for medical reasons, primarily for the purpose of further exploration of the modifying effects of age at exposure, attained age, and time since exposure (Little and others 1998, 1999a, 1999c; Little, 1999).
Although these analyses provide valuable information on the comparability of risks and of modifying factors in different cohorts, the results for the A-bomb survivor cohort itself generally confirm the findings reported earlier in the chapter, and they are not discussed further here. Biologically based models have also been applied to the A-bomb survivor data (Kai and others 1997; Pierce and Mendelsohn 1999).
SITE-SPECIFIC CANCERS
Because the exposure of A-bomb survivors was whole-body exposure, studies of the LSS cohort afford the opportunity to compare cancer risks by site. Inferences for site-specific cancers are based on smaller numbers than those for all solid cancers and involve smaller ERRs than leukemia. This often means that there is considerable uncertainty in quantifying risk, in evaluating modifying factors, and even in determining whether or not there is a dose-response relationship. Although it is likely that radiosensitivity varies across sites, it is often not possible to separate true differences from chance fluctuations. Cancers at some sites may fail to exhibit associations because of small numbers of cases and diagnostic misclassification, which is more problematic for mortality data than for incidence data.
Preston and colleagues (2003) used common models for expressing risks for cancers at different sites. Specifically, 15 sites were analyzed with parameters expressing the modifying effects of age at exposure and attained age set equal to those for all solid cancers. Results of these analyses are summarized in Figure 6-3, which shows the ERR/Sv for exposure at age 30 and attained age 70. Except for sex-specific cancers, estimates are averaged for the two sexes. Preston and colleagues (2003) note that the variability in this plot is generally consistent with what would be expected if the true site-specific ERRs were all equal to that for all solid cancers. More detailed analyses of the five most common types of solid cancer (stomach, colon, liver, lung, and female breast) were conducted. With ERR models, the age-time patterns were similar for these sites, although the decrease in risk with attained age was more rapid for colon cancer. With EAR models, statistically significant departures from the solid cancer temporal model were found for lung cancer, which increased more rapidly with attained age than other solid cancers, and breast cancer, which decreased more rapidly with age at exposure than other solid cancers.
Data from the Hiroshima and Nagasaki tumor registries are preferable to mortality data for evaluating site-specific risks. These data have the major advantages of including
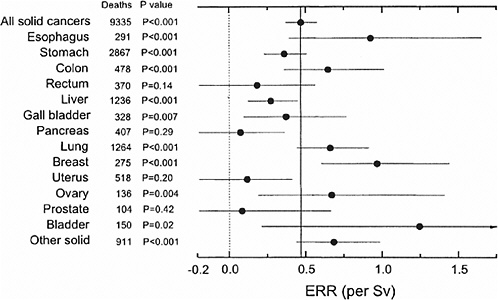
FIGURE 6-3 Estimates of the site-specific solid cancer mortality ERR with 90% confidence intervals and one-sided p-values for testing the hypothesis of no dose-response. Except for sex-specific cancers (breast, ovary, uterus, and prostate) the estimates are averaged over sex. All estimates and p-values are based on a model in which the age-at-exposure and attained-age effects were fixed at the estimates for all solid cancers as a group. The light dotted vertical line at 0.0 corresponds to no excess risk; the dark solid vertical line indicates the sex-averaged risk for all solid cancers. SOURCE: Reproduced with permission from Preston and others (2003).
nonfatal cancers and of more accurate diagnostic information with data on histological types of cancer. Results based on analyses by the committee of updated incidence data (1958–1997) are discussed in Chapter 12.
Thompson and colleagues evaluated cancer incidence data from 1958 to 1987 for the cancer sites shown in Figure 6-4 and Table 6-2. For each site, they evaluated whether there was a significant association with dose, whether there were departures from linearity, and whether risks were modified by city, sex, age at exposure, attained age, or time since exposure.
Of the cancer sites shown in Figure 6-4 and Table 6-2, the largest ERR/Sv was for breast cancer. Relatively large values were also seen for nonmelanoma skin cancer and for cancers of the ovary, urinary bladder, and thyroid. In addition to these sites, the 95% confidence intervals excluded zero for cancers of the stomach, colon, liver, and lung. It should be noted that the size of the ERR/Sv may be affected by the size of the baseline risk. These ERRs/Sv were obtained from a model with no modifying factors and are not strictly comparable to those based on mortality data and shown in Figure 6-3, which included modifying factors and were intended to be applicable to a person exposed at age 30 at attained age 70.

FIGURE 6-4 Excess relative risk at 1.0 Sv (RBE 10) for solid cancer incidence and 95% confidence interval, 1958–1987. SOURCE: Reproduced with permission from Thompson and others (1994).
In addition to analyses by Thompson and colleagues (1994), several papers provide further analyses that, in some cases, give more attention to histological type and, in other cases, are based on case-control studies that include data on possible modifying factors that were not available for the full cohort. These results are summarized below for selected cancer sites.
Female Breast Cancer
In a case-control interview study nested within the LSS cohort and including cases occurring in 1950–1985, Land and colleagues (1994b) investigated known risk factors for breast cancer: age at the time of a first full-term pregnancy, number of children, and cumulative period of breast-feeding. The influence of these factors on breast cancer risks in women in the LSS cohort was similar to that found in other studies. The relationship of these factors and radiation exposure was reasonably well described by a multiplicative model (in which known risk factors for breast cancer do not modify the ERR/Sv), whereas an additive model could be rejected.
Preston and colleagues (2002a) conducted pooled analyses of breast cancer incidence in eight cohorts. Analyses from this paper based on the LSS cohort alone that included cases
TABLE 6-2 Summary of Risk Estimates for Solid Cancer Incidence by Cancer Site or Organ System
|
Cancer Site or Organ System |
Percentage of Total Casesa |
ERR1Sv |
EAR per 10,000 PY-Sv |
AR,b % |
|
Total solid tumors |
100.0 |
0.63 (0.52, 0.74)c |
29.7 (24.7, 34.8) |
11.6 (10.2, 14.3) |
|
Oral cavity and pharynx |
1.5 |
0.29 (−0.09, 0.93) |
0.23 (−0.08, 0.65) |
9.1 (−3.0, 25.9) |
|
Digestive system |
55.7 |
0.38 (0.25, 0.52) |
10.4 (7.0, 14.0) |
7.8 (5.3, 10.6) |
|
Esophagus |
2.1 |
0.28 (−0.21, 1.0) |
0.30 (−0.23, 1.0) |
6.5 (−5.0, 22.5) |
|
Stomach |
30.9 |
0.32 (0.16, 0.50) |
4.8 (2.5, 7.4) |
6.5 (3.5, 10.5) |
|
Colon |
5.3 |
0.72 (0.29, 1.3) |
1.8 (0.74, 3.0) |
14.2 (5.9, 23.9) |
|
Rectum |
4.1 |
0.21 (−0.17, 0.75) |
0.43 (−0.35, 1.5) |
4.4 (−3.6, 14.6) |
|
Liver |
6.8 |
0.49 (0.16, 0.92) |
1.6 (0.54, 2.9) |
10.9 (3.6, 19.4) |
|
Gallbladder |
3.4 |
0.12 (−0.27, 0.72) |
0.18 (−0.41, 1.1) |
2.2 (−5.1, 13.1) |
|
Pancreas |
2.8 |
0.18 (−0.25, 0.82) |
0.24 (−0.36, 1.1) |
3.5 (−5.2, 15.3) |
|
Respiratory system |
11.9 |
0.80 (0.50, 1.2) |
4.4 (2.9, 6.1) |
16.3 (10.6, 22.6) |
|
Trachea, bronchus, and lung |
10.1 |
0.95 (0.60, 1.4) |
4.4 (2.9, 6.0) |
18.9 (12.5, 26.0) |
|
Nonmelanoma skin |
2.0 |
1.0 (0.41, 1.9) |
0.84 (0.40, 1.4) |
24.1 (11.5, 38.6) |
|
Female breast |
6.1 |
1.6 (1.1, 2.2) |
6.7 (4.9, 8.7) |
31.9 (23.2, 41.1) |
|
Uterus |
8.4 |
−0.15 (−0.29, 0.10) |
−1.1 (−2.1, 0.68) |
−3.3 (−6.4, 2.1) |
|
Ovary |
1.5 |
0.99 (0.12, 2.3) |
1.1 (0.15, 2.3) |
17.7 (2.4, 37.3) |
|
Prostate |
1.6 |
0.29 (−0.21, 1.2) |
0.61 (−0.46, 2.2) |
7.0 (−5.3, 25.5) |
|
Urinary organs and kidney |
3.8 |
1.2 (0.62, 2.1) |
2.1 (1.1, 3.2) |
22.3 (11.8, 34.2) |
|
Urinary bladder |
2.4 |
1.0 (0.27, 2.1) |
1.2 (0.34, 2.1) |
16.3 (4.8, 30.1) |
|
Kidney |
0.8 |
0.71 (−0.11, 2.2) |
0.29 (−0.50, 0.79) |
15.2 (−2.6, 41.3) |
|
Nervous system |
1.5 |
0.26 (−0.23, 1.3) |
0.19 (−0.17, 0.81) |
5.7 (−5.3, 24.5) |
|
Thyroid |
2.6 |
1.2 (0.48, 2.1) |
1.6 (0.78, 2.5) |
25.9 (12.4, 40.7) |
|
a254 solid cancers of other and ill-defined sites are included in the total solid tumors category. bAR is the attributable risk, which in this case is the percentage of cases in exposed survivors attributed to radiation exposure. cValues in parentheses are the 95% confidence limits. SOURCE: Thompson and others (1994). |
||||
occurring in the period 1958–1993 showed a clear decline in the ERR/Sv with either age at exposure or attained age when evaluated separately. The EAR was also found to decrease with age at exposure, but to increase with attained age at least up to age 50. These analyses, as well as earlier analyses by Tokunaga and colleagues (1994) and by Thompson and coworkers (1994), found that the dose-response for breast cancer was well described by a linear function. Tokunaga and colleagues (1994) also report a strong attained age effect, with an ERR/Sv of 13 for breast cancer occurring before age 35 compared to an ERR/Sv of about 2 for breast cancer occurring after age 35.
Land and colleagues (2003) reported on an incidence survey of breast cancers diagnosed during 1950–1990. As in previous analyses a strong linear dose-response was found. A modified isotonic regression approach, which required only that the ERR/Sv be monotonic in age, was used to evaluate in detail the modification of the dose-response by age at exposure and attained age. The abstract notes that “exposure before age 20 was associated with higher ERR1Sv compared to exposure at older ages, with no evidence of consistent variation by exposure age under 20. ERR1Sv was observed to decline with increasing attained age, with by far the largest drop around age 35.”
Thyroid Cancer
Like breast cancer, thyroid cancer risks are described well by a linear dose-response function and also show a strong dependence on age at exposure. In fact, there is little evidence of a dose-response for persons exposed in adulthood (Thompson and others 1994; Ron and others 1995a), while the ERRs/Sv for those exposed as children were large (9.5 for persons exposed under age 10, and 3.0 for those exposed at ages 10–19; Thompson and others 1994). Although several other cohorts provide data on thyroid cancer risks from external radiation exposure in childhood (Ron and others 1995a), the LSS cohort is the only cohort providing much information on thyroid cancer risk from external radiation exposure in adulthood.
Salivary Gland Cancer
Because some types of salivary gland tumors are not readily identified by the conventional disease classification codes used by tumor registries, a special evaluation that included pathology reviews of both benign and malignant salivary gland tumors was undertaken by Land and colleagues (1996). This resulted in an estimated ERR/Sv of 3.5 (95% CI
1.5, 7.5) for malignant tumors, higher than any of the ERR/Sv shown in Table 6-2, although very uncertainly estimated. The ERRs/Sv was 0.7 (0.1, 1.7) for benign tumors. Most of the dose-response for malignant tumors resulted from mucoepidermoid carcinoma with an ERR/Sv of 8.3 (2.5, 29.6), whereas most of the dose-response for benign tumors resulted from Warthin’s tumor with an ERR/Sv of 3.1 (0.6, 10.3).
Stomach Cancer
This site merits special comment primarily because stomach cancer is the most common type of cancer in Japan and, specifically, in the LSS cohort. Based on cancer incidence data evaluated by Thompson and colleagues (1994), stomach cancer had a relatively small but precisely estimated ERR/Sv of 0.32 (0.16, 0.50). The ERR/Sv for females was about three times that for males, and the ERR/Sv decreased with increasing age at exposure. Nearly one-third (31%) of the solid cancer cases included in the incidence data were stomach cancers, so this cancer potentially has a strong impact on overall solid cancer results. However, analyses of solid cancer mortality data with stomach cancer excluded resulted in parameter estimates that were similar to those obtained for all solid cancers (Preston and others 2003).
Liver Cancer
Liver cancer is one of the most frequently occurring cancers in Japan and the third most common cancer (after stomach and lung) in the LSS. Liver cancers reported on death certificates might in fact be cancers originating in other organs because the liver is a frequent site for metastatic cancer. This can be a problem even for tumor registry data, since some cases were based only on death certificate information. For this reason, Cologne and colleagues (1999) conducted a study of primary liver cancer based on extensive pathology review of known or suspected cases of liver cancer. This study showed a clear dose-response with an estimated ERR/Sv (with 95% CI) of 0.81 (0.32, 1.43). The ERRs/Sv for males and females were very similar (0.81 and 0.78, respectively), in contrast to findings for many other cancers, and somewhat remarkable given that background rates for males were about three times those for females. The modifying effect of age at exposure was also different from that for other cancers, with excess risk peaking for those exposed in their twenties, but little evidence of excess risk for those exposed under age 10 or over age 45.
Of the 364 cases analyzed, there were 307 hepatocellular carcinomas (HCCs), 53 cholangiocarcinomas, two mixed hepatocellular-cholangiocarcinomas, and one each of hepatoblastoma and hemangiosarcoma. This is in contrast to liver cancers associated with Thorotrast exposure, which are dominated by cholangiocarcinomas and hemangiosarcomas. Cologne and colleagues found no difference in the dose-response for HCC compared to cholangiocarcinoma, although this may have been because the number of cancers of the latter type was small.
It has been estimated that more than 60–75% of HCC cases in Japan are related to chronic hepatitis C infection and that 20–25% are positive for hepatitis B surface antigen (Fujiwara and others 2000). Neriishi and others (1995) reported a radiation dose related increase in the prevalence of hepatitis B surface antigen in atomic bomb survivors. Fujiwara and colleagues (2000) did not find such a relationship for hepatitis C infection, but their data suggest that the radiation dose-response for chronic liver disease was greater for survivors who were positive for hepatitis C antibody than for survivors who were negative.
Lung Cancer
Next to stomach cancer, lung cancer was the most common cancer in the LSS cohort. This cancer showed a strong sex association with the ERR/Sv for females about four times as large as that for males based on the incidence data evaluated by Thompson and colleagues (1994), which probably reflects at least in part the larger baseline risks for males. Lung cancer also deviated from the usual pattern of decreasing risk with increasing age at exposure. Instead, lung cancer risks appeared, if anything, to increase with increasing age at exposure, although, based on the incidence data, this trend was not statistically significant.
Recently, Pierce and coworkers (2003) evaluated the joint effects of smoking and radiation on lung cancer incidence through 1994 in a subset of about 45,000 members of the LSS cohort for whom both radiation dose and smoking data were available. The smoking data were obtained from mail surveys of the LSS cohort and clinical interviews of members of the AHS conducted during 1963–1993. Pierce and colleagues (2003) found that the effects of smoking and radiation were significantly submultiplicative and consistent with an additive model. They note that the aging of the cohort and higher smoking levels among more recent birth cohorts resulted in a stronger basis for evaluating the joint effects of smoking and radiation than in previous analyses by Kopecky and colleagues (1986), Prentice and colleagues (1983), and the National Research Council (NRC 1988); these earlier investigations were unable to distinguish between additive and multiplicative effects. Pierce and colleagues (2003) also found that adjustment for smoking substantially reduced the female-to-male ERR/Sv ratio; about 85% of the men and 16% of the women were smokers. With adjustment for smoking, there was evidence of a decline in the ERR/Sv with increasing attained age (comparable to other solid cancer sites), but no evidence of modification by age at exposure.
Skin Cancer
Ron and colleagues (1998b) conducted a detailed study of skin cancer that included pathologic review of cases. Basal cell carcinoma (80 cases) was found to be associated with
radiation dose with some evidence of nonlinearity in the dose-response, but with no evidence of an interaction with ultraviolet radiation. No dose-response association was found for squamous cell carcinoma (69 cases). The relationships with dose for melanoma (10 cases) and Bowen’s disease (26 cases) were not statistically significant, but estimates of the ERR/Sv were large.
Central Nervous System Cancers
See discussion of central nervous system tumors at the end of the section “Benign Neoplasms.”
Lymphoma
Analyses of mortality data by Pierce and colleagues (1996) showed no evidence of an association for lymphoma; with the mortality data, it was not possible to distinguish between Hodgkin’s and non-Hodgkin’s cases. Lymphoma was not included in more recent mortality analyses. The incidence data included 210 lymphoma cases, of which 22 were Hodgkin’s and 188 were non-Hodgkin’s. A statistically significant dose-response was found for males, but not for females, for whom the estimated ERR/Sv was negative (Preston and others 1994).
Multiple Myeloma
Multiple myeloma exhibited a statistically significant dose-response based on the mortality data (Pierce and others 1996), but incidence data showed little evidence of such an association (Preston and others 1994). The discrepancy in these findings appears to be due to deaths with questionable diagnoses and second primary tumors that were included in the mortality analyses, but not the incidence analyses.
CANCERS RESULTING FROM EXPOSURE IN UTERO
Delongchamp and colleagues (1997) analyzed data on cancer mortality among atomic bomb survivors who were exposed either in utero or, for comparison, during the first 5 years of life. These analyses covered the period 1950–1992, adding an additional 8 years of follow-up to data available to the BEIR V committee (Yoshimoto and others 1988). Analyses were restricted to cancers occurring between the ages of 17 and 45. Ten cancers were observed in the cohort exposed in utero, and a significant dose-response was observed with an estimated ERR/Sv of 2.1 (90% CI 0.2, 6.0). This estimate did not differ significantly from that observed for survivors exposed during the first 5 years of life. An unusual aspect of the finding was that 9 of the 10 cancers occurred in females, and significant differences between the sexes persisted even when the three female cancer sites (breast, ovary, and uterus) were excluded.
BENIGN NEOPLASMS
Studies addressing benign neoplasms have generally been based on either the AHS or the tumor registries. Fujiwara and colleagues (1992) used the AHS to investigate hyperparathyroidism in Hiroshima survivors. About 4000 individuals with DS86 doses were tested for hyperparathyroidism, and a dose-response relationship was found (p < .001). The estimated relative risk at 1 Gy was 4.1 (95% CI 1.7, 14.0), and a decrease in relative risk with increasing age at exposure was suggested. The authors concluded that doses lower than those used in radiotherapy might induce this disorder. Nagataki and colleagues (1994) used Nagasaki AHS data to investigate thyroid diseases in 2587 subjects with diagnoses based on uniform procedures including ultrasonic scanning. Significant dose-response relationships were observed for all solid nodules (females), adenoma, and nodules without histological diagnosis (females). An association was also found for autoimmune hypothyroidism, one of the nonneoplastic end points investigated. However, the dose-response for hypothyroidism was not monotonic; risk increased to about 0.7 Sv and then decreased.
Ron and colleagues (1995b) used data from the Hiroshima and Nagasaki tumor and tissue registries to evaluate benign tumors of the stomach, colon, and rectum for 1958–1989. A total of 470 cases with histologically confirmed benign gastrointestinal tumors (163 stomach, 215 colon, and 92 rectum) were identified. A positive dose-response relationship was observed for stomach tumors, with an estimated ERR/Sv of 0.52 (95% CI 0.01–1.43), similar to that for stomach cancer. There was little evidence of dose-response for either colon or rectal tumors.
Tokunaga and colleagues (1993) investigated proliferative and nonproliferative breast disease using breast tissue samples from 88 high-dose and 225 low-dose autopsy cases of members of the LSS cohort. Both proliferative disease in general and atypical hyperplasia in particular were found to be positively associated with radiation dose, with the strongest association for subjects who were 40–49 years of age at exposure. The authors hypothesized that this finding might be “related to the age dependence of radiation-induced breast cancer, in that potential cancer induced in this age group by radiation exposure may receive too little hormonal promotion to progress to frank cancers.”
Kawamura and colleagues (1997) conducted a study of uterine myoma based on ultrasound examination of 1190 female AHS participants in Hiroshima. The reason for conducting this study was concern that the previously identified dose-response associations (Wong and others 1993), discussed below, might have resulted from bias in case detection. This study resulted in an estimated ERR/Sv of 0.61 (95% CI 0.12, 1.31). It was judged unlikely that bias could explain the association. In earlier analyses by Wong and colleagues, time since exposure was found to be a significant modifier for uterine myoma, with younger survivors show-
ing a decrease with time and older survivors showing an increase with time.
Preston and colleagues (2002b) investigated tumors of the nervous system and pituitary gland based on cases ascertained through the Hiroshima and Nagasaki Tumor and Tissue Registries and through medical records from RERF and major medical institutions in Hiroshima and Nagasaki. Histologic diagnoses were obtained by having four pathologists independently review slides and medical records. The majority of the 228 central nervous system tumors included in the study were benign. A statistically significant dose-response association was observed for all nervous system tumors with an estimated ERR/Sv of 1.2 (95% CI 0.6, 2.1). The ERR/Sv was highest for schwannomas (4.5; 95% CI 1.9, 9.2), but the dose-response for all other central nervous system tumors evaluated as a group was also statistically significant. The dose-responses for all nervous system tumors and for schwannomas were both statistically significant when limited to subjects with doses of less than 1 Sv, and there was no evidence that the slope for this low-dose range was different from that for the full range. Modification of risk by sex, age at exposure, and attained age was also investigated.
NONNEOPLASTIC DISEASE
Findings Based on Mortality Data
A statistically significant dose-response relationship with mortality from nonneoplastic disease in A-bomb survivors was demonstrated by Shimizu and colleagues (1992) based on mortality data for 1950–1985. The addition of five years of mortality data (through 90) strengthened the evidence for this effect and allowed a more detailed evaluation (Shimizu and others 1999). In these analyses, statistically significant associations were seen for the categories of heart disease, stroke, and diseases of the digestive, respiratory, and hematopoietic systems.
Preston and colleagues (2003) updated these results and present analyses of deaths from all causes excluding neoplasms, blood diseases, and external causes such as accidents or suicide. They give considerable attention to the fact that for a few years after the atomic bomb explosions, baseline risks for noncancers in proximal survivors (within 3000 m of the hypocenter) were markedly lower than those in distal survivors. They refer to this as the “healthy survivor effect” and note that it could lead to distortion of the dose-response, particularly in the early years of follow-up. They also note that a small difference (2%) in baseline risks for proximal and distal survivors persisted in later years, which they consider likely to be due to demographic factors such as urban-rural differences. They address this potential source of bias by conducting analyses restricted to the period 1968–1997 and by including an adjustment for differences in proximal and distal survivors (although results without the adjustment are also presented).
The estimated ERR/Sv for noncancers based on a linear model with no dependence on age at exposure or sex was 0.14, generally lower than that for all solid cancers (where the ERR/Sv depends on age and sex). There was no evidence of a statistically significant dependence on either age at exposure or sex, but the data were compatible with effects similar to those estimated for solid cancers. A linear dose-response function fitted the data well, but it was not possible to rule out a pure quadratic model or a model with a threshold as high as 0.5 Sv. Similar to Shimizu and colleagues (1999), significant dose-response relationships were found for heart disease, stroke, respiratory disease, and digestive disease. There was no evidence of radiation effects for infectious diseases or all other noncancer diseases in the group evaluated. Lifetime noncancer risks for people exposed to 1 Sv were estimated to be similar to those for solid cancer for those exposed as adults, and about half those for solid cancer for those exposed as children. Because baseline risks for the noncancer category evaluated are greater than those for all solid cancers, even the relatively small ERR/Sv leads to a fairly large absolute lifetime risk.
Because small ERRs can easily arise from bias, Shimizu and colleagues (1999) evaluated several potential sources of bias, including misclassification of cause of death, confounding, and cohort selection effects. Although Preston and coworkers (2003) discuss cohort selection effects in detail, they did not reevaluate other sources of bias. The committee summarizes the discussion provided by Shimizu and colleagues in the remainder of this section.
With regard to misclassification, they note that Sposto and coworkers (1992) investigated the possibility of bias from this source using mortality data through 1985. These investigators used estimated age-dependent misclassification probabilities obtained from RERF autopsy data to conduct analyses that corrected for misclassification and found that estimates for noncancer mortality were reduced by 20%, but remained highly statistically significant. Shimizu and colleagues (1999) used mail survey and interview data to examine the possible effect of several potential confounders including educational history and smoking. Although most of the factors evaluated were found to affect noncancer mortality, they were not found to be associated strongly with dose. Analyses adjusted for various confounders, based on survivors with available data, resulted in ERRs/Sv that were very similar to the unadjusted values.
Shimizu and colleagues (1999) also evaluated noncancer diseases of the blood, benign neoplasms, and deaths from external causes. Because these categories were not reevaluated by Preston and coworkers (2003), the committee summarizes these findings. The ERR/Sv for the 191 deaths from noncancer diseases of the blood was estimated to be 1.9 (90% CI 1.2, 2.9), larger than the estimated values for most solid cancers. The accuracy of death certificate diagnosis is known
to be poor for this category and likely to include many misclassified leukemias and malignant lymphoma deaths. Among 128 deaths for which additional diagnostic information was available, there were 57 nonneoplastic disease deaths. When these deaths were analyzed separately, the resulting ERR/Sv was 2.0 (90% CI 0.6, 4.4), nearly identical to that based on the full 191 deaths. Analyses suggested that the effect was limited to nonaplastic anemias (29 cases), since the estimate for aplastic anemias (31 cases) was essentially zero. There was also a suggestion of a strong dose-response based on 13 deaths from myelodysplastic syndrome, a neoplastic disease thought to be a precursor of acute myelogenous leukemia.
Although the data evaluated by Shimizu and colleagues (1999) included 379 deaths attributed to benign neoplasms or neoplasms of unspecified nature, only 31 deaths were specifically indicated on the death certificate as being due to benign neoplasms. There was no convincing evidence of a dose-response for these 31 deaths.
With regard to deaths from external causes, suicide rates showed a statistically significant decline with increasing dose, whereas no evidence of a dose-response relationship was found for deaths from other external causes.
Findings Based on the Adult Health Study (AHS) or on Autopsy Data
Wong and colleagues (1993) evaluated the relationship between exposure to radiation and the incidence of 19 nonmalignant disorders using data from the AHS cohort for 1958–1986. They found statistically significant positive dose-response relationships (p < .05) for thyroid disease (p < .001), chronic liver disease and cirrhosis (p = .007), and uterine myoma (p < .001). In addition, myocardial infarction showed a significant dose-response for 1968–1986 among those who were under 40 years of age at exposure (p = .03). Statistically significant relationships were not detected for hypertension, hypertensive heart disease, ischemic heart disease, occlusion and stenosis of precerebral and cerebral arteries, aortic aneurysm, stroke, cataract, gastric ulcer, duodenal ulcer, viral hepatitis, calculus of kidney and ureter, cervical polyp, hyperplasia of prostate, dementia, and Parkinson’s disease. Modification of the ERR/Sv by sex, city, age at exposure, and time since exposure was also investigated for those end points that showed overall associations. Age at exposure was found to be a significant modifier of risk for thyroid disease (decreasing ERR/Sv with increasing age); modifying effects for uterine myoma are discussed above (“Benign Neoplasms”).
Kodama and colleagues (1996) reviewed results of studies addressing noncancer diseases and their relationship to radiation exposure in A-bomb survivors. They also update some of the analyses by Wong and colleagues (1993) to include data through 1990, but do not present nearly as much detail as the latter. They found a statistically significant association for myocardial infarction based on all of the data (p = .02), with an estimated ERR/Sv of 0.17 (95% CI 0.01, 0.36). The association remained significant when analyses were adjusted for various risk factors including blood pressure and cholesterol. Positive dose-response relationships were also found for several other end points of atherosclerosis, which the authors interpreted as supporting a real association between radiation exposure and atherosclerosis. Kodama and colleagues (1996) confirmed previously identified radiation associations for uterine myoma, hyperparathyroidism, and chronic liver disease with an ERR/Gy of 0.46 (0.27, 0.70), 3.1 (0.7, 13), and 0.14 (0.04, 0.27) for the three respective end points.
Wong and colleagues (1999) used AHS data to examine long-term trends in total serum cholesterol levels over the 28 years from 1958 to 1986. Dose-response relationships for the increase in cholesterol levels over time were demonstrated for women in general but only in the youngest birth cohort (1935–1945) for men. Age, body mass index, city, and birth year were considered in the analyses, and some analyses were adjusted for cigarette smoking. These results may partially explain the dose-response relationship for coronary heart disease that has been observed in other studies of atomic bomb survivors.
LIFE SHORTENING
Cologne and Preston (2000) investigated life shortening in the LSS cohort using mortality data through 1995. Although dose-related increases in both cancer and noncancer mortality imply that longevity is also related to dose, earlier papers addressing these effects (Pierce and others 1996; Shimizu and others 1999) did not specifically attempt to quantify the degree of radiation-induced life shortening, an end point that reflects the effects of both cancer and noncancer mortality. The investigation of longevity was undertaken in part because of earlier reports in both the scientific literature and the press that certain atomic bomb survivors had greater-than-average life expectancy.
A clear decrease in median life expectancy with increasing radiation dose was found. Among cohort members with estimated doses between 0.005 and 1.0 Gy, the median loss of life was estimated to be about 2 months, while among cohort members with estimated doses of 1 Gy or more, the median loss of life was estimated to be about 2.6 years. The median loss of life among all cohort members with doses estimated to be greater than zero was about 4 months.
Cologne and Preston (2000) present estimates of life expectancy for groups defined by dose. For those with zero dose, separate estimates are presented for groups defined by distance from the hypocenter, including estimates for those who were not in the city (>10 km from the hypocenter). Although the relative mortality for all nonzero-dose groups compared to the combined in-city, zero-dose group was 1.0 or greater, results for those in the lowest-dose category
(0.005–0.25 Gy) were somewhat dependent on the choice of comparison group. Cohort members in this low-dose category had a median life expectancy that was shorter than that of zero-dose survivors who were within 3 km of the hypocenter (229 d), shorter than the not-in-city group (365 d), but slightly longer (52 d) than survivors located 3 km or more from the hypocenter. These results do not support the hypothesis that life expectancy for atomic bomb survivors exposed at low doses is greater than that for comparable unexposed persons.
SUMMARY
The LSS cohort of survivors of the atomic bombings in Hiroshima and Nagasaki continues to serve as a major source of information for evaluating health risks from exposure to radiation, and particularly for developing quantitative estimates of risk from exposure to ionizing radiation. Its advantages include its large size, the inclusion of both sexes and all ages, a wide range of doses that have been estimated for individual subjects, and high-quality mortality and cancer incidence data. In addition, the whole-body exposures received by this cohort offer the opportunity to assess risks for cancers of a large number of specific sites and to evaluate the comparability of site-specific risks. The full LSS cohort consists of approximately 120,000 persons who were identified at the time of the 1950 census. However, most recent analyses have been restricted to approximately 87,000 survivors who were in the city at the time of the bombings and for whom it is possible to estimate doses. Special studies of subgroups of the LSS have provided clinical data, biological measurements, and information on potential confounders or modifiers.
Mortality data for the period 1950–1997 have been evaluated in detail, adding 12 years to the follow-up period available at the time BEIR V (NRC 1990) was published. The longer follow-up period not only increases statistical precision, but also allows more reliable assessment of the long-term effects of radiation exposure, including modification or risk by attained age and time since exposure. Importantly, cancer incidence data from both the Hiroshima and the Nagasaki tumor registries became available for the first time in the 1990s. These data not only include nonfatal cancers, but also offer diagnostic information that is of higher quality that that based on death certificates, which is especially important for evaluating site-specific cancers. Although published evaluations described in Chapter 6 are based on DS86 dosimetry, a revised DS02 system—the result of a major international effort to reassess and improve survivor dose estimates—has recently become available and was used to develop BEIR VII risk models. An initial evaluation indicates that this revision will slightly reduce risk estimates.
The more extensive data on solid cancer that are now available have allowed more detailed evaluation of several issues pertinent to radiation risk assessment. Several investigators have evaluated the shape of the dose-response, focusing on the large number of survivors with relatively low doses. These analyses have generally confirmed the appropriateness of linear functions to describe the data. The modifying effects of sex, age at exposure, and attained age have also been explored in detail using both ERR and EAR models. The ERR/Sv has been found to decrease with both increasing age at exposure and increasing attained age, and it now appears that both variables may be necessary to provide an adequate description of the data. By contrast, the EAR shows a sharp increase with increasing attained age and a decrease with increasing age at exposure.
The availability of high-quality cancer incidence data has resulted in several analyses and publications addressing specific cancer sites. These analyses often include special pathological review of the cases and sometimes include data on additional variables (e.g., smoking for evaluation of lung cancer risks). Papers focusing on the following cancer sites have been published in the last decade: female breast cancer, thyroid cancer, salivary gland cancer, liver cancer, lung cancer, skin cancer, and central nervous system tumors. Special analyses have also been conducted of cancer mortality in survivors who were exposed either in utero or during the first 5 years of life.
Health end points other than cancer have been linked to radiation exposure in the LSS cohort. Of particular note, a dose-response relationship with mortality from nonneoplastic disease was demonstrated in 1992, and subsequent analyses in 1999 and 2003 have strengthened the evidence for this association. Statistically significant associations were seen for the categories of heart disease, stroke, and diseases of the digestive, respiratory, and hematopoietic systems. The data were inadequate to distinguish between a linear dose-response, a pure quadratic response, or a dose-response with a threshold as high as 0.5 Sv.














