10
Integration of Biology and Epidemiology
INTRODUCTION
Previous chapters of this report have reviewed major elements of experimental and epidemiologic studies relating to the tumorigenic and heritable effects of low-LET (linear energy transfer) ionizing radiation. The development of views on the risks to health from exposure to ionizing radiation depends increasingly upon the establishment of scientific coherence between judgments that stem from knowledge of the biological mechanisms underlying radiation-induced health effects and the direct epidemiologic quantification of such effects. The epidemiologic modeling of radiation-induced health effects for the purposes of risk estimation relies in many cases on biological concepts developed from experimental studies with cultured cells and laboratory animals. This chapter draws together the most important conclusions reached from the reviews of the data. The principal topics considered here are the intimate relationship between cellular responses to DNA damage and health effects; the possible implications of the knowledge of cancer mechanisms for projections of cancer risk over time and the transport of that risk between populations; the shape of the dose-response relationship for cancer risk at low doses; dose and dose-rate effects for cancer risk; the possible implications for cancer risk or other forms of cellular response to radiation; genetic factors in radiation cancer risk; and the heritable effects of radiation.
DNA DAMAGE RESPONSE AND CANCER RISK
Chapters 2 and 3 review the largely cellular and molecular data that strongly support the proposition that chromosomal DNA, the genetic material of the cell, represents the principal target for the deleterious effects of ionizing radiation. In brief, energy deposition from low-LET electron tracks intersecting DNA or its local environment can lead to radical-mediated disruption of covalent bonds in DNA. The cell responds to the presence of such DNA damage in a biochemically complex fashion, but the outcome of greatest importance is the repair or misrepair of critical DNA lesions. Depending on its location, misrepaired DNA damage can lead to the appearance of gene and chromosomal mutations in both somatic (Chapter 2) and germline cells (Chapter 4).
The establishment of an intimate relationship between DNA damage responses, somatic mutation, and cancer development represents one of the most important advances in cancer research during the last decade (Vogelstein and Kinzler 1993; UNSCEAR 2000b). There is good evidence that this relationship applies to a range of human tumor types arising spontaneously or induced by certain environmental carcinogens (UNSCEAR 1993, 2000b).
Epidemiologic studies (Chapters 5–9) show that exposure to low-LET radiation can lead to the age- and time-dependent development of a wide range of tumor types that, in general, are not distinguishable from those arising in nonirradiated populations; studies with experimental animals provide essentially the same message (Chapter 3). Therefore, an initial conclusion would be that the multistage process of cancer development after ionizing radiation is unlikely to be substantially different from that which applies generally (i.e., that the DNA-damaging capacity of radiation is a crucial element in cancer risk). DNA or chromosomal mutations and the heritable effects of radiation are summarized in a subsequent section of this chapter. This initial conclusion receives much support from reviews of data on the links between radiosensitivity and DNA damage response deficiency in humans and mice (Chapters 2 and 3) and findings of candidate radiation-associated mutations in tumors of humans and experimental rodents (Chapter 3). This broad conclusion, while not excluding other mechanistic components of radiation cancer risk, particularly at high doses, underpins many of the judgments summarized below.
PROJECTION OF RISKS OVER TIME
Although the Life Span Study (LSS) cohort (Hiroshima and Nagasaki) has been followed for more than 50 years,
most survivors who were young (under age 20) at the time of the bombings are still alive, and thus their risks at older ages, when baseline risks are greatest, have not yet been studied. This is also true of other exposed cohorts. For leukemia, risks in A-bomb survivors had dropped to negligible levels by the end of the follow-up period (Preston and others 1994; Pierce and others 1996). However, estimating lifetime risks of solid cancer for those who are young at exposure requires assumptions about the time-response patterns of disease. Approaches that have been used in past risk assessments include a multiplicative projection based on the assumption that the excess cancer rate increases in direct proportion to the baseline cancer rate and an additive projection based on the assumption that the excess rate is constant and independent of the background rate. Currently available data on A-bomb survivors and other cohorts make it clear that the additive projection method is not appropriate, and this method has not been used in recent years.
From a biological standpoint, a multiplicative projection of risk implies a mechanism whereby all host and environmental factors that modify the background cancer rate have an equivalent impact on radiation-induced disease. This would be the case if radiation were to act predominantly on an early stage in multistage tumorigenesis (i.e., as a tumor initiator). By contrast, additive projection of risk would apply if radiation acted independently as one of many cancer-modifying factors during postinitiation cellular development (e.g., as a tumor promoter). Cytogenetic and molecular studies on tumorigenic mechanisms in experimental animals (Chapter 3) suggest that acute doses of low-LET radiation act predominantly to initiate tumorigenesis rather than to promote its development. Thus, the monoclonal tumorigenic mechanism of initiation proposed for low-LET radiation is also most consistent with a multiplicative projection of cancer risk. In addition, epidemiologic studies of Japanese A-bomb survivors and of persons exposed for medical reasons indicate that exposure early in life results in greater risks than exposure later in life, which also argues against strong tumor-promoting activity and favors an initiation role.
Although multiplicative risk projection is clearly better supported than additive risk projection, current epidemiologic data indicate that relative risks may decrease with increasing attained age or time since exposure, especially for those who were young at exposure (Thompson and others 1994; Little and others 1998; Preston and others 2002b). Thus, it may not be appropriate to use the multiplicative projection method without modification. Risk assessments conducted by the United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR 2000), the National Institutes of Health (NIH 2003), and this committee have allowed for a decline in relative risk with attained age (see Chapter 12). Because experimental animal data seldom include detailed information on age-specific baseline and radiation-associated cancer, these data do not inform us about a decline in the relative risk with time since exposure or attained age.
Finally, because follow-up is now reasonably complete for all but the youngest A-bomb survivors, there is less uncertainty in projecting risks forward in time than in past risk assessments.
THE TRANSPORT OF CANCER RISK BETWEEN DIFFERENT POPULATIONS
Another important issue in risk assessment is applying risks estimated from studying a particular exposed population to another population that may have different genetic and life-style characteristics and different baseline cancer risks. Specifically, the application of risk estimates developed from Japanese atomic bomb survivors to a U.S. population is a concern. Two approaches that have been used are multiplicative or relative risk transport, in which it is assumed that the risks resulting from radiation exposure are proportional to baseline risks, and additive or absolute risk transport, in which it is assumed that radiation risks (on an absolute scale) do not depend on baseline risk and thus are the same for the United States and Japan. Estimates based on relative and absolute risk transport can differ substantially. For example, baseline risks for stomach cancer are much higher in Japan than in the United States, and for this reason, estimates of stomach cancer risks from radiation exposure from a recent report based on absolute risk transport are nearly an order of magnitude higher than those based on relative risk transport (UNSCEAR 2000).
In general, if the factors that account for the difference in baseline risks act multiplicatively with radiation, then relative risk transport would be appropriate, whereas if they act additively, then absolute risk transport would be appropriate. If some factors act multiplicatively and others additively, the correct estimate might be intermediate to those obtained with the relative or absolute transport models. Whether a factor acts multiplicatively or additively with radiation will depend on whether radiation and the factor of interest act principally as initiators of cancer or act at later stages in multistage cancer development as discussed below.
Two approaches based on epidemiologic data can inform us regarding the most appropriate transport method. The first is to compare risk estimates based on A-bomb survivors with those obtained from studies of non-Japanese populations, particularly predominantly Caucasian populations. If estimates of the excess relative risk (ERR)1 per sievert are comparable, this suggests that relative risk transport may be appropriate, whereas if estimates of the excess
absolute risk (EAR)2 per 104 person-year (PY) per sievert are comparable, this suggests that absolute risk may be appropriate. However, other differences in the populations often confound such comparisons. Most of the relevant exposures occured for medical reasons, were generally protracted, and often were at higher doses than those received by atomic bomb survivors, making it difficult to interpret comparisons. Additional difficulties are dosimetry uncertainties and statistical variation, which is quite large in some studies. Furthermore, although many studies report estimates of the ERR per gray (ERR/Gy), few report estimates of the EAR per gray. Comparisons of estimates from the LSS and medical studies are also discussed in the material below on breast cancer and at the end of Chapter 12 after the BEIR VII risk estimates have been presented.
A second approach based on epidemiologic data is to investigate interactions of various risk factors with radiation. However, there are few studies with available data on both radiation and other risk factors and with sufficient power to distinguish multiplicative and additive interactions. Relevant data are reviewed below. A detailed discussion of interactions is given by UNSCEAR (2000b, Appendix H).
In the sections that follow, the committee first discusses the type of interaction that would be expected based on consideration of whether radiation and other risk factors act primarily as initiators or promoters. Because the correct transport model is not necessarily the same for all cancer sites, this is followed by a discussion of cancers of each of several specific sites. The etiology of each site-specific cancer is discussed briefly, including the role of various risk factors. A discussion of epidemiologic studies that address interactions of radiation and other risk factors then follows.
Although baseline risks for all solid cancers (as a single category) do not differ greatly between the United States and Japan, this occurs because of the canceling out of site-specific cancers that are higher in the United States (including breast, colon, lung, and prostate) and site-specific cancers that are higher in Japan (including stomach and liver). If the correct transport models differ by site, estimates of all solid cancers based on relative and absolute risk transport may not fully reflect the transport uncertainty.
Postirradiation Cancer Mechanisms and Choice of Transport Model
Animal studies (Chapter 3) suggest that low-LET radiation acts principally as an initiator of tumorigenesis and is at best a weak tumor promoter. In addition, for many tumor types, relative risks (ratio of radiation-associated and spontaneous risks) are more comparable across animal strains than are absolute risks (Storer and others 1988). Thus, quantitative animal tumorigenesis data are most consistent with a relative risk transport model, although there are exceptions.
Current knowledge implies the following: (1) at low doses, radiation acts principally as an initiator of cancer (Chapter 3), and (2) many of the known cancer risk factors such as hormonal or reproductive factors, particularly for breast cancer risk, and chronic inflammation associated with microbial infection, for stomach and liver cancers (discussed in this chapter), tend to act at later stages in multistage tumorigenesis. In these latter cases, cancer risk modification is believed to be associated largely with the postinitiation clonal expansion of preneoplastic or malignant cells (Chapter 3). Genetic factors acting throughout cancer development may also modify risk (Chapter 3).
Biologically based risk projection models provide a simplistic, but useful, intuitive framework to evaluate the possible role of radiation in populations with different distributions of risk factors for specific cancer types. An example of such modeling approaches is given in Annex 10A, which summarizes judgments that can be made on the transport of cancer risk using the Moolgavkar and Knudson two stage clonal expansion model, viewing low-LET radiation as a tumor initiator. In simple terms, the model predicts that in the case of a radiogenic tumor type with a strong influence of promoters, one would favor a relative risk transportation model, whereas in the case of a tumor type with a strong influence of initiators, one would favor an absolute risk transportation model.
Etiology of Cancer at Different Sites
As briefly illustrated in Annex 10A, knowledge of the mechanistic factors that underlie tumor etiology can provide an important input to judgments on the most appropriate methodology for transportation of radiation cancer risk between different populations. This section provides an overview of the etiology of a selection of radiogenic human tumors.
Stomach Cancer
Stomach cancer is a disease with a much higher background incidence in Japan than in the United States (IARC 2002). Risk factors for gastric cancer include the presence of conditions such as chronic atrophic gastritis, gastric ulcer, atrophic gastritis, and autoimmune gastritis associated with pernicious anemia. These cause an excessive rate of cell proliferation in the gastric epithelium and are therefore likely to act as promoters, increasing the chance of fixation of replication errors induced by radiation and dietary carcinogens (IARC 2003). Helicobacter pylori infection of the
stomach appears to be a strong risk factor for stomach cancer, and its effect is likely to be mainly through tumor promotion (although there is increasing evidence that it may also cause tumor initiation; Parsonnet and others 1994; Aromaa and others 1996; Goldstone and others 1996). Environmental risk factors include low consumption of fruit and vegetables; consumption of salted, smoked, or poorly preserved foods; and cigarette smoking (Fuchs and Mayer 1995). The majority of these agents are likely to influence the promotion of tumors.
The above considerations would therefore suggest that for stomach cancer, relative risk transport may be better supported than absolute risk transport. This is also supported by a study of predominantly male peptic ulcer patients, where the estimated ERR/Gy based on patients with doses to the stomach of less than 10 Gy (mean 8.2 Gy) was 0.20 (95% CI 0, 0.73), very similar to that based on male A-bomb survivors (Carr and others 2002; see Table 12-2).
Liver Cancer
The incidence of liver cancer (mainly hepatocellular carcinoma) is also much higher in Japan than in the United States (IARC 2002). The main risk factors for this disease are chronic infection with hepatitis B or C virus, dietary exposure to aflatoxins, and chronic alcohol consumption (IARC 2003). Tobacco smoking also plays a role in the etiology of liver cancer (IARC 2004).
Aflatoxins induce mutations in several genes involved in hepatocellular carcinoma and are thus likely to be involved in the early or initiating stages of carcinogenesis. Hepatitis B and C infections and alcohol consumption, on the other hand, are likely to be involved in the promotion of tumors. They are thought to increase the risk of liver cancer through inflammation that may result in liver cirrhosis. The latter is the major clinical determinant of hepatocellular carcinoma, with 70–90% of these tumors developing in patients with macronodular cirrhosis (IARC 2003).
Baseline risks for liver cancer are much higher in Japan than in the United States, and rates of infection with hepatitis B and C undoubtedly contribute to this difference. The mechanistic arguments above and the limited epidemiologic data tend to support the use of the multiplicative transportation model.
Lung Cancer
Lung cancer is the most common cancer worldwide and the major cause of death from cancer, particularly among men (IARC 2003). In the United States, based on SEER (Surveillance, Epidmiology, and End Results) registry data, the annual incidence rates, age-standardized to the world population, were 55.7 and 33.5 per 100,000, respectively, in men and women in 1993–1997. Comparable rates in Hiroshima and Nagasaki during the same period were lower (40–44 per 100,000 in men and 11.8–12.9 per 100,000 in women), particularly among women (IARC 2002).
The major risk factors for lung cancer are tobacco consumption, occupational exposure to a number of carcinogens, and air pollution (Pope and others 2002; IARC 2003). Geographic and temporal differences in lung cancer incidence are determined overwhelmingly by tobacco consumption (IARC 2003).
Tobacco smoke contains approximately 4000 specific chemicals, including nicotine, polycyclic aromatic hydrocarbons, N-nitroso compounds, aromatic amines, benzene, and heavy metals. Lung cancer is not thought to be attributable to any one chemical component, but rather to the effect of a complex mixture of chemicals in tobacco smoke, which may act at different stages of the carcinogenic process. Based on the mechanistic arguments above, this suggests that neither a pure absolute nor a pure relative risk transport model is appropriate.
The estimated ERRs/Gy for lung cancer in several studies involving medical exposures in predominately Caucasian patients are lower than those based on A-bomb survivors (Table 6-3), and this might be interpreted as indicating that absolute risks are more comparable than relative risks. However, the lower ERR estimates may also have resulted from other differences in the study populations, particularly the much higher doses in several of the medical studies.
Pierce and colleagues (2003) evaluated the joint effect of smoking and radiation exposure on lung cancer risks in A-bomb survivors and found that they were significantly submultiplicative and consistent with an additive model. They also demonstrate that inferences about the modifying effects of gender and age at exposure on the ERR/Gy can be distorted if analyses do not account for smoking; this is because smoking habits in the LSS cohort depend strongly on both factors.
By contrast, studies of lung cancer risks in underground miners exposed to radon (NRC 1999) or of Hodgkin’s disease (HD) patients treated with high doses of radiation (Gilbert and others 2003) rejected additive interactions and found that multiplicative interactions were compatible with the data. However, these studies may be less relevant for estimating the risks of low doses of low-LET radiation than those of A-bomb survivors. Underground miners were exposed to α-emitting (high-LET) radon progeny. In addition, the evidence for a multiplicative relation of radiation and smoking comes primarily from analyses of data on miners in Colorado and China, where doses to the lung (in sieverts) were much higher than in the LSS cohort (NRC 1999). Although data on miners were compatible with a multiplicative effect and not with an additive one, the estimated interaction was submultiplicative. HD patients were also exposed to very high doses (mean dose to the lung 25 Gy) and, in addition, were subject to the immunodeficiency
inherent to this lymphoma and associated with the chemotherapy that was also given to many of these patients.
In summary, the absolute risk transport model has greater support for lung cancer than for stomach or liver cancer. Mechanistic considerations suggest that the correct model may be intermediate between relative and absolute risk.
Breast Cancer
Breast cancer is the most common cancer and one of the leading causes of death from cancer among women worldwide, with nearly 1,000,000 new cases per year. Known risk factors for breast cancer include reproductive factors, postmenopausal increased weight, and history of proliferative benign breast disease (IARC 2003). Differences in cancer incidence between U.S. and Japanese populations have been attributed to the tumor promotion effects of hormonal factors (Moolgavkar and others 1980).
In addition, a strong genetic contribution to the risk of spontaneous breast cancer has been shown by the increased cancer incidence among women with a family history of breast cancer. A number of genes involved in DNA damage response pathways, including BRCA1, BRCA2, and less certainly ATM, have been found to confer genetic susceptibility to breast cancer. Alterations in the activity of ATM, BRCA1, and BRCA2 proteins may have far-reaching consequences in the control of genetic stability and the risk of tumor development. The presence of sequence variants that alter either the expression or the function of these genes could therefore influence gene-environment interactions and enhance the increased breast cancer risk in women following radiation exposure (see Chapter 3).
There is no study published on BRCA1 or BRCA2 mutation frequency in the Japanese population. However, since the prevalence of these mutations in relatively large studies of breast and breast-ovarian cancer in Japanese families is similar to that in Europe and North America, it is likely that BRCA1 and BRCA2 mutation frequencies will be the same in Japanese and Caucasians. In Caucasians, the frequency of BRCA1 was estimated to be 0.051% (95% CI 0.021, 0.125) and of BRCA2 0.068% (95% CI 0.033, 0.141; Antoniou and others 2002). Thus, slightly more than one individual in 1000 is a carrier of the BRCA1 or BRCA2 mutation. For ATM there is no information about the frequency of heterozygotes in the Japanese population. However, for ATM and other possible breast cancer genes, as a first approximation it is assumed that there are not major differences in gene frequencies among populations in Japan and Europe or North America.
Thus, in the absence of more detailed data on mutation and polymorphism frequencies in Japan and the United States, the main differences in breast cancer incidence between these two countries are judged to relate to reproductive history and, implicitly, to hormonal factors that would be expected to act as tumor promoters. The above considerations would therefore suggest that the preferred transportation model for breast cancer should be based on a multiplicative model.
The female breast is one of the few cancer sites for which extensive epidemiologic data on predominantly Caucasian populations are available, and this makes it possible to base risk estimates directly on Caucasian data, avoiding the need to transport risks. Nevertheless, it is useful to evaluate what these data tell as about appropriate transportation models.
Land and colleagues (1980) conducted parallel analyses of cancer incidence data in Japanese A-bomb survivors, Massachusetts tuberculosis fluoroscopy patients, and New York women treated with radiation for mastitis, and found that absolute risks were comparable for the three cohorts whereas relative risks were much larger in the Japanese cohort. This was recently confirmed in a pooled analysis of breast cancer incidence in several cohorts by Preston and coworkers (2002a). In this study, models that were similar in form could be used to describe breast cancer incidence in A-bomb survivors and in U.S. women (Massachusetts fluoroscopy patients and the Rochester infant thymus irradiation cohort). The overall ERR/Gy was about three times as large in the Japanese cohort, whereas the EAR/Gy was similar for the LSS and the U.S. cohorts. However, since fluoroscopy exposure is protracted and involves lower-energy photons than A-bomb exposure, these differences in exposures might confound the comparison. Also, in a pooled analysis of breast cancer mortality in Canadian fluoroscopy patients and A-bomb survivors, neither the ERRs nor the EARs were found to differ significantly between the cohorts (Howe and McLaughlin 1996), although the ERR for the combined LSS women was nearly four times that for non-Nova Scotia Canadian women. Little and Boice (1999) and Brenner (1999) provide additional discussion of these issues with a commentary by Ullrich (1999).
In a case-control study of breast cancer among A-bomb survivors, Land and colleagues (1994a) evaluated the interaction of several risk factors for breast cancer with radiation and found that the relationship was better described by a multiplicative model than an additive one. This, together with the etiological and mechanistic considerations above, would seem to favor relative risk transport, in contradiction to the higher ERR/Gy observed in A-bomb survivors and noted in the preceding paragraph; these observations, however, might have come about because of other differences between the Japanese and U.S. cohorts.
In summary, mechanistic considerations and some epidemiologic data support relative risk transport. However, direct use of data on predominantly Caucasian populations results in estimates that are comparable to those based on A-bomb survivors on an absolute risk scale, but not on a relative risk scale.
Thyroid Cancer
Cancer of the thyroid is a rare disease, accounting for only about 1% of cancer cases in developed countries. The incidence is highest in Iceland and Hawaii (IARC 2002). Annual incidence rates in Japan and the United States are similar (of the order of 2–3 per 100,000 among men and 7–10 per 100,000 in women, for rates age-standardized to the world population), and incidence rates have been increasing worldwide in the last decades. Thyroid cancer in childhood is a very rare disease, with an annual incidence of less than one case per million per year in most developed countries.
Thyroid cancer is about three times as frequent in women as in men, suggesting that hormonal factors may play a role in its etiology, although results from epidemiologic studies of reproductive factors are inconsistent. Iodine deficiency is thought to be involved in the development of papillary thyroid cancer, as may the consumption of some cruciferous and goitrogenic vegetables (IARC 2003). Experimental studies have shown that excessive long-term stimulation of the thyroid gland by thyroid-stimulating hormone, such as results from iodine deficiency, can lead to tumor formation with or without addition of a mutagenic agent (Thomas and Williams 1991).
History of goiter and benign thyroid nodules is associated with papillary thyroid cancer risk, as is family history of thyroid cancer; the possible role of increased thyroid screening in these associations is unclear at present. Medullary thyroid carcinoma, a rare type of thyroid cancer, has a very strong genetic component (IARC 2003).
Because the majority of the risk factors listed above (hormones, iodine deficiency) are likely to influence the promotion of tumors, mechanistic considerations suggest that the preferred transportation model for thyroid cancer should be based on relative risk transport. It is noted that the BEIR model for thyroid cancer risk is based on a combined analysis of epidemiologic studies carried out in different countries (U.S., Japan, Israel). The multiplicative model developed by Ron and coworkers (1995b) was applied directly with the uncertainty that reflects international variation in thyroid cancer risk.
Leukemia
Leukemia comprises about 3% of all incident cancers worldwide; the age-standardized incidence in the United States (standardized to the world population), based on SEER registry data, was 10.8 and 6.7 per 100,000, respectively, in men and women during 1993–1997. Rates in Nagasaki prefecture during the same period were similar (9.4 and 6.2 per 100,000, respectively, in men and women), while they were lower in Hiroshima (6.1 and 4.7 per 100,000, respectively; IARC 2002). It should be noted that these rates include chronic lymphocytic leukemia, which is known to be rare in Japan but is more frequent in the United States.
The etiology of leukemia is not well established. Apart from ionizing radiation, occupational exposure to agents such as benzene can increase the risk of leukemia, as can exposure to some chemotherapeutic agents. Some risk factors such as Down’s syndrome and exposure to extremely low frequency magnetic fields have been postulated as risk factors for childhood leukemia. Infection by the HTLV-1 virus is responsible for adult T-cell leukemia, a disease observed in Japan, but rarely in the United States (IARC 2003). Conversely, chronic lymphocytic leukemia, a neoplasm of B lymphocytes, is rare in Japan but more frequent in the United States.
Based on the above, it is not currently possible to draw conclusions about mechanisms of carcinogenesis, and therefore transport models, except to note that the different prevalence of infection with a number of viruses including HTLV-1 and viruses involved in B-cell lymphomas may account for a difference in the incidence of specific leukemia subtypes between Japan and the United States.
Conclusions
At present, neither knowledge of biological mechanisms nor data from epidemiologic studies are sufficient to allow definitive conclusions regarding the appropriate method for transporting risks, although mechanistic considerations suggest somewhat greater support for relative risk than for absolute risk transport. For this reason, the committee provides estimates based on both relative risk and absolute risk transport. When a single estimate is needed, a weighted mean of the two estimates can be used. For cancer sites other than breast, thyroid, and lung, the committee recommends a weight of 0.7 for the estimate obtained using relative risk transport and a weight of 0.3 of the estimate obtained using absolute risk transport with the weighting done on a logarithmic scale. This choice of weights, which clearly involves subjective judgment, was made because the mechanistic considerations discussed above suggest somewhat greater support for relative risk transport, particularly for cancer sites (such as stomach, liver, and female breast) for which known risk factors act mainly on the promotion or progression of tumors. The choice reflects uncertainty regarding which model is correct and also allows for the possibility that some factors interact additively with radiation, whereas others interact multiplicatively. The uncertainty involved in this choice is reflected in the subjective confidence intervals that are provided as discussed in Chapter 12.
Exceptions to the approach noted above are made for cancers of the breast, thyroid, and lung. For breast and thyroid cancer, extensive data on Caucasian populations are available and can be used directly to estimate risks. The committee’s preferred models, which are described in Chapter 12, make use of these data. For lung cancer, analyses of the A-bomb survivor data by Pierce and colleagues (2003)
support an additive interaction of smoking and radiation. Since differences in smoking habits undoubtedly contribute to the differences in baseline risks in Japan and the United States, this finding supports the use of absolute risk transport. Furthermore, lung cancer analyses of A-bomb survivor data based on EAR models may provide a more reliable evaluation of the dependence of radiation risk on factors such as gender and age at exposure than do ERR models, as discussed above. As indicated in Chapter 12, relative risk transport estimates are based on ERR models, whereas absolute risk transport estimates are based on EAR models. Thus, for lung cancer, the weighting scheme used for most other solid cancers is reversed, and a weight of 0.7 is used for the estimate obtained with absolute risk transport and a weight of 0.3 for the estimate obtained with relative risk transport.
For sites other than breast, thyroid, and lung, it is likely that the correct transport model varies by site. However, the committee judged that current knowledge was insufficient to provide separate approaches for other specific sites.
FORM OF THE DOSE-RESPONSE FOR RADIATION TUMORIGENESIS
Follow-up of cancer incidence and mortality in Japanese A-bomb survivors (the LSS study) continues to provide the most informative epidemiologic data on the shape of the dose-response for solid tumors and leukemia (Chapter 6), although studies of large-scale populations with low-dose chronic exposures are increasingly informative about the effects of low doses.
Atomic bomb survivor data for solid tumors combined provide statistical evidence of a radiation-associated excess at doses down to around 100 mSv; these combined data are well described by a linear no-threshold dose-response, although some low-dose nonlinearity is not excluded (Pierce and Preston 2000; Preston and others 2003). Indeed, dose-response relationships for individual tumor types in the LSS can differ, and for nonmelanoma skin cancer the dose response is highly curvilinear with an excess seen only at doses higher than around 500 mSv. The LSS dose-response for leukemia is also clearly curvilinear, with a statistically significant excess being evident at doses around 200 mSv.
The above human data well illustrate the problems of limited statistical power that surround epidemiologically based conclusions on the shape of the low dose-response for radiation cancer risk and how it might vary between tumor types. Similar difficulties surround judgments based on data obtained using experimental animals; many studies are broadly consistent with a linear no-threshold dose response, but there are a number of examples of highly curvilinear, threshold-like relationships (Chapter 3).
It is abundantly clear that direct epidemiologic and animal approaches to low-dose cancer risk are intrinsically limited in their capacity to define possible curvilinearity or dose thresholds for risk in the range 0–100 mSv. For this reason the present report has placed much emphasis on the mechanistic data that can underpin such judgments.
The following data and conclusions are given in Chapters 1, 2, and 3 and are most pertinent to radiation risks in the dose range 0–100 mSv where epidemiologic and animal data are inadequate.
First, there is evidence that most cancers are monoclonal in origin (i.e., they develop from progeny of a single abnormal cell; UNSCEAR 1993). Whatever molecular mechanism is envisaged for radiation, at very low doses (e.g., 0–5 mGy low LET), increases in dose simply increase the probability that a given single cell in the tissue will be intersected by an electron track which will have a nonzero probability of inducing a biological effect. Therefore, at these very low doses, a linearity of response is almost certain (Chapter 3).
Second, given the intimate relationship established between DNA damage response, gene or chromosomal mutations, and cancer development, the form of the dose-response for mutation induction in single cells should be broadly informative for cancer initiation. Data from a large-scale study noted in Chapter 2 suggest a linear relationship between low-LET dose and chromosomal mutation down to around 20 mGy.
A central question addressed in this report is the nature of critical DNA lesions after low-LET radiation and the extent to which they may be repaired by the cell without errors. This is a crucial judgment in radiation tumorigenesis since, at the level of cancer-associated gene or chromosomal mutation, the presence of a true dose threshold demands totally error-free DNA damage response and repair.
The detailed information available on the importance of a chemically complex DNA double-strand break (DSB) induced by a single ionization cluster for postirradiation biological effects (Chapter 1), together with the predominance of error-prone nonhomologous end joining (NHEJ) repair in postirradiation cellular response, argues strongly against a DNA repair-mediated low-dose threshold for cancer initiation (Chapters 1–3). The same data provide a strong counter to pro-threshold arguments based on the relative abundance of spontaneously arising and radiation-induced DNA damage. Those arguments fail to take account of the quality of the repair achievable for simple and complex forms of DNA damage.
In principle, complex DNA DSBs may be repaired with full fidelity by homologous recombination (HR) pathways. Since HR operates almost exclusively between sister chromatids in cells that have newly replicated their DNA (Chapters 1 and 2), the cell has a limited cell cycle window for such error-free repair. At any one time, only a small fraction of stem-like target cells in tissues are expected to reside within this postreplication window—many will be in a nonreplicative, quiescent state (e.g., Potten and Hendry 1997; Kountouras and others 2001; Young 2004). On this basis HR-mediated error-free repair is unlikely to be the
dominant feature of in vivo cellular response and tumor induction.
Finally, evidence is emerging that the DNA deletions that are characteristic molecular footprints of NHEJ-mediated misrepair and gene loss in cultured cells are also seen as early events in radiation-induced tumors in rodents; there is also preliminary evidence pointing toward the involvement of NHEJ misrepair in the genesis of early arising RET gene rearrangements in post-Chernobyl childhood thyroid cancer (Chapter 3).
When considered together, these in vitro and in vivo data are seen to provide a scientifically coherent linkage between error-prone postirradiation repair of chemically complex DNA DSBs in target cells in vivo and tumor induction.
Mechanistic uncertainties remain, but the weight of available evidence would argue against the presence of a low dose threshold for tumor induction based on error-free repair of initial DNA damage. In summary, the committee judges that the balance of scientific evidence at low doses tends to weigh in favor of a simple proportionate relationship between radiation dose and cancer risk.
DOSE AND DOSE-RATE EFFECTS ON TUMOR INDUCTION
Since much of the informative epidemiologic data on low-LET radiation cancer risk derives from the study of acute exposures, it is necessary to make somewhat indirect judgments about the magnitude of the expected reduction in risk associated with low doses and dose protraction. This reduction in risk is conventionally described by the dose and dose-rate effectiveness factor (DDREF). As illustrated and discussed in Chapter 2 (see Figure 2-1), the reduction in risk for low doses (DEF) and the reduction in risk for dose protraction (i.e., low dose rates; DREF) are assumed to be equal; therefore, the term DDREF is used for estimating effects for either low doses or low dose rates.
Information from cellular and molecular studies strongly suggests that dose and dose-rate effects of low-LET radiation are determined largely by the activity of DNA damage response process in cells. For the induction of gene and chromosomal mutations in cultured somatic cells, values for DDREF generally fall in the range of 2–4 (Lloyd and others 1992; Thacker 1992; UNSCEAR 1993, 2000b; Cornforth and others 2002), although higher and lower values have been recorded in some mutation systems. Together, these data are consistent with the view that the temporal abundance of radiation-induced DNA damage is a major factor in the efficiency or fidelity of DNA repair and hence the frequency of induced mutation (Chapter 2).
In vivo effects of dose protraction or fractionation are likely to be more complex, but available data on animal tumorigenesis show that the reduction of tumor yield with dose fractionation is determined by processes that operate on a time scale of up to 24 h. This time scale is more consistent with the activity of cellular DNA repair than with that of postirradiation whole-tissue remodeling, thus drawing together dose-rate effects at the cellular and whole-animal levels (Chapter 3).
Animal tumorigenesis data and related information from life-shortening studies (Chapter 3) may be used to provide judgments on DDREF that vary up to a value of 10 or more (UNSCEAR 1994). However, when those tumor types that, atypically, depend strongly on cell killing are excluded and analysis is restricted to doses up to a few grays, the DDREF values obtained are in the range of 2–3 (Chapter 3). These values are similar to those of gene mutation and, thereby, broadly consistent with the recurring theme of a close association between DNA damage response, mutation induction, and cancer.
The biological picture overall is that cellular and animal data relating to protracted radiation exposures provide a convincing argument for the inclusion of DDREF in judgments about cancer risk at low doses and low dose rates. The animal data showing reduction in carcinogenic effectiveness, including life shortening, following protracted exposure constitute the strongest element in this argument; the coherence of the mechanistic data adds additional weight.
An alternative approach is to estimate DDREF on the basis of the degree of curvature of the dose-response for excess cancer after acute irradiation. Conventional radiobiological theory holds that the initial linear (α) term of a linear-quadratic (αD + βD2) dose-response (where D is the dose) will represent the low-dose and low-dose-rate response. Accordingly, the α and β terms of the acute dose-response may be used to provide an estimate of DDREF. Note that the BEIR V committee did not apply a DREF (sic) in its analysis of solid tumor data and used a linear-quadratic model for leukemia (NRC 1990). Also, the UNSCEAR (2000) committee commented that the LSS data suggested a “value of about 1.5” for the DDREF. In its report, the International Commission on Radiological Protection (ICRP 1990) stated that “the Commission has decided to recommend that for radiation protection purposes the value of 2 be used for the DDREF, recognizing that the choice is somewhat arbitrary and may be conservative.”
The committee has taken a computational approach to the estimation of DDREF that is based on a Bayesian analysis of combined dose-response data. The data sets considered were (1) solid cancer incidence in the LSS cohort of Japanese atomic bomb survivors; (2) cancer and life shortening in animals; and (3) chromosome aberrations in human somatic cells.
Derivation of the Dose and Dose Rate Reduction Factor by Bayesian Analysis
The BEIR VII cancer risk estimates are based on risk models derived primarily from analyses of data on the LSS cohort of Japanese atomic bomb survivors. Historically, and
with the exception of leukemia, there has been little statistical evidence of a need for curvature in the LSS dose-response models and substantial reliance on models in which risk is simply a linear function of radiation dose (Pierce and Preston 2000; Preston and others 2003). There is stronger evidence of curvature from radiobiological considerations and experimental results. The DDREF has been used in the past as a device for allowing risk estimates to conform to this expected curvature but without abandoning the LSS linear models (ICRP 1991; NCRP 1993; EPA 1999; UNSCEAR 2000b; NIH 2003).
A rationale for DDREF is illustrated in Figure 10-1 for a setting that mimics a simple animal experiment on cancer induction by acute-dose low-LET radiation in which risks are observed only at two doses: zero and some particular “high dose.” If the true dose-response relationship is concave up to that dose, as the radiobiological data tend to suggest, then a line connecting the excess risk at high dose to the origin would tend to have a larger slope than a line that approximates the dose-response curve at doses near zero. The DDREF in this case is the ratio of these two slopes (i.e., the risk per unit of dose at high dose divided by the risk per unit of dose at low dose). If this ratio is known then it can be used to convert a risk estimate from the high-dose linear approximation to the more appropriate low-dose linear approximation, as shown in the figure. The association between the form of the dose-response at acute doses and the effects of dose-rate is discussed in Chapter 2 and in Annex 10B.
This DDREF clearly must depend on what is meant by high dose and should not be mistakenly thought of as a universal low-dose correction factor. Furthermore, of particular interest here is what might more appropriately be called an LSS DDREF, where a curvature adjustment to risk estimates from LSS-estimated linear models is based on a wide range of doses. The line analogous to the “high-dose linear approximation” of Figure 10-1 is the one that results from linear model estimation with the LSS data. If a certain degree of curvature is presumed, then it is possible to define an LSS DDREF that correctly adjusts LSS linear risk in order to estimate cancer risk at low doses. Such a definition is provided after the discussion of a numerical characterization of dose-response curvature upon which it is based.
If, over some dose range of interest, the dose-response curve can be approximated by a linear-quadratic (LQ) function, αDose + βDose2, then the slope of the high-dose linear
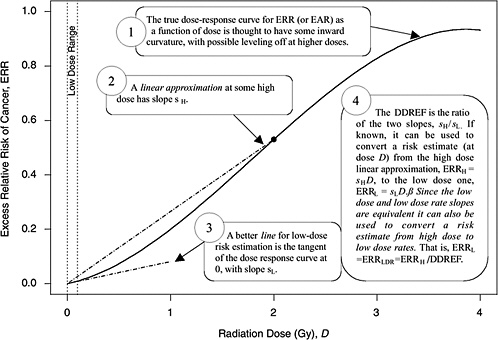
FIGURE 10-1 A hypothetical dose-response curve with a linear approximation for low doses (i.e., the tangent of the curve at dose zero) and a linear approximation based on risk at one particular high dose (i.e., the line that passes through the origin and the true dose-response curve at the high dose), when the high dose is taken to be 2 Gy. The DDREF at this high dose is the larger slope divided by the smaller slope. An explanation of why this low-dose effect also applies to low-dose-rate effects is provided in Chapter 3.
approximation (sH in Figure 10-1) at a particular high dose DH is α + βDH, the slope of the low-dose linear approximation (sL in Figure 10-1) is α, and the DDREF corresponding to DH is their ratio, 1 + (β / α)DH (UNSCEAR 1993). A natural numerical quantity for curvature characterization, therefore, is β / α, which is not tied to any particular high dose. This ratio is referred to here as the LQ “curvature” and is represented by the symbol θ (i.e., the reciprocal of the so-called crossover dose).
If the correct curvature, θ, is known, then an LSS DDREF may be defined through the following steps: an LQ model for ERR or EAR is estimated from the LSS data in such a way that the curvature is constrained to be θ, that is, by fitting the relative risk model αLQ(Dose + θDose2) for fixed θ and with unknown linear component αLQ. A separate linear model is estimated from the same data: αLDose, with linear component αL. The LSS DDREF is the estimate of the ratio of the two linear components, αL / αLQ. The resulting DDREF can be used to convert a risk estimate based on the linear model projection to one based on the linear component of an estimated LQ model with curvature determined by a given choice of the value of θ. Figure 10-2 illustrates the definition for two possible choices of this value.
The two definitions of DDREF as a function of LQ curvature must be clearly distinguished: the fixed high-dose DDREF (or UNSCEAR definition), DDREF = 1 + θ × high dose, and the LSS DDREF defined by the estimation process in the preceding paragraph. The first is a function of θ and some particular high dose. The second is a function of θ and the LSS data. Their relationship, as illustrated in Table 10-1, indicates that the LSS DDREF based on A-bomb survivors with doses of 1.5 Sv or less is roughly equivalent to the fixed high-dose DDREF at an effective high dose of about 1 Sv. In other words, in terms of the familiar UNSCEAR single high-dose definition, one can act as if the nonzero LSS doses were concentrated at a dose of 1 Sv.
Table 10-1 may be used as an aid in interpreting radiobiological evidence for curvature. If, for example, radiobiology data indicate that a DDREF of 2 is appropriate for adjusting risks based on a linear model derived at the single high dose of 2 Sv, then the implicit curvature is 0.5 Sv−1 and the corresponding LSS DDREF is 1.5.
The committee estimates LSS DDREF in this report by combining radiobiological and LSS evidence concerning curvature via a Bayesian statistical analysis and applying the definition of LSS DDREF to the result. As detailed in Annex 10B, the
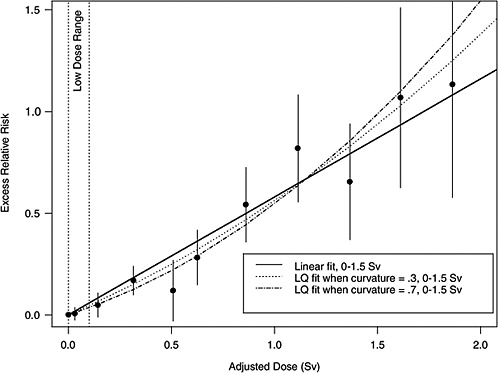
FIGURE 10-2 Illustration of LSS DDREF. Plotted points are the estimated ERRs for solid cancer incidence (averaged over sex, for individuals exposed at age 30 at attained age 60) from LSS subjects in each of 11 dose categories. The vertical lines extend two standard errors above and below the estimates. The solid line is a linear fit to the data for dose range 0–1.5 Sv, with slope αL = 0.56. The other two curves are estimated LQ models for the same dose range, when the curvature, θ, is constrained to be 0.3 Sv−1 (resulting in estimated linear coefficient αLQ = 0.43) and 0.7 Sv−1 (resulting in estimated linear coefficient αLQ = 0.32). The LSS DDREFs that result from these are 0.56 / 0.43 = 1.3 and 0.56 / 0.32 = 1.8, respectively.
TABLE 10-1 UNSCEAR Definition of DDREF and LSS DDREFa Corresponding to Three Values of Curvature
|
UNSCEAR DDREFb |
||||
|
Curvature (θ, Sv−1) |
High Dose = 1Sv |
High Dose = 2Sv |
High Dose = 3Sv |
LSS DDREFc |
|
0.5 |
1.5 |
2.0 |
2.5 |
1.5 |
|
1.0 |
2.0 |
3.0 |
4.0 |
2.1 |
|
2.0 |
3.0 |
5.0 |
7.0 |
3.1 |
|
aFor incidence of solid cancers and based on doses between 0 and 1.5 Sv, as in Figure 10-2. bDDREF = 1 + θ × high dose. cFrom estimating LQ models forced to have curvature θ. |
||||
10B, the radiobiological information comes from mouse experiments, via models estimated from direct cancer risk data and models estimated from cancer-associated life-shortening data. The resulting posterior distribution for possible values of LSS DDREF is displayed in Figure 10-3.
Table 10-2 summarizes the graphical results of Figure 10-3. A single estimate of curvature is the median of the posterior distribution: 0.5 Sv−1, corresponding to an LSS DDREF of 1.5. On the basis of these analyses, there is little disagreement between the radiobiological and LSS estimates of LSS DDREF. While a quadratic term in an LSS LQ model is not significantly different from zero (twosided p-value = .2, for the 0–1.5 Sv dose range), the single best estimate of LSS DDREF from the LSS subset is 1.3. If the radiobiological estimate of 1.5 seems low, the committee believes that it is due not to a new interpretation of radiobiological curvature but rather to the use of an LSS DDREF that is specific to the needs of LSS linear model adjustment to account for the curvature. As evident in Table 10-1, a DDREF suitable for LSS adjustment is less than that expected for low-dose extrapolation of estimates based on high doses of 2 to 3 Sv.
The Bayesian approach formalizes the connection among the DDREF, the LQ curvature in radiobiology, and the LSS data. However, there are two reasons for the continuing uncertainty in the estimation of DDREF: (1) there is substantial inconsistency and imprecision in the data from animal experiments; and (2) the curvature estimates from radiobio-
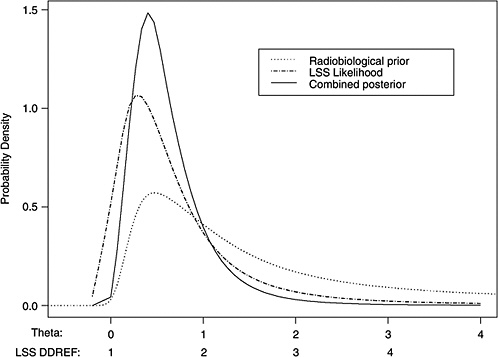
FIGURE 10-3 Results of a Bayesian statistical analysis of dose-response curvature and associated LSS DDREF values. The probability density labeled “radiobiological prior” expresses the belief about curvature deduced from animal data, as detailed in Annex 11B. Regions of high density correspond to more believable values of curvature. The LSS likelihood is the likelihood function of curvature θ from the data displayed in Figure 10-2. The “combined” density is the Bayesian posterior obtained by updating the radiobiological density to account for information from the LSS data. The scale below the plot shows the implied values of LSS DDREFs corresponding to the θ scale. NOTE: The committee judges it preferable to choose a cutoff dose that lies within the lower rather the higher portion of the possible range.
TABLE 10-2 Maximum Likelihood Estimates of Curvature and Corresponding Estimates of LSS DDREFa and the Posterior Median from the Bayesian Analysis that Combines the Two
logical data and from LSS data are sensitive to the range of doses used for estimation.
As shown in Annex 10B and evident in Figure 10B-1, there is a statistically significant difference in curvatures for the different mouse strains, sex, and cancer outcome combinations investigated (p-value < .001). Some results indicate large curvature, some no curvature, and some curvature in the opposite direction. The combined effect is weak evidence for small curvature. Because of the wide variability, the analysis is sensitive to the particular studies chosen and the approach for estimating a curvature that is presumed to be constant across studies.
The numerical results also are not robust because of the somewhat arbitrary choice in dose range subset for estimating linear-quadratic models, both from animal experiments and from LSS data. If the LQ model is fitted to a dose range that includes doses at which leveling off of the dose-response curve has occurred (as illustrated in Figure 10-1), the result will be biased for the intended purpose. If the dose range is too low, meaning it excludes doses for which the LQ approximation is still good, the estimates will be less precise than what is possible but will not lead to any bias. Given these consequences, it is judged preferable to choose a cutoff dose that is too low rather than one that is too high. The cutoffs of 1.5–2 Gy for animal experiments and 1.5 Sv for LSS data were chosen subjectively, based on the belief that these were sufficiently low that leveling off is not of great concern. Nevertheless, the fact remains that the relationships shown in Figure 10-3 would be quite different if different dose ranges were used.
The cutoff of 1.5 Sv for the LSS data is important for assessing curvature. The resulting LSS DDREF is appropriate for adjusting risks from linear models based on the same dose range. Since the LSS estimated linear model is insensitive to the choice of subset however, the particular choice of dose range upon which to estimate the linear model is not critical.
More generally, since a linear model fits the LSS data over the entire range (for cancers other than leukemia), it is important to question why the expected curvature fails to materialize and whether the absence of curvature necessarily implies that the LSS low-dose slope is too large. It could be that a linear relationship is the result of some cancelation of inward curvature and high-dose leveling-off. It is not obvious that the linear relationship resulting from such cancelation overestimates low-dose risk.
Given these unresolved issues, it is comforting that the estimate of LSS DDREF is consistent with the best-fitting LQ model based on LSS data alone; that is, low-dose risk estimates based on LSS linear models with DDREF adjustment will be essentially the same as risk estimates based on the best-fitting LQ model from LSS data over the range 0 to 1.5 Sv. In Figure 10-2, for example, it is clear that the linear component of an LQ curve with curvature 0.5 Sv−1 over the low-dose range is consistent with the data. The difference between that estimate and one based on the unadjusted linear model will be small relative to the size of the associated confidence interval.
The DDREF analysis has used LSS data on solid cancer incidence. A recent similar analysis on cancer mortality (Preston and others 2004) has provided the somewhat larger estimated curvature 0.94 Sv−1 (90% CI 0.16, 8.4) for the best-fitting LQ model over the range 0 to 2 Sv. Since there is considerable imprecision in the calculations, this result is not inconsistent with the committee’s conclusions.
In summary, the approach used by the committee to make an analytical judgment about the value of DDREF has employed a combined Bayesian analysis of dose-response curvature for cancer risk using animal radiobiological data and human evidence from the LSS. The committee found a believable range of DDREF values for adjusting linear risk estimates from the LSS cohort to be 1.1–2.3. Based on this analysis, the committee elected to use the value of 1.5 for solid tumors; also, a linear-quadratic model was used for leukemia. The committee recognizes the limitations of the data and the uncertainties in estimating the DDREF.
OTHER FORMS OF CELLULAR AND ANIMAL RESPONSE TO RADIATION
This report has given much attention to biological responses to radiation that, although not well understood, may influence the development of views on tumorigenic mechanisms and the modeling of epidemiologic data.
Adaptive Responses
Adaptive responses to radiation are represented in a range of studies that purport to demonstrate that a low priming dose of radiation can influence the subsequent response of cells or experimental animals to subsequent challenge by a second higher dose. It is claimed by some that these adaptive
responses will reduce low-dose cancer risk substantially, perhaps to zero, or even be beneficial to health (see Calabrese and Baldwin 2003 and references therein).
Cellular data and mechanistic considerations on adaptive responses are reviewed in Chapter 2. From this review it is concluded that adaptive responses are not expressed robustly in cells and that a mechanistic basis for the phenomena, particularly in the form of well-characterized DNA damage response, has yet to be established. This situation may be contrasted with the detailed knowledge that has accrued on many other aspects of DNA damage recognition or repair and cellular response (see Chapters 1 and 2). Accordingly, cellular and mechanistic data on adaptive responses are as yet insufficient to develop specific judgments on the fundamental aspects of low-dose cancer risk.
Recent animal studies on adaptive responses to radiation and cancer risk are considered in Chapter 3. These studies provide some evidence that under certain conditions, a low priming dose of radiation can modestly influence the rate of development of certain tumors. However this response is not accompanied by a reduction of overall lifetime cancer risk. Uncertainties remain about the specific conditions of irradiation under which this form of adaptive response is expressed, and its mechanistic basis is a matter of speculation. Accordingly, these animal data, although of considerable scientific interest, are not sufficiently well developed to influence the modeling and interpretation of epidemiologic data.
Induced Genomic Instability
Induced genomic instability is a term used to describe a set of cellular phenomena whereby radiation exposure alters the state of a cell in a way that generally leads to a persistent elevation of mutation rate over many cell generations. The cellular data reviewed in Chapter 2 highlight the inconsistent mode of expression of this phenomenon and the current lack of information on the cellular mechanisms that might be involved. It is notable that many of these data sets relate to cells established in culture for many years. Despite these problems of interpretation, there has been speculation that radiation-induced genomic instability might make a significant contribution to cancer induction in vivo and thereby confound the interpretation of epidemiologic data. Chapter 3 considers the in vivo expression of radiation-induced genomic instability, possible mechanistic links with cancer induction in animal models, and the expression of such instability in radiation-associated human tumors. Although some uncertainty remains, these in vivo data strongly question the proposition that radiation-induced, genome-wide instability plays a major role in radiation tumorigenesis. One possible exception to this is the instability of altered telomeric sequences at chromosome termini that may trigger ongoing cycles of chromosomal associations and rearrangement (Chapters 2 and 3). However, given the great uncertainty about the contribution of induced and persistent genomic instability to postirradiation tumor development, there is at present no meaningful way in which the phenomenon can be included in the general interpretation of epidemiologic data and, thereby, the derivation of new estimates of low-LET cancer risk.
Bystander Cellular Effects
Chapter 2 details the almost exclusively cellular data for high-LET radiation, indicating that cellular damage response signals may be passed from an irradiated cell to a nonirradiated neighbor. There are few consistent data sets for low-dose, low-LET radiation. The stress-related mechanisms that have been suggested to underlie postirradiation signal transfer via cellular gap junctions or cell culture medium are not well understood. In addition, the in vivo expression of bystander effects and their impact on tumor development have yet to be adequately addressed. For these reasons, the committee judges that current knowledge of these phenomena is insufficient for the purpose of interpreting epidemiologic data and developing judgments on cancer risks at low doses of low-LET radiation.
GENETIC SUSCEPTIBILITY TO CANCER
The data reviewed in Chapters 1 and 3 provide coherent evidence from cellular, animal, and clinical or epidemiologic studies that inheritance of certain germline gene mutations can predispose to radiation-induced cancer. The qualitative linkage between such epidemiologic or clinical and experimental data are particularly strong for rare, strongly expressing human mutations. However, with current knowledge, experimental data cannot quantitatively inform about the magnitude of the increased radiation risk in such genetic disorders. Accordingly, only broad judgments are possible—principally that strongly expressing human mutations of relevance to radiation cancer risk are too rare to an appreciably distort population-based estimates of low-dose risk as derived from epidemiologic data (Chapter 3).
The implication for population risk of weakly expressing but potentially common variant genes is a most difficult issue. Genetic studies with mice (Chapter 3) provide evidence of the potential complexity of germline gene-gene interactions in radiation tumorigenesis. However, human molecular epidemiologic studies in this area are at a very early stage of development, and no specific judgments are possible on the extent to which common genetic variation influences epidemiologic measures of radiation risk. The general judgment made in Chapter 3 is that the potential impact of such variant genes on radiation cancer risk in the population will depend on a complex interplay between their frequency in the population, their tissue specificity, and the strengths of the gene-gene and gene-radiation interactions that may apply.
HERITABLE EFFECTS OF RADIATION
As in the BEIR V report (NRC 1990), estimates of the risks of adverse heritable effects of radiation exposure are made indirectly through extrapolation from mouse data on rates of radiation-induced germ cell mutations using population genetic theory and a set of plausible assumptions (see Chapter 4). These estimates are expressed as increases in the frequencies of genetic diseases relative to their baseline frequencies in the population. The method that is used for this purpose is referred to as the “doubling dose method.” Equation (10-1) below summarizes the method:
(10-1)
where P is the baseline frequency of the disease class under consideration, DD is the doubling dose (i.e., the dose of radiation required to double the rate of spontaneous mutation in a generation, estimated as a ratio of rates of spontaneous and induced mutations in defined genes), MC is the mutation component (a measure of the responsiveness of the disease class to an increase in mutation rate), and PRCF is the potential recoverability correction factor (the fraction of induced mutations that are compatible with live births and cause disease).
This report incorporates several important advances that have been made since the publication of BEIR V (NRC 1990), among which are those that relate to the four quantities mentioned above. It suffices to note that the estimates for P, MC, and PRCF are different for Mendelian and multifactorial diseases; however, the DD estimate of 1 Gy (for low-dose or chronic low-LET exposure) is common to both classes of disease.
The risk estimates provided in Chapter 4 are about 3000 to 4700 cases of excess genetic disease per million first-generation progeny per gray of radiation to the parental generation. Compared to the natural (i.e., baseline) risk of genetic diseases of 738,000 per million live births in the population, the radiation risk (per gray) is very low (about 0.4 to 0.6% of the baseline).
As mentioned earlier, the results of the extensive genetic epidemiologic studies of A-bomb survivors in Japan have shown no adverse effects in the progeny that could be attributed to the radiation exposures (of the order of 0.4 Sv) sustained by most survivors. The indicators of adverse effects used in these studies were untoward pregnancy outcomes (UPOs), mortality of live born children through a period of about 26 years (exclusive of those resulting from malignant tumors), malignancies in the F1 children, frequency of balanced structural rearrangements of chromosomes, frequency of sex chromosomal aneuploids, frequency of mutations affecting protein charge or function, sex ratio shift among children of exposed mothers, and growth and development of F1 children. The important point here is that these indicators of adverse effects cannot be compared readily to what are formally called genetic diseases.
The total numbers of children included in the analyses to ascertain radiation effects were about 41,000 in the “unexposed” and 31,000 in the “exposed” groups, although the numbers were different for different indicators (e.g., ~8000 children each in the exposed and control groups for balanced structural chromosomal rearrangements and sex chromosomal aneuploidy; ~41,000 in the exposed and ~31,000 in the exposed groups for malignancies in F1).
Although no statistically significant effects of parental radiation exposures were found, Neel and colleagues (1990) estimated doubling doses on the basis of data for five of the indicators (i.e., UPO, F1 mortality, F1 cancers, sex chromosomal aneuploids, mutations) that would be consistent with the findings. In order to do this, several assumptions had to be made (discussed in Annex 4G). The oft-quoted DD estimated from these data, corrected for low-dose or chronic, low-LET radiation conditions is 3.4 to 4.5 Sv.
The perception remains that the above estimate of the DD is indicative of far lower heritable risk than that implied by the DD of 1 Gy used by the present BEIR committee and UNSCEAR (2001; since 1/DD, the relative mutation risk per unit dose, is a smaller fraction with the Japanese DD). It should be stressed that comparison of the DDs alone does not present the correct picture of risks for the following reasons: (1) the Japanese DDs are estimated retrospectively from empirical observations using measures of genetic ill health that are totally different from those used by this committee; besides, these measures have not shown any significant differences between the control and radiated groups; and (2) the DD of 1 Gy used by the present committee (and by UNSCEAR 2001) is based on data on mutations in defined genes and is used prospectively as one of the four factors in predicting the risk of genetic diseases. Nonetheless, the principal message that emerges from the Japanese epidemiologic studies and the present risk estimates projected from mouse data on radiation-induced mutations is the same—namely, that at low or chronic doses of low-LET irradiation, the genetic risks are very small compared to the baseline risk in the population.
SUMMARY
The principal objective of this chapter is to highlight the ways in which cellular, molecular, and animal data considered in this report may be integrated with epidemiologic findings in order to develop coherent judgments on the health effects of low-LET radiation. Emphasis is placed on data integration for the purposes of modeling these health risks.
The principal conclusions from this work can be summarized as follows:
-
Current knowledge of the cellular or molecular mechanisms of radiation tumorigenesis tends to support the appli-
-
cation of models that incorporate the ERR projection over time.
-
The choice of models for the transport of cancer risk from Japanese A-bomb survivors to the U.S. population is influenced by mechanistic knowledge and information on the etiology of different cancer types. Where specific epidemiologic evidence is lacking, the committee recommends that the weights attaching to relative and absolute risk transport should be 0.7 and 0.3, respectively.
-
A combined Bayesian analysis of A-bomb epidemiologic information and experimental data has been employed to provide an estimate of the DDREF for cancer risk. The committee found a believable range of DDREF values to be 1.1 to 2.3 and uses a median value of 1.5 to estimate solid cancer risks.
-
Knowledge of adaptive responses that may act to reduce radiation cancer risk was judged to be insufficient to be incorporated in a meaningful way into the modeling of epidemiologic data. The same judgment is made in respect of the possible contribution to cancer risk of postirradiation genomic instability and bystander signaling effects.
-
Genetic variation in the population is a potentially important factor in the estimation of radiation cancer risk. Strongly expressing cancer-predisposing mutations are judged from modeling studies to be too rare to distort population-based estimates of risk appreciably but are a significant issue in some medical irradiation settings. The position regarding potentially more common variant genes that express only weakly remains uncertain.
-
The estimation of the heritable effects of radiation by the committee takes advantage of new information on human genetic disease and on mechanisms of radiation-induced germline mutations. The application of a new approach to genetic risk estimation leads the committee to conclude that low-dose induced genetic risks are very small compared to baseline risks in the population.
-
The committee judges that the balance of evidence from epidemiologic, animal, and mechanistic studies tends to favor a simple proportionate relationship at low doses between radiation dose and cancer risk. Uncertainties in this judgment are recognized and noted.
ANNEX 10A: APPLICATION OF THE MOOLGAVKAR AND KNUDSON TWO-STAGE CLONAL EXPANSION MODEL TO THE TRANSPORT OF RADIATION CANCER RISK
In the case of tumors whose background incidence is strongly influenced by initiating factors, one would expect the EAR to be directly transportable from one population to another. If one considers, for example, the Moolgavkar and Knudson two-stage clonal expansion model (Moolgavkar and Knudson 1981; Moolgavkar and Luebeck 1990) shown in Figure 10A-1, the hazard function h(t) at time t is given approximately by the following formula:
where μ(t) and ν(t) denote, respectively, the first and second mutation rates at time t; α(t) is the rate of division of intermediate (or initiated) cells; and β(t) is the rate of death or differentiation of intermediate cells at time t.
If ionizing radiation and the other main risk factors for the tumor of interest are predominantly cancer initiators, their effect would be modeled additively on the first mutation rate μ, as follows:
The resulting relative risk would then be of the form:
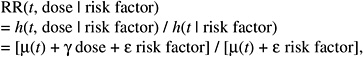
while the absolute risk (AR) would be of the form:
According to this formulation, the effect of radiation would tend to be independent of the other risk factors on the AR scale. The AR per sievert could therefore be transported from one population to another.
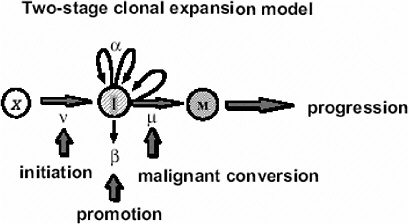
FIGURE 10A-1 The two-stage clonal expansion model. SOURCE: Luebeck and others (1999).
If, on the contrary, the background incidence of a given tumor type is heavily influenced by host or environmental promoting factors (e.g., breast cancer, stomach cancer), the effects of these factors can be thought to affect the expansion (increasing α to a value αr, decreasing β to βr, or both) of the clone of initiated or transformed cells and, thus, the expression of tumors. The resulting relative risk would then be of the form:
This formulation is independent of the magnitude of the effect of promoting factors on the cell division and mortality rates αr and βr. Hence the ERR can be exported directly from one population to another.
Expressed in simple terms, low-LET radiation (viewed here as a tumor initiator) will tend to act additively with other tumor initiators and multiplicatively with tumor promoters. Thus, in the case of a radiogenic tumor type with a strong influence of promoters (e.g., stomach cancer), one would favor an RR transportation model, while in the case of a tumor with strong influence of initiators, one would favor an AR transportation model.
The preceding formulations are consistent with more general analyses of the nature of risk relationships involving exposure to two carcinogens (Kodell and others 1991; Zielinski and others 2001).
ANNEX 10B: EVIDENCE FOR THE CONNECTION BETWEEN DOSE EFFECTS AND DOSE-RATE EFFECTS IN ANIMAL EXPERIMENTS
First consider fractionated acute exposures. If the relative risk due to the sum of K acute exposures of equal dose, D / K, administered at separate times, is the sum of the individual relative risks, and if an LQ dose-response model describes the effects at each fraction, then the total relative risk due to all K exposures is
Thus, for a given total dose D, the importance of the quadratic term diminishes with increasing number of fractions of exposure. The RR due to a protracted exposure may be thought of, at least approximately, as the limit as K approaches infinity. In this way, the total RR due to a protracted exposure is simply αD, where α is the linear coefficient in the LQ model. Therefore, if a risk estimate corresponding to a protracted exposure D is based on an LSS linear model, it should be adjusted to correspond to the linear component of the estimated LQ model, which is exactly what the DDREF presented in this chapter is designed to do.
Figure 10B-1 shows data from mouse experiments that fitted to the model above (data from Table 6 of Edwards 1992). These data show that the slope in the linear dose-response for chronic exposure approximates the linear component of the LQ model for acute exposure.
Details of DDREF Estimation
An LQ model for ERR or EAR, with curvature constrained to be θ, may be written as αLQ[Dose + θDose2]. A Bayesian statistical analysis is used to update information about dose-response curvature from animal carcinogenesis studies with the information concerning curvature from the LSS cohort of Japanese A-bomb survivors (over the dose range 0–1.5 Sv). A posterior distribution for LSS DDREF follows directly from this, via its definition as a function of θ. The LSS DDREF is essentially 1 + θ for the 0–1.5 Sv dose range and for values of θ of interest here. Pierce and Vaeth (1991) provide a more detailed discussion of this relationship over different dose ranges.
Two forms of animal experiment data were used to estimate curvature: estimated cancer risks and mean survival times (referred to as life-shortening data). These are two different summarizing results from the same experiments, so they are not independent but address the curvature in different ways. LQ models for risk as a function of dose can be estimated for each separate cancer and combined to form a single estimate of curvature, θ. On the other hand, the life-shortening studies ignore cause of death and therefore represent a cumulative effect of all radiation-induced deaths, the majority of which are cancer related. By using the relationship between survival rate and risk, the curvature of interest can be estimated from these, as detailed below.
The estimated risks of relevant cancers, plotted versus radiation dose in Figure 10B-2, were extracted from the summary tables of Edwards (1992), but exclude (1) the results in Tables 1 and 2 because those risk estimates were not adjusted for competing causes of death; (2) results for doses greater than 2 Gy; and (3) results on lymphomas, ovarian cancer, reticulum cell carcinoma, and nonmyeloid leukemias, because these are thought to arise via atypical biological mechanisms, as discussed in Chapter 3, or to reflect an ill-defined combination of cancer types. The risks presented here are based on acute exposures only.
There is substantial evidence that the curvature, θ, is not the same in all 11 situations (p-value < .0001, from a likelihood ratio test). Despite this evidence, the model with common curvature explains 97% of the variability and the model with different curvatures explains 98% of the variability in estimated risks, so the practical significance of the different curvatures may not be too important. Note in Figure 10B-2 that although the LQ curves seem to be highly divergent, the
FIGURE 10B-1 Risks of lung cancer versus dose from experiments in which doses were administered fractionally or chronically. Each plotted point corresponds to an estimated risk from one experiment. The plotting symbol shows the number of fractions (number of separate acute exposures) or “C” if the administration was chronic. The curves show an estimated LQ model for risk from dose D administered in K fractions, αD + βD2 / K, for five different values of K (where K is taken to be infinity for chronic exposure).
dotted lines tend to intersect most of the error bars—the evidence for different curvatures is not as extreme as it might appear from simple visual inspection.
By acting as if there is a single value of θ, the evidence for it is summarized by the likelihood function labeled “Animal Experiments” in Figure 10B-4. This is a scaled profile likelihood function for θ from a model in which the risk estimates of Figure 10B-2 are normally distributed with variances that are proportional to the reciprocal of the squared standard errors. The means are modeled to depend on the particular condition—corresponding to each of the 11 graphs in Figure 10B-2—with linear-in-dose coefficients that depend on the particular condition and with a quadratic coefficient that is θ divided by the linear coefficient. Thus, the different conditions have different linear and quadratic terms, but the ratio of the quadratic to linear term is held constant.
The “life-shortening” data used here are the mean survival times of mice exposed acutely and chronically to γ-rays at various doses (Storer and others 1979). Indications of a dose-rate effect from these data stem from the observation that the mean survival times are longer for chronically exposed mice than for acutely exposed mice given the same total dose. However, to extract specific information about curvature, it is necessary to understand the connection between age-specific failure rate and survival time. The human risk models estimated with the LSS data are for age-specific failure rates, also known as hazard functions. Interest here therefore concerns LQ models for hazard functions. Data on mouse survival times may, in principle, be used directly to estimate the hazard function, by employing standard statistical tools of survival analysis, but the unavailability of the raw data precluded this approach by the committee. If the survival times are assumed to follow an exponential probability distribution, then the hazard function is the reciprocal of the mean survival time. By using this exponential assumption (which is probably incorrect but useful nonetheless for extracting information about curvature, at least roughly), the
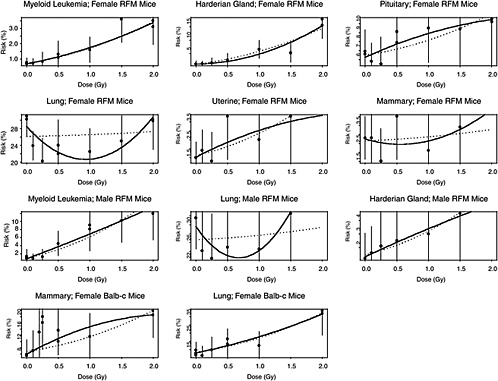
FIGURE 10B-2 Estimated risk of cancer versus radiation dose from various mouse experiments. SOURCE: Data from A.A. Edwards (1992) for cancer site, mouse strain, and sex combinations. Vertical bars extend two standard errors above and below each estimate. Solid curves are estimated LQ models based on each condition individually. Dotted curves are the best-fitting LQ models when curvature is constrained to be the same for all 11 conditions.
curvature of interest can be ascertained by fitting an LQ model to the reciprocal of the mean survival.
Figure 10B-3 shows the reciprocal mean survival times plotted versus dose, with different plotting characters for means based on acutely and chronically exposed mice. Also shown on the plot are the fits to the model that has the age-specific death rate equal to a constant plus αDose for chronically exposed mice and the same constant plus α(Dose + θDose2) for acutely exposed mice, following the reasoning in the first section of this Annex. (The estimates are maximum likelihood estimates based on normality of the reciprocal means, which are estimates from a large number of mice.) The estimates depend highly on the dose range considered. This presents a difficulty since leveling off of the dose-response is expected (as shown in Figure 10-1), but the dose at which leveling off occurs is difficult to determine, both theoretically and empirically. The decision was made by the committee to use the 0–1.5 Gy dose range, but this is subjective and open to debate.
The (profile) likelihood function for θ is shown in Figure 10B-4. It is evident that the life-shortening data indicate slightly more curvature than the direct cancer risk results. While it is appropriate to multiply two likelihoods from independent data sets, these data sets are not independent. Instead, an average of the two is obtained, shown as the solid curve in Figure 10B-4, to represent an average effect based on the two ways of dealing with the data. The maximum likelihood estimate of θ from the average likelihood is 0.5, corresponding to an LSS DDREF of 1.5.
Evidence of curvature at the cellular level comes primarily from studies of chromosomal aberrations in human cells. Table 10B-1 shows estimated LQ models for the regression of chromosome aberration induction on dose. These results may be included weakly, by specifying a probability distribution with mean and variance equal to the sample mean and sample variance of the three curvatures in the table. The result of including such a distribution in the averaging of Figure 10B-4 is to increase the width of the resulting average likelihood, with little effect on the center of the distribution. Since they do not alter the results and because of the extra theoretical demand in incorporating cellular data into models for human cancer rates, chromosome aberration data were not included in the analysis.
The final step in the LSS DDREF estimation involves combining animal radiobiological information with LSS information about curvature. The average likelihood in Figure 10B-4
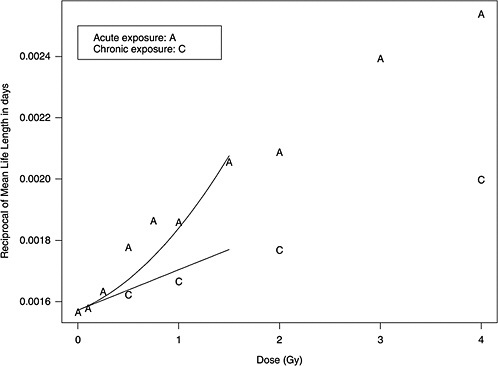
FIGURE 10B-3 Life-shortening data from Tables 1, 2, and 3 of Storer and others (1979). Plotted are the reciprocals of the mean life lengths of RFM female mice versus the dose of exposure, with different plotting symbols for acute (A) and chronically (C) exposed groups. The curves are the result of estimation of an LQ model for age-specific mortality rate fit to the 0–1.5 Gy dose range.
10B-4 is used as a “Bayesian prior distribution” in a Bayesian analysis. The resulting “posterior distribution” that results when this prior is multiplied by the LSS likelihood function is shown in Figure 10-3. The posterior density in the
TABLE 10B-1 Estimates of Linear and Quadratic Coefficients from Chromosome Aberration Induction Studies and the Implicit Curvatures
|
Human Cell Type |
Radiation |
α |
β |
θ |
|
Lymphocytesa |
Cobalt-60 |
0.015 |
0.06 |
4.0 |
|
Lymphocytesa |
250 kV X-rays |
0.04 |
0.06 |
1.5 |
|
Primary human fibroblastsb |
Cesium-137 (acute) |
0.059 |
0.029 |
0.5 |
|
Primary human fibroblastsb |
Cesium-137 (chronic) |
0.019 |
|
|
|
aFrom Lloyd and others (1992). bFrom Cornforth and others (2002). |
||||
graph indicates the likely values of curvature and corresponding values of the LSS DDREF.
It should be evident that further study beyond that accomplished here could possibly lead to a better summarization of radiobiological information about curvature than provided in Figure 10B-4. Even a more thorough study, however, would similarly be obstructed by the subjectivity involved in the choice of dose range upon which LQ models are fit, by the inconsistency of animal experiment results, and by the difficulty in translating mouse results to human cancer rates.
The posterior density can be used directly to describe the uncertainty in LSS DDREF for the uncertainty analysis in Chapter 12. This distribution probably understates the uncertainty in knowledge of LSS DDREF, however, because of the various subjective choices involved. In an attempt to be more realistic about the state of knowledge of LSS DDREF, an inflated variance (of the distribution of the logarithm of LSS DDREF) is used in the uncertainty analysis.
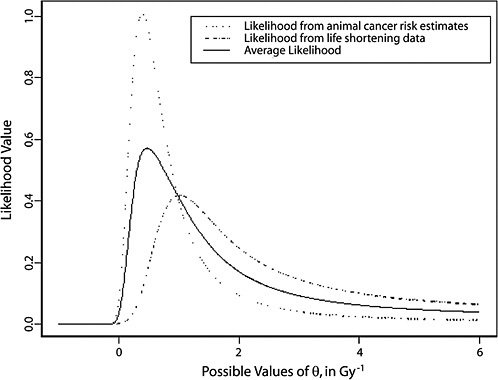
FIGURE 10B-4 A summary of radiobiological evidence for curvature: the (profile) likelihood for curvature from the risk estimate data in Figure 10B-2, the (profile) likelihood from the life shortening data in Figure 10B-3, and their average.




















