B
Some Physics-Based Constraints on Autonomous Vehicles: Scaling, Energy, Sensing, and Communications
The purpose of this appendix is to provide a technical discussion of autonomous vehicle (AV) scaling, energy, sensing, communications, and related topics. Although these areas are touched upon in this report’s chapters on unmanned aerial vehicles (UAVs), unmanned surface vehicles/unmanned undersea vehicles (USVs/UUVs), and unmanned ground vehicles (UGVs)—that is, in Chapters 4, 5, and 6, respectively—the details and physics-based constraints are discussed at greater length in this appendix.
RANGE AND ENDURANCE
For most missions of interest, the range and endurance of an autonomous vehicle are crucial parameters that affect the suitability of that vehicle for any particular mission. The cost of the system that can accomplish a mission grows with requirements for increasing range and endurance. It is important to understand how basic physics determines the variations in size, mass, and cost of autonomous systems in response to variations in the needed range and endurance for individual missions.
The principal factor affecting range and endurance is energy storage. For an atmospheric or underwater vehicle, the basic physics is that the drag force is proportional to V2, where V is the velocity of the vehicle. The drag power is proportional to V3. Both vary with the surface area, or with R2, where R is the radius of the vehicle’s fuselage or hull. The amount of energy storage available in the vehicle is proportional to the volume, and so is proportional to R3. So a simplistic, back-of-the-envelope estimate of the endurance time t of a vehicle
that maintains a velocity V is t = kR/ρV3, and the total distance covered is S = Vt = kR/ρV2. Here, k is a constant that depends on the type of energy storage and on geometric factors relating to how streamlined the vehicle is. For vehicles that derive their energy from chemical storage and which are streamlined with the usual 12:1 length-to-diameter aspect ratio appropriate for conventional high-strength materials, the value of k can range up to about 1011 in metric units. This factor k can vary by a modest amount, depending on the specific chemicals used for energy storage, the fraction of total volume devoted to fuel, and so on. The Greek letter “rho” (ρ) is the density of the medium that the vehicle moves through (1,025 kg/m3 for seawater and 1.29 kg/m3 for air at sea level).
Thus, both range and endurance are expected to be roughly proportional to the scale of the vehicle. Smaller vehicles can be used if one is willing to make a proportionate sacrifice in range and endurance. The mass of the vehicle, which generally determines the cost and the difficulty of handling logistics, is proportional to R3. So range and endurance are found to be proportional to M1/3, where M is the gross (fully loaded) mass of the vehicle. Furthermore, range varies inversely with V2, and endurance varies inversely with V3. Thus, it is very important that the vehicle move only as fast as necessary to accomplish its mission, but no faster.
For endurance, a lower bound on velocity is primarily determined by the fluid disturbances that the vehicle must fight. In both atmospheric and underwater vehicles, the natural disturbances with which the vehicle must contend are driven by solar power. The fluid disturbances in the atmosphere and under water rarely exceed the power densities (½ ρV3) of the incident solar power flux (1,350 W/m2). Under water, this means that characteristic currents are 1.4 m/s (2.7 knots). In the atmosphere, because the density of air is so much lower, the velocity of typical disturbances is higher, about 14 m/s (27 knots) at sea level and 36 m/s (70 knots) at 18 km altitude (59,000 ft). Most autonomous vehicles designed for long endurance cruise at a speed that ranges from 1.3 to 5 times faster than these disturbances, so that they have sufficient command authority to loiter over a stationary point and to reach new targets of interest despite the occasional flow that exceeds the solar power flux. One side effect of the solar origin of these disturbances is that an infinite-endurance solar-powered aircraft is barely possible, since the wing area can collect power at about the same rate at which a minimal vehicle expends it.1
The simple analysis here shows that the endurance of a vehicle varies inversely with ρV3, which itself is just a fixed multiple of the solar constant, and so the endurance of a vehicle that has a fixed velocity margin over the natural
|
1 |
See, for example, the Web site <http://www.aerovironment.com/area-aircraft/unmanned.html>. Last accessed on April 1, 2004. |
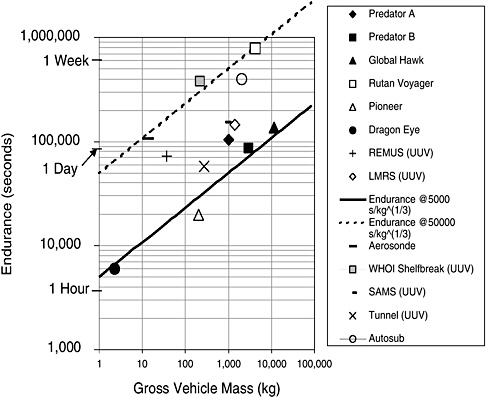
FIGURE B.1 Endurance versus mass for typical vehicles. NOTE: A list of acronyms is provided in Appendix D.
disturbances is found to be approximately independent of the density of the fluid that it moves through. This means that unmanned aerial vehicles and unmanned underwater vehicles will have the same endurance-mass relationship. Shown in Figure B.1 is a plot of gross vehicle mass versus endurance for several vehicles, along with two curves for constant endurance per kg1/3. All the UAVs and UUVs lie within the same band of constant endurance per kg1/3, as predicted by this simple model, over a range of four orders of magnitude.
One example near the extreme in Figure B.1 is the Rutan Voyager, which flew nonstop around the world without refueling; that flight took place in December 1986 over a period of 9 days, with two pilots onboard. The Rutan Voyager was built using the most advanced composite materials and methods, and it demonstrates that significant advances in endurance are possible, even though it is far too fragile a craft for naval operations. If current research (e.g., in carbon nanotubes) is successful in creating useful materials with a strength-to-weight ratio up to two orders of magnitude higher than that of conventional materials, it
may be possible to build vehicles that equal or exceed the performance of the Rutan Voyager and yet are rugged enough for naval operations.
All of the vehicles listed in Figure B.1 are highly streamlined, and for aircraft they all use a high-aspect-ratio, high-lift-to-drag-ratio wing. If other considerations force the vehicle design away from this approach, the endurance can be expected to suffer accordingly. It is perhaps worth noting that aircraft normally carry only one of the two chemical reactants needed for energy storage and ingest the needed oxygen from the air. This makes chemical energy storage for aircraft somewhat more efficient than that for underwater vehicles, which generally carry both components of the chemical reaction. But an aircraft must lift its own weight, and so it requires a large wing and its associated drag, while the UUV is neutrally buoyant. These two effects roughly cancel one another.
It is perhaps worth discussing briefly the possibility that something other than chemical energy might be used. Nuclear power has its own scaling difficulties, since a critical mass of fissionable material is of a fixed size, not to mention the severe political, environmental, and practical handling problems once the vehicle structure is thoroughly bombarded with neutrons. Radioisotope thermal power sources currently have specific power densities of only ~5 W/kg, compared with chemical engines, which have useful outputs of 1 to 2 kW/kg. So the power density of radioisotope power is too low for aircraft but might work for very slow submersibles. An interesting possibility is beamed power, involving laser or microwave energy directed at the vehicle from a remote source to completely break all of these scaling relations. And lastly, as previously mentioned, infinite-endurance solar-powered aircraft are possible (they store extra energy in the daytime for use at night or simply glide all night). At this time, none of these alternative energy sources is highly attractive for naval operations.
While endurance is approximately the same for UAVs and UUVs of the same mass, the range of the vehicles is radically different. Since ρV3 is roughly constant for all of these vehicles, V is proportional to ρ1/3. This means that the speed of a low-altitude UAV will be about 9 times faster than that of a UUV, and a high-altitude UAV will be at least 25 times faster than a UUV. So over the same endurance time, a UAV will cover much more distance than can be covered by a UUV of the same mass, as one would expect intuitively. The fact that range and endurance suffer so badly from increases in velocity (inversely with V2 and V3, respectively) makes it unattractive to have the vehicles “sprint” to their operational stations. This logic suggests air deployment of UUVs when the mission calls for them to be a long way from the fleet, perhaps using UAVs designed for this purpose.
In-flight refueling of UAVs and UUVs is also attractive: small, low-signature vehicles will have limited endurance, but they could rendezvous with a much larger “tanker,” which has significant endurance. Since the tanker would not carry the expensive sensor package, it could be much cheaper than the smaller
vehicles. Unfortunately, the existing fleets of KC-130 aerial tankers operated by the Air Force have a minimum speed that is much too great for UAVs to match, given the scaling issues addressed here. Some C-130 tankers configured for in-flight refueling of helicopters may be suitable for refueling UAVs.
A key point here is that the Navy should not try to make UAVs that are compatible with the existing jet-refueling tankers, since the high-speed requirement is so contrary to the need for long endurance. And it may not be practical, at least initially, to build a new fleet of tankers specifically for UAVs. It is perhaps most important to deploy a system that is capable, yet highly affordable in all stages of deployment. Deploying “Predator-class” UAVs and torpedo-tube-compatible UUVs from the fleet will accomplish most missions at low cost and low risk without in-flight refueling and without onerously frequent launch and recovery. In October 1996, the Predator Marinization Feasibility Study, conducted by the Program Executive Office, Cruise Missiles and Unmanned Aerial Vehicles (PEO(CU)) under the direction of Commander Kurt Engel, USN, concluded, “The assessment finds that the marinization of the Predator-A system to takeoff and land on CV/LH [aircraft carrier/amphibious assault] class ships is feasible with moderate costs.” There were a number of issues, including those of using a heavy-fuel engine versus avgas, the wind over deck margin, and problematic flying qualities in the aft deck burble, but the study concluded that the issues were resolvable.
The endurance of the marinized version of the Predator was estimated at 22 hours. It would seem that a redesigned, perhaps slightly larger vehicle could be made so that it could launch at the beginning of a flight-deck operations shift on one day and not be recovered until the end of the shift on the following day, greatly increasing the total number of vehicles that the fleet can sustain. The cost of these UAVs could perhaps be made significantly less than the cost of shooting them down, especially if each of them carried suitable suppression of enemy air defense (SEAD) implements. With clever design it should be possible to pack multiple Predator-class UAVs in the space of a single manned aircraft belowdecks, given that a combat aircraft has a mass of more than 30 tons at launch, while each UAV is only 1 or 2 tons. For example, the UAVs could be designed with their wings hinged on each side about halfway out, and then the whole wing would pivot to line up with the fuselage so that it all fit in a “cigar tube” whose length is about half of the UAV’s deployed wingspan (the same configuration as that of the small Finder UAV developed by the Naval Research Laboratory; Figure B.2). The 18 m length of a manned aircraft is more than twice the length of a Predator-class vehicle packed this way, so it seems possible to have a 3 × 5 × 2 array (30 total) of UAVs stowed in the same space as a current combat aircraft. Once combat operations begin, these “boxed and stacked” vehicles will necessarily come out and stay out “on their tires” for the duration of operations. But if they have an endurance of 2 days, then during combat opera-

FIGURE B.2 The Finder unmanned aerial vehicle developed by the Naval Research Laboratory has a folding and pivoting wing to stow in a “cigar-tube” shape. SOURCE: Office of the Secretary of Defense. 2002. Unmanned Aerial Vehicles Roadmap 2002-2027, Department of Defense, Washington, D.C., December.
tions, at most half are onboard at any time. If each UAV has a highwing that pivots over the fuselage, they could be parked with the fuselages almost side by side and still be on their tires (e.g., each on a 9 × 1.7 m spot). Each unpacked UAV would take perhaps three times the “spot factor” of the stacked units, but half of them would be in the air, so instead of having a ratio of 30 per current manned vehicle, one might effectively have 20.
Where does this very simplistic analysis fail to capture the essential issues? For very small vehicles, the dimensionless Reynolds number that characterizes the fluid flow around a body gets outside the range in which the drag coefficient is roughly constant, as assumed. To date, human-built vehicles at extremely small scales have had even lower range and endurance than this simple analysis would indicate, because of this effect. However, the animal world gives numerous examples showing that this need not be so. For example, a well-fed housefly has an endurance of about an hour, which is possible only because the wing of the fly is able to take remarkable advantage of “swimming in its own vortices” in a manner not yet fully understood. For larger aircraft, the simple model used here predicts
that the range and endurance can be increased without bound by making the vehicle large enough. This is not quite true. To understand further, consider that most aircraft have a lift-to-drag ratio (L/D) between 10 and 40. If all of the lift is used to carry fuel of mass M, then L = Mg , where g is the acceleration of gravity. The drag D times the velocity V is the mechanical power needed to sustain flight, which is the energy E contained by the fuel divided by the endurance t, so DV = E/t. But the best fuels have a specific energy E/M of about 50 MJ/kg, so L/D = Mg/(E/Vt) = (M/E)/(Vt) or Vt = (L/D)(E/M)/g. The product of velocity times endurance is range; thus, the maximum possible range of a vehicle, at any scale, is roughly the lift-to-drag ratio of the airframe times the specific energy of the fuel divided by the acceleration of Earth’s gravity. For L/D = 10, this maximum range turns out to be 50,000 km, or slightly more than the circumference of Earth.
This result means that the feat of the Rutan Voyager in flying around the world without refueling was not something that could be easily achieved simply by making a bigger vehicle. Instead, it was required that the product of the lift-to-drag ratio and the overall power efficiency of the propulsion system had to be about 10, which is very difficult to achieve at any scale. Once again this analysis is somewhat simplistic, in the sense that, as fuel burns off and the vehicle becomes lighter, the angle of attack of the airfoil can be reduced to lower the drag. This effect has been neglected; in principle it could be used (in the extreme case by staging away unneeded surfaces as fuel is spent, much like a rocket is staged) to give endurance limited only by the strength-to-weight ratio of the structural materials. In normal practice the maximum endurance of a vehicle is proportional to the product of the lift-to-drag ratio, the effective specific energy of the fuel (after accounting for the conversion efficiency of the propulsion system), and (again much like a rocket) the logarithm of the ratio of the wet mass to the dry mass of the aircraft (i.e., with and without fuel, respectively). Note that this formula for range does not involve velocity, since the airframe can be designed to have the needed lift and a good lift-to-drag ratio at any reasonable, preselected subsonic speed and altitude. However, velocity does affect endurance. Since the endurance time is the range divided by the velocity, the loiter time of such a vehicle is inverse with V. Once again, high velocity implies lower endurance, as concluded previously.
The transition region between a UAV whose endurance is proportional to M1/3 (as is the original simplistic analysis) and where it levels off independent of M (this latter analysis involving L/D and E/M) occurs when all of the fuel fits into the wings, so that the vehicle has no fuselage. The longest-endurance, greatest-range systems would be expected to be large, flying wings. For a small vehicle this is not possible, because the volume of a small, thin wing is too low to achieve normal wing loading only with the fuel that fits inside. (Normal wing loading is about 25 kg/m2 for a sailplane—3 times that for a civil aviation aircraft, 9 times that for the Global Hawk, or 27 times that for a modern fighter aircraft.) Even
with the light wing loading of a sailplane, the average wing thickness would need to be about 3 cm to hold all of the fuel. A wing chord (the distance from the leading to the trailing edge) is typically about 10 times the wing thickness, and, for a high L/D, the wingspan is often 20 or 30 times the chord. Thus, the smallest maximal-endurance flying wing possible with chemical fuels has a wingspan of about 10 m, and in practice it might be 2 or 3 times that big. Smaller vehicles must have a fuselage to hold the fuel that does not fit in the wing, and the drag of this fuselage follows the initial simplistic scaling laws used here.
In summary, a simple scaling analysis points out that vehicles with reasonable endurance tend to be moderately large, but are still much smaller than corresponding manned vehicles. Very small vehicles will have very limited range and endurance, as one would expect intuitively. Because of the strong dependence of velocity on range and endurance, it would be very helpful to base the vehicle close to the theater of operations (e.g., on ships), since either it could take the vehicle a very long time to get there on its own, or else it would need to give up a large fraction of its endurance to sprint to the theater. (Actually, for the vehicles in consideration, the dimensionless Reynolds number that characterizes the fluid flow varies from ~104 to ~107 between the smallest, slowest vehicles and the largest, fastest vehicles. There is a significant drop in drag coefficient over that range, so endurance is observed to vary less rapidly than with the inverse cube of the velocity between vehicles optimized at each design point. Empirically, this exponent is found to be slightly less than 2, which is still high enough to impose a significant penalty for high speed.) In any event, both UAVs and UUVs will need to have a mass of 1 ton or a few tons, if only to limit the launch and recovery frequency to an acceptable level, except for those vehicles used for extremely short-duration or short-range missions such as for hand-deployed units used by Special Operations Forces or frontline troops.
Attempts to combine long endurance, substantial payload, high speed, and stealth (e.g., poor aerodynamics) in a single vehicle face tremendous obstacles. The basic physics suggests a separation of functions, using a slow, high-altitude UAV to get the targeting information to call in strikes using other forms of attack, or having a small missile or two on the “big-wing” UAV for really time-critical targets. Presumably most or all combat (as opposed to intelligence, surveillance, and reconnaissance (ISR)) aircraft will slowly be replaced with UAVs as the technology advances. These combat UAVs will need to be much more massive than the ISR UAVs in order to achieve all of the endurance, payload, speed, and stealth requirements. The current uninhabited combat air vehicle-Navy (UCAV-N) under development is an example of this larger size, although it is still smaller than a manned aircraft designed for the same mission—two of the UCAV-Ns fit in the space needed for a normal carrier-based combat aircraft.
LAUNCH AND RECOVERY
Launch and recovery of aircraft from ships constitute a major issue. For example, the launch catapult and landing arrestor on aircraft carriers are designed for vehicles at least an order of magnitude heavier than the UAVs considered here. Fortunately, long-endurance UAVs fly slowly, so they can take off and land at speeds that barely exceed the speed of the fleet when it is under way. Thus, it should be possible to arrange a separate launch-and-recovery apparatus that would only need to deliver or absorb about 1 percent or less of the energy of the traditional systems for these ISR UAVs, if such an apparatus is needed at all. (Both C-130 transport aircraft and U-2 reconnaissance jets have successfully landed and taken off from aircraft carriers without either launch catapults or landing arrestors.2) The combat UAVs, as mentioned, will be comparable in mass to current manned aircraft and therefore should be able to use the same launch-and-recovery systems. (Being unmanned, these UAVs can take the higher acceleration that being lighter implies.) Carrier-deck operations currently require that UAVs maneuver and respond in the same way as manned aircraft to radio commands, hand signals, and so on. This requirement suggests that initially each UAV needs to be controlled by a human pilot via a direct, high-bandwidth, low-latency, “telepresence-style” data link during launch and recovery operations. Having such a control mode also may continue to be required for operation with the current civil air-traffic-control system as is needed for many routine transit operations and training purposes.
Having a moderately large vehicle has other advantages beyond endurance. At the very least, a larger vehicle is able to devote more mass and power to sensing and communications than a small vehicle can. Also, basic physics dictates that sensor angular resolution is inversely proportional to the sensor aperture. For wavelengths and resolutions of interest (e.g., a few-centimeter resolution at several tens of kilometers of slant range using visible imagery or synthetic aperture radar (SAR)), the needed apertures tend to be a significant fraction of a meter. So, serendipitously, the radius of the vehicle should be about the size needed for adequate endurance, just to get the aperture sizes needed for reasonable standoff from the target. The vehicle could be moved closer, of course, but then it would be much more vulnerable, have much less sensor coverage, and be subject to the weather. A similar scaling argument shows that it takes a fairly large and sophisticated system to destroy a hard-to-see, low-power aircraft at ~20 km altitude—the argument based both on the energy needed for the vehicle to get up that high quickly and on the illumination power and resolution needed for the
|
2 |
For the history of the C-130, see the Web site <http://www.aerospaceweb.org/question/history/q0097.shtml>; and for the history of the U-2, see <http://www.aerospaceweb.org/question/history/q0050.shtml>. Last accessed on April 1, 2004. |
sensor to see the target. This large, sophisticated system will itself be vulnerable and will have a cost comparable to that of the UAV. Similar arguments about sensor apertures apply to submersibles. Thus, one finds that aerial or underwater autonomous vehicles having enough range and endurance to avoid nearly continuous launch-and-recovery operations will have a mass of 1 ton or a few tons, will move relatively slowly, will be based relatively close to the target area, and will be able to have superb sensor resolution and relative immunity from attack, especially when viewed in terms of the cost ratio compared with potential countermeasures.
COMMUNICATIONS
Another key issue for autonomous vehicles is communications. Sensors on an approximately 1 ton autonomous aircraft are capable of generating huge amounts of information (~1017 bits per second), based on diffraction-limited resolution and Poisson-limited shot noise, taking full advantage of the large number of thermal and visible photons that flood the environment. Real sensor systems today only deliver a very small fraction of this theoretical limit, but still they frequently overwhelm the available communications bandwidth. However, the basic physics of communications between UAVs, surface combat units, satellites, and ships suggests that it may be possible to return essentially all of the data collected by UAVs.
Moderately large UAVs, as described above, flying at relatively high altitude (to obtain greater sensor coverage, all-weather performance, and relative immunity from attack) generally have a line of sight to other UAVs, to satellites, and often to surface or low-altitude assets as well as to ships at sea. Focused beams of radio-frequency (RF) power can be transmitted between these systems, with modest frequency allocation limitations and very little signature. In particular, RF communications using focused beams between similar UAVs at ranges up to 550 km per leg (the “clear air” horizon limit at 18 km altitude) can carry huge amounts of information. The pointing, tracking, and vehicle-position and attitude knowledge requirements for such communications are not greater than those needed for the basic sensing and targeting functions of the vehicle. (It is especially crucial to know the vehicle attitude precisely for targeting, a fact that has been overlooked in some prior systems. One way to do this for high-altitude UAVs is with a star tracker, which can provide a low-cost, low-mass way to get precise orientation at high altitude, even in the daytime, since the bright stars are visible in the dark sky.)
The Office of the Secretary of Defense is proceeding vigorously with the Global Information Grid (GIG), which seems well tailored to the needs of UAVs and allows transport of large amounts of information from these vehicles to the fleet, to the continental United States (CONUS), or to Marines on the frontlines,
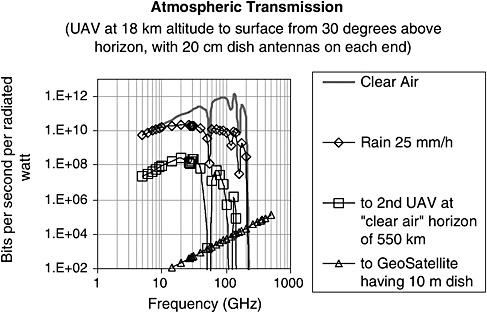
FIGURE B.3 Communications between unmanned aerial vehicles (UAVs) and the ground, other UAVs, and a geosynchronous satellite.
at or near the limits imposed by fundamental physics. As this system matures and deploys, the currently large gap between the ability of UAV sensors to create data and the ability of the communications network to deliver them should disappear. It is important to note that, while the GIG architecture includes satellite communications as part of the grid, this may not be the most important part relevant to UAV systems. Instead, a rich network of point-to-point RF communications between dozens or hundreds of unmanned vehicles will offer tremendous volumes of data through a relatively robust system. The GIG architecture seems well crafted to manage the complexity and dynamic routing requirements of this future environment.
Many presentation packages from all of the military Services depict a future scenario with a densely connected grid of communications over the battlespace. However, it is not clear that any of the Services is making detailed plans or taking responsibility for making this communications grid a reality. It may be that UAVs, and naval UAVs in particular, are especially well suited for making this essential battlespace infrastructure possible. Figure B.3 shows a plot of the theoretical maximum data rate per transmitted watt from a UAV at 18 km altitude to the ground, under various weather conditions. It is assumed that each end of the
link uses a 20 cm (8 in.) diameter parabolic dish antenna. Note that, with the exception of the oxygen absorption band between 50 and 60 GHz, it is possible to transmit over 10 gigabits per second (Gbps) per watt at any frequency from about 8 GHz to over 100 GHz, even through heavy rain (1 inch per hour). Also plotted is the maximum data rate between two UAVs at the “clear-air” horizon distance of 550 km (maintaining the line of sight above 12 km so as to be above essentially all weather). Real communications systems will have a performance less than this theoretical maximum, of course, but even with existing technology the actual performance will be close to these curves. To be immune from jamming, it is generally assumed that between 100 and 1,000 times as much energy per bit is required above this theoretical minimum. Because the sidelobes of the antenna pattern are so much smaller at high frequencies, less jamming margin is needed there, and the link is much more clandestine. Thus, one might speculate that it is possible to build a robust communications link at almost 100 GHz that communicates almost 100 megabits per second (Mbps) per watt between the UAV network and small mobile units on the ground. Given that a typical cellular phone transmits up to 3 W, this level of performance seems good enough for even small units of Marines to obtain a real-time picture of events from the UAVs.
In Figure B.3 it is assumed that the UAV is 30 degrees above the horizon of the unit on the ground. To have one UAV at least 30 degrees above the horizon for every spot in a 1000 × 1000 km battlespace would require about 730 UAVs, which could be hosted by a single aircraft carrier if they had a mass of only 1 ton each and had at least 2 days’ endurance, as described previously. Since the most useful information for the unit on the ground probably comes from the UAV in direct line of sight, there may not be a tremendous load on the network transmitting between UAVs in support of ground operations. Most units would request ISR data from “their” UAV overhead. It does not seem difficult to endow each UAV with a half-dozen or more 8 in. dishes to talk to people on the ground for this purpose. As an “antenna farm,” these UAVs would not be especially stealthy, but they could be fairly small and fairly cheap. The same basic airframe with an electro-optical infrared (EO/IR) sensor (needed by the pilot anyway) and communications package, with a payload bay that can accommodate a SAR, extra fuel tanks, a couple of joint direct attack munitions (JDAMs), or other payloads, can be imagined.
Also plotted in Figure B.3 is the corresponding data rate per watt for a UAV transmitting to a geosynchronous satellite, as is done by the Global Hawk and the Predator. Note that the data rate per watt is generally at least a million times worse than it is between the UAVs and the ground, despite the assumption made here that the satellite uses a large, 10 m (33 ft) dish antenna. This severe performance penalty comes from the extreme distance to geosynchronous orbit, with the attendant inverse-square losses. The bulbous nose of the Global Hawk and the Predator come from the need to use a very large antenna for satellite communica-
tions, which substantially affects the aircraft’s drag, mass, complexity, cost, and endurance. It is not clear that many or any of the UAVs actually need or benefit from satellite communications.
An additional element of the communications system is the need for an omnidirectional, low-bandwidth link for making requests for access to the precisely pointed antenna system. Since each unit will know its own IMU (inertial measurement unit)-augmented Global Positioning System (GPS) location, only a small amount of data needs to be transmitted to allow the two ends of the link to align for the high-bandwidth communications session. Cellular-phone-class systems should be capable of performing this function for ground units wishing to connect to the data network, while UAVs at long range from each other can get the location of new UAVs entering the grid using low-bandwidth links from the fleet or from satellites. The low-bandwidth omnidirectional system will presumably operate at very high frequency/ultrahigh frequency (VHF/UHF), and thus also allow communications of modest amounts of data to units under forest canopies and in other heavily cluttered regions.
It seems that the mass versus endurance argument makes the Navy the logical home for this UAV communications system. A fleet-based system is going to be an order of magnitude lighter and more fuel-efficient and will have a similar savings in logistics tail compared with a system that has the same capability but is based some 2,000 miles from the action. Recent global political events make it clear that any reliance on foreign basing may be problematic in some future conflicts. A fleet-based UAV network would allow line-of-sight relay to the battlespace without the large antennas and severe UAV power drains of satellite communications. Critical information could be fed from the fleet into the national grid via satellite. Since the Navy is presumably the first Service to project force into a region, the UAV communications grid would arrive with it and thus be available for all of the Services to use. Once the Marine Corps has established a secure base in theater, part or all of the maintenance of this UAV grid can be moved on land if that is logistically superior to continued fleet basing.
One particular advantage of the fleet-based UAV grid is that the speed-of-light delay is negligible. It is axiomatic in autonomous vehicle development (at least for those hoping to field systems of acceptable complexity and cost) that one should close only the control loops on the vehicle that are essential owing to latency or bandwidth concerns. In this case, the fundamental bandwidth and latency limitations are so minor that there is actually no formal need to close any of the loops on the vehicle. But in fact it is so trivial to make the vehicle perform behaviors such as to navigate through a series of GPS waypoints that it would be pointless not to include this feature, at the very least so that the vehicle can both finish its primary mission and return back to base if communications are lost.
Indeed, because a GIG/UAV communications system should provide abundant bandwidth even when there are huge numbers of UAVs in the theater, the
one reason for onboard intelligence is health monitoring and fault recovery, especially as related to the communications system. Fortunately there has been considerable progress in such autonomous health monitoring and fault recovery. Other autonomy functions can augment or replace human operator intelligence at the control station first (where computing mass and power are effectively infinite). Later, these functions may migrate up to the vehicle in an orderly fashion as Moore’s law reduces the mass, power, and cost of ever-more-sophisticated onboard computers. Using current-generation commercial off-the-shelf processing at the control station, the state of autonomy development is such that it should be possible to have a single human operator control multiple vehicles within the very near future. Presumably humans will be involved in target identification and weapons release authority for a very long time. Also, the ability of an intelligent adversary to “spoof” even (maybe especially) sophisticated automated systems should not be underestimated. The need for human “eyes on target” (via remote sensing) to satisfy any plausible rules of engagement is a powerful reason to design a system that has adequate bandwidth to transmit the necessary high-resolution images without much delay. This architecture effectively makes autonomy enhancing but not enabling, which is reassuring considering the slow pace of autonomy successes over the past few decades.
The GIG communications architecture permits telepresence for the human operator so long as the operator is in theater. If the geosynchronous relay satellite component of the GIG is used (e.g., for operators in the CONUS), then the speed-of-light latency will be too great for fleet launch and retrieval operations. Thus, at a minimum, pilots who manage the launch and recovery of the UAVs should be based in the fleet. It may be desirable to hand off control to other pilots located elsewhere during the mission. Technology for launch and recovery of UUVs from the torpedo tubes of submarines is already in an advanced state of development. UUVs with perhaps weeks of endurance that cannot fit in a standard torpedo tube, such as might be needed for a submarine track-and-trail mission, will need new developments for launch and recovery.
The situation for communications with underwater vehicles is completely different from that for UAVs. Those UUVs whose mission allows them to continuously or periodically rise to the surface (to snorkel for air-breathing power, get a GPS fix, and so on) can use tight high-frequency beams to the UAV network and the GIG system for high-bandwidth communications. Fortunately, many or most UUV missions fall into this category.
One of the most demanding missions is searching for mines emplaced on or under the seafloor. This effort requires that the vehicle descend to 100 m or more of depth so that short-range sensors can locate the mines. However, it is a relatively modest mission demand to require that the vehicle bring a low-observable antenna to the surface every few kilometers, getting a GPS fix and allowing the exchange of huge amounts of data with the GIG/UAV network. Thus, the principal onboard autonomy requirement for the UUV is to be able to navigate effec-
tively for a period of an hour or so, through a combination of inertial and topography-matching techniques, both of which are relatively mature. (Also, in some situations acoustic beacons can be emplaced to form a local underwater “GPS-like” navigation grid.) Since navigation can be fairly accurate, it is acceptable to have a strategy by which, for example, minelike objects are cataloged along with their detailed sensor profiles, which are then reviewed by human and sophisticated offboard processing following a GIG interchange, with the UUV being sent back to those objects that are determined to be worthy of further scrutiny, tagging, or destruction. There are other attractive architectures for UUVs, such as using acoustic communications to surface transponders into the GIG network, although acoustic communications create a distinctive broadcast signature that tightly focused beams useable by UAVs will not have. This signature might compromise certain missions.
IN SUMMARY
It can be concluded that a very attractive system of autonomous vehicles is composed of a collection of relatively slow undersea and airborne vehicles, each with a launch mass of 1 ton or a few tons and the usual streamlined form factor. These vehicles are essentially flying fuel tanks that can be capable of relatively long endurance, so a large effort does not have to be spent in nearly continuous launch-and-recovery operations.
Each vehicle can return huge amounts of data (at gigabits per second, if necessary) for ship- or ground-based processing. Generally it is not important to miniaturize sensors so that what would be a standard sensor fits in a miniature vehicle, since the basic physics favors sensor apertures more appropriate for the moderate-sized vehicle. To avoid very long delays in getting on-station, these “slow” UAVs should be based close to the action (e.g., on the fleet). Recent political events show that reliance on foreign powers for land basing or overflight rights is fragile, arguing in favor of ship basing.
Needed onboard autonomy can be modest, at least at first, since there are no serious latency or bandwidth limits imposed by the physics of the deployment. The ability to navigate through GPS waypoints is trivial to include. Automated health monitoring, fault recovery, and return-to-base should be relatively easy to implement, especially if effort is focused initially on situations involving loss of communications. At first, all serious data processing can be done at the base station. As the technology advances to do this processing automatically, it will progressively reduce the number of human operators per vehicle and the overall system life-cycle cost. At the very least, humans will certainly be required for a very long time for weapons-release authority and for target identification to outwit the camouflage, concealment, and deception of an intelligent adversary.
Each UAV would have multiple, gimbaled, pointing platforms that are able to maintain accurate pointing and tracking. Some would be gimbaled mirrors
used for sensing, and some would be the gimbaled dishes used for high-bandwidth communications, employing focused beams at high frequencies. In all cases they can and perhaps should be inertially stabilized so that they only slew in inertial space precisely as commanded but do not require constant, high-rate servoing in order to reject airframe disturbances. This need suggests that all can use the same pointing technology and common hardware as much as possible to reduce costs, and that it may be desirable to incorporate a reaction wheel in each reflector assembly (e.g., spin the reflecting dish as is done on the Sidewinder missile) to provide inertial stabilization of each reflector. Since it is desired that each UAV support multiple communications channels and relays, it may be that one or more pods on each wing should provide such gimbaled pointing platforms in both the forward and aft directions, with as large an unobstructed field of view and range of gimbal motion as possible. It is important not to underestimate the value of UAVs as high-bandwidth communications relays, a role that may ultimately approach or eclipse their importance as information-gathering devices.
This scaling discussion does not apply to ground vehicles, but the complexity of negotiating jungles, urban rubble piles, areas inside buildings and sewers, and so on with a ground vehicle is so daunting that it leads one to examine the ducted-fan, vertical-takeoff-and-landing, organic air vehicles and micro-air-vehicles now being developed under funding from the Defense Advanced Research Projects Agency. This scaling analysis does apply to them, and since they are small, they have low range and endurance. As such, they are presumably close to the ground troops that deploy them and so can be recovered, refueled, and redeployed as needed, to stay ahead of the forward troops. Also, they can “perch and stare” for longer endurance. Larger, tanklike autonomous ground vehicles that will be used by the Marine Corps will presumably be developed by the Army (i.e., as part of the Future Combat System, which relies heavily on robotic vehicles as part of its basic architecture). Such vehicles are outside the scope of this appendix, except that they can benefit greatly from the UAV communications network.
It is important to recognize that “humanlike performance” will perhaps be achieved with fully autonomous machines, but probably not for many decades. That is because the human brain represents some 1017 operations per second of equivalent computing performance (~1011 neurons, each with a few thousand synapses operating at a few hundred hertz). Today’s desktop processors perform about 109 operations per second. Assuming that Moore’s law continues unabated—increasing processor throughput by a factor of two every 18 months as progression is made from planar two-dimensional structures to fully integrated three-dimensional computing structures—it will take 40 years to close the gap. Very clever software may reduce the computing requirement by a few orders of magnitude, but it still seems quite possible that humanlike performance in compact, affordable systems is 30 to 50 years away. (The largest supercomputers may
reach rough “human equivalence” within a decade.) A key point for the deployment of UAVs in support of naval operations is that the basic physics does not impose a serious bandwidth or latency constraint (unlike, for example, the case of planetary exploration by the National Aeronautics and Space Administration) that prevents appropriate levels of human involvement with the unmanned vehicles; this feature will allow the total system to have performance comparable to that of a manned system with much less cost and risk. The GIG communications architecture being deployed by the Office of the Secretary of Defense appears to offer all of the necessary features for high-speed, point-to-point communications using secure, focused beams at high frequency. Autonomy (in the sense of onboard computing of those functions that are usually thought to require human intelligence) can be infused as it becomes available, to further reduce cost or risk or to increase performance. But advanced autonomy is not “enabling” except for those missions (some urban, cave, or tunnel warfare scenarios) in which line-of-sight communications cannot be made available.

















