5
Computational Modeling and Simulation as Enablers for Biological Discovery
While the previous chapter deals with the ways in which computers and algorithms could support existing practices of biological research, this chapter introduces a different type of opportunity. The quantities and scopes of data being collected are now far beyond the capability of any human, or team of humans, to analyze. And as the sizes of the datasets continue to increase exponentially, even existing techniques such as statistical analysis begin to suffer. In this data-rich environment, the discovery of large-scale patterns and correlations is potentially of enormous significance. Indeed, such discoveries can be regarded as hypotheses asserting that the pattern or correlation may be important—a mode of “discovery science” that complements the traditional mode of science in which a hypothesis is generated by human beings and then tested empirically.
For exploring this data-rich environment, simulations and computer-driven models of biological systems are proving to be essential.
5.1 ON MODELS IN BIOLOGY
In all sciences, models are used to represent, usually in an abbreviated form, a more complex and detailed reality. Models are used because in some way, they are more accessible, convenient, or familiar to practitioners than the subject of study. Models can serve as explanatory or pedagogical tools, represent more explicitly the state of knowledge, predict results, or act as the objects of further experiments. Most importantly, a model is a representation of some reality that embodies some essential and interesting aspects of that reality, but not all of it.
Because all models are by definition incomplete, the central intellectual issue is whether the essential aspects of the system or phenomenon are well represented (the term “essential” has multiple meanings depending on what aspects of the phenomenon are of interest). In biological phenomena, what is interesting and significant is usually a set of relationships—from the interaction of two molecules to the behavior of a population in its environment. Human comprehension of biological systems is limited, among other things, by that very complexity and by the problems that arise when attempting to dissect a given system into simpler, more easily understood components. This challenge is compounded by our current inability to understand relationships between the components as they occur in reality, that is, in the presence of multiple, competing influences and in the broader context of time and space.
Different fields of science have traditionally used models for different purposes; thus, the nature of the models, the criteria for selecting good or appropriate models, and the nature of the abbreviation or simplification have varied dramatically. For example, biologists are quite familiar with the notion of model organisms.1 A model organism is a species selected for genetic experimental analysis on the basis of experimental convenience, homology to other species (especially to humans), relative simplicity, or other attractive attributes. The fruit fly Drosophila melanogaster is a model organism attractive at least in part because of its short generational time span, allowing many generations in the course of an experiment.
At the most basic level, any abstraction of some biological phenomenon counts as a model. Indeed, the cartoons and block diagrams used by most biologists to represent metabolic, signaling, or regulatory pathways are models—qualitative models that lay out the connectivity of elements important to the phenomenon. Such models throw away details (e.g., about kinetics) implicitly asserting that omission of such details does not render the model irrelevant.
A second example of implicit modeling is the use of statistical tests by many biologists. All statistical tests are based on a null hypothesis, and all null hypotheses are based on some kind of underlying model from which the probability distribution of the null hypothesis is derived. Even those biologists who have never thought of themselves as modelers are using models whenever they use statistical tests.
Mathematical modeling has been an important component of several biological disciplines for many decades. One of the earliest quantitative biological models involved ecology: the Lotka-Volterra model of species competition and predator-prey relationships described in Section 5.2.4. In the context of cell biology, models and simulations are used to examine the structure and dynamics of a cell or organism’s function, rather than the characteristics of isolated parts of a cell or organism.2 Such models must consider stochastic and deterministic processes, complex pleiotropy, robustness through redundancy, modular design, alternative pathways, and emergent behavior in biological hierarchy.
In a cellular context, one goal of biology is to gain insight into the interactions, molecular or otherwise, that are responsible for the behavior of the cell. To do so, a quantitative model of the cell must be developed to integrate global organism-wide measurements taken at many different levels of detail.
The development of such a model is iterative. It begins with a rough model of the cell, based on some knowledge of the components of the cell and possible interactions among them, as well as prior biochemical and genetic knowledge. Although the assumptions underlying the model are insufficient and may even be inappropriate for the system being investigated, this rough model then provides a zeroth-order hypothesis about the structure of the interactions that govern the cell’s behavior.
Implicit in the model are predictions about the cell’s response under different kinds of perturbation. Perturbations may be genetic (e.g., gene deletions, gene overexpressions, undirected mutations) or environmental (e.g., changes in temperature, stimulation by hormones or drugs). Perturbations are introduced into the cell, and the cell’s response is measured with tools that capture changes at the relevant levels of biological information (e.g., mRNA expression, protein expression, protein activation state, overall pathway function). Box 5.1 provides some additional detail on cellular perturbations.
The next step is comparison of the model’s predictions to the measurements taken. This comparison indicates where and how the model must be refined in order to match the measurements more closely. If the initial model is highly incomplete, measurements can be used to suggest the particular components required for cellular function and those that are most likely to interact. If the initial model is relatively well defined, its predictions may already be in good qualitative agreement with measurement, differing only in minor quantitative ways. When model and measurement disagree, it is often
|
1 |
See, for example, http://www.nih.gov/science/models for more information on model organisms. |
|
2 |
Section 5.1 draws heavily on excerpts from T. Ideker, T. Galitski, and L. Hood, “A New Approach to Decoding Life: Systems Biology,” Annual Review of Genomics and Human Genetics 2:343-372, 2001; and H. Kitano, “Systems Biology: A Brief Overview,” Science 295(5560):1662-1664, 2002. |
|
Box 5.1 Perturbation of biological systems can be accomplished through a number of genetic mechanisms, such as the following:
SOURCE: Adapted from T. Ideker, T. Galitski, and L. Hood, “A New Approach to Decoding Life: Systems Biology,” Annual Review of Genomics and Human Genetics 2:343-372, 2001. |
necessary to create a number of more refined models, each incorporating a different mechanism underlying the discrepancies in measurement.
With the refined model(s) in hand, a new set of perturbations can be applied to the cell. Note that new perturbations are informative only if they elicit different responses between models, and they are most useful when the predictions of the different models are very different from one another. Nevertheless, a new set of perturbations is required because the predictions of the refined model(s) will generally fit well with the old set of measurements.
The refined model that best accounts for the new set of measurements can then be regarded as the initial model for the next iteration. Through this process, model and measurement are intended to converge in such a way that the model’s predictions mirror biological responses to perturbation. Modeling must be connected to experimental efforts so that experimentalists will know what needs to be determined in order to construct a comprehensive description and, ultimately, a theoretical framework for the behavior of a biological system. Feedback is very important, and it is this feedback, along with the global—or, loosely speaking, genomic-scale—nature of the inquiry that characterizes much of 21st century biology.
5.2 WHY BIOLOGICAL MODELS CAN BE USEFUL
In the last decade, mathematical modeling has gained stature and wider recognition as a useful tool in the life sciences. Most of this revolution has occurred since the era of the genome, in which biologists were confronted with massive challenges to which mathematical expertise could successfully be brought to bear. Some of the success, though, rests on the fact that computational power has allowed scientists to explore ever more complex models in finer detail. This means that the mathematician’s talent for abstraction and simplification can be complemented with realistic simulations in which details not amenable to analysis can be explored. The visual real-time simulations of modeled phenomena give
more compelling and more accessible interpretations of what the models predict.3 This has made it easier to earn the recognition of biologists.
On the other hand, modeling—especially computational modeling—should not be regarded as an intellectual panacea, and models may prove more hindrance than help under certain circumstances. In models with many parameters, the state space to be explored may grow combinatorially fast so that no amount of data and brute force computation can yield much of value (although it may be the case that some algorithm or problem-related insight can reduce the volume of state space that must be explored to a reasonable size). In addition, the behavior of interest in many biological systems is not characterized as equilibrium or quasi-steady-state behavior, and thus convergence of a putative solution may never be reached. Finally, modeling presumes that the researcher can both identify the important state variables and obtain the quantitative data relevant to those variables.4
Computational models apply to specific biological phenomena (e.g., organisms, processes) and are used for a number of purposes as described below.
5.2.1 Models Provide a Coherent Framework for Interpreting Data
A biologist surveys the number of birds nesting on offshore islands and notices that the number depends on the size (e.g., diameter) of the island: the larger the diameter d, the greater is the number of nests N. A graph of this relationship for islands of various sizes reveals a trend. Here the mathematically informed and uninformed part ways: simple linear least-squares fit of the data misses a central point. A trivial “null model” based on an equal subdivision of area between nesting individuals predicts that N~ d2, (i.e., the number of nests should be roughly proportional to the square of island area). This simple geometric property relating area to population size gives a strong indication of the trend researchers should expect to see. Departures from this trend would indicate that something else may be important. (For example, different parts of islands are uninhabitable, predators prefer some islands to others, and so forth.)
Although the above example is elementary, it illustrates the idea that data are best interpreted within a context that shapes one’s expectations regarding what the data “ought” to look like; often a mathematical (or geometric) model helps to create that context.
5.2.2 Models Highlight Basic Concepts of Wide Applicability
Among the earliest applications of mathematical ideas to biology are those in which population levels were tracked over time and attempts were made to understand the observed trends. Malthus proposed in 1798 the fitting of population data to exponential growth curves following his simple model for geometric growth of a population.5 The idea that simple reproductive processes produce
exponential growth (if birth rates exceed mortality rates) or extinction (in the opposite case) is a fundamental principle: its applicability in biology, physics, chemistry, as well as simple finance, is central.
An important refinement of the Malthus model was proposed in 1838 to explain why most populations do not experience exponential growth indefinitely. The refinement was the idea of the density-dependent growth law, now known as the logistic growth model.6 Though simple, the Verhulst model is still used widely to represent population growth in many biological examples. Both Malthus and Verhulst models relate observed trends to simple underlying mechanisms; neither model is fully accurate for real populations, but deviations from model predictions are, in themselves, informative, because they lead to questions about what features of the real systems are worthy of investigation.
More recent examples of this sort abound. Nonlinear dynamics has elucidated the tendency of excitable systems (cardiac tissue, nerve cells, and networks of neurons) to exhibit oscillatory, burst, and wave-like phenomena. The understanding of the spread of disease in populations and its sensitive dependence on population density arose from simple mathematical models. The same is true of the discovery of chaos in the discrete logistic equation (in the 1970s). This simple model and its mathematical properties led to exploration of new types of dynamic behavior ubiquitous in natural phenomena. Such biologically motivated models often cross-fertilize other disciplines: in this case, the phenomenon of chaos was then found in numerous real physical, chemical, and mechanical systems.
5.2.3 Models Uncover New Phenomena or Concepts to Explore
Simple conceptual models can be used to uncover new mechanisms that experimental science has not yet encountered. The discovery of chaos mentioned above is one of the clearest examples of this kind. A second example of this sort is Turing’s discovery that two chemicals that interact chemically in a particular way (activate and inhibit one another) and diffuse at unequal rates could give rise to “peaks and valleys” of concentration. His analysis of reaction-diffusion (RD) systems showed precisely what ranges of reaction rates and rates of diffusion would result in these effects, and how properties of the pattern (e.g., distance between peaks and valleys) would depend on those microscopic rates. Later research in the mathematical community also uncovered how other interesting phenomena (traveling waves, oscillations) were generated in such systems and how further details of patterns (spots, stripes, etc.) could be affected by geometry, boundary conditions, types of chemical reactions, and so on.
Turing’s theory was later given physical manifestation in artificial chemical systems, manipulated to satisfy the theoretical criteria of pattern formation regimes. And, although biological systems did not produce simple examples of RD pattern formation, the theoretical framework originating in this work motivated later more realistic and biologically based modeling research.
5.2.4 Models Identify Key Factors or Components of a System
Simple conceptual models can be used to gain insight, develop intuition, and understand “how something works.” For example, the Lotka-Volterra model of species competition and predator-prey7 is largely conceptual and is recognized as not being very realistic. Nevertheless, this and similar models have played a strong role in organizing several themes within the discipline: for example, competitive exclusion, the tendency for a species with a slight advantage to outcompete, dominate, and take over from less advantageous species; the cycling behavior in predator-prey interactions; and the effect of
resource limitations on stabilizing a population that would otherwise grow explosively. All of these concepts arose from mathematical models that highlighted and explained dynamic behavior within the context of simple models. Indeed, such models are useful for helping scientists to recognize patterns and predict system behavior, at least in gross terms and sometimes in detail.
5.2.5 Models Can Link Levels of Detail (Individual to Population)
Biological observations are made at many distinct hierarchies and levels of detail. However, the links between such levels are notoriously difficult to understand. For example, the behavior of single neurons and their response to inputs and signaling from synaptic connections might be well known. The behavior of a large assembly of such neurons in some part of the central nervous system can be observed macroscopically by imaging or electrode recording techniques. However, how the two levels are interconnected remains a massive challenge to scientific understanding. Similar examples occur in countless settings in the life sciences: due to the complexity of nonlinear interactions, it is nearly impossible to grasp intuitively how collections of individuals behave, what emergent properties of these groups arise, or the significance of any sensitivity to initial conditions that might be magnified at higher levels of abstraction. Some mathematical techniques (averaging methods, homogenization, stochastic methods) allow the derivation of macroscopic statements based on assumptions at the microscopic, or individual, level. Both modeling and simulation are important tools for bridging this gap.
5.2.6 Models Enable the Formalization of Intuitive Understandings
Models are useful for formalizing intuitive understandings, even if those understandings are partial and incomplete. What appears to be a solid verbal argument about cause and effect can be clarified and put to a rigorous test as soon as an attempt is made to formulate the verbal arguments into a mathematical model. This process forces a clarity of expression and consistency (of units, dimensions, force balance, or other guiding principles) that is not available in natural language. As importantly, it can generate predictions against which intuition can be tested.
Because they run on a computer, simulation models force the researcher to represent explicitly important components and connections in a system. Thus, simulations can only complement, but never replace, the underlying formulation of a model in terms of biological, physical, and mathematical principles. That said, a simulation model often can be used to indicate gaps in one’s knowledge of some phenomenon, at which point substantial intellectual work involving these principles is needed to fill the gaps in the simulation.
5.2.7 Models Can Be Used as a Tool for Helping to Screen Unpromising Hypotheses
In a given setting, quantitative or descriptive hypotheses can be tested by exploring the predictions of models that specify precisely what is to be expected given one or another hypothesis. In some cases, although it may be impossible to observe a sequence of biological events (e.g., how a receptor-ligand complex undergoes sequential modification before internalization by the cell), downstream effects may be observable. A model can explore the consequences of each of a variety of possible sequences can and help scientists to identify the most likely candidate for the correct sequence. Further experimental observations can then refine one’s understanding.
5.2.8 Models Inform Experimental Design
Modeling properly applied can accelerate experimental efforts at understanding. Theory embedded in the model is an enabler for focused experimentation. Specifically, models can be used alongside experiments to help optimize experimental design, thereby saving time and resources. Simple models
give a framework for observations (as noted in Section 5.2.1) and thereby suggest what needs to be measured experimentally and, indeed, what need not be measured—that is how to refine the set of observations so as to extract optimal knowledge about the system. This is particularly true when models and experiments go hand-in-hand. As a rule, several rounds of modeling and experimentation are necessary to lead to informative results.
Carrying these general observations further, Selinger et al.8 have developed a framework for understanding the relationship between the properties of certain kinds of models and the experimental sampling required for “completeness” of the model. They define a model as a set of rules that maps a set of inputs (e.g., possible descriptions of a cell’s environment) to a set of outputs (e.g., the resulting concentrations of all of the cell’s RNAs and proteins). From these basic properties, Selinger et al. are able to determine the order of magnitude of the number of measurements needed to populate the space of all possible inputs (e.g., environmental conditions) with enough measured outputs (e.g., transcriptomes, proteomes) to make prediction feasible, thereby establishing how many measurements are needed to adequately sample input space to allow the rule parameters to be determined.
Using this framework, Salinger et al. estimate the experimental requirements for the completeness of a discrete transcriptional network model that maps all N genes as inputs to all N genes as outputs in which the genes can take on three levels of expression (low, medium, and high) and each gene has, at most, K direct regulators. Applying this model to three organisms—Mycoplasma pneumoniae, Escherichia coli, and Homo sapiens—they find that 80, 40,000, and 700,000 transcriptome experiments, respectively, are necessary to fill out this model. They further note that the upper-bound estimate of experimental requirements grows exponentially with the maximum number of regulatory connections K per gene, although genes tend to have a low K, and that the upper-bound estimate grows only logarithmically with the number of genes N, making completeness feasible even for large genetic networks.
5.2.9 Models Can Predict Variables Inaccessible to Measurement
Technological innovation in scientific instrumentation has revolutionized experimental biology. However, many mysteries of the cell, of physiology, of individual or collective animal behavior, and of population-level or ecosystem-level dynamics remain unobservable. Models can help link observations to quantities that are not experimentally accessible. At the scale of a few millimeters, Marée and Hogeweg recently developed9 a computational model based on a cellular automaton for the behavior of the social amoeba Dictyostelium discoideum. Their model is based on differential adhesion between cells, cyclic adenosine monophosphate (cAMP) signaling, cell differentiation, and cell motion. Using detailed two- and three-dimensional simulations of an aggregate of thousands of cells, the authors showed how a relatively small set of assumptions and “rules” leads to a fully accurate developmental pathway. Using the simulation as a tool, they were able to explore which assumptions were blatantly inappropriate (leading to incorrect outcomes). In its final synthesis, the Marée-Hogeweg model predicts dynamic distributions of chemicals and of mechanical pressure in a fully dynamic simulation of the culminating Dictyostelium slug. Some, but not all, of these variables can be measured experimentally: those that are measurable are well reproduced by the model. Those that cannot (yet) be measured are predicted inside the evolving shape. What is even more impressive: the model demonstrates that the system has self-correcting properties and accounts for many experimental observations that previously could not be explained.
5.2.10 Models Can Link What Is Known to What Is Yet Unknown
In the words of Pollard, “Any cellular process involving more than a few types of molecules is too complicated to understand without a mathematical model to expose assumptions and to frame the reactions in a rigorous setting.”10 Reviewing the state of the field in cell motility and the cytoskeleton, he observes that even with many details of the mechanism as yet controversial or unknown, modeling plays an important role. Referring to a system (of actin and its interacting proteins) modeled by Mogilner and Edelstein-Keshet,11 he points to advantages gained by the mathematical framework: “A mathematical model incorporating molecular reactions and physical forces correctly predicts the steady-state rate of cellular locomotion.” The model, he notes, correctly identifies what limits the motion of the cell, predicts what manipulations would change the rate of motion, and thus suggests experiments to perform. While details of some steps are still emerging, the model also distinguishes quantitatively between distinct hypotheses for how actin filaments are broken down for purposes of recycling their components.
5.2.11 Models Can Be Used to Generate Accurate Quantitative Predictions
Where detailed quantitative information exists about components of a system, about underlying rules or interactions, and about how these components are assembled into the system as a whole, modeling may be valuable as an accurate and rigorous tool for generating quantitative predictions. Weather prediction is one example of a complex model used on a daily basis to predict the future. On the other hand, the notorious difficulties of making accurate weather predictions point to the need for caution in adopting the conclusions even of classical models, especially for more than short-term predictions, as one might expect from mathematically chaotic systems.
5.2.12 Models Expand the Range of Questions That Can Meaningfully Be Asked12
For much of life science research, questions of purpose arise about biological phenomena. For instance, the question, Why does the eye have a lens? most often calls for the purpose of the lens—to focus light rays—and only rarely for a description of the biological mechanism that creates the lens. That such an answer is meaningful is the result of evolutionary processes that shape biological entities by enhancing their ability to carry out fitness-enhancing functions. (Put differently, biological entities are the result of nature’s engineering of devices to perform the function of survival; this perspective is explored further in Chapter 6.)
Lander points out that molecular biologists traditionally have shied away from teleological matters, and that geneticists generally define function not in terms of the useful things a gene does, but by what happens when the gene is altered. However, as the complexity of biological mechanism is increasingly revealed, the identification of a purpose or a function of that mechanism has enormous explanatory power. That is, what purpose does all this complexity serve?
As the examples in Section 5.4 illustrate, computational modeling is an approach to exploring the implications of the complex interactions that are known from empirical and experimental work. Lander notes that one general approach to modeling is to create models in which networks are specified in terms of elements and interactions (the network “topology”), but the numerical values that quantify those interactions (the parameters) are deliberately varied over wide ranges to explore the functionality of the network—whether it acts as a “switch,” “filter,” “oscillator,” “dynamic range adjuster,” “producer of stripes,” and so on.
|
10 |
T.D. Pollard, “The Cytoskeleton, Cellular Motility and the Reductionist Agenda,” Nature 422(6933):741-745, 2003. |
|
11 |
A. Mogilner and L. Edelstein-Keshet, “Regulation of Actin Dynamics in Rapidly Moving Cells: A Quantitative Analysis,” Biophysical Journal 83(3):1237-1258, 2002. |
|
12 |
Section 5.2.12 is based largely on A.D. Lander, “A Calculus of Purpose,” PLoS Biology 2(6):e164, 2004. |
Lander explains the intellectual paradigm for determining function as follows:
By investigating how such behaviors change for different parameter sets—an exercise referred to as “exploring the parameter space”—one starts to assemble a comprehensive picture of all the kinds of behaviors a network can produce. If one such behavior seems useful (to the organism), it becomes a candidate for explaining why the network itself was selected; i.e., it is seen as a potential purpose for the network. If experiments subsequently support assignments of actual parameter values to the range of parameter space that produces such behavior, then the potential purpose becomes a likely one.
5.3 TYPES OF MODELS13
5.3.1 From Qualitative Model to Computational Simulation
Biology makes use of many different types of models. In some cases, biological models are qualitative or semiquantitative. For example, graphical models show directional connections between components, with the directionality indicating influence. Such models generally summarize a great deal of known information about a pathway and facilitate the formation of hypotheses about network function. Moreover, the use of graphical models allows researchers to circumvent data deficiencies that might be encountered in the development of more quantitative (and thus data-intensive) models. (It has also been argued that probabilistic graphical models provide a coherent, statistically sound framework that can be applied to many problems, and that certain models used by biologists, such as hidden Markov models or Bayesian Networks), can be regarded as special cases of graphical models.14)
On the other hand, the forms and structures of graphical models are generally inadequate to express much detail, which might well be necessary for mechanistic models. In general, qualitative models do not account for mechanisms, but they can sometimes be developed or analyzed in an automated manner. Some attempts have been made to develop formal schemes for annotating graphical models (Box 5.2).15
Qualitative models can be logical or statistical as well. For example, statistical properties of a graph of protein-protein interaction have been used to infer the stability of a network’s function against most “deletions” in the graph.16 Logical models can be used when data regarding mechanism are unavailable and have been developed as Boolean, fuzzy logical, or rule-based systems that model complex networks17 or genetic and developmental systems.
In some cases, greater availability of data (specifically, perturbation response or time-series data) enables the use of statistical influence models. Linear,18 neural network-like,19 and Bayesian20 models have all been used to deduce both the topology of gene expression networks and their dynamics. On the
|
13 |
Section 5.3 is adapted from A.P. Arkin, “Synthetic Cell Biology,” Current Opinion in Biotechnology 12(6):638-644, 2001. |
|
14 |
See, for example, Y. Moreau, P. Antal, G. Fannes, and B. De Moor, “Probabilistic Graphical Models for Computational Biomedicine, Methods of Information in Medicine 42(2):161-168, 2003. |
|
15 |
K.W. Kohn, “Molecular Interaction Map of the Mammalian Cell Cycle: Control and DNA Repair Systems,” Molecular Biology of the Cell 10(8):2703-2734, 1999; I. Pirson, N. Fortemaison, C. Jacobs, S. Dremier, J.E. Dumont, and C. Maenhaut, “The Visual Display of Regulatory Information and Networks,” Trends in Cell Biology 10(10):404-408, 2000. (Both cited in Arkin, 2001.) |
|
16 |
H. Jeong, S.P. Mason, A.L. Barabasi, and Z.N. Oltvai, “Lethality and Centrality in Protein Networks,” Nature 411(6833):41-42, 2001; H. Jeong, B. Tombor, R. Albert, Z.N. Oltvai, and A.L. Barabasi, “The Largescale Organization of Metabolic Networks,” Nature 407(6804):651-654, 2000. (Cited in Arkin, 2001.) |
|
17 |
D. Thieffry and R. Thomas, “Qualitative Analysis of Gene Networks,” pp. 77-88 in Pacific Symposium on Biocomputing, 1998. (Cited in Arkin, 2001.) |
|
18 |
P. D’Haeseleer, X. Wen, S. Fuhrman, and R. Somogyi, “Linear Modeling of mRNA Expression Levels During CNS Development and Injury,” pp. 41-52 in Pacific Symposium on Biocomputing, 1999. (Cited in Arkin, 2001.) |
|
19 |
E. Mjolsness, D.H. Sharp, and J. Reinitz, “A Connectionist Model of Development,” Journal of Theoretical Biology 152(4):429-453, 1999. (Cited in Arkin, 2001.) |
|
20 |
N. Friedman, M. Linial, I. Nachman, and D. Pe’er, “Using Bayesian Networks to Analyze Expression Data,” Journal of Computational Biology 7(3-4):601-620, 2000. (Cited in Arkin, 2001.) |
|
Box 5.2 A large fraction of today’s knowledge of biochemical or genetic regulatory networks is represented either as text or as cartoon-like diagrams. However, text has the disadvantage of being inherently ambiguous, and every reader must reinterpret the text of a journal article. Diagrams are usually informal, often confusing, and thus fail to present all of the information that is available to the presenter of the research. For example, the meanings of nodes and arcs within a diagram are inconsistent—one arrow may mean activation, but another arrow in the same diagram may mean transition of the state or translocation of materials. To remedy this state of affairs, a system of graphical representation should be powerful enough to express sufficient information in a clearly visible and unambiguous way and should be supported by software tools. There are several criteria for a graphical notation system, including the following:
No current graphical notation system satisfies all of these criteria fully, although a number of systems satisfy some of them.1 SOURCE: Adapted by permission from H. Kitano, “A Graphical Notation for Biochemical Networks,” Biosilico 1(5):159-176. Copyright 2003 Elsevier. |
other hand, statistical influence models are not causal and may not lead to a better understanding of underlying mechanisms.
Quantitative models make detailed statements about biological processes and hence are easier to falsify than more qualitative models. These models are intended to be predictive and are useful for understanding points of control in cellular networks and for designing new functions within them.
Some models are based on power law formalisms.21 In such cases, the data are shown to fit generic power laws, and the general theory of power law scaling (for example) is used to infer some degree of causal structure. They do not provide detailed insight into mechanism, although power law models form the basis for a large class of metabolic control analyses and dynamic simulations.
Computational models—simulations—represent the other end of the modeling spectrum. Simulation is often necessary to explore the implications of a model, especially its dynamical behavior, because
human intuition about complex nonlinear systems is often inadequate.22 Lander cites two examples. The first is that “intuitive thinking about MAP [mitogen-activated protein] kinase pathways led to the long-held view that the obligatory cascade of three sequential kinases serves to provide signal amplification. In contrast, computational studies have suggested that the purpose of such a network is to achieve extreme positive cooperativity, so that the pathway behaves in a switch-like, rather than a graded, fashion.”23 The second example is that while intuitive interpretations of experiments in the study of morphogen gradient formation in animal development led to the conclusion that simple diffusion is not adequate to transport most morphogens, computational analysis of the same experimental data led the opposite conclusion.24
Simulation, which traces functional biological processes through some period of time, generates results that can be checked for consistency with existing data (“retrodiction” of data) and can also predict new phenomena not explicitly represented in but nevertheless consistent with existing datasets. Note also that when a simulation seeks to capture essential elements in some oversimplified and idealized fashion, it is unrealistic to expect the simulation to make detailed predictions about specific biological phenomena. Such simulations may instead serve to make qualitative predictions about tendencies and trends that become apparent only when averaged over a large number of simulation runs. Alternatively, they may demonstrate that certain biological behaviors or responses are robust and do not depend on particular details of the parameters involved within a very wide range.
Simulations can also be regarded as a nontraditional form of scientific communication. Traditionally, scientific communications have been carried by journal articles or conference presentations. Though articles and presentations will continue to be important, simulations—in the form of computer programs—can be easily shared among members of the research community, and the explicit knowledge embedded in them can become powerful points of departure for the work of other researchers.
With the availability of cheap and powerful computers, modeling and simulation have become nearly synonymous. Yet, a number of subtle differences should be mentioned. Simulation can be used as a tool on its own or as a companion to mathematical analysis.
In the case of relatively simple models meant to provide insight or reveal a concept, analytical and mathematical methods are of primary utility. With simple strokes and pen-and-paper computations, the dependence of behavior on underlying parameters (such as rate constants), conditions for specific dynamical behavior, and approximate connections between macroscopic quantities (e.g., the velocity of a cell) and underlying microscopic quantities (such the number of actin filaments causing the membrane to protrude) can be revealed. Simulations are not as easily harnessed to making such connections.
Simulations can be used hand-in-hand with analysis for simple models: exploring slight changes in equations, assumptions, or rates and gaining familiarity can guide the best directions to explore with simple models as well. For example, G. Bard Ermentrout at the University of Pittsburgh developed XPP software as an evolving and publicly available experimental modeling tool for mathematical biologists.25 XPP has been the foundation of computational investigations in many challenging problems in neurophysiology, coupled oscillators, and other realms.
Mathematical analysis of models, at any level of complexity, is often restricted to special cases that have simple properties: rectangular boundaries, specific symmetries, or behavior in a special class. Simulations can expand the repertoire and allow the modeler to understand how analysis of the special cases
relates to more realistic situations. In this case, simulation takes over where analysis ends.26 Some systems are simply too large or elaborate to be understood using analytical techniques. In this case, simulation is a primary tool. Forecasts requiring heavy “number-crunching” (e.g., weather prediction, prediction of climate change), as well as those involving huge systems of diverse interacting components (e.g., cellular networks of signal transduction cascades), are only amenable to exploration using simulation methods.
More detailed models require a detailed consideration of chemical or physical mechanisms involved (i.e., these models are mechanistic27). Such models require extensive details of known biology and have the largest data requirements. They are, in principle, the most predictive. In the extreme, one can imagine a simulation of a complete cell—an “in silico” cell or cybercell—that provides an experimental framework in which to investigate many possible interventions. Getting the right format, and ensuring that the in silico cell is a reasonable representation of reality, has been and continues to be an enormous challenge.
No reasonable model is based entirely on a bottom-up analysis. Consider, for example, that solving Schrödinger’s equation for the millions of atoms in a complex molecule in solution would be a futile exercise, even if future supercomputers could handle this task. The question to ask is how and why such work would be contemplated: finding the correct level of representation is one of the key steps to good scientific work. Thus, some level of abstraction is necessary to render any model both interesting scientifically and feasible computationally. Done properly, abstractions can clarify the sources of control in a network and indicate where more data are necessary. At the same time, it may be necessary to construct models at higher degrees of biophysical realism and detail in any event, either because abstracted models often do not capture the essential behavior of interest or to show that indeed the addition of detail does not affect the conclusions drawn from the abstracted model.28
It is also helpful to note the difference between a computational artifact that reproduces some biological behavior (a task) and a simulation. In the former case, the relevant question is: “How well does the artifact accomplish the task?” In the latter case, the relevant question is: “How closely does the simulation match the essential features of the system in question?”
Most computer scientists would tend to assign higher priority to performance than to simulation. The computer scientist would be most interested in a biologically inspired approach to a computer science problem when some biological behavior is useful in a computational or computer systems context and when the biologically inspired artifact can demonstrate better performance than is possible through some other way of developing or inspiring the artifact. A model of a biological system then becomes useful to the computer scientist only to the extent that high-fidelity mimicking of how nature accomplishes a task will result in better performance of that task.
By contrast, biologists would put greater emphasis on simulation. Empirically tested and validated simulations with predictive capabilities would increase their confidence that they understood in some fundamental sense the biological phenomenon in question. However, it is important to note that because a simulation is judged on the basis of how closely it represents the essential features of a biological system, the question “What counts as essential?” is central (Box 5.3). More generally, one fundamental focus of biological research is a determination of what the “essential” features of a biological system are,
|
Box 5.3 Consider the following modeling task. The phenomenon of interest is a monkey learning to fetch a banana from behind a transparent conductive screen. The first time, the monkey sees the banana, goes straight ahead, bumps into the screen, and then goes around the screen to the banana. The second time, the monkey, having discovered the existence of the screen that blocks his way, goes directly around the screen to the banana. To model this phenomenon, a system is constructed, consisting of a charged ball and a metal sheet. The charged metal ball is hung from a string above the banana and then held at an angle so the screen separates the ball and the banana. The first time the ball is released, the ball swings toward the screen, and then touches it, transferring part of its charge to the screen. The similar charges on the screen and the ball now repel each other, and the ball swings around the screen. The second time the ball is released, the ball sees a similarly charged screen and goes around the screen directly. This model reproduces the behavior of the monkey in the first instance. However, no one would claim that it is an accurate model of the learning that takes place in the monkey’s brain, even though the model replicates the most salient feature of the monkey’s learning consistently: both the ball and the monkey dodge the screen on the second attempt. In other words, even though it demonstrates the same behavior, the model does not represent the essential features of the biological system in question. |
recognizing that what is “essential” cannot be determined once and for all, but rather depends on the class of questions under consideration.
5.3.2 Hybrid Models
Hybrid models are models composed of objects with different mathematical representations. These allow a model builder the flexibility to mix modeling paradigms to describe different portions of a complex system. For example, in a hybrid model, a signal transduction pathway might be described by a set of differential equations, and this pathway could be linked to a graphical model of the genetic regulatory network that it influences. An advantage of hybrid models is that model components can evolve from high-level abstract descriptions to low-level detailed descriptions as the components are better characterized and understood.
An example of hybrid model use is offered by McAdams and Shapiro,29 who point out that genetic networks involving large numbers of genes (more than tens) are difficult to analyze. Noting the “many parallels in the function of these biochemically based genetic circuits and electrical circuits,” they propose “a hybrid modeling approach that integrates conventional biochemical kinetic modeling within the framework of a circuit simulation. The circuit diagram of the bacteriophage lambda lysislysogeny decision circuit represents connectivity in signal paths of the biochemical components. A key feature of the lambda genetic circuit is that operons function as active integrated logic components and introduce signal time delays essential for the in vivo behavior of phage lambda.”
There are good numerical methods for simulating systems that are formulated in terms of ordinary differential equations or algebraic equations, although good methods for analysis of such models are still lacking. Other systems, such as those that mix continuous with discrete time or Markov processes with partial differential equations, are sometimes hard to solve even by numerical methods. Further, a particular model object may change mathematical representation during the course of the analysis. For example, at the beginning of a biosynthetic process there may be very small amounts of product so its
concentration would have to be modeled discretely. As more of it is synthesized, the concentration becomes high enough that a continuous approximation is justified and is then more efficient for simulation and analysis.
The point at which this switch is made is dependent not just on copy number but also on where in the dynamical state space the system resides. If the system is near a bifurcation point, small fluctuations may be significant. Theories of how to accomplish this dynamic switching are lacking. As models grow more complex, different parts of the system will have to be modeled with different mathematical representations. Also, as models from different sources begin to be joined, it is clear that different representations will be used. It is critical that the theory and applied mathematics of hybrid dynamical systems be developed.
5.3.3 Multiscale Models
Multiscale models describe processes occurring at many time and length scales. Depending on the biological system of interest, the data needed to provide the basis for a greater understanding of the system will cut across several scales of space and time. The length dimensions of biological interest range from small organic molecules to multiprotein complexes at 100 angstroms to cellular processes at 1,000 angstroms to tissues at 1-10 microns, and the interaction of human populations with the environment at the kilometer scale. The temporal domain includes the femtosecond chemistry of molecular interactions to the millions of years of evolutionary time, with protein folding in seconds and cell and developmental processes in minutes, hours, and days. In turn, the scale of the process involved (e.g., from the molecular scale to the ecosystem scale) affects both the complexity of the representation (e.g., molecule base, concentration based, at equilibrium or fully dynamic) and the modality of the representation (e.g., biochemical, genetic, genomic, electrophysiological, etc.).
Consider the heart as an example. The macroscopic unit of interest is the heartbeat, which lasts about a second and involves the whole heart of 10 cm scale. But the cardiac action potential (the electrical signal that initiates myocellular contractions) can change significantly on time scales of milliseconds as reflected in the appropriate kinetic equations. In turn, the molecular interactions that underlie kinetic flows occur on time scales on the order of femtoseconds. Across such variation in time scales, it is not feasible to model 1015 molecular interactions in order to model a complete heartbeat. Fortunately, in many situations the response with the shorter time scale will converge quickly to equilibrium or quasi-steady-state behavior, obviating the need for a complete lower-level simulation.30
For most biological problems, the scale at which data could provide a central insight into the operation of the whole system is not known, so multiple scales are of interest. Thus, biological models have to allow for transition among different levels of resolution. A biologist might describe a protein as a simple ellipsoid and then in the next breath explain the effect of a point mutation by the atomic-level structural changes it causes in the active site.31
Identifying the appropriate ranges of parameters (e.g., rate constants that govern the pace of chemical reactions) remains one of the difficulties that every modeler faces sooner or later. As modelers know well, even qualitative analysis of simple models depends on knowing which “leading-order terms” are to be kept on which time scales. When the relative rates are entirely unknown—true of many biochemical steps in living cells—it is hard to know where to start and how to assemble a relevant model, a point that underscores the importance of close dialogue between the laboratory biologist and the mathematical or computational modeler.
Finally, data obtained at a particular scale must be sufficient to summarize the essential biological activity at that scale in order to be evaluated in the context of interactions at greater scales of complexity. The challenge, therefore, is one of understanding not only the relationship of multiple variables operating at one scale of detail, but also the relationship of multivariable datasets collected at different scales.
5.3.4 Model Comparison and Evaluation
Models are ultimately judged by their ability to make predictions. Qualitative models predict trends or types of dynamics that can occur, as well as thresholds and bifurcations that delineate one type of behavior from another. Quantitative models predict values that can be compared to actual experimental data. Therefore, the selection of experiments to be performed can be determined, at least in part, by their usefulness in constraining a model or selecting one model from a set of competing models.
The first step in model evaluation is to replicate and test a computational model of biological systems that has been published. However, most papers contain typographical errors and do not provide a complete specification of the biological properties that were represented in the model. One should be able to extract the specification from the model’s source code, but for a whole host of reasons it is not always possible to obtain the actual files that were used for the published work.
In the neuroscience field, ModelDB (http://senselab.med.yale.edu/senselab/modeldb/) is being developed to answer the need for a database of published models used in neuroscience research.32 It is part of the SenseLab project (http://senselab.med.yale.edu/), which is supported through the Human Brain Project by the National Institute of Mental Health (NIMH), the National Institute of Neurologist disorders and Stroke (NINDS), and the National Cancer Institute (NCI).
ModelDB is a curated database that is designed for convenient entry, search, and retrieval of models written for any programming language or simulation environment. As of December 10, 2004, it contained 141 downloadable models. Most of these are for NEURON, but 40 of them are for MATLAB, GENESIS, SNNAP, or XPP, and there are also some models in C/C++ and FORTRAN. Database entries are linked to the published literature so that users can more easily determine the “scientific context” of any given model.
Although ModelDB is still in a developmental or research stage, it has already begun to have a positive effect on computational modeling in neuroscience. Database logs indicate that it is seeing heavy usage, and from personal communications the committee has learned that even experienced programmers who write their own code in C/C++ are regularly examining models written for NEURON and other domain-specific simulators, in order to determine key parameter values and other important details. Recently published papers are beginning appear that cite ModelDB and the models it contains as sources of code, equations, or parameters. Furthermore, a leading journal has adopted a policy that requires authors to make their source code available as a condition of publication and encourages them to use ModelDB for this purpose.
As for model comparison, it is not possible to ascertain in isolation whether a given model is correct since contradictory data may become available later, and indeed even “incorrect” models may make correct predictions. Suitably complex models can be made to fit to any dataset, and one must guard against “overfitting” a model. Thus, the predictions of a model must be viewed in the context of the number of degrees of freedom of the model, and one measure that one model is better than another is a judgment about which model best explains experimental data with the least model complexity. In some cases, measures of the statistical significance of a model can be computed using a likelihood distribution over predicated state variables taking into account the number of degrees of freedom present in the model.
At the same time, lessons learned over many centuries of scientific investigation regarding the use of Occam’s Razor may have limited applicability in this context. Because biological phenomena are the result of an evolutionary process that simply uses what is available, many biological phenomena are simply cobbled together and in no sense can be regarded as the “simplest” way to accomplish something.
As noted in Footnote 28, there is a tension between the need to capture details faithfully in a model and the desire to simplify those details so as to arrive at a representation that can be analyzed, understood fully, and converted into scientific “knowledge.” There are numerous ways of reducing models that are well known in applied mathematics communities. These include dimensional analysis and multiple time-scale analysis (i.e., dissecting a system into parts that evolve rapidly versus those that change on a slower
time scale). In some cases, leaving out some of the interacting components (e.g., those whose interactions are weakest or least significant) may be a workable method. In other cases, lumping together families or groups of substances to form aggregate components or compartments works best. Sensitivity analysis of alternative model structures and parameters can be performed using likelihood and significance measures. Sensitivity analysis is important to inform a model builder of the essential components of the model and to attempt to reduce model complexity without loss of explanatory power.
Model evaluation can be complicated by the robustness of the biological organism being represented. Robustness generally means that the organism will endure and even prosper under a wide range of conditions—which means that its behavior and responses are relatively insensitive to variations in detail.33 That is, such differences are unlikely to matter much for survival. (For example, the modeling of genetic regulatory networks can be complicated by the fact that although the data may show that a certain gene is expressed under certain circumstances, the biological function being served may not depend on the expression of that gene.) On the other hand, this robustness may also mean that a flawed understanding of detailed processes incorporated into a model that does explain survival responses and behavior will not be reflected in the model’s output.34
Simulation models are essentially computer programs and hence suffer from all of the problems that plague software development. Normal practice in software development calls for extensive testing to see that a program returns the correct results when given test data for which the appropriate results are known independently of the program as well as for independent code reviews. In principle, simulation models of biological systems could be subject to such practices. Yet the fact that a given simulation model returns results that are at variance with experimental data may be attributable to an inadequacy of the underlying model or to an error in programming.35 Note also that public code reviews are impossible if the simulation models are proprietary, as they often are when they are created by firms seeking to obtain competitive advantage in the marketplace.
These points suggest a number of key questions in the development of a model.
-
How much is given up by looking at simplified versions?
-
How much poorer, and in what ways poorer, is a simplified model in its ability to describe the system?
-
Are there other, new ways of simplifying and extracting salient features?
-
Once the simplified representation is understood, how can the details originally left out be reincorporated into a model of higher fidelity?
Finally, another approach to model evaluation is based on notions of logical consistency. This approach uses program verification tools originally developed by computer scientists to determine whether a given program is consistent with a given formal specification or property. In the biological context, these tools are used to check the consistency and completeness of a model’s description of the biological system’s processes. These descriptions are dynamic and thus permit “running” a model to observe developments in time. Specifically, Kam et al. have demonstrated this approach using the languages, methods, and tools of scenario-based reactive system design and applied it to modeling the well-characterized process of cell fate acquisition during Caenorhabditis elegans vulval development. (Box 5.4 describes the intellectual approach in more detail.36)
|
33 |
L.A. Segel, “Computing an Organism,” Proceedings of the National Academy of Sciences 98(7):3639-3640, 2001. |
|
34 |
On the basis of other work, Segel argues that a biological model enjoys robustness only if it is “correct’’ in certain essential features. |
|
35 |
Note also the well-known psychological phenomenon in programming—being a captive of one’s test data. Programming errors that prevent the model from accounting for the data tend to be hunted down and fixed. However, if the model does account for the data, there is a tendency to assume that the program is correct. |
|
36 |
N. Kam, D. Harel, H. Kugler, R. Marelly, A. Penueli, J. Hubbard, et al., “Formal Modeling of C. elegans Development: A Scenario-based Approach,” pp. 4-20 in Proceedings of the First International Workshop on Computational Methods in Systems Biology (CMSB03; Rovereto, Italy, February 2003), Vol. 2602, Lecture Notes in Computer Science, Springer-Verlag, Berlin, Heidelberg, 2003. This material is scheduled to appear in the following book: G. Ciobanu, ed., Modeling in Molecular Biology, Natural Computing Series, Springer, available at http://www.wisdom.weizmann.ac.il/~kam/CelegansModel/Publications/MMB_Celegans.pdf. |
|
Box 5.4 Our understanding of biology has become sufficiently complex that it is increasingly difficult to integrate all the relevant facts using abstract reasoning alone. [Formal modeling presents] a novel approach to modeling biological phenomena. It utilizes in a direct and powerful way the mechanisms by which raw biological data are amassed, and smoothly captures that data within tools designed by computer scientists for the design and analysis of complex reactive systems. A considerable quantity of biological data is collected and reported in a form that can be called “condition-result” data. The gathering is usually carried out by initializing an experiment that is triggered by a certain set of circumstances (conditions), following which an observation is made and the results recorded. The condition is most often a perturbation, such as mutating genes or exposing cells to an altered environment…. [and] a large proportion of biological data is reported as stories, or “scenarios,” that document the results of experiments conducted under specific conditions. The challenge of modeling these aspects of biology is to be able to translate such “condition-result” phenomena from the “scenario”-based natural language format into a meaningful and rigorous mathematical language. Such a translation process will allow these data to be integrated more comprehensively by the application of high-level computer-assisted analysis. In order for it to be useful, the model must be rigorous and formal, and thus amenable to verification and testing. We have found that modeling methodologies originating in computer science and software engineering, and created for the purpose of designing complex reactive systems, are conceptually well suited to model this type of condition-result biological data. Reactive systems are those whose complexity stems not necessarily from complicated computation but from complicated reactivity over time. They are most often highly concurrent and time-intensive, and exhibit hybrid behavior that is predominantly discrete in nature but has continuous aspects as well. The structure of a reactive system consists of many interacting components, in which control of the behavior of the system is highly distributed amongst the components. Very often the structure itself is dynamic, with its components being repeatedly created and destroyed during the system’s life span. The most widely used frameworks for developing models of such systems feature visual formalisms, which are both graphically intuitive and mathematically rigorous. These are supported by powerful tools that enable full model executability and analysis, and are linkable to graphical user interfaces (GUIs) of the system. This enables realistic simulation prior to actual implementation. At present, such languages and tools—often based on the object-oriented paradigm—are being strengthened by verification modules, making it possible not only to execute and simulate the system models (test and observe) but also to verify dynamic properties thereof (prove)…. [M]any kinds of biological systems exhibit characteristics that are remarkably similar to those of reactive systems. The similarities apply to many different levels of biological analysis, including those dealing with molecular, cellular, organ-based, whole organism, or even population biology phenomena. Once viewed in this light, the dramatic concurrency of events, the chain-reactions, the time-dependent patterns, and the event-driven discrete nature of their behaviors, are readily apparent. Consequently, we believe that biological systems can be productively modeled as reactive systems, using languages and tools developed for the construction of man-made systems…. SOURCE: N. Kam et al., “Formal Modeling of C. elegans Development: A Scenario-based Approach,” pp. 4-20 in Proceedings of the First International Workshop on Computational Methods in Systems Biology (CMSB03; Rovereto, Italy, February 2003), Vol. 2602, Lecture Notes in Computer Science, Springer-Verlag, Berlin, Heidelberg, 2003, available at http://www.wisdom.weizmann.ac.il/~kam/CelegansModel/Publications/MMB_Celegans.pdf. Reprinted with permission from Springer-Verlag. |
5.4 MODELING AND SIMULATION IN ACTION
The preceding discussion has been highly abstract. This section provides some illustrations of how modeling and simulation have value across a variety of subfields in biology. No claim is made to comprehensiveness, but the committee wishes to illustrate the utility of modeling and simulations at levels of organization from gene to ecosystem.
5.4.1 Molecular and Structural Biology
5.4.1.1 Predicting Complex Protein Structures
Interactions between proteins are crucial to the functioning of all cells. While there is much experimental information being gathered regarding protein structures, many interactions are not fully understood and have to be modeled computationally. The topic of computational prediction of protein-protein structure remains to be solved and is one of the most active areas of research in bioinformatics and structural biology.
ZDOCK and RDOCK are two computer programs that address this problem, also known as protein docking.37 ZDOCK is an initial stage protein docking program that performs a full search of the relative orientations of two molecules (referred to by convention as the ligand and receptor) to determine their best fit based on surface complementarity, electrostatics and desolvation. The efficiency of the algorithm is enhanced by discretizing the molecules onto a grid and performing a fast Fourier transform (FFT) to quickly explore the translational degrees of freedom.
RDOCK takes as input the ZDOCK predictions and improves them using two steps. The first step is to improve the energetics of the prediction and remove clashes by performing small movements of the predicted complex, using a program known as CHARMM. The second step is to rescore these minimized predictions with more detailed scoring functions for electrostatics and desolvation.
The combination of these two algorithms has been tested and verified with a benchmark set of proteins collected for use in testing docking algorithms. Now at version 2.0, this benchmark is publicly available and contains 87 test cases. These test cases cover a breadth of interactions, such as antibody-antigen, and cases involving significant conformational changes.
The ZDOCK-RDOCK programs have consistently performed well in the international docking competition CAPRI (Figure 5.1). Some notable predictions were for the Rotavirus VP6/Fab (50 of 52 contacting residues correctly predicted), and SAG-1/Fab complex (61 of 70 contacts correct), and the cellulosome cohesion-dockerin structure (50 of 55 contacts correct). In the first two cases, the number of contacts in the ZDOCK-RDOCK predictions were the highest among all participating groups.
5.4.1.2 A Method to Discern a Functional Class of Proteins
The DNA-binding helix-turn-helix structural motif plays an essential role in a variety of cellular pathways that include transcription, DNA recombination and repair, and DNA replication. Current methods for identifying the motif rely on amino acid sequence, but since members of the motif belong to different sequence families that have no sequence homology to each other, these methods have been unable to identify all motif members.
A new method based on three-dimensional structure was created that involved the following steps:38 (1) choosing a conserved component of the motif, (2) measuring structural features relative
|
37 |
For more information, see http://zlab.bu.edu. |
|
38 |
W.A. McLaughlin and H.M. Berman, “Statistical Models for Discerning Protein Structures Containing the DNA-binding Helix-Turn-Helix Motif,” Journal of Molecular Biology 330(1):43-55, 2003. |
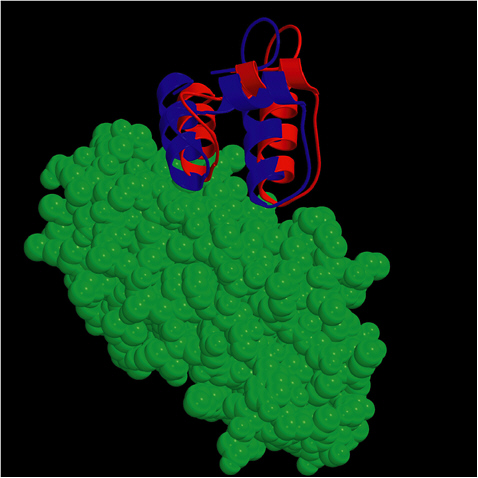
FIGURE 5.1 The ZDOCK/RDOCK prediction for dockerin (in red) superposed on the crystal structure for CAPRI Target 13, cohesin/dockerin. SOURCE: Courtesy of Brian Pierce and Zhiping Weng, Boston University.
to that component, and (3) creating classification models by comparing measurements of structures known to contain the motif to measurements of structures known not to contain the motif. In this case, the conserved component chosen was the recognition helix (i.e., the alpha helix that makes sequence-specific contact with DNA), and two types of relevant measurements were the hydrophobic area of interaction between secondary structure elements (SSEs) and the relative solvent accessibility of SSEs.
With a classification model created, the entire Protein Data Bank of experimentally measured structures was searched and new examples of the motif were found that have no detected sequence homology with previously known examples. Two such examples are Esa1 histone acetyltransferase and isoflavone 4-O-methyltransferase. The result emphasizes an important utility of the approach: sequence-based methods used to discern a functional class of proteins may be supplemented through the use of a classification model based on three-dimensional structural information.
5.4.1.3 Molecular Docking
Using a simple, uniform representation of molecular surfaces that requires minimal parameterization, Jain39 has constructed functions that are effective for scoring protein-ligand interactions, quantitatively comparing small molecules, and making comparisons of proteins in a manner that does not depend on protein backbone. These methods rely on computational approaches that are rooted in understanding the physics of molecular interactions, but whose functional forms do not resemble those used in physics-based approaches. That is, this problem can be treated as a pure computer science problem that can be solved using combinations of scoring and search or optimization techniques parameterized with the use of domain knowledge. The approach is as follows:
-
Molecules are approximated as collections of spheres with fixed radii: H = 1.2; C = 1.6; N = 1.5; O = 1.4; S = 1.95; P = 1.9; F = 1.35; Cl = 1.8; Br = 1.95; I = 2.15.
-
A labeling of the features of polar atoms is superimposed on the molecular representation: polarity, charge, and directional preference (Figure 5.2, subfigures A and B).
-
A scoring function is derived that, given a protein and a ligand in some relative alignment, yields a prediction of the energy of interaction.
-
The function is parameterized in terms of the pairwise distances between molecular surfaces.
-
The dominant terms are a hydrophobic term that characterizes interactions between nonpolar atoms and a polar term that captures complementary polar contacts with proper directionality.
-
The parameters of the function were derived from empirical binding data and 34 protein-ligand complexes that were experimentally determined.
-
The scoring function is described in Figure 5.2, Subfigure C. The hydrophobic term peaks at approximately 0.1 unit with a slight surface interpenetration. The hydrophobic term for an ideal hydrogen bond peaks at 1.25 units, and a charged interaction (tertiary amine proton (+1.0) to a charged carboxylate (−0.5)) peaks at about 2.3 units. Note that this scoring function looks nothing like a force field derived from molecular mechanics.
-
Figure 5.2, Subfigure D compares eight docking methods on screening efficiency using thymidine kinase as a docking target. For the test, 10 known ligands and 990 random ligands were used. Particularly at low false-positive rates (low database coverage), the scoring function approach shows substantial improvements over the other methods.
5.4.1.4 Computational Analysis and Recognition of Functional and Structural Sites in Protein Structures40
Structural genomics initiatives are producing a great increase in protein three-dimensional structures determined by X-ray and nuclear magnetic resonance technologies as well as those predicted by computational methods. A critical next step is to study the relationships between protein structures and functions. Studying structures individually entails the danger of identifying idiosyncratic rather than conserved features and the risk of missing important relationships that would be revealed by statisti-
|
39 |
See A.N. Jain, “Scoring Noncovalent Protein Ligand Interactions: A Continuous Differentiable Function Tuned to Compute Binding Affinities,” Journal of Computer-Aided Molecular Design 10(5):427-440, 1996; W. Welch, J. Ruppert, and A.N. Jain, “Hammerhead: Fast, Fully Automated Docking of Flexible Ligands to Protein Binding Sites,” Chemistry & Biology 3(6):449-462, 1996; J. Ruppert, W. Welch, and A.N. Jain, “Automatic Identification and Representation of Protein Binding Sites for Molecular Docking,” Protein Science 6(3):524-533, 1997; A.N. Jain, “Surflex: Fully Automatic Flexible Molecular Docking Using a Molecular Similarity-based Search Engine,” Journal of Medicinal Chemistry 46(4):499-511, 2003; A.N. Jain, “Ligand-Based Structural Hypotheses for Virtual Screening.” Journal of Medicinal Chemistry 47(4):947-961, 2004. |
|
40 |
Section 5.4.1.4 is based on material provided by Liping Wei, Nexus Genomics, Inc., and Russ Altman, Stanford University, personal communication, December 4, 2003. |
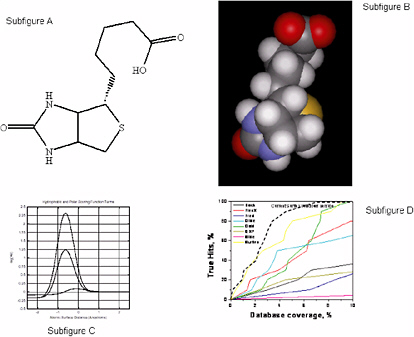
FIGURE 5.2 A Computational Approach to Molecular Docking. SOURCE: Courtesy of A.N. Jain, University of California, San Francisco.
cally pooling relevant data. The expected surfeit of protein structures provides an opportunity to develop computational methods for collectively examining multiple biological structures and extracting key biophysical and biochemical features, as well as methods for automatically recognizing these features in new protein structures.
Wei and Altman have developed an automated system known as FEATURE that statistically studies the important functional and structural sites in protein structures such as active sites, binding sites, disulfide bonding sites, and so forth. FEATURE collects all known examples of a type of site from the Protein Data Bank (PDB) as well as a number of control “nonsite” examples. For each of them, FEATURE computes the spatial distributions of a large set of defined biophysical and biochemical properties spanning multiple levels of details in order to capture conserved features beyond basic amino acid sequence similarity. It then uses a nonparametric statistical test, the Wilcoxin Rank Sum Test, to find the features that are characteristic of the sites, in the context of control nonsites. Figure 5.3 shows the statistical features of calcium binding sites.
By using a Bayesian scoring function that recognizes whether a local region within a three-dimensional structure is likely to be any of the sites and a scanning procedure that searches the whole structure for the sites, FEATURE can also provide an initial annotation of new protein structures. FEATURE has been shown to have good sensitivity and specificity in recognizing a diverse set of site types, including active sites, binding sites, and structural sites and is especially useful when the sites do not have conserved residues or residue geometry. Figure 5.4 shows the result of searching for ATP (adenosine triphosphate) binding sites in a protein structure.
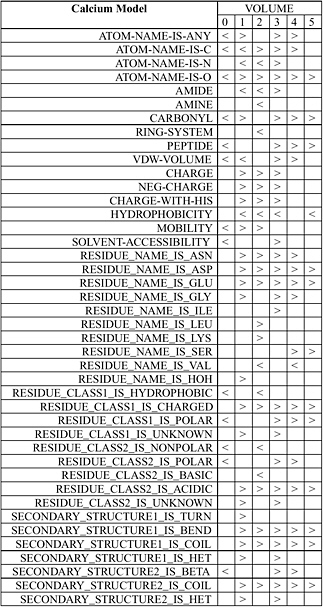
FIGURE 5.3 Statistical features of calcium binding sites determined by FEATURE. The volumes in this case correspond to concentrate radial shells 1 Å in thickness around the calcium ion or a control nonsite location. The column shows properties that are statistically significantly different (at p-value cutoff of 0.01) in at least one volume between known examples of calcium binding sites and those of control nonsites. A “>” (greater than sign) indicates that the calcium binding sites have significantly higher value for that property at that volume compared to control nonsites. A “<” (less than sign) indicates the opposite. An empty box indicates the lack of statistically significant difference. SOURCE: Courtesy of Liping Wei, Nexus Genomics, Inc., and Russ Altman, Stanford University, personal communication, December 4, 2003.
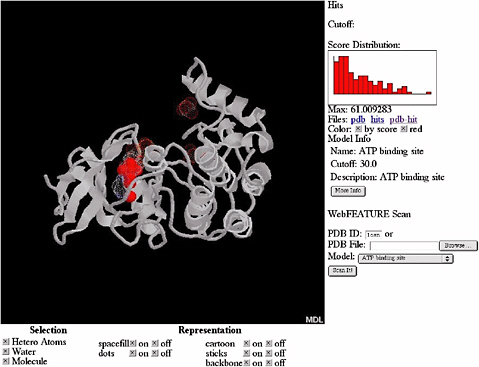
FIGURE 5.4 Results of automatic scanning for ATP binding sites in the structure of casein kinase (PDB ID 1csn) using WebFEATURE, a freely available, Web-based server of FEATURE. The solid red dots show the prediction of FEATURE, they correspond correctly with the true location of the ATP binding site, shown as white cloud. SOURCE: Courtesy of Liping Wei, Nexus Genomics, Inc., and Russ Altman, Stanford University, personal communication, December 4, 2003.
5.4.2 Cell Biology and Physiology
5.4.2.1 Cellular Modeling and Simulation Efforts
Cellular simulation requires a theoretical framework for analyzing the interactions of molecular components, of modules made up of those components, and of systems in which such modules are linked to carry out a variety of functions. The theoretical goal is to quantitatively organize, analyze, and interpret complex data on cell biological processes, and experiments provide images, biochemical and electrophysiological data on the initial concentrations, kinetic rates, and transport properties of the molecules and cellular structures that are presumed to be the key components of a cellular event.41 A simulation embeds the relevant rate laws and rate constants for the biochemical transformations being modeled. Based on these laws and parameters, the model accepts as initial conditions the initial concentrations, diffusion coefficients, and locations of all molecules implicated in the transformation, and generates predictions for the concentration of all molecular species as a function of time and space. These predictions are compared against experiment, and the differences between prediction and experiment are used to further refine the model. If the system is perturbed by the addition of a ligand, electrical stimulus, or other experimental intervention, the model should be capable of predicting changes as well in the relevant spatiotemporal distributions of the molecules involved.
|
41 |
A brief introduction to the rationale underlying cellular modeling can be found at the National Resource for Cell Analysis and Modeling (http://www.nrcam.uchc.edu/applications/applications.html). |
TABLE 5.1 Sample Simulation Programs
|
Name |
Descriptorsa |
Web Site |
|
Gepasi/Copasi |
fkFW |
|
|
BioSim |
qWMU |
|
|
Jarnac |
krfbFWS |
|
|
MCELL |
rsU |
|
|
Virtual Cell |
ksDFWMU |
|
|
E-Cell |
kWUS |
|
|
Neuron |
ksFWMUS |
|
|
Genesis |
ksUS |
|
|
Plas |
kfbFW |
|
|
Ingeneue |
qkFMWUS |
|
|
DynaFit |
kfW |
|
|
Stochsim |
rS |
|
|
T7 Simulator |
kUS |
|
|
Molecularizer/Stochastirator |
krUS |
|
|
NOTE: All packages have facilities for chemical kinetic simulation of one sort or another. Some are better designed for metabolic systems, others for electrochemical systems, and still others for genetic systems. aThe descriptors are as follows: b, bifurcation analyses and steady-state calculation; f, flux balance or metabolic control and related analyses; k, deterministic kinetic simulation; q, qualitative simulation; r, stochastic process models; s, spatial processes; D, database connectivity; F, fitting, sensitivity, and optimization code; M, runs on Macintosh; S, source code available; U, runs on Linux or Unix; W, runs on windows. |
||
There are many different tools for simulating and analyzing models of cellular systems (Table 5.1). More general tools, such as Mathematica and MATLAB or other systems that can be used for solving systems of differential or stochastic-differential equations, can be used to develop simulations, and because these tools are commonly used by many researchers, their use facilitates the transfer of models among different researchers. Another approach is to link data gathering and biological information systems to software that can integrate and predict behavior of interacting components (currently, researchers are far from this goal, but see Box 5.5 and Box 5.6). Finally, several platform-independent model specification languages are under development that will facilitate greater sharing and interoperability. For example, SBML,42 Gepasi,43 and CellML44 are specialized systems for biological and biochemical modeling. Madonna45 is a general-purpose system for solving a variety of equations (differential equations, integral equations, and so on).
Rice and Stolovitzky describe the task of inferring signaling, metabolic, or gene regulatory pathways from experimental data as one of reverse engineering.46 They note that automated, high-throughput methods that collect species- and tissue-specific datasets in large volume can help to deal with the risks in generalizing signaling pathways from one organism to another. At the same time, fully detailed kinetic models of intracellular processes are not generally feasible. Thus, one step is to consider models that describe network topology (i.e., that identify the interactions between nodes in the system—genes, proteins, metabolites, and so on). A model with more detail would describe network topology that is causally directional (i.e., that specifies which entities serve as input to others). Box 5.7 provides more detail.
|
Box 5.5 BioSPICE, the Biological Simulation Program for Intra-Cellular Evaluation, is in essence a modeling framework that provides users with model components, tools, databases, and infrastructure to develop predictive dynamical models of cellular function. BioSPICE seeks to promote a synergy between experiment and model, in which model predictions drive experiment and experimental results identify areas in which a given model needs to be improved, and the intent is that researchers go from data to models to analysis and hypothesis generation, iteratively refining their understanding of the biological processes. An important component of BioSPICE is a library of experimentally validated (and hence trusted) model components that can be used as starting points in larger-scale simulations, as elements from this library are composed in new ways or adapted to investigate other biological systems. Many biological parts and processes are represented as components, including phosphorylization events, chemotaxis, and conserved elements of various pathways. Also, because BioSPICE is designed as an open-source environment, it is hoped that the user community itself will make available a repertoire of model components that span a wide range of spatial, temporal, and functional scales, including those that simulate a single chemical reaction with high fidelity, those that simulate entire pathways, and those that simulate more abstract higher-order motifs. BioSPICE tools are intended to enable researchers to use public databases and local resources to formulate a qualitative description of the cellular process of interest (e.g., models of networks or pathways), to annotate the links between entities with biochemical interactions, and finally to convert this annotated qualitative description to a set of equations that can be analyzed and simulated. In addition, BioSPICE provides a number of simulation engines with the capability to simulate ordinary, stochastic, and partial differential equations and other tools that support stability and bifurcation analysis and qualitative reasoning that combines probabilistic and temporal logic. SOURCE: Sri Kumar, Defense Advanced Research Projects Agency, June 30, 2003. |
An example of a cellular simulation environment is E-CELL, an open-source system for modeling biochemical and genetic processes. Organizationally, E-CELL is an international research project aimed at developing theoretical and functioning technologies to allow precise “whole cell” simulation; it is supported by the New Energy and Industrial Technology Development Organization (NEDO) of Japan.
E-CELL simulations allow a user to model hypothetical virtual cells by defining functions of proteins, protein-protein interactions, protein-DNA interactions, regulation of gene expression, and other features of cellular metabolism.47 Based on reaction rules that are known through experiment and assumed concentrations of various molecules in various locations, E-CELL numerically integrates differential equations implicitly described in these reaction rules, resulting in changes over time in the concentrations of proteins, protein complexes, and other chemical compounds in the cell.
Developers hope E-CELL will ultimately allow investigators a cheap, fast way to screen drug candidates, study the effects of mutations or toxins, or simply probe the networks that govern cell behavior. One application of E-CELL has been to construct a model of a hypothetical cell capable of
|
47 |
See http://www.e-cell.org/project/. For a view of the computer science challenges, see also K. Takahashi, K. Yugi, K. Hashimoto, Y. Yamada, C.J.F. Pickett, and M. Tomita, “Computational Challenges in Cell Simulation: A Software Engineering Approach,” IEEE Intelligent Systems 17(5):64-71, 2002. |
|
Box 5.6 A variety of computer-aided models has been developed to simulate biological networks, typically focusing on specific cellular processes or single pathways.1 Cytoscape is a modeling environment particularly suited to the analysis of global data on network interactions (from high-throughput screens for protein-protein, protein-DNA, and gene interactions) and on network states (including data on gene expression, protein abundance, and metabolite concentrations.) The Java-based, open-source software uses plug-ins to incorporate analyses of individual processes and pathways.2 A model in Cytoscape is organized as a network graph, with molecular species represented as nodes and interactions represented as edges between nodes. Nodes and edges are mapped to specific data values called attributes that can be text strings, discrete or continuous numbers, URLs, or lists, either loaded from a data repository or generated dynamically. Layered onto attributes are annotations, which represent a hierarchical classification of progressively more specific descriptions (such as functions) of groups of nodes and edges. It is possible to have many levels of annotation active simultaneously, each displayed as a different attribute of a node or edge. To visualize the network, Cytoscape supports several layout algorithms that fix the relative locations of specific nodes and edges in the graphical window. An attribute-to-visual mapping facility allows attributes to determine the appearance (color, shape, size) of their associated nodes and edges. Graph selection and filtering reduces the complexity of the network by selectively displaying subsets of nodes and edges according to a variety of criteria. Cytoscape’s plug-in extensibility addresses the challenge of bridging high-level information (relationships among network components) with lower-level information (reaction rates, binding constants) of specific processes. A plug-in that organizes the network layout according to putative functional attributes of genes was used to study energy transduction pathways in Halobacterium.3 Another plug-in allows Cytoscape to simulate stochastic SBML-biochemical models.4 The authors hope a community will further develop and enhance Cytoscape. SOURCE: Adapted from P. Shannon, A. Markiel, O. Ozier, N.S. Baliga, J.T. Wang, D. Ramage, N. Amin et al., “Cytoscape: A Software Environment for Integrated Models of Biomolecular Interaction Networks,” Genome Research 13(11):2498-2504, 2003. |
transcription, translation, energy production, and phospholipid synthesis with only 127 genes. Most of these genes were taken from Mycoplasma genitalium, the organism with the smallest known chromosome (the complete genome sequence is 580 kilobases).48 E-CELL has also been used to construct a computer model of the human erythrocyte,49 to estimate a gene regulatory network and signaling
|
48 |
M. Tomita, K. Hashimoto, K. Takahashi, Y. Matsuzaki, R. Matsushima, K. Saito, K. Yugi, et al., “E-CELL Project Overview: Towards Integrative Simulation of Cellular Processes,” Genome Informatics 9:242-243, 1998, available at http://giw.ims.u-tokyo.ac.jp/giw98/cdrom/Poster-pdf/poster02.pdf. |
|
49 |
M. Tomita et al., “In Silico Analysis of Human Erythrocyte Using E-Cell System,” poster session, The Future of Biology in the 21st Century: 2nd International Conference on Systems Biology, California Institute of Technology, Pasadena, November 4-7, 2001, available at http://www.icsb2001.org/Posters/032_kinoshita.pdf. |
|
Box 5.7 On Topology. In this level, we are only concerned with identifying the interaction between nodes (genes, proteins, metabolites, etc.) in the system. The goal is the generation of a diagram of non-directional connections between all interacting nodes. For example, many have sought to develop large-scale maps of protein–protein interactions derived from various sources. Two-hybrid studies have produced genome-wide interaction maps for E. coli bacteriophage T7, yeast, Drosophila, and C. elegans. Although this approach can be comprehensive in regard to being genome wide, many interactions are not reproducible (a potential source of false negatives) and putative interactions occur between unlikely protein combinations (a potential source of false positives)…. Another approach to constructing large-scale connection maps is by mining databases. Specific databases of protein interactions are being developed, the largest of which are DIP and BIND. These databases combine data from many high-throughput experiments along with data from other sources, such as published literature…. Along other lines, investigators have attempted to identify topological links by analyzing the dynamic behavior of networks. Pioneering work in this area shows that metabolic network topologies can be derived from correlation of time-series measurements of species concentrations. The method is further refined to better identify connections in non-linear systems using mutual information instead of correlation. In another method, pair-wise correlation of gene expression data is used to predict functional connections that could then be combined into “relevance networks” of linked genes. Other methods may seek to use some combination of data sources, although this may not be completely straightforward. On Inferring Qualitative Connections. In this level, we include not only associations between cellular entities but also the causal relations of such associations, such as which entities serve as input to others…. Researchers have proposed methods that infer connectivities from the estimations of the Jacobian matrix for metabolic, signaling, and genetic networks. Ross and co-workers have proposed a method based on propagated perturbations of chemical species that can reconstruct causal sequences of reactions from synthetic and experimental data. To reconstruct gene regulatory systems, methods include fuzzy logic analysis of facilitator/repressor groups in the yeast cell cycle and reconstruction of binary networks. However, the wide application of such methods is often limited because the continuous nature of many biological systems prevents easy abstractions into coarser signals. Recently, there has been considerable work using Bayesian network inference. Examples include inferring gene regulation using gene expression data from the yeast cell cycle or using data from synthetic gene networks. SOURCE: Reprinted by permission from J.J. Rice and G. Stolovitzky, “Making the Most of It: Pathway Reconstruction and Integrative Simulation Using the Data at Hand,” Biosilico 2(2):70-77. Copyright 2004 Elsevier. (References omitted.) |
pathway involved in the circadian rhythm of Synechococcus sp. PCC 7942,50 and to model mitochondrial energy metabolism and metabolic pathways in rice.51
Another cellular simulation environment is the Virtual Cell, developed at the University of Connecticut Health Center.52 The Virtual Cell is a tool for experimentalists and theoreticians for computationally testing hypotheses and models. To address a particular question, these mechanisms (chemical kinetics, membrane fluxes and reactions, ionic currents, and diffusion) are combined with a specific set of experimental conditions (geometry, spatial scale, time scale, stimuli) and applicable conservation laws to specify
|
50 |
F. Miyoshi et al., “Estimation of Genetic Networks of the Circadian Rhythm in Cyanobacterium Using the E-CELL system,” poster session, presented at US-Japan Joint Workshop on Systems Biology of Useful Microorganisms, September 6-18, 2002, Keio University, Yamagata, Japan, available at http://nedo-doe.jtbcom.co.jp/abstracts/35.pdf. |
|
51 |
E. Wang et al., “e-Rice Project: Reconstructing Plant Cell Metabolism Using E-CELL System,” poster session presented at Systems Biology: The Logic of Life—3rd International Conference on Systems Biology, December 13-15, 2002, Karolinska Institutet, Stockholm, available at http://www.ki.se/icsb2002/pdf/ICSB_222.pdf. |
|
52 |
L.M. Loew and J.C. Schaff, “The Virtual Cell: A Software Environment for Computational Cell Biology,” Trends in Biotechnology 19(10):401-406, 2001. |
a concrete system of differential and algebraic equations. This experimental geometry may assume well-mixed compartments or a one-, two-, or three-dimensional spatial representation (e.g., experimental images from a microscope). Models are constructed from biochemical and electrophysiological data mapped to appropriate subcellular locations in images obtained from a microscope. A variety of modeling approximations are available including pseudo-steady state in time (infinite kinetic rates) or space (infinite diffusion or conductivity). In the case of spatial simulations, the results are mapped back to experimental images and can be analyzed by applying the arsenal of image-processing tools that is familiar to a cell biologist. Section 5.4.2.4 describes a study undertaken within the Virtual Cell framework.
Simulation models can be useful for many purposes. One important use is to facilitate an understanding of what design properties of an intracellular network are necessary for its function. For example, von Dassow et al.53 used a simulation model of the gap and pair-rule gene network in Drosophila melanogaster to show that the structure of the network is sufficient to explain a great deal of the observed cellular patterning. In addition, they showed that the network behavior was robust to parameter variation upon the addition of hypothetical (but reasonable) elements to the known network. Thus, simulations can also be used to formally propose and justify new hypothetical mechanisms and predict new network elements.
Another use of simulation models is in exploring the nature of control in networks. An example of exploring network control with simulation is the work of Chen et al.54 in elucidating the control of different phases of mitosis and explaining the impact of 50 different mutants on cellular decisions related to mitosis.
Simulations have also been used to model metabolic pathways. For example, Edwards and Palsson developed a constraint-based genome-scale simulation of Escherichia coli metabolism (Box 5.8). By applying successive constraints (stoichiometric, thermodynamic, and enzyme capacity constraints) to the metabolic network, it is possible to impose limits on cellular, biochemical, and systemic functions, thereby identifying all allowable solutions (i.e., those that do not violate the applicable constraints). Compared to the detailed theory-based models, such an approach has the major advantage that it does not require knowledge of the kinetics involved (since it is concerned only with steady-state function). (On the other hand, it is impossible to implement without genome-scale knowledge, because only genome-scale knowledge can bound the system in question.) Within the space of allowable solutions, a particular solution corresponds to the maximization of some selected function, such as cellular growth or a response to some environmental change. A more robust model accounting for a larger number of pathways is also described in Box 5.8.
The Edwards and Palsson model has been used to predict the evolution of E. coli metabolism under a variety of environmental conditions. In the words of Ibarra et al., “When placed under growth selection pressure, the growth rate of E. coli on glycerol reproducibly evolved over 40 days, or about 700 generations, from a sub-optimal value to the optimal growth rate predicted from a whole-cell in silico model. These results open the possibility of using adaptive evolution of entire metabolic networks to realize metabolic states that have been determined a priori based on in silico analysis.”55
Simulation models can also be used to test design ideas for engineering networks in cells. For example, very simple models have been used to provide insight into a genetic oscillator and a switch in E. coli.56 Models have also been used to test designs for the control of cellular networks, as illustrated by
|
Box 5.8 A. In Silico Model1 The Escherichia coli MG1655 genome has been completely sequenced. The annotated sequence, biochemical information, and other information were used to reconstruct the E. coli metabolic map. The stoichiometric coefficients for each metabolic enzyme in the E. coli metabolic map were assembled to construct a genome-specific stoichiometric matrix. The E. coli stoichiometric matrix was used to define the system’s characteristics and the capabilities of E. coli metabolism. The effects of gene deletions in the central metabolic pathways on the ability of the in silico metabolic network to support growth were assessed, and the in silico predictions were compared with experimental observations. It was shown that based on stoichiometric and capacity constraints the in-silico analysis was able to qualitatively predict the growth potential of mutant strains in 86% of the cases examined. Herein, it is demonstrated that the synthesis of in silico metabolic genotypes based on genomic, biochemical, and strain-specific information is possible, and that systems analysis methods are available to analyze and interpret the metabolic phenotype. B. Genome-scale Model2 An expanded genome-scale metabolic model of E. coli (iJR904 GSM/GPR) has been reconstructed which includes 904 genes and 931 unique biochemical reactions. The reactions in the expanded model are both elementally and charge balanced. Network gap analysis led to putative assignments for 55 open reading frames (ORFs). Gene to protein to reaction associations (GPR) are now directly included in the model. Comparisons between predictions made by iJR904 and iJE660a models show that they are generally similar but differ under certain circumstances. Analysis of genome-scale proton balancing shows how the flux of protons into and out of the medium is important for maximizing cellular growth…. E. coli iJR904 has improved capabilities over iJE660a [a model that accounted for 660 genes and 627 unique biochemical reactions and was itself a slight modification of the original model described in the above paragraph]. iJR904 is a more complete and chemically accurate description of E. coli metabolism than iJE660a. Perhaps most importantly, iJR904 can be used for analyzing and integrating the diverse datasets. iJR904 will help to outline the genotype-phenotype relationship for E. coli K-12, as it can account for genomic, transcriptomic, proteomic and fluxomic data simultaneously.
|
Endy and Yin in using their T7 model to propose a pharmaceutical strategy for preventing both T7 propagation and the development of drug resistance through mutation.57
Given observed cell behavior, simulation models can be used to suggest the necessity of a given regulatory motif or the sufficiency of known interactions to produce the phenomenon. For example, Qi et al. demonstrate the sufficiency of membrane energetics, protein diffusion, and receptor-binding kinetics to generate a particular dynamic pattern of protein location at the synapse between two immune cells.58
The following sections describe several simulation studies in more detail.
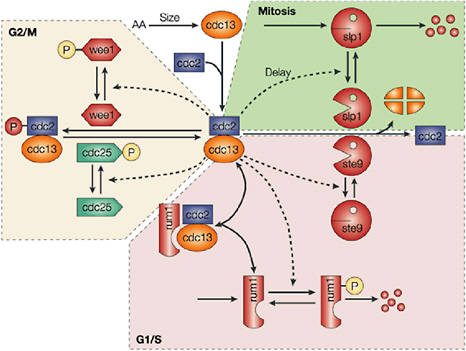
FIGURE 5.5 The cell-cycle control system in fission yeast. This system can be divided into three modules, which regulate the transitions from G1 into S phase, from G2 into M phase, and exit from mitosis. SOURCE: J.J. Tyson, K. Chen, and B. Novak, “Network Dynamics and Cell Physiology,” Nature Reviews of Molecular Cell Biology 2(12):908-916, 2001. Figure and caption reproduced with permission from Nature Reviews of Molecular Cell Biology. Copyright 2001 Macmillan Magazines Ltd.
5.4.2.2 Cell Cycle Regulation
Biological growth and reproduction depend ultimately on the cycle of DNA synthesis and physical separation of the replicate DNA molecules within individual cells. In eukaryotes, these processes are triggered by cyclin-dependent protein kinases (CDKs). In fission yeast, CDK activity (cdc2 = kinase subunit, cdc13 = cyclin subunit) is regulated by a network of protein interactions (Figure 5.5), including cyclin synthesis and degradation, phosphorylation of cdc2, and binding to an inhibitor.
A network of such complexity, with multiple feedback loops, cannot be understood thoroughly by casual intuition. Instead, the network is converted into a set of nonlinear differential equations, and the physiological implications of these equations are studied.59 Numerical simulation of the equations (Figure 5.6) provides complete time courses of every component and can be interpreted in terms of observable events in the cell cycle. Simulations can be run, not only of wild-type cells but also of dozens of mutants constructed by deleting or overexpressing each component singly or in multiple combinations. From the observed phenotypes of these mutants it is possible to reverse-engineer the regulatory network and the set of kinetic constants associated with the component reactions.
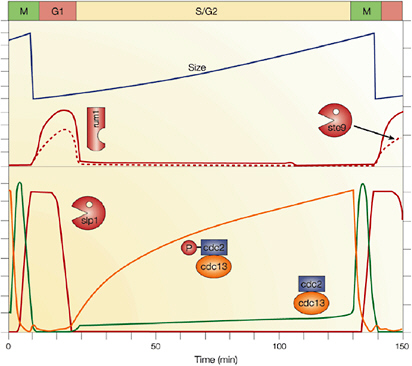
FIGURE 5.6 Simulated time courses of cdc2 and related proteins during the cell cycle of fission yeast. Numerical integration of the full set of differential equations that describe the wiring diagram in Figure 5.5 yields these time courses. Time is expressed in minutes; all other variables are given in arbitrary units. “Size” refers to the number of ribosomes per nucleus. Notice the brief G1 phase, when ste9 is active and rum1 is abundant. After a long S/G2 phase, during which cdc2 is tyrosine phosphorylated, the cell enters M phase, when cdc25 removes the inhibitory phosphate group. After some delay, slp1 activates and degrades cdc13. As cdc2–cdc13 activity falls, the cell exits mitosis. Size decreases twofold at nuclear division. SOURCE: J.J. Tyson, K. Chen, and B. Novak, “Network Dynamics and Cell Physiology,” Nature Reviews of Molecular Cell Biology 2(12):908-916, 2001. Figure and caption reproduced with permission from Nature Reviews of Molecular Cell Biology. Copyright 2001 Macmillan Magazines Ltd.
For understanding the dynamics of molecular regulatory systems, bifurcation theory is a powerful complement to numerical simulation. The bifurcation diagram in Figure 5.7 presents recurrent solutions (steady states and limit cycle oscillations) of the differential equations as functions of cell size. The control system has three characteristic steady states: low cdc2 activity (G1 = pre-replication), medium cdc2 activity (S/G2 = replication and post-replication), and high cdc2 activity (M = separation of replicated DNA molecules). G1 and S/G2 are stable steady states; M is unstable because of a negative feedback loop as shown in Figure 5.5 (cdc2-cdc13 activates Slp1, which degrades cdc13).
When the time courses of size and cdc2 activity from Figure 5.6 are superimposed on the bifurcation diagram (curve labeled “size”), one sees how progress through the cell cycle is governed by the bifurcations that turn stable steady states into unstable steady states and/or stable oscillations. A mutation changes a specific rate constant, which changes the locations of the bifurcation points in Figure 5.7, which changes how cells progress through (or halt in) the cell cycle. By this route one can trace the dynamical consequences of genetic information all the way to observable cell behavior.
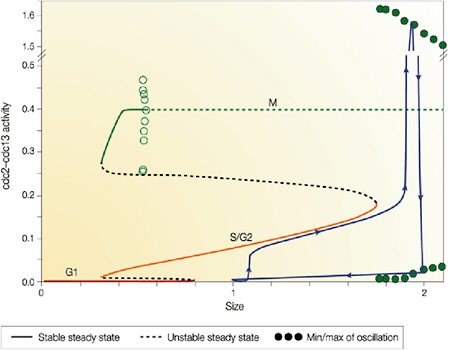
FIGURE 5.7 Bifurcation diagram for the full cell-cycle control network…. [T]he full diagram is not a simple sum of the bifurcation diagrams of its modules. In particular, oscillations around the M state are greatly modified in the composite control system. Superimposed on the bifurcation diagram is a “cell-cycle orbit” (line on the right with arrows): from the time courses in Figure 5.6, we plot size on the abscissa and cdc2–cdc13 activity on the ordinate for representative times between birth and division. Notice that, at small cell size, all three modules support stable steady states. Notice how the cell-cycle orbit follows the attractors of the control system. SOURCE: J.J. Tyson, K. Chen and B. Novak, “Network Dynamics and Cell Physiology,” Nature Reviews Molecular Cell Biology 2(12):908-916, 2001. Figure and caption, reproduced with permission from Nature Reviews Molecular Cell Biology. Copyright 2001 Macmillan Magazines Ltd.
5.4.2.3 A Computational Model to Determine the Effects of SNPs in Human Pathophysiology of Red Blood Cells
The completion of the Human Genome Project has led to the construction of single nucleotide polymorphism (SNP) maps. Single nucleotide polymorphisms are common DNA sequence variations among individuals. A result of the construction of SNP maps is to determine the effects of SNPs on the development of disease(s) since sequence variations can lead to altered biological function or disease.
Currently, it is difficult to determine the causal relationship between the variations in sequence, SNPs, and the physiological function. One way to analyze this relationship is to create computational models or simulations of biological processes. Since erythrocyte (red blood cell) metabolism has been studied extensively over the years and many SNPs have been characterized, Jamshidi et al. used this information to build their computational models.60
Two important metabolic enzymes, glucose-6-phosphate dehydrogenase (G6PD) and pyruvate kinase (PK), were studied for alterations in their kinetic properties in an in silico model to calculate the overall effect of SNPs on red blood cell function. Defects in these enzymes cause hemolytic anemia.
Clinical data taken from the published literature were used for the measured values of the kinetic parameters. These values were then used in model simulations to determine whether a direct link could be established between the SNP and the disease (anemia).
The computational modeling revealed two results. For the G6PD and PK variants analyzed, there appeared to be no clear relationship between their kinetic properties as a function of sequence variation or SNP. However, upon assessment of overall biological function, a correlation was found between the sequence variation of G6PD and the severity of the clinical disease. Thus, in silico modeling of biological processes may aid in analysis and prediction of SNPs and pathophysiological conditions.
5.4.2.4 Spatial Inhomogeneities in Cellular Development
Simulation models can be used to provide insight into the significance of spatial inhomogeneities. For example, the interior of living cells does not resemble at all a uniform aqueous solution of dissolved chemicals, and yet this is the implicit assumption underlying many views of the cell. This assumption serves traditional biochemistry and molecular biology reasonably well, but research increasingly demonstrates that the physical locations of specific molecules are crucial. Multiprotein complexes act as machines for internal movements or as integrated circuits in signaling. Messenger RNA molecules are transported in a highly directed fashion to specific regions of the cell (in nerve axons, for example). Cells adopt highly complex shapes and undergo complex movements thanks to the matrix of protein filaments and associated proteins within their cytoplasm.
5.4.2.4.1 Unraveling the Physical Basis of Microtubule Structure and Stability
Microtubules are cylindrical polymers found in every eukaryotic cell. Microtubles play a role in cellular architecture and as molecular train tracks used to transport everything from chromosomes to drug molecules. An understanding of microtubule structure and function is key not just to unraveling fundamental mechanisms of the cell, but also to opening the way to the discovery of new antiparasitic and anticancer drugs.
Until now, researchers have known that the microtubules, constructed of units called protofilaments in a hollow, helical arrangement, are rigid but not static, and undergo periods of growth and sudden collapse. Yet the mechanism for this construction-destruction had eluded researchers.
Over the past several years, McCammon and his colleagues have pioneered the use of a combination of an atomically detailed model for a microtubule and large-scale computations using the adaptive Poisson-Boltzmann Solver to create a high-resolution, 1.25-million-atom map of the electrostatic interactions within the microtubule.61
More recently, David Sept and Nathan Baker of Washington University and McCammon used the same technique to successfully predict the helicity of the tubule with a striking correspondence to experimental observation.62 Based on the lateral interactions between protofilaments, they determined that the microtubule prefers to be in a configuration in which the protofilaments assemble with a seam at each turn, rather than spiraling smoothly upward with alpha and beta monomers wrapping the microtubule as if it were a barber’s pole. At the end of each turn, a chain of alphas is trailed by a chain of betas, then after that turn, a chain of alphas, and so on. It is as if the red and white stripes on the barber’s pole traded places with every twist (Figure 5.8).
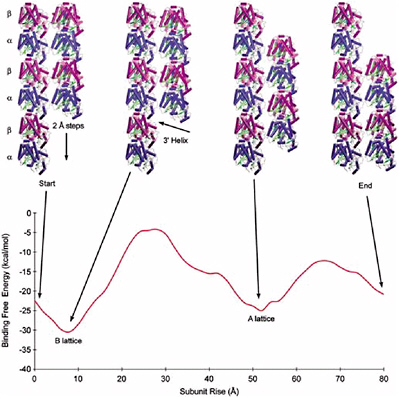
FIGURE 5.8 The binding free energy between two protofilaments as a function of the subunit rise between adjacent dimmers. Sept et al. used electrostatic calculations to determine the binding energy between two protofilaments as a function of the subunit rise between adjacent dimers. Viewed from the growing (+) end of the tubule, the graph demonstrates the most favorable configuration at various points during assembly. SOURCE: Reprinted by permission from D. Sept, N.A. Baker, and J.A. McCammon, “The Physical Basis of Microtubule Structure and Stability,” Protein Science 12:2257-2261, 2003. Copyright 2003 by the Protein Society.
5.4.2.4.2 The Movement of Listeria Bacteria
Alberts and Odell have developed a computational model of Listera monocytogenes based on an explicit simulation of a large number of monomer-scale biochemical and mechanical interactions,63 representing all protein-protein binding interactions with on-rate and off-rate kinetic equations. These equations characterize individual actin filaments: the bulk properties of the actin “gel” arise from the contributions of the many individual filaments of the actin network; and the growth of any particular filament depends on that filament’s precise location, orientation, and biochemical state, all of which change through time. Mechanical interactions, which resolve collisions and accommodate the stretching of protein-protein linkages, follow Newton’s laws.
The model is based on a large set of differential equations that determine how the relevant state variables change with time. These equations are solved numerically, taking into account the fact that discontinuities in time occur frequently as objects suddenly collide and as objects suddenly spring into existence or disappear (due to new filament nucleation and depolymerization). The model accommo-
|
63 |
J.B. Alberts and G.M. Odell, “In Silico Reconstitution of Listeria Propulsion Exhibits Nano-Saltation,” PLoS Biology 2(12):e412, 2004, available at http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=532387. |
dates arbitrary geometries, explicit stochastic input, and specific small-scale events. Because the model is built from the ground up, it can predict emergent behavior that would not be apparent from intuition or qualitative description of the behavior of individual parts. On the other hand, the simulation requires multiple runs of its stochastic, individual molecule-based model, and parametric relationships emerge not from closed-form equations that demonstrate qualitative functional dependencies but from ensembles of many repeated simulations.
The trajectories generated by this model of L. monocytogenes motility display repeated runs and pauses that closely resemble the actual nanoscale measurements of bacterial motion.64 Further analysis of the simulation state at the beginning and ends of simulated pauses indicate that there is no characteristic step-size or pause duration in these simulated trajectories and that pauses can be caused both by correlated Brownian motion and by synchronously strained sets of ActA-actin filament mechanical links.
5.4.2.4.3 Morphological Control of Spatiotemporal Patterns of Intracellular Signaling
Fink and Slepchenko studied calcium waves evoked by activation of the bradykinin receptor in the plasma membrane of a neuronal cell.65 The neuromodulator bradykinin applied to the cells produced a calcium wave that starts in the neurite and spreads to the soma and growth cones. The calcium wave was monitored with digital microscope imaging of a fluorescent calcium indicator. The hypothesis was that interaction of bradykinin with its receptor on the plasma membrane activated production of inositol-1,4,5-trisphosphate (InsP3) that diffused to its receptor on the endoplasmic reticulum, leading to calcium release.
Using the Virtual Cell software environment, they assembled a simulation model of this phenomenon.66 The model contained details of the relevant receptor distributions (via immunofluorescence) within the cell geometry, the kinetics of InsP3 production (via biochemical analysis of InsP3 in cell populations and photorelease of caged InsP3 in individual cells), the transport of calcium through the InsP3 receptor calcium channel and the sarcoplasmic/endoplasmic reticulum calcium ATPase (SERCA) pump (from literature studies of single-channel kinetics and radioligand flux), and calcium buffering by both endogenous proteins and the fluorescent indicator (from confocal measurements of indicator concentrations).
The mathematical equations generated by this combination of molecular distributions and reaction and membrane transport kinetics were then solved to produce a simulation of the spatiotemporal pattern of calcium that could be directly compared to the experiment. The characteristic calcium dynamics requires rapid, high-amplitude production of [InsP3]cyt in the neurite. This requisite InsP3 spatiotemporal profile is provided, in turn, as an intrinsic consequence of the cell’s morphology, demonstrating how geometry can locally and dramatically intensify cytosolic signals that originate at the plasma membrane. In addition, the model predicts and experiments confirm that stimulation of just the neurite, but not the soma or growth cone, is sufficient to generate a calcium response throughout the cell.
5.4.3 Genetic Regulation
The problem of genetic regulation—how and under what circumstances and the extent to which genes are expressed as proteins—is a central problem of modern biology. The issue originates in an apparent paradox—every cell in a complex organism contains the same DNA sequences, and yet there are many cell types in such organisms (blood cells, skin cells, and so on). In particular, the proteins that comprise any given cell type are different from those of other cell types, even though the genomic information is the same in both. Nor is genomic information the whole story in development—cells also respond to their environment, and external signals coming into a cell from neighboring cells influence which proteins the cell makes.
Genetic regulation is an extraordinarily complex problem. Molecular biologists distinguish between cis-regulation and trans-regulation. Cis-regulatory elements for a given gene are segments of the genome that are located in the vicinity of the structural portion of a gene and regulate the expression of the gene. Trans-regulatory elements for a given gene refer to proteins not structurally associated with a gene that nevertheless regulate its expression. The sections below provide examples of several constructs that help shed some light on both kinds of regulation.
5.4.3.1 Cis-regulation of Transcription Activity as Process Control Computing
It has been known for some time that the genome contains both genes and cis-regulatory elements.67 The presence or absence of particular combinations of these regulatory elements determines the extent to which specific genes are expressed (i.e., transcribed into specific proteins). In pioneering work undertaken by Davidson et al.,68 it was shown that cis-regulation could—in the case of a specific gene—be viewed as a logical process analogous to a computer program that connected various inputs to a single output determining the precise level of transcription for that gene.
In particular, Davidson and his colleagues developed a high-level computer simulation of the cis-regulatory system governing the expression of the endo16 gene in the sea urchin (endo16 is a gut-specific gene of the sea urchin embryo). In this context, the term “high-level” means a highly abstracted representation, consisting at its core of 18 lines of code. This simulation enabled them to make predictions about the effect of specific manipulations of the various regulatory factors on endo16 transcription levels that could be tested against experiment.
Some of the inputs to the simulation were binary values. The value 1 indicated that a binding site was both present and productively occupied by the appropriate cis-regulatory factor. A 0 indicated that the site was mutationally destroyed or inactive because its factor was not present or was inactive. The other inputs to the simulation were continuous and varied with time, and represented outputs (protein concentrations) in other parts of the system. The output of this process in some cases was a continuous time-varying variable that regulated the extent to which the specific gene in question was transcribed.
Davidson et al. were able to confirm the predictions made by their computational model, concluding that all of the regulatory functions in question (and the resulting system properties) were encoded in the DNA sequence, and that the regulatory system described is capable of processing complex informational inputs and hence indicates the presence of a multifunctional organization of the endo16 cis-regulatory system.69
|
67 |
For purposes of the discussion in this subsection (Section 5.4.3.1), regulation refers to cis-regulation. |
|
68 |
C.H. Yuh, H. Bolouri, and E.H. Davidson, “Genomic Cis-regulatory Logic: Experimental and Computational Analysis of a Sea Urchin Gene,” Science 128(5):617-629, 1998. Some of this discussion is also adapted from commentary on this article: G.A. Wray, “Promoter Logic,” Science 279(5358):1871-1872, 1998. |
|
69 |
In this context, a multifunctional organization of the regulatory system means that the protein associated with the endo16 gene is differentially expressed in various cells in the sea urchin. |
The computational model undoubtedly provides a compact representation of the relationships between different inputs and different outputs.70 Perhaps a more interesting question, however, is the extent to which it is meaningful to ascribe a computational function to the biochemical substrate underlying the regulatory system. Davidson et al. argue that the DNA sequence in this case specifies “what is essentially a hard-wired, analog computational device,” resulting in system properties that are “all explicitly specified in the genomic DNA sequence.”71
It is highly unlikely that the precise computational structure of endo16’s regulatory system will generalize to the regulatory systems of other genes. From the perspective of the biologist, the reason is clear—organisms are not designed as general-purpose devices. Indeed, the evolutionary process virtually guarantees that individualized solutions and architectures will be abundant, because specific adaptations are the rule of the day. Nevertheless, insight into the computational behavior of the endo16 cis-regulatory system provides a new way of looking at biological behavior.
Can the regulatory systems of some other genes be cast in similar computational terms? If and when future work demonstrates that such casting is possible, it will become increasingly meaningful to view the genome as thousands of simple computational devices operating in tandem. Davidson’s work suggests the possibility that a class of regulatory mechanisms, complex though they might be with respect to their behavior, may be governed by what are in essence hard-wired devices whose essential functionality can be understood in computational terms through a logic of operation that is in fact relatively simple at its core. Prior to Davidson’s work and despite extensive research, the literature had not revealed any apparent regularity in the organization of regulatory elements or in the ways in which they interact to regulate gene expression.
Indeed, while many promoters appear either to have a simpler organization or to operate less logically than that of endo16, few promoters have been examined with the many precise quantitative assays that were carried out by Davidson et al., and nonquantitative assays would have completely missed most of the functions that the majority of the regulatory system’s elements encode.72 So, it is at this point an open question whether this computational view has applicability beyond the specific case of endo16.
5.4.3.2 Genetic Regulatory Networks as Finite-state Automata
Trans-regulation (as contrasted to cis-regulation) is based on the notion that some genes can have regulatory effects on others.73 In reality, the network of connections between genes that regulate and genes that are regulated is highly complex. In an attempt to gain insight into genetic regulatory networks from a gross oversimplification, Kaufmann proposed that actual genetic regulatory networks might be modeled as randomly connected Boolean networks.74
Kaufmann’s model made several simplifying assumptions:
|
70 |
E.F. Keller, Making Sense of Life: Explaining Biological Development with Models, Metaphors, and Machines, Harvard University Press, Cambridge, MA, 2002, p. 241. |
|
71 |
This is not to argue that DNA sequence alone is responsible for the specification of system properties. Epigenetic control mechanisms also influence system properties as do environmental conditions and cell state that are not specified in DNA. An analogy might be that although a memory dump of a computer specifies the state of the computer, many contingent activities may affect the actual execution path. For example, the behavior (and timing) of specific input-output activities are likely to be relevant. |
|
72 |
G.A. Wray, “Promoter Logic,” Science 279(5358):1871-1872, 1998. |
|
73 |
For purposes of the discussion in this subsection (Section 5.4.3.2), regulation refers to trans-regulation. |
|
74 |
Much of this work is due to the pioneering work of Stuart Kauffman. See for example, S.A. Kauffman, The Origins of Order: Self-Organization and Selection in Evolution, Oxford University Press, New York, 1993. An alternative discussion of this material can be found at http://www.smi.stanford.edu/projects/helix/bmi214/ (May 13); lecture notes of Russell Altman. |
-
The total number of genes involved is N, a number of order 30,000.
-
The number of genes that regulate a given target is a constant (call it K) for all regulated genes; K is a small integer.
-
The regulatory signal associated with a connection or the expression of a gene is either on or off. (In fact, almost certainly it is not just the fact of a connection between genes that influences regulation, but rather the nature of that connection as a continuous time-varying value such as a molecular concentration over time.)
-
Every gene is governed by the same transition rule (i.e., a Boolean function) that specifies its state (on or off) as a function of the activities of its K inputs at the immediately earlier time.
-
The regulatory network operates synchronously (and, by implication, kinetics are unimportant).
-
Secondary effects on genetic regulation arising from the nondigital characteristics of DNA (such as methylation) can be neglected.
-
The genes that regulate and genes that are regulated (which may overlap) are connected at random.
Box 5.9 provides more details about this model. Because the model treats all genes as identical (i.e., all obey the same transition rule) and assigns connections between genes at random, it obviously lacks fidelity to any specific genome and cannot predict the biological phenomenology of any specific organism. Yet, it may provide insight into biological order that emerges from the structure of the genetic regulatory network itself.
Simulations of the operation of this model yielded interesting behavior, which depends on the values of N and K. For K = 1 or K > 5, the behavior of the network exhibits little interesting order, where order is defined in terms of fixed cycles known as attractors. If K = 1, the networks are static, with the number of attractors exponential in the size of the network and the cycle length approaching unity. If K > 5, there are few attractors, and it is the cycle length that is exponential in the size of the network. However, for K = 2, the network does exhibit order that has potential biological significance—both the number of attractors and the cycle length are proportional to N1/2.75
What might be the biological significance of these results?
-
The trajectory of an attractor through its successive states would reflect the fact that, over time, different genes are expressed in a biological organism.
-
The fact that there are multiple attractors within the same genome suggests that multiple biological structures might exist, even within the same organism, corresponding to the genome being in one of these attractor states. An obvious candidate for such structures would be multiple cell types. That is, this analysis suggests that a cell type corresponds to a given state cycle attractor, and the different attractors to the different cell types of the organism. Another possibility is that different but similar attractors correspond to cells in different states (e.g., disease state, resting state, perturbed state).
-
The fact that an attractor is cyclic suggests that it may be related to cyclic behavior in a biological organism. If cell types can be identified with attractors, the cyclic trajectory in phase space of an attractor may correspond to the cell cycle in which a cell divides.
-
States that can be moved from one trajectory (for one attractor) to another trajectory (and another attractor) by changing a single state variable are not robust and may represent the phenomenon that small, apparently minor perturbations to a cell’s environment may kick it into a different state.
-
The square root of the number of genes in the human genome (around 30,000) is 173. Under the assumption of K = 2 scaling, this would correspond to the number of cyclic attractors and thus to the number of cell types in the human body. This is not far from the number of cell types actually observed
|
Box 5.9 In Kaufmann’s Boolean representation of a genetic regulatory network, there are N genes, each with two states of activity (expressed or inhibited), and hence 2N possible states (i.e., sets of activities) in the network. The number of possible connections is combinatorial in N and K. Starting at time t, each gene makes a transition to a new state at time t + 1 in accord with the transition rule and the K inputs that it receives. Thus, the state of the network at a time t + 1 is uniquely determined from its state at time t. The trajectory of the network as t changes (i.e., the sequence of states that the network assumes) is analogous to the process by which genes are expressed. This network is an instantiation of a finite-state automaton. Since there are a finite number of states (2N), the system must eventually find itself in a state previously encountered. Since the system is deterministic, the network then cycles repeatedly through a fixed cycle, called an attractor. Every possible system state either leads to some attractor or is part of an attractor. Different initial conditions may or may not lead to different attractors. All of the initial conditions that lead to the same attractor constitute what is known as a “basin” for that attractor. Any state within a basin can be exchanged with any other state in the same basin without changing the behavior of the network in the long run. In addition, given a set of attractors, no attractor can intersect with another (i.e., pass through even one state that is contained in another attractor). Thus, attractors are intrinsically stable and are analogous to the genetic expression pattern in a mature cell. An attractor may be static or dynamic. A static attractor involves a cycle length of one (i.e., the automaton never changes state). A dynamic attractor has a cycle length greater than one (i.e., a sequence of states repeats after some finite number of time increments). Attractors that have extremely long cycle lengths are regarded as chaotic (i.e., they do not repeat in any amount of time that would be biologically interesting). Two system states differing in only a small number of state variables (i.e., having only a few bits that differ out of the entire set of N variables) often lie on dynamical trajectories that converge closer to one another in state space. In other words, their attractors are robust under small perturbations. However, there can be states within a basin of attraction that differ in only one state variable from a trajectory that can lead to a different attractor. |
-
(about 200). Such a result may be numerological coincidence or rooted in the fact that nearly all cells in a given organism (even across eukaryotes) share the same basic housekeeping mechanisms (metabolism, cell-cycle control, cytoskeletal construction and deconstruction, and so on), or it may reflect phenotypic structure driven by the large-scale connectivity in the overall genetic regulatory network. More work will be needed to investigate these possibilities.76Box 5.10 provides one view on experimental work that might be relevant.
To illustrate the potential value of Boolean networks as a model for genetic regulatory networks, consider their application to understanding the etiology of cancer.77 Specifically, cancer is
|
76 |
This point is discussed further in Section 5.4.2.2 and the references therein. |
|
77 |
Z. Szallasi and S. Liang, “Modeling the Normal and Neoplastic Cell Cycle with ‘Realistic Boolean Genetic Networks’: Their Application for Understanding Carcinogenesis and Assessing Therapeutic Strategies,” Pacific Symposium on Biocomputing, pp. 66-76, 1998. |
|
Box 5.10 Because of the extreme simplifications embedded in the Boolean network model, detailed predictions (e.g., genes A and B turn on gene C) are unlikely to be possible. Instead, the utility of this approach as a way of looking at genetic regulation will depend on its ability to make qualitative predictions about large-scale structure and trends. Put differently, can Boolean networks behave in biologically plausible ways? Under certain circumstances, Boolean networks do exhibit certain regularities. Thus, the operative question is whether these features have reasonable biological interpretations that afford insight into the integrated behavior of the genomic system. Consider the following:
SOURCE: Stuart Kauffman, Santa Fe Institute, personal communication, September 20, 2002. |
widely believed to be a pathology of the hereditary apparatus. However, it has been clear for some time that single-cause, single-effect etiologies cannot account for all or nearly all occurrences of cancer.78
If the correspondence between attractor and cell is assumed, malignancy can be viewed as an attractor similar in most ways to that associated with a normal cell,79 and the transition from normal to malignant is represented by a “phase transition” from one attractor to another. Such a transition might be induced by an external event (radiation, chemical exposure, lack of nutrients, and so on).
As one illustration, Szallasi and Liang argue that changes in large-scale gene expression patterns associated with conversion to malignancy depend on the nature of attractor transition in the underlying genetic network in three ways:
-
A specific oncogene can induce changes in the state of downstream genes (i.e., genes for which the oncogene is part of their regulatory network) and transition rules for those genes without driving the system from one attractor to another one. If this is true, inhibition of the oncogene will result a reversion of those downstream changes and a consequent normal phenotype. In some cases, just such phenomenology has been suggested,80 although whether or not this mechanism is the basis of some forms of human cancer is unknown as yet.
-
A specific oncogene could force the system to leave one attractor and flow into another one. The new attractor might have a much shorter cycle time (implying rapid cell division and reproduction) and/or be more resistant to outside perturbations (implying difficulty in killing those cells). In this case, inhibition of the oncogene would not result in reversion to a normal cellular state.
-
A set of “partial” oncogenes may force the system into a new attractor. In this case, no individual partial oncogene would induce a phenotypical change by itself—however, the phenomenology associated with a new attractor would be similar.
These different scenarios have implications for both research and therapy. From a research perspective, the operation of the second and third mechanisms implies that the network’s trajectory through state space is entirely different, a fact that would impede the effectiveness of traditional methodologies that focus on one or a few regulatory pathways or oncogenes. From a therapeutic standpoint, the operation of the latter two mechanisms implies that a focus on “knocking out the causal oncogene” is not likely to be very effective.
5.4.3.3 Genetic Regulation as Circuits
Genetic networks can also be modeled as electrical circuits.81 In some ways, the electrical circuit analogy is almost irresistible, as can be seen from a glance at any of the known regulatory pathways: the tangle of links and nodes could easily pass for a circuit diagram of Intel’s latest Pentium chip. For example, McAdams and Shapiro described the regulatory network that governs the course of a λ-phage infection in E. coli as a circuit, and included factors such as time delays, which are critical in biological networks (gene transcription and translation are not instantaneous, for example) and indeed, in electrical networks, as well.
More generally, nature’s designs for the cellular circuitry seems to draw on any number of techniques that are very familiar from engineering: “The biochemical logic in genetic regulatory circuits provides real-time regulatory control [via positive and negative feedback loops], implements a branch-
TABLE 5.2 Points of Similarity Between Genetic Logic and Electronic Digital Logic in Computer Chips
|
Characteristic |
Electronic Logic |
Genetic Logic |
|
Signals distribution |
Electron concentrations Point-to-point (by wires or by electrically encoded addresses) |
Protein concentrations Distributed volumetrically by diffusion or compartment-to-compartment by active transport mechanisms |
|
Organization logic type |
Hierarchical Digital, clocked, sequential logic |
Hierarchical Analog, unclocked (can approximate asynchronous sequential logic; dependent on relative timing of signals) |
|
Noise |
Inherent noise due to discrete electron events and environmental effects |
Inherent noise due to discrete chemical events and environmental effects |
|
Signal-to-noise ratio |
Signal-to-noise ratio high in most circuits |
Signal-to-noise ratio low in most circuits |
|
Switching speed |
Fast (>10−9 s−1) |
Slow (<10−2 s−1) |
|
SOURCE: Excerpted with permission from H. McAdams and A. Arkin, “Simulation of Prokaryotic Genetic Circuits,” Annual Review of Biophysics and Biomolecular Structure 27:199-224, 1998, available at http://caulo.stanford.edu/usr/hm/pdf/1998_McAdams_simulation_genetic_circuits.pdf. Originally published by Annual Review of Biophysics and Biomolecular Structure. |
||
ing decision logic, and executes stored programs [in the DNA] that guide cellular differentiation extending over many cell generations.”82Table 5.2 describes some of the similarities.
Of course, taking an engineering view of biological circuits does not make understanding them trivial. For example, consider that cellular regulatory circuits implement a complex adaptive control system. Understanding this system is greatly complicated by the fact that at the biochemical implementation level, the distinction between the controlling mechanisms and the controlled processes is not as clear as it is when such control is engineered into a human-designed artifact. In a biochemical environment, control reactions and controlled functions are composed of intermingled molecules interacting in ways that make identification of roles much more complex.
Nor does the analogy to electrical circuits always carry over perfectly. Because critical molecules are often present in the cell in extremely small quantities, to take the most notable example, certain critical reactions are subject to large statistical fluctuations, meaning that they proceed in fits and starts, much more erratically than their electrical counterparts.
5.4.3.4 Combinatorial Synthesis of Genetic Networks83
Guet et al. have demonstrated the feasibility of creating synthetic networks, composed of well-characterized genetic elements, that provide a framework for understanding how diverse phenotypi-
|
82 |
H.H. McAdams and A. Arkin, “Simulation of Prokaryotic Genetic Circuits,” Annual Reviews of Biophysical and Biomolecular Structure 27:199-224, 1998. |
|
83 |
Section 5.4.3.4 is based on C.C. Guet, M.B. Elowitz, W. Hsing, and S. Leibler, “Combinatorial Synthesis of Genetic Networks,” Science 296(5572):1466-1470, 2002. |
cal functionality can (but does not always) arise from changes in network topology rather than changes in the elements themselves. This functionality includes networks that exhibit the behavior associated with negative and positive feedback loops, oscillators, and toggle switches. By showing that functionality can change dramatically due to changes in topology, Guet et al. argue that once a simple set of genes and regulatory elements is in place, it is possible to jump discontinuously from one functional phenotype to another using the same “toolkit” of genes simply by modifying the regulatory connections. Such discontinuous changes are different from the more gradual effects driven by successive point mutations.
Such discontinuities reflect the nonlinear nature of genetic networks. Furthermore, the topology of connectivity of a network does not necessarily determine its behavior uniquely, and the behavior of even simple networks built out of a few well-characterized components cannot always be inferred from connectivity diagrams alone. Because genetic networks are nonlinear (and stochastic as well), the unknown details of interactions between components might be of crucial importance to understanding their functions. Combinatorially developed libraries of simple networks may thus be useful in uncovering the existence of additional regulatory mechanisms and exploring the limits of quantitative modeling of cellular systems.
The system of Guet et al. uses a small number of elements restricted to a single type of interaction (transcriptional regulation), but the range of biochemical interactions can be extended by including other modular genetic elements. For example, the approach can be extended to include linking input and output through cell-cell signaling molecules, such as those involved in quorum sensing. Also, this combinatorial strategy can be used to search for other dynamic behaviors such as switches, sensors, oscillators, and amplifiers, as well as for high-level structural properties such as robustness or noise resistance.
5.4.3.5 Identifying Systems Responses by Combining Experimental Data with Biological Network Information
Mawuenyega et al. have developed a method to identify specific subnetworks in large biological networks.84 A biological network is constructed by identifying components (genes, proteins, transcription factors, chemicals) and interactions between components (protein-protein, protein-DNA, signal transduction, gene expression, catalysis) from genome context information as well as from external sources (databases, literature, and direct interaction with experimentalists). By superimposing experimental data such as expression values or identified proteins, it is possible to identify a best-scored subnetwork in the large biological network. This subnetwork is known as the response network, identifying a system’s response with respect to the experimental scenario and data used.
Proteomic mass spectroscopy (MS) analysis was used to identify and characterize 1,044 Mycobacterium tuberculosis (TB) proteins and their corresponding cellular locations. From these 1,044 identified, 70 proteins were selected that are known to function in lipid biosynthesis (20) and fatty acid degradation (50). It is striking that the identified proteins involved in fatty acid degradation were distributed between the different cellular compartments in an almost exclusive fashion (e.g., in the subnetwork centered on fadB2 and fadB3) (Figure 5.9).
In addition, Forst and colleagues performed a response network analysis of mycobacterium tuberculosis to isoniazid (INH) drug treatment.85 The entirety of the FAS-II fatty acid synthase group (except
|
84 |
K.G. Mawuenyega, C.V. Forst, K.M. Dobos, J.T. Belisle, J. Chen, M.E. Bradbury, A.R. Bradbury, and X. Chen, “Mycobacterium Tuberculosis Functional Network Analysis by Global Subcellular Protein Profiling,” Molecular Biology of the Cell 16:396-404, 2005. |
|
85 |
L. Cabusora, E. Sutton, A. Fulmer, and C.V. Forst, “Differential Network Expression During Drug and Stress Response,” Bioinformatics 21:2898-2905, 2005, available at http://bioinformatics.oupjournals.org/cgi/content/abstract/bti440v1. |
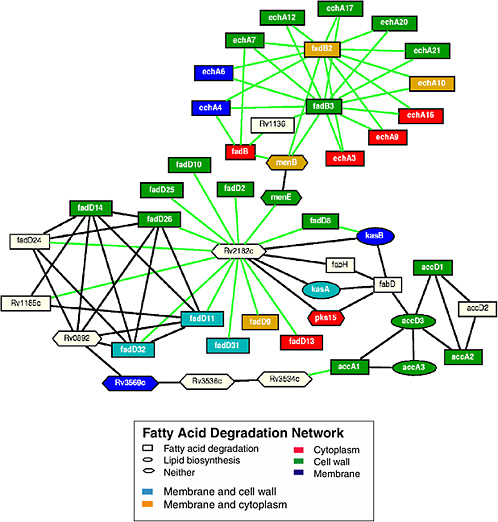
FIGURE 5.9 Fatty acid degradation network. SOURCE: Courtesy of Christian Forst, Los Alamos National Laboratories, December 8, 2004.
acpM, which was not included in the interaction data used to construct the original, whole network) showed up in the INH response network, all with significant up-regulation (Figure 5.10). Furthermore, the specific removal of these genes (kasA, kasB, fabD, accD6) from the initial set of genes did not affect their presence in the INH response subnetwork: the newly calculated network continued to contain each of them. Forst concluded that INH does directly interfere with the FAS-II fatty acid production pathway, in confirmation of earlier results.
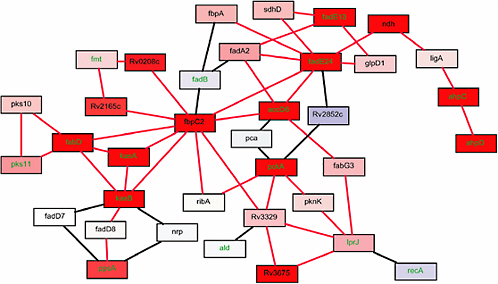
FIGURE 5.10 The isoniazid (INH) response network. Red nodes indicate up-regulated genes. Blue nodes indicate down-regulated genes. SOURCE: Courtesy of Christian Forst, Los Alamos National Laboratories, December 8, 2004.
5.4.4 Organ Physiology
Sydney Brenner has noted that “genes can only specify the properties of the proteins they code for, and any integrative properties of the system must be ‘computed’ by their interactions.”86 In this context, subcellular behavior and function represents a first level of “computed” interaction; cellular behavior and function, a second level. Organization of cells into organs provides a context for cellular behavior, and in the words of Denis Noble, “successful physiological analysis requires an understanding of the functional interactions between the key components of cells, organs, and systems, as well as how these interactions change in disease states. This information resides neither in the genome nor even in the individual proteins that genes code for. It lies at the level of protein interactions within the context of subcellular, cellular, tissue, organ, and system structures. There is therefore no alternative to copying nature and computing these interactions to determine the logic of healthy and diseased states. The rapid growth in biological databases; models of cells, tissues, and organs; and the development of powerful computing hardware and algorithms have made it possible to explore functionality in a quantitative manner all the way from the level of genes to the physiological function of whole organs and regulatory systems.”87
5.4.4.1 Multiscale Physiological Modeling88
Physiological modeling is the modeling of biological units at a level of aggregation larger than that of an individual cell. Biological units can be successively decomposed into subunits (e.g., an organism may consist of subsystems for circulatory, pulmonary, digestive, and cognitive function; a digestive
|
86 |
S. Brenner, “Biological Computation,” The Limits of Reductionism in Biology. Wiley, Chichester, UK, 1998, pp. 106-116. |
|
87 |
D. Noble, “Modeling the Heart—from Genes to Cells to the Whole Organ,” Science 295(5560):1678-1682, 2002. |
|
88 |
Much of the material in Section 5.4.4.1 is based on excerpts from A.D. McCulloch and G. Huber, “Integrative Biological Modelling in Silico,” Novartis Foundation Symposium 247:4-19, 2002. |
system may consist of esophagus, stomach, and intestines; and so on down to the level of organelles within cells and molecular functions within organelles), and every unit depends on the coordinated interaction of its subunits.
Given the complexity of physiological modeling, it makes sense to replicate this natural organization. Thus, models of tissue, organs, and even entire organisms are relevant subjects of physiological modeling. Functional behavior in each of these entities depends on activity at all spatial and temporal scales associated with structure from protein to cell to tissue to organ to whole organism (Box 5.11) and requires the integration of interacting physiological processes such as regulation, growth, signaling, metabolism, excitation, contraction, and transport processes. One term sometimes used for work that involves such integration is “physiome” (or by analogy to genomics,“physiomics”).89
Integration of such models presents many intellectual challenges. Following McCulloch and Huber,90 it is helpful to consider two different types of integration. Structural integration implies integration across physical scales of biological organization from protein to whole organism, while functional integration refers to the integrated representation of interacting physiological processes. Structurally integrative models (e.g., models of molecular dynamics and other strategies that predict protein function from structure) are driven by first principles and hence tend to be computation-intensive. Because they are based on first principles, they impose constraints on the space of possible organismic models. Functionally integrative models are strongly data-driven and therefore data-intensive, and are needed to bridge the multiple time and space scales of substructures within an organism without leaving the problem computationally intractable. Box 5.12 provides a number of examples of intersection between structurally and functionally integrated models.
Predictive simulations of subcomponents at various levels of the hierarchy of complexity are generally based on physicochemical first principles. Integrating such simulations, of which micromechanical tissue models and molecular dynamics models are examples, with each other across scales of biological organization is highly computationally intensive (and requires a computational infrastructure that enables distributed and heterogeneous computational resources to participate in the integration and facilitates the modular addition of new models and levels of organization).
5.4.4.2 Hematology (Leukemia)
Childhood acute lymphoblastic leukemia (ALL) is a lethal but highly treatable disease. However, successful treatment depends on the ability to deliver the correct intensity of therapy. Improper intensity can result in an excess of deaths caused by toxicity, decreased mental function over the long term, and undertreatment for high-risk cases.
The appropriate intensity is determined today through an extensive—and expensive—range of procedures including morphology, immunophenotyping, cytogenetics, and molecular diagnostics. However, Limsoon Wong has developed a relatively inexpensive single-platform microarray test that uses gene expression profiling to identify each of the known clinically important subgroups of childhood ALL (Figure 5.11) and hence the appropriate intensity of treatment.91 This is confirmed using computer-assisted supervised learning algorithms, in which an overall diagnostic accuracy of 96 percent was achieved in a blinded test sample. To determine whether expression profiling at diagnosis
|
89 |
J.B. Bassingthwaighte, “Toward Modeling the Human Physionome,” pp. 331-339 in Molecular and Subcellular Cardiology: Effects on Structure and Function, S. Sideman and R. Beyar, eds., Plenum Press, New York, Volume 382 in Advanced Experiments in Medical Biology, 1995; http://www.physiome.org/. |
|
90 |
A.D. McCulloch and G. Huber, “Integrative Biological Modelling in Silico,” pp. 4-25 in ‘In Silico’ Simulation of Biological Processes No. 247, Novartis Foundation Symposium, G. Bock and J.A. Goode, eds., John Wiley & Sons Ltd., Chichester, UK, 2002. |
|
91 |
L. Wong, “Diagnosis of Childhood Acute Lymphoblastic Leukemia and Optimization of Risk-Benefit Ratio of Therapy,” PowerPoint presentation presented at the Institute for Infocomm Research, 2003, Singapore, available at http://sdmc.lit.org.sg:8080/~limsoon/psZ/wls-aasbi03.ppt. |
might further help identify those patients who are likely to relapse up to 4 years later, the expression profiles of four groups of leukemic samples with different outcomes were compared. Distinct gene expression profiles for each of these groups were identified.
5.4.4.3 Immunology
The immune system provides protection for human beings from pathogens. (For purposes of this discussion, the immune system of interest here refers to the adaptive immune system. The human body also has an innate immune system that provides a first response to pathogens that is essentially independent of the specific pathogen—in essence, its role is to give the adaptive immune system time to build a more specific response.) To do so, the immune system must first identify an entity within the body as a harmful pathogen that it should attack or eliminate and then mount a response that does so.
In principle, the identification of harmful pathogens might be based on a list of known pathogens. If an entity is found within the human body that is sufficiently similar to a known pathogen, it could be marked for later attack and destruction. However, a list-based approach to pathogen identification suffers from two major weaknesses. First, any such list would have to be large enough to include most of the possible pathogens that an organism might encounter in its lifetime; some estimates of the number of different foreign molecules that the human immune system is capable of recognizing are as high as 1016.92 Second, because pathogens evolve (and, thus, new pathogens are created), an a priori list could never be complete.
Accordingly, nature has developed an alternative mechanism for pathogen identification based on the notion of “self” versus “nonself.” In this paradigm, entities or substances that are recognized as self are deemed harmless, while those that are nonself are regarded as potentially dangerous. Thus, the immune system has developed a variety of mechanisms to differentiate between these two categories. Note that this distinction is highly simplistic, as not all nonself entities are bad for the human body (e.g., transplanted organs that replace original organs damaged beyond repair). Nevertheless, the self-nonself distinction is not a bad point of departure for understanding the human immune system.
The immune system relies on a process that generates detectors for a subset of possible pathogens and constantly turns over those detectors for new detectors capable of identifying a different set of pathogens. When the immune system identifies a pathogen, it selects one of several immunological mechanisms (e.g., those associated with the different immunoglobulin [Ig] groups) to eliminate it. Furthermore, the immune system retains memory of the pathogen, in the form of detectors that are specifically configured for high affinity to that pathogen. Such memory enables the immune system to confer long-lasting resistance (immunity) to pathogens that may be encountered in the future and to mount a stronger response to such future encounters.
Many of the broad outlines of the immune system are believed to be understood, and computational modeling of the immune system has shed important light on its detailed workings, as described in Box 5.13. A medical application of simulation models in immunology has been to evaluate the effects of revaccinating someone yearly for influenza. Because of the phenomenon of immune memory, a vaccine that is too similar to a prior year’s vaccine will be eliminated rapidly by the immune response (a negative interference effect). A simulation model by Smith et al. has examined this effect and suggests some circumstances under which individuals who are vaccinated annually will have greater or less protection than those with a first-time vaccination.93 The Smith et al. results also suggested that in the production of flu vaccine, a choice among otherwise equivalent strains (i.e., strains thought to be
|
Box 5.11 One helpful approach is to consider a set of different, but interrelated, levels of biological organization:
The approach described above—of integrating models across structural and functional lines—is generally adaptable to other tissues and organs, especially those with physical functions, such as lung and cartilage. |
|
Box 5.12 There are a number of examples of intersection between structurally and functionally integrated models, including the following:
SOURCE: A.D. McCulloch and G. Huber, “Integrative Biological Modelling in Silico,” pp. 4-19 in ‘In Silico’ Simulation of Biological Processes No. 247, Novartis Foundation Symposium, G. Bock and J.A. Goode, eds., John Wiley & Sons Ltd., Chichester, UK, 2002. Reproduced with permission from John Wiley & Sons Ltd. |
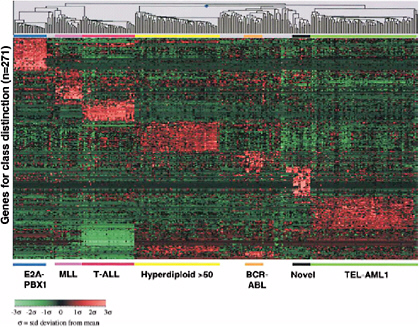
FIGURE 5.11 Microarray expression groupings indicating known clinically important subgroups of childhood acute lymphoblastic leukemia (ALL). Note in particular the second column from the right, labeled “novel.” In this instance, the hierarchical clustering of gene expression reveals a novel subtype of childhood ALL. SOURCE: Courtesy of L. Wong, Institute for Infocomm Research, Singapore, 2003.
equally good guesses of the upcoming epidemic strain and equally appropriate for manufacture) should be resolved in favor of the strain that is most different from the one used in the previous year, because this choice would reduce the effects of negative interference and thus potentially increase vaccine efficacy in recipients of repeat vaccines.
5.4.4.4 The Heart
The heart is an organ of primary importance in vertebrates, and heart disease is one of the primary causes of death in the Western world. At the same time, the heart is an organ of high complexity. Although it is in essence an impulsive pump, it is a pump that must operate continuously and repair itself if necessary while in operation. Its output must be regulated according to various physiological conditions in the body, and its performance is affected by the characteristics of the arterial and vein networks to which it is connected.
The heart brings together many subsystems that interact mutually through fundamental physiological processes. As a general rule, physiological processes have both functional and structural dimensions. For example, cells are functionally specialized—blood cells and myocytes (heart cells) do different things. Furthermore, blood cells and heart cells are themselves part of a collective of other blood cells and heart cells; thus, the structure within which an individual cell is embedded is relevant.
An integrated computational model of the heart would bring together all of the relevant physiological processes (Box 5.14).94 Were such a model available, it would be possible to investigate common
|
Box 5.13 In basic immunology, issues related to mutation also have been the focus of mathematical modeling and intense experimentation…. [For example,] during the course of an immune response, B lymphocytes within germinal centers can rapidly mutate the genes that code for antibody variable regions. The immune system thus provides an environment in which evolution occurs on a time scale of weeks. Among the large number of mutant B cells that are generated, selection chooses for survival those B cells that have increased binding affinity for the antigen that initiated the response. After 2 to 3 weeks, antibodies can have improved their equilibrium binding constant for antigen by one to two orders of magnitude, and may have sustained as many as 10 point mutations. How can the immune system generate and select variants with higher fitness this rapidly and this effectively? An optimal control model has suggested that mutation should be turned on and off episodically in order to allow new variants time to expand without being subjected to the generally deleterious effects of mutation. Time-varying mutation could be implemented by having cells recycle through one region of the germinal center, mutating while there, and proliferating in a different region of the germinal center. This suggestion has generated new experimental investigations of events that occur within germinal centers. Opportunities exist for a range of models that address basic questions about in vivo cell population dynamics and evolution, as well as more detailed questions involving the immunological mechanisms underlying affinity maturation. Control of the immune response is another area ripe for modeling. What determines the intensity of a response? How is the response shut off when the antigen is eliminated? Feedback mechanisms may exist to control the response intensity, response length, and type of response (cellular or antibody). Some models of a basic feedback mechanism involving two types of helper T cells, TH1 and TH2, have been developed; others are needed. Regulatory mechanisms involve interactions among many cell populations that communicate by direct cell-cell contact and through the secretion of cytokines. Diagrams representing the elements of regulatory schemes commonly have scores of elements. Because of the complexities involved, theorists have an opportunity to lead experimentation by providing suggestions as to what needs to be measured and how such measurements can be used to provide an insightful view of possible control mechanisms. A fundamental feature of the immune system is its diversity. Successful recognition of antigens appears to require a repertoire of at least 105 different lymphocyte clones. The diversity of the immune system has challenged experimentalists, and many recent advances have come from developing experimental models with limited immune diversity. However, models based on ecological concepts may provide insights into the control of clonal diversity, and modern computational methods now make it practical to consider models with tens of thousands of clones. Thus, it is possible to develop models that start to approach the size of small immune systems. Simulations have suggested that from simple rules of cell response, emergent phenomena arise that may have immunological significance. The challenge in using computation is to develop models that address important questions, are realistic enough to capture the relevant immunology, and yet are simple enough to be revealing. SOURCE: Reprinted by permission from S.A. Levin, B. Grenfell, A. Hastings, and A.S. Perelson, “Mathematical and Computational Challenges in Population Biology and Ecosystems Science,” Science 275(5298):334-343. Copyright 1997 AAAS. (References omitted.) |
heart diseases and to probe cardiac structure and function in different places in the heart—a point of some significance in light of the fact that heart failure is usually regional and nonhomogeneous. The graphic in Box 5.14 emphasizes functional integration in the heart, and the majority of functional interactions take place at the scale of the single cell. However, an organism’s behavior depends on interactions that span many orders of magnitude of space and time (from molecular structures and events to whole-organ anatomy and physiology). Thus, high-fidelity modeling of an organism or organ system within an organism demands the integration of information across similar scales.
An example of a functional model of a single cell is the work of Winslow et al. in modeling the cardiac ventricular cell, and specifically the relationship between various current flows in the cell and
|
Box 5.14 … [Integrative cardiac modelling has sought] to integrate data and theories on the anatomy and structure, hemodynamics and metabolism, mechanics and electrophysiology, regulation and control of the normal and diseased heart. The challenge of integrating models of many aspects of such an organ system, including its structure and anatomy, biochemistry, control systems, hemodynamics, mechanics and electrophysiology, has been the theme of several workshops over the past decade or so. Some of the major components of an integrative cardiac model that have been developed include [models of] ventricular anatomy and fiber structure, coronary network topology and hemodynamics, oxygen transport and substrate delivery, myocyte metabolism, ionic currents, impulse propagation, excitation-contraction coupling, neural control of heart rate and blood pressure, cross-bridge cycling, tissue mechanics, cardiac fluid dynamics and valve mechanics, and ventricular growth and remodelling…. …. [T]hese models can be extended and integrated with others [by considering the role in] several major functional modules … as shown in the figure below…. They include:
… While [Figure 5.14.1] does show different scales in the structural hierarchy, it emphasizes functional integration, and thus it is not surprising that the majority of functional interactions take place at the scale of the single cell…. [A functionally integrated] model of functionally interacting networks in the cell can be viewed as a foundation for structurally coupled models that extend to multicellular networks, tissue, organ and organ system. But it can also be viewed as a focal point into which feed structurally based models of protein function and subcellular anatomy and physiology. … Predictive computational models of various processes at almost every individual level of the hierarchy have been based on physicochemical first principles. Although important insight has been gained from empirical models of living systems, models become more predictive if the number of adjustable parameters is reduced by making use of detailed structural data and the laws of physics to constrain the solution. These models, such as molecular dynamics simulations, spatially coupled cell biophysical simulations, tissue micromechanical models and anatomically based continuum models are usually computationally intensive in their own right…. This will require a computational infrastructure that will allow us to integrate physically based biological models that span the hierarchy from the dynamics of individual protein molecules up to the regional physiological function of the beating heart…. Investigators have developed large-scale numerical methods for ab initio simulation of biophysical processes at the following levels of organization: molecular dynamics simulations based on the atomic structure of biomolecules; hierarchical models of the collective motions of large assemblages of monomers in macromolecular structures; biophysical models of the dynamics of cross-bridge interactions at the level of the cardiac contractile filaments; whole-cell biophysical models of the regulation of muscle contraction; microstructural constitutive models of the mechanics of multicellular tissue units; continuum models of myocardial tissue mechanics and electrical impulse propagation; and anatomically detailed whole organ models. They have also investigated methods to bridge some of the boundaries between the different levels of organization. We [McCulloch and Huber] and others have developed finite-element models of the whole heart, incorporating microstructural constitutive laws and the cellular biophysics of thin filament activation. Recently, these mechanics |
|
models have been coupled with a non-linear reaction-diffusion equation model of electrical propagation incorporating an ionic cellular model of the cardiac action potential and its regulation by stretch. At the other end of the hierarchy, Huber has recently developed a method, the Hierarchical Collective Motions method, for integrating molecular dynamics simulation results from small sections of a large molecule into a quasi-continuum model of the entire molecule. 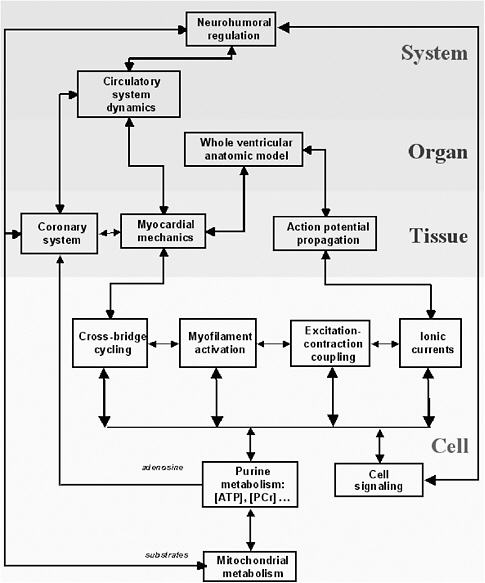 FIGURE 5.14.1 Some major functional subsystems of an integrated heart model and their hierarchical relationships from cell to tissue to organ and cardiovascular system. SOURCE: A.D. McCulloch and G. Huber, “Integrative Biological Modelling in Silico,” pp. 4-19 in ‘In Silico’ Simulation of Biological Processes No. 247, Novartis Foundation Symposium, G. Bock and J.A. Goode, eds., John Wiley & Sons Ltd., Chichester, UK, 2002. Text and figure reproduced with permission from John Wiley & Sons Ltd. (References omitted.) |
|
Box 5.15 Example 1: Results from Single-cell Modeling Winslow et al. have developed and applied a model of the normal and failing canine ventricular myocyte to analysis of the functional significance of changes in gene expression during tachycardia pacing-induced heart failure. Using the data on mRNA and protein expression levels cited above, these investigators defined a minimal model of end-stage heart failure as (1) 33 percent reduction of IK1; (2) 66 percent reduction of Ito1; (3) 68 percent reduction of the SR [sacroplasmic reticulum] Ca2+-ATPase; and (4) 75 percent upregulation of the Na+-Ca2+ exchanger. They incorporated these changes sequentially into the computational model and used the model to predict the functional consequences of each alteration of gene expression in this disease. Results show that the minimal HF [heart failure] model can reproduce the increased APD [action potential duration] observed in failing myocytes relative to normal myocytes. The minimal model can also account for the reduced amplitude and slowed relaxation of the Ca2+ transients observed in failing versus normal myocytes. Most importantly, model simulations reveal that reduced expression of the outward potassium currents Ito1 and IK1 have relatively little impact on APD, whereas altered expression of the Ca2+ handling proteins has a profound impact on APD. These results suggested a strong interplay between APD and the properties of Ca2+ handling in canine myocytes. The nature of this interplay was examined in the model. The model indicated that reductions in expression level of the SR Ca2+-ATPase and increased expression of the Na+-Ca2+ exchanger both contribute to a reduction of JSR Ca2+ load. This reduction in the junctional SR (JSR) Ca2+ load in turn produces a smaller Ca2+ release from SR, reduced subspace Ca2+ levels, and therefore reduced Ca2+-mediated inactivation of the Ca2+ current. The enhanced Ca2+ current then contributes to prolongation of APD. This is an important insight, because identifies the heart failure-induced reduction in JSR Ca2+ load as a critical factor in APD prolongation and in the accompanying increased risk of arrhythmias related to repolarization abnormalities. Analyses of the type described above are likely to become increasingly important in determining the functional role of altered gene and protein expression in various disease states as more comprehensive large-scale data on genome and protein expression in disease become available. |
its contractile behavior.95 In particular, Winslow has used this model to show that the reduced contractility (i.e., reduction in the strength with which a ventricular muscle contracts, which is associated with heart failure) is caused largely by changes in the calcium ion currents in those cells, rather than changes in potassium ion currents as was widely speculated before this work (Example 1 in Box 5.15). Such an insight suggests that the development of drugs to cope with heart failure would thus be better focused on those that can regulate calcium flow. Examples 2 and 3 in Box 5.15 illustrate some of the scientific insights that can be gained with a computational model integrated across functional and structural lines.
Integrating these various perspectives on the heart (and other organs as well) is the mission of the Physiome Project, which seeks to construct models that incorporate the detailed anatomy and tissue structure of an organ in a way that allows the inclusion of cell-based models and spatial structure and distribution of proteins. The Physiome project has developed a computational framework for integrating the electrical, mechanical, and biochemical functions of the heart:96
|
95 |
R.L. Winslow, D.F. Scollan, A. Holmes, C.K. Yung, J. Zhang, and M.S. Jafri, “Electrophysiological Modeling of Cardiac Ventricular Function: From Cell to Organ,” Annual Reviews of Biomedical Engineering 2:119-155, 2002. |
|
96 |
P.J. Hunter, “The IUPS Physiome Project: A Framework for Computational Physiology,” Progress in Biophysics and Molecular Biology 85(2-3):551-569, 2004. |
|
Results from Integrated Modeling (Examples 2 and 3) In the clinical arrhythmogenic disorder long-QT syndrome, a mutation in a gene coding for a cardiomyocyte sodium or potassium-selective ion channel alters its gating kinetics. This small change at the molecular level affects the dynamics and fluxes of ions across the cell membrane and thus affects the morphology of the recorded electrocardiogram (prolonging the QT interval and increasing the vulnerability to life-threatening cardiac arrhythmia). Such an understanding could not be derived by considering only the single gene, channel, or cell; it is an integrated response across scales of organization. A hierarchical integrative simulation could be used to analyze the mechanism by which this genetic defect can lead to sudden cardiac death, for example, by exploring the effects of altered repolarization on the inducibility and stability of reentrant activation patterns in the whole heart. A recent study made excellent progress in spanning some of these scales by incorporating a Markov model of altered channel gating, based on the structural consequences of the genetic defect in the cardiac sodium channel, into a whole-cell kinetic model of the cardiac action potential that included all the major ionic currents. … [It] is becoming clearer that mutations in specific proteins of the cardiac muscle contractile filament system lead to structural and developmental abnormalities of muscle cells, impairment of tissue contractile function, and the eventual pathological growth (hypertrophy) of the whole heart as a compensatory response. In this case, the precise physical mechanisms at each level remain speculative, although much detail has been elucidated recently, so an integrative model will be useful for testing various hypotheses regarding the mechanisms. The modeling approach could be based on the same integrative paradigm commonly used by experimental biologists, in which the integrated effect of a specific molecular defect or structure can be analysed using techniques such as in vivo gene targeting. SOURCE: R.L. Winslow, D.F. Scollan, A. Holmes, C.K. Yung, J. Zhang, and M.S. Jafri, “Electrophysiological Modeling of Cardiac Ventricular Function: From Cell to Organ,” Annual Review of Biomedical Engineering 2:119-156, 2000. Adapted by permission from Annual Review of Biomedical Engineering. (References and citations omitted.) |
-
The underlying anatomical descriptions are based on finite element techniques, and orthotropic constitutive laws based on the measured fiber-sheet structure of myocardial tissue drive the dynamics of the large deformation soft-tissue mechanics involved.
-
Patterns of electrical current flow in the heart are computed using reaction-diffusion equations on a grid of deforming material points which access systems of ordinary differential equations representing the cellular processes underlying the cardiac action potential; these result in representations of the activation wavefronts that spread around the heart and initiate contraction.
-
Coronary blood flow is computed based on the Navier-Stokes equations in a system of branching blood vessels embedded in the deforming myocardium and the delivery of oxygen and metabolites is coupled to the energy-dependent cellular processes.
These models of different cardiac phenomena have been been implemented with “horizontal” integration of mechanics, electrical activation and metabolism, together with “vertical” integration from cell to tissue to organ. Thus, these models can be said to deconstruct an organ into a set of (submodels for) constituent functions, with explicit feedback and connection between them represented in the overall model of the whole organ.
5.4.5 Neuroscience
In recent years, neuroscience has expanded its horizons beyond the microstructure of the brain—neurons, synapses, neurotransmitters, and the like—to focus on the brain’s large-scale cognitive architecture. Drawing on dramatic advances in mapping techniques, such as functional magnetic resonance imaging (MRI) and magnetoencephalography, neuroscientists hope to give a computational account of precisely what each specialized region of the brain is doing and how it interacts with all the other active regions to produce high-level thought and behavior.
5.4.5.1 The Broad Landscape of Computational Neuroscience
Neuroscience seeks to probe the details of the brain and the mechanisms by which the nervous systems develops, is organized, processes information, and establishes mental abilities. Research in neuroscience spans many levels of organization, from atomic and molecular events on the order of one-tenth to one nanometer, up to the entire nervous system on the order of a meter or more. In addition, there are on the order of 1011 neurons and thousands to tens of thousands of synapses per neuron.
Information processing in the brain occurs through the interactions and spread of chemical and electrical signals both within and among neurons. Acting within the extensive but intricate architecture of the neurons and their interconnections, the mechanisms are nonlinear and span a wide range of spatial and temporal scales.97 Understanding how the nervous system and brain work thus requires an interdisciplinary approach to the challenging multiscale integration of experimental data, computational data, and theory.
It is helpful to describe the nervous system’s functional processes and their mechanisms at several different levels of detail, depending on the goal of a given effort. Table 5.3 and Figure 5.12 describe the numerous spatial and temporal scales relevant to neuroscience research, and provide some indication of the complexity of such research.
To illustrate, a low level of analysis might involve consideration of individual neurons. In this analysis, functional properties of neurons such as electronic structure, nerve cell connections (synapses), and voltage-gated ion channels are important. At a higher level, it is recognized that individual neurons connect in networks—an analysis at this level examines how individual neurons interact to form functioning circuits. The mathematics of dynamic systems and visual neuroscience are notably relevant at this level. At a still higher level, individual networks—each with its own specific architecture and information-processing capabilities—interact to form neural nets and carry out cognition, speech
TABLE 5.3 Scales of Neuroscience Research
|
Spatial Scale |
Component |
|
1 meter |
Central nervous system |
|
10 centimeters |
Systems |
|
1 centimeter |
Maps |
|
1 millimeter |
Networks |
|
100 microns |
Neurons |
|
1 micron |
Synapses |
|
10 angstroms |
Molecules |
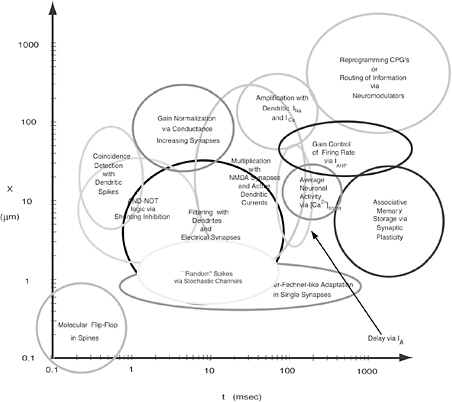
FIGURE 5.12 Temporal and spatial scales of neuroscience research. SOURCE: Courtesy of Christof Koch, Caltech.
perception, and imaging. At this level, computational analysis of nervous system networks and (connectionist) modeling of psychological processes is the primary focus.
Computational neuroscience provides the basis for testing models of the nervous system’s functional processes and their mechanisms, and computational modeling at several levels of detail is important, depending on the purposes of a given effort. Box 5.16 describes simulators that operate at different levels of detail for different purposes.
5.4.5.2 Large-scale Neural Modeling98
To better understand a system as complex as the human brain, it is necessary to develop techniques and tools for supporting large-scale, similarly complex simulations. Recent advances in understanding how single neurons represent the world,99 how large populations of neurons cooperate to build more complex representations,100 and how neurobiological systems compute functions over their representations make large-scale neural modeling a highly anticipated next step.
|
98 |
Section 5.4.5.2 is based largely on material supplied by Chris Eliasmith, University of Waterloo, September 7, 2004. |
|
99 |
F. Rieke, D. Warland, R. de Ruyter van Steveninick, and W. Bialek, Spikes: Exploring the Neural Code, MIT Press, Cambridge, MA, 1997; D. Warland, M. Landolfa, J. Miller, and W. Bialek, “Reading Between the Spikes in the Cercal Filiform Hair Receptors of the Cricket,” Analysis and Modeling of Neural Systems, F. Eeckman, ed., Kluwer Academic Publishers, Boston, MA, 1992. |
|
100 |
L. Abbott and T. Sejnowski, Neural Codes and Distributed Representations: Foundations of Neural Computation, MIT Press, Cambridge, MA, 1999; R.S. Zemel, P. Dayan, and A. Pouget, “Probabilistic Interpretation of Population Codes,” Neural Computation 10, 1998. |
|
Box 5.16 The nervous system is extraordinarily complex. A single cubic centimeter in the brain’s cerebral cortex contains on the order of 5 billion synapses, and these differ in size and shape. The transmission of chemical signals is very complex, with many molecules involved, and is an area of intense study. With the introduction of more powerful computer hardware and advances in algorithms, quantitative modeling and realistic simulation in three-dimensions of the interplay of biological ultrastructure and neuron physiology have become possible and have provided insight into the variability in signaling and plasticity of the system. To deal with the complexity, multiscale range of space and time, and nonlinearity of neural phenomena, a number of specialized computational tools have been developed. MCell (a Monte Carlo simulator of cellular microphysiology) simulates individual connections or synapses between neurons and groups of synapses. MCell simulations provide insights into the behavior and variability of real systems comprising finite numbers of molecules interacting in spatially complex environments. MCell incorporates high-resolution physical structure into models of ligand diffusion and signaling and thus can take into account the large complexity and diversity of neural tissue at the subcellular level. Monte Carlo algorithms are used to simulate ligand diffusion using three-dimensional random walk movements for individual molecules. Effector sites and surface positions are mapped spatially, and the encounters during ligand diffusion are detected. Bulk solution rate constants are converted into Monte Carlo probabilities so that the diffusing ligands can undergo stochastic chemical interactions with individual binding sites such as receptor proteins, enzymes, and transporters. GENESIS (the General Neural Simulation System) is a tool for building structurally realistic simulations of biological neural systems that quantitatively embed what is known about the anatomical structure and phys- |
Recent theoretical work has suggested that it is possible to generally characterize the dynamics, representation, and computational properties of any neural population (Figure 5.13).101 Applications of these methods have been used successfully to generate models of working memory, rodent navigational tasks (path integration; see Figure 5.14), eye position control, representation of self-motion, lamprey and fish motor control, and deductive reasoning (Figure 5.15).
Box 5.17 illustrates the use of computational modeling to understand how dopamine functions in the prefrontal cortex. The box also illustrates the often-present tension between those who believe that simple models (in this case, advocates of a connectionist model) can provide useful insight and those who believe that simple models cannot capture the implications of the complex dynamics of individual neurons and their synapses and that the addition of considerable biophysical and physiological detail is needed for real understanding. Many of these models require large numbers of individual, spiking neurons to be simulated concurrently, which results in significant computational demands. In addition, calculating the necessary connection weights requires the inversion of extremely large matrices. Thus, high-performance computing resources are essential for expanding these simulations to include more neural tissue, and hence more complex neural function.
|
iological characteristics of the neural system of interest. GENESIS reflects the modeling perspective that spatial organization and structure are important for understanding neural function. GENESIS is organized around neurons constructed out of components such as compartments (short sections of cellular membrane) and variable conductance ion channels that receive inputs, perform calculations on them, and then generate outputs. Neurons in turn can be linked to form neural circuits. GENESIS originally was used largely for realistic simulations of cortical networks and of the cerebellar Purkinje cell and, more recently, to interconnect cell and network properties to biochemical signaling pathways. NEURON is similar to GENESIS in many ways, but contains optimizations that enable it to run very fast on networks in which cable properties play a crucial role, that involve system sizes ranging from parts of single cells to small numbers of cells, and that involve complex branched connections. Furthermore, the performance of NEURON degrades very slowly with increasing complexity of morphology and membrane mechanisms, and it has been applied to very large network models (104 cells with six compartments each and a total of 106 synapses in the network. Using a high-level language known as NMODL, NEURON has also been extended to investigate new kinds of membrane channels. The morphology and membrane properties of neurons are defined with an object-oriented interpreter, allowing for voltage control, manipulation of current stimuli, and other biological parameters. SOURCES: For more information, see http://www.mcell.cnl.salk.edu; J.R. Stiles and T.M. Bartol, Jr., “Monte Carlo Methods for Simulating Realistic Synaptic Microphysiology Using MCell,” pp. 87-127 in Computational Neuroscience: Realistic Modeling for Experimentalists, E. de Shutter, ed., Boca Raton, FL, CRC Press, 2000; J.R. Stiles, T.M. Bartol, Jr., E.E. Salpeter, M.M. Salpeter, T.J. Sejnowski, “Synaptic Variability: New Insights from Reconstructions and Monte Carlo Simulations with MCell,” pp. 681-731 in Synapses, W.M. Cowan, T.C. Sudhof, C.F. Sudhof, eds., Johns Hopkins University Press, Baltimore, 2001; J.M. Bower, D. Beeman, and M. Hucka, “The GENESIS Simulation System,” The Handbook of Brain Theory and Neural Networks, Second Edition, M.A. Arbib, ed., MIT Press, Cambridge, MA, 2003, pp. 475-478, available at http://www.genesis-sim.org/GENESIS/hbtn2e-bower-etal/hbtn2e-bower-etal.html; M.L. Hines and N.T. Carnevale, “The NEURON Simulation Environment,” Neural Computation 9(6):1179-1209, 1997, available at www.neuron.yale.edu/neuron/papers/nc97/nsimenv.pdf. |
5.4.5.3 Muscular Control
Muscles are controlled by action potentials—brief, rapid depolarizations of membranes in nerves and muscles. The timing of action potentials transmitted from motor neurons coordinates the contraction of the muscles they innervate. Rhythmic activity of the nervous system often takes the form of complex bursting oscillations in which intervals of action potential firing and quiescent intervals of membrane activity alternate. The relative timing of action potentials generated by different neurons is a key ingredient in the function of the nervous system.
Changes in the electrical potential of membranes are mediated by ion channels that selectively permit the flow of ions such as sodium, calcium, and potassium across the membrane. Individual channels are protein complexes containing membrane-spanning pores that open and close randomly at rates that depend on many factors. Cellular and network models of membrane potential represent these systems as electrical circuits in which voltage gated channels function as “nonlinear” resistors whose conductance depends on membrane potential. Information is transmitted from one neuron to another through synapses where action potentials trigger the release of neurotransmitters that bind to channels of adjacent cells, stimulating changes in the ionic currents of these cells. (The action potential is the basic neuronal signaling “packet” of ionic flow through a cell membrane.)
The most basic model of this mechanism is the Hodgkin-Huxley model, which refers to a set of differential equations that describe the action potential.102 Specifically, the Hodgkin-Huxley equations
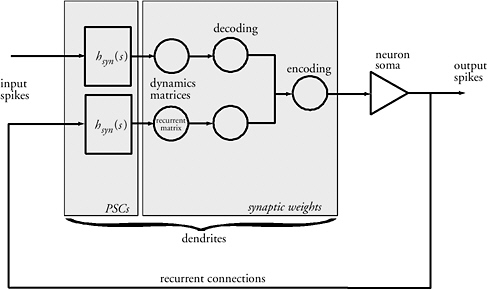
FIGURE 5.13 A generic neural subsystem. The diagram depicts the mathematical analysis of a neural subsystem and its mapping onto the biological system—a population of neurons. Labels outside the gray boxes indicate the relevant biological structures and processes. Neural action potentials (spikes) coming from a previous neural population generate weighted post-synaptic currents (PSCs) in the dendrites of the neurons to which they are connected. The subsequent voltage changes travel to the neural somata, where action potentials are generated, resulting in output spikes. Because the input and output are neural spikes, this kind of subsystem can be linked to others like it, permitting the construction of larger, more complex neural circuits (see Figure 5.15 for an example). Note that labels inside the gray boxes are generated based on understanding of the purpose of the neural system being modeled and on current understanding of neural representation (encoding), computation (decoding), and dynamics (dynamics matrices and hsyn). Building simulations using these methods leads to a better understanding of how neural systems perform the complex functions they do. SOURCE: Courtesy of Chris Eliasmith, University of Waterloo.
express quantitatively the feedback entailed in the relationship between changing ionic flows and changing membrane potential. Originally based on data collected from experiments on the giant axon of the squid, the physical model used is that of a membrane separating two infinite regions, each of which is homogeneous on its side of the membrane.
In the nervous system, different kinds of ions pass through the membrane, and the flow of ions through these channels is voltage dependent. In the model, a circuit is used to represent the ion flows and potential differences that drive ion flow. The semipermeable cell membrane separating the interior of the cell from the extracellular liquid is modeled as a capacitor, and each ion channel is modeled as a separately variable resistor. In series with each variable resistor is a battery representing the Nernst potential arising from the difference in ion concentration on each side of the membrane. All of these components are connected in parallel and are driven by a time-varying current source to ground. If a time-varying input current is injected into the cell, it may add further charge on the capacitor, or the added charge may leak through the channels in the cell membrane. Because of active ion transport through the cell membrane, the ion concentration inside the cell is different from that in the extracellular liquid. The potential generated by the difference in ion concentration is represented by a battery.
Elementary circuit theory allows the construction of a set of differential equations relating the different ion currents to the potential difference across the membrane. Using this set of differential equations, certain essential features of neural behavior can be modeled. For example, assuming appro-
FIGURE 5.14 Rodent navigation. These figures depict the behavior of a neurally realistic simulation of the path integrator in a rat. The simulation was generated by using a single (recurrent) generic neural subsystem. (A) When the simulation is given random noise, it spontaneously generates a stable, localized bump of neural activity over the neural sheet, which represents the rat’s current location. This demonstrates that a stable attractor (a widely accepted model of how the rat’s path integrator is organized) has been implemented. (B) This model also implements control (i.e., updating of the current location based on the rat’s motion) of the path integrator in a neurally plausible way. Here, straight-line motion in a rightward direction is shown. (C) The model correctly integrates the circular path of the rat, demonstrating that it can path integrate in any direction that the rat might move. This simulation has very little error compared to the simulations of past models. SOURCE: Chris Eliasmith, University of Waterloo, personal communication, September 7, 2004, and A. Samsonovich and B.L. McNaughton, “Path Integration and Cognitive Mapping in a Continuous Attractor Model,” Journal of Neuroscience 17(15):5900-5920, 1997.
priate parameter values, a constant input current larger than a certain critical value and turned on at a given instant of time results in the potential difference across the membrane taking the form of a regular spike train—which is reminiscent of how a real neuron fires. More realistic current inputs (e.g., stochastic ones) result in a much more realistic-looking output.
Despite lack of information about much of the cellular and molecular basis of neuronal excitation at the time, Hodgkin and Huxley were able to provide a relatively accurate quantitative description of how an action potential was generated by voltage-dependent ionic conductivities. The Hodgkin-Huxley model provided the basis for research for more than five decades, spinning off a new field of neurophysiology: in large part, this field rests on the foundation created by their model. Recent research on membrane ion channels can be related directly to the seminal ideas and (more importantly) precise mechanism that their model described.
The “plain vanilla” Hodgkin-Huxley model is still interesting today. For example, a recent study demonstrated previously unobserved dynamics in the Hodgkin-Huxley model, namely, the existence of chaotic solutions in the model with its original parameters.103 The significance of chaos in this context is that the excitability of a neural membrane with respect to firing is likely to be more complex than can be explained by a simple sub- or super-threshold potential.
Simulation and mathematical analysis of models have become essential tools in investigations of the complicated processes underlying rhythm generation in the nervous system. There are many types of channels and synapses. The number of channels and synapses and their locations distinguish different types of neurons from one another. Simulation of networks consisting of model neurons with
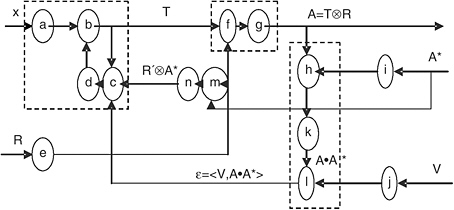
FIGURE 5.15 System for learning and performing deductive reasoning. The graphic describes the proposed system used during solution of the Wason card selection task; see P.C. Wason and P.N. Johnson-Laird, Psychology of Reasoning: Structure and Content, Harvard University Press, Cambridge, MA, 1972. This task requires determining when a logical rule is valid or invalid, and so is a form of deductive reasoning. Humans perform notoriously badly on many versions of this task, but well on other versions. This kind of context/content sensitivity is captured by this model; see C. Eliasmith, “Learning Context Sensitive Logical Inference in a Neurobiolobical Simulation,” pp. 17-19 in Compositional Connectionism in Cognitive Science: Papers from the AAAI Fall Symposium, S.D. Levy and R. Gayler, Program Co-chairs, October 21-24, 2004, The AAAI Press, Arlington, VA, Technical Report FS-04-03, 2004. The depicted large-scale circuit consists of 14 neural subsystems, distributed across frontal and ventral areas of the brain. This is a good example of the degree of complexity that can be built into a neurally realistic simulation using these new techniques. Populations a-d learn and apply the appropriate context for interpretation of the rule (R) encoded by population e. Populations f and g apply the relevant transformation (T) to the rule, giving the current answer (A). Populations h, k, and l determine the degree of correctness or incorrectness of the suggested answer (either given the correct answer, or given a reward or punishment signal), resulting in an error signal e. Populations m and n provide a guess at the best possible transformation. This guess and the error signal are integrated into the learning algorithm. SOURCE: Courtesy of Chris Eliasmith, University of Waterloo.
specified conductances and synapses enables researchers to test their intuitions regarding how these networks function. Simulations also lead to predictions of the effects of neuromodulators and disorders that affect the electrical excitability of the systems. Nonetheless, simulation alone is not sufficient to determine the information we would like to extract from these models. The models have large numbers of parameters, many of which are difficult or impossible to measure, and the goal is to determine how the system behavior depends on the values of all of these parameters.
Dynamical systems theory provides a conceptual framework for characterizing rhythms. This theory explains why there are only a small number of dynamical mechanisms that initiate or terminate bursts of action potentials, and it provides the foundations for algorithms that compute parameter space maps delineating regions with different dynamical behaviors. The presence of multiple time scales is an important ingredient of this analysis because the rates at which different families of channels respond to changes in membrane potential or ligand concentration vary over several orders of magnitude.
Figure 5.16 illustrates this type of analysis using a model for bursting in the pre-Bötzinger complex, a neural network in the brain stem that controls respiration. The first panel shows voltage recordings from intracellular recordings of a medullar slice from neonatal rats. Butera and colleagues measured conductances in this preparation and constructed a model for this system.104 Simulations of the burst-
|
Box 5.17 Connectionist Models of Dopamine Neuromodulation A long-held hypothesis suggests that catecholamine neurotransmitters, including dopamine (DA), modulate target neuron responses, by increasing their signal-to-noise (SNR) ratio (i.e. by increasing the differentiation between background or baseline firing rates and those that are evoked by afferent stimulation). For example, studies in the striatum showed that DA potentiated the response of target neurons to the effect of both excitatory and inhibitory signals. However, the precise biophysical mechanisms underlying these effects were not well understood. Moreover, the view that DA acts as a modulator in the pre-frontal cortex (PFC) has been controversial, because, for many years, DA application or stimulation of DA neurons reliably inhibited spontaneous PFC activity. Thus, many investigators argued that DA served as an inhibitory transmitter in PFC. The first explicit computational models of the neuromodulatory function of catecholamines, and DA in particular, were developed within the connectionist framework, and focused on their effects on information processing. Although such models do not typically incorporate biophysical detail, by virtue of their simplicity they have the advantage of simulating system level function and performance in a wide variety of cognitive tasks. Within this framework, DA effects were simulated as a change in the slope (or gain) of the sigmoidally shaped input-output activation function of processing units. Thus, in the presence of DA, both the excitatory and inhibitory influences of afferent inputs are potentiated. Computational analyses showed that this modulatory function would not improve the SNR characteristics of single neurons, but could do so at the network level. Models implementing these ideas proved useful for accounting for a wide range of phenomena, including the pharmacological effects of DA on performance in tasks thought to rely on PFC and the effects of disturbances of DA in schizophrenia. Biophysically Detailed Models In recent work, computational studies have focused on more biophysically detailed accounts of DA action within PFC. Models by Durstewitz et al. and Brunel and Wang, all include data on the different biophysical effects of DA on specific cellular processes. These models have been used to simulate the dynamics of activity in networks that closely parallel the patterns observed in vivo within PFC…. These models synthesize the rapidly growing, but often confusing literature on the neurophysiology of DA within PFC. For example, the biophysical effects of DA are shown to produce a suppressive influence on spontaneous activity, explaining its apparent inhibitory actions, while at the same time causing an enhanced excitability in response to afferent drive. Furthermore, the selective enhancement of inputs from recurrent versus external afferents provides a mechanism for stabilizing sustained activity patterns within PFC that are resistant to interference from external inputs. These computational analyses support the characterization of DA as a modulatory neurotransmitter, rather than a classical excitatory or inhibitory one, and explain its role in support sustained activity within PFC. Strikingly, these models are remarkably consistent with the original hypothesis that DA increases SNR within the PFC, and the expression of this idea in earlier connectionist models. The underlying assumption in both types of models is that short-term storage of information in PFC occurs through recirculating activity within local recurrent networks, which can be described as fixed-point attractor systems. DA activity helps to stabilize attractor states, both by making high activity states more stable (active maintenance), and low activity states (spontaneous background activity) less likely to spuriously transition to high activity states in the absence of strong afferent input. This is accomplished by the concurrent potentiation of excitatory and inhibitory transmission, implemented as changes in ion channel properties in biophysically detailed models and “summarized” as a change in the gain of the sigmoidal activation function in connectionist models. These mechanisms can be used to simulate the effects of DA on performance in cognitive tasks that rely on PFC function. For example, in a task emphasizing the role of PFC in working memory, increased DA activation in the Durstewitz et al. model enhanced the stability of PFC working memory representations by making them less susceptible to interference from the intervening distractors. Within connectionist models, similar effects have been demonstrated by changing the gain of the activation function, and simulating human performance in tasks known to rely on PFC, tasks similar to those simulated by Durstewitz et al. and Brunel and Wang. SOURCE: Reprinted by permission from J.D. Cohen, T.S. Braver, and J.W. Brown, “Computational Perspectives on Dopamine Function in Prefrontal Cortex,” Current Opinion in Neurobiology 12(2):223-229. Copyright 2002 Elsevier. (References omitted.) |
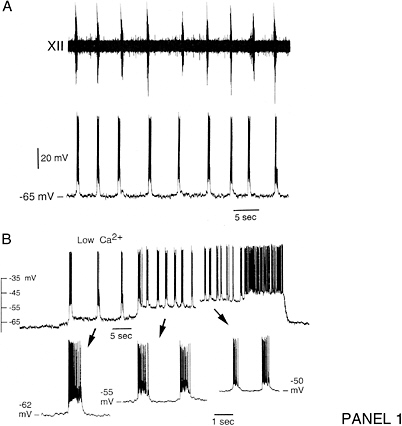
FIGURE 5.16 Bursting in the pre-Botzinger complex.
Panel 1: Example of voltage-dependent properties of pre-Bötzinger complex (pre-BötC) inspiratory bursting neurons. Traces show whole-cell patch-clamp recordings from a single candidate pacemaker neuron in the pre-BötC of a 400-µm-thick neonatal rat transverse medullary slice with rhythmically active respiratory network. Recordings in A and B were obtained respectively before and after block of synaptic transmission by low Ca2+ conditions identical to those described in Johnson et al. (1994) (i.e., 0.2 mM Ca2+, 4 mM Mg2+, 9 mM K+ in slice bathing solution). Patch pipette solution and procedure for whole-cell recording were as described previously (Smith et al. 1991, 1992). Before block of synaptic transmission, the neuron bursts in synchrony with the inspiratory phase of network activity as monitored by the inspiratory discharge recorded on the hypoglossal (XII) nerve (Smith et al. 1991). After block of synaptic activity (30 minutes under low-Ca2+ conditions), the cell exhibits intrinsic voltage-dependent oscillatory behavior. As the cell is depolarized by constant applied current, it undergoes a transition from silence (baseline potential below 65 mV, left) to oscillatory bursting to beating (baseline potential above 45 mV, right). In the bursting regime, the burst period and duration decreases (see expanded time-base traces in B) as the baseline membrane potential is depolarized. SOURCE: Reprinted by permission from R.J. Butera, Jr., J. Rinzel, and J.C. Smith, “Models of Respiratory Rhythm Generation in the Pre-Bötzinger Complex. I. Bursting Pacemaker Neurons,” Journal of Neurophysiology 82(1):382-397, 1999. Copyright 1999 American Physiological Society.
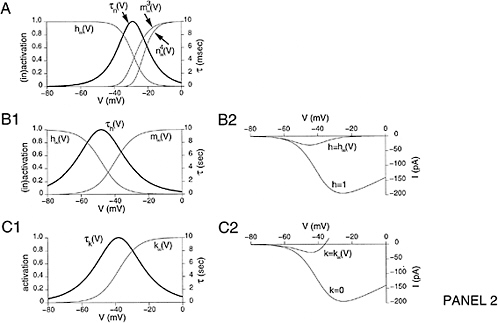
Panel 2: Gating and I-V characteristics of components of models 1 and 2. (A) spike-generating kinetics: m∞3(V) and h∞(V) of INa and n∞(V) and τn(V) of IK; note that h=1− n. (B1) gating characteristics of INaP: m∞(V), h∞(V), and τh(V) (bold); left: y-axis scale for steady-state gating functions; right: y-axis scale for τh(V). (B2) I-V plots of INaP for h=h∞(V) and h=1. First case results in a small window current at subthreshold potentials; second case corresponds to INaP-h with complete removal of inactivation. (C1) gating characteristics of IKS: k∞(V) and τk(V) (bold); left: y-axis scale for activation function; right: y-axis scale for τk(V). (C2) I-V plots of INaP+IKS for k=k∞(V) and k=0. First case results in a small current at subthreshold potentials; second case corresponds to INaP with complete removal of the opposing IKS.
SOURCE: Reprinted by permission from R.J. Butera, Jr., J. Rinzel, and J.C. Smith, “Models of Respiratory Rhythm Generation in the Pre-Bötzinger Complex. I. Bursting Pacemaker Neurons,” Journal of Neurophysiology 82(1):382-397, 1999. Copyright 1999 American Physiological Society.
ing rhythms displayed by this model are shown in the second panel. The third panel shows a map of the simulated trajectory that illustrates the relationship of the bursting to slow and fast variables in the system.
5.4.5.4 Synaptic Transmission
The intercellular signaling process of synaptic transmission is a much-studied problem. Much has been learned about synaptic structure and function through the classical techniques of neuropharmacology, electron microscopy (EM) neuroanatomy, and electrophysiology, and correlation of the observations made through these various techniques has led to the development of computational models of synaptic microphysiology. However, the scope of previous modeling attempts has been limited by available computing power, modeling framework, and lack of high-resolution three-dimensional ultrastructural data in an appropriate machine representation.
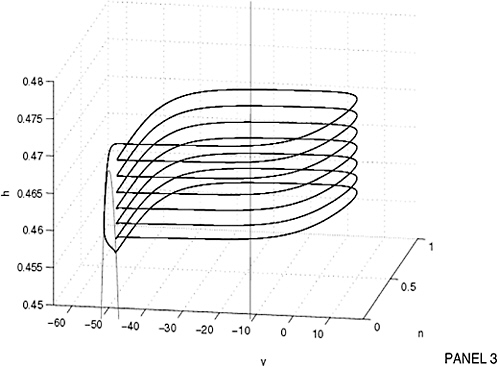
Panel 3: Projection of trajectory onto fixed points of fast subsystem. The axes are v: membrane potential; h: inactivation of the HH sodium channel (there is also a persistent sodium channel in the model); and n: activation of the HH “delayed rectifier” potassium channel. The voltage traces show the changes of voltage as a function of time. The values of h and n also change with time. Think of v, n, h as the three coordinates of a point moving through space. This plot depicts the path taken by this point in a bursting oscillation of the model. The curves are states at which the motion through this space is particularly slow, becoming zero in the limit so that the slower currents in the model are not allowed to change at all. SOURCE: Derived from Figure 4, Panel A3, in R.J. Butera Jr., J. Rinzel, and J.C. Smith, “Models of Respiratory Rhythm Generation in the Pre-Bötzinger Complex. I. Bursting Pacemaker Neurons,” Journal of Neurophysiology 82(1):382-397, 1999. Copyright 1999 American Physiological Society. Used by permission.
What has been missing is an appropriate set of tools for acquiring, building, simulating, and analyzing biophysically realistic models of subcellular microdomains. Coggan et al. have developed and used a suite of such computational tools to build a realistic computational model of nicotinic synaptic transmission based on serial electron tomograms of a chick ciliary ganglion somatic spine mat.105
The chick ciliary ganglion somatic spine mat is a complex system with more than one type of neurotransmitter receptor, possible alternative locations for transmitter release, and a tortuous synaptic geometry that includes a spine mat and calyx-type nerve terminal. Highly accurate models of the synaptic ultrastructure are obtained through large-scale, high-resolution electron tomography; com-
puter-aided methods for extracting accurate surfaces and defining in-silico representations of their molecular properties; and physiological underpinnings from a variety of studies conducted by the involved laboratories and from the literature.
These data are then used as the framework for advanced simulations using MCell running on high-performance supercomputers as well as distributed or grid-based computational resources. This project pushes development of tools for acquisition of improved large-scale tomographic reconstructions of cellular interfaces down to supramolecular scales. It also drives improvements in the software tools both for the distribution of molecular components within the surface models extracted from the tomographic reconstructions and for the deposition and retrieval of relevant information for the MCell simulator (Box 5.18) in the tomography and Cell-Centered Database (CCDB) environment.
Realistic modeling of synaptic microphysiology (as illustrated in Figure 5.17) requires the following:
-
Acquisition of high-resolution, three-dimensional synaptic ultrastructure—this is accomplished with serial EM tomography.
-
Segmentation of pre- and postsynaptic membrane from the tomographic volume—this is accomplished using the tracing tool in Xvoxtrace.
-
Three-dimensional reconstruction of the membrane surface topology to form a triangle mesh—this is accomplished using the marching cubes isosurface extraction tool in Xvoxtrace.
-
Subdivision of the membrane surface meshes into physiologically relevant regions (e.g., spine versus nonspine membrane and PSD [phosphorylation site domain] versus non-PSD regions)—this is accomplished using the mesh tagging tool in DReAMM.
-
Placement of effector molecules (e.g., receptors, enzymes, reuptake transporters) onto membrane surfaces with the desired distribution and density—this is accomplished using the MCell model description language (MDL). Effector distribution and density may be determined by labeling and imaging studies.
-
Specification of the diffusion constant, quantity, and location of neurotransmitter release—this is accomplished using MCell MDL.
-
Specification of the reaction mechanisms and kinetic rate constants governing the mass action kinetics interaction of neurotransmitter and effector molecules—this is accomplished using MCell MDL.
-
Specification of what quantitative measures should be made during the simulation—this is accomplished using MCell MDL.
-
Simulation of the defined system—this is accomplished using the MCell compute kernel.
-
Analysis of the results at various points in the parameter space defined by the system—this is accomplished using analysis tools of the investigator’s discretion.
Analysis of miniature excitatory postsynaptic currents (mEPSCs) recorded in electrophysiological experiments shows that mEPSCs in the CG somatic spine mat occur in a broad spectrum of amplitudes, rise times, and fall times. The differential kinetics and complementary distributions of α3 and α7 nAChRs are expected to lead to mEPSCs whose characteristics are highly dependent on the location of neurotransmitter release within the spine mat. Realistic simulation makes it possible to explore and quantify the degree to which this hypothesis is true and to make quantitative comparisons of the simulation and electrophysiological results. Figure 5.18 summarizes the results of simulations designed to explore the limits of mEPSC behavior by virtue of the choice of neurotransmitter release locations. The results not only confirm the qualitative expectations at each site but also predict their quantitative behavior, allowing fine discriminations to be made.
The process briefly outlined above represents a significant advance in the ability to create realistic computational models of subcellular microdomains from actual cellular ultrastructure. The preliminary results presented are just the beginning of exciting computational experiments that can now be performed on the CG model in an effort to illuminate and inform further bench experiments. Among all of the things learned, perhaps the most important is which of the physical characteristics of the CG are the
|
Box 5.18 MCell is a general Monte Carlo simulator of cellular microphysiology. MCell simulations provide insights into the behavior and variability of real systems comprising finite numbers of molecules interacting in spatially complex environments. MCell incorporates high-resolution physical structure into models of ligand diffusion and signaling, and thus can take into account the large complexity and diversity of neural tissue at the subcellular level. MCell is based on the use of rigorously validated Monte Carlo algorithms to track the evolution of biochemical events in time and three-dimensional space for individual ligand and effector molecules. That is, the Monte Carlo approach is based on the use of random numbers and probabilities to effect the simulation of individual cases of the system’s behavior. In the MCell models used in neural signaling employing a Brownian dynamics random walk algorithm, individual ligand molecules move according to a three-dimensional Brownian dynamics random walk and encounter membrane boundaries and effector molecules as they diffuse. Bulk solution rate constants are converted into Monte Carlo probabilities so that the diffusing ligands can undergo stochastic chemical interactions with individual binding sites such as receptor proteins, enzymes, and transporters. These interactions are governed by user-specified reaction mechanisms. The diffusion algorithms are grid-free, and the reaction algorithms are at the level of interactions between individual molecules and thus do not involve solving systems of differential equations. Membrane boundaries are represented as triangle meshes and may be of arbitrary complexity. The Monte Carlo approach has certain important advantages over the finite element (FE) approach often used to include spatial information in kinetic modeling. The FE approach divides three-dimensional space into a regular grid of contiguous subcompartments, or voxels. It assumes well-mixed conditions within each voxel and uses differential equations to compute fluxes between, and reactions within, each voxel. Mass action equations are based on continuum processes and predict average concentrations. In large, simple volumes with great numbers of a few types of molecules (e.g., reactions in a test tube), fluctuations are relatively small, and knowledge of average concentrations accounts most of the interesting phenomena. However, synaptic signaling is inherently discrete and stochastic because the number of molecules involved is small; hence, the FE method will fail to describe accurately the biochemistry of synaptic signaling because these methods provide only averaged data. Furthermore, complex cellular structures—such as the structures that characterize the synapse—require that the voxel grid be very fine and irregular in shape, making an FE approach both computationally expensive and difficult to implement. MCell is very general because it includes a high-level model description language (MDL), which allows the user to build subcellular structures and signaling pathways of virtually any configuration. MCell’s algorithms scale smoothly from typical workstations to shared-memory multiprocessor machines to massively parallel supercomputers. SOURCE: For more information, see http://www.mcell.cnl.salk.edu; J.R. Stiles and T.M. Bartol, Jr., “Monte Carlo Methods for Simulating Realistic Synaptic Microphysiology Using MCell,” pp. 87-127 in Computational Neuroscience: Realistic Modeling for Experimentalists, E. de Schutter, ed., CRC Press, Boca Raton, FL, 2000; J.R. Stiles, T.M. Bartol, Jr., E.E. Salpeter, M.M. Salpeter, and T.J. Sejnowski, “Synaptic Variability: New Insights from Reconstructions and Monte Carlo Simulations with MCell,” pp. 681-731 in Synapses, W. Cowan, T.C. Sudhof, and C.F. Stevens, eds., Johns Hopkins University Press, Baltimore, MD, 2001. Discussion of the pros and cons of FE versus MC is from K.M. Franks and T.J. Sejnowski, “Complexity of Calcium Signaling in Synaptic Spines,” BioEssays 24(12):1130-1144, 2002. |
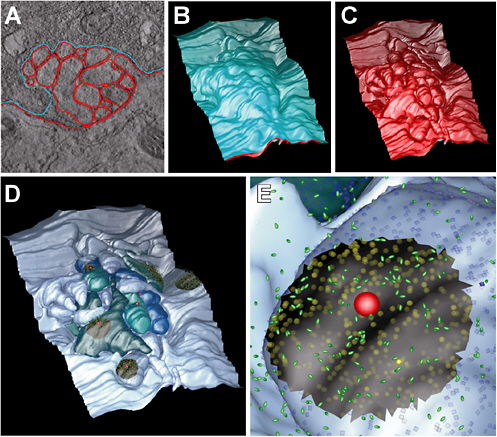
FIGURE 5.17 Constructing the geometry of a chick ciliary ganglion (CG) somatic spine mat model. A serial EM tomogram of a CG spine mat was obtained at ~4 nm per voxel resolution. The serial tomogram encompassed a volume of ~27 mm3 (~3 µm × 3 µm × 3 µm).
(A) A typical slice through the tomographic volume together with hand-traced contours of the pre- and postsynaptic membranes. Tracing and segmentation of presynaptic (cyan) and postsynaptic (red) membrane contours generated using Xvoxtrace.
(B) Three-dimensional reconstruction of pre- and postsynaptic membrane surfaces as triangle meshes—view looking down onto intracellular face of presynaptic membrane (visualized using DReAMM). The presynaptic mesh is composed of 100,000 triangles and the postsynaptic mesh is composed of 300,000 triangles.
(C) Postsynaptic membrane surface—view of extracellular face of membrane (presynaptic membrane invisible).
(D) Completed model including postsynaptic membrane subdivided into distinct spines, PSD areas (black regions with yellow borders), receptor molecules (tiny blue particles on membrane surface), and several neurotransmitter release sites (red spheres). The membrane was subsequently populated with the desired distributions and densities of nicotinic acetylcholine receptor (nAChR) types and acetylcholine esterase (AChE) enzyme. Also visible in
(D) are several acetylcholine (ACh) vesicular release sites whose locations are most clearly illustrated in Figure 5.18A.
(E) Magnified view of the state of a simulation of synaptic transmission model as simulated by MCell. State of system 300 ms after release of 5,000 molecules of acetylcholine (small green ellipsoids) is shown. α7 nAChR types are shown in blue, and α3* nAChR types are shown in yellow (inactive receptors are semitransparent, and open receptors are opaque).
SOURCE: Courtesy of Tom Bartol, Salk Institute, San Diego, California.
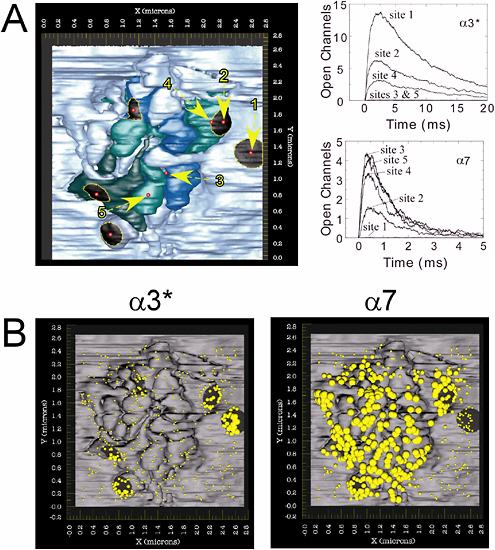
FIGURE 5.18 Summary of synaptic transmission simulations.
(A) Location of selected transmitter release sites and their associated simulated mEPSC traces, each decomposed into their α3 and α7 nAChR components. Each trace is the average of 100 simulations using MCell. Site 1 is located at a PSD on nonspine membrane. This site is expected to have a large α3 response and a very small α7 response. At the other extreme of behavior, sites 3 and 5 are placed over non-PSD spine membrane. Rich in α7 receptors and poor in α3 receptors, these sites are expected to have large α7 responses and minimal α3 responses. The other sites are placed at locations expected to give rise to mEPSCs of mixed nAChR origin.
(B) mEPSC amplitudes (decomposed into their α3 and α7 nAChR components) at each of 550 distinct vesicular release sites. The mEPSC amplitudes are indicated by the diameter of the yellow spherical glyph and demonstrate a strong dependence on location and underlying geometry.
SOURCE: Courtesy of Tom Bartol, Salk Institute, San Diego, CA.
FIGURE 5.19 The hippocampus in situ. SOURCE: Courtesy of Michael Miller, Johns Hopkins University.
least constrained, are least understood, and have the greatest impact on synaptic function. Specifically, the results clearly demonstrate that synaptic geometry, receptor distribution, and vesicle release location each have a profound quantitative impact on the efficacy of the postsynaptic response. This means that attention to accuracy in the model-building process must be a prime concern.
5.4.5.5 Neuropsychiatry106
The field of computational neuropsychiatry has been exploding with applications of large-deformation brain mapping technology that provide mechanisms for discovering neuropsychiatric disorders of many types. The hippocampus is a region of the brain (depicted in green in Figure 5.19) that has been implicated in schizophrenia and other neurodegenerative diseases such as Alzheimer’s. Using large-deformation brain mapping tools in computational anatomy, researchers can define, visualize, and measure the volume and shape of the hippocampus. These methods allow for precise assessment of changes in hippocampal formation.
Researchers at the Center for Imaging Science (CIS) used mapping tools to compare the left and right hippocampi (Figure 5.20) in 15 pairs of schizophrenic and control subjects. In the schizophrenic
|
106 |
Section 5.4.5.5 is based on L. Wang, S.C. Joshi, M.I. Miller, and J.G. Csernansky, “Statistical Analysis of Hippocampal Asymmetry in Schizophrenia,” Neuroimage 14(3):531-545, 2001; J.G. Csernansky, L. Wang, S. Joshi, J.P. Miller, M. Gado, D. Kido, D. McKeel, et al., “Early DAT Is Distinguished from Aging by High-dimensional Mapping of the Hippocampus,” Neurology 55(11):1636-1643, 2000. |
FIGURE 5.20 Left and right hippocampuses. SOURCE: Courtesy of Michael Miller, Johns Hopkins University.
subjects, deformations were localized to hippocampal subregions that send projections to the prefrontal cortex. The deformations strongly distinguish schizophrenic subjects from control subjects. The pictures indicate inward deformations by cooler colors, outward deformations by warmer colors, and little deformation by a neutral green color. These results support the current hypothesis that schizophrenia involves a disturbance of hippocampal-prefrontal connections.
In a separate study, CIS researchers also compared asymmetry between the left and right hippocampi. The left and the right side of normal brains develop at different rates. Structures on both sides of the brain are similar, but not identical. This is normal brain asymmetry. If a different asymmetry pattern exists in schizophrenic subjects, it may indicate a disturbance of the left-right balance during early stages of brain development. Researchers found that the left hippocampus was narrower along the outside edge than the right hippocampus. This asymmetry was similar in schizophrenic and normal subjects (Figure 5.21, left image). However, further comparison revealed a significant difference in asymmetry patterns of the hippocampal area called the subiculum (Figure 5.21, right image). People with schizophrenia tend to have a more pronounced depression and a downward bend in the surface of that structure.
As part of Washington University’s Healthy Aging and Senile Dementia (HASD) program, CIS researchers have also applied brain mapping tools to assess the structure of the hippocampus in older human subjects (depicted in Figure 5.22). They compared measurements of hippocampal volume and shape in 18 subjects with early dementia of the Alzheimer type (DAT) with 18 healthy elderly and 15 younger control subjects. Hippocampal volume loss and shape deformities observed in subjects with DAT distinguished them from both elderly and younger control subjects. The pattern of hippocampal
FIGURE 5.21 Asymmetry in schizophrenia. SOURCE: Michael Miller, Johns Hopkins University.
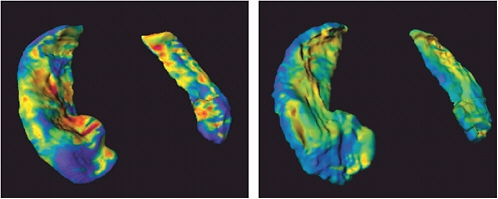
FIGURE 5.22 Hippocampal structure in normal aging (left) versus in Alzheimer’s disease patients (right). SOURCE: Courtesy of Michael Miller, Johns Hopkins University.
deformities in subjects with DAT was largely symmetric and suggested damage to the CA1 hippocampal subfield.
Hippocampal shape changes were also observed in healthy elderly subjects, which distinguished them from healthy younger subjects. These shape changes occurred in a pattern distinct from the pattern seen in DAT and were not associated with substantial volume loss. These assessments indicate that hippocampal volume and shape derived from computational anatomy large deformation brain mapping tools may be useful in distinguishing early DAT from healthy aging.
5.4.6 Virology
Mathematical and computational methods are increasingly important to virology. For example, a primary and surprising phenomenological aspect of HIV infection is that progression to AIDS usually
|
Box 5.19 Mathematical models of HIV infection and treatment have provided quantitative insights into the major biological processes that underlie HIV pathogenesis and helped establish the treatment of patients with combination therapy. This in turn has changed HIV from a fatal disease to a treatable one. The models successfully describe the changes in viral load in patients under therapy and have yielded estimates of how rapidly HIV is produced and cleared in vivo, how long HIV-infected cells survive while producing HIV, and how fast HIV mutates and evolves drug resistance. They have also provided clues into the process of T-cell depletion that characterizes AIDS. The models have also provided means to rapidly screen antiviral drug candidates for potency in vivo, thus hastening the introduction of new antiretroviral therapies. On average, HIV takes about 10 years to advance from initial infection to immune dysfunction (or AIDS). During this period the amount of virus measured in a person’s blood hardly changes. Because of this slow progression and the unchanging level of virus it was initially thought that this infection was slow and it was unclear whether treating this disease early, when symptoms were not apparent, was worthwhile. Recognizing that constant levels of virus meant only that the rates of viral production and clearance were in balance, but not necessarily slow, Perelson and David Ho from Rockefeller University used experimental drug therapy to “perturb” the viral steady state. Mathematically modeling the response to this perturbation using a system of ordinary differential equations that kept track of the concentrations of infected cells and HIV, and fitting the experimental data to the model, revealed a plethora of new features of HIV infection. Figure 5.19.1 shows that after therapy is initiated at time 0, levels of HIV RNA (a surrogate for virus) fall ten-to a hundredfold in the first week or two of therapy. This suggested that HIV has a half-life (t1/2) of 1-2 days, and thus maintaining the pre-therapy constant level of virus requires enormous virus production—in fact, the amount of virus in the body must double every 1-2 days. Detailed analysis showed that this viral decay was governed by two processes, clearance of free virus particles (t1/2 < 6 hours) and loss of productively infected cells (t1/2 < 1.6 days). From this rapid clearance of virus one could compute that at steady state, ~1010 virions are produced daily and given the mutation rate of HIV, that each single and most double mutations of the HIV genome are produced daily. Thus, effective drug therapy  FIGURE 5.19.1 Model predictions (lines) of the biphasic decay of HIV viral load compared with typical patient data (symbols). SOURCE: Courtesy of A.S. Perelson, Los Alamos National Laboratory. |
|
would require drug combinations that can sustain at least three mutations before resistance arises, and this engendered the idea of triple combination therapy. Other analyses showed that the slope of viral decay was proportional to the drug combinations’ antiviral efficacy, providing a means of comparing therapies. Following the rapid 1-2 week “first phase” loss, the rate of HIV RNA decline slows. Models of this “second phase” of decline, when fitted to the kinetic data, suggested that a small fraction of infected cells might live a period of weeks while infected (t1/2 ~ 14 days). Following upon the success of these joint modeling and experimental efforts, many similar studies were undertaken and revealed a fourth, much longer time-scale for the decay of latently infected cells of 6-44 months. Latently infected cells, which harbor the HIV genome but do not produce virus, can hide from the immune system and reignite infection when the cells are stimulated into proliferation. Clearing latently infected cells is one of the last remaining obstacles to eradicating HIV from the body. |
takes a very long time, and individuals who have not progressed to full-blown AIDS are asymptomatic. As Box 5.19 suggests, computational models have been able to shed considerable light on this phenomenology, and these insights have altered the view of AIDS from a static picture in which the virus is essentially dormant and does not do very much for a long time to a much more dynamic picture of a rough balance between the virus and the immune system, both working very hard, for that period of time. These findings have had tangible impact, because they have affected drug treatment regimes considerably.
More specifically, the average rate of HIV production in the human body is on the order of 1010 copies per day as noted in Box 5.19. Empirical data indicate that errors in HIV replication occur at a rate on the order of 10−4 to 10−5 per base per generation, and since the HIV genome is 10,000 base pairs long, the likelihood that a replicated genome will contain at least one error is 10 percent to nearly unity (and the vast majority of these errors are errors in a single base). Because there are only four possible bases in DNA (and hence each base can change into only one of three other bases), there are only 30,000 possible single-base mutations of a given genome. An error rate of 10−4 to 10−5 per base per generation distributed among 1010 copies each with 104 bases means that each generation produces 109 to 1010 mutations, which are distributed over the set of 30,000 possible mutations. Put differently, every new day brings to life on the order of 105 instances of every possible single-base variant of HIV.
Thus, a drug known to bind to a particular sequence of amino acids at a certain location in a protein today will face 105 to 106 new variants tomorrow against which its effectiveness will be questionable. This fact suggests that drug treatment regimes must target multiple binding sites, and hence combination drug therapy is likely to be more effective because drug-resistant variants must then be the result of multiple errors in the replication process (which occur much less frequently). This in fact reflects recent experience with combination drug regimes.107
5.4.7 Epidemiology
Epidemiology is the study of the dynamics of disease in a population of individuals. Of particular interest is the epidemiology of infectious diseases, which arise from contact between an environmental
|
107 |
For further discussion, see A.G. Rodrigo, “HIV Evolutionary Genetics,” Proceedings of the National Academy of Sciences 96(19):10559-10561, 1999; B.A. Cipra, “Will Viruses Succumb to Mathematical Models?” SIAM News 32(2), 1999, available at http://www.siam.org/siamnews/03-99/viruses.pdf. |
|
Box 5.20 One of the best illustrations of [the significance of spatial heterogeneity] is provided by the highly dynamic spatiotemporal epidemic pattern of measles. An important set of analyses of simple, homogeneous models predicted the possibility of chaotic dynamics; however, the resulting large-amplitude [predicted] epidemics generate unrealistically low persistence of infection in small communities. Adding successive layers of social and geographical space—and moving from deterministic to stochastic models—improves spatial realism and may reduce the propensity for chaos. The major computational challenge in these highly nonlinear stochastic systems is to represent hierarchical spatial complexity and especially its impact on vaccination strategies. Depending on the problem, all scales—from the individual level to big cities—may be important, both in terms of social space [family and school infection dynamics] and in terms of geographic spread and coherency. … [A] central question is: How spatially aggregated and parsimonious a model can provide useful results in a given context? This is particularly important in comparisons between directly transmitted human infections—where long-range movements may bring infection dynamics comparatively close to mean field behavior (in which every individual is assumed to have equal contact with every other individual, thus experiencing the mean or average field)—and the equivalent infections in natural populations, where more restricted movements and host population dynamics add extra complexities. It is risky to model at a given level of detail without having data at the relevant spatial grain. Notifiable infectious diseases are unusually well [documented], with large and often as yet uncomputerized spatiotemporal data sets. These data provide a huge potential testbed for developing methods for characterizing spatiotemporal dynamics in nonlinear, nonstationary stochastic systems. An encouraging development is that the current, generally nonparametric, approaches to characterizing chaos and other nonlinear behaviors are increasingly incorporating lessons from mechanistic epidemiological models. SOURCE: Reprinted by permission from S.A. Levin, B. Grenfell, A. Hastings, and A.S. Perelson, “Mathematical and Computational Challenges in Population Biology and Ecosystems Science,” Science 275(5298):334-343, 1997. Copyright 1997 AAAS. (References omitted.) |
agent and an individual (e.g., an insect that bites an individual) or between individuals (e.g., an individual who sneezes in a room filled with people) that leads to the transmission of disease. The dynamics of infectious diseases depend on many things, such as the likelihood of transmission between carrier agent and infected individual given that contact has been made, the geographical distribution of carrier agents and individuals, and the susceptibility of individuals to the disease.
A central problem in epidemiology is how the dynamics of disease play out across geographical space.108 Problems of spatial heterogeneity play out at many different levels of aggregation: individuals, families, work groups and firms, neighborhood, and cities. Box 5.20 provides an example taken from the study of measles.
At the same time, spatial heterogeneity is not the only inhomogeneity of interest. For example, the epidemiology of sexually transmitted diseases (STDs) cannot be separated from a consideration of their dynamics in different social groups. For example, patterns of STDs in prostitutes and intravenous drug
|
108 |
K. Dietz, “The Estimation of the Basic Reproduction Number for Infectious Diseases,” Statistical Methods in Medical Research 2(1):23-41, 1993; A.D. Cliff and P. Haggett, Atlas of Disease Distributions: Analytic Approaches to Epidemiologic Data, Blackwell LTD, Oxford, UK, 1988; D. Mollison and S.A. Levin, “Spatial Dynamics of Parasitism,” pp. 384-398 in Ecology of Infectious Diseases in Natural Populations, B.T. Greenfell and A.P. Dobson, eds., Cambridge University, Cambridge, UK, 1995. |
|
Box 5.21 The main focus for modeling social space (the space of social interactions) and disease is, of course, on AIDS and other sexually transmitted infections. Simple models illustrated clearly that heterogeneities in contact rates can substantially alter the predicted course of epidemics. This area has seen an explosion of research, both in data analysis of contact structures and in graph-theoretic and other approaches to modeling. Models and data analysis are most productive when combined, especially in allowing the observations to limit the universe of possible networks. The major computational challenge is how to deal with the complexity of networks, where concurrency of partnerships often means that closure to a few moments of the distribution is difficult. This problem is especially acute given the sensitivity of obtaining data for STD networks, in that the nature of the network is generally only partially and imperfectly known. The use of mathematical models for human immunodeficiency virus (HIV) transmission will be especially important in assessing the impact of potential vaccines. Another major computational challenge—which developed with the AIDS epidemic and is currently being applied to another pathogen, the bovine spongiform encephalopathy agent—is to estimate the parameters of transmission models from disease incidence and other demographic data. One hope for the future for both of these areas is network information embedded in viral genomes. A body of recent work indicates exciting possibilities for estimating epidemiological parameters from the birth and death processes of pathogen evolutionary trees. More generally, new mathematical and computational techniques will be needed to understand the epidemiological implications of the rapidly accumulating data on pathogen sequences, especially in the context of parasite genetic diversity and the host immunological response to it. SOURCE: Reprinted by permission from S.A. Levin, B. Grenfell, A. Hastings, and A.S. Perelson, “Mathematical and Computational Challenges in Population Biology and Ecosystems Science,” Science 275(5298):334-343,1997. Copyright 1997 AAAS. (References omitted.) |
users exhibit different dynamical patterns than those in the general population because of factors such as rates of sexual contact with others (both inside and outside the individual’s own social group) and different sexual practices of individuals in each group (e.g., use of condoms). Box 5.21 elaborates on this notion in greater detail.
5.4.8 Evolution and Ecology
5.4.8.1 Commonalities Between Evolution and Ecology
No two fields in biology encompass such a broad range of levels of biological organization as ecology and evolutionary biology. Although the two fields ask different questions, they both contend with factors of space and time, and share common theories about relationships between individuals, populations, and communities. The two intertwined fields view these relationships in different ways. Evolutionary biologists want to understand and quantify the effect of environment (e.g., natural selection) on individuals and populations; ecologists want to understanding the role of individuals and populations in shaping their environment (ecological inheritance, niche construction).
The two fields encompass a diverse assemblage of topics with applications in resource management, epidemiology, and global change. In these fields, data have been relatively difficult to collect in ways that relate directly to mathematical or computational models, although this has been changing over the past 10 years. Thus, both fields have relied heavily on theory to advance their insights. In fact, ecology and evolution have been the substrate for the development of important mathematical concepts. The quantitative study of biological inheritance and evolution provided the context for statistics, probability theory, stochasticity, and dynamical systems theory.
Among the fundamental questions in the study of evolution are those that seek to know the relative strengths of natural selection, genetic drift, dispersal processes, and genetic recombination in shaping the genome of a population—essentially the forces that provide genetic variability in a species. Both ecologists and evolutionary biologists want to know how these forces lead to morphological changes, speciation, and ultimately, survival over time. The fields seek theory, models, and data that can account for genetic changes over time in large heterogeneous populations in which genetic information is exchanged routinely in an environment that also exerts its influence and changes over time.
In addition to interest in genetic variability and fitness within a single species, the two fields are interested in relationships between multiple species. In ecology, this manifests itself in questions of how the individual forces of variability within and between species affect their relative ability to compete for resources and space that leads to their survival or extinction—in other words, forces that determines the biodiversity of an ecosystem (i.e., a set of biological organisms interacting among themselves and their environment). Ecologists want to understand what determines the minimum viable population size for a given population, the role of keystone species in determining the diversity of the ecosystem, and the role of diversity in preservation of the ecosystem.
For evolutionary biologists, questions regarding relationships between species focus on trying to understand the flow of genetic information over long periods of time as a measure of the relatedness of different species and the effects of selection on the genetic contribution to phenotypes. Among the great mysteries for evolutionary biologists is whether and how evolution relates to organismal development, an interaction for which no descriptive language currently exists.
How will ecologists and evolutionary biologists answer these questions? These fields have had few tools to monitor interactions in real time. But new opportunities have emerged in areas from genomics to satellite imaging and in new capabilities for the computer simulation of complex models.
5.4.8.2 Examples from Evolution
A plethora of genomic data is beginning to help untangle the relationship between traits, genes, developmental processes, and environments. The data will serve as the substrate from which new statistical conclusions can be drawn, for example, new methods for identifying inherited gene sequences such as those related to disease. To answer question about the process of genome rearrangement, the possibility of comparing gene sequences from multiple organisms provides the basis for testing tools that discern repeatable patterns and elucidate linkages.
As more detailed DNA and protein sequence information is compiled for more genes in more organisms, computational algorithms for estimating parameters of evolution have become extremely complex. New techniques will be needed to handle the likelihood functions and produce satisfactory statistics in a reasonable amount of time. Studies of the role of environmental and genetic plasticity in trait development will involve large-scale simulations of networks of linked genes and their interacting products. Such simulations may well suggest new approaches to such old problems as the nature-nurture dichotomy for human behaviors.
New techniques and the availability of more powerful computers have also led to the development of highly detailed models in which a wide variety of components and mechanisms can be incorporated. Among these are individual unit models that attempt to follow every individual in a population over time, thereby providing insight into dynamical behavior (Box 5.22).
Levin argues that such models are “imitation[s] of reality that represent at best individual realization of complex processes in which stochasticity, contingency, and nonlinearity underlie a diversity of possible outcomes.”109 From the collective behaviors of individual units arise the observable dynamics
|
Box 5.22 Avida is a simulation software system developed at the Digital Life Laboratory at the California Institute of Technology.1 In it, digital organisms have genomes comprised of a sequence of instructions that operate on a virtual machine. These instructions include the ability to perform simple mathematical operations, copy values from memory location to memory location, provide input and output, and check conditions. Through a sequence of instructions, these organisms can copy their genome, thereby reproducing asexually. Since the software can simulate many hundreds of thousands of generations of evolution for thousands of organisms, their digital evolution not only can be observed in reasonable lengths of time, but also can be precisely inspected (since there are no inconvenient gaps in the fossil record). Moreover, alternate scenarios can be explored by going back into evolutionary history and reversing the effects of mutations, for example. At a minimum, this can be seen as experiment by analogy, revealing potential avenues for investigation or hypotheses to test in actual biological evolution. A stronger argument holds that evolution is an abstract mathematical process and will operate under similar dynamics whether embodied in DNA in the physical world or in digital simulations of it. Avida has been used to explore how complex features can arise through mutation, competition, and selective pressure.2 In a series of experiments, organisms were provided with a limited supply of energy units necessary for the execution of their genome of instructions. However, organisms that performed any of a set of complex logical operations were rewarded with an increased allowance and thus increased opportunities to reproduce. More complicated logical operations provided proportionally greater rewards. The experiment was seeded with an ancestral form that could perform none of those operations, containing only the instructions to reproduce. Mutation arose through imperfect copying of the genome during reproduction. EQU, the most complex logical operation checked for [representing the logical statement (A and B) or (~A and ~B)], arose in 23 out of 50 populations studied where the simpler operations also provided rewards. The sequence of instructions that evolved to perform the operation varied widely in length and implementation. However, in other simulations where only EQU was rewarded, no lineages ever evolved it. This evidence agrees with the standard theory of biological evolution—stated as early as Darwin—that complex structures arise through the combination and modification of useful intermediate forms. |
of the system. “The challenge, then, is to develop mechanistic models that begin from what is understood about the interactions of the individual units, and to use computation and analysis to explain emergent behavior in terms of the statistical mechanics of ensembles of such units.” Such models must extrapolate from the effects of change on individual plants and animals to changes in the distribution of individuals over longer time scales and broader space scales and hence in community-level patterns and the fluxes of nutrients.
5.4.8.2.1 Reconstruction of the Saccharomyces Phylogenetic Tree
Although the basic structure and mechanisms underlying evolution and genetics are known in principle, there are many complexities that force researchers into computational approaches in order to gain insight. Box 5.23 addresses complexities such as multiple loci, spatial factors, and the role of frequency dependence in evolution, and discusses a computational perspective on the evolution of altruism, a behavioral characteristic that is counterintuitive in the context of individual organisms doing all that they can to gain advantage in the face of selection pressures.
|
Box 5.23 The dynamics of alleles at single loci are well understood, but the dynamics of alleles at two loci are still not completely understood, even in the deterministic case. As a rule, two-locus models require the use of a variety of computational approaches, from straightforward simulation to more complex analyses based on optimization or the use of computer algebra systems. Three-locus models can be understood only through numerical approaches, except for some very special cases. Compare these analytical capabilities to the fact that the number of loci exhibiting genetic variation in populations of higher organisms is well into the thousands. Thus, the number of possible genotypes can be much larger than the population. In such a situation, the detailed population simulation (i.e., a detailed consideration of events at each locus) leads to problems of substantial computational difficulty. An alternative is to represent the population as phenotypes—that is, in terms of traits that can be directly observed and described. For example, certain traits of individuals are quantitative in the sense that they represent the sum of multiple small effects. Efforts have been undertaken to integrate statistical models of the dynamics of quantitative traits with more mechanistic genetic approaches, though even under simplifying assumptions concerning the relation between genotype and phenotype, further approximations are required to obtain a closed system of equations. Frequency dependence in evolution refers to the phenomenon in which the fitness of an individual depends both on its own traits and on the traits of other individuals in the population—that is, selection is dependent on the frequency with which certain traits appear in the population, not just on pressures from the environment. This point arises most strongly in understanding how cooperation (altruism) can evolve through individual selection. The simplest model is the game of prisoner’s dilemma, in which the game-theoretic solution for a single encounter between parties is unconditional noncooperation. However, in the iterated prisoner’s dilemma, the game theoretic solution is a strategy known as “tit-for-tat,” which begins with cooperation and then uses the strategy employed by the other player in the previous interaction. (In other words, the iterated prisoner’s dilemma stipulates repeated interactions over time between players.) Although the iterated prisoner’s dilemma yields some insight into how cooperative behavior might emerge under some circumstances, it is a highly and perhaps oversimplified model. Most importantly, it does not account for possible spatial localizations of individuals—a point that is important in light of the fact that individuals who are spatially separated have low probabilities of interacting. Because the evolution of traits dependent on population frequency requires knowledge of which individuals are interacting, more realistic models introduce some explicit spatial distribution of individuals—and, for these, simulations are required to dynamical understanding. These more realistic models suggest that spatial localization affects the evolution of both cooperative and antagonistic behaviors. SOURCE: Adapted from S.A. Levin, B. Grenfell, A. Hastings, and A.S. Perelson, “Mathematical and Computational Challenges in Population Biology and Ecosystems Science,” Science 275(5298):334-343, 1997. (References in the original.) |
Along these lines, a particularly interesting work on the reconstruction of phylogenies was reported in 2003 by Rokas et al.110 One of the primary goals of evolutionary research has been understanding the historical relationships between living organisms—reconstruction of the phylogenetic tree of life. A primary difficulty in phylogenetic reconstruction is that different single-gene datasets often result in different and incongruent phylogenies. Such incongruences occur in analyses at all taxonomic levels, from phylogenies of closely related species to relationships between major classes or phyla and higher taxonomic groups.
Many factors, both analytical and biological, may cause incongruence. To overcome the effect of some of these factors, analysis of concatenated datasets has been used. However, phylogenetic analyses of different sets of concatenated genes do not always converge on the same tree, and some studies have yielded results at odds with widely accepted phylogenies.
Rokas et al. exploited genome sequence data for seven Saccharomyces species and for the outgroup fungus Candida albicans to construct a phylogenetic tree. Their results suggested that datasets consisting of a single gene or a small number of concatenated genes had a significant probability of supporting conflicting topologies, but that use of the entire dataset of concatenated genes resulted in a single, fully resolved phylogeny with the maximum likelihood. In addition, all alternative topologies resulting from single-gene analyses were rejected with high probability. In other words, even though the individual genes examined supported alternative trees, the concatenated data exclusively supported a single tree. They concluded that “the maximum support for a single topology regardless of method of analysis is strongly suggestive of the power of large data sets in overcoming the incongruence present in single-gene analyses.”
5.4.8.2.2 Modeling of Myxomatosis Evolution in Australia
Evolution also provides a superb and easy-to-understand example of time scales in biological phenomena. Around 1860, a nonindigenous rabbit was introduced into Australia as part of British colonization of that continent. Since this rabbit had no indigenous foe, it proliferated wildly in a short amount of time (about 20 years). Early in the 1950s Australian authorities introduced a particular strain of virus that was deadly to the rabbit.
The data indicated that in the short term (say, on a time scale of a few months), the most virulent strains of the virus were dominant (i.e., the virus had a lethality of 99.8 percent). This is not surprising, in the sense that one might expect virulence to be a measure of viral fitness. However, in the longer term (on a scale of decades), similar measurements indicate that these more virulent strains were no longer dominant, and the dominant niche was occupied by less virulent strains (lethality of 90 percent or less). The evolutionary explanation for this latter phenomenon is that an excessively virulent virus would run the risk of killing off its hosts at too rapid a rate, thereby jeopardizing its own survival. The underlying mechanism responsible for this counterintuitive phenomenon is that transmission of the virus depended on mosquitoes feeding from live rabbits. Rabbits that were infected with the more virulent variant died quickly, and thus, fewer were available as sources of that variant.
The above system was modeled in closed form based on a set of coupled differential equations; this model was successful in reproducing the essential qualitative features described above.111 In 1990, this model was extended by Dwyer et al. to incorporate more biologically plausible features.112 For example, the evolution of rabbit and virus reacting to each other was modeled explicitly. A multiplicity of
|
110 |
A. Rokas, B.L. Williams, N. King, and S.B. Carroll, “Genome-scale Approaches to Resolving Incongruence in Molecular Phylogenies,” Nature 425(6960):798-804, 2003. |
|
111 |
S. Levin and D. Pimentel, “Selection of Intermediate Rates of Increase in Parasite-Host Systems,” The American Naturalist 117(3), 1981. |
|
112 |
G. Dwyer, S.A. Levin, and L.A. Buttel, “A Simulation Model of the Population Dynamics and Evolution of Myxomatosis,” Ecological Monographs 60(4):423-447, 1990. |
virus vectors was modeled, each with different transmission efficiencies, rather than assuming a single vector. The inclusion of such features, cou pled with exploitation of a wealth of data available on this system, allowed Dwyer et al. to investigate questions that could not be addressed in the earlier model. These questions included whether the system will continue to evolve antagonistically and whether the virus will be able to control the rabbit population in the future.
More broadly, this example illustrates the important lesson that both time scales are equally significant from an evolutionary perspective, and one is not more “fundamental” than the other when it comes to understanding the dynamical behavior of the system. Furthermore, it demonstrates that pressures for natural selection can operate at many different levels of complexity.
5.4.8.2.3 The Evolution of Proteins
By making use of simple physical models of proteins, it is possible to model evolution under different evolutionary, structural, and functional scenarios. For example, cubic lattice models of proteins can be used to model enzyme evolution involving binding to two hydrophobic substrates. Gene duplication coupled to subfunctionalization can be used to predict enzyme gene duplicate retention patterns and compare with genomic data.113 This type of physical modeling can be expanded to other evolutionary models, including those that incorporate positive selective pressures or that vary population genetic parameters. At a structural level, they can be used to address issues of protein surface-area-to-volume ratios or the evolvability of different folds. Ultimately, such models can be extended to real protein shapes and can be correlated to the evolution of different folds in real genomes.114
The role of structure in evolution during potentially adaptive periods can also be analyzed. A subset of positive selection will be dictated by structural parameters and intramolecular coevolution. Common interactions, like RKDE ionic interactions can be detected in this manner. Similarly, less common interactions, like cation-p interactions, can also be detected and the interconversion between different modes of interactions can be assessed statistically.
One important tool underlying these efforts is the Adaptive Evolution Database (TAED), a phylogenetically organized database that gathers information related to coding sequence evolution.115 This database is designed to both provide high-quality gene families with multiple sequence alignments and phylogenetic trees for chordates and embryophytes and to enable answers to the question, “What makes each species unique at the molecular genomic level?”
Starting with GenBank, genes have been grouped into families, and multiple sequence alignments and phylogenetic trees have been calculated. In addition to multiple sequence alignments and phylogenetic trees for all families of chordate and embryophyte sequences, TAED includes the ratio of nonsynonymous to synonymous nucleotide substitution rates (Ka/Ks) for each branch of every phylogenetic tree. This ratio, when significantly greater than 1, is an indicator of positive selection and potentially a change of function of the encoded protein in closely related species, and has been useful in the construction of phylogenetic trees with probabilistic reconstructed ancestral sequences calculated using both parsimony and maximum likelihood approaches. With a mapping of gene tree to species tree, the branches whose ratio is significantly greater than 1 are collated together in a phylogenetic context.
|
113 |
F.N. Braun and D.A. Liberles, “Retention of Enzyme Gene Duplicates by Subfunctionalization;” International Journal of Biological Macromolecules 33(1-3):19-22, 2003. |
|
114 |
H. Hegyi, J. Lin, D. Greenbaum, and M. Gerstein, “Structural Genomics Analysis: Characteristics of Atypical, Common, and Horizontally Transferred Folds,” Proteins 47(2):126-141, 2002. |
|
115 |
D.A. Liberles, “Evaluation of Methods for Determination of a Reconstructed History of Gene Sequence Evolution.” Molecular Biology and Evolution 18(11):2040-2047, 2001; D.A. Liberles, D.R. Schreiber, S. Govindarajan, S.G. Chamberlin, and S.A. Benner, “The Adaptive Evolution Database (TAED),” Genome Biology 2(8):research0028.1-0028.6, 2001; C. Roth, M.J. Betts, P. Steffansson, G. Sælensminde, and D.A. Liberles, “The Adaptive Evolution Database (TAED): A Phylogeny-based Tool for Comparative Genomics,” Nucleic Acids Research 33(Database issue):D495-D497, 2005. |
The TAED framework is expandable to incorporate other genomic-scale information in a phylogenetic context. This is important because coding sequence evolution (e.g., as reflected in the Ka/Ks ratio) is only one part of the molecular evolution of genomes driving phenotypic divergence. Changes in gene content116 and phylogenetic reconstructions of changes in gene expression and alternative splicing data117 can indicate where other significant lineage-specific changes have occurred. Altogether, phylogenetic indexing of genomic data presents a powerful approach to understanding the evolution of function in genomes.
5.4.8.2.4 The Emergence of Complex Genomes
How did life get started on Earth? Today, life is based on DNA genomes and protein enzymes. However, biological evidence exists to suggest that in a previous era, life was based on RNA, in the sense that genetic information was contained in RNA sequences and phenotypes were expressed as catalytic properties of RNA.118
An interesting and profound issue is therefore to understand the transition from the RNA to the DNA world, one element of which is the fact that DNA genomes are complex structures. In 1971, Eigen found an explicit relationship between the size of a stable genome and the error rate inherent in its replication, specifically that the size of the genome was inversely proportional to the per-nucleotide replication error rate.119 Thus, for a genome of length L to be reasonably stable over successive generations, the maximum tolerable error rate in replication could be no more than 1/L per nucleotide. However, more precise replication mechanisms tend to be more complex. Given that the replication mechanism must itself be represented in the genome, the puzzle is that a precise replication mechanism is needed to maintain a complex genome, but a complex genome is required to encode such a mechanism.
The only possible answer to this puzzle is that complex genomes evolved from simpler ones. Szabó et al. investigated this possibility through computer simulations.120 They constructed a population of digital genomes subject to evolutionary forces and found that under a certain set of circumstances, both genome size and replication fidelity increased with the run time of the simulation. However, such behavior was dependent on the existence of a sufficient amount of spatial isolation of the evolving population. In the absence of separation (i.e., in the limit of very rapid diffusion of genomes across the two-dimensional surface to which they were confined), genome complexity and replication fidelity were both limited. However, if diffusion is slow (i.e., the characteristic time constant of diffusion is less than the time scale of replication), both complexity and fidelity increase.
In addition, Johnston et al. have synthesized in the laboratory a catalytic RNA molecule that contains about 200 nucleotides and synthesizes RNA molecules of up to 14 nucleotides, with an error rate of about 3 percent per residue.121 This laboratory demonstration, coupled with the computational finding described above, suggest that a small RNA genome that operates as an RNA replicase with
|
116 |
E.V. Koonin, N.D. Fedorova, J.D. Jackson, A.R. Jacobs, D.M. Krylov, K.S. Makarova, R. Mazumder, et al., “A Comprehensive Evolutionary Classification of Proteins Encoded in Complete Eukaryotic Genomes,” Genome Biology 5(2):R7, 2004. (Cited in Roth et al., “The Adaptive Evolution Database,” 2005.) |
|
117 |
R. Rossnes, “Phylogenetic Reconstruction of Ancestral Character States for Gene Expression and mRNA Splicing Data,” M.Sc. thesis, Universtiy of Bergen, Norway, 2004. (Cited in Roth et al., 2005.) |
|
118 |
See, for example, G.F. Joyce, “The Antiquity of RNA-based Evolution,” Nature 418(6894):214-221, 2002. |
|
119 |
M. Eigen, “Selforganization of Matter and the Evolution of Biological Macromolecules,” Naturwissenschaften 58(10):465-523, 1971. |
|
120 |
P. Szabó, I Scheuring, T. Czaran, and E. Szathmary, “In Silico Simulations Reveal That Replicators with Limited Dispersal Evolve Towards Higher Efficiency and Fidelity,” Nature 420(6913):340-343, 2002. A very helpful commentary on this article can be found in G.F. Joyce, “Molecular Evolution: Booting Up Life,” Nature 420(6894):278–279, 2002. The discussion in Section 5.4.8.2.4 is based largely on this article. |
|
121 |
W.K. Johnston, P.J. Unrau, M.S. Lawrence, M.E. Glasner, and D.P. Bartel, “RNA-catalyzed RNA Polymerization: Accurate and General RNA-Templated Primer Extension,” Science 292(5520):1319-1325, 2001. |
modest efficiency and fidelity could evolve a succession of ever-larger genomes and ever-higher replication efficiencies.
5.4.8.3 Examples from Ecology122
Simulation-based study of an ecosystem considers the dynamic behavior of systems of individual organisms as they respond to each other and to environmental stimuli and pressures (e.g., climate) and examines the behavior of the ecosystem in aggregate terms. However, no individual run of such a simulation can be expected to predict the detailed behavior of each individual organism within an ecosystem. Rather, the appropriate test of a simulation’s fidelity is the extent to which it can, through a process of judicious averaging of many runs, predict features that are associated with aggregation at many levels of spatial and/or temporal detail. These more qualitative features provide the basis for descriptions of ecosystem dynamics that are robust across a variety of dynamical scenarios that are different at a detailed level and also provide high-level descriptions that can be more readily interpreted by researchers.
Because of the general applicability of the approach described above, simulations of dynamical behavior can be developed for aggregations of any organisms as long as they can be informed by adequate understandings of individual-level behavior and the implications of such behavior for interactions with other individuals and with the environment.
Note also the key role played by ecosystem heterogeneity. Spatial heterogeneity is one obvious way in which nonuniform distributions play a role. But in biodiversity, functional heterogeneity is also important. In particular, essential ecosystem functions such as the maintenance of fluxes of certain nutrients and pollutants, the mediation of climate and weather, and the stabilization of coastlines may depend not on the behavior of all species within the ecosystem but rather on a limited subset of these species. If biodiversity is to be maintained, the most fragile and functionally critical subsets species must be identified and understood.
The mathematical and computational challenges range from techniques for representing and accessing datasets, to algorithms for simulation of large-scale spatially stochastic, multivariate systems, to the development and analysis of simplified description. Novel data acquisition tools (e.g., a satellite-based geographic information system that records changes for insertion in the simulations) would be welcome in a field that is relatively data poor.
5.4.8.3.1 Impact of Spatial Distribution in Ecosystems
An important dimension of ecological environments is how organisms interact with each other. One often-made computationally simple assumption is that an organism is equally likely to interact with every other organism in the environment. Although this is a pragmatic assumption, actual ecosystems are physical and organisms interact only with a very small number of other organisms—namely, the ones that are nearby in a spatial sense. Moreover, localized selection—in which a fitness evaluation is undertaken only under nearest neighbors—is also operative.
Introducing these notions increases the speciation rate tremendously, and the speculation is that in a nonlocalized environment, the pressures on the population tend toward population uniformity—everything looks similar, because each entity faces selection pressure from every other entity. When localization occurs, different species emerge in different spatial areas. Further, the individuals that are evolving will start to look quite different from each other, even though they have (comparably) high
|
122 |
Section 5.4.8.3 is based largely on material taken from S.A. Levin, B. Grenfell, A. Hastings, and A.S. Perelson, “Mathematical and Computational Challenges in Population Biology and Ecosystems Science,” Science 275(5298):334-343, 1997. |
fitness ratings. (This phenomenon is known as convergent evolution, in which a given environment might evolve several different species that are in some sense equally well adapted to that environment.)
As an example of spatial localization, Kerr et al. developed a computational model to examine the behavior of a community consisting of three strains of E. coli,123 based on a modification of the lattice-based simulation of Durrett and Levin.124 One of the strains carried a gene that created an antibiotic called colicin. (The colicin-producing strain, C, was immune to the colicin it produced.) A second strain was sensitive to colicin (S), while a third strain was resistant to colicin (R). Furthermore, the factors that make the S strain sensitive also facilitate its consumption of certain nutrients, and the R strain is less able to consume these nutrients. However, because the R strain does not have to produce colicin, it avoids a metabolic cost incurred by the C strain. The result is that C bacteria kill S bacteria, S bacteria thrive where R bacteria do not, and R bacteria thrive where C bacteria do not. The community thus satisfies a “rock-paper-scissors” relationship.
The intent of the simulation was to explore the spatial scale of ecological processes in a community of these three strains. It was found found (and confirmed experimentally) that when dispersal and interaction were local, patches of different strains formed, and these patches chased one another over the lattice—type C patches encroached on S patches, S patches displaced R patches and R patche invaded C patches. Within this mosaic of patches, the local gains made by any one type were soon enjoyed by another type; hence the diversity of the system was maintained. However, dispersal and interaction were no longer exclusively local (i.e., in the “well-mixed” case in which all three strains are allowed to interact freely with each other): continual redistribution of C rapidly drove S extinct, and R then came to dominate the entire community
5.4.8.3.2 Forest Dynamics125
To simulate the growth of northeastern forests, a stochastic and mechanistic model known as SORTIE has been developed to follow the fates of individual trees and their offspring. Based on species-specific information on growth rates, fecundity, mortality, and seed dispersal distances, as well as detailed, spatially explicit information about local light regimes, SORTIE follows tens of thousands of trees to generate dynamic maps of distributions of nine dominant or subdominant species of tree that look like real forests and match data observed in real forests at appropriate levels of spatial resolution. SORTIE predicts realistic forest responses to disturbances (e.g., small circles within the forest boundaries within which all trees are destroyed), clear-cuts (i.e., large disturbances), and increased tree mortality.
SORTIE consists of two units that account for local light availability and species life history for each of nine tree species. Local light availability refers to the availability of light at each individual tree. This is a function of all of the neighboring trees that shade the tree in question. Information on the spatial relations among these neighboring tree crowns is combined with the movement of the sun throughout the growing season to determine the total, seasonally averaged light expressed as a percentage of full sun. In other words, the growth of any given tree depends on the growth of all neighboring trees.
The species life history (available for each of nine tree species) provides the relationship between radial growth rates as a function of its local light environment and is based on empirically estimated life-history information. Radial growth predicts height growth, canopy width, and canopy depth in accordance with estimated allometric relations. Fecundity is estimated as an increasing power function of tree size, and seeds are dispersed stochastically according to a relation whereby the probability of
|
123 |
B. Kerr, M.A. Riley, M.W. Feldman, and B.J. Bohannan, “Local Dispersal Promotes Biodiversity in a Real-life Game of Rock-Paper-Scissors,” Nature 418(6894):171-174, 2002. |
|
124 |
R. Durrett and S. Levin, “Allelopathy in Spatially Distributed Populations,” Journal of Theoretical Biology 185(2):165-171, 1997. |
|
125 |
Section 5.4.8.3.2 is based largely on D.H. Deutschman, S.A. Levin, C. Devine, and L.A. Buttel, “Scaling from Trees to Forests: Analysis of a Complex Simulation Model,” Science Online supplement to Science 277(5332), 1997, available at http://www.sciencemag.org/content/vol277/issue5332. Science Online article available at http://www.sciencemag.org/feature/data/deutschman/home.htm. |
dispersal declines with distance. Mortality risk is also stochastic and has two elements: random mortality and mortality associated with suppressed growth.
Because SORTIE is intended to aggregate statistical properties of forests, an ensemble of simulation runs is necessary, in which different degrees of smoothing and aggregation are used to determine how much information is lost by averaging and to find out where error is compressed and where it is enlarged in the course of this process. SORTIE is a computation-intensive simulation even for individual simulations, because multiple runs are needed to generate the necessary ensembles for statistical analysis. In addition, simulations carried out for heterogeneous environments require an interface between large dynamic simulations and geographic information systems, providing real-time feedbacks between the two.
5.5 TECHNICAL CHALLENGES RELATED TO MODELING
A number of obstacles and difficulties must be overcome if modeling is to be made useful to life scientists more broadly than is the case today. The development of a sophisticated computational model requires both a conceptual foundation and implementation. Challenges related to conceptual foundations can be regarded as mathematical and analytical; challenges related to implementation can be regarded as computational or, more precisely, as related to computer science (Box 5.24).
Today’s mathematical tools for modeling are limited. Nonlinear dynamics and bifurcation theory provide some of the most well-developed applied mathematical techniques and offer great successes in illuminating simple nonlinear systems of differential equations. But they are inadequate in many situations, as illustrated by the fact that understanding global stability in systems larger than four equations is prohibitively hard, if not unrealistic. Visualization of high-dimensional dynamics is still problematic in computational as well as analytical frameworks; the question remains as to how to represent such complex dynamics in the best, most easily understood ways. Moreover, many high-dimensional systems have effectively low-dimensional dynamics. A challenge is to extract the dynamical behavior from the equations without first knowing what the low-dimensional subspace is. Box 5.25 describes one new and promising approach to dealing with high-dimensional multiscale problems.
Other mathematical methods and new theory will be needed to find solutions that apply not only to biological problems, but to other scientific and engineering applications as well. These include methods for global optimization and for reverse engineering of structure (of any “black box,” be it a network of genes, a signal transduction pathway, or a neuronal system) based on data elicited in response to stimuli and perturbations.
Identification of model structure and parameters in nonlinear systems is also nontrivial. This is especially true in biological systems due to incomplete knowledge and essentially limitless types of interactions. Decomposition of complex systems into simpler subsystems (“modules”) is an important challenge to our ability to analyze and understand such systems (a point discussed in Chapter 6). Development of frameworks to incorporate moving boundaries and changing geometries or shapes is essential to describing biological systems. This is traditionally a difficult area. Ideally, it would be desirable to be able to synthesize and analyze models that have nonlinear deterministic as well as stochastic elements, and continuous as well as discrete, algebraic constraints, with other more traditional nonlinear dynamics. (See Section 5.3.2 for greater detail.) All of these can be viewed as challenges in nonlinear dynamics aspects of modeling.
Further developing both computational (numerical simulation) methods and analytical methods (bifurcation, perturbation methods, asymptotic analysis) for large nonlinear systems will invariably mean great progress in the ability to build more elaborate and detailed models. However, with these large models come large challenges. One is how to find methodical ways of organizing parameter space exploration for systems that have numerous parameters. Another is the development of ways to codify and track assumptions that have gone into the construction of a model. Understanding these assumptions (or simplifications) is essential to understanding the limitations of a model and when its predictions are no longer biologically relevant.
|
Box 5.24 Integration Methods
Models
Validation
SOURCE: U.S. Department of Energy, Report on the Computer Science Workshop for the Genomes to Life Program, Gaithersburg, MD, March 6-7, 2002, available at http://DOEGenomesToLife.org/compbio/. |
|
Box 5.25 Yannis Kevrikides of Princeton University and his colleagues have developed a framework for computer-aided multiscale analysis. This framework enables models at a “fine” (microscopic, stochastic) level of description to perform modeling tasks at a “coarse” (macroscopic, systems) level. These macroscopic modeling tasks, yielding information over long time and large space scales, are accomplished through appropriately initialized calls to the microscopic simulator for only short times and small spatial domains: “patches” in macroscopic space-time. In general, traditional modeling approaches require the derivation of macroscopic equations that govern the time evolution of a system. With these equations in hand (usually partial differential equations (PDEs)), a variety of analytical and numerical techniques for their solution is available. The framework of Kevrikides and colleagues, known as the equation-free (EF) approach can, when successful, bypass the derivation of the macroscopic evolution equations when these equations conceptually exist but are not available in closed form. The advantage of this approach is that the long-term behavior of the system bypasses the computationally intensive calculations needed to solve the PDEs that describe the system. That is, the EF approach enables an alternative description of the physics underlying the system at the microscopic scale (i.e., its behavior on relatively short time and space scales) provide information about the behavior of the system over relatively large time and space scales directly without expensive computations. In effect, the EF approach constitutes a systems identification-based, “closure on demand” computational toolkit, bridging microscopic-stochastic simulation with traditional continuum scientific computation and numerical analysis. SOURCE: The EF approach was first introduced by Yannis Kevrikides and colleagues in K. Theodoropoulos et al., “Coarse Stability and Bifurcation Analysis Using Timesteppers: A Reaction Diffusion Example,” Proceedings of the National Academy of Sciences 97:9840, 2000, available at http://www.pnas.org/cgi/reprint/97/18/9840.pdf. The text of this box is based on excerpts from an abstract describing a presentation by Kevrikides on April 16, 2003, to the Singapore-MIT Alliance program on High Performance Computation for Engineered Systems (HPCES); abstract available at http://web.mit.edu/sma/events/seminar/kevrekidis.htm. |
In the second category, issues related to implementing the model arise. Often such issues involve the actual code used to implement the model. Computational models are, in essence, large computer programs; issues of software development come to the fore. As the desire for and utility of computational modeling increase, the needs for software are growing rather than diminishing as hardware becomes more capable. On the other hand, progress in software development and engineering over the last several decades has not been nearly as dramatic as progress in hardware capability, and there appears to be no magic bullets on the horizon that will revolutionize the software development process.
This is not to say that good software engineering does not or should not play a role in the development of computational models. Indeed, the Biomedical Information Science and Technology Initiative (BISTI) Planning Workshop of January 15-16, 2003, explicitly recommended that NIH require grant applications, proposing research in bioinformatics or computational biology to adopt as appropriate, accepted practices of software engineering.126Section 4.5 describes some of the elements of good software engineering in the context of tool development, and the same considerations apply to model development.
A second important challenge as large simulation models become more prevalent is a standard specification language to unambiguously specify the model, its parameters, annotations, and even the means by which it is to be scored against data. The challenge will be to provide a language flexible enough to capture all interesting biological processes and incorporate models at different levels of abstraction and in different mathematical paradigms, including stochastic differential, partial differential, algebraic, and discrete equations. It may prove necessary to develop a set of nested languages—for example, a language that specifies the biological process at a very high level and a linked language that specifies the mathematical representation of each process. There are some current attempts at these languages based on the XML framework. SBML and CellML are attempts in this direction.
Finally, many biological modeling applications involve a problem space that is not well understood and may even be intended to explore queries that are not well formulated. Thus, there is a high premium on reducing the labor and time involved to produce an application that does something useful. In this context, technologies for “rapid prototyping” of biological models have considerable interest.127
|
126 |
|
|
127 |
Note, however, that in the rapid prototyping process often used to create commercial applications, there is a dialogue between developer and user that reveals what the user would find valuable: once the developer knows what the user really wants, the software development effort is straightforward. By contrast, in biological applications, it is nature that determines the appropriate structuring and formulation of a problem, and a problem cannot be structured in a certain way simply because it is convenient to do so. Thus, technologies for the rapid prototyping of biological models must afford the ability to rearrange model components and connections between components with ease. |
























































































