3
Framework for Evaluating Medical and Physical Standards
This chapter discusses and develops a framework for evaluating and setting medical and physical standards. The first section describes some general considerations for validating standards by linking them to specific outcomes, the second section describes a cost trade-off approach that has been used successfully to validate education and aptitude standards, and the third section discusses some of the health databases that might be needed to develop successful validation procedures. Some of the material in this chapter is technical and is intended primarily for policy analysts and others who formulate and evaluate enlistment standards. The function of this chapter is to describe the methodological approach and data needed to evaluate medical and physical enlistment standards in terms of such outcomes as injury, lost time, and attrition.
The setting of military enlistment standards does not follow a single, strict procedure. There are multiple reasons for setting particular standards and, accordingly, there are varying approaches for determining standards. As mentioned in Chapter 2, physical and medical standards are generally set to increase the likelihood that recruits will be able to meet the rigorous requirements of military jobs and missions. Unlike physical and medical standards, the standards for both education and aptitude characteristics are set by fairly formal procedures for validating standards against specific outcomes, such as attrition or job performance.
LINKING STANDARDS TO OUTCOMES
To some extent, the methods used to set enlistment standards have been influenced by the type of characteristic under consideration. Many medical and physical standards are determined by the presence of disqualifying conditions that are justified on prima facie grounds: examples are serious diseases, physiological abnormalities, and such physical impairments as blindness or deafness. For these types of serious medical or physical conditions, a formal validation methodology is usually unnecessary.
More formal, quantitative methods have been developed for validating education and mental aptitudes for two reasons (National Research Council, 1988). First, a characteristic like aptitude is a continuum rather than a present/absent dichotomy; one therefore has to develop cutoff scores to determine eligibility. Second, while education can be considered a dichotomous characteristic (high school graduate versus nongraduate), being a nongraduate is not disqualifying on its face in the same way that blindness might be. Rather, nongraduates (and lower aptitude recruits) can reduce military effectiveness in various ways, such as having high attrition rates or poor performance with respect to certain military duties. Thus, there is a trade-off between effectiveness or performance and the proportion of recruits with these characteristics.
Although formal trade-off models have not been applied to the validation of medical and physical standards, they may be useful when medical or physical attributes are similar to education and aptitude. For example, they could be applied to continuous conditions, such as weight and strength, for which no disqualifying level can be established clinically, or to dichotomous conditions, such as marijuana use or asthma, the presence of which may reduce effectiveness but is not automatically disqualifying.
Elements of a Formal Model
Generally, in order to develop a formal trade-off model, there must be a correlation between a selection characteristic and some desired or necessary outcome. If there is no correlation, then the validation process basically ends with no need for a selection standard, since the characteristic is not related to a valued outcome. At the other extreme, if every person with a certain characteristic at entry has an undesired outcome, then there is no need for a trade-off analysis, since everyone with that characteristic should be disqualified. In effect, for those medical and physical conditions that lead to automatic disqualification, it is assumed that all recruits with those characteristics are unable to perform any military specialty at a
satisfactory level. Of course, for any particular medical or physical condition, this assumption could be subjected to closer scrutiny.
If there is a correlation between the selection criterion and an important outcome, then specific standards can be set based on some type of utility or cost trade-off analysis. The Department of Defense has developed cost trade-off models to set standards for education levels and cognitive aptitudes (National Research Council, 1994). We describe how these models could be adapted for use with appropriate medical and physical standards.
In summary, the process of establishing a standard for an appropriate physical or medical condition consists of several steps. The first step is to determine a valued outcome that corresponds to some aspect of military effectiveness. The second step is to establish an empirical correlation between the condition and the valued outcome. The third step is to determine a specific standard or a cutoff value in the case of continuous conditions, such as body mass index (BMI), using a cost trade-off analysis of some type.
Selecting Outcomes
The outcome used to evaluate an enlistment condition is usually a goal or condition related to military objectives or requirements, such as completion of training, on-the-job performance, or combat effectiveness. The evaluation of education standards, for example, uses the outcome of first-term attrition. The justification is that enlistees who leave before the end of their first term increase training costs, since more recruits must be trained to fill unit manpower requirements. Thus, an enlisted force with 20 percent attrition has to train 125 recruits to fill 100 manpower unit slots, while a force with 40 percent attrition has to train 167 recruits to fill the same unit requirement. This increased recruiting burden represents an increase in training costs of about 40 percent.
Another example is the evaluation of aptitude requirements. In this case, job performance has been the preferred outcome because it is well established that cognitive abilities are good predictors of actual job performance in virtually all military specialties (Armor and Roll, 1994). As the proportion of persons with low cognitive aptitudes increases in a unit, there is a corresponding reduction of combat effectiveness. The concern of recruiting sufficient numbers of people with good cognitive skills has been heightened by the growing technological requirements of many military occupations and activities. Unlike attrition, the assessment of military job performance is an arduous and complex undertaking.
In the case of physical and medical standards, a range of outcomes can be considered. And for some of them, the use of attrition appears warranted. Recruits with certain physical conditions, such as obesity or a very low level of physical fitness, may not be able to complete basic training or may not be able to adapt to difficult combat environments. Attrition might therefore be a reasonable outcome for evaluating specific standards for these conditions. The same might be said for such medical conditions as asthma, orthopedic disorders, and so forth.
Physical conditions such as obesity and fitness and medical conditions like orthopedic disorders can also be evaluated using performance outcomes of various types. For example, many military jobs may involve tasks that require minimum levels of strength, agility, or endurance. The advantage of using these types of performance outcomes is that screening devices might be designed that offer good predictive validity of the outcomes, such as the Assessment of Recruit Motivation and Strength test being tested by the Accessions Medical Standards Analysis and Research Activity (AMSARA).
Finally, another outcome that can be used for many physical and medical conditions is lost time on the job and the medical costs of injuries and sickness (including disability expenditures) arising from these conditions. The outcomes of lost time and medical costs may be especially appropriate for such physical conditions as obesity and fitness or such medical conditions as orthopedic disorders.
Establishing a Correlation
Given the selection of an appropriate outcome, the second step in a validity study is to establish a correlation or association between the physical or medical condition and the outcome. This usually requires an empirical study of some sort. The study may use existing military data, particularly when attrition rates are the outcome of interest. In other cases, an original prospective data collection effort may be required. The latter is usually necessary if the outcome is some type of job performance outcome that is not captured by military records.
Before discussing how a correlation is established empirically, it may be helpful to discuss the nature of this correlation and to understand approaches to validity assessments in various fields. In medical and some behavioral science research, the validity of a screening test is established by its effectiveness in detecting certain conditions (e.g., disease, impairment). Effectiveness of the screen is evaluated by several statistics, including sensitivity and specificity. These are illustrated using a two-by-two table (Table 3-1).
TABLE 3-1 Hypothetical Validity Relationship
|
|
|
Condition (C) |
|
|
|
|
Absent = 0 |
Present = 1 |
|
Screen (S) |
Neg = 0 |
a |
b |
|
|
Pos = 1 |
c |
d |
Sensitivity is defined as the proportion of persons with the condition (C = 1) who are flagged positive by the screen, or
(the conditional probability having a positive screen if the condition is present). Specificity is defined as the proportion of persons without the condition who are negative on the screen, or
Generally, the most effective screening tests are those with high sensitivity and specificity (e.g., .9 or so).
These two statistics are actually components of a summary measure of association derived by regressing the screen on the condition (scored as dummy variables). The regression coefficient can be calculated in this case as
or the sum of sensitivity and specificity minus one. In the case of high sensitivity and specificity measures, which are desirable for most screening tests, the regression coefficient would be quite high; for example, the regression coefficient would be .8 if both sensitivity and specificity were .9.
In the case of military enlistment standards, validity has a somewhat different meaning and therefore validity studies have taken a somewhat different approach. In the military standards context, validity means the extent to which a screen predicts a future outcome rather than an existing condition. Even a fairly weak relationship (e.g., a modest regression coefficient) between a screen and a future outcome could justify a particular standard, depending on the cost of that outcome.
For example, Table 3-2 illustrates the approximate relationship between high school education and 24-month attrition. The specificity is fairly high at .8, but the sensitivity is quite low at .4, and the overall
TABLE 3-2 Approximate Relationship Between Education and Attrition
|
|
|
High School Dropout |
|
|
|
|
No (0) |
Yes (1) |
|
24-month |
No (0) |
0.8 |
0.6 |
|
attrition |
Yes (1) |
0.2 |
0.4 |
regression coefficient is only .2. The relationship nevertheless justifies an enlistment standard that restricts nongraduates because of the costs of replacing and retraining recruits who leave military service within one or two years. This cost trade-off approach is discussed further in the next section.
Continuing with the examples of education and aptitude standards, the validity of education standards has been established by correlating education levels with first-term attrition rates, as in Table 3-2. The validation of aptitude standards with on-the-job performance outcomes required a massive original data collection effort that took place over a period of nearly 10 years (National Research Council, 1991).
Even assuming that attrition rates are being used as the outcome for a particular standard, reliable entry data cannot be assumed in the case of many medical conditions, which rely on self-report by military applicants. Moreover, some medical conditions observable during the physical exam may be missed. So the availability and reliability of physical and medical conditions at entry cannot be assumed, and obtaining good data may require special prospective studies and data collection such as that being carried out at AMSARA. Of particular interest here are special longitudinal studies being conducted by the Services, such as the Army Research Institute study of the 1999 cohort (McCloy and Putka, 2004).
Special job performance assessment may be appropriate for certain physical conditions such as obesity and fitness. For example, it may be possible to track BMI measurements or fitness test performance as enlistees move through the first term to determine whether entry condition predicts later levels of BMI and fitness. It also may be possible to collect data on the unit commander’s evaluation of an enlistee’s physical fitness or related characteristics.
Special prospective studies would be necessary to evaluate changing a standard that now causes automatic disqualification. Of course, this depends on whether there are any conditions at the present time that experts feel should not be disqualifying.
Finally, it may be possible to examine various medical outcomes, such as injuries, illnesses, or hospitalizations during the first term that could be related to initial medical or physical conditions, some of which might be subject to disqualification waivers. This type of analysis would involve merging files of the U.S. Military Entrance Processing Command (MEPCOM) with medical record files, which may require special approvals but should be technically possible.
Determining the Standard
The final step, assuming that a physical or medical condition is reliably correlated with an acceptable outcome, is to determine a specific standard for that condition. There are at least two scenarios. On one hand, if the physical or medical condition is a simple binary “present” or “absent,” then, as mentioned earlier, the standard may simply be a decision to disqualify a potential recruit if the condition is present (which assumes that a person with that condition cannot perform military duties). If, on the other hand, the condition has a continuous underlying metric, such as BMI, a score on a fitness test, or blood pressure, then a specific cutoff value is required.
The process of determining a specific cutoff value ranges from simple to complex, depending on the way in which utility is assessed. In the simplest case, military experts may be able to use a qualitative procedure based on experience that determines a value above or below which a recruit is highly unlikely to meet the requirement in question.
In the more complex case, particularly when there is no expert opinion about acceptable levels of the condition (or even sometimes when there is an expert opinion), a cost-performance trade-off model can be applied. For example, if BMI or some type of substance abuse is correlated with attrition or some performance outcome, one can compare the cost of disqualifying persons above certain values (based on supply information about the cost of recruits) with the cost of various performance or attrition levels (e.g., training costs associated with different rates of attrition).
COST-PERFORMANCE TRADE-OFF MODELS
In this section, we discuss an example of the type of cost-performance trade-off model that has been applied to aptitudes and education. The full model is a computer-based optimization model that evaluates enlistment standards along two dimensions: high school graduation status and aptitudes. We present a much simplified version of this model and illustrate it with high school graduation status, a characteristic not unlike such medical conditions as asthma or drug use. We use this model later for those
medical and physical standards for which a trade-off analysis might be useful.
High school graduate status is associated with attrition. Recruits with a high school diploma are valued because years of research and experience show that those with a high school diploma are more likely to complete their initial three years of service, as shown in Table 3-2.
The better retention associated with those who complete high school saves money. According to an estimate by the U.S. General Accounting Office (1997, 1998) the cost of first-year attrition is in the range of $15,000-$35,000. In our examples, we use an estimate of $20,000 as the cost of first year attrition. On one hand, this argues for recruitment of those who are most likely to adjust to the rigors of military life and stay the course. The high school diploma is a reliable indicator of “adaptability” and “perseverance.” On the other hand, if all nongraduates are excluded from the enlistment pool, it forces recruiters to draw from the pool of graduates, and these individuals may be more expensive to recruit because they may have more opportunities for jobs elsewhere. This problem is compounded if one adds aptitudes to the mix and wants to exclude (or minimize) those with low aptitude scores.
The objective of a cost-performance trade-off optimization model is to choose an enlistment cohort that minimizes the cost of recruiting, training, and compensating the cohort, subject to meeting staffing goals by occupation over the first term of service. The complexity of this formulation may exceed what is necessary for setting most medical or physical standards, but the basic concept can be applied to setting any standard.
The intuition underlying the model is relatively straightforward. Since high school graduates leave the military prematurely at lower rates, they generate more staff years per recruit and lower training cost. However, the additional cost of recruiting high school graduates is greater than that of nongraduates, at the mix typically recruited. The optimization model implicitly makes trade-offs between the higher staff years and lower training costs of the high school graduate recruits and the lower recruiting cost, but also lower staff years and greater attrition, of nongraduate recruits. The graduate/nongraduate mix of recruits the model chooses is that which meets staffing goals most efficiently.1
TABLE 3-3 Example of Cost-Performance Trade-off Analysis ($ millions)
|
Standard |
High School Graduates (percentage) |
Nongraduates (percentage) |
Recruiting Cost |
Training/Comp Costs |
Total Costs |
|
Old |
90 |
10 |
$504 |
$7,814 |
$8,318 |
|
New |
100 |
0 |
$941 |
$7,559 |
$8,500 |
Illustration Using the Army Education Standard
To illustrate how the model provides an “optimal” (i.e., cost-minimizing) enlistment standard, consider a hypothetical (but realistic) Army example. We first let the model choose a cost-minimizing high school diploma graduate mix of graduate and nongraduate recruits that meets a given staffing requirement at the lowest cost. For a given set of staffing goals, economic conditions, and other factors, the model solves for an optimal mix of recruits consisting of 89.6 percent high school diploma and 10.4 percent nongraduates. Hence, an enlistment standard that set the high school diploma graduate goal at about 90 percent would be close to optimal.2
Now, let us assume that standards are arbitrarily changed, so applicants without a high school diploma are no longer eligible to enlist. The standard under this constraint is 100 percent high school diploma graduates and 0 percent nongraduates.
Which set of standards is best? The new standard results in lower training and compensation costs because, with nongraduates ineligible to enlist, there is lower attrition. However, the new standard results in significantly higher recruiting costs. Table 3-3 compares the two sets of standards.
The higher standards implied by screening out all nongraduates does indeed reduce training and compensation costs relative to the old standard, which includes about 10 percent nongraduates. This is because attrition is lower, so fewer recruits must be trained to achieve a given staffing level. However, the new standard in this example goes too far. By making all nongraduates ineligible, recruiting costs are raised significantly, as recruiters must replace nongraduates with the more difficult to recruit (at the margin) graduates. The increase in recruiting costs more
than outweighs the savings in reduced attrition-related costs, resulting in higher total costs.3
A Simple Model for Evaluating Medical or Physical Standards
This type of trade-off and balance may exist for many physical and medical entry standards. For example, in principle, the weight standard as measured by BMI is a trade-off between lower attrition-related costs associated with a higher standard and increased recruiting costs, resulting from disqualifying a portion of the recruiting market due to higher standards. The right balance, then, and the optimal weight standard is one that minimizes cost by balancing the higher recruiting costs associated with a more stringent standard with the savings in attrition costs.
Of course, there will not be an optimization model for all physical and medical standards. However, we can use this trade-off framework to help determine the correct direction of change in standards. If a particular medical or physical condition is correlated with attrition and various standards are set that raise or lower the proportion of recruits with this condition, then what is the effect on cost? For a given cost of attrition, this will provide an estimate of the change in attrition costs. If the proportion of the relevant recruit population that is made ineligible by the modest increase in the standard can be determined, then the recruiting cost function can be used to estimate the change in recruiting costs.
In some of the chapters in this report, we apply a simple cost-performance analysis that uses a number of parameters defined below. In the notation, the subscript 1 refers to the value of the parameter under existing or current standards, while the subscript 2 refers to the value of the parameter after changing standards (i.e., reducing the number of or disqualifying persons who have a given medical or physical characteristic):
-
the probability of attrition for those with or without a given characteristic, aw and awo (the cost model here assumes a 12-month attrition rate).
-
the difference in attrition rates for those with and without the characteristic, d = awo − aw (normally, awo < aw).
-
the cohort 12-month attrition rates before and after changing standards, a1 and a2.
-
the unit cost of attrition (cost of training through 12 months), C.
-
the proportion of recruits with the characteristic before and after changing the standard, p1 and p2 (before changing standards, p1 is assumed to be the same for the recruit population and the larger youth population).
-
the size of the eligible youth population before and after changing standards, POP1 and POP2.
-
the size of the force needed at 12 months (posttraining), F.
-
the number of recruits needed before and after changing standards, N1 and N2, in order to attain a given force size F (N2 will be less than N1).
-
recruiting costs as a function of the number recruited and the recruit-eligible population, which we denote by the function R(N,POP) with dR/dN > 0 and dR/d POP < 0.
The enlistment standard, in this analysis, is used to screen out populations that have higher expected attrition rates in the first year of service than the general population. The benefit associated with screening out a population is that attrition will be lower. The cost is that, because some in the population will no longer be able to enlist, recruiting costs may be higher.
Because there are lower attrition rates, the number of recruits leaving prior to completing a year will be lower. Let a1 be the average attrition rate before the standard is in place and let a2 be the average attrition rate after the standard is in place. Then, if N1 is the number recruited and C is the unit cost of attrition, then ![]() is, to a first-order approximation, the savings in attrition costs. However, because attrition rates are lower, fewer individuals must be recruited in the first place to fill a given number of spaces at the end of the year. Let the number of spaces to be filled equal F. Then, N1, the number originally recruited, is equal to F/(1 − a1). If expected average attrition were to fall to a2 with the enlistment standard in effect, the number of recruits needed would be N2, equal to F/ (1 − a2). Hence, a more precise estimate of the savings in attrition costs is calculated as the difference in costs before and after the enlistment standard is introduced:
is, to a first-order approximation, the savings in attrition costs. However, because attrition rates are lower, fewer individuals must be recruited in the first place to fill a given number of spaces at the end of the year. Let the number of spaces to be filled equal F. Then, N1, the number originally recruited, is equal to F/(1 − a1). If expected average attrition were to fall to a2 with the enlistment standard in effect, the number of recruits needed would be N2, equal to F/ (1 − a2). Hence, a more precise estimate of the savings in attrition costs is calculated as the difference in costs before and after the enlistment standard is introduced:
Now, we ask, how does a1, the average attrition rate prior to the introduction of the enlistment standard, differ from a2, the average attrition rate after the introduction of the enlistment standard? Let the expected attrition rate (probability of attrition) for those without the characteristic to be subject to the enlistment standard be denoted awo and the expected
attrition rate (probability of attrition) for those with the characteristic be denoted aw. Then, let the proportion of the recruits with the characteristic, before the standard is in place, be equal to p1. The average attrition rate before introducing the enlistment standard, is
where d is the difference between the expected attrition rate for those without and those with the characteristic in question. Now, with the enlistment screen, the proportion of recruits with the characteristic falls to p2. Hence, the average attrition rate after applying the enlistment screen is
Note that if all are screened out, p2 = 0, and the attrition rate is simply the “without” attrition rate. We can rewrite the equation for the average cost savings as:
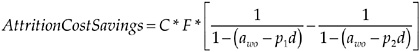
In addition to the benefits of lower attrition costs, an enlistment standard that screens out recruits reduces the effective population from which to recruit. This increases recruiting costs, most probably in a nonlinear way. Recruiting costs are a function of the number of recruits, N, and the population available to recruit from, POP.
The additional recruiting costs are given by
where we adopt the assumption that the effect on the relevant recruiting population is proportionate to the effect that the standard has on the number of recruits. Hence,
The number of recruits required is adjusted downward because attrition is expected to be lower. The number required to recruit to reach a
given goal is reduced, lowering recruiting costs somewhat. However, the population available for recruiting is also reduced, raising recruiting costs.
DATA RELEVANT TO EVALUATING MEDICAL AND PHYSICAL STANDARDS
DoD maintains many databases necessary, if not critical, for evaluating medical and physical standards. One of the factors that complicates carrying out studies of this type is that some of these databases, particularly health databases, are held by separate agencies, making cross-reference and linkage difficult and problematic. Another issue is the validity and reliability of the data in these sources. This section discusses some of the administrative and research issues pertaining to these databases.
Overview of Databases
A simple sort by function reveals four types of databases relevant to evaluating medical and physical standards: health care system management data, health surveillance data, health research data, and personnel data. These databases encompass a personnel and health care system unique in the world for its global scope, the number of personnel, and comprehensive health care. Those eligible for health care include all active-duty personnel, their immediate family members, and Reserve and National Guard personnel assigned to duty with the active force.
Since the population eligible for this health care system in general mirrors the U.S. population from ages 17 to 18 to the beginning of military retirement after 20 years of service, these databases could be a powerful resource not only for DoD but also for the country as a whole, in terms of health demographics, occupational health, and the formulation of health policy. Access to information in DoD health databases, however, is tightly controlled.
The primary purposes of the health databases are to protect and preserve the health of the fighting force in the field and to enhance health care delivery to beneficiaries. All those seeking information from these databases, whether DoD agencies or their contractors, other federal government agencies, or individuals or organizations outside DoD, must show in their request some benefit to the health of the fighting force or some benefit to delivery of health care to beneficiaries (S. Jenkins, privacy officer, Health Affairs, Office of the Assistant Secretary of Defense, personal communication, June 13, 2005 [http://tricare.osd.mil/tmaprivacy]).
The health databases are by definition those operated by the Army, Navy, and Air Force medical departments and by the Health Affairs component of the Office of the Secretary of Defense (OSD/HA). Databases
maintained outside the medical departments and OSD/HA contain considerable health information, including some identified to specific individuals, but these databases are not subject to the controls cited above. Most importantly for this study, MEPCOM is not a medical command, but rather a recruit processing command. As a consequence, even though MEPCOM performs medical functions, such as physical examinations, the medical records created by these functions do not become subject to medical record controls until each enlistee, carrying his or her medical record, is sworn in as a member of the U.S. armed forces at a military entrance processing station (MEPS) (S. Jenkins, personal communication).
The flow of information from health databases is governed by the Privacy Act of 1974 and by the Health Insurance Portability and Accountability Act of 1996 (HIPAA). Generally, DoD health databases include specific identifiers of individuals associated with health events being reported. For this reason, legitimate requests for information can be complicated by requirements of these federal privacy laws. Security rules in DoD to protect sensitive information also apply. As a consequence, responsiveness to requests for information can be slow. If the request for information requires what is judged to be a research effort, then an institutional review board (IRB) approval is required before any search for data can be undertaken. In addition, searches for information not routinely reported can be undertaken only when the requestor provides funding for the effort.
A listing and brief description of each of the major databases that may be relevant to evaluating medical and physical standards is presented in an appendix to this chapter.
Data Linkage Issues
There clearly exists a wealth of information about individual service members that is gathered, stored, updated, and maintained, beginning with an applicant’s first contact with a military recruiter and continuing throughout the service member’s career. Much of this information is stored in sophisticated central databases, although some information is maintained only locally and on paper. There have been some successful attempts at integrating—or at least connecting—these databases. For example, the MEPCOM Integrated Resource System (MIRS) is the source for building the initial personnel records maintained by the Defense Manpower Data Center, some of whose record data are provided to the Total Army Injury and Health Outcomes Database.
General connectivity between medical and personnel databases does not exist, however. There are serious privacy issues associated with the
maintenance and availability of medical databases and the maintenance costs can be high. At the same time, the ability to link personnel and medical databases, including individual-level information, is a central requirement for doing the kinds of longitudinal studies and analyses needed to support decision making in the area of physical, medical, and mental health standards for enlistment; these questions cannot be adequately addressed by data collected on a study-by-study basis. In particular, the linking of databases has the potential to permit multivariate analyses of a variety of phenomena. Analyses of the joint and interactive effects of physical, medical, and mental health variables on outcomes of interest would be of great value.
CONCLUSIONS AND RECOMMENDATIONS
Some standards are justified on prima facie grounds, based on an incontrovertible link between the standard and fitness for service (e.g., blindness, deafness, paralysis). Many, however, are based on a presumed link between the standard and an outcome of interest. The evaluation framework linking standards to outcomes outlined in this chapter is applicable to all physical and medical enlistment standards.
Recommendation 3-1: We recommend that data be collected that would allow the study of empirical links between physical and medical characteristics and performance-based outcomes, such as attrition and injury.
Application of a cost trade-off methodology requires valid data on enlistee health and fitness throughout the tour of duty as well as the ability to link health and fitness measures to such outcomes as lost work time and attrition. This requires ready access to and linkage between health and personnel databases.
Recommendation 3-2: We recommend that DoD undertake a project to develop the data and technology necessary for a cost-performance trade-off model that could be applied to setting and evaluating medical and physical standards.
Recommendation 3-3: We recommend that DoD commission a review of the medical databases necessary for evaluating and assessing medical and physical enlistment standards and create a mechanism for integrating or linking the medical databases with existing personnel databases at the Defense Manpower Data Center, subject to all legal requirements.
APPENDIX 3-A OVERVIEW OF DATABASES
Management Databases
The Office of the Assistant Secretary of Defense for Health Affairs maintains two separate management databases, one for inpatients and one for outpatients. They are global in scope and cover all three military departments. The general purpose of these databases is to match health care assets to patient demands. The Army, Navy, and Air Force each have their own health care management databases for the same general purpose. (The Navy provides health care services for the Marine Corps.)
Surveillance Databases
Defense Medical Surveillance System
DoD’s global Defense Medical Surveillance System (DMSS) (accessible on the Internet at http://amsa_army_mil) is assigned organizationally to the U.S. Army Center for Health Promotion and Preventive Medicine (USACHPPM) in Aberdeen Proving Ground, Maryland, and is maintained at the Walter Reed Army Medical Center in Washington, DC. It was established in 1994 in the aftermath of the first Persian Gulf War. It is an operational database serving operational needs and is supported by operational funds, but it has proven to be very useful for conducting research. The database receives information according to a specific reporting protocol on every inpatient and outpatient visit to any DoD health care facility worldwide. Every event is to be documented with the appropriate International Classification of Diseases (ICD-9) code. DMSS publishes monthly reports, both electronically and in print, and performs analyses for medical leadership. DMSS also has a component called the Reportable Medical Events System, which publishes monthly reports on communicable diseases in the military of public health significance, in parallel with the civilian reporting system of the Centers for Disease Control and Prevention. DMSS does not link directly to personnel databases; however, it receives data from the Defense Manpower Data Center and other sources, including demographics and occupational data, to permit population-based routine medical surveillance and to answer basic surveillance questions, such as rates by gender, rates for specific deployments, rates by age, and reportable diseases.
Service Health Surveillance Systems
For many years, each Service has maintained a health surveillance system of its own personnel.
Service Occupational Health Databases
Each Service maintains health databases on personnel with military occupational specialties of importance to their global operations. Examples are the longitudinal health databases on all aviators in the Air Force.
Research Databases
Total Army Injury and Health Outcome Database
The Total Army Injury and Health Outcome Database (TAIHOD) is an administrative electronic database with origins in 1994 as a component of the Women’s Health Initiative. Over time the database has grown into its present form. It uses datasets common to DMSS but is structured differently to serve research, in contrast with operational surveillance needs. This database is limited to the Army because injury and disability reporting is not standardized across Services and because safety and accident reporting is also not standardized. The database is maintained at the U.S. Army Research Institute of Environmental Medicine. There is an initiative to broaden this database further. Currently, 25,000 medical records of Army personnel accessed in 1998, 1999, and 2000 are being reviewed and scanned into the database.
Accession Medical Standards Analysis and Research Activity Databases
The Accession Medical Standards Analysis and Research Activity (AMSARA) (available on the Internet at http://amsara.amedd.army.mil) was established in 1996 to support the Accession Medical Standards Steering Committee of the Under Secretary of Defense (Personnel and Readiness). AMSARA is located in the Division of Preventive Medicine at Walter Reed Army Institute of Research, Washington, DC. AMSARA study datasets are structured to answer specific queries from sponsors. Collectively they represent many individual databases rather than a single, multipurpose database. They are constructed by AMSARA researchers who examine individual recruit medical and personnel records and MEPCOM and Service data pertaining to the accession of recruits.
Because of this hands-on process at the individual record level, these databases have high validity. All investigations by AMSARA have institutional review board approval and oversight.
Nonmedical Databases
Army Accessions Command Database
Army Accessions Command is the executive agent for the acting under secretary of defense, military personnel policy, for screening and processing potential recruits. Its database of importance for this study is the one maintained by its subordinate command, MEPCOM.
The MEPCOM Integrated Resource System is the database that provided information to the committee for this study. This is an administrative database encompassing many management functions of MEPCOM. It contains all data on each applicant relevant to the accession process, including outcome information on physical examinations, medical failure codes, ICD codes for all failures, and waiver status. Individual applicants are identified by their Social Security numbers. This database does not include health information acquired by recruiters of individual Service recruiting commands from individual applicants.
Defense Manpower Data Center Databases
The Defense Manpower Data Center (DMDC) maintains the largest archive of personnel, manpower, training, and financial data in the Department of Defense. Of the numerous individual databases it maintains, several are routinely used for personnel research, studies, and analyses. For example, the Active Duty Military Personnel File provides an inventory of all individuals on active duty. It is a standardized and centralized database of present and past members of the active-duty force. Historical data back to 1971 are available. This file includes such data elements as the following:
-
Personal data, including Social Security numbers, education level, home of record, date of birth, marital status, number of dependents, race, and ethnic group.
-
Military data, including Service, pay grade, Armed Forces Qualification Test percentile, military primary duty and secondary occupation, unit identification code, months of service, duty location, estimated termination of service date, basic active-duty service date, date of current rank, pay entry base date, foreign language ability, and major command code.
Similarly, databases such as the Active Duty Military Enlisted Cohort File, the Active Duty Military Personnel Transaction File, and the MEPCOM Examination and Accession File, are often used for research, studies, and analyses.
Validity of Administrative Databases
The issue of the validity of these administrative databases has been addressed in research publications by users of these databases. An example is a recent publication by Hoge et al. (2005) in which the authors found a very high correlation in their results among different administrative data systems. Also cited were publications by Miller et al. (2000) and Bell et al. (2003).



















