Part II
HOW CHILDREN LEARN SCIENCE
In Part II, we present reviews of the research on science learning in early childhood through early adolescence. Over the past 50 years, new tools, techniques, and theories about learning—coinciding with the emergence of computer technology, cognitive and sociocultural learning theories, and new theory-building views of the nature of science—have expanded and focused understandings of the ways in which science learning occurs. The chapters in this part, organized around the four strands of science proficiency (see Box 2-1), synthesize research on learning, science learning, and the dynamics involved in the growth of scientific knowledge.
Across the five chapters, we examine the literature on concept learning, scientific reasoning, children’s understanding of the structure of scientific knowledge, and the ways in which communication and representation practices that characterize scientific discourse and decision making impact learning. In most cases, we draw on research that was not explicitly organized around the strands framework but is useful nonetheless in illuminating the process of science learning within and across the four strands.
Chapter 3 reviews research on young children and provides an overview of the knowledge and skills they bring to school which provide a foundation for learning science. Chapter 4 reviews literature related to Strand 1: Know, use, and interpret scientific explanations of the natural world. Chapter 5 discusses evidence related to Strand 2: Generate and evaluate scientific evidence and, explanations. Chapter 6 summarizes the research evidence related to Strand 3: Understand the nature and development of scientific knowledge. Finally, Chapter 7 discusses research related to Strand 4: Participate productively in scientific practices and discourse.
A major theme across the chapters is how findings from research have increasingly revealed interconnections between the four strands as children develop scientific understanding at all grade levels. The evidence is especially strong that knowledge of the natural world (Strand 1, Chapter 4) and the ability to generate and evaluate evidence and explanations (Strand 2, Chapter 5) are closely intertwined. Work on the connections between Strands 1 and 2 and Strand 3—understanding the nature and development of scientific knowledge (Chapter 6)—is more recent. However, this connection has strong theoretical support, and emergent empirical work documenting the links is compelling. Connections between Strand 4 (Chapter 7), productive participation in science, and the other three strands have less direct empirical support in science. However, work in other subject areas, such as mathematics and reading, supports the idea that there is a connection and that the connection depends on incorporating certain science practices, like modeling, and discourse practices, like argumentation, into science learning environments.
Another major theme across Part II is the strong evidence from current research that children are more capable than was once thought and that implementation of the strands framework could begin as early as kindergarten. In fact, basic research in cognitive development over the past few decades has revolutionized the view of how children’s minds develop, from infancy through adolescence. It turns out that children come to school with a great capacity for learning in general as well as for science learning, and they are able to engage in surprisingly sophisticated scientific thinking in the early grades.
Finally, across the four chapters we review research on how science reasoning and the growth of scientific knowledge develops in the elementary and middle school grades. The research reveals surprisingly diverse capabilities within a given age group as well as variation within a single individual depending on the nature of the task, problem, or inquiry at hand.
3
Foundations for Science Learning in Young Children
Major Findings in the Chapter:
-
In contrast to the commonly held and outmoded view that young children are concrete and simplistic thinkers, the research evidence now shows that their thinking is surprisingly sophisticated. Important building blocks for learning science are in place before they enter school.
-
Children entering school already have substantial knowledge of the natural world, which can be built on to develop their understanding of scientific concepts. Some areas of knowledge may provide more robust foundations to build on than others, because they appear very early and have some universal characteristics across cultures throughout the world.
-
By the end of preschool, children can reason in ways that provide helpful starting points for developing scientific reasoning. However, their reasoning abilities are constrained by their conceptual knowledge, the nature of the task, and their awareness of their own thinking.
Regardless of one’s theoretical orientation, by the time children enter elementary school, no one would argue that their minds are empty vessels awaiting enlightenment in the form of instruction. They come to school after years of cognitive growth in which they have developed a wide range of ways of understanding and reasoning about the world around them. Our goal in this chapter is to describe the knowledge and skills that children bring to school, beginning with the earliest understandings of infants. The past 20 to 30 years of research paint a picture of young children as surpris-
ingly competent and able to engage in learning across all four strands of scientific proficiency from the very beginning of their science education.
We begin with a discussion of young children’s knowledge of the natural world. This knowledge can emerge as a consequence of a child’s everyday interactions with the world as well as a result of the ways in which the culture and its adult members explicitly impart information to children. In some areas of instruction, such as reading, the role of preexisting knowledge and understanding may be relatively modest, but in the area of science education, children bring a great deal that is relevant. A major challenge is to build on students’ existing knowledge of the natural world to help them understand and use scientific knowledge.
Next we identify aspects of young children’s thinking that can serve as the foundation for developing scientific reasoning in the elementary grades. For example, young children understand that one thing can represent another (such as a toy airplane or a scale model), which provides a starting point for modeling. Finally, we consider precursors to children’s understanding of how scientific knowledge is constructed. We include here their understanding of the ideas and beliefs held by other people and their ability to assess the credibility of different sources of knowledge.
ORGANIZING THEMES
Several themes run repeatedly through the research on young children’s emerging understandings of natural systems and their reasoning. The following three themes help organize the research summaries that follow:
-
Concern with explanation and investigation are central to children’s learning and thinking at all ages. Even the youngest children are sensitive to highly abstract patterns and causal relations. They use this information to guide the ways in which they generalize, make inferences, and make sense of the world. There is increasing recognition of the richness and variability of children’s understandings that involve implicit and explicit, nonsymbolic and symbolic, associative and explanatory components. There is no simple concrete to abstract progression in children’s development.
-
Children develop explanatory insights in specific domains. Some key domains of understanding may have a privileged status in helping with the emergence of science. These include mechanics, folk biology, some aspects of chemistry (e.g., an initial understanding of different substances), and folk psychology, as explained below. These four domains have universal shared components throughout the world and for children from all backgrounds in the United States. They form an important cognitive common ground on which to build more sophisticated scientific understandings. Roots of these
-
domains extend back to preverbal thought and are therefore a legacy of infancy.
-
Not only does the growth of scientific understanding involve a sense of the patterns special to such domains as physics and biology, but it also requires much broader cognitive skills that cut across domains. These include an ability to stand back and look at one’s knowledge and learning, heuristics that enable one to efficiently process large amounts of information, and strategies for acquiring, maintaining, and transmitting information. This interplay between domain-specific forms of learning and domaingeneral ones is central to any account of the emergence of scientific thought.
This chapter illustrates these three themes and how they are central to recent research findings concerning how many of the building blocks of scientific understanding emerge prior to school.
Much of the current science education curriculum is based on dated assumptions about the nature of cognitive development and learning, assumptions that lead to suboptimal teaching of science (Metz, 1995). It has been common to view younger children as deficient in some manner, resulting in a focus on what they cannot do rather than what they can do (Gelman and Baillargeon, 1983). That focus is a legacy going back more than 85 years to Jean Piaget’s early studies of the ways in which normal children failed on early versions of the standardized tests that later became widely used as intelligence tests. It asks what children are “missing” and leads to analyses asking when they acquire a certain component of thinking. As a result—in a somewhat distorted interpretation of Piaget’s work (e.g., Bruner, 1964; Werner and Kaplan, 1963)—cognitive development has often been understood as a series of artificial dichotomies in which children do or do not have a particular skill. The transition from being without the skill to having the skill is understood as going through a developmental stage. Problems with this perspective have long been recognized (Flavell, 1971; Linn, 1978; Pulos and Linn, 1978; see also Metz, 1995, for an extensive discussion of the misapplication of Piagetian ideas).
The emphasis on deficits and stages of abilities tends to look at highly general characterizations of children’s capacities, emphasizing global deficits that apply to almost all areas of thought. For example, preschool children have often been claimed to be concrete, preoperational, precausal, prelogical, and lacking the ability to think in relational terms. Only during the elementary school years, or in some cases not until adolescence, were children thought to transition to “higher” forms of thought. If these claims were true as absolute deficits, they would suggest that children bring a radically different way of understanding the world with them when they enter the elementary school classroom.
One review has characterized three false and outmoded views about limitations in elementary children’s thinking that are still widely embraced by education practitioners (Metz, 1995): (1) Elementary schoolchildren think in concrete as opposed to abstract terms. (2) Elementary schoolchildren can make sense of their world primarily in terms of ordering and classifying objects and relations and not in terms of explanatory understanding or the building of intuitive theories. (3) Elementary schoolchildren cannot use experimentation to develop their ideas. All three of these views, as well as other views of broad cognitive limitations of elementary schoolchildren, and even many preschoolers, are no longer accepted by the cognitive developmental research community (see Carey, 1985; Gelman and Baillargeon, 1983; Gelman and Kalish, 2005; and Metz, 1995, for reviews).
EARLY CONCEPTUAL UNDERSTANDING OF NATURAL SYSTEMS
In all cultures, whether they are highly technological or profoundly traditional, there are natural systems that everyone encounters in common and must explain. These form our point of departure for discussing what children bring to school in terms of scientific understanding. Four systems have been extensively studied in infants and young children: the simple mechanics of solid bounded objects, the behaviors of psychological agents, the actions and organization of living things, and the makeup of substances and materials. Infants throughout the world seem to understand these four natural systems in the same way and, to the extent that cross-cultural work has been done with older children, there are considerable commonalities for preschoolers as well. Although these common sets of understandings may diverge more and more in the elementary school years and beyond, they do represent a shared understanding that is a critical foundation for the teaching and learning of science. In older children, there has also been considerable study of their understanding of cosmology and larger scale earth systems, such as weather, ecology, and such processes as volcanic eruptions, tides, and mountain formation. Beliefs in these areas can vary dramatically across cultures and form an interesting contrast to systems that seem to be partially grasped at a much earlier age, but even with large-scale earth systems, there are important common threads.
Naïve Physics
Simple and universal rules govern the behaviors of the physical world, or at least seemingly simple ones at a macroscopic scale. Consider, for example, bounded solid objects, such as rubber balls, wooden doors, and rigid sticks. One knows that solid objects cannot move through each other, that
any changes in their movements are the result of forces outside them, either through direct contact, such as in a collision, or through gravity. One knows that action at a distance between two objects, such as with magnets, is unusual. One also knows that objects tend to endure over space and time. They cannot blink out of existence and then reappear at a different time or in a different place, except in science fiction.
It might seem that knowledge of this sort takes years to acquire. A baby and a young toddler would have to carefully observe the behaviors of physical objects and gradually, from this observational data, induce a set of beliefs that would become their intuitive theory of physics. Given that the simple and elegant rules of Newtonian mechanics were not apparent until Newton himself labored over the topic for many years, how could one expect an infant or a toddler to have any set of coherent expectations about the physical world? It now is clear that, well before their first birthday, infants do have such expectations and they continue to develop in the preschool years. They are definitely not in the form laid down in Newton’s Principia, but they do enable infants and children to anticipate and interpret many aspects of their physical worlds.
The research literature on infants’ conceptions of physical objects has burgeoned in the past two decades and cannot possibly be fully surveyed here (see Baillargeon, 2004; Cohen and Cashon, 2006; Mandler, 2004; Munakata, Casey, and Diamond, 2004, for discussions of large segments of this literature). Instead, we provide a few examples of the ways in which infants are and are not successful. One set of studies concerns intuitions about object permanence and solidity. It now appears that, at least by the fourth month of life, infants “know” that solid objects cannot interpenetrate and that they continue to exist over space and time even when out of sight.
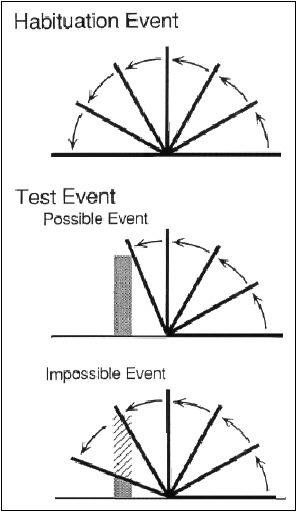
One now classic line of studies in this area had infants observe a flat barrier swinging both toward and away from them through 180 degrees of arc on a surface, such as a table. Infants were shown the 180 degree event several times until they became disinterested (i.e., habituated) to the stimulus. They were then shown a small solid object that was placed behind the barrier in such a way that would prevent the barrier from swinging through the full 180 degrees (see Box 3-1 for diagram). Infants looked longer at displays in which the barrier went through the full 180 degrees (the hidden object disappeared through a trap door) than at displays in which the barrier stopped, for the first time, at say 110 degrees, a novel stopping position but one that was consistent with assumptions about object solidity and permanence (Baillargeon, 1987; Baillargeon, Spelke, and Wasserman, 1985).
In other studies, infants expected that a small vehicle moving behind a barrier would reemerge only when a block behind the barrier was not directly in its path (Baillargeon, 1986). In still other lines of work, infants looked longer when a vertically dropped object seemed to end up in a
position that implies it must have moved through an intervening, but occluded, solid platform (Spelke, 1991). Longer looking by infants is widely accepted as an indication that they have seen an event that violates their expectations.
There is also, not surprisingly, considerable learning about the physical world during infancy. For example, younger infants are sensitive only to large and obvious conflicts between the barrier and obscured block and will not notice smaller discrepancies, such as when the barrier stops 30 degrees too early (Baillargeon, 1995). Thus, they need to learn to calibrate the geometry of physical events with their consequences. Similarly, an appreciation that an unsupported object will fall down takes time to develop (Spelke and Kyeong, 1992). Other researchers argue that competing ways of thinking about objects during infancy are resolved only gradually, over a period of several months (Munakata et al., 1997). Regardless of the details of how quickly infants gain a single clear view of the nature of the physical world, there is substantial agreement that, by the end of the first year of life, they have expectations about objects that fit with many principles governing the behaviors of bounded physical objects.
By 12 months of age, infants are capable of taking into account physical dimensions and magnitudes and their consequences for events. As noted earlier, they consider the angle of movement of a swinging barrier as it relates to the size of an object behind it. They also understand that bigger objects in motion are likely to have bigger consequences. For example, when 11-month-olds observe a cylinder roll down a ramp and move another object through collision, they infer that a larger novel cylinder will move the object more and that a smaller cylinder will move it less (Kotovsky and Baillargeon, 1994). More broadly, while starting early with some very general ideas about solidity and spatiotemporal continuity (Spelke et al., 1992, 1995), infants are constantly refining those ideas into forms that enable more subtle inferences about objects and their behaviors over intervals of time and space (Baillargeon, 2004). By the end of the first year, infants also have a clear sense of causation as opposed to mere correlation or contiguity. Thus, even if one event reliably occurs before another one, infants may not infer causation unless there is also some degree of plausible mechanism, such as one object launching another through collision (Leslie and Keeble, 1987). They can also make inferences about unreasonable versus reasonable hidden causes of the motion of an inanimate object (Saxe, Tenenbaum, and Carey, 2005).
Ongoing research is now asking how a 1-year-old’s mental representations of the world should be best characterized. Should her ability to anticipate the behaviors of physical objects be seen as her having beliefs like those of an adult, or could it reflect mental processes that are less explicit and belief-like in nature? (See Leslie, 1994, for further discussion of these
issues.) To what extent can the 1-year-old flexibly use those mental representations to understand more novel problems with physical objects? Answers to these questions will help to clarify not only how older children’s physical knowledge becomes more explicit but also how that explicit knowledge interacts with earlier preverbal forms.
One intriguing example of the limits of physical understanding in infancy is seen in tasks in which toddlers fail what seem to be the same solidity problems that infants pass. In one task, children observed a display in which several wooden boards could block a ball rolling down a ramp on which the blocks were placed. A low wall was put in front of the blocks and ramp, occluding most of the ramp but keeping the tops of the blocks visible, and a ball was then put into motion on the high part of the ramp that was still visible. When 2-year-olds were asked to open a door where they think a rolling ball will be, they often open the door that would require the ball to move through a salient solid barrier (Keen, 2003). The same children do much better when the two doors are opened simultaneously by another person and they merely have to react to expected and unexpected outcomes. Such actions as retrieval or catching add new levels of complexity in terms of representing the spatial arrangements of hidden objects, levels that can overwhelm 2-year-olds (Freeman et al., 2004; Hood, 2004; Kloos and Keen, 2005).
More broadly, one sees that, in certain tasks, some elements of physical object knowledge are emerging very early, but that the ability to use this knowledge in a wider range of tasks, including those that require planning or coordinating sequences of actions on the part of the child, takes considerable time to develop. In addition, children through their own actions often provide critical feedback that adults might not normally provide. Thus, while adults rarely put objects on surfaces from which they will topple off because they aren’t adequately supported, younger children and infants (e.g., Baillargeon, 2004) will do so and will therefore gain valuable new information concerning the mechanics of physical objects. Finally, knowledge can sometimes be implicit in a child’s action before it is accessible for other, more explicit uses. For example, 5-year-olds will adjust the angle and strength of their throws of a ball in ways that nicely anticipate the trajectories needed for projectiles to hit particular targets, at the same time showing strong errors in their guesses of correct launch speeds for the same targets (Krist, Fieberg, and Wilkening, 1993; see also Shanon, 1976). Over the next several years, their explicit ability to predict projectile trajectories gradually improves, although even in adults there are vestiges of the kindergarten errors (Krist et al., 1993; Shanon, 1976). Indeed, a large literature has shown that several naïve errors about physical trajectories persist in most adults (Bertamini, Spooner, and Hecht, 2004; Carmazza, McCloskey, and Green, 1981; Clement, 1982; Hecht and Bertamini, 2000).
Preschoolers have a quite sophisticated sense of the sort of mechanical causality that is intrinsic to the motion of simple physical solids. For example, when two events precede another one, they will usually correctly sense which is more physically plausible and then prefer it as the cause (Bullock, Gelman, and Baillargeon, 1982; Gelman and Lucariello, 2002). When preschoolers’ spontaneous explanations of various entities are examined in large transcriptions of everyday speech, the children flexibly and easily employ causal reasoning, using different kind of explanations depending on whether the events are thought of as physical, psychological, or biological (Hickling and Wellman, 2001). They show similar distinctions in more experimental tasks (Heyman, Phillips, and Gelman, 2003). Indeed, when asked to explain anomalies in physical regularities, children use very different patterns of reasoning than when explaining anomalies in social conventions of moral rules (Lockhart, 1981).
Preschoolers are also adept at inferring hidden causes. Thus, they assume that similar external motions of animate and inanimate objects are governed by radically different internal causes (Gelman, Durgin, and Kaufman, 1995). They understand that unseen factors must be linked to observable ones in systematic ways that are mechanistically mediated (Yoachim and Meltzoff, 2003). Moreover, preschoolers are quite sophisticated at using complex patterns of covariation over time to infer hidden causes and not just correlations (Gopnik et al., 2004), although often such inferences may be constrained by prior mechanistic theories that they are applying to those tasks (Griffiths, Baraff, and Tenenbaum, 2004). Finally, preschoolers will track a sequence of events occurring in causal chains and infer that the first event in that chain is most likely to be the most important cause (Ahn et al., 2000), a strategy frequently used by adults as well.
A vast literature on science “misconceptions” argues that erroneous beliefs about the physical world are held by many, ranging from preschoolers to adults. And many of these beliefs are highly resistant to change by instruction (Chi, 2005). Much of that literature, especially in the area of mechanics, has focused on high school and college students (e.g., Brown and Clement, 1987; Carmazza, McCloskey, and Green, 1981; Minstrell, 1983, 1988; Clement, 1982); there have been many fewer studies of younger preschool or elementary schoolchildren (Doran, 1972; Ioannides and Vosniadou, 2002; Viennot, 1979). This literature makes clear, however, that the elegant theoretical construction of Newtonian mechanics (including its three primary laws of motion) is by no means obvious even to high school or college students who have had courses in introductory mechanics.
Student misconceptions are sometimes revealed in tasks in which they are asked to predict the trajectories of objects or evaluate whether an observed trajectory is possible or impossible, but even more often when they are asked to identify and explain the forces acting on an object in a given
situation. For example, many students predict that a moving object emerging from a circular tube will continue in a circular trajectory once it emerges from the tube (rather than flying off in a straight line path), or they predict that a person running off a cliff will (as in a Wile E. Coyote cartoon) continue a short way off the cliff before abruptly falling straight down.
Although even young children, like adults, have an explicit concept of force that they use to explain what happens in different physical situations, the meaning of force is an intuitive one, very different from the mathematicized notion embodied in Newtonian mechanics. They tend to think of forces as active pushes or pulls that are needed to explain an object’s motion, rather than coming in interactive action-reaction pairs that are needed to explain not an object’s motion but its change in motion (acceleration). Thus, they see forces in situations in which a physicist has no need to postulate a force (e.g., when a coin is thrown upward, they postulate an upward force is imparted to the object from the hand for the duration of the upward trajectory to explain why it continues to go up), and they fail to see forces that are essential to a Newtonian analysis (e.g., many of the action-reaction pairs that are so central to a Newtonian analysis, such as the force exerted by a table on a book when it is resting on the table). They do not clearly distinguish between force and momentum, acceleration, position, and speed or between instantaneous and average velocity. In light of these findings, some have suggested that high school students may have an alternative naïve theory of motion, akin in many respects to historically naïve impetus views of the sort proposed by Aristotle or the medieval impetus theorists (Caramazza, McCloskey, and Green, 1981; Espinoza, 2005).
Others have argued that viewing these misconceptions as stemming from a highly coherent alternative impetus theory is misleading for several reasons (diSessa, 2004; Smith, diSessa, and Roschelle, 1993). First, it suggests that students are more consistent in their erroneous reasoning than they actually are. Although they may appeal to impetus notions in some tasks, they may not use them in other tasks in which they would be relevant. Second, it overlooks many other notions that students appeal to in their physical explanations, such as balancing, overcoming, or resisting. DiSessa argues that everyday physics is better thought of as exploiting a fairly large and diverse number of these low-level (often inarticulate) explanatory fragments that are evoked, often quite independently, in different contexts. Third, the naïve theories account overlooks many of the points at which students’ intuitions are actually in accord with mature physical analysis. For example, although students may not see the balance of forces in the situation of a book on a table, they do provide this analysis when analyzing a book on an outstretched hand. Thus, they are not as devoid of positive intuitions as the misconceptions literature would suggest. On this analysis there is much valuable knowledge, though admittedly often at an inarticulate subconceptual
level, acquired from rich everyday experience with objects that can be drawn on as resources in physics teaching.
Considerable research is still needed to map out the ways in which infant expectations about physical objects transition into the expectations and beliefs held by preschoolers and elementary schoolchildren. However those studies turn out, however, it is clear that children entering elementary school should not be characterized as merely having a batch of misconceptions. The many ways in which they do correctly sense some of the behaviors of simple mechanical objects should be central to their teaching and learning of science.
Naïve Psychology
People, as well as many other organisms, behave in ways that are immediately interpreted in terms of their having goals, desires, and beliefs that help to explain their actions. Moreover, their actions have a different quality from those of the inanimate world (Spelke, Phillips, and Woodward, 1995). People can easily act on each other at a distance. A facial expression, a comment, or a gesture can cause another agent to spring into action in ways that are directly related to that first event, even though it may be spatially quite distinct. Causes have no obvious proportionality to their effects. A whisper might cause an eruption of action, while a shout may cause inhibition of action. In a different situation, the opposite may occur. Animate things can change their direction midcourse, while simple objects require an external force to change their trajectories. There are patterns of contingency between people that are quite distinctive, so that one person tends to respond to the actions of the other after a characteristic temporal delay (Scassellati and Gold, in press).
The domain of people (and other intentional agents) and their actions corresponds roughly to the research areas of psychology and cognitive science. Although psychology and cognitive science are not typically areas of science instruction in the elementary school, much of the scholarship in those fields arises from experimental research very much in the tradition of the biological and physical sciences.The contrast between simple mechanical objects and intentional agents is one of the most robust and earliest emerging cognitive distinctions in development. Children’s emerging understanding of psychology may be a critical component that they bring to the learning of science in elementary school. For example, understanding and engaging with the beliefs and ideas of other people play an important role in science discourse.
Infants are quite sensitive to the differences in the behavior of people (or other entities considered to be intentional) and inanimate solid objects. They have different expectations about the focus or location of future ac-
tions when they perceive an entity to be goal directed. For example, if an inanimate rod reaches out to touch a particular object, such as a teddy bear, in a given location, such as the left of a screen, 5-month-old infants will expect the rod to return to the same location regardless of what object is there. By contrast, if a hand reaches out to the teddy bear, they will expect it to go to the same object regardless of its location, presumably because they infer that the object is desired by the animate creature possessing the hand (Woodward, 1998). As another example, if an object responds to an infant’s vocalizations by making nonsense sounds back with a slight temporal lag, and if the object then turns 90 degrees, 12-month-old infants will turn as well to see where the object is “looking,” even though there are no obvious facial features on the side that was initially facing them (Johnson, and Carey, 1998; see also Watson, 1979). In other words, the infant uses the pattern of vocalization to infer that the object is like a person (i.e., it has intentions). In addition, a certain kind of contingency-based movement of a simple triangle is enough to trigger in infants inferences of a social agent with specific intentions when the same triangle might otherwise be seen as a simple inanimate object (Kuhlmeier, Bloom, and Wynn, 2005).
Infants use a wide variety of cues, ranging from facial features to contingent responding, to infer that an object is an intentional agent, and, once they make that categorization, they have radically different expectations about the entity (Johnson, 2003; Woodward, Sommerville, and Guajardo, 2001). They also expect very different paths of movement. They think it odd that a cylinder should act on another one across a spatial gap, but they do not think it odd that people should do so (Spelke, Phillips, and Woodward, 1995), and they assume that animate creatures can move in ways that inanimates cannot (Kuhlmeier, Bloom, and Wynn, 2005). For example, they assume that, if a ball has repeatedly hopped over a barrier on its way to a destination, it will continue to do so when the barrier is removed. Yet if cues are provided that the ball is an intentional agent, 12-month-olds will assume that the intentional ball will now go on an entirely new straight-line trajectory right toward the destination (Gergeley et al., 1995; Csibra et al., 1999). Thus, they seem to assume that the laws of classical mechanics are suspended as soon as an entity is assumed to have goals, desires, and beliefs. As with the case of mechanics, it is still not known to what extent the infant’s knowledge of psychology is explicit and within the infant’s awareness as opposed to being implicit knowledge that consists mainly of automatic responses (Leslie, 1994).
After infancy, the young child’s understanding of the mind develops quite dramatically. One of the most discussed developments concerns the emergence, during the third year of life, of an ability to understand that intentional agents might have false beliefs that lead them to behave differently from when they might have true beliefs (Perner, Leekam, and Wimmer,
1987; see Box 3-2 for examples of tasks used to study theory of mind). Children seem to progress from seeing agents as simply driven by desires to being driven by beliefs and desires that interact in a systematic and reliable way (Wellman, 1990). Over much of childhood, there continue to be advances in thinking in even more subtle ways about how mental states and processes are causally related to actions (Flavell, 1999).
The nature of thought about intentional agents is vividly revealed through the study of individuals with autism. Although their understanding of motion in the physical world may be relatively intact, their understanding of other people’s beliefs may be seriously deficient (Baron-Cohen, 1995). Such results give support to the idea that cognitive development proceeds somewhat independently in each domain of knowledge.
In short, from early in infancy, the social world is seen as patterning in dramatically different ways from the physical world. Infants have entirely different sets of expectations about entities in the two worlds, expectations
|
BOX 3-2 Tasks Used to Study Children’s Ideas About the Mind In a standard test for children’s understanding of false belief (Wimmer and Perner, 1983), children watch while a doll puts some chocolate in a cupboard and leaves the room. The chocolate is then moved in the doll’s absence, and the doll returns. Children are told that the doll now wants the chocolate, and they are asked to say where the doll will search. Before children have an understanding of others’ minds, they are more likely to say the doll will search in the new location. Once they have developed an understanding of false belief, they will predict that the doll will search in the old location. In fact, there is a robust improvement between age 3 and age 5 in children’s ability to predict that the doll will search in the old rather than the new location. A number of other tasks have also been used to explore children’s developing understanding of the mind. For example, they may be asked to explain a character’s actions in a story (e.g., Jane is looking for her kitty under the piano. Why is she doing that?) (Bartsch and Wellman, 1989). In another task, children watch as Coke is taken out of a Coke can and replaced with milk out of sight of a story character. They are then asked how the character feels about being offered the can to drink, before the character has taken a sip and discovered it is milk; 3- and 4-year-olds often refer to what they themselves know about the contents of the can (it is milk), rather than what the character would believe (it is Coke) (Harris et al., 1989). |
that influence later developments in more elaborate and explicit beliefs about the minds of others. There are two ways in which a developing folk psychology and cognitive science are relevant to science education. First, they are domains of scientific activity, and the child’s intuitive knowledge can be understood as forming the basis for later explicit instruction on the topic. Second, the cognitive science of science itself is an important part of the science education of the child (Klahr, 2000). For example, an understanding of the subjectivity of knowledge and of potential distortions in communication is essential to being able to engage in science and is deeply dependent on an understanding of the mind and how it acquires and uses knowledge.
Naïve Biology
Given the extraordinary changes in conceptions of the living world over the past few hundred years, it is obvious that the very young child could not possibly have a fully accurate grasp of current biological knowledge. After all, only a few hundred years ago, some of the most learned members of Western society thought that the brain might simply be a large cooling organ for the rest of the body (Zimmer, 2004). Modern molecular biology is a product of the past 60 years or so, and introductory college biology courses of the 1940s have almost no overlap with those of today. In light of these dramatic historical changes, it might seem that a preschooler, let alone an infant, might have no sense whatsoever of the biological world as a distinct domain of causal regularities, mechanisms, and principles.
There is little evidence that infants appreciate the biological world as distinct. They do easily discriminate biological motions, such as walking, from nonbiological ones (Bertenthal, 1993; Booth, Pinto, and Bertenthal, 2002); however, the ability of newborn chicks to make similar discriminations illustrates the point that a mere ability to discriminate biological motion from nonbiological forms should not be overinterpreted in terms of its role in the emergence of biological thought (Vallortigara, Regolin, and Marconato, 2005). Many organisms—whether predator, prey, or both—may have strong reasons for needing a dedicated perceptual system tuned to detect biological motions in the surrounding environment.
Older human infants will classify animals together even when they differ dramatically from each other in appearance, and they will keep apart animals and artifacts (such as birds and toy planes) even when they have strikingly similar appearances (Mandler, 2004). But those acts of categorization, albeit at an apparently abstract level, may be based on seeing the animals as intentional agents compared with the inanimate objects. Along those lines, one view of the emergence of biological thought argues that the infant and the young child initially have no sense of the living world as such and instead only think of living things either as social beings (most animals)
or as inanimate objects (most plants) (Carey, 1985). An understanding of the biological world as a domain with its own principles is thought not to emerge until well into the elementary school years (Carey, 1985, 1988). Animals are distinctive only insofar as they are also understood as social agents with desires, goals, and other cognitive and emotional states that help explain their actions. Since young children will often attribute properties to animals on the basis of their psychological similarities to humans (e.g., dogs eat but worms do not because eating is understood as feeling hungry and feeling satiated or as requiring a clearly visible mouth), they often mistakenly underattribute biological properties to simpler organisms in both the animal and plant kingdoms (Carey, 1985, 1988).
Young children can also be remarkably ignorant about many of the mechanisms that underlie biological processes, such as digestion, movement, and reproduction. Thus, preschoolers may grossly misconstrue the inner workings of the body that digest food; they have little sense of how the body breaks down food into simpler compounds through mechanical and chemical means (Gellert, 1962; Nagy, 1953). Similarly, they have no sense of how organic molecules release energy units that are used to contract muscles and enable movement. Nor do most children know about sex gametes, how they come into contact, and how they result in a fertilized egg that differentiates into a fetus. Because of these clear deficits, it is easy to infer that young children have no understanding of the living world. Moreover, their tendency in some contexts to generalize properties based on psychological similarity suggests that they might be understanding biological entities and processes in psychological terms.
At a different level, however, there is considerable evidence suggesting more precocity in children’s abilities to track the distinctive nature of causal and relational patterns in the biological world (Inagaki and Hatano, 2006; Keil, 2003). Consider again the case of digestion. Although young children do not understand the physiology of digestion in any sort of detail, they do seem to figure out early on that food is transformed in some manner that gives organisms the ability to grow and to move (Inagaki and Hatano, 2002). They understand that an organism will physically deteriorate if it cannot ingest food, they know that the transformation of food is essential to its being usefully employed by the body, and they know that only plants and animals transform food and need to digest it (Toyama, 2000). It therefore seems that, at a more abstract functional level, preschoolers do have a sense of some of the distinctive operations and processes that are essential to digestion. In that way, they are not so different from adults. Most adults also have poor or mistaken knowledge of biological mechanisms, believing for example that most of the solid mass of plants arises from the soil, often completely missing the huge contribution from gaseous carbon dioxide (Driver et al., 1994). At this mechanistic level of analysis, one can find a huge array
of misconceptions about biology not only in children but also in most adults (Driver et al., 1994). Moreover, people of all ages think that they understand such mechanisms far better than they really do, leading to a false impression of having detailed mechanistic understandings (Rozenblit and Keil, 2002; Lawson, in press; Mills and Keil, 2005).
The story for digestion is repeated for most other areas of biology. Both children and adults have glaring gaps in their knowledge and often outright false mechanistic details, at the same time sensing higher level functional patterns quite well. They understand general patterns of growth and regrowth (Hickling and Gelman, 1995; Backscheider, Shatz, and Gelman, 1993), what sorts of properties are likely to be inherited (Springer and Keil, 1989; Gimenez and Harris, 2002), and how something extracted from food helps enable movement (Inagaki and Hatano, 2002). Active debates remain concerning the extent to which children are thinking about living things as a distinct and neatly bounded group. Beyond those debates, children appear to pick up on patterns related to function that help support their thinking about biological kinds (Gelman, 2003; Gelman and Hirschfeld, 1999). Also, children in other cultures may not be swayed by psychological similarity in the same way that North American children are when making judgments about biological properties (Atran et al., 2001; Medin, Unsworth, and Hirschfeld, in press). Indeed, as is the case with physics, a core sense of biological entities as such may often be present but obscured by the context of a task and how it is framed. For example, if preschoolers carrying out a task are given brief cues suggesting that they should attend to internal mechanisms rather than social factors, they will make inductions that are based on biological as opposed to psychological similarity (Gutheil, Vera, and Keil, 1998).
Children may zero in on the domain of living things by realizing that they occur at the intersection of two kinds of causal and relational patterns, each of which individually may apply to entities in multiple domains, but which in concert uniquely pick out the living world (Keil, 1992). Consider, for example, three such patterns: (1) a rich internal, microstructural essence (that is, a true, underlying nature); (2) deep taxonomic embedding (i.e., placed in an ordered system of groups and categories that indicates relationships); and (3) teleological interpretations (i.e., being seen as having a purpose). It is common to think of all categories of natural entities, such as chemical elements and biological species, as having essences (e.g., atomic number, DNA) but artifacts do not (there is no inner essence of chair) (Gelman, 2003; Keil, 1989). This essentialist view for natural kinds is not strictly correct (Keil and Richardson, 1999), but it is a useful heuristic. It is also common to think about parts of biological systems as having purposes, but it is not common to do so for nonliving natural kinds. This teleological stance, in combination with the essentialist bias, helps children pick out all and only
living kinds. Finally, the idea that biological entities are embedded in rich and deep taxonomies may not be strictly true for only living things, but when used with the essentialist bias and teleological interpretations, it helps to further demarcate the set of living things. Moreover, there are strong cross-cultural universals in the use of folk biological taxonomies, suggesting a way of organizing the living world that remains robust across both culture and development (Lopez et al., 1997).
The use of a teleological or “design” stance to understand living things is particularly interesting. When children are asked to explicitly reject or accept whether functional attributions can be made about nonliving natural kinds, such as rocks, preschoolers tend to give a functional attribution (Kelemen, 1999). Yet the ability to make explicit judgments about whether a teleological explanation is applicable may emerge later. Young children may in fact have a more tacit understanding that is revealed in their spontaneous use of such explanations in attempts to learn more about the biological and physical worlds. For example, when preschoolers are shown novel artifacts and living things, their spontaneous questions about them reveal sharply contrasting patterns for artifacts and living things. They tend to ask more questions about the purposes of whole artifacts and about the parts of animals rather than about the purposes of whole animals (Greif et al., 2006). Thus, when children later enter a more formal setting of science education, their competence may be underestimated if they are assessed in terms of their judgments of the appropriateness of certain forms of explanation for certain phenomena. Greater competence may be revealed by looking at their spontaneous use of questions.
Overall, well before elementary school begins, children are sensitive to a variety of high-level causal and relational patterns that are particularly useful for reasoning about living things. The most dramatic cases of cognitive change seem to involve learning about more detailed mechanisms of biological systems, much of this occurring during the elementary school years. In addition, an explicit awareness of plants and animals as a distinct domain governed by unique sets of mechanistic principles may undergo considerable development during childhood; it may change from a simple notion of seeing plants and animals as special because of a vital force to seeing them as engaging in unique metabolic activities (Inagaki and Hatano, 2002, 2006).
Substances and Their Transformations
As adults, people think of chemistry as the study of the composition of matter and changes that it can undergo, both in isolation and in combination with other forms of matter. There is a great deal of knowledge involved in mature scientific notions of chemistry, ranging from atomic theory, to mecha-
nisms of chemical bonding, to the dynamics of phase changes. Again, it is clear that children cannot possibly be expected to know the details of organic and inorganic chemistry, the thermodynamics of compounds changing states, or why there are clusters of elements in the periodic table with similar chemical properties. Most adults have only the most shallow grasp of such matters, even those with advanced degrees. As with other domains, it is easy to document a host of dramatic misconceptions if one approaches naïve ideas related to chemistry in this manner. There are, however, other ways of thinking about matter, substance, and transformation that appear to have much earlier developmental roots. Although there has been much less research on infants’ and preschool children’s understandings of matter and materials than their understandings in other domains, a consistent pattern is suggested.
Infants may have no conception of the makeup of matter, but they do seem early on to know that substance and the stuff that things are made of apply to a different level of conceptual analysis from thinking of things as objects. Preverbally, they seem to know that food is often understood most importantly in terms of the substance it is made of, whereas tools are often most importantly understood in terms of their shapes (Santos, Hauser, and Spelke, 2002). In the earliest stages of word learning, they know that mass nouns (some x) will refer to substance, whereas count nouns (an x) refer to bounded objects, apparently building on a earlier emerging prelinguistic understanding of this fundamental contrast (Imai and Genter, 1997; Soja, Carey, and Spelke, 1992). During the preschool years, children learn not only words that name specific kinds of objects (e.g., boats, cups, airplanes) or bounded entities (e.g., lakes, puddles, rivers), but also words that name specific kinds of materials (e.g., wood, glass, plastic, water, juice, sand) and the perceivable properties of things (e.g., large/small, heavy/light, rough/ smooth, red/green, shiny/dull, hot/cold, sweet/salty). Such naming practices could not proceed without some sense of the substances that objects are made of and the ways in which the substance itself confers properties on an object (Gelman and Kalish, 2005).
Although preschoolers still have much to learn about distinguishing and relating object and material levels of description, they are by no means clueless about the patterning of properties at these levels. Indeed, they have several emerging high-level insights that they can build on in subsequent learning. First, in several studies with children from both middle and lower middle-class backgrounds, 3- and 4-year-olds seemed to appreciate the homogeneous structure of materials (Au, 1994). For example, they often judged that an arbitrary portion of a chunk/pile of a given substance was still the same kind of substance as the whole chunk/pile. They also began to distinguish substance-relevant properties (such as taste, smell, whether it melts or burns, the color it turns when in certain reactions) that would be maintained
across different portion sizes and more entity-relevant properties (such as coarseness, its capacity to blow away or break another object, fit into a certain space, or its shape) that would not.
Although children were far from perfect in their judgments, especially when materials have been ground into powders or invisible pieces, these and other studies (e.g., Gelman and Markman, 1986, 1987) have shown that preschool children, like adults, can use a notion of material kinds as a basis for making inductive inferences about the properties of things, even when such judgments are pitted against judgments based on global perceptual similarity. In addition, from about age 4, they realize that the same type of object can be made from different materials (e.g., a toy airplane made of paper or wood, a spoon made of plastic or metal) or that two different objects (e.g., a spoon and a cup) could be made of the same materials (Dickinson, 1987). They also realize that transformations (such as cutting, grinding, or breaking) that destroy object identity do not need to change the identity of the kind of material an object is made of. For example, if one cut a wooden toy airplane into pieces, it would no longer be an airplane, but it would still be wood (Smith, Carey, and Wiser, 1985).
Another somewhat early developing notion is the belief in conservation of “amount of matter or stuff” under certain simple transformations in shape, as evidenced in Piaget and Inhelder’s famous conservation studies (1974). For example, 5- to 7-year-old children are beginning to realize that changing the shape of an object (rolling a clay ball into a long thin snake-like shape or pouring a liquid from one shaped container to another) does not change the amount of stuff in the object or the amount of liquid in the container. Again, children are beginning to look beyond differences in surface appearance to make inferences about some theoretically important quantity that has been conserved—in this case, “the amount of matter or stuff.” These are perhaps some of the most widely studied and replicated findings in all of developmental psychology, although the replications suggest that many features of how the tasks are presented can affect how well the questions are understood, children’s pattern of judgment, and the age at which they give “conservation” answers (Gelman and Baillargeon, 1983).
Initially, children who make these conservation judgments base their arguments on references to features of transformation history—nothing appeared to be added or removed—or base their arguments on qualitative compensation arguments (e.g., general trade-off between height and width of containers). They generally have no means yet of directly measuring, quantifying, or comparing the amount of matter in the two samples. Developing a deeper understanding of the (approximate) conservation of amount of matter and mass across a much broader range of transformations (including dissolving and across chemical and phase changes), in contrast, is a protracted process and requires more explicit science instruction and self-
conscious theory-building on the child’s part, learning to measure volume and weight and, in some cases, developing an atomic-molecular framework of matter (Smith et al., 2006; Stavy, 1995).
Chemistry is a domain in which some of the clearest cases of dramatic conceptual change have been documented during childhood, at both the macroscopic and atomic-molecular levels. For example, although even preschool children understand that objects vary in their size and weight, their initial understanding of these magnitudes is grounded in their perceptual experiences, rather than an explicitly articulated theory of matter. Size is “perceived global bigness,” in which different spatial dimensions have not yet been differentiated. Weight is “felt weight,” in which weight and density have not yet been differentiated as distinct physical magnitudes. Children often judge that some light objects, like a small piece of Styrofoam, weigh “nothing at all” because they exert no force on their hand (Smith, Carey, and Wiser, 1985; Smith, Solomon, and Carey, 2005). Hence, their understanding of these properties undergoes dramatic change as they construct distinct measures of weight and volume, come to see them as central properties of all matter, and interrelate these quantities in a distinct concept of density tied to their notion of material kind (Lehrer et al., 2001; Smith, Carey, and Wiser, 1985; Smith et al., 1997; Smith, Solomon, and Carey, 2005).
Furthermore, when young children are beginning to develop an explicit concept of matter that includes both solids and liquids, it is initially grounded in more commonsense perceptual properties—something one can see, feel, or touch—rather than as something that takes up space and has mass (Carey, 1991; Stavy, 1991). Thus, children have difficulty recognizing that matter continues to exist when divided into pieces too small to see (Carey, 1991; Smith et al., 1997) and generally do not appreciate the material nature of gases (Lee et al., 1993; Stavy, 1988; Smith et al., 1997).
Even more challenging to their everyday experiences of matter and materials are the assumptions of the atomic-molecular theory of matter. Not only does this theory call for them to imagine matter at a scale far removed from their everyday experiences, but it also makes theoretical commitments that violate their metaphysical beliefs (e.g., there is no vacuum). Everyday experience—the experience that matter is continuous—is deeply entrenched, and the experience that the kinds of materials in the world are infinitely varied is not easily reconciled with the notion that there are only about 100 different kinds of atoms on earth (Nussbaum, 1985; Lee et al., 1993). However, although there is still much for children to learn, even in preschool they are making some distinctions between object and material levels of description in organizing their knowledge of the natural world. They are beginning to ask themselves what are things made of, what changes and what stays the same across different transformations, and learning to count things and even to build some initial causal accounts of why things have the
properties that they do. All of these initial insights and interests can and should be drawn on in science teaching.
Earth Systems and Cosmology
In some respects there could hardly be more diversity across cultures than there is with respect to cosmology. Views of the nature of the heavens and of heavenly bodies have varied enormously over the years and from society to society. It might therefore seem that views of the earth, the heavens, extraterrestrial bodies, and the interactions between them would show markedly different developmental patterns depending on the culture involved. Yet the past decade of research suggests a more nuanced pattern. There may be a considerable common ground to early views of the earth and the heavens, with divergence tending to emerge later on.
One view sees preschool children as developing a coarse set of beliefs or “framework theory” (see Wellman, 1990) that helps guide the emergence of later more culture-specific views (Nussbaum, 1979; Nussbaum and Novak, 1976; Nussbaum and Sharoni-Dagan, 1983; Vosniadou, 1994; Vosniadou and Brewer, 1990, 1992, 1994; Vosniadou and Ioannides, 1998). By this account, young children become convinced of two very salient “facts” about their external world: it is essentially flat, and unsupported objects fall down. As they grow older and become immersed in their culture, they strive to fit these two universal framing beliefs with what the culture tells them about the earth, the moon, and the stars. This process of fitting these strong early beliefs with what their culture tells them often results in distortions as they either attempt to reconcile the two or simply develop compartmentalized and internally contradictory beliefs. For example, their firsthand experience of flatness and things falling down may be very difficult to reconcile with being told that the earth is round. Children will try to reinterpret “round” as not meaning a sphere but instead as something like a flat disc or a hollowed out hemisphere in which people live. In fact, the mental models that the children create of the earth, the sun, and the moon tend to come from a relatively small family of alternatives in most cultures (e.g., Samarapungavan, Vosniadou, and Brewer, 1996).
Cosmology and earth sciences offer an especially interesting case in which the history of science and cognitive development can be compared and contrasted for mutually reinforcing insights (Duschl, 2000). Certainly, views of a flat earth, of the heavens as a curtain with pinholes representing stars, or of the sun revolving around the earth are well known for their prominent roles in the Western historical tradition. It is useful to therefore ask about the extent to which very early emerging beliefs, such as those about flatness and about the downward descent of unsupported objects, have had a framing effect on belief systems for millennia and how, as formal
science emerged, it managed to override those early belief systems. Those accounts may well help clarify the ways in which science education today might encounter such beliefs and work with them.
There are, of course, many other features of early knowledge that influence the development of cosmology and an intuitive earth science. The large literature on how children conceptualize the spatial layout, for example, is critical to understanding how they start to build models of the arrangement of bodies in space (Newcombe et al., 1998). Similarly, the development of the ability to understand the representational meanings of maps and three-dimensional models (such as globes) undergoes dramatic changes during the preschool and early elementary school years (DeLoache, 1987, 2004; Liben, Kastens, and Stevenson, 2002) and is therefore essential to understanding how cultural artifacts may influence the teaching and learning of earth science. Moreover, the particular symbols and representations used influence the nature of the spatial representations that are constructed (Uttal, 2002), making clear the importance of understanding the ways in which children of different ages naturally conceive of spatial information and the ways in which they are and are not able to glean information from maps and models.
In short, the emergence of a folk cosmology and an intuitive earth science in the preschool and early elementary school years forms a critical skeletal structure within which more formal science curricula must function. Of all five domains considered here, some of the most dramatic changes may occur during the elementary school years with respect to cosmology; but these changes hardly occur in an intellectually empty or unformed mind. Children bring with them a substantial set of interrelated beliefs and expectations about the earth and the heavens that must be taken into account.
UNDERPINNINGS OF SCIENTIFIC REASONING
As we have shown above, young preschoolers can be exquisitely sensitive to abstract patterns in the world and use that sensitivity to guide how they think about the behaviors of objects, the nature of living things, and the layout of things in space, among many other problems (Keil et al., 1998). Young children and preverbal infants seem to have a strong sense of principles of cause and effect and do not merely notice spatial and temporal contiguity (Leslie, 1984). Moreover, they have reasonable expectations about how causes precede effects and how certain kinds of causes are linked to specific kinds of effects (Bullock, Gelman, and Baillargeon, 1982; Koslowski, 1996). Categorization, induction, and many other forms of reasoning seem to be guided by such abstract forms of information. At the same time, infants and young children can have enormous difficulty explicitly talking about abstract patterns, a difficulty that may well contrib-
ute to a false impression that they are hopelessly concrete (Simons and Keil, 1995). That difficulty in itself is an important developmental factor to consider in its own right.
Children can use many processes that can be thought of as the underpinnings of scientific reasoning (at least in certain contexts), certainly by the end of the preschool years and often well before. These include deductive reasoning, inductive reasoning, Bayesian reasoning and screening off, sensitivity to covariation, correlation, and contingency patterns in stimulus input, the ability to evaluate simple quantified and if-then rules, the ability to distinguish determinate and indeterminate evidence, and some general problem-solving heuristics and reasoning biases. In this sense, children are more competent than has been commonly supposed and bring a wealth of capacities to the learning process.
For example, reasoning about covariation and cause has been an active area of research on scientific reasoning in older children. Research has demonstrated that even preschool children are adept at using a variety of cues from the environment to identify the cause of an event from a set of potential candidates. Among these cues are temporal contiguity, spatial contiguity, consistent covariation between the candidate cause and the effect, and mechanism—that is, whether there is a plausible mechanism that would account for A causing B (Leslie, 1984; Shultz, 1982). There is mounting evidence that even very young children (ages 2, 3, and 4) are able to draw inferences about cause from viewing patterns of covariation of events.
In a series of investigations, Gopnik and her colleagues (Gopnik et al., 2004; Gopnik and Sobel, 2000; Gopnik, et al., 2001; Kushnir and Gopnik, 2005; Schulz and Gopnik, 2004) explored both how young children learn about new causal relations and whether these learning systems are domain specific or apply across different domains of knowledge, such as biological and physical systems. The strategy was to observe children as they went about learning a novel causal relation that they had not previously encountered or been taught.
In one series of studies, children were shown several small blocks and told that one or more of them were blickets. They were then introduced to the “blicket detector,” a machine that lights up and plays music when (and only when) “blickets” are placed on it. Children were asked to identify which of the blocks were the blickets, either by observing the response of the blicket detector as the researcher placed blocks on it, or, in some studies, by themselves placing blocks on the detector. Across trials within a study and across studies, the patterns of evidence that children used to make inferences became increasingly complex, ultimately including multiple causes and probabilistic relationships. In most cases, even the 2-year-olds made correct conclusions about causality by observing patterns of contingency, although younger children did not perform as well as older preschoolers on
more complex tasks. Children seemed to use similar kinds of causal learning principles across different content domains of knowledge.
Young children also demonstrate capacities that can be seen as the foundation for modeling. The developmental literature illustrates that there are myriad ways in which even preschool children come to regard one thing as representing another. For example, long before they arrive at school, children have some appreciation of the representational qualities of toys, pictures, scale models, and video representations (DeLoache, 2004; DeLoache, Pierroutsakos, and Uttal, 2003; Troseth, 2003; Troseth and DeLoache, 1998; Troseth, Pierroutsakos, and DeLoache, 2004). In pretend play, children treat objects as stand-ins for others (a block stands in for a teacup; a banana for a telephone), yet they still understand that the object has not really changed its original identity, character, or function (Leslie, 1987). Later in school, they capitalize on very similar understandings to use counters for “direct modeling” to solve simple early arithmetic problems that involve grouping and separating.
Although young children demonstrate many early symbolic capacities that provide a foundation for modeling, they are not yet able to engage in all the key aspects of modeling in science. As Lehrer and Schauble (2000) note, “Mature modeling includes the self-conscious separation of a model and its referent, the explicit consideration of measurement error, and the understanding that alternative models are possible and may in fact be preferable.” In contrast, although they certainly know the difference between a model and its referent, children do not usually self-consciously think about the separation of the model and the modeled world. Consequently, they often show a preference for copies over true models, because they tend to resist symbolic depictions that leave out information, even if the information is not important to the current theoretical purposes (Grosslight et al., 1991; Lehrer and Schauble, 2000). For example, children using paper strips to represent the height of plants may insist on the strips being colored green (like the plant stems), and demand that each strip be adorned with a flower (Lehrer and Schauble, 2002).
Children are also unlikely to spontaneously consider issues of precision and error of a representation or the implications of deviations between the model and the modeled world in light of current goals (although they certainly have intuitions that are helpful as starting points; see Masnick and Klahr, 2003; Petrosino, Lehrer, and Schauble, 2003). They also have difficulty entertaining the idea that there are many possible alternative representations. Indeed, the search for and evaluation of rival models in evaluating alternative hypotheses is a form of argument that does not typically emerge spontaneously (Driver et al., 1996; Grosslight et al., 1991).
In sum, the evidence is strong that children can engage in sophisticated forms of reasoning in some contexts. However, there are certainly many
problems and tasks in which they do not display these abilities (a fact that explains, in part, why psychologists and teachers have often thought of them as lacking some of these abilities). Researchers are now more aware of the conditions that affect the use of many forms of reasoning. Significantly, many of the same variables that affect adults’ use of these forms of reasoning act in similar ways with children. In this sense, there is much greater continuity across development in basic reasoning processes than has been commonly supposed, as well as more variability and context sensitivity for a given individual. Three important conditions on reasoning are (1) knowledge of relevant conceptual relations, (2) whether a problem makes sense to the child, and (3) whether implicit or nonverbal reasoning comes into play.
One of the foremost conditions on reasoning is the role of children’s knowledge of relevant conceptual relations in promoting deeper reasoning (i.e., reasoning based on causal, taxonomic relations rather than surface similarity or perceptual cues). Thus, rather than reasoning being independent of knowledge, there are deep interactions between domain knowledge and many forms of reasoning (Gotwals and Songer, 2006). For example, studies of young children’s causal reasoning suggest an interaction of domain-general reasoning processes and knowledge of the specific domain being investigated (Gopnik et al., 2001).
Another important condition is that the problem an individual is asked to reason about has to make (pragmatic) sense to him or her. When a problem does not make sense, people often transform it into one that does. When care is taken to present a reasoning problem in a form in which it makes sense to children, they show much more competence. For example, many problems that involve reasoning with counterfactual information do not make sense to either young children or lay adults (e.g., All snow is black. Tom sees some snow. Is it black?). However, even preschool children can reason about counterfactuals if the problem is presented in a context in which such reasoning makes sense. For example, Leevers and Harris (1999, 2000) found that 4- and 5-year-old children could reason syllogistically about incongruent content when the problems were presented in fantasy mode or when they were encouraged to think about the problems and imagine what it would be like if it were true. Many classic tasks showing apparent deep conceptual failures can be changed through pragmatic manipulations into ones where the children succeed.
Finally, in many contexts, reasoning processes are implicit and outside of children’s conscious control, rather than explicit. Work in infancy suggests that even nonverbal infants have ways of representing and evaluating ideas, independent of language or other culturally transmitted symbol systems. Thus, there are many implicit and nonverbal aspects to reasoning that need to be understood and that may persist in important ways into the adult years. For example, detecting covariation and contingency and inferring causal
relations from this information is likely to be an implicit process for young children (and for adults). That is, they are not fully conscious of the reasoning they use and cannot describe their thinking processes to someone else (Gopnik et al., 2001). Developing more awareness of our reasoning processes can give us conscious control over them and allows us to choose when and how we use different strategies.
YOUNG CHILDREN’S UNDERSTANDING OF KNOWLEDGE AND OF SCIENCE
Understanding how scientific knowledge is constructed and reflecting on the status of one’s own knowledge of scientific concepts is challenging for many students and for adults. While young children clearly do not have a complete grasp of the scientific enterprise, research suggests that they do have important insights that can serve as resources to their learning about science as a way of knowing. These resources include children’s understanding of their own and others’ ideas, beliefs, and knowledge and their ability to assess sources of knowledge.
Understanding Ideas, Beliefs, and Knowledge
An extensive research literature describes young children’s understanding of knowledge. The preschool years are a time of enormous accomplishments in this regard. Most notably, children develop an initial theory of mind, which provides a framework for their beginning to think of themselves and others as more or less knowledgeable. The research literature on children’s theory of mind is concerned with their increasing sophistication in understanding and predicting the behaviors of others. Central to this development is the transition from a “copy theory” of mind to a “representational” theory of mind (Wellman, 1990), enabling such insights as false belief and how access to different information can lead to different inferences. In the words of Gopnik and Wellman, 5-year-olds appreciate that “all mental life has the same representational character” (Gopnik and Wellman, 1994, p. 267). This work describes an important foundation for children’s understanding of knowledge and the construction of scientific knowledge. For example, it reveals the child’s growing understanding of the active role of the knower in knowledge construction, negating any simple correspondence between observing and knowing.
Understanding what ideas are and what they are not is prerequisite to doing science in a meaningful way. As early as 2 years of age, children begin to use words like “think” in ways that suggest that ideas carry varying degrees of certainty (Perner, 1991); by age 3, they use a cluster of words that distinguish among different mental states (e.g., “think,” “know,” “forget,”
and “pretend”). These are the early markers of their growing awareness of their own minds and the fact that their own understandings may be tentative, incomplete, or incorrect in relation to those of other people. Beyond recognizing ideas as such, by about the age of 4 (if not sooner) children also understand that individuals can believe things that may be false. False belief is an essential component to mature learning as well as scientific practice. The inquiry process hinges on treating ideas as plausible and testing them empirically before determining their value.
By school age, most children will easily distinguish objects from simple symbols representing those objects (e.g., an actual milk bottle from a drawing of one) (see, e.g., DeLoache, 2004). Their ability to understand symbol systems and representational models underpins a capacity to understand and formulate explanatory models in science. This capacity emerges quite early and is in place before children enter school. For example, in studies conducted by DeLoache and her colleagues, children see an object hidden in a small-scale model of a room, and they are asked to find the object in the actual room. To be successful at this task, children must achieve the insight that the scale model is both an object in its own right and that it represents something about the larger room. This task is quite difficult for 2½-year-olds, although on versions of the task using scale models, by 3 years of age, children typically succeed.
Understanding Sources of Knowledge
Young children are also surprisingly sophisticated in the sources of information they consider. Contrary to pervasive views of children as “lone scientists” or “concrete operators” who rely only on firsthand observations and experiments, children actually draw on information from a range of sources. These include their own perception, as well as the testimony of other children and adults, and the inferences they draw from observations and testimony (Harris, 2002). Furthermore, they also track the sources of information that influence their thinking. In the preschool years, children begin to identify clear sources of their beliefs. They accurately attribute their ideas to perception, the testimony of others, or inference from observations (Montgomery, 1992; Perner, 1991; Sodian and Wimmer, 1987; Taylor, 1988; Wellman, 1990).
Scientific practice and mature learning involve making informed judgments of the quality and truthfulness of evidence and arguments, as well as identification of reliable sources of expert knowledge. By the time children reach kindergarten, the rudiments of these intellectual skills are in hand. Children as young as age 2 make basic distinctions in the sources from which they gather information. For example, children viewing the same scene on TV and through a window will treat their observations differently
(Troseth and DeLoache, 1998). By the age of 3 or 4, children acquire a sense of the credibility of reports. Koenig, Clement, and Harris (2004), for example, presented groups of 3- and 4-year-olds with two adult “labelers” who, respectively, identified novel objects correctly and incorrectly. The older preschool children in their sample were quite capable of identifying accurate and inaccurate informants, and many tracked the accurate labeler and tended to rely on that labeler’s testimony in novel scenarios.
Learning in science and in general also entails sensing the terrain of knowledge in other minds: determining who is expert on particular topics of interest (Keil, 1989). Children are surprisingly good at getting a sense of the divisions of cognitive labor around them and how to evaluate people’s credibility. In preschool and through the first years of schooling, children develop a crude but impressive sense that there are experts in different broad domains corresponding roughly to physics, psychology, biology, chemistry, and political science. They know that expertise is bounded, and that not everyone knows everything. They also show marked changes during late preschool and early elementary school in their ability to discount information given by others if they see that person as having suspect motivations. In addition, they start to understand the general nature of testimony and the different pressure points that can make it fallible.
Another way of thinking about sources of knowledge is distinguishing between one’s own beliefs (or theories) and empirical evidence. Kuhn and Pearsall (2000) report a study that provides evidence of an initial fragile contrast between theory and evidence by about age 6. They investigated whether children ages 4 to 6 were sensitive to evidence as a source of knowledge to support the truth of a claim, and as distinguishable from theory that enhances plausibility of the claim. Participants were shown a sequence of pictures in which, for example, two runners compete in a race. Cues in the images suggested a theory as to why one will win (e.g., one runner sports fancy running shoes, the other does not). The final image depicts one runner holding a winner’s trophy.
When asked to indicate the outcome and to justify this knowledge, 4-year-olds show a fragile distinction between the two kinds of justification, “How do you know?” and “Why is it so?” (the evidence for the claim versus an explanation). In contrast, 6-year-olds, while still prone to errors, were right most of the time, and adults made no errors. Other researchers have reported similar findings that reveal children’s ability to distinguish beliefs from evidence (Sodian, Zaitchick, and Carey, 1991).
Understanding Scientific Knowledge
The research literature has not extensively investigated what young children may know about science as a distinct way of knowing by the start of
elementary school. In this category, we include both knowledge of the enterprise of science per se, as well as knowledge about processes that are at the heart of doing science (such as the coordination of theory and evidence). Whereas for the most part, children will have had limited experience with science, there is enormous variability in this regard. For example, some children will have gone to science museums, been read various science books, perhaps seen TV scientists performing experiments, or even had a parent who is a scientist. Such differences in experience are likely to translate into variations in children’s ideas about the enterprise of science. However, very little research has explored this issue.
Some suggestions about what first graders may think about science comes from the work of Gertrude Hennessey, a science education researcher as well as a grade 1-6 science teacher, who asked her students to respond to the question “What is science?” Typical responses from first graders indicated that they did not think about science as a unique enterprise of knowledge production. Their responses included that “science is”
-
learning about things,
-
learning about the human body,
-
having fun and learning about what it was like in the olden days, and
-
about learning and listening.
These anecdotal responses suggest that early elementary students have some idea that science involves learning new things, although they may not yet have much idea what might be distinctive or special about science as a way of knowing and learning.
CONCLUSION
The notion of young children as hopelessly concrete and incapable of abstract thought is undermined by their early emerging abilities to track all sorts of highly abstract relations in the world around them. They have rich knowledge of natural phenomena. They are able to reason in ways that provide a foundation for scientific thinking, including potential precursors of modeling, designing experiments, and reasoning about theory and evidence. They also enter school with a broad and impressive set of knowledge skills that allow them to use and work with knowledge in sophisticated ways, although they may lack a clear sense of what is unique about science.
Across all five domains of knowledge of the natural world considered in this chapter, there is a consistent pattern in which preschoolers, and often even preverbal infants, are found to be tracking a wide range of relational and causal properties of the world around them. Beyond just tracking those regularities, however, they also come to link them to broad domains, such as
those corresponding to physical mechanics, cognitive and motivational processes, matter, the living world, and cosmology. They are not always correct and often have huge gaps in their understandings, but they certainly aren’t mere bundles of misconceptions. Instead, they are more profitably construed as active exploratory agents who have successfully learned about regularities in these broad domains in ways that help them interpret, anticipate, and explain their worlds. They do have misconceptions, and some persist into most adults’ mental lives, but these misconceptions are more revealing and better understood in the broader context of considering children’s positive abilities.
In conjunction with their knowledge of the natural world, young children are also able to engage in reasoning that can be used as starting points for supporting the generation and evaluation of evidence. For example, young children’s understanding of symbols and scale models can be used to help them engage in modeling activities. Likewise, their ability to distinguish cause and effect is a critical foundation for designing informative experiments. These early reasoning abilities are constrained, however, by the depth of children’s conceptual knowledge, the nature of the task, and their awareness of their own thinking (metacognition). The latter, metacognition or the ability to think about one’s own thinking, is recognized as critical to learning in general (see National Research Council, 2000) and emerges again and again as important to science learning.
Finally, children’s early beliefs about knowledge may serve as precursors to developing an understanding of how scientific knowledge is constructed. During the preschool years, children develop an awareness of other people’s minds that reveals a growing understanding of the active role of the knower in knowledge construction. This ability to consider ideas and beliefs as separate from the material world is foundational for engaging in debates about the interpretation of evidence. Children’s beliefs about knowledge also encompass some aspects of the nature of knowledge, such as its degree of uncertainty and the relative credibility of knowledge sources. These epistemological beliefs can function as a starting point for learning about the nature and development of science knowledge in the classroom, providing rich resources on which to build, as well as limitations.
Many questions remain about the mental representations that children use to help make sense of their world, such as how different they are from the more formal theories of science and how easy it is for them to access information for use across a wide range of contexts. It is important for science educators to balance a deep appreciation of what is genuinely conceptually difficult, “non obvious,” and novel about many central principles of modern science, with an equally deep appreciation of the many intellectual resources that children bring to the science learning task. It is these resources in combination with the new knowledge and tools provided in sci-
ence instruction itself that will make successful science learning possible. There is now abundant evidence that, along with whatever misconceptions they may appear to have, children also bring to the classroom a rich and valuable set of knowledge structures and processes that should be exploited more fully as points of departure for science education. Furthermore, their reasoning abilities and understanding of knowledge mean that they can engage in and profit from instruction that incorporates relatively complex scientific practices from the very beginning of their schooling.
REFERENCES
Ahn, W., Gelman, S.A., Amsterlaw, J.A., Hohenstein, J., and Kalish, C.W. (2000). Causal status effects in children’s categorization. Cognition, 76, 35-43.
Atran, S., Medin, D.L., Lynch, E., Vapnarsky, V., Ucan Ek’, E., and Sousa, P. (2001). Folkbiology doesn’t come from folkpsychology: Evidence from Yukatec Maya in cross-cultural perspective. Journal of Cognition and Culture, 1, 4-42.
Au, T.K. (1994). Developing an intuitive understanding of substance kinds. Cognitive Psychology, 27(1), 71-111.
Backscheider, A.G., Shatz, M., and Gelman, S.A. (1993). Preschoolers’ ability to distinguish living kinds as a function of regrowth. Child Development, 64, 1242-1257.
Baillargeon, R. (1986). Representing the existence and the location of hidden objects: Object permanence in 6- and 8-month-old infants. Cognition, 23, 21-41.
Baillargeon, R. (1987). Object permanence in 3.5- and 4.5-month-old infants. Developmental Psychology, 23, 655-664.
Baillargeon, R. (1995). A model of physical reasoning in infancy. In C. Rovee-Collier and L. Lipsitt (Eds.), Advances in infancy research (vol. 9, pp. 305-371). Norwood NJ: Ablex.
Baillargeon, R. (2004). How do infants learn about the physical world? Current Directions in Psychological Science, 3, 133-140.
Baillargeon, R., Spelke, E.S., and Wasserman, S. (1985). Object permanence in five-month-old infants. Cognition, 20, 191-208.
Baron-Cohen, S. (1995). Mindblindness: An essay on autism and theory of mind. Cambridge, MA: MIT Press.
Bartsch, K., and Wellman, H. (1989). Young children’s attribution of action to beliefs and desires. Child Development, 60, 946-964.
Bertamini, M., Spooner A., and Hecht, H. (2004). The representation of naive knowledge about physics. In G. Malcolm (Ed.), Multidisciplinary approaches to visual representations and interpretations. Amsterdam: Elsevier.
Bertenthal, B.I. (1993). Infants’ perception of biomechanical motions: Intrinsic image and knowledge-based constraints. In C. Granrud (Ed.), Visual perception and cognition in infancy (pp. 175-214). Hillsdale, NJ: Lawrence Erlbaum Asociates.
Booth, A.E., Pinto, J., and Bertenthal, B.I. (2002). Perception of the symmetrical patterning of human gait by infants. Developmental Psychology, 38(4), 554-563.
Bullock, M., Gelman, R., and Baillargeon, R. (1982). The development of causal reasoning. In W.J. Friedman (Ed.), The developmental psychology of time. New York: Academic Press.
Brown, D.E., and Clement, J. (1989). Overcoming misconceptions via analogical reasoning: Abstract transfer versus explanatory model construction. Instructional Science, 18, 237-261.
Bruner, J. (1964). The course of cognitive growth. American Psychologist, 19, 1-15.
Caramazza, A., McCloskey, M., and Green, B. (1981). Naive beliefs in “sophisticated” subjects: Misconceptions about trajectories of objects. Cognition, 9, 117-123.
Carey, S. (1985). Conceptual change in childhood. Cambridge, MA: MIT Press.
Carey, S. (1988). Conceptual differences between children and adults. Mind and Language, 3, 167-181.
Carey, S. (1991). Knowledge acquisition: Enrichment or conceptual change? In S. Carey and R. Gelman (Eds.), The epigenesis of mind: Essays on biology and cognition (pp. 257-291). Hillsdale, NJ: Lawrence Erlbaum Associates.
Chi, M.T.H. (2005). Commonsense conceptions of emergent processes: Why some misconceptions are robust. Journal of the Learning Sciences, 14(2), 161-199.
Clement, J. (1982). Students’ preconceptions in introductory mechanics. American Journal of Physics, 50, 66-71.
Cohen, L.B., and Cashon, C.H. (2006). Infant cognition. In W. Damon and R.M. Lerner (Eds.), Handbook of child psychology, 6th Edition. Hoboken, NJ: Wiley.
Csibra, G., Gergely, G., Biró, S., Koós, O., and Brockbank, M. (1999). Goal-attribution without agency cues: The perception of ‘pure reason’ in infancy. Cognition, 72, 237-267.
DeLoache, J.S. (1987). Rapid change in the symbolic functioning of very young children. Science, 238, 1556-1557.
DeLoache, J.S. (2004). Becoming symbol-minded. Trends in Cognitive Sciences, 8, 66-70.
DeLoache, J.S., Pierroutsakos, S.L., and Uttal, D.H. (2003). The origins of pictorial competence. Current Directions in Psychological Science, 12, 114-118.
Dickinson, L. (1987). Self-instruction in language learning. Cambridge, MA: Cambridge University Press.
diSessa, A.A. (2004). Metarepresentation: Native competence and targets for instruction. Cognition and Instruction, 22(3), 293-331.
Doran, R.L. (1972). Misconceptions of selected science held by elementary school students. Journal of Research in Science Teaching, 9, 127-137.
Driver, R., Leach, J., Millar, R., and Scott, P. (1996). Young people’s images of science. Buckingham, England: Open University Press.
Driver, R., Squires, A., Rushworth, P., and Wood-Robinson, V. (1994). Making sense of secondary science: Research into children’s ideas. New York: Routledge.
Duschl, R. (2000). Making the nature of science explicit. In R. Millar, J. Leech, and J. Osborne (Eds.), Improving science education: The contribution of research (pp. 187-206). Philadelphia, PA: Open University Press.
Espinoza, F. (2005). Experience conflicts with and undermines instruction and its legacy: Examples from two-dimensional motion. Physics Education, 40(3), 274-280.
Flavell, J. (1971). Stage-related properties of cognitive development. Cognitive Psychology, 2, 421-453.
Flavell, J.H. (1999). Cognitive development: Children’s knowledge about the mind. Annual Review of Psychology, 16, 21.
Freeman, N.H, Hood, B.M., and Meehan, C. (2004). Young children who abandon error behaviorally still have to free themselves mentally: A retrospective test for inhibition in intuitive physics. Developmental Science, 7, 277-282.
Gellert, E. (1962). Children’s conceptions of the content and function of the human body. Genetic Psychology Monographs, 65, 293-405.
Gelman, R., and Baillargeon, R. (1983). A review of some Piagetian concepts. In J.H. Flavell and E.M. Markman (Eds.), Handbook of child psychology (vol. 3, pp. 167-230). Hoboken, NJ: Wiley.
Gelman, R., Durgin, F., and Kaufman, L. (1995). Distinguishing between animates and inanimates: Not by motion alone. In D. Sperber, D. Premack, and A.J. Premack (Eds.), Causal cognition: A multidisciplinary debate (pp. 150-184). Oxford, England: Clarendon Press.
Gelman, R., and Lucariello, J. (2002). Role of learning in cognitive development. In H. Pashler (Series Ed.) and R. Gallistel (Vol. Ed.), Stevens’ handbook of experimental psychology: Learning, motivation, and emotion (vol. 3, 3rd ed., pp. 395-443). Hoboken, NJ: Wiley.
Gelman, S.A. (2003). The essential child: Origins of essentialism in everyday thought. Oxford, England: Oxford University Press.
Gelman, S.A., and Hirschfeld, L.A. (1999). How biological is essentialism? In D.L. Medin and S. Atran (Eds.), Folkbiology(pp. 403-446). Cambridge, MA: MIT Press.
Gelman, S., and Kalish, C. (2005). Conceptual development. In R.S. Siegler and D. Kuhn (Eds.), Handbook of child psychology volume 2, cognition, perception, and language, 6th edition (pp. 687-733). Hoboken, NJ: Wiley.
Gelman, S.A., and Markman, E. (1986). Categories and induction in young children. Cognition, 23, 183-209.
Gelman, S.A., and Markman, E.M. (1987). Young children’s inductions from natural kinds: The role of categories and appearances. Child Development, 58, 1532-1541.
Gergeley, G., Nadasdy, Z., Csibra, G., and Biro, S. (1995). Taking the intentional stance at 12 months of age. Cognition, 56, 165-193.
Gimenez, M., and Harris, P.L. (2002). Understanding constraints on inheritance: Evidence for biological thinking in early childhood. British Journal of Developmental Psychology, 20, 307-324.
Gopnik, A., Glymour, C., Sobel, D., Schulz, L., Kushnir, T., and Danks, D. (2004). A theory of causal learning in children: Causal maps and Bayes nets. Psychological Review, 111, 1-31.
Gopnik, A., and Sobel, D.M. (2000). Detecting blickets: How young children use information about novel causal powers in categorization and induction. Child Development, 71, 1205-1222.
Gopnik, A., Sobel, D.M., Schulz, L., and Glymour, C. (2001). Causal learning mechanisms in very young children: Two, three, and four-year-olds infer causal relations from patterns of variation and covariation. Developmental Psychology, 37, 620-629.
Gopnik, A., and Wellman, H. (1994). The “theory theory.” In L. Hirschfield and S. Gelman (Eds.), Domain specificity in culture and cognition. New York: Cambridge University Press.
Gotwals, A., and Songer, N. (2006). Measuring students’ scientific content and inquiry reasoning. In S. Barab and K. Hay (Eds.), Proceedings of the international conference of the learning sciences. Ann Arbor: University of Michigan Press.
Greif, M., Nelson, D., Keil, F., and Gutierrez, F. (2006). What do children want to know about animals and artifacts? Domain-specific requests for information. Psychological Science, 17(6), 455-459.
Griffiths, T.L., Baraff, E.R., and Tenenbaum, J.B. (2004). Using physical theories to infer hidden causal structure. In K. Forbes, D. Gentner, and J. Regier (Eds.), Proceedings of the 26th annual meeting of the cognitive science society (pp. 500-505). Mahwah, NJ: Lawrence Erlbaum Associates.
Grosslight, L., Unger, C., Jay, E., and Smith, C. (1991). Understanding models and their use in science: Conceptions of middle and high school students and experts. Journal of Research in Science Teaching, 28(9), 799-822.
Gutheil, C., Vera, A., and Keil, F.C. (1998). Do houseflies think? Patterns of induction and biological beliefs in development. Cognition, 66(1), 33-49.
Harris, P. (2002). What do children learn from testimony? In P. Carruthers, S. Stich, and M. Siegal (Eds.), The cognitive basis of science (pp. 316-334). New York: Cambridge University Press.
Harris, P., Johnson, C.N., Hutton, D., Andrews, G., and Cooke, T. (1989). Young children’s theory of mind and emotion. Cognition and Emotion, 3, 379-400.
Hecht, H.H., and Bertamini, M. (2000). Understanding projectile acceleration. Journal of Experimental Psychology: Human Perception and Performance, 26(2), 730-746.
Heyman, G.D., Phillips, A.T., and Gelman, S.A. (2003). Children’s reasoning about physics within and across ontological kinds. Cognition, 89(1), 43-61.
Hickling, A., and Gelman, S. (1995). How does your garden grow? Evidence of an early conception of plants as biological kinds. Child Development, 66, 856-876.
Hickling, A.K., and Wellman, H.M. (2001). The emergence of children’s causal explanations and theories: Evidence from everyday conversation. Developmental Psychology, 5, 668-683.
Hood, B.M. (2004). Children’s understanding of the physical world. In R.L. Gregory (Ed.), The Oxford companion to the mind, 2nd edition. New York: Oxford University Press.
Imai, M., and Gentner, D. (1997). A crosslinguistic study of early word meaning: Universal ontology and linguistic influence. Cognition, 62, 169-200.
Inagaki, K., and Hatano, G. (2002) Young children’s naïve thinking about the biological world. New York: Psychology Press.
Inagaki, K., and Hatano, G. (2006). Young children’s conception of the biological world. Current Directions in Psychological Science, 15(4), 177.
Ioannides, C.H., and Vosniadou, S. (2002). The changing meanings of force. Cognitive Science Quarterly, 2(1), 5-62.
Johnson, S.P. (2003). Theories of development of the object concept. In J.G. Bremner and A.M. Slater (Eds.), Theories of infant development (pp. 174-203). Cambridge, MA: Blackwell.
Johnson, S., and Carey, S. (1998). Knowledge enrichment and conceptual change in folkbiology: Evidence from Williams Syndrome. Cognitive Psychology, 37, 156-200.
Keen, R. (2003). Representation of objects and events: Why do infants look so smart and toddlers look so dumb? Current Directions in Psychological Science, 12, 79-83.
Keil, F.C. (1989). Concepts, kinds, and cognitive development. Cambridge, MA: MIT Press.
Keil, F.C. (1992). The origins of an autonomous biology. In M.R. Gunnar and M. Maratsos (Eds.), Modularity and constraints in language and cognition. The Minnesota Symposia on Child Psychology (vol. 25, pp. 103-137). Hillsdale, NJ: Lawrence Erlbaum Associates.
Keil, F.C. (2003). That’s life: Coming to understand biology. Human Development, 46, 369-377.
Keil, F.C., and Richardson, D.C. (1999). Species, stuff, and patterns of causation. In R. Wilson (Ed.), Species: New interdisciplinary essays (Chapter 10). Cambridge, MA: MIT Press.
Keil, F.C., Smith, C.S., Simons, D., and Levin, D. (1998). Two dogmas of conceptual empiricism. Cognition, 65, 103-135.
Kelemen, D. (1999). The scope of teleological thinking in preschool children. Cognition, 70(3), 241-272.
Klahr, D. (2000). Exploring science: The cognition and development of discovery processes. Cambridge, MA: MIT Press.
Kloos, H., and Keen, R. (2005). An exploration of toddlers’ problems in a search task. Infancy, 7(1), 7-34.
Koenig, M., Clement, F., and Harris, P. (2004). Trust in testimony: Children’s use of true and false statements. Psychological Science, 15(10), 694-698.
Koslowski, B. (1996). Theory and evidence: The development of scientific reasoning. Cambridge, MA: MIT Press.
Kotovsky, L., and Baillargeon, R. (1994). Calibration-based reasoning about collision events in 11-month-old infants. Cognition, 51, 107-129.
Krist, H., Fieberg, E.L., and Wilkening, F. (1993). Intuitive physics in action and judgment: The development of knowledge about projectile motion. Journal of Experimental Psychology: Learning Memory and Cognition, 19(4), 952-966.
Kuhlmeier, V., Bloom, P., and Wynn, K. (2005). Do 5-month-old infants see humans as material objects? Cognition, 94, 95-103.
Kuhn, D., and Pearsall, S. (2000). Developmental origins of scientific thinking. Journal of Cognition and Development, 1, 113-129.
Kushnir, T., and Gopnik, A. (2005). Young children infer casual strength from probabilities and interventions. Psychological Science, 16(9), 678-683.
Lawson, R. (in press). The science of cycology: Failures to understand how everyday objects work. Memory and Cognition.
Lee, O., Eichinger, D.C., Anderson, C.W., Berkheimer, G.D., and Blakeslee, T.D. (1993). Changing middle school students’ conceptions of matter and molecules. Journal of Research in Science Teaching, 30(3), 249-270.
Leevers, H.J., and Harris, P.L. (1999). Persisting effects of instruction on young children’s syllogistic reasoning with incongruent and abstract premises. Thinking and Reasoning, 5, 145-173.
Leevers, H.J., and Harris, P.L. (2000). Counterfactual syllogistic reasoning in normal 4-year-olds, children with learning disabilities, and children with autism. Journal of Experimental Child Psychology, 76, 64-87.
Lehrer, R., and Schauble, L. (2000). Inventing data structures for representational purposes: Elementary grade students’ classification models. Mathematical Thinking and Learning, 2, 51-74.
Lehrer, R., and Schauble, L. (2002). Symbolic communication in mathematics and science: Co-constituting inscription and thought. In J. Byrnes and E.D. Amsel, (Eds.), Language, literacy, and cognitive development: The development and consequences of symbolic communication (pp. 167- 192). Mahwah, NJ: Lawrence Erlbaum Associates.
Lehrer, R., Schauble, L., Strom, D., and Pligge, M. (2001). Similarity of form and substance: Modeling material kind. In D. Klahr and S. Carver (Eds.), Cognition and instruction: 25years of progress (pp. 39-74). Mahwah, NJ: Lawrence Erlbaum Associates.
Leslie, A.M. (1984). Spatiotemporal continuity and the perception of causality in infants. Perception, 13, 287-305.
Leslie, A.M. (1987). Pretense and representation: The origins of “theory of mind.” Psychological Review, 94, 412-426.
Leslie, A.M. (1994). ToMM, ToBY, and agency: Core architecture and domain specificity. In L.A. Hirschfeld and S.A. Gelman (Eds.), Mapping the mind: Domain specificity in cognition and culture (pp. 119-148). New York: Cambridge University Press.
Leslie, A.M., and Keeble, S. (1987) Do six-month-old infants perceive causality? Cognition, 25, 265-288.
Liben, L.S., Kastens, K.A., and Stevenson, L.M. (2002). Real-world knowledge through real-world maps: A developmental guide for navigating the educational terrain. Developmental Review, 22, 267-322.
Linn, M.C. (1978). Formal operations: Construct or conglomerate. Formal Operator, 1(4), 2-4.
Lockhart, K. (1981). The development of knowledge about uniformities in the environment: A comparative analysis of the child’s understanding of social, moral, and physical rules. Dissertation Abstracts International, 41(7-B), 2793.
Lopez, A., Atran, S., Coley, J.D., Medin, D.L., and Smith, E.E. (1997). The tree of life: Universal and cultural features of folkbiological taxonomies and induction. Cognitive Psychology, 32(3), 251-295.
Mandler, J.M. (2004). The foundations of mind: Origins of conceptual thought. Oxford, England: Oxford University Press.
Masnick, A.M., and Klahr, D. (2003). Error matters: An initial exploration of elementary school children’s understanding of experimental error. Journal of Cognition and Development, 4, 67-98.
Medin, D.L., Unsworth, S.J., and Hirschfeld, L. (in press). Cultures, categorization, and reasoning. In S. Kitayama and D. Cohen (Eds.), Handbook of cultural psychology. New York: Guilford Press.
Metz, K.E. (1995). Reassessment of developmental constraints on children’s science instruction. Review of Educational Research, 65, 93-127.
Mills, C., and Keil, F.C. (2005). The development of cynicism. Psychological Science, 16, 385-390.
Minstrell, J. (1983). Getting the facts straight. Science Teacher, 50(l), 52-54.
Minstrell, J. (1988). Teaching science for education. In L.B. Resnick and L.E. Klopfer (Eds.), Toward the thinking curriculum: ASCD yearbook. Hillsdale, NJ: Lawrence Erlbaum Associates.
Montgomery, D. (1992). Young children’s theory of knowing: The development of a folk epistemology. Developmental Review, 12, 410-430.
Munakata, Y., Casey, B.J., and Diamond, A. (2004). Developmental cognitive neuroscience: Progress and potential. Trends in Cognitive Science, 8, 122-128.
Munakata, Y., McClelland, J.L., Johnson, M.H., and Siegler, R. (1997). Rethinking infant knowledge: Toward an adaptive process account of successes and failures in object permanence tasks. Psychological Review, 104, 686-713.
Nagy, M.H. (1953). The representations of “germs” by children. Journal of Genetic Psychology, 83, 227-240.
National Research Council. (2000). How people learn: Brain, mind, experience, and school. Committee on Developments in the Science of Learning. J.D. Bransford, A.L. Brown, and R.R. Cocking (Eds.). Washington, DC: National Academy Press.
Newcombe, N., Huttenlocher, J., Drummey, A.B., and Wiley, J.G. (1998). The development of spatial location coding: Place learning and dead reckoning in the second and third years. Cognitive Development, 13, 185-201.
Nussbaum, J. (1979). Children’s conceptions of the earth as a cosmic body: A crossage study. Science Education, 63, 83-93.
Nussbaum, J. (1985). The particulate nature of matter in the gaseous phase. In R. Driver, E. Guesne, and A. Tiberghien (Eds.), Children’s ideas in science. Philadelphia, PA: Open University Press.
Nussbaum, J. and Novak, J.D. (1976). An assessment of children’s concepts of the earth utilizing structured interviews. Science Education, 60, 535-550.
Nussbaum, J. and Sharoni-Dagan, N. (1983). Changes in second grade children’s preconceptions about the earth as a cosmic body resulting from a short series of audio-tutorial lessons. Science Education, 67, 99-114.
Perner, J. (1991). Understanding the representational mind. Cambridge, MA: Bradford Books/MIT Press.
Perner, J., Leekam, S.R., and Wimmer, H. (1987). Three-year-olds’ difficulty with false belief: The case for a conceptual deficit. British Journal of Developmental Psychology, 5, 125-137.
Petrosino, A., Lehrer, R., and Schauble, L. (2003). Structuring error and experimental variation as distribution in the fourth grade. Mathematical Thinking and Learning, 5(2-3), 131-156.
Piaget, J., and Inhelder, B. (1974). The child’s construction of quantities. London, England: Routledge and Kegan Paul.
Pulos, S., and Linn, M.C. (1978). Pitfalls and pendulums. Formal Operator, 1(2), 9-11.
Rozenblit, L.R., and Keil, F.C. (2002). The misunderstood limits of folk science: An illusion of explanatory depth. Cognitive Science, 26, 521-562.
Samarapungavan, A., Vosniadou, S., and Brewer, W.F. (1996). Mental models of the earth, sun, and moon: Indian children’s cosmologies. Cognitive Development, 11, 491-521.
Santos, L.R., Hauser, M.D., and Spelke, E.S. (2002). Domain-specific knowledge in human children and non-human primates: Artifact and food kinds. In M. Bekoff (Ed.), The cognitive animal. Cambridge, MA: MIT Press.
Saxe, R., Tenenbaum, J.B., and Carey, S. (2005). Inferences about hidden causes by 10 and 12 month old infants. Psychological Science, 16(12), 995-1001.
Scassellati, B., and Gold, K. (in press). Learning acceptable windows of contingency. Connection Science: Special Issue on Developmental Learning, (18)2.
Schulz, L., and Gopnik, A. (2004). Causal learning across domains. Developmental Psychology, 40(2), 162-176.
Shanon, B. (1976). Aristotelianism, Newtonianism and the physics of the layman. Perception, 5, 241-243.
Shultz, T.R. (1982). Rules of causal attribution. Monographs of the Society for Research in Child Development, 47(1).
Simons, D.J., and Keil, F. (1995). An abstract to concrete shift in the development of biological thought: The insides story. Cognition, 56, 129-163.
Smith, C., Carey, S., and Wiser, M. (1985). On differentiation: A case study of the development of size, weight, and density. Cognition, 21(3), 177-237.
Smith, C., Maclin, D., Grosslight, L., and Davis, H. (1997). Teaching for understanding: A study of students’ preinstruction theories of matter and a comparison of the effectiveness of two approaches to teaching students about matter and density. Cognition and Instruction, 15, 317-393.
Smith, C., Solomon, G., and Carey, S. (2005). Never getting to zero: Elementary school students’ understanding of the infinite divisibility of number and matter. Cognitive Psychology, 51(2), 101-140.
Smith, C.L., Wiser, M., Anderson, C.W., and Krajcik, J. (2006). Implications of research on children’s learning for standards and assessment: A proposed learning progression for matter and the atomic molecular theory. Measurement: Interdisciplinary Research and Perspectives, 4(1-2), Focus Article.
Smith, J., di Sessa, A., and Roschelle, J. (1993). Misconceptions reconceived: A constructivist analysis of knowledge in transition. Journal of the Learning Sciences, 3, 115-163.
Sodian, B., and Wimmer, H. (1987). Children’s understanding of inference as a source of knowledge. Child Development, 58, 424-433.
Sodian, B., Zaitchik, D., and Carey, S. (1991). Young children’s differentiation of hypothetical beliefs from evidence. Child Development, 62(4), 753-766.
Soja, N.N., Carey, S., and Spelke, E.S. (1992). Ontological categories guide young children’s inductions of word meaning: Object terms and substance terms. Cognition, 43(1), 85-91.
Spelke, E.S. (1991). Physical knowledge in infancy: Reflections on Piaget’s theory. In S. Carey and R. Gelman (Eds.), The epigenesis of mind: Essays on biology and cognition (pp. 133-169). Hillsdale, NJ: Lawrence Erlbaum Associates.
Spelke E.S., Katz, G., Purcell, S.E., Ehrlich, S.M., and Breinlinger, K. (1992). Early knowledge of object motion: Continuity and inertia. Cognition, 51, 131-176.
Spelke, E.S., and Kyeong, K.I. (1992). Infants’ sensitivity to effects of gravity on visible object motion. Journal of Experimental Psychology: Human Perception and Performance, 8(2), 385-393.
Spelke, S.S., Phillips, A.T., and Woodward, A.L. (1995). Infants’ knowledge of object motion and human action. In A. Premack (Ed.), Causal understanding in cognition and culture (pp. 47-78). Oxford, England: Clarendon Press.
Springer, K., and Keil, F. (1989). On the development of biologically specific beliefs: The case of inheritance. Child Development, 60, 637-648.
Stavy, R. (1988). Children’s conception of gas. International Journal of Science Education, 10(5), 553-560.
Stavy, R. (1991). Children’s ideas about matter. School Science and Mathematics, 91(6), 240-244.
Stavy, R. (1995). Conceptual development of basic ideas in chemistry. In S. Glynn and R. Duit (Eds.), Learning science in the schools: Research reforming practice (pp. 131-154). Hillsdale, NJ: Lawrence Erlbaum Associates.
Taylor, M. (1988) Conceptual perspective taking: Children’s ability to distinguish what they know from what they see. Child Development, 59, 703-718.
Toyama, N. (2000). What are food and air like inside our bodies? Children’s thinking about digestion and respiration. International Journal of Behavioral Development, 24(2), 222-230.
Troseth, G.L. (2003). Getting a clear picture: Young children’s understanding of a televised image. Developmental Science, 6(3), 247-253.
Troseth, G.L., and DeLoache, J.S. (1998). The medium can obscure the message: Young children’s understanding of video. Child Development, 69, 950-965.
Troseth, G.L., Pierroutsakos, S.L., and DeLoache, J.S. (2004). From the innocent to the intelligent eye: The early development of pictorial competence. Advances in Child Development and Behavior, 32, 1-35.
Uttal, W.R. (2002). A behaviorist looks at form recognition. Mahwah, NJ: Lawrence Erlbaum Associates.
Vallortigara, G., Regolin, L., and Marconato, F. (2005). Visually inexperienced chicks exhibit spontaneous preference for biological motion patterns. PLoS Biology, 3(7), 1312-1316 (e208).
Viennot, L. (1979). Spontaneous reasoning in elementary dynamics. European Journal of Science Education, 1, 205-221.
Vosniadou, S. (1994). Capturing and modeling the process of conceptual change. Learning and Instruction, 4, 45-69.
Vosniadou, S., and Brewer, W.F. (1990). A cross-cultural investigation of children’s conceptions about the earth, the sun, and the moon: Greek and American data. In H. Mandl, E. DeCorte, N. Bennett, and H.F. Friedrich (Eds.), Learning and instruction: European research in an international context (pp. 605-629). Oxford, England: Pergamon Press.
Vosniadou, S., and Brewer, W.F. (1992). Mental models of the earth: A study of conceptual change in childhood. Cognitive Psychology, 24, 535-585.
Vosniadou, S., and Brewer, W.F. (1994). Mental models of the day/night cycle. Cognitive Science, 18, 123-183.
Vosniadou, S., and Ioannides, C. (1998). From conceptual development to science education: A psychological point of view. International Journal of Science Education, 20(10), 1213-1230.
Watson, J.S. (1979). Perception of contingency as a determinant of social responsiveness. In E.B. Thoman (Ed.), Origins of the infant’s social responsiveness (pp. 33-64). Hillsdale, NJ: Lawrence Erlbaum Associates.
Wellman, H.M. (1990). The child’s theory of mind. Cambridge, MA: MIT Press.
Werner, H., and Kaplan, B. (1963). Symbol formation: An organismic developmental approach to language and the expression of thought. Hoboken, NJ: Wiley.
Wimmer, H., and Perner, J. (1983). Beliefs about beliefs: Representations and constraining functions of wrong beliefs in young children’s understanding of deception. Cognition, 13, 103-128.
Woodward, A.L. (1998). Infants selectively encode the goal object of an actor’s reach. Cognition, 69(1), 1-34.
Woodward, A.L., Sommerville, J.A., and Guajardo, J.J. (2001). How infants make sense of intentional action. In B.F. Malle, L.J. Moses, and D.A. Baldwin (Eds.), Intentions and intentionality. Foundations of social cognition (pp. 149-170). Boston, MA: MIT Press.
Yoachim, C.M., and Meltzoff, A.N. (2003, October). Cause and effect in the mind of the preschool child. Poster presented at the biennial meeting of the Cognitive Development Society, Park City, UT.
Zimmer, C. (2004). Soul made flesh. New York: Free Press.