2
Key Questions in Particle Physics
Particle physics had relatively simple origins, beginning with the study of natural sources of particles, either radioactive atoms or cosmic rays from space. As one discovery led to another, surprises proliferated. New questions emerged, and newer and more powerful instruments were developed to answer them.
Now particle physics has advanced to the point that it can ask some very deep questions:
-
Can all the forces between particles be understood in a unified framework?
-
What do the properties of particles reveal about the nature and origin of matter and the properties of space and time?
-
What are dark matter and dark energy, and how has quantum mechanics influenced the structure of the universe?
Some of these questions have a long history going back to the earliest days of particle physics and even before that. Some of them are new questions raised by contemporary discoveries. What the questions have in common is that progress in experiment and theory has revealed new clues and created fundamentally new ways of answering them. The committee deals with each of these key questions in turn.1
CAN ALL THE FORCES BETWEEN PARTICLES BE UNDERSTOOD IN A UNIFIED FRAMEWORK?
Even in preindustrial times, people knew about static electricity, lodestones (or magnetized rocks), and light. From a modern point of view, this means that one of the fundamental forces of nature—electromagnetism—was observed without any modern technology. Of course, preindustrial people did not know that static electricity, magnetism, and light are different aspects of the same thing. This only became clear when James Clerk Maxwell combined electric and magnetic forces into the theory of electromagnetism in the mid-19th century. Maxwell’s equations—together with the discovery of the first elementary particle, the electron, in 1897—led to the invention of radio and, ultimately, to today’s electronic technologies.
One other fundamental force was known before the 20th century—gravity. Gravity is vastly weaker than the other forces—so weak that the gravitational forces between individual elementary particles are too small to observe. Yet the gravitational effects of many particles are cumulative. Thus for everyday objects gravity is clearly observable, and gravity is the dominant force for galaxies and in the universe as a whole today.
The advanced technology of the 20th century was required to discover and understand the two other forces that influence the behavior of particles. Some atoms decay radioactively by emitting electrons and neutrinos. In the 20th century these decays were shown to be the product of weak force interactions. The weak force—which is critically important in stellar processes, the formation of the elements beyond iron, and the evolution of the early universe—is just as fundamental as electromagnetism or gravity, but it is far less obvious in everyday experience.
Recognition of the strong, or nuclear, force resulted from research into the atomic nucleus. The nucleus consists of protons and neutrons that are bound together in a tiny ball. Protons have a positive electric charge, which makes them repel each other. However, something keeps the nucleus from flying apart. This something is the strong force.
Understanding the strong and weak forces depends centrally on quantum mechanics. In the 1920s, physicists began studying the properties and behaviors of particles, in part to understand the forces between them. This process culminated a half century later with the emergence of the Standard Model. The Standard Model, in a remarkably concise way, describes and explains many of the phenomena that underlie particle physics and captures with astonishing precision an incredible range of observational data.
The Standard Model has another important feature. It reveals a deep analogy between the four forces, in keeping with Einstein’s goal of unifying all of the
fundamental forces. All are described by similar equations. In the Standard Model, the electromagnetic force, weak interactions, and the strong force are described by equations called the Yang-Mills equations, which generalize Maxwell’s equations of electromagnetism. These Yang-Mills equations have a close analogy with Einstein’s equations of gravity in his general theory of relativity. Understanding the similarities and differences among these forces and their mathematical representations will be a key to realizing Einstein’s dream.
In the Standard Model, each force is carried by a different kind of particle. That is, forces are exerted by the exchange of certain particles between two objects. The photon, which is the basic quantum unit of light, carries the electromagnetic force. The weak force is carried by particles known as W and Z bosons. The strong force, now understood as the force that binds quarks to form particles such as protons and neutrons, is carried by particles known as gluons. Like quarks, gluons are not seen in isolation because of the strength of the forces binding them together. The gluons, therefore, must be observed indirectly, by the patterns of particle production that they cause in high-energy experiments. These patterns have been studied, and the results match the theory over a wide range of energies.
According to the Standard Model, electromagnetism and the weak force have a related origin, which is why the two are sometimes described as electroweak interactions. Electromagnetism is mediated by photons that obey Maxwell’s equations. Weak interactions are mediated by W and Z particles that obey the analogous Yang-Mills equations. The W and Z bosons have a very large mass—nearly one hundred times the mass of a proton. Why are the masses of the W and Z particles so large, whereas the photon has no mass? Why are the force-carrying particles so different, with the photon being detectable by our eyes while the W and Z particles can be observed only with the most sophisticated equipment? Settling this question, which would explain why the weak interactions are weak, is a major goal of particle physics for the coming decade.
To put the question differently, if the equations are so similar, why are the forces so different? According to the Standard Model, the mechanism for breaking the symmetry between the two forces is something called “spontaneous symmetry breaking” (see Box 2-1). Exactly how this symmetry breaking occurs remains unknown. This process determines which particle of the three (the photon, the W particle, the Z particle) remains massless while the others become massive. Furthermore, the theory predicts that there must be at least one more particle associated with the symmetry breaking. In the Standard Model, there is a single such particle: the Higgs boson. The field associated with this particle gives mass to matter by acting as a kind of invisible quantum liquid that fills the universe. Interactions with this quantum liquid give all particles mass. Heavier objects, such as the W and Z particles, are more strongly affected by the Higgs field, lighter ones
|
BOX 2-1 Symmetry Breaking One of the most important concepts in physics is spontaneous symmetry breaking. The laws of nature often have a good deal more symmetry than the phenomena that we actually observe. The reason is that the lowest energy state of a system often does not have the full symmetry inherent in the laws. An example is provided by a ball placed at the top of a sombrero, as in Figure 2-1-1. 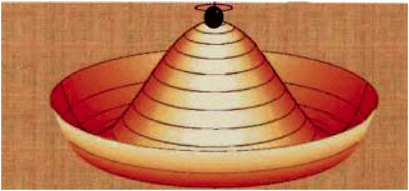 FIGURE 2-1-1 An example of spontaneous symmetry breaking. |
interact less with it, and massless particles like the photon slip through the field without feeling it at all.
The Higgs particle, which is the particle associated with the Higgs field, has not yet been seen. One major goal of upcoming accelerator experiments is to discover whether a simple Higgs particle causes the breaking of the symmetry between the weak interactions and electromagnetism, as in the Standard Model, or whether there is some more complicated mechanism. The mass of the Higgs particle (or whatever breaks the electroweak symmetry) can be roughly estimated. The masses of the W and Z particles are 80 and 91 GeV. (GeV refers to giga-electron volts, which is a way of describing the mass of a particle in terms of its energy equivalent; 1 GeV is approximately the mass of a proton, and 1,000 GeV equals 1 TeV.) Existing accelerators would have observed the Higgs particle if its mass had been less than 115 GeV and if it decayed as predicted by the Standard Model. Since it has not been observed, it must be more massive than that. However, the Standard
|
When the ball sits on top of the hill, the configuration is symmetric—the ball and the hat appear identical from all sides. But the ball won’t stay perched at the top for very long! To lower the system’s energy, the ball will roll down the hill in one direction or another. It could roll in any direction, but it has to pick some direction: At that point, the symmetry becomes broken. Spontaneous symmetry breaking describes a system where the lowest energy state has less symmetry than the equations that describe that system. Nature has many other examples. Another easy one to picture is a broom handle that is balanced, standing vertically on one end on a flat (circular) table. The equations that describe this system are completely symmetric with respect to rotations about the axis defined by the vertical broom, but when the broom falls over, it must fall in some direction and thus break this symmetry spontaneously. Likewise, any chunk of magnetized iron is an example of spontaneous symmetry breaking. When the iron is molten the spins of the individual atoms point in all directions and the equations describing their interactions have rotational symmetry, but as the iron cools it has a lowest energy state in which the spins are predominantly aligned in some direction, giving the iron a magnetic axis that breaks the rotational symmetry. The symmetry that is broken in particle physics is the symmetry between the different particle types of the electroweak force—the photon, the W boson, and the Z boson. Experimentally, they look completely different. We see photons with our eyes, but it takes accelerators to detect W and Z bosons. Yet the fundamental equations describing these different particles (and the forces they mediate) are almost the same. The difference is largely responsible for the nature of our universe. As go the particles, so go the forces that they mediate. Because of the symmetry breaking between the photons and the W and Z boson, electricity (mediated by the photon) is the basis of the modern world, and weak forces (mediated by the W and Z bosons) are mostly hidden inside individual atoms. By discovering the Higgs particle at accelerators, or possibly something more complex, physicists hope to learn how nature broke the symmetry between the different particles and forces. |
Model is mathematically inconsistent if the Higgs particle—or whatever replaces it—is too much heavier than the W and Z. Thus, combined with experimental measurements, the Higgs particle should weigh no more than around 300 GeV. It may be within reach of experiments at Fermilab’s Tevatron, and it is certainly within reach of the Large Hadron Collider (LHC) currently being constructed at CERN.
Two more potentially important approaches to unifying the particle forces are “grand unification” and “supersymmetry.” These ideas, which are explained in more detail below, are responsible for a good deal of the excitement about potential new discoveries at the Terascale.
Grand unification is the idea that all three of the Standard Model interactions (the weak, electromagnetic, and strong forces) are different aspects of a single larger set of interactions that has a larger, but spontaneously broken, symmetry. One powerful argument in favor of this idea is that the coupling strengths of the
different interactions change with energy, and all appear to become roughly the same at a very high energy scale. Furthermore, the distinct types of particles observed in nature fit together beautifully in the larger symmetry patterns predicted by grand unification. Some signatures of grand unification may be accessible to experimental study at the Terascale, and others are best investigated by experiments that probe neutrino masses, the polarization of the cosmic microwave radiation, proton decay, and other rare or unusual phenomena.
Supersymmetry is a new type of symmetry that uses quantum variables to describe space and time. If supersymmetry is a symmetry of our world, space and time have new quantum dimensions as well as the familiar dimensions that we see in everyday life. Ordinary particles vibrating in the new quantum dimensions would then appear as new elementary particles, which could be detected using accelerators. Supersymmetry suggests that every known particle has an as-yet-undiscovered superpartner particle. If the symmetry were exact, the partners would have mass equal to that of the observed particles. This is not the case (or the superpartners would already have been observed), so this symmetry, too, must be broken.
Why do particle physicists think that supersymmetry is likely to be correct? The reason is that without it, it is very hard to understand how the scale of electroweak symmetry breaking (characterized by the W, Z, and Higgs boson masses) can be so small compared to the scale of possible unification, where the strengths of the strong, weak, and electromagnetic forces become equal. That is, above the scale of symmetry breaking between the electromagnetic and weak forces, one would expect the strengths of the forces to be equivalent, but this only happens at a much higher energy scale. Thus, supersymmetry makes it possible to understand why the W and Z have masses around 100 GeV. In addition, supersymmetry makes the unification of the three couplings occur more precisely. Of the superpartners predicted by supersymmetry, the lightest neutral superpartner particle, a neutralino, is thought to be an excellent candidate to account for some or all of the dark matter in the universe. Theoretical arguments strongly suggest that some of the new supersymmetric particles will be produced at the LHC. Supersymmetry is one of the most stimulating and challenging new ideas that physicists will be exploring in the Terascale regime.
There is one more important force in nature that is not usually regarded as a particle force, because its effects are unmeasurably small for individual elementary particles. This is gravity, which is the dominant force for stars, galaxies, and the universe as a whole but is so weak at the atomic level that it is not included in the Standard Model. Nevertheless, gravity is actually very similar to the other forces in that the mathematics of the Standard Model is stunningly similar to the math-
|
BOX 2-2 String Theory An idea that may someday result in a full unification of all the forces appeared on the scene in the 1970s. Known as string theory, the idea in its most naïve form says that an elementary particle is not a point particle but a loop or a strand of vibrating string. Like a violin or piano string, one of these strings can vibrate with many different shapes or forms. In string theory the different forms of vibration of the string correspond to the various elementary particles—electrons, neutrinos, quarks, W particles, and so on. Unification of all forms of matter and of all the forces is achieved because the different matter particles and the carriers of the forces all arise from different forms of vibration of the same string. Can string theory be tested? One testable idea associated with string theory is supersymmetry. Supersymmetry can exist without string theory, but string theories almost always have supersymmetry, and, indeed, the idea arose from early string theory work. Discovering the superpartner particles associated with supersymmetry at accelerators would help update relativity in the light of quantum mechanics and would give a major boost to string theory. |
ematics used to describe gravity in Einstein’s general theory of relativity. Thus, in contemporary physics, all the known forces are described in very similar ways.
Are these forces merely similar, or does this similarity point toward a truly unified theory that includes gravity as well as the particle forces? Within the usual theoretical framework, the differences lead to an impasse, and no combination of the two theories, the Standard Model and Einstein’s general relativity, can be found. Understanding how to combine quantum mechanics and gravity is one of the goals of string theory (see Box 2-2). Combining quantum mechanics and gravity and finding ways to experimentally test these ideas are big challenges. Yet these challenges must be met to understand the development of the universe.
WHAT DO THE PROPERTIES OF PARTICLES REVEAL ABOUT THE NATURE AND ORIGIN OF MATTER AND THE PROPERTIES OF SPACE AND TIME?
Though particle physics focuses on the fundamental particles of the universe, it involves far more than just developing a taxonomy of esoteric phenomena studied in accelerator laboratories. An underlying quest of particle physics has been to understand how the detailed properties of particles and their interactions have influenced (and, in turn, been influenced by) the evolution of the cosmos.
At the beginning of the 20th century, the electron, which had just been discovered, was the only known particle that is today considered elementary. But the newly discovered phenomenon of atomic radioactivity gave physicists their first
access to particles that, by the standards of the day, had high energies. (The energy of a particle emitted by a radioactive atom is about a million times greater than the energy of an electron that comes from a battery—and it is a million times smaller than the highest energy reached in modern particle accelerators.) With particle beams from naturally occurring radioactive sources, physicists made a host of major discoveries. The atomic nucleus, the proton, and the neutron all were discovered in this way, and the existence of the neutrino was inferred from studies of atomic radioactivity.
A new source of naturally occurring particles was discovered in 1912: Earth is constantly bombarded with cosmic rays from space. Besides giving physicists a fascinating new window from which to explore the universe, cosmic rays made possible fundamental discoveries about nature, mainly because cosmic rays have higher energies than do the particles emitted by radioactive atoms. The first antimatter particle, the positron (which is the antiparticle of the electron), was discovered in cosmic rays in 1932. Other important particles, including the muon, the pion, and the first strange particles, were discovered in cosmic rays in the 1940s and 1950s.
By then it was clear that many surprises lurked in the subatomic world. Beginning in the 1950s, man-made particle accelerators made it possible to achieve a combination of high energy and precision that could not be reached with naturally occurring particle sources. The first results brought chaos in the 1950s and the 1960s, as accelerators discovered literally hundreds of new kinds of particles that experience the strong force that holds the atomic nucleus together. All these particles are cousins of the familiar proton and neutron, which are the building blocks of atomic nuclei.
The Standard Model, which emerged in the early 1970s, brought some order to this chaos (see Box 2-3). According to the Standard Model, the multitude of particles arises by combining in many different ways a much smaller number of more fundamental entities called quarks. The strong force, which is mediated by particles known as gluons, binds the quarks together to form protons, neutrons, and other strongly interacting particles. Within atomic nuclei, the strong force arises as a consequence of the quarks and gluons in one neutron or proton interacting with those of another. The existence of quarks was confirmed in electron scattering experiments at the Stanford Linear Accelerator Center (SLAC) and in neutrino scattering experiments at CERN in the early 1970s. The gluon particle that binds together quarks was discovered at the Deutsches Elektronen-Synchrotron laboratory (DESY) in Germany in 1979.
Reinterpreting the multitude of particles produced at accelerators in terms of quarks and gluons gave a simpler explanation of how nature works. It also gave an entirely new foundation for thinking about unification of the forces of nature.
|
BOX 2-3 Particles in the Standard Model The Standard Model contains six quarks with the names up (u), down (d), charm (c), strange (s), top (t), and bottom (b). The quarks are classified into three families or generations. The Standard Model also contains three electrically charged leptons—the electron (e), the muon (µ), and the tau (τ)—and three uncharged neutrinos (νe, νµ, and ντ) (see Figure 2-3-1). The particles in each higher generation are identical to the particles in the previous generation except they have higher masses and quickly decay into other particles. Understanding why there are three generations is an open question. Experimental evidence suggests there can only be three light neutrinos and so only three generations of particles. At the same time, quantum mechanics shows that three generations is the minimum number that can accommodate a mechanism known as CP violation, which allows matter and antimatter to behave slightly differently and which may have been critical in the formation and evolution of the universe. 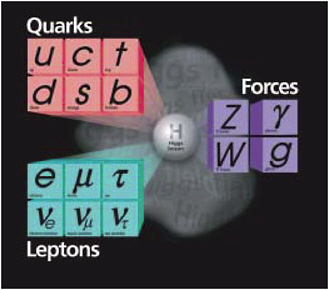 FIGURE 2-3-1 The particles of the Standard Model. Recent discoveries about neutrinos indicate that this picture of the Standard Model must be revised. The neutrino states (the νe, νµ, and ντ) in this old version are now understood not to be particles with definite mass like their partners in each generation, the quarks and charged leptons. Instead, the νe, νµ, and ντ are mixtures (combinations) of definite-mass neutrinos, which leads to the phenomenon of neutrino oscillations, which has recently been established experimentally. This discovery requires the first significant revision of the Standard Model in decades. Courtesy of Fermilab Visual Media Services. |
Quarks obey equations similar to the equations obeyed by electrons, and gluons obey equations similar to the equations obeyed by photons, or light waves. The analogy was further improved when the CERN accelerator in 1983 discovered the W and Z particles, which are responsible for the weak atomic force and obey the same sort of equations as gluons or photons. At DESY in the 1990s, the properties of the strong force and the numbers and energy distributions of quarks and gluons in high-speed protons were measured with great precision; these results have been important inputs into the expectations for LHC physics. Again, new discoveries made at high energies showed that at a fundamental level the different forces are all very similar, giving physicists a new foundation for seeking to unify the laws of nature.
The Standard Model further reduces the observed complexity of particles by organizing quarks and leptons (the most familiar of which is the electron) into three “generations.” The first generation contains the particles making up ordinary atoms—the up and down quarks and the electron, along with a more elusive entity called the electron neutrino. Such neutrinos are created in the radioactive decays of certain types of nuclei. Neutrinos interact so weakly with matter that when they were first hypothesized in the 1930s, physicists thought they would be undetectable. The invention of nuclear reactors changed the situation by making available intense sources of electron antineutrinos, leading to the detection of the neutrino in 1955.
One generation of particles would suffice to construct ordinary matter. Oddly, nature repeats itself with two more generations of particles. These additional particles, which are short-lived, are usually only produced in high-energy collisions and detected by their decay remnants. While they are subject to precisely the same forces as the first-generation particles, they decay so quickly that they are harder to study. But in the early universe they appear to have been just as important as the first-generation particles. Physicists do not yet understand why particle generations exist, much less why there are three of them.
It is, however, believed that the number of generations is precisely three. The best indication of this comes from studies of the Z particle, which carries the weak force. All types of neutrinos can be produced when the Z particle decays, provided that they are less massive than half the Z mass. The pattern of Z production and decay shows that it decays into only three types of neutrinos, so a fourth neutrino type can exist only if it is very heavy. The amount of helium produced in the early universe is also sensitive to the number of neutrino types, and measurements of this abundance are consistent with the existence of just three types of light neutrinos. Since all known neutrino types are very light, this tells us that there is no fourth generation of particles that follows the same pattern as the first three with a very light neutrino.
First-generation particles are present all around us in ordinary matter. But how do we know about the other two generations? The discovery of the second generation began in the 1930s and 1940s, when the muon and mesons, which consist of a quark and an antiquark, were discovered in cosmic rays. When these high-energy particles from space strike the atmosphere, the collisions are energetic enough to produce many mesons containing the second-generation strange quark. The mesons then decay, many of them by a weak interaction process that produces a muon and a neutrino.
In the 1950s, particle accelerators with enough energy to create second-generation particles were built for studying the behavior of particles in controlled experiments. By 1962, using high-energy neutrino beams created at accelerators, the second-generation neutrino was discovered; an experiment at Brookhaven National Laboratory demonstrated that the neutrinos created along with muons in meson decays are distinct from the first-generation neutrinos created in decays of radioactive atoms. The discovery of the second generation was completed when evidence for the charm quark was found at particle accelerators, beginning with the discovery of the J/Ψ particle (which consists of a charm quark and an anticharm quark) in November 1974 at SLAC and Brookhaven.
Experimental discovery of the third generation began when the tau lepton was discovered in 1975 at SLAC, after which particles containing the bottom quark were discovered in 1977 at Fermilab and at Cornell. Once the tau lepton and bottom quark were observed, the search began for the third-generation top quark. But what would it weigh? All that was known was that the top quark would have to be heavier than the bottom quark, or it would have been found at the energy levels already explored. The bottom quark weighs about 5 GeV, or about five times the mass of the proton (which contains three of the much lighter quarks).
By the early 1990s, experiments provided an indirect estimate of the mass of the top quark. Even if a particle is not produced in a given reaction, it can influence that reaction through quantum effects. According to quantum mechanics, particles and their antiparticles can wink in and out of existence for unobservably short times, thereby producing small but measurable effects on particle interactions. By the early 1990s, the data on the properties of Z bosons were precise enough to be sensitive to quantum effects due to top quarks. This led to an estimate that the top quark’s mass was 150 to 200 GeV. For a mass outside this range, the measurements could not fit with Standard Model predictions.
This mass range was just barely in reach of the Tevatron, and in 1995 the top quark was discovered at Fermilab, with a mass since measured to be 174 GeV. The initial discovery was based on just a few dozen events, in which a top quark and antiquark were produced and decayed to other particles, including bottom quarks and leptons, in a characteristic and expected pattern.
Completion of the third generation required confirmation that the third generation has its own neutrino type. Thus, the neutrino produced in association with a tau particle should make only tau particles when it interacts with a W particle. This confirmation was achieved at Fermilab in 2000. With the tau neutrino observation, three of the four particles of the Standard Model’s third generation had been discovered at Fermilab.
Observing neutrino effects is hard, but an even bigger challenge for particle physics has been to detect and measure the masses of the neutrinos. Those masses still have not been precisely determined, yet they are suspected to be very important clues about particle unification. There are several approaches to detecting neutrino masses, the most sensitive of which depends on the fact that there are multiple types of neutrinos. If neutrinos have mass, a quantum mechanical effect known as “neutrino oscillations” can come into play. As a neutrino of one type travels through space, it can spontaneously convert to another type. For example, a muon neutrino can convert spontaneously to a tau neutrino or to an electron neutrino. Later it can revert to being a muon neutrino, which is why neutrino types are said to oscillate. The probability for oscillation depends on the differences in the masses between the neutrinos, and it takes very large distances for these changes to occur with a high probability.
Neutrinos created in the sun travel 93 million miles before they reach Earth, which makes them likely candidates to undergo oscillations. Beginning with pioneering measurements made almost 40 years ago in the Homestake Gold Mine in South Dakota, every measurement of the number of electron neutrinos reaching Earth from the sun has given an unexpectedly small result. Subsequent observations, notably in laboratories in Japan and Canada, have found similar anomalies in the properties of neutrinos created in Earth’s atmosphere by cosmic rays, neutrinos from nuclear reactors, and neutrinos produced in accelerators. All these observations are understood today in terms of neutrino masses and oscillations.
When the second generation first emerged—with the discovery of the muon in cosmic rays—it fell from the sky to everyone’s surprise. I.I. Rabi famously asked: “Who ordered that?” By contrast, the existence of a third generation was suggested in advance as a possible explanation of what is called CP violation (see below).
One of the surprising predictions from combining quantum mechanics with special relativity is the existence of antimatter. Antimatter was first discovered in cosmic rays as antielectrons (positrons). The antiproton was first created artificially at one of the early high-energy accelerators, the Lawrence Berkeley National Laboratory Bevatron. For every type of particle, there is a corresponding antiparticle with the same mass and spin but with opposite electric charge. When particle and antiparticle meet, they can annihilate into radiation. The laws of physics for
matter and antimatter are very similar, but in the universe today there is lots of matter and very little antimatter. The reason for this is a mystery.
In 1964 it was discovered at Brookhaven that matter and antimatter behave slightly differently. In this experiment, scientists prepared a beam of kaon particles such that it was about half matter and half antimatter. By carefully studying the particles, they observed that the matter particles behaved differently than the antimatter ones (see Box 2-4). This discovery was a great surprise, not only because it violated the presumed equivalence of matter and antimatter but also because it
|
BOX 2-4 Sakharov, Antimatter, and Proton Decay Andrei Sakharov (1921-1989) is best known to the general public as the architect of the Soviet nuclear bomb who later became a fearless advocate of human rights and peace. The Nobel peace prize committee called him “a spokesman for the conscience of mankind.” Many credit him with helping to end the cold war. Sakharov also conceived the idea of building a toroidal magnetic coil (tokamak) to generate fusion energy. This is a key concept behind the current international fusion energy collaboration known as ITER. But particle physicists also know Sakharov for a daring cosmological proposal he made in 1967. Sakharov wanted to explain why the universe seems to be filled with matter, while antimatter is nowhere to be seen—except when it is produced by cosmic rays or radioactive atoms. Since matter and antimatter seem to have equivalent properties, why is the universe filled with one and not the other? Sakharov’s concept was that the very early universe was filled with a huge density of matter and antimatter at a vast temperature. The temperature and the density that Sakharov assumed are far beyond anything that exists in the current universe, even at the center of stars or in particle accelerators. Then, Sakharov said, as the universe expanded and cooled, almost all of the matter and antimatter annihilated and disappeared. But a slight asymmetry developed, and as the antimatter annihilated, a tiny bit of matter remained. From that small remnant of the cosmos’s origin, according to Sakhavov, stars, planets, and people ultimately formed. For this to work, Sakharov showed, two very subtle particle physics effects would be needed. The first is a tiny asymmetry between the behavior of matter and antimatter that is known as CP violation. This had been discovered in 1964 at Brookhaven National Laboratory in careful studies of the decays of elementary particles known as kaons, or K particles. That discovery provided an important clue for Sakharov’s work. Intensive studies of CP violation continue to the present day, notably at the B factories at SLAC in California and at KEK in Japan. Sakharov boldly predicted a second subtle effect that is needed for his approach to cosmology to work: The proton cannot live forever. It must decay. Thus, all ordinary atoms (which contain protons in their nuclei) must ultimately decay. Intensive experimental searches for proton decay have not yet been successful. Yet, since Sakharov’s work, new reasons have emerged to suspect that the proton does decay. The search goes on. |
suggested a connection between the microphysics of elementary particles and the macrophysical question of the amount of antimatter in the universe. This small but fundamental asymmetry in physical laws between matter and antimatter is the above-mentioned CP (or charge parity) symmetry violation. Since then, important experiments at Fermilab in 1999 studied the kaon system further and confirmed the presence of CP violation not only in the behavior of the kaons but also in their decays.
The early universe was filled with matter and antimatter, and modern particle and cosmology theory strongly suggest that they both were equally represented. As the universe cooled, matter and antimatter annihilated each other. If the laws of nature had had perfect symmetry between matter and antimatter, the cooling universe would have maintained equal amounts of matter and antimatter, which would have been capable of completely annihilating into photons. By the time “ordinary” temperatures were reached (in this context, a million degrees is low enough), the matter and antimatter would all have disappeared, leaving only photons and dark matter. The result would have been a very dull universe.
Instead, the early universe seems to have produced a slight excess of matter over antimatter. After the bulk of the matter and antimatter annihilated each other, only this excess remained. Today the universe contains more than a billion photons for every proton, neutron, and electron. In the overall universe, therefore, the leftover matter is just a trace, but it has condensed into dense regions to form galaxies, stars, and planets.
In the Standard Model, CP violation cannot occur in a two-generation world; it requires a third generation. With the third generation included, the Standard Model leads to an elegant theory of CP violation. To test it effectively requires experiments with third-generation particles, because CP-violating effects are so tiny for the first two generations.
A particle called the B meson (a particle containing one b quark and one lighter quark or antiquark) is the right one for the job. Careful study at the Cornell Electron Storage Ring (CESR) and at the DORIS storage ring at DESY in Hamburg showed that the B meson can change into an anti-B meson (and back again) and that the bottom quark undergoes rare weak decays to an up quark, both of which are key if CP violation is to be observable. Furthermore, experiments at particle accelerators showed that the B meson survives a trillionth of a second before decaying, which is surprisingly long for such a massive particle. This is long enough for CP-violating effects to take place—and for them to be observed.
The critical advance in this area was the construction of “B factories” at SLAC and at KEK in Japan. A B factory is an electron-positron collider designed to create a very large number of B mesons. In fact, these accelerators have the greatest luminosity, measured by the rate of particle-antiparticle collisions, of any accelera-
tor ever built. This high rate is needed because the study of CP violation depends on recording many very rare particle decays.
The B factories incorporate novel techniques to make these experiments feasible. The beams are asymmetric (one of the colliding beams has more energy than the other), so that the resulting B particles are produced with high velocity. This makes it possible to measure the tiny times (corresponding to flight-length distances of a few hundred microns in the detector) involved in B particle decays. The B factories have made many important new measurements of CP violation. These measurements fit together exactly as expected by the Standard Model, providing a unique precision test of its predictions.2
However, although measurements of CP violation at the B factories matched the Standard Model, they cannot account for the asymmetry in the amounts of matter and antimatter in the universe. That is, cosmological observations about the relative abundances of matter and antimatter in the universe are not explained by Standard Model physics of the early universe.
Extremely precise measurements of parameters provide extremely sensitive tests of particle theory: Thus, extra precision has important dividends. There are several avenues to achieving greater precision. In some cases, greater precision is possible by collecting more data, which may require more intense particle beams, more sensitive equipment, or other technical advances. In other instances, one must develop new techniques of measurement or a capability for performing entirely new types of experiments.
Measurements of weak interactions over the past decade provide a good example of the usefulness of large data samples. Since electrons and positrons are relatively simple, well-understood particles, the greatest precision in testing detailed predictions often has come from experiments using them. At the beginning of the 1990s, the energy available in electron-positron collisions reached the mass of the Z particle. This energy became available in electron-positron collisions at the Stanford Linear Collider (SLC) at SLAC and at the Large Electron and Positron (LEP) collider at CERN with higher luminosity. After a few years of LEP data, measurements of Z particles became available based on millions of events rather than thousands.
|
2 |
The two experiments at Fermilab’s Tevatron, CDF and D0, have recently announced the first measurements of the mixing frequency for a special type of B particle, the Bs. These observations of the properties of this subatomic particle suggest that it oscillates between matter and antimatter in one of nature’s fastest rapid-fire processes—many trillions of times per second. Please see <http://www.fnal.gov/pub/presspass/press_releases/CDF_04-11-06.html> and <http://www.fnal.gov/pub/presspass/press_releases/DZeroB_s.html> for more information. |
Another improvement in precision measurements of the weak interactions came after 1995, when the energy of LEP was doubled by adding accelerating cavities to the machine. This made it possible to produce the W particle in pairs and to measure the mass and properties of the W more precisely. Along with measurements of the W and top quark masses at Fermilab, the production of W particles in pairs led to indirect estimates of the mass of the Higgs particle in the Standard Model, due to its quantum effects on these quantities. For all the pieces to fit together with a single set of Standard Model parameters, a Higgs particle must exist with a mass below about 300 GeV. If experiments at the LHC do not discover a Higgs particle within the expected range, the mechanism that produces particle masses must be more complicated than the hypothesis incorporating a single Higgs boson.
As the examples in the previous paragraphs demonstrate, precise measurements in particle physics do not always require the highest possible energies to probe for new physics effects (see Box 2-5). New particles or processes that can only be directly observed at very high energies can cause effects at lower energies. Such effects could change the decay properties of lighter particles containing strange, charm, or bottom quarks from the predictions of the Standard Model. As long as all the various measurements taken together fit Standard Model predictions, they also provide lower limits on the masses, or combinations of masses and couplings, of any particles that may exist at very high energies, because any such particles would contribute to all decays via these quantum effects.
Thus, precision measurements are windows onto energies far above those that can be created in the laboratory. By comparing the experimental measurements with predictions from the Standard Model, particle physicists look for tiny deviations from Standard Model predictions. Any such deviations can be interpreted as signals for particles not in the Standard Model that exist at a higher energy scale than is possible to produce directly at an accelerator. These deviations also could be interpreted as signals for new physical structures of the universe such as dimensions in addition to the three we observe with our eyes.
Experiments using beams of muons or kaons (which contain strange quarks) and experiments observing the decay of D mesons (which contain charm quarks) have ruled out some departures from the Standard Model as small as one part in a trillion, eliminating many models with unseen particles at masses up to the Terascale. Similarly, CESR and the B factories at SLAC and KEK have used decays of bottom quarks to rule out other hypotheses. Important limits on transitions from one type of charged lepton to another that do not include the expected types of neutrino partners have been established at HERA in Germany, the Los Alamos National Laboratory, and the Paul Scherrer Institute in Switzerland.
In a similar fashion, neutrino masses can be a window onto unknown physics
|
BOX 2-5 Magnetic Moments of the Leptons: A Precision Measurement Historically, one of the first very precise measurements in particle physics was the measurement of the magnetic moment of the electron in 1950, originally with a precision of about one part in a thousand. The electron has a tiny spin, like a quantum gyroscope, and also behaves as a tiny magnet, giving it a magnetic moment. Over the years, measurements of the electron’s magnetic moment have improved, as have theoretical calculations. Measurement of the magnetic moment is important because of the sensitivity to phenomena that are not yet understood; that is, the rare opportunity offered in measuring the magnetic moment is not only that experimentalists can extract a very precise value but that theorists can make a very precise prediction using the tools of the Standard Model. By comparing these two results (the observed value and the predicted value) to high precision, particle physicists have constructed a very sensitive test of the accuracy of the Standard Model. (In general, just because a theorist can make a prediction doesn’t mean an experimenter can prove whether that prediction is right or wrong!) The latest measurement of the electron magnetic moment, reported in 2004, has an accuracy of better than one part in a trillion, which is perhaps the greatest precision with which any physical quantity has ever been measured. This measurement does not require an accelerator. It is made with a single electron stored in a tabletop device, in which the electron can be manipulated and studied with great precision for a long time. Because this quantity also can be calculated in the Standard Model to a high level of precision, the data and theoretical calculations together provide one of the most sensitive tests available today of the form of the new physics and the precise constraints on it. The muon (the second-generation cousin of the electron) also has a magnetic moment. However, the techniques for measuring it are rather different, since muons are short-lived and can be produced only at accelerators. The most recent measurement of the muon magnetic moment, reported at Brookhaven in 2004, has a precision of about one part in ten billion, which also places this measure among the most precise in nature. Comparisons between the experimentally measured magnetic moments of the electron and muon and the precise predictions of the Standard Model place important restrictions on the allowed masses of the new particles predicted in some extensions of the Standard Model. |
occurring at high energy scales. Nonzero neutrino masses can be accommodated through models that contain new and as-yet-undiscovered particles. Detailed studies of the patterns of neutrino masses can give insight into physics at the high energy scales where these new particles are presumed to exist. Such particles are a necessary component of some models of unified forces and are predicted to exist at an energy scale far past the range of any foreseeable accelerator. Neutrino masses also open the door to CP violation in the neutrino world, similar to that already seen in the quark sector. This understanding of CP violation in the neutrino sector may lead to new explanations of how matter came to dominate antimatter in the early universe.
WHAT ARE DARK ENERGY AND DARK MATTER AND HOW HAS QUANTUM MECHANICS INFLUENCED THE STRUCTURE OF THE UNIVERSE?
Astronomers looking at the night sky used to assume that what they saw was pretty much what there was. Then, in 1933, astronomers studied the motion of galaxies and found that they were moving much faster than could be explained by the known gravitational forces due to other nearby galaxies. This was the beginning of the dark matter problem. To account for the unexpectedly rapid motion of the galaxies—and, as later became clear, the rapid motion of individual stars making up galaxies—one must assume that galaxies are surrounded by clouds of dark matter. In recent times, scientists have found more and more ways to observe the gravitational effects of dark matter but have not yet learned what the dark matter is. All that is known for sure about the dark matter cloud surrounding a galaxy is that, typically, it is considerably larger and heavier than the visible part of the galaxy. In fact, according to the most recent measurements by NASA’s Wilkinson Microwave Anisotropy Probe (WMAP) satellite, dark matter accounts for about six times as much of the universe as the ordinary matter that can be seen.
Different theories of dark matter have led to different strategies for detecting it, none of which have been successful so far. If dark matter is a cloud of elementary particles, it may be detectable in sensitive particle detectors placed deep underground for shielding from ordinary cosmic rays. Calculations show that a cloud of Terascale particles would have just about the right properties to agree with what is known about dark matter. Underground laboratories are approaching the sensitivity at which such a cloud could be detected, so there is a chance of uncovering the nature and properties of dark matter in the near future.
Dark matter is only one of the surprising discoveries made by astronomers about the content of the universe. Since the discovery in the 1920s that the universe is expanding, astronomers and physicists have assumed that the expansion is slowing because of the gravitational attraction between galaxies. Numerous attempts were made to measure this presumed deceleration of the cosmic expansion, but the attempts were frustrated by the difficulty of estimating precise distances to remote galaxies.
Then, in the 1990s, measurements of large-scale structure in the universe, including clusters and superclusters of galaxies, and of the radiation that permeates the universe suggested that most of the energy in the universe consists of dark energy, a smoothly distributed, all-pervasive form of energy that causes the expansion of the universe to accelerate. Supernovae in distant galaxies were also used to gauge cosmic distances and provided direct evidence that the expansion of the universe is speeding up.
The dark energy responsible for this accelerated expansion of the universe might be interpreted theoretically in terms of what Einstein called the cosmological constant. It is not yet clear whether this interpretation is correct or whether some more elaborate theory of dark energy is needed. In any event, the acceleration of the cosmic expansion calls for a fundamental modification of existing ideas about nature. Calculations of the amount of dark energy in the Standard Model using the most reasonable assumptions differ from the experimental result by at least 60 orders of magnitude! Obviously, the current understanding of the situation is incomplete.
This problem is closely related to the effort to unify the Standard Model and general relativity. Indeed, the problem of dark energy combines considerations of quantum mechanics, which contributes to the vacuum energy via quantum fluctuations, with Einstein’s theory of gravity, without which the energy of the vacuum would be unobservable. No formalism has yet been devised that combines the theory of gravity and quantum mechanics in a satisfactory way.
The overwhelming scientific interest in dark matter and dark energy is driven by the fact that these seemingly exotic substances were discovered because of their very real effects on the structure and evolution of the universe.
Another challenging idea about cosmology is the idea of the inflationary universe, which is closely linked to particle physics. According to this hypothesis, the vast and nearly homogeneous universe that we see today originated in a period soon after the big bang, when the universe underwent a period of accelerated expansion that was 100 orders of magnitude faster than the acceleration due to dark energy. The cause of this rapid expansion is thought to be a field dubbed the “inflaton,” which dominated the universe for a brief instant after the big bang and then disintegrated into the matter and radiation observed today. During that brief period, the inflaton stretched the universe by a factor of 10100 or more, making it smooth and flat. However, the quantum process associated with the disappearance of the inflaton field caused the distribution of the remaining energy and radiation to be slightly nonuniform after the inflation was complete.
Surprisingly, it has proved possible to test the inflationary hypothesis using the fact that space is filled with a diffuse radiation called the cosmic microwave background (CMB), which is interpreted as radiation that was created at the beginning of the universe. The CMB has a temperature of about 2.7 K. This is the temperature that one would measure if one placed a thermometer in outer space far from any star. The CMB is highly isotropic, which means that the temperature appears to be nearly the same no matter in which direction one looks (see Box 2-6).
However, in the 1970s, researchers realized that to account for the formation of clusters of galaxies, the CMB must be slightly anisotropic, with slightly different temperatures in different regions of space. When the idea of inflation was intro-
|
BOX 2-6 The Cosmic Microwave Background: Footprints of the Early Universe The 21st century will be the first time in history when humans view the universe with high precision all the way out to the cosmic horizon. The light traveling from the most distant reaches of space will provide detailed information about the universe in its early stages, when the temperature and density of the universe exceeded what can be achieved at the highest energy accelerators imaginable, including the LHC and the ILC. For this reason, cosmology and elementary particle physics have become intimately intertwined, providing information that simultaneously improves understanding of both the smallest and largest entities in the cosmos. Breakthroughs in cosmology have been made possible by a confluence of new, highly advanced technologies. For example, the first highly precise microwave, infrared, and x-ray surveys of the distant universe have been completed; the three-dimensional structure of the nearby universe has been mapped out by the first red shift surveys; and views of the first stars and galaxies have been captured by the Hubble Space Telescope and by giant segmented-mirror telescopes on the ground. The snapshot of the infant universe taken by the WMAP satellite—sure to be one of the icons of 21st century science—is emblematic of this generation of powerful new probes (see Figure 2-6-1). In early 2006, a new, more detailed picture of the infant universe was released. Colors indicate “warmer” (red) and “cooler” (blue) spots. The white bars show the polarization direction of the oldest light. This seemingly formless pattern is chock-full of valuable information. First, it shows in detail the distribution of energy in the universe more than 13 billion years ago, when the first atoms formed. In this pattern can be identified the regions that later gave birth to galaxies like our own Milky Way (red and yellow) or that grew into giant, nearly vacuous voids (blue). Second, by studying how the number of spots and energy concentration vary with the spot size, cosmologists can derive a precise measure of the composition of the universe, providing the best evidence that the universe contains 4 percent ordinary matter, 20 percent dark matter, and more than 75 percent dark energy. Perhaps most exciting is the information an improved map of the cosmic background radiation and forthcoming measurements of its polarization will provide about the events that created the splotches in the first place. The measurements may prove that inflation accounts for the structure of the universe, as most cosmologists believe, and provide insights about the ultra-high-energy physics effects that caused inflation. 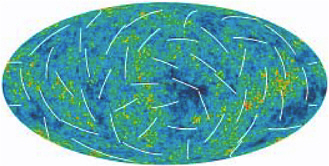 FIGURE 2-6-1 Infant universe as seen by WMAP. Courtesy of the NASA/WMAP Science Team. |
duced a decade later, it was realized that the early periods of inflation solved the problem of generating the density lumps need to explain the splotches in the CMB. In 1992, a dedicated satellite experiment, the Cosmic Background Explorer (COBE), was launched, and the predicted anisotropy of the background radiation was indeed detected. The temperature differences among the splotches were found to be only a few hundred-thousandths of a degree. A much more precise measurement of the temperature variations was made by WMAP in 2003 and in 2006. The temperature pattern found thus far is in excellent accord with the inflationary prediction, although the inflationary picture is not the only hypothesis consistent with the data.
To confirm the inflationary universe hypothesis (or an alternative) requires improved instruments that can make more precise measurements of how the CMB radiation varies with position in the sky. Among the most important tests will be measurements of the polarization pattern of the CMB radiation. The polarization of an electromagnetic wave is the direction along which its electric field oscillates. When the CMB radiation scatters from the sea of electrons and begins to stream toward us, it becomes polarized by an amount that depends on the cosmological model. This polarization was observed for the first time in 2002, but not yet with the sensitivity needed to definitively test the inflationary theory of the universe.
ROLES OF ACCELERATOR- AND NON-ACCELERATOR-BASED EXPERIMENTS
This recent history of particle physics underscores the interplay between experiments involving accelerators and those that do not involve accelerators. For instance, nonaccelerator experiments have helped drive the scientific frontiers of particle physics and have brought the field into closer contact with nuclear physics, cosmology, and astrophysics. Historically, many important discoveries first came from nonaccelerator experiments, in some cases simply because appropriate accelerators did not exist at the time. In fact, there is an impressive list of particle physics discoveries that did not involve accelerators. To name just a few:
-
Discovery of the neutron,
-
First evidence for the neutrino,
-
Detection of antimatter (discovery of the positron),
-
Discovery of parity violation,
-
Detailed exploration of the weak interaction,
-
Discovery of muons,
-
Discovery of pions,
-
Discovery of V particles (later called kaons),
-
Direct detection of neutrinos, and
-
Recently, discovery of neutrino mass and mixing.
Accelerator-based experiments, on the other hand, have also led to important accomplishments:
-
Discovery of the electron.
-
Discovery of the composite nature of the proton.
-
The era of particle “zoology” in the mid-1900s, when 100 or so particles and resonances were found, which in turn called for a simpler framework. The ultimate solution was the proposal of the quark model.
-
Discovery of the antiproton and antineutron. This discovery validated and solidified the Dirac theory of antiparticles. Even though the positron, found in cosmic rays, was already known to exist, physicists were not sure about every particle having an antiparticle.
-
Discovery of the KL meson. Although the kaon was discovered in cosmic rays, its rich physical properties were elucidated in accelerators. Resolution of the puzzle of a particle with two lifetimes led to the discovery of CP violation. CP violation was key to the attempt to understand matter-antimatter asymmetry in the universe.
-
Discovery of the second-generation neutrino.
-
The 1974 discovery at SLAC and Brookhaven National Laboratory of the charm quark.
-
Discovery of jets in electron and positron collisions.
-
Discovery of the gluon at DESY, and confirmation of the existence of a particle carrying the strong force.
-
Discovery at CERN of the W and Z, the carriers of the weak force, and confirmation of the gauge theory of weak interaction.
-
Discovery of the tau lepton at SLAC, proving that there must be at least three families of leptons.
-
Discovery of bottom quark particles at Fermilab and Cornell, demonstrating that there are three families of quarks in parallel with three families of leptons.
-
Precision tests of the Standard Model using measurements at LEP, SLAC, Fermilab, DESY, CESR, and elsewhere (for example, measurements of particle masses, quantum numbers, and quark couplings and mixing rates).
-
Measurement at LEP of light neutrino families that couple to the Z, showing that there can only be three families.
-
Discovery of the top quark at Fermilab, completing the Standard Model.
-
More recently, confirmation of neutrino oscillations and mixing through accelerator-based experiments at KEK in Japan and at Fermilab.
Without the contributions from accelerator experiments, modern particle physics would be far less advanced than it is today. There is no question that accelerators have been essential in particle physics and there is a clear role for them in uncovering the secrets of the Terascale. Indeed, much of the drama surrounding the Terascale comes from the expectation that accelerators will finally expose and then directly investigate the cracks in the Standard Model.
A remarkable aspect of particle physics today is that answers to many of the questions described in this chapter are within the reach of tools that can be built with currently available technologies. The next chapter explores the tools that will be available in the next decade to address the grand questions of particle physics, including those that will enable exploration of the Terascale.























