Section 2
Selected Workshop Papers
THE ECONOMICS OF GENDER DIFFERENCES IN EMPLOYMENT OUTCOMES IN ACADEMIA*
Donna K. Ginther
Department of Economics
University of Kansas
Abstract
This paper summarizes research that examines the relationship between hiring, promotion, and salary for tenure track science and social science faculty using data from the Survey of Doctorate Recipients (SDR). Gender differences in hiring and promotion can be explained by observable characteristics. However, gender differences in salaries persist at the full professor rank. In particular, women in science and social science are less likely to have tenure track jobs within five years of the doctorate when compared with men. However, when controls for marital status and children are included in the analysis, the research finds that unmarried women are significantly more likely to have tenure track jobs than unmarried men. Marriage provides a significant advantage for men relative to women. Presence of children, especially young children, significantly disadvantages women while having no impact on men in obtaining tenure track jobs. The research also finds no significant gender differences in the probability of obtaining tenure in life science, physical science, and engineering. These results also hold for promotion to full professor. However, significant gender promotion differences are evident in the social sciences, in particular, economics. Finally, the research finds large gender differences in salaries are partially explained by academic rank. However, gender salary differences for full professors, on the order of 13% in the sciences, are not fully explained by observable characteristics.
In his examination of the salaries and appointments of men and women in academia, the Director of Research at the American Association of University Professors (AAUP) observes: “Substantial disparities in salary, rank, and tenure
between male and female faculty persist despite the increasing proportion of women in the academic profession” (Benjamin, 1999). While the evidence presented by AAUP is striking, the gender comparisons of salaries do not control for characteristics that contribute to pay differentials such as academic field or publication record. Simply comparing salaries of male and female academic scientists without taking into consideration these factors could overstate the gender salary gap. Disentangling the causes of gender disparities in employment outcomes requires an in-depth examination of the data. This report summarizes research that examines the relationship between hiring, promotion, and salary for tenure track faculty using data from the Survey of Doctorate Recipients (SDR).
The Economic Perspective
Economic theory provides the underpinnings of this research. I start by assuming that employment outcomes are determined by market forces. Wages and hiring are determined by the supply of and demand for PhD scientists. Equally productive workers irregardless of gender will be paid the same and hired in similar numbers given market forces. Given these assumptions, one should not observe hiring, promotion, and salary differences for equally productive workers of either gender. However, persistent gender wage and employment differentials persist on average in the market as a whole (Altonji and Blank, 1999) and for scientists in particular (Ginther, 2001). I use economic theory to explain observed gender differences in hiring, promotion and salary.
Beginning with Becker’s seminal work on discrimination (Becker, 1971), economists have developed models to understand gender and racial disparities in employment outcomes. Becker argues that taste-based discrimination (prejudice) will be eliminated by competitive forces. Given employer, employee, or customer prejudice, those firms that pay premiums to favored workers will have higher costs. Thus, the nondiscriminating firm will have a competitive advantage by hiring women or minorities, and the market will eventually compete away the discriminating wage differential. Becker’s prediction relies on the assumption that markets are perfectly competitive—an assumption one can reject for academic institutions.
Given Becker’s results, economic theory has developed other explanations besides discrimination to account for observed gender differences in employment outcomes. These explanations may be divided into differences in “preferences” or choices and other factors. The preference-based explanations argue that gender differences in employment outcomes result from choices, in particular, differences in productivity. Economic theory holds that equally productive workers will be paid the same, thus, gender salary differences are the result of differences in productivity. A second preference-based explanation is that women chose to marry and have children, which in turn affects their attachment to their careers and overall productivity.
Other theoretical explanations include monopsony models of the labor market. A monopsonist is a single employer of labor that has more bargaining power in the employment contract than the worker. Monopsonists pay workers less than the competitive wage and may be able to pay different wages to different types of workers depending upon their relative mobility. Thus if female faculty have fewer outside job opportunities, this will generate a gender wage differential. One may convincingly argue that academic institutions have monopsony power relative to faculty in most fields. However, for monopsony to explain gender employment disparities, women would need to be less mobile than men.
Job-matching models may also explain gender differences in employment outcomes. In this model workers who are the best match for the job earn the highest salaries. In loose terms, the job-matching model suggests that women are paid less because they are not as capable (not as good of a match) in science compared to men.
If the researcher cannot explain the gender differences in employment outcomes using one of the above explanations, then the residual gender difference in hiring, promotion, or salary may be attributed to discrimination. Statistical discrimination suggests that imperfect information on the part of employers generates wage differentials. In this model, an employer attributes the average characteristics of a group to an individual member of this group—essentially the employer uses a stereotype in making hiring decisions or setting wages. As a result, we observe gender differences in employment outcomes. However, direct measures of statistical discrimination are difficult to come by. Thus, discrimination may be inferred when other plausible explanations have been ruled out.
Using economic theory as a guide, the research summarized in this report is organized using three basic principles. First, there is no single scientific labor market. As a result, this research disaggregates the data by scientific field. Second, gender differences in employment outcomes need a context in order to make meaningful comparisons. Thus, the research compares employment outcomes across academic fields in order to ascertain the relative status of women in academic science and social science. Finally, employment outcomes are interrelated. One cannot understand gender differences in salary without considering related outcomes of hiring and promotion. Given these principles, my research poses the question: Does science discriminate against women? I evaluate gender differences in hiring, promotion, and salary and can largely explain the first two outcomes using observable characteristics. However, I find large gender differences in the salaries of full professors that I cannot explain as a function of productivity or other choices.
Data and Methods
This study uses data from the Survey of Earned Doctorates (SED) and the Survey of Doctorate Recipients (SDR) to examine the distribution of women
across scientific fields and gender differences in salary. The SED is a census of doctorates awarded in the United States each year. I use the 1974–2004 waves of the survey to evaluate changes in the distribution of women in scientific fields. The SDR is a nationally representative sample of PhD scientists in the United States used by the National Science Foundation to monitor the scientific workforce and fulfill its congressional mandate to monitor the status of women in science. This study uses data from the 1973-2001 waves of the SDR. The SDR collects detailed information on doctorate recipients including demographic characteristics, educational background, employer characteristics, academic rank, government support, primary work activity, productivity, and salary. Although the SDR has comprehensive measures of factors that influence academic salaries, the data lack information on some quantitative measures, such as laboratory space and extensive measures of publications. Measures of academic productivity are largely missing from the SDR data, but the SDR does ask questions about publications in the 1983, 1995, and 2001 surveys. I use these data to create rough measures of productivity for each year following the doctorate.1
Academics in the life sciences, physical sciences, engineering, and social science are included in the analysis. Life science includes biological sciences and agriculture and food science. Physical science includes mathematics and computer science, chemistry, earth science and physics. Social science includes economics, psychology, sociology and anthropology, and political science. Engineering includes all engineering fields. The SDR collected information on doctorate recipients in the humanities between 1977 and 1995. In some of the analysis that follows, I include comparisons across the three broad disciplines of humanities, sciences, and social sciences.
I begin the analysis by analyzing the percentage of doctorates awarded and the percentage of tenured faculty who are female. Figures 2-1 and 2-2 indicate that women are not equally distributed across scientific fields. Figure 2-1 graphs the percentage of doctorates awarded to females between 1974 and 2004 using data from the SED. If we consider only life science fields, we may conclude, like the National Research Council (2001), that women have indeed moved ‘from scarcity to visibility’ in terms of doctorates granted. By 2004 almost half of all doctorates in life science and more than half of all doctorates in social science were awarded to women. However, both physical science and engineering awarded less than one-third of doctorates to women. In the year 2004, less than 18% of engineering doctorates and less than 27% of physical science doctorates were granted to women.
Despite the increasing numbers of doctorates awarded to women, the representation of women among tenured academic scientists remains quite low. Figure 2-2 uses data from the 1973–2001 waves of the SDR to graph the percentage of
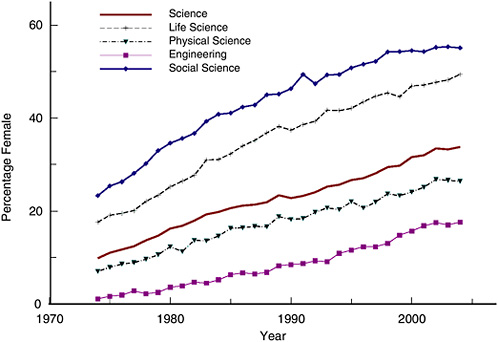
FIGURE 2-1 Percentage of doctorates granted to females, 1974–2004.
SOURCE: 1974-2004 Survey of Earned Doctorates.
tenured faculty who are female in life science, physical science, social science, and engineering. As expected, social science and life science have the highest percentages of tenured female faculty at 28 and 25% respectively in 2001. Physical science and engineering have far fewer tenured female faculty at 11 and 5%, respectively. Given the large differences between the percentages of doctorates awarded to women and the percentages of tenured faculty who are women, I turn to potential explanations.
Gender Differences in Hiring and Promotion
Hiring
The underrepresentation of women in tenured academic ranks may result from gender differences in hiring or promotion. Ginther and Kahn (2005) examine gender differences in hiring by evaluating whether women in science are more or less likely than men to get tenure track jobs within five years of receiving their doctorate. Women and men who leave academia immediately following the doctorate are dropped from the sample. Figure 2-3 shows three sets of estimates of the effect of being female on getting a tenure track job using samples of over
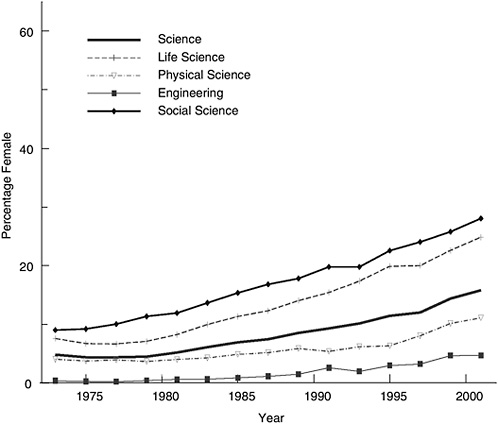
FIGURE 2-2 Percentage of tenured faculty who are female, by discipline, 1973–2001.
SOURCE: 1973-2001 Survey of Doctorate Recipients.
12,000 scientists and over 3,000 social scientists from 1973–2001. Negative numbers indicate that women are less likely whereas positive numbers indicate that women are more likely to get a tenure track job within five years of PhD. Numbers that are underlined are statistically significant at the 5% level. The first bar in Figure 2-4 shows that women are between 4 to 6% less likely than men to have tenure-track jobs in all science fields combined, social science, and life science. There is no significant difference between men and women getting a tenure-track job in physical science and engineering. The second bar in Figure 2-4 includes controls for academic field, race, age at PhD, year of PhD, marital status, and children. The estimated gender gap falls for all science and social science fields but does not change appreciably for the disaggregated science fields.
The third bar includes controls that interact female with marital status and children. These interaction terms allow the impact of marriage and children to be different for men and women in the model. The estimates are strikingly different.
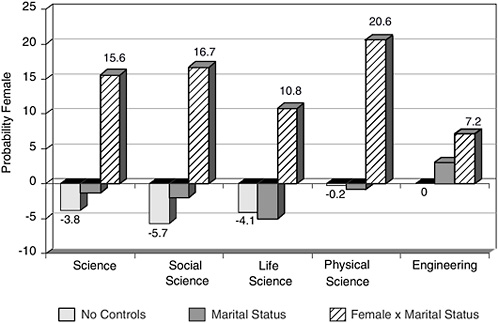
FIGURE 2-3 Gender differences in tenure-track job within 5 years of PhD.
Notes: Estimates from Ginther and Kahn (2005) using 1973-2001 Survey of Doctorate Recipients.
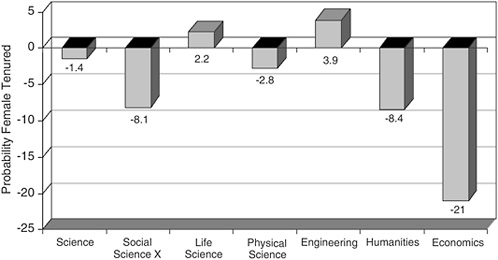
FIGURE 2-4 Gender differences in promotion to tenure 10 years past PhD.
Notes: Estimates from Ginther and Kahn (2004) and Ginther and Hayes (2003). Science and Social Science estimates from 1973-2001 SDR. Humanities estimates from 1977-1995 SDR. Economics, humanities, and social science X (excluding economics) are statistically significant (p = 0.01).
Women are between 7 to 21% more likely than men to get a tenure-track job within 5 years of PhD provided they are unmarried and do not have children. These results indicate that much of the underrepresentation of women in academic science is the result of having children. Single women are 16% more likely in science and 17% more likely in social science to get tenure-track jobs than single men. Marriage has a positive and significant impact of 22% on men getting a tenure-track job whereas the effect of marriage on women ranges between 0 and 8% for all science, life science, and social science fields. The exception is engineering where marriage increases women’s chances of having a tenure-track job by 23%. Children, especially young children, significantly decrease the likelihood of women obtaining a tenure-track job between 8 to 10% in all science fields, life science, and social science while having no significant impact on men.
The positive impact of marriage and children on men’s tenure-track employment echoes the positive impact of men’s marriage and children on wages and promotion in the labor market as a whole. The negative impact of children on women’s tenure-track employment may result from a number of factors. Women may choose to have children instead of pursuing an academic career because of the coincident timing of the tenure and biological clocks. The dual-career problem may also play a role. Career hierarchies in marriage often result in the husband’s career taking precedence over the wife’s career. If it is difficult to obtain two tenure-track jobs, she may choose to have children instead of investing in her career.
Furthermore, women are often the primary caregivers of children and this may hamper investments in their careers. The availability of tenure-track jobs may be limited to such an extent that women choose to invest more in marriage and family than in their careers. I suggest that the relative lack of academic jobs may be playing a significant role. By way of example, approximately half of all medical students are women and increasing numbers of women are practicing medicine. The demand for doctors is much higher than the demand for academic scientists, and this demand results in more women practicing medicine. It follows that the lack of academic jobs may be contributing to women’s underrepresentation in academic science.
Finally, the timing of women’s departure from academia may also indicate problems with the post-doctoral system in academic science. Studies suggest that the post-doctoral process is taking longer because the number of post-doctoral positions has expanded without a similar expansion of academic jobs (Davis, 2005). These results suggest that some combination of factors at the early stages of women’s careers are affecting married women’s choice of or access to tenure-track jobs. I now examine what happens to women as they progress through the tenure track.
Promotion
Once women have tenure-track jobs, their prospects for getting tenure in science are very promising but less so in social science. Figure 2-4 is derived from estimates in Ginther and Kahn (2004, 2005) and Ginther and Hayes (2003). It shows gender differences in the promotion to tenure 10 years past the doctorate in the fields of science, social science excluding economics, life science, physical science, engineering, humanities, and economics. These latter two disciplines are included to provide a context for the remaining fields. Women are between 1 to 3% less likely to get tenure in all scientific fields combined and in physical science 10 years past the doctorate. Women are between 2 and 4% more likely to get tenure in life science and engineering. These results indicate that gender differences in promotion to tenure are small for women in scientific fields.
This is not true for social science (excluding economics) and the humanities where women are 8% less likely than men to get tenure. Economics is the outlier—women are 21% less likely to get tenure than men 10 years past the doctorate. These differences in economics cannot be fully explained by gender differences in productivity, marital status, or presence of children (Ginther and Kahn, 2004).
Ginther and Kahn (2005) estimate gender differences in promotion to tenure and promotion to full professor in scientific fields. They find no statistically significant gender differences in promotion to either rank. Thus, we can conclude that gender differences in promotion in science are negligible. However, gender differences in promotion in social science are large, especially in economics. I now consider gender differences in salaries.
Gender Differences in Salaries
There are several factors that affect the salaries of academics. Demographic characteristics such as race, marital status, fertility, and years of work experience may have a positive or negative effect on salaries. For example, on average, marriage increases male salaries while having a negative effect on female salaries. Employer characteristics such as working at a public or private institution, liberal arts or a doctoral institution, and the Carnegie ranking of the employer may also affect salaries. Top research institutions pay more than liberal arts colleges. Public institutions have state-mandated salary scales that tend to be more restrictive than those at private institutions. Employee characteristics such as the academic rank and tenure status of the individual also influence salaries, with salaries increasing with academic rank and tenure.
Measures of productivity also affect salaries. These include factors such as whether the individual receives government support, primary work activities, and publications. If men are more likely to work at top-ranked research universities, the gender salary gap will be larger. Salary differences may also result from dif-
ferential treatment reflected in differences in estimated coefficients. For example, at private institutions if men are paid more than women and private institutions are equally likely to employ both, then the gender salary gap will increase. Taken together, these observable characteristics may explain a substantial portion of the gender salary gap.
The analysis reported here updates estimates in Ginther (2001, 2003, 2004) and Ginther and Hayes (2003) using the 2001 SDR data. The first bar in Figure 2-5 shows the average gender salary gap for all tenure-track and tenured faculty combined in science, social science, life science, physical science, engineering, and humanities. The salary gap ranges from a low of 11% in the humanities2 to a high of 21% in engineering. This combined gender salary gap is very large. However, previous research by Ginther and Hayes (1999, 2003) shows that the majority of the gender salary gap in the humanities disappears when separate salary regressions are estimated for each academic rank.
The remaining bars in Figure 2-5 show the gender salary gap for assistant, associate, and full professor ranks. Similar to Ginther and Hayes (1999, 2003), the gender salary gap at the assistant and associate professor ranks falls from close to 20% to just over 5% for assistant and associate professors in science and social science. However, the full professor salary gap increases to 8% for social science and as high as 14% for life scientists. In contrast, the gender salary gap for full professors in the humanities is less than 2%.
Using regression techniques, these salary gaps can be decomposed into factors that are explained by observable characteristics and factors that result from differential treatment of men and women. One-third of the salary gap for all science fields combined cannot be explained by observable characteristics such as productivity. Three-quarters of the salary gap for engineering cannot be explained by observable characteristics. I now evaluate whether economic theory can explain the gender salary gap for full professors.
Explanations for the Salary Gap
To determine whether publication differences could account for a substantial portion of the unexplained salary gap for full professors, I use publications measures from the 2001 SDR (Ginther, 2004). The sample includes measures of papers published and papers presented at conferences within the last five years. Including productivity measures only reduced the unexplained portion of the gap by 0.3 percentage points from 3.8 to 3.5%. Thus, productivity does not appreciably reduce the unexplained gender salary gap for full professors for all science fields combined. However, productivity differences do explain a significant portion of the salary gap in physical science and engineering.
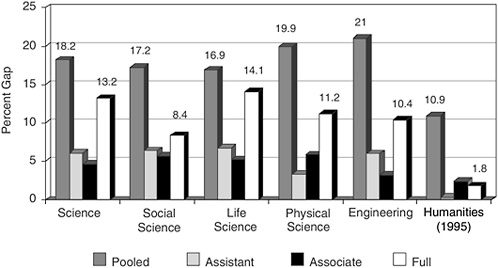
FIGURE 2-5 Gender salary gap by academic rank, 2001 SDR.
Notes: Estimates for Humanities from Ginther and Hayes (2003) based on 1995 SDR.
Next, I consider other factors that may explain the gender salary gap. In particular, women who have children are often paid less than women without children (Waldfogel, 1998). Since women are often the primary care-givers for children, having a child may reduce a woman’s productivity. My analysis shows that the total number of children and presence of children under the age of six have little or no impact on either the explained or unexplained portion of the gender salary gap for full professors.
Economic models of monopsony (where the university acts as the sole purchaser of labor) may also explain the gender salary gap. In monopsonistic models of academic labor markets developed by Ransom (1993), senior faculty have higher moving costs and receive lower salary offers. It is possible that tenured women faculty have higher moving costs than their male colleagues because of dual career considerations or fewer job opportunities. In related research, Booth, Frank, and Blackaby (2002) suggest that universities may consider women to be “loyal servants” who are less likely to change academic employers. As a result, universities can make lower salary offers and adjustments to women scientists. Both the monopsony and loyal servant explanations would be evident in the effect of job tenure on wages. If women have higher moving costs due to monopsony or are perceived to be “loyal servants,” their wages would be reduced more than men’s for each additional year of job tenure with the same employer. However, the data show the opposite is true. Male salaries are reduced more than female salaries for each additional year of job tenure. Thus, neither monopsony models nor the loyal servant hypothesis provide an adequate explanation of the gender salary gap in science.
Job matching models suggest that women are paid less than men because they are not as well suited (matched) to scientific careers. Whereas this may explain part of the salary gap for lower ranks, it is difficult to argue that women full professors of science are not well suited to academic science.
Although productivity, children, and economic models do not provide an adequate explanation for the gender salary gap, there are other variables that are associated with the gender gap. In my analysis, the single most important factor contributing to both the explained and unexplained gender gap is work experience—measured by years since PhD. Virtually all of the explained salary gap for full professors results from men having relatively more work experience. In addition, virtually all of the unexplained salary gap for full professors results from men having a higher return on experience than women. Although the effect of experience on wages is almost the same for men and women in the assistant and associate professor ranks, it differs for men and women at the full professor rank. Each additional year of work experience increases the salaries for male full professors but has zero effect on the salaries of female full professors, thus contributing to the unexplained salary gap.
The effect of experience suggests that the gender salary gap may result from a subtle mechanism such as the cumulative advantage model described by Zuckerman (1987). In this model, some groups receive greater opportunities than others. Recipients are enriched and nonrecipients are impoverished. Over time as advantages and disadvantages accumulate, a gender gap develops. The estimated impact of experience on the salary gap is consistent with the cumulative advantage model.
Conclusions and Policy Recommendations
I began this analysis by posing the question: does science discriminate against women in hiring, promotion, and salaries? The answers to these questions provide questions for further research and policy recommendations.
First, women in science and social science are less likely to have tenure track jobs within 5 years of the doctorate when compared with men. However, when controls for marital status and children are included in the analysis, the research finds that unmarried women are significantly more likely to have tenure track jobs than unmarried men. Marriage provides a significant advantage for men relative to women. Presence of children, especially young children, significantly disadvantages women while having no impact on men in obtaining tenure track jobs. Second, the research finds no significant gender differences in the probability of obtaining tenure in life science, physical science, and engineering. These results also hold for promotion to full professor. However, significant gender promotion differences are evident in the social sciences, in particular, economics. Finally, the research finds large gender differences in salaries are partially explained by academic rank. However, gender salary differences for full professors, on the
order of 13% in the sciences, are not fully explained by observable characteristics. The gender differences in salaries are most consistent with the cumulative advantage model where advantages accrue to men more often than women and generate salary differentials.
The results of this research provide both research and policy recommendations. The gender differences in hiring and salary summarized in this paper can only be partially explained with existing data. In order to understand the complex causes of gender disparities in employment outcomes for women in science and social science, better data are required. The Survey of Doctorate Recipients is the best source of data on academic labor markets. However the quality of the data should be enhanced along two dimensions. First, additional questions should be included in the SDR to allow for the comparison of resource allocations. These questions include the following:
-
Information on publications and citations
-
Dollar amount and duration of grant awards
-
Laboratory size
-
Numbers of graduate students and post-doctoral students advised.
This series of questions would allow researchers to determine whether gender differences in resource allocation and productivity contribute to the gender salary gap.
Second, additional questions related to post-doctoral appointments and dual career issues should be include in the SDR. These questions include:
-
Number, quality, and productivity of post-doctoral appointments
-
Spouse information including education, employment and earnings
-
Childcare time
This series of questions would allow researchers to determine whether the post-doctoral process or work-family trade-offs lead to fewer women in academic science.
In addition to the SDR, I recommend that agencies such as the NSF and NIH collect information on the demand for scientists. In particular, researchers could make great use of data on the number of academic and nonacademic jobs available in scientific fields. It is my belief that the excess supply of scientists in certain fields disproportionately disadvantages women. Finally, I recommend that the NSF create an advisory panel of researchers who use the SDR to make recommendations on data collection, survey design, survey questions, and dissemination of the data.
The hiring and salary gaps summarized in this research also lead to specific policy recommendations. In terms of hiring, universities should be encouraged to develop family friendly policies such as tenure clock stops for childbirth, paid parental leave, and on-site childcare. These policies would ease the burden of having and caring for children. Dual career hiring policies may also benefit
women. At most institutions, accommodations for the trailing spouse are ad hoc or nonexistent. This poses a special problem for women who are more likely to married to professional or academic spouses. Universities that wisely invest in academic couples may be able to hire and retain higher quality faculty because couples are less mobile than individuals. Finally, I would recommend institutional review of salaries on a regular basis in order to adjust obvious gender salary discrepancies.
References
JG Altonji and RM Blank (1999). Race and Gender in the Labor Market. Handbook of Labor Economics, Volume 3, Eds. O Ashenfelter and D Card. Amsterdam: Elsevier Science.
GS Becker (1971). The Economics of Discrimination, 2nd edition. Chicago: University of Chicago Press.
E Benjamin (1999). Disparities in the salaries and appointments of academic women and men. Academe 85(1):60-62.
AL Booth, J Frank, and D Blackaby (2002). “Outside Offers and the Gender Pay Gap: Empirical Evidence from the UK Academic Labour Market”. Mimeo, University of Essex.
G Davis (2005). “The Productive Postdoc: Assessing the Impact of Recommended Changes to the Postdoctoral Experience”. Mimeo, Sigma Xi.
DK Ginther (2001). Does Science Discriminate Against Women? Evidence from Academia, 1973-97. Federal Reserve Bank of Atlanta Working Papers 2001-02 (2001):66. http://www.frbatlanta.org/publica/work_papers/wp01/wp0102.htm.
DK Ginther (2003). Is MIT the exception? Gender pay differentials in academic science. Bulletin of Science, Technology, and Society 23(1):21-26.
DK Ginther (2004). Why women earn less: Economic explanations for the gender salary gap in science. AWIS Magazine 33(1):6-10.
DK Ginther and KJ Hayes (1999). Gender differences in salary and promotion in the humanities. American Economic Review Papers and Proceedings 89(2):397-402.
DK Ginther and KJ Hayes (2003). Gender differences in salary and promotion for faculty in the humanities, 1977-1995. The Journal of Human Resources 38(1):34-73.
DK Ginther and S Kahn (2004). Women in economics: Moving up or falling off the academic career ladder? Journal of Economic Perspectives 18(3):193-214.
DK Ginther and S Kahn (2005). Does Science Promote Women? Evidence from Academia 1973-2001. Mimeo, University of Kansas.
National Research Council (2001). From Scarcity to Visibility. Washington, DC: National Academy Press.
M Ransom (1993). Seniority and monopsony in the academic labor market. American Economic Review 83(1):221-233.
SV Rosser (2004). The Science Glass Ceiling. New York: Routledge.
J Waldfogel (1998). The family gap for young women in the United States and Britain: Can maternity leave make a difference? Journal of Labor Economics 16(3):505-545.
H Zuckerman (1987). “The Careers of Men and Women Scientists: A Review of Current Research.” Reprinted in eds. H Zuckerman, JR Cole, and JT Bruer, The Outer Circle: Women in the Scientific Community. New York: WW Norton.
BIOPSYCHOSOCIAL CONTRIBUTIONS TO COGNITIVE PERFORMANCE*
Diane F. Halpern
Berger Institute for Work, Family, and Children
Claremont McKenna College
Abstract
Females and males are both similar and different in their cognitive performance. There is no evidence to support claims for a smarter sex. Males and females have different average scores on different cognitive measures; some show an advantage for females and others show an advantage for males. Females are achieving at higher rates in school at all levels and in all subjects, including subjects in which they obtain lower scores on aptitude/ability tests (e.g., advanced mathematics). Although there is much overlap in the female and male distributions, on average, females excel on many memory tasks including memory for objects and location, episodic memory, reading literacy, speech fluency, and writing. Males excel at visuospatial transformations, especially mental rotation, science achievement, mathematics tests that are not tied to a specified curriculum (possibly due to use of novel visuospatial representations and transformations), and males are more variable on many cognitive tests. A biopsychosocial model that recognizes the reciprocal relationships among many types of variables is used as an explanatory framework.
There have been remarkable changes in the lives of women and men in the blink of history that was the 20th century. College enrollments went from consisting largely of men from the privileged classes near the start of the 20th century to men from all socioeconomic classes and literally, all stripes, as they returned from World War II near mid-century. College enrollments for women at the same time consisted mostly of women of privilege, or exceptional talent, or high moti-
vation, or some combination of all three. But, by the time the post-war baby boom reached college age, women were attending college at an increasingly higher rate than earlier generations, in part because the baby boomers faced more competition as they entered an overcrowded work force. By 1982, the number of women enrolled in and graduating from college exceeded that of men, and the gap in favor of women has continued to widen ever since.
Among women between 25 and 34 years old, 33% have completed college, compared to 29% of men. Women also get higher grades in school, on average, in every subject area (Dwyer and Johnson, 1997; Kimball, 1989). These changes have occurred faster than any gene can mutate or any theory of evolution can explain, so it is not surprising that most people look to societal explanations for the changing roles of men and women. Although women still dominate enrollments in the “helping professions,” such as teaching, social work, and nursing, they have been increasing their enrollments in traditional male disciplines. Males have been much slower to enter the traditional female disciplines. There have been many initiatives to accelerate the increase in the numbers of women in academic areas commonly known as STEM—Science, Technology, Engineering, and Mathematics—however the underrepresentation of women, particularly at the full professor level in university faculties, was brought into a near frenzy of public debate when Lawrence Summers (January 14, 2005), president of Harvard University, offered his personal beliefs about this topic. Summers identified these three broad hypotheses as possible reasons for the large disparities in the percentage of women in academic positions in universities: (1) high-powered job hypothesis; (2) differential availability of aptitude at the high end, and (3) different socialization and patterns of discrimination in the faculty search process. Summers eliminated the third hypothesis quite simply by concluding that there could not be discrimination against women in the process of searching and hiring professors because discrimination would have to occur on every campus in the United States. If there were one or even a few campuses that did not discriminate against women scientists, then these campuses would have many outstanding women at the level of full professor who had been discriminated against at the other campuses; since there are no such campuses, there could not have been discrimination in the hiring or promotion process. Summers’ hasty dismissal of all that is known about implicit stereotyping (Banaji and Hardin, 1996), social expectations, in-group and out-group behaviors (Shelton and Richeson, 2005), and social psychology created a firestorm of controversy. He later retracted his statements and pledged $50 million to enhance faculty diversity and support women’s programs at Harvard. The other two hypotheses proposed by Summers are addressed in greater detail below.
Summers’ statements raised a serious question that is often not asked at the many symposia and talk shows that have followed as a result of his remarks: Are there too few women with the cognitive abilities to become our highest level scientists and mathematicians?
There are many science disciplines and women are dominating some of them. Women now comprise 75% of all graduating veterinarians, a field that is sometimes considered one of the most difficult of the sciences because there are multiple biological systems to be learned; women are obtaining 50% of medical school degrees, and 44% of the PhDs in the biological and life sciences, so women clearly have the innate ability to succeed in science. By contrast, women are getting only 29% of the doctorates in mathematics; 17% in engineering; and 22% in computer/information sciences. These percentages are higher than they used to be, but not equal to the number of males in these areas. On the other hand, should we be just as concerned about the low percentage of men who obtain only 32% of PhDs in psychology, 37% in health sciences, 34% in education (U.S. Department of Education, 2000)? Clearly women have the cognitive ability to learn and succeed in math and science, although there are sex differences in the fields of sciences in which they are selecting. The differences among these fields are sometimes described by a theory that suggests that biological or life sciences are preferred by women and inorganic sciences are preferred by men, but when psychologists look over this list, alternative categorizations emerge. For example, Lippa (1998) found that women, by a large margin, prefer to work with people— a career preference that also fits with women’s success in the field of law, which used to be dominated by men, versus men’s, strong preference for working with “things.” Ackerman et al. (2001) studied how trait complexes, which consist of abilities, interests, and personality variables, combine to influence achievement and career goals.
These data raise interesting philosophical questions about values and opportunities: would we expect or want all fields of study and all careers to become approximately equal in the numbers of men and women, and if so, at what cost are we willing to pursue that goal?
Biopsychosocial Model
When it comes to understanding cognitive performance, males and females are both similar and different, and some of the differences are small and some are large. There are cognitive tasks and tests that show, on average, some differences that favor females and some that favor males. There is also much overlap, so we do not have distinctly different groups, but overlapping distributions. In thinking about the differences, some of them have not changed over the decades for which we have data. Most people prefer environmental explanations, but are willing to settle for an explanation the will give a percentage of the “explanation” to nurture, a percentage to nature, and a percentage to their interaction. But nature and nurture cannot act independently, and they cannot “just interact.” Nature and nurture mutually influence each other in reciprocal ways and cannot be separated. It is not as though there is a number that exists in the real world and if researchers are very clever they will discover the percentage that can be attributed to nature
or nurture and their interaction. Nature and nurture have no meaning without each other—nature needs nurture and vice versa.
The distinction between biology and experience is hopelessly blurred, so asking whether nature or nurture plays the greater part in determining a cognitive sex difference is the wrong question. Consider, for example, the brain. It is the quintessential “biological” organ, yet, it is also shaped extensively by experience. There are many sex differences in the architecture of the brain, but it cannot be assumed that differences in female and male brains result solely from genetic or hormonal action. The importance of experience was demonstrated in a study of London cab drivers that found that the cabbies had enlarged portions of their right posterior hippocampus relative to a control group of adults whose employment required less use of spatial navigational skills (Maguire et al., 2000). The cab drivers showed a positive correlation between the size of the region of the hippocampus that is activated during recall of complex routes and the number of years they worked in this occupation. The finding that size of the hippocampus varied as a function of the number of years spent driving taxis makes it likely that it was a lifetime of complex way-finding that caused the brain structure used in certain visual-spatial tasks to increase in size.
The burgeoning field of hormone replacement therapies for men and women is providing evidence that hormones continue to be important in cognition throughout the life span, although the field is complex and rife with controversies. The best evidence for a beneficial effect is the effect of estrogen on verbal memory in old age. Even though there are many studies that have failed to find beneficial effects for hormone replacement in elderly women, a substantial number of studies suggest that exogenous estrogen (pill, patch, cream, or other form) causes positive effects on the cognition of healthy older women and possibly for women in early stages of Alzheimer’s disease. This conclusion is in accord with Sherwin’s (1999) meta-analytic review of 16 prospective, placebo-controlled studies in humans, where she concludes that “Estrogen specifically maintains verbal memory in women and may prevent or forestall the deterioration in short- and long-term memory that occurs with normal aging. There is also evidence that estrogen decreases the incidence of Alzheimer disease or retards its onset or both” (p. 315). The results of these studies and others provide a causal link between levels of adult hormones and sex-typical patterns of cognitive performance.
A graphic depiction of the biopsychosocial model is shown in Figure 2-6 as a continuous, dynamic loop, essentially blurring the distinction between biology and environment. Learning, for example, is both a biological and environmental variable, with the brain differentially responsive to new learning based on prior learning, genetic factors, nutrition, and much more. Even hormones, which are usually considered “biological” variables, do not act in fixed or preprogrammed ways, but act within a context. We now know, for example, that testosterone can increase or decrease depending on whether an individual wins or loses a game (Schultheiss et al. 2005) and that some cognitive measures vary slightly over the
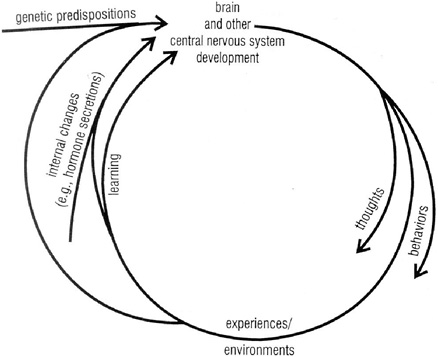
FIGURE 2-6 Biopsychosocial model in which the nature-nurture dichotomy is replaced with a continuous feedback loop.
menstrual cycle for cycling women and over the diurnal cycle for men, but the size of the fluctuations in cognitive performance are too small to be meaningful in everyday life (Halpern and Tan, 2001; Moffat and Hampson, 1996). The biopsychosocial model also makes it easier to understand that although sex differences are often (not always) found on some cognitive tasks, these differences are not immutable or inevitable and “biological” variables are developed in environments that are more or less favorable to their development and maintenance.
Sex Differences in Cognitive Performance
In understanding sex differences in cognitive performance, Hyde’s (2005) recent meta-analyses remind us that the sexes are similar in more ways than they are different. The standardized intelligence tests were written and normed to show no overall sex differences, but even a comparison of cognitive tests that were not deliberately normed to eliminate sex differences provide no evidence of overall sex differences in intelligence (Jensen, 1998). These tests do, however, show predictable sex differences on their subscores.
Some researchers object to the study of sex differences because they fear that it promotes false stereotypes and prejudice, but, there is nothing inherently sexist in a list of cognitive sex differences; prejudice is not intrinsic in data, but can be
seen in the way people misuse data to promote a particular viewpoint or agenda. Prejudice also exists in the absence of data. Research is the only way to separate myth from empirically supported findings. A necessarily very brief overview of the largest differences is presented here. For a more complete review, see Halpern (2000).
Female:
-
Writing and comprehending complex prose. In a report published by the U. S. Department of Education, entitled, “Trends in Educational Equity of Girls and Women,” the data on reading and writing achievement are described this way, “Females have consistently outperformed males in writing achievement at the 4th, 8th, and 11th grade levels between 1988 and 1996. Differences in male and female writing achievement were relatively large. The writing scores of female 8th graders were comparable to those of 11th grade males” (U.S. Department of Education, 2000, p. 18). A meta-analysis by Hedges and Nowell (1995) called the sex difference in writing that favored girls to be so large as to be “alarming”. The female advantage in writing may be one reason why females get higher grades in school, on average. Any assessment that relies on writing provides an advantage to females.
-
Rapid access to and use of phonological, semantic, and episodic information in long term memory. Many laboratory tests show females are better at generating synonyms, recalling information about events, and numerous standard memory tasks such as object location and identity (Herlitz, Nilsson, & Baeckman, 1997, Levy, Astur, & Frick, 2005).
-
Speech articulation and fine motor tasks. Females are much less likely to stutter and have better fine motor skills (e.g., O’Boyle, Hoff, & Gill, 1995). These results could be interpreted as females are “naturally” better at typing, or small motor repair, or brain surgery.
Male:
-
Visuospatial transformations, especially mental rotation. This is a well-replicated and large effect that has not declined in over 30 years (between 0.9 to 1.0 standard deviations; Halpern & Collaer, 2005; Masters & Sanders, 1993; Nordvik & Amponsah, 1998). In addition, performance on mental rotations tasks improve with practice and the improved performance transfers to novel mental rotation stimuli, but performance improves equally for women and men (Peters et al. 1995). Numerous replications with training do not find a sex by training interaction. Females do not especially benefit from training. An example of a mental rotation task is shown in Figure 2-7. The task is to determine if the pairs of figures can be rotated to be identical. When this test is administered on a com-
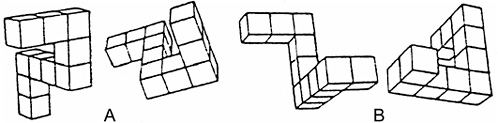
FIGURE 2-7 An example of a mental rotation task. Can the pairs of figures in A and B be rotated so that they are identical? Reaction times and correct answers are recorded.
-
puter, both the number (and percentage) correct is recorded with the reaction time for each item. Men not only get more items correct, but they also rotate the items more quickly than most women.
-
Fluid (novel) reasoning tasks in math and science. The advantage for males in mathematics is seen on some math tests. As already noted, females get higher grades in school, even in advanced math and science courses, although there are usually many fewer females enrolled in these courses. The advantage for males in math and science is found on high stakes tests that are not tied to a specific curriculum, which means that the problems require novel approaches, most frequently visuospatial problem representation or transforming visuospatial information in working memory (Gallagher, Levin & Cahalan, 2002). The size of the male advantage gets larger as the population sampled becomes more selective. In other words, the difference between males and females grows larger as the sample moves from high school to college-going students, from college-going students to graduate schools students, and from graduate students to those who are most gifted in math and science among graduate students. As this sample becomes more selective, so does the demand for visuospatial mental representation and transformation, which may be the underlying factor in this cognitive performance differential between males and females.
-
More variable in cognitive performance. There are more males at both the high and low ends of many cognitive performance distributions. The greater variability for males means that there are more males with mental deficiencies, and there are more males that score at the very high end on many tests of intelligence and achievement. The SAT-M, the mathematics test administered by the Educational Testing Service that is used by many universities for college admissions is one of the tests that shows an excess of males on the extreme high end. The quantitative test of the Graduate Record Examination (GRE-Q), which is used for admissions for graduate school also has a greater proportion of males scoring at its highest end (Webb, Lubinski, & Benbow, 2002).
Distribution of Aptitude
Several researchers have argued that the excess of males at the very high end of the abilities distributions for mathematics can account for the underrepresentation of females in physical sciences and math careers. When Summers referred to the different availability of aptitude at the high end, he was referring the finding that the ratio of males to females in the tails of distributions such as the GRE-Q is very high and gets higher the farther out in the tail that the distribution is cut, so that at the top 1% or 0.5 % there are many more males than females. There are flaws in this line of reasoning as an explanation of the underrepresentation of women in science and math academic careers because there is a lack of females at all ability ranges in science and math, not just at the highest ability range (Halpern, in press). There are many males in science and math who are not in the highest ability ranges because, by definition, only a very small percentage of the population is in this range. In other words, it is not as if we have only mediocre women in sciences and math with a lack at the top—women are underrepresented across the board.
Although the relative scarcity of females in the extreme tails of distributions cannot explain the absence of females in science and math careers overall, a surprising finding showed that for the very highest scoring SAT-M students at age 13, having a “genius” level score made a difference in their own career choices and achievements 20 years later (Wai, Lubinski, and Benbow, 2005). Researchers found that among precocious youth, there were differences in career choices and achievements 20 years later between those youth who scored in the top quartile of the top 1% on the SAT-M and those who scored in the bottom quartile of the top 1% on the SAT-M. Most psychologists would have believed, and probably still believe, that if an individual has achieved a threshold level of ability, additional ability beyond that level has little or no effect on life success because other variables such as motivation, interest, and opportunity would be far more important. These results remind researchers that high level ability is an important determinant of life outcomes, assuming that people have the opportunities to develop their abilities.
In looking over this abbreviated list of areas in which there are cognitive sex differences, one point should be evident—everyone except the profoundly retarded can improve in these cognitive areas with appropriate education, which is why we have schools. We really do not know if we could close, reverse, or increase any or all of the average differences between males and females with learning experiences, “selective breeding” (which was not discussed), hormone manipulations, or with combinations of all of these.
International Comparisons
Some differences between females and males are found consistently in international assessments. International comparisons of males and females are shown
in Figure 2-8. The left hand column shows data from 15 year-old students from 25 countries who participated in the Program for International Assessment (PISA). As seen in this figure, all of these countries showed significantly different effects favoring girls in reading literacy. The mathematics achievement and science achievement data are taken from the Third International Math and Science Study (U.S. Department of Education, 1997). The sex differences in math achievement at 8th grade are not as impressive on this assessment as it is on more advanced measures, but as indicated earlier, the size of the sex difference depends on what is assessed and it grows with more select samples. The cross-national consistency of the science achievement data is striking. In looking over these data, it is apparent that the results all show that males performed better than females and that the differences are statistically significant.
Readers may be wondering whether these effects are large enough to be important or meaningful in “real world” contexts. The question of when an effect is large enough to be meaningful has been the subject of much debate. In Valian’s (1998) analysis of women’s slow advancement in academia and other professions, she showed how small disparities can be compounded over time to create larger disparities, so a seemingly “small” percentage of variance accounted for can be meaningful, depending on the context and variable being assessed. Rosenthal, Rosnow, and Rubin (2000, pp. 15-16), three leading statisticians weigh in on this critical matter: “Mechanically labeling … ds automatically as ‘small,’ ‘medium,’ ‘and ‘large’ can lead to later difficulties. The reason is that even ‘small’ effects can turn out to be practically important.”
In a research paper on the mental rotation test, Peters et al. (1995) report that sex accounted for only 18% of the variance, but when they calculated a Binomial Effect Size Display (BESD), they found that 15% of the females exceed the mean of the males on this test. If the mean value of the male distribution were selected as the cut point for selection for an engineering program or some similar program, 50% of men would be admitted and 15% of women would be admitted, so even a seemingly “small” percentage of variance would have a devastating effect on the number of women admitted to this hypothetical program for further training.
Grades-Tests Disparities
Although females, in general, are doing better in school than their male counterparts (boys are more likely to repeat a grade, be victimized in school, or show up for school unprepared; U.S. Department of Education, 2000), males do better, in general, on standardized tests that are not linked to any specific curriculum, such as the SATs and GREs, which are used for college and graduate school admissions. The grades-tests disparity implies that the SAT-V (verbal) and SAT-M under-predict women’s grades in college, which is empirically supported (Cullen, Hardison, and Sackett, 2004). One explanation of the underprediction of women’s grades by tests that are not linked to the curriculum is that women are better

FIGURE 2-8 Gender differences in achievement: 15 year old* and 8th grade students.
students. Class grades also include classroom behavior and other noncognitive variables that are part of the good student role—a social role that is more compatible with the female sex role than the male sex role.
Average scores on the SAT-M for entering college classes from 1967 to 2004 are shown for men and women are shown in Figure 2-9. Despite the huge changes in number of women enrolled in mathematics courses and their higher grades in
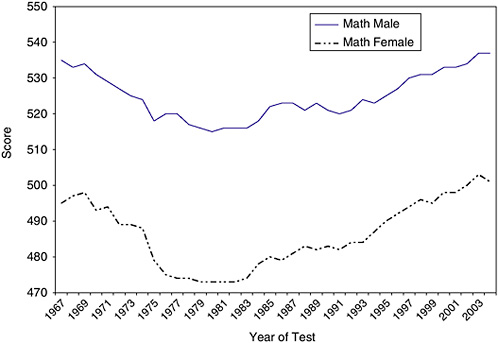
FIGURE 2-9 Average SAT scores of entering college classes, 1967-2004.
SOURCE: The College Board (2004). Table 2: Average SAT scores of entering college classes, 1967-2004. Date retrieved June 15, 2005, from http://www.collegeboard.com/prod_downloads/about/ness_info/cbsenior/yr2004/links.html.
mathematics courses, the male advantage on this test has remained fairly constant over the last 36 years.
Cognitive Process Taxonomy
How can we understand the grade-tests disparity? One way to consider the underlying cognitive processes used in executing the cognitive tasks being assessed when females or males excel at a cognitive task. Using a basic framework that was derived from the empirical literature on sex differences, Halpern (2000) proposed that females, in general, have faster access to information in episodic memory, to word knowledge and phonetic information; greater language fluency and implicit use of grammatical rules (in writing). Males, in general have faster access to visuospatial information and more accurate transformations of visuospatial information. In a study of the strategies used to solve mathematical problems, Gallagher et al. (2000) used the framework proposed by Halpern to see if boys and girls differed systematically in their use of mathematical strategies for different types of problems. In a series of several studies, they found that overall,
the male students were more likely to use a flexible set of general strategies and more likely to solve problems that required a spatial representation, a short cut, or the maintenance of information in spatial working memory. Females were more likely to correctly solve problems with context that was familiar for females, used verbal skills, or required retrieval of a known solution or algebraic or multi-step solution.
Building on the cognitive processing model, Gallagher, Levin and Cahalan (2002) examined cognitive patterns of sex differences on math problems on the Graduate Record Examination (GRE). They found the same results as predicted from the processes involved in solving the specific math problems, with differences favoring males for problems where there was an advantage to using a spatially-based solution strategy (use of a spatial representation), but not when solution strategies were more verbal in nature or similar to the ones presented in popular math textbooks. Similarly, the usual male advantage was found with math problems that had multiple possible solution paths, but not on problems that had multiple steps, so the differences in the performance of males and females on GRE math problems lie in the recognition and/or selection of a solution strategy that may be novel and not in the load on working memory. They found that the usual male advantage on standardized math tests can be minimized, equated, or maximized by altering the way problems are presented and the type of cognitive processes that are optimal for their solution.
These are important findings because they advance our understanding of problem solving in general and math problem solving for all learners. These findings also suggest ways to help everyone improve at what is often the “funnel”— or sieve—in education. Everyone can be taught how to create spatial representations and how to use successful strategies when they are appropriate for a specific type of mathematical problem. This is one example where the study of sex differences can move us toward a better understanding of the cognitive processes people use and new ways to improve strategies for math problem solving.
Noncognitive Variables
There are many context variables that influence cognitive performance. The president of Harvard, Lawrence Summers (2005, January 14) offered a “high-powered job” hypothesis as one possible reason for the low participation rate of women at the full professor level in the sciences and math that considers the larger context of higher education. There are few women full professorships in any discipline at research universities—they are underrepresented in all disciplines. Higher education is one of the few places that has an early “up or out” system. Law and accounting firms that require early partnership are the only other comparable models where young talented employees must prove themselves in the first six or seven years of their careers. For a scientist, who will usually have a postdoc position after receiving a doctorate, tenure decisions will be made
around age 36, which means that tenure clocks run in the same time zone as biological clocks. A recent study found that early babies—before tenure—hurt women’s careers in academe, but help men’s (Mason and Goulden, 2004). Women who want a career in academic science will have to make greater sacrifices than men, because in general, women have greater care responsibilities than men do. The inflexibility of the tenure system to accommodate to the reality of women’s lives is the more likely and proximal cause of the underrepresentation of women in academic science, which in addition to the other requirements in the academy, includes long hours in the laboratory.
Thus, although there are sex differences in cognitive performance on many tests, and despite the many unanswered and important questions about the interplay of social, assessment, and biological variables on cognitive performance, the most immediate route to helping talented women gain entry and move through career in science and mathematics is by recognizing the family and other care-taking demands that most usually fall on women. Many talented women resent the choice between children and career that society is not asking of their male peers. Egalitarian households would go a long way to achieving workplace equity, but until we achieve that reality, part-time tenure track appointments without retaliation and other family-compatible options for men and women will be needed so that the nation can take advantage of the talent in the new workforce.
References
PL Ackerman, KR Bowen, ME Beier, and R Kanfer (2001). Determinants of individual differences and gender differences in knowledge. Journal of Educational Psychology 93:797-825.
MR Banaji and CD Hardin (1996). Automatic stereotyping. Psychological Science 7:136-141.
MJ Cullen, CM Hardison, and PR Sackett (2004). Using SAT-grade and ability-job performance relationships to test predictions derived from stereotype threat theory. Journal of Applied Psychology 89:220-239.
CA Dwyer and LM Johnson (1997). Grades, accomplishment, and correlates. In: Gender and fair assessment, Eds. WW Willingham and NS Cole, Mahwah, NJ: Erlbaum.
AM Gallagher, R De Lisi, PC Holst, AV McGillicuddy-De Lisi, M Morely, and C Cahalan (2000). Gender differences in advanced mathematical problem solving. Journal of Experimental Child Psychology 75:165-190.
A Gallagher, J Levin, and C Cahalan (2002). GRE Research: Cognitive patterns of gender differences in mathematics admissions test (ETS Report 02-19). Princeton, NJ: Educational Testing Service.
DF Halpern (2000). Sex differences in cognitive abilities (3rd ed.). Mahwah, NJ: Erlbaum.
DF Halpern (in press). Science, sex, and good sense. In: Are Sex Differences in Cognition Responsible for the Underrepresentation of Women in Scientific Careers? Eds. S Ceci and W Williams, Washington, DC: American Psychological Association.
DF Halpern and ML Collaer (2005). Sex differences in visuospatial abilities: More than meets the eye. In: The Cambridge Handbook of Visuospatial Thinking, Eds. P Shah and Miyake, Cambridge, MA: Cambridge University Press.
DF Halpern and U Tan (2001). Stereotypes and steroids: Using a psychobiosocial model to understand cognitive sex differences. Brain and Cognition 45:392-414.
LV Hedges and A Nowell (1995). Sex differences in mental test scores, variability, and numbers of high-scoring individuals. Science 269:41-45.
A Herlitz, L-G Nilsson, and L Baeckman (1997). Gender differences in episodic memory. Memory and Cognition 25:801-811.
JS Hyde (2005). The gender similarities hypothesis. American Psychologist 60:581-592.
MM Kimball (1989). A new perspective on women’s math achievement. Psychological Bulletin 105:198-214.
AR Jensen (1998). The g Factor: The Science of Mental Ability. New York: Praeger.
LJ Levy, RS Astur, and KM Frick (2005). Men and women differ in object memory but not performance of a virtual radial maze. Behavioral Neuroscience 119:853-862.
R Lippa (1998). Gender-related individual differences and the structure of vocational interests of the people-things dimension. Journal of Personality and Social Psychology 74:996-1009.
EA Maguire, DG Gadian, IS Johnsrude, CD Ashburner, RSJ Frackowiak, and CD Frith (2000). Navigation-related structural change in the hippoccampi of taxi drivers. Proceedings of National Academy of Sciences 97:4398-4403.
MA Mason and M Goulden (2004). Do babies matter? The effect of family formation of the lifelong careers of academic men and women. Academe. Retrieved on-line March 28, 2005 from http://www.aaup.org.
MS Masters and B Sanders (1993). Is the gender difference in mental rotation disappearing? Behavior Genetics 23:337-341.
SD Moffat and E Hampson (1996). A curvilinear relationship between testosterone and spatial cognition in humans: Possible influence of hand preference. Psychoneuroendocrinology 21:323-337.
H Nordvik and B Amponsah (1998). Gender differences in spatial abilities and spatial activity among university students in an egalitarian educational system. Sex Roles 38:1009-1023.
MW O’Boyle, EJ Hoff, and HS Gill (1995). The influence of mirror reversals on male and female performance in spatial tasks: A componential look. Personality and Individual Differences 18:693-699.
M Peters, B Laeng, K Latham, M Jackson, R Zaiyouna, and C Richardson (1995). A redrawn Vandenberg and Kuse mental rotations test: Different versions and factors that affect performance. Brain and Cognition 28:39-58.
R Rosenthal, RL Rosnow, and DB Rubin, (2000). Contrasts and effect sizes in behavioral research: A correlational approach. Cambridge, UK: Cambridge University Press.
OC Schultheiss, MM Wirth, CM Torges, JS Pang, MA Villacota, and KM Welsh (2005). Effects of implicit power motivation on men’s and women’s implicit learning and testosterone changes after social victory or defeat. Journal of Personality and Social Psychology 88:174-188.
JN Shelton and JA Richseon. (2005). Intergroup contact and pluralistic ignorance. Journal of Personality and Social Psychology 88:91-107.
BB Sherwin (1999). Can estrogen keep you smart? Evidence from clinical studies. Journal of Psychiatry and Neuroscience 24:315-321.
LH Summers (2005, January 14). Remarks at NBER Conference on Diversifying the Science and Engineering Workforce, Cambridge, MA. Available online: http://www.president.harvard.edu/speeches/2005/nber.html. Retrieved: March 18, 2005.
U.S. Department of Education (1997). The Third International Mathematics and Science Study. Washington, DC: U.S. Department of Education. (http://www.ed.gov/nces.).
U.S. Department of Education (2000). National Center for Education Statistics, Trends in Educational Equity for Girls and Women NCES 2000-030, by Y Bae, S Choy, C Geddes, J Sable, and T Snyder. Washington, DC: U.S. Printing Office.
V Valian (1998). Why So Slow? The Advancement of Women. Cambridge, MA: The MIT Press.
MR Webb, D Lubinski, and CP Benbow (2002). Mathematically facile adolescents with math-science aspirations: New perspectives on their educational and vocational development. Journal of Educational Psychology 94:785-794.
J Wai, D Lubinski, and CP Benbow (2005). Creativity, and occupational accomplishments among intellectually precocious youths: An age 13 to 33 longitudinal study. Journal of Educational Psychology 97:484-492.
WOMEN IN SCIENCE AND MATHEMATICS: GENDER SIMILARITIES IN ABILITIES AND SOCIOCULTURAL FORCES*
Janet Shibley Hyde
Department of Psychology
University of Wisconsin
Abstract
Success in engineering and the physical sciences requires many abilities (Handelsman et al., 2005). Chief among them are mathematical, spatial, and verbal abilities, the first two for doing the science and the third for presenting one’s work in scientific articles and at conferences. All three have been stereotyped as showing gender differences. Researchers have amassed mountains of data on gender differences in mathematical, spatial, and verbal abilities and have synthesized the finding using meta-analysis. This paper reviews these meta-analyses and other related research, concluding that gender differences in these abilities are generally small.
Success in engineering and the physical sciences requires many abilities (Handelsman et al., 2005). Chief among them are mathematical, spatial, and verbal abilities, the first two for doing the science and the third for presenting one’s work in scientific articles and at conferences. All three have been stereotyped as showing gender differences. Researchers have amassed mountains of data on gender differences in mathematical, spatial, and verbal abilities. These data have been synthesized using a statistical technique called meta-analysis. Therefore, before reviewing the evidence on gender differences in abilities, I provide a brief explanation of meta-analysis.
Meta-Analysis
Meta-analysis is a statistical method for aggregating research findings across many studies of the same question (Hedges and Becker, 1986). It is ideal for synthesizing research on gender differences, an area in which often dozens or even hundreds of studies of a particular question have been conducted.
Crucial to meta-analysis is the concept of effect size, which measures the magnitude of the effect—in this case, the magnitude of the gender difference. In gender meta-analyses, the measure of effect size typically is d (Cohen, 1988).
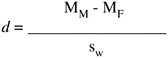
where MM is the mean score for males, MF is the mean score for females, and sw is the within-sex standard deviation. That is, d measures how far apart the male and female means are, in standardized units. In meta-analysis, the effect sizes computed from all individual studies are then averaged to obtain an overall effect size reflecting the magnitude of gender differences across all studies. Here I follow the convention that negative values of d mean that females scored higher and positive values of d indicate that males scored higher.
Although there is some disagreement among experts, a general guide is that an effect size d of 0.20 is a small difference, a d of 0.50 is moderate, and a d of 0.80 is a large difference (Cohen, 1988). As an example of a large effect, for the gender difference in throwing distance, d = +1.98 (Thomas and French, 1985).
Meta-analyses generally proceed in three steps: (1) The researchers locate all studies on the topic being reviewed, typically using databases such as PsychINFO and carefully chosen search terms. (2) Statistics are extracted from each report and an effect size is computed for each study. (3) An average of the effect sizes is computed to obtain an overall assessment of the direction and magnitude of the gender difference when all studies are combined.
Conclusions based on meta-analyses are almost always more powerful than conclusions based on an individual study, for two reasons. First, because meta-analysis aggregates over numerous studies, a meta-analysis typically represents the testing of tens of thousands—sometimes even millions—of participants. As such, the results should be far more reliable than those from any individual study. Second, findings from gender differences research are notoriously inconsistent across studies. For example, in the meta-analysis of gender differences in mathematics performance discussed later in this paper, 51% of the studies showed males scoring higher, 6% showed exactly no difference between males and females, and 43% showed females scoring higher (Hyde, Fennema, and Lamon, 1990). This makes it very easy to find a single study that supports one’s prejudices. Meta-analysis overcomes this problem by synthesizing all available studies.
Gender Differences in Mathematics Performance
A major meta-analysis of studies of gender differences in mathematics performance surveyed 100 studies, representing the testing of more than 3 million
persons (Hyde, Fennema, and Lamon, 1990). Averaged over all samples of the general population, d = –0.05, a negligible difference favoring females.
An independent meta-analysis confirmed the results of the first meta-analysis (Hedges and Nowell, 1995). It found effect sizes for gender differences in mathematics performance ranging between 0.03 and 0.26 across large samples of adolescents—all differences in the negligible to small range. Results from the International Assessment of Educational Progress also confirm that gender differences in mathematics performance are small across numerous countries including Hungary, Ireland, Israel, and Spain (Beller and Gafni, 1996).
For issues of the underrepresentation of women in the physical sciences, however, this broad assessment of the magnitude of gender differences is probably less useful than an analysis by both age and cognitive level tapped by the mathematics test. These results from one meta-analysis are shown in Table 2-1. Ages were grouped roughly into elementary school (ages 5-10 years), middle school (11-14), high school (15-18), and college age (19-25). Insufficient studies were available for older ages to compute mean effect sizes. Cognitive level of the test was coded as assessing either simple computation (requires the use of only memorized math facts, such as 7 × 8 = 56), conceptual (involves analysis or comprehension of mathematical ideas), problem solving (involves extending knowledge or applying it to new situations), or mixed. The results indicated that girls outperform boys by a small margin in computation in elementary school and middle school and there is no gender difference in high school. For understanding of mathematical concepts, there is no gender difference at any age level. For problem solving there is no gender difference in elementary or middle school, but a small gender difference favoring males emerges in high school and the college years. There are no gender differences, then, or girls perform better, in all areas except problem solving beginning in the high school years.
This gender difference in problem solving favoring males deserves attention because problem solving is essential to success in occupations in engineering and the physical sciences. Perhaps the best explanation for this gender difference, in
TABLE 2-1 The Magnitude of Gender Differences in Mathematics Performance as a Function of Age and Cognitive Level of the Test
|
Age group |
Cognitive Level |
||
|
Computation |
Concepts |
Problem solving |
|
|
5-10 |
–0.20 |
–0.02 |
0.00 |
|
11-14 |
–0.22 |
–0.06 |
–0.02 |
|
15-18 |
0.00 |
0.07 |
0.29 |
|
19-25 |
NA |
NA |
0.32 |
|
SOURCE: Hyde et al. (1990). |
|||
view of the absence of a gender difference at earlier ages, is that it is a result of gender differences in course choice, i.e., the tendency of girls not to select optional advanced mathematics courses and science courses in high school. The failure to take advanced science courses may be particularly crucial because mathematics curricula often do not teach problem solving, whereas it typically is taught in chemistry and physics.
Gender Differences in Verbal Ability
A meta-analysis of studies of gender differences in verbal ability indicated that, overall, the difference was so small as to be negligible, d = –0.11 (Hyde and Linn, 1988). The negative value indicates better performance by females, but the magnitude of the difference is quite small. There are many aspects to verbal ability, of course. When analyzed according to type of verbal ability, the results were as follows: for vocabulary, d = –0.02; for reading comprehension d = –0.03; for speech production d = –0.33; and for essay writing d = –0.09. The gender difference in speech production favoring females is the largest and confirms females’ better performance on measures of verbal fluency (not to be confused with measures of talking time). The remaining effects range from small to zero. Moreover, the magnitude of the effect was consistently small at all ages. Overall, then, gender difference in verbal ability are tiny and, if anything, favor females on measures such as essay writing and speech production, which should contribute to success in science. A second meta-analysis confirmed these findings using somewhat different methods (Hedges and Nowell, 1995).
Gender Differences in Spatial Ability
Spatial ability tests may tap any of several distinct skills: spatial visualization (finding a figure in a more complex one, like hidden-figures tests), spatial perception (identifying the true vertical or true horizontal when there is distracting information, such as the rod-and-frame task), and mental rotation (mentally rotating an object in 3 dimensions). Two meta-analyses are available on the question of gender differences in spatial performance. One found that the magnitude of gender differences varied substantially across the different types of spatial performance: d = 0.13 for spatial visualization, 0.44 for spatial perception, and 0.73 for mental rotation, all effects favoring males (Linn and Peterson, 1985). The last difference is large and potentially influential. The other meta-analysis found d = 0.56 for mental rotation (Voyer, Voyer, and Bryden, 1995), a somewhat smaller effect but nonetheless a substantial one. Gender differences in spatial performance—specifically, mental rotation—are important because mental rotation is crucial to success in several fields of engineering, chemistry, and physics (Hegarty and Sims, 1994).
Sociocultural Influences on Gender Differences in Mathematical and Spatial Abilities
The evidence on social and cultural influences on gender differences in mathematical and spatial abilities is plentiful and varied. I consider three categories of evidence: research on family and school influences, training studies, and cross-cultural analyses.
Family and School Influences
Abundant evidence exists for the multiple influences of parents and the schools on children’s development. Here I focus on these influences specifically in the domains of abilities and academic performance. A limitation to some of these studies is that they report simply a correlation, for example, between parents’ estimates of the child’s mathematics ability and the child’s score on a standardized test. From this correlation, we cannot infer the direction of causality with complete certainty. We cannot tell whether the parents’ beliefs in the child influence the child’s performance or whether the opposite process occurs—that children’s test scores influence their parents’ estimates of abilities. Moreover, it may be that both processes occur.
Numerous studies have confirmed the finding that parents’ expectations for their children’s academic abilities and success predict the children’s self-concept of their own ability and their subsequent performance (e.g., Bleeker and Jacobs, 2004; Eccles, 1994). When engaged in a science task—playing with magnets— mothers talk about the science process (e.g., use explanations, generate hypotheses) more with boys than with girls (Tenenbaum et al., 2005). Moreover, the amount of mothers’ science-process talk predicts children’s comprehension of readings about science 2 years later. Observations of parents and children using interactive science exhibits at a museum showed that parents were three times more likely to explain science to boys than to girls (Crowley et al., 2001). Girls essentially grow up in a different family science environment than boys do.
Schools may exert their influence in multiple ways, including teachers’ attitudes and behaviors, curriculum, ability grouping, and sex composition of the classroom. The availability of hands-on laboratory experiences is especially critical for learning in the physical sciences in middle school and high school. An important point is that, although laboratory experiences do not improve the physical science achievement of boys, they do improve the achievement of girls, thereby helping to close the gender gap in achievement in the physical sciences (Burkam, Lee, and Smerdon, 1997; Lee and Burkam, 1996). In science and mathematics classes, teachers are more likely to encourage boys than girls to ask questions and to explain (American Association of University Women, 1995; Jones and Wheatley, 1990; Kelly, 1988). In one study of high school geometry classrooms, teachers directed 61% of their praise comments to boys and 55% of
their high-level open questions to boys (Becker, 1981). Experiences such as these are thought to give children a deeper conceptual knowledge of and more interest in science.
Students also exercise choice in school activities. Crucial to this discussion is their choice in high school to take advanced mathematics and science courses. The gender gap in mathematics course taking has narrowed over the last decade, so that by 1998 girls were as likely as boys to have taken advanced mathematics courses, including AP/IB calculus (National Science Foundation, 2005). Girls were actually slightly more likely than boys to take advanced biology (40.8% of girls, 33.8% of boys), AP biology (5.8% of girls, 5.0% of boys), and chemistry (59.2%, 53.3%). Boys, however, were more likely to take AP chemistry (3.3% of boys, 2.6% of girls) and physics (31% of boys, 26.6% of girls), and were twice as likely to take AP physics (2.3% of boys, 1.2% of girls) (National Science Foundation, 2005). The science pipeline heading toward physics, then, begins to leak early as fewer girls take the necessary high school courses to prepare themselves for college-level physics. It is beyond the scope of this article to review what psychologists know about the reasons why adolescents choose or do not choose to take challenging math and science courses. Readers wanting more information can look to a massive program of research conducted by Eccles (e.g., Eccles, 1994).
Training Studies
Environmental input is essential to the development of spatial and mathematical abilities (Baenninger and Newcombe, 1995; Newcombe, 2002; Spelke, 2005). Babies are not born knowing how to work calculus problems. Children acquire these skills through schooling and other experiences.
A meta-analysis found that spatial ability can indeed be improved with training, with effect sizes ranging between d = 0.40 to 0.80, depending on the length and specificity of the training (Baenninger and Newcombe, 1989). The effects of training were similar for males and females; that is, both groups benefited about equally from the training, and there was little evidence that the gender gap was closed or widened by training. A more recent study showed that the gender difference could be eliminated by carefully conceptualized training (Vasta et al., 1996). Unfortunately, most school curricula contain little or no emphasis on spatial learning. Girls, especially, could benefit greatly from such a curriculum.
The most recent development is multimedia software that provides training in 3-dimensional spatial visualization skills (Gerson, Sorby, Wysocki, and Baartmans, 2001). It has been used successfully with first-year engineering students. Most notably for the topic under discussion, there were improvements in the retention of women engineering students who took the spatial visualization course; without the course, the retention rate for women was 47%, whereas with the course it was 77%.
Cross-Cultural Analyses
The International Assessment of Educational Progress (IAEP) tested the math and science performance of 9- and 13-year-olds in 20 nations around the world. The effect sizes for gender differences for selected countries are shown in Table 2-2 (Beller and Gafni, 1996). Focusing first on the results for mathematics, we see that the gender differences are small in all cases. Most importantly, effect sizes are positive (favoring males) in some countries, negative (favoring females) in other countries, and several are essentially zero. The Trends in International Mathematics and Science Study (TIMSS, 2003, formerly the Third International Mathematics Study) found similar results, with some positive and some negative effect sizes, and most < 0.10. In the TIMSS data for eighth graders, the magnitude of the gender difference was 0.09 in Chile (country average score 379), 0.02 in the United States (country average 502), 0.01 in Japan (country average 569), and –0.05 in Singapore (country average 611). That not only the magnitude, but also the direction of gender differences in mathematics performance varies from country to country is powerful testimony to the importance of sociocultural factors in shaping those differences. Perhaps most importantly, though, the gender difference is very small in most nations.
Focusing next on the results for science performance (Table 2-2), we can see that the effect sizes more consistently favor males and are somewhat larger, although not large for any nation. When the results are broken down by science, gender differences are smaller in life sciences knowledge (0.11 and 0.20 at ages 9 and 13, respectively, averaged over all countries) and somewhat larger for physical sciences (0.22 and 0.33) (Beller and Gafni, 1996).
TABLE 2-2 Effect Sizes for Gender Differences in Mathematics and Science Test Performance Across Countries
|
Country |
Mathematics |
|
Science |
|
|
9 years |
13 years |
9 years |
13 years |
|
|
Hungary |
–0.03 |
–0.02 |
0.09 |
0.25 |
|
Ireland |
–0.06 |
0.19 |
0.20 |
0.31 |
|
Israel |
0.16 |
0.15 |
0.23 |
0.24 |
|
Korea |
0.28 |
0.10 |
0.39 |
0.31 |
|
Scotland |
–0.01 |
–0.02 |
–0.01 |
0.20 |
|
Spain |
0.01 |
0.18 |
0.25 |
0.24 |
|
Taiwan |
0.03 |
0.02 |
0.25 |
0.08 |
|
U. S. |
0.05 |
0.04 |
0.09 |
0.29 |
|
All countries |
0.04 |
0.12 |
0.16 |
0.26 |
|
SOURCE: Beller and Gafni, 1996, Table 2 and Appendix. |
||||
It is important to note that cross-cultural differences in mathematics performance are enormous compared with gender differences in any one country. For example, in one cross-national study of 5th graders, American boys (M = 13.1) performed better than American girls (M = 12.4) on word problems, but 5th grade Taiwanese girls (M = 16.1) and Japanese girls (M = 18.1) performed far better than American boys (Lummis and Stevenson, 1990). Culture is considerably more important than gender in determining mathematics performance.
In perhaps the most sophisticated analysis of cross-national patterns of gender differences in mathematics performance, the researchers found that, across nations, the magnitude of the gender difference in mathematics performance for eighth graders correlated significantly with a variety of measures of gender stratification in the countries (Baker and Jones, 1993). For example, the magnitude of the gender difference in math performance correlated –0.55, across nations, with the percentage of women in the workforce in those nations. That is, the more that women participate in the labor force (an index of gender equality), the smaller the gender difference in mathematics achievement.
The Gender Similarities Hypothesis
I propose an alternative to our cultural and scientific obsession with gender differences. The alternative is the Gender Similarities Hypothesis, which I formalized in an article that appeared in the American Psychologist this year (Hyde, 2005). For that paper, I essentially meta-analyzed meta-analyses. That is, I found all the meta-analyses of psychological gender differences that I could. I found 46 relevant meta-analyses, and from them I extracted 124 effect sizes—d’s—for gender differences. The meta-analyses spanned a wide range of psychological characteristics, including abilities, communication, aggression, leadership, personality, and self-esteem.
I organized those 124 effect sizes into ranges— those that are close to zero, i.e., in the range 0 to 0.10, those that are small, 0.11 to 0.35, those that are moderate in magnitude, 0.36 to 0.65, those that are large, 0.66 to 1.00, and those that are very large, > 1.00. The results indicated that 30% of those effect sizes were in the close-to-zero range, and another 48% were small. So, 78% of the effect sizes were small or close to zero—that is the gender similarities hypothesis—psychologically, women and men are more similar than they are different. There are a few exceptions of large differences, but the big picture is one of gender similarities.
Implications: How Can We Close the Gender Gap in Engineering and the Physical Sciences?
One conclusion of this review is that, overall, there are no gender differences in math performance, but a gender difference favoring males in complex problem solving does emerge in high school. Mathematical problem solving is crucial to
success in the physical sciences, so this gap must be addressed. The evidence also indicates a gender gap in favor of males in spatial ability, specifically in mental rotation. This ability, too, is crucial to success in the physical sciences and must be addressed.
The following policy recommendations flow from the data reviewed here:
-
Focusing on the gender difference in spatial skill, we need to institute a spatial learning curriculum in the schools. Girls are seriously disadvantaged by its absence.
-
Colleges of engineering should have a spatial skills training program for entering students. Theoretically, such a program should help in physics and chemistry as well.
-
We should require 4 years of math and 4 years of science in high school— or at least require it for university admission. Otherwise, girls will elect not to take some advanced science courses and, without carefully making the decision, close themselves out of outstanding careers in engineering and the sciences.
-
The mathematics curriculum in many states continues to need attention. It needs far more emphasis on real problem solving, and that approach will benefit not only girls, but boys as well.
-
Hands-on science labs will benefit girls and help to close the gender gap. And, they represent good science education practice.
-
Teachers and high-school guidance counselors need to be educated about the findings on gender similarities in math performance. Otherwise, teachers will believe the stereotypes about girls’ math inferiority that pervade our culture, the teachers will have lower expectations for girls’ math performance, and those expectations will convey themselves to the students.
If we do all this—and much more—we can all look forward to a day when girls and women will have equal access to careers in engineering and the sciences. And our nation will benefit from maximizing women’s contributions.
References
American Association of University Women (1995). How schools shortchange girls. Washington, DC: AAUW.
M Baenninger and N Newcombe (1989). The role of experience in spatial test performance: A meta-analysis. Sex Roles 20:327-344.
M Baenninger and N Newcombe (1995). Environmental input to the development of sex-related differences in spatial and mathematical ability. Learning and Individual Differences 7:363-379.
DP Baker and DP Jones (1993). Creating gender equality: Cross-national gender stratification and mathematical performance. Sociology of Education 66:91-103.
JR Becker (1981). Differential treatment of females and males in mathematics classes. Journal for Research in Mathematics Education 12:40-53.
M Beller and N Gafni (1996). The 1991 International Assessment of Educational Progress in Mathematics and Sciences: The gender differences perspective. Journal of Educational Psychology 88:365-377.
MM Bleeker and JE Jacobs (2004). Achievement in math and science: Do mothers’ beliefs matter 12 years later? Journal of Educational Psychology 96:97-109.
DT Burkam, VE Lee, and BA Smerdon (1997). Gender and science learning early in high school: Subject matter and laboratory experiences. American Educational Research Journal 34: 297-331.
J Cohen (1988). Statistical power analysis for the behavioral sciences. 2nd ed., Hillsdale, NJ: Erlbaum.
K Crowley, MA Callanan, HR Tenenbaum, and E Allen (2001). Parents explain more often to boys than to girls during shared scientific thinking. Psychological Science 12:258-261.
JS Eccles (1994). Understanding women’s educational and occupational choices: Applying the Eccles et al. model of achievement-related choices. Psychology of Women Quarterly 18:585-610.
H Gerson, SA Sorby, A Wysocki, and BJ Baartmans (2001). The development and assessment of multimedia software for improving 3-D spatial visualization skills. Computer Applications in Engineering Education 9:105-113.
J Handelsman, N Cantor, M Carnes, D Denton, E Fine, B Grosz, V Hinshaw, C Marrett, S Rosser, D Shalala, and J Sheridan (2005). More women in science. Science 309:1190-1191.
LV Hedges and BJ Becker (1986). Statistical methods in the meta-analysis of research on gender differences. In J. S. Hyde & M. C. Linn (Eds.), The psychology of gender: Advances through meta-analysis (pp. 14-50). Baltimore: Johns Hopkins University Press.
LV Hedges and A Nowell (1995). Sex differences in mental test scores, variability, and numbers of high-scoring individuals. Science 269:41-45.
M Hegarty and VK Sims (1994). Individual differences in mental animation during mechanical reasoning. Memory and Cognition 22(4):411-430.
JS Hyde (2005). The gender similarities hypothesis. American Psychologist 60:581-592.
JS Hyde, E Fennema, and SJ Lamon (1990). Gender differences in mathematics performance: A meta-analysis. Psychological Bulletin 107:139-155.
JS Hyde and MC Linn (1988). Gender differences in verbal ability: A meta-analysis. Psychological Bulletin 104:53-69.
MG Jones and J Wheatley (1990). Gender differences in teacher-student interactions in science classrooms. Journal of Research in Science Teaching 27:861-874.
A Kelly (1988). Gender differences in teacher-pupil interactions: A meta-analytic review. Research in Education 39:1-23.
VE Lee and DT Burkam (1996). Gender differences in middle grade science achievement: Subject domain, ability level, and course emphasis. Science Education 80:613-650.
MC Linn and AC Petersen (1985). Emergence and characterization of sex differences in spatial ability: A meta-analysis. Child Development 56:1479-1498.
M Lummis and HW Stevenson (1990). Gender differences in beliefs and achievement: A cross-cultural study. Developmental Psychology 26:254-263.
National Science Foundation (2002). Science and engineering degrees, 1966-2000 (NSF 02-327), Author Susan T. Hill. Arlington, VA: National Science Foundation. http://ww.nsf.gov/sbe/srs/ stats.htm.
National Science Foundation (2005). Science and engineering indicators 2004: Elementary and secondary education, mathematics and science coursework and student achievement. Arlington, VA: National Science Foundation. http://www.nsf.gov/statistics/seind04/.
NS Newcombe (2002). The nativist-empiricist controversy in the context of recent research on spatial and quantitative development. Psychological Science 13:395-401.
E Spelke (2005). Sex differences in intrinsic aptitude for mathematics and science? A critical review. American Psychologist 60(9):950-958.
HR Tenenbaum, CE Snow, KA Roach, and B Kurland (2005). Talking and reading science: Longitudinal data on sex differences in mother-child conversations in low-income families. Applied Developmental Psychology 26:1-19.
JK Thomas and KE French (1985). Gender differences across age in motor performance: A meta-analysis. Psychological Bulletin 98:260-282.
Trends in International Mathematics and Science Study (TIMSS) (2003). http://nces.ed.gov/pubs2005/ timss03.
R Vasta, JA Knott, and CE Gaze (1996). Can spatial training erase the gender differences on the water-level task? Psychology of Women Quarterly 20:549-568.
D Voyer, S Voyer, and MP Bryden, (1995). Magnitude of sex differences in spatial abilities: A meta-analysis and consideration of critical variables. Psychological Bulletin 117:250-270.
CREATING AN INCLUSIVE WORK ENVIRONMENT*
Sue V. Rosser
Ivan Allen School of Liberal Arts and Technology
Georgia Institute of Technology
Abstract
Faced with a severe shortage of scientists and engineers, exacerbated by changes in immigration policies in the wake of 9/11, the United States has renewed its efforts to diversify the scientific and technological workforce, including attracting and retaining women in academic science and engineering. At the dawn of the 21st century, several promising developments, particularly the National Science Foundation’s ADVANCE program, indicate the willingness of the scientific and engineering professions and the academy to address the under-representation of women in academic ranks that has continued for decades, despite federally and foundation-funded programs to increase the number of female faculty members (Rosser and Lane, 2002).
In March 1999 the Massachusetts Institute of Technology released “A Study on the Status of Women Faculty in Science at MIT”1 creating a stir that spread far beyond the institutional boundaries of MIT. More than one year later, MIT President Charles Vest hosted a meeting of the presidents, chancellors, provosts, and twenty-five women scientists from some of the most prestigious research univer-
|
* |
Paper presented at the National Academies Convocation on Maximizing the Success of Women in Science and Engineering: Biological, Social, and Organizational Components of Success, held December 9, 2005, in Washington, DC. |
|
1 |
Published in the MIT Faculty Newsletter XI (4). Available at http://web.mit.edu/fnl/women/women.html. |
sities in the country. At the close of the meeting on January 29, 2001, they issued a joint statement recognizing “that this challenge will require significant review of, and potentially significant change in, the procedures within each university, and within the scientific and engineering establishments as a whole.” (Campbell, 2001), thus acknowledging that institutional barriers have prevented women scientists and engineers from having a level playing field and that science and engineering might need to change to accommodate women.
Almost simultaneously, the National Science Foundation (NSF) initiated ADVANCE, a new awards program that provided funding of $17 million for fiscal year 2001. The program offers an award for institutional, rather than individual solutions to empower women to participate fully in science and technology. NSF encouraged institutional solutions because of “increasing recognition that the lack of women’s full participation at the senior level of academe is often a systemic consequence of academic culture” (NSF, 2001a). Under ADVANCE, NSF grants Institutional Transformation Awards, ranging up to $750,000 per year for up to five years, to promote the increased full participation and advancement of women; Leadership Awards recognize the work of outstanding organizations of individuals and enable them to sustain, intensify and initiate new activity (NSF, 2001a).
ADVANCE Institutions
In October, 2001 the first eight institutions receiving ADVANCE awards were announced (NSF, 2001b): Georgia Tech, New Mexico State, the University of California-Irvine, the University of Colorado-Boulder, the University of Michigan, the University of Puerto Rico, the University of Washington, and the University of Wisconsin-Madison. Hunter College joined the first round of ADVANCE awardee institutions in early 2002.
In 2003, NSF announced 10 second round institutional transformation grants: Case Western Reserve, Columbia University, Kansas State University, University of Alabama-Birmingham, University of Maryland-Baltimore County, University of Montana, University of Rhode Island, University of Texas-El Paso, Utah State, and Virginia Tech. The third round of ADVANCE institutional proposals should be announced early in 2006.
ADVANCE promises to go beyond individual research projects of women scientists and engineers that previous NSF initiatives such as Professional Opportunities for Women in Research and Education (POWRE), Faculty Awards for Women (FAW), Career Advancement Awards (CAA), and Visiting Professorships for Women (VPW) (Rosser & Lane, 2002) supported to solve problems with broader systemic and institutional roots such as balancing career and family.
Institutional Initiatives
The NSF-funded ADVANCE initiative and the MIT Report have brought attention to the need for institutional transformation to improve the daily lives of all faculty, particularly women scientists and engineers. Other institutions have undertaken transformation initiatives using their own funds. In the wake of issues raised by the comments made by President Summers on January 14, 2005, Harvard announced a $50 million initiative on May 16, 2005 in an attempt to address these issues (Pope, 2005). Princeton has undertaken several efforts, including an automatic one year family leave extension on the tenure track for both men and women, rather than placing the onus on the faculty member to ask for the extension (Bartlett, 2005).
Priorities for Institutional Change: Lessons from POWRE
To be most effective, proposed institutional changes should address the institutional barriers identified as most problematic by women scientists and engineers. Data from the almost 400 respondents to an e-mail survey of fiscal years 1997, 1998, 1999, and 2000 NSF Professional Opportunities for Women in Research and Education (POWRE) awardees reveal the barriers academic women scientists and engineers identify as most challenging to their careers. POWRE awardees were women who received peer-reviewed funding from a focused National Science Foundation program (NSF, 1997) from fiscal years (FY) 1997-2000. Because POWRE was the NSF initiative that ADVANCE replaced in 2001, the quantitative and qualitative data from the entire POWRE awardee cohort are particularly relevant in exposing the barriers that institutions should change to empower and enable women scientists and engineers.
Women scientists and engineers who were U.S. citizens at any rank in tenured, tenure track, or nontenure track positions at any four-year college, comprehensive, or research university were eligible to apply to POWRE. Although a few tenured full professors, faculty from four-year institutions, and/or nontenure track individuals received awards, the vast majority of POWRE awardees were untenured assistant professors in tenure track positions at research universities.
All POWRE new grant awardees were sent questionnaires via e-mail that included the question “What are the most significant issues/challenges/opportunities facing women scientists today as they plan their careers?” Overwhelming numbers of respondents across all 4 years found “balancing work with family” (Response 1) to be the most significant challenge facing women scientists and engineers (Table 2-3). When analyzed by disciplines, the responses of women remained remarkably similar across the disciplines, with balancing work with family responsibilities as the major issue for women from all disciplines (Rosser and Lane, 2002).
Table 2-4 groups the responses to Question 1 into four categories. Adding
TABLE 2-3 Total Responses to Question 1
|
Question 1: What are the most significant issues/challenges/opportunities facing women scientists today as they plan their careers? |
|||||||||
|
|
|
1997 |
1998 |
1999 |
2000 |
||||
|
Categories |
% of responses |
% of responses |
% of responses |
% of responses |
|||||
|
1 |
Balancing work with family responsibilities (children, elderly relatives, etc.) |
62.7 |
(42/67) |
72.3 |
(86/119) |
77.6 |
(76/98) |
71.4 |
(75/105) |
|
2 |
Time management/balancing committee responsibilities with research and teaching |
22.4 |
(15/67) |
10.1 |
(12/119) |
13.3 |
(13/98) |
13.3 |
(14/105) |
|
3 |
Low numbers of women, isolation and lack of camaraderie/mentoring |
23.9 |
(16/67) |
18.5 |
(22/119) |
18.4 |
(18/98) |
30.5 |
(33/105) |
|
4 |
Gaining credibility/respectability from peers and administrators |
22.4 |
(15/67) |
17.6 |
(21/119) |
19.4 |
(19/98) |
21.9 |
(23/105) |
|
5 |
“Two career” problem (balance with spouse’s career) |
23.9 |
(16/67) |
10.9 |
(13/119) |
20.4 |
(20/98) |
20.0 |
(21/105) |
|
6 |
Lack of funding/inability to get funding |
7.5 |
(5/67) |
4.2 |
(5/119) |
10.2 |
(10/98) |
8.6 |
(9/105) |
|
7 |
Job restrictions (location, salaries, etc.) |
9.0 |
(6/67) |
9.2 |
(11/119) |
7.1 |
(7/98) |
5.7 |
(6/105) |
|
8 |
Networking |
6.0 |
(4/67) |
<1 |
(1/119) |
0 |
(0/98) |
4.8 |
(5/105) |
|
9 |
Affirmative action backlash/discrimination |
6.0 |
(4/67) |
15.1 |
(18/119) |
14.3 |
(14/98) |
12.4 |
(13/105) |
|
10 |
Positive: active recruitment of women/more opportunities |
6.0 |
(4/67) |
10.1 |
(12/119) |
9.2 |
(9/98) |
14.3 |
(15/105) |
|
11 |
Establishing independence |
3.0 |
(2/67) |
0 |
(0/119) |
6.1 |
(6/98) |
2.9 |
(3/105) |
|
12 |
Negative social images |
3.0 |
(2/67) |
3.4 |
(4/119) |
2.0 |
(2/98) |
<1 |
(1/105) |
|
13 |
Trouble gaining access to nonacademic positions |
1.5 |
(1/67) |
1.7 |
(2/119) |
1.0 |
(1/98) |
1.9 |
(2/105) |
|
14 |
Sexual harassment |
1.5 |
(1/67) |
<1 |
(1/119) |
2.0 |
(2/98) |
1.9 |
(2/105) |
|
15 |
No answer |
0 |
(0/67) |
<1 |
(1/119) |
1.0 |
(1/98) |
1.9 |
(2/105) |
|
16 |
Cut-throat competition |
— |
— |
— |
— |
1.0 |
(1/98) |
1.9 |
(2/105) |
TABLE 2-4 Categorization of Question 1 Across Year of Award
|
Question 1: What are the most significant issues/challenges/opportunities facing women scientists today as they plan their careers? |
||||||
|
|
|
|
Means of responses |
|||
|
Categories |
Response numbersb |
1997 |
1998 |
1999 |
2000 |
|
|
A |
Pressures women face in balancing career and family |
1, 5, 7 |
31.9% |
30.8% |
35.0% |
32.4% |
|
Ba |
Problems faced by women because of their low numbers and stereotypes held by others regarding gender |
3, 4, 8, 10, 12 |
12.3% |
10.1% |
9.8% |
14.5% |
|
Ca |
Issues faced by both men and women scientists and engineers in the current environment of tight resources, which may pose particular difficulties for women |
2, 6, 16 |
10.0% |
4.8% |
8.2% |
7.9% |
|
D |
More overt discrimination and harassment |
9, 11, 13, 14 |
3.0% |
4.4% |
5.8% |
4.8% |
|
aThe alphabetic designation for categories B and C have been exchanged, compared with earlier papers (Rosser and Zieseniss, 2000) to present descending response percentages. bGiven the responses from all four years, after receiving faculty comments at various presentations of this research, and after working with the data, we exchanged two questions from both category B and D to better reflect the response groupings. Specifically, responses 10 and 12 (considered in category D in Rosser and Zieseniss, 2000) were moved to category B. Similarly, responses 11 and 13 (included in category B in Rosser and Zieseniss, 2000) were placed into category D. |
||||||
restrictions because of spousal situations (Responses 5 and 7) to “balancing work with family responsibilities” (Response 1) suggests that Category A-pressures women face in balancing career and family is the most significant barrier identified by women scientists and engineers. A second grouping (Responses 3, 4, 8, 10, and 12) appears to result from the low numbers of women scientists and engineers and consequent stereotypes that surround expectations about their performance. Isolation and lack of mentoring as well as gaining credibility and respectability from peers and administrators typify Category B. Category C (Responses 2, 6, 16) includes issues men and women scientists and engineers face in the current environment of tight resources that may pose particular difficulties for women because of their low numbers or their balancing act between career and family. For example, time management issues such as balancing committee responsibilities with research and teaching (Response 2) can be a problem for male as well as female faculty. However, because of their low numbers in science and engineering, women faculty are often asked to serve on more committees to meet gender diversity needs, even while they are still junior, and to advise more students, either formally or informally (Rosser and Zieseniss, 2000). Cut-throat competition makes it difficult for both men and women to succeed and obtain funding. Gender stereotypes that reinforce women’s socialization to be less overtly competitive may make it more difficult for a woman scientist or engineer to succeed in a very competitive environment. Category D (Responses 9, 11, 13, 14) identifies barriers of overt harassment and discrimination women scientists and engineers face. Sometimes even a positive response, such as active recruitment of women (Response 10) leads to backlash and difficulty gaining credibility from peers who assume a woman obtained her position because of affirmative action.
Example quotations from the respondents from all 4 years provide the qualitative context for the categories:
Category A: Pressures Women Face in Balancing Career and Family
-
“At the risk of stereotyping, I think that women generally struggle more with the daily pull of raising a family or caring for elderly parents, and this obviously puts additional demands on their time. This is true for younger women, who may struggle over the timing of having and raising children, particularly in light of a ticking tenure clock, but also for more senior women, who may be called upon to help aging parents (their own or in-laws). Invariably they manage, but not without guilt.” (2000 respondent 63)
-
“Managing dual-career families (particularly dual academic careers). Often women take the lesser position in such a situation. PhD women are often married to PhD men. Most PhD men are not married to PhD women.” (2000 respondent 16)
Category B: Problems Faced by Women Because of Their Low Numbers and Stereotypes Held by Others Regarding Gender
-
“The biggest challenge that women face in planning a career in science is not being taken seriously. Often women have to go farther, work harder, and accomplish more in order to be recognized.” (2000 respondent 21)
-
“In my field (concrete technology), women are so poorly represented that being female certainly creates more notice for you and your work, particularly when presenting at conferences. This can be beneficial, as recognition of your research by your peers is important for gaining tenure; it can also add to the already large amount of pressure on new faculty.” (2000 respondent 70)
Category C: Issues Faced by Men and Women Scientists and Engineers in the Current Environment of Tight Resources, Which May Pose Particular Difficulties for Women
-
“I have noticed some problems in particular institutions I have visited (or worked at) where women were scarce. As a single woman, I have sometimes been viewed as ‘available,’ rather than as a professional co-worker. That can be really, really irritating. I assume that single men working in a location where male workers are scarce can face similar problems. In physics and astronomy, usually the women are more scarce.” (1997 respondent 26)
-
“I still find the strong perception that women should be doing more teaching and service because of the expectation that women are more nurturing. Although research as a priority for women is given a lot of lip service, I’ve not seen a lot of support for it.” (2000 respondent 1)
Category D: More Overt Discrimination and/or Harassment
-
“There are almost no women in my field, no senior women, and open harassment and discrimination are very well accepted and have never been discouraged in any instance I am aware of.” (1998 respondent 53)
-
“I have often buffered the bad behavior of my colleagues—and over the years I have handled a number of sexual harassment or ‘hostile supervision’ cases where a more senior person (all of them male) was behaving inappropriately toward a lower social status woman (or in rarer cases a gay man).” (1999 respondent 59)
Models for best practices
Considerable research has revealed barriers such as balancing career and family, dual career issues, isolation, dearth of mentoring, and possible unconscious bias in search processes, negotiation, evaluation, as well as promotion and tenure, that may differentially impact appointment, retention, and advancement of women faculty. Coupling this research with evidence from climate surveys and experiences raised by faculty at their own institutions, models for some best practices have begun to emerge from ADVANCE institutions.
At the time of this conference, none of the ADVANCE institutions had completed their five-year institutional transformation grant, so evaluation of the success of these programs is not possible. However, progress towards goals may be gleaned from examination of the reports submitted annually to NSF on the projects (http://www.nsf.gov/advance) and from many of the ADVANCE institution websites. Although most of the efforts have centered on advancing junior women to senior ranks, anecdotal evidence and some preliminary data from my current research suggest that senior women scientists and engineers face different obstacles. Institutions need also to address these barriers to retain senior women and insure they reach their full potential. Preliminary data from the Georgia Tech ADVANCE project grant, which ends in fall 2006, suggest that more women have been promoted to full professor, endowed chairs, and administrative positions since the grant was obtained in October, 2001. See Figures 2-10, 2-11A, and 2-11B.
Family friendly policies and practices
To facilitate the balancing of career and family, perceived overwhelmingly by women scientists and engineers, particularly those of younger ages, as the major issues (Rosser, 2004), Georgia Tech instituted the following family friendly policies and practices: stop the tenure clock; active service, modified duties; lactation stations; and day care.2 Many other institutions have similar and additional policies, including for flexible work hours at Johns Hopkins3 and the University of Wisconsin,4 and shared positions for dual career couples at Cornell5 and Grinnell.6
|
2 |
The specific details of these policies can be accessed under Family and Work Policies at http://www.advance.gatech.edu. Retrieved on June 23, 2005. |
|
3 |
http://hrnt.jhu.edu/worklife/benefits/flex/index.cfm. Retrieved on November 21, 2005. |
|
4 |
http://www.secfac.wisc.edu/governance/legistlaiton/Pages300-399.htm#308. Retrieved on November 21, 2005. |
|
5 |
http://www.policy.cornell.edu/PDF_6613_Workplace_Flexibility.cfm. Retrieved on November 21, 2005. |
|
6 |
http://www.grinnell.edu/offices/dean/chairinfo/sharedpos/. Retrieved on November 21, 2005. |
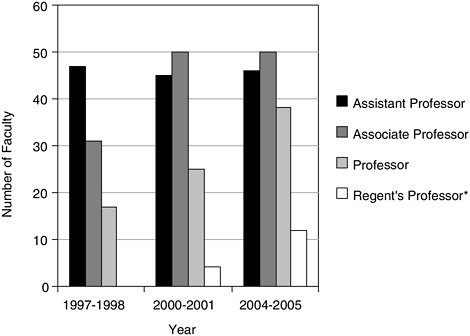
FIGURE 2-10 Georgia Institute of Technology female faculty by rank and year, institution-wide.
* Regent’s Professorships are a rare, distinguished promotion above the level of full professor, which are open to both men and women faculty at the research institutions in the University System of Georgia. A Regent’s Professorship is awarded only upon the unanimous recommendation of the president, the dean of the graduate school, the administrative dean, the academic dean, and three other members of the faculty to be named by the president, and upon the approval of the Chancellor and the Committee on Education.
Speed-mentoring
To assist junior faculty in preparation for tenure and/or promotion, Georgia Tech ADVANCE Professor Jane Ammons developed a workshop in which junior faculty members consult for 15 to 20 minutes with each of four experienced tenure case reviewers who identify gaps and offer suggestions for strengthening the tenure case. Even more women seeking promotion to full professor than tenure and promotion to associate professor attended the workshop, confirming information revealed in the climate survey that individuals understand the parameters less well for promotion to full professor.
Training of search committees
The University of Wisconsin-Madison has designed workshops to train search committees in good search methods, including sensitization to bias.7 This training includes cultivation of professional relationships with promising women scholars at professional meetings, active solicitation of applications from qualified women, and deliberate actions to overcome unconscious bias such as encouraging time for thorough review and evaluation of each individual to insure focus on data rather than impressions. Denice Denton, while at the University of Washington, developed a Faculty Recruitment Toolkit.8 The University of Michigan developed the STRIDE program, led by faculty to improve diversity and excellence in recruiting.9
Training of chairs and deans
Because top administrators can set the climate and standards for fostering inclusivity, programs to train department chairs to recognize and combat isolation, while nurturing inclusion become critical. The ADVANCE program at the University of Michigan worked with an interactive theater program that portrays typical academic situations and engages academic audiences in discussion around interpersonal behaviors affecting these issues. The University of Washington has developed a National UW ADVANCE Summer Leadership Workshop for Department Chairs.10
Training of tenure and promotion committees
To minimize gender, racial, and other biases in promotion and tenure, the Provost at Georgia Tech, who also serves as Principal Investigator on its ADVANCE grant, appointed a Promotion and Tenure ADVANCE Committee (PTAC) to assess existing promotion and tenure processes, explore potential forms of bias, provide recommendations to mitigate against them, and elevate awareness of both candidates and committees for expectations and best practices in tenure and promotion. After one year of study, the committee developed nine case studies with accompanying sample curriculum vitae that served as the basis for an interactive Web-based instrument. This interactive Web tool, Awareness
|
7 |
http://wiseli.engr.wisc.edu/products.htm. Retrieved on November 21, 2005. |
|
8 |
http://www.washington.edu/admin/eoo/forms/ftk_01.html. Retrieved on November 21, 2005. |
|
9 |
http://www.umich.edu/%7Eadvproj/stridepresents_files/fram.htm. Retrieved on November 21, 2005. |
|
10 |
http://www.engr.washington.edu/advance/workshops/National/Workshop/chair-workshop.html. Retrieved on November 21, 2005. |
of Decision in Evaluation of Promotion and Tenure (ADEPT), is designed to allow individuals to participate in a virtual promotion and tenure meeting.11
Each ADVANCE institution has evolved programs and policies to address similar issues on its campus. Most have at least one program that is unique, which if successful, might serve as a model for other institutions. Virginia Tech hosts the ADVANCE portal website for all ADVANCE institutional transformation awardees.12 As these models spread to other campuses where they undergo implementation and improvements, a national transformation of science and engineering may occur that fulfills the promise of the Science and Technology Equal Opportunities Act to create a scientific and technological community reflective of our diverse society.
References
T Bartlett (2005). More time. The Chronicle of Higher Education 52(2):A-16.
K Campbell (2001). Leaders of 9 universities and 25 women faculty meet at MIT, agree to equity reviews. MIT News Office. Available at http://web.mit.edu/newsoffice/nr/2001/gender.html.
National Science Foundation. (1997). Professional opportunities for women in research and education. Program announcement. Arlington, VA: National Science Foundation.
National Science Foundation. (2001a). ADVANCE. Program solicitation. Arlington, VA: National Science Foundation.
National Science Foundation. (2001b). ADVANCE Institutional Transformation Awards. http:// www.nsf.gov/advance. Retrieved on October 1, 2001.
J Pope (2005). Harvard to commit $50M to women’s programs. The Boston Globe (17 May). http:// www.boston.com/news/education/higher/articles/2005/05/17/html.
SV Rosser 2004. The Science Glass Ceiling: Academic Women Scientists and the Struggle to Succeed. New York: Routledge.
SV Rosser and EO Lane (2002). Key barriers for academic institutions seeking to retain women scientists and engineers: Family-unfriendly policies, low numbers, stereotypes, and harassment. Journal of Women and Minorities in Science and Engineering 8(2):161-190.
SV Rosser and M Zieseniss (2000). Final report on professional opportunities for women in research and education (POWRE) workshop. Gainesville, FL: Center for Women’s Studies and Gender Research.
|
11 |
The Web-based instrument, along with best practices from PTAC, and resources on bias can be accessed at http://www.adept.gatech.edu/ptac. Retrieved on June 23, 2005. |
|
12 |
The portal can be accessed at http://www.advance.vt.edu. Retrieved on June 23, 2005. |
LONG TIME NO SEE: WHY ARE THERE STILL SO FEW WOMEN IN ACADEMIC SCIENCE AND ENGINEERING?*
Joan C. Williams
UC Hastings College of the Law
Center for WorkLife Law
Abstract
After all these years, all these reports, all these initiatives, why does the percentage of women academics in science and engineering remain so low? The traditional response is to point to the “chilly climate” for women. That metaphor is outdated. What keeps women back is gender bias, although it does “not look like what we thought discrimination looked like.” The time has come to link the chilly climate with two literatures that have flowered since the “climate” metaphor was invented in 1982 by Roberta Hall and Bernice Sandler (Sandler et al., 1996; Sullivan, 2005).
The first is the growing literature in experimental social psychology on stereotyping and cognitive bias, which shows that many of the patterns that create a “built-in headwinds” for women in the sciences and engineering reflect documented patterns of gender bias (Griggs v. Duke Power Co., 401 U.S. 424 (1971)). The second is antidiscrimination law, which increasingly accepts stereotyping evidence in court and highlights that “chilly climate” patterns may be illegal. This article provides a very brief introduction to both literatures. Before it does so, it provides an even briefer introduction to a third discipline that provides crucial data for understanding why women’s progress has been so glacially slow: demography (Valian, 1998).
“It did not look like what we thought discrimination looked like.”
(MIT, 1999)
This article looks briefly at the demography that provides crucial context for understanding why women’s progress has been so glacially slow in academic positions in science and engineering. It then provides a brief introduction to the law and experimental social psychology relevant to understanding the “chilly climate.”
The ideal-worker schedule
The single most important statistic for understanding the dearth of academic women in science and engineering is that 95% of mothers aged 25 to 44 work less than 50 hours per week year-round1 (Williams, 2000, p. 2). All a university has to do to drive most mothers off the tenure track is to define full time as 50-60 hours a week. Given that roughly 82% of women have children, driving away most mothers means driving away a very high percentage of women (Williams & Cooper, 2004).
Thus schedule alone goes a long way towards explaining why there are so few women in academic science and engineering (the “STEM disciplines”): the average workweek for scientists in education is 50.6 hours/week (NSF, 2005).
Just as most men want a career that does not require them to sacrifice conventional family life, so do most women.2 For men, an academic career in the STEM disciplines typically does not require this sacrifice. For example, 68% of female physicists, but only 17% of male physicists, are married to other scientists, making the women much less likely than the men to have partners who can take care of the home front and leave the scientists with few responsibilities apart from working very long hours (McNeil, 1999).
Given that grant eligibility often is defined in terms of a certain number of years from PhD and that grant schedules typically do not allow time off for maternity leave, the STEM disciplines tend to idealize the worker who takes no time off for children. One result is that only 50% of tenured women academics in the STEM disciplines (but 70% of their male counterparts) have children (Mason and Goulden, 2002).
Indeed, the single-mindedness—and geographic mobility—required of academics in the STEM disciplines often mean that women sacrifice not only children but also marriage. This happens for two reasons. First, males are more likely to have a spouse who will follow them (Bielby, 1992); second, while career success in men is often considered an aphrodisiac (think Donald Trump), career success in women is a turn-off to many men.3 Thus tenured women in academia are twice as likely as men to remain unmarried (Mason and Goulden, 2002).
When women “opt out” of academic careers in the STEM disciplines (Belkin, 2003), it is often because they are faced with different choices than their male counterparts. Men are opting into a field that offers them a highly respected and intellectually challenging career that they can enjoy along with marriage and children. Women are opting out of a field that offers them a far less certain career path (due to glass-ceiling bias, described below), along with a high probability that they will have to sacrifice children and/or marriage along the way. Given their different contexts, that men and women make different choices is not (as we nonscientists like to say) rocket science.
Beyond culture and climate metaphors: glass-ceiling and maternal-wall stereotyping
In physics, “we select for assertiveness and single-mindedness.”
(Georgi, 2000)
As suggested above, the ideal worker is designed around men’s bodies (they need no time off for childbirth) and men’s life patterns (American women still do 65-80% of the childrearing) (Sayer, 2001). The result is gender stereotyping in professional norms and everyday interactions.
One of the problems with the “chilly climate” and “culture” metaphors is that they provide little guidance for employers seeking to achieve a proportional representation of women.4 WorkLife Law5 (which I founded and direct) has worked hard to describe patterns of stereotyping in a way that provides clear guidance on what universities can do to eliminate the patterns of bias that plague the lives of many women.
The first, and most familiar, pattern is “glass-ceiling” bias many women encounter simply because they are women. WorkLife Law has documented that working women often encounter a second major form of gender bias, which we term the “maternal wall.”6 This term refers to the fact that many women who do not experience glass-ceiling bias find themselves facing discrimination triggered by family responsibilities once they become mothers (Biernat, Crosby and Williams, 2004; Williams and Segal, 2003).
In an era when the number of gender discrimination suits is falling, maternal wall suits are rising sharply. WorkLife Law has identified over 600 cases involving family responsibilities discrimination, a 400% increase in the last decade
|
4 |
The chilly climate literature actually does better than the “climate” literature in describing the specific patterns that create problems for women. |
|
5 |
WorkLife Law is housed at UC Hastings College of the Law; http://www.worklifelaw.org. |
|
6 |
The “maternal wall” metaphor was introduced in Deborah J. Swiss and Judith P. Walker, Women and the Work/Family Dilemma (1993). |
(Still, 2005). Because maternal wall cases have a higher win-rate than do civil rights cases in general (50% versus 27%), the potential for liability is substantial (Still, 2005). Thirty-seven verdicts and settlements have topped $100,000, with one over $11 million (Calvert, 2005).
A new role is emerging for gender stereotyping in maternal-wall cases. The traditional way of proving discrimination under Title VII of the Civil Rights Act of 1964 is by comparing the experience of a woman plaintiff to the experience of a “comparator”: a similarly situated man. Yet in Back v. Hastings-on-Hudson, 365 F.3d. 107 (2d Cir. 2004), the Second Circuit Federal Court of Appeals allowed a case to go to trial despite the fact that the plaintiff lacked a comparator: She could not point to a similarly situated male school psychologist, because school psychologists typically are women. Yet Elana Back could, and did, identify significant evidence of gender stereotyping of mothers, notably the view (expressed by her principal and the head of human resources) that mothers are not committed to their careers.
Back clarified how stereotyping evidence can be used in federal discrimination cases, building on the glass-ceiling case of Price Waterhouse v. Hopkins, 490 U.S. 228 (1989). Price Waterhouse, through expert testimony of prominent social psychologist Susan Fiske, established that stereotyping evidence could be used to help a plaintiff prove sex discrimination. Price Waterhouse involved “hostile prescriptive stereotyping.” A highly successful woman candidate for partner was told that she needed to “walk more femininely, talk more femininely, wear make-up,” and “go to charm school”; in effect, behaving in a traditionally feminine manner was treated as a job requirement.
A third case added another key piece of the puzzle. In Lust v. Sealy Inc., 383 F.3d 580 (7th Cir. 2004), the jury awarded the plaintiff over $1 million (later reduced). The lower court decision was upheld in a Seventh Circuit opinion that turned, in part, on a form of stereotyping called “cognitive bias.” Cognitive bias is the bias that stems from the way our minds work in processing information (Krieger, 1995; Blasi, 2002). In Lust, the supervisor engaged in a form of cognitive bias called “attribution bias.” When a man told the supervisor that he was interested in a promotion, the supervisor assumed that he was ready, willing, and able to move his family, whereas when Ms. Lust told the supervisor that she was interested in a promotion, he assumed (without asking her) that she would not move to take the job.
Price Waterhouse, Back, and Lust seem to signal that courts are ready, willing, and able to begin accepting evidence of gender stereotyping in discrimination cases. This interpretation seems all the more convincing given that while the opinion in one of the landmark 2004 cases (Back) was written by a liberal judge (Judge Guido Calibresi, former dean of Yale Law School), the opinions in the two others were written by leading conservative judges (Judges Richard Posner and Frank Easterbrook). These developments suggest a movement to accept stereotyping evidence that crosses ideological boundaries in an era when the
federal courts are becoming increasingly conservative. Courts’ increasing willingness to rely on stereotyping evidence is particularly important in academic cases because it provides an alternative method of proving discrimination in an employment context where comparators are often hard to find (AAUW, pp. 20-21).
Making bias visible in academic workplaces
Currently, the stereotyping literature is largely limited to experimental studies or meta-analyses confined to a specific theoretical approach. To be useful in guiding everyday workplace interactions, this literature must be consolidated and described in a way that is both scientifically responsible and readily understandable. What follows is WorkLife Law’s attempt to do so.
The glass ceiling
The glass ceiling is composed of two distinct patterns: one makes it more difficult for women to establish themselves as competent; the other penalizes women for being too competent. Each pattern is described very briefly below, followed by an example from academia (from sciences or engineering, if one could readily be found) as well as references to the experimental social psychology literature.7
Trying twice as hard to achieve half as much: Patterns that make it more difficult for women to be perceived as competent
-
Women are judged on their accomplishments; men on their potential (Williams, 2003, pp. 416-417; McCracken, 2000, p. 159).
-
He’s a “nascent scholar…soon to blossom”; she is unqualified due to lack of publications (Lam v. University of Hawaii, 59 Fair Empl. Prac. Cas. (BNA) 113 (1991))
-
“She’s too feminine.”
-
One faculty member voting against a female faculty member’s tenure commented, “[her] problem in attracting graduate students was that she was too ‘feminine’ in that she was too ‘unassuming, unaggressive, unassertive and not highly motivated for vigorous interpersonal competition.’” (Zahorick v. Cornell University, 729 F.2d 85, 89-90 (2d Cir. 1984); West, 1994, p. 132) Note the covert reliance on the association of femininity with low competence.
-
An accomplished female chemistry professor was characterized as “nice” and “nurturing” but not tenure material; a similarly accomplished man might well be seen as a good colleague and a good mentor.8 (Weinstock v. Columbia University, 224 F.3d 33 (2nd Cir. 2000); Williams, 2004, pp. 45-47)
-
“He’s skilled; she’s lucky.” Social psychologists long ago noted the tendency to attribute a man’s successes to skill, while a woman’s successes tend to be attributed to luck. This is an instance of “attribution bias” (Williams, 2003, p. 416; Swim & Sana, 1996).
-
“Anger is unseemly in a woman.” Another example of attribution bias: An angry woman is a witch or a bitch, while an angry man is excused on the grounds that he understandably would not tolerate being “jerked around.”
-
Recall bias. “Recall bias” is when women’s mistakes are remembered forever but men’s are soon forgotten (Williams, 2003, p. 417; Heilman, 1995, p. 6).
-
Gender-biased rewards. Men are sometimes given greater rewards than women for the same accomplishment (Williams, 2003, p. 418; Brewer, 1996, p. 63).
-
Objective rules are no guarantee of objectivity. Rules that are apparently objective can be framed around men or masculinity in ways that systematically disadvantage women. In addition, studies have documented leniency bias, when objective rules are applied rigidly to women, but flexibly to men (Williams, 2003, p. 415; Brewer, 1996, p. 65).
-
Polarized evaluations. In some institutions, woman superstars thrive, but women who are merely excellent are given much lower evaluations than similarly situated men. This key question is “whether a female schlemiel can do as well as a male schlemiel” (Williams, 2003, p. 418; Krieger, 1995, p. 1193; Yoder, 1994).
-
Are women isolated and “out of the loop”? Many academic departments in the STEM disciplines are overwhelmingly male. Studies have shown that women experience the problems of tokenism until women comprise 18-20% of a given workplace or department, a statistic that suggests that most women in science and engineering are at risk of being isolated and out of the loop (Williams, 2004; Biernat, 1998, p. 304; Taylor, 1981, p. 84).
-
Social isolation is one reason single women without children in the bench sciences consider leaving academia (Mason and Goulden, 2002).
-
Is the job defined in terms of masculine patterns? Recall the quote that academic physics is defined in terms of assertiveness and single-mindedness (Georgi, 2000). Single-mindedness, as noted above, is a polite way of describing the requirement that, to be successful, a scientist must either eschew family life or enjoy a flow of domestic services from a spouse that is common among men but
-
rare among women. Assertiveness signals that the personality characteristics assumed to be required for success in science often track those traditionally associated with men. When a job is defined in terms that confuse masculinity with job qualifications, bias against women occupants of the job is likely to be commonplace (Williams, 2003, pp. 408-409; Heilman, 1993, p. 280).
-
Mother, princess, pet. An extremely important point, rarely understood, is that environments plagued by gender bias do not affect all women in the same way. Women are stereotyped by subtype, not as a generalized group (Glick and Fiske, 2001, p. 113; Williams, 2003, p. 419). In some departments, women who play stereotypically feminine roles are taken into the in-group and do well, while women who do not adhere to traditionally feminine behavior are stigmatized. Established feminine roles documented by social psychologists include the mother, who may take charge of departmental teas and comfort; the princess, who aligns herself with powerful men; the pet, who is nonthreatening and cuddly; and Ms. Efficiency, who acts as a glorified but subservient secretary (Taylor, 1981, p. 84).
-
“[Faculty] don’t realize that often they—men and women—expect women to make [their colleagues] feel comfortable, and [they] don’t expect men to make [their colleagues] feel comfortable.” (AAUW, 2004, p. 35)
-
“[My wife did not get tenure because] she had not played at being a good daughter to the older and more traditional men on the faculty, giggling at their jokes and massaging their egos.” (West, 1994, p. 145, quoting Robert Reich)
-
Subtype revisited: feminist. Stereotype content studies show negative associations with the label “feminist”. (Glick and Fiske, 2002) When a woman stands up for herself or women’s rights and is characterized as “shrill,” “a feminazi,” or a “fanatical feminist,” this is evidence of gender bias. (Note that we no longer hear claims that African-Americans “have it coming” if they are “too uppity”: Women, too, should be able to stand up for their group without being demonized.)
Patterns that penalize women for being too competent
Sometimes women are disadvantaged because they do not conform to their colleagues’ image of how women should behave.
-
“He’s assertive, she’s aggressive” (Taylor, 1981, p. 103).
-
According to Martin Snyder of the American Association of University Professors, recent collegiality cases “all came down to the same thing. They’re all-male dominated departments that hadn’t tenured a woman in a long time, or ever, and there’s some language about how the woman ‘just doesn’t fit in.’ What comes through is that these are aggressive women who are seen as uppity.” (Lewin, 2002)
-
“To get ahead here [at MIT], you have to be so aggressive. But if women are too aggressive they’re ostracized …” (Haak, 1999)
-
Catch-22. “… and if they’re not aggressive enough they have to do twice the work.” (Haak, 1999). The leading case, Price Waterhouse v. Hopkins, 490 U.S. 228, 250 (1989), christened this a “Catch-22” and treated it as potentially illegal gender discrimination.
-
Ambivalent sexism. In some departments, a woman may have to choose between being liked, but not respected, or respected, but not liked (Glick and Fiske, 1999). Neither path leads to tenure.
-
Her colleagues were “indifferent, if not hostile, to her accomplishments.... Ironically, her prestige and status outside the university grew as her status at the university diminished and became more precarious.” (AAUW, 2004, p. 58)
-
She’s a “bitter, selfish” effective manager. Women managers tend to be categorized as either unqualified because they are ineffective managers or as unqualified because they are effective but have personality problems (Heilman, 2001). This again stems from the fact that the qualities associated with traditionally masculine professions such as scientist, engineer, and manager closely track the qualities associated with a typical man, but not those associated with a typical woman.
-
“There might be a perception that, as a woman, [a woman candidate] should have a warm and fuzzy personality. [Name of candidate] is not a warm and fuzzy person…”. (AAUW, 2004, p. 35)
-
“She’s a shameless self-promoter; he knows his own worth”. Particularly if a woman colleague is socially isolated, she may well have no mentor who can highlight her accomplishments. Yet if she does so herself, studies show that self-promotion in women may well trigger negative reactions not triggered by self-promotion in men (Eagley and Karau, 2002, p. 584; Williams, 2003, p. 425).
-
Sexual harassment of successful women. Sexual harassment is one way sexist men have of controlling women they find threatening. This is typically a “no win” situation for women: A survey by the American Management Association found that even if the woman is the victim, she is just as likely as the offender to be dismissed or transferred (Grimsley, 1996).
The maternal wall
-
Jobs defined in masculine terms, revisited. As noted above, the ideal academic worker reflects a template designed around masculinity (Williams, 2000). When the ideal worker designed around men, no wonder so few women measure up.
-
An unsuitable job for a mother: role incongruity. Particularly when the ideal worker is defined as requiring a 24/7 commitment, being an academic may be seen as inconsistent with being a mother. (Williams, 2003, pp. 430-431; Etaugh and Gilomen, 1989; Eagly and Steffen, 1986, p. 254; Kobrynowicz and Biernat, 1997, p. 593).
-
In a case with a reported settlement of nearly $500,000, a memo was
-
circulated saying, “As a mother of two infants, she had responsibilities that were incompatible with those of a full-time academician.”9 (Schneider, 2000).
-
“Loose lips”: prescriptive stereotyping, benevolent or hostile (Glick and Fiske, 2001; Burgess and Borgida, 1999). Hostile prescriptive stereotyping prescribes that mothers should stay home with their children. Kinder, gentler “benevolent” prescriptive stereotyping is when a department attempts to do a mother a favor by, for example, not allocating travel funds because they assume that children need their mothers and that mothers will not want to travel. (Note that the solution is to simply ask the mother, rather than making assumptions.)
-
A department chair argued that a woman did not need her job as much as a man because she was married (and presumably her husband could support her) (AAUW, 2004, p. 5).
-
Maternal wall attribution bias. An absent man is giving a paper; an absent woman is assumed to be home with her children (even if she is at a conference). (Williams, 2003, pp. 433-434; Eagley and Karau, 2002, p. 589; Kennelly, 1999, p. 176)
-
Maternal wall leniency bias. Mothers are held to longer hours and to higher performance and punctuality standards. (Williams, 2003, p. 433; Correll and Benard, 2005)
-
Negative competence assumptions associated with motherhood. A 2005 study found that “relative to other kinds of applicants, mothers were rated as less competent, less committed, less suitable for hire, promotion, and management training, and deserving of lower salaries.” (Correll & Benard, 2005)
-
According to one scientist, “The perception of me [after] having a child is that my profession is not the priority anymore….” (Bombardieri, 2005)
-
“Several female professors believed that pregnancy had hampered their chances for tenure because they were viewed as less serious about or committed to their careers” (AAUW, 2004, p. 27).
Earlier stereotype content studies show that, although businesswomen are rated as high in competence, similar to businessmen, housewives are rated as extremely low in competence, alongside stigmatized groups such as the elderly, blind, “retarded,” and disabled (Glick and Fiske, 2002; Eckes, 2002, p. 110).
-
“If you…have your child on campus, colleagues who recognize you when you are by yourself now only see you as a walking uterus and ignore you.” (Mason, 2003, p. 2)
-
Part-time work is an independent trigger for negative competence assumptions. Women who work part-time may get the worst of both worlds: They are seen as less competent workers than women who work full time and less compe-
-
tent mothers than homemakers10 (Williams, 2004, p. 388). (Note that women who trigger negative competence assumptions often are held to a higher standard, which is illegal under federal antidiscrimination law, as discussed below.)
-
A female professor claimed that her pregnancy, which has caused her to switch to part-time tenure track (among other things) led her institution to hold her to a higher standard than similarly situated males (AAUW, 2004, p. 50).
-
The maternal wall can trigger gender wars among women. Often the maternal wall triggers fights among professional women, which can be particularly acute in the sciences given that 50% of women academic scientists have no children (Mason and Goulden, 2002). Some of these women are childfree—cultural entrepreneurs who are trying to invent an image of a full, female life without children, and may feel that mothers who demand “special treatment” are reinforcing stereotypes that women can’t measure up (Burkett, 2000). Others are childless, regretful they did not have children. They may well ask why mothers should “have it all” when they themselves had to make a choice between career and having a family (ignoring the fact that most male academics “have it all” as a matter of course) (Hewlett, 2002). When the maternal wall pits women against women, this is a result of gender discrimination; yet it is often cited as evidence that “this is not a gender problem.”
-
Family responsibilities discrimination against men. The technical name for maternal wall discrimination is family responsibilities discrimination (FRD), because it can affect men as well as women. When men seek to take on traditionally feminine caregiving roles, they may well suffer even more severe consequences than do women. A study of over 500 employees found that, when compared to mothers, fathers who took a parental leave were recommended for fewer rewards and viewed as less committed, and fathers with even a short work absence due to a family conflict were recommended for fewer rewards and had lower performance ratings (Dickson, 2004).
-
An untenured professor told his mentor that he did not dare even to ask about parental leave, much less take it (Source: confidential).
-
A father was denied a child-rearing leave routinely available to women (Shafer v. Board of Public Education, 903 F.2d 243, 244 (3rd Cir. 1990)).
Chilly climate patterns may be evidence of illegal gender discrimination
While this is not the forum for a full discussion of the potential for legal liability, a brief review of the applicable law serves to highlight that many pat-
terns that comprise the “chilly climate” are potentially illegal. Where available, an academic example or two is provided.
Title VII of the Civil Rights Act of 1964: Disparate treatment
(42 USC § 2000e-2 (a)(1))
As noted above, the first way of proving disparate treatment is to show that a woman plaintiff is treated differently than a comparator, as when a man is hired based on his potential, but a woman with the same qualifications is not hired because she is judged strictly on what she has already accomplished. As also noted above, even in the absence of a comparator (or in addition to comparator evidence), a plaintiff can rely on evidence of gender stereotyping (Back, 2004).
-
A psychology professor called the WorkLife Law hotline. She had outstanding job evaluations from peers and students—until she had a baby. After her baby was born, she still got high evaluations from students, but not from her colleagues. The head of her department engaged in intense scrutiny of her office hours, although he did so for no other member of the department, a classic example of a woman being treated differently than the relevant male comparators. In addition, the department head and members of her tenure committee stated that, “[P]eople who prioritize family do not make tenure,” a statement that reflects maternal wall stereotyping.
Title VII of the Civil Rights Act of 1964: Disparate impact
(42 USC § 2000e-2 (a)(2))
A facially neutral policy that disproportionately impacts women may be illegal if it is not justified by business necessity. Even if the policy is justified by business necessity, the employer may be liable if the plaintiff can show that an alternative less discriminatory policy could accomplish the same goal. (42 USC § 2000e-2 (k)(1)(A). An example of a policy that has a disparate impact on women is a university policy that denies proportional benefits to professors on part-time tenure track; the university would argue business necessity.
Title VII of the Civil Rights Act of 1964: Sexual harassment
(42 USC § 2000e-2)
Quid pro quo (your body or your job)
-
A senior professor remarked to a woman colleague that her refusal of his sexual advances was “no way to get tenure.” (AAUW, 2004, p. 61)
Hostile environment
-
Some women academics have reported that they themselves are sexually harassed when they blow the whistle against other faculty members who have harassed women. (AAUW, 2004, p. 13)
-
One woman professor alleged hostile work environment when a department celebrated a colleague’s birthday with a “boob cake.” A male faculty called her a lesbian because she turned down dates with male faculty members. Women signed up for the department athletic team only to be turned down and insulted. The plaintiff was given unusually heavy teaching and service loads but was not allowed to teach graduate courses. Women were asked to appear at many functions to present an image that the department had a substantial number of women on the faculty (which they did not) (AAUW, 2004, p. 29).
Title VII of the Civil Rights Act of 1964: Constructive discharge
Constructive discharge occurs when an employer imposes intolerable working conditions stemming from unlawful discrimination or harassment that would compel a reasonable person to quit (Center for WorkLife Law, 2006, pp. 29-31).
Title VII of the Civil Rights Act of 1964: Retaliation (42 USC § 2000e-3(a))
An employer is prohibited from retaliating against women for engaging in conduct Title VII protects. In some jurisdictions, retaliation is defined narrowly, and covers only situations in which a woman reports alleged harassment and discrimination to a civil rights enforcement agency. In others, retaliation is defined more broadly, and also covers reporting discrimination or harassment to management, having a lawyer write a letter alleging discrimination, refusing to settle a prior claim of discrimination, or stating an intention to file a civil rights complaint (Center for WorkLife Law, 2006, pp. 33-37). Retaliation may well be easier to prove than the underlying discrimination case.
-
A woman professor was denied tenure after she advocated better treatment of female graduate students and faculty; in particular, she publicly objected to the disproportionate service responsibilities assigned to women (AAUW, 2004, p. 17).
-
A women professor was retaliated against when she complained of pay inequity in violation of the EPA and of her denial of tenure (AAUW, 2004, p. 21).
-
A professor who objected to the treatment of women after childbirth was branded a troublemaker and fired at the first opportunity (AAUW, 2004, p. 26).
Equal protection (a constitutional claim) (42 USC. § 1983)
Academics who teach in public universities can recover if they can prove that men were disadvantaged as compared with women, as when leave is routinely offered to women but men are forbidden or severely discouraged from taking it. Women in public universities also can sue if they are not given equal protection of the law.
Equal Pay Act
It is illegal to pay higher salaries to men than to women doing “equal work” in jobs that require substantially “equal skill, effort, and responsibilities … under equal working conditions” (29 USC § 206(d)(1)). One federal case, Lovell v. BBNT Solutions, LLC, 295 F. Supp. 2d 611 (E.D. VA. 2003), refused to apply a categorical rule excluding a part-time chemist from being compared to full-time chemists, in a ruling that suggests that professors on part-time tenure track should be paid the proportion of their salary equal to the proportion of a full-time schedule they work (for example, 75% pay for a 75% workload).
-
When a female professor was hired she was told that the institution was prohibited from paying her more than a specified base salary and $5,000 as an administrative stipend, only to later discover that other professors were paid more (AAUW, 2004, p. 22).
Pregnancy Discrimination Act (PDA) (42 USC § 2000e-(k))
Employers are required to treat pregnant professors “the same” as other workers whose ability to work is similar. Evidence of a violation of the PDA includes stereotyping pregnant women as incompetent or not committed to their careers, stripping a pregnant woman of duties and opportunities, or imposing conditions on her that are not applied to nonpregnant employees.
-
One professor alleged that, in her department, pregnant professors’ chances for tenure were hampered because they were viewed as less serious, less committed to their careers, and because of animosity stemming from the way their teaching responsibilities were reallocated to their colleagues (AAUW, 2004, p. 27).
-
Another professor alleged that pregnant women were not treated the same as other professors because, while the university gave assistant professors an extra year for a variety of reasons, it refused to stop the tenure clock after she had a baby, thereby making her record appear weaker than those of her colleagues. Another colleague had the clock stopped for a year but was not told that the university expected an extra year’s publications despite their agreement to stop the clock.
-
An institution required pregnant women to choose between the parental
-
leave benefit available to men and women (a course release) and their 6- to 8-week maternity disability leave; other faculty members were granted disability leave without being required to sacrifice another benefit in order to obtain it.
Family Medical Leave Act of 1993 (FMLA) (29 U.S.C. § 2601)
Denial of leave: The FMLA gives professors the legal right to up to 12 weeks of unpaid leave per year if the employee or her child, partner, or parent has a serious health condition, or if she has or adopts a child. Giving leave is mandatory.
Interference with leave: In addition to denying leave, covered employers are prohibited from interfering with leave.
-
Female faculty hesitated to take the four-week disability leave immediately after birth, sensing “pressure … not to take it.” Candidates for leave were told that “[t]aking a four week maternity leave may be seen by some members of the committee as a lack of commitment to career, and a premeditated plan to [impose on their colleagues].” In this context, a female faculty member was in the classroom five days after she gave birth11 (AAUW, 2004, p. 28).
Americans with Disabilities Act (ADA) (42 USC § 12101)
Employees may not be discriminated against because they are caring for a family member whose illness or disability is covered by the ADA.
Title IX (20 USC § 1681)
The federal government can block all federal funding to an academic institution if it discriminates on the basis of sex, parental status, primary caregiver status, or pregnancy in its educational programs. This “atom bomb” sanction is rarely used. Title IX also allows professors to sue for discrimination, although some jurisdictions limit their ability to receive damages (Center for WorkLife Law, 2006, pp. 63-64).
Conclusion
This article introduces a very different language for talking about gender bias in the STEM disciplines than the traditional metaphors of the “chilly climate” or the “academic culture” (Sandler, et al., 1996; Stanford, 1993; Mervis, 2002; Trower and Chait, 2002). While these metaphors have played a useful role, it is
time to re-examine them. Developments in experimental social psychology and the law offer more concrete and effective guidance on how to improve the status of women.
The approach outlined here, I believe, is important for two reasons. First, recent studies show that, while diversity training shows no demonstrable effect in increasing the numbers of minorities and women, litigation—or the potential for it—does often spur institutional change (Kalev, Dobbin, and Kelly, 2005; Pedriana and Stryker, 1997). Second, the booming literature on cognitive bias shows that while stereotype activation is automatic, stereotype application can be controlled (Sommers and Ellsworth, 2001; Blair, 2002). Before stereotypes can be controlled, however, they must first be recognized. The approach outlined in this article has the potential to spur that process by making stereotyping and bias visible in the STEM disciplines.
References
American Association of University Women (2004). Tenure denied: cases of sex discrimination in academia. Washington, DC: AAUW Education Foundation and Legal Advocacy Fund, http://www.case.edu/president/aaction/TenureDenied.pdf.
Back v. Hastings-on-Hudson Union Free School District, 365 F.3d. 107 (2d Cir. 2004).
L Belkin (2003). The opt-out revolution. New York Times Magazine October 26:42.
WT Bielby and D Bielby (1992). I will follow him: family ties, gender-role beliefs, and reluctance to relocate for a better job. American Journal of Sociology 97(5):1241-1267.
M Biernat, CS Crandall, LV Young, D Kobrynowicz, and SM Halpin (1998). All you can be: stereotyping of self and others in a military context. Journal of Personality and Social Psychology 75(2):301-317.
M Biernat, FJ Crosby, and JC Williams (2004). The maternal wall. Journal of Social Issues 60(4):675-683.
IV Blair (2002). The malleability of automatic stereotypes and prejudice. Personality and Social Psychology Review 6:242-261.
G Blasi (2002). Advocacy against the stereotype: Lessons from cognitive social psychology. University of California, Los Angeles Law Review 49(5):1241-1281.
M Bombardieri (2005). Reduced loan lets faculty meld family, tenure track. Boston Globe. October 4.
MB Brewer (1996). In-group favoritism: the subtle side of intergroup discrimination. In Codes of conduct: behavioral research into business ethics, eds. DM Messick and AE Tenbrunsel, New York: Russell Sage Foundation.
E Burkett (2000). The baby boom. New York: The Free Press.
D Burgess and E Borgida (1999). Who woman are, who women should be: descriptive and prescriptive gender stereotypes in sex discrimination. Psychology, Public Policy and Law 5:665-687.
C Calvert (2005). E-mail to Joan C. Williams. November 7, 2005.
Center for WorkLife Law (2006). WorkLife Law’s guide to caregiver discrimination (forthcoming).
Civil Rights Act of 1964, Title VII. 42 USCS § 2000e-2.
SJ Correll and S Benard (2005). Getting a job: Is there a motherhood penalty? Presentation at American Sociological Association Annual Meeting, August 15, 2005, Philadelphia, PA. http://sociology.princeton.edu/programs/workshops/Correll_Benard_manuscript.pdf.
CE Dickson (2004). The impact of family supportive policies and practices on perceived family discrimination, (dissertation).
AH Eagly and SJ Karau (2002). Role incongruity theory of prejudice toward female leaders. Psychology Review 109:537-598.
AH Eagly and VJ Steffen (1986). Gender stereotypes, occupational roles, and beliefs about part-time employees. Psychology of Women 10:252-262.
T Eckes (2002). Paternalistic and envious gender prejudice: testing predictions from the stereotype content model. Sex Roles 47:99-114.
Equal Pay Act. 29 USC § 206 (d)(1).
Equal Protection. Section 1983, 42 USC § 1983.
C Etaugh and G Gilomen (1989). Perceptions of mothers: effects of employment status, marital status, and age of child. Sex Roles 20:59-70.
C Etaugh and C Moss (2001). Attitudes of employed women toward parents who choose full-time or part-time employment following their child’s birth. Sex Roles 44:611-619.
Family and Medical Leave Act of 1993. (29 U.S.C. § 2601).
H Georgi (2000). Is their an unconscious discrimination against women in science? The American Physical Society News 9(1):27-30. http://www.aps.org/apsnews/0100/010016.cfm.
P Glick and ST Fiske (2002). A model of (often mixed) stereotype content: competence and warmth respectively follow from perceived status and competition. Journal of Personality and Social Psychology 82:878-902.
P Glick and ST Fiske (2001). An ambivalent alliance: hostile and benevolent sexism as complementary justifications for gender inequality. American Psychology 58:109-118.
P Glick and ST Fiske (1999). (Dis)respecting versus (dis)liking: Status and interdependence predict ambivalent stereotypes of competence and warmth. Journal of Social Issues 55:473-489.
Griggs v. Duke Power Co., 401 U.S. 424 (1971).
American Management Association survey cited in KD Grimsley (1996). Co-Workers Cited in Most Sexual Harassment Cases; Management Group’s Study Disputes Stereotype. The Washington Post, June 14, p. D01.
L Haak (1999). Women in Neuroscience: The first twenty years. Journal of the History of Neuroscience 11:70-79.
S Hewlett (2002). Creating a life: professional women and the quest for children. New York: Talk Miramax Books.
ME Heilman (2001). Description and prescription: How gender stereotypes prevent women’s ascent up the organizational ladder. Journal of Social Issues 57:657-674.
ME Heilman (1995). Sex stereotypes and their effects in the workplace: What we know and what we don’t know. Journal of Social Behavior and Personality 10 (3):3-26.
ME Heilman (1993). Sex bias in work settings: The lack of fit model. In Research in Organizational Behavior, eds. LL Cumings and BM Staw. Greenwich, CT: JAI Press.
A Kalev, F Dobbin, and E Kelly (2005). Best Practices or Best Guesses? Diversity Management and the Remediation of Inequality. Working Paper. Department of Sociology, Harvard University.
I Kennelly (1999). That single mother element: How white employers typify black women. Gender and Society 14:168-192.
D Kobrynowicz and M Biernat (1997). Decoding subjective evaluations: How stereotypes provide shifting standards. Journal of Experimental Social Psychology 33:579-601.
LH Krieger (1995). The content of our categories: A cognitive bias approach to discrimination and equal employment opportunity. Stanford Law Review 47:1161-1248.
Lam v. University of Hawaii, 59 Fair Empl. Prac. Cas. (BNA) 113 (1991).
T Lewin (2002). “Collegiality” as a tenure battleground. New York Times, July 12, p. A12.
Lovell v. BBNT Solutions, LLC, 295 F. Supp. 2d 611 (E.D. Va. 2003).
Lust v. Sealy, 383 F.3d 580 (7th Cir. 2004).
C MacKinnon (1987). Feminism unmodified: discourses of life and law. Cambridge, MA: Harvard University Press.
MA Mason (2003). UC Berkeley faculty work and family survey: preliminary findings, http:// universitywomen.stanford.edu/reports/UCBfacultyworknfamilysurvey.pdf.
MA Mason and M Goulden (2002). Do babies matter? The effect of family formation on the lifelong careers of academic men, and women. Academe, November-December. http://www.aaup.org/ publications/Academe/2002/02nd/02ndmas.htm.
Massachusetts Institute of Technology (1999). A study on the status of women faculty in science at MIT. The MIT Faculty Newsletter 11 (4):14-26, http://web.mit.edu/fnl/women/women.html.
DM McCracken (2000). Winning the talent war for women: Sometimes it takes a revolution. Harvard Business Review, http://hbswk.hbs.edu/item.jhtml?id=1840&t=organizations.
L McNeil (1999). Dual-career-couples: Survey results. http://www.physics.wm.edu/~sher/survey3.html.
J Mervis (2002). Can equality in the sports be repeated in the lab? Science 298:356.
National Science Foundation (2005). All in a week’s work: average work weeks of doctoral scientists and engineers, http://www.nsf.gov/statistics/infbrief/nsf06302/nsf06302.pdf.
N Pedriana and R Stryker (1997). Political culture wars 1960s style: Equal employment opportunity-affirmative action law and the Philadelphia plan. American Journal of Sociology 103(3):633-691.
Pregnancy Discrimination Act 42 USC § 2000e (k).
Price Waterhouse v. Hopkins, 490 U.S. 228 (1989).
BR Sandler, LA Silverberg, and RM Hall (1996). The Chilly Classroom Climate: A Guide to Improve the Education of Women. Washington, DC: The National Association of Women in Education.
LC Sayer (2001). Time, use, gender, and equality: Differences in men’s and women’s market, non-market, and leisure time. Unpublished doctoral dissertation, University of Maryland, College Park.
A Schneider (2000). University of Oregon settles tenure lawsuit over maternity leave. The Chronicle of Higher Education (July 21), p. A12.
Shafer v. Board of Public Education, 903 F.2d 243 (3rd Cir. 1990).
SR Sommers and PC Ellsworth (2001). White juror bias: An investigation of racial prejudice against Black defendants in the American courtroom. Psychology, Public Policy, and Law 7:201-229.
Stanford University (1993). Report of the Committee on the Recruitment and Retention of Women Faculty at Stanford. M. Strober, Chair.
M Still (2005). E-mail to Joan C. Williams, December 7.
AV Sullivan (2005). Breaking anonymity: The chilly climate for women faculty by the chilly collective, http://fcis.oise.utoronto.ca/~hep/Sullivan.html.
JK Swim and LJ Sana (1996). He’s skilled, she’s lucky: a meta-analysis of observers’ attribution for women’s and men’s successes and failures. Personality and Social Psychology Bulletin 22(5):507-519.
DJ Swiss and JP Walker (1993). Women and the Work/Family Dilemma. New Jersey: John Wiley and Sons.
SE Taylor (1981). A categorization approach to stereotyping. In Cognitive Processes in Stereotyping and Intergroup Behavior, ed. DL Hamilton. New Jersey: Lawrence Erlbaum Associates.
CA Trower and RP Chait (2002). Faculty diversity: Too little for too long. Harvard Magazine (March-April):33-38. http://www.harvardmagazine.com/on-line/030218.html.
V Valian (1998). Why so slow? The advancement of women. Cambridge, MA: MIT Press.
Weinstock v. Columbia University, 224 F.3d 33 (2nd Cir. 2000)
M West (1994). Gender bias in academic robes: The law’s failure to protect women faculty. Temple Law Review 67:68-178.
JC Williams (2004). Hitting the maternal wall. Academe, http://www.aaup.org/publications/Academe/ 2004/04nd/04ndwill.htm.
JC Williams and HC Cooper (2004). The public policy of motherhood. Journal of Social Issues 60(4):849-865.
JC Williams and N Segal (2003). Beyond the maternal wall: relief for family caregivers who are discriminated against on the job. Harvard Women’s Law Journal 26:77-162.
JC Williams (2003). The social psychology of stereotyping: Using social science to litigate gender discrimination cases and defang the “cluelessness” defense. Employee Rights and Employment Policy Journal 7(2):401-458.
JC Williams (2000). Unbending gender: Why work and family conflict and what to do about it. New York, NY: Oxford University Press.
JD Yoder (1994). Looking beyond numbers: the effect of gender status, job prestige, and occupational gender-typing on tokenism processes. Social Psychology Quarterly 57:150-159.
Zahorick v. Cornell University, 729 F.2d 85, 89-90 (2d Cir. 1984)
SOCIAL INFLUENCES ON SCIENCE AND ENGINEERING CAREER DECISIONS1
Yu Xie
University of Michigan
Abstract
Our study on the career processes and outcomes of women in science has four major components. First, rather than focusing on specific segments of a science/engineering (S/E) career, we studied the entirety of a career trajectory. Second, we analyzed seventeen large, nationally representative datasets. Third, we tried to be as objective and “value-free” as possible and to emphasize empirical evidence. Finally, we based the book on a life-course approach, a combination of special methodological perspectives which recognize the following phenomena:
-
Interactive effects across multiple levels, such as the individual level, the family level, and the school level. Individuals do not live or work in isolation from one another.
-
Interactive effects across multiple domains, such as education, family, and work. What we do in one domain of our lives affects what we do in other domains.
-
Individual-level variations in career tracks resulting from differences among individuals, even those with the same demographic characteristics.
-
The cumulative nature of the life course. What happened before affects what happens now, and what is happening now affects what comes next. This is also called “path-dependency.” Because of path dependency, small differences at particular points in time can deflect trajectories and subsequently generate large differences in career outcomes.
|
1 |
This presentation is based on the book Yu Xie co-authored with Kimberlee Shauman entitled, Women in Science: Career Processes and Outcomes, published by Harvard University Press in 2003. |
*Paper presented at the National Academies Convocation on Maximizing the Success of Women in Science and Engineering: Biological, Social, and Organizational Components of Success, held December 9, 2005, in Washington, DC.
The life course approach places a high demand on data. Ideally, we would like to have longitudinal data over the entire career of many scientists and non-scientists. We looked very hard but were not able to find a perfect data set. Lacking such a data set, we were still able to carry out our study by piecing together many datasets to paint a composite picture of gender differences in science careers, a method which is called synthetic cohort in demography. Figure 2-12 shows the data sets that we used to look at different segments of science/engineering careers.
Needless to say, our study contains complicated and nuanced analyses. These analyses led us to conclude that women’s severe underrepresentation in science and engineering is an extremely complex social phenomenon that defies any attempt at simplistic explanations. Due to the complex and multi-faceted nature of women scientists’ career processes and outcomes, especially how these processes and outcomes affect, and are affected by, other life course events such as marriage and childbearing, we were uncomfortable recommending concrete policy interventions intended to increase women’s representation in science and engineering No single explanation or hypothesis testing should or could substitute for the richness of the empirical results from these analyses, though we did consider and reject several widely accepted hypotheses, as the following discussion shows.
The “Critical Filter” Hypothesis
One longstanding hypothesis in the literature is that women are less likely to pursue science/engineering careers because they are handicapped by deficits in high school mathematics training. In a classic statement of this position, Sells (1980) claims that “[a] student’s level of high-school mathematics achievement acts as a critical filter for undergraduate college admission for blacks and limits choices of an undergraduate major for women in general once they are admitted to college.” This hypothesis is appealing for its simplicity and the clear remedy it implies.
From our research, we find that the gender gap in average mathematics achievement is small and has been declining since the 1960s (see Table 2-5). The numbers in Table 2-1 are mean gender differences in math achievement scores (in standard deviation units). The declining trend shown in Table 2-5 casts doubt on the interpretation that the gender gap in math achievement reflects innate, perhaps biological, differences between the sexes. We also find that the gender gap in representation among top achievers remains significant (see Table 2-6). This finding was cited by Harvard President Larry Summers in his remarks at an NBER conference on January 14, 2005, which made international news. However, President Summers failed to cite the following finding: gender differences in neither average nor high achievement in mathematics explain gender differences in the likelihood of majoring in science/engineering fields.2
TABLE 2-5 Standardized Mean Gender Difference of Math Achievement Scores Among High School Seniors by Cohort
|
School Cohort |
Mean Difference (d) |
Data Source |
|
1960 |
–0.25*** |
NLS-72 |
|
1968 |
–0.22*** |
HSBSr |
|
1970 |
–0.15*** |
HSBSo |
|
1978 |
–0.13** |
LSAY1 |
|
1980 |
–0.09*** |
NELS |
|
*p<.05 **p<.01 ***p<.001 (two-tailed test), for the hypothesis that there is no mean difference between males and females. |
||
TABLE 2-6 Female-to-Male Ratio of the Odds of Achieving in the Top 5% of the Distribution of Math Achievement Test Scores Among High School Seniors by Cohort
|
School Cohort |
Achievement Ratio |
Data Source |
|
1960 |
0.45*** |
NLS-72 |
|
1968 |
0.47*** |
HSBSr |
|
1970 |
0.48*** |
HSBSo |
|
1978 |
0.25*** |
LSAY1 |
|
1980 |
0.60*** |
NELS |
|
*p<.05 **p<.01 ***p<.001 (two-tailed test), for the hypothesis that there is no mean difference between males and females. |
||
The Pipeline Paradigm
A dominant perspective in the literature on women in science is the “pipeline” paradigm. According to this paradigm, the process of becoming a scientist can be conceptualized as a pipeline, called the “science pipeline,” which is essentially a developmental process. Change in the developmental process along the life course is unidirectional—leaving science versus staying in science.
However, we find career processes to be fluid and dynamic. Exit, entry, and reentry are real possibilities. Many persons, especially women, become scientists through complicated processes rather than by just staying in the pipeline. Also, we show that participation gaps are greatest at the transition from high school to college. This is illustrated in Figure 2-13.
In Figure 2-13, we observe that in the senior year of high school, women are much less likely than men to plan a science/engineering major in college. In addition, women experience a much larger attrition from the science/engineering educational trajectory than men do at the transition from high school to college. In the later college years, however, we find women and men to have similar transition rates to attaining degrees in science and engineering.
The “Productivity Puzzle”
In an influential paper, Cole and Zuckerman (1984) state that “women published slightly more than half (57%) as many papers as men.” They found that the gender gap had persisted for many decades at this level and could not find any explanations for it. Out of despair, they called this gender difference the “productivity puzzle.” Later, Long (1992), after considering possible explanations, reaffirms this characterization with the observation that “none of these explanations has been very successful.”
We analyzed data from four nationally representative surveys of faculty in postsecondary institutions in 1969, 1973, 1988, and 1993.3 Two major findings emerged from our work about the puzzle. First, sex differences in research productivity declined sharply between the 1960s and the 1990s, even without any controls. This is shown in Figure 2-14. Women scientists’ research productivity has improved because their overall structural positions, such as institutional affiliation, have improved. This improvement in women’s productivity relative to men’s suggests that the large gender gap observed for earlier decades should not be attributed to innate biological differences between men and women.
Second, most of the observed sex differences in research productivity can be attributed to sex differences in background characteristics, employment positions and resources, and marital status. This is shown in Table 2-7. The first line of Table 2-7 reproduces the observed trends presented earlier in Figure 2-14. In lower lines, we included statistical adjustments for the fact that women and men differ in relevant characteristics, such as rank, year from a bachelor’s degree to PhD, and institutional affiliation. Thus, even in the earlier decades, the observed sex differences in productivity can be explained once these relevant attributes are controlled for.
Family Life and Women Scientists’ Careers
A common theme is the importance of considering the family in studies of women in science. In particular, we find that it is not marriage per se that hampers women’s career development. Married women appear to be disadvantaged only if
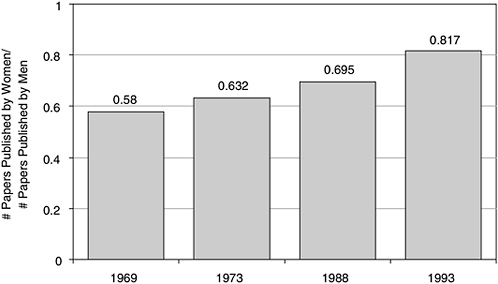
FIGURE 2-14 Trends in female-male ratio of publication rate.
TABLE 2-7 Estimated Female-to-Male Ratio of Publication
|
Model Description |
1969 |
1973 |
1988 |
1993 |
|
(0): Sex |
0.580*** |
0.632*** |
0.695** |
0.817 |
|
(1): (0) + Field + Time for PhD + Experience |
0.630*** |
0.663*** |
0.800 |
0.789* |
|
(2): (1) + Institution + Rank +Teaching + Funding + RA |
0.952 |
0.936 |
0.775 |
0.931 |
|
(3): (2) + Family/Marital Status |
0.997 |
0.971 |
0.801 |
0.944 |
|
*p<.05 **p<.01 ***p<.001 (two-tailed test), for the hypothesis that there is no mean difference between males and females. |
||||
they have children. For example, we show that, relative to their male counterparts, married women with children are less likely to pursue careers in science and engineering after the completion of science/engineering education4 less likely to be in the labor force or employed, less likely to be promoted,5 and less likely to be geographically mobile.6 Although some of the gender differences are attributable to the advantages that marriage and parenthood bestow upon men, they clearly suggest that being married and having children create career barriers that are unique to women—as opposed to men—scientists.
TABLE 2-8 Female-to-Male Odds Ratio of Post-Baccalaureate Career Paths by Family Status
|
Family Status |
Grad School or Work |
Grad School |
Grad School in S/E |
Work in S/E |
|
Single |
0.90 |
1.02 |
0.77 |
0.78** |
|
Married without children |
0.28*** |
0.67 |
0.11** |
0.72** |
|
Married with children |
0.05*** |
0.35* |
|
0.39*** |
|
*p<.05 **p<.01 ***p<.001 (two-tailed test), for the hypothesis that there is no mean difference between males and females. |
||||
Table 2-8 presents the female-to-male odds ratio of post-baccalaureate career paths by family status. There are five destinations for graduates with a bachelor’s degree in science and engineering: (1) out of work and school altogether, (2) graduate school in science/engineering, (3) graduate school in nonscience/ engineering, (4) work in science/engineering, and (5) work in nonscience/engineering. For the five outcomes, we made four contrasts and found that in all four, married women with children are disadvantaged in terms of science/engineering careers. Column 1 shows that married women with children are less likely than men to either work or attend graduate school. In column 2, we see that they are less likely than men to be in graduate school rather than working. Furthermore, married women with children are less likely than men to be in science/engineering, either in work (column 3) or in graduate school (column 4). Similarly, we also find married women with children disadvantaged in terms of other labor force outcomes.7
Summary
While the conventional wisdom often draws on casual analyses of non-representative data, our tentative conclusions are based on very good data and careful analyses. Table 2-9 shows the contrast between conventional wisdom and our findings.
There appear to be two types of simplistic explanations. At one extreme, some observers claim that gender differences in science are all due to innate biological differences between men and women. At the other extreme, some scholars are tempted to make a sweeping claim that all gender differences are due to discrimination against women in school and at work. Our research shows that both positions are wrong. Otherwise, it would not be possible to explain either the rapid improvement of women’s position in science, which cannot be attributed to
TABLE 2-9 Comparison Between Conventional Thinking and Our Findings
|
Conventional Wisdom |
Our Findings |
|
|
change in biological differences between the sexes, or the interaction between gender and parental status, which suggests that factors outside educational and work settings play an important role.
Women’s underrepresentation in science/engineering has deep social, cultural, and economic roots that will not be transformed by a few isolated policy interventions or programs. Increasing women’s representation in science/engineering requires many social, cultural, and economic changes that are large-scale and interdependent. After spending ten years searching for explanations, our research indicates we should stop looking for simple explanations and easy fixes, as attractive as they may be to us as human beings. Instead, we should look at the actual social processes that generate gender differences in science, and base policy interventions on empirical knowledge about these processes. Finally, while there may be policy changes that could address some of the complex reasons for women’s underrepresentation, we should not expect any individual policy change to bring about gender equity in science overnight.
References
JR Cole and H Zuckerman (1984). The productivity puzzle: Persistence and change in patterns of publication of men and women scientists. Advances in Motivation and Achievement 2:217-258.
JS Long (1992). Measures of Sex Differences in Scientific Productivity. Social Forces 71:159-178.
LW Sells (1980). The mathematics filter and the education of women and minorities. In: Women and the Mathematical Mystique, eds. L Fox, L Brody, and D Tobin. Baltimore, MD: Johns Hopkins University Press.
Y Xie and KA Shauman (1998). Sex differences in research productivity revisited: New evidence about an old puzzle. American Sociological Review 63:847-870.
Y Xie and KA Shauman (2003). Women in Science: Career Processes and Outcomes. Cambridge, MA: Harvard University Press.