4
Between “Design” and “Bricolage”: Genetic Networks, Levels of Selection, and Adaptive Evolution
ADAM S. WILKINS
The extent to which “developmental constraints” in complex organisms restrict evolutionary directions remains contentious. Yet, other forms of internal constraint, which have received less attention, may also exist. It will be argued here that a set of partial constraints below the level of phenotypes, those involving genes and molecules, influences and channels the set of possible evolutionary trajectories. At the top-most organizational level there are the genetic network modules, whose operations directly underlie complex morphological traits. The properties of these network modules, however, have themselves been set by the evolutionary history of the component genes and their interactions. Characterization of the components, structures, and operational dynamics of specific genetic networks should lead to a better understanding not only of the morphological traits they underlie but of the biases that influence the directions of evolutionary change. Furthermore, such knowledge may permit assessment of the relative degrees of probability of short evolutionary trajectories, those on the microevolutionary scale. In effect, a “network perspective” may help transform evolutionary biology into a scientific enterprise with greater predictive capability than it has hitherto possessed.
BioEssays Editorial Office, 10/11 Tredgold Lane, Napier Street, Cambridge CB1 1HN, United Kingdom.
The analysis of complex molecular networks has become widespread in biology in recent years. The initiating event for this development was the publication of some landmark papers that argued for the ubiquity of so called “scale-free” networks in numerous biological systems and human communications networks (Barabasi and Albert, 1999; Jeong et al., 2000). Subsequent analysis (Doyle et al., 2005) has undermined the case for the near-universality of scale-free networks, but the general importance of networks as organizational devices is undisputed. In biology, an understanding of the structure and dynamics of genetic networks, in particular, is now widely viewed as crucial to understanding phenomena as diverse as metabolic systems, phage developmental switches, protein interaction systems, transcriptional controls, and complex developmental traits. Indeed, the study of molecular and genetic networks is central to the new field of systems biology (Strogatz, 2003).
The fundamental concept of genetic networks, however, is hardly new. A hint of the intricacy of the genetic architecture that underlies complex morphological traits, and of the complexity of the genetic interactions involved, can be found in a seminal paper on the gene by H. J. Muller (1922). Furthermore, the concept of genetic networks was implicit in much of C. H. Waddington’s work (1940, 1957), although he did not use the term. Most importantly, however, the structure of genetic networks (in particular, one class of genetic networks, those underlying the biochemistry of mammalian coat colors) was central to the work of S. Wright (1968, 1980). Beyond these three great pioneers of 20th century biology, S. Kauffman added a molecular dimension to network-thinking with an early, if necessarily rather abstract, exploration of the generic structural properties of regulatory genetic networks (Kauffman, 1971). Not least, R. H. Britten and E. Davidson produced some thought-provoking schemes of how transcriptional networks might operate (Britten and Davidson, 1969, 1971). These specific hypotheses have not held up, but the basic thinking was prescient. It was, however, only the confluence, more than two decades later, of advances in genetics and molecular techniques in the 1990s with the then-new graph theory analyses of various networks (Barabasi and Albert, 1999; Jeong et al., 2000) that launched the current wave of interest amongst biologists, in networks generally and, more specifically, in genetic networks (reviewed in Wilkins, 2007a).
An important part of this recent scientific development has been a focus on the evolutionary dynamics of networks (Dorogovtsev and Mendes, 2003; Barabasi and Oltvai, 2004; Berg et al., 2004; Manke et al., 2006). In principle, this theoretical work should provide a significant bridge between systems biology and evolutionary biology. In reality, however, there has remained a gap between the theoretical work on genetic network evolution and its application to understanding organismal evolution.
There seem to be two major reasons for this persisting “disconnect” between systems biology and evolutionary biology. First, the actual analysis of the kind of genetic networks that underlie complex morphological traits is more difficult, at both the conceptual and technical levels, than the analysis of some of the other kinds of networks (metabolic, protein interactomes, etc.) (Wilkins, 2007b). Second, a great deal of highly productive work in understanding the genetic basis of adaptive trait evolution is possible without reference to networks, simply through the traditional focus on individual genes and their immediate interacting partners, as will be discussed below. In effect, it seems that the importance of genetic networks for development and evolution can be fully accepted at the theoretical level while being essentially ignored in the experimental exploration of evolutionary change.
In this article, however, I will present the case that a genuine integration of network-thinking into evolutionary genetics can greatly enrich our understanding of evolutionary events. In particular, in the final part, I will present an argument that a deeper understanding of particular genetic networks, in conjunction with an appreciation of the generic properties of such networks, can, in principle, permit a larger predictive (or “retrodictive”) element in evolutionary biology than has hitherto been possible.
EVOLUTIONARY METAPHORS AND THINKING ABOUT GENETIC NETWORKS
Each kind of network has its own distinctive kind of components and its own dynamics of behavior. Hence, each category requires a distinct analytical approach to identify its elements, dynamics, and evolutionary potentialities. However, in general, identifying the elements and boundaries of developmental genetic networks, which underlie morphological traits, is especially difficult (Wilkins, 2007b). These practical difficulties compound the interpretative problems in understanding the evolution of these networks. In the light of those vagaries, it becomes pertinent to ask what general perspective one should adopt for thinking about genetic networks and organismal evolution. The pioneering work of S. Wright (1968) on biochemical networks treated their genetic foundations as fixed entities, in both composition and connectivity, whose alternative behaviors were solely a function of the allelic properties of particular components. Developmental genetic networks, however, are evolutionarily more fluid entities, with a much wider range of capabilities for genetic alteration in both composition and behavior, as will be explained below. It becomes important, therefore, to be clear about the conceptual framework these networks require before proceeding to their detailed analysis or the
exploration of their evolution. Inevitably, that perspective will be influenced by the general evolutionary metaphor that one subscribes to.
Judging from their ubiquity, metaphors seem to be a universal aid to thinking, both in normal life and in science. For instance, the large number of creation myths to explain the origins of the world may differ greatly between different cultures, but nearly all are extended metaphors of either construction or birth. As these myths illustrate, the general appeal of metaphors is that they concretize otherwise mysterious processes, events, or objects and make them more accessible. At the same time, if used repetitively, or taken too literally, they can constrict thinking and obscure deeper understanding, as exemplified by the hold that the various creation myths have in various religious and ethnic subcultures.
In evolutionary biology, perhaps more than in any other branch of biology, the use of metaphors is especially marked. Evolutionary biology, in fact, was founded on a metaphor, “natural selection,” which was Darwin’s explanation of the evolutionary process by means of a term that leaned on the ways that breeders artificially select and develop new varieties of animals and plants. Other, and later, evolutionary metaphors include such figures of speech as “the adaptive landscape,” “the Red Queen hypothesis,” “the molecular clock,” and “Muller’s ratchet.” Two of the most prominent metaphors, however, are those of “design” and “bricolage.” Design, in fact, figures in the title of the Colloquium from which this article results, and, as Francisco Ayala discusses in this volume (Chapter 1), the challenge for evolutionary biologists is to explain how seemingly well designed features of organisms, where the fit of function to biological structure and organization often seems superb, is achieved without a sentient Designer. In reality, although organisms often seem designed efficiently for one trait, much is clearly suboptimal and many morphological/anatomical traits are baroque in their construction, defying the simplest notions of what constitutes good design. Furthermore, even the optimality of the well designed features is often at the slight expense of other traits, the phenomenon of “tradeoffs” (Sibly, 2002).
In contrast, the alternative metaphor of evolution as a tinkerer, engaged in piecemeal construction or bricolage, seems at first to be more apposite than that of design. Evolution clearly works by adapting preexisting structures to new purposes, many in ways that no sensible human engineer would have used. The evolution of certain reptilian jaw joint bones into two of the middle ear bones of the mammalian ear is a classic example of such evolutionary tinkering (Hopson and Crompton, 1969). Although the general concept of makeshift evolutionary construction from preexisting features was inherent in Darwin’s thinking (Darwin, 1886), it was given prominence in contemporary evolutionary biology by Francois Jacob (1977). His special insight was that evolutionary tinkering takes
place not only at the morphological level but at the genetic level as well, with the use of “old” genes for new purposes. This latter process is now referred to as either “gene co-option” (Raff, 1996; True and Carroll, 2002) or “gene recruitment” (Wilkins, 2002), and its ubiquity and importance in evolution have been amply documented since Jacob’s landmark paper (Duboule and Wilkins, 1998; True and Carroll, 2002).
MOLECULAR CONSTRAINTS ON EVOLUTIONARY TINKERING
Although the metaphor of bricolage seems far more appropriate for describing the evolutionary process than design, it too is somewhat misleading. It implies a higher degree of freedom about the elements that are borrowed and used in new evolutionary ways than is probably the case. The verb in French, “bricoler,” often connotes an almost haphazard throwing of things together to see what happens and what works rather than the slightly more methodical procedure one associates with the term “tinkerer.” Although there are no experimental studies yet of the constraints involved in gene recruitment, consideration of the basic properties of the properties of molecules and of the requirements of the process suggest that there are two kinds of general constraint that must operate. The first is the set of preexisting properties of the recruited molecule, permitting its adoption for new roles. When a transcription factor (TF) is evolutionarily recruited for a new activity (Duboule and Wilkins, 1998; True and Carroll, 2002), it must possess certain properties that confer capability for the new function, properties not shared with many other TFs. In effect, not any TF has equal potential for turning on, or repressing, a new gene or set of genes; the gain-of-function activity that a TF gene recruitment event comprises is determined by both the structure of the TF and the TF-binding sites in the enhancers of the target gene(s) (Davidson, 2001; Wray et al., 2003). Second, the recruited gene must be already expressed in the cell/tissue where its new function initially takes place, or the mutation that leads to the recruitment event is one that prompts the de novo expression of the recruited TF, making it available for a new use. In the latter cases, presumably additional mutations would be required to optimize the expression or the function (or both) of the recruited molecule. There is, as yet, no direct evidence for such optimization after recruitment, but it seems an unavoidable conclusion from what is known about structure–function relationships in regulatory macromolecules. There is, however, good comparative evidence from bacteria for the converse situation, namely the relationship of structural properties to the probability of evolutionary loss of function. Evolutionary loss or substitution of TFs is influenced both by the kind of activity possessed by the factor (whether
positive, negative, or both) and the chromatin structure in which such factors operate (Hershberg and Margalit, 2006).
Hence, the tinkering/borrowing process at the molecular level is somewhat more channeled, thus restricted, than the metaphor of bricolage might suggest. In addition, however, it has become equally clear over the past decade that the recruitment process is often not a gene at a time but a functional grouping of genes, a network “module” (Davidson, 2006). This is most obviously relevant in the cases where a preexisting signal transduction pathway becomes recruited, via an enabling mutation, to a new use. But it almost certainly also involves certain functional groupings of TFs. The Six-Dach-eya functional ensemble of TFs was first identified as a key component in the fruit fly eye development network (reviewed in Kumar, 2001) but later found in muscle development (Heanue et al., 1999) and then in still other developmental processes (Li 2003). In principle, the initial mutational event may elicit only a single activity, but that single recruited gene then induces or activates other members of the network modules. The distinction is that between “primary” and “secondary” recruitment (Wilkins, 2002). The induction of eye development in nonstandard sites by ectopic expression of Pax6 in Drosophila (Halder et al., 1995) is currently one of the best pieces of evidence that network module recruitment can take place in this way. The crucial point is that the recruitment of modules is made possible by the prior evolutionary-selective history that constructed and optimized performance of the network module.
The relevance of these points to organismal evolution is that it is the particular combination of network modules used that determines the composition of the entire genetic network governing a trait (Fig. 4.1) (Davidson, 2006; Wilkins, 2007b). Each module, however, is not, in itself, a rigidly delimited gene set, in either evolution or development, particularly in its downstream (“output”) target genes. The set of target genes is almost certainly evolutionarily labile (Davidson, 2006) while it seems inevitable that the overall molecular machinery, with its plethora of regulatory devices (from alternative splicing to a host of posttranslational modifications), will affect the particular degree of activity of various members of the output target gene set differentially in different cellular contexts (within and between organisms).
The network module, however, is only one kind of modular unit in the genetic and regulatory machinery that influences the outcomes of genetic recruitment events. The fact that most complex proteins are made up of distinct domains, with different kinds of domains shared between members of the same or even distantly related gene families (Alberts et al., 1989), constitutes a further layer of modular complexity and one that influences the behavior of those gene products that have this structure.
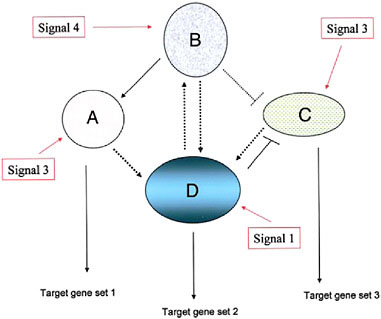
FIGURE 4.1 A schematic diagram of a simple genetic network, consisting of four component modules, signified by ovals and circles (with the component, interacting genes not indicated). Each module’s expression is evoked by an external signal that can be one derived external to the cell (environmental, cell matrix-derived, hormonal, etc.) or by an internal gene product from another genetic module. Three of the modules depicted here have outputs in the form of target gene sets including cytodifferentiation gene products (A, D, and C) whereas one module (B) is purely regulatory. (Adapted from Wilkins, 2007b.)
Finally, there is the modular nature of the enhancer and silencer units that control whether and where and how long a particular gene product is expressed (reviewed in Davidson, 2001, 2006; see also Prud’homme et al., 2007, Chapter 6, this volume).
Mutational events that affect either the structure or the presence/ absence of particular domains within the encoded gene product or that affect the transcriptional modular units must influence how the respective genes are used in particular recruitment events. An example is the use of alternative v domains in the adhesion protein CD44 (Ruiz et al., 1995),), which can dramatically alter specific cellular capabilities of the expressing cells. The ubiquity of alternative splicing as a source of functionally altered proteins (Xing and Lee, 2006), however, serves as a general indicator of the importance of alterations in domain structure and composition as an input to regulatory change (Alonso and Wilkins, 2005). With respect to
transcription, the detailed structural organization of enhancer/silencer modules clearly establishes their activity as on/off switches (Davidson, 2001). In effect, mutational events at both the protein domain and transcription module levels must exert influences “upward” in the sequence of molecular interactions while selection must influence which ones are preserved and then amplified within the population in which those mutational events first occur. The relationships between these modular levels and the screening activity of natural selection is diagrammed in Fig. 4.2. If this point of view is validated by further analysis and experimental findings, it must be taken into account in the continuing debate about “levels of selection.” Thus, below the level of the individual organism (the primary Darwinian “unit of selection”) there are not just genes (as in the traditional levels-of-selection argument) but additional levels of genetic–molecular organization, namely genetic networks and their modules, that natural selection actively screens.
To sum up: if one accepts this view of a molecular sequence of upward interactions, with the effects of mutational events feeding through from the DNA sequence level, at the lowest modular levels, to that of network modules and networks, and selection screening downward through this
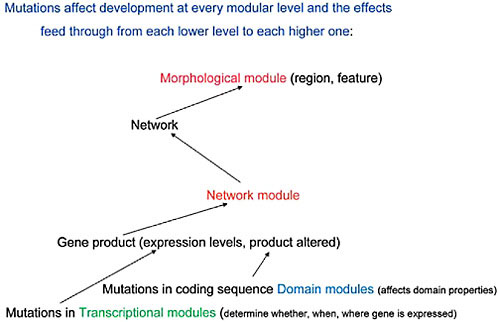
FIGURE 4.2 A diagrammatic representation of the effects of mutations at each modular level and the ways these transmit upward, within the developing organism, to affect the next modular level of organization.
hierarchy, then the nature of the gene tinkering process is seen to be much less haphazard than the process connoted by the term “bricolage,” having more built-in molecular constraints yet, at the same time, lacking the goal-directed nature of a process that is implied by the term “design.”
BUT IS A NETWORK PERSPECTIVE TRULY NECESSARY TO UNDERSTAND ADAPTIVE EVOLUTIONARY CHANGES?
All of the above statements can be accepted, however, without embracing the idea that the network perspective is needed for experimental research in evolution. A case can be made that a sufficient understanding of the genetic basis of adaptive evolutionary changes emerges from classic quantitative trait locus and molecular single gene-based experimental perspectives and that neither the concept of networks nor detailed knowledge of particular networks is needed for actual progress. This position is seemingly bolstered by recent success in understanding the genetic foundations of several adaptive traits, work that has underlined the key importance of a small number of specific genes. These cases involve finch beak dimensions in Darwin’s finches, characteristics related directly to specific feeding adaptations (Abzhanov et al., 2004, 2006); the adaptive evolution of bat wings for flight (Sears et al., 2006; Weatherbee et al., 2006); and the adaptive loss of pelvic armature in freshwater sticklebacks (Shapiro et al., 2004; Colosimo et al., 2004).).
The adaptive radiation of Darwin’s finches, with their different kinds of beaks suitable for different feeding adaptations, is one of the classic instances of evolutionary divergence due to natural selection (Lack, 1947). Abzhanov et al. (2004) have identified two key gene activities that are associated, respectively, with beak depth and width, on one hand and beak length on the other. The first characteristic, beak depth and width, is correlated with and evidently determined by an elevated level of activity of bone morphogenetic protein 4 (BMP4) during a critical phase of beak development. In contrast, finch beak length is evidently linked to a specific elevation of calmodulin activity during beak development (Abzhanov et al., 2006).).
The analysis of the genetic basis of bat wing evolution bears some similarity. A key component in the evolution of the distinctive wings of bats is the elevation in activity during a key phase of forelimb development in the embryo of another TGF-β activity, also a member of the BMP family, BMP2, which promotes the selective growth of the metacarpals to extend the key digits (Sears et al., 2006). Making a batwing, however, involves more than just exaggerated digit length; it also involves suppression of the waves of apoptosis that eliminate interdigital material in tetrapods with distinct digits. In the case of bats, the maintenance of
interdigital webbing, however, is due to the specific inhibition of at least three BMP activities in the post-outgrowth phase of the interdigital regions (Weatherbee et al., 2006).).
The finch and bat examples involve the control of differential growth and differential apoptosis (in the case of the interdigital webbing in bats) at key phases by regulation of expression of members of the TGF-β family, specifically of the BMP subfamily of this superfamily. In contrast, the loss of stickleback pelvic armature in at least three independent speciation events involves the transcriptional down-regulation of a specific key TF, namely Pitx1. The genetic analysis indicates that this loss of armature, which appears to be adaptive as an energy-saving measure in lakes that are essentially predator-free zones, also involves several minor loci (as determined by quantitative trait locus analysis), but the key major locus is Pitx1, and the loss of pelvic regional expression of this TF is due, apparently, to mutations in cis-linked enhancer modules that normally boost its specific regional activity (Shapiro et al., 2004).).
As informative and important as the findings of these impressive studies are, they provide only the first stage of an understanding of the respective cases. This is most obvious in the differential growth stories of finch beaks and bat wings. In these cases, the pinpointed key molecules whose changes in amount are essential for the developmental process are well known components of ubiquitously used signal transduction pathways. Those pathways are used in a host of different developmental processes, with a wide range of different phenotypic outcomes, both within and amongst the different animal systems in which they are used. Such ubiquitously used regulatory modules have been termed “plug-ins” by Eric Davidson (2006). It follows that identifying neither the particular plug-in module nor, even less, a particular rate-limiting component (e.g., BMP2, calmodulin, BMP4) can fully explain the developmental change that lies at the heart of the respective evolutionary change. The still missing parts of the explanation, in all of these instances, involve the genetic network of which the respective identified molecule is a part and how that network then regulates selective cell proliferation (and apoptosis in the case of the bat’s interdigital webbing) in the relevant developing primordium.
At first glance, however, the loss of pelvic armature in sticklebacks seems to present quite a different situation. Ignoring, for the moment, the relatively small contributions from the minor loci that contribute to the phenotype, the key element in explaining the phenotypic change is a change in expression in one gene, namely the TF gene Pitx1. One does not need to understand in detail what genes Pitx1 regulates, in specifying the development of the pelvic armature, to understand how down-regulation of its expression in selected sites leads to the loss of that structure, with
the consequent adaptive benefit in predator-free environments. If, however, one inspects the earlier part of stickleback evolutionary history and inquires about the initial gain of the pelvic armature in the stickleback lineage, one is immediately confronted with the question of how the genetic network that specifies the pelvic armature evolved. One hypothetical scenario is given in Fig. 4.3. Although the details of this scheme may well prove wrong and the picture is, at best, highly schematic, it illustrates the fact that this evolutionary change must have been a multistep process of network construction, involving several (possibly many) mutations and, presumably, either multiple or continuing selection pressures (from predation).
Although three traits in three organisms create far too small a sample from which to draw firm general conclusions, one can offer a few tentative generalizations. For new or modified evolutionary traits (e.g., finch beaks, bat wings), knowing the genetic network, with its component modules, is essential for understanding in depth what the phenotypic change actually involves. Single-gene stories, however informative in themselves, cannot provide comparable understanding. For loss of traits, however, as in the stickleback example, knowing the genetic networks responsible for those traits may be unnecessary. It is sufficient to know which genes

FIGURE 4.3 A tentative evolutionary scenario for the evolution of the genetic network underlying the pelvic armature of sticklebacks. The essential general feature is that it involves a stepwise (gradualistic mode) process of construction of the network. A particular aspect to note is that Pitx1 is seen as having been recruited at an intermediary step, after evolution of the basic network/module structure for constructing skeletal elements, permitting it to have well defined regional control effects and its loss of expression to affect only that region.
in the network can be made rate-limiting for the trait to understand how their inactivation (partial or incomplete) can lead to loss of the trait. Such losses are genetically simple but can have large potential adaptive evolutionary significance. Nevertheless, loss-of-function evolutionary traits are, by definition, derivative traits. For most of the adaptive complex phenotypic traits that are of interest to evolutionists, the primary story lies in the acquisition of those traits. In turn, comprehending those evolutionary innovations requires understanding the underlying genetic networks.
USING GENETIC NETWORKS TO ASSESS RELATIVE PROBABILITIES OF MICROEVOLUTIONARY TRAJECTORIES
A network perspective, however, has further value for evolutionary biology. A detailed knowledge of genetic networks, which necessarily includes an understanding of their component modules, can provide even more: such knowledge provides a platform from which to assess the relative a priori probabilities of certain evolutionary trajectories. Such assessment would necessarily be approximate, but even that degree of understanding would be sufficient to allow the beginnings of a predictive approach to evolutionary trajectories, extending the potential range of hypothesis testing in evolutionary biology. It will be remembered that it was the apparent dearth of falsifiable hypotheses in evolution that led K. Popper initially to question whether evolutionary biology was truly science or simply a “metaphysical” framework of thought (Popper, 1972), although he later modified his stance (Popper, 1978).
The basis of using genetic network information to estimate relative probabilities of different evolutionary paths depends on understanding two generic properties that are shared by all developmental genetic networks. The first of these general properties is that each interactive step within a module, or between modules, is either an activation of the next gene activity (+) or an inhibition (−). This generalization is independent of the molecular mechanism involved in each such interaction and the stringency of any quantitative requirements. Thus, in a wild-type genetic network each step functions as either an activation (+) or a repression (−). In principle, therefore, one can encode each sequence of steps in a network, or network module, from the first triggering input signals, as a sequence of pluses and minuses.
The second general property concerns the structure of networks. Every network can be analytically decomposed into three kinds of elements (Wilkins, 2007b), which might be termed “functional connectivity motifs.” This may not be immediately obvious from the existing genetic network diagrams, which show an initially bewilderingly complex array of lines, arrows, and bars. (See for instance the diagrams in Davidson et
al., 2002, and Stathopoulos and Levine, 2005.) Yet closer inspection of such diagrams validates the claim. The first of these functional connectivity patterns consists of linear sequences of action between genes, namely genetic pathways. In reality, each gene may (and most do) connect to more than one gene (both upstream and downstream), but if one follows each gene–gene link, from one to the next, a linear sequence of causal activation/inhibition steps is always found (although many gene activations, in particular, require multiple inputs from several gene products). The second set of structural elements are the functional links between the linear segments, the pathways. Again, the connecting links function as either + or − steps. The third class of element is that of feedback loops. These are either positive (+) feed-forward steps or inhibitory (−) negative feedback functions. For both sign types, such feedback loops can either involve a gene product acting on itself (or the encoding gene) or interact with other genes/gene products either upstream or downstream in the sequence.
These two generic properties of networks, namely, the +/− choice at each step and the decomposability into three structural motifs, ensures that if one knows all of the potentially rate-limiting (nonredundant) members of a network/network module, plus all of the relevant inputs (and which ones are being used in a particular developmental process), and, not least, the specific functional relationships (whether + or −) between each pair of interacting genes, one can determine whether a particular set of inputs will trigger a particular set of outputs of the whole functional unit. This principle was first noted by Kauffman (1971), who used the term “forcing structure” to denote this deterministic property of networks, but it has most recently been discussed by Davidson (2006).
This property is most easily illustrated in the abstract for the case of simple, linear pathways. Such sequences always consist of all activating (+) steps, all negative (−) steps (although this group is undoubtedly a minority class), or a mixture of + and − steps (which is almost certainly the most common category of pathways). These are illustrated in Fig. 4.4 for the putative wild-type situation in each case. In addition, the figure shows the effect of a complete loss-of-function mutation in an early (“upstream”) gene of each kind of pathway. For all three pathway types, the effect of such a mutation is the complete reversal of sign of all of the following (“downstream”) gene activities. Thus, not only does the pathway structure allow one to predict outcomes in the wild-type case if one knows which inputs have been applied in any instance, but it also allows you to predict the effect of loss-of-function mutations on pathway/module output. In contrast, the effects of gain-of-function mutations are less predictable, at least where it is a + step that is affected in a pathway that has already been triggered. If, however, the activation step caused by a constitutive gain-

FIGURE 4.4 Three kinds of genetic pathways and the effects on their outputs from upstream loss-of-function mutations. In pathway 1, all of the steps in the pathway are activation (+) events; in pathway 2, the causal chain of gene expression events involves both activation and inhibition (−) steps; in pathway 3, all of the steps are inhibitory (−). For all three kinds of pathway, the effect of an upstream loss-of-function mutation is to change the sign of activity for all successive downstream activities, from + to − or from − to +. [Reproduced with permission from Wilkins (2007b) (Copyright 2007, Novartis).]
of-function mutation occurs in a gene in a previously inactive pathway, such gain-of-function mutations will, in principle, lead to ectopic activations of all steps downstream of the affected gene. (Whether this happens will depend, in part, on what other kinds of regulatory mechanisms are in operation in those cells and how they functionally link to the activated downstream functions.)
Pathways are, indeed, relatively simple structures, but similar reasoning can be used to predict outputs in functionally linked pathway
situations as well, such cross-linked pathways constituting the simplest kind of network situation. For instance, a loss-of-function mutation in a pathway upstream of a cross-inhibitory step should, in principle, activate the linked pathway below the point of functional linkage in the second pathway (Wilkins, 2007b).
This possibility, of predicting phenotypic outcomes from mutations in well characterized pathways, is, of course, only a potential for future work. At present, there is insufficient knowledge of any network, and of few network modules, to allow this kind of analysis. Furthermore, knowing the probability of a developmental outcome is only the beginning of estimating the chances of a particular evolutionary trajectory, which will be influenced at many steps by selective opportunities, genetic drift, the occurrence of rare external disasters (e.g., mass extinctions), or other chance events. Yet, knowing which phenotypic outcomes are more likely than others would provide a first step toward assessing the likelihood of certain trajectories vs. others. That there are certain propensities toward certain evolutionary trajectories is shown by the numerous instances of parallel evolution in related lineages that evolutionists have found. Although the traditional emphasis to explain this phenomenon is similarity of selective pressures, there must also be some inherent biases built into the genetics and development of the branching lineages that display it (Wilkins, 2004). Even instances of convergent evolution, e.g., the independent origination of shearing teeth in carnivorous marsupials and in the placental carnivores, may well involve the independent activation of highly conserved network modules within similar cellular developmental contexts in the unrelated lineages.
Clearly, evolutionary biology will never have the capacity for exact, flawless “retrodiction” (explaining why past events occurred in a certain way), with consequent capacity for formulating falsifiable hypotheses, on which a strict Popperian might insist. A network perspective, however, when coupled with the kind of detailed knowledge of network modules and networks, can, in principle, move the science of evolution toward a somewhat more predictive capability. Without such, it is difficult to see how the kinds of studies focusing on single genes or small numbers of genes can ever have the kind of full explanatory capability that, ideally, evolutionary biology should aim for.
Given the plethora of networks and morphologies, however, that there are to explore and the costs (in money, time, and sheer hard work) of characterizing developmental genetic networks (Wilkins, 2007b), the prospects sketched above might seem so distant as to be unachievable in the foreseeable future. Yet a simple consideration of microevolutionary morphological patterns suggests which networks and network modules might be most profitably explored. This number is considerably smaller
than the totality of possibilities. Specifically, when one looks at any group of animals, at the genus or family level, what strikes one is that the great majority of variations are in either growth properties (regional, appendage, or whole-organism level) or color patterns, or both. There are, of course, major structural novelties, which distinguish groups separated by large macroevolutionary distances and whose evolutionary origins demand an explanation (Muller and Newman, 2005). Yet, at the microevolutionary level, most speciation events, when reflected in or correlated with certain morphological characteristics, involve differential growth and/or color patterning. When one considers the high degree of functional conservation of basic patterning mechanisms in general (Carroll et al., 2001; Wilkins, 2002), it seems not unreasonable that growth and pigmentation may also exhibit a degree of conservation in the immediately upstream genetic network modules that govern them.
The analysis of growth is, of course, a major subject area in biology, involving such disciplines as cell biology, traditional developmental biology, developmental genetics, and cancer biology. Yet there is still a relative dearth of information about the connections between developmental patterning mechanisms for specific structures and regions and the growth controls that directly regulate the rate and extent of cell proliferation in those regions. Nevertheless, progress is also being made in this area, and some of the relevant networks are beginning to be elucidated (Cho et al., 2006). How widely conserved such networks might be and whether there are widely conserved network modules in the metazoa for evoking pigmentation patterns is not known, but these are at least possibilities and can be investigated. My principal suggestion here is that analyses of the networks or network modules that link developmental patterning mechanisms to growth and pigmentation patterns could have special importance in understanding the genetic basis of many microevolutionary-scale events. Furthermore, simple calculations involving gene size and mutation rate indicate that even relatively modest-sized genetic networks, found in organisms of moderately sized populations, should harbor significant standing variation of potential phenotype-changing capacity (Wilkins, 2007b). This sort of quantitative consideration further illustrates the value of, and need for, a network-based perspective on evolution.
CONCLUSIONS
This article has explored the ways that evolutionary trajectories are influenced by (i) the properties of gene products, (ii) the on/off switches that control transcription of individual genes, and (iii) the structured properties of the regulatory ensembles we know as genetic network modules. It would be overstating the case to call the biases created by these selection-
honed properties “constraints,” which connotes strong barriers, but it seems certain that these properties must exert some preferential influence or channeling effects at the start of every evolutionary departure. Such molecular attributes make possible the kinds of “facilitated variation” described by Gerhart and Kirschner (Chapter 3, this volume). Their perspective is both fully consistent with and complementary to the one sketched here.
The central point of this chapter, however, is that a knowledge of the network modules that constitute particular genetic networks, underlying specific developmental processes in particular organisms (hence, their morphological traits), can greatly enrich understanding of the ways in which particular genetic changes promote particular developmental changes. Furthermore, an appreciation of the generic properties of networks and the ways that they transmit effects along functional linear pathways can, when the knowledge of the composition of a network and its inputs and outputs is reliable, lead to predictions about the effects of mutations within network modules on eventual phenotypes. With this sort of analytical framework in place, evolutionary biology will possess a greater degree of predictive capability and potential for the falsification of hypotheses than has hitherto been possible.


















