5
The Frailty of Adaptive Hypotheses for the Origins of Organismal Complexity
MICHAEL LYNCH
The vast majority of biologists engaged in evolutionary studies interpret virtually every aspect of biodiversity in adaptive terms. This narrow view of evolution has become untenable in light of recent observations from genomic sequencing and population-genetic theory. Numerous aspects of genomic architecture, gene structure, and developmental pathways are difficult to explain without invoking the nonadaptive forces of genetic drift and mutation. In addition, emergent biological features such as complexity, modularity, and evolvability, all of which are current targets of considerable speculation, may be nothing more than indirect by-products of processes operating at lower levels of organization. These issues are examined in the context of the view that the origins of many aspects of biological diversity, from gene-structural embellishments to novelties at the phenotypic level, have roots in nonadaptive processes, with the population-genetic environment imposing strong directionality on the paths that are open to evolutionary exploitation.
Although biologists have always been concerned with complex phenotypes, the matter has recently become the subject of heightened speculation, as a broad array of academics, from nearly every branch of science other than evolutionary biology itself, claim to be in
Department of Biology, Indiana University, Bloomington, IN 47405.
possession of novel insights into the evolution of complexity. The claims are often spectacular. For example, Kirschner and Gerhart (2005) argue that evolutionary biology has been “woefully inadequate” with respect to understanding the origins of complexity and promise “an original solution to the long-standing puzzle of how small random genetic change can be converted into complex, useful innovations.” However, this book and many others like it (e.g., Depew and Weber, 1985; Kauffman, 1993; Carroll, 2005a; Davidson, 2006) provide few references to work done by evolutionary biologists, making it difficult to understand the perceived areas of inadequacy, and many of the ideas promoted are known to be wrong, making it difficult to appreciate the novelty. Have evolutionary biologists developed a giant blind spot; are scientists from outside of the field reinventing a lot of bad wheels; or both?
Evolutionary biology is treated unlike any science by both academics and the general public. For the average person, evolution is equivalent to natural selection, and because the concept of selection is easy to grasp, a reasonable understanding of comparative biology is often taken to be a license for evolutionary speculation. It has long been known that natural selection is just one of several mechanisms of evolutionary change, but the myth that all of evolution can be explained by adaptation continues to be perpetuated by our continued homage to Darwin’s treatise (1859b) in the popular literature. For example, Dawkins’ (1976, 1986, 1996) agenda to spread the word on the awesome power of natural selection has been quite successful, but it has come at the expense of reference to any other mechanisms, a view that is in some ways profoundly misleading. There is, of course, a substantial difference between the popular literature and the knowledge base that has grown from a century of evolutionary research, but this distinction is often missed by nonevolutionary biologists.
The goal here is to dispel a number of myths regarding the evolution of organismal complexity (Table 5.1). Given that life originated from inorganic matter, it is clear that there has been an increase in phenotypic complexity over the past 3.5 billion years, although long-term stasis has been the predominant pattern in most lineages. What is in question is whether natural selection is a necessary or sufficient force to explain the emergence of the genomic and cellular features central to the building of complex organisms.
NOTHING IN EVOLUTION MAKES SENSE EXCEPT IN LIGHT OF POPULATION GENETICS
Although the basic theoretical foundation for understanding the mechanisms of evolution, the field of population genetics, has long been in place, the central significance of this framework is still occasionally
TABLE 5.1 A Summary of Some Common Misconceptions About Evolution and Complexity, and Contrasting Views
|
Myth |
Reality |
|
1. Evolution is natural selection. |
Natural selection is just one of four primary evolutionary forces. |
|
2. Characterization of interspecific differences at the molecular and/or cellular levels is tantamount to identifying the mechanisms of evolution. |
The resources deployed in evolutionary change reside at the molecular level, but whereas the cataloging of such differences at the interspecific level identifies the end products of evolution, it does not reveal the population-genetic processes that promoted such change. |
|
3. Microevolutionary theory based on gene-frequency change is incapable of explaining the evolution of complex phenotypes. |
No principle of population genetics has been overturned by an observation in molecular, cellular, or developmental biology, nor has any novel mechanism of evolution been revealed by such fields. |
|
4. Natural selection promotes the evolution of organismal complexity. |
There is no evidence at any level of biological organization that natural selection is a directional force encouraging complexity. In contrast, substantial evidence exists that a reduction in the efficiency of selection drives the evolution of genomic complexity. |
|
5. Natural selection is the only force capable of promoting directional evolution. |
Both mutation and gene conversion are nonrandom processes that can drive the patterning of genomic evolution in populations with sufficiently small effective sizes (common in multicellular lineages). |
|
6. Genetic drift is a random process that leads to noise in the evolutionary process, but otherwise leaves expected evolutionary trajectories unaltered. |
By reducing the efficiency of selection, random genetic drift imposes a high degree of directionality on evolution by increasing the likelihood of fixation of deleterious mutations and decreasing that of beneficial mutations. |
|
7. Mutation merely creates variation, whereas natural selection promotes specific mutant alleles on the basis of their phenotypic effects. |
Mutation operates as a weak selective force by differentially eliminating alleles with structural features that magnify mutational target sizes. |
|
Myth |
Reality |
|
8. Phenotypic and genetic modularity are direct products of natural selection. |
There is no evidence that the modular structure of gene regulatory regions or genetic networks is directly advanced by selective mechanisms. However, the processes of duplication, degenerative mutation, and random genetic drift can lead to the passive emergence of modularity in populations with genetic effective sizes of the magnitude found in multicellular species. |
|
9. Natural selection promotes the ability to evolve. |
There is no evidence that phylogenetic variation in the pathways open to evolutionary exploration is anything more than a by-product of physical processes that passively arise with expansions in genome size and generation length. There are no abrupt transitions in aspects of genomic architecture or gene structure between unicellular and multicellular species, nor between viruses, prokaryotes, and eukaryotes. |
questioned, as exemplified in this quote from Carroll (2005a), “Since the Modern Synthesis, most expositions of the evolutionary process have focused on microevolutionary mechanisms. Millions of biology students have been taught the view (from population genetics) that “evolution is change in gene frequencies.’ Isn’t that an inspiring theme? This view forces the explanation toward mathematics and abstract descriptions of genes, and away from butterflies and zebras…. The evolution of form is the main drama of life’s story, both as found in the fossil record and in the diversity of living species. So, let’s teach that story. Instead of “change in gene frequencies,’ let’s try “evolution of form is change in development’.” Even ignoring the fact that most species are unicellular and differentiated mainly by metabolic features, this statement illustrates two fundamental misunderstandings. Evolutionary biology is not a story-telling exercise, and the goal of population genetics is not to be inspiring, but to be explanatory. The roots of this contention are fourfold.
First, evolution is a population-genetic process governed by four fundamental forces. Darwin (1859b) articulated one of those forces, the process of natural selection, for which an elaborate theory in terms of genotype frequencies now exists (Crow and Kimura, 1970; Bürger, 2000). The remaining three evolutionary forces are nonadaptive in the sense that they are not a function of the fitness properties of individuals: mutation is the ultimate source of variation on which natural selection acts, recombi-
nation assorts variation within and among chromosomes, and genetic drift ensures that gene frequencies will deviate a bit from generation to generation independent of other forces. Given the century of work devoted to the study of evolution, it is reasonable to conclude that these four broad classes encompass all of the fundamental forces of evolution.
Second, all four major forces play a substantial role in genomic evolution. It is impossible to understand evolution purely in terms of natural selection, and many aspects of genomic, cellular, and developmental evolution can only be understood by invoking a negligible level of adaptive involvement (Kimura, 1983; Lynch, 2007). Because all three nonadaptive forces of evolution are stochastic in nature, this conclusion raises some significant technical challenges. It is tempting to think that stochastic processes have no implications for the direction of evolution. However, the effects of mutation and recombination are nonrandom, and by magnifying the role of chance, genetic drift indirectly imposes directionality on evolution by encouraging the fixation of mildly deleterious mutations and discouraging the promotion of beneficial mutations.
Third, the field of population genetics is now so well supported at the empirical level that the litmus test for any evolutionary hypothesis must be its consistency with fundamental population-genetic principles. Grounded in basic Mendelian processes and sampling theory, many of these principles were laid down before the elucidation of the structure of DNA. Shortly after the genetic code was cracked, a series of technological breakthroughs advanced our ability to reveal molecular variation: protein sequencing in the 1950s, surveys of protein variants in the 1960s, ribosomal RNA sequencing in the 1970s, gene sequencing in the 1980s, and whole-genome sequencing in the 1990s. Each of these episodes brought the need for new methods for analysis and interpretation, and in each case the framework was drawn largely from preexisting population-genetic theory. Thus, although we do not yet fully understand the connections between evolution at the molecular and phenotypic levels, we can be confident that the machinery to do so is in place.
Fourth, some attempts to marginalize the contributions of population genetics to our understanding of evolution have pointed to the “bean bag” genetics debate that occurred in the middle of the last century (see Felsenstein, 1975). However, this is a misunderstanding, as the tensions during this period were not about the population-genetic basis of evolutionary change, but about the need to incorporate epistasis into the existing framework, something that population geneticists have now invested heavily in (Wolf et al., 2000; Carter et al., 2005). From the standpoint of its phenotypic products, evolution is more than a change in gene frequencies. Organisms are more than the sum of their parts, just as genes are more than the sum of their functional components. But if we are concerned with
the process of evolutionary change, then evolution is indeed a change in genotype frequencies.
In summary, population genetics provides an essential framework for understanding how evolution occurs, grounding us in reality by clarifying the pathways that are open to evolutionary exploitation. To quote Carroll (2005a) again, “Simplification may indeed be necessary for news articles, but it can distort the more complex and subtle realities of evolutionary patterns and mechanisms.”
INTERNAL VERSUS EXTERNAL EVOLUTIONARY FORCES
The literature is permeated with dogmatic statements that natural selection is the only guiding force of evolution, with mutation creating variation but never controlling the ultimate direction of evolutionary change (for a review, see Stoltzfus, 2006a). This view derives from two types of arguments. First, hundreds of artificial selection experiments have generated changes in mean phenotypes well beyond the observed range in the base population in just a few dozen generations (Falconer and Mackay, 1996), inspiring the view that quantitative variation is distributed over an effectively infinite number of loci with minuscule effects (Kimura, 1965; Lande, 1975; Bulmer, 1980). Second, much of the earliest work in theoretical population genetics downplayed the ability of mutation to overcome the force of selection (Fisher, 1930; Haldane, 1932). Both arguments ignore significant complications that arise in finite populations, and it is now known that genome composition is governed by biases in mutation and gene conversion, some of which (e.g., mobile-element proliferation) operate via internal drive-like mechanisms (Lynch, 2007).
The notion that mutation pressure can be a driving force in evolution is not new (Darwin, 1859b, 1866; Morgan, 1925; Dover, 1982; Nei, 1987, 2005; Cavalier-Smith, 1997; Yampolsky and Stoltzfus, 2001; Stoltzfus, 2006b), and the conditions that must be fulfilled if mutation is to alter the direction of evolution relative to adaptive expectations are readily derived. Consider two alternative states at a locus, A and a, with the mutation rate of a → A being m times that of A → a, but with type A having a fractional selective advantage s over type a. Further progress requires that we specify the effective number of gene copies per locus at the population level. This quantity, Ng, which is equivalent to the effective size of a haploid population and approximately twice that for an outcrossing diploid species, is influenced by many factors, including the breeding system, temporal fluctuations in population size, and the level of recombination (which influences the sensitivity of a locus to spurious hitch-hiking effects), and is generally orders of magnitude smaller than the absolute number of reproductive adults in a population (Lynch, 2007). With these definitions in
hand, standard theory (Kimura, 1983) shows that the fixation probability of a mutation to A is es times that for a mutation to a, where S = 2 Ngs is twice the ratio of the power of selection to the power of random genetic drift (1/Ng). Because the population-level rate of transition from one allelic type to another is equal to the product of the mutation rate and the fixation rate, the ratio of probabilities of being in states A versus a at selection-mutation-drift equilibrium is simply mes (Fig. 5.1). This simple expression leads to two general conclusions: (i) regardless of the strength of selection, if 1/Ng >> |s| the population will be driven to a state expected under mutation pressure alone; and (ii) the equilibrium composition of a population depends not on the absolute power of mutation, but on the relative rates of forward and reverse mutations (the mutation bias).
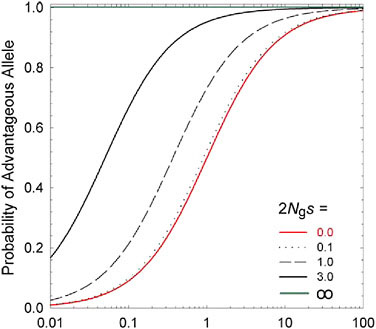
FIGURE 5.1 The long-term probability that an allele residing at a biallelic locus will be of the selectively advantageous type, given a selective advantage s, an effective population number of gene copies of Ng, and a mutation rate to the beneficial allele m times that in the reverse direction. The lowest curve (2 Ngs = 0.0) denotes neutrality, whereas the upper line (2Ngs = ∞) denotes an effectively infinite population, such that genetic drift is a negligible force.
THE PASSIVE EMERGENCE OF GENOME COMPLEXITY BY NONADAPTIVE PROCESSES
Most biologists are so convinced that all aspects of biodiversity arise from adaptive processes that virtually no attention is given to the null hypothesis of neutral evolution, despite the availability of methods to do so (Lande, 1976; Lynch and Hill, 1986; Lynch, 1994). Such religious adherence to the adaptationist paradigm has been criticized as being devoid of intellectual merit (Gould and Lewontin, 1979), although the field of molecular evolution has long been obsessed with potential for the “nearly neutral” accumulation of very slightly deleterious mutations (Ohta, 1972, 1973, 1974). The condition for near-neutrality is fulfilled when the ratio of the powers of selection and drift is substantially <1, i.e., |2Ngs| << 1.
This simple relationship has considerable utility in attempts to evaluate the potential role of nonadaptive mechanisms in the evolution of genomic architecture (Lynch and Conery, 2003; Lynch, 2006, 2007). Striking phylogenetic variation exists at the level of gene and genomic architecture. The genomes of multicellular eukaryotes are invariably packed with mobile elements, and individual genes are generally subdivided by multiple introns, harbor multiple transcription-factor binding sites, and are transcribed into units containing substantial untranslated flanking sequences. In contrast, prokaryotic genomes are usually nearly completely devoid of mobile elements and introns and have genes with very simple regulatory structures, often transcribed into polycistronic units (operons) with negligible leader and trailer sequences. Most unicellular eukaryotic genomes exhibit structural features on a continuum between these two extremes.
Understanding the origins of eukaryotic genome complexity in adaptive terms is rendered difficult by the fact that each embellishment added to a gene magnifies its vulnerability to mutational inactivation, thereby encouraging its elimination from the population (Lynch 2006, 2007). If a particular embellishment requires that n nucleotides be conserved for proper gene function, the mutational disadvantage is nu, where u is the mutation rate per nucleotide site. Each intron added to a protein-coding gene requires that n ≈ 30 nucleotide sites within the intron and adjacent exons be reserved for proper spliceosomal recognition (Lynch, 2002). Transcription-factor binding sites are ≈10 bp in length (e.g., Gasch et al., 2004), so the addition of each such site to a gene increases the degenerative mutation rate by ≈10u. The average eukaryotic 5′ UTR increases the degenerative mutation rate by ≈4u by providing substrate for mutations to premature translation-initiation codons (Lynch et al., 2005). Even completely nonfunctional intergenic DNA is a mutational hazard because it serves as a substrate for inappropriate gain-of-function mutations (Hahn et al., 2003).
Numerous observations suggest that the amount of regulatory DNA associated with the average gene in a multicellular species is at least as great as the length of the coding region, and such genes typically also contain ~5–7 introns (Lynch, 2007). Thus, the average mutational target sizes of genes in multicellular eukaryotes are more than two to three times those for prokaryotes. To become established, the modifications that led to such mutational hazards must have either had a substantial immediate selective advantage or arisen in populations with effective sizes sufficiently small to render them immune to selection. Letting s = nu, the latter condition requires that 2Ngnu < 1, and because the mutational cost of individual modifications is small, generally <30u, it is difficult to reject the hypothesis that incremental expansions of eukaryotic gene complexity were largely driven by nonadaptive processes.
More formal justification for this claim derives from molecular population-genetic data. Assuming the silent sites of protein-coding genes to be effectively neutral, the average number of silent-site substitutions between randomly sampled nucleotide sites within a population is a function of the rates of input of new variation by mutation (2u) and loss by genetic drift (1/Ng). At mutation-drift equilibrium, the expected level of silent-site divergence within a population is equal to the ratio of these rates, 2Ngu. Average estimates of 2Ngu are 0.104 for prokaryotes, 0.057 for unicellular eukaryotes, 0.026 for invertebrates, 0.015 for land plants, and 0.004 for vertebrates (Lynch, 2006). Because some weak selective forces may operate on silent sites, the average estimates of 2Ngu for unicellular species (with high Ng) are almost certainly downwardly biased. Thus, rearranging the criterion for effective neutrality to 2Ngu << 1/n, an embellishment that increases the mutational target size of a vertebrate gene by n < 250 will be largely immune from selection, and hence free to drift to fixation, whereas the critical value of n for a prokaryote is <<10.
These observations indicate that the paths open to evolutionary exploration are fundamentally different between unicellular and multicellular species for reasons completely unassociated with organismal complexity. Because of their relatively small Ng, multicellular species are expected to accumulate gratuitous gene-structural changes without any direct selection for them and to become laden with other deleterious genomic features (Lynch and Conery, 2003; Lynch, 2007). In contrast, unicellular lineages are expected to maintain streamlined genomes, not necessarily for metabolic reasons, but because of the exceptionally high efficiency of selection opposing the accumulation of mutationally hazardous DNA.
The hypothesis that expansions in the complexity of genomic architecture are largely driven by nonadaptive evolutionary forces is capable of explaining a wide range of previously disconnected observations (Lynch, 2006, 2007) (Table 5.2). This theory may be viewed as overly simplistic.
TABLE 5.2 Aspects of Gene and Genomic Architectural Evolution That Appear to Be Explainable Only After Accounting for Variation in the Relative Power of Nonadaptive Evolutionary Forces
|
Genomic streamlining in microbial species versus genome bloating in multicellular lineages. |
|
Nucleotide composition variation within and among genomes: genomewide A/T composition, strand asymmetry, isochores, and codon-usage bias in unicellular species. |
|
Differential proliferation of mobile elements in unicellular versus multicellular species. |
|
Gene number: preservation of duplicate genes by degenerative mutations (subfunctionalization). |
|
Origin of the spliceosome by subfunctionalization and proliferation of introns in lineages of multicellular species. |
|
Expansion of UTRs of the messenger RNAs of eukaryotes. |
|
Origin of modular regulatory regions in eukaryotic genes. |
|
Demise of operons in eukaryotes. |
|
Variation in organelle genome architecture: lean in animals; bloated in land plants. |
|
Messenger RNA editing in plant organelle genomes. |
|
Restriction of sex chromosomes to multicellular lineages. |
However, simply making the counterclaim that natural selection is all powerful (without any direct evidence) is not much different from invoking an intelligent designer (without any direct evidence). If a successful adaptive counterargument is to be mounted, simpler nonadaptive models must be shown to be inadequate, and to accomplish that, something must be known about the expected pattern of evolution in the absence of selection. If nothing else, the ideas presented above provide the basis for a null model for genomic evolution. Certainly, many of the above-mentioned embellishments of eukaryotic genes have adaptive functions in today’s multicellular species, but observations on current deployment may have little bearing on matters of initial origins. Most of the repatterning of the genomic real estate of eukaryotes occurred before the evolution of multicellularity (Lynch, 2007).
ARE THE ORIGINS OF ORGANISMAL COMPLEXITY ALSO ROOTED IN NONADAPTIVE PROCESSES?
Multicellularity is widely viewed as a unique attribute of eukaryotes, somehow made possible by the origin of a more complex cellular architecture and, without question, with the assistance of natural selection. However, it is difficult to defend this assertion in any formal way. Complex, multicellularity has only arisen twice, once in animals and once in vascular plants. One might add fungi to the list, although the number of fungal cell types is not large, and there is some question as to whether multicellularity was ancestral to the phylogenetic group that contains animals, fungi, and slime molds. In any event, the probability that two or three origins of multicellularity simply arose by chance within eukaryotes as opposed to prokaryotes is somewhere on the order of 1/4 to 1/2, well below the general standards of statistical validity. Of course, many other eukaryotes are capable of producing a few different cell types, but the same is true for prokaryotes, some of which produce radically different cell morphologies.
Nevertheless, King (2004) states that “this historical predisposition of eukaryotes to the unicellular lifestyle begs the question of what selective advantages might have been conferred by the transition to multicellularity;” and Jacob (1977) argues that “it is natural selection that gives direction to changes, orients chance, and slowly, progressively produces more complex structures, new organs, and new species.” The vast majority of biologists almost certainly agree with such statements. But where is the direct supportive evidence for the assumption that complexity is rooted in adaptive processes? No existing observations support such a claim, and given the massive global dominance of unicellular species over multicellular eukaryotes, both in terms of species richness and numbers of individuals, if there is an advantage of organismal complexity, one can only marvel at the inability of natural selection to promote it. Multicellular species experience reduced population sizes, reduced recombination rates, and increased deleterious mutation rates, all of which diminish the efficiency of selection (Lynch, 2007). It may be no coincidence that such species also have substantially higher extinction rates than do unicellular taxa (Raup, 1978; Stanley, 1985).
Although some aspects of the roots of the cellular interactions that constitute development are likely to reside in the resolution of adaptive conflicts between the advantages of cell–cell cooperation versus going it alone (e.g., Maynard Smith and Szathmáry, 1995; Michod, 1999), it need not follow that natural selection is a sufficient force for the exit from the unicellular world. Many developmental genes previously thought to have originated in the vertebrate lineage, owing to their absence in arthropods and nematodes, are now known to be present in basal lineages of animals
lacking mesoderm (the cnidarians), and by inference must have simply been lost from various invertebrate phyla (Technau et al., 2005). Numerous examples of morphological simplification exist in animals (e.g., limb loss in lizards and salamanders, coelom loss in nematodes, and mouth and anal loss in hydrothermal-vent worms), and a plausible, albeit controversial, case has even been made that prokaryotic cell architecture is a simplified derivative of that of eukaryotes (Kurland et al., 2006).
Could nonadaptive processes have played a role in the evolution of something as intricate as cell architecture or developmental complexity? There are at least two ways by which such a cascade of events might be precipitated. First, intrinsically deleterious genome-level changes, such as those resulting from intron and mobile-element proliferation, must impose selection pressures for cellular defense mechanisms. It has been argued that by imposing a need to process mRNAs before their exposure to ribosomes, the establishment of spliceosomal introns provided the evolutionary pressure that led to the origin of the nuclear membrane (Lopez-Garcia and Moreira, 2006; Martin and Koonin, 2006), and Koonin (2006) has further suggested that the nonsense-mediated decay (NMD) and ubiquitin signaling pathways evolved as secondary mechanisms for minimizing the accumulation of aberrant transcripts and proteins resulting from splicing errors. This line of thinking could be taken in a number of additional directions. For example, the assembly of spliceosomal subunits occurs within intranuclear Cajal bodies (Stanek and Neugebauer, 2006), and aberrant transcripts flagged by the NMD pathway are degraded in cytoplasmic P bodies (Sheth and Parker, 2006). The nature of cause and effect in these relationships is difficult to resolve, as all hypothetical lines of defense against introns appear to have been present in the stem eukaryote (Lynch et al., 2006), raising the possibility that the colonization of nuclear genes by introns followed the origin of permissive cellular features, rather than the other way around. Nevertheless, the idea that internal constraints played a role in cellular evolution is secure under either scenario.
Second, because cellular and developmental features reflect the transformation of gene-level information into gene expression, the opportunities for phenotypic evolution must ultimately be constrained by the physical resources existing at the genomic level, which as noted above are strongly influenced by nonadaptive aspects of the population-genetic environment. Reductions in Ng are expected to lead to increases in intron number and size, expansions in UTR lengths, losses of operons, the modularization of regulatory regions, and the preservation of duplicate genes by subfunctionalization (among other things; Table 5.2). Thus, as will be discussed more fully below, to the extent that an increase in gene-architectural complexity is a precondition for the emergence of greater complexity at the organismal level (including the hallmarks of multicellularity: multiple cell
types, complex patterns of gene expression, and mechanisms of cell signaling), a long-term synergism may exist between nonadaptive evolution at the DNA level and adaptive evolution at the phenotypic level. There is no need to abandon the idea that many of the external morphological and/or behavioral manifestations of multicellularity in today’s organisms are adaptive. However, if the view promoted above is correct, the relatively simple phenotypes of the Earth’s smallest organisms is not an inevitable outcome of the prokaryotic body plan nor a reflection of selection for metabolic efficiency, but an indirect consequence of the barrier to the passive emergence of genomic complexity imposed by high Ng.
In summary, the near-complete absence of the concept of nonadaptive processes from the lexicon of those concerned with cellular and developmental evolution does not reflect any formal demonstration of the negligible contribution of such mechanisms, and indeed, there is no fundamental reason why development should be uniquely immune to non-adaptive evolutionary forces. One could even argue that the stringency of natural selection is reduced in complex organisms with behavioral and/or growth-form flexibilities that allow individuals to match their phenotypic capabilities to the local environment. Some of these shortcomings have recently attracted attention, and a scaffold for connecting evolutionary genetics, genomics, and developmental biology is slowly beginning to emerge (Johnson and Porter, 2000, 2001; Stern, 2000; True and Haag, 2001; Delattre and Felix, 2002; Rockman and Wray, 2002; Wray et al., 2003; Force et al., 2005).
THE PASSIVE EMERGENCE OF MODULAR GENE INTERACTIONS
King and Wilson (1975) inspired the view that modularity and repatterning of regulatory-element utilization are the central determinants of the evolution of organismal complexity (Carroll, 2005a,b; Davidson, 2006). Although this view is not universally accepted even among developmental biologists (Alonso and Wilkins, 2005), because development always involves cross-talk between gene products, one must start with a consideration of the origins of the mechanisms that allow such transactions to take place. There is no evidence that gene-regulatory modules associated with complex functions arise as de novo integrated units, although some biologists seem to feel otherwise (Davidson and Erwin, 2006). Rather, like all aspects of evolution, the origins of changes in genetic pathways must be a function of descent with modification. Mutant alleles arise independently at individual loci, with features being defined by prior historical contingencies. Thus, although the idea that regulatory modules with functional significance in today’s organisms can only have arisen via natural
selection is seductive, it remains to be determined how the stepwise alterations necessary for the construction of genetic pathways come about. The following is a preliminary outline of one approach to understanding the evolution of organismal complexity via the development of a formal population-genetic framework for the emergence of alternative forms of gene interactions.
Although compelling adaptive arguments are always accompanied by a formal rejection of simpler nonadaptive hypotheses, credible null hypotheses have rarely been pursued in evolutionary developmental biology. This concern is not trivial, as it has been shown that modular gene-regulatory structures (with unique transcription factors governing expression in different spatial/temporal contexts) can emerge passively, without any direct selection for modularity per se, starting from an initial state in which the entire expression breadth of the gene is under unified control (Force et al., 2005). Under the scenario outlined in the top two tiers of Fig. 5.2, during the entire transition to a modular form of gene regulation, the spatial/temporal pattern of gene expression remains constant, with only the underlying molecular mechanisms for achieving this fixed pattern being modified. Thus, the new regulatory architecture emerges beneath a constant phenotype, without any bottleneck in fitness during the transitional phase of mixed genotypes. Such neutral transitions may help explain apparent cases of “developmental system drift,” whereby closely related species achieved similar morphological structures by substantially different mechanisms (Sommer, 1997; Johnson and Porter, 2000; Ludwig et al., 2000; True and Haag, 2001; Ruvinsky and Ruvkun, 2003; Tsong et al., 2006).
The emergence of modular gene structure by the nonadaptive processes of duplication, degenerative mutation, and genetic drift is fully compatible with the known magnitudes of these forces in multicellular species (Lynch, 2007). For example, the rate of duplication of entire genes
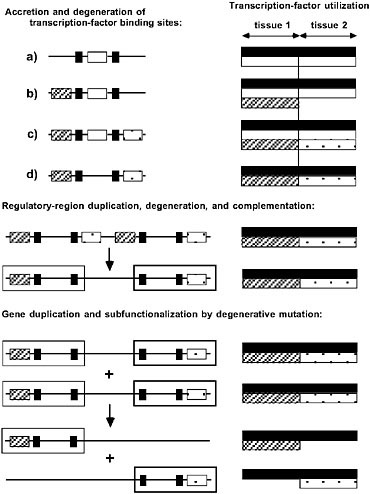
FIGURE 5.2 The passive emergence of specialized gene functions via nonadaptive processes of duplication, degenerative mutation, and random genetic drift. (Left) Regulatory elements (transcription-factor binding sites) are depicted on the left, with each regulatory element coded according to the transcription factor that binds to it. (Right) Allele-specific utilizations of transcription factors are depicted. Transcription factors denoted by black and white are ubiquitously expressed, whereas those denoted by hatching and crosshatching are each expressed in single, non-overlapping tissues. For this particular gene, within their respective tissues, the hatched and crosshatched transcription factors are redundant with respect to the white factor, but the additional black factors are essential for complete expression. Three hypothetical phases of gene architectural modification are shown. (Top) Accretion and degeneration of transcription-factor binding sites. The initial allele (a) is expressed in an identical manner in both tissues, but the regulatory region sequentially acquires the hatched and crosshatched elements. The redundant white element is then vulnerable to loss by degenerative mutation, yielding a descendant allele with a semi-independent mode of expression, as the black element is still essential to expression in both tissues. At this stage all four alleles (a–d) are interchangeable, as each of them achieves the same pattern of phenotypic expression. (Middle) Regulatory-region duplication, degeneration, and complementation. The entire enhancer region is tandemly duplicated, with each component then losing a complementary (hatched/crosshatched) element. The resultant allele has become modularized in the sense that it harbors two independently mutable subfunctions denoted by the hatched and crosshatched open boxes; a mutation in either region has effects confined to a single tissue. (Bottom) Gene duplication and subfunctionalization by degenerative mutation. The entire gene is duplicated, with each copy becoming silenced by degenerative mutation for a complementary subfunction. The expression of each copy is now confined to a single tissue.
is ~1% per gene per million years, and because small fragments of DNA are tandemly duplicated at much higher rates than entire genes (Katju and Lynch, 2003), variation in the regulatory modules of genes must arise at least as rapidly as single-nucleotide polymorphisms. However, because of the mutational cost of allelic complexity, the likelihood of completion of semineutral modularization processes becomes negligible once 1/Ng becomes smaller than the excess mutational burden (Force et al., 2005). Thus, contrary to popular belief, natural selection may not only be an insufficient mechanism for the origin of genetic modularity, but population-genetic environments that maximize the efficiency of natural selection may actually promote the opposite situation, alleles under unified transcriptional control. Under this view, the reductions in Ng that likely accompanied both the origin of eukaryotes and the emergence of the animal and land-plant lineages may have played pivotal roles in the origin of modular gene architectures on which further developmental complexity was built.
Despite the initial invariance of phenotypic expression patterns during this type of gene-architectural repatterning, the emergence of independently mutable subfunctions in modularized alleles can contribute to adaptive evolution in significant ways. For example, if the ancestral allele under unified control was subject to pleiotropic constraints associated with shared regulatory regions, modularization may open up previously inaccessible evolutionary pathways. Relief from pleiotropy can be even further facilitated following the duplication of the entire gene (bottom of Fig. 5.2), as complementary degenerative mutations partition cellular tasks among paralogous copies (Force et al., 1999). This process of subfunctionalization is known to be a frequent fate of duplicate genes in multicellular species (Prince and Pickett, 2002; Lynch, 2007), and theory suggests that it too is most likely to occur in populations with small Ng, again because of the mutational burden of distributing a fixed number of subfunctions over multiple genes (Lynch et al., 2001). Thus, the joint operation of both processes (the emergence of gene subfunctions and their subsequent partitioning among paralogs) in the small to moderate population-size environment that exists in multicellular species provides a powerful mechanism for the passive remodeling of entire developmental genetic pathways (Lynch, 2007).
Another peculiar aspect of developmental pathways that has defied explanation is their seemingly baroque structure (Wilkins, 2002, 2005). It is common for linear pathways to consist of a series of genes whose products are essential to the activation/deactivation of the next downstream member, with only the expression of the final component in the series having an immediate phenotypic effect. For example, the product of gene D may be necessary to turn on gene C, whose product turns on gene B, whose
product finally turns on gene A, which carries out an essential organismal function. Pathways involving only inhibitory steps also exist, and these lead to an alternating series of high and low expression, depending on the state of the first gene in the pathway. It is often unclear whether such complexity has any advantages over the simple constitutive expression or self-regulation of the final member of the pathway.
In principle, pathway augmentation may be driven entirely by the nonadaptive processes of duplication, degeneration, and genetic drift. Consider the series of regulatory states for gene A in Fig. 5.3. In the simplest case, A carries out some function in a self-sufficient fashion, but in a series of steps, it can become completely reliant on upstream activation by transcription factor B. A scenario like this could unfold in the following way. Initially, A becomes sensitive to activation by B, either because gene A has acquired a binding site for factor B, or because factor B acquires a fortuitous mutation that causes it to serve as an activator of A. At this point, gene A has redundant activation pathways, and is therefore insensitive to loss of one of them. Should a degenerative mutation cause a redundantly regulated allele of A to lose the ability to self-regulate, B will have been established as an essential activator, i.e., the pathway will have been augmented by a step. In principle, this process could be repeated anew as B acquires sensitivity to a further upstream gene C and loses the ability to constitutively express.
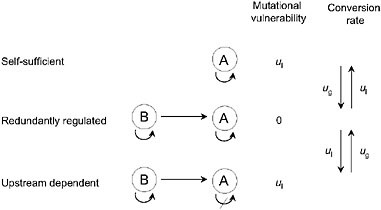
FIGURE 5.3 A series of allelic states for locus A, defined by the ability to self-express and/or be activated by an upstream transcription factor B. Mutational rates of gain and loss of regulatory abilities are denoted by ug and ul, here for simplicity assumed to be the same for both self-activation and upstream activation. The redundantly regulated allele is invulnerable to single-loss mutations.
As in the case of subfunction fission and duplicate-gene subfunctionalization, the probability of establishment of these types of changes will depend on Ng. This is because a redundantly regulated allele has a weak mutational advantage equal to the rate of loss of a regulatory site (ul); one such mutation will result in the nonfunctionalization of either a self-regulated or an upstream-dependent allele, but will leave the function of a redundantly regulated allele unaltered. If 1/Ng > u1, such an advantage will be too small to be influenced by selection, and the population will evolve to an allelic state that simply depends on the relative rates of gain and loss of regulatory sites (ug and ul in Fig. 5.3). In contrast, if 1/Ng < u1, the accumulation of upstream-dependent alleles will be inhibited by their weak mutational burden and their lack of function in genetic backgrounds that fail to support A–B crosstalk. Thus, whereas small Ng may promote the passive elongation of genetic pathways, large Ng has the opposite effect. This does not mean that the augmentation of obligatory pathways cannot occur in very large populations, but if such changes are to occur, they must be of immediate selective advantage.
EVOLVABILITY
All replicating populations are capable of evolution, but it has recently been argued that some species are better at it than others, with natural selection directly advancing features of genomic architecture, genetic networks, and developmental pathways to promote the future ability of a species to adaptively evolve. Such speculation, which is almost entirely restricted to molecular and cell biologists and those who study digital organisms (e.g., Gerhart and Kirschner, 1997; Kirschner and Gerhart, 1998, 2005; Rutherford and Lindquist, 1998; True and Lindquist, 2000; Caporale, 2003; Earl and Deem, 2004; Bloom et al., 2006; Federici and Downing, 2006), has been subject to considerable criticism by evolutionary biologists (e.g., Williams, 1966; Dickinson and Seger, 1999; Partridge and Barton, 2000; Brookfield, 2001; Sniegowski and Murphy, 2006). The term evolvability has long been in use in quantitative genetics, where it has a precise definition closely related to the concept of heritability, i.e., the relative amount of standing variation that is subject to a response to natural selection (Houle, 1992; Lynch and Walsh, 1998). However, the above-mentioned authors use the word in a rather different way, loosely defining evolvability to be the ability of a lineage to generate useful adaptive variation via mutational flexibility. Regardless of the definition, the idea that variation in evolvability exists among species is secure, as it has long been known that organisms and classes of traits vary in their propensities to respond to natural selection (Falconer and Mackay, 1996). Less secure is the idea that the ability to evolve itself is actively promoted by directional selection. Four reasons for skepticism follow.
First, evolution is a population-level feature. Thus, if an organismal feature that modifies the ability to evolve is to be advanced directly by adaptive mechanisms, selection must operate efficiently at a higher level of organization than the individual. This requires a significantly subdivided population structure, with levels of evolvability being positively correlated with population longevity and/or productivity. Because populations survive longer than individuals, such group selection is expected to be a much weaker force than individual selection, and necessarily operates on much longer time scales. If evolvability is to be subject to selective advancement, at least three stringent conditions must be met: (i) the group advantages of the genomic attribute that enhances evolvability must exceed any conflicting pressures operating at the individual level; (ii) the enhanced capacity for rapid evolutionary change must persist over the time scale of group selection; and (iii) while en route to fixation at the population level, the alleles that promote evolvability must remain tightly linked to the loci whose evolution is advantageous. Do such conditions ever exist in nature? The evidence for individual-level selection is overwhelming (Endler, 1986; Kingsolver et al., 2001), but aside from the matter of kin selection in behavioral evolution (Hamilton, 1964a,b; Wilson, 1975), the evidence for the operation of group selection is weak, although some investigators remain more optimistic than others (Coyne et al., 2000; Goodnight and Wade, 2000).
Second, it is by no means clear that an enhanced ability to evolve is generally advantageous. The dynamics of genetic variance for quantitative traits is complex, with selection modifying allele frequencies at epistatically interacting loci in ways that can either increase or decrease heritabilities, regardless of the advantage of the traits under selection (Carter et al., 2005). In addition, one can just as easily point to a long list of pathologies that can arise from an overly rapid proliferation of a new phenotype, and such scenarios have motivated a completely alternative, and equally speculative, view, that selection can favor mechanisms that suppress evolvability (Altenberg, 2005). Furthermore, theoretical studies have shown that the kinds of complexities that are often focused on by those enamored with evolvability (e.g., increased dimensionality and modularity) can actually inhibit the rate of adaptive evolution (Orr, 2000; Welch and Waxman, 2003; Haygood, 2006). Although the arguments are technical, they are no more abstract than the verbal reasoning of the evolvability school.
Third, there is no evidence that phylogenetic variation in evolutionary features reflects anything more than diversity in variation-generating factors that exist for purely physical reasons. For example, the biological features most likely to influence the ability to evolve, recombination and mutation rates, vary by orders of magnitude among species, with no
sudden discontinuities in the lineages imagined to be most evolvable (animals and land plants) (Lynch, 2006, 2007). Such variation appears to be a simple by-product of alterations in chromosome lengths and numbers of germ-line cell divisions: because chromosome number is independent of genome size, and there is typically one meiotic cross-over event per chromosome, a doubling in genome size generally results in a 50% reduction in the recombination rate per physical distance; and because a large fraction of mutations are generated during replication, a doubling in the number of germ-line cell divisions doubles the per-generation mutation rate.
Fourth, comparative genomics provides no support for the idea that genome architectural changes have been promoted in multicellular lineages so as to enhance their ability to evolve (Lynch, 2007). Indeed, other than the appearance of spliceosomal introns, some forms of mobile elements, and organelles in the stem eukaryote, there are no discontinuities in the basic features of genomes across the entire domain of cellular life. Moreover, as noted above, the additional genomic complexities of multicellular eukaryotes appear not to have arisen by positive selection but instead to have emerged passively in population-genetic environments where the efficiency of selection is relaxed, quite contrary to the view espoused by the evolvability school. Many unicellular species are excluded from certain evolutionary pathways that are open to multicellular species, and vice versa, but this is simply an indirect consequence of the altered power of nonadaptive evolutionary forces in these different contexts, not a direct outcome of natural selection for the ability to engage in particular evolutionary pursuits.
CLOSING COMMENTS
Because it deals with observations on historical outcomes, frequently in the face of incomplete information, the field of evolution attracts significantly more speculation than the average area of science. Nevertheless, a substantial body of well tested theory provides the basis for understanding the pathways that are open to evolutionary exploration in various population-genetic contexts. Four of the major buzzwords in biology today are complexity, modularity, evolvability, and robustness, and it is often claimed that ill-defined mechanisms not previously appreciated by evolutionary biologists must be invoked to explain the existence of emergent properties that putatively enhance the long-term success of extant taxa. This stance is not very different from the intelligent-design philosophy of invoking unknown mechanisms to explain biodiversity. Although those who promote the concept of the adaptive evolution of the above features are by no means intelligent-design advocates, the burden of evidence for invoking an all-powerful guiding hand of natural selection
should be no less stringent than one would demand of a creationist. If evolutionary science is to move forward, the standards of the field should be set no lower than in any other area of inquiry.
The field of population genetics is technically demanding, and it is well known that most biologists abhor all things mathematical. However, the details do matter in the field of evolutionary biology. As discussed above, many aspects of biology that superficially appear to have adaptive roots almost certainly owe their existence in part to nonadaptive processes. Such conclusions would be difficult to reach without a formal population-genetic framework, but they equally rely on observations from molecular, genomic, and cell biology. Such conclusions also raise significant challenges. If complexity, modularity, evolvability, and/or robustness are entirely products of adaptive processes, then where is the evidence? What are the expected patterns of evolution of such properties in the absence of selection, and what types of observations would be acceptable as a falsification of a null, nonadaptive hypothesis?
This tone of dissent is not meant to be disrespectful. The development of a mature field of evolutionary biology requires the participation of not just population geneticists, but molecular, cell, and developmental biologists. However, the integration of these fields needs to be a two-way street. Because the forces of mutation, recombination, and genetic drift are now readily quantifiable in multiple species, there is no longer any justification for blindly launching suppositions about adaptive scenarios without an evaluation of the likelihood of nonadaptive alternatives. Moreover, if the conclusion that nonadaptive processes have played a central role in driving evolutionary patterns is correct, the origins of biological complexity should no longer be viewed as extraordinarily low-probability outcomes of unobservable adaptive challenges, but expected derivatives of the special population-genetic features of DNA-based genomes. A similar point has been made previously by Kauffman (1993), although his conclusions were derived from models far removed from mainstream population genetics.
ACKNOWLEDGMENTS
Helpful input has been provided by E. Haag, M. Hahn, H. Malik, S. Otto, A. Stoltzfus, G. Wray, and the two reviewers. This work was supported by the National Institutes of Health and National Science Foundation.






















