2
Paleoclimatic Modeling—A Review with Reference to Problems and Prospects for the Pre-Pleistocene
W.LAWRENCE GATES
Oregon State University
INTRODUCTION
While problems of paleoclimate have long held the attention of geologists, biologists, and climatologists, they have only recently been regarded as a subject to which mathematical modeling could be applied successfully. From painstakingly assembled evidence of climatic changes in the geologic past at scattered locations around the world, the volume of paleoclimatic data has caused a veritable flood during recent years as new techniques of dating and new sources of information have been developed. The unifying key to this evidence of global pre-Pleistocene climates is the theory of plate tectonics, through which the relative global geometry of the continents and oceans may be at least tentatively reconstructed. These reconstructions provide the large-scale boundary conditions for climate, whereas the accompanying biological and geophysical data provide verifying evidence for climatic change; what is missing is the reconstruction of the paleoclimate itself, so that the global distribution and evolution of the climate over geologic time may be seen in parallel to the large-scale changes of the Earth’s surface and the evolution of the Earth’s flora and fauna. This reconstruction of the Earth’s climatic history is one of the great unsolved problems of geophysics and poses a particularly exciting challenge to the climate modeler.
In addition to its unifying role in paleoclimatic research, the modeling of the structure and evolution of climate over geologic time presents a unique opportunity to test the performance of climate models under the widest possible variety of boundary conditions. The comparison of modeled paleoclimates with the paleoclimatic evidence is a valuable supplement to the models’ calibration, which would otherwise be confined to modern climates, and thereby increases confidence in the models’ use in the estimation of possible future climates. The systematic evaluation of model-simulated paleoclimates may also be expected to serve as a guide in the identification of the accuracy needed in paleoclimatic data and in the assembly and analysis of new data in regions of particular climatic significance. In view of the uncertainty that surrounds the global distribution of many of the pre-Pleistocene boundary conditions required by climate models, disagreement between the modeled and “observed” paleoclimate may be at least partly due to this source; experimentation with alternate but plausible distributions of mountains and shallow seas, for example, may improve the accuracy of both the simulated climate and
the geologic reconstruction. Once a best fit is obtained for a particular geologic epoch, further experimentation may permit the testing of hypotheses of paleoclimatic change and thereby provide the elements of a consistent physical synthesis of pre-Pleistocene climates.
The purpose of this chapter is to review and evaluate climate modeling as a tool for paleoclimatic research. To this end, I shall first present an overview of the techniques and present status of climate modeling, followed by a brief review of past applications of climate models to paleoclimatology. With this background, I shall then consider the development of a research strategy for modeling pre-Pleistocene climates in particular. More comprehensive reviews of climate modeling have been given by Schneider and Dickinson (1974) and Saltzman (1978), and current model performance has been reviewed by the World Meteorological Organization (1979).
THE CLIMATE SYSTEM AND CLIMATE MODELING
Underlying much of the resurgence of interest in the problem of climate that has occurred in the past decade or so is the increasingly clear demonstration that numerical models are capable of simulating many important aspects of the global climate with considerable accuracy. This has prompted the use of such models to study the climatic impacts of a variety of factors, such as increased CO2 concentration in the atmosphere and changes in the character of the Earth’s surface. Even though climate models have not yet been applied extensively to the prediction of the time-dependent evolution of future climate in terms of specific seasons or specific years, experimentation with climate models has provided new insight into the many factors that can influence climate and its changes.
The Physical Basis of Climate Modeling
The Earth’s climate is the result of the interaction among a wide variety of physical processes, many of which are familiar as the ingredients of daily weather. On the longer time scales of climate, however, it is not only the atmosphere that is involved but also the behavior of the world’s oceans and ice masses and the nature of the land surface and the associated biomass. These elements are usually identified as components of the climate system, which thus formally includes the atmosphere, hydrosphere, cryosphere, surface lithosphere, and global biomass (NRC Panel on Climatic Variation, U.S. Committee for GARP, 1975). These components of the complete climate system are shown schematically in Figure 2.1, together with some of the principal interactions among them.
The atmosphere is of course the most prominent and familiar component of the climate system and is central to the common perception of climate itself. In addition to the average of statistical distribution of the wind, pressure, temperature, and humidity, the atmospheric climate includes the distribution of cloudiness and precipitation, the distribution of shortwave and long-wave radiation, and the atmospheric composition and aerosol concentration. On the global scale the distribution of many of these atmospheric properties is closely related to the surface properties of the ocean, including the ocean’s configuration relative to the continents. The oceanic climate itself includes the statistical distribution of ocean temperature, salinity, and current, together with the distribution of dissolved gases and suspended matter. Of particular importance to the atmosphere is the distribution of the sea-surface temperature, which largely controls the vertical flux of heat and moisture through the atmospheric boundary layer.
In addition to the properties of the atmosphere and ocean, the global distribution of ice and snow is an important compo-
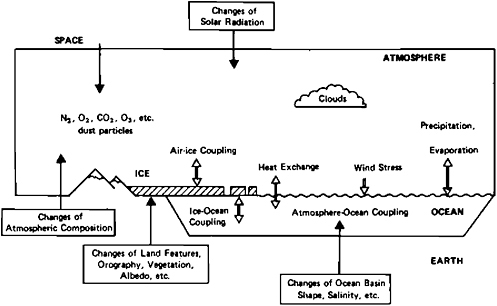
FIGURE 2.1 Schematic representation of the climate system and the principal interactions between its components (from NRC Panel on Climatic Variation, U.S. Committee for GARP, 1975).
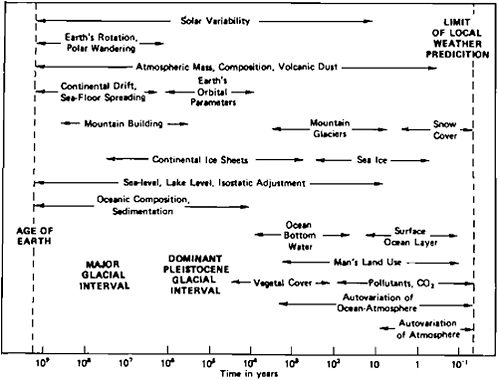
FIGURE 2.2 The characteristic time scales over which possible internal and external causes of climatic change take place (from NRC Panel on Climatic Variation, U.S. Committee for GARP, 1975).
nent of the climate system. The climate of the world’s ice masses includes the statistics of their areal extent and thickness, and their temperature and motion, whether for the continental ice sheets, mountain glaciers, sea or lake ice, or surface snow cover. These latter elements respond relatively rapidly to atmospheric and oceanic conditions, while the former and more massive elements change much more slowly. In this respect the climate of the cryosphere is like that of the land surface and associated biomass, both of which contain elements of widely differing response times to the prevailing atmospheric (and oceanic) conditions. The climate of the Earth’s land surface and biomass in turn includes the statistics of the temperature and water content of the surface soil, the surface’s albedo or reflective characteristics for solar radiation, and the surface vegetation or land use, all of which have important effects on surface evapotranspiration and surface heat and moisture fluxes.
Taken together, these climatic statistics or characteristics constitute the total climate system, which also formally includes the variability (and higher-order statistics) of the various climatic elements in addition to the distribution of the means. Defined in this way the climate of the Earth has not yet been completely determined, for large portions of the global atmosphere and ocean remain unobserved on a systematic basis, and the analysis necessary for an adequate description of even the atmosphere’s variability has not yet been completed. The determination of climate is further complicated by the fact that the statistics (or climate) of the complete climatic system can in principle change in response to a wide variety of influences originating outside the system, as well as in response to influences from within the system itself. As illustrated in Figure 2.1, a distinction is therefore made between internal and external causes of climate change, with the latter presumably being independent of the climate of the (internal) system.
In view of many processes that serve to relate one portion of the climate system to another, and the disparate response times of the system’s atmospheric, oceanic, cryospheric, land surface, and biomass components to these internal processes as well as to external ones, the history of the Earth’s climate can be expected to show variations over a wide range of time scales. As illustrated in Figure 2.2, these variations extend from the age of the atmosphere itself to the shortest-term climatic variation (about 1 month) that can be identified. Even if the external factors causing climate change were concentrated in welldefined frequencies, the high degree of coupling or interaction among internal processes in the climate system would be sufficient to create a virtually continuous spectrum of climatic variation. It is precisely these nonlinear feedback processes, the most prominent of which are illustrated in Figures 2.1 and 2.2, that make the analysis of climate and climate change a difficult if not impossible task without the assistance of models. (As we shall see, however, even with models there remain significant uncertainties, although the process is now at least a systematic one.)
Although a truly comprehensive climate model would include the interactions among all components of the climate system, usually only a portion of the complete system is modeled at any one time, with the remaining components held fixed (or ignored). This tactic is due both to our limited observational understanding of many of the interactions involving the nonat-
mospheric portions of the system and to the difficulty of coping with the vastly different time scales over which different portions of the climate system respond (see Figure 2.2).
The fastest-responding component of the climate system is of course the atmosphere, which effectively adjusts to new external conditions on time scales of the order of months. This relatively rapid response is determined by the characteristic growth rate of synoptic-scale baroclinic disturbances (the familiar transient highs and lows of mid-latitudes) and their associated transports of heat and momentum and by the more rapid adjustments that occur through smaller-scale convective and turbulent processes. The response of the ocean occurs over time scales ranging from the order of months in the surface waters in response to atmospheric changes to the order of centuries in the case of the deeper ocean. These time scales are determined by the vertical mixing of the upper ocean by wind and convection and by the relatively high thermal and mechanical inertia of the bulk of the oceanic water mass. Except for the synoptic-scale and seasonal variation of sea ice and surface snow cover as a result of surface oceanic and atmospheric heat fluxes, the response to the cryosphere may be even slower than that of the oceans; mountain glaciers typically respond to changes in atmospheric conditions and snow accumulation over time scales of centuries, while the more massive continental ice sheets respond over thousands of years. These time scales are determined by the relatively high viscosity, latent heat, and albedo of the ice and by the large volumes of ice involved. Finally, the response of the land surface and associated biomass occurs on time scales from months in the case of seasonal vegetative cover to centuries and beyond in the case of changes in surface-soil properties by erosion and desertification. These and other aspects of the physical basis of climate and climate modeling are reviewed in more detail elsewhere (World Meteorological Organization, 1975).
Faced with this complexity of space and time scales, it has been found convenient to introduce a scientific definition of climate. We may define climate, or more precisely a climatic state, as the statistics of one or more components of the climatic system over a specified domain and specified time interval, including the mean, variance, and other moments (NRC Panel on Climatic Variation, U.S. Committee for GARP, 1975). We may therefore speak, for example, of the atmospheric climate of Washington or of North America during July or of the climate of the global atmosphere-ocean system over a year, decade, or century. This definition recognizes that the climate varies significantly in both space and time and avoids the sometimes troublesome questions of homogeneity and statistical equilibrium. Climatic change may then be defined as the difference between climatic states of the same kind, and we may speak, for example, of the interannual climatic change between two Januaries or of the climatic change between two decades. When practical applications of climate are considered, these definitions are often further restricted to apply to only the atmosphere near the surface and to the more readily observed variables, as in the traditional classifications of climate in terms of the average seasonal regimes of surface-air temperature and precipitation. There are therefore many types of climate and climatic change, the most important aspect of which is the identification of the space and time scales involved for that portion of the climate system being considered.
The Formulation and Structure of Climate Models
For the present purposes, climate models may be considered to be physical-mathematical representations of the structure and variation of the large-scale climate. Most of these focus on the atmosphere, although there are some that consider aspects of the coupled atmosphere-ocean-ice system. For the most part, the continental ice sheets, which play such a large part in the geologic history of the Earth’s surface, have not been fully incorporated into the interactive climate system nor have the longer-term changes of the land surface and biomass been adequately modeled.
The dynamical basis of climate models rests on the fundamental equations that presumably govern the system’s motion, mass, and energy, together with whatever additional physical information is necessary to describe the system and its boundary conditions. For the atmosphere, these relations may be written in the form of the equations describing the conservation of horizontal momentum, the conservation of heat, and the conservation of mass:
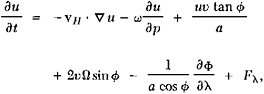
(2.1)
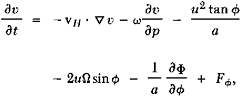
(2.2)
(2.3)
(2.4)
(2.5)
where a is the radius of an assumed spherical Earth with latitude ![]() longitude λ, and rotation rate Ω, and ∇ is a gradient operator on an isobaric surface. Here the dependent variables are the eastward (u) and northward (υ) components of the horizontal wind vH, the vertical mass flux ω (=dp/dt in the isobaric coordinate system in which the pressure p plays the role of the vertical independent variable), the geopotential Φ of an isobaric surface, the temperature T, and the atmospheric specific humidity q. Together with the hydrostatic equation ∂Φ/∂p=−α and the atmospheric equation of state pα=RT,
longitude λ, and rotation rate Ω, and ∇ is a gradient operator on an isobaric surface. Here the dependent variables are the eastward (u) and northward (υ) components of the horizontal wind vH, the vertical mass flux ω (=dp/dt in the isobaric coordinate system in which the pressure p plays the role of the vertical independent variable), the geopotential Φ of an isobaric surface, the temperature T, and the atmospheric specific humidity q. Together with the hydrostatic equation ∂Φ/∂p=−α and the atmospheric equation of state pα=RT,
where α is the specific volume and R the gas constant, Eqs. (2.1)–(2.5) constitute a closed dynamical system in terms of the variables u, υ, ω, T, q, and α once the frictional forces Fλ and ![]() the diabatic heating Q, the net evaporation E minus the net condensation C, and the necessary boundary conditions are specified. For most applications, the Earth’s geophysical constants (Ω, a, and gravity), the Earth-Sun geometry, the atmospheric composition, and the distribution and elevation of the continents relative to the oceans are assumed given.
the diabatic heating Q, the net evaporation E minus the net condensation C, and the necessary boundary conditions are specified. For most applications, the Earth’s geophysical constants (Ω, a, and gravity), the Earth-Sun geometry, the atmospheric composition, and the distribution and elevation of the continents relative to the oceans are assumed given.
Equations (2.1)–(2.4) describe the local variation of the velocity, temperature, and moisture with time (t) as a result of the horizontal and vertical advection accompanying the largescale field of motion over the spherical Earth, the Coriolis forces induced by the Earth’s rotation, the pressure forces, and the local frictional, heating, and moisture source/sink effects; Eq. (2.5), on the other hand, serves to determine the vertical motion in terms of the isobaric divergence of the horizontal velocity and is a diagnostic relation in contrast to the prognostic Eqs. (2.1)–(2.4). These equations, often with further approximations, are the basis of the numerical weather-prediction methods now used routinely by the National Weather Service. Similar equations exist for the variation of the velocity, temperature, and salinity of the ocean and form the basis of operational models for predicting the large-scale oceanic circulation and sea-surface temperature. The amount of water in the surface soil and the depth of snow on the surface are sometimes also treated as dependent variables through equations describing their net accumulation as a function of the local precipitation, evaporation, and surface runoff and/or melting.
For the purposes of climate, however, some of the most important physical processes are not those displayed explicitly in these equations (all of which can in principle be determined with reasonable accuracy) but rather those that are contained implicitly in the frictional and heating terms. Included in the symbol F, for example, are all the smaller-scale convective and turbulent transfers of momentum within the atmosphere and between the atmosphere and the underlying surface, whether it is ocean, land, or ice; in the case of the ocean, this includes the wind stress at the sea surface and the ocean’s frictional drag against the bottom and lateral boundaries of the basin. These frictional effects serve as a brake on the intensity of the circulation, which is otherwise sustained by the kinetic energy converted from the total potential and internal energy of the system, the ultimate source of which is the Sun’s radiation. The symbol Q contains not only this net heating from insolation but also the heating from the transfer of long-wave radiation within the atmosphere and between the atmosphere, the clouds, and the Earth’s surface. Also included in Q is the latent heating accompanying the processes of condensation and evaporation and the transfers of sensible heat by conduction and convection.
Many of these momentum and heat fluxes occur in the boundary layer near the Earth’s surface and in the convective-scale motions associated with clouds in the case of the atmosphere. Generally, these fluxes are not explicitly resolved in climate models, in spite of the fact that they contain much of the model’s physics, and their successful parameterization or representation in terms of the large-scale variables is an important aspect of modeling. Such parameterization usually rests heavily on empirical information and affords an opportunity to adjust or tune the model to some extent to observed (present) conditions. On the time scales of climate such model parameterization is of particular importance, because in the long run it is the accumulation of small imbalances in friction and heating that may cause the climate to change as the system seeks a new statistical equilibrium. The net incoming and outgoing radiation at the top of the atmosphere are in only approximate balance over periods of a year or longer, and it is possible for the deeper oceans and the ice sheets, for example, to store or release large amounts of heat effectively over long periods of time by slow but progressive changes in their temperature and volume.
The remaining aspect of the formulation of a climate model is the specification of the boundary conditions necessary for its solution. In the case of the atmosphere, these conditions consist of the incoming solar radiation at the top of the (model) atmosphere and the elevation and albedo of the Earth’s surface. Without the ocean and ice included as interactive components, it is also necessary to specify the sea-surface temperature and the distribution of surface ice as boundary conditions for the atmospheric model as sketched in Figure 2.3. The boundary conditions for an oceanic model are the net fluxes of momentum, heat, and moisture at the ocean surface (which would automatically be determined by a coupled atmosphere) and the geometry of the ocean basin. Similarly, for models of the ice sheets and land surface the necessary boundary conditions
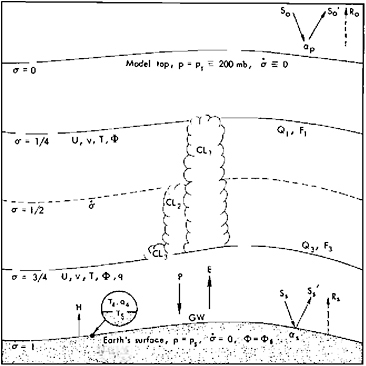
FIGURE 2.3 Schematic representation of the structure and principal variables of an atmospheric GCM. Symbols are as defined in the text, except for σ, which is a scaled vertical coordinate=(p−pT)(ps−pT)−1, sensible heat flux H, ground wetness GW, solar radiation S, terrestrial radiation R, cloudiness CL, and albedo α (from Schlesinger and Gates, 1979).
are the net fluxes of water and heat with the overlying atmosphere and the geometry of the Earth’s surface.
Because the atmosphere is the central conduit (and the smallest reservoir) of the climate system’s energy and contains most of the high-frequency variations, it is the resolution of the atmospheric portion of a climate model that is usually the most demanding. An exception to this occurs when the atmosphere is itself treated in a parametric or statistical fashion, in which case the necessary resolution is determined by the highest-frequency component of the climate system that is explicitly modeled. The climate models of lowest spatial resolution are those that effectively represent the entire atmosphere as a single point; those of highest spatial resolution are capable of resolving features of several-hundred-kilometer horizontal dimension and a few kilometer vertical dimension. Because the computational effort involved in solving a model generally varies as the cube of the spatial resolution, the higher-resolution models generally proceed relatively slowly on even the fastest of modern computers, whereas models of less spatial resolution proceed hundreds or thousands of times faster. This computational disparity effectively restricts the more detailed climate models to the simulation of a few years or decades. The more highly parameterized (and therefore less-detailed) models are able to simulate effectively the behavior of at least some aspects of the climate over much longer periods of time. As we shall see, the problems of paleoclimate require an effective solution to this computational dilemma.
In general, atmospheric and oceanic models (and hence climate models) are conveniently classified as either general-circulation models (GCMs) or statistical-dynamical models (SDMs), depending on whether synoptic-scale motions are resolved. In the atmosphere these motions are the familiar cyclones and anticyclones of mid-latitude weather, which occur on characteristic scales of the order of 103 km, whereas the corresponding motions in the ocean (the so-called mesoscale oceanic eddies) occur on scales of the order of 102 km. Most of the kinetic energy in both fluids is associated with these transient disturbances, and they represent the dominant mode of instability whereby potential and internal energy is transformed into kinetic energy; these motions also play an important role in the maintenance of the global balances of angular momentum, heat, and total energy. GCMs are therefore essentially weather models that have been designed to run on climatic time scales and from which the statistics of the climate are extracted by averaging the solutions over the desired intervals of time (and possibly space as well). SDMs, on the other hand, may be regarded as more directly addressing the climatic averages themselves, although not without a possibly serious loss of information. Depending on the essential space and time scales of the problem being considered, both modeling approaches may be useful; for the problem of pre-Pleistocene climates in particular, a blending of the two approaches is indicated, as will be discussed below.
As already noted, climate models are invariably solved with the aid of high-speed computers. This requires the design of appropriate numerical algorithms to replace the physical differential equations [such as Eqs. (2.1)–(2.5)], as well as the adoption of resolution intervals in both space and time; in a well-designed numerical scheme the solution of the approximating equations should be reasonably close to the (generally unknown) solution of the basic differential equations themselves. Although other techniques are available, most GCMs are solved with the aid of either finite-difference inite-difference or spectral approximations to the models’ physical equations, in which case the maximum allowable time step is limited to the order of 1 h in order to ensure the solution’s computational stability. Moreover, it is also generally desirable to design the numerical solution of a GCM in such a way that the basic integral invariants of the flow (such as the total energy, total angular momentum, and total square of the vorticity) will be at least approximately conserved in the absence of sources and sinks.
When these conditions are met, the numerical solution of an atmospheric GCM proceeds on modern computers at speeds between roughly 10 and 1000 times the speed of the evolving climate itself, depending primarily on the number of levels in the vertical and the amount of sophistication included in the parameterization of the friction, heating, and moisture source terms. The numerical solution of SDMs, on the other hand, may be carried out without the restrictions of computational stability, which so severely slow a GCM’s solution because they do not explicitly resolve the atmospheric (or oceanic) synoptic-scale motions. It is therefore not uncommon for a time-dependent SDM to advance in steps of several years, although special attention is sometimes given to seasonal changes. SDMs also lend themselves readily to the examination of equilibrium or time-independent solutions, such as those that are built around the requirement of an exact heat balance at the Earth’s surface, By employing different degrees of spatial averaging, SDMs may be developed in zero-, one-, two-, or three-dimensional versions (Saltzman, 1978); a zero-dimensional model is one in which averaging is performed both horizontally and vertically over the climate system, a one-dimensional model has only vertical or latitudinal resolution, and two-dimensional models are usually developed in either the meridional or horizontal planes. Zonally averaged atmospheric models in particular have been widely used to study the latitudinal dependence of climate, although they necessarily obscure the longitudinal structure of climate features such as those due to the relative spacing of oceans and continents and require parameterization of the effects of synoptic-scale disturbances.
When examining the output of a climate model, whether in the form of an extended numerical integration of a GCM or the equilibrium numerical solution of an SDM, it is usually assumed that the statistical properties of the solution (i.e., the climate) depend only on the specification of the model’s internal physical properties and on the specified boundary conditions. In this deterministic view of climate, the initial conditions from which a particular integration is started are viewed as unimportant in the determination of the statistical properties of the equilibrium climatic state; when the more slowly responding components of the climatic system are included, however, more time will generally be required to achieve statistical equilibrium. As reasonable as this sounds, it is known that the climate given by at least some relatively simple models is not unique and that more than one stable solution exists for identical boundary conditions. This property has its origin in the
model’s parameterization of nonlinear feedback effects, and whether it is also present in more general climate models has not yet been satisfactorily determined. The solutions of certain simplified climate systems under invariant boundary conditions are also known to switch in a seemingly irregular and unpredictable manner between two seemingly distinct states; whether such behavior is (or has been) exhibited by the Earth’s climate is not known. Lest these considerations cast doubt on the validity of paleoclimatic reconstruction, it should be noted that the Earth’s climate has necessarily followed only one climatic path during geologic time even if multiple paths were available and that this uniqueness should therefore in principle be reproducible.
Characteristic Model Performance
To give a clear idea of the nature and accuracy of the solutions to be expected from climate models, we first consider the characteristic performance of current atmospheric GCMs. The distribution of the average sea-level pressure simulated for the month of July in a recent integration of a two-level atmospheric GCM is shown in Figure 2.4, along with the observed climatological distribution (Schlesinger and Gates, 1979). While a number of local simulation errors may be noted (the most prominent of which is the model’s evident failure to simulate correctly the position of the quasi-stationary high-pressure cells over the mid-latitude oceans in the summer hemisphere), the model has satisfactorily portrayed most of the large-scale features of the pressure field. A similar level of skill is present in the corresponding solutions from other GCMs and for other months of the year when the insolation and the sea-surface temperature are assigned their observed seasonal variations. Figure 2.4 also illustrates the typical resolution of the continents and oceans achieved by global GCMs, which in this case is that given by a 4° latitude and 5° longitude grid.
The global distribution of total precipitation simulated during July in the same model integration just considered is shown in Figure 2.5, together with the climatological average July precipitation. As was the case with sea-level pressure, the model can be seen to have successfully simulated the largescale distribution of precipitation, including the band of maximum rainfall near the equator and the low precipitation in the subtropical desert and semiarid regions. Although there are errors of 100 percent or more in the estimate of local precipitation in some areas, the coherence in the simulated precipitation pattern and its systematic shift with the seasons (not shown here) lends confidence to the overall realism of this and other similarly performing GCMs. This performance is especially
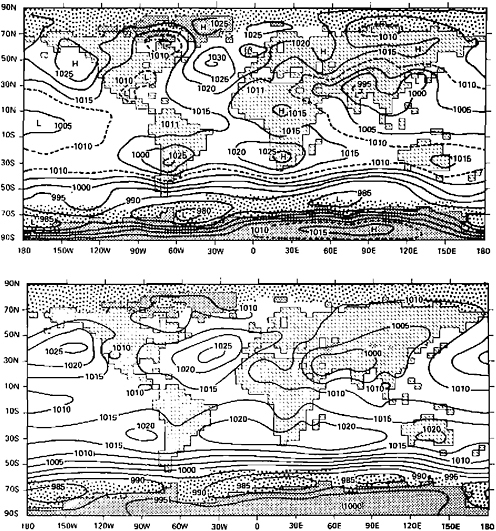
FIGURE 2.4 The distribution of July sealevel pressure (in millibars) as simulated (above) and as observed (below). Here stippling over the ocean denotes the assigned locations of sea ice (from Schlesinger and Gates, 1979).
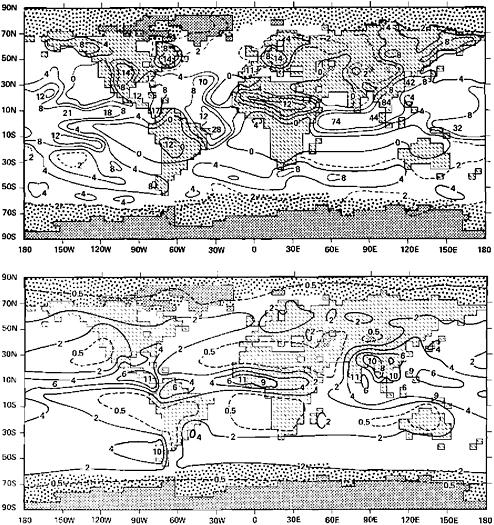
FIGURE 2.5 Same as Figure 2.4 except for July precipitation (in millimeters per day).
noteworthy in the case of precipitation, of which approximately half of that in mid-latitudes and nearly all of that in low latitudes is simulated to occur in association with convective-scale motions; the effective parameterization of this convective rainfall is one of the more difficult and sensitive aspects of climate modeling.
The characteristic performance of atmospheric SDMs may be illustrated by the zonally averaged distribution of mean air temperature simulated by a simple energy-balance mode, as shown in Figure 2.6, along with the observed average distribution (North and Coakley, 1979). This model (and most other SDMs with latitudinal resolution) has obviously reproduced the climatological meridional surface-temperature variation, especially in middle and higher latitudes, with an accuracy equal to that achieved by GCMs. As is usually the case with the more highly parameterized models, however, the extent to which this agreement with observation has been caused by the use of climatological data in the tuning or adjustment of the model’s overall heat balance needs to be determined. In spite of this proviso (or perhaps because of it), SDMs have generally shown an acceptable level of accuracy in simulating other elements of the climate, including the pressure and zonal winds (not shown here), and have proven useful in the depiction of at least a first-order solution for those aspects of the climate that are least sensitive to parameterization and spatial averaging.
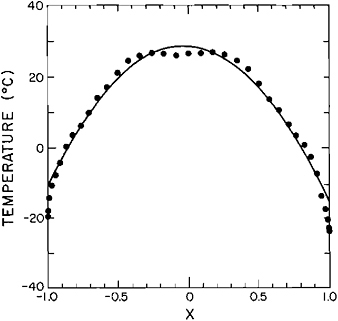
FIGURE 2.6 The distribution of the zonally averaged mean atmospheric temperature (in degrees Celsius) during March, April, and May as simulated by a simple climate model (curve) and as observed (dots). The abscissa X is the sine of the latitude (from North and Coakley, 1979).
More detailed information on the performance of current atmospheric GCMs and SDMs has been given by the World Meteorological Organization (1979).
In parallel with atmospheric GCMs, general circulation models have also been developed for the global ocean. The characteristic performance of these oceanic GCMs is illustrated in Figure 2.7 by the distribution of the annual average sea-surface temperature simulated by a six-level oceanic model in response to atmospheric wind stress and heat flux at the surface (Bryan et al., 1975). In comparison with the observed average distribution, which is also shown, the model has successfully reproduced the large-scale features of the sea-surface temperature distribution even though there are local errors of several degrees Celsius. The success of this simulation, as well as that of similar oceanic GCMs, is partly the result of the advection of temperature by the large-scale current systems, which the model successfully simulates (not shown here) and partly due to the model’s depiction of the local vertical mixing of heat. This performance is of particular importance to the atmosphere in view of the close correspondence observed between the variations of sea-surface temperature and rainfall in the lower latitudes—a result of the surface temperature’s control of surface evaporation and the subsequent convective condensation. There is therefore an expectation that when these mechanisms are allowed to interact freely in a coupled ocean-atmosphere GCM, there will be an improvement in at least the tropical simulation of both the sea-surface temperature and precipitation; the fact that this has not occurred to a marked degree in the few integrations of coupled GCMs that have been made so far is testimony to the difficulty of properly parameterizing the turbulent fluxes in the back-to-back atmospheric and oceanic surface-boundary layers and to the lack of an adequate treatment of the disparate response times of the largescale atmospheric and oceanic circulation to these mutually determined surface fluxes.
In addition to the atmosphere and ocean, models have also been successfully developed for the cryosphere. Among these are numerical models of the growth and movement of sea ice,
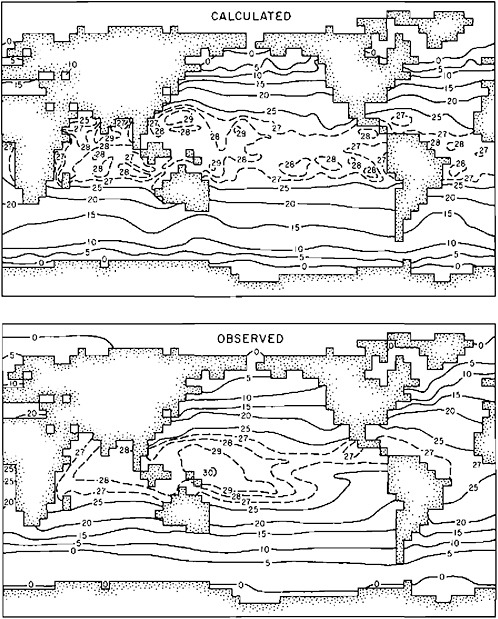
FIGURE 2.7 The distribution of annually averaged sea-surface temperature (in degrees Celsius) as simulated by an oceanic GCM (above) and as observed (below) (from Bryan et al., 1975; with permission of the American Meteorological Society).
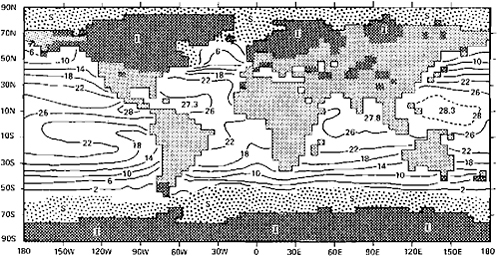
FIGURE 2.8 The distribution of sea-surface temperature (in degrees Celsius), sea ice (S, denoted over the oceans by stippling) and land ice (l, denoted over the land by cross-hatching). Here the continental outlines correspond to a sea-level lowering of 85 m as seen on a 4° latitude and 5° longitude grid (from Gates, 1976a; copyright 1976 by the American Association for the Advancement of Science).
which are usually integrated as part of the solution of an oceanic model. The seasonal variations of sea ice in the Arctic and Antarctic are reasonably well simulated by the simpler of such models that consider only the local vertical fluxes of heat above and beneath the ice. Of at least equal importance to the overall modeling of the climatic system are the models of the ice sheets (and to a lesser extent, models of mountain glaciers). In response to a prescribed net surface accumulation of mass and to a prescribed net surface-heat flux (which are the most important elements of the local atmospheric climate as far as the ice sheet is concerned), dynamical ice-sheet models that consider both the sheet’s internal temperature and velocity have successfully simulated the development of ice sheets on continental dimensions. Whereas these models may be regarded as ice-sheet GCMs, their dynamics are somewhat simpler than those of their atmospheric and oceanic counterparts because of the high viscosity of the ice. The integration of such models can therefore be carried out relatively easily. In solutions extending over hundreds and thousands of years the friction with the underlying ground and the possibility that the ice may melt at the bottom may exert a major influence on the behavior of an ice sheet as it either approaches or retreats from an equilibrium configuration (Budd, 1969). It might also be noted that an ice-sheet GCM has not yet been solved in concert with an atmospheric or oceanic GCM, so the long-term effects of their mutual interaction cannot be adequately assessed; this interaction, however, is likely to be an important element in the history of the Earth’s glaciation.
PALEOCLIMATIC MODELING
On the basis of the background and review of climate modeling given above, we are now in a position to consider the specific problem of modeling the paleoclimate, with particular reference to the pre-Pleistocene. After reviewing the problem of paleoclimatic data assembly and the present status of paleoclimatic numerical experiments, we shall consider a specific strategy for pre-Pleistocene climate modeling.
Paleoclimatic Data Assembly and Model Testing
The relative scarcity of suitable paleoclimatic records and the difficulty that usually accompanies their extraction dictates that careful consideration be given to all paleoclimatic data. These proxy data are typically found at scattered locations over the globe and can be interpreted in terms of only a limited number of climatic variables. As shown elsewhere in this volume, such paleoclimatic “data of opportunity” are also generally less abundant as one proceeds to older geologic periods.
From the viewpoint of climate modeling, paleoclimatic data serve two purposes: first, they are necessary for the realistic specification of the boundary conditions at the Earth’s surface that are required by climate models, and, second, they are necessary for the verification of at least portions of the models’ simulated climate. As has been noted previously, the most demanding surface-boundary conditions are those required by atmospheric GCMs; these consist of the location and elevation of the land surface relative to a possibly changed sea level, the sea-surface temperature, the distribution (and elevation) of ice sheets and sea ice, and the surface albedo, which serves to distinguish land-surface types and vegetative cover. Ideally these data should be provided at every point of the model’s global grid and be changed with the seasons if appropriate for the model’s time integration. No paleoclimatic data set fully meets these requirements, although that assembled by the CLIMAP Project Members (1976) for the Wisconsin ice age of about 18,000 yr. B.P. (years before present) shown in Figure 2.8 comes closest. For earlier epochs atmospheric climate modelers will have to proceed on the basis of less precise knowledge of conditions at the Earth’s surface and will have to develop the grid-point boundary-condition data sets required by GCMs with the help of interpolation schemes and the most physically consistent estimates that can be made.
In the paleoclimatic application of oceanic GCMs, the required boundary conditions consist of the location and geometry of the global ocean basins and the water mass and heat fluxes at the ocean surface. From the growing body of data col-
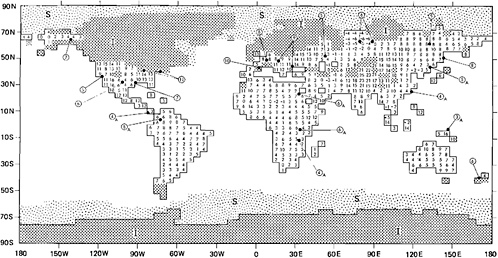
FIGURE 2.9 The distribution of the difference (present minus ice age) of July surface air temperature (in degress Celsius) over ice-free continental areas as simulated by an atmospheric GCM for the Wisconsin ice age (18,000 yr B.P.). Here the stippled areas over the ocean denote the locations of ice-age sea ice (S), and the more heavily shaded areas denote the locations of ice-age land ice (l). The encircled data are the “observed” changes as assembled by CLIMAP from pollen analyses and periglacial evidence, with the subscript A denoting observed annual (rather than July) changes (from Gates, 1976a; copyright 1976 by the American Association for the Advancement of Science).
lected in association with studies of plate tectonics, the history of the shape, depth, and global position of the major ocean basins is now emerging from which it may be possible to extract the information required by models (Smith et al., 1973; Smith and Briden, 1977; Scotese et al., 1979; Ziegler et al., 1979). Of particular importance for the large-scale oceanic circulation, and hence for the distribution of global climate, is the presence (or absence) of zonal passages and shallow seas and the geographic locations of intermediate and bottom water formation. In the simulation of a paleo-ocean, it may be expected that the surface layers will show a relatively rapid adjustment to the imposed surface fluxes and that the response of deeper water will require many years. The details of the surface fluxes are probably not critical for the study of the ocean’s spin-up characteristics, although these fluxes should be made compatible (or actually be coupled) with an atmospheric model if the oceanic climate is to achieve a realistic equilibrium state. A similar remark applies to the application of ice-sheet models, which as previously noted have not yet been integrated in concert with their atmospheric and oceanic counterparts.
After a climate model has been integrated under suitable paleoclimatic conditions, there remains the question of verifying its results against whatever paleoclimatic data are available (and have not already been used as boundary conditions for the model). Using an atmospheric GCM as an example, the time history of a climate simulation will generally yield the global distribution of a wide variety of surface climatic variables (in addition to variables in the free atmosphere itself). These include the surface-air temperature, pressure and wind velocity, surface evaporation and sensible heat flux, net surface fluxes of long-wave and shortwave radiation, precipitation in the form of either rain or snow, degree of ground wetness, local snow depth (if any), and cloudiness. If the model simulation extends over seasonal or annual time scales, then the corresponding seasonal and interannual variability of such variables is automatically furnished as well. Because the detail of the simulated data far exceeds that which is ever likely to be available for even relatively recent geologic periods, model verification will generally consist of the comparison with limited “observed” proxy data at selected locations. If such comparison shows reasonable agreement, and especially if agreement occurs for more than one variable and in more than one location, then the model’s results may be accepted provisionally. The importance of such verification for multiple variables at multiple sites is an especially important factor in our appraisal of the realism of the simulated climate, observed climate, or both as the elements of the simulated climate at least are guaranteed to be physically consistent with one another and in their spatial distribution. While it is of course true that a model is never better than the data on which it rests, a locally poor verification of a particular simulated climatic variable may be due to the low quality of the verifying proxy data rather than to a failure of the model itself.
Although these two uses of paleoclimatic data—for boundary conditions and for verification—are formally independent from the modeler’s viewpoint, they are often closely related in practical paleoclimatic work. For example, the derivation of one proxy data set may depend on another set, as in the calibration of paleobotanical evidence in terms of either temperature and rainfall or the implications that the specification of the land-surface albedo has in terms of surface vegetation. Furthermore, a proxy data set that serves as a boundary condition for one model may serve as verification data for another, more general model, as in the case of the sea-surface temperature inferred from the analysis of oceanic sediments. In the CLIMAP effort, most of the available proxy data were for the specification of model surface-boundary conditions, leaving relatively little independent data for verification. It is hoped that this allocation will be reversed as paleoclimatic data assembly proceeds in parallel with climatic reconstructions with progressively more comprehensive models.
Paleoclimatic Model Experiments
As a preview of the results that may be expected from future model simulations of the pre-Pleistocene, it is useful to review in more detail some of the results that have been obtained for the Wisconsin (Pleistocene) ice age. The first application of a comprehensive atmospheric model to the simulation of ice-age climate was that of Alyea (1972), who used a hemispheric geostrophic model in conjunction with idealized surface-boundary conditions representing an ice age. He found, as might have been anticipated, a generally cooler and drier climate along with indications of slight shifts in the pattern of the zonal wind circulation. Generally similar results were subsequently found by Williams et al. (1974), who used a global GCM but with surface-boundary conditions drawn from diverse estimates that schematically represented conditions during the Wisconsin ice age. Only a qualitative verification of these model experiments was attempted, and the degree of model dependence in the results has not been determined satisfactorily.
By far the most comprehensive paleoclimatic data assembly yet achieved is that of the CLIMAP Project Members (1976). These data, representing conditions at the height of the Wisconsin ice age about 18,000 yr B.P., include the global distribution of sea-surface temperature and sea ice (inferred from the fossil record in deep-sea sediments), the extent and thickness of ice sheets (reconstructed from glacial evidence and ice-sheet budgets), the albedo of the land surfaces (inferred from botantical evidence and soil characteristics), and a specification of global sea level relative to the present (inferred from coral-reef data and ice-volume estimates). These data have been used by Gates (1976a, 1976b) and Manabe and Hahn (1977) in the reconstruction of the July ice-age climate with global GCMs. The results of these experiments (in which seasonal effects were omitted) are represented in Figures 2.9 and 2.10, which show the simulated change of July surface-air temperature (with respect to the model’s simulation for present-day conditions) and the simulated ice-age July sea-level pressure, respectively. In Figure 2.9 the model is seen to have simulated an ice-age cooling of 10°C or more in extensive ice-free areas over the continents, even though the average specified cooling of the ice-age oceans relative to modern July was only about 2°C. In comparison with the limited verification data also shown in Figure 2.9, the model’s simulated cooling is considered reasonably accurate.
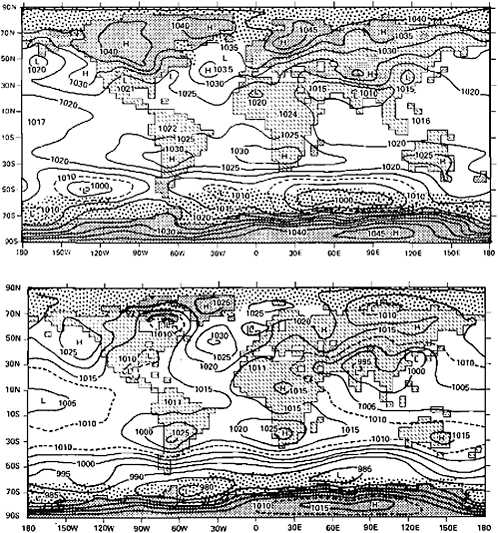
FIGURE 2.10 The distribution of July sea-level pressure (in millibars) as simulated for Wisconsin ice-age conditions (above) and for modern conditions (below); see also Figure 2.8 (from Gates, 1976b; with permission of the American Meteorological Society).
From the simulated July sea-level pressure shown in Figure 2.10, the major ice-age change in the surface circulation is seen to be that associated with the semipermanent anticyclones found over the major ice sheets in North America and Europe; this pattern implies a drastic change from the present characteristic July climate over the eastern and southern portions of these continents. Although the models of both Gates (1976a, 1976b) and of Manabe and Hahn (1977) show the July ice-age climate in general to be slightly drier than at present, less confidence can be placed in the models’ simulated changes of local precipitation (not shown here) for reasons discussed earlier. These results have been generally confirmed in new GCM experiments using the revised global data sets for both January and July recently assembled by CLIMAP (Peterson et al., 1979).
The performance of SDMs in paleoclimatic reconstruction is illustrated in Figure 2.11 by the results of Saltzman and Vernekar (1975) for glacial maximum conditions. Here the simulated ice-age changes of zonally averaged temperature, wind, and the evaporation-precipitation difference are generally similar to the zonal average of the results given by GCMs. Other SDMs have been used to simulate glacial-interglacial cycles in response to either variations of the Earth’s orbital parameters (Pollard, 1978) or to internal feedback between the ice albedo and temperature (Held and Saurez, 1974). A preliminary attempt to simulate the climatic effects of changed continental positions has also been made by Donn and Shaw (1975). Such experiments serve to illustrate the sensitivity of the climate in such models (and perhaps in all models) to the relative absorption of heat by the atmosphere, ocean, and ice. Without additional paleoclimatic data it is difficult to verify such models adequately even for the Pleistocene, although they may nevertheless prove useful in conjunction with other models in the exploration of earlier climates.
A Strategy for Modeling Pre-Pleistocene Climate
In view of the complexity of the climate system and the effort involved in achieving even a modest degree of success for modern and recent Holocene climates, it is not realistic to expect a rapid breakthrough in the simulation of pre-Pleistocene climate; it will in all likelihood require several decades of work before the paleoclimatic data and modeling techniques necessary for satisfactory results will be in hand. And even if virtually unlimited computing resources were available (which is certainly not the case), it would be utterly unrealistic to expect
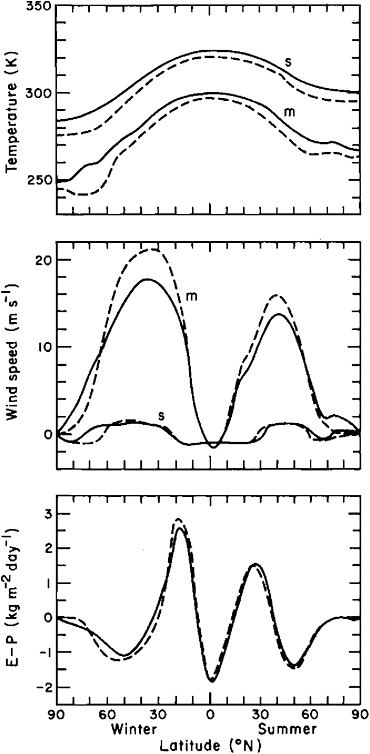
FIGURE 2.11 The distribution of zonally averaged potential temperature (top panel), zonal wind (middle panel), and evaporation-precipitation difference (bottom panel) as simulated by an atmospheric SDM for modern conditions (full line) and for 18,000 yr B.P. glacial conditions (dashed line). In the top and middle panels the letters s and m refer to surface values and mean atmospheric values, respectively (from Saltzman and Vernekar, 1975).
to simulate with GCMs the day-by-day evolution of climate over pre-Pleistocene time scales. What is needed is a modeling strategy that combines the valuable features of both GCMs and SDMs in an economical and effective fashion while guiding the acquisition of new proxy data and the development of new modeling techniques.
Such a strategy in fact is suggested by a basic characteristic of the climate system itself, namely, the widely differing response times of the system’s major atmospheric, oceanic, cryospheric, land surface, and biomass components. The behavior of the more inertial portions of the system suggests that these components effectively respond to the average or integral of the climatic information from the more rapidly varying components and that they therefore require such information only at relatively widely separated times. Hence, in the solution of an atmospheric model (and specifically an atmospheric GCM) it is permissible to neglect the variation of all other components of the system (except perhaps the oceanic surface layer and associated sea ice) and to integrate only over that time interval sufficient to generate a statistically representative atmospheric climate; this interval is certainly longer than a season but probably less than a decade. For an oceanic GCM (and perhaps also for the surface biomass) whose response time is intermediate between that of the ice sheets and the atmosphere, this strategy suggests that integration needs to be performed in response to a periodically updated atmospheric climate only over that time interval sufficient to generate a representative oceanic climate, with the land surface and ice sheets held fixed as boundary conditions; this interval is probably of the order of a few centuries. Finally, for the ice sheets themselves (and perhaps also for the land surface), this in turn suggests that models describing their variation need to be integrated in response to a periodically updated climate only over that time interval sufficient to generate a representative ice-sheet climate.
As summarized in Figure 2.12, this strategy results in a series of snapshots of the climate of the various components of the climate system, with each snapshot exposed only long enough to acquire representative information for use by another component and with the interval between snapshots selected in accord with each component’s natural response time. Although there are many conceivable variations of such a modeling strategy, its basic philosophy appears to offer a way in which long climatic time scales can be addressed without unnecessary computation. In this scheme, a climate-system component is linked to any slower-reacting components by boundary conditions and to any faster-reacting components by their climatic statistics; the common practice of using an atmospheric model with all other variables held fixed may be recognized as a part of this procedure. If the complete strategy is implemented, the evolution of the slow components will periodically update the boundary conditions for the faster components, whereas the transfer of climatic statistics in the other directions affords an opportunity for the development and use of appropriate parameterizations or entire SDMs.
Such a snapshot strategy for modeling paleoclimate may be initiated at any particular point in geologic time (or extended into the future, for that matter). Although we do not yet know the behavior of the climate system under different arrange-
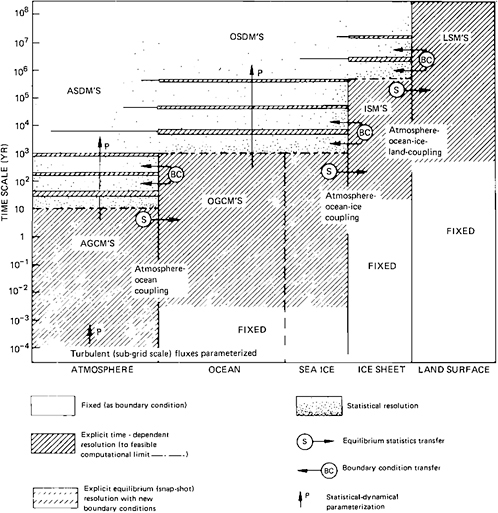
FIGURE 2.12 Schematic summary of a snapshot strategy for integrating the components of the coupled climate system. Here the symbol S denotes the transfer of equilibrium climatic statistics from one component to a more slowly varying component, BC denotes the provision of boundary-condition information in the reverse direction, and P denotes the possibility of parameterization (from Gates, 1975).
ments of the continents and oceans, there are certain times when the climate should be more interesting to study than at other times; these include in particular those periods when the continents were away from the poles and when the global ocean was free of meridional obstructions in low latitudes (Frakes, 1979). This suggests that the late Cambrian and early Devonian might be interesting times at which to attempt a reconstruction of the climate, perhaps starting with a prescribed ocean and then progressively relaxing this constraint with the strategy described above. Other considerations, not the least of which is the likely availability of appropriate paleoclimatic data, suggest that simulating the climate at some time during the Carboniferous, Permian, and Jurrasic would also be of considerable interest.
SUMMARY AND CONCLUDING REMARKS
From this review it is seen that the successful application of climate modeling to the pre-Pleistocene will depend primarily on (1) the assembly of the paleoclimatic data necessary for the specification of the model boundary conditions and for model verification and (2) the development of a modeling strategy for treating the disparate characteristic response times of the interacting components of the climatic system. It is particularly important that the geometry and relative positions of the oceans and continents be specified as accurately as possible for those geologic periods chosen for study and that data that may be used for verification of the model-simulated climate be assembled for as many climatic elements and locations as possible. These considerations are perhaps more important than the absolute accuracy of the individual data or their spatial density, in view of the inevitable questions concerning the representativeness of local data. Finally, it may be remarked that in the assembly of paleoclimatic proxy data for either model boundary conditions or verification particular attention should be given to the rapidly accumulating body of quantitative information from paleomagnetic, tectonic, and isotopic evidence, in addition to the use of the more qualitative climatic information from biogeographic sources.
Although there is always room for improvement, available models of the atmosphere and ocean are clearly capable of simulating the global structure of the currently observed seasonal climates with acceptable accuracy, and the limited application that has been made of atmospheric models to the simulation of the Wisconsin ice-age climate has given encouraging results. The most serious shortcomings of present climate models (aside from the errors associated with inadequate resolution) are believed to occur as a result of the improper parameterization of the surface-boundary layer and of the unresolved convective-scale motions. For successful application to the simulation of paleoclimates, and especially those of the prePleistocene, there is the additional need for an effective and economical method of treating the widely differing response rates of the atmosphere, ocean, ice sheets, and land surface.
One such method is a snapshot strategy, whereby interacting components of the climate system are intermittently coupled to provide the statistics of the forcing functions, boundary conditions, or both needed for a sustained integration. Such a strategy can serve as the key organizing element of a comprehensive paleoclimatic research program (NRC Panel on Climatic Variation, U.S. Committee for GARP, 1975; NRC Committee on Geology and Climate, 1978), wherein there is an active interplay between the identification, assembly,. and analysis of paleoclimatic data on the one hand and the design, application, and evaluation of a hierarchy of climate models on the other. Whereas such a program calls for the dedication of considerable resources over several decades, and will require an extraordinary degree of collaboration among Earth, atmospheric, and oceanic scientists, it is probably the most effective way to advance the scientific study of pre-Pleistocene climates.
REFERENCES
Alyea, F.F. (1972). Numerical simulation of an ice-age paleoclimate, Atmos, Sci. Paper No. 193, Colorado State U., Ft. Collins, Colorado, 134 pp.
Bryan, K., S.Manabe, and R.C.Pacanowski (1975). A global oceanatmosphere climate model, Part II. The oceanic circulation, J. Phys. Oceanogr. 5, 30–46.
Budd, W.F. (1969). The dynamics of ice masses, ANARE Science Report, Ser. A (IV), No. 108, Melbourne.
CLIMAP Project Members (1976). The surface of the ice-age Earth, Science 191, 1131–1137.
Donn, W.L., and D.Shaw (1975). The evolution of climate, Proc. WMO/IAMAP Symp. Long-Term Climatic Fluctuations (18–23 August 1975, Norwich), WMO No. 421, World Meteorological Organization, Geneva, pp. 53–62.
Frakes, L.A. (1979). Climates Throughout Geologic Time, Elsevier, Amsterdam, 310 pp.
Gates, W.L. (1975). Numerical modelling of climate change: A review of problems and prospects, Proc. WMO/IAMAP Symp. Long-Term Climatic Fluctuations (18–23 August 1975, Norwich), WMO No. 421, World Meteorological Organization, Geneva, pp. 343–354.
Gates, W.L. (1976a). Modeling the ice-age climate, Science 191, 1138–1144.
Gates, W.L. (1976b). The numerical simulation of ice-age climate with a global general circulation model, J. Atmos. Sci. 33, 1844–1873.
Held, I.M., and M.J.Saurez (1974). Simple albedo feedback models of the icecaps, Tellus 26, 613–629.
Manabe, S., and D.G.Hahn (1977). Simulation of the tropical climate of an ice age, J. Geophys. Res. 82, 3889–3911.
NRC Committee on Geology and Climate (1978). Geological Perspectives on Climatic Change, National Academy of Sciences, Washington, D.C., 46 pp.
NRC Panel on Climatic Variation, U.S. Committee for GARP (1975). Understanding Climatic Change—A Program for Action, National Academy of Sciences, Washington, D.C., 239 pp.
North, G.R., and J.A.Coakley (1979). Simple seasonal climate models, Report of the JOC Study Conference on Climate Models; Performance Intercomparison and Sensitivity Studies, W.L.Gates, ed., CARP Publications Series No. 22, Vol. 11, World Meteorological Organization, Geneva, pp. 715–727.
Peterson, G.M., T.Webb III, J.E.Kutzbach, T.van der Hammen, T.A.Wijmstra, and F.A.Street (1979). The continental record of
environmental conditions at 18,000 yr B.P.: An initial evaluation, Quat. Res. 12, 47–82.
Pollard, D. (1978). An investigation of the astronomical theory of the ice ages using a simple climate-ice sheet model, Nature 272, 233–235.
Saltzman, B. (1978). A survey of statistical-dynamical models of the terrestrial climate, Adv. Geophys. 20, 183–304.
Saltzman, B., and A.D.Vernekar (1975). A solution for the northern hemisphere climatic zonation during a glacial maximum, Quat. Res. 5, 307–320.
Schlesinger, M.E., and W.L.Gates (1979). Numerical simulation of the January and July global climate with the OSU two-level atmospheric general circulation model, Report No. 9, Climatic Research Institute, Oregon State U., Corvallis, 102 pp.
Schneider, S.H., and R.E.Dickinson (1974). Climate modeling, Rev. Geophys. Space Phys. 12, 447–493.
Scotese, C.R., R.K.Bambach, C.Barton, R.van der Voo, and A.M. Ziegler (1979). Paleozoic base maps, J. Geol. 87, 217–277.
Smith, A.G., and J.C.Briden (1977). Mesozoic and Cenozoic paleocontinental maps, Cambridge U., Cambridge, England.
Smith, A.G., J.C.Briden, and G.E.Drewry (1973). Phanerozoic world maps, Organisms and Continents Through Time, Spec. Pap. Palaeontol. No. 12, Paleontol. Assoc., London, 42 pp.
Williams, J., R.G.Barry, and W.M.Washington (1974). Simulation of the atmospheric circulation using the NCAR global circulation model with ice age boundary conditions, J. Appl. Meteorol. 13, 305–317.
World Meteorological Organization (1975). The Physical Basis of Climate and Climate Modelling, GARP Publications Series No. 16, World Meteorological Organization, Geneva, 265 pp.
World Meteorological Organization (1979). Report of the JOC Study Conference on Climate Models: Performance, Intercomparison and Sensitivity Studies, W.L.Gates, ed., GARP Publication Series No. 22, World Meteorological Organization, Geneva, Vols. 1 and 2, 1049 pp.
Ziegler, A.M., C.R.Scotese, W.S.McKerrow, M.E.Johnson, and R.K.Bambach (1979). Paleozoic paleogeography, Ann. Rev. Earth Planet. Sci. 7, 473–502.

















