6
Weighting and Interpreting ACS Multiyear Estimates
The series of monthly samples that constitute the American Community Survey (ACS) can be combined in a variety of ways to produce survey estimates. The previous chapter has described the weighting methods being used to produce 1-year period estimates, combining all the data collected within a calendar year. This chapter examines the weighting methods that the Census Bureau is planning to use to produce 3-year and 5-year period estimates. The same weighting methods could also be used to produce estimates for other periods, such as 2-year and 8-year estimates. Similar methods can also be used to produce subannual estimates—perhaps without the population controls—as indeed the Census Bureau has done for areas affected by Hurricanes Katrina and Rita (see Section 1-B.2.b). As users gain experience with the ACS products, the Census Bureau should consult them about the usefulness of producing estimates for other periods.
The weights to be used in analyzing survey data need to be developed in relation to the population parameters—or estimands—to be estimated. There are several alternative estimands that can be considered when analyzing multiyear data from ACS. Three such estimands are discussed in Section 6-A.
The Census Bureau has chosen multiyear period parameters as the quantities to be estimated from ACS data accumulated over multiple years. Section 6-B reviews the weighting scheme the Census Bureau plans to use to produce estimates of the multiyear period parameters and the interpretation of these estimates.
Section 6-C then discusses the estimation of changes over time based
on the multiyear period estimates, assuming no change in population size and demographic composition, geographic boundaries, or question wording over the applicable period. The complications associated with population changes are addressed in Section 6-D. Other changes that potentially affect multiyear period estimates, such as changes in geographic boundaries or question wording, and the problem of discontinuities in population and housing controls around the time of the 2010 census are addressed elsewhere in the report.
6-A
ALTERNATIVE ESTIMANDS FROM MULTIYEAR DATA
During the panel’s early deliberations, various alternative estimands based on 3- and 5-years of ACS data were under consideration. The discussions focused on three main forms of estimand. For the majority of applications, the most attractive estimand is the population parameter for the most recent year of the multiyear period (provided that it can be estimated with adequate precision). A second estimand is the population parameter for the middle year. The third estimand is a multiyear period parameter comparable to the 1-year period parameter. The choice between these and other parameters needs to be based not only on which is preferred from a user perspective, but also on how well the parameters can be estimated. The paper by Jay Breidt in Appendix C, commissioned by the panel, discusses methods for comparing these and other estimands.
6-A.1
Single-Year Estimands from Multiyear Data
The rationale behind the use of multiyear data for producing estimates for any single year—such as the middle year or the end year—is that the estimation can “borrow strength” from the ACS data collected in other years. The process requires a statistical model that relates the estimands across time.
Some simplifying assumptions are made in order to illustrate the key issues in developing model-dependent estimates of single-year estimands from multiyear data. It is assumed that the population of the area for which the estimate is required remains constant over the multiyear period, that the sample size is the same for each year in that period, and that the standard error of each of the 1-year estimates in the period is the same, say σ.
Let the multiyear estimate be a simple weighted combination of the 1-year estimates, denoted by ![]() , where yi is the 1-year estimate for year i and wi is a weight such that ∑wi = 1. Under the above assumptions, the variance of
, where yi is the 1-year estimate for year i and wi is a weight such that ∑wi = 1. Under the above assumptions, the variance of ![]() is then σ2∑wi2.
is then σ2∑wi2.
The optimum choice of the wi depends on which estimand is selected and on the way in which the 1-year parameters are assumed to vary across
time. In the simplest case in which the 1-year parameters are assumed constant across time, then the optimum choice for the values for the wi is to set them all equal (i.e., wi = 0.33 for 3-year estimates, or wi = 0.2 for 5-year estimates) since this choice minimizes the variance of ![]() . In this simple case, the multiyear estimate can be viewed as an estimate for any of the years or for any combination of years.
. In this simple case, the multiyear estimate can be viewed as an estimate for any of the years or for any combination of years.
When the 1-year parameters are assumed to vary across years, the choice of the wi needs to take account of both the variance and bias of ![]() in estimating the chosen estimand. In this situation the 1-year estimate is an unbiased estimate for the estimand for any specific year, but that estimate will be too imprecise for small areas. In many cases a natural assumption to make is that the 1-year estimates for years close to the given year will be less biased in estimating the parameter for the given year than the 1year estimates for years farther away. This assumption leads to assigning weights wi that are largest for the given year and decline as the other 1-year estimates get farther away. Thus, for example, the weights for an estimate for the latest year of a 5-year period might be 0.06, 0.08, 0.14, 0.25, and 0.47, with greatest weight to the fifth year and declining weights for earlier years, like exponential smoothing (see Appendix C). Under the assumption made, these weights lead to a less biased estimate than equal weights, but the variance of this estimate is substantially increased. With equal weights, the variance of the 5-year estimate is 0.2σ2, whereas with this alternative weighting scheme it is 56 percent larger at 0.31σ2, and the standard error is 25 percent larger. In fact, the use of a 5-year estimator with this weighting scheme produces a final-year estimate with about the same variance as a 3-year estimator with an equal weighting scheme, which has a variance of 0.33σ2. (However, the mean square errors of these two estimators are not the same since they have different biases when used as estimators for the year 5 estimand.)
in estimating the chosen estimand. In this situation the 1-year estimate is an unbiased estimate for the estimand for any specific year, but that estimate will be too imprecise for small areas. In many cases a natural assumption to make is that the 1-year estimates for years close to the given year will be less biased in estimating the parameter for the given year than the 1year estimates for years farther away. This assumption leads to assigning weights wi that are largest for the given year and decline as the other 1-year estimates get farther away. Thus, for example, the weights for an estimate for the latest year of a 5-year period might be 0.06, 0.08, 0.14, 0.25, and 0.47, with greatest weight to the fifth year and declining weights for earlier years, like exponential smoothing (see Appendix C). Under the assumption made, these weights lead to a less biased estimate than equal weights, but the variance of this estimate is substantially increased. With equal weights, the variance of the 5-year estimate is 0.2σ2, whereas with this alternative weighting scheme it is 56 percent larger at 0.31σ2, and the standard error is 25 percent larger. In fact, the use of a 5-year estimator with this weighting scheme produces a final-year estimate with about the same variance as a 3-year estimator with an equal weighting scheme, which has a variance of 0.33σ2. (However, the mean square errors of these two estimators are not the same since they have different biases when used as estimators for the year 5 estimand.)
For a midyear estimand from 5-year data, the corresponding weights might be 0.14, 0.19, 0.34, 0.19, and 0.14. The pattern of these weights around the middle year is symmetric, with the weight for the middle year estimate being the largest. The variance of this weighted estimate is 0.23σ2, only 13.5 percent larger than that for the equally weighted estimate. If an estimand for a single year is required, based on this approach, a midyear estimand is thus preferable to an end-year estimand in terms of the precision of the estimate.
6-A.2
Multiyear Period Estimand from Multiyear Data
Whatever weighting scheme is adopted with multiyear data, for practical reasons a single set of weights is needed for application for all analyses. If a single-year estimand and associated weighting scheme are adopted,
there will likely be characteristics for which the resulting estimates for some areas will be seriously biased due to the pattern of changes in the characteristic over the period. The use of a period estimand, averaged over the time period, avoids this concern about bias. The Census Bureau has decided to adopt the approach of period estimation for the multiyear data from the ACS, which, under the assumptions made above in Section A.1, also leads to the equal weighting scheme and hence lowest variance. However, the period estimation approach achieves its benefits by placing considerable burden on users to interpret the estimates in an appropriate manner.
As discussed in Section 3-C.1.b and later in this chapter, period estimates are difficult to interpret, and users must assess them in terms of external information about changes that have occurred during the period. For example, a 5-year period estimate of the percentage of poor families of 10 percent could reflect any of the following: a constant percentage across the 5 years; a steady increase from, say, 7 percent to 13 percent; a corresponding steady decrease; a rise and decline in the percentage across the years; and so on. To obtain an indication of the likely pattern that underlies a 5-year (or 3-year) estimate, users need to apply local knowledge of the conditions in the area over the period. They can also examine the published 1-year estimates for a larger area that contains the area of interest.
6-B
MULTIYEAR PERIOD ESTIMATION
Conceptually, multiyear period estimation is the same as 1-year period estimation, merely extended over a longer period. The starting point for producing multiyear period estimates is to concatenate the 1-year data files over the 3 or 5 years involved, in the same way that 1-year estimation is based on concatenating the monthly data collected within a calendar year. Then the weighting scheme the Census Bureau is proposing for multiyear estimation from the concatenated file is broadly the same as that used for the 1-year estimation, as described in Chapter 5.
A natural and very simple way to develop weights for use with a multiyear concatenated file is to take the existing weights on each of the 1-year files and divide them by the number of years involved (3 or 5). A variant of this simple approach takes advantage of revised, updated housing and population controls for earlier years in the period, which may have become available by the time when the weights for the period estimates are being developed. Under this variant, the 1-year weights would be revised by using the applicable updated housing and population controls, and the revised weights would then be divided by 3 or 5.
The Census Bureau is planning, however, to use a similar but somewhat different approach. In its method, the first two steps in the 1-year weighting process (that is, base weights and variation in monthly response factor—see
Box 5-1) are retained, but then noninterview factors 1 and 2, the mode bias noninterview factor, and the housing unit control and population control factors are applied differently. Instead of applying these factors separately for each year, they are applied to the concatenated sample for the multiple years.
The housing unit and population controls used are the averages of the 1-year controls for the multiple years, using any revisions that have been made to the controls since the 1-year period estimates were first produced. The advantage of the Census Bureau’s method is that, by pooling the sample across years first, the controls are applied to a larger sample. (This is also an advantage for the noninterview adjustments.) As a result, greater control on the population counts by age, sex, and race/ethnicity within estimation areas is possible because less collapsing of control cells is needed.
There are trade-offs to be considered between the simple approach and the Census Bureau’s planned approach. The Census Bureau’s approach gives greater control on demographic characteristics but lacks control over the yearly representation of the sample. The simple scheme has the benefit of ensuring that each year is represented in its right proportion in the estimation process but employs control over the demographic characteristics only to the extent that this is achieved for the 1-year estimates.
While the greater control on the demographic controls afforded by the Census Bureau’s scheme appears attractive, the issue of the quality of those controls must be considered. As discussed in Section 5-D, the panel has serious concerns about the quality of the population estimates at this level of detail and recommends that the Census Bureau should carry out research on this step in the 1-year weighting process, including alternative possibilities of less detailed demographic controls, applying the controls on a marginal basis by raking, or applying the controls at a higher level of aggregation. The results of this research may lead to a population control weighting step that does not require the collapsing of control cells. In this case, the simple scheme for producing multiyear weights by dividing the 1-year weights by the number of years, or rather the variant of it with updated controls, may be preferred because it also provides temporal control. Research is needed in this area.
Another area of research on multiyear weighting is to investigate the application of the housing unit and population controls at the county level rather than at the estimation area level used in the 1-year weighting. A key concern is whether the housing unit and population estimates for small counties are of adequate quality for this use. A possible approach would be to apply a housing unit control at the county level and to use a raking algorithm to apply a total population control at the county level and demographic controls at the estimation level. (Total population and housing unit controls could also be applied for cities within counties.) Note that
the preferred weighting scheme for 3-year estimation may be different from that for 5-year estimation because of the difference in sample sizes.
The Census Bureau has recently begun research into the introduction of an additional step in the weighting procedure based on linking administrative data to housing units on the MAF. This step, which involves a calibration weighting adjustment applied just to the linked units, can be applied at the tract level (Fay, 2005, 2006). The initial goal of this research was to improve the precision of 5-year estimates for tracts, but, if successful, it could improve the precision of estimates for subcounty areas more generally. Elsewhere in this report the panel has pointed out the need to improve the precision of ACS estimates for small geographical areas. Thus, this line of research warrants further investigation.
Recommendation 6-1: The Census Bureau should conduct research to examine the bias and variance properties of the planned multiyear weighting scheme and compare these properties with those of some alternative schemes.
6-C
ESTIMATION OF CHANGE OVER TIME
The production of estimates every year, rather than every 10 years as with the decennial census long-form sample, is a major asset of the ACS. Users will be able to study changes in estimates over the years. For areas for which 1-year estimates are provided, users will have a time series of 1-year estimates from which annual, biannual, and other changes are easily obtained, and to which more sophisticated methods of time series analysis can be applied. The Census Bureau will also provide margins of error for changes from one year to the next. With areas for which only multiyear period estimates are produced, the study of change over time is more complicated.
There are two main questions to be addressed in assessing changes in multiyear period estimates over time: (1) How is the change between two multiyear estimates to be interpreted (that is, what is the estimand)? (2) What is the precision of the estimated change? Two simplifying assumptions help to convey the essential points to be made in answering these questions. One is that each multiyear estimate for an area is a simple average of its 1-year estimates. This assumption is approximately valid for areas with populations that change little over time. The second assumption is that the precision of the 1-year estimates remains the same over time. Given the first assumption, the second assumption is a reasonable approximation, even though, when estimating a proportion (for example, the proportion poor), the magnitude of an estimate’s sample error depends on the value of the proportion.
6-C.1
Interpreting Estimates of Change Between Multiyear Period Estimates
Let the time series of 1-year estimates be y1, y2, y3, …, yt, …. Let ![]() and
and ![]() be 3-year and 5-year period estimates, respectively, where t denotes the last 1-year estimate in the multiyear estimate. Under the first assumption, the multiyear estimates are simply 3- or 5-year moving averages of the 1-year estimates. Thus, for example, for 3-year estimates,
be 3-year and 5-year period estimates, respectively, where t denotes the last 1-year estimate in the multiyear estimate. Under the first assumption, the multiyear estimates are simply 3- or 5-year moving averages of the 1-year estimates. Thus, for example, for 3-year estimates,
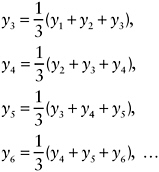
and, for 5-year estimates,
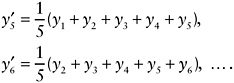
With the 3-year period estimates, pairs of estimates that are only 1 year apart have 2 years in common, and those that are 2 years apart have 1 year in common. There is no overlap when the pair of years is more than 2 years apart. With the 5-year period estimates, estimates that are only 1 year apart have 4 years in common, those that are 2 years apart have 3 years in common, those that are 3 years apart have 2 years in common, and those that are 4 years apart have 1 year in common. It is only when two 5-year period estimates are 5 or more years apart that there is no overlap.
The extent of overlap between two multiyear estimates determines the estimand that the difference between them is estimating. Consider the difference between two 3-year estimates, with one being ![]() and the other being
and the other being ![]() with t > 3. With t = 4, because of the 2-year overlap, the difference between
with t > 3. With t = 4, because of the 2-year overlap, the difference between ![]() and
and ![]() is
is
(1)
that is, one-third of the change between year 1 and year 4. With t = 5, with a one-year overlap, the difference between ![]() and
and ![]() reduces to [(y4 – y1)
reduces to [(y4 – y1)
+ (y5 – y2)]/3. This quantity can be viewed as estimating two-thirds of the average difference between two pairs of years that are 3 years apart—that is, years 1 and 4 and years 2 and 5. With t = 6, with no overlap, the difference between ![]() and
and ![]() is [(y4 – y1) + (y5 – y2) + (y6 – y3)]/3—that is, the average difference over three pairs of years for years that are 3 years apart. In general, for all pairs of nonoverlapping estimates, the difference between
is [(y4 – y1) + (y5 – y2) + (y6 – y3)]/3—that is, the average difference over three pairs of years for years that are 3 years apart. In general, for all pairs of nonoverlapping estimates, the difference between ![]() and
and ![]() is given by [(yt–2 – y1) + (yt–1 – y2) + (yt – y3)]/3—that is, the average difference for years that are (t – 3) years apart. Similar results apply for differences between 5-year estimates.
is given by [(yt–2 – y1) + (yt–1 – y2) + (yt – y3)]/3—that is, the average difference for years that are (t – 3) years apart. Similar results apply for differences between 5-year estimates.
These results indicate the importance of distinguishing between nonoverlapping and overlapping multiyear estimates. On one hand, with nonoverlapping estimates, the estimand can be simply viewed as an average difference across a set of 3 or 5 individual years that are apart by the number of years that the multiyear estimates are apart. On the other hand, with overlapping multiyear estimates, the estimand is only a fraction of the average 3- or 5-year difference.
To elaborate on the interpretation of differences in multiyear estimates, consider two alternative scenarios for changes in the estimands over time: one is a steady linear trend in the 1-year values, with the values increasing by, say, δ from one year to the next; the second is one in which the 1-year values stay at a constant level until year 6, at which point they increase by γ and then remain constant at the increased level after that. For simplicity of the presentation, for the latter scenario, we consider changes in 3-year estimates.
Under the first scenario, the estimand corresponding to the difference between multiyear estimates—both 3- and 5-year estimates—that are k years apart is kδ, irrespective of whether the estimates are overlapping or not. Thus, the difference between adjacent multiyear estimates is an estimate of the constant annual change δ, the difference between multiyear estimates that are two years apart is an estimate of twice the annual change, and so on. These points are illustrated in Table 6-1, in which an increase in the percentage of poor families is assumed to be 1 percent per year. The 3-year estimates also increase by 1 percent per year, so that the difference between adjacent 3-year estimates is 1 percent, between 3-year estimates 2 years apart it is 2 percent, and so on. While expressing the difference
TABLE 6-1 Estimates of Poor Families in an Area Assuming a 1 Percent Annual Increase, in Percent
|
Year |
1 |
2 |
3 |
4 |
5 |
6 |
|
1-Year Estimate |
10 |
11 |
12 |
13 |
14 |
15 |
|
3-Year Estimate |
|
|
11 |
12 |
13 |
14 |
TABLE 6-2 Estimates of Poor Families in an Area Assuming a 3 Percent Increase in Year 6, in Percent
|
Year |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1-Year Estimate |
10 |
10 |
10 |
10 |
10 |
13 |
13 |
13 |
|
3-Year Estimate |
|
|
10 |
10 |
10 |
11 |
12 |
13 |
in terms of annual change is attractive, it can be misleading if the annual change is not constant, as the second scenario demonstrates (see Table 6-2). Under the second scenario, the annual population values can be represented as Y for the first 3 years and Y + γ thereafter. The 3-year average for the first 3 years is then Y3 = Y, and subsequent 3-year averages are
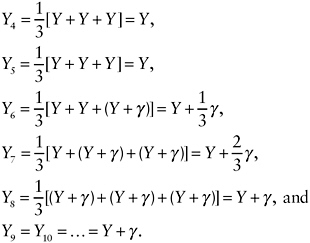
The estimand for the difference between the 3-year estimates for years 3 and 4, ![]() –
– ![]() , and for years 3 and 5,
, and for years 3 and 5, ![]() –
– ![]() , is thus 0 since no change has occurred over the first 5 years. The estimand for the difference between the 3-year estimates for years 3 and 6—which do not overlap—is γ/3. This difference is an average of no difference between years 1 and 4 and between years 2 and 5 and a difference of γ between years 3 and 6. Similarly, the estimand for the difference between the 3-year estimates for years 3 and 7 is 2γ/3, which represents an average of no difference between years 1 and 5 and a difference of γ between years 2 and 6 and years 3 and 7. The full estimate of γ is obtained only when the 3-year estimate for year 8 is obtained, after the increase has been in effect for 3 years. This point is illustrated in Table 6-2, in which a permanent increase of 3 percent in the estimated percentage of poor families occurs in year 6. It is not until year 8 that this increase is fully reflected in the 3-year estimate, and it is only in the differences between the 3-year estimates for year 8 and for years prior to year 6 that the full 3 percent change is observed.
, is thus 0 since no change has occurred over the first 5 years. The estimand for the difference between the 3-year estimates for years 3 and 6—which do not overlap—is γ/3. This difference is an average of no difference between years 1 and 4 and between years 2 and 5 and a difference of γ between years 3 and 6. Similarly, the estimand for the difference between the 3-year estimates for years 3 and 7 is 2γ/3, which represents an average of no difference between years 1 and 5 and a difference of γ between years 2 and 6 and years 3 and 7. The full estimate of γ is obtained only when the 3-year estimate for year 8 is obtained, after the increase has been in effect for 3 years. This point is illustrated in Table 6-2, in which a permanent increase of 3 percent in the estimated percentage of poor families occurs in year 6. It is not until year 8 that this increase is fully reflected in the 3-year estimate, and it is only in the differences between the 3-year estimates for year 8 and for years prior to year 6 that the full 3 percent change is observed.
6-C.2
Precision of Estimates of Change Between Multiyear Period Estimates
To assess the precision of the estimates of the differences between multiyear estimates, it helps to invoke the second simplifying assumption, namely, that the variance of each of the 1-year estimates is the same, say, σ2. Since the ACS annual samples are approximately independent of each other, the variance of a sum or difference between any two 1-year estimates is 2σ2, and, indeed, the variance of any equally weighted combination of sums and differences of k 1-year estimates is kw2σ2, where w is the weight attached to each estimate (w = 1/3 or 1/5).
Application of these results to obtain the variances of the difference between nonoverlapping multiyear estimates is straightforward. Since there are six 1-year estimates involved in the difference between two nonoverlapping 3-year estimates (k = 6), and each is weighted by 1/3, the variance and the standard error of the difference are 6σ2/9 = 0.67σ2 and 0.82σ, respectively. The corresponding variance and standard error for differences between nonoverlapping 5-year estimates are 10σ2/25 = 0.4σ2 and 0.63σ. By comparison, the variance and standard error of the difference between any two 1-year estimates are 2σ2 and 1.41σ.
In the case of the difference between two overlapping multiyear estimates, some of the 1-year estimates cancel out as indicated, for example, in equation (1) above. After removing the overlapping 1-year estimates in the difference, the above formula still applies: the only consequence is that the number of 1-year estimates, k, is reduced. If the multiyear estimates are 1 year apart, then k = 2; if they are 2 years apart, then k = 4; if they are 3 years apart, then k = 6; and if they are 4 years apart with 5-year estimates, then k = 8. As a result of the reduction in k with overlapping multiyear estimates, the variance and standard error of the difference are smaller than for nonoverlapping estimates. However, as noted in Section 6-C.1 above, the estimand is also different.
To aid understanding of the relationship between the different estimands and their standard errors, Table 6-3 summarizes results on standard
TABLE 6-3 Standard Errors of Estimates of Change for Various Values of the Gap Between Two Period Estimators as Multiples of the Standard Errors of a 1-Year Estimator
errors for estimates of change between two period estimates that are a specific number of years apart. The table expresses the results in terms of multiples of the standard error of a 1-year estimate, σ, using the formulas given above. The multiples for the 3-year and 5-year change estimates indicate the lower standard errors that occur when using nonoverlapping multiyear estimates as compared with 1-year estimates (0.82 and 0.63, compared with 1.41). However, in a situation in which a multiyear estimate is required, the standard error of the 1-year estimate, σ, is large. Since the standard errors of the differences between both 3-year and 5-year nonoverlapping estimates are sizable proportions of σ, the standard errors of the differences will also be large. Thus, only large changes are likely to be detected as significantly different.
When the two multiyear estimates being compared overlap, there is a further reduction in the multiples, as seen on the left side of the table, but this occurs because the estimands are not comparable. Consider, for example, changes in 3-year estimates under the linear trend scenario, with the 1-year parameter increasing (or decreasing) by a constant amount, δ, each year. The estimand corresponding to the difference between two 3-year estimates with a gap of 3 years between them is 3δ, while the estimands for the differences between 3-year estimates that overlap by 1 year or 2 years are only 2δ and δ, respectively. To convert these overlapping estimates of change to estimates of the 3-year change, they need to be multiplied by 3 and 1.5, respectively. When the overlapping estimates of change are increased in this way, the standard errors of 3-year change estimates are increased by the corresponding factors given in Table 6-3. Thus, for example, the standard error of the estimate of the full 3-year change between two 3-year estimates that are 1 year apart is 3 × 0.47σ = 1.41σ, which is the same as that for comparing two 1-year estimates. For two 3-year estimates that are 2 years apart, the corresponding standard error is 1.5 × 0.67σ = σ. The fact that 3-year estimates are being compared in a situation in which a 1-year estimate with a standard error of σ is deemed too imprecise to be published implies that change estimates between overlapping 3-year estimates are very imprecise—they have standard errors as large as or larger than a 1-year estimate.
The same situation applies with estimates of differences between overlapping 5-year estimates. The most favorable case is when two 5-year estimates overlap by only 1 year. In this case, the standard error of the full estimate of the 5-year change is (5/4) × 0.57σ = 0.71σ. In situations in which 5-year estimates are needed, the large size of this standard error makes comparisons of overlapping 5-year estimates rarely likely to be of interest.
The results in Table 6-3 are presented in terms of multiples of the standard errors of 1-year estimates. However, users will generally have
TABLE 6-4 Standard Errors of Estimates of Change for Various Values of the Gap Between Two Period Estimators as Multiples of the Standard Errors of the Corresponding Period Estimator
available only the standard errors, or rather measures of error (based on 90 percent confidence intervals), of the 3-year or 5-year estimates. Under the assumptions made, the results in Table 6-3 are readily converted to multiples of standard errors of the multiyear estimates in Table 6-4 by noting that the standard errors of 3-year and 5-year estimates are simply σ ![]() and σ
and σ ![]() , respectively. The multiples for the standard errors of 3-year and 5-year estimates are thus simply
, respectively. The multiples for the standard errors of 3-year and 5-year estimates are thus simply ![]() = 1.73 and
= 1.73 and ![]() = 2.24 times the corresponding multiples in Table 6-3, and these multiples also apply to the published measures of error. Thus, for example, for two nonoverlapping 5-year estimates (or 3-year estimates) for which the average of their measures of error is ±5 percent, the measure of error of the difference between the estimates from Table 6-4 is around ±7.1 percent (5 × 1.41), whereas for two 5-year estimates that are 2 years apart with the same average measure of error of ±5 percent, the measure of error of the difference is around ±4.5 percent (5 × 0.89).
= 2.24 times the corresponding multiples in Table 6-3, and these multiples also apply to the published measures of error. Thus, for example, for two nonoverlapping 5-year estimates (or 3-year estimates) for which the average of their measures of error is ±5 percent, the measure of error of the difference between the estimates from Table 6-4 is around ±7.1 percent (5 × 1.41), whereas for two 5-year estimates that are 2 years apart with the same average measure of error of ±5 percent, the measure of error of the difference is around ±4.5 percent (5 × 0.89).
6-C.3
Conclusions
The overall conclusions from these analyses are that estimates of change based on differences between overlapping 3-year or 5-year period estimates are generally not useful. Furthermore, even with nonoverlapping estimates, the estimates of differences will generally be fairly imprecise. Analyses of change will be most productive only when major changes have occurred or when 1-year estimates are precise enough to be published. Of course, the multiyear period estimates remain an improvement over the once-a-decade long-form sample because they are updated every year and therefore provide a more timely picture of the characteristics of an area than is possible from the long-form sample.
A final point regarding differences between multiyear period estimates is that, just like the estimates themselves, they can reflect a variety of pat-
terns in the underlying 1-year estimates. For example, a 2 percent change between two nonoverlapping 3-year estimates could occur because all the increase—a 6 percent increase—occurred in the latest year, because a 2 percent increase occurred in the interval between the two estimates, or because of other patterns of change. Users need to be aware of the possible underlying patterns and find ways to distinguish between them based on other sources or on ACS data at other levels of aggregation.
6-D
EFFECTS OF CHANGES IN POPULATION SIZE AND CHARACTERISTICS
The treatment thus far in this chapter has assumed that the population of an area has been static, or at least has changed in only minor ways, during the time period of a 3- or 5-year period estimate. While this may be a reasonable assumption for many areas, there will be some areas that experience major changes in population size or composition or both. Moreover, major changes are most likely to occur in small governmental units and census tracts, areas for which 3-year and 5-year estimates are needed.
Population changes that recur within a year, such as the seasonal patterns discussed in Section 3-C.3, affect each year of a multiyear period estimate in the same way that they affect a 1-year period estimate. The additional population changes that affect multiyear period estimates are year-to-year changes, such as population growth over time, which may be concentrated in certain demographic subgroups. The Census Bureau’s planned weighting procedures for multiyear estimates reflect such changes by using the 3- or 5-year averages of the independent housing unit estimates and the independent population estimates by demographic subgroup as controls.
Users need to consider the potential effects of the planned weighting scheme on ACS estimates. For this discussion, it is useful to distinguish between two types of ACS estimates: estimates of proportions, such as the proportion of poor people, and estimates of totals, such as the number of poor people. In the case of proportions, if an area had major growth, say, an influx of young persons, the ACS multiyear period estimates of the characteristics of young people will be weighted toward their characteristics in the later years of the period, and the influx will similarly affect other estimates in which young people are included. Even if it seems likely that a characteristic of interest has remained stable over the period, the changes in the population composition will lead to differences in the proportions of the population with that characteristic over the time period. Consider, for instance, the comparison of the multiyear estimates of the unemployment rates between this area and a stable or declining area. In this case, users
will need to be cognizant that the influx of young people may affect the comparison.
The situation is even more complex when the multiyear estimates are totals and the area’s population changes appreciably during the period. A multiyear period estimate of a total then reflects not only changes in the prevalence of the characteristic (for example, the unemployment rate) due to temporal changes and to changes in the composition of the population, but also changes in the size of the population. As a result of these complexities, users may find multiyear estimates of totals for areas that change markedly in size to be problematic. They may prefer to develop model-based estimates of totals for the current population or for the population of the latest year of the estimation period.
In the case of counties, one possible approach for developing estimates of totals for the latest year of the estimation period (or a subsequent year) takes advantage of the county population estimates reported annually by the Census Bureau’s Population Division. The simplest model assumes for the county that the prevalence rates for the characteristic of interest have remained approximately constant over the estimation period within demographic subgroups and that the population estimates by demographic subgroup for the latest year are accurate. The ACS multiyear period estimates are then used as estimates of the latest-year prevalence rates within specified demographic subgroups, and these rates are applied to the latest-year county population estimates for those subgroups. The sum of the resulting subgroup estimates then serves as an estimate of the number of persons with the given characteristic in the county in the latest year.
Although the model assumptions involved in producing such estimates are problematic, the resulting estimates may suit user needs better than the standard multiyear estimates for counties that have experienced major population changes. The extension of this simple model to produce subcounty estimates of totals introduces the further complexity that no estimates of population sizes are readily available at levels below the county. Thus an additional step is needed to produce population estimates for such areas as census tracts and small cities. Simply applying the proportion of the county’s population in the area from the ACS period estimates to the current population county estimates is questionable but is a possibility if there is no better local information available.
In summary, multiyear period estimates are highly complex when the population of an area changes substantially in size or composition or both during the estimation period. Users need to pay careful attention to their interpretation in such cases and, particularly when estimating totals, they need to assess whether the estimates meet their needs.
Recommendation 6-2: The Census Bureau should consult users about the utility of the currently proposed multiyear period estimates—particularly for estimates of totals—for areas that change markedly in population size. It should investigate whether there are other forms of estimates that could be produced and would better serve user needs.
















