C
Alternatives to the Multiyear Period Estimation Strategy for the American Community Survey
F. Jay Breidt
Colorado State University
ABSTRACT
A class of estimation strategies that includes simple moving averages and direct estimates as special cases is evaluated for small area estimation in the American Community Survey. The evaluation is based on both operational and theoretical considerations. Operationally, the estimation strategies considered are feasible in a massive-scale production environment. Theoretically, the estimation strategies are compared using simple decision-theoretic tools, which suggest good compromise strategies that borrow strength across time in a robust way. Strategies outside the class considered here can be evaluated with these same decision-theoretic tools.
C–1
INTRODUCTION
C–1.1
Proposed Multiyear Estimation Strategy for the ACS
The publication plans for estimates from the American Community Survey (ACS) are to produce 1-year estimates for areas with populations of 65,000 persons or more, 3-year estimates for areas with 20,000 persons or more, and 5-year estimates for all areas (all governmental units, census tracts, and block groups). When the survey is fully established, 1-year, 3-year, and 5-year estimates will be produced every year based on the latest prior year or set of prior years. The National Research Council’s Panel on the Functionality and Usability of Data from the American Community Survey (ACS) asked me to address the multiyear estimation strategy for the ACS. The weighting scheme currently proposed by the Census Bureau involves pooling the survey data across the 3 or 5 years. The weights will be developed starting with the inverse selection probabilities of sampled households.
A number of adjustments will then be made including nonresponse adjustments and poststratification adjustments to postcensal housing unit and population estimates produced by the Census Bureau’s Population Division. The housing and population controls are averages of the 1-year controls for the multiple years. Details of the weighting procedures are given in Chapters 5 and 6 of the panel’s report.
The multiyear estimates produced by the Census Bureau’s weighting scheme can be viewed as period estimates: they represent averages that reflect both changing characteristics and changes in the area’s populations across the years. The limitation of these estimates, and changes in them over time, is that they can be difficult to interpret and may not suit user needs. The panel therefore invited me to investigate other estimation strategies for the multiyear data, and in particular the use of several years of data to produce an estimate for a single year (e.g., year 3 or 5 from 5 years of ACS data) in place of the period estimate. The fact that any strategy that is adopted would have to implemented in a massive production environment imposes constraints: It needs to be simple and require no auxiliary data; and each unit (household or person) should have only one analysis weight within the given 3- or 5-year data set in order to enable a wide range of consistent analyses across variables and areas of different sizes.
There are strong arguments that one can make in support of a strategy that uses different weights for producing single-year estimates for areas of different sizes from multiyear data. For example, there are definite advantages to borrowing strength over more years for areas with small populations and for variables that are more stable in time. However, ACS data users would likely find the non-uniformity an unwelcome complication and possibly undesirable, at least during the start up phase of ACS. The paper therefore focuses exclusively on uniform strategies.
Two simplifying assumptions are made throughout the paper in order to convey the essence of a principled strategy for producing single-year estimates with desirable properties from multiyear data. The first is that the population size of an area does not change over the 3- or 5-year estimation period. This assumption may hold reasonably well for many areas, but there will be areas for which it does not hold. The second assumption is that the 1-year estimates for each of the years in the period have the same variance. With the assumption of a constant population size, the ACS sample size in an area is likely to be approximately the same each year. Thus, if the element variances are about the same across the years, the second assumption will hold approximately. While element variances may often be reasonably equal, that will not always be the case.
Under these two assumptions, and ignoring the nonresponse and calibration weighting adjustments, the Census Bureau’s period estimate reduces to a simple average of the 1-year estimates for the period. In order to produce
estimates for a given year within the period, this paper examines a strategy that assigns differential weights to the 1-year estimates, with largest weight given to the year in question and the next larger weights to the neighboring years. Each year the ACS will update the 3- and 5-year estimates by replacing the earliest year by the latest year. For this reason, the estimates produced are described here as moving average (MA) estimates.
Although the simple MA is operationally convenient and easily understood, a number of questions arise regarding its appropriateness. It can be applied to any sort of characteristics across any geographic and demographic domains, but does it give efficient estimates for those characteristics on those domains? Is the method defensible? Is it a principled approach for obtaining estimates, with some theoretical justification? Can it be extended in a logical way to novel estimation problems?
C–1.2
Signal-Plus-Noise Model
To address these questions, I begin with a general model for annual ACS estimates, written as a time series {Yt}. Assume the classical signal-plus-noise formulation
where the signal, θt, represents the true unobserved population characteristic in year t, and et represents both sampling and variable nonsampling error (the estimates are assumed to be unbiased). See, for example, Scott and Smith (1974) as well as Binder and Hidiroglou (1988) and the references therein. On one hand, presumably, the sampling error would have some negative correlation by design, since the ACS rolls through the population, avoiding selection of the same households month-to-month. On the other hand, the variable nonsampling error would be expected to have some positive month-to-month correlation (e.g., due to nonresponse follow-up with common computer-assisted telephone and personal interviewing staffs from month to month). Assume that at the annual level of aggregation considered here, these correlations are negligible, so that {et}is uncorrelated.
It is convenient to let
denote the vector consisting of the m most recent annual true values of the characteristic of interest. Furthermore, consider the random vector of m ACS annual estimates,
so that
with et ~(0, σe2I), where I is the m × m identity matrix.
I consider linear estimators of θt given by some known m × m matrix S multiplied by ![]() . (Note that such estimators use only data from the m-year time window, for direct comparability with the ACS 3- and 5-year estimates. Given the various dynamics that the ACS will be subject to, it makes sense to limit the data used to a small number of years, although of course some information is lost by this restriction.)
. (Note that such estimators use only data from the m-year time window, for direct comparability with the ACS 3- and 5-year estimates. Given the various dynamics that the ACS will be subject to, it makes sense to limit the data used to a small number of years, although of course some information is lost by this restriction.)
Various population characteristics might be of interest, several of which can be written as linear functions zTθt for some known m × 1 vector z. Examples of linear functions for m = 5 include zT= [0, 0, 0, 0, 1] for current level, zT = [0, 0, 1, 0, 0] for midpoint level, and zT= [1/5, 1/5, 1/5, 1/5, 1/5] for temporal average. Each of these linear functions can be estimated in the obvious way as
Estimates of change are more complicated, since there are at least two obvious estimation strategies. The first is to define, for k < m, the k-year change as a linear function of θt, with
and estimate k-year change by
exactly as above. Note that this “current” estimator uses only data from the current m-year time window.
The second estimation strategy for change is to compute the difference between the published level estimate for year t and year t – k. Note that this “final” estimator uses data from both the current m-year time window and the lagged m-year time window. For example, in estimation of 1-year change, the “current” estimate of change is computed from only the current 5-year window, while the “final” estimate of change is computed from consecutive 5-year windows. The final change estimate is presumably the one that would be published in order to maintain consistency with published level estimates.
C–1.3
Classes of Estimation Strategies
The matrix S can be chosen in a number of ways. It could be constructed from principles of filter design commonly used in time series: for example, one can construct a filter that passes a quadratic trend without distortion while eliminating certain seasonal components or attenuating noise at certain frequencies (Brockwell and Davis, 1991, Chapter 1).
More formally, strategies may be based on temporal models, either stochastic or deterministic. If the temporal model is stochastic, then optimal filters can be computed using well-known principles; for example, the Kalman filter does these computations recursively for large classes of linear state-space models.
If the state-space model is a random walk plus noise (a special case of a process that is integrated of order one, or I(1)), then the Kalman filter becomes equivalent to exponential smoothing as m → 8 (Harvey, 1989, p. 440). If the state-space model is a particular type of local linear trend (a special case of an I(2) process), then the Kalman filter yields double exponential smoothing (Harvey, 1989, p. 177).
The temporal model might, however, be deterministic, specifying only that the true values θt evolve as a smooth unknown function of time. In this case, methods from nonparametric regression, such as localpolynomial kernels or smoothing splines, could be used to derive estimation strategies. It is interesting to note the connections between the stochasticand deterministic cases. First, exponential smoothing can be derived as a special case of non-parametric regression: the Nadaraya-Watson kernel smoother (zero-th order polynomial) with a particular form of half-kernel (Gijbels, Pope, and Wand, 1999). Second, smoothing splines can be derived as the optimal filtering solution for a local linear trend stochastic model (Durbin andKoopman, 2001, p. 61).
Other strategies might be devised based on spatial or spatiotemporal considerations, but it seems difficult to develop spatial methods applicable in a large-scale production environment. On one hand, defining spatial neighborhoods would be difficult, since they would vary substantially across space. On the other hand, defining temporal neighborhoods is straightforward. In addition, there may be political complications that arise from borrowing strength across governmental units that are not raised by temporal averaging, because of the interest in comparisons among governmental units.
C–1.4
Framework for Comparing Estimation Strategies
It is tempting to use existing theory for either Kalman filtering in the stochastic case or nonparametric regression in the deterministic case, to evaluate the performance of various estimation strategies. However, these methods typically assume that m → ∞, which is not the case in the ACS application. I use other techniques to evaluate the performance of estimation strategies.
Given the large number of possible estimation strategies, one needs a principled approach to comparing them and choosing a reasonable compromise among them. In comparing these strategies theoretically, it is critical to keep in mind the operational constraint that it is not feasible or desir-
able to develop separate estimation strategies for each governmental unit of interest. The strategies must be quite generic.
With this in mind, I propose a simple decision-theoretic framework for comparing strategies. I focus on squared error loss
for which the corresponding risk is the prediction mean squared error (MSE) zTΩz, where
C–2
METHODS
This framework for comparing estimation strategies is bestillustrated by focusing on a particular class of strategies. I use the class of I(1) strategies as formulated by William Bell in a presentation at a 1998 Committee on National Statistics workshop on the ACS (National Research Council, 2001). The I(1) strategies are derived from a random walk plus noisemodel, but this derivation is not important in what follows. The strategy to be evaluated might be derived from a formal model or might be entirely ad hoc, but in either case it can be evaluated with the methods to be described.
Define

with the subscript suppressed when the dimension is clear, and let
with α ≥ 0 prespecified. Define the smoother matrix
Note that the rows of S sum to 1 for any choice of a, since Δ1 = 0.
A few numerical examples of S demonstrate the breadth of the I(1) estimation strategies. Consider the case m = 5. With α = 0, the smoother matrix is
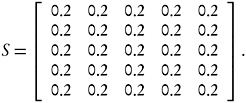
In this case, the estimate of current level becomes
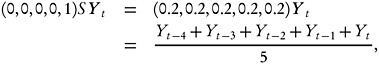
which corresponds to the 5-year period estimate proposed by the Census Bureau.
The other extreme is obtained as α → ∞, in which case the smoother matrix is

In this case the estimate of current level is simply
the direct estimate in the current year. This is the estimator produced by the Census Bureau for areas of more than 65,000 persons.
Between these two extremes lies a continuum of smoothing possibilities. Consider, for example, α = 0.4206232, in which case the smoother matrix is
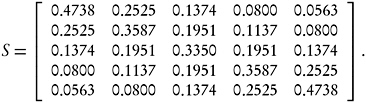
The estimate of current level in this case is
a weighted average with weights that look much like the exponential smoothing weights
A useful summary of the amount of smoothing is given by the degrees offreedom (df) of the smoother matrix,
This value varies continuously between 1 and m. One df represents maximum smoothing; it corresponds to the simple moving average,or fitting of a common mean over the m-year window. No smoothing is represented by m df; this corresponds to the direct estimates, or fitting of separate means for each year. Other values of df correspond to different amounts of smoothing between the maximum and minimum values. A few examples are given in the following table:
|
df |
α |
|
|
1 |
0 |
moving average: S = (1/5)11T |
|
2 |
0.4206232 |
|
|
3 |
1.545009 |
|
|
4 |
5.380712 |
|
|
5 |
∞ |
direct estimates: S = I5 |
Note that the α = 0.4206232 case considered above corresponds to two degrees of freedom and roughly corresponds to exponential smoothing with parameter 1/2.
C–3
RESULTS
C–3.1
General Results
Assume that changes in the signal are uncorrelated with the noise,
(C.1)
and that
(C.2)
where the (m − 1) × (m − 1) matrix M does not depend on t. (That is, the covariance matrix for the differenced signal is time-invariant.) The matrix M depends on the model for the signal; several examples of M are given below under different models. The scalar is interpreted as a signal-to-noise ratio (SNR).
The risk for estimation of the linear function zTθ under squared error loss is then zTΩz, where
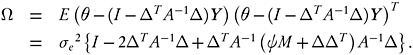
(C.3)
We can effectively take σe2 = 1and interpret all risks in units of noise variance. Note that (C.3) then depends on the smoothing parameter α through
A and on the true model through φM. Also, observe that the term depending on φM is the squared bias under model (C.2), and all other terms are attributable to variance from the noise.
Two special cases of this risk computation are worth considering, before moving on to consideration of the general case. First, for the direct estimates, S = I and the risk is
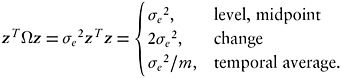
(C.4)
These are useful benchmark values in looking at risk surfaces as functions of α.
The second special case arises in estimating the temporal average. The risk is given in the following result.
Result 1 For any choice of the smoothing parameter α and for any model satisfying the conditions (C.1) and (C.2) above, the risk for estimating the temporal average m-11Tθtis σe2m−1.
This result is immediate from the fact that Δ1 = 0. The result implies that if one is interested in estimating the temporal average only, then any strategy in this class is equally good, and the result does not depend on parameterization of the true model. The temporal average is unusual in this regard. In general, the risk surface depends nontrivially on the strategy and on the model. We need to remove the dependence on the model and then choose an optimal strategy.
One linear function of interest that is not included in the discussion above is “final” estimation of k-year change, computed as the difference of level estimates, as discussed in Section C–1.2. For k = 1, 1-year change is computed as follows: ![]() is estimated on the basis of Y t−1,
is estimated on the basis of Y t−1, ![]() is estimated on the basis of Y t, and the 1-year change is estimated ast
is estimated on the basis of Y t, and the 1-year change is estimated ast ![]() . The prediction error is therefore
. The prediction error is therefore
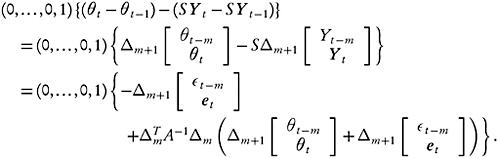
Extension to k-year change for k > 1 is straightforward.
C–3.2
Results for the I(1) Strategy Under the I(1) Model
The I(1) strategy was derived under an I(1) model, but the use of this strategy does not require that the I(1) model holds. Supposefor the moment that the I(1) model does hold. That is,
where “WN” signifies that {ηt}are “white noise” or uncorrelated; B is the backshift operator (BkXt = Xt−k for k = 0, ±1, ±2…); and the SNR φ and model matrix M from (C.2) are given by
Under this formulation, consider the risk surfaces in Figure C.1, which are functions of the strategy through df (or equivalently, through α) and are functions of the model (through the SNR = φ).
Consider the upper left contour plot in Figure C.1, corresponding to the risk for estimation of current level. Note that this contour plot is in units of σe2. The rightmost edge of this plot corresponds to the direct estimator, at 5 df. The risk for the direct estimator is identically 1, as given in equation (C.4). The lower left corner corresponds to the simple MA (1 df) with SNR = 0 (constant mean function). In this case, the risk is σe2/5, or 0.2.
Similarly, the upper right contour plot corresponds to riskfor estimation of the middle year values, or midpoint. Once again, the right edge is identically 1, and the lower left corner is 0.2. The bottom two plots correspond to estimates of 1-year change. The lower left plot is the “current” estimate of change computed from only the 5-year window, while the lowerright plot is the “final” estimate of change computed from consecutive 5-year windows. This “final” estimate is the difference between current level estimates and presumably is the estimate that would be published. In both cases, the right edge is identically 2.
To choose an optimal strategy, it is necessary to remove the dependence on the model, which in this context means removing dependence on the SNR, φ, since M is parameter-free. Two standard approaches are to compute the supremum risk over all models, or the average risk over all models.
The supremum risk corresponds to the worst-case scenario. The strategy that minimizes the maximum risk is the minimax strategy. For each strategy, find the model that maximizes the risk; that is, find the maximum on the risk surface along a vertical slice at a particular df. Then choose the strategy that minimizes this maximum risk curve. Clearly the minimax strategy is a very conservative approach.
For df = 5 in Figure C.1, the contour is identically 1, and so the maximum risk at df = 5 is 1. For any df < 5, the risk increases without bound as
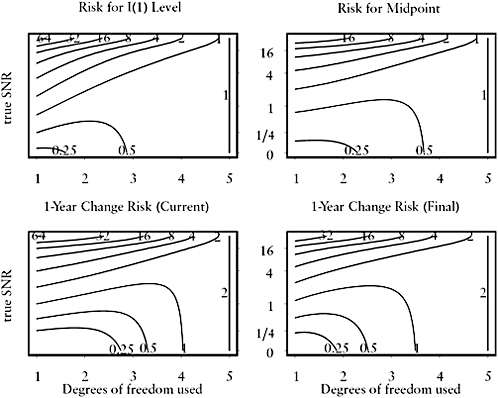
FIGURE C.1 Risk surfaces under I(1) model and I(1) strategy for estimation of current level, level at midpoint of 5-year time window, and 1-year change.
NOTE: “Current” estimate of change uses only 5-year time window, while “Final” uses consecutive 5-year time windows. Horizontal axis is degrees of freedom used in the smoother, from 1 = simple moving average to 5 = direct estimates. Vertical axis is true signal-to-noise ratio (SNR). Contours of risk surface are in units of ![]() .
.
the SNR increases. The supremum is therefore 1 for df = 5, and infinity for df < 5, so the minimax strategy is df = 5, the direct estimators.
This result can be generalized. Consider a model in which the matrix M does not depend on SNR φ or on any other unknown parameter and in which all elements of M are finite. Then for any α < ∞, maximizing the risk with respect to φ is equivalent to maximizing
with respect to φ. If Q(φ) ≠ 0, then Q(φ) is unbounded in φ for any α < ∞, but finite for α = ∞. In this case, the direct estimates (df = m) are minimax.
The second approach to removing the dependence of the risk on the model is to consider the average or Bayes risk. Assume that the SNR has a
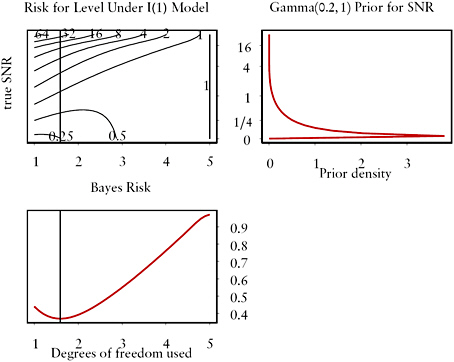
FIGURE C.2 Computation of Bayes risk for estimation of current level.
NOTE: Horizontal axis is degrees of freedom used in the smoother, from 1 = simple moving average to 5 = direct estimates. Vertical axis is true signal-to-noise ratio (SNR). Bottom left plot is Bayes risk, obtained by averaging risk surface in upper left with respect to prior density on SNR shown in upper right (Gamma(0.2,1) with prior mean 0.2). Bayes strategy under this prior is indicated by vertical line at 1.5394 df (α = 0.2). Risk surface under I(1) model and I(1) strategy for estimation of current level is shown in upper left.
prior distribution, π(φ). For each strategy, find the average risk, computed with respect to the prior distribution. Then choose the strategy that minimizes this average risk curve. This is the Bayes strategy. The procedure is illustrated in Figure C.2. The upper right plot of the figure shows the prior density for the SNR (rotated 90 degrees since the priordensity applies to the vertical axis of the upper left plot). The prior in this case, which is Gamma(0.2,1) with mean φ0 = 0.2, assigns most mass to SNRs less than 0.5. Integrating the risk surface in the upper left along the vertical slice at df = 5 is the same as integrating the constant 1 against the prior, and so the average risk at df = 5 is 1, as shown in the lower left plot. For df slightly less than 5, the integral puts most mass on risks less than 1, and almost no mass on risks greater than 1, so the average risk is less than 1. For df = 1, the risks greater than one contribute nontrivially to the integral. At about 1.5934 df (α = 0.2), the average risk attains its minimum, and so this is the Bayes strategy for estimation of current level under the given prior.
In fact, it is easy to find the Bayes strategy analytically under the I(1) model and to show that this same strategy is Bayes for estimation of any linear function. This is the content of the following result.
Result 2 Assume that the I(1) model holds and that the SNR ![]() has prior π(φ) with prior mean φ0. Then the Bayes strategy for estimation of any linear function zTθ using Y tis obtained with α = φ0:
has prior π(φ) with prior mean φ0. Then the Bayes strategy for estimation of any linear function zTθ using Y tis obtained with α = φ0:
that is, this strategy minimizes expected risk among all rules of the form ZT (I − ΔT (αI + ΔΔT)−1) Y t. The Bayes risk for this strategy is
A consequence of Result 1 is that all strategies have the same average risk for estimating the temporal average, and so all strategies are equally successful. Ignoring this special case, an immediate consequence of Result 2 is that the simple MA is not Bayes for the I(1) model unless the prior is degenerate; that is, φ = 0 with probability 1. (In other words, with an SNR = 0, the mean process is not changing in time, and therefore a simple average is optimal.)
Figure C.3 was constructed with the same prior shown in Figure C.2, but for a variety of linear functions. Figure C.3 illustrates the fact that all of these linear functions have minimum average risk at the same strategy, corresponding to α = φ0.
C–3.3
Results for the I(1) Strategy Under Non-I(1) Models
I now turn to the robustness question of what happens if the proposed I(1) strategy is used with a non-I(1) model. For numerical illustration, it is convenient to consider models under which M is parameter-free, so that the risk depends on the model only through the single SNR parameter φ. Some examples follow.
The I(2) Model
First, consider the I(2) model,
where ![]() and (1 – B)θ0 is a constant. Then
and (1 – B)θ0 is a constant. Then
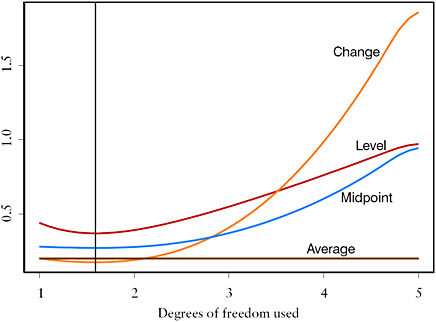
FIGURE C.3 Bayes risk of I(1) strategy for various linear functions under I(1) model with Gamma(0.2,1) prior on SNR.
NOTE: For each linear function, a Bayes strategy under this prior is to smooth with 1.5394 df (α = 0.2), indicated by the vertical line.
with T being the lower triangular matrix of one’s,
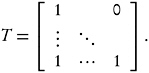
The risk surfaces under this I(2) model are shown in Figure C.4. Note that the bottom edges of each of the plots in the figure agree with the corresponding bottom edges in Figure C.1, because the I(1) and I(2) models are identical when the SNR is zero.
Dependence of the risk on the model could be removed in the same way as in the I(1) case. The minimax strategy is again to use the direct estimators, and the Bayes strategy could be derived given a suitable prior on the SNR. Unlike in the I(1) case, the Bayes strategy will depend on which linear function is of interest. Since more than one linear function is usually of interest, some compromise strategy would need to be selected.
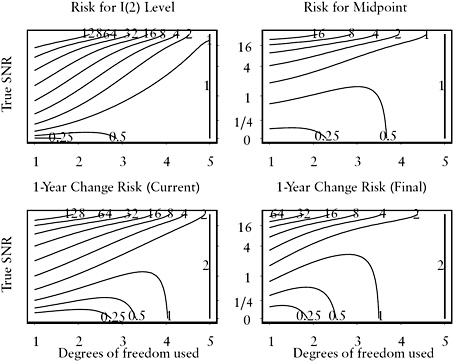
FIGURE C.4 Risk surfaces under I(12) model and I(1) strategy for estimation of current level, level at midpoint of 5-year time window, and 1-year change.
NOTE: “Current” estimate of change uses only 5-year time window, while “Final” uses consecutive 5-year time windows. Horizontal axis is degrees of freedom used in the smoother, from 1 = simple moving average to 5 = direct estimates. Vertical axis is true signal-to-noise ratio (SNR). Contours of risk surface are in units of ![]() .
.
The Linear Model With No Population Error
These same comments apply to all of the following models, derived for a linear model with no population-level error (admittedly unrealistic):
In particular, for a population that is perfectly linear, θt = β0 + βt,
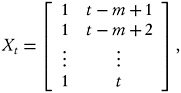
and
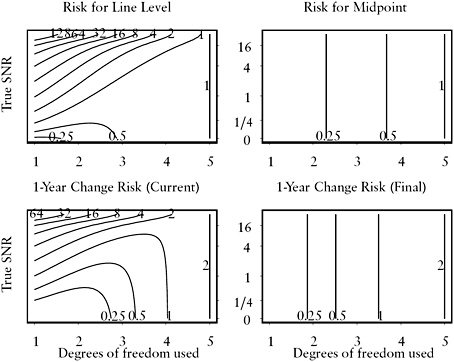
FIGURE C.5 Risk surfaces under Line model and I(1) strategy for estimation of current level, level at midpoint of 5-year time window, and 1-year change.
NOTE: “Current” estimate of change uses only 5-year time window, while “Final” uses consecutive 5-year time windows. Horizontal axis is degrees of freedom used in the smoother, from 1 = simple moving average to 5 = direct estimates. Vertical axis is true signal-to-noise ratio (SNR). Contours of risk surface are in units of ![]() .
.
The risk surface is given in Figure C.5. Note the vertical contours for risk in estimation of the midpoint, since the midpoint is unaffected by the slope of the line. Because of these vertical contours, the optimal strategy for estimation of the midpoint level is the simple MA. For a population that is constant until a 1-year level shift of size δ (in year t − m + 2 or later, since a shift in year t − m + 1 cannot be detected in a time window that only goes back to year t − m + 1),
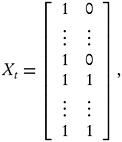
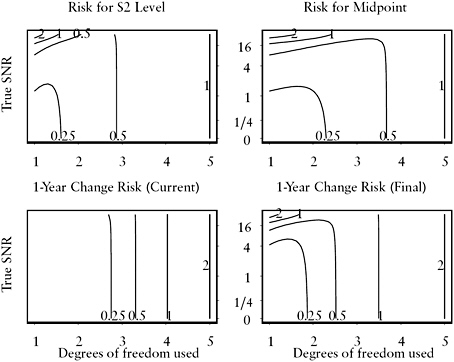
FIGURE C.6 Risk surfaces under model with level shift in year 2 (S2) and I(1) strategy for estimation of current level, level at midpoint of 5-year time window, and 1-year change.
NOTE: “Current” estimate of change uses only 5-year time window, while “Final” uses consecutive 5-year time windows. Horizontal axis is degrees of freedom used in the smoother, from 1=simple moving average to 5=direct estimates. Vertical axis is true signal-to-noise ratio (SNR). Contours of risk surface are in units of ![]() .
.
and
with 1 in the (k − 1)th diagonal position. Figures C.6–C.9 show the risk surfaces associated with these level shift models. The later the shift, the more difficult the estimation of current level or 1-year change. Note also the symmetry in the risk surfaces for the midpoint between S2 and S5 and S3 and S4; that is, level shifts two years before and two years after the midpoint are equally difficult, and level shifts one year before or one year after the midpoint are equally difficult.
As David Binder pointed out in discussion of this paper, all of the models considered here can be considered as special cases of the local linear trend model (e.g., Harvey, 1989, p. 45). Thus, with a small number of parameters and a joint prior on those parameters, Bayes strategies could be derived.
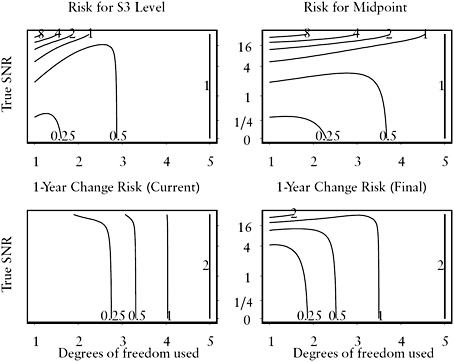
FIGURE C.7 Risk surfaces under model with level shift in year 3 (S3) and I(1) strategy for estimation of current level, level at midpoint of 5-year time window, and 1-year change.
NOTE: “Current” estimate of change uses only 5-year time window, while “Final” uses consecutive 5-year time windows. Horizontal axis is degrees of freedom used in the smoother, from 1=simple moving average to 5=direct estimates. Vertical axis is true signal-to-noise ratio (SNR). Contours of risk surface are in units of ![]() .
.
This would be an excellent model for further theoretical and empirical investigation. I did not consider it here and instead restricted attention to single-parameter models for purposes of illustration.
Prior Determination and Empirical Results for the I(1) Strategy
The previous sections have shown that it is possible to derive optimal strategies, given a model and a prior distribution for the model parameters. In practice, the ACS will produce multiyear estimates for many characteristics in governmental units at many different levels (e.g., states, counties, places, townships, school districts). These governmental units vary widely in size. As noted in the introduction, I focus here on uniformstrategies. The results on optimal strategies in the previous sections can be used to choose sensible uniform strategies, which reflect a compromise among strategies.
To use the optimal strategy results, it is necessary to identify models for
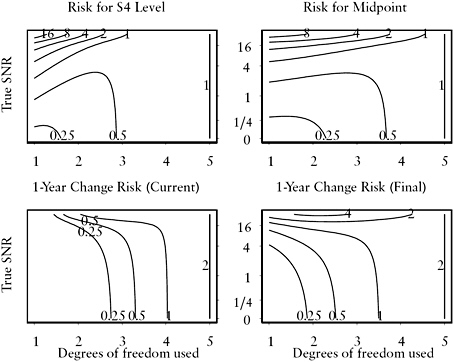
FIGURE C.8 Risk surfaces under model with level shift in year 4 (S4) and I(1) strategy for estimation of current level, level at midpoint of 5-year time window, and 1-year change.
NOTE: “Current” estimate of change uses only 5-year time window, while “Final” uses consecutive 5-year time windows. Horizontal axis is degrees of freedom used in the smoother, from 1=simple moving average to 5=direct estimates. Vertical axis is true signal-to-noise ratio (SNR). Contours of risk surface are in units of ![]() .
.
ACS characteristics, to determine numerical values for the associated model parameters, and to use the empirical distribution of model parameters as the prior distribution in identifying an optimal strategy. The optimal strategy under this empirical “prior” is then one uniform strategy that compromises among the optimal strategies for the various characteristics.
There is considerable information on the various characteristics studied by the ACS, from sources such as the ACS test sites during 1996–1999, the C2SS in 2000, the ACS test surveys in 2001 through 2004, and the ACS in 2005. In addition, there are other ongoing government surveys. It thus seems possible in principle to identify reasonable classes of models and reasonable numerical values for the associated SNRs. That is, for a given model class, determine a prior from historical data for which the model class is appropriate. Given the prior, compute the Bayes strategy for that model class. Finally, choose a compromise strategy from among the computed Bayes strategies.
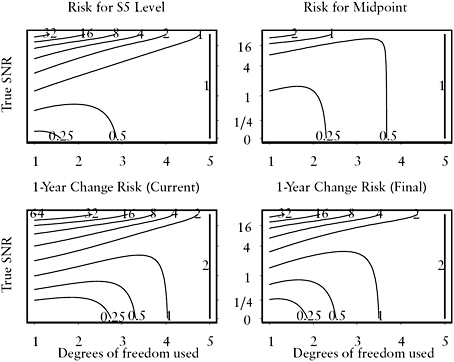
FIGURE C.9 Risk surfaces under model with level shift in year 5 (S5) and I(1) strategy for estimation of current level, level at midpoint of 5-year time window, and 1-year change.
NOTE: “Current” estimate of change uses only 5-year time window, while “Final” uses consecutive 5-year time windows. Horizontal axis is degrees of freedom used in the smoother, from 1=simple moving average to 5=direct estimates. Vertical axis is true signal-to-noise ratio (SNR). Contours of risk surface are in units of ![]() .
.
Alternatively, construct a prior as a mixture across model classes. Determine the frequency with which each model class is represented among the ACS characteristics of interest and then determine prior distributions for the model parameters in each model class. The final prior is then the mixture of these component priors, weighted by model class frequency.
As a simple numerical example (purely for illustration; not intended to be a realistic modeling exercise), consider the four years of demographic, social, economic, and housing characteristics from the ACS in Multnomah County, Oregon. Fitting the line+error model to each such series, we obtain the estimated SNR values:
Some of these values are estimated as infinity because the line fits perfectly. These infinities are trimmed from the set of estimated SNRs, and the stem-and-leaf plot of the remaining estimates is given in Figure C.10.
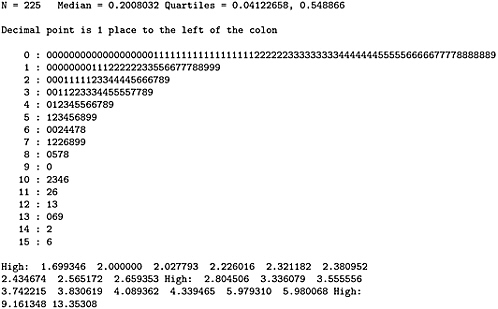
FIGURE C.10 Stem-and-leaf plot of estimated signal-to-noise ratios inthe line model fitted to four years of ACS data on demographic, social, economic, and housing characteristics in Multnomah County, Oregon.
With this empirical prior for SNR, the Bayes risk for various linear functions can be computed. These risks are shown in Figure C.11. The Bayes strategy for estimation of current level uses approximately 2.8 df. Since the model is a line, the Bayes strategy for estimation of the midpoint level uses 1 df. Any strategy is Bayes for estimation of the temporal average. Finally, the Bayes strategy for 1-year change uses approximately 2 df. Depending on the relative importance of estimation of the various linear functions, some compromise df could be chosen. In this numerical illustration, 2 df might be a sensible compromise: it is close to optimal for most of the linear functions considered and does not give up too much efficiency for current level.
This empirical example illustrates the choice of a data-driven compromise strategy, in which the compromise is across characteristics. The same sort of approach might be used to choose a single, compromise strategy across multiple areas in which the SNRs vary spatially.
C–4
SUMMARY
There are many possible sources of estimation strategies for a survey repeated over time, like the ACS. I have focused on the I(1) strategy in this
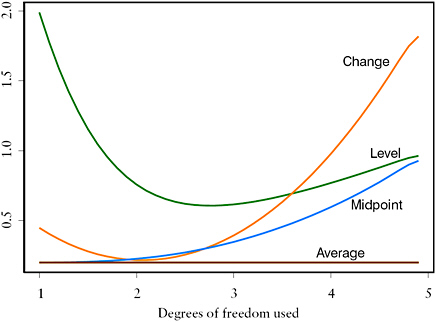
FIGURE C.11 Bayes risk for various linear functions using empirical prior fitted from Multnomah County ACS data.
NOTE: See Figure C.10 for derivation of the empirical prior using the “line” model as the true model.
case, evaluating it using simple decision-theoretic tools for various population characteristics, under various models, across a rangeof unknown model parameters.
The proposed MA strategy does poorly in this evaluation. It is not minimax (although this extremely conservative criterion is not very useful in practice). More importantly, it is generally not Bayes under any reasonable prior on the SNR. For example, under the I(1) model (and ruling out the temporal average for which all strategies are equally effective), MAs are Bayes only if the true SNR is zero, or equivalently if the true values are constant over time.
The question for this research was to determine if there are viable alternatives to the proposed MA strategy. The I(1) strategy meets the criteria set out at the beginning of this paper. It is simple and consistent. Its weights are unequal but fixed, so that large-scale implementation is no harder than MA, and comparability across domains is ensured. Its linear form means that tables add up. Guidance for users would seem to be no worse for a weighted MA than for an unweighted MA.
The I(1) strategy can be made robust. This paper has indicated methods by which compromise df can be chosen empirically for reasonable efficiency across a range of characteristics and population parameters. Finally, the I(1) strategy is defensible. It has a motivating statistical model but does not require correctness of that model. Choice of a particular strategy can build on extensive knowledge of related populations. If novel estimation problems are encountered, appropriate estimation techniques can be developed theoretically by going back to the motivating model, and then those techniques could be evaluated with decision-theoretic criteria when the motivating model does not hold.
Finally, it is important to note that although this paper has focused on the class of α-smoothers derived from an I(1) strategy, any other strategies could be evaluated with similar decision-theoretic criteria.
REFERENCES
Binder, D.A., and Hidiroglou, M.A. (1988), Sampling in time, in Handbook of statistics, Vol. 6, eds. P.R. Krishnaiah and C.R. Rao, pp. 187–211. Amsterdam: North-Holland.
Brockwell, P.J., and Davis, R.A. (1991). Time series: Theory and methods, 2nd ed. New York: Springer-Verlag.
Durbin, J., and Koopman, S.J. (2001). Time series analysis by state space methods. Oxford, England: Oxford University Press.
Gijbels, I., Pope, A., and Wand, M.P. (1999). Understandingexponential smoothing via kernel regression. Journal of the Royal Statistical Society, Series B, 61, 39– 50.
Harvey, A.C. (1989). Forecasting, structural time series models and the Kalman filter. Cambridge, England: Cambridge University Press.
National Research Council. (2001). The American Community Survey: Summary of a Workshop. Committee on National Statistics. Washington, DC: National Academy Press.
Scott, A.J., and Smith, T.M.F. (1974). Analysis of repeatedsurveys using time series methods. Journal of the American Statistical Association, 69, 674–678.























