9
Applying Population-Based Results to Individuals: From Observational Studies to Personal Compensation
The previous chapters address problems of inferring causation from observational studies in the context set by other types of evidence. We also provide a classification scheme for the level of evidence in support of causation in general. Having determined that the level of evidence is sufficient to infer causation, two additional matters are of interest: (1) What is the burden of disease among those exposed that is caused by the exposure? and (2) What is the likelihood that the disease was caused by exposure in a particular individual? Information pertinent to the first question is relevant to forecasting the administrative and financial implications of the causal determination. Information relevant to the second question may be of value in handling individual cases.
In the present chapter we address these topics, beginning with the simplifying assumption that a causal association has been established in the population, and that we have an accurate estimate of relative risk (RR) among exposed people. We turn to an epidemiologic measure, the attributable fraction (AF), to answer these questions. This chapter also addresses the complexities of using the AF in devising compensation approaches. It provides a conceptual foundation that should prove useful in the further elaboration of the Committee’s framework and its implementation.
ATTRIBUTABLE FRACTION
Definitions and Assumptions
The attributable fraction (AF) is used several ways in the literature (Rothman and Greenland, 1998). We use the term in a way most relevant to compensation by the Department of Veterans Affairs (VA), namely as the proportion of disease in an exposed group that can be attributed to the exposure. This report uses the terminology service-attributable fraction (SAF) when the exposed group is a military population. We begin with two simplifying assumptions: (1) exposure produces new cases of the disease that would not have occurred otherwise, and (2) the additional RR from exposure is stable over age and across subgroups within the population of exposed veterans. Later we discuss complications that might occur when these assumptions do not hold. Under these two assumptions, the AF is interpreted as the probability that among the exposed people with the disease, their disease has actually been caused by the exposure.
Crucial Properties of the AF
In applying the AF, there are two key properties. First, it is not a statement about whether the exposure is able to cause the disease. In calculating the AF, we take as given that the exposure does, in fact, cause the disease. However, even among exposed persons, the exposure does not necessarily cause all cases of the disease—most diseases have many possible causes. When an exposed person gets the disease, the chance that the disease is caused by the exposure is almost certainly less than one. The AF represents this probability.
The second important aspect of the AF is that it cannot specifically tell us which exposed people have their disease because of the exposure. All the AF can provide is an estimate of the average probability for all exposed persons. We can refine this estimate in various ways (e.g., by age or levels of exposure), but even with perfect information it is seldom, if ever, possible with current methods to identify which particular cases of a disease with multiple causes were caused by the exposure and which were not.
Estimating the AF
An AF is based on an estimation of RR, which is the ratio of disease risk among exposed persons compared to the risk among otherwise similar, but unexposed persons. RR is the most common expression of disease risk in epidemiologic studies. As discussed in Chapter 7, odds ratios from case-control studies approximate the RR.
The AF is calculated by the following formula:
This may also be expressed as: AF = (RR − 1)/RR.
Consider the example of smoking and lung cancer. The RR for lung cancer among smokers is around 20. Applying the formula above, a RR of 20 yields an attributable risk of 95 percent, AR = (20 − 1)/20. In other words, 95 percent of all lung cancers among smokers can be attributed to their smoking, possibly acting in combination with other factors, while the remaining 5 percent of the lung cancers of smokers come from other causes. For another example, smoking and cardiovascular disease, the RR is close to 2. Thus, only half of the cases of cardiovascular disease among smokers, 50 percent = (2 − 1)/2, can be attributed to smoking. The lower the RR, the less likely it is that the disease in an exposed person is caused by the exposure, and the more likely that other factors are the cause.
Factors That Can Distort the AF
Broadly speaking, there are two problems that can bias an estimate of disease burden due to an exposure when using the AF. One is portability—that is, the degree to which the RR estimated from one population can be properly applied to another population. The second problem is error in the measurement of exposure. We consider each of these limitations below.
Problems in Portability
Chapter 7 discusses the biases and confounding that can distort estimates of RR. Even if these problems have been carefully handled in the original estimation of RR, the application of a valid RR to a new group introduces a fresh set of opportunities for distortions. This problem goes under the general rubric of portability, that is, the ability of a valid RR in one population to be applied to a new population. The portability of RRs and hence of AFs is often uncertain because of differing characteristics of the population in which the AF was estimated compared to those in which it is to be applied.
A simple example of a problem with portability is effect modification by gender. Suppose that, at a given level of exposure, the RR of disease differs by gender of the exposed person (a common observation). If the distribution of men and women in the study group is different from the exposure group to which the RR is being applied, and gender is ignored,
the resulting AF will be incorrect. This particular problem can be handled by applying gender-specific RRs to gender strata of the exposed population. However, more complicated scenarios of confounding or effect modification can be readily anticipated; methods to handle these have been proposed by Bruzzi et al. (1985) and Benichou (2001). Although such methods work in principle, they may require detailed data for subgroup-specific RRs that are difficult to obtain.
A similar problem can arise when the RR is estimated in a population with high exposure (as in an occupational setting) and then applied to a population with lower levels of exposure. The RR will tend to overestimate the AF for the lower-exposed population. With enough information from epidemiologic studies on exposure-specific risk and information on levels of exposure in the population of interest, the appropriate adjustments of the AF can be made to account for exposure.
In summary, problems of portability do not call into question the validity of the original RR, but rather its generalizability—that is, the validity of its application to a new population and the estimate of the AF. Even when the causal association is certain (as we assume here), the problems of portability raise questions about the strength of the disease risk in the population of interest—and thus the size of the AF.
Problems in Exposure Classification
The second distortion that can occur with the AF is when the RR is applied to a population in which some persons classified as exposed were not in fact exposed. (This problem is especially relevant in the context of the charge of this Committee, in that VA is frequently unable to establish actual exposure during military service, and therefore must infer it—with inevitable error.) Usually the decision is to err in the direction of assuming people are exposed when they may not be exposed.
When an “exposed” group includes some people who are not actually exposed, the AF for the whole “exposed” group would be
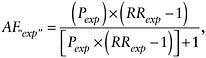
where AF“exp” = the AF for an “exposed” group containing some unexposed people, Pexp = the proportion of the supposedly “exposed” group who are truly exposed, and RRexp = the RR for the truly exposed group.
Typically, we do not know what proportion of those reported as exposed were actually exposed. However, we can make reasonable assumptions and
see how much difference such errors might make. In our previous smoking example, if only half of the “exposed” group had truly been exposed, then the true AF for the “exposed” group would be 90 percent instead of 95 percent. Thus, exposure misclassification introduces a trivial difference between the true AF and the calculated AF when the RR is high.
This is not true when the RR is lower (as is often the case). Taking the example of RR = 2 (for smoking and cardiovascular disease), the true AF is 50 percent when every person in the “exposed” group was truly exposed, but only 33 percent, if half of the “exposed” group had actually been unexposed. Thus, when the RR is low, misclassification of exposure results in an estimated AF that is an overestimate of the true AF.
Reconsidering the Assumptions of the AF and Alternatives
A basic assumption in calculating the AF is that the RR is known. In the real world, RRs are only estimates and typically include some measure of the statistical imprecision of that estimate. The implications of such uncertainty can be explored by calculating a range of AFs under different assumptions for the RR.
What if other assumptions about the AF are untrue? For example, what if the exposure accelerates disease among persons who were going to get the disease anyway, instead of causing disease in persons who would not otherwise have gotten the disease? In this more complex scenario, the AF may not adequately capture the total burden of disease caused by the exposure. Alternatives to the AF that attempt to capture the total impact of exposure on disease include “years of life lost” (YLL) (Robins and Greenland, 1989a; Steenland and Armstrong, 2006) and “years of life lived with disability” (YLD).
Methods for the calculation of YLL, YLD, and disability-adjusted life years (DALYs) have been recently reviewed (Steenland and Armstrong, 2006). YLL is the total number of deaths caused by the disease of interest multiplied by the average number of years of survival expected beyond the age of death from that disease. YLD is the product of the number of incident cases, a disability weight, and mean duration of disease; in the absence of incidence data an estimate can be based on mortality data and case-fatality rates. The total burden of disease can be estimated as the sum of YLL and YLD and is known as disability-adjusted life years, or DALYs. YLL, YLD, and DALYs caused specifically by military service exposure can be calculated by multiplying them by the AF (Steenland and Armstrong, 2006). In the case of military service, we refer to this as the service-attributable fraction (SAF). Because the AF is a fundamental element of these alternatives to the AF, they are subject to the same caveats about portability and misclassification of exposure as the AF itself. In the section
“Promoting the Use of AFs in Determining Compensation for Veterans” we return to this discussion with regard to the AF and the SAF.
Further Refinements of the AF
Once we have estimated the total disease burden caused by the exposure using the AF, it may be possible to refine this estimate further by considering characteristics of persons, including features of their exposure, that make their individual risk of disease higher or lower than in the exposed population as a whole. In other words, we can move from an estimate of overall AF, applied equally to all, to estimates for subgroups or even individuals, based on additional information regarding their risk factors. This refined expression of the AF as estimated for individuals has usually been designated as the probability of causation, or PC, although in actuality it is simply the AF estimated for subgroups of those exposed.
PROBABILITY OF CAUSATION FOR AN INDIVIDUAL
The AF attempts to apportion the disease burden in a population between the exposure and other factors causing the disease. In contrast, the PC attempts to address the question of whether the exposure could have caused a particular disease in an individual, given that individual’s particular characteristics of genetic makeup, lifestyle, and personal history—that is, the characteristics that determine individual susceptibility. For the past two decades, estimates of the PC have been available to guide the compensation of atomic veterans and others exposed to ionizing radiation (DHHS, 2002; NIH, 1985; Thomas, 2000). These estimates have been possible because of the extensive information on cancer risk in relation to radiation exposure.
PC Definition
A precise definition of PC will help illustrate the challenges in estimating it. Following the National Institutes of Health (NIH) Working Group (1985), the PCi is the probability that individual i’s disease was caused by the exposure, given i’s unique set of characteristics (call them Xi). Symbolically, PCi, is defined using two terms—the probability that the individual would have developed the disease given no exposure, (Ē),[P(D,Ē|Xi)] and the probability that the individual developed the disease given the exposure, [P(D,E|Xi]:
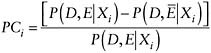
|
PCi = probability of causation for an individual P = probability D = disease E = exposure Ē = no exposure Xi= an individual’s unique set of characteristics |
Notice the equation represents an allocation of the probability of disease between the exposed and unexposed. The probability that the background caused the disease in individual i is simply 1 − PCi. If everyone in the population is identical in susceptibility to the disease and in the extent of exposure, and if the exposure-induced cases are completely independent of other cases (i.e., cases that were caused by something else), then the PC for every individual in the population is given by the population AF. Implications of not meeting these assumptions are discussed below in “Promoting the Use of AFs in Determining Compensation for Veterans.” Still, additional information on the levels of exposure, age at exposure, time since exposure, mechanism of disease causation, and other factors can be used to define subgroups within populations, and then to estimate AFs for these subgroups. As described below, these subgroup measures provide the basis for better estimates of PCs for individuals within these classes.
Because individuals may vary in susceptibility to a particular exposure because of genetics, lifestyle, and other factors, estimates of PCs are not necessarily expected to resemble the true probability that an individual’s disease was caused by the exposure. The term assigned share (AS) has been used in place of PC, especially as it pertains to issues of compensation (Lagakos and Mosteller, 1986). The NIH Ad Hoc Working Group to Develop Radioepidemiological Tables (NIH, 1985) (for use in compensating cancer victims exposed to ionizing radiation) found itself constrained by legislative mandate to use the term probability of causation rather than assigned share. Reflecting on the history of the use of the terms, a more recent National Research Council (NRC) committee decided to use the terms synonymously (NRC, 2000).
Refining Estimates by Differences in Exposure Levels
Exposures to any given chemical or other disease-causing factor would be expected to vary substantially among veterans in any theater of war or duty, with corresponding large differences in individual risk and hence PCs. Also, the pattern of exposure can be important. For the same cumulative dose, the dose rate, timing, and duration may play a significant role in determining those who get the disease and those who do not. Route and exposure pathways are also to be considered. Although obtaining accurate estimates of exposure among veterans will typically be challenging, in some cases exposures may differ by orders of magnitude, and it may be possible to develop at least crude exposure estimates.
If exposure can be quantified and the relationship between risk and exposure is understood, the AF can be expressed as a function of exposure. For example, dose-response relationships can be derived from occupational epidemiologic data for various carcinogens. As the example below shows, it can be important to stratify by the degree of exposure if this information is available, because the AF can vary substantially with exposure level.
Consider the following simple relationship between the lifetime probability of cancer P, or risk, and the air concentration, D, and the duration of exposure t, P(D) = 1 − exp(− a − bDt), which at P less than 10 percent is closely approximated by a simple linear relationship P(D) = a + bDt, where a, the intercept, is the risk in the absence of exposure, and b, the slope, describes the incremental increase in risk with increasing air concentration and time. Here RR is given by
and the AF is given by
which, substituting in the above, reduces to
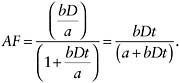
|
P = lifetime probability (or risk) of cancer D = air concentration t = duration of exposure a = risk in the absence of exposure b = incremental increase in risk with increasing air concentration and time RR = relative risk AF = attributable fraction |
Benzene provides an example of how very different AFs can result from differently exposed subgroups. We show how when exposure is taken into account PC estimates can be made for individuals with different levels of exposure. Benzene is an established cause of acute myelogenous leukemia (AML) in humans (Austin et al., 1988). Benzene exposures are ubiquitous; for example, benzene is a constituent of gasoline and also cigarette smoke. The general population in the United States is exposed to levels averaging from 1 to 5 ppb in indoor and outdoor air, and it would be anticipated that Service members would be similarly exposed. In addition, some in the service may have duties that result in exposures to considerably higher levels of benzene (e.g., those servicing airplanes or working in garage facilities). We might assume that some service jobs result in exposures as high as 10 ppm.
AML is relatively uncommon, with a lifetime risk of diagnosis (an estimate for parameter a in the equation above) of about 0.3 percent. A lifetime exposure to 1 ppm causes AML in roughly 5 percent of those so exposed, corresponding to an estimate of b in the above equation of 0.00062/ppm-years (= 0.05/ppm/78 years). Applying these parameter estimates, AFs can be derived, while acknowledging the caveats and limitations noted above, including the issue of portability since the b was estimated from occupational cohorts in China and the United States (OEHHA, 2001). Service members who contract AML after being exposed during a tour of duty of 3 years to general background levels (e.g., 5 ppb) have a 0.2 percent chance that their leukemia arose because of their military exposure (AF = [0.00062 × 0.005 × 3]/[0.003 + 0.00062 × 0.005 × 3]). Thus, any case of AML among the exposed Service members would be highly unlikely to have resulted from military exposure. The AF associated with military service lasting 30 years is higher, at 3 percent. In contrast, Service members with a 3-year tour of duty who were exposed to 10 ppm during work hours, or a daily average of approximately 5 ppm, have an
AF of 76 percent: AF = (0.00062 × 5 × 3)/(0.003 + 0.00062 × 5 × 3). This simple example illustrates the importance of segregating groups in terms of the magnitude and duration of exposure when those data are available. It also illustrates the importance of identifying those most heavily exposed in determining whether disease caused by an exposure to a given factor deserves compensation.
As illustrated below, it is occasionally possible to classify or otherwise identify individuals or groups of individuals in terms of their exposure duration, age at exposure, exposure intensity, as well as other factors to derive exposure group-specific AFs and hence more refined estimates of PCs for individuals.
Refining Estimates in the Presence of Multiple Known Causes of Disease
Many illnesses considered for compensation have multiple causes. For example, lung cancer has many known causes in addition to smoking, including asbestos, arsenic, radiation, and environmental tobacco smoke (NCI, 2006). Some lung cancers occur in individuals without significant exposures to any known cause. The proportion of disease that is attributable to military service exposure can be estimated when there are valid RR estimates for (1) the military service-related exposure in the absence of the other known causes (RRE), (2) other known causes that individuals in the group were subjected to (such as smoking—RRS), and (3) the joint exposure of both military service and other specific known causes (RRboth).
As an illustration, the proportion of disease attributable to military exposure and smoking, separately and jointly, is estimated for the hypothetical case described in Chapter 7. This is derived for two cases below, with smoking and military exposure interacting either additively or multiplicatively. In the additive model, smoking adds a constant RR over background (RRS − 1) regardless of whether there is military exposure. Thus, in the presence of both exposures, the RR is RRboth= RRE + RRS − 1. In the multiplicative model, RRboth = RRE × RRS.
We introduce new terminology to aid in the derivation of AFs for the joint and separate effects of these multiple known causal exposures. The population attributable fraction (PAF) is the proportion of disease in the entire population attributable to an exposure or any other factor. (The relation of the PAF to the AF will be discussed below.)
Assume that all disease in the population is attributed either to the background or to the two identified causes. PAF0 is the proportion of disease attributable to background factors unrelated to smoking or military exposure. PAFboth is the proportion of disease attributable to smoking and military exposures. The two sum to unity 1 = PAF0 + PAFboth. Analogous to the AF, the PAFboth is given by
Thus PAF0 is given by
which reduces to
PAFE, the proportion attributable to military exposure alone, is simply the proportion of disease attributable to background factors multiplied by the excess RR above the background (RRE − 1):
which reduces to
Similarly PAFS, the proportion attributable to smoking acting alone, is
The additional proportion attributable to the two factors acting in combination (i.e., interacting), PAFInt is
|
PAF0 = proportion of disease attributable to background factors unrelated to smoking or military exposure PAFboth = proportion of disease attributable to smoking and military exposures PAFE = proportion of disease attributable to military exposure alone PAFS = proportion of disease attributable to smoking acting alone PAFInt= the additional proportion of disease attributable to the two factors acting in combination RRE= RR estimates for military service-related exposure in the absence of the other known causes RRS = RR estimate for other known causes that individuals in the group were subjected to (e.g., smoking) RRboth = RR for the joint exposure of both military service and other specific known causes |
Table 9-1 provides the parameter values for the hypothetical case described in Chapter 7 for the two different cases—when smoking and military exposure interact multiplicatively and when they interact additively.
The calculations of AFs to the separate and joint exposures for this hypothetical example are laid out in Table 9-2. For the multiplicative example, one might be tempted to conclude that the contribution of military exposure was very small, since in the absence of the smoking interaction, the AF is only 6.7 percent. However, due to its interaction with smoking, the total contribution of military exposure is 66.7 percent (Table 9-2). (Note that this is the same PAFE as for nonsmokers, [3 − 1]/3 = 67 percent [Table 9-1], revealing that under a multiplicative model, the total PAFE
TABLE 9-1 Hypothetical Example of Risks from Multiple Causal Exposures
|
Military Exposure |
Smoking Habit |
Number at Risk |
Cancer Cases |
|
Relative Risk |
|
No |
Never |
1,000 |
10 |
|
1 |
|
No |
Current |
1,000 |
100 |
|
10 |
|
Yes |
Never |
1,000 |
30 |
|
3 |
|
Yes |
Current |
1,000 |
Multiplicative |
300 |
30 |
|
|
|
|
Additive |
120 |
12 |
TABLE 9-2 Hypothetical PAFs Due to Smoking and Military Exposure
|
PAF Due to |
Multiplicative Model |
Additive Model |
|
Background only, PAF0 |
1/30 = 3.3% |
1/12 = 8.3% |
|
Military exposure only, PAFE |
2/30 = 6.7% |
2/12 = 16.7% |
|
Smoking only, PAFS |
9/30 = 30% |
9/12 = 75% |
|
Military exposure and smoking interaction, PAFInt |
(30 − 3 − 10 + 1)/30 = 60% |
(12 − 3 − 10 + 1)/12 = 0% |
|
Total: PAF0 + PAFE + PAFS + PAFInt |
3.3 + 6.7 + 30 + 60 = 100% |
8.3 + 16.7 + 75 = 100% |
|
SAF: Disease preventable by eliminating military exposure, PAFE + PAFInt |
6.7 + 60 = 66.7% |
16.7 + 0 = 16.7% |
does not depend upon smoking.) Of course, the same calculation applied to smoking would yield an estimate of 90 percent for the total fraction attributable to that factor. If one were naively to add these two figures, it would appear that more than 100 percent of the risk would be accounted for, but of course, this is simply because the interaction contribution has been counted twice. In terms of prevention, 66.7 percent of the cancer cases in this group could have been prevented had the military exposure not occurred (or 90 percent [30 percent + 60 percent] if they had not smoked or 96.7 percent [30 percent + 60 percent + 6.7 percent] if both causes were eliminated [Table 9-2]).
Under a purely additive model, there is no interaction, no proportion of disease is attributable to the interaction, and the term PAFInt becomes zero (Table 9-2). Among smokers, then, the proportion attributable to military exposure is 16.7 percent, considerably lower than in the multiplicative case. Among nonsmokers, however, military exposure accounts for 67 percent of the cases (PAFE = [3 − 1]/3 = 67 percent [Table 9-1]), revealing that under an additive model (or any less-than-multiplicative model), the PAFE will be larger for nonsmokers than for smokers. This holds even if the relative effect of smoking is much larger than exposure.
Chapter 7 also considered a scenario where one of the two factors was an intermediate variable on a causal pathway from exposure to disease (the example was smoking resulting from an amputation and leading to lung cancer). In this case, one would not want to partition the AF in this manner, because the direct effect of smoking on lung cancer was itself a consequence
of the exposure (battle trauma) and is therefore part of the total lung cancer burden attributable to that trauma.
Turning to the concept of the AF that was introduced at the beginning of this chapter, as the fraction of disease in the population that would not have occurred had the exposure not occurred, the AF can be derived from PAFs computed in this manner. It is simply
As before, the AF can be refined to provide estimates for individuals in specific subgroups, with the same caveats and cautions discussed earlier. For the multiplicative case in the hypothetical illustration above, the SAF is thus estimated to be 66.7 percent (Table 9-2). The elimination of exposure would have eliminated the excess cases due to exposure acting alone and those due to its joint action with smoking. Hence, both components are counted in deriving the SAF. For the additive case, with the interaction term (PAFInt) equal to zero, the SAF estimate is 16.7 percent. This underscores the importance of understanding the potential for interaction among multiple causal factors when evaluating the SAF for specific subgroups to be applied to individuals.
Using Data on Susceptibility and Exposure to Refine an AF Estimate
People differ in their susceptibility to disease and predispositions toward certain disabilities. Some of these differences are within an individual’s control (e.g., food choices and eating habits), while other differences (e.g., genetics, age, and gender) are not. Differences in susceptibility remain to a great extent unquantifiable for most diseases, and thus are a source of uncertainty that in turn cannot be quantified in estimating the PC for individuals. When the background risk (in the absence of the exposure in question) varies substantially among individuals in the group, or there are strong interactions between background factors and exposure, the PCs among individuals can vary substantially, even for the same exposure level, and these will be misestimated by the AFs calculated for specific subgroups that cannot incorporate information on background risk.
Epidemiologic data may provide the basis for refining estimates of the AF for subgroups to be applied to individuals. As illustrated above, data on smoking or other causes of a disease not related to military service may allow refinement of the SAF. A variety of susceptibility and other factors have been used to refine estimates of the AF for radiation-induced cancers. In 1985, a set of radioepidemiological tables was released that provided probability of causation estimates for radiation exposures in terms of a
person’s gender, age at exposure, age of cancer diagnosis, dose, and other factors (DHHS, 2002; NIH, 1985) (see the case study on radiation in Appendix I for details). These tables have since been updated using mathematical models of risk incorporating the characteristics of the individual claimant. In addition to gender, age at exposure and diagnosis, and smoking status, the dose, type, and energy intensity of the radiation are addressed. These estimates can now be obtained using an interactive computer program. The program also explicitly accounts for uncertainty in model inputs to “help minimize the possibility of denying compensation to claimants under the Energy Employees Occupational Illness Compensation Program (EEOICPA) for those employees with cancers likely to have been caused by occupational radiation exposures” (NIOSH, 2007, p. 3). Few if any other exposures lend themselves to such precise adjustments of risk.
Other Complexities of the AF
Most of the above discussion treats RR of exposure as fixed. A typical assumption for cancers is that, following a latency period after exposure, d, there is an age-specific incidence p(t,d) that is a fixed multiplicative factor above the nonexposed
In other words, there is a constant RR at any age t. An alternative assumption—constant excess risk—is that a given exposure d increases the absolute risk in the exposed by a fixed amount g(d), so that p(t,d) = g(d) + p(t,0). Because background incidence of every type of cancer changes with age, the constant excess risk model is incompatible with the assumption of constant RR. Another aspect of this problem is that for some diseases there are ages at which an individual is more susceptible to certain diseases. For radiation carcinogenesis there are considerable data for evaluating dose-response relationships that account for exposure level and duration, and age at exposure, and still uncertainty remains regarding how best to model these relationships for the purpose of calculating AFs for individuals (DHHS, 2002). For other cancer causes and other diseases there is usually much greater uncertainty about these relationships.
AF AND COMPENSATION
Earlier in this chapter, the concepts of the AF and the SAF were further developed after being initially introduced in Chapter 6. The extension of these concepts to attempt to estimate refined AFs that could be applied to
individuals was then introduced and discussed. We now bring these concepts to bear on the issue of compensation.
Considerations in Assessing Alternative Compensation Schemes
Exposure-Based Schemes
Compensation can theoretically be based on any number of considerations, not all of which make use of the notion of causation. For example, compensation could simply be based on a determination that certain types of exposure are so hazardous or extreme that they merit compensation regardless of whether they cause a disease. The Prisoner of War (POW) experience could reasonably be a candidate for an experience worthy of compensation on the basis of exposure alone, regardless of whether any illnesses resulted from this “exposure,” and with perhaps some consideration of the severity of the experience. Similarly, when an exposure strongly increases the risk of a specific disease or condition, compensation could be granted regardless of whether the disease actually occurs. This approach was considered by the Presidential Commission on Catastrophic Nuclear Accidents and discarded (Presidential Commission, 1990). These approaches to compensation will not be considered further here, as they are matters of policy. We restrict our discussion to the compensation of persons whose exposure was causally linked to a health outcome and who were actually diagnosed with the outcome of interest.
A Traditional Approach Using the PC
For most questions of compensation, the decision rests on whether a specific exposure has been established as the cause of a disease or condition. It is usually not possible to establish the fact of causation for individuals (also referred to as causation in fact or individual causation) because the exposed cases caused by the exposure cannot be distinguished from the exposed cases caused by something else (Presidential Commission, 1990, pp. 107, 110). Furthermore, it is often difficult, if not impossible, to reconstruct the past doses, or even the exposures, when the latency period is very long. One approach to establishing the fact of causation in these circumstances has been to use an estimate of the probability of causation (PC) to determine whether compensation should be provided (OSTP, 1988). This estimate of PC (which is itself sometimes also referred to as PC), as discussed above, is the AF refined to be applicable to subgroups of individuals and is used to assign group risk to exposed individuals with the condition. A minimum threshold value of this estimated PC is then selected to determine whether one is eligible for compensation. This PC can also then be
used to determine, in those below this threshold, what lesser degrees of compensation might be provided.
The Presidential Commission on Catastrophic Nuclear Accidents used this approach when it recommended, in the context of radiation exposure, that someone for whom PC was determined to be more likely than not (i.e., PC > 0.50) would merit full compensation (Presidential Commission, 1990). At the other end of the spectrum, those in which it was determined that “it is extremely unlikely that an illness results from” an exposure would receive no compensation. For those who fell in between those two extremes, a “proportional recovery” approach was recommended in which compensation was awarded in relation to the PC (Presidential Compensation, 1990, p. 10). This approach, then, uses PC at a threshold of 0.5 to determine full compensability, with PC being determined by estimated exposure dose. Information on dose is then again brought to bear in determining the amount of compensation for those who do not meet the threshold PC, but who have received a dose that could possibly have caused the disease. Some of these issues are developed in more detail below (see “Possible Applications of the AF in Determining Individual Compensation”).
A cogent critique has been developed that argues against the use of PC for the purpose of determining compensation (Cox, 1984, 1987; Greenland, 1999; Greenland and Robins, 1988, 2000; Robins, 2004; Robins and Greenland, 1989a,b, 1991). This critique has important implications as to whether the AF itself should be used in compensation. We later summarize the relevant aspects of this critique in the context of promoting use of AFs for this purpose as it relates to veterans (see “Promoting the Use of AFs in Determining Compensation for Veterans”).
Use of YLL, YLD, and DALYs in Compensation
As an alternative to the use of PC or AF, Greenland and Robins proposed an approach to compensation based on expected years of life lost (YLL) (Greenland and Robins, 2000) (see above, “Reconsidering the Assumptions of the AF and Alternatives,” where YLL, YLD, and DALYs are defined). Compensation would then be based on some reasonably assessed amount per year of life lost. An important feature of such a scheme is that it takes into account when an exposure caused death rather than merely whether it caused death. A compensation scheme based on YLL, it is argued, is economically rational because the total compensation payable under such a scheme corresponds to the total health burden caused by an exposure (at least as reflected by mortality), a quantity that can be estimated from epidemiologic data. However, because YLL cannot be estimated for any individual from epidemiologic data, it is not possible to determine the correct apportionment of the total YLL among those exposed (Robins and Greenland, 1991).
Apportioning compensation among exposed individuals would still require a policy decision based on unverifiable, but—one hopes—realistic, assumptions. Because mortality is not as relevant for veterans’ compensation as illness and disability, the above scenario can use YLD and DALYs instead.
Applying Concepts of Sensitivity and Specificity to Compensation Schemes
Criteria for determining compensation make both explicit and implicit assumptions. One set of assumptions involves sensitivity and specificity (see Chapter 6). Sensitivity in this context is the probability that someone whose condition (or disease) was caused by a specific exposure is identified as such. Specificity is the probability that someone whose condition (or disease) was caused by something other than the specific exposure is identified as such. Typically when one improves sensitivity, specificity deteriorates, and vice versa. By trying to provide compensation for everyone whose condition was caused by the exposure, we typically increase the likelihood of mistakenly compensating some whose condition was not caused by the exposure. Conversely, in trying to exclude from compensation those who do not warrant it, we increase the chance of excluding those whose disease was in fact caused by exposure.
It is difficult to maximize both sensitivity and specificity. Optimizing one or the other means making some kind of mistake: either we optimize sensitivity by compensating some whose disease was not caused by exposure or we optimize specificity by failing to compensate some whose disease was caused by exposure.
The closely related concepts of true positive (TP) and false positive (FP), and true negative (TN) and false negative (FN), describe making the right and the wrong decisions (Table 9-3). True positives are those correctly identified by some criteria. False positives are those mistakenly identified by the criteria. False negatives are those not identified by the criteria, but who should have been. True negatives are those who were correctly not identified by the criteria.
Sensitivity is TP/(TP + FN)—the proportion of those whose condition was in fact caused by the exposure (TP + FN) who are correctly identified
TABLE 9-3 True and False Positive and Negative Rates
|
|
|
Disease Caused by Exposure |
|
|
Yes |
No |
||
|
Compensation criteria |
Met |
TP |
FP |
|
Not met |
FN |
TN |
|
as such (TP). Specificity is TN/(TN + FP)—the proportion of those whose condition was in fact not caused by the exposure (TN + FP) who are correctly identified as such (TN).
The positive predictive value (PPV) and negative predictive value (NPV) are important related concepts that are also defined from Table 9-3. The PPV is the proportion of those who meet the criteria whose condition was caused by the exposure, namely, PPV = TP/(TP + FP). The NPV is the proportion of those who do not meet the criteria whose condition was not caused by the exposure, namely, NPV = TN/(TN + FN).
A hypothetical example using two alternative criteria for compensation will be used to help clarify these concepts. Consider a disease, D, caused by an exposure, E, and service in a theater, T, the only theater in which exposure to E was known to have occurred. First, criteria that would provide compensation to all veterans who are eventually diagnosed with D and who served in T, and who would therefore have potentially been exposed to E, are very sensitive criteria (Criteria A in Table 9-4). No veteran whose disease D was caused by exposure to E would be missed by using these criteria (i.e., sensitivity is excellent). However, because we have elected to make sure that all veterans whose disease D was caused by exposure to E are compensated, we likely mistakenly also compensate those individuals whose disease D had another cause (i.e., specificity is poor). The use of criteria in this case to make certain that everyone in whom the disease was caused by exposure to E is compensated results in compensating many with the disease in whom it was not caused by E.
In contrast, criteria that would provide compensation only to veterans with the disease D who, for example, also had documented exposure to E for a specified period of time and of a specified intensity, and who also were diagnosed with D within a specified number of years of their first exposure, would be very “specific” criteria (Criteria B in Table 9-4). One can be more certain that if any group of veterans got D from exposure to E, those who were provided compensation by these criteria would be most likely to
TABLE 9-4 Comparing Sensitivity and Specificity of Two Hypothetical Sets of Compensation Criteria
|
|
|
Specificity |
|||
|
excellent |
good |
some |
poor |
||
|
Sensitivity |
excellent |
|
|
|
Criteria A |
|
good |
|
|
|
|
|
|
some |
Criteria B |
|
|
|
|
|
poor |
|
|
|
|
|
belong to that group (i.e., specificity is excellent). However, these specific criteria could potentially result in not providing compensation to some of those in whom D was in fact caused by E (i.e., sensitivity is compromised). The use of specific criteria increases the likelihood of denying compensation to some whose disease was in fact caused by E.
Sensitivity and specificity are not affected by the AF (the proportion of those with the condition whose condition was caused by the exposure). However, PPV and NPV are strongly influenced by the AF. Because the PPV indicates what fraction (or percentage) of veterans compensated for a condition actually had their disease caused by the exposure, varying the AF will change the likelihood that those compensated will have had their disease caused by the exposure. The following tables illustrate how this works. It is assumed that the compensation criteria have fixed excellent sensitivity (0.90) and relatively poor specificity (0.20)—a realistic scenario. What happens when the AF is allowed to vary? In Table 9-5, we begin with a hypothetical scenario in which half of the veterans with the disease will have gotten it as a result of the exposure (AF = 0.50). Here the PPV is 9,000/17,000 = 0.53, or 53 percent of those who are compensated will have had the disease caused by the exposure.
In Table 9-6, a lower and in some instances a more realistic AF of 0.09 is assumed, produced here by decreasing the number of those whose disease was caused by the exposure 10-fold. Here the PPV is 900/8,900 = 0.10, which means only 10 percent of those compensated will have it caused
TABLE 9-5 Hypothetical Scenario 1: PPV When AF = 50 Percent
|
|
|
Disease Caused by Exposure |
Total |
|
|
Yes |
No |
|||
|
Compensation criteria |
Met |
9,000 |
8,000 |
17,000 |
|
Not met |
1,000 |
2,000 |
3,000 |
|
|
Total |
10,000 |
10,000 |
20,000 |
|
TABLE 9-6 Hypothetical Scenario 2: PPV When AF = 9 Percent
|
|
|
Disease Caused by Exposure |
Total |
|
|
Yes |
No |
|||
|
Compensation criteria |
Met |
900 |
8,000 |
8,900 |
|
Not met |
100 |
2,000 |
2,100 |
|
|
Total |
1,000 |
10,000 |
11,000 |
|
by the exposure, but 90 percent will have been compensated without the exposure having played a role. If the AF is even lower, say 0.02 (2 percent), then PPV falls to 0.02 and only 2 percent of those compensated will actually have had it caused by exposure while 98 percent will have been compensated without the exposure having contributed (Table 9-7).
The definition of exposure as used in these calculations plays a large role in determining whether the AF is large or small. For example, if exposure is defined precisely based on documented exposure to a specific agent, then a larger AF may be realistic. However, if a nonspecific exposure is used, such as presence in a given theater where relevant exposure to the agent is relatively uncommon, then the AF might be expected to be very small, meaning that the proportion of disease caused merely by being in a given theater would often most likely be small. As discussed above, while the AF can clearly vary depending on level of exposure, in this case, it is the definition of exposure that strongly influences the AF.
The Receiver Operator Characteristics Curve
A more flexible and informative way of displaying these concepts is by the use of the receiver operator characteristics (ROC) curve (Obuchowski, 2003). An ROC curve (Figure 9-1) can display similar features as Table 9-4, but allows sensitivity (the proportion of true positives) and specificity (in this case reflected by the proportion of false positives [1 – specificity]) to be expressed on a continuous scale. The straight line of identity indicates combinations of sensitivity and specificity for criteria that do no better than chance in distinguishing those with disease caused by the exposure from those with disease not caused by exposure; the ability of criteria along this line to distinguish the two is no greater than that of tossing a coin.
Points on curved lines that are displaced upwards and to the left of the line of identity indicate combinations of sensitivity and specificity corresponding to specific criteria (cut points) that perform better than chance. Points on a line are generated using different criteria and produce an empirical ROC curve. The resulting curve illustrates how sensitivity and the
TABLE 9-7 Hypothetical Scenario 3: PPV When AF = 2 Percent
|
|
|
Disease Caused by Exposure |
Total |
|
|
Yes |
No |
|||
|
Compensation criteria |
Met |
180 |
8,000 |
8,180 |
|
Not met |
20 |
2,000 |
2,020 |
|
|
Total |
200 |
10,000 |
10,200 |
|
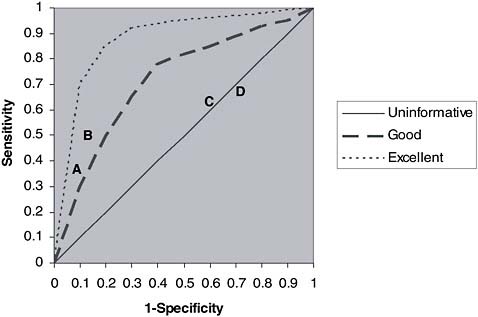
FIGURE 9-1 Example of ROC curves.
NOTE: Example of ROC curves. Different individual compensation criteria (A and B, and C and D) are displayed for different sets of criteria (dashed and dotted lines).
specificity vary together for different criteria. Each curved line corresponds to a different set of criteria for which varying the criteria within each set corresponds to different points along the line. Those curves displaced further upwards to the left than curves with lesser degrees of displacement generally perform better in distinguishing those with disease caused by exposure from those in which it was not caused by exposure. The point at the extreme upper left corner indicates largely unachievable criteria in which there is both perfect sensitivity and specificity—all those whose disease was caused by exposure receive compensation and none of those whose disease was not caused by the exposure receive compensation. The relevant advantages of an ROC curve over the table presented above are that the ROC curve (1) displays all possible criteria, (2) displays the relationship between sensitivity and specificity for different criteria, and (3) allows the performance of different sets of criteria (curves) to be directly compared.
The hypothetical example of disease D and exposure E can also serve to attempt to make ROC curve concepts clearer. A set of criteria were presented above in which compensation was provided only to veterans who developed D with documented exposure to E for a specified period
of time and of a specified intensity, and who also were diagnosed with D within a specified number of years of their first exposure. Using this set of criteria, alternative specific criteria can be considered. Criteria that favor specificity (A, Figure 9-1) might require cumulative exposure to E of at least 3 months of direct dermal or inhalational exposure and diagnosis of D within 10 years of first exposure (i.e., a latency of diagnosis of less than 10 years). Alternative criteria (B) that favored sensitivity might only require 1 week of direct dermal or inhalational exposure to E, with the same latency requirement. Each of these criteria would correspond to a specific point on an ROC curve, with corresponding sensitivity and specificity.
Another set of criteria could be considered that only uses information on exposure E, for example, but did not incorporate information on latency of diagnosis of D; this set of criteria would generate a new curve, with points corresponding only to different criteria for exposure. Another curve could be generated that only used information on time in theater T, for example 6 months (C) or 3 months (D), without any attempt to incorporate information either on exposure E or on latency. These criteria would be less specific, but probably more sensitive, than criteria A or B.
A feature shared by the ROC curve, and sensitivity and specificity, since the ROC curve simply displays sensitivity and specificity, is that there is no allowance for graded decisions. Compensation does not necessarily need to be an either-or decision, but instead could incorporate a mechanism (see below) that allows degrees of compensation. Sensitivity and specificity, and therefore the ROC curve, cannot accommodate such decisions.
In the earlier discussion pertaining to the AF and compensation (“A Traditional Approach Using the PC” in which PC terminology was used in place of AF terminology) it was noted that the level of the AF can be used to determine compensation. Note that selection of a specific AF for this purpose necessarily implies some sensitivity and specificity. Selection of a large AF would be less sensitive but more specific (i.e., with the more stringent criteria entailed by a larger AF, more people whose disease was caused by the exposure would not be compensated, but those compensated would be less likely to have had their disease caused by something besides the exposure), while a small AF would be more sensitive, but less specific.
Valuing Sensitivity or Specificity
Another feature of ROC curves, as was also noted above in discussing sensitivity and specificity, is that they are not affected by the proportion of a disease caused by the exposure (i.e., the AF) and therefore do not directly incorporate information on PPV and NPV. However, consideration of the AF can inform deliberations as to which criteria along an ROC curve are better than others. Specifically, the ROC curve does not tell us whether
we should place more value on improving sensitivity at the expense of specificity, or vice versa. The AF, by identifying the proportion of those with the disease that is caused by the exposure and thereby allowing us to calculate PPV, provides information that allows us to quantify the mistakes entailed in using different criteria.
The value (or cost) placed on these mistakes will play an important part in determining which mistake is least (or more) tolerable, and therefore whether it is better to optimize sensitivity or specificity. One could argue, using an analogy from the battlefield, that it is intolerable to think of leaving any wounded behind on the battlefield. In the compensation context, this sentiment might translate into optimizing sensitivity to make sure that no one whose disease was in fact caused by the exposure was denied compensation, even at the expense of mistakenly providing compensation to many whose disease was not caused by the exposure. Alternatively, if economic concerns were paramount (for example, if there were severe budgetary constraints on the total amount of money available to a compensation program), then it might be better to optimize specificity, making sure that only those whose disease was caused by exposure received compensation, even at the expense of mistakenly not providing compensation to some whose disease was in fact caused by the exposure.
Options for compensation criteria lie on the spectrum that ranges from complete sensitivity (top right corner of the ROC curve) to complete specificity (bottom left corner). Obviously, there is no universally correct choice from among the options along this spectrum. However, whether this is done explicitly, or whether this is merely implicit in the decisions (which is normally the case), a compensation policy chooses some combination of sensitivity and specificity. Typically such decisions favor one over the other. In the case of a common disease or illness, if there is a fixed budget available for compensation, then use of very sensitive criteria, such as motivated by the battlefield analogy, might result in many receiving only a small amount of compensation. If the budget is not fixed, use of very sensitive criteria would result in the total amount of compensation paid out becoming exceedingly large. These issues are further developed in the following section.
Developing a Basis for Compensation Based on AF
In earlier sections of this chapter, we discussed the properties of the AF, its underlying assumptions, and its inherent limitations. Here we discuss a critique of AF as a tool for determining compensation and propose justifications for its continued use in the context of veterans’ compensation. We also explore options for the application of AF for this purpose.
Promoting the Use of AFs in Determining Compensation for Veterans
In the 1980s, Cox published an important critique of using epidemiologic data based on groups (and therefore the AF that is derived from these data) to draw conclusions about individuals, as is done in compensation settings (Cox, 1984, 1987). This theme was extended in a series of papers published from 1988 to 2004 by Robins and Greenland in which they developed their own critique of using probability of causation, and by implication, AF, as a basis for compensation or liability (Greenland, 1999; Greenland and Robins, 1988, 2000; Robins, 2004; Robins and Greenland, 1989a,b, 1991). There are at least three points in their critique that are relevant to the issue of AF and compensation.
First, compensation schemes based on AF alone allow consideration only of whether a disease occurs, not when the disease occurs. Although RRs, and the AFs derived from them, can vary by time in the sense that they can be estimated for different ages and for varying times since exposure, they do not reflect time lost due to disability or death. Those who live with a disease for a longer period of time, or had their life shortened by a longer period of time, presumably deserve more compensation. Approaches that use YLD or YLL (or DALYs) reflect when disease occurs and therefore provide an attractive alternative. (It should be recalled that the AF is a component of any calculation of YLD or YLL that tries to estimate the portion due to exposure [Steenland and Armstrong, 2006], and so any limitations inherent to the estimation of the AF itself will also apply to these extensions of the AF.)
Second, with an RR we cannot distinguish a situation where an exposure causes new disease in a few that would otherwise not have occurred from the extreme case where an exposure accelerates the onset of disease that would have occurred anyway in all of the exposed (Robins, 2004). In fact any RR, no matter how little elevated above a no-effect RR of 1.0, is as consistent with the exposure accelerating the onset of disease in all exposed as it is with the exposure causing the disease in the fraction of the exposed represented by the AF. One important implication is that an RR of 2.0 (and hence an AF of 0.5) does not equate to a 50 percent probability that exposure contributed to the disease in either the population or in an individual. That is, an RR of 2.0 does not make it as likely as not that the exposure caused the disease. It is important to understand that the distinction between accelerating the onset of a disease and causing disease that would not have occurred without the exposure is a blurry one. For example, because most men have latent prostate cancer by age 80 (Oh et al., 2003), it is often assumed that all men, if they were to live long enough, will get prostate cancer. Yet we have no hesitation in referring to exposures as potential causes of prostate cancer even though any exposure
would in reality have accelerated the onset in all who got it as a result of the exposure.
Third, when there is heterogeneity in baseline disease risks (i.e., when the risk of disease in the absence of exposure is different for different people, which is the usual situation), the AF does not necessarily equal the average of the probabilities that exposure caused the disease in each individual. This follows from the general principle that a nonlinear function (in this case a ratio) of averages does not in general equal the average of individual nonlinear functions (i.e., individual ratios). In the case here, the ratio of averages is the AF, and the average of ratios is the average of individual probabilities that exposure caused the disease. The greater the individual differences in the baseline probabilities, the greater the disparity between the AF and the average of individual probabilities.
In light of these compelling arguments, why would the AF continue to be recommended in compensation plans? Part of the answer relates to the features of a given compensation plan. A compensation plan that pays a lump sum to a veteran (or spouse/survivor) in direct proportion to the AF would be open to the criticisms of Robins and Greenland. VA compensation does not work in this way. VA compensation has many features of a compensation plan based on YLD or YLL. For diseases associated with disability only (which is common), monthly VA disability benefits begin when a case is approved for compensation and continue until death. VA compensation therefore accounts for the period of time a veteran lives with a disability.
Further, the amount of each monthly payment is intended to reflect the amount of disability, another feature incorporated in YLD (Steenland and Armstrong, 2006). Even though VA compensation does not directly account for YLL, spouse/survivor benefits for diseases that result in early mortality continue for the lifetime of the spouse/survivor. Thus, if the spouse/survivor outlives the veteran by many years because the veteran’s life was shortened by many years due to the disease, the total payment would reflect this degree of life shortening. Although this might not be true in any individual case (if the spouse/survivor also dies early, for example) VA compensation nonetheless accounts for YLL at least indirectly.
Although we acknowledge the limitations, we also recognize the simplicity and transparency of the AF as a measure of disease burden. As others have deliberated similar issues of AF and assigned shares (NRC, 2000), we accept the utility of the AF as an input to compensation. In the following section we explore ways in which the AF might be applied for VA compensation.
Possible Applications of the AF in Determining Individual Compensation
There are several possible criteria for choosing among compensation plans. We focus here on two: economic rationality and fairness.
An economically rational basis for compensation is one in which the total compensation provided to the population is equal to the total burden of disease caused by exposure in the exposed group (as defined by the AF). Thus, the total compensation given to the exposed group is determined by the total disease burden caused by their exposure. For example, if the AF is 50 percent (and we make the simplifying assumption that half of the cases of disease among the exposed are due to the exposure), then the total economically rational compensation is the amount needed to compensate half of the afflicted persons. Unless the AF were 100 percent (a rare occurrence), the total economically rational compensation is always less than full compensation to every person with the disease.
One problem with the economically rational approach is that it says nothing about how to divide the total fairly among the eligible persons. The “correct” way would be to compensate each person according to his or her particular burden of disease caused by the exposure. We have discussed ways in which better information on exposure or individual susceptibility might improve estimates of individual PC. Ultimately, however, it is almost always impossible to determine which person’s disease was caused by military exposure. This is because most disabilities and diseases have multiple causes, and each exposed person is also exposed to other causes of the condition. Even with perfect research, it is not usually possible to determine which case of the disease was caused by the military exposure and which was not. This is a central feature and problem of compensation for military exposure.
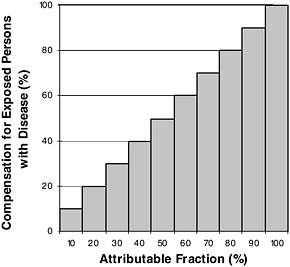
Given this problem, one approach would be to spread the total compensation evenly among all exposed persons who have the disease. For example, if half of the disease cases among the exposed were caused by the exposure (AF = 50 percent), then half compensation could be given to everyone. More generally, under this plan every exposed person with the disease would get a percent of compensation equal to the AF for their disease. This plan is illustrated in Figure 9-2. This approach has been used in class-action suits, but to our knowledge has not been used for military compensation.
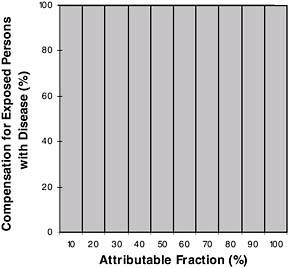
A criticism of this approach is that even if we cannot identify them, we know there are probably some people whose disease was actually caused by their military exposure. Such people get only partial compensation, which can be construed as unfair. The only way to guarantee this never happens is to compensate everyone 100 percent, regardless of the likelihood that their disease was caused by their exposure (Figure 9-3). Such an approach achieves
extremely high sensitivity, but at high cost. This plan is not economically rational, in that it provides more compensation to the exposed population (in some cases, far more compensation) than the total disease burden would justify. It is worth noting that other criteria may legitimately be regarded by policy makers as more important than economic rationality.
The two plans described in Figures 9-2 and 9-3 define the boundaries of practical plans for compensation. The economically rational model provides the minimum rational compensation (Figure 9-2) and the compensation-to-all model provides the maximum possible compensation (Figure 9-3). All remaining plans discussed here fall somewhere between.
One in-between approach would be to establish a level of AF necessary for 100 percent compensation. The usual criterion is 50 percent—that is, the chance that the disease in an exposed person was caused by their exposure is at least 50:50. This approach is shown in Figure 9-4.
A criticism of the “50 percent criterion” is its all-or-none property. Because of uncertainty in the estimate of RR, there is little real difference between an RR of 2.1 and 1.8 (producing AFs of 52 percent and 44 percent), and yet a disease with the first AF might get 100 percent compensation, and a disease with the other might get none. By the criterion of economic rationality, the plan in Figure 9-4 undercompensates persons when the AF is less than 50 percent, and overcompensates them when it is 50 percent or greater.
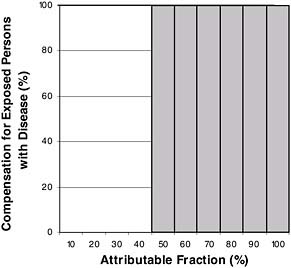
FIGURE 9-4 Complete compensation for all exposed persons only when attributable fraction is 50 percent or more.
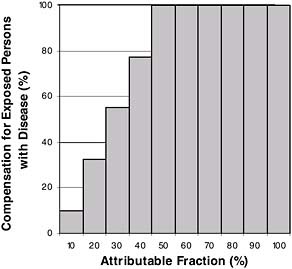
FIGURE 9-5 Complete compensation for an AF of 50 percent or more, plus graduated compensation below 50 percent.
This problem of all or none has been addressed in an alternative compensation scheme. The 1984 NRC Oversight Committee (NRC, 1984) suggested that when the AF was 50 percent or greater, compensation should be 100 percent, and when it is less than 50 percent, it should be linearly scaled down to 10 percent. This is shown in Figure 9-5.
A graded strategy of compensation (such as Figure 9-5), is more fair than an arbitrary cutoff of 50 percent and comes closer to achieving economic rationality—although at any given AF, it still provides total payouts much larger than the total burden of disease.
In the past, there has been a policy not to compensate individuals at levels less than 10 percent. Such a threshold would be relevant if any these models generated estimated compensations under 10 percent.
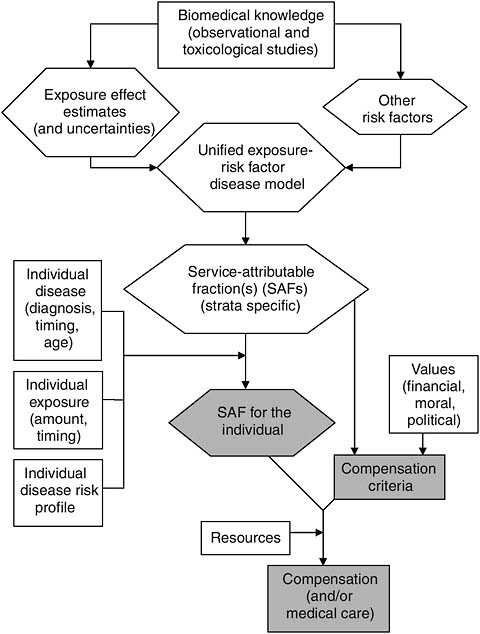
INTEGRATIVE SYNTHESIS: ROLES FOR PRESUMPTIONS
In this chapter the factors that can serve as information inputs to the decision-making process underlying the determination of veterans’ compensation have been identified and discussed. These factors and the point(s) in the process at which they come into play are displayed in Figure 9-6. Additional inputs to the compensation process that are not strictly informational in nature are also displayed. These consist of ethical, political, and economic considerations that in practice can be critical determinants of the
outcome of the process, but do not lend themselves to the type of exploration that has been undertaken in this chapter.
A Rational Compensation Determination Process
The compensation determination process for veterans displayed in Figure 9-6 is, we argue, a scientifically based and rational scheme, albeit necessarily somewhat idealized for most situations. Scientific findings here form the foundation for compensation. These scientific findings are more typically observational in nature, although toxicological or other experimental findings, depending on the specific exposure or disease, can either complement the observational findings or occasionally comprise the bulk of the findings. However, to be useful in this scheme, science must provide estimates of exposure effect that can be used to derive estimated AFs, and such effect estimates are best derived from observational data. Measures of uncertainty in the effect estimates could potentially play a role in some compensation schemes, although we have not here presented applications of how this might work. Toxicological findings, or the lack of them, could be reflected in the measures of uncertainty.
The size of effect estimates are affected by the extent of exposure and, by definition, effect modifiers. These, then, also affect the SAFs. Moreover, as we have seen, the SAF can be affected by how other risk factors interact with the exposure in causing disease, being affected not at all if they interact multiplicatively, but potentially dramatically if they interact additively (see Table 9-2 and corresponding discussion). To make use of these influences on the AF in the compensation process, science must not only provide information on how exposure and effect modifiers influence effect estimates, but also provide information on the form of interactive effects of other disease risk factors.
Armed with a host of exposure SAFs that correspond to levels (strata) of exposure, to states (strata) of the modifying factors, and to states of other risk factors if their interactions with the exposure are other than additive, individual SAFs can be estimated. Assuming that this information on exposure and these factors are also available for a given veteran seeking compensation, a corresponding SAF can be assigned to the veteran in lieu of our ability to know any individual’s PC.
A compensation scheme for a specific exposure-disease combination that is economically rational (i.e., one that provides a total award reflecting the total disease burden of the exposed group) is formulated. A compensation scheme can potentially incorporate features relating to the certainty of the scientific information that is used in estimating the SAF, although we have not provided examples as to how this might be done. Criteria that define who is eligible for some form of compensation
implicitly assume some sensitivity and specificity, and for the population of concern, corresponding false positive and false negative rates. The AF, as shown above (Tables 9-5 to 9-7), has a great impact on both of these rates for a fixed sensitivity and specificity, and therefore could influence the selection of compensation criteria apart from its role in determining the individual SAF. Because of the trade-offs involved in choosing one set of criteria over another, the choice will always entail invoking values of some sort, for example, ethical, political, or financial (i.e., resource) values.
For many cases, including those involving veterans, this version of a compensation process may seem farfetched. It is unlikely that any single instance involving determination of compensation for veterans has features that look exactly like this. Nevertheless, it is instructive to consider how individual processes differ from this version. First, by identifying how actual cases differ from this framework, insight can be gained into some not so obvious assumptions that have been made in these cases. Second, this framework might help pinpoint or clarify the critical influences on any given compensation process. Finally, this framework can serve to identify information needs that, if met, would improve the specific presumptive disability decision-making process.
One way of viewing presumptions is as compromises necessitated by either poor or absent information on one or several of the inputs to the veterans’ compensation determination process. For example, absent information on exposures of Service members in a specific theater, a presumption could be used to make the determination that any Service member who served in that theater was exposed. As another example, epidemiologic and other evidence about the association between a specific exposure and disease may be inadequate for estimating the AF. A presumption could be used to determine that any veteran with the disease who had been exposed most likely had the disease caused by the exposure. Or, there may be no information on how risk factors other than the exposure of interest influence the risk of disease, or how timing of disease occurrence influences the likelihood that the exposure was relevant. Even if this information existed, there may be no reliable way of obtaining this information for a veteran. A presumption might be used to determine that all exposed veterans, regardless of gender, age, the time since exposure, or exposure to other suspected disease risk factors, have the same AF.
Some Case Studies Revisited
It is instructive to again examine some of the case studies in light of this view of presumptions, and to assess characteristics of presumptions pertaining to sensitivity and specificity, and positive and negative predictive
value. The contrasting cases of Agent Orange and type 2 diabetes and of radiation and lung cancer will be used for this purpose.
With Agent Orange and type 2 diabetes, much of the information needed to apply our proposed process is unavailable or of poor quality (see Agent Orange and type 2 diabetes case study in Appendix I). First, scientific information that can be used to estimate an SAF indicates that the SAF is small, at best, and uncertain. Consequently, it is difficult based on this information to provide meaningful SAFs that correspond to different levels of exposure, or SAFs that correspond to different strata of possible modifying factors. There is information on the effect of several diabetes risk factors, but none is available on how any of these interact with Agent Orange exposure to influence diabetes risk.
Assuming that meaningful SAFs could be estimated, information about the veteran to make use of the SAFs is needed. First, information on exposure to Agent Orange is needed, including first and foremost whether exposure occurred, and the intensity and duration of exposure. Although there has been little attempt to make use of possible sources of exposure information for Agent Orange in Vietnam veterans for the purpose of compensation, attempting to characterize exposure based on current information will nevertheless be difficult. Information on the time of onset of diabetes, the certainty of diagnosis, and diabetes risk factors, while not perfect, is comparatively good.
Compensation schemes for Agent Orange and type 2 diabetes could take several forms, any of which might require some type of presumptions. We assume that the scientific findings indicate that exposure to constituents of Agent Orange causes type 2 diabetes, with some degree of certainty. With the SAF being small, even among those with well-documented exposure, the total disease burden is relatively small. This is true whether total disease burden is estimated directly from the SAF or using the SAF to modify a YLD or DALY. For compensation to be economically rational, the total compensation award to the veterans affected would then also be relatively small. Alternatively, if the overall cost of compensation for Agent Orange and type 2 diabetes is not relevant, then economic rationality is also not pertinent. With a small SAF, it is also likely that the proportion of those who would receive compensation under any scheme whose diabetes was actually caused by Agent Orange exposure would also be small (i.e., the false positive rate would be high). With crude measures of exposure that would include large numbers of veterans without the degree of exposure needed to cause disease, the SAF would be smaller still, with a correspondingly high proportion mistakenly compensated.
Any available information on the above inputs to the compensation process could restrict the scope of presumptions needed for Agent Orange and type 2 diabetes. Clearly the use of some information on exposure to
Agent Orange would reduce the effect on reduction of the SAF caused by including unexposed veterans. In the absence of better scientific information on Agent Orange exposure and type 2 diabetes, it will not be possible to utilize veteran information on potential modifying factors such as age of exposure, age of disease onset, or latency period to provide strata of SAF, although assumptions might have a role. For example, a hypothetical case could be made to limit the number of years allowable between exposure to Agent Orange and onset of diabetes. Regarding the presence of other diabetes risk factors that modify baseline risk, in the absence of good information on the form of interactions with Agent Orange, an assumption of additivity of risks might be made that could make it possible to provide stratified SAFs. A later age of diabetes onset in this case, for example, would increase baseline risk and reduce the SAF.
The current presumption for Agent Orange and type 2 diabetes has implicit assumptions as to sensitivity and specificity. With a presumption that requires service in Vietnam and diagnosed type 2 diabetes, sensitivity, TP/(TP + FN), is nearly 1.0 as there are essentially no FNs. That is, any Vietnam veteran who got diabetes from Agent Orange exposure will receive compensation. On the other hand, specificity, TN/(TN + FP), is 0 since there are no TNs. That is, no Vietnam veterans whose diabetes was caused by something other than Agent Orange will not be compensated. The positive predictive value of compensation, TP/(TP + FP) is very small because FP is exceedingly large due to the small SAF. That is, only a small fraction of those who receive compensation will actually have had their diabetes caused by exposure. The negative predictive value, TN/(TN + FN), is almost meaningless because both TN and FN are essentially nonexistent. These characteristics of this particular presumption are therefore quite extreme.
The case of radiation and lung cancer presents distinct contrasts to that of Agent Orange and type 2 diabetes. As detailed earlier (see radiation case study in Appendix I), here the case for causation is strong, uncertainty is relatively well estimated, and there is extensive information on dose-response relationships. Information on the effects of other factors, principally smoking and age, is also relatively extensive. However, even in this case there are deficiencies in the state of the information that invite presumptions. These deficiencies include (1) poor individual person-dose estimation; and (2) inadequate information on the form of the radiation interaction model for other risk factors, again principally smoking.
Based on the above information it is clear that the estimated SAF is relatively large for radiation and lung cancer and has less associated uncertainty than most exposures. As noted before, the radioepidemiological tables (NIH, 1985) provide estimated PCs for radiation in lung cancer by exposure dose, age at exposure and at cancer diagnosis, latency, and cigarette smoking history. However, there is little agreement on the form of the
radiation-smoking interaction in lung cancer, with initial evidence favoring additive effects and more recent interpretations favoring multiplicative (or submultiplicative) effects (see radiation case study in Appendix I). Because the form of the interaction has a large impact on estimation of the SAF, uncertainty about the form complicates use of an SAF even for lung cancer (see discussion on effects on the positive predictive value below).
The current presumption for radiation and lung cancer also has implicit assumptions as to sensitivity and specificity. Sensitivity, TP/(TP + FN), is good as there will only be a few FNs. That is, most radiation-exposed veterans who get lung cancer from radiation exposure will receive compensation, at least when based on a presumption of exposure. Specificity, TN/(TN + FP) is also good because those with low radiation risk, such as those with low estimated exposure, are less likely to receive compensation, although because of inaccuracies in the estimated exposure, some will (these will be FPs). The positive predictive value of compensation, TP/(TP + FP), is very good because FPs are relatively uncommon because of the large AF. That is, a large fraction of those who receive compensation will actually have had their lung cancer caused by exposure. The negative predictive value, TN/(TN + FN), is also very good because FNs are relatively uncommon. These characteristics of this particular presumption therefore seem to be reasonable.
However, even for the case of radiation and lung cancer, the above assessment of these characteristics is dependent on the way other disease risk factors, for example smoking, are determined to interact with the effect of radiation. For nonsmokers the above assessment is reasonable and does not depend on the form of the interaction. For smokers the assessment varies depending on whether smoking is determined to interact additively or multiplicatively with radiation exposure. With a multiplicative interaction, exposure RR and therefore AF is the same regardless of smoking status. In the additive case, the RR and the AF can vary dramatically by smoking status (see Tables 9-1 and 9-2, above). This will have no effect on sensitivity or specificity, as these are unaffected by the AF. However, positive and negative predictive values will be affected as both change as a function of the AF. Because the AF is substantially smaller in smokers than nonsmokers under an additive model, the positive predictive value is likewise smaller, indicating that for smokers a substantial percentage of those receiving compensation will not have gotten lung cancer as a result of exposure to radiation. The AF (and the PC derived from it) in the radioepidemiological tables is therefore critically dependent on the form of the interaction that is determined to be the case. Therefore, even with better scientific information than is available for any other military exposure, there is still room for presumptions. However, the better the information, the more focused and limited in scope the presumptions can be.
Science and Compensation Presumptions
The inability to identify the disease role of specific military exposures in any individual veteran partly motivates the need for compensation presumptions. The scope of a presumption is, in turn, partly determined by the available scientific information and corresponding information on any given veteran. The more scientific information available on the causal relationship between a service exposure and disease, and the more information available on an individual veteran’s exposure and disease risk, the more narrow in scope the presumption needs be. The contrasting cases of Agent Orange and type 2 diabetes, and radiation and lung cancer, discussed above serve to make these points.
It is likely that there will be substantial advances in our ability to quantify exposure and other disease risks in individual veterans, perhaps through the use of specific biomarkers of exposure or disease for example, and by exploiting findings from toxicogenetics and toxicogenomics. These advances could possibly refine the scope of presumptions or conceivably do away with the need for some presumptions.
Earlier chapters laid out a framework for determining when a compensation presumption may be considered based on the state of scientific information. The intent in this chapter has been to identify concepts and tools that can be utilized in making decisions as to the form and content of a compensation presumption. These include (1) a set of SAFs that is as refined as the science permits; (2) features of alternative presumptions, such as sensitivity, specificity, and positive predictive value, that characterize and quantify the relative strengths and unavoidable mistakes (and therefore costs) implicit in each presumption; and (3) an appreciation of the relationship between the SAFs and some of these features, namely the positive and negative predictive values.
It has not been the intent here to determine whether a specific presumption and its form are justified or sensible or to identify better alternatives. These are issues on which VA and Congress deliberate. It is hoped, however, that the framework outlined can be used in these deliberations to allow for more rational, science-based decisions about the content of specific presumptions than may have been the case in the past.
REFERENCES
Austin, H., Delzell, E., and Cole, P. 1988. Benzene and leukemia: A review of the literature and a risk assessment. American Journal of Epidemiology 127:419-439.
Benichou, J. 2001. A review of adjusted estimators of attributable risk. Statistical Methods in Medical Research 10:195-216.
Bruzzi, P., S. B. Green, D. P. Byar, L. A. Brinton, and C. Schairer. 1985. Estimating the population attributable risk for multiple risk factors using case-control data. American Journal of Epidemiology 122(5):904-914.
Cox, A. T. 1984. Probability of causation and the attributable proportion of risk. Risk Analysis 4(3):221-230.
Cox, A. T. 1987. Statistical issues in the estimation of assigned shares for carcinogenesis liability. Risk Analysis 7(1):71-80.
DHHS (Department of Health and Human Services). 2002. 42 CFR Parts 81 and 82. Guidelines for determining the probability of causation and methods for radiation dose reconstruction under the Employees Occupational Illness Compensation Program Act of 2000; Final Rules. Federal Register 67(85):22296-22330.
Greenland, S. 1999. Relation of probability of causation to relative risk and doubling dose: A methodologic error that has become a social problem. American Journal of Public Health 89:1166-1169.
Greenland, S., and J. M. Robins. 1988. Conceptual problems in the definition and interpretation of attributable fractions. American Journal of Epidemiology 128:1185-1197.
Greenland, S., and J. M. Robins. 2000. Epidemiology, justice and the probability of causation. Jurimetrics 40:321-340.
Lagakos, S. W., and F. Mosteller. 1986. Assigned shares in compensation for radiation-related cancers. Risk Analysis 6(3):345-357.
NCI (National Cancer Institute). 2006. Lung cancer prevention. http://www.cancer.gov/cancertopics/pdq/prevention/lung/Patient/page2 (accessed May 23, 2007).
NIH (National Institutes of Health). 1985. Report of the National Institutes of Health Ad Hoc Working Group to Develop Radioepidemiological Tables. Responding to the congressional mandate under Section 7(b) of the Orphan Drug Act of January 4, 1983 (PL-97-414). NIH Pub. No. 85-2748. Washington, DC: U.S. Government Printing Office.
NIOSH (National Institute of Occupational Safety and Health). 2007. Users guide for the Interactive RadioEpidemiological Program (NIOSH-IREP). Version 5.5.2. http://0-www.cdc.gov.mill1.sjlibrary.org/niosh/ocas/pdfs/irep/irepug0607.pdf (accessed July 28, 2007).
NRC (National Research Council). 1984. Assigned share for radiation as a cause of cancer, review of radioepidemiologic tables assigning probabilities of causation. Washington, DC: National Academy Press.
NRC. 2000. A review of the draft report of the NCI-CDC Working Group to Revise the 1985 Radioepidemiological Tables. Washington, DC: National Academy Press.
Obuchowski, N. A. 2003. Receiver operating characteristic curves and their use in radiology. Radiology 229:3-8.
OEHHA (Office of Environmental Health Hazard Assessment). 2001. Public health goal for benzene in drinking water. California Environmental Protection Agency. http://www.oehha.ca.gov/water/phg/pdf/BenzeneFinPHG.pdf (accessed February 7, 2007).
Oh, W. K., Hurwitz, M., D’Amico, A. V., Richie, J. P., Kantoff, P. W. 2003. Neoplasms of the prostate (Ch. 111). In: Holland-Frei Cancer Medicine 6, 6th ed. Hamilton, ON: BC Decker.
OSTP (Office of Science Technology and Policy). 1988. Use of probability of causation by the Veterans Administration in the adjudication of claims of injury due to exposure to ionizing radiation. OSTP Committee on Interagency Radiation Research and Policy Coordination. Executive Office of the President, Washington, DC.
Presidential Commission. 1990. Ch. 4. Standards and procedures for latent illnesses. Presidential Commission on Catastrophic Nuclear Accidents: Report to Congress. Washington, DC.
Robins, J. 2004. Should compensation schemes be based on the probability of causation or expected years of life lost? Journal of Law and Policy 12:537-548.
Robins, J. M., and S. Greenland. 1989a. Estimability and estimation of excess and etiologic fractions. Statistics and Medicine 8:845-859.
Robins, J., and S. Greenland. 1989b. The probability of causation under a stochastic model for individual risk. Biometrics 45:1125-1138.
Robins, J., and S. Greenland. 1991. Estimability and estimation of expected years of life lost due to a hazardous exposure. Statistics and Medicine 10:79-93.
Rothman, K. J., and S. Greenland. 1998. Modern Epidemiology, 2nd ed. Philadelphia, PA: Lippincott-Raven. Pp. 54-55.
Steenland, K., and B. Armstrong. 2006. An overview of methods for calculating the burden of disease due to specific risk factors. Epidemiology 17(5):512-519.
Thomas, D. C. 2000. The probability of causation can be used in an equitable manner to resolve radiation tort claims and design compensation claims. Radiation Research 154(6):718-719.