1
Study Background
Models have a long and illustrious history as tools for helping to explain scientific phenomena and for predicting outcomes and behavior in settings where empirical observations may not be available. Fundamentally, all models are simplifications. Complex relationships are reduced, some relationships are unknown, and ones perceived to be unimportant are eliminated from consideration to reduce computational difficulties and to increase transparency. Thus, all models face inherent uncertainties because human and natural systems are always more complex and heterogeneous than can be captured in a model.
This report looks at a specific aspect of computational modeling, the use of environmental models in federal regulatory activities, particularly at the U.S. Environmental Protection Agency (EPA). The use of computational models is central to the decision-making process at EPA because it must do prospective analysis of its policies, including projecting impacts into the future. In addition, obtaining a comprehensive set of measured data to support a decision is typically impracticable in terms of time and resources or is technically and ethically impossible. The agency uses model results to augment and assess measured data. The results of models can become the basis for decisions, such as initiating environmental cleanup and regulation. In sum, models help to inform and set priorities in environmental policy development and implementation at EPA through the ability to evaluate alternative regulations, provide a
framework to assess compliance, and summarize available knowledge needed for regulatory decisions.
EARLY ENVIRONMENTAL MODELS
The earliest uses of mathematics to explain the physical world, an important element of environmental models, came in response to the desire to explain and predict the movement of the night sky, the relationship of notes in a musical scale, and other scientific observations (Mahoney 1998; Eagleton 1999; O’Connor and Robertson 2003; Schichl 2004). Later developments of basic conceptual models that helped further the connections of mathematics and modeling to science include the thirteenth century Fibonacci sequences of rabbit population, Paracelsus’s connection of dose to disease in the fifteenth century, and the Copernican model of planetary motions in the sixteenth century. The role that mathematics would play in explaining the physical world is evident in the seventeenth century roots of differential calculus, where physical observations of moving objects led to conceptual models of motion, mathematical representations of motions, and finally predictions of locations (Herrmann 1997).
A large expansion in the use of computational models for understanding environmental science and management came in the nineteenth and early twentieth centuries.1 Mathematical formulations of basic models were developed for many problems, including atmospheric plume motion (Taylor 1915), human dose-response relationship (Crowther 1924), predator-prey relationships (Lotka 1925), and national economy (Tinbergen 1937). An early example of the level of sophistication possible in computational models is Arrhenius’s climate model for assessing the greenhouse effect (Arrhenius 1896). Arrhenius’s model is a seasonal, spatially disaggregated climate model that relies on a numerical solution to a set of differential equations that represent surface energy balance. The numerical computations required months of hand calculations (Weart 2003), similar to many early numerical models. The computa-
tional difficulties associated with such models prompted Lewis Richardson, an early pioneer in the use of computational fluid dynamics in weather modeling, to imagine a “forecast-factory,” having thousands of people performing flow calculations directed by a forecast leader coordinating activities with telegraph and colored lights (Fluent Inc. 2006).
Holmes and Wolman (2001) discussed how other model applications during this same era began to spell out the systems-analysis approach to environmental problems that recognizes the interrelationship of physically disparate elements in the environment and the need to understand these relationships through modeling to develop environmental mitigations. A seminal work for understanding the modeling complexity that developed before the invention of digital computers is the Miami Conservancy District flood control project, planned and constructed from 1914 to 1923 (Morgan 1951; Burgess 1979). This project, under the direction of Arthur Morgan, pioneered the use of complex hydrological, economic, and design optimization models coupled with benefit-cost analysis and expert elicitation to quantitatively assess pre- and post-construction conditions of a complex flood control system (Bock 1918; Woodward 1920; Houk 1921; Engineering Staff of the Miami Conservancy District 1922). Morgan and staff used sophisticated computational and graphical techniques to simulate the operation of their flood control design during flood conditions, develop optimizing techniques to increase the project’s efficiency, and perform a detailed economic appraisal of the project’s impact on more than 77,000 individual properties.
TRENDS IN ENVIRONMENTAL REGULATORY MODEL USE
The past 25 years has seen a vast increase in the number, variety, and complexity of computational models available for regulatory purposes at EPA. Models have increased in capabilities and sophistication through advances in computer technology, data availability, developer creativity, and increased understanding of environmental processes. Demand for models expanded as the participants in regulatory processes, Congress, EPA, Office of Management and Budget (OMB), stakeholders, and the general public required improved analysis of environmental issues and the consequences of proposed regulations. Demands also increased as policy makers have attempted to improve the ability of environmental regulatory activities to achieve the desired environmental benefits and reduce implementation costs. Individual histories are com-
plex, and regulatory model use in specific fields is tied to specific regulatory and scientific developments. However, regulatory needs and model capabilities are often not aligned perfectly. Box 1-1 briefly describes the history of ozone air quality modeling, one area with a lengthy modeling and regulatory history, and the uneven interactions between policy and science.
While the demand for models has grown, the conceptualization of what a model is has shifted in recent years, especially among those closest to the modeling process. Models are viewed less as truth-generating machines and much more as tools designed to fulfill specific tasks and purposes (Beck et al. 1997). As tools, models serve in the decision-
|
BOX 1-1 Ozone Modeling and the Irregular Swings Between Policy and Science The formation of ozone in the lower atmosphere (troposphere) is an exceedingly complex chemical process involving the interaction of oxides of nitrogen (NOx), volatile organic compounds (VOCs), sunlight, and dynamic atmospheric processes. The basic chemistry of ozone formation was known in the early 1960s (Leighton 1961). Reduction of ozone concentrations in general requires control of either NOx or VOC emissions or a combination of both. Due to the nonlinearity of atmospheric chemistry, the selection of the emission-control strategy has traditionally relied on air quality models. One of the first attempts to include the complexity of atmospheric ozone chemistry in the decision-making process was a simple observations-based model, the so-called Appendix J curve (36 Fed. Reg. 8186 [1971]) (see Figure 1-1). The curve was based on measurements for six U.S. cities where such data were available. Reliable NOx data were virtually nonexistent at that time. On the basis of the maximum ozone concentrations observed at these cities and their estimated VOC emissions, the curve purported to indicate the percentage of VOC emission reduction required to attain the ozone standard in an urban area as a function of the peak concentration of photochemical oxidants observed in that area. The Appendix J curve was based on the hypothesis that reductions of VOC emissions were the most effective emission-control path, and this conceptual model helped define legislative mandates enacted by Congress that emphasized controlling these emissions. The next step in modeling complexity was the empirical kinetic modeling approach (EKMA) (Dimitriades 1977). EKMA used the improved uncertainty of chemical mechanisms that were under intense development in |
|
the late 1970s and early 1980s (Atkinson and Lloyd 1984) to simulate the airshed of interest, assuming that it is a well-mixed box. The final result of the modeling was three-dimensional plots of ozone concentrations as a function of VOC and NOx emissions (Figure 1-2) that could be used for the design of emission-control strategies. 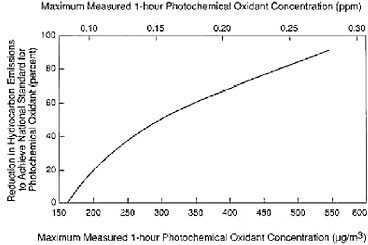 FIGURE 1-1 Appendix J curve. Required hydrocarbon emission control as a function of photochemical oxidant concentration. Source: EPA 1971. 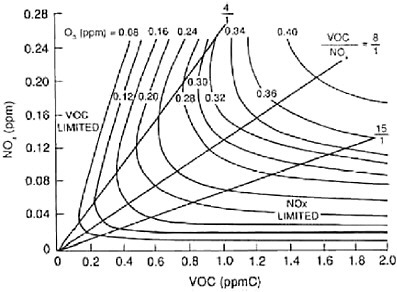 FIGURE 1-2 Typical EKMA diagram. Source: NRC 1991, adapted from Dodge 1977. |
|
The resulting EKMA plots captured the major features and complexities of the NOx, VOC, and ozone system. For example, they suggested that at low VOC and high NOx emissions levels, decreases in VOC emissions will reduce peak ozone concentrations, but decreases in NOx emissions will have the opposite result. Based on the available emissions inventories at the time (1977 to 1982), which turned out to greatly underestimate VOC emissions, many urban areas appeared to be near or above the ridge of the diagram, suggesting that VOC controls were the efficient path. Another characteristic of the EKMA plots is that they suggest that implementation of either VOC or NOx controls alone is practically always preferable to controlling both ozone precursors. The EKMA approach was heavily used for regulatory applications in the late 1970s and 1980s and supported VOC control as the principal path to attain the ozone standard. The development of three-dimensional grid models capable of simulating the dynamics and spatial variability of ozone formation (commonly termed 3D chemical transport models or CTMs) also began in the 1970s, although computational demands prevented their use in regulatory activities. EPA in the mid-1970s had committed its research efforts to supporting the development of the urban airshed model (UAM). At the same time, other models (for example, the CIT model) were developed and used by the scientific community (Reynolds et al. 1973). California played a major role in supporting the development and evaluation of these first CTMs. The emphasis of these models was on comprehensive descriptions of the atmospheric system without adjustable parameters (no calibration). During the 1970s, UAM was used only for the Los Angles basin. In the 1980s, the use of 3D models spread to other major metropolitan areas, and the 1990 Clean Air Act Amendments specifically called for the use of such models for all ozone nonattainment areas. The first applications of UAM in the eastern United States also supported the need for VOC controls. Thus, from the early 1970s to the early 1990s, EPA and Congress, with few exceptions, promoted VOC control as the principal path to attaining the ozone standard (for example, required NOx reductions from motor vehicles). These VOC reductions had little effect on the ozone concentrations. The incomplete and often erroneous VOC inventories used during this period were one of the major reasons for the choice of suboptimal strategies. For example, biogenic VOC emissions were not included in the inventories until the late 1980s. An influential paper by Chameides et al. (1988) found that when biogenic VOC emissions were included in the inventory in Atlanta and the southeastern United States, NOx controls were favorable. Additional field and theoretical studies in California suggested that VOC emissions had been underestimated by a factor of approximately two, in large part because of the underestimation of mobile-source emissions. Furthermore, the increased use of regional ozone models that incorporated |
|
long-range transport of ozone and its precursors also demonstrates the importance of NOx control, especially for regional control of ozone. The debate over a more balanced approach, including control of NOx emissions, reached a head in the NRC report Rethinking the Ozone Problem (NRC 1991; Dennis 2002). The report concluded, “to substantially reduce ozone concentrations in many urban, suburban, and rural areas of the United States, the control of NOx emissions will probably be necessary in addition to, or instead of, the control of VOCs.” An important aspect of this refocused effort was the need for multistate modeling necessary for addressing transport problems. Although it was originally assumed that ozone problems within a given area were largely caused by emissions within that area, by the end of the 1980s, it was clear that some air quality problems had a larger multistate component and that a substantial contribution to an area’s ozone problem could arise from upwind emissions sources. That finding in turn resulted in the formation of multistate organizations, such as the Ozone Transport Commission and Ozone Transport Assessment Group, to develop technical information related to the nature of the transport problem and identify policy options (NRC 2004a). Regional scale modeling is an integral part of understanding the science behind new ambient air quality standards for ozone and fine particulate matter. There has clearly been a long exchange between policy and science regarding regulations for controlling tropospheric ozone. The choice in the 1970s to concentrate on VOC controls was supported by early results from models. While new results regarding the higher than expected biogenic VOC emissions were being gathered in the 1980s, EPA continued on its path of emphasizing VOC controls, in part because the schedule set by Congress and EPA for attainment of ozone ambient air quality standards was not conducive to reflection on the basic elements of the science (Dennis 2002). The shift in the 1990s toward regulatory activities focusing on NOx controls from both large stationary sources and mobile sources (along with some VOC controls) was a correction to the prior policy of focusing almost exclusively on VOC reductions. A further complication in the exchange between policy and science during this history was the realization that historical estimates of emissions and the effectiveness of various control strategies in reducing emissions were not accurate. Thus, part of the reason ozone concentrations have not been reduced as much as hoped for over the past 3 decades has been because emissions of some pollutants were much higher than originally estimated and have not been reduced as much as originally predicted. The results of policy decisions to control NOx takes many years to fully implement, delaying a full understanding of its effectiveness for reducing ozone concentrations. For example, the emissions standards for new on-road diesel engines will not be fully implemented until 2010, and a full fleet turnover will take many years beyond that. While these policies are being implemented, observations of higher weekend ozone when ozone precursor emissions are low (Lawson 2003) and results from an intensive atmospheric observation field cam |
|
paign in the Houston-Galveston, Texas, area, where highly reactive VOCs seem to play a critical role in ozone formation (Daum et al. 2002), provide new complications to the understanding of the effectiveness of VOC versus NOx controls. The long history of the exchange between tropospheric ozone science and modeling and policy demonstrates several critical points. Regulations go forward despite imperfect models and information. The potential harm from environmental hazards can cause regulatory activities to proceed before the science and models are perfected. The long history of controlling VOC and NOx emissions shows that the inability of the models to predict accurately may reflect not only imperfections in the models but also inputs to the models. In the case of ozone modeling, the inputs to the models (emissions inventories in this case) are often more important than the model science (description of atmospheric transport and chemistry in this case) and require as careful an evaluation as the evaluation of the model. These factors point to the potential synergistic role that measurements play in model development and application. Finally, it is clear that there has been an irregular exchange between modeling/science and policy, which Dennis (2002) describes as “a jerky exchange” between the two, where the policy process has been out of sync with the latest science. |
making process as (1) succinctly encoded archivers of contemporary knowledge; (2) interpreters of links between health and environmental harm from environmental releases to motivate the making of a regulatory decision or policy; (3) instruments of analysis and prediction to support the making of a decision or policy; (4) devices for communicating scientific notions to a scientifically lay audience; and (5) exploratory vehicles for discovery of our ignorance. This committee’s task in looking at model use in the regulatory process is 1 and 2, the use of models in understanding environmental impacts and developing and evaluating policy alternatives, that are most prominent. Such analysis of relations and regulatory proposals form the core of regulatory modeling analysis. However, this is not to imply that the other uses of models are not also important for regulatory modeling activities.
It is important to consider why the transition from regarding models as “truth” to regarding models as “tools” might have occurred. Clearly, oversight agencies, such as the OMB, and stakeholders have made an effort to open up the modeling process to external peer review and public scrutiny. As a result, there might be a greater willingness to discuss model shortcomings or at least to disclose them. As regulators become more experienced with the use of models, there might also be a greater appreciation and awareness of the inherent strengths and limitations of
models. Finally, the transition to regarding models as tools might represent a push by modelers to educate decision makers that, although models can play an important role in regulatory analysis, models cannot provide “the answer,” which is often what the regulatory process demands.
MODEL LIMITATIONS AND ASSUMPTIONS
All models are simplifications of the systems or relations they represent. As a result, the spatial and temporal attributes of processes within a model cannot be resolved fully against observations. Chave and Levin (2003) highlight the intractability of this problem, noting that there is no single correct scale at which to study the dynamics of a natural system. At one end of the spectrum, a model might not simulate at a high enough resolution to represent all critical processes or at scales that capture system heterogeneities. At the other end of the spectrum, an extremely detailed model might not capture large-scale features. These limitations produce two types of uncertainties inherent to models (Morgan 2004). One uncertainty is in the values of key parameters, which are uncertain because of a lack of knowledge and a natural variability. The second uncertainty is in the structure of the model itself. Model uncertainty relates to whether the structure of the model fundamentally represents the system or decision of interest.
These limitations and uncertainties contribute to an inability to ever fully validate or verify numerical models of natural systems (Oreskes et al. 1994). Fundamentally, natural systems are never closed, and model results are never unique. Models of natural systems are never complete, and any match between observations and model results might occur because processes not represented in the model canceled each other. The combination of model formulation and parameters that results in a good match between observations and results is never unique because another combination of model formulation and parameters could result in an equally good match.
In addition, all regulatory model applications have assumptions and default parameters incorporated into them, some of which may include science policy judgments (NRC 1994; EPA 2004a). Assumptions and defaults are unavoidable, as there is never a complete data set to develop a model, but they might have a larger impact on modeling results. Models are commonly used to predict values into the future or under different environmental conditions for which the models were developed, so the
assumptions and defaults are subject to debate. Further, the policy settings for regulatory models are framed by more than scientific, technological, and economic ones. Factors related to public values and social and political considerations enter into the modeling process and influence modeling assumptions and defaults.
Although these fundamental uncertainties and limitations are critical to understand when using environmental regulatory models, they do not constitute reasons why modeling should not be performed. When done in a manner that makes effective use of existing science and in a way understandable to stakeholders and the public, models can be very effective for assessing and choosing amongst environmental regulatory activities and communicating with decision makers and the public.
Finally, model results and the observations used to evaluate those results may be at different temporal and/or spatial scales, making it difficult to compare model estimates to actual conditions. For examples, models of climate change, regional groundwater contaminant transport, or human health impacts may make estimates for time scales where observations are not available. Other models, such as air and water quality models, may produce average pollutant concentrations for a wide spatial extent (a grid cell within the model) whereas observations may be available only at a single point within that grid cell.
ORIGIN OF STUDY AND CHARGE TO COMMITTEE
Since the 1980s, EPA recognized the need for agency-wide guidance on the use and development of models, including general model evaluation protocols to test and confirm the accuracy of models. The EPA’s Science Advisory Board (SAB), which provides independent scientific and engineering advice to the agency, first issued general guidance on model review in 1989 and recommended that a model’s predictive capability could be enhanced through: (1) obtaining external stakeholder input; (2) documenting the model’s explicit and implicit assumptions; (3) performing sensitivity analyses; (4) testing model predictions against laboratory and field data; and (5) conducting peer reviews. In 1994 the Report on the Agency Task Force on Environmental Regulatory Modeling—Guidance, Support Needs, Draft Criteria, and Charter (EPA 1994a) included guidance for conducting external peer review of models. Other guidance from EPA has come from its Science Policy Council’s Peer Review Handbook (EPA 2006a) and its National
Center for Environmental Assessment’s Guidelines for Exposure Assessment (EPA 1992), Guidelines for Ecological Risk Assessment (EPA 1998), and Guidelines for Carcinogenic Risk Assessment (EPA 2005a).
Despite these efforts to establish and follow appropriate standards, EPA models have become part of the controversies over environmental decision making. At times, Congress has examined models and model results during public hearings, sponsored external reviews of models, or directed EPA to perform a particular analysis (for example, Hearings before the Subcommittee on Oversight and Investigations of the Committee on Commerce, 104th Cong., 1st Sess. 16 [1995]; GAO 1996; NRC 2000, 2001a; EPA 2001a). In addition, models and their results can be prominent in the litigation that results from environmental regulatory activities. EPA has had several environmental regulations overturned because, in the opinion of the courts, the model was considered to be so inaccurate that the regulation was deemed “arbitrary and capricious.” McGarity and Wagner (2003) document instances where courts have ruled against the agency because EPA had not sufficiently explained model simplifications, justified the application of a generic model to a specific location, or justified the application of a model to new activities or conditions not originally envisioned when the model was developed. On the other hand, courts have sometimes upheld EPA regulations by ruling in part that EPA’s modeling adequately supported their position. In a recent example, the DC Circuit Court of Appeals substantially upheld EPA proposed regulations on “upwind” nitrogen oxides emissions for urban ozone control in part by ruling that the agency’s modeling was sufficient to support the determination as to which states should be regulated (D.C. Circuit Court of Appeals, Appalachian Power Co. v. EPA; May 2001).
More recently, the executive branch has been interested in the quality of information produced by government agencies, including EPA. The Office of Management and Budget recently issued guidelines calling for each regulatory agency to develop its own guidance to ensure the quality, objectivity, utility, and integrity of information (OMB 2001). Recognizing the critical roles that models have in developing information, EPA issued information-quality guidelines that include guidance to ensure that the models used in regulatory proceedings be objective, transparent, and reproducible (EPA 2002a). OMB has also issued guidance on peer review (OMB 2004), which EPA has incorporated into its evaluation of models (EPA 2006a).
To help support modeling activities across the agency, EPA established the Council for Regulatory Environmental Modeling (CREM) in 2000. CREM was established to promote consistency and consensus within the agency on mathematical modeling issues, including modeling guidance, development, and application, and to enhance both internal and external communications on modeling activities. CREM is now focused on helping to generate information to determine whether a model and its analytical results are of a quality sufficient to serve as the basis for a decision (Foley 2004). Specifically, the EPA administrator, tasked CREM with developing a guidance document on the development, assessment and use of environmental models; making publicly accessible an inventory of EPA’s most frequently used models; consulting with stakeholders concerning modeling issues; holding regional workshops; and engaging with the National Academy of Sciences to produce a report on the use of environmental and human health models for decision making (EPA 2003a). This report is the response to the last charge. Recognizing the importance of EPA regulatory models in their activities, the U.S. Department of Transportation also participated in this study through additional funding and presentations to the committee.
In 2005, the National Research Council (NRC) established the Committee on Models in the Regulatory Decision Process. The Statement of Task set forth to the committee is as follows:
A National Research Council committee will assess evolving scientific and technical issues related to the selection and use of computational and statistical models in decision-making processes at EPA. The committee will provide advice concerning the development of guidelines and a vision for the selection and use of models at the agency. Through public workshops and other means, the committee will consider cross-discipline issues related to model use, performance evaluation, peer review, uncertainty, and quality assurance/quality control. The committee will assess scientific and technical criteria that should be considered in deciding whether a model and its results could serve as a reasonable basis for environmental regulatory activities. It will also use case examples of EPA’s model development, evaluation, and application practices to further elucidate guiding principles. The objective of the committee will be to provide a report that will serve as a fundamental guide for the selection and use of models in the regulatory process at EPA—the goal is to produce a report on models similar to the NRC’s 1983 “Red
Book” on risk assessment (NRC 1983). As part of its scientific assessment, the committee will need to carefully consider the realities of EPA’s regulatory mission so as to provide practical advice on model development and use. The report will avoid an overly prescriptive and stringent set of guidelines and will recognize the need for regulatory and policy decisions in the face of incomplete information and uncertainty. In particular, the committee will not attempt to define a numerical standard for accuracy that all models must attain before they can be used in the decision-making process.
The task statement asks the committee to address the following specific issues:
-
What scientific and technical factors should be considered in developing model acceptability and application criteria that address the needs of EPA, as well as those of interested and affected parties?
-
How can the agency provide guidance on procedures for appropriate use, peer review, and evaluation of models that is applicable across the range of interdisciplinary regulatory activities undertaken by EPA?
-
How can issues related to input data quality, model sensitivity, uncertainty, and the use of model outputs be addressed in a unified manner across the multiple disciplines that encompass modeling at EPA?
-
Models developed outside of the agency must meet the same acceptability and application criteria as models developed within EPA. How can users of proprietary models meet acceptability and application criteria for the use of models in environmental regulatory applications while maintaining the possible proprietary nature of the code?
-
Are there unique evaluation issues associated with different categories of models, such as statistical dose-response models based on epidemiological data?
-
How can models be improved in an adaptive management process to allow simpler tools and models to be used now while having the flexibility to incorporate new data, scientific advances, and advances in modeling in the future?
-
How can uncertainties and limitations of models be effectively communicated to policy makers and others who are not
-
experts in the details of the models? How should secondary uses of models be treated, including communication of model uncertainties and limitations?
-
What are the emerging scientific and technological advances that may affect the selection and use of models? Specifically, what are the emerging sources of data (such as remote sensing and other spatially resolved environmental data, and genomic/proteomic data) and developments in information technology for which EPA will need to prepare?
COMMITTEE APPROACH TO THE CHARGE
The task statement and the interpretation of the task by the committee required it to review and provide recommendations for a wide array of regulatory modeling activities at EPA. The committee is composed of members from many disciplines. Thus, the committee’s expertise and the study charge have led it to provide broad recommendations on guidance and principles for improving the general field of regulatory environmental modeling. When individual modeling efforts are examined in the report, it is for illustrative purposes with respect to the study charge. The committee’s approach begins with several fundamental definitions.
Basic Definitions
The committee’s charge calls for the study to focus on environmental regulatory models. This is clearly a subset of all models used in science, policy making, and elsewhere. To help differentiate environmental regulatory models from other models, the committee defines four basic terms: model, conceptual model, computational model, and environmental regulatory model.
Recognizing the wide usage of the term in academia, policy making, and elsewhere, the committee defines a model as
a simplification of reality that is constructed to gain insights into select attributes of a particular physical, biological, economic, or social system. Models can be of many different forms. They can be computational. Computational models include those that express the relationships among components of a system using mathemati-
cal relationships. They can be physical, such as models built to analyze effects of hydrodynamic or aeronautical conditions or to represent landscape topography. They can be empirical, such as statistical models used to relate chemical properties to molecular structures or human dose to health responses. Models also can be analogs, such as when nonhuman species are used to estimate health effects on humans. And they can be conceptual, such as a flow diagram of a natural system showing relationships and flows amongst individual components in the environment, a business model that broadly shows the operations and organization of a business, or a model that includes the relationships among both natural and economic components. The above definitions are not mutually exclusive. For example, a computational model may be developed from conceptual and physical models and an animal analog model can be the basis for an empirical model of human health impacts.
Although models range widely in terms of how they are constructed, models share the common objective of aiding in the understanding of a complex and poorly accessible physical, biological, economic, or social system. Figure 1-3 shows one type of model, a physical model for representing planetary motions. Models help generate information to better understand the relationship among components in a system, to extrapolate the behavior of a system to alternate designs, or to projected future conditions. Figure 1-4 shows a second type of model, an analog model where a white mouse is used as analog for estimating human health impacts. This figure also shows one of the issues that arise from using such a model, the need to extrapolate from the range of exposures for a mouse down to the range of exposures for humans. Although the question of whether a mouse is an appropriate analog model for estimating human health impacts is not part of this study, issues related to the statistical models that are used to extrapolate from mice to humans are part of this study.
The process of building computational, physical, and other models begins with a basic conceptualization of a system. A conceptual model is an abstract representation that provides the general structure of a system and the relationships within the system that are known or hypothesized to be important. Many conceptual models have as a key component a graphical or pictorial representation of the system.
Although the environmental regulatory process typically requires numerical analysis of proposed regulations, the conceptual model
provides critical synoptic or summary understanding of the principle factors that influence the effectiveness of policies and, thus, is critical for regulatory analysis. In the context of environmental regulatory model applications, conceptual models are critical for both guiding quantitative analysis and communicating with decision makers, stakeholders, and the interested public.
A subset of all models are those that use measurable variables, numerical inputs and mathematical relationships to produce quantitative outputs. The committee defines a computational model as
a model that is expressed in formal mathematics using equations, statistical relationships, or a combination of the two. Although values, judgment, and tacit knowledge are inevitably embedded in the structure, assumptions, and default parameters, computational models are inherently quantitative, relating phenomena through mathematical relationships and producing numerical results.

FIGURE 1-3 An orrery or physical model of the solar system. Source: C. Mollan, National Inventory of Scientific Instruments, Royal Dublin Society. Image courtesy of Miruna Popescu. Reprinted with permission; copyright 2004, Armagh Observatory.
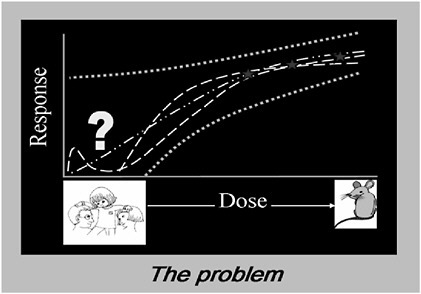
FIGURE 1-4 The use of a mouse model for estimating human health risks. Source: Conolly 2005.
Two examples of computational models are shown in Figures 1-5 and 1-6. Figure 1-5 (taken from Morales et al. 2000) shows the use of statistical models to characterize the lifetime risk of developing bladder cancer among males living in southwestern Taiwan as a function of exposure to arsenic in drinking water (measured in micrograms per liter). Each dot in the three panels represents the estimated lifetime risk for subjects exposed in increments of 100 µg/L, with each panel representing a separate population. We will come back to these figures later in the report, since they provide a very clear illustration of the impact of model choice on estimated dose response. Figure 1-6 shows the conceptual structure of the integrated exposure uptake biokinetic (IEUBK) model that is used to estimate blood lead levels in children. This model has been used in both air quality and hazardous waste-site applications to support standards and cleanup goals (NRC 2005a).
Finally, the committee’s task statement concentrates on the application of environmental regulatory models at the EPA. The committee defines an environmental regulatory model as
a computational model used to inform the environmental regulatory process. Some models are independent of a specific regulation, such as water quality or air quality models that are used in an array
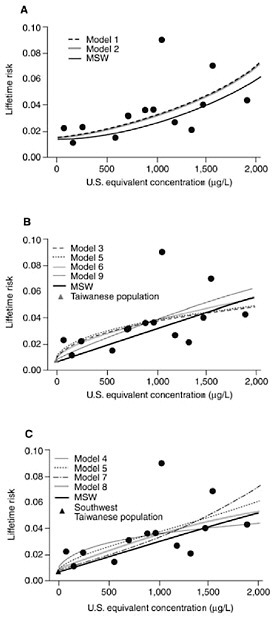
FIGURE 1-5 Examples of dose-response models for estimating lifetime risk for male bladder cancers due to arsenic in drinking water for various exposed populations. A shows the estimated lifetime death risk for male bladder cancer without comparison population; B shows the estimated lifetime death risk for male bladder cancer with Taiwanese-wide comparison population; and C shows the estimated lifetime death risk for male bladder cancer and the southwestern Taiwanese region comparison population. Note that several possible statistical models are fit to each data set. Source: NRC 2001b, from Morales et al. 2000.
of application settings. Other models are created to provide a regulation-specific set of analyses completed during the development and assessment of specific regulatory proposals. The approaches can range from single parameter linear relationship models to models with thousands of separate components and many billions of calculations.
Environmental regulatory models range from those that come complete with source code, documentation, and cellophane packaging to those that are simply a system of algebraic equations or statistical operations. Models also are often coupled together for environmental regulatory applications.
In the context of their use in environmental regulatory activities, the differentiation between a model and its application can be difficult. For example, some models developed for a single set of analysis may be viewed by users as inseparable from their applications, and treated
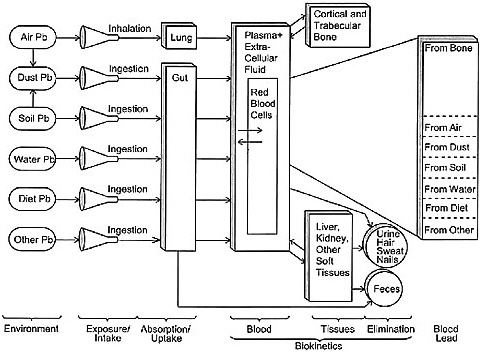
FIGURE 1-6 Components and functional arrangements of the IEUBK model that predict blood lead levels in children. Source: EPA 1994b.
synonymously. In Figure 1-3, each line is from a different model fitted through the same data, resulting in several possible dose-response curves. In other cases, general models are adapted to a particular location or particular contaminant through problem-specific input data or modification of particular assumptions. To further blur the distinction, analysts may use the term “model” to refer to a particular application of a general model.
In some ways this is merely a semantic difference. However, the development and application of a model pose differing evaluation issues. Further, although a model may be applicable to a given setting, its actual application to that setting may be problematic if input parameters for that application are not available or incorrectly specified. Thus, it is necessary to differentiate between evaluation of a general model, evaluation of the applicability of that model to a particular circumstance, and the ultimate implementation of that model, including the specification of parameter and/or input values. This report is not entirely about de novo model development and use, but also the application of previously developed models to specific applications.
What Types of Models Are Within Study Scope
A broad array of environmental models is used in the implementation of EPA’s regulatory mission. This includes the use of models in the assessment and regulation of toxic substances, the setting of emissions and environmental standards, and the development of mitigation plans. For example, models are used to
-
Assess exposures to contaminants and effects, as well as the relationships between them.
-
Project future conditions or trends.
-
Extrapolate and interpolate values to situations in which observations are not available.
-
Assess the contributions of individual sources to a problem that results from aggregate and/or cumulative exposures.
-
Evaluate attributes and impacts of different policy alternatives or future scenarios.
-
Evaluating the post-implementation adequacy of a regulation to achieve its goals.
-
Consider how the actions of regulated parties might be impacted by alternate policy instruments such as emissions standards versus emissions trading.
The types of models used in this regulatory analysis include those for emissions, environmental fate and transport, exposure, dose (pharmacokinetic models), health effects, ecological impacts, engineering, and economics. Chapter 2 provides more discussion of these models and how they are used in the regulatory process. These models vary widely in complexity. One of the simplest environmental regulatory modeling applications is the use of one-dimensional groundwater flow equations in the assessment of regulatory actions for leaking underground storage tanks (Weaver 2004). Such models use an exact solution to simple differential equations that describe straight-line flow and transport in a homogeneous aquifer. A similar model complexity is a simple linear doseresponse model that fits a straight line to a series of individual dose-response points. At the other end of the spectrum is the highly complex Community Multiscale Air Quality (CMAQ) model and its associated meteorological and emissions processing models that simulates the transport, transformation, and formation of multiple atmospheric pollutants. These three models (CMAQ for the simulation of the chemical transformation and fate of pollutants, an emissions model for anthropogenic and natural emissions that are injected into the atmosphere, and a meteorological model for the description of atmospheric states and motion) form a coupled modeling system. CMAQ uses as inputs the results of the emissions and meteorological models. Thus, this suite of individual models can be an even more complex model. Regardless of their level of complexity, all environmental regulatory models provide a quantitative tool for the development, implementation, and assessment of environmental policies.
What Types of Models Are Outside the Study Scope
Although the environmental modeling considered part of the committee’s charge encompasses a substantial portion of EPA’s modeling activities, some modeling applications are outside of the primary scope. Foremost, the committee is not constituted to comment on the development and use of laboratory animal analog models of human health responses to environmental pollutants. Assessing issues related to the use
of an animal species as an analog for human health impacts is outside the expertise of this committee. Another NRC report describes issues related to the use of animal analog models (NRC 2001b). However, computational models, particularly statistical dose-response models, that are used to extrapolate laboratory animal data to humans are included.
Additionally, the committee’s focus is on models used in the development, assessment, and implementation of environmental regulatory actions. EPA also uses models in a variety of other applications including planning, project scheduling, data collection, research, prediction, and forecasting. In so far as these models are computational, the committee’s recommendations may be useful for these models and their applications. But the committee in no way focused on some of the unique attributes of model selection and use at EPA in these other activities. Because of the wide array of environmental modeling at the agency, there is sometimes not a clear distinction between models used for regulatory purposes that are within the scope of this study and models considered to be used for nonregulatory purposes. For example, the same model may be used for both a regulatory application and a research application. In this way there is sometimes a continuum from models clearly in the regulatory domain under the purview of this study and other applications clearly outside the scope of work. However, not all model applications at EPA directly lead to regulation and there are clearly some model applications that fall outside the committee’s scope.
REPORT CONTENTS
This report documents the committee’s response to the charge described above. The report consists of six chapters and a summary. Chapter 2 describes the diversity of model use at EPA, how the agency currently integrates models into its policies, and some of the challenges to model use. Chapter 3 discusses the major steps in environmental regulatory model development, focusing on the main lessons learned from previous efforts in EPA. Chapter 4 discusses the evaluation of these models. Chapter 5 describes issues that arise in selecting models for their application in environmental regulatory activities. The report closes by discussing future environmental regulatory model activities in Chapter 6.






















