6
Regional and Global Aspects
RALPH A. LLEWELLYN
Indiana State University
WARREN M. WASHINGTON
National Center for Atmospheric Research
6.1
ESTIMATES OF ENERGY CONSUMPTION
Worldwide energy use has increased at an average annual rate of about 3½ percent over the past 50 years, accelerating to about 5½ percent during the latter half of this period, but with a perceptible slowing beginning in the late 1960’s (Darmstadter, 1971; Hubbert, 1971). By 1971, the per capita consumption of energy among the developed countries had reached 164 × 106 Btu/year, having tripled since the beginning of the Industrial Revolution (Cook, 1971).
This dramatic increase was accompanied by an equally significant rise in world population, estimated to have reached 4 billion in March 1976. The combined result of population increases, changing patterns of population densities, and escalating per capita energy consumption has been to concentrate in some regions of the world very large energy fluxes per unit area (energy flux density) when compared with the world average. For example, in 1971, the world average was 1.43 × 109 Btu/km2 of land area-year, while Japan’s energy consumption per unit area was 2.52 × 1010 Btu/km2-year or nearly 20 times larger. In that year, New York City’s Manhattan Island had a total energy flux density of approximately 6.0 × 1012 Btu/km2-year, very nearly equal to the global average of solar radiation at the surface and roughly 1000 times the average man-made energy flux density for the world’s land areas.
The developing countries, on the other hand, consume energy at a much lower rate. The developing nations of Africa, for example, had an average energy flux density of 4.69 × 107 Btu/km2-year for 1971 (United Nations Statistical papers, 1973), or about 3 percent of the average for the world’s land areas and roughly 8 × 10−6 of that of Manhattan. However, data gathered over the past several years indicate the possibility that the situation is slowly but steadily changing. Since 1950, the net population growth rate for the developing countries has risen sharply, largely a result of declining infant death rates. This, coupled with increasing concern and ability on the part of these nations for improving the living conditions of their people, has resulted in rising energy consumption to the extent that the ratio of per capita energy consumption for the developed to the developing countries has remained nearly constant at about 8 since 1960. Said differently, even though the population of the developing world is increasing more rapidly
than that in the developed world, the difference in per capita energy consumption has not changed markedly, indicating that the aggregate energy consumption by the developing countries is becoming a larger fraction of the world total as times goes on (Figure 6.1).
This trend, if it persists, will lead to a more rapid increase of energy flux densities in the developing countries than in the developed nations. Indeed, aggregate consumption of all fuels by the developing nations will equal that among the present developed nations in less than 120 years (United Nations Statistical Papers, 1973), if both groups maintain the average annual increase in energy use typical of the past 15 years. No one is suggesting that such trends can easily continue, particularly in the absence of clearly adequate and acceptable alternatives to the fossil fuels; however, pressure on the world’s social systems will be to maintain the trends to the degree possible (i.e., continue to improve standards of living via energy expenditures). If anything, the energy conservation strategies being explored in many developed countries may reduce the time to energy equity to significantly less than 120 years.
In suggesting that the upward trend of energy use may persist in the developing countries, we are not assuming a rapid rise in the numbers of automobiles, televisions, air conditioners, and the like throughout the world. The pressure to feed the increasing population will provide the main thrust. Providing India’s people with the minimum 3000 kcal/day considered necessary would require that nation to devote more energy to agriculture than it currently uses for all purposes combined. To raise the caloric intake of all the world’s people to this level would demand that 80 percent of the world’s current total energy consumption be devoted to agriculture (Steinhart and Steinhart, 1974). The problem is monumental, but the effort will probably be made to solve it.
Without concern at this point for possible solutions and the details of new technologies that may contribute to, or the extent to which rapidly depleting fossil fuel reserves may impede, the implementation of potential solutions, it must be recognized that man-made energy flux densities
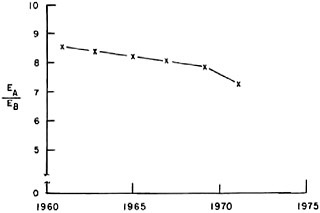
FIGURE 6.1 Ratio of energy use by developed countries (EA) to energy use by developing countries (EB), 1960– 1971.
will likely continue to increase, with those in the developing countries increasing more rapidly than elsewhere. These increases seem sure to continue through this century and, with obviously less certainty, well into the twenty-first century.
Our interest here is directed toward what the current trends in energy flux densities may suggest concerning the earth’s climate on various scales ranging from convective to synoptic, i.e., from areas smaller than 102 km2 to those 106 km2 or larger (Figure 6.5). As Hosler and Landsberg point out in Chapter 5, the effects of man’s activities in modifying the weather on a microclimate scale (areas up to several hundred km2) are well documented. Microclimate effects due to heat generated by cities and major electric generating stations have been previously noted in the literature. Included among the observed effects have been increments in various atmospheric parameters ranging from cloud cover and temperature to the frequency of thunderstorms and tornadoes. The important point is that changes in these indicators also occur without the benefit of man’s intervention; so it is essential to assess carefully whether man-made heat rejected to the atmosphere over small areas, such as cities, really produces significant departures from ordinary fluctuations resulting from natural energy inputs to the atmosphere. The evidence seems substantial that on the convective scale it certainly does (Landsberg, 1956; Hosler, 1971; Changnon, 1973).
Whether the same conclusion is valid for larger areas is another question. In Chapter 2, Mitchell observes that the size of the region over which the climate is affected by a given factor and the geographical extent of that factor are rather closely related. Changnon (1973) noted observable effects on rainfall, thunderstorms, and hail frequency over areas of urban dimensions (St. Louis, Chicago, etc.), which reject heat to the atmosphere with energy flux densities of the order of 10 11–1012 Btu/km2-year. For similar effects to occur on a continental or global scale, presumably man-made energy flux densities of similar magnitude would be necessary over the larger region, unless, of course, there are potential positive feedbacks not yet recognized that could become significant at less than macrodimensions. In the absence of such feedbacks, it does not seem likely that man’s production of heat energy at current levels will have any influence on climate that can be distinguished from effects arising from natural causes at other than microclimate scales.
The key phrase in the last sentence of the preceding paragraph is “at current levels.” As pointed out earlier in this paper and by Perry and Landsberg in Chapter 1, neither current levels of energy consumption nor current global patterns of energy flux density are likely to continue. Although the mix of fuels will change in a way not yet clear, total consumption will undoubtedly continue to rise, and higher energy flux densities will probably become more widely distributed geographically.
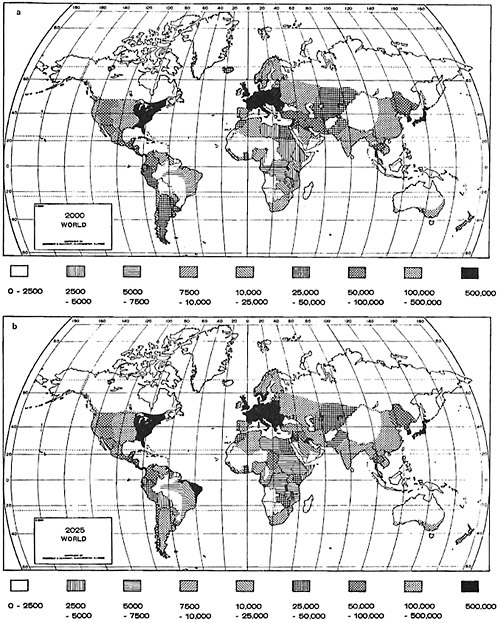
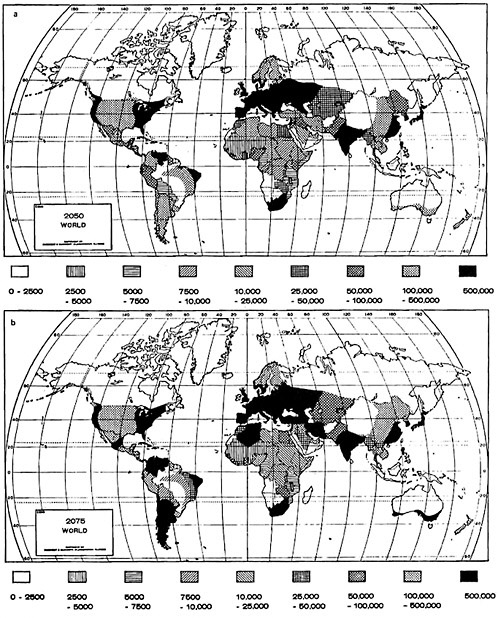
As one example of how the energy flux density patterns might change in the future, we have computed flux densities for 1970, 2000, 2025, 2050, and 2075, those after 1970 being projected on the basis of present values and recent trends in per capita energy consumptions and population
densities. Calculations are on a country-by-country basis, except where available data made possible smaller geographical computations. The data are displayed in Figures 6.2, 6.3, and 6.4. The displays, of course, differ from those of Weinberg and Hammond (1970) and Washington (1972), where a uniform per capita consumption (15 kW in the latter) and an ultimate population density based on current values were assumed.
It is not yet clear whether the techniques used herein will result in energy flux density projections of any more value to meteorologists and climatologists than Washington’s results. Work is continuing on developing displays with better and more geostrophically precise input data in the expectation that successively more useful outputs will be obtained.
6.2
MODELING CLIMATE IMPACT
SURFACE ENERGY BALANCE
It is possible to suggest mechanisms by which man’s activities might influence local weather events (such as clouds and precipitation), but is is difficult to prove that they definitively change regional and global climate (Landsberg, 1970). The problem is in separating natural fluctuations from those possibly caused by man’s generation of heat, particularly when the effects of such quantities of heat are relatively small. One promising approach for testing regional and global effects is through the use of theoretical models of the atmosphere and oceans. The basis and development of such models are discussed in Chapter 9. We cover here the preliminary use of such models for estimating the effects, but it may be useful first to review the major factors influencing the surface temperature of the earth.
The earth’s surface temperature over continents and oceans is determined by a balance of thermal energy transports. Thus, we can define a surface energy balance equation as
(1)
where
F = F1 – F2 = net long-wave radiation at the ground,
F1 = upward long-wave radiation from surface,
F2 = downward long-wave radiation from atmosphere, (1 – A) Q = absorbed solar flux at surface,
A = albedo of ground surface,
Q = solar flux arriving at surface,
H = sensible heat flux to atmosphere,
L·Eυ = latent heat flux to atmosphere,
Eυ = evaporative flux to atmosphere,
M = conduction of heat to subsurface,
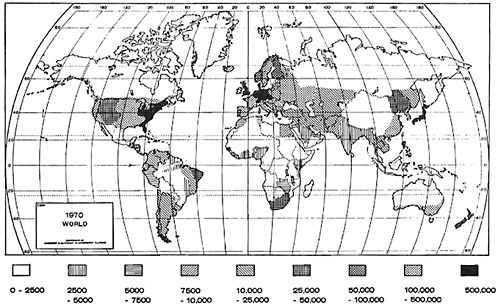
FIGURE 6.2 World energy flux density (kg of coal/km2/year), A.D. 1970.
Sm = melting of snow and ice,
l = latent heat of fusion,
L = latent heat of evaporation Lc or latent heat of sublimation Le + l,
EP = man-made heat sources.
The effects of horizontal transports of heat have been neglected in Eq. (1). This is a reasonable assumption over continents and ice-snow regions, but, of course, they cannot be neglected over ocean areas— particularly along the western boundary currents such as the Gulf Stream, where enormous amounts of heat are transported poleward. The mechanical generation of heat by wind and tides is also ignored in the definition of Eq. (1). It is assumed in the model studies carried out thus far that thermal heat release EP is at the surface or in the planetary boundary layer. The proper vertical placement of heat release in the atmosphere may not be a serious problem on regional or global space scales because vertical mixing caused by convection and surface roughness is usually quite efficient in distributing heat in the vertical. There are exceptions where the atmosphere is quite stable as far as thermal or moist convection, and, thus, heat would be trapped in lower layers.
The first terms of Eq. (1) dealing with radiation can be grouped as
(2)
Following Sellers (1965), in Table 6.1 we divide the mean latitudinal values of components of the surface energy balance equation into oceans, continents, and the earth as a whole. In the polar region, the values represent snow and ice cover. The features of Table 6.1 are that R tends to balance latent heat L·Eυ and sensible heat H, with the remainder being the transport of sensible heat by the oceans. Vonder Haar and Oort (1973) estimated that ocean transport is 40 percent of the poleward heat flux in the northern hemisphere, suggesting that the role of oceans in heat transport is greater than previously thought. R is positive, except in polar regions, where net long-wave radiation exceeds solar radiation absorbed at the ground. Note that global values of the earth as a whole (including ocean transport) show R as 95 W m−2; later this value will be compared with the present and predicted values of man-made generated heat.
GLOBAL AND REGIONAL CLIMATE IMPACT
It is useful to review model estimates of possible global climatic impacts due to waste heat. Budyko (1969, 1972a, 1972b) and Sellers (1969) used simple steady-state, earth-atmosphere, globally averaged models to estimate the effects. See also the survey of simplified climate models by Schneider and Dickinson (1974). Budyko assumed that the release of waste heat increased by 4 percent each year so that after 200 years waste heat, rather than solar energy, would be the controlling factor in climate. This assumption is not realistic when compared with our estimates. As pointed out, current levels of waste heat probably will not continue to increase indefinitely, and, thus, Budyko’s assumption appears quite unrealistic. Schneider and Dennett (1975) estimated that current levels of energy consumption are
TABLE 6.1 Mean Latitudinal Values of Components of the Surface Energy Balance Equation (W m−2) from Sellers (1965)
|
|
Oceans |
Continents |
Earth |
||||||
|
Latitude |
R |
L·Eυ |
H |
R |
L·Eυ |
H |
R |
L·Eυ |
H |
|
80–90° N |
|
|
|
|
|
|
−12 |
4 |
−13 |
|
70–80 |
|
|
|
|
|
|
1 |
12 |
−1 |
|
60–70 |
30 |
44 |
21 |
26 |
18 |
8 |
28 |
26 |
13 |
|
50–60 |
38 |
51 |
21 |
40 |
25 |
15 |
40 |
37 |
18 |
|
40–50 |
67 |
70 |
18 |
59 |
32 |
28 |
63 |
50 |
22 |
|
30–40 |
110 |
114 |
17 |
79 |
30 |
49 |
96 |
78 |
32 |
|
20–30 |
149 |
139 |
12 |
91 |
26 |
65 |
127 |
96 |
32 |
|
10–20 |
157 |
131 |
8 |
94 |
38 |
55 |
140 |
107 |
21 |
|
0–10 |
152 |
106 |
5 |
95 |
63 |
32 |
139 |
95 |
15 |
|
0–10° S |
152 |
111 |
4 |
5 |
66 |
29 |
139 |
100 |
13 |
|
10–20 |
149 |
137 |
7 |
96 |
54 |
42 |
137 |
119 |
15 |
|
20–30 |
133 |
132 |
9 |
92 |
37 |
55 |
124 |
109 |
21 |
|
30–40 |
108 |
106 |
11 |
82 |
37 |
45 |
106 |
98 |
15 |
|
40–50 |
75 |
73 |
12 |
54 |
28 |
26 |
74 |
70 |
13 |
|
50–60 |
37 |
41 |
13 |
41 |
26 |
15 |
37 |
41 |
15 |
|
60–70 |
|
|
|
|
|
|
17 |
13 |
15 |
|
70–80 |
|
|
|
|
|
|
−3 |
4 |
−5 |
|
80–90 |
|
|
|
|
|
|
−15 |
0 |
−15 |
|
Globe |
108 |
98 |
11 |
65 |
33 |
32 |
95 |
78 |
17 |
TABLE 6.2 Thermal Energy Generation
|
Time |
Energy Use per Capita (kilowatts/capita) |
Population (× 109) |
Total Energy Use (× 1012 W) |
|
1970a |
2 |
4 |
8 |
|
2000a |
10 |
7 |
70 |
|
2050a |
20 |
10 |
200 |
|
“Ultimate” orb “steady state” |
20 |
20 |
400 |
|
aFrom Häfele (1973). bEnergy use per capita from Weinberg and Hammond (1971); population from Weinberg and Hammond (1970). |
|||
10−4 of the solar flux absorbed at the earth’s surface and, therefore, are insignificant in the global heat budget. However, they did point out that other industrialization activities may have many times the direct effect of waste heat, e.g., changes in cloudiness, CO2, and aerosols. These aspects are discussed in Chapter 2 and in Schneider and Mesirow (1976). In Tables 6.2 and 6.3, Kutzbach (1974) compared the Budyko and Sellers global and continental values of energy flux densities with 1/4 the solar constant and net radiation R at the earth’s surface, These values can be compared further with those in Table 6.1. If we follow through Budyko’s arguments, we would expect the polar ice covers to retreat and eventually disappear. Sellers, with a model similar to Budyko’s but applied at 10° latitude bands, spread 20 W m−2 of waste heat into these bands— roughly equivalent to the present distribution of large cities. He found changes in surface temperature of the order of 20°C near the north pole and about 11°C in the tropics and concluded that this would eliminate the permanent ice fields. However, models such as Budyko’s and Sellers’ have highly simplified feedback mechanisms, such as cloud cover, and do not explicitly compute the dynamics of the atmosphere.
Figure 6.5 (Kutzbach, Center for Climatic Research, University of Wisconsin, personal communication) is a graph of energy flux density versus area. Note the solid line showing net radiation balance at the surface, the dashed line representing years circa 1970 and 2050, and the scale of meteorological processes at the bottom. Sources for the estimates of energy consumption appear in the legend. As seen from the slope of the dashed lines, the current energy usage is comparable to the natural energy balance at smaller scales. It will also probably take until 2050 for much effect to be seen on regional and synoptic scales. The general circulation model experiment referred to later is closer to the 2050 estimate.
Without a theoretical model, Sawyer (1974) estimated the effects of sea-surface temperature anomalies on the increase of sensible and latent heat fluxes from the ocean to the atmosphere and compared these with present levels of waste energy fluxes. He concluded that the effects of waste heat fluxes are much less than those caused by natural sea-surface anomalies. From the SMIC report (Matthews
TABLE 6.3 Man-Generated and Natural Energy Flux Densities (W m−2)
|
|
Globe |
Continents |
|
(a) Man-generated |
|
|
|
1970 |
0.015 |
0.054 |
|
2000 |
0.14 |
0.47 |
|
2050 |
0.39 |
1.4 |
|
“Ultimate” |
0.78 |
2.7 |
|
“Extrapolation”a |
(20) |
(65) |
|
(b) Natural |
|
|
|
1/4 solar constant |
350 |
350b |
|
Net radiation, surface |
95 |
65 |
|
aExtrapolation to circa 2150, based upon continued 4 percent per annum growth rate of energy flux density (Budyko, 1969; Sellers, 1969). bShould be used with caution over continental areas. |
||
et al., 1971), current values of waste heat releases over western Europe and the eastern United States (~106 k m 2) are 0.74 and 1.11 W m−2, respectively. These small amounts appear insignificant when compared with natural values R, H, or LE in the higher latitudes (Table 6.1). Sawyer, therefore, concluded that a fiftyfold increase is needed before it affects the natural climatic fluctuations. This agrees with the North Pacific anomaly numerical experiments (Chervin et al., 1976), which indicated that for realistic anomaly patterns in the North Pacific the effects did not have much statistical significance except directly over the warm anomaly. They found relatively little downstream effect.
CLIMATE IMPACT EXPERIMENTS WITH GENER AL CIRCULATION MODELS
Some preliminary calculations with a three-dimensional atmospheric general circulation model were carried out with the restriction of a fixed ocean temperature (Washington, 1971, 1972; Murphy et al., 1976). These experiments were conducted to show the atmospheric response to man-made heat uncoupled from ocean changes and should not be regarded as true climate-change experiments. In the first
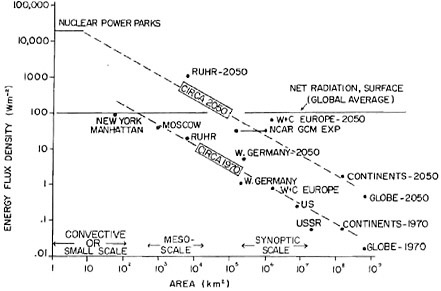
FIGURE 6.5 Energy consumption (W m−2) plotted versus area (km2) from Kutzbach (1974). Sources; Nuclear power parks, RUHR, W. Germany, continents, globe (Häfele, 1973). Manhattan, Moscow, Europe, United States, Soviet Union (Matthews, 1971). NCAR GCM Experiment (Washington, 1972).
set of experiments by Washington (1971), 24 W m−2 of waste heat was added to Eq. (1) over all continental and ice regions—approximately 100 times the heat energy released over the entire United States in 1965, or approximately one third of the surface radiation balance over continental areas. To see how this energy input compares with other terms of the surface energy budget, see Table 6.1 and Figure 6.5. The experiment was compared with a January simulation that did not include waste heat. The surface temperature in the waste-heat experiment rose 1–2° in the tropics and 8° over Siberia and northern Canada within 15 days and thereafter leveled off. The greater response in the northern polar regions than in the tropics was due to a small or zero solar flux in the northern hemisphere winter simulation. In other words, the ratio of thermal heat to net radiation balance (EP/R) was quite large in the winter hemisphere. The main shortcomings with these experiments, aside from the fixed ocean temperature, were too large an estimate of EP and assumed uniform distribution. In collaboration with Weinberg and Hammond of Oak Ridge National Laboratory and Hanna of the National Oceanic and Atmospheric Administration, Washington (1972) performed a more realistic set of experiments, still with fixed ocean temperatures. A geographical distribution of thermal pollution was based upon the current population density (this distribution is similar to that shown in Figure 6.2). Following Weinberg and Hammond (1970), Washington assumed a per capita energy usage of 15 kW and an ultimate population of 20 billion. In total energy, this was approximately six times smaller than in the earlier experiments. Figure 6.6 shows the geographical distribution of waste heat. The population assumption ignored the fact that people in the tropics probably require less energy for heating and cooling than those in the polar or midlatitude regions. One million megawatts over a 5° latitude-longitude square in the mid-latitudes is equivalent to an energy flux of approximately 6 W m−2. The maximum is approximately 37 W m−2 in the most densely populated areas, and the minimum much less than the average 6 W m−2. The maximum is four times smaller than R in the tropics. Four experiments were performed: the first—the control—did not include the effect of waste heat; the second—with waste-heat distribution—was termed thermal pollution. To determine if the differences between the control and thermal pollution experiments were large with respect to the natural fluctuations of the statistics, two other experiments were carried out—one adding negative thermal pollution (i.e., – EP) and one including a small initial random error in the control. Figure 6.7 shows the geographical difference of time means of temperature at the lowest level of the model (1.5 km) between the control and random thermal pollution, control and positive thermal pollution, and control and negative thermal pollution. H denotes warmer than control and C cooler. The temperature changes between the positive thermal pollution and control were up to 10°C in the northern hemisphere and about 1–2°C in the tropics, The same pattern emerged for the other experiments, The experiments deviated from the control in the same way, indicating that the thermal pollution effects were not large compared to the noise level for a 29-day, time-averaged January simulation. Put another way, the atmospheric effects of thermal pollution could not be separated from the natural fluctuations of the model for this averaging period. This contrasts markedly with results of the first experiments where the forcing, and therefore response, was much larger. Later Chervin et al. (1974, 1976) investigated the effects of time-averaging on the “noise levels” of general circulation model statistics, so that it is possible to obtain some measure of statistical significance in experiments when a change is made in the model or its boundary conditions.
For additional insight into regional effects and their statistical significance, another January experiment was
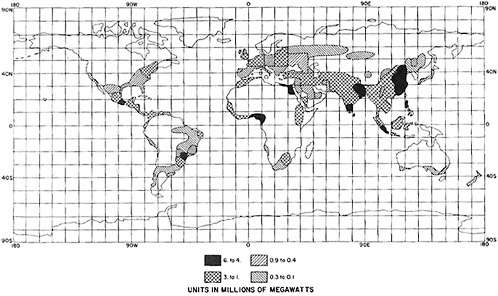
FIGURE 6.6 Geographical distribution of expected levels of man-made heat from Weinberg, Hammond, and Hanna (see Washington, 1972).
performed at the National Center for Atmospheric Research (NCAR). We assumed an urban population distribution for the year 2000 from Pickard (1973; see also Sundquist, 1975), showing a densely populated area from the Atlantic Seaboard to the Great Lakes to Florida, to which we added thermal pollution effects. We further assumed that the energy consumption is equal to that of present Manhattan—approximately 90 W m−2 (Figure 6.5). To keep the experiment simple, other regions of the globe were not modified. The experiment was run from days 0–60, averaged over days 31– 60, and the results compared with a control experiment without anomalous heating. Figure 6.8(a) shows the time mean temperature difference between the anomaly and control in the boundary layer (i.e., near the ground) ![]() Note that the temperature differences rise to 12°C in the vicinity of anomalous heating. Although we show only part of the globe here, no other location has such a high maximum, and it is safe to assume that this is a direct result of the heating. However, it is more difficult to make this point for other levels without statistical analysis.
Note that the temperature differences rise to 12°C in the vicinity of anomalous heating. Although we show only part of the globe here, no other location has such a high maximum, and it is safe to assume that this is a direct result of the heating. However, it is more difficult to make this point for other levels without statistical analysis.
The temperature difference at 1.5 km, representing a layer thickness of 3 km, is shown in Figure 6.8(b); here the anomalous effect is not obvious. To obtain a quantitative statistical measure, we compute the standard deviation σ of the average January 1.5-km temperature in the model from five separate control runs in which small differences were introduced into the initial data (see Chervin et al., 1976, for details and comparison with observed). Figure 6.8(c) shows the general distribution of 1–3°C in the midlatitudes and somewhat smaller values over the oceans or in the tropical latitudes. If we define ratio r of the absolute difference of the time means of control and anomaly experiments ∆ to the the standard deviation, we obtain
(3)
Following Chervin et al. (1976), we can relate r to the widely used t test in statistics to obtain an objective measure of significance. The significance level is an estimation of the probability that a given value of r could be exceeded by chance (i.e., by merely random fluctuations generated in the model). The confidence level is one minus the significance level. In the experiments here, we have only five samples to estimate standard deviation and, thus, we have four degrees of freedom. The distribution of r in Figure 6.8(d) shows over the eastern United States values of 1 and 2 yielding significance levels of 52 percent and 23 percent, respectively (Table 6.4). Therefore, the differences in this region should be treated with lower confidence than in the boundary layer [Figure 6.8(a)]. In the first case, there is a 52 percent chance of being random, and in the second, 23 percent. Caution should be noted with some of the large values of
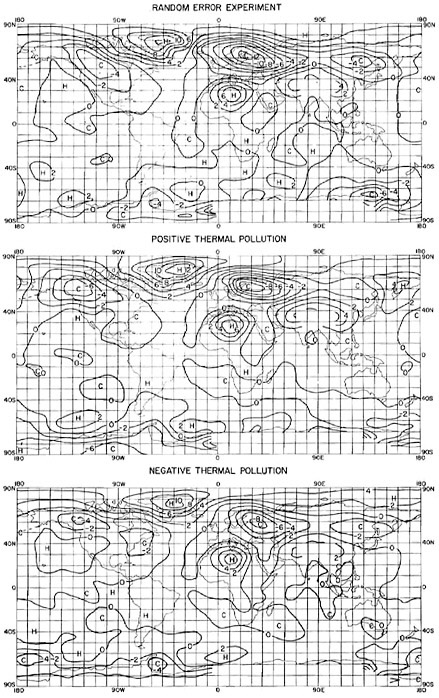
FIGURE 6.7 Geographical difference of time means of global temperature at 1.5 km between control and random initial error experiments, control and positive thermal pollution, and control and negative thermal pollution. H denotes warmer than control experiment and C denotes cooler; contour interval is 2° C.
r in Figure 6.8(d). These are often caused by unrealistically small values (due to the small sample size) of σ in Eq. (3) and could have been avoided somewhat in Figure 6.8(d) by limiting σ to 0.5°C (a reasonable value from observational data). The major conclusion here is that the changes induced by waste heat are large in the boundary layer but do not seem to have as much influence above it. Remember that because this was a January simulation and the northern hemisphere was mostly stably stratified, the addition of waste heat caused a large temperature change in the boundary layer. In summer over the continents, we expect the effects to be less because solar flux dominates waste heat flux and, because of more convection, the extra heat would not be trapped at the surface as in winter.
In recent January numerical experiments using the United Kingdom Meteorological Office general circulation model,
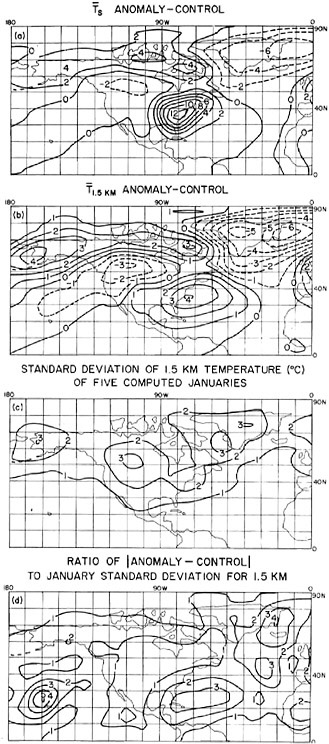
FIGURE 6.8 (a) Difference maps of boundary layer temperature ![]() between anomaly and control averaged in time over days 31– 60. Units are °C. (b) Same as (a) except for
between anomaly and control averaged in time over days 31– 60. Units are °C. (b) Same as (a) except for ![]() (c) Geographical distribution of standard deviation σ from five Januaries simulated by the NCAR GCM. Units are °C. (d) Ratio r maps of the differences of 1.5-km temperature averaged from days 31–60 to the standard deviation.
(c) Geographical distribution of standard deviation σ from five Januaries simulated by the NCAR GCM. Units are °C. (d) Ratio r maps of the differences of 1.5-km temperature averaged from days 31–60 to the standard deviation.
TABLE 6.4 Significance Levels for Temperature Differences
|
r |
Significance Level (%); 4 Degrees of Freedom |
|
1 |
51.69 |
|
2 |
22.86 |
|
3 |
10.02 |
|
4 |
4.69 |
|
5 |
2.38 |
|
6 |
1.31 |
|
7 |
0.77 |
|
8 |
0.47 |
|
9 |
0.31 |
Murphy et al. (1976) investigated the effects of waste heat from energy parks. They conducted two experiments, adding 375 W m−2 to each over two energy parks with a total area 8 × 105 km2 (approximately four grid boxes in their model). The heat was added to the lowest layer of the model which is 200 mbar thick. This heat is equivalent to the total heat used by Washington (1972) and is approximately four times the energy density of Manhattan (Figure 6.5). In the first experiment, the parks were located in the North Atlantic southwest of England (48° N and 15° W) and in the North Pacific east of Japan (36° N and 148° E). They carried out a second experiment with the Atlantic park located west of Africa (9° N and 22° W), but we discuss here only the first experiment Two further assumptions were made: (1) all energy was added to four grid boxes in the model (see striped area in Figure 6.9), and (2) the heat is in sensible form only. In future experiments, they will add the park heat in both sensible and latent forms by computing the ocean temperature change in the park region.
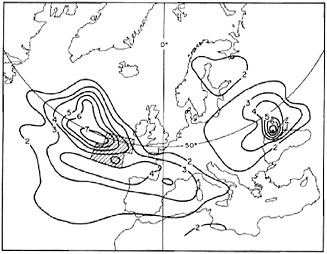
FIGURE 6.9 Ratio of pressure differences to one half of the range of sea-level pressures in the four controls over the Atlantic and Europe.
The North Atlantic energy park (4 × 105 km2 in area) experiment produced surface pressure falls east of the park, which extended over the entire western Atlantic with a maximum of −14 mbar, and rises west of the park, extending to eastern Scandinavia with a maximum of +12 mbar. This pattern is consistent with known relationships between atmospheric heating and large-scale pressure patterns. They also found large upstream and downstream effects on precipitation.
Figure 6.9 shows the ratio of sea-level pressure difference between the control and the anomaly divided by one half the range of sea-level pressure in four separate control experiments. This is a type of t test for which values of 3.18 in Figure 6.9 are statistically significant at the 0.05 level (for a two-sided test). With four control experiments, they have three degrees of freedom. We see in Figure 6.9 that increases in sea-level pressure difference over the western edge of the park, as well as south of the park, are highly significant. The differences east of the park are less significant. Over the Crimea, a large ratio occurs, which is not significant because the denominator of the ratio becomes too small. As mentioned earlier with Eq. (3), this can occur because of the small sample size. The statistical significance of the precipitation differences is not shown, although the observed changes are consistent (in a physical sense) with the pressure changes. These effects and those of other energy parks are being investigated in greater detail by a group at the International Institute for Applied Systems Analysis in Laxenburg, Austria (Häfele et al., 1976).
It would be a wrong interpretation of these preliminary experiments to say that thermal pollution can or cannot seriously affect regional and global climate. The experiments described here are extreme. What has been learned is that the effects can be sizable, given levels of waste heat much higher than at present. Model experiments must be performed and averaged over long periods to determine the statistical significance of relatively small effects. These small effects can be important for human affairs. Ultimately, this will require coupled atmosphere-ocean-snow-ice models to account for the total climatic response, and development of such models must continue.
6.3
ACKNOWLEDGMENTS
We thank R. Chervin, S. Schneider, and J. Kutzbach for their comments on the manuscript. We appreciate the editorial assistance of A. Modahl.
REFERENCES
Budyko, M. I. (1969). The effect of solar radiation variations on the climate of the earth, Tellus 21, 611.
Budyko, M. I. (1972a). The Influence of Man on Climate (in Russian), Hydrometeorological Publishing House, Leningrad.
Budyko, M. I. (1972b). The future climate. ![]() Trans. Am. Geophys. Union 53, 868.
Trans. Am. Geophys. Union 53, 868.
Changnon, S. A., (1973). Urban-industrial effects on clouds and precipitation, in Proc. Workshop on Inadvertent Weather Modification, Utah State U., Logan, Utah, Aug. 1973, pp. 111–139.
Chervin, R. M., W. L. Gates, and S. H. Schneider (1974). The effect of time averaging on the noise level of climatological statistics generated by atmospheric general circulation models, J. Atmos. Sci. 31, 2216.
Chervin, R. M., W. M. Washington, and S. H. Schneider (1976). Testing the statistical significance of the response of the NCAR general circulation model to North Pacific Ocean surface temperature anomalies, J. Atmos. Sci. 33, 413.
Cook, E. (1971). The flow of energy in an industrial society, in Energy and Power, W. H. Freeman and Co., New York, pp. 134–147.
Darmstadter, J. (1971). Energy in the World Economy, Johns Hopkins U. Press, Baltimore, Md., pp. 9–35.
Häfele, W. (1973). Energy systems. Proc. IIASA Planning Conference on Energy Systems, International Institute for Applied Systems Analysis, Laxenburg, Austria, 17–20 July 1973, IIASA-PC-3, pp. 9–78.
Häfele, W., et al. (1976). Possible impacts of waste heat on global climate patterns, Research Report RR-76-1, Second Status Report of the IIASA Project on Energy Systems, 1975, International Institute for Applied Systems Analysis, Laxenburg, Austria, pp. 134–148.
Hosler, C. L. (1971). Wet Cooling Tower Plume Behavior, C.E.P. Tech. Manual No. T40. AIChE, p. 1.
Hubbert, M. K. (1971). Energy resources of the earth, in Energy and Power, W. H. Freeman and Co., New York, pp. 60–87.
Kutzbach, J. E. (1974 ). Possible impact of man’s energy generation on climate, Report of GARP Study Conference on the Physical Basis of Climate and Climate Modelling, Stockholm, Sweden, 29 July-10 August 1974.
Landsberg, H. E. (1956). The Climate of Towns; Man’s Role in Changing the Face of the Earth, U. of Chicago Press, Chicago, Ill., pp. 584–603.
Landsberg, H. E. (1970). Man-made climatic changes, Science 170, 1265.
Matthews, W. H., W. W. Kellogg, and G. D. Robinson, eds. (1971). Inadvertent Climate Modification, Study of Man’s Impact on Climate (SMIC). MIT Press, Cambridge, Mass.
Murphy, A. H., A. Gilquist, W. Häfele, G, Krömer, and J. Williams, (1976). The impact of waste heat release on simulated global climate, RM-76 –79, International Institute for Applied Systems Analysis, Laxenburg, Austria.
Pickard, J. P. (1973). Urbanization and economic change in North American regions, in Sundquist (1975).
Sawyer, J. W. (1974). Can man’s waste heat affect the regional climate? Talk presented at the IAMAP Symposia, Melbourne, Australia, January.
Schneider, S. H., and R. E. Dickinson (1974). Climate modeling, Rev. Geophys. Space Phys. 12, 447.
Schneider, S. H., and R. D. Dennett (1975). Climatic barriers to long-term energy growth, Ambio 4, 65.
Schneider, S. H., with L. E. Mesirow (1976). The Genesis Strategy, Climate and Global Survival, Plenum Press, New York.
Sellers, W. D. (1965). Physical Climatology, The U. of Chicago Press, Chicago, Ill.
Sellers, W. D. (1969). A global climatic model based on the energy balance of the earth-atmosphere system, J. Appl. Meteorol. 8, 392.
Steinhart, J. S., and C. E. Steinhart (1974). Energy and use in the U.S. food system, Science 184, 307.
Sundquist, J. L. (1975). Dispersing population: What America can
learn from Europe, Brookings Institution, Washington, D.C., pp. 24 –32.
United Nations Statistical Papers (1973). World energy supplies, 1968–1971. Ser. J/16, 6– 40.
Vonder Haar, T. H., and A. H. Oort (1973). New estimate of annual poleward energy transport by northern hemisphere ocean, J. Phys. Oceanog. 3, 169.
Washington, W. M. (1971). On the possible uses of global atmospheric models for the study of air and thermal pollution, in Inadvertent Climate Modification—Study of Man’s Impact on Climate, W. H. Matthews et al., eds., MIT Press, Cambridge, Mass., pp. 265–276; also in Air and Water Pollution, W. E. Brittin et al., eds., Colorado Associated U. Press, Boulder, Colo., pp. 599–613.
Washington, W. M. (1972). Numerical climatic-change experiments The effect of man’s production of thermal energy, J. Appl. Meteorol. 11, 768.
Weinberg, A. M., and R. P. Hammond (1970). Limits to the use of energy, Am. Sci. 58, 412.
Weinberg, A. M., and R. P. Hammond (1971). Global effects of increased use of energy, in Proc. Fourth International Conference on Peaceful Uses of Atomic Energy, Geneva, Switzerland, Sept.