11
Reproductive Decisions Under Ecological Constraints: It’s About Time
PATRICIA ADAIR GOWATY and STEPHEN P. HUBBELL
The switch point theorem (SPT) is the quantitative statement of the hypothesis that stochastic effects on survival, mate encounter, and latency affect individuals’ time available for mating, the mean and variance in fitness, and thus, originally favored the evolution of individuals able to make adaptively flexible reproductive decisions. The SPT says that demographic stochasticity acting through variation in (i) individual survival probability, s; (ii) individual encounter probability, e; (iii) latency, l; (iv) the number of potential mates in the population, n; and (v) the distribution of fitness conferred, the w distribution, together affect average lifetime fitness, and induce adaptive switches in individual reproductive decisions. The switch point is the rank of potential mates at which focal individuals switch from accepting to rejecting potential mates, a decision rule that the SPT proves maximizes the average lifetime fitness of a focal individual under given values of ecological constraints on time. The SPT makes many predictions, including that the shape of the distribution of fitness conferred affects individual switch points. All else equal, higher probabilities of individual survival and encounter decrease the fraction of acceptable potential mates, such that focal individuals achieve higher average lifetime fitness by rejecting more potential mates. The primary prediction of the SPT is that each decision a focal
Department of Ecology and Evolutionary Biology and Institute of the Environment, University of California, Los Angeles, CA 90095 and Smithsonian Tropical Research Institute, APO, AA 34002.
individual makes is determined jointly by e, s, l, n, and the w distribution.
When Darwin’s critics said that natural selection (Darwin, 1859) could not explain the evolution of traits such as the outrageous tails of peacocks that reduce their bearers’ survival probabilities, he countered with sexual selection (Darwin, 1871). He argued that costly traits would evolve if they also increased males’ abilities to attract females or to win behavioral contests over access to females. In “Principles of Sexual Selection,” the first chapter of Part II of The Descent of Man, and Selection in Relation to Sex (Darwin, 1871), Darwin defined sexual selection as that type of selection that “depends on the advantage which certain individuals have over other individuals of the same sex and species, in exclusive relation to reproduction” (1871, p. 256). Darwin distinguished sexual selection from natural selection as selection that arises from some individuals having a reproductive advantage over other same-sex, conspecific individuals, not from different “habits of life,” but from reproductive competition with rivals. Darwin’s discussion focused overwhelmingly on traits in males that could be explained by 2 mechanisms of sexual selection—male-male competitive interactions and female choice—each of which could result in variation among males in fitness and thereby favor traits that helped males win fights and attract females (see Jones and Ratterman, Chapter 9, this volume). Most modern discussions of typical sex roles begin with Darwin’s 1871 volume, and statements about choosy females and profligate, competitive males. However, Darwin probably suspected that male choice was common; he argued in Part I of the 1871 book that men’s choice of mates was seemingly more common than women’s at least in “civilized societies.” He even argued that the beauty of women was due to male choice. In Part II he also described cases of male domestic and companion animals refusing to copulate with some females. He was aware too of gaudy, pugnacious, and competitive females in some bird species. Controversy over whether females had the esthetic capability for discrimination dogged Darwin and his followers into the 20th century.
After most people finally agreed that females had the sensibilities to choose, focus narrowed so that modern students of sexual selection simply assumed that males were competitive and indiscriminate and females “coy,” passive, and discriminating. For example, when Bateman (1948) studied sex differences in fitness variances in Drosophila melanogaster, he attributed the larger variances of males to their “undiscriminating eagerness” and the “discriminating passivity” of the females (p. 367), even though he did not watch behavior (Dewsbury, 2005). Bateman’s study
also led many to infer that female multiple mating was unlikely to be very common as it was unlikely to enhance female fitness.
Resistance to such “narrow-sense sexual selection” was afoot in Darwin’s century [see citations in Gowaty (2007)], and accelerated with the flush of empirical papers that followed Parker et al. (1972) and Trivers (1972). Parker argued that the sexes are what they are because of the size of the gametes they carry: females having large, relatively immobile, resource-accruing gametes and males having smaller, mobile gametes that competed for access to the larger ones. Trivers argued, echoing Williams (1966), that females were usually the choosy sex because in most species females bore the greater cost of reproduction. Challenges to the generalizations of parental investment theory included Hrdy’s (1981) book about the near ubiquity of competitiveness of primate females and their anything but “coy” and “passive” sexual behavior; discovery that females fight females to defend “genetic maternity” in birds (Gowaty, 1981; Gowaty and Wagner, 1987), documentation of multiple mating by wild-living female Drosophila pseudoobscura (Anderson, 1974), Sialia sialis and other bird species (Gowaty and Karlin, 1984; Gowaty, 1985); and the first study of male mate choice in beetles with typical female-biased parental investment (Johnson and Hubbell, 1984). Importantly, Sutherland (1985a,b, 1987) showed theoretically that the sex differences in fitness variances could arise in the absence of mate choice and intramale competition and could be due entirely to chance. Building on Sutherland’s insights, Hubbell and Johnson (1987) showed that the variation in lifetime mating success results from chance and selection, so that measures of selection should rely only on the residual variance that cannot be ascribed to known and quantifiable nongenetic life history variation. Hrdy and Williams (1983) and Hrdy (1986) offered an explanation for why, in the face of so much evidence, so many biologists seem invested in the “myth of the coy female.” In response to the failures of the simpler versions of parental investment theory, new theory to explain reproductive decisions appeared (Hubbell and Johnson, 1987; Crowley et al., 1991; Clutton-Brock and Parker, 1992) predicting that variation in encounters, latencies, survival, and their more complex proxies (relative reproductive rate, the operational sex ratio, and density) favored shifts in mean behavior of the sexes, and as a result more nuanced reports of ecologically induced variation in sex-typical behavior appeared [e.g., Magnhagen (1991), Forsgren (1992), Shelly and Bailey (1992), Berglund and Rosenqvist (1993), Hedrick and Dill (1993), Berglund (1994, 1995), Poulin (1994), Simmons (1995), Dill et al. (1999), Grand and Dill (1999), Itzkowitz and Haley (1999), Gowaty et al. (2002), Jiggins (2002), Drickamer et al. (2003)]. Currently, few investigators think that sex role behavior is entirely fixed for either sex, particularly in females in species with female-biased parental investment in which many observations of
changes in mating behavior exist (Magnhagen, 1991; Gong, 1997; Grand and Dill, 1999). Nevertheless, we know little about how male mate choice behavior varies under ecological constraints, because few investigators study male mate choice in species with female-biased parental investment. The possibility of sex role flexibility has seldom been simultaneously tested in both sexes (Gowaty et al., 2003b).
Most modern theories of sex roles begin with Trivers’s (1972), and Parker et al.’s (1972) ideas about sex differences to predict further sex differences. The derivative theories assume that the origin theories are an accurate reflection of past selection, which is an intuitive place to begin in refinement of theory—until one seriously considers the explicit challenges to the embedded assumptions about sex differences in fitness variances. Consider what Hubbell and Johnson (1987) proved theoretically: that demographic stochasticity gives rise to chance variances in lifetime reproductive success. They proved that nonheritable environmental variation in an individual’s lifetime number of mates could have favored the evolution of mate assessment in the first place. They showed that variances in number of mates similar or identical to those usually attributed to sexual selection could arise without mate choice and other sources of intrasexual competition. In other words, the arrow of causation linking classic mechanisms of sexual selection to fitness variances can go in either direction (Gowaty and Hubbell, 2005). This means that fitness variances can arise from demographic stochasticity, acting through chance effects on individual encounter probabilities with potential mates, individual survival probabilities, and latencies, which are variables that can then induce individual behavior (Fig. 11.1). This conclusion is turned around from the usual conclusion that mate choice and intrasexual competition cause fitness variances. This observation was profound, just as Sutherland’s (1985a) earlier one was, because it showed that the usual linkage between

FIGURE 11.1 Scheme showing a scenario of the evolution of switches in reproductive decisions.
SOURCE: Modified from Gowaty and Hubbell (2005).
mechanisms of sexual selection and means and variances in number of mates is best interpreted as correlation rather than causation until one partitions the deterministic and stochastic components of means and variances in number of mates.
Most recent sex roles research has focused on female mate choice for fancy male traits, much of which was inspired by Hamilton and Zuk’s (1982) hypothesis that fancy male traits indicate good genes for offspring viability, a compelling hypothesis given Red Queen dynamics between hosts and pathogens. Later quantitative genetics theory suggested that indirect fitness effects are less likely than direct fitness effects to favor the evolution of such traits (Kirkpatrick, 1985; Wolf and Wade, 2001). Additionally, until relatively recently, few data existed in support of the good genes hypothesis of mate choice. However, female and male choice studies in flies (Anderson et al., 2007), cockroaches (Moore et al., 2001, 2003), ducks (Bluhm and Gowaty, 2004a,b), and mice (Drickamer et al., 2000, 2003; Gowaty et al., 2003a) have demonstrated that offspring viability was significantly higher when choosers were mated with discriminatees they preferred, as was productivity (the number of offspring surviving to reproductive age). In contrast, fecundity (the numbers of eggs laid or offspring born) was almost always lower and sometimes significantly lower when choosers were experimentally paired with partners they preferred compared with partners they did not prefer (Gowaty et al., 2007). These findings are consistent with the hypothesis of reproductive compensation (Gowaty, 2008) and inconsistent with theories predicting that mate choice favors enhanced fecundity.
Why were these studies (Drickamer et al., 2000, 2003; Moore et al., 2001, 2003; Bluhm and Gowaty, 2004a,b; Anderson et al., 2007; Gowaty et al., 2007) successful in showing the predicted associations between mate choice and offspring viability, when others were not? There are at least 3 reasons. First, the studies had controls that eliminated the effects of intrasexual behavioral contests and intersexual coercion that often confound mate choice studies (Kingett et al., 1981). Second, these studies were not designed to understand the evolution of traits mediating preferences, but to test the effects of mate choice independent of their effect on the evolution of discriminatee traits. The investigators picked choosers and discriminatees at random with respect to their phenotypes, so these studies are silent about the traits in the discriminatees that mediated choosers’ preferences. Questions about the evolution of fancy traits are really 2 separate questions: one about the fitness payouts of preferences, and the other about the evolution of the traits that mediate the preferences. Multiple traits may mediate preferences (Candolin, 2003). However, few have evaluated the hypothesis that fancy traits may exploit preexisting sensory biases that could manipulate choosers in ways that could decrease rather
than increase their fitness. Third, the investigators (Gowaty et al., 2007) were motivated to study the effects of constraints on the free expression of mate preferences, so their methodologies were designed to get unambiguous pretouching behavioral indicators that choosers preferred one discriminatee more than the other. Once the investigators knew whom the choosers liked and did not like, they randomly assigned the choosers to breed with one of the discriminatees. In that way, they captured the effects of constraints on the fitness payouts for choosers in unconstrained and constrained partnerships.
Why are these studies (Drickamer et al., 2000, 2003; Moore et al., 2001, 2003; Gowaty et al., 2003a, 2007; Bluhm and Gowaty, 2004a,b; Anderson et al., 2007) of interest in an article on sex roles? (i) They provide powerful empirical counterpoint to theory that argues that indirect fitness effects are unlikely to accrue from mate preferences. (ii) They demonstrate tradeoffs in components of fitness for choosers breeding under constraints, thus suggesting that to understand selection from mate choice, investigators may profit from knowing about as many components of fitness as possible, including fecundity, productivity, and offspring viability, when individuals breed under constraints. (iii) They show that individuals—both males and females—can and do make pretouching assessments of likely fitness payouts before mating. They made clear that males, not just females, are able to modify their behavior and physiology when breeding under constraints (Gowaty et al., 2007), observations inconsistent with typical ideas about sex role variation in species with female-biased parental investment.
What is needed now is a theory that will allow investigators to parse differential effects on fitness and behavior, and the direction of their effects on each other (behavior to fitness/fitness to behavior) on both females and males. Such a theory will allow investigators to attribute reproductive decisions and behavior to 3 causal factors: (i) chance variation in ecological contingencies that may induce flexible and adaptive individual reproductive decisions; (ii) competitive forces including natural and sexual selection; and (iii) fixed sex differences. The model we present facilitates these goals.
To describe the model, which we call the switch point theorem (SPT), we (i) discuss individual reproductive time budgets, which encapsulate some of the most important ecological constraints on reproduction. (ii) We introduce the concept of the fitness conferred by alternative potential mates. (iii) We verbally describe the steps in model construction (the mathematical description is in the Appendix to this chapter). (iv) We show some of the results of the model. In the discussion, we (v) list what the SPT does and does not do, and (vi) describe several possible empirical tests and applications of the SPT.
CONSTRAINTS ON INDIVIDUAL REPRODUCTIVE TIME BUDGETS
For all mortal individuals, their time is finite. Time available for mating affects means and variances in number of mates (Fig. 11.1) (Gowaty and Hubbell, 2005), and chance effects on life history that affect time available for mating can have strong effects on fitness means and variances (Sutherland, 1985a; Hubbell and Johnson, 1987). The simplest set of parameters to affect lifetime variance in numbers of mates is based on stochastic effects on an individual’s survival and the individual’s encounters with potential mates, and, if the individual is a nonvirgin (i.e., a remating individual), its latency from one copulation to receptivity for the next (Sutherland, 1985a; Hubbell and Johnson, 1987; Gowaty and Hubbell, 2005). Indeed, in order for a receptive individual to mate, it must encounter a potentially mating opposite-sex individual; thus an individual’s encounter probability (e) with potential mates affects how much time the focal individual spends searching for mates. Likewise, for already-mated individuals in iteroparous species, the time they spend “handling” the reproductive consequences of mating, during which they are in latency (l) and unavailable for further mating, affects the time remaining for future matings and the opportunity cost of the past mating (Sutherland, 1985a,b, 1987; Gowaty and Hubbell, 2005). Importantly, individuals vary in reproductive life span, a function of their survival probability (s). All else equal, when search time and latencies are short, and life span is long, individuals have more time for reproduction than when search time and latencies are long, and life span is short. Individuals with short search times and long lives have more opportunities to mate than individuals whose search time is long and whose probability of future life is short. Intuitively (Fig. 11.2), it is easy to see that when opportunities vary, the costs and benefits of accepting or rejecting potential mates also vary. This means that for individuals with many opportunities, the costs of rejecting more potential mates are smaller, whereas, when focal individuals have fewer opportunities, the costs of rejecting potential mates are greater. However, relative opportunities predict only means and variances in number of mates; to predict adaptive, flexible reproductive decisions of an individual, one must also know the fitness that would be conferred if a focal individual were to mate with any given alternative potential mate.
FITNESS DISTRIBUTIONS
Just as most models of mate preferences do (Andersson, 1994), the SPT assumes that individuals assess the fitness that would be conferred (w) by potential mates before making reproductive decisions. We further assume that individuals obtain information during their development of
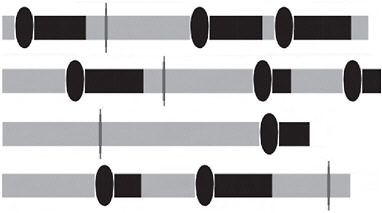
FIGURE 11.2 Four stick models of idealized reproductive careers of 4 individuals. On each stick, the gray bars represent the stage, search. The ovals attached to black bars represent the time used when an individual encounters and accepts for mating a potential mate, and enters a latency, a period during which the individual is unreceptive to further mating. The gray vertical ovals attached to gray bars represent encountering and rejecting a potential mate, after which the individual reenters search. Some sticks are longer than others, indicating that some individuals die before others, when they enter the absorbing state, death.
the distribution of fitness that would be conferred (the w distribution) by potential mates in their population. To conceptualize the meaning of w distributions, imagine an experiment with no carryover effects in which every female in a population is mated with every male and every male with every female. Fill in every cell of a matrix with the fitness that would result from each pairwise mating. This matrix specifies what we mean by “fitness conferred by alternative potential mates.” We assume that focal individuals have information about the distribution, which is a key component of expected mean reproductive success. The fitness components one might consider empirically or theoretically include: fecundity (the number of eggs laid or offspring born), productivity (the number of their offspring that survive to reproductive age), or offspring viability (the proportion of eggs laid or offspring born that survive to reproductive age). On completion, one would have a matrix of values representing “fitness conferred by alternative potential mates, w.” One can imagine a variety of scenarios for how fitnesses are distributed in such a fitness matrix. For example, one might observe a situation in which w is as an absolute, meaning that all focal individuals rank a potential mate the same way, as predicted by many theories of sexual selection (Andersson, 1994). Alternatively, w might often differ from one focal individual to another, as we think likely, and be an interaction effect and self-referential, meaning that each focal individual will not rank specific potential mates in the
same way. Such self-referential mate preferences occur in mice and other organisms (Ryan and Altmann, 2001; Ryan and Lacy, 2003). The entries in the fitness matrix have some statistical distribution, which we call the w distribution.
In the SPT, we assume the w distributions are beta distributions. The beta distribution is convenient because a beta random variate takes values from 0 to 1, as fitness does, and a beta distribution can assume a very large diversity of shapes depending on its 2 parameters, nu (ν) and omega (ω), from flat to strongly unimodal, left or right skewed, and even bimodal. We illustrate several possible fitness distributions in the analyses including beta (1, 1), which gives a uniform probability density from 0 to 1; beta (8, 3), which is skewed to high values; beta (3, 8), which is skewed to low values; and beta (5, 5), which has a strong central tendency. Note that although we use a beta probability density function in the SPT, there is no necessity for the w distribution to be beta for the SPT to be valid.
THE SWITCH POINT THEOREM
The SPT arises from a Markov chain state transition model. The SPT is a generalization of an earlier model (Hubbell and Johnson, 1987; Gowaty and Hubbell, 2005) in which focal individuals made mating decisions when potential mates occurred in only 2 qualities. In the current model, focal individuals make mating decisions when potential mates may occur in up to n qualities, where n is the number of potential mates in the population, so that there is a state for mating each potential mate. In Markov state transition models, individuals move from one state to another with some probability. The model is an absorbing Markov chain, so individuals continue to move through states until death (a terminal state individuals cannot leave). The solution to the model is a theorem that specifies the mean and the variance of the number of times the individual enters each state. The solution to the SPT (below) is f*, the number of potential mates a focal individual finds acceptable that maximizes relative lifetime fitness. The SPT says that focal individuals should accept all potential mates whose rank (with 1 being the highest fitness rank) is less than or equal to the rank at which average lifetime fitness would be maximized (f*); and reject all whose fitness rank is above f*.
The SPT assumes that individuals encounter potential mates at random with respect to their rank, and shows that focal individuals who follow the mating decision rule to accept any potential mate i for which wi > wf*, and reject any potential mate j for which wj < wf*, will maximize their average lifetime reproductive fitness. Note that any given focal individual in this stochastic ensemble may not actually mate with all individuals having wi > wf*, in their lifetime. However, the rule that maxi-
mizes lifetime reproductive success is to find acceptable any individual encountered whose w is greater than wf*, the fitness of the potential mate at rank f* (Fig. 11.3).
DERIVATION OF THE SPT
The SPT proof is provided in the Appendix. Here, we describe the steps that allowed us to analytically solve for the number of potential mates that a focal individual should find acceptable to maximize the focal’s average lifetime fitness.
In step 1, we constructed a series of absorbing Markov chain models for each decision rule associated with n, under specified ecological constraints affecting values of e, s, l, and the w distribution. If n = 3, for example, there are 3 decision rules, and 3 matrices are required to deduce the rule that would maximize average lifetime fitness: (i) accept the potential mate ranked 1 and reject potential mates ranked 2 and 3; (ii) accept potential mates ranked 1 and 2 and reject the potential mate ranked 3; and (iii) accept all 3 potential mates. If n = 100, there are 100 decision rules and, without the SPT proof by induction, 100 matrices would have been required to deduce the rule that would maximize the focal individual’s
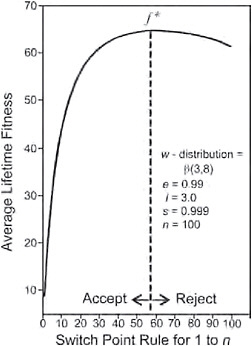
FIGURE 11.3 An example of a switch point graph.
average lifetime fitness under specified values of e, s, l, n, and w distribution. The 100 rules take the following form: accept up to rank f* (where f* equals the highest acceptable rank), reject all from rank n − f*. The probabilities associated with e, s, and l determine the mean number of times the focal will pass through each cell in each matrix. It is possible to solve this algebraically without specifying numerical values of e, s, l, or n.
In step 2, we computed for each decision rule the mean number of times that an individual passed through the mating state with each acceptable potential mate and multiplied this mean by the fitness, w, that would be conferred if the focal actually mated with the acceptable mate. The w for each potential mate comes from the specified beta distribution.
In step 3, we summed up these products from each decision rule for a focal with specified e, s, l, n, and w distribution to find f*, the decision rule that would maximize average lifetime fitness, if the focal actually mated with each acceptable mate.
Because of social and ecological constraints (Gowaty et al., 2007), it is unlikely that focal individuals actually mate with all potential mates who are acceptable to them. Therefore, we characterize the rule as the switchpoint at which focal individuals switch from accepting potential mates to rejecting them. That is, it is important to keep in mind that the SPT does not state that individuals actually mate up to f*, only that they will accept any potential mate they encounter whose rank is 1 to f*. Thus, the SPT is only a decision rule, not a statement of how many mates a focal individual will have. The SPT specifies whether to accept or reject a potential mate under chance effects from demographic and environmental stochasticity. The information embodied in the SPT is about future opportunities, and, if one actually mates with a potential mate, the opportunity costs associated with having mated with a particular potential mate. We hypothesize that individuals use this information to adjust their reproductive decisions as their ecological circumstances change. The two body problem that occurs when 2 individuals meet and one accepts but the other rejects cannot be studied in the current Markov chain model.
The analytical solution for a switch point set at f, for which the derivation is the SI, is:
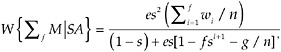
(1)
where g = n − f.
The solution is the decision rule f* that maximizes Eq. 1. Note that e, s, l, n, and the w distribution could be functions of 1 or more of the other parameters. There is nothing in the theorem that precludes such functional interactions between the parameters. We have presented the version without interaction for heuristic simplicity.
The SPT allows us to predict how an individual’s switch point changes with changing ecological and life-history circumstances that affect e, s, l, n, and w distribution, which we present next.
RESULTS
Fitness Distributions Affect the Switch Points of Focal Individuals
Figs. 11.4 and 11.5 show how the switch point changes for a focal individual experiencing identical values of e, s, l, and n, when the w distribution varies. When the w distribution is right skewed, the fitness conferred at f* is on average higher than when the w distribution is left skewed; and the fraction of acceptable mates is greater when w distributions are strongly right skewed with many potential mates conferring high fitness.
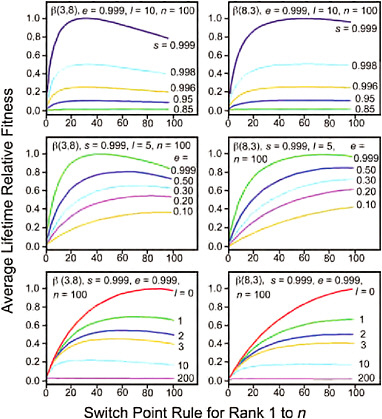
FIGURE 11.4 Comparison of the effects of different w distributions on the switch point when e, s, l, and n are held constant.
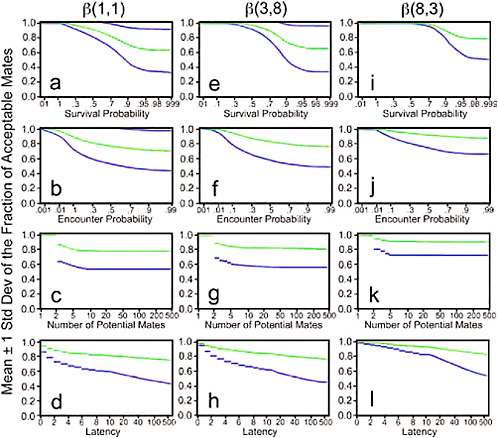
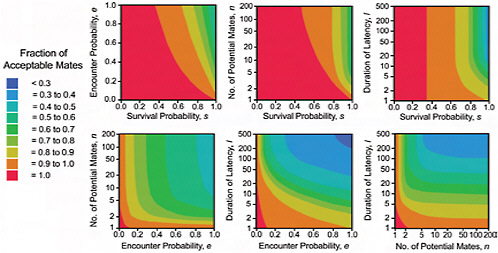
FIGURE 11.5 The means (top lines) plus or minus 1 standard deviation (bottom lines) of the fraction of acceptable mates for the marginal distributions of s, e, n and l for three different distributions of fitness. The left panel is for β(1,1), the middle for β(3,8), and the right for β(8,3). The standard deviations are plotted as lines below and above the means. Because no values can be above 1 in these graphs, most show the standard deviation below the mean.
Variation in Number of Potential Mates
In populations of different sizes, individuals with identical e will see different numbers of potential mates, with those in larger populations seeing more than those in small. The SPT predicts that individuals in larger populations, when holding e, s, l, and the w distribution constant, reject a larger fraction of potential mates than those in smaller populations (see Fig. 11.6). This is because for a given e, s, or l a larger n allows focal individuals to sample a larger portion of the fitness distribution. Likewise, for a given e, s, and l, individuals in smaller populations will
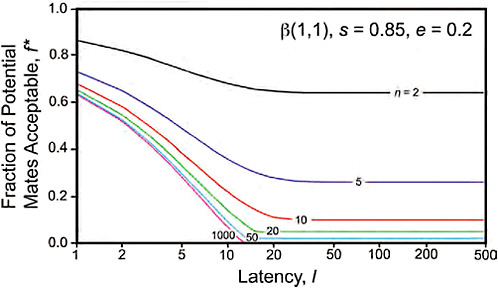
FIGURE 11.6 Effect of latency l and population size n on the fraction of acceptable mates, for a uniform w-distribution of fitnesses conferred, β(1,1). Encounter probably e = 0.2; survival probability s = 0.85.
accept more mates, because they will sample a smaller portion of the fitness distribution.
Variation in s Changes Individual Switch Points Most
A sensitivity analysis of Eq. 1 indicates that changes in fitness with respect to changes in s, e, and l are such that dw/ds > dw/de > dw/dl (Figs. 11.7 and 11.8 and further discussion in the Appendix). Of the 3 parameters, the greatest sensitivity is to s, and the least sensitivity is to l. As s → 1, the focal individual has a longer and longer mean life span, and the derivatives increase without bound. This is because total lifetime fitness at f* is the sum of mean fitness conferred over all acceptable mates from rank 1 to rank f*. Lifetime fitness at f* is approximately 2 orders of magnitude less sensitive to changes in e than to changes in s. Lifetime fitness at f* is least sensitive to l. The parameters also interact in their sensitivity effects on fitness. The interactions are manifest in the fact that the sensitivity of the fitness function at f* to e, s, and l is a function of the specific values of the other parameters. For example, increasing e increases the sensitivity of fitness to s. Similarly, increasing s strongly increases the sensitivity of fitness to e.
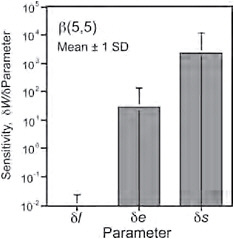
FIGURE 11.7 The mean and standard deviation in the rate of change in log average lifetime fitness relative to changes in s, e, and l for a beta distribution with a strong central tendency.
Time Available for Mating Affects the Switch Points of Focal Individuals
Increases in e, s, and n decrease the time to finding potential mates, thereby increasing reproductive opportunities for focal individuals, an effect that enhances the fitness benefit of rejecting more potential mates. The SPT shows that within a sex, individuals experiencing longer latencies must make up opportunity costs relative to individuals that experienced shorter latencies.
Changing More Than One Parameter at a Time
All else is seldom equal, and the SPT allows evaluation of the effects of variation in e, s, l, n, and w distribution on f* while varying only 1 parameter, 2 parameters (Fig. 11.9), or all 5 parameters at a time.
DISCUSSION
What the SPT Does and Does Not Do
The SPT makes no assumptions about underlying sex differences. We assume that individuals’ time available for reproduction is finite, and we characterize variation in individual reproductive careers in terms of constraints on time available for mating. We simplify the parameters of previous theories and unify them in a general framework that provides
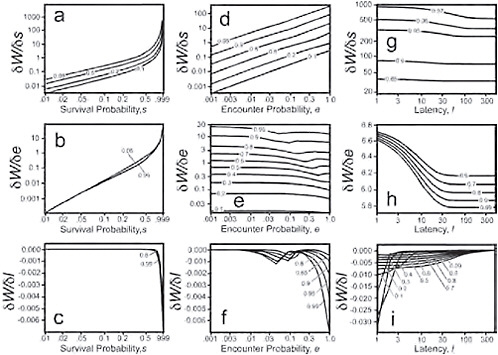
FIGURE 11.8 Top three panels: Sensitivity of the derivative of lifetime fitness at the switch point f* with respect to the survival probability s, a. as a function of survival probability s (x axis), for several sample values of the probability of encounter e (contour lines), and for a latency l = 10; d: as a function of encounter probability e (x axis), for several sample values of the probability of survival s (contour lines), and for a latency of l = 10; g: as a function of latency l (x axis), for several sample values of the probability of survival s (contour lines), and an encounter probability e = 0.99. Middle three panels. Sensitivity of the derivative of lifetime fitness at the switch point f* with respect to the encounter probability e, b. as a function of survival probability s (x axis), for several sample values of the probability of encounter e (contour lines), and for a latency l = 10; e: as a function of encounter probability e (x axis), for several sample values of the probability of survival s (contour lines), and for a latency of l = 10; h: as a function of latency l (x axis), for several sample values of the probability of survival s (contour lines), and an encounter probability e = 0.99. Bottom three panels. Sensitivity of the derivative of lifetime fitness at the switch point f* with respect to latency l, c. as a function of survival probability s (x axis), for several sample values of the probability of encounter e (contour lines), and a latency l = 10; f: as a function of encounter probability e (x axis), for several sample values of the probability of survival s (contour lines), and for a latency of l = 10; i: as a function of latency l (x axis), for several sample values of the probability of survival s (contour lines), and an encounter probability e = 0.99.
a unique way to think about reproductive decisions (Fig. 11.1). We start simply with an individual and its time budget.
The SPT predicts the fraction of potential mates that a focal individual finds acceptable to mate. Each calculation of the switch point is about a single individual under specific values of ecological constraints on their time available for future reproduction. The SPT assumes that individuals assess the likely fitness that would be conferred by alternative potential mates before accepting or rejecting a potential mate. Furthermore, it ranks potential mates from highest fitness conferred (rank 1) to lowest fitness conferred (rank n, where n is the total number of alternative potential mates in the population). The SPT assumes that focal individuals encounter potential mates at random with respect to the rank the focal assigns them. The switch point is the rule (what lowest fitness rank to accept), which if obeyed, maximizes average lifetime fitness for a focal individual under specified time constraints. These constraints arise from social or ecological factors. The primary prediction of the SPT is that e, s, l, n, and the w distribution jointly determine each reproductive decision a focal individual makes.
The SPT is silent about how many times a focal individual actually mates, so that the SPT is accurately characterized as a model of the decision rule that a focal individual would use, if it encounters a particular potential mate. Because the absorbing Markov chain model is stochastic, some focal individuals may be unlucky during their entire lives and never encounter a potential mate. Because the SPT provides an analytical solution, one can calculate how many focal individuals, under different time constraints, may never encounter a potential mate. So, the SPT is a model of the decision rules—accept this one, reject that one, when potential mates come in up to n qualities, if the focal individual encounters that potential mate. We hypothesize that flexible individuals should use these rules under variation in opportunities for future matings and opportunity costs of realized matings.
The SPT is silent also about the proximate mechanisms mediating preferences. The SPT may be used to inform models of trait evolution under sexual selection (see below), but the SPT by itself is not a model about the evolution of traits in preferred individuals.
With the SPT, we are able to design studies to answer whether sex differences primarily are due to past selection on females for choosy behavior and on males for profligate, competitive behavior. With it, we are able to ask by what ways, and to what effects on fitness, do ecological and social constraints influence sex roles. With it, we are able to determine if contemporary assessments of future fitness costs and benefits induce individual reproductive decisions.
Are Both Sexes Flexible?
It is possible to empirically test the hypothesis that both sexes make flexible reproductive decisions, as the SPT predicts. Imagine an experiment in which individuals of both sexes develop in social environments in which they have controlled exposures to future potential mates. Imagine also that the population has been managed so that the w distribution for all individuals of either sex has the same shape (such as might occur in large outbred populations without sex-biased dispersal) and that n is equal. In our thought experiment, investigators move all individuals into same-sex holding arenas just before they reach sexual maturity to guarantee that mating does not occur. Then, they carry out pretouching arena [such as the one pictured in Anderson et al. (2007)] tests, to measure the fraction of potential mates acceptable to focal individuals. Note that the experiments evaluating accept/reject responses must be tightly controlled so that subjects’ responses are not contaminated by intrasexual interactions among the discriminatees or sexual coercion (Kingett et al., 1981). Then investigators manipulate one variable, say, e so that in similar time periods some focal individuals encounter fewer potential mates, and in other trials the same focal individuals encounter more potential mates. This experimental procedure would vary the focal individual’s encounter rate with potential mates and, if carried out, would provide a strong within-subject test of the prediction that focal individuals reject more potential mates as e increases. Importantly, the SPT predicts that if e, s, l, n, and the w distribution are the same for all tested individuals, males and females will show no significant differences in their accept/reject behavior.
The SPT is an Alternative Hypothesis to Anisogamy Theory
The SPT is not only a predictive hypothesis of when individuals should switch their reproductive decisions. It is also a strong alternative hypothesis that can be simultaneously tested along with classic ideas about the evolution of sex roles. Anisogamy theory is silent about ecological and temporal constraints on reproductive decision making. It predicts that in species with gamete size asymmetries, such as D. pseudoobscura and D. melanogaster, the sex with the larger gametes will reject more potential mates (i.e., “be choosier”) than individuals of the sex with the smaller gametes. In species such as Drosophila hydei, with little or no gamete size asymmetries, anisogamy theory predicts that males and females should be similarly “choosy” and similarly “indiscriminate.” In contrast the SPT predicts that for both sexes in all 3 species, individuals will flexibly adjust their decisions to accept or reject particular mates as e, s, l, n, and w distribution vary. These alternatives could be tested with a crucial experiment (Platt, 1964) in which a test of a single prediction—about accepting or
rejecting potential mates—could simultaneously reject one hypothesis and provide support for the alternative.
The SPT is an Alternative Hypothesis to Parental Investment Theory
For species in which parental investment is biased toward one sex, investigators could compete the predictions of the SPT with parental investment theory. Controlling for s, e, n, l, and w distribution for experimental subjects, the predicted behavior of individuals of different sexes would be the same under the SPT. Parental investment theory, by contrast, predicts that in a species with female-biased parental investment, females would reject more and males would accept more potential mates, whereas, in a species with male-biased parental investment, females would accept more and males reject more potential mates. Another valuable test would be of virgins of both sexes, for whom l = 0, in species with female-biased parental investment and in species with male-biased parental investment. As with anisogamy theory, these alternative predictions of the SPT and parental investment theory could be tested with a crucial experiment.
Almost Nothing Is Known Empirically About w Distributions
The w distribution has only been characterized for a few populations (unpublished data), and no one to our knowledge has tested the effects of w distributions on individual reproductive decisions. For laboratory populations of flies and other organisms with short generation times and no sex biases in dispersal, it is relatively easy to estimate the shape of the w distribution, measuring fecundity, productivity, and offspring viability from a sample of random pairs breeding under enforced monogamy. An experiment that we plan to do will begin with flies cultured under inbreeding and outbreeding, which may produce w distributions with different shapes, and then to test the predictions (Fig. 11.7) for virgins (l = 0) when e, s, and n are held constant, using pretouching arenas.
Implications for Experimental Studies of Mate Preferences for Fancy Male Traits
The SPT is not a hypothesis for the evolution of fancy male traits, nor does it predict the evolution of traits mediating preferences. Nevertheless, the SPT suggests that selection should favor traits that increase a focal individual’s encounters with potential mates. Enhanced encounters increase reproductive opportunities, thereby reducing the opportunity costs of accepting potential mates who would confer low w. Traits, such as bizarre or easily seen plumage, loud calls, songs, or pheromones that travel over
large distances may attract more potential mates to the focal individual. In contrast to classic sexual selection ideas, however, the SPT predicts a different payout, not necessarily more mates, but in more reproductive opportunity. The SPT thus predicts that attractive focal individuals reject more potential mates than other, less attractive same-sex conspecifics, all else equal (i.e., if s, l, n, and w distribution are equal for attractive and unattractive focals). This prediction has not been made by any hypothesis of classic sexual selection.
The SPT suggests that many previous failures to associate fitness rewards for female mate choice for fancy traits in males might be explained by experimentally uncontrolled variation in e, s, l, n, or w distribution. The SPT predicts that a focal individual exposed only to a small number of potential mates would fail to show a preference. It is also possible that investigators have exposed females to males of nearly equivalent fitness. If this were the case, adaptively flexible females would more often accept potential mates, because the differences in w between potential mates may be very small, thus reducing the opportunity costs from any particular mating. Thus, the SPT may inform previous ambiguities in mate preference studies.
The Ecology of Sex Roles
Thinking about time constraints on reproductive decisions suggests a new, powerful framework for sex differences research. If individuals of different sexes have different feeding niches and/or different exposure to pathogens or predators, there are likely to be associated differences in e, s, and l experienced by individuals of different sexes and, as the SPT predicts, differences in the typical reproductive decisions of individuals of different sexes. Or, if species in which one sex disperses, but the other does not, individuals of different sexes may see different w distributions and therefore express differences in the fraction of potential mates acceptable. Thus, it is possible that sex differences in typical reproductive decisions may have more to do with what Darwin called “habits of life,” rather than with fixed sex differences. Data on how different habits of life affect e, s, l, n, and w distribution of individuals are not yet systematically collected to our knowledge, and may prove interesting indeed, perhaps providing a path toward resolution of the some of the controversies that have dogged Darwin and his followers up to the current day.
ACKNOWLEDGMENTS
We thank John Avise and Francisco Ayala for inviting P.A.G. to contribute to the Arthur M. Sackler Colloquium of “In the Light of Evolution
III: Two Centuries of Darwin and J. P. Drury, Brant Faircloth, Graham Pyke, Steve Shuster, and Elliott Sober for comments on a previous version of the manuscript. This work was supported by National Science Foundation grant Beyond Bateman, which has allowed us and our collaborators, W.W. Anderson and Y.K. Kim, to study variances in number of mates and reproductive success in 3 species of flies with different gamete size asymmetries.
APPENDIX
In this Appendix, we derive Eq. 1 for the switch point theorem given in the paper, and we also give the equations used in the sensitivity analysis of lifetime fitness to changes in each of the model parameters. We also present some graphical results.
Derivation of the Switch Point Theorem
The switch point theorem is an analytical solution to the question of how many potential mates a focal individual should accept or reject to maximize lifetime fitness. Consider a focal individual with a finite reproductive life span, during which the individual searches for potential mates, accepting some and rejecting others, and having to take time out from searching and mating every time it mates and reproduces, a latency period from the onset of one copulation to receptivity to remating. We can represent movement of the individual through its reproductive lifetime as a series of states, each lasting 1 time unit, such as searching but no potential mate is encountered in a given time step, searching and potential mate i is encountered, mating with potential mate i, and in time period j of a latency period of length l.
Let e be the probability that a potential mate is encountered per unit time. Let there be n potential mates, and let pi be the probability that the encountered potential mate is individual i, where ∑pi = 1. The relative fitness conferred on the focal individual by mating with potential mate i is a beta-distributed random variable, β(ω,ν) where ω and ν determine the shape of the fitness distribution. Let s be the probability of survival of the focal individual over 1 unit of time. The reproductive life span of the focal individual is the time from the onset of reproductive maturity until the individual’s death. In terms of the probability of survival per unit time, the expected reproductive life span of the focal individual is 1/(1− s). Note that small changes in the probability of survival when s is near unity can cause large changes in life span. Thus, for example, survival probabilities of 0.9, 0.99, and 0.999 correspond to mean life span of 10, 100, and 1000 time units, respectively. In a Markov chain there are discrete time steps. When s = 0, the individual lives one time step and dies. When s = 1, the
ratio of 1/1 − s is infinite and the reproductive life span is infinite, the individual lives forever. Thus, s = 1 is not a biologically meaningful value. Values of s > 0 and s < 1 are the biologically meaningful values and these are the ones we use in our sensitivity analyses.
The relative fitness of potential mates influences whether the focal individual should or should not mate a particular potential mate. To illustrate the Markovian process, we analyze a case of 3 potential mates (n = 3). In this simple case, we can distinguish 3 possible decisions. A focal individual could accept all 3 potential mates as encountered. Or an individual might accept 2 and reject 1 of the 3 potential mates. Or a focal individual might accept only 1 of 3, rejecting the other 2 potential mates.
Consider the “accept all” 3 case first. The state of the focal individual can be receptive and searching for a mate, but it does not encounter a potential mate in the current time step. Label this state SA. Or the focal individual may encounter a potential mate in the current time step, in which case there are 3 possible states: encountering potential mate number 1 (state S1), encountering potential mate number 2 (state S2), or encountering potential mate number 3 (state S3). Because the focal individual accepts all 3, it will then mate with the potential mates as encountered (i.e., enter mating states M1, M2, and M3, respectively). Let l be the length of time that the focal individual is in latency before returning to the pool of receptive individuals. Measure the duration of the latency period in the same time units used for measuring s and e. In this example, let the latency l = 1. Let the state of latency be labeled L1, and the absorbing state of death D. The matrix of transition probabilities for the case “accept all 3” is thus:
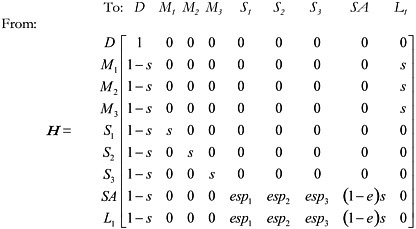
[1]
We list “to” and “from” states along the top and left side of matrix H, respectively. The column state (“to”) is the next state reached after the states (“from”) listed on the rows. Note that the focal individual has a probability 1 − s of dying during every time step, and moving to state D (death). If death occurs, this is the terminating point of the absorbing
Markov chain. In the accept all 3 case, whenever the focal individual encounters a potential mate, it mates, with a probability simply equal to the survival probability (because the only behavior the individual exhibits next is to mate) (e. g., Pr{M1 | S1} = Pr{M2 | S2} = Pr{M3 | S3} = s). During search, the focal individual encounters a potential mate of quality i with probability Pr{SAS|S1} = espi. Since the encounter probability is e, the probability that the search fails in the current time step and the focal individual has to continue searching in the next time step is: Pr{SA | SA} = (1 − e)s.
We can solve Eq. (1) for the expected number of times the focal individual passes through each state before death, by computing E = (I−H)−1. Matrix E always exists and its element ei,j is the expected number of times over its lifetime that the focal individual is in column state j given that the focal individual starts in row state i. By convention we assume a newly mature focal individual begins the reproductive portion of its life in state SA, searching for a mate. From Eq. (1), the expected number of matings of a focal individual with potential mate i is
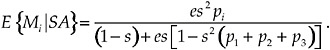
[2]
Therefore, the total lifetime mating success of the focal individual over all potential mates is
[3]
Generalizing this expression to a latency of 1 time units yields a total lifetime mating success of

[4]
The total lifetime mating success for a latency of two time units (l = 2) is therefore
[5]
Generalizing this expression to a latency of l time units yields a total lifetime mating success of
[6]
Now, consider when a focal individual mates with 2 of the 3 potential mates but not the third. In this case, state M3 no longer exists (although potential mate 3 is still encountered, which is state S3), so the transition matrix becomes:
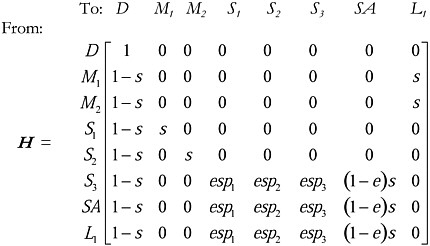
[7]
Note that when the focal individual encounters potential mate 1 (S1) it moves to the state of mating with individual 1 (M1) and likewise when the focal individual encounters potential mate 2 (S2), it moves to mating that individual (M2). However, note that when potential mate 3 is encountered, the focal individual does not mate with it (there is no state M3), but it resumes search, enters states S1, S2, S3, and SA, depending on what the search results are.
For a focal individual with a latency of 1, this decision rule yields a total lifetime mating success of:
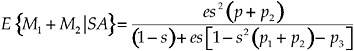
[8]
and for a focal individual with a latency of l time units:
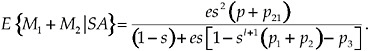
[9]
In the case in which the focal individual mates with only 1 of the 3 possible potential mates, 1 but not 2 or 3, the transition matrix is
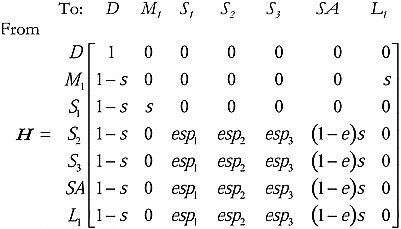
[10]
Focal individuals with a latency, l = 1, with this decision rule gain a lifetime mating success of
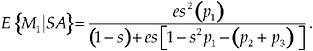
[11]
For the generalization of this decision rule to focal individuals with latency of l time units, expected lifetime mating success becomes
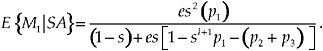
[12]
One can find by induction the general solution for the lifetime mating success of a decision rule in which the focal individual mates with f individuals out of a total of n total potential mates, where f ≤ n. The solution is
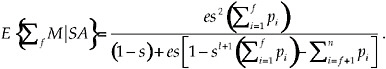
[13]
We are now in a position to evaluate the cumulative lifetime fitness for focal individuals exhibiting this decision rule. If the fitness of the focal individual of mating with potential mate i is wi, then the focal individual’s cumulative lifetime fitness is simply its mating success with potential mate i multiplied by wi, summed over all of the focal individuals’ mates:
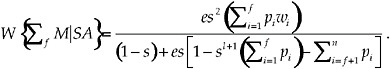
[14]
The expression in Eq. (14) is the analytically derived mean of cumulative lifetime fitness computed over an stochastic ensemble of focal individuals, each of whom assesses the fitness distribution of potential mates in the same way, experiences the same values of e, s, and l, and has the same mating decision rule. Eq. (14) takes on different values as we change f, the number of acceptable mates, out of a total of n potential mates. The objective is to find the value of f, call it f*, which maximizes Eq. (14); f* is the switch point. Given values of e, s, and l and a distribution of fitnesses wi across a set of n potential mates, the recipe for maximizing Eq. (14) is as follows: (1) Rank the n potential mates in fitness conferred on the focal individual from high to low. (2) Next, compute the average focal individual’s expected cumulative lifetime reproductive fitness for these parameters and fitness distribution, assuming that the focal individual mates with only one potential mate, the highest fitness-conferring individual, and rejects the remaining n – 1 individuals. This corresponds to f = 1 in the Eq (14). (3) Now, repeat step 2, but assume that the focal individual mates with the top two potential mates, so that f = 2 in Eq .(14). (4) Continue this process, adding 1 more mate at a time and computing the expression in Eq. (14) until f = n. (5). Plot the curve of reproductive fitness as a function of f, the number of ranked potential mates that are accepted, and find that value of f, f*, that produces the highest average reproductive fitness. This is the switch point, and f*/n is the fraction of acceptable mates that maximizes the cumulative lifetime fitness.
If the potential mates are equally likely to be encountered, then we can further simplify Eq. (14)
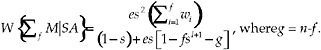
[15]
This is the expression given by Eq. (1) in the text of the paper.
Sensitivity Analysis
We studied the sensitivity of the fitness function to changes in the encounter probability e, the survival probability s, and the latency l, by computing the derivatives of Eq. (14) with respect to each of the parameters. We evaluated the derivatives at the switch point, f*. The sensitivity of the fitness function at f* to changes in encounter probability e is given by
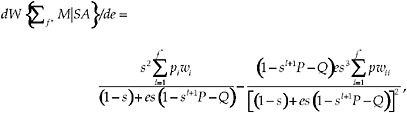
[16]
where ![]()
The sensitivity of the fitness function at f* to changes in the survival probability s is
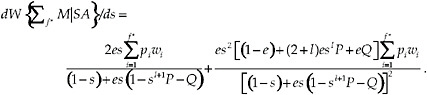
[16]
Finally, the sensitivity of the fitness function at f* to changes in latency l is
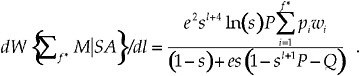
[18]
Results
Fig. 11.6 shows the effect of varying latency l and the population size of acceptable mates n on the fraction of mates acceptable, for a w distribution of β(1,1). The fraction of acceptable mates declines with population
size, and with increasing latency, but the effect of latency is minimal for long latency times. Fig. 11.5 shows how the mean fraction of acceptable mates and its standard deviation change as a function of the w distribution and of each of the model parameters. The left-most column of graphs (a–d) are for a uniform w distribution of β(1,1). The middle column of graphs (e–h) are for a w distribution, β(3,8), skewed to low fitness values, and the right-most columns of graphs (i – l) are for a w distribution, β(8,3), skewed to high fitness values. Note that a higher fraction of potential mates are acceptable when the fitness distribution is skewed high than when it is skewed low or is uniform. Fig. 11.8 presents a graphical representation of the results of the sensitivity analysis. The top row of panels (a, d, g) represents how the sensitivity of lifetime fitness to survival rate s is affected by variation in s, e, and l. The middle row of panels (b, e, h) show how the sensitivity of lifetime fitness to encounter rate e is affected by variation in s, e, and l. The bottom row of panels (c, f, i) show how the sensitivity of lifetime fitness to latency l is affected by variation in s, e, and l. Note that in general, the sensitivity of lifetime fitness to survival is much greater than sensitivity to encounter rate, which in turn is much greater than the sensitivity to latency. Note also that the parameters interact in complex nonlinear ways in their impact on the sensitivity.