C
Experimental Design Strategies
FRACTIONAL FACTORIAL DESIGNS
Factorial designs are used to study the joint effect of several factors on a response. In a factorial design we assume that there are a number of factors present and each factor has several levels. In a 2k factorial design there are k factors and every factor has only two levels (e.g., high versus low or experimental versus control). Thus the total number of level combinations is 2k. Consider an example of a 23 factorial design where the three factors are denoted by A, B, and C. The eight combinations of levels are denoted by 1, a, b, c, ab, bc, ca, abc. Here, a is the main effect of the factor A, ab is the interaction effect of the factors A and B. All other level combinations have similar interpretations. The main goal of a factorial design is to study the main effects of factors involved in the design. An experimenter may also be interested in studying the two factor interaction effects or even higher-order interactions. To run a complete 2k factorial design, the experimenter needs to have 2k experimental conditions (e.g., groups). Sometimes, to achieve better efficiency, the design is replicated several times. To estimate the average of the main effect of factor A in a 23 factorial design replicated n times, we use the following formula:
where abc is the total number of observations in n replicates with all factors at the high level, and all other symbols have similar interpretations.
The interaction effect of A and B is
The sum of squares due to factor A, denoted by SSA, is
Similarly, the sum of squares due to the AB interaction is
The total sum of squares SST is
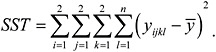
To get the sum of squares due to error (i.e., SSE) we subtract the sum of all the 7 factor level combinations (except 1) from SST. The degree of freedom for any factor combination is 1 and that of SSE is 8(n – 1). The significance of the interaction effect AB is tested by constructing the F-statistic,
As we see from the previous discussion, if the number of factors k in a 2k factorial design increases, the total number of runs in a complete factorial design outgrows the resources of most experimenters. If the experimenter believes that higher-order interactions are negligible, the main effects and the lower-order interactions can be estimated by running only a fraction of the complete experiment. Let us assume that in a 23 factorial design the second-order interactions are not significant and the experimenter can provide only four conditions (i.e., experimental
and/or control groups) to estimate the main effects. In order to conduct this experiment in only four conditions to estimate the main effects we have to select the treatment level combinations appropriately. To choose the appropriate level of treatment combinations we first define a generator that is generally a higher-order interaction. Let our generator be ABC. In each of the above average factor effect expressions (i.e., A, B, etc.) 1 has either a + or − a sign. Choose only those factor levels effects that have −1 sign (those are A, B, C, and ABC). The average effects of these factors in this ½ fractional factorial design are determined by
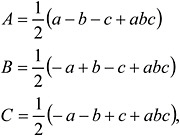
and the sums of squares due to these factors are
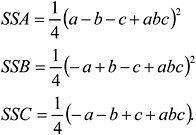
No degrees of freedom are left for the error. Hence we can estimate the main effects but we cannot test their significance. Generally, this is not the case for ½ fractional factorial designs in which there are four or more factors.
In terms of confounding, 23 ½ fractional replicate designs can estimate main effects, but they are confounded with two-factor interactions. 24 ½ fractional replicate designs can estimate main effects that are unconfounded by two-factor interactions; however, the two-factor interactions may be confounded with other two-factor interactions. 25 ½ fractional replicate designs can estimate unconfounded main effects and two-factor interactions, but three-factor interactions may be confounded
with two-factor interactions. Finally, 26 ½ fractional replicate designs can estimate main effects and two-factor interactions unconfounded by three-factor or less interactions, but three-factor interactions may be confounded with other three-factor interactions.
The previous examples illustrate the resolution of the fractional factorial design. Resolution II designs are completely undesirable because even the main effects are confounded with each other. Resolution III designs (e.g., 23-1 which represents a ½ replicate of a 23 design) can estimate main effects, but the main effects may be confounded with two-factor interactions. Resolution IV designs can estimate both main effects and two-factor interactions, but some of the two-factor interactions are confounded with each other. Resolution V designs can estimate main effects that are unconfounded by three-factor (or less) interactions, and two-factor interactions that are unconfounded by other two-factor interactions, but the two-factor interactions may be confounded with three-factor interactions. Finally, resolution VI designs can estimate unconfounded main effects (four-factor or less) and two-factor interactions (three-factor or less), and estimate three-factor interactions, but they may be confounded by other three-factor interactions. As such, if we are interested in preserving the integrity of both main effects and two-factor interactions in a 2k fractional factorial design, we require a resolution V or higher design. If all that we care about are the main effects, a resolution III design will allow us to estimate them, but a resolution IV design is required if we want to both estimate and test the significance of the main effects. Resolution IV 2k fractional factorial designs include 24-1, 26-2, 27-2, 27-3, 28-3, 28-4, 29-3, 29-4 designs, where for example, a 29-4 design reduces the total number of experimental conditions (i.e., factor level combinations) from 29 = 512 to a far more manageable 25 = 32 and still permits estimates and tests of main effects that are unconfounded by two-factor interactions. Resolution V 2k fractional factorial designs include 25-1, 28-2.
An alternative strategy is to use a resolution III fractional factorial design to conduct a screening experiment, which would then be followed by a more complete but lower-dimensional factorial design. For example, Neter et al. (1996) describe a resolution III 210-6 design, involving 16 experimental conditions out of the 1,024 conditions needed for a full factorial design, that was used to study the effects of six process variables and four ingredient variables on the extent of crystallization in ice cream. The 16 conditions included in the screening study are as follows:
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
|
–1 |
–1 |
–1 |
–1 |
–1 |
–1 |
–1 |
–1 |
+1 |
+1 |
|
+1 |
–1 |
–1 |
–1 |
+1 |
–1 |
+1 |
+1 |
–1 |
–1 |
|
–1 |
+1 |
–1 |
–1 |
+1 |
+1 |
–1 |
+1 |
–1 |
–1 |
|
+1 |
+1 |
–1 |
–1 |
–1 |
+1 |
+1 |
–1 |
+1 |
+1 |
|
–1 |
–1 |
+1 |
–1 |
+1 |
+1 |
+1 |
–1 |
–1 |
+1 |
|
+1 |
–1 |
+1 |
–1 |
–1 |
+1 |
–1 |
+1 |
+1 |
–1 |
|
–1 |
+1 |
+1 |
–1 |
–1 |
–1 |
+1 |
+1 |
+1 |
–1 |
|
+1 |
+1 |
+1 |
–1 |
+1 |
–1 |
–1 |
–1 |
–1 |
+1 |
|
–1 |
–1 |
–1 |
+1 |
–1 |
+1 |
+1 |
+1 |
–1 |
+1 |
|
+1 |
–1 |
–1 |
+1 |
+1 |
+1 |
–1 |
–1 |
+1 |
–1 |
|
–1 |
+1 |
–1 |
+1 |
+1 |
–1 |
+1 |
–1 |
+1 |
–1 |
|
+1 |
+1 |
–1 |
+1 |
–1 |
–1 |
–1 |
+1 |
–1 |
+1 |
|
–1 |
–1 |
+1 |
+1 |
+1 |
–1 |
–1 |
+1 |
+1 |
+1 |
|
+1 |
–1 |
+1 |
+1 |
–1 |
–1 |
+1 |
–1 |
–1 |
–1 |
|
–1 |
+1 |
+1 |
+1 |
–1 |
+1 |
–1 |
–1 |
–1 |
–1 |
|
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
Three factors were identified as important, and these factors were then studied in a 23 full factorial design.
The 2k-f designs that have highest possible resolution have been identified and catalogued for choices of k and f that are of general interest by Box and colleagues (2005) and are also provided online by the National Institute of Standards and Technology at http://www.itl.nist.gov/div898/handbook/pri/section3/pri3347.htm.
Response Surface Methodology
The previous discussion of fractional factorial designs is based on discrete levels of each factor (e.g., high or low, experimental or control). In some cases, the factors of interest may be continuous variables, for which simple dichotomization is not possible. An alternative approach for exploring the effects of individual factors, low-level interactions, and nonlinear relations is based on response surface methodology (RSM). In RSM we first model the response function, which is influenced by several variables, and then we optimize this function. Suppose that we have a quantitative index of carcinogenicity Y in a test animal that depends on the length-to-width ratio (x1) and size (x2) of a particular mineral particle to which the animal is exposed. The scientific objective is to determine the levels of x1 and x2 in order to achieve a certain value of Y, say y0. Let
us assume that the relationship between Y and (x1, x2) is modeled by a function f: i.e., y = f(x1, x2) + ε, where ε represent noise in response y. Let E(Y) = η = f(x1, x2). The surface represented by η = f(x1, x2) is called the response surface. In RSM the functional form of f is unknown. We generally try a linear function or a polynomial function to model this relation. When there is a variation of this relation from laboratory to laboratory, a mixed-effects polynomial model can be used and the method of maximum likelihood or marginal maximum likelihood can be used to estimate model parameters. Once the parameters have been estimated, we can use the estimated response surface to evaluate the values of x1 and x2 for a specific targeted value of y0—for example, a carcinogenetic threshold. A contour plot may help in this regard to estimate levels of x1 and x2 corresponding to a particular level of carcinogenic risk. The RMS method may not provide a reasonable solution for the true functional relationship over the entire space of the independent variables x1 and x2. In that case a small region for the independent variables is chosen and RMS is used sequentially. The interested reader is referred for further discussion on these issues to Box and Draper (2007).
REFERENCES
Box, G. E. P., and N. Draper. 2007. Response surfaces, mixtures, and ridge analyses, 2nd edition. Wiley Series in Probability and Statistics. New York: John Wiley & Sons.
Box, G. E. P., J. S. Hunter, and W. G. Hunter. 2005. Statistics for experimenters: Design, innovation, and discovery, 2nd edition. New York: John Wiley & Sons.
Neter, J., M. H. Kutner, C. J. Nachtsheim, and W. Wasserman. 1996. Applied linear statistical models, 4th edition. Burr Ridge, IL: Irwin.






