B
Counting Strategies1
In reviewing the literature on asbestos fiber counting, there appears to be considerable variability in counts from analyst to analyst within a given laboratory as well as between laboratories. As a consequence, a new observed count from a particular analyst in a particular laboratory may have considerable deviation from the true value. In an effort to provide a connection between observed and true counts and to characterize the uncertainty in the true count, Dulal Bhaumik and colleagues have extended the ideas of Gibbons and Bhaumik (2001) and Bhaumik and Gibbons (2005) to the case of a Poisson random variable, which is the appropriate distribution for rare-event count data. This appendix provides a brief sketch of a potential methodology for addressing the variability and includes an illustration of this methodology using data from the New York state inter-laboratory asbestos testing program.
POTENTIAL METHODOLOGY
Let yij be the jth observation from the ith laboratory, j = 1, … , ni, and i = 1, … , k. We assume that the count variable yij follows a Poisson distribution with parameter λij. To model the interlaboratory variability,
we assume a mixed-effect Poisson regression model with random parameters β0 and β1. We further assume that the joint distribution of β0 and β1 is bivariate normal, with mean vector γ0 and covariance matrix Σ. Hence, regarding the complete distributions of yij, our assumptions are as follows:
where β0i and β1i are respectively the random intercept and slope parameters for the ith laboratory and xij is the true count in the jth measurement from the ith laboratory. Of course, we never know the true count (i.e., xij ), but a reasonable substitute is a consensus estimate based on a series of leading laboratories or analysts.
At this stage, we assume that all of the yij and the corresponding xij are known. We estimate the model parameter Σ by the method of marginal maximum likelihood (MML). The resulting estimate of Σ denoted by ![]() is consistent and MML also provides the standard error of
is consistent and MML also provides the standard error of ![]() . Given MML estimates of the means and covariance matrix, we can obtain empirical Bayes estimates of β0i and β1i, denoted by
. Given MML estimates of the means and covariance matrix, we can obtain empirical Bayes estimates of β0i and β1i, denoted by ![]() and
and ![]() .
.
Let yil be a new observation from the ith laboratory. We do not know the value of the corresponding true observation xil. Our goal is to estimate xil and construct a confidence region for xil using the previous estimates ![]() ,
, ![]() , and
, and ![]() of Σ, β0i , and β1i, respectively. We follow the likelihood-based procedure to estimate xil (i.e., maximize the likelihood function of yil with respect to xil using
of Σ, β0i , and β1i, respectively. We follow the likelihood-based procedure to estimate xil (i.e., maximize the likelihood function of yil with respect to xil using ![]() ,
, ![]() , and
, and ![]() ). Denote this estimate of xil by
). Denote this estimate of xil by ![]() . The expression of
. The expression of ![]() is as follows:
is as follows:
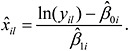
(1)
This estimate is valid provided yil > 0. In the case of yij = 0 we must set xil = 0. Also note that the above estimate of xil becomes nega-
tive if ![]() . In such a scenario we also set xil = 0.
. In such a scenario we also set xil = 0. ![]() is asymptotically unbiased for large values of
is asymptotically unbiased for large values of ![]() , where
, where ![]() . The standard errors of
. The standard errors of ![]() and
and ![]() are obtained directly via MML. The laboratory-specific estimate of the conditional variance of yil is
are obtained directly via MML. The laboratory-specific estimate of the conditional variance of yil is ![]() . Using the Delta method, we obtain the estimate of the variance of ln(yil) as
. Using the Delta method, we obtain the estimate of the variance of ln(yil) as ![]() . Hence an approximate expression for the variance of
. Hence an approximate expression for the variance of ![]() is
is ![]() . Thus, the standard error of
. Thus, the standard error of ![]() is
is ![]() . Let us denote the 95 percent asymptotic confidence region of xil by
. Let us denote the 95 percent asymptotic confidence region of xil by ![]() , where
, where
(2)
The aforementioned confidence region of xil is based on the assumption that we had samples from the ith laboratory and we estimated the laboratory-specific parameters and also estimated Σ borrowing strength from all of the laboratories. However, if the new observation yil comes from an arbitrary new laboratory and the estimates of its parameters are not available, then we should estimate xil globally (i.e., based on the expected values of the laboratory-specific parameters).
Based on these methods, we can now obtain a point estimate of the true number of asbestos fibers in the sample (xij), and a 95 percent confidence region for that true count. There are several useful things that we can do with these quantities. First, we can now always provide an uncertainty interval surrounding our best estimate of the true fiber count. Second, we can determine if the lower confidence limit is greater than zero. If it is, then we can have 95 percent confidence that the true number of asbestos fibers in the sample is greater than 0. Third, we can determine the detection limit, which is the smallest observed count for which the true count is greater than zero. To do this, we begin by setting the true count to zero (i.e., xij = 0 ) and then compute the upper 95 percent prediction limit for the observed y. Any observed y greater than the prediction limit will indicate that the true count is greater than zero. The
prediction limit for y given x = 0 can be computed via simulation using the following expressions of the unconditional mean and variance of y:
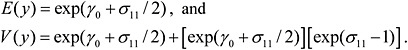
ILLUSTRATION
To illustrate the statistical methodology for inter-laboratory calibration of counts and to obtain a better feel for the magnitude of the variability within and between laboratories, we obtained de-identified data from the New York State inter-laboratory asbestos testing program, which were graciously provided by Dr. James Webber of the Wadsworth Center of the New York State Department of Health. Results based on both transmission electron microscopy (TEM) and phase contrast microscopy (PCM) were analyzed. For TEM, there were a total of 327 samples from 43 laboratories. For PCM there were a total of 9400 airborne asbestos samples analyzed by several hundred laboratories, though participation in a single round ranged from 100 to 150 laboratories. The data were collected as a part of the New York State Environmental Laboratory Approval Program (ELAP) based on the semiannual proficiency testing of laboratories analyzing airborne asbestos, based on the Asbestos Hazard Emergency Response Act (AHERA) criteria and of laboratories analyzing airborne fibers by the NIOSH 7400 method (NIOSH, 1994b). For TEM, our analysis focuses on cummingtonite-grunerite (amosite; AM) counts from 11 rounds. Two additional rounds were not considered because they contained impractically high counts (>6,000 structures/mm2). (All data are expressed in structures/mm2.)
In order to apply the previously described methodology based on a mixed-effects Poisson regression model, we must obtain an estimate of true count for each sample. To this end, we used the overall mean count over all of the laboratories that analyzed each sample. In addition to fitting the Poisson regression model, we also used the alternative minimum level described by Gibbons et al. (1997), Zorn et al. (1997) and Gibbons and Coleman (2001), to obtain estimates of the critical level (LC), detection limit (LD) and quantification limit (LQ) for these data (see Currie, 1968, for an excellent review). The LC is a threshold used to determine whether or not detection has occurred. The LD is the lowest
level for which there is simultaneous high confidence that: (a) detection will occur if the true value is at the detection limit; (b) there will NOT be detection if the true value is zero. The LQ is the lowest level at which a specified (estimated) relative standard deviation is achieved, typically 10 percent, 20 percent, or 30 percent.
TEM Analyses
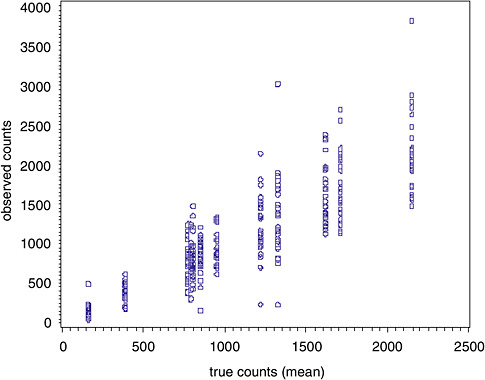
Figure B-1 displays the raw TEM asbestos counts on the y-axis and the mean asbestos counts on the x-axis (i.e., best available estimate of the true count).
Figure B-1 reveals that the absolute variability is proportional to the true (i.e., average) count. This is consistent with a Poisson random variable and can be modeled either via a Poisson regression model or a model that allows for non-constant variability in the calibration function as described by Gibbons and colleagues (1997, 2001). We next fit a mixed-effects Poisson regression model to the TEM AM asbestos data. The model is ln(λ) = (γ0 + γ1x) + (u0 + u1x) where u has a normal distribution with mean 0 and a variance-covariance matrix Σ. x is the true count divided by 1,000 (done to obtain parameter estimates in a metric of reasonable magnitude for the purpose of interpretation since the model is for the log count as shown above). The parameter estimates, standard errors and tests of significance are displayed in Table B-1.
The term Σ(2,2) is the variance of the slopes of the inter-laboratory calibration curves, which reveals a standard deviation of 0.58, which is 58 percent of the mean slope (1.0128) of the calibration curve over all of the 45 laboratories. This is an enormous relative standard deviation, indicating that the laboratories exhibit considerable variability in their individual calibration curves (i.e., differential sensitivity to changing numbers of particles from lab to lab).
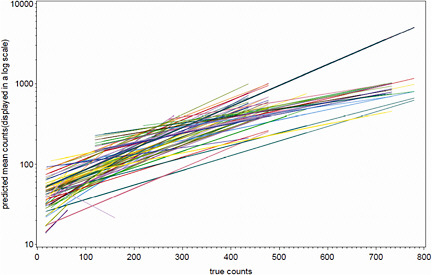
Figure B-2 presents empirical Bayes estimates of the individual laboratory calibration functions. Note that the y-axis is in log-scale. Figure B-2 confirms that there is considerable variability in the slopes of the estimated calibration functions.
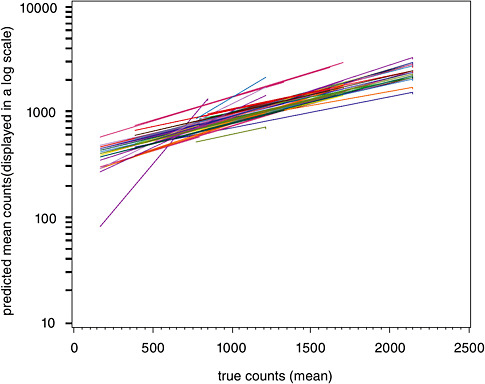
FIGURE B-2 Individual laboratory estimated calibration functions.
NOTE: The y-axis is in a log scale with base = 10.
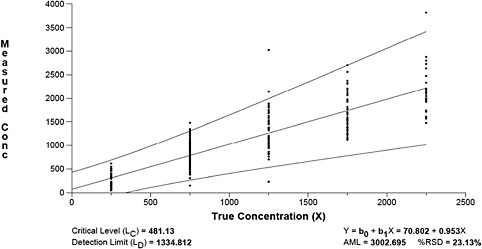
Next, we estimated detection and quantification limits from these data using the AML method described by Gibbons and colleagues (1997). The results are displayed graphically in Figure B-3.
Figure B-3 reveals that the critical level (LC) is 481 fibers, the detection limit (LD) is 1335 fibers and the quantification limit (LQ) is 3003 fibers. At the LQ, the relative standard deviation is still reasonably large (i.e., 23 percent).
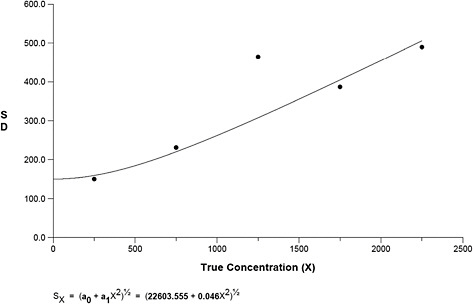
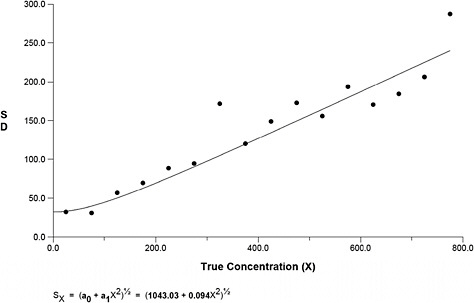
Figure B-4 presents the variance function, for which the best fit was based on the Rocke and Lorenzato Model (Rocke and Lorenzato, 1995) and reveals that the variability increases linearly from 100 to 2,500 fibers.
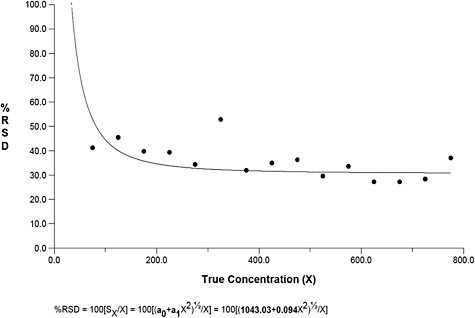
Finally, Figure B-5 displays a plot of the relationship between average counts and the relative standard deviation (RSD). This figure reveals that considerable uncertainty exists in asbestos counts throughout all of the samples investigated, regardless of the number of fibers. However, the RSD stabilizes at around 20 percent for true concentrations around 2,000.
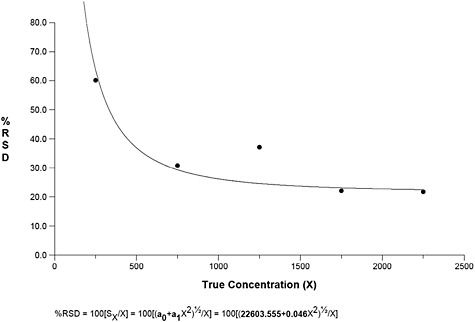
FIGURE B-5 Percent relative standard deviation vs. concentration for asbestos TEM samples in mm2.
PCM Analyses
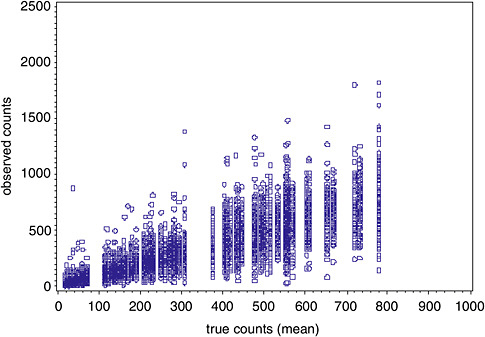
In contrast to TEM, there were several extreme values (in excess of counts of 5,000) associated with the PCM data, despite the fact that the highest average concentration never exceeded 800 counts (see Figure B-6).
Exclusion of the 12 extreme counts reveals a more consistent pattern in the raw data (see Figure B-7). Results of the analysis of the raw PCM data excluding outliers are presented in Table B-2. For PCM, the true counts were divided by 100 to place the estimates on a scale that is more easily interpreted.
The inter-laboratory standard deviation is 0.40, which is 67 percent of the mean slope (0.60) of the calibration curve over all of the laboratories. This is an even larger relative standard deviation than obtained for TEM, indicating also that the laboratories exhibit considerable variability in their individual calibration curves (i.e., differential sensitivity to changing numbers of particles from lab to lab) for PCM.
FIGURE B-6 Raw PCM data.
TABLE B-2 Marginal Maximum Likelihood Estimates of the Mixed-effects—Poisson Regression Model for PCM Data
|
Parameters |
Estimates |
SE |
z-value |
p-value |
|
γ0 |
3.8559 |
0.0864 |
44.63 |
< .0001 |
|
γ1 |
0.6006 |
0.0498 |
12.07 |
< .0001 |
|
Σ(1,1) |
0.5158 |
0.0526 |
|
|
|
Σ(1,2) |
−0.2128 |
0.0265 |
|
|
|
Σ(2,2) |
0.1593 |
0.0182 |
|
|
Figure B-8 presents empirical Bayes estimates of the individual laboratory calibration functions. Note that the y-axis is in log-scale. This figure confirms that there is considerable variability in the slopes of the estimated calibration functions.
Next, we estimated detection and quantification limits for the PCM data. The results are displayed graphically in Figure B-9. This figure reveals that the critical level (LC) is 127 fibers, the detection limit (LD) is 589 fibers and the quantification limit (LQ) is 924 fibers. At the LQ, the relative standard deviation is still quite large (i.e., 32 percent). Figure B-9 also reveals that outliers still remain in the data; however, the prediction intervals are conservative due to the large number of measurements.
Figure B-10 presents the variance function, for which the best fit was based on the Rocke and Lorenzato Model (Rocke and Lorenzato, 1995). The figure reveals that the variability is constant below 100 fibers and then increases linearly from 100 to 800 fibers.
Finally, Figure B-11 displays a plot of the relationship between average counts and the relative standard deviation. The figure shows that considerable uncertainty exists in PCM asbestos counts throughout all of the samples investigated, regardless of the number of fibers. However, the RSD stabilizes at around 30 percent for fiber counts around 500.
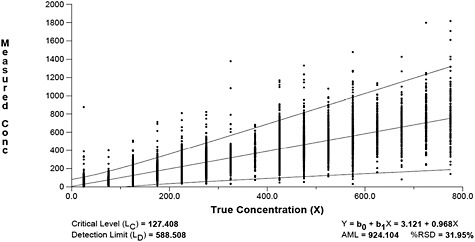
FIGURE B-9 Alternative minimum level model with 99 percent prediction interval for asbestos PCM samples in mm2.
Discussion
Fiber-counting protocols must be considered as a contributor to variability. The AHERA method was produced in 1987 as a simplification of the EPA Level II analysis (U.S. EPA, 1987). “Clusters” of fibers are counted as one structure under the AHERA method, whereas a more detailed and prescriptive method, ASTM D6281, requires the analyst to count and measure individual fibers within clusters (ASTM, 2008). In fact, a separate inter-laboratory study, which used AM filters from one of the batches discussed here, produced a relative standard deviation of only 11 percent at a concentration of ~400 s/mm2 when the ASTM D6281 method was used. No inter-laboratory data are available for the NIOSH 7402 TEM method, where PCM-equivalent fibers (length >5-μm, width >0.25 μm, aspect ratio >3) are counted (NIOSH, 1994a). Variability would probably be similar to the ASTM method, but NIOSH 7402 does not allow counting of fibers thinner than 0.25 μm, so this method would not monitor the very thin fibers that are considered to be the most hazardous.
Filter type and preparation techniques are other sources of variability. MCE filters sometimes have surficial defects that cause skewed deposition across the filter face, but the skewing is not obvious once the filter is collapsed. Furthermore, differences in collapsing methods and in etching rates (poorly defined and inconsistently calibrated) add to the variability (Webber et al., 2007).
Another source of variation that cannot be de-coupled is the difference in filters received by each laboratory for each PT batch. In-house validation of homogeneity of AM filters has been checked by analyzing 5 filters from each generation batch of 109 filters. Relative standard deviations for these counts, by the same analyst and same instrument, are typically 10 percent around a concentration of 1,000 s/mm2.
In both the examples, asymptotic normality is used (see Tables B-1 and B-2) in order to arrive at the reported p-values. This is appropriate since the sample sizes are large. However, if the number of laboratories and/or the count data within each lab are sparse, asymptotic methods for hypothesis testing may yield biased results. One option is to use small sample asymptotic theory that has recently become available (see Brazzale et al., 2007 and Bellio, 2003). The relevant theory would need to be developed for the mixed effects Poisson regression model proposed here and is likely to be quite valuable in the context of the Rocke-Lorenzato model as well.
Taken as a whole, the current analysis reveals that there is considerable variability in asbestos fiber counting under both TEM and PCM methodologies. Although detection limits are smaller for PCM than for TEM, PCM cannot be considered an alternative because it cannot detect the thin fibers of most concern and it cannot even determine if a fiber is asbestos. It is critically important for the analytic community to address the issue of TEM variability so that more reliable exposure concentrations can be determined.
THE PROBLEM OF NON-DETECTS
A complication in the statistical analysis of environmental data in general and asbestos in particular is the presence of non-detects. Even if the measured concentrations have a known distribution (e.g., normal, lognormal, Poisson) the overall distribution may not because of a mass of probability associated with a count of zero, or samples in which the material has not been detected. In the case of an asbestos count, it may be the case that there are more zeros (i.e., non-detects) than are expected based on a Poisson distribution. In this case, one may consider extensions to the Poisson model, such as a zero-inflated Poisson model (Lambert, 1992). General discussions of the treatment of nondetects in environmental data analysis can be found in Helsel (2005) and Gibbons et al. (2009).
REFERENCES
ASTM (American Society for Testing and Materials). 2008. Annual book of ASTM standards, 2008. Volume 11.07: Atmospheric Analysis. West Conshohocken, PA: ASTM International.
Bellio, R. 2003. Likelihood methods for controlled calibration. Scandinavian Journal of Statistics 30:339–353.
Bhaumik, D. K., and R. D. Gibbons. 2005. Confidence regions for random-effects calibration curves with heteroscedastic errors. Technometrics 62:223–230.
Brazzale, A. R., A. C. Davison, and N. Reid. 2007. Applied asymptotics: Case studies in small-sample statistics. Cambridge: Cambridge University Press.
Currie, L. A. 1968. Limits for qualitative detection and quantitative determination: Application to radiochemistry. Analytical Chemistry 40:586–593.
Gibbons, R. D., and D. Bhaumik. 2001. Weighted random-effects regression models with application to inter-laboratory calibration. Technometrics 43:192–198.
Gibbons, R. D. and D. E. Coleman. 2001. Statistical methods for detection and quantification of environmental contamination. New York: John Wiley & Sons.
Gibbons, R. D., D. E. Coleman, and R. F. Maddalone. 1997. An alternative minimum level definition for analytical quantification. Environmental Science and Technology. 31:2071–2077.
Gibbons, R. D., D. K. Bhaumik, and S. Aryal. 2009. Statistical methods for groundwater monitoring, 2nd edition. New York: John Wiley & Sons.
Helsel, D. R. 2005. Nondetects and data analysis: Statistics for censored environmental data. New York: John Wiley & Sons.
Lambert, D. 1992. Zero-inflated poisson regression, with an application to defects in manufacturing. Technometrics 34(1):1–14.
NIOSH (National Institute for Occupational Safety and Health). 1994a. NIOSH Method 7402 asbestos by TEM, Revision 2. Cincinnati: NIOSH.
NIOSH. 1994b. NIOSH Method 7400 asbestos and other fibers by PCM. Issue 2. Cincinnati: NIOSH.
Rocke, D. M., and S. Lorenzato. 1995. A two-component model for measurement error in analytical chemistry. Technometrics 37:176– 184.
U.S. EPA (U.S. Environmental Protection Agency). 1987. 40 CFR Part 763. Asbestos-containing materials in schools: Final rule and notice. Federal Register 52(21):41826–41905.
Webber, J. S., A. G. Czuhanich, and L. J. Carhart. 2007. Performance of membrane filters used for TEM analysis of asbestos. Journal of Occupation and Environmental Hygiene 4:780–789.
Zorn, M. E., R. D. Gibbons, and W. C. Sonzogni. 1997. Weighted least squares approach to calculating limits of detection and quantification by modeling variability as a function of concentration. Analytical Chemistry 69:3069–3075.