A7
THE SEVERITY OF PANDEMIC H1N1 INFLUENZA IN THE UNITED STATES, FROM APRIL TO JULY 2009: A BAYESIAN ANALYSIS50
Anne M. Presanis,51 Daniela De Angelis,52 The New York City Swine Flu Investigation Team,53,54 Angela Hagy,55 Carrie Reed,56 Steven Riley,57 Ben S. Cooper,58 Lyn Finelli,59 Paul Biedrzycki,60 Marc Lipsitch61
Abstract
Background
Accurate measures of the severity of pandemic (H1N1) 2009 influenza (pH1N1) are needed to assess the likely impact of an anticipated resurgence in the autumn in the Northern Hemisphere. Severity has been difficult to measure because jurisdictions with large numbers of deaths and other severe outcomes have had too many cases to assess the total number with confidence. Also, detection of severe cases may be more likely, resulting in overestimation of the severity of an average case. We sought to estimate the probabilities that symptomatic infection would lead to hospitalization, ICU admission, and death by combining data from multiple sources.
|
50 |
Reprinted with permission from Presanis et al. 2009. The severity of pandemic H1N1 influenza in the United States, from April to July 2009: a Bayesian analysis. PLoS 6(12), http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2762775/ (accessed December 15, 2009). |
|
51 |
Medical Research Council Biostatistics Unit, Cambridge, United Kingdom. |
|
52 |
Medical Research Council Biostatistics Unit, Cambridge, United Kingdom. Statistics, Modelling and Bioinformatics Department, Health Protection Agency Centre for Infections, London, United Kingdom. |
|
53 |
Department of Health and Mental Hygiene, City of New York, New York, New York, United States of America. |
|
54 |
Membership of The New York City Swine Flu Investigation Team is provided in the Acknowledgments. |
|
55 |
Department of Health, City of Milwaukee, Milwaukee, Wisconsin, United States of America. |
|
56 |
Influenza Division, Centers for Disease Control and Prevention, Atlanta, Georgia, United States of America. |
|
57 |
Department of Community Medicine and School of Public Health, Li Ka Shing Faculty of Medicine, The University of Hong Kong, Hong Kong SAR, China. |
|
58 |
Statistics, Modelling and Bioinformatics Department, Health Protection Agency Centre for Infections, London, United Kingdom. |
|
59 |
Influenza Division, Centers for Disease Control and Prevention, Atlanta, Georgia, United States |
|
60 |
Department of Health, City of Milwaukee, Milwaukee, Wisconsin, United States of America. |
|
61 |
Center for Communicable Disease Dynamics, Departments of Epidemiology and Immunology & Infectious Diseases, Harvard School of Public Health, Boston, Massachusetts, United States of America E-mail: mlipsitc@hsph.harvard.edu. |
Methods and Findings
We used complementary data from two US cities: Milwaukee attempted to identify cases of medically attended infection whether or not they required hospitalization, while New York City focused on the identification of hospitalizations, intensive care admission or mechanical ventilation (hereafter, ICU), and deaths. New York data were used to estimate numerators for ICU and death, and two sources of data—medically attended cases in Milwaukee or self-reported influenza-like illness (ILI) in New York—were used to estimate ratios of symptomatic cases to hospitalizations. Combining these data with estimates of the fraction detected for each level of severity, we estimated the proportion of symptomatic patients who died (symptomatic case-fatality ratio, sCFR), required ICU (sCIR), and required hospitalization (sCHR), overall and by age category. Evidence, prior information, and associated uncertainty were analyzed in a Bayesian evidence synthesis framework. Using medically attended cases and estimates of the proportion of symptomatic cases medically attended, we estimated an sCFR of 0.048% (95% credible interval [CI] 0.026%–0.096%), sCIR of 0.239% (0.134%–0.458%), and sCHR of 1.44% (0.83%–2.64%). Using self-reported ILI, we obtained estimates approximately 7–9 × lower. sCFR and sCIR appear to be highest in persons aged 18 y and older, and lowest in children aged 5–17 y. sCHR appears to be lowest in persons aged 5–17; our data were too sparse to allow us to determine the group in which it was the highest.
Conclusions
These estimates suggest that an autumn–winter pandemic wave of pH1N1 with comparable severity per case could lead to a number of deaths in the range from considerably below that associated with seasonal influenza to slightly higher, but with the greatest impact in children aged 0–4 and adults 18–64. These estimates of impact depend on assumptions about total incidence of infection and would be larger if incidence of symptomatic infection were higher or shifted toward adults, if viral virulence increased, or if suboptimal treatment resulted from stress on the health care system; numbers would decrease if the total proportion of the population symptomatically infected were lower than assumed.
Please see later in the article for the Editors’ Summary.
Introduction
The H1N1 2009 influenza (pH1N1) pandemic has resulted in over 209,000 laboratory-confirmed cases and over 3,205 deaths worldwide as of 11 September 2009 (http://www.who.int/csr/don/2009_09_11/en/index.html, accessed 14 Sep-
tember 2009), but national and international authorities have acknowledged that these counts are substantial underestimates, reflecting an inability to identify, test, confirm, and report many cases, especially mild cases. Severity of infection may be measured in many ways, the simplest of which is the case-fatality ratio (CFR), the probability that an infection causes death. Other measures of severity, which are most relevant to the burden a pandemic exerts on a health care system, are the case-hospitalization and case-intensive care ratios (CHR and CIR, respectively), the probabilities that an infection leads to hospitalization or intensive care unit (ICU) admission. In the absence of a widely available and validated serologic test for infection, it is impossible to estimate these quantities directly, and in this report we instead focus on the probabilities of fatality, hospitalization, and ICU admission per symptomatic case; we denote these ratios sCFR, sCHR, and sCIR respectively.
Although it is difficult to assess these quantities, estimates of their values and associated uncertainty are important for decision making, planning, and response during the progression of this pandemic. Initially, some national and international pandemic response plans were tied partly to estimates of the CFR, but such plans had to be modified in the early weeks of this pandemic, as it became clear that the CFR could not at that time be reliably estimated (Lipsitch et al., 2009a). Costly measures to mitigate the pandemic, such as the purchase of medical countermeasures and the use of disruptive social distancing strategies may be acceptable to combat a more severe pandemic but not to slow a milder one. While past experience (Jordan et al., 1958) and mathematical models (Ferguson et al., 2006; Halloran et al., 2008; Mills et al., 2004) suggest that between 40% and 60% of the population will be infected in a pandemic with a reproduction number similar to those seen in previous pandemics, the number of deaths and the burden on the health care system also depend on the age-specific severity of infection, which varies by orders of magnitude between pandemics (Miller et al., 2008) and even between different waves in the same pandemic (Andreasen et al., 2008). Reports from the Southern Hemisphere suggest that a relatively small fraction of the population experienced symptomatic pH1N1 infection (7.5% in New Zealand, for example; Baker et al., 2009), although these numbers are considered highly uncertain (Baker et al., 2009). On the other hand, primary care utilization for influenza-like illness (ILI) has been considerably higher than in recent years (Baker et al., 2009), and anecdotal reports in the Southern Hemisphere have indicated that some intensive care units (ICUs) have been overwhelmed and surgery postponed due to a heavy burden of pH1N1 cases (Bita, 2009; Newton, 2009).
The problem of estimating severity of pH1N1 infection includes the problem of estimating how many of the infected individuals in a given population and time period subsequently develop symptoms, are medically attended, hospitalized, admitted to ICU, and die due to infection with the virus. No large jurisdiction in the world has been able to maintain an accurate count of total pH1N1 cases once
the epidemic grew beyond hundreds of cases, because the effort required to confirm and count such cases is proportionate to the size of the exponentially growing epidemic (Lipsitch et al., 2009b), making it impossible to reliably estimate the frequency of an event (e.g., death) that occurs on the order of 1 in 1,000 patients or fewer. As a result, simple comparisons of the number of deaths to the number of cases suffer from underascertainment of cases (making the estimated ratio too large), and underascertainment of deaths due to inability to identify deaths caused by the illness and due to delays from symptom onset to death (making the estimated ratio too small; Lipsitch et al., 2009a). Imperfect ascertainment of both numerator and denominator will lead to biased estimates of the CFR. Estimating the number of persons at these varying levels of severity therefore depends on estimating the proportion of true cases that are recognized and reported by existing surveillance systems. Similar problems affect estimates of key parameters for other diseases, such as HIV. In HIV, a solution to this problem—which now forms the basis for the UK’s annual HIV prevalence estimates published by the Health Protection Agency (Health Protection Agency Centre for Infections, 2009a, b)—has been to synthesize evidence from a variety of sources that together provide a clearer picture of incidence, prevalence, and diagnosis probabilities. This synthesis is performed within a Bayesian framework that allows each piece of evidence, with associated uncertainties, to be combined into an estimate of the numbers of greatest interest (Goubar et al., 2008; Presanis et al., 2008).
Here we use a similar framework to synthesize evidence from two cities in the United States—New York and Milwaukee—together with estimates of important detection probabilities from epidemiologic investigations carried out by the US Centers for Disease Control and Prevention (CDC) and other data from CDC. We estimate the severity of pH1N1 infection from data from spring– summer 2009 wave of infections in the United States. The New York City and Milwaukee health departments pursued differing surveillance strategies that provided high-quality data on complementary aspects of pH1N1 infection severity, with Milwaukee documenting medically attended cases and hospitalizations, and New York documenting hospitalizations, ICU/ventilation use, and fatalities. These are the numerators of the ratios of interest.
The denominator for these ratios is the number of symptomatic pH1N1 cases in a population, which cannot be assessed directly. We use two different approaches to estimate this quantity. In the first (Approach 1), we use self-reported rates of patients seeking medical attention for ILI from several CDC investigations to estimate the number of symptomatic cases from the number of medically attended cases, which are estimated from data from Milwaukee. In the second (Approach 2), we use self-reported incidence of ILI in New York City, and making the assumption that these ILI cases represent the true denominator of symptomatic cases, we directly estimate the ratio between hospitalizations, ICU admissions/mechanical ventilation, and deaths (adjusting for ascertainment) in New York City. Each of these two methods provides estimates for the general
population, and also for broad age categories 0–4, 5–17, 18–64, and 65+ years. The result of each approach is a tiered severity estimate of the pandemic.
Methods
Methods Overview
The overall goal of this study was to estimate, for each symptomatic pH1N1 case, the probability of hospitalization, ICU admission or mechanical ventilation, or death, overall and by age group. The challenge is that in any population large enough to have a significant number of patients with these severe outcomes, there is no reliable measure of the number of symptomatic pH1N1 cases. This problem was approached in two ways. Approach 1 was to view the severity of infection as a “pyramid” (Garske et al., 2009), with each successive level representing greater severity; to estimate the ratio of the top level to the base (symptomatic cases), we estimated the ratios of each successive level to the one below it (Figure A7-1, left side). Thus we broke down (for example) the sCFR (Figure A7-1, black), i.e., the probability of death per symptomatic case, into components for which data were available –the probability of a case coming to medical attention given symptomatic infection (CDC survey data); the probability of being hospitalized given medical attention (Milwaukee data); and the probability of dying given hospitalization (New York data, including a correction for those who died of pH1N1 but were not hospitalized). Approach 2 was to use the self-reported incidence of ILI from a telephone survey in New York City as the estimate of total symptomatic pH1N1 disease, and the total number of confirmed deaths in New York City as the estimate of the deaths (after accounting for imperfect ascertainment, in this case due to possibly imperfect viral testing sensitivity). In each case, prior distributions were used to quantify information on the probability that cases at each level of severity were detected; these prior distributions reflected the limited data available on detection probabilities and associated uncertainty.
All of these estimates were combined within a Bayesian evidence synthesis framework. This framework permits the estimation of probabilities for the quantities of interest (the sCFR, sCIR, and sCHR) and associated uncertainty (expressed as credible intervals [CIs]). These credible intervals appropriately reflect the combined uncertainties associated with each of the inputs to the estimate—mainly, the true numbers of cases at each level of severity, after accounting for imperfect detection—as well as the uncertainties due to sampling error (chance).
Study Populations
Data were obtained from enhanced pandemic surveillance efforts by the City of Milwaukee Health Department and the New York City Department of Health and Mental Hygiene (DOHMH). Details of testing policies, data acquisition, and
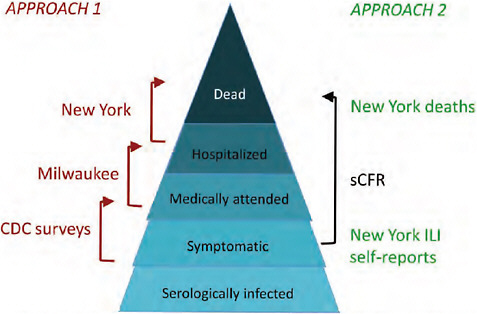
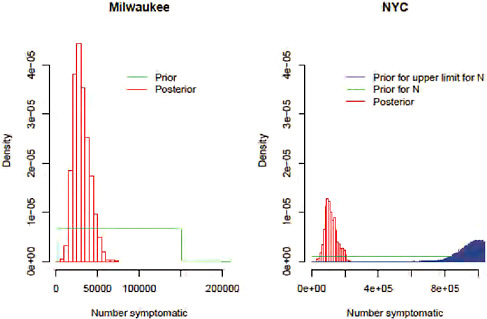
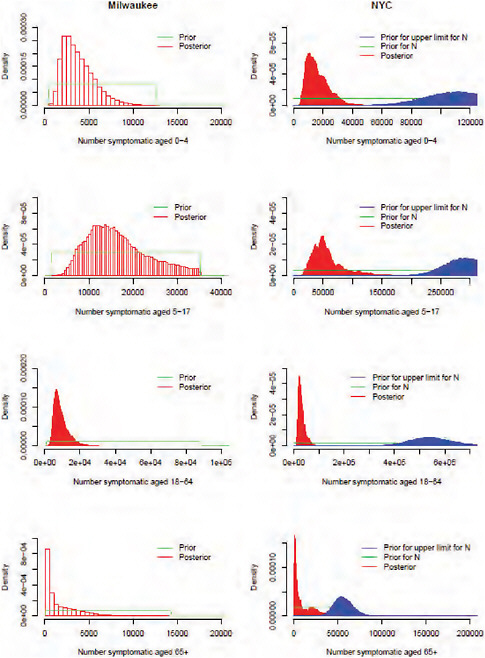
FIGURE A7-1 Diagram of two approaches to estimating the sCFR. Approach 1 used three datasets to estimate successive steps of the severity pyramid. Approach 2 used self-reported IU for the denominator, and confirmed deaths for the numerator, both from New York City. Both approaches used prior distributions, in some cases informed by additional data, to inform the probability of detecting (confirming and reporting) cases at each level of severity (not shown in the diagram; see text S1). The Bayesian evidence synthesis framework was used as a formal way to combine information and uncertainty about each level of severity into a single estimate and associated uncertainty that reflected all of the uncertainty in the inputs.
analysis are given in Text S1. All data were analyzed first in aggregate and then by age category.
Milwaukee Data
Between April 6 and July 16, 2009, Milwaukee recorded 3,278 confirmed cases and four deaths due to pH1N1, reflecting sustained efforts to test patients reporting ILI and their household contacts from the start of the epidemic in April until mid-July. On April 27, Milwaukee initiated protocols including recommendations for testing persons with influenza symptoms and travel history to areas reporting novel H1N1 cases, using a reverse transcriptase polymerase chain reaction (RT-PCR) test specific for pH1N1. By May 7, Milwaukee issued testing guidance updated to recommend testing persons with moderate to severe symptoms, except that test-
ing continued to be recommended for health care workers with mild, moderate or severe symptoms. We used a line list dated July 21, and in a preliminary analysis examined the frequency of hospitalization among cases by “episode date” (the earliest date in their case report). The proportion of confirmed cases hospitalized was stable around 3% up to May 20, after which it increased markedly to 6%–8% in the following weeks. We judged that this change reflected reduced testing of mild cases and limited our analysis (used to inform the ratio of hospitalizations to medically attended cases) to the 763 cases with an episode date up to or including May 20. While Milwaukee data were not the main source of estimates of ICU admission or death probabilities, we did employ hospitalized cases up to an episode date of June 14 to contribute to estimates of the ratio of deaths or ICU admissions to hospitalizations, since these should not be affected by failure to test mild cases.
New York Case Data
New York City maintained a policy from April 26 to July 7, 2009 of testing hospitalized patients with ILI according to various criteria. These criteria evolved up to May 12, from which point they remained as follows: all hospitalized ILI patients received a rapid influenza antigen test. Those patients who tested positive on rapid test (which is known to have low sensitivity for seasonal influenza (Uyeki et al., 2009) and for pH1N1 (CDC, 2009)), and any patient in the ICU or on a ventilator, regardless of rapid test result, received RT-PCR tests for pH1N1. We obtained a line list of confirmed or probable hospitalized cases dated July 7, and found in a preliminary analysis that all patients in this line list had a date (onset or admission) in their record no later than June 30, 7 d prior to the date of the line list. Given that >90% of hospitalizations were reported in New York within 7 d, we used this entire line list without accounting for delays in reporting of hospitalizations. Also, given that 98% of admissions occurred after May 12, we did not attempt to account for changes in testing practices before May 12. This line list included a field indicating whether the patient had been admitted to the ICU or ventilated; patients were not followed up after admission to determine if this status changed. However, a chart review of 99 hospitalized cases indicated that none had been admitted to the ICU after admission, so no effort was made to account for this limitation.
Separately, we obtained a list of 53 patients whose deaths were attributed to pH1N1, of whom 44 (83%) had been hospitalized before dying. All patients with known influenza or unexplained febrile respiratory illness at the time of death had postmortem samples and/or samples taken before they died sent for PCR testing.
New York Telephone Survey Data
To estimate levels of ILI in New York City, DOHMH conducted 1,006 surveys between May 20 and May 27, 2009, and 1,010 between June 15 and
June 19. Interviews lasted 5 min and were conducted with households in both English and Spanish. The survey used a random-digit dialing (RDD) telephone sampling methodology to obtain data from a random sample of residential households in New York City. A nonrandom individual from each selected household was interviewed and provided information about all household members. Sampled numbers were dialed between five and 15 times to contact and interview a household, or until the sampled number was determined to be nonworking.
To account for this design, the data were weighted to the 2007 American Community Survey (ACS); respondents were weighted to householders by borough, age, gender, and race/ethnicity, and the population was weighted by age to the borough of residence.
The survey’s RDD sampling methodology gave a useful overview of ILI in the community, but it has limitations. The design does not include individuals living in households only reachable by cellular telephone but not by a landline telephone number, and it omitted those living in group or institutional housing. Although households were randomly selected, for the sake of efficiency the interviewed adult was not. Instead, an available adult in the household provided information about all household members and themselves, which may have introduced bias. The results of the survey are being compiled for publication elsewhere. Here, we use summaries of these results by age group (see Text S1) as one means to provide denominators of symptomatic cases.
Data on Detection Probabilities from CDC Investigations
Sources of data include two community surveys on ILI and health-seeking behavior, and two field investigations conducted during early outbreaks of pH1N1 in the US. These sources are described in further detail elsewhere (Reed et al., 2009), but are summarized here briefly. In 2007, the Behavioral Risk Factor Surveillance Survey (BRFSS), an RDD telephone survey, included a module on ILI in nine states. This module included questions to assess the incidence of ILI, health-seeking behavior, physician diagnosis of influenza, and treatment of influenza with antiviral medications during the annual 2006–2007 influenza season. In May 2009, following the emergence of pH1N1, an RDD telephone survey sampled similar to the BRFSS was conducted in the same nine states using only the ILI module from the 2007 BRFSS and limited demographic questions. In addition, some data were available from field investigations conducted during large outbreaks of pH1N1 in one community in Chicago and a university campus in Delaware. Investigations of these outbreaks consisted of household interviews in a Chicago neighborhood and an online survey of students and faculty in Delaware. These data were used to inform detection probabilities. In addition, these data were used to inform a prior distribution on the ratio between symptomatic and medically attended cases, cM|S: these surveys estimated that between 42% and 58% of symptomatic ILI patients sought medical attention (Reed et al., 2009).
Analysis
Estimation of the probabilities of primary interest, cH|S, cI|S, and cD|S, respectively the sCHR, sCIR, and sCFR, was undertaken using a Bayesian evidence synthesis framework (Goubar et al., 2008). Details are given in Text S1, and a schematic illustration of the model is given in Figure A7-2. Briefly, in this framework, prior information about the quantities of interest (including the uncertainty associated with this prior information) is combined with the information coming from the observed cases at each severity level to derive a posterior distribution on these quantities. This posterior distribution fully reflects all information about the quantities of interest that is contained in the prior distribution and the observed data. Specifically, it was assumed that detected cases O at each level of severity—medically attended (M), hospitalized (H), ICU-admitted (I), and fatal (D)—represented binomially distributed samples from the true number of cases N at the corresponding level of severity, in the given location (New York, abbreviated N or Milwaukee, abbreviated W), with probability equal to the probability of detection at each level (d). The probability d for each level was informed by evidence on the probability of testing at each level of severity (which may have depended on the sensitivity of the rapid test if this was required for PCR testing) and the sensitivity of the PCR test (Table A7-1). Thus, for example, we defined
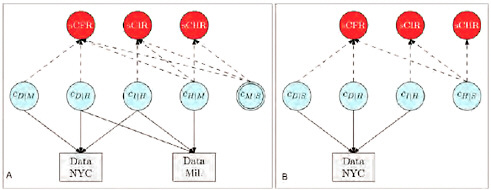
FIGURE A7-2 Schematic illustration of the relationship between the observed data (rectangles) and the conditional probabilities (blue circles). The key quantities of interest, sCHR, sCIR, and sCFR, are products of the relevant conditional probabilities. (A) Approach 1, synthesizing data from New York City and Milwaukee. Note that cM/S (double circle) is informed by prior information (Reed et al., 2009) rather than observed data. (B) Approach 2, using data from New York City only, including the telephone survey. Variables: cD/M: the ratio of non-hospitalized deaths to medically-attended cases; cD/H: the ratio of deaths to hospitalized cases; cI/H: the ratio of cases admitted to intensive care or using mechanical ventilation to hospitalized cases; cH/M: the ratio of hospitalized cases to medically attended cases; cM/S: the ratio of medically attended cases to symptomatic cases; cD/S: the ratio of deaths to symptomatic cases; cH/S: the ratio of hospitalized cases to symptomatic cases.
TABLE A7-1 Detection Probabilities and Their Prior Distributions
|
Detection Probability |
Components |
Distributions |
Rationale |
|
dM Medically attended illness |
dM1 probability of testing, follow-up, and reporting among medically attended patients |
Uniform (0.2,0.35) |
Data from CDC epi-aids in Delaware and Chicago (Reed et al., 2009) |
|
dM = dM1dM2 |
dM2 PCR test sensitivity |
Uniform (0.95,1) |
Assumption (Reed et al., 2009) |
|
dHW Hospitalization (Milwaukee) |
dHW1 probability of testing, follow-up, and reporting among hospitalized patients |
Uniform (0.2,0.4) |
Assumption (Reed et al., 2009) |
|
dHW = dHW1dHW2 |
dHW2 PCR test sensitivity |
Uniform (0.95,1) |
Assumption (Reed et al., 2009) |
|
dIW ICU admission (Milwaukee) |
dIW1 probability of testing, follow-up, and reporting among hospitalized patients |
Uniform (0.2,0.4) |
Assumption (Reed et al., 2009) |
|
dIW = dIW1 dIW2 |
dIW2 PCR test sensitivity |
Uniform (0.95,1) |
Assumption (Reed et al., 2009) |
|
dDW Deaths (Milwaukee) |
PCR test sensitivity and other detection |
Beta (45,5) |
Assumption (Reed et al., 2009) (mean 0.9, standard deviation 0.05) |
|
dHW Hospitalization (New York City) |
dHN1 probability of oerforming PCR (rapid A positive or ICU/ventilated) |
0.27+0.73 (Uniform (0.2,0.71)) |
27% of test cases were ICU-admitted so received PCR test; remainder were tested if rapid A positive, which has a sensitivity of 0.2 (Uyeki et al., 2009) to 0.71 (sensitivity among ICU patients in NYC) |
|
dHN = dHN1dHN2 |
dHN2 PCR test sensitivity |
Uniform (0.95,1) |
Assumption (Reed et al., 2009) |
|
dIN ICU/ventilation (New York City) |
PCR test sensitivity |
Uniform (0.95,1) |
Assumption (Reed et al., 2009) |
|
dDN Deaths (New York City) |
PCR test sensitivity and other detection |
Beta (45,5) |
Assumption (Reed et al., 2009) |
the probability of detecting a hospitalized case in New York as dHN = dHN1dHN2, where dHN1 was the probability of performing an RT-PCR–based test and dHN2 was the sensitivity of that test. Hence, the observed number of hospitalized patients in New York, OHN, was assumed to be distributed as Binomial(NHN,dHN).
We noted that the ratios cH|S, cI|S, and cD|S can be built up multiplicatively from simpler components: for instance, the ratio of deaths to symptomatic infections may be expressed as cD|S = cD|HcH|McM|S, the product of the ratios of deaths: hospitalizations, of hospitalizations:medically attended cases, and of medically attended cases:symptomatic cases. These ratios of increasing severity are similar to conditional probabilities but are not strictly so in all cases, since for example some deaths in New York City occurred in persons who were not hospitalized. For this reason we model deaths separately among hospitalized and nonhospitalized patients, i.e., cD|S = cD|HcH|McM|S + cD|McM|S. For each observed level of severity (medically attended, hospitalized, ICU, death), the true number of cases was modeled as a binomial sample from the true number of cases at an appropriate lower level, hence
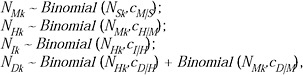
where the first subscript indicates severity and the second indicates the population (New York, Milwaukee to May 20, Milwaukee to June 14).
In Approach 1 (New York and Milwaukee data combined), for the unobserved level of severity (symptomatic cases) we used a prior distribution of cM|S ~ Beta (51.5,48.5) to represent uncertainty between 42% and 58% (Reed et al., 2009); this distribution has 90% of its mass in this range, with a mean of 0.515. The main analysis of this first approach was performed using prior information to inform the detection probabilities. An additional “naïve” analysis was performed, in which the detection probabilities d were set equal to 1 at all levels of severity. Our prior distributions for the number of symptomatic cases in New York (overall and by age) were taken as ranging uniformly between zero and the proportion reporting ILI in the telephone survey (with the upper bound of that distribution itself having a prior distribution reflecting the confidence bounds of the survey results; details in Text S1). For Milwaukee, the prior distribution on symptomatic cases was taken as uniform between 0 and 25% of the population.
In Approach 2 (New York case data and telephone survey data), we made the assumption that self-reported ILI cases represented symptomatic pH1N1 infection, and used the mean and 95% confidence intervals from that survey to define a prior distribution on the number of symptomatic cases overall and by age group. We then used observed hospitalizations, ICU/ventilator use, and fatalities along with prior distributions on detection probabilities as above to inform estimates
of true numbers of hospitalizations, ICU/ventilator use, and fatalities, and these in turn were used to estimate sCHR, sCIR, and sCFR.
The evidence was synthesized through a full probability model in a Bayesian framework, implemented in the OpenBUGS software (Thomas et al., 2006), which uses Markov chain Monte Carlo to sample from the posterior distribution.
Results
Table A7-2 shows the numbers of medically attended cases, hospitalizations, ICU admissions, and deaths in the two cities, with the Milwaukee data separated into the period (to May 20) for which we believe medically attended cases were consistently detected, and the period (to June 14) for which we consider only hospitalized cases, ICU admissions, and deaths.
Approach 1
We considered two alternatives to estimate the ratios of interest from the combined New York and Milwaukee data, using self reported rates of seeking medical attention to establish the denominator. First, we obtained a naïve estimate of the ratios of deaths to hospitalizations, ignoring differences in detection across levels of severity; and second, we obtained an estimate that incorporated evidence and expert opinion on the detection probabilities at each level of severity.
The naïve estimate would suggest a median (95% CI) ratio of deaths to hospitalizations (cD|H) of 4.3% (95% CI 3.2%–5.5%), of ICU admissions to hospitalizations (cI|H) of 25% (95% CI 22%–27%), and of hospitalizations to medically attended cases (cH|M) of 3.1% (95% CI 2.0%–4.4%). The ratio of deaths outside of hospitals to medically attended cases (cD|M) is estimated to be 0.03% (95% CI 0.01%–0.06%). Incorporating the prior evidence that 42%–58% of symptomatic ILI is medically attended, this would imply a naïve estimate of the sCFR (cD|S = cD|HcH|McM|S + cD|McM|S) of 0.081% (95% CI 0.049%–0.131%), a corresponding estimate of the sCIR (cI|S = cI|HcH|McM|S) of 0.38% (95% CI 0.24%–0.58%), and an estimate of the sCHR (cH|S = cH|McM|S) of 1.55% (95% CI 0.98%–2.32%). If one assumes that detection probabilities are no worse at higher levels of severity than at lower levels, then these figures would be reasonable upper bounds on the symptomatic CFRs and CIRs.
Incorporating prior evidence of the detection probabilities at each level of severity, and thus accommodating structural and statistical uncertainties in these probabilities, we estimated that ratio of deaths to hospitalizations (cD|H) of 2.7% (95% CI 1.8%–3.8%) of ICU admissions to hospitalizations (cI|H) of 17% (95% CI 12%–21%) and of hospitalizations to medically attended cases (cH|M) of 2.9% (95% CI 1.6%–5.0%). The ratio of deaths outside of hospitals to medically attended cases (cD|M) is estimated to be 0.02% (95% CI 0.01%–0.04%).
TABLE A7-2 Cases at Each Level of Severity
|
Location |
Age Group |
Severity |
||||
|
Medically Attended |
Hospitalized |
ICU-admitted |
Dead |
|||
|
to May 20 |
to May 20 |
to Jun 14 |
to Jun 14 |
to Jun 14 |
||
|
Milwaukee |
0-4 |
126 (16%) |
7(28%) |
27 (18%) |
5(20%) |
0 |
|
|
5-17 |
470 (60%) |
6 (24%) |
29 (20%) |
7 (26%) |
2 (50%) |
|
|
18-64 |
189 (24%) |
12 (48%) |
87 (59%) |
14 (52%) |
2 (50%) |
|
|
65+ |
3(0.4%) |
0 |
4 (13%) |
1 (4%) |
0 |
|
|
Total |
788 |
25 |
147 |
25 |
4 |
|
|
Age Group |
Medically Attended |
Hospitalized |
|
ICU-admitted |
Dead (total)/Dead but not hospitalized |
|
New York |
0-4 |
— |
225 (23%) |
|
44 (17%) |
2(4%)/2 |
|
|
5-17 |
— |
197 (20%) |
|
51 (20%) |
2 (4%)/2 |
|
|
18-64 |
— |
518 (52%) |
|
147 (57%) |
46 (87%)/6 |
|
|
65+ |
— |
56 (6%) |
|
15 (6%) |
3(6%)/0 |
|
|
Total |
— |
996 |
|
257 |
53/9 |
Table A7-3 shows the estimates for the quantities of primary interest, overall and by age group, in the analysis that incorporated prior evidence of detection probabilities. Here, the posterior median estimate for the sCFR is 0.048% (95% CI 0.026%–0.096%) and for the sCIR is 0.239% (95% CI 0.134%–0.458%). The sCHR is estimated as 1.44% (95% CI 0.83%–2.64%).
Estimates of each of these severity measures vary dramatically by age group, with the lowest severity by each measure in the 5–17 year age group. Comparing the two groups for which we have the most data, the relative risk of death for a symptomatic 18–64-year-old compared to a symptomatic 5- to 17-year-old is 15 (95% CI 5– 57). The corresponding relative risks of ICU admission and hospitalization are 5 (95% CI 2–13) and 5 (95% CI 2–12) respectively. The Bayesian framework provides a natural way to estimate confidence (measured as the posterior probability) that one rate is higher than another. The probability that severity is higher in the 18- to 64-y age group than in the 5–17 age group is >99.9%, for each of fatality, ICU admission, and hospitalization respectively. The data are too sparse to say with confidence whether adults over 65 or under 65 have greater severity. For example, among the four age groups, the symptomatic case-fatality ratio is highest in the 18- to 64-y age group with posterior probability 62%, and in those 65 and over with probability 38%. The symptomatic case-ICU admission ratio is highest in 18- to 64-year-olds with posterior probability 51% and in those over 65 with posterior probability 38%. The sCHR is highest in 18- to 64-year-olds with posterior probability 37% and in those over 65 with posterior probability 37%.
TABLE A7-3 Posterior Median (95% CI) Estimates of the sCFR, sCIR, and sCHR, by Age Group, Based on a Combination of Data from New York City and Milwaukee, and Survey Data on the Frequency of Medical Attendance for Symptomatic Cases
|
Age |
sCFR |
sCIR |
sCHR |
|
0-4 |
0.026% |
0.321% |
2.45% |
|
|
(0.006%-0.092%) |
(0.133%-0.776%) |
(1.10%-5.56%) |
|
5-17 |
0.010% |
0.106% |
0.61% |
|
|
(0.003%-0.031%) |
(0.043%-0.244%) |
(0.27%-1.34%) |
|
18-64 |
0.159% |
0.542% |
3.00% |
|
|
(0.066%-1.471%) |
((0.230%-1.090%) |
(1.35%-5.92%) |
|
65+ |
0.090% |
0.327% |
1.84% |
|
|
(0.008%-1.471%) |
(0.035%-4.711%) |
(0.21%-25.38%) |
|
Total |
0.048% |
0.239% |
1.44% |
|
|
(0.026%-0.096%) |
(0.134%-0.458%) |
(0.83%-2.64%) |
Approach 2
Table A7-4 shows the estimates for the sCFR, sCIR, and sCHR, by age group, when self-reported ILI is used as the denominator for total symptomatic cases. Overall these estimates are: sCFR= 0.007% (95% CI 0.005%–0.009%), sCIR =0.028% (95% CI 0.022%–0.035%) and sCHR =0.16% (95% CI 0.12%–0.26%). Compared to Approach 1, these estimates are nearly an order of magnitude smaller, and the age distribution differs. The relative risks for each severity in the 18- to 64-year-old group compared to the 5- to 17-year-old group are 7 (95% CI 3–25) for fatalities, 1.5 (95% CI 0.9–2.5) for ICU admissions, and 1.4 (95% CI 0.9–2.1) for hospitalizations. The CFR is highest in the 18–64 y group with posterior probability 52%. In contrast to Approach 1, the CIR is highest among 0- to 4-year-olds, with posterior probability 79%, and the CHR is highest among 0- to 4-year-olds, with posterior probability 99%.
Discussion
We have estimated, using data from two cities on tiered levels of severity and self-reported rates of seeking medical attention, that approximately 1.44% of symptomatic pH1N1 patients during the spring in the US were hospitalized; 0.239% required intensive care or mechanical ventilation; and 0.048% died. Within the assumptions made in our model, these estimates are uncertain up to a factor of about 2 in either direction, as reflected in the 95% credible intervals associated with the estimates. These estimates take into account differences in detection and reporting of cases at different levels of severity, which we believe, based on some evidence, to be more complete at higher levels of severity. With-
TABLE A7-4 Posterior Median (95% CI) Estimates of the sCFR, sCIR, and sCHR by Age Group, Using Self-Reported ILI as the Denominator of Symptomatic Cases
|
Age |
sCFR |
sCIR |
sCHR |
|
0-4 |
0.004% |
0.044% |
0.33% |
|
|
(0.001%-0.011%) |
(0.026%-0.078%) |
(0.21-0.63%) |
|
5-17 |
0.002% |
0.019% |
0.11% |
|
|
(0.000%-0.004%) |
(0.013%-0.027%) |
(0.08%-0.18%) |
|
18-64 |
0.010% |
0.029% |
0.15% |
|
|
(0.007%-0.016%) |
(0.021%-0.040%) |
(0.11%-0.25%) |
|
65+ |
0.010% |
0.030% |
0.16% |
|
|
(0.003%-0.025%) |
(0.016%-0.055%) |
(0.10%-0.30%) |
|
Total |
0.007% |
0.028% |
0.16% |
|
|
(0.005%-0.009%) |
(0.022%-0.035%) |
(0.12%-0.26%) |
out such corrections for detection and reporting, estimates are approximately two-fold higher for each level of severity. Using a second approach, which uses self-reported rates of influenza-like illness in New York City to estimate symptomatic infections, we have estimated rates approximately an order of magnitude lower, with a symptomatic sCHR of 0.16%, an sCIR of 0.028%, and an sCFR of 0.007%. In both approaches, the sCFR was highest in adults (in Approach 1, 18–64 y, while Approach 2 cannot distinguish whether it is higher in that group or in those 65y and older) and lowest in school-aged children (5–17 y). Data on children 0–4 and adults 65 and older were relatively sparse, making statements about their ordering more difficult. Nonetheless, these findings, along with surveillance data on the age specific rates of hospitalization and death in this pandemic (http://www.cdc.gov/vaccines/recs/ACIP/downloads/mtg-slidesoct09/12-2-flu-vac.pdf), indicate that the burden of hospitalization and mortality in this pandemic falls on younger individuals than in seasonal influenza (Thompson et al., 2009). A shift in mortality toward nonelderly persons has been observed in previous pandemics and the years that immediately followed them (Simonsen et al., 1998).
These estimates are valuable for attempting to project, in approximate terms, the possible severity of a fall–winter wave of pH1N1, under the assumption that the virus does not change its characteristics. In the 1957 and 1968 pandemics, it appears that perhaps 40%–60% of the population was serologically infected, and that of those, 40%–60% were symptomatic (Jordan et al., 1958; Clarke et al., 1958; Davis et al., 1970; Foy et al., 1976). Current estimates of the transmission of pH1N1 range between about 1.4 and about 2.2, consistent with estimates of the reproduction numbers from prior pandemics (Boelle et al., 2009; Fraser et al., 2009; Nishiura et al., 2009a; White et al., 2009; Pourbohloul et al., 2009). To convert our estimates into population impacts, one needs to make an assumption about the attack rate and its age distribution. For each 10% of the US population symptomatically infected (with the same age distribution observed in the spring wave), our Approach 1 estimates suggest that approximately 7,800–29,000 deaths (3–10 per 100,000 population), 40,000–140,000 intensive care admissions (13–46 per 100,000 population), and 250,000–790,000 hospitalizations (170–630 per 100,000 population) will occur. These estimates scale up or down in proportion to the attack rate; for example, they should be doubled if 20% of the population were symptomatic, producing for example 15,000–58,000 deaths (6–20 per 100,000 population). Approach 2 suggests much smaller figures (for each 10% of the population symptomatic) of 1,500–2,700 deaths (0.5–0.9 per 100,000), 6,600–11,000 ICU admissions/uses of mechanical ventilation (22–35 per 100,000), and 36,000–78,000 hospitalizations (12–26 per 100,000). Again, these numbers should be scaled in proportion to the attack rate.
To date, symptomatic attack rates seem to be far lower than 25% in both the completed Southern Hemisphere winter epidemic and the autumn epidemic in progress in the US; severe outcomes seem to be considerably less numerous than those described for Approach 1 with a 25% attack rate. In New Zealand, just
under 2% of the population consulted a general practitioner (GP) for ILI during the winter wave of the pandemic (http://www.moh.govt.nz/moh.nsf/indexmh/influenza-a-h1n1-update-138-180809), which is consistent with an attack ratesignificantly lower than 25%, though somewhat higher than the GP consultation rate observed in severe seasonal flu outbreaks such as those in 2003 and 2004 (http://www.surv.esr.cri.nz/PDF_surveillance/Virology/FluWeekRpt/2004/FluWeekRpt200444.pdf).
The level of severity estimated for the United States reflects in part the availability of antiviral treatment and other medical interventions that will not be available in all populations. Oseltamivir use was common in Milwaukee (Milwaukee Department of Health, unpublished data), and although the health care system was put under strain in both cities studied, there was no shortage of intensive care or other life-saving medical resources. In a situation of greater stress on the health system, as has been observed in certain locations in the Southern Hemisphere (Bita, 2009; Newton, 2009); http://www.capegateway.gov.za/eng/your_gov/3576/news/2009/aug/185589), or in areas that lack a high-quality health care system, severity might increase in proportion to decreased availability of adequate medical attention. Worryingly, our estimates of the proportion of symptomatic cases requiring mechanical ventilation or ICU care was approximately 4–5 × our estimate of the sCFR. It is possible that a substantial proportion of those admitted to ICUs could have died without intensive care. In populations without widespread access to intensive care, our results suggest that the same burden of disease could lead to a death rate 4–5 × higher. Likewise, a change in the virus to become more virulent or resistant to existing antiviral drugs, or the emergence of more frequent bacterial coinfections, could increase the severity of infection compared to that observed so far.
Estimates of severity for an infection such as influenza are fraught with uncertainties (Lipsitch et al., 2009a). Our analysis has accounted for many of these uncertainties, including imperfect detection and reporting of cases, bias due to delays between events (such as the delay from illness onset to death), and the statistical uncertainties associated with limited numbers of cases, hospitalizations, and deaths. Another major source of difficulty is the spatial and temporal variation in reporting effort for mild and severe cases; for example, most jurisdictions in the US stopped reporting mild cases on or before the second week of May, but this change varied by jurisdiction. We have attempted to avoid this difficulty by focusing on individual jurisdictions—New York and Milwaukee—for which the approach to reporting was relatively stable over time. One limitation is that Milwaukee changed its guidance during our surveillance period from testing of all symptomatic cases to testing of all symptomatic health care workers but only moderate-tosevere cases in non-health care workers. We believe that testing policies did not change dramatically during this period, because the proportion of hospitalized cases remained fairly constant; however, the sample size before this change in guidance was
small. Thus, our estimates should be seen as being the risk of severe outcome among persons with symptoms, possibly biased somewhat toward those with more severe symptoms.
Despite our efforts to account for sources of uncertainty, several others remain and have not been accounted for in our analysis. First, we have assumed that for each level of severity (from medically attended up to fatal), case reporting was equal across age groups; for example, we assumed that medically attended cases were as likely to be reported for young children as for adults. It is possible that this is not the case, for example that mild cases were more likely to come to medical attention if they occurred in children than if they occurred in adults. If this were true, our conclusion that severity was higher in adults than children could be partly a result of differential reporting.
Second, the overall estimates of severity (not stratified by age group) reflect the age composition of cases in the sample we studied, especially the age composition of the lowest level of severity examined, medically attended illness. Among medically attended cases in Milwaukee, 60% were in the 5–17 y age group, the one in which severe outcomes were the least likely. A preponderance of cases within this age group may be typical of the early part of influenza epidemics, and while it has been argued that there is a shift from younger to older age groups in seasonal influenza (Brownstein et al., 2005) as the epidemic progresses, there is evidence, at least from the 1957 pandemic, that attack rates remain higher in children than adults throughout the course of the epidemic (Jordan et al., 1958). Since severity of pH1N1 influenza appears to be considerably higher in adults, a shift in the burden of disease from children to adults as the epidemic progresses would lead to an increase in average severity.
We note that the association between age and severity may also affect observed trends in the characteristics of cases. The World Health Organization has noted worldwide a shift from younger to older mean age among confirmed cases (http://www.who.int/csr/disease/swineflu/notes/h1n1_situation_20090724/en/index.html). If severity is lowest among children, this upward shift in age distribution may partially reflect a shift toward detection of more severe cases, rather than a true shift in the ages of those becoming infected.
Third, the symptomatic CFR, CIR, and CHR are dependent upon our estimates of the true number of symptomatic cases, NiSk, and hence are sensitive to the choice of prior distribution for these, as well as to our prior assumptions on the detection probabilities. In particular, if the probability that symptomatic patients seek medical attention and are confirmed is lower than we assume in our prior distributions, then there are more cases than are inferred by our model, and severity is correspondingly lower than our estimates. If the probability of detecting severe outcomes (hospitalizations, deaths, ICU) is lower than our prior distributions reflect, then there are more severe outcomes than our model infers, so severity is correspondingly higher.
Finally, the small sample sizes in some age groups, the over-65 year olds in
particular, lead to large uncertainty in the age-specific estimates. This level of uncertainty is reflected in the wide 95% credible intervals for the estimates.
Our two approaches yield estimates that differ by almost an order of magnitude in the severity of the infection, on each of the three measures considered. How should planners evaluate these contrasting estimates? The lower estimates, using the denominator of self-reported ILI in New York City, may reasonably be considered lower bounds on the true ratios. ILI is thought to be relatively rare in May–June, hence true ILI was probably largely attributable to pH1N1 during this period in New York City. However, self-reported ILI is notoriously prone to various biases, most of which suggest that true rates are probably lower than selfreported rates. A previous telephone survey conducted in New York City found that 18.5% of New Yorkers reported ILI in the 30 d prior to being surveyed in late March 2003 (Metzger et al., 2004), which represented a period of above-baseline but declining influenza activity nationally and no known influenza outbreaks in New York City (Metzger et al., 2004). The survey was repeated in October–November 2003, prior to the appearance of significant influenza activity, and 20.8% reported ILI in the 30 d prior (Metzger et al., 2004). If these surveys represent a baseline level of self-reported ILI in the absence of significant influenza activity, then the approximately 12% self-reported ILI in the telephone survey is substantially lower than this out-of-season baseline, suggesting that it likely overstates the total burden of symptomatic pH1N1 disease. The lower estimates are also broadly consistent with estimates from New Zealand, which has experienced a nearly complete influenza season (Baker et al., 2009), and from Australia (http://www.health.gov.au/internet/main/publishing.nsf/Content/cda-surveil-ozflu-flucurr.htm/$FILE/ozflu-no14-2009.pdf). The higher estimates, on the other hand, were obtained using ratios of hospitalizations to confirmed medically attended cases and self-reported rates of seeking medical attention for ILI, which have been consistently measured in the range of about 40%–60%. It is possible that the special efforts of the New York City health department to identify pH1N1-related fatalities (including those not hospitalized) provides a fuller picture of the total number of deaths from this infection. Interestingly, New York City reports about the same number of hospitalizations for our study period (996) as New Zealand reports up to mid-August (972), but 3.5 × as many deaths (53 versus 16) (Baker et al., 2009). If this discrepancy reflects more complete ascertainment of deaths in New York City, it may account for much of the difference between our higher estimates of case-fatality ratios and those from New Zealand. Given the number of uncertainties cataloged above (which apply also to other jurisdictions within and outside the US), we believe that our two approaches probably bracket the reasonable range of severity for the US spring wave.
Age-specific severity patterns as estimated here are largely consistent with those one would obtain by simply comparing the incidence of confirmed cases, hospitalizations, and deaths in the US as a whole for a similar period (Reed et al., 2009), although the estimates for persons over age 65 are highly uncertain,
with 95% credible intervals spanning several orders of magnitude, due to the very small number of individuals in our sample from that age group.
The estimates provided here may be compared to those for seasonal influenza. Compared to seasonal influenza, these estimates (assuming a 25% symptomatic attack rate) suggest a number of deaths in the US that could range from about half the number estimated for an average year to nearly twice the number estimated for an average year (Thompson et al., 2003) (Approach 1), or a range about 10-fold lower than that (Approach 2); however, the deaths would be expected to occur in younger age groups, compared to the preponderance of deaths in persons over 65 in seasonal influenza. Such a shift in age distribution is typical for pandemics and the years that follow them (Simonsen et al., 1998). Under Approach 1, and assuming a typical pandemic symptomatic attack rate of 25%, the estimated number of hospitalizations for an autumn–winter pandemic wave is considerably more than the approximately 300,000 estimated for typical seasonal influenza (Thompson et al., 2004), whereas Approach 2 suggests a number between 1/3 and 2/3 of that observed in typical seasonal influenza. It should be noted that most hospitalizations, and about 90% of deaths attributed to seasonal influenza, are categorized as respiratory and circulatory, not including the more specific diagnoses of pneumonia and influenza; that is, they are due to myocardial infarction, stroke, and other proximate causes, but are nonetheless likely initially caused by influenza infection (Reichert et al., 2004). The deaths included in our study may have reflected more directly influenza-related causes and may not reflect these indirect causes of influenza-related death. Indeed, it is unclear whether the proportion of indirect respiratory and circulatory causes of death and hospitalization will be as high in this pandemic year, given the younger ages involved in most severe cases. Given these differences between the estimates here based on virologically confirmed deaths and the ecological statistical approach to estimating influenza-attributable deaths and hospitalizations for seasonal influenza, it will be difficult to interpret comparisons between the two types of estimates until (after the pandemic has finished) comparisons can be made between the ecological and the confirmed-case approach to estimating burden of hospitalization and deaths.
Our estimate of the sCFR is lower than those provided by Garske et al. (2009), which ranges from 0.11% to 1.47% overall, and between 0.59% and 0.78% in the US, but which was based on confirmed plus probable (rather than symptomatic) cases. Nishiura et al. (2009b) estimate that between 0.16% and 4.48% of confirmed cases in the United States and Canada were fatal. Our Approach 1 includes a probability of approximately 1/8 (~50% probability of symptomatic patients seeking care × ~28% probability of testing and report for a symptomatic × ~97% test sensitivity, with associated ranges for each; Table A7-1) to convert symptomatic into medically attended cases, and this factor accounts for most of the difference between our estimates and the earlier estimates based on confirmed or confirmed plus probable cases. Wilson and
Baker (2009), on the other hand, use a denominator of infections (rather than symptomatic or confirmed cases) and estimate a range of CFR from 0.0004% up to 0.6%. Our estimates fall in the middle part of this range. More recently, Baker et al. (2009) used their estimates of the total incidence of symptomatic disease in New Zealand to estimate an sCFR of 0.005%, equal to the lower end of the credible interval for our Approach 2 estimate, and considerably below our Approach 1 estimate. The generally downward trend in the estimates of severity reflects early ascertainment of more severe cases (e.g., mainly hospitalized cases in the early Mexican outbreak); the authors of each of these earlier reports recognized and discussed the issue of ascertainment and its potential biasing effect on severity estimates.
While we have been careful to highlight uncertainties in the estimates of severity, our results are sufficiently well-resolved to have important implications for ongoing pH1N1 pandemic planning. The estimated severity indicates that a reasonable expectation for the autumn–winter pandemic wave in the US is a death toll less than or equal to that which is typical for seasonal influenza, though possibly with considerably more deaths in younger persons. If attack rates in the autumn match those of prior pandemics and hospitalization rates are comparable to our estimates using Approach 1, the surge of ill individuals and subsequent burden on hospitals and intensive care units could be large. However, using Approach 2, estimates of hospitalizations and ICU admissions are considerably lower. Either set of estimates places the epidemic within the lowest category of severity considered in pandemic planning conducted prior to the appearance of pH1N1 in the United States, which considered CFRs up to 0.1% (http://www.flu.gov/professional/community/community_mitigation.pdf).
Continued close monitoring of severity of pandemic (H1N1) 2009 influenza is needed to assess how patterns of hospitalization, intensive care utilization, and fatality are varying in space and time and across age groups. Increases in severity might reflect changes in the host population—for example, infection of persons with conditions that predispose them to severe outcomes—or changes in the age distribution of cases—for example a shift toward adults, in whom infection is more severe. Changes in severity might also reflect changes in the virus or variation in the access and quality of care available to infected persons.
Supporting Information
Text S1 Supplementary methods.
Found at: doi:10.1371/journal.pmed.1000207.s001 (0.43 MB DOC)
Acknowledgments
We thank Michael Baker for helpful discussions and Carolyn Bridges for useful comments on earlier drafts.
The 2009 New York City Swine Flu Investigation Team participated in the response to the pandemic and preparation of this manuscript: Joel Ackelsberg, Alys Adamski, Gail Adman, Elisabeth Agbor-Tabi, Christopher Aston, Josephine Atamian, Peter Backman, Sharon Balter, Oxiris Barbot, Sara T. Beatrice, Gary Beaudry, Elizabeth Begier, Geraldine Bell, Debra Berg, Magdalena Berger, James Betz, Susan Blank, Katherine Bornschlegel, Brooke Bregman, Meghan Burke, Barbara Butts, Liqun Cai, Alejandro Cajigal, Marilyn Campbell, Lorraine Camurati, Shadi Chamany, Dan Cimini, James Cone, Heather Cook, Debra Cook, Catherine Corey, Roseann Costarella, Christiana Coyle, Bindy Crouch, Cherry-Ann Da Costa, Alexandria Daniels, Berta Darkins, Arlene DeGrasse, Susanne DeGrechie, Otto Del Cid, Bisram Deocharan, Luis Diaz, Kathleen DiCaprio, Laura DiGrande, Damon Duquaine, James Durrah, Joanna Eavey, Zadkijah Edghill, Barbara Edwin, Joseph Egger, Donna Eisenhower, Martin Evans, Shannon Farley, Richard Feliciano, Marcial Fernandez, Christine Fils-Aime, Anne Fine, Ana Maria Fireteanu, Kelly Fitzgerald, Anne Marie France, Thomas Frieden, Stephen Friedman, Jie Fu, Lawrence Fung, Latchmidat Girdharrie, Michelle Glaser, Christopher Goranson, Francine Griffing, Leena Gupta, Carol Hamilton, Heather Hanson, Scott Harper, Ian Hartman-O’Connell, Qazi Hasnain, Sonia Hedge, Michael Heller, Debra Hendrickson, Arnold Herskovitz, Kinjia Hinterland, Roosevelt Holmes, Jeanne Hom, Jeffrey Hon, Tana Hopke, Jennifer Hsieh, Scott Hughes, Stephen Immerwahr, Anne Marie Incalicchio, John Jasek, Julia Jimenez, Michael Johns, Lucretia Jones, Hannah Jordan, Chrispin Kambili, Jisuk Kang, Deborah Kapell, Adam Karpati, Bonnie Kerker, Kevin Konty, John Kornblum, Gary Krigsman, Fabienne Laraque, Marcelle Layton, Ellen Lee, Lillian Lee, Stephen Lee, Sungwoo Lim, Melissa Marx, Emily McGibbon, Kevin Mahoney, Gilbert Marin, Thomas Matte, Rene McAnanama, Ryan McKay, Carolyn McKay, Katherine McVeigh, Eric Medina, Wanda Medina, Danielle Michelangelo, Juliet Milhofer, Irina Milyavskaya, Mark Misener, Joseph Mizrahi, Linda Moskin, Matt Motherwell, Christa Myers, Hemanth P. Nair, Yuk-Wah (Fran) Ng, Trang Nguyen, Diana Nilsen, Janet Nival, Jennifer Norton, William Oleszko, Carolyn Olson, Marc Paladini, Lucille Palumbo, Peter Papadopoulos, Hilary Parton, Jacob Paternostro, Lynn Paynter, Krystal Perkins, Sharon Perlman, Haresh Persaud, Charles Peters, Melissa Pfeiffer, Roger Platt, Lindsay Pool, Amado Punsalang, Zahedur Rasul, Valerie Rawlins, Vasudha Reddy, Anne Rinchiuso, Teresa Rodriguez, Ramon Rosal, Maureen Ryan, Michael Sanderson, Allison Scaccia, Amber Levanon Seligson, Jantee Seupersad, Joanne Severe-Dildy, Asma Siddiqi, Ulirike Siemetzki, Tejinder Singh, Sally Slavinski, Meredith Slopen, Timothy Snuggs, David Starr, Catherine Stayton, Alaina Stoute, Jacqueline Terlonge, Alexandra Ternier, Lorna Thorpe, Catherine Travers, Benjamin Tsoi, Kimberly Turner, Joan Tzou, Shameeka Vines, Elizabeth Needham Waddell, Donald Walker, Connie Warner, Isaac Weisfuse, Don Weiss, Antoinette Williams-Akita, Elisha Wilson, Eliza Wilson, Marie Wong, Charles Wu, David Yang, Mohammad Younis, Sulaimon Yusuff, Christopher Zimmerman, and Jane Zucker.
Author Contributions
ICMJE criteria for authorship read and met: AMP DDA TNYCSFIT AH CR SR BSC LF PB ML. Agree with the manuscript’s results and conclusions: AMP DDA TNYCSFIT AH CR SR BSC LF PB ML. Designed the experiments/the study: TNYCSFIT SR BSC LF ML. Analyzed the data: AMP LF ML. Collected data/did experiments for the study: TNYCSFIT AH LF PB. Enrolled patients: TNYCSFIT AH. Wrote the first draft of the paper: ML. Contributed to the writing of the paper: AMP DDA TNYCSFIT AH CR SR BSC LF PB. Contributed to model development: AMP. Contributed to model development and assessment: DDA. The New York City Swine Flu Investigation Team, who designed the surveillance for NYC, collected, cleaned, and did initial analyses of the data, is responsible for the data integrity of the NYC data and shared it with the other authors, and played a significant role in revising the paper and thinking through the analyses.
Editor’s Summary
Background
Every winter, millions of people catch influenza—a viral infection of the airways—and about half a million people die as a result. In the US alone, an average of 36,000 people are thought to die from influenza-related causes every year. These seasonal epidemics occur because small but frequent changes in the virus mean that an immune response produced one year provides only partial protection against influenza the next year. Occasionally, influenza viruses emerge that are very different and to which human populations have virtually no immunity. These viruses can start global epidemics (pandemics) that kill millions of people. Experts have been warning for some time that an influenza pandemic is long overdue and in, March 2009, the first cases of influenza caused by a new virus called pandemic (H1N1) 2009 (pH1N1; swine flu) occurred in Mexico. The virus spread rapidly and on 11 June 2009, the World Health Organization declared that a global pandemic of pH1N1 influenza was underway. By the beginning of November 2009, more than 6,000 people had died from pH1N1 influenza.
Why Was This Study Done?
With the onset of autumn—drier weather and the return of children to school help the influenza virus to spread—pH1N1 cases, hospitalizations, and deaths in the Northern Hemisphere have greatly increased. Although public-health officials have been preparing for this resurgence of infection, they cannot be sure of its impact on human health without knowing more about the severity of pH1N1 infections. The severity of an infection can be expressed as a case-fatality ratio
(CFR; the proportion of cases that result in death), as a case- hospitalization ratio (CHR; the proportion of cases that result in hospitalization), and as a case- intensive care ratio (CIR; the proportion of cases that require treatment in an intensive care unit). Because so many people have been infected with pH1N1 since it emerged, the numbers of cases and deaths caused by pH1N1 infection are not known accurately so these ratios cannot be easily calculated. In this study, the researchers estimate the severity of pH1N1 influenza in the US between April and July 2009 by combining data on pH1N1 infections from several sources using a statistical approach known as Bayesian evidence synthesis.
What Did the Researchers Do and Find?
By using data on medically attended and hospitalized cases of pH1N1 infection in Milwaukee and information from New York City on hospitalizations, intensive care use, and deaths, the researchers estimate that the proportion of US cases with symptoms that died (the sCFR) during summer 2009 was 0.048%. That is, about 1 in 2,000 people who had symptoms of pH1N1 infection died. The “credible interval” for this sCFR, the range of values between which the “true” sCFR is likely to lie, they report, is 0.026%–0.096% (between 1 in 4,000 and 1 in 1,000 deaths for every symptomatic case). About 1 in 400 symptomatic cases required treatment in intensive care, they estimate, and about 1 in 70 symptomatic cases required hospital admission. When the researchers used a different approach to estimate the total number of symptomatic cases—based on New Yorkers’ self-reported incidence of influenza-like-illness from a telephone survey—their estimates of pH1N1 infection severity were 7- to 9-fold lower. Finally, they report that the sCFR and the sCIR were highest in people aged 18 or older and lowest in children aged 5–17 years.
What Do These Findings Mean?
Many uncertainties (for example, imperfect detection and reporting) can affect estimates of influenza severity. Even so, the findings of this study suggest that an autumn–winter pandemic wave of pH1N1 will have a death toll only slightly higher than or considerably lower than that caused by seasonal influenza in an average year, provided pH1N1 continues to behave as it did during the summer. Similarly, the estimated burden on hospitals and intensive care facilities ranges from somewhat higher than in a normal influenza season to considerably lower. The findings of this study also suggest that, unlike seasonal influenza, which kills mainly elderly adults, a high proportion of deaths from pH1N1 infection will occur in nonelderly adults, a shift in age distribution that has been seen in previous pandemics. With these estimates in hand and with continued close monitoring of the pandemic, public-health officials should now be in a better position to plan effective strategies to deal with the pH1N1 pandemic.
Additional Information
Please access these Web sites via the online version of this summary at http://dx.doi.org/10.1371/journal.pmed.1000207.
-
The US Centers for Disease Control and Prevention provides information about influenza for patients and professionals, including specific information on pandemic H1N1 (2009) influenza
-
Flu.gov, a US government Web site, provides access to information on H1N1, avian and pandemic influenza
-
The World Health Organization provides information on seasonal influenza and has detailed information on pandemic H1N1 (2009) influenza (in several languages)
-
The UK Health Protection Agency provides information on pandemic influenza and on pandemic H1N1 (2009) influenza
-
More information for patients about H1N1 influenza is available through Choices, an information resource provided by the UK National Health Service
References
Andreasen V, Viboud C, Simonsen L (2008) Epidemiologic characterization of the 1918 influenza pandemic summer wave in Copenhagen: Implications for pandemic control strategies. J Infect Dis 197: 270–278.
Baker MG, Wilson N, Huang QS, Paine S, Lopez L, et al. (2009) Pandemic influenza A(H1N1)v in New Zealand: The experience from April to August 2009. Euro Surveill 14: pii: 19319. Available: http://www.eurosurveillance.org/ViewArticle.aspx?ArticleId=19319. Accessed: 15 September 2009.
Bita N (2009 August 04) No bed for swine flu man on life support. The Australian.
Boelle PY, Bernillon P, Desenclos JC (2009) A preliminary estimation of the reproduction ratio for new influenza A(H1N1) from the outbreak in Mexico, March-April 2009. Euro Surveill 14: pii =19205.
Brownstein JS, Kleinman KP, Mandl KD (2005) Identifying pediatric age groups for influenza vaccination using a real-time regional surveillance system. Am J Epidemiol 162: 686–693.
CDC (2009) Evaluation of rapid influenza diagnostic tests for detection of novel influenza A (H1N1) Virus - United States, 2009. MMWR Morb Mortal Wkly Rep 58: 826–829.
Clarke SK, Heath RB, Sutton RN, Stuart-Harris CH (1958) Serological studies with Asian strain of influenza A. Lancet 1: 814–818.
Davis LE, Caldwell GG, Lynch RE, Bailey RE, Chin TD (1970) Hong Kong influenza: The epidemiologic features of a high school family study analyzed and compared with a similar study during the 1957 Asian influenza epidemic. Am J Epidemiol 92: 240–247.
Ferguson NM, Cummings DA, Fraser C, Cajka JC, Cooley PC, et al. (2006) Strategies for mitigating an influenza pandemic. Nature 442: 448–452.
Foy HM, Cooney MK, Allan I (1976) Longitudinal studies of types A and B influenza among Seattle schoolchildren and families, 1968-74. J Infect Dis 134: 362–369.
Fraser C, Donnelly CA, Cauchemez S, Hanage WP, Van Kerkhove MD, et al. (2009) Pandemic potential of a strain of influenza A (H1N1): early findings. Science 324: 1557–1561.
Garske T, Legrand J, Donnelly CA, Ward H, Cauchemez S, et al. (2009) Assessing the severity of the novel influenza A/H1N1 pandemic. BMJ 339: b2840.
Goubar A, Ades AE, De Angelis D, McGarrigle CA, Mercer CH, et al. (2008) Estimates of human immuno deficiency virus prevalence and proportion diagnosed based on Bayesian multi parameter synthesis of surveillance data. J R Stat Soc Ser A 171: 1–27.
Halloran ME, Ferguson NM, Eubank S, Longini IM Jr, Cummings DA, et al. (2008) Modeling targeted layered containment of an influenza pandemic in the United States. Proc Natl Acad Sci U S A 105: 4639–4644.Jordan WS Jr, Denny FW Jr, Badger GF, Curtiss C, Dingle JH, et al. (1958) A study of illness in a group of Cleveland families. XVII. The occurrence of Asian influenza. Am J Hyg 68: 190–212.
Health Protection Agency Centre for Infections (2009) HIV in the United Kingdom: 2008 Report. Available: http://www.hpa.org.uk/hivuk2008. Accessed: 15 September 2009.
Health Protection Agency Centre for Infections (2009) Sexually transmitted infections and men who have sex with men in the United Kingdom: 2008 report. Available: http://www.hpa.org.uk/hivmsm2008. Accessed: 15 September 2009.
Jordan WS Jr, Denny FW Jr, Badger GF, Curtiss C, Dingle JH, et al. (1958) A study of illness in a group of Cleveland families. XVII. The occurrence of Asian influenza. Am J Hyg 68: 190–212.
Lipsitch M, Riley S, Cauchemez S, Ghani AC, Ferguson NM (2009a) Managing and reducing uncertainty in an emerging influenza pandemic. N Engl J Med 361: 112–115.
Lipsitch M, Hayden FG, Cowling BJ, Leung GM (2009b) How to maintain surveillance for novel influenza A H1N1 when there are too many cases to count. Lancet 374: 1209–1211.
Metzger KB, Hajat A, Crawford M, Mostashari F (2004) How many illnesses does one emergency depart ment visit represent? Using a population-based telephone survey to estimate the syndromic multiplier. MMWR Morb Mortal Wkly Rep 53 Suppl: 106–111.
Miller MA, Viboud C, Olson DR, Grais RF, Rabaa MA, et al. (2008) Prioritization of infl uenza pandemic vaccination to minimize years of life lost. J Infect Dis 198: 305–311.
Mills CE, Robins JM, Lipsitch M (2004) Transmissibility of 1918 pandemic influenza. Nature 432: 904–906.
Newton K (2009 July 18) Swine flu puts hold on surgery. The Dominion Post Wellington, NZ.
Nishiura H, Castillo-Chavez C, Safan M, Chowell G (2009a) Transmission potential of the new influenza A(H1N1) virus and its age-specificity in Japan. Euro Surveill 14: pii: 19227. Available: http://www.eurosurveillance.org/ViewArticle.aspx?ArticleId=19205. Accessed: 1 November, 2009.
Nishiura H, Klinkenberg D, Roberts M, Heesterbeek JA (2009b) Early epidemiological assessment of the virulence of emerging infectious diseases: a case study of an influenza pandemic. PLoS One 4: e6852. doi:10.1371/ journal.pone.0006852.
Pourbohloul B, Ahued A, Davoudi B, Meza R, Meyers LA, et al. (2009) Initial human transmission dynamics of the pandemic (H1N1) 2009 virus in North America. Influenza Other Respi Viruses 3: 215–222.
Presanis AM, De Angelis D, Spiegelhalter DJ, Seaman S, Goubar A, et al. (2008) Conflicting evidence in a Bayesian synthesis of surveillance data to estimate human immunodeficiency virus prevalence. J R Stat Soc Series A Stat Soc 171:915–937.
Reed C, Angulo F, Swerdlow D, Lipsitch M, Meltzer M, et al. (2009) Estimating the burden of pandemic influenza A/H1N1–United States, April-July 2009. Emerg Infect Dis. In press.
Reichert TA, Simonsen L, Sharma A, Pardo SA, Fedson DS, et al. (2004) Influenza and the winter increase in mortality in the United States, 1959–1999. Am J Epidemiol 160: 492–502.
Simonsen L, Clarke MJ, Schonberger LB, Arden NH, Cox NJ, et al. (1998) Pandemic versus epidemic influenza mortality: A pattern of changing age distribution. J Infect Dis 178: 53–60.
Thomas A, O’Hara B, Ligges U, Sturtz S (2006) Making BUGS Open. R News 6: 12–17.
Thompson WW, Weintraub E, Dhankhar P, Cheng PY, Brammer L, et al. (2009) Estimates of US influenza-associated deaths made using four different methods. Influenza Other Respi Viruses 3: 37–49.
Thompson WW, Shay DK, Weintraub E, Brammer L, Cox N, et al. (2003) Mortality associated with influenza and respiratory syncytial virus in the United States. JAMA 289: 179–186.
Thompson WW, Shay DK, Weintraub E, Brammer L, Bridges CB, et al. (2004) Influenza-associated hospitalizations in the United States. JAMA 292: 1333–1340.
Uyeki TM, Prasad R, Vukotich C, Stebbins S, Rinaldo CR, et al. (2009) Low sensitivity of rapid diagnostic test for influenza. Clin Infect Dis 48: e89–92.
White LF, Wallinga J, Finelli L, Reed C, Riley S, et al. (2009) Estimation of the reproductive number and the serial interval in the current influenza A/H1N1 outbreak. Influenza Other Respi Viruses 3: 267–276.
Wilson N, Baker MG (2009) The emerging influenza pandemic: estimating the case fatality ratio. Euro Surveill 14: pii: 19255. Available: http://www.eurosurveillance.org/ViewArticle.aspx?ArticleId=19255. Accessed 15 September, 2009.
SUPPLEMENTARY METHODS: THE SEVERITY OF PANDEMIC H1N1 INFLUENZA IN THE UNITED STATES, APRIL – JULY 2009
Anne M. Presanis,62 Daniela De Angelis,62,63 The New York City Swine Flu Investigation Team,64 Angela Hagy,65 Carrie Reed,66 Steven Riley,67 Ben S. Cooper,64 Lyn Finelli,67 Paul Biedrzycki,66 Marc Lipsitch68
1.
Introduction
In this Supplementary Material we provide additional details about the statistical model employed (Section 2), the data (Section 3), the detection probabilities (Section 4), the relationship between medically attended and symptomatic illness (Section 5), and the software implementation of our model (Section 6).
2.
Model
Of ultimate interest is to estimate three quantities:
-
the case-fatality ratio, defined as the ratio of the true number of H1N1pdmattributable deaths to the true number of H1N1pdm infections; we denote this cDInf because it is a conditional probability, Pr{death | infection};
-
the case-ICU admission ratio, defined as the ratio of the true number of H1N1pdm -attributable ICU admissions to the true number of H1N1pdm infections; we denote this cI|Inf = Pr{ICU | infection}; and
-
the case-hospitalization ratio, defined as the ratio of the true number of H1N1pdm-attributable hospitalizations to the true number of H1N1pdm infections; this is denoted cH|Inf = Pr{hospitalization | infection}.
Ascertainment of all infections, whether symptomatic or not, requires serological surveys, which are not yet available for H1N1pdm. Without such surveys, it is not possible to estimate the relationship between infection and more severe outcomes. We therefore attempt to estimate the ratio of severe outcomes to symptomatic infection: namely, the symptomatic case-fatality ratio cD|S = Pr{death | symptomatic infection}, the symptomatic case-ICU admission ratio cI|S = Pr{ICU admission | symptomatic infection} or the symptomatic case-hospitalization ratio cH|S = Pr{hospitalization | symptomatic infection}.
No jurisdiction in the United States conducted case-based surveillance for a long enough period, in a large enough population to estimate this quantity directly; in particular, jurisdictions with intensive case-finding (such as Milwaukee) did not have enough deaths or ICU admissions to make a statistically robust estimate, while jurisdictions with enough deaths and ICU admissions (such as New York) had too many cases to pursue intensive case-finding for the period over which deaths and ICU visits were registered.
Given that we do not have data on all severity levels for both locations, we aim to estimate cD|S, cI|S and cH|S, using two approaches. First, we combine data from both Milwaukee and New York on medically attended symptomatic cases, hospitalizations, ICU admissions and deaths, together with information from the Centers for Disease Control (CDC) on ascertainment probabilities and proportions of symptomatic cases seeking medical attention, to estimate the ratios cD|S, cI|S and cH|S, assuming the conditional probabilities are equal, but age-specific, across the two jurisdictions. Second, we use data on hospitalizations, ICU admissions and deaths just from New York City, together with data on self-reported incidence of influenza-like illness (ILI) in New York, assuming that these ILI cases represent the true number of symptomatic cases, to estimate cD|S, cI|S and cH|S.
2a.
Severity Model
Approach 1 We start from the simple assumption that the following hierarchy in the severity level holds: death ![]() hospital admission
hospital admission ![]() medical attendance
medical attendance ![]() symptomatic case, and similarly, ICU admission
symptomatic case, and similarly, ICU admission ![]() hospital admission
hospital admission ![]() medical attendance
medical attendance ![]() symptomatic case, where
symptomatic case, where ![]() represents inclusion. Under this assumption,
represents inclusion. Under this assumption,
cD|S = Pr {death | symptoms}
= Pr {death | hospital}Pr{hospital | medical attendance} Pr{medical attendance | symptoms},
= cD|HcH|McM|S
cI|S = Pr{ICU | symptoms}
= Pr{ICU | hospital} Pr{hospital | medical attendance} Pr{medical attendance | symptoms}
= cI|HcH|McM|S
and
cH|S = Pr{hospital | symptoms}
= Pr{hospital | medical attendance} Pr{medical attendance | symptoms}
= cH|McM|S
where cD|H and cI|H are the probabilities of true H1N1pdm-attributable deaths or ICU admissions, respectively, conditional on true H1N1pdm-attributable hospitalizations; cH|M is the probability of true H1N1pdm-attributable hospitalization, conditional on being a true H1N1-positive medically attended case, and cM|S is the probability of being a true H1N1pdm-positive medically attended case, conditional on true symptomatic infection with H1N1pdm.
Clearly, these subset relations may not strictly hold. Indeed, in New York, data are available on H1N1pdm-attributable deaths which occur outside of hospital. So we instead make the assumption that
cD|S = Pr {death | symptoms}
= Pr {death among hospitalized ![]() death among medically attended but not hospitalized | symptoms}
death among medically attended but not hospitalized | symptoms}
= Pr{death among hospitalized | symptoms} + Pr{death among medically attended but not hospitalized | symptoms}
![]()
(see Figure A7-3).
We consider age-group specific values for all of these conditional probabilities so all carry a subscript i for age group and we denote the actual number of people who reached a given level of severity in a given jurisdiction by Ns for symptomatic cases, NM for medically attended cases, NH for hospitalizations, NI
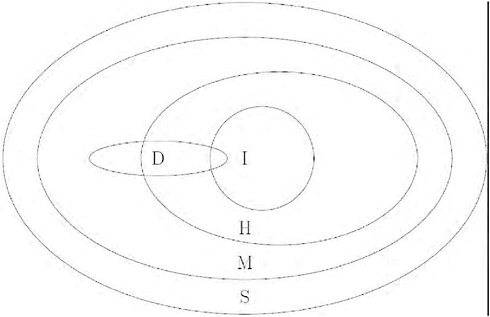
FIGURE A7-3 Assumed severity hierarchy.
for ICU admissions and ND for deaths. Each of these true numbers also varies by age group i and location k (Milwaukee, k = W or NYC, k = N). We assume that in each age group, for each level of severity, the true number of persons at that level of severity is binomially distributed based on the corresponding conditional probability and the true number at the preceding level of severity:
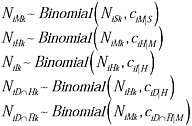
(1a)
NiSk is given a prior reflecting our uncertainty about the number of symptomatic cases (see details in section on symptomatic vs. medically attended infection).
Approach 2 For the NYC only analysis, we do not consider the medically attended level, such that
cH|S is given by
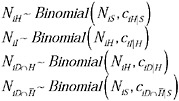
(1b),
and NiS ~ Binomial (NiP,ciS|P) where NiP is the NYC population size (considered constant), and ciS|P are given priors, to reflect estimates from the NYC telephone survey, see section on symptomatic vs. medically attended infection.
2b.
Observation Model
For a variety of reasons, detection at each level of severity will be imperfect, and thus the true values N are not observed. However, we do observe detected medically attended cases OiMW and detected hospitalizations OiHW in Milwaukee, and we observe detected hospitalizations OiHN, detected ICU stays OiIN, and detected deaths OiDN in New York City. We assume that these observations O are related to the true numbers N as follows:
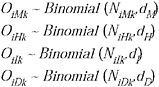
(2)
where for each level of severity j, dj is the detection probability, i.e. the probability that a case enters our database.
2c.
Combining the models—a Bayesian approach
Given (1a) or (1b) and (2), we wish to estimate the values of the age-specific cij, which can then be multiplied appropriately to estimate the age-specific (symptomatic) case-hospitalization, case-ICU and case-fatality ratios.
Figure A7-4 is a schematic representation of the relationship between the quantities we wish to estimate and the quantities we observe. The figure shows only a small part of the whole model in approach 1, for one generic age group and
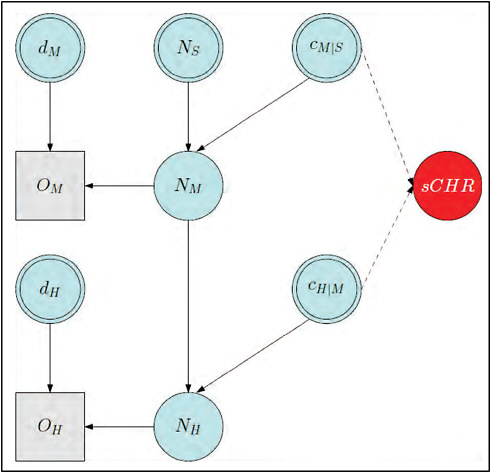
FIGURE A7-4 Simplified directed acyclic graph displaying the dependencies in part of the model.
location, and for the first three levels of severity (symptomatic to hospitalized). Circles denote parameters, double circles denote parameters for which we have prior information, and squares denote observations. Solid lines denote distributional relationships and dashed lines denote functional relationships. The arrows represent the process by which the parameters, if known, would generate the data. In our case, the problem is reversed, i.e. to infer the values of the parameters given the available information. The figure provides an illustration of the flow of information from the observations and prior distributions to the unknown parameters. So for example, the information on OH (the observed number of hospitalizations) together with the prior on dH gives information on NH, the true number of hospitalizations. Note that estimation of the parameters of primary interest (e.g. sCHR, the symptomatic case-hospitalization ratio) is informed indirectly
by the combination of prior and sample information on intermediate but related parameters (OH and OM, together with dM, dH, NS and cM|S, via the true numbers N and the conditional probabilities c).
More generally, the complete set of unknown parameters is ![]() , and we have observations
, and we have observations ![]() Inference is then carried out in a Bayesian setting using the prior information,
Inference is then carried out in a Bayesian setting using the prior information, ![]() , and the likelihood of the observations given the parameters,
, and the likelihood of the observations given the parameters, ![]() to obtain, via Bayes’ Theorem, the posterior distribution
to obtain, via Bayes’ Theorem, the posterior distribution ![]() of the parameters.
of the parameters.
3.
Data
3a.
Milwaukee
On April 27th, Milwaukee sent out messaging to local healthcare providers recommending testing anyone presenting with signs and symptoms characteristic of influenza (fever >100 degrees, cough or sore throat, myalgia) and travel to an area with documented H1N1. By May 7th more than 100 confirmed cases had been identified, and testing guidance was updated to recommend testing persons with moderate to severe symptoms (temperature of > 101.5 and significant respiratory symptoms and significant constitutional symptoms). Testing of persons with mild symptoms was limited to health care workers. On June 15th providers were told to begin testing on a fee-for-service basis. Throughout the outbreak, healthcare providers have been asked to report any suspect, probable or confirmed case of H1N1. Providers were advised about concerns regarding the accuracy of rapid flu tests and urged to use PCR as the preferred method for analysis. All confirmed and probable cases were entered into a line list on a rolling basis, and we used a line list dated July 21.
Because our primary focus for Milwaukee was on hospitalization probabilities, in a preliminary analysis we plotted the frequency of hospitalization by week of “episode date,” the earliest date (of illness onset, report or hospitalization) in an individual record. The hospitalization frequency was around 3% overall with no temporal trend up to an episode date of May 20, after which there was a dramatic upward trend in the proportion hospitalized, with 8.2%, 6.0%, and 7.0% hospitalized in the weeks that followed. We interpreted this increased hospitalization rate as evidence of declining ascertainment of mild cases, and we therefore restricted our attention to cases with illness onset date up to and including May 20. This also obviated the need to deal with censoring, as the date of the line list was two months later, far longer than the delay in reporting for nearly all cases. This created a data set of 763 cases, of whom 25 (3%) were hospitalized.
While the main source of data on the probability of ICU admission or death was New York City, such data were available, albeit in small numbers, for
Milwaukee. To inform the ratio of ICU+ventilation:hospitalization and death:-hospitalization, we used a larger subset of the data, on the assumption that the change in ascertainment after May 20 was due to reduced ascertainment of mild cases, not changes in ascertainment of hospitalized or more severe cases. Therefore, we considered the 147 hospitalizations with episode date up to and including June 14. Again, this was more than 30 days prior to the close of the line list, so we did not correct for censoring. Of these 147 hospitalizations, 25/147 (17%) were admitted to the ICU and/or ventilated, and 4 (3%) died.
3b.
New York City
From April 26 to July 7, 2009, New York City maintained a policy of testing hospitalized patients with influenza-like illness (ILI) under various criteria. Criteria for testing varied up to May 12, after which point all hospitalized patients with influenza-like illness (ILI) were tested with a rapid influenza antigen test. Those patients who tested positive, and also any patient on a ventilator or in an intensive care unit (ICU) regardless of rapid test result, were tested for H1N1pdm by PCR. We obtained a line list of confirmed cases dated August 24, 2009, including 996 hospitalizations, of whom 882 had a known date of onset. Preliminary analysis indicated that >99% of hospitalizations were reported within 21 days of symptom onset. Since the last date of admission in the data set was July 6, 49 days prior to the date of the line list (August 24), we did not restrict this data set. Also, >97% of admissions in the data set were after May 12, so we did not attempt to account for differences in testing prior to May 12.
Separately, we obtained a list of 53 deaths attributed to H1N1pdm, of whom 44 (83%) had been hospitalized before dying. The dates of death ranged from 17 May to 19 July, but the dates of case report to New York City ranged from 13 May to 4 July; hence, these cases were all included within the time frame in which hospitalizations were being investigated. Based on the time-to-death distribution and the timing of hospitalizations, we estimated that >99.9% of deaths which would be reported from the hospitalized cases had already been reported. We therefore made no effort to account for censoring of deaths.
The data are shown in Table A7-1 of the main text.
4.
Detection Probabilties
We require information on the detection probabilities, dM, dH, dI, dD. In general, these are assumed location-specific, and may consist of multiple components. We present below the evidence or prior assumptions available to inform estimates of these detection probabilities.
4a.
Detection of medically attended illness
The detection probability for medically attended (M) illness (in Milwaukee), dMW, may be expressed as
dMW = Pr{specimen collected & tested | true M case already M} Pr{test positive | specimen collected & tested for a true M case}
= dMW1dMW2
where dMW2 is the sensitivity of the PCR-based tests recommended for use in Milwaukee. We assume dMW1 ~ Uniform(.2,.35), dMW2 ~ Uniform(.95,1), and that the probability of censoring is 0, for the reasons described in Section 3. These assumptions are based on estimates from Reed et al. (2009), using data from seasonal influenza and from Epi-Aids in Delaware and Chicago and are not Milwaukee-specific. Unlike Reed et al., we do not assume a separate probability for specimens being sent for confirmatory testing, since Milwaukee recommended against use of rapid antigen testing for screening (which would have led to false negatives and reduced detection) and since Milwaukee recommended testing of all persons with moderate to severe symptoms.
4b.
Detection of hospitalizations (Milwaukee)
We define dHW, the detection probability for hospitalization (in Milwaukee) as
dHW = Pr{report hosp case | test pos} Pr{test pos | true hosp case already hosp and tested}Pr{tested | true hosp case already hosp}
= dHW1dHW2
By using the July 21 line list but restricting analysis to cases with an episode date prior to or on May 20 (or June 14) we believe it reasonable to assume the probability of censoring is 0. We have no Milwaukee-specific data on the probability that some true hospitalizations go unreported, either because testing was not performed, or because a positive case was not reported. Hence we again follow Reed et al. in assuming
dHW1 = Pr{report hosp case | test pos} Pr{tested | true hosp case already hosp} ~ Uniform(.2,.4) and dHW2 ~ Uniform(.95,1) to account for imperfect PCR test sensitivity.
We assume the same priors for the detection probabilities in ICU admissions.
4c.
Detection of deaths (Milwaukee)
dDW is the detection probability for deaths in Milwaukee. As with hospitalizations, we assume no censoring, since the date of the line list is a month after the last episode date in the data set we are considering (episode dates up to 14th June), so that dDW = Pr{report death | true H1n1pdm-attributable death (already died)}. We have no data to assess the probability of a death being tested for H1N1pdm, hence we assume a prior reflecting failure to detect of dDW ~ Beta(45,5) giving a prior mean of 0.9 and standard deviation 0.05 (a range of 0.8 – 1, as in New York, see below), covering both test sensitivity and failure to detect.
4d.
Detection of hospitalizations (New York)
dHN is the detection probability for hospitalization (in New York). In New York, rapid antigen testing was used as a screen for most patients. From May 12, PCR testing for H1N1pdm was performed only on hospitalized patients who (a) tested positive on a rapid influenza A test, or (b) were in the ICU or on ventilator, regardless of their rapid influenza A status. Thus one component of dHN is dHN1, the probability of PCR testing. 27% (242/909) of hospitalized H1N1pdm patients in New York were in the ICU, so for these we assume that the probability of PCR testing was 1. For the other 73% we assume the probability of PCR testing was equal to the sensitivity of the rapid test, which we model as Uniform(.2,.71). Thus we model dHN1~.27+.73(Uniform(.2,.71)). Finally we account for imperfect sensitivity of the PCR, dHN2 ~ Uniform(.95,1). Because of active surveillance for hospitalized cases, we assume that testing was performed as advised and was reported in all cases; hence we do not assume a separate factor for failure to test or report. As noted above, we made no effort to account for censoring of hospitalized cases.
4e.
Detection of ICU admissions, New York
Here we assume that detection is equal to the sensitivity of the PCR test, dIN ~ Uniform(.95,1), since rapid testing was not required for PCR testing. As with hospitalizations, we assume the probability of censoring is 0.
A limitation is that we only detect ICU admissions that are known by the time the hospitalized case is reported to the NYC Department of Health. Later admissions from the ward are not reported. Thus we will underestimate the proportion of ICU admissions among hospitalized cases. However, a chart review of 99 hospitalizations found that 24 (24%) were admitted to the ICU during their entire stay, a proportion indistinguishable from that in our overall dataset. Hence we conclude that this underestimation is not severe.
4f.
Detection of deaths, New York
New York had a policy of PCR testing all unexplained respiratory deaths involving fever. We have no data to assess the completeness of such testing. Given issues of PCR sensitivity and possible failure to test, we assume a prior distribution for ascertainment of deaths of, dDN ~ Beta(45,5) giving prior mean 0.9 and standard deviation 0.05), reflecting possible failure to detect H1N1pdm-attributable deaths.
5.
Symptomatic vs. Medically Attended Infection
We have no direct data on the number of symptomatic but not medically attended H1N1pdm infections. However, multiple epidemiological investigations have estimated the proportion of influenza-like illness that is medically attended; these estimates range from 42% to 58% (Reed et al., 2009) and include data both from prior influenza seasons and from the spring 2009 H1N1pdm influenza period. Thus we model the conditional probability of being medically attended given symptomatic infection, cM|S ~ Beta(51.5,48.5) giving a mean of 0.515 and standard deviation 0.05, with 90% of the probability mass between 0.42 and 0.58.
For approach 1, we also require prior distributions for the true number of symptomatic infections, NS. For Milwaukee, we assume NiSW ~ Uniform(HiMW, 0.25 × popniW), i.e. a lower limit of the observed number of medically attended cases, with an upper limit of 25% of the population size. This implies a maximum clinical attack rate of 25%. For New York, we assume NiSN ~ Uniform(0,upperiN × popniN): we have not observed medically attended cases in New York, so cannot use the observation as a lower limit. We used an upper bound of symptomatic infection in New York City based on the number of persons reporting ILI in a telephone survey conducted by the New York City Department of Health and Mental Hygiene covering a 30-day period in May-June at the height of the spring epidemic (NYC DOHMH, unpublished data):
upper0-4,N ~ Beta(18.2,72)
upper5-17,N ~ Beta (50.4,178)
upper18-64,N ~ Beta(38.7,338)
upper65+,N ~ Beta(27.6,446)
upperall,N ~ Beta(91.4,654)
In approach 2, the telephone survey data is used directly to inform priors for the proportion of the NYC population with symptomatic infection, rather than an upper bound:
c0-4,S|P ~ Beta(18.2,72)
c5-17,S|P ~ Beta(50.4,178)
c18-64,S|P ~ Beta(38.7, 338)
c65+,S|P ~ Beta(27.6,446)
cAll,S|P ~ Beta(91.4,654)
6.
Implementation
The Bayesian model described in Section 2 used the data and priors as presented in Sections 3 to 5, and was implemented in the OpenBUGS software. This uses Markov chain Monte Carlo to obtain samples from the posterior distributions of the parameters of interest. Three chains of 1,000,000 iterations each were run, starting from different initial values. Summary statistics were based on the last 200,000 iterations of each chain, after discarding the first 800,000 as a burn-in period.
Convergence for the quantities of primary interest which were reported in the main text, the conditional probabilities cij, was assessed both visually and using Gelman-Rubin-Brooks plots and we are satisfied the chains converged for these in most age groups. In approach 1, the probability of hospitalization given medical attendance did not reach quite the same level of convergence as the other cij, particularly for the 65+ age group. This is due to the paucity of data available for this ratio: only data from Milwaukee is available, up till May 20th, the period for which ascertainment of mild cases was assumed constant over time. The observed numbers of hospitalizations in particular are very small, with 0 hospitalizations observed in the 65+ age group. This has a knock-on effect on the true numbers of medical attendances and symptomatic infections (NiSk and NiMk), so that their Markov chains also did not quite reach the same level of convergence as the chains for the true numbers of hospitalizations, ICU admissions and deaths.
The posterior estimates for the symptomatic case-fatality, case-ICU admission and case-hospitalization ratios are reliant on the estimates of NiSk, the true number of symptomatic cases, and are hence sensitive to the choice of prior. Convergence for NiSk improves as the upper limit for its prior is reduced, i.e. as the maximum clinical attack rate becomes smaller. However, it would not be reasonable to assume a maximum clinical attack rate of less than the telephone survey estimates for New York or less than 25% for Milwaukee, given our lack of prior knowledge on these. For this reason we do not report estimates of the total number symptomatic. Despite the uncertainty, there is some information available in the likelihood to update the estimates of the number symptomatic: the posteriors do not simply reflect the prior distributions (Figures A7-5 and A7-6).
In approach 2, we are satisfied that the chains converged for the conditional probabilities cij in all age groups.