3
Fiscal Prudence
Whatever people’s values and choices about government and the budget, in the long run many widely shared policy goals that require federal spending will be unattainable if the budget is not on a sustainable path. It will be difficult to simply continue the programs that people have come to expect, let alone allow sufficient flexibility for future generations to develop new policies for a changing world. In this chapter we offer a first step toward dealing with the country’s fiscal challenge by specifying concrete and usable tests that any proposed budget must meet to move toward sustainability in a prudent manner.
The committee’s members embody a range of disciplinary perspectives and practical experience in dealing with the federal budget. We hold quite varied views of the nation’s priorities and how best to achieve them, including the proper size and role of government. We do not necessarily agree, for example, about the extent to which the federal budget ought to aim at expanding individual responsibility and choice or at promoting economic security; whether the nation should limit the use of carbon fuels or eschew such limits to facilitate economic growth; or how much to emphasize national security concerns versus expanding education and other programs that may promote equality of economic and social opportunity. What the committee members do agree on is the need for a set of straightforward criteria that anyone can use to assess the fiscal responsibility of any budget proposal for the overall federal budget from a long-term perspective.
In its work, the committee sought to apply these criteria to the development of an illustrative set of policy and budget scenarios that demonstrate several possible paths to sustainability. These scenarios are detailed in
Chapter 9. The criteria also can be applied to the President’s budget or any alternative set of budget proposals, as discussed in Chapter 11.
LIMITING THE GROWTH OF FEDERAL DEBT
In consequence of our concerns about the current trajectory of the federal budget, the committee believes the overriding goal of long-term budget policy should be to slow the rate of future accumulation of the federal public debt—through some combination of revenue increases and spending restraints—so that such debt first ceases to grow faster than the economy and then subsequently returns to a prudent proportion of gross domestic product (GDP) within a reasonable period of time. The choice of a particular path for deficit reduction will ultimately be made by elected leaders, in light of the information available to them when they make budget decisions. But the committee believes that the projected level of federal government debt relative to GDP is an appropriate benchmark for assessing the prudence of long-term budget policy, and that aiming for a level of 60 percent within a decade of initiating policy actions that could begin as soon as fiscal year 2012 is prudent under current circumstances.
The remainder of this section explains our rationale for these views. The trajectory of a nation’s level of debt relative to its GDP has been widely used by U.S. government agencies, international organizations, and other countries as a benchmark for assessing a nation’s fiscal condition (see Peterson-Pew Commission on Budget Reform, 2009; also see Appendix G). The three major federal agencies that regularly make long-term projections each highlight the debt as a percentage of GDP as a principal measure of the budget outlook: (1) the Congressional Budget Office (2009c), (2) the General Accountability Office (2009), and (3) the U.S. Office of Management and Budget (2009a:Ch. 13).
The most recent assessment of the state of public finances in advanced economies and emerging markets by the International Monetary Fund (IMF) (2009b) uses the ratio of total public debt to GDP as the basis for international comparisons (International Monetary Fund, 2009b). The IMF also used simulations to project the evolution of public debt as a percentage of GDP as a way of judging which countries are most vulnerable to an adverse debt dynamic following the current downturn. Those simulations noted, for example, that “[projected] increases are particularly large in absolute terms for the United Kingdom and the United States, where debt levels rise sharply” (International Monetary Fund, 2009b:18). Similarly, the Center for Budget and Policy Priorities has estimated that “driven primarily by health care costs, rapidly growing deficits will push the debt held by the public up to roughly 300 percent of gross domestic product by 2050, or nearly three times as large as the record level reached at the end of World War II” (Cox et al., 2009:1).
The Congressional Budget Office (2009e) and others (e.g., Auerbach, 1994) have calculated another measure that is useful in assessing the long-term fiscal outlook, termed the “fiscal gap.” It is the amount that spending has to be reduced or revenues increased as a percentage of GDP so that the debt is the same at the end of a specified projection period as today, expressed as a percentage of today’s GDP. It is similar to our measure in that the debt is eventually stabilized relative to GDP, but it is more stringent in that it depends on stabilizing the debt ratio at today’s level. Because the stimulus plan, financial bailouts, and the lingering effects of the recession have the debt ratio on a strong upward course, the committee believes that the total elimination of the fiscal gap would require an overly painful change in tax and spending policies.1
Yet another alternative fiscal yardstick would be the size of the annual budget deficit. A different target and an even more stringent goal than ours for budget policy in the long term would be a return to the easily grasped idea that budgets should be balanced—either year-by-year or on average—and as expeditiously as possible. Because the government’s debt in dollar terms would be constant if budgets were balanced, the economy’s growth would gradually reduce the federal debt as a percentage of GDP. A balanced budget, although not consistently achieved, was the norm over most of U.S. history (Schick, 2007). Adopting this more stringent approach would, over time, provide a widening margin for error in case projections are overly optimistic or adverse developments ensue. However, the committee concluded that such a goal is unnecessarily restrictive: It would both be extraordinarily difficult to achieve in the foreseeable future—and goes well beyond what prudent fiscal policy requires for sustainability over a long period. Moreover, many would argue that running modest deficits to finance wise public investments that will benefit future generations is appropriate (see also the discussion in Box 3-1 of the relationship between deficits and GDP growth).
Having selected the ratio of debt to GDP as a reasonable (albeit not the only possible) indicator of fiscal prudence, the committee then considered possible targets for it and on what time line the target should be reached. Within certain bounds, the choice of a target for debt is a matter of judgment, but that does not mean that it is arbitrary.2 The federal government could eventually stabilize its debt at a substantially higher percentage of GDP than our chosen level of 60 and could run larger deficits in the meantime (which would in part accommodate the resulting additional debt service). Or, it could stabilize debt at a smaller percentage of GDP, requiring larger policy adjustments to reach the goal in a given period of time.3 Box 3-1 provides illustrations of the relationship among interest rates, the primary budget balance, growth in incomes and GDP, and the debt-to-GDP ratio.
There is no magic number either for the debt target as a percentage of
|
BOX 3-1 The Arithmetic of the Debt Suppose borrowing were used only to finance the interest portion of spending, that is, revenues were always sufficient to cover noninterest (“primary”) spending. And suppose that the interest rate on the debt equals the growth rate of incomes (or GDP, given that incomes and GDP grow at nearly the same rate). Under those conditions, the debt will grow at the same rate as incomes, and the debt-to-GDP ratio will remain constant. For example, if the interest rate on the debt is 5 percent and the U.S. Treasury borrows just enough to cover it, the debt will grow 5 percent annually. If GDP also were to grow at 5 percent, the debt-to-GDP ratio would remain constant. At 60 percent of GDP, which is the target ratio the committee proposes, debt service at an interest rate of 5 percent would be 3 percent of GDP (0.6 × 5). If all spending totaled about 20 percent of GDP, interest on the debt would be 15 percent of all spending. With revenues at 17 percent of GDP, the budget would be balanced except for interest on the debt. The annual budget deficit—equal to the additional borrowing or growth of debt—would be 3 percent of GDP and the debt would grow by that amount or at a rate of 5 percent (3/60). If GDP grew 4 percent in one year, then debt at the end of the year would be 60.6 percent of GDP.a If budgeters wanted to prevent the debt from growing, they could either raise revenues or reduce primary spending as a percentage of GDP. This “solution” might not be practical for long, however, given that the study’s baseline projects primary spending to grow faster than GDP if no changes in policy are made. In that case, it would become increasingly difficult to either limit or offset spending growth in order to keep debt stable. The simple relationship between growth rate of the economy and the federal debt is summarized by the following equation (adapted from von Furstenberg, 1991): where R is revenues, P is noninterest spending, and Dt−.5 is the average publicly held federal debt during the year, all expressed as percents of GDP. The average interest rate on debt is represented by r, n is the growth rate of GDP, and t is the fiscal year. When r − n is zero, revenues can equal primary spending plus the change in the debt resulting from borrowing the amount needed that year for interest on the debt paid that year. If r − n is negative, either revenues can be lowered or spending increased without increasing the debt. Conversely, in a year when r − n is positive, the debt will grow unless revenues are increased or spending reduced as a percentage of GDP. As the debt grows, so does the burden of interest on that debt. Even if r − n were always zero, if P is on a rising path, as this study’s baseline projects, then to keep the debt from increasing relative to GDP, R must rise by the same amount. Or, to keep R constant as P rises, D must fall instead. However, r − n can be (and often has been) positive, as in the example above. Although n can be (and often has been) greater than r, it is precisely when the opposite is true that the nation can least afford to run primary surpluses, so these circumstances deserve special attention (Bohn, 1995). The most recent downturn serves as an example. In 2008 and 2009, n turned negative while r fell slowly, P rose as a result of additional spending demands and efforts to stimulate recovery, and R fell with the drop in employment, incomes, and profits: the result was a rapid rise in federal debt, D. |
|
The following example illustrates how quickly D can rise as a percentage of GDP in and following a less severe downturn than the one we have experienced. Assume that at the recession’s onset Dt = .60 and r = n. The primary deficit, Pt+1− Rt+1, suddenly equals .08, and n falls to −.05 while r = .05. Rearranging the budget constraint, Then, substituting the assumed numbers, we have The recession has raised D by 11.3 percentage points. Now assume a partial recovery next year. The primary deficit improves to .02, n = .02, and r remains at .05. The debt has risen by over 15 percent of GDP in only2 years. This exercise illustrates how fast D can rise in a recession and its aftermath. Suppose that interest rates on the debt doubled in the future while annual GDP growth continued to average 4 percent. In that case, debt service would more than double in a few years as the debt grew relative to GDP and as maturing debt rolled over and was replaced by new debt carrying higher rates. If annual interest payments on the debt doubled from 3 to 6 percent of GDP, for example, then one of three things would have to happen: the additional interest spending would be covered by borrowing and the debt would grow by that amount; noninterest spending would be reduced by about 18 percent (equal to 3 percent of GDP, assuming total spending is 20 percent of GDP); or revenues would be increased by3 percent of GDP. The first option would put the budget on an unsustainable path. The other two options would be very painful but perhaps barely manageable. If the debt reaches much more than 60 percent of GDP, an interest rate doubling might be too difficult to manage. Suppose instead that the debt is stabilized at 80 percent rather than 60 percent of GDP. With the interest rate at 5 percent, the interest bill would be 4 percent of GDP (0.8 × 5), that is, interest spending would be one-third higher than at a 60 percent debt ratio. Even if GDP growth matches interest rates, absent a decision to increase revenues by1 percent or to reduce noninterest spending by 1 percent, the deficit would increase from 3 to 4 percent of GDP because of the additional interest spending. Not only would annual interest payments be higher on this larger debt, but the margin for future spending and revenue increases would be reduced. In the budget baseline used for this study, the publicly held debt is projected to increase by more than 40 percentage points of GDP from 2008 to 2021. Suppose that after some years the United States faced one or a series of economic or other emergencies of magnitude comparable to the 2008-2009 financial crisis and downturn, contributing to a comparable increase in borrowing, which would put the debt at 120 percent of GDP. At that level, even with no increase in borrowing rates, annual interest payments would be 6 percent of GDP, requiring a decision about whether to borrow, raise revenues, or lower spending to cover the higher interest payments. If revenues are not increased or noninterest spending reduced in this case, the debt would begin to grow as a percentage of GDP. If interest rates doubled, debt service would consume 12 percent of GDP; if other spending were maintained at 17 percent of GDP, spending would equal 29 percent of GDP, and interest would be 41 percent of total spending. |
the GDP or for the number of years until the target is reached. These choices must follow from the underlying purpose of adopting such a standard. The federal budget will be sustainable if investors around the world (including the United States) are willing to lend to the Treasury at affordable interest rates. Maintaining that willingness to lend now and in the future requires, in our view, a credible public commitment to responsible fiscal behavior.
The choice of the target and the time line are important. A target or a schedule that is too stringent risks failure because it imposes such painful policy choices. A failure to achieve a publicized goal could shake the confidence of domestic and international financial markets. An excessively rigorous standard might require either what would be viewed as excessive taxation or forgoing government services that most people believe are essential.
The higher the level of debt, the closer the nation would be at any time to a major problem as the result of any adverse events—such as an economic downturn or a national security crisis—that can drive revenues down and increase spending needs. In fact, the IMF (2009b:21) found that the size of the fiscal stimulus during 2008-2010 was inversely related in large
countries to the initial level of public debt. Presumably, those with higher debt burdens were more constrained either politically or economically than others. Furthermore, the larger the debt and the government’s interest obligations, the more the budget would be vulnerable to any upward spike in interest rates.
Both theory and evidence suggest that higher debt itself will tend to increase the long-term interest rate on government debt (Engen and Hubbard, 2004; International Monetary Fund, 2009b). The observed effects are even larger “for countries that start from high debt ratios or deficit levels, or that confront faster population aging” (International Monetary Fund, 2009b:21-22). With interest payments as a larger share of spending, the task of maintaining debt at a given percentage of GDP in the face of an interest rate rise becomes harder. There is a danger of a debt spiral. The tax increases or spending cuts necessary to finance a growing interest bill become more difficult politically as they become larger. Legislators may lag in enacting them. The deficit grows, and interest pressures become more severe. Faced with such pressures, many countries throughout history have simply given up and decided to finance deficits by creating money (Reinhart and Rogoff, 2009). The hyperinflation that follows destroys personal wealth and government programs. It is often said that cannot happen here, but the prospect is so terrible that we must be extremely vigilant in avoiding even the smallest probability of such an outcome.
It can also be argued that an “easy” standard would result in a government that many people would believe is too large. The larger the debt, all else equal, the more the government must spend on interest payments before it can spend to meet any of the nation’s needs. Larger government borrowing competes with other uses of capital, including productive business investment, and can increase interest costs for other borrowers. To the extent that productive investment is crowded out or the United States must rely on borrowing from abroad, either wage growth is slowed or a higher portion of our income must be devoted to paying interest and dividends to foreigners.
The committee believes that some combination of revenue increases and spending restraints should be implemented soon to constrain the growth of federal debt as a percentage of GDP within a decade to a level that provides an appropriate balance between the risks associated with a higher ratio and the additional difficulties of implementing policies that would be consistent with a lower ratio. The committee judged that a debt of 60 percent of GDP reflects an appropriate balance and is an achievable target within a decade—and is therefore useful to guide policy choices that will ultimately be made by elected leaders. This is a different ratio than the committee would have likely proposed under different circumstances. Indeed, it will surely be seen by some as too high and by others as too low.
But the committee believes it is the lowest ratio that is practical given the fiscal outlook and reflects the best balancing of practicality and risk, taking into account a range of concerns.
In establishing a debt target, the nation needs a standard that balances risk—maintaining credibility, but not excessively constraining public services or raising taxes—through either too low a constraint on debt or too high a level of debt service. Maintaining credibility will require a debt target that is within a reasonable range, based on the nation’s economic history. Although the U.S. economy survived a debt in excess of its GDP in the years immediately following World War II, those were extraordinary—probably unique—times. There was enormous pent-up demand for domestic goods and services as a result of war-time rationing, the labor force grew enormously with the return of the troops, and the federal government had not yet made sizeable commitments for retirement and health care that would later cause spending to automatically rise much faster than revenues. As a result, the debt-to-GDP ratio fell rapidly as the GDP grew quickly, and the budget remained close to balance from 1947 through 1960. Today, this favorable situation is almost completely reversed, as the post-World War II baby boom generation is just beginning to retire, both slowing the potential growth of the labor force and the economy and (along with rising health care costs) putting severe pressures on the budget.
Our target of stabilizing the ratio of debt to GDP at 60 percent still would leave the public debt relative to the size of its economy at its highest point since 1952. Assuming as a rough rule of thumb that the average interest rate on the debt is 5 percent, that would leave the government’s net interest cost at 3 percent of GDP—which would be higher than in any years other than the period of high deficits and elevated interest rates of 1985 through 1997.4
With the future spending and higher debt relative to GDP implicit in the nation’s promises to the elderly both larger than at any time in the past, the credibility of a target debt level of 60 percent of GDP is not a foregone conclusion. However, a 60 percent target would have institutional confirmation in the financial world. The European Monetary Union (EMU) set as its standard for membership the achievement and maintenance of a debt-to-GDP ratio of 60 percent.5 Of course, just as the U.S. debt has increased in the current economic and financial crisis, so have the debts of EMU members. However, should the United States articulate and pursue a target for the public debt of 60 percent of GDP, there is a strong probability that the financial credibility of the nation in world financial markets will be maintained.
In considering feasibility, we concluded on the basis of the analysis in this report that a debt target of 60 percent of GDP could be reached consistent with appropriate levels of spending and taxation. In fact, there are many plausible policy combinations that would produce this result if action
is taken in our proposed time frame. We note again that the members of the committee would choose different levels of taxation and of spending in different categories of the budget. Those decisions ultimately must be made by the citizens of the nation, through their elected representatives. Our findings demonstrate that many reasonable choices are available to meet the standard that we have chosen.
Apart from the numerical target for the debt as a percentage of GDP, there are further specific questions about how quickly it should be reached. We selected fiscal 2012 (which begins October 1, 2011) as a reasonable time to start—to first slow the rapid increase of the debt relative to the economy and then, over several years, to reduce it to a more prudent level. We expect the economy to find its feet by that date. The longer the time taken to change course, the longer the debt will continue to rise relative to GDP and the higher the level before it begins to be stabilized or reduced, raising all of the concerns about excessive debt. However, given the situation as the committee writes its report—and with an economy that is still fragile and in a slow recovery—sharply and quickly raising revenues or reducing spending quickly could be a mistake, even with a debt-to-GDP ratio above 50 percent and rising rapidly as it currently is in the United States. With-drawing purchasing power from the economy while the recovery is fragile could return the economy to a recession. The committee is aware both of the many spending demands that the federal government must meet in the immediate future and the dangers of quickly raising revenues or reducing spending relative to their current paths. We believe that articulating an extended adjustment path from the outset would help to cushion the impact on the economy, reducing the risk of extending the recent slowdown. We note that once a 60 percent debt-to-GDP ratio is reached, the government can run annual deficits (after 2022) that average between 2 and 3 percent of GDP at the projected rate of interest on the debt without causing the debt to grow in proportion to the economy.6
A target or schedule that is delayed too long could itself lose the nation’s credibility with investors by failing to assure that the nation’s debt-servicing obligations will be met. In fact, we believe that the reassurance of financial markets that would come from the national determination to meet a clear fiscal standard would help keep interest rates lower than they otherwise would be, facilitating the economic recovery and ultimate expansion. We then believe that 10 years would prove to be a sufficient time horizon to achieve the necessary savings in a nondisruptive manner.
The choice of the starting date and time line, as with the level of the target will ultimately be a decision of elected leaders, taking into account the best information available to them when they must make budget choices. However, we judge that waiting longer to begin changing course or enacting a less stringent target (thereby allowing the debt to GDP ratio to rise even further before its rise is arrested and reduced to the proposed target) will
only add to the ultimate budgetary cost—and the economic risk. This, in turn, will add to the political difficulty and pain of reaching the 60 percent target. The budget costs of such delays are highlighted by an analysis, presented in Chapter 9, showing the budget effects of waiting 5 or 10 years longer before beginning to introduce similar policy changes.
As the discussion of illustrative policy options in the following chapters makes clear, achieving the committee’s proposed stabilization of the debt-to-GDP ratio by 2022 would require the adoption of painful policies. The fact that the goal is so politically challenging to reach is an indication of the depth of the nation’s fiscal hole. The committee would prefer a more ambitious goal for the very long run, but believes that it is unrealistic to aim for a significantly lower debt ratio within the next 20 to 25 years. Thus, we selected a 60 percent debt-to-GDP target as reasonable and reachable within this time frame—particularly since a higher target or longer glide path would leave the nation at too much risk of being unable to cope with unforeseeable shocks that require a vigorous federal response. Chapters 4 through 9 present first an overview of, and then describe, specific sets of, policy options and possible combinations that would put the U.S. budget on a path to achieve this target federal debt-to-GDP ratio by 2022. The committee’s different scenarios are intended as an illustrative, but by no means, definitive or exhaustive, set of trajectories toward a sustainable fiscal future.
Reasonable people may differ with our views about what target and time path to choose, and there should be a full and rich debate about those decisions. However, the committee urges those who differ significantly on these choices—especially those who would choose a less ambitious target or a slower time path—to consider seriously the benefits in terms of credibility from formally setting some target and some schedule to reach it. We believe that such a public commitment would be beneficial even if the target and schedule chosen were different from ours.
TESTS FOR FISCAL PRUDENCE
Having set a long-term target for sustainability, the committee suggests that people apply to any comprehensive set of budget proposals three primary fiscal prudence tests, on the debt target and on the long-term relationship between revenues and spending. We also offer secondary fiscal prudence tests on the deficit, age-related programs, cost-effectiveness and growth, and effects on states.
Primary Tests for Fiscal Prudence
A budget must be judged primarily by the extent to which it moves from the current unsustainable path to one that is sustainable for the
foreseeable future. The committee proposes three primary tests to assess whether it puts the country on a path of economic sustainability.
-
Does the proposed federal budget include policy actions that start to reduce the deficit in the near future in order to reduce short-term borrowing and long-term interest costs?
The budget should include proposals that begin to close the gap between revenues and spending, first slowing the growth of the debt and then gradually reversing its growth. This cannot be done overnight, but it can be done gradually and steadily over a decade or more. It is important to minimize near-term annual deficits that add to the future size of the federal debt and the costs of servicing that debt, in part because many policy changes to entitlement programs will take a long time to yield substantial budget savings, even if enacted soon.
-
Does the proposed budget put the government on a path to reduce the federal debt within a decade to a sustainable percentage of GDP?
Given the fiscal outlook and the committee’s analysis of the many factors that affect economic outcomes, the committee believes that the lowest ratio of debt to GDP that is economically manageable within a decade, as well as practical and politically feasible, is 60 percent. If the budget is put on a path beginning in 2012 to reach that target, savings from interest payments that are avoided by reducing borrowing requirements would accumulate slowly at first, but would equal nearly $800 billion in the first 10 years (2012 through 2021), exceeding $5.7 trillion by 2031 and multiplying quickly thereafter: see Figure 3-1. These estimates are derived from the scenarios developed and analyzed in Chapters 4 through 9.
In addition to contributing directly to deficit reduction, less borrowing in this period would contribute to creditors’ confidence in the United States’ ability to manage its affairs and thereby reduce the risks of a disruptive financial crisis that could harm the economy, as well as greatly illustrative complicate efforts to achieve budget sustainability.
-
Does the proposed budget align revenues and spending closely over the long term?
Projections of the long-term path (75 years or beyond) implied by a proposed or enacted budget should show revenues and spending that are roughly aligned and parallel and appear likely to remain so beyond the end of the projection period. The size and timing of changes that affect the budget’s path matter a great deal. It may be too much politically to ask
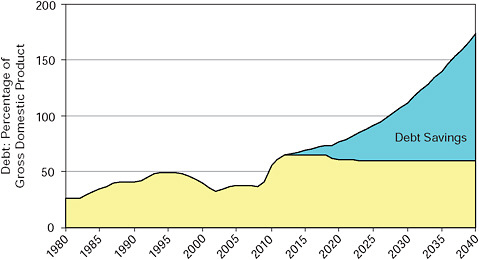
FIGURE 3-1 Debt savings from stabilizing debt-to-GDP ratio in 12 years.
leaders to provide specific policies in a single year’s budget sufficient to accomplish the entire, large task of aligning spending and revenues. However, each year’s budget should demonstrate a credible commitment to policy changes that substantially move toward sustainability, with an explicit commitment to the longer-term goal of aligning revenues and spending over the long term.
Secondary Tests for Fiscal Prudence
The standards of fiscal prudence proposed above address the overall long-term balance between revenues and spending. The additional criteria discussed in this section can help people assess whether budgets are moving in the right direction. Most analysts are likely to agree on these in principle, although they may disagree on how to apply them in practice. The three secondary criteria offered below are applicable to any budget, but they are particularly important given the current path of the U.S. budget.
-
Does the proposed budget restrain health care cost growth and introduce changes now in the major entitlement programs and in other spending and tax policies that will have cumulative beneficial fiscal effects over time?
For entitlement programs, peoples’ reasonable expectations about current benefits will be honored. Changes will be easier to manage if spending restraints or revenue increases are introduced soon, but applied in a way
that minimizes their effects on current beneficiaries. This means that even budget savings from changes introduced immediately would take effect slowly—so the sooner the effort is started the better.
If programs can be designed that truly yield productivity gains by restructuring major sectors of the economy or the budget (or both), investments in these may increase spending in the short run but yield permanent gains from more productive use of resources. Proposed investments in information technology for health and investments in new forms of energy, if they yield hoped-for gains in productive capacity and other social benefits, fall into this category.
For both sets of policies, it may take many years after major policy changes are made before they achieve results of the magnitude required to help bring revenues and spending into stable alignment. For this reason, if policy changes are deemed necessary to yield large long-term changes in levels of spending or revenues relative to the baseline, they should be introduced as soon as possible. The costs of waiting—in forgone budget savings and accumulated additional borrowing to finance deficits—are high.
-
Does the budget include spending and revenue policies that are cost-effective and promote more efficient use of resources in both the public and private sectors?
A budget should include those investments—perhaps in education, preventive health, infrastructure, and scientific research—that can be shown to yield high returns. A budget should raise revenues in ways that do not create undue distortions and inefficiency in private-sector decisions about the best use of resources, which slow growth. And a budget should eliminate or curtail programs that have proven ineffective or inefficient and use information about performance to redirect public resources to more effective programs addressing the most important national objectives.
-
Does the federal budget reflect a realistic assessment of the fiscal problems facing state and local governments?
It would be easy for the federal government to improve its books by simply dumping its burdens onto state and local governments. Because cutting federal transfers to states and localities adds to their fiscal burdens, applying this test requires consideration of the fiscal stresses that are facing state and local governments. In the medium and longer term, states will face daunting fiscal pressures from some of the same sources as the federal government, including commitments for health and retirement. Their freedom of action is more limited than that of the federal government because in most cases they have, at most, limited borrowing capacity to finance
these commitments. Shifts of responsibilities to state and local governments should be predicated on evidence that these will improve overall government efficiency and responsibility to local circumstances. However, arguments for devolving to states some functions traditionally performed at a national level—if these changes are made thoughtfully—are stronger now than in the past. States’ governing capacities have increased and become more uniform over time, and state governments are often leaders in both policy innovation and service administration. States can be expected to do more than some years ago partly because of convergence among states in their economies and policies. In particular, many southern states whose economies were so weak they could not easily provide basic services to their residents or have had a history of racial discrimination are today closer to economic parity with other states. However, the principal test for deciding whether to devolve some federal responsibilities to state and local government is whether those government can better take account of local conditions and be more responsive to people’s varied demands than the federal government.
In a broad sense, these secondary tests help to ensure that the federal government makes the most efficient possible use of its share of the nation’s resources, allowing other governments and private actors to allocate the rest.
APPLYING THE FRAMEWORK
The framework presented in this and the preceding chapter is intended to have immediate practical application. A proper understanding of how values and beliefs shape budget choices provides a starting point for understanding how to approach the difficult choices that face the country. A set of practical tests of fiscal prudence will enable every person to judge how far a proposed or enacted budget goes to meet the looming fiscal challenge and put the budget on a sustainable course. The committee believes that these tests ought to be applied by everyone to all proposed budgets, starting with the budget that the President will present for the next fiscal year.
The tests outlined above do not, of course, help policy makers and others decide what combination of reductions to spending, increases in revenues, or both to choose. If policy makers agree that the nation must reduce the debt and bring spending and revenues into long-term alignment, then some combination of the following must occur soon: some objectives must be abandoned or pursued by means other than federal spending, government spending must yield much more for each dollar, or government spending will take a larger share of the economy’s resources and must be financed by higher revenues. If the majority decision is to continue to pursue the federal government’s long and growing list of responsibilities with the same vigor, and perhaps to take on new challenges, either such efficiencies must
be achieved or more revenue will have to be raised. If the majority decision is to avoid or minimize tax increases, then the rate of spending growth must be slowed even more, and, eventually, quite dramatically.
Several aspects of the relationship between value choices and budget choices are becoming increasingly clear. First, to bring spending and revenues into alignment over the next two decades and then keep them there will require not merely tactical changes but rethinking the way government is used to achieve the goals Americans consider most important. Explicit and deep debate over these questions is needed to inform choices. If political leaders are to act responsibly without being punished at the polls, the culture and character of the nation’s politics—typically dominated by organized clienteles lobbying to protect or expand narrow benefits—may need to change to represent better the more diffuse public benefits and the lower but perhaps more concentrated costs of a prudent fiscal policy.
Second, unless revenues are raised to a level consistent with spending over the long term, some federal responsibilities on which people place great value eventually will have to be sacrificed or significantly reduced. This change can be achieved in part by shifting resource decisions to state and local governments or to the private sector or by mandating specific use of private resources through federal regulation.
Third, if the nation fails to bring spending and revenues into closer alignment over the long term, then all of the values that are now reflected in federal programs and fiscal policy will be threatened by a financial melt-down. If the nation fails, everyone’s ox may be gored.
Fortunately, perhaps, values do not translate directly or consistently into positions on particular policies, as discussed above. People with similar values may arrive at different positions on questions of policy. And conversely, those with sharply different values may be able to agree or compromise on a particular policy. A proper framing of the problem can help. The hard fiscal choices facing everyone in the country put a premium on rational discussion. There is no magic formula for resolving value and other differences and reaching the consensus and accommodation that are necessary. In Chapter 10 we suggest some process changes that can help. In a democratic society, different values and interests, and differing views of how to pursue them, are eventually compromised or reconciled through healthy argument and bargaining. Ultimately, the nation will have to rely on democratic politics, shaped by responsible leaders, to set a new course.
NOTES
|
|
1. The fiscal gap represents the government’s long-term projected flows of revenues and spending by a single number, which is the present value of future payments to and from the Treasury, discounted for the time value of money to make them comparable with payments today; see Appendix A. The fiscal gap would be zero if it was expected that |
|
|
over a long period the debt would remain the same proportion of GDP. Although the committee might have constructed such a measure and set a target on this basis, the debt target is more easily understood and communicated. |
|
|
2. In December 1991 the Maastricht Treaty of the European Union (EU) set future targets for deficits and debt that were to be used as conditions for membership in the European Monetary Union. The debt criterion was that publicly held debt may not exceed 60 percent of GDP. However, several EU member nations currently do not meet this standard. An official of the International Monetary Fund noted in a conference call in July 2009 that there is no “magic number” for debt-to-GDP (International Monetary Fund, 2009c). Buiter (2006) has written about the nature of the 1991 EU debt and deficit targets and the subsequent failure to enforce them, either as originally defined or with modifications. |
|
|
3. Stabilizing the ratio of debt to GDP implies and is equivalent to stabilizing deficits at a constant percentage of GDP (or deficits minus debt service, the so-called primary deficit, as a percentage of GDP). The target could as easily be expressed in these terms. As discussed below, stabilizing the budget at a higher debt-to-GDP ratio would permit the government to run larger annual deficits. |
|
|
4. With a 1-year respite in 1994, when debt service was 2.9 percent of GDP. |
|
|
5. The IMF has used a target of 60 percent by 2030 as the basis for measuring “the aggregate adjustment required to restore advanced economy ratios to safer levels” (2009b:23). |
|
|
6. The projections assume that inflation is generally well behaved during the projection period. A higher inflation rate allows a higher deficit, because the real value of past debt is being eroded. But the effect is limited in the United States because so much of its debt is short term and the average interest rate on the debt will adjust upward quickly. |
















