Optical Antennas: A New Technology That Can Enhance Light-Matter Interactions
LUKAS NOVOTNY
University of Rochester
Rochester, New York
The purpose of optical antennas is to convert the energy of free propagating radiation to localized energy, and vice versa. Although this is similar to what radio wave and microwave antennas do, optical antennas exploit the unique properties of metal nanostructures, which behave as strongly coupled plasmas at optical frequencies. It is hoped that optical antennas can increase the efficiency of light-matter interactions in important applications, such as light-emitting devices, photovoltaics, and spectroscopy.
Electromagnetic antennas, a key enabling technology for devices such as cellular phones and televisions, are mostly used in the radio-wave or microwave regime of the electromagnetic spectrum. At optical frequencies, on the contrary, electromagnetic fields are controlled by re-directing the wave fronts of propagating radiation by means of lenses, mirrors, and diffractive elements. Because this type of manipulation is based on the wave nature of electromagnetic fields, it cannot be used to control fields on the subwavelength scale. In contrast, radio wave and microwave technology predominantly uses antennas to manipulate electromagnetic fields, controlling them on the subwavelength scale and interfacing efficiently between propagating radiation and localized fields.
Recent research in nano-optics and plasmonics has generated considerable interest in optical antennas, and several current studies are exploring ways of translating established radio wave and microwave antenna theories into the optical frequency regime. The introduction of the antenna concept into the optical
frequency regime will lead to new technological applications, such as enhancing absorption cross-sections and quantum yields in photo-voltaics, releasing energy efficiently from nanoscale light-emitting devices, boosting the efficiency of photochemical or photophysical detectors, and improving spatial resolution in optical microscopy.
BACKGROUND
The word antenna most likely derives from the prefix an- (meaning “up”) and the Indo-European root ten- (meaning “to stretch”) (Tucker, 1931; Watkins, 2000). Therefore, from an etymological perspective, an antenna is that which stretches or extends upward (Klein, 1966). Today, we refer to an electromagnetic transmitter or receiver as an antenna, but these were originally called aerials in English (Simpson and Weiner, 1989). In 1983, IEEE defined an antenna as a means of radiating or receiving radio waves (IEEE, 1983).
Radio antennas were developed as solutions to a communication problem, whereas optical antennas were developed for use in microscopy. Analogous to its radio wave and microwave counterparts, we define an optical antenna as a device designed to efficiently convert free propagating optical radiation to localized energy, and vice versa (Bharadwaj et al., 2009). In the context of microscopy, an optical antenna, which can concentrate external laser radiation to dimensions smaller than the diffraction limit, can effectively replace a conventional focusing lens or objective.
In a letter to Albert Einstein dated April 22, 1928, Edward Hutchinson Synge describes a microscopic method (Figure 1) in which the field scattered from a tiny particle could be used as a light source (Novotny, 2007b). The particle would convert free propagating optical radiation into a localized field that would interact with a sample surface. If we think of the surface as a receiver, the particle can be viewed as an optical antenna. Synge’s method was probably inspired by the development of dark-field microscopy, a technique invented at the turn of the twentieth century by Richard Adolf Zsigmondy, an Austrian chemist (Elsevier, 1966).
In 1988, Ulrich Ch. Fischer and Dieter W. Pohl carried out an experiment similar to Synge’s proposal, but instead of a solid metal particle, they used a gold-coated polystyrene particle as a local light source (Fischer and Pohl, 1989). They imaged a thin metal film with 320 nanometer (nm) holes and demonstrated a spatial resolution of ~ 50nm. Later, laser-irradiated metal tips were proposed as optical antenna probes for near-field microscopy and optical trapping (Novotny et al., 1997, 1998), and since then various other antenna geometries have been studied (e.g., rods and bowties).
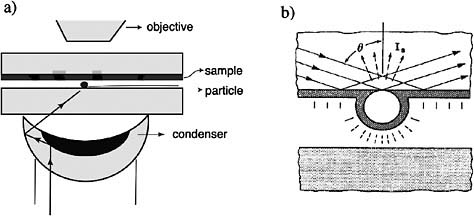
FIGURE 1 (a) Synge’s original proposal of near-field optical microscopy based on using scattered light from a particle as a light source. Source: Adapted from Synge’s letter to Einstein dated April 22, 1928, cited by Novotny, 2007b. (b) 1988 experiment in which the near-field probe consists of a gold-coated polystyrene particle. Source: Fischer and Pohl, 1989. Reprinted with permission.
HOW OPTICAL ANTENNAS WORK
Although optical antennas are strongly analogous to their radio-frequency (RF) and microwave counterparts, there are crucial differences in their physical properties and scaling behavior. Most of these differences arise because metals are not perfect conductors at optical frequencies, but are strongly correlated plasmas described as a free electron gas. Optical antennas are also not typically powered by galvanic transmission lines; instead, localized oscillators are brought close to the feed point of the antennas, and electronic oscillations are driven capacitively (Pohl, 2000). Moreover, optical antennas can take various unusual forms (e.g., tips or nanoparticles), and their properties may be strongly shape- and material-dependent due to surface plasmon resonances.
Typically, an optical antenna interacts with a receiver or transmitter in the form of a discrete quantum system, such as an atom, molecule, or ion. Because the antenna enhances the interaction between the receiver or transmitter and the radiation field, it may control the light-matter interaction on the level of a single quantum system. On the one hand, the presence of the antenna modifies the properties of the quantum system, such as its transition rates and, in the case of a strong interaction, even the energy-level structure. On the other hand, the properties of the antenna depend on the properties of the receiver/transmitter. Thus, the two must be regarded as a coupled system. The efficiency of the interaction can be expressed in terms of established antenna terminology, such as antenna gain, efficiency, impedance, directivity, and aperture (Bharadwaj et al., 2009).
RADIATION ENHANCEMENT WITH NANOPARTICLE ANTENNAS
A spherical nanoparticle is probably the simplest model antenna (Anger et al., 2006; Bharadwaj and Novotny, 2007; Bharadwaj et al., 2007; Kühn et al., 2006). Although this simple antenna geometry is not very efficient, quantitative comparisons can be made by simple analytical means (Bharadwaj and Novotny, 2007). As shown in the inset of Figure 2a, we can consider a transmitter in the form of a single fluorescent molecule optically pumped by external laser radiation. For weak excitation intensities, the radiation rate Γrad can be expressed as
(1)
where Γexc is the excitation rate and ηrad is the quantum yield. Both Γexc and ηrad depend on the antenna’s properties and the separation, z, between antenna and molecule. ηrad corresponds to the radiation efficiency, and the rates, Γi, can be expressed in terms of powers as Pi = Γihνi, with hνi corresponding to the atomic transition energy.
Figure 2a shows the experimentally recorded photon emission rate of a single dye molecule as a function of its separation from an 80nm silver nanoparticle. The superimposed curve is a theoretical calculation based on a simple electromagnetic model in which the molecule is treated as a classical oscillating dipole (Bharadwaj and Novotny, 2007). The data demonstrate that, as the silver particle is brought closer to the molecule, the fluorescence emission rate first increases and then is suppressed. The initial fluorescence enhancement is due to the antenna effect of the silver particle. The excitation rate, Γexc, increases because of the enhanced local fields near the nanoparticle.
However, for separations shorter than z = 10nm, the radiation efficiency ηrad decreases rapidly as more and more of the energy is absorbed in the silver nanoparticle. At a distance of z ~ 3nm, the rapid decrease of ηrad wins over the increase of Γexc, and the fluorescence of the molecule is quenched. Hence, there is an optimal separation between molecule and antenna.
Figure 2b shows a near-field fluorescence image of single dye molecules dispersed on a flat glass surface. The fluorescence emission rate was recorded pixel by pixel, while the dye sample was raster scanned under a laser-irradiated nanoparticle antenna held at a fixed distance of z ~ 5nm above the sample surface by means of a shear-force feedback mechanism (Anger et al., 2006; Höppener et al., 2009; Karrai and Grober, 1995). The resolution achieved in this type of near-field imaging is determined by the antenna size. With an 80nm silver or gold particle, we typically achieve resolutions of ~ 65nm. The different fluorescence patterns in Figure 2b are due to different orientations of the molecular transition dipole axis (Frey et al., 2004; Novotny et al., 2001).
The results of similar experiments performed with other quantum systems,
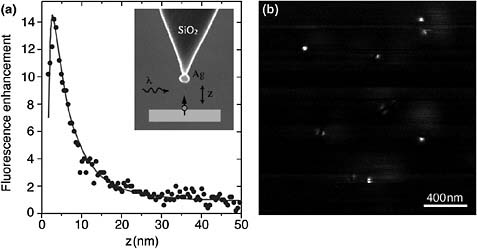
FIGURE 2 Enhancement of the radiation rate of a single molecule with a silver nanoparticle antenna. (a) Normalized fluorescence rate as a function of antenna-molecule separation. Dots are data, and the curve is the result of a theoretical calculation. Inset: scanning electron microscope image of a nanoparticle antenna. The particle is held by a dielectric tip, λ= 488nm. (b) Fluorescence rate image recorded by raster scanning of a sample with dispersed dye molecules in a plane z = 5nm underneath a nanoparticle antenna. The different fluorescence patterns are due to different orientations of the molecular transition dipole axis. Source: Adapted from Bharadwaj and Novotny, 2007.
such as quantum dots and carbon nanotubes, are consistent with the results for single fluorescent molecules. An important finding is that for systems with weak intrinsic quantum efficiency (ηi) the radiation efficiency can be enhanced by the optical antenna. In the example discussed here, in which we assumed ηi = 1, the antenna can only decrease the radiation efficiency. However, for poor emitters, such as carbon nanotubes, the antenna can increase the radiation efficiency by more than a factor of 10 (Hartschuh et al., 2005). In general, the lower the ηi, the more the antenna increases the overall efficiency, an effect that was first observed by Wokaun et al. in 1983.
This method of increasing the quantum efficiency of weak emitters might be a promising development that could boost the efficiency of organic light-emitting devices (OLEDs), silicon-based lighting, and solid-state lighting (SSL) in the yellow and green spectral region (Pillai et al., 2007; Wetzel et al., 2004).
The nanoparticle antenna is a model antenna, and its predictions have been tested in various recent experiments. However, much higher efficiencies can be achieved with optimized antenna designs, such as the optical half-wave antenna.
NEAR-FIELD RAMAN SCATTERING
The hallmark of optical antennas, their ability to influence light on the nanometer scale, leads naturally to nano-imaging applications. In the context of nanoscale imaging, an optical antenna represents a near-field optical probe that can interact locally with an unknown sample surface. For a near-field optical image, the optical antenna is guided over the sample surface in close proximity, and an optical response (e.g., scattering, fluorescence, antenna detuning) is detected for each image pixel.
The vibrational spectra provided by Raman scattering define a unique chemical fingerprint for the material under study. Raman scattering involves the absorption and emission of photons, almost identical in energy; thus a nearby antenna can amplify both the incoming and outgoing fields. The total Raman scattering enhancement is therefore proportional to the fourth power of the field enhancement (Novotny and Hecht, 2006).
In tip-enhanced Raman scattering (TERS), optical antennas (e.g., metal tips) are used for point-by-point Raman spectroscopy (Hartschuh, 2008; Hartschuh et al., 2003; Stöckle et al., 2000), similar to the original idea of Wessel (1985). Raman enhancements achieved with metal tips are typically in the range of 104–108, corresponding to field enhancements of 10 to 100.
Our TERS studies are focused on localized states (due to defects and dopants) in carbon nanotubes (Anderson et al., 2005; Maciel et al., 2008). Figure 3 shows (a) the simultaneously recorded topography and (b) near-field Raman image of a single-walled carbon nanotube sample. The image contrast in the near-field

FIGURE 3 Near-field Raman imaging of a single-walled carbon nanotube sample. (a) Topography showing a network of carbon nanotubes covered with small droplets. (b) Raman image of the same sample area recorded by integrating, for each image pixel, the photon counts, which fall into a narrow spectral bandwidth centered around ν= 2615 cm−1 (indicated by shading in 3c). (c) Raman scattering spectrum recorded on top of the nanotube. Source: Adapted from Hartschuh et al., 2003.
Raman image (c) is defined by the intensity of the G’line (vibrational frequency of ν = 2615 cm−1) highlighted in the spectrum.
WAVELENGTH SCALING
At optical frequencies, electrons in metals have considerable inertia and cannot respond instantaneously to the driving fields. Typically, the skin depth is on the order of tens of nanometers, comparable to the dimensions of the antenna. Traditional design rules that prescribe antenna parameters only in terms of an external wavelength are thus no longer valid. The metal must be rigorously treated as a strongly coupled plasma, which leads to the antenna “seeing” a reduced effective wavelength (Novotny, 2007a). This effective wavelength, λeff, is related to the external (incident) wavelength, λ, by a surprisingly simple relation
(2)
where λp is the plasma wavelength of the metal, and n1 and n2 are constants that depend on the geometry and dielectric parameters of the antenna. λeff is shorter, by a factor of 2 to 6, than the free space, λ, for typical metals (e.g., gold, silver, aluminum) and realistic antenna thicknesses (Bryant et al., 2008; Novotny, 2007a).
The shortening of wavelength from λ to λeff has interesting implications. For example, it implies that the radiation resistance of an optical half-wave antenna is on the order of just a few Ohms (Alu and Engheta, 2008; Burke et al., 2006; Novotny, 2007a). To see this, we note that the radiation resistance of a thin-wire antenna is roughly Rrad = 30 π2(L/λ)2, with L being the antenna length. For a half-wave antenna at RF frequencies, L = λ/2 and Rrad ~73Ω. However, for an optical half-wave antenna, L = λeff/2 and hence Rrad = (30/4) π2 (λeff/λ)2. In other words, the radiation resistance at optical frequencies is a factor of (λeff/λ)2 smaller than at RF frequencies. For λeff = λ/5 we find Rrad = 3Ω.
Figure 4a shows the intensity distribution near a gold half-wave antenna of length L = 110nm and radius R = 5nm resonantly excited at λ= 1170nm. The effective wavelength is λeff = 220nm. The induced current density j = iωεo [ε(ω) – 1] E evaluated along the axis of the antenna is found to be nearly 180° out of phase with respect to the exciting field.
The notion of an effective wavelength can be used to extend familiar design ideas and rules into the optical frequency regime. For example, the optical analog of the λ/2 dipole antenna becomes a thin metal rod of length λeff/2. Since λeff for a silver rod of radius 5nm is roughly λ/5.2 (Figure 4c), this means that the length of a “λ/2” dipole antenna is surprisingly small, about λ/10.4. One can similarly construct antenna arrays like the well established Yagi-Uda antenna developed in the 1920s for the UHF/VHF region (Novotny, 2007a; Taminiau et al., 2008).
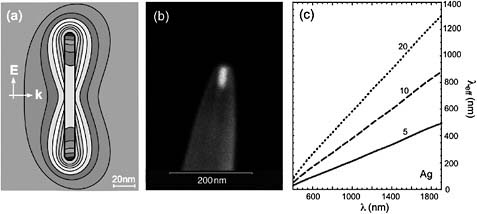
FIGURE 4 Effective wavelength scaling for linear optical antennas. (a) Intensity distribution (E2, factor of 2 between contour lines) for a gold half-wave antenna irradiated with a plane wave (λ = 1150nm). (b) Scanning electron microscope image of a half-wave antenna resonant at λ = 650nm, fabricated by placing a gold nanorod ~ 65nm long into the opening of a quartz nanopipette. (c) Effective wavelength scaling for silver rods of different radii (5, 10, and 20nm). Source: Novotny, 2007a.
ENHANCED LIGHT-MATTER INTERACTIONS
The localized fields near an optical antenna open up new interaction mechanisms between light and matter, such as higher order multipole transitions and momentum-forbidden transitions. These interactions, which are inaccessible in free space, have the potential to enrich optical spectroscopy and provide new strategies for optical sensing and detection. In free space, the momentum of a photon with energy, E, is p = E/c. However, the momentum of an unbound electron with the same energy is two to three orders of magnitude greater, and the photon momentum can be neglected in electronic transitions.
Near an optical antenna, the photon momentum is no longer defined by its free space value. Instead, localized optical fields are associated with a photon momentum defined by the spatial confinement, D, which can be as small as 1 to 10nm. Thus in the optical near field the photon momentum can be drastically increased to a level comparable with the electron momentum, especially in materials with small effective mass, m*. Hence, localized optical fields can give rise to “diagonal” transitions in an electronic band diagram thereby increasing overall absorption strength, which can be useful for devices such as silicon solar cells. The increase of photon momentum in optical near fields has been discussed in the context of photoelectron emission (Shalaev, 1996) and photoluminescence (Beversluis et al., 2003).
The strong field confinement near optical antennas also has implications for selection rules in atomic and molecular systems. Usually, the light-matter interac-
tion is treated in the dipole approximation where the spatial variation of the fields is much weaker than the spatial variation of quantum wave functions. However, the localized fields near optical antennas give rise to spatial field variations of a few nanometers; hence it may no longer be legitimate to invoke the dipole approximation. This is the case in semiconductor nanostructures, for example, where the low effective mass gives rise to quantum orbitals with large spatial extent.
CONCLUSIONS AND OUTLOOK
Research in the field of optical antennas is currently driven by the need for high field enhancement, strong field localization, and large absorption cross sections. Antennas for high-resolution microscopy and spectroscopy, photovoltaics, light emission, and coherent control are being investigated. In one way or another, optical antennas make processes more efficient or increase the specificity of gathered information.
As in canonical antenna theory, there is no universal antenna design, and optical antennas have to be optimized separately for each application. However, to achieve the highest level of efficiency, the internal energy dissipation of any antenna must be minimized. For a quantum emitter, such as an atom, molecule, or ion, a good antenna yields a low nonradiative decay rate.
New ideas and developments are emerging at a rapid pace, and it is now clear that the optical antenna concept will provide new opportunities for optoelectronic architectures and devices. Today, the building blocks for optical antennas are plasmonic nanostructures that can be fabricated either from the bottom up by colloidal chemistry or from the top down with established nanofabrication techniques, such as electron-beam lithography and focused ion-beam milling. It is also conceivable that future optical antenna designs will draw inspiration from biological systems, such as light-harvesting proteins in photosynthesis.
ACKNOWLEDGMENTS
This work is supported by the U.S. Department of Energy, the National Science Foundation, and the Air Force Office of Scientific Research. I thank all of the students and postdoctoral researchers of the Nano-Optics Group who have contributed to this work.
REFERENCES
Alu, A., and N. Engheta. 2008. Input impedance, nanocircuit loading, and radiation tuning of optical nanoantennas. Physical Review Letters 101(4): 043901.
Anderson, N., A. Hartschuh, S. Cronin, and L. Novotny. 2005. Nanoscale vibrational analysis of single-walled carbon nanotubes. Journal of the American Chemical Society 127(8): 2533–2537.
Anger, P., P. Bharadwaj, and L. Novotny. 2006. Enhancement and quenching of single molecule fluorescence. Physical Review Letters 96(11): 113002.
Beversluis, M.R., A. Bouhelier, and L. Novotny. 2003. Continuum generation from single gold nanostructures through near-field mediated intraband transitions. Physical Review B 68(11): 115433.
Bharadwaj, P., and L. Novotny. 2007. Spectral dependence of single molecule fluorescence enhancement. Optical Express 15(21): 14266–14274.
Bharadwaj, P., P. Anger, and L. Novotny. 2007. Nanoplasmonic enhancement of single-molecule fluorescence. Nanotechnology 18: 044017.
Bharadwaj, P., B. Deutsch, and L. Novotny. 2009. Optical antennas. Advances in Optics and Photonics 1(3): 438–483.
Bryant, G.W., F.J.G. de Abajo, and J. Aizpurua. 2008. Mapping the plasmon resonances of metallic nanoantennas. Nano Letters 8(2): 631–636.
Burke, P.J., S. Li, and Z. Yu. 2006. Quantitative theory of nanowire and nanotube antenna performance. IEEE Transactions on Nanotechnology 5(4): 314–334.
Elsevier. 1966. Nobel Lectures, Chemistry 1922–1941. Amsterdam: Elsevier Publishing Co.
Fischer, U.C., and D.W. Pohl. 1989. Observation of single-particle plasmons by near-field optical microscopy. Physical Review Letters 62(4): 458–461.
Frey, H.G., S. Witt, K. Felderer, and R. Guckenberger. 2004. High-resolution imaging of single fluorescent molecules with the optical near-field of a metal tip. Physical Review Letters 93(20): 200801.
Hartschuh, A. 2008. Tip-enhanced near-field optical microscopy. Angewandte Chemie International Edition 47(43): 8178–8191.
Hartschuh, A., E. Sanchez, X. Xie, and L. Novotny. 2003. High-resolution near-field Raman microscopy of single-walled carbon nanotubes. Physical Review Letters 90(9): 095503.
Hartschuh, A., H. Qian, A.J. Meixner, N. Anderson, and L. Novotny. 2005. Nanoscale optical imaging of excitons in single-walled carbon nanotubes. Nano Letters 5(11): 2310.
Höppener, C., R. Beams, and L. Novotny. 2009. Background suppression in near-field optical imaging. Nano Letters 9(2): 903908.
IEEE (Institute of Electrical and Electronics Engineers Inc.). 1983. Antenna Standards Committee of the IEEE Antennas and Propagation Society, IEEE Std 145-1983. New York: IEEE.
Karrai, K., and R.D. Grober. 1995. Piezoelectric tip-sample distance control for near field optical microscopes. Applied Physics Letters 66(14): 1842–1844.
Klein, E. 1966. Antenna. P. 82 in A Comprehensive Etymological Dictionary of the English Language. Amsterdam: Elsevier Publishing Company.
Kühn, S., U. Hakanson, L. Rogobete, and V. Sandoghdar. 2006. Enhancement of single molecule fluorescence using a gold nanoparticle as an optical nanoantenna. Physical Review Letters 97(1): 017402.
Maciel, I.O., N. Anderson, M.A. Pimenta, A. Hartschuh, H. Qian, M. Terrones, H. Terrones, J. Campos-Delgado, A.M. Rao, L. Novotny, and A. Jorio. 2008. Electron and phonon renormalization at defect/doping sites in carbon nanotubes. Nature Materials 7: 878–883.
Novotny, L. 2007a. Effective wavelength scaling for optical antennas. Physical Review Letters 98(26): 266802.
Novotny, L. 2007b. The History of Near-Field Optics. Pp. 137–180 in Progress in Optics, Vol. 50, edited by E. Wolf. Amsterdam: Elsevier Publishing Co.
Novotny, L., and B. Hecht. 2006. Principles of Nano-Optics. Cambridge: Cambridge University Press.
Novotny, L., R.X. Bian, and X.S. Xie. 1997. Theory of nanometric optical tweezers. Physical Review Letters 79(4): 645–648.
Novotny, L., E.J. Sanchez, and X.S. Xie. 1998. Near-field optical imaging using metal tips illuminated by higher-order Hermite-Gaussian beams. Ultramicroscopy 71(1): 21–29.
Novotny, L., M.R. Beversluis, K.S. Youngworth, and T.G. Brown. 2001. Longitudinal field modes probed by single molecules. Physical Review Letters 86(23): 5251.
Pillai, S., K. Catchpole, T. Trupke, and M. Green. 2007. Surface plasmon enhanced silicon solar cells. Journal of Applied Physics 101(9): 093105.
Pohl, D.W. 2000. Near-field Optics Seen as an Antenna Problem. Pp. 9–21 in Near-field Optics, Principles and Applications, edited by X. Zhu and M. Ohtsu. Singapore: World Scientific.
Shalaev, V.M. 1996. Electromagnetic properties of small-particle composites. Physics Reports 272(2–3): 61–137.
Simpson, J.A., and E.S.C. Weiner. 1989. Antennas. P. 506 in The Oxford English Dictionary. New York: Oxford University Press.
Stöckle, R.M., Y.D. Suh, V. Deckert, and R. Zenobi. 2000. Nanoscale chemical analysis by tip-enhanced Raman spectroscopy. Chemical Physics Letters 318(1–3): 131–136.
Taminiau, T.H., F.D. Stefani, and N.F. van Hulst. 2008. Enhanced directional excitation and emission of single emitters by a nano-optical Yagi-Uda antenna. Optics Express 16(14): 10858–10866.
Tucker, T.G. 1931. Antemna, antenna. P. 19 in A Concise Etymological Dictionary of Latin. Halle/Saale, Germany: Max Niemeyer Verlag.
Watkins, C. 2000. “ten-” P. 90 in The American Heritage Dictionary of Indo-European Roots. Boston: Houghton Mifflin Company.
Wessel, J. 1985. Surface-enhanced optical microscopy. Journal of the Optical Society of America B 2(9): 1538–1541.
Wetzel, C., T. Salagaj, T. Detchprohm, P. Li, and J.S. Nelson. 2004. GaInN/GaN growth optimization for high power green light emitting diodes. Applied Physics Letters 85(6): 866.
Wokaun, A. H.P. Lutz, A.P. King, U.P. Wild, and R.R. Ernst. 1983. Energy transfer in surface enhanced luminescence. Journal of Chemistry and Physics 79(1): 509–514.












