5
Mitigation
Impacts on Earth by near-Earth objects (NEOs) are inevitable. The impactors range from harmless fireballs, which are very frequent; through the largest airbursts, which do not cause significant destruction on the ground, on average occurring once in a human lifetime; to globally catastrophic events, which are very unlikely to occur in any given human lifetime but are probably randomly distributed in time. The risks from these NEOs, or more specifically scientists’ assessment of the risks in the next century, will be changing as surveys are carried out. Given the inevitability of impacts, and noting that the entire point of surveys is to enable appropriate action to be taken, how can the effects of potential impacting NEOs be mitigated?
The amount of destruction from an event scales with the energy being brought by the impacting object. Because the range of possible destruction is so huge, no single approach is adequate for dealing with all events. For events of sufficiently low energy, the methods of civil defense in the broadest sense are the most cost-effective for saving human lives and minimizing property damage. For larger events, changing the path of the hazardous object is the appropriate solution, although the method for changing the path varies depending on the amount of advance notice available and the mass of the hazardous object. For the largest events, from beyond global catastrophe to events that cause mass extinctions, there is no current technology capable of sufficiently changing the orbital path to avoid disaster.
In this chapter the committee considers four categories of mitigation:
-
Civil defense—involving such efforts as evacuating the region around a small impact,
-
Slow-push or -pull methods—gradually changing the orbit of an NEO so that it misses Earth,
-
Kinetic impact—delivering a large amount of momentum (and energy) instantaneously to an NEO to change its orbit so that it misses Earth, and
-
Nuclear detonation—delivering a much larger amount of momentum (and energy) instantaneously to an NEO to change its orbit so that it misses Earth.
For impacting NEOs that are sufficiently small (tens of meters to perhaps 100 meters in diameter) and not very strong (typically not iron meteoroids), the destruction on Earth will be caused by an airburst and its associated blast wave and thermal pulse, as was the case of the Tunguska event above Siberia in 1908. Events like this cause destruction over areas up to thousands of square kilometers, and evacuation and sheltering are not only plausible but often the most cost-effective approach for saving human lives. Airburst events will also be the most frequent,
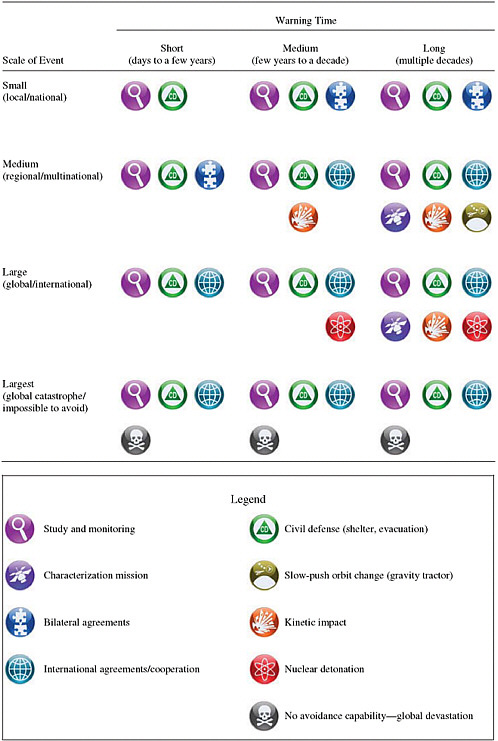
occurring on average every couple of centuries. They are also the events that are likely to have the least advance warning. For larger events, actively changing the orbit of the hazardous object is likely desirable. The choice among the three methods—the slow-push and -pull method, kinetic impact, and nuclear detonation—depends both on the mass of the NEO that has to be moved and on how early the NEO is determined to be hazardous, as well as on the details of the orbit. The mitigation options are laid out in Table 5.1, which lists the applicability of each option to a given threat. Table 5.2 shows the regimes in which each mitigation method is applicable. Note that Table 5.2 brings in an additional important aspect of the problem, international coordination, which is discussed in more detail in Chapter 7 of this report.
Although all of the primary mitigation strategy methods are conceptually valid, none is now ready to implement on short notice. Civil defense and kinetic impactors are probably the closest to deployable but even these require additional study before they can be relied on.
In all cases, the decision to initiate mitigation is a sociopolitical decision, not a technical decision. This decision is implicit in earlier sociopolitical decisions about which methods of mitigation to develop, and it also depends on the level of probability that is considered to require mitigation. The committee’s recommendations regarding the minimum approach to mitigation and more aggressive approaches are discussed later.
The subject of mitigation is rife with uncertainty. The effect on Earth of a given NEO depends critically on the velocity at which the NEO impacts Earth, a factor that is traditionally ignored in studies of the hazard. The decisions on mitigation must be based on the mass of the NEO rather than on its diameter, because mass is the quantity that most affects the effectiveness of any mitigation and the diameter for a given mass can vary by roughly a factor of two. The variation in diameter implies a factor-of-two variation, depending on the NEO’s density, of the size of an NEO that can be moved far enough to miss Earth. Clearly an earlier warning allows a smaller action to be sufficient, but quantifying this relation is very uncertain. The effectiveness of most but not all methods also depends critically on the physical properties of the NEO. Humanity’s ability to mitigate depends on the details of the intercepting trajectory. There are also significant differences depending on whether the discussion of mitigation is limited to current technology or includes likely future technology such as the next generation of heavy-lift launch vehicles. Thus the committee’s discussion of the range of applicability will show overlapping and uncertain ranges.
Realistic mitigation is likely to include more than one technique, if for no other reason than to provide confidence. In any case of mitigation, civil defense will undoubtedly be a component, whether as the primary response or as the ultimate backup.
Finding: No single approach to mitigation is appropriate and adequate for completely preventing the effects of the full range of potential impactors, although civil defense is an appropriate component of mitigation in all cases. With adequate warning, a suite of four types of mitigation is adequate to mitigate the threat from nearly all NEOs except the most energetic ones.
TABLE 5.1 Summary of Primary Strategies for Mitigating the Effects of Potential Impacting Near-Earth Objects
|
Strategy |
Range of Primary Applicability |
|
Civil defense (e.g., warning, shelter, and evacuation) |
Smallest and largest threats. Threat of any size with very short warning time. |
|
Slow push (e.g., “gravity tractor” with a rendezvous spacecraft) |
A fraction (<10%) of medium-size threats. Usually requires decades of warning time. |
|
Kinetic impact (e.g., interception by a massive spacecraft) |
Most medium-size threats. Requires years to decades of warning time. |
|
Nuclear detonation (e.g., close-proximity nuclear explosion) |
Large threats and short-warning medium-size threats. Requires years to decades of warning time. |
CIVIL DEFENSE: DISASTER PREPARATION AND RECOVERY
Of the two generic approaches to the mitigation of an impact hazard—(1) active orbital change or the destruction of the incoming body, and (2) passive, traditional natural-disaster mitigation based on “all-hazards” protocols for evacuation, sheltering, response and recovery, and so on—people in contemporary society would very likely be faced with evacuation and sheltering rather than orbital change or destruction during their lifetimes. The most probable event will be a very late warning of a small NEO (tens of meters in diameter or less). At the opposite end of the size spectrum for impacts approaching or exceeding the level of “civilization-threatening impacts” (100 to many hundreds of meters in diameter), there are inadequate precedents. For comparable events, one might think of the Black Death, world wars, or the fictional end-of-the-world stories in On the Beach (Shute, 1957) or, more relevantly, Lucifer’s Hammer (Niven and Pournelle, 1977). Whether human civilization would be fragile or robust in the face of such an event is unclear to us.
Although civil defense is the most likely response to any impact hazard, the committee did not possess the expertise needed to address fully the political and economic aspects of even a small-asteroid impact. This issue requires additional study.
There is a spectrum of potential events that might invoke one or more of the social, scientific, and emergency-management approaches to disaster mitigation. Some typical examples of such potential events, in rough order of increasing severity, include the following:
-
News media reports of a low-probability near- or long-term impact, warranting appropriate response informed by lessons in risk communication. Such occasions have happened frequently in the past decade and require no further societal action.
-
The prediction of an unusually high likelihood of a major impact (such as the Apophis case in 2004-2005 [Giorgini et al., 2008]) at some point in future decades. As planning was developed for a rational approach to orbit change, the “risk corridor” for locations where the impact might occur would be known. There could be some immediate economic and political implications (e.g., concerns about property values in potentially threatened locations), although further astronomical observations may change the probability of impact to zero.
-
The prediction of an imminent impact (in hours to days) impact by a very small object (1 to 10 meters in size) on an impact trajectory. This type of warning might begin to occur once every few years if telescopic searches are optimized for discovering such imminent impactors. Although it is very likely that such an impact would be harmless for people on the ground, prudent people near ground zero should stay indoors, away from windows, and perhaps not gaze at the atmospheric explosion. Such events might rain down meteorites or cause an on-ground explosive cratering event as in the case of the Carancas impact event in Peru in 2007, and could possibly break windows. Practicing risk communication would be important and would need to be planned in advance (see, too, Chapter 7).
-
A prediction with a short-term warning (days to weeks) of an impact by a small NEO (10 to 25 meters in diameter). Such an event is likely to occur during this century. Such impacts are near the threshold of causing significant and potentially lethal damage in a zone a modest few tens of kilometers wide near ground zero, warranting prudent evacuation if the impact occurred on or near land. Here, the approaches would be similar to established procedures for other predictable, localized natural disasters such as a flooding river or a volcano ready to explode. Of course, first responders would lack knowledge of the characteristics of such devastating events in locations where floods, volcanoes, and so on are not relevant. Thus plans should be made to ensure adequate knowledge transfer from experienced first-responders in the event that such a circumstance might materialize.
-
An unpredicted destructive impact by a modest-sized (10 to 100 meters) NEO. This case is about as likely as the previous one. Such an event could have modest to severe local consequences, but the customary response-and-recovery methodologies employed after natural and human-made disasters would generally be as applicable in this case as in any generic disaster. The kinds of damage from a modest-sized NEO in the atmosphere or impact into the ground would be similar to the kinds of damage from other natural disasters, including building collapse, fires, social confusion, injuries, and death. Of course, the cause of this particular type of disaster is unusual and would possibly evoke uninformed, exaggerated responses, such as fears that the impact was a harbinger of more
-
and larger impacts to follow, as exemplified in numerous recent television shows and movies. This fear is very unlikely to be correct, so appropriate risk communication and the public involvement of NEO impact experts should be helpful.
-
The prediction of a very unlikely, but possible, impact by a dangerously large NEO (30 to many hundreds of meters in diameter) in the next decades. Such predictions will be common in future years, especially after next-generation telescopic surveys become operational, but the initial responses should emphasize refining the prediction and possible preparations for NEO orbit-change missions. The chances of such an impact occurring during the next century are tens of percent. Should the probability of an impact increase to certainty and the regional locale of ground zero become identified, then preparations should be begun in order to minimize the potential losses to life and property in the event that orbit-change measures failed or were not implemented. These preparations would involve augmenting provisions for shelter, medical care, food for displaced persons; provision for pets; and so on, including advanced planning for communications, evacuation, and so on.
-
The prediction of an imminent (in days to a few years) impact by a very dangerously large NEO (100 to many hundreds of meters in diameter). The final procedures would be similar to those described in the previous case, except that the planning for implementation would be less localized. Because the nature of the disaster could be similar in consequences to those of other large disasters (the worst earthquakes in history, the Indian Ocean tsunami of 2004, World War II), lessons from those historical cases could inform the preparations for and responses to the inevitable disaster (since the prevention of the impact might not be feasible for technical and/or political reasons). The cause of such a disaster would have no precedent, and misunderstandings based on badly mistaken popular culture (movies, television programs) could have negative repercussions, so reliable risk communication would be especially important.
-
The prediction of a possible impact by a potentially civilization-destroying (and species-destroying) NEO in the next decades. Such a potential catastrophe would be unprecedented in human history. Reliance could be placed on efforts to avert the disaster by orbital change. But prior to successful orbital change (or after unsuccessful change), if the impact was within a decade of happening, concurrent international efforts could begin to ameliorate the consequences of any impact that might occur, noting that there would likely be a tendency for the entire social structure to collapse. These efforts would be most effective if they attempted to increase the robustness of all elements of society, ranging from appropriate risk communications and warning; to making provisions for medical care; to preparing for the provision of food and water and shelter; to shoring up the global infrastructures in the financial, electronic, social, and law-enforcement arenas; to preparing for the inevitable response-and-recovery operations.
-
The predicted short-term impact (in a few years or less) by a civilization or species-destroying NEO. While this apocalyptic possibility is extraordinarily unlikely to happen in the lifetime of anyone living now, traditional approaches to preparing for disaster would become irrelevant.
Finding: Civil defense (evacuation, sheltering in place, providing emergency infrastructure) is a cost-effective mitigation measure for saving lives from the smallest NEO impact events and is a necessary part of mitigation efforts for larger events. If an NEO was predicted to impact on a specific, inhabited location, there would likely be strong pressure for implementing more than the most cost-effective method for saving lives.
SLOW-PUSH-PULL METHODS
This section considers the first of three approaches to prevent an impact rather than to protect against an impact. “Slow-push-pull” means the continuous application of a small but steady force to the NEO, thereby causing a small acceleration of the body relative to its nominal orbit. The effect of such small accelerations is most productive if applied along or against the NEO’s direction of motion, as this causes a net shift of the NEO along its orbit. This shift can avert an impact by causing the NEO to “show up” at Earth’s orbit earlier or later than Earth does. A simple rule-of-thumb formula predicts the drift along the NEO’s orbit for a given applied acceleration
(Eq. 5.1)
where Δs represents the shift in the NEO’s position relative to its nominal orbit, A represents the induced acceleration of the NEO, ta represents the time during which the acceleration is applied, and tc represents the coast time after the application of the acceleration. For estimating the range of NEOs for which a given method is applicable, the committee considers orbital changes large enough to move the NEO by 15,000 kilometers, enough to provide a safe miss as long as the orbit is well determined. Assume that a 10-ton spacecraft is the maximum possible with current launch capability and that a 50-ton spacecraft might be possible with future heavy-lift launch vehicles (see later discussion and the accompanying Table 5.4). Of course multiple launches are possible and may be desirable to scale up the effect or to provide backup in case of failure.
The proposed slow-push techniques can be sorted into four categories: the enhancement of natural effects, the enhanced evaporation of surface material, the application of contact force, and the application of gravitational force. Only the last of these techniques, which is likely the easiest from an engineering standpoint, has been studied sufficiently to show that it is feasible. With any slow-push technique, the efficiency of the approach and possible unintended consequences must be seriously considered. As the accelerations are quite small, overlooked physical phenomena or efficiency losses may substantially change the actual effect.
Enhancement of Natural Effects
In this approach involving the enhancement of natural effects, a natural source of momentum—most typically the use of photon pressure or solar energy—is used to accelerate the NEO. Changing the NEO’s thermal response or reflectivity is one such technique, as this then modifies the natural forces that produce slight deviations from purely gravitational motion for small NEOs. A major drawback of such techniques is the lack of precision and predictability with which they can be applied to the body. Owing to this lack, a conservative approach would require overcompensating by a large factor. One simple way to bound the level of acceleration possible using such an approach is to estimate the maximum acceleration that impinging solar radiation pressure can induce on an NEO, realizing that only a fraction of this natural acceleration will be available for modifying the orbit. For an asteroid with a density of 2 grams per cubic centimeter (g/cm3), the total solar radiation pressure on a 2-kilometer-diameter asteroid induces an acceleration at 1 AU from the Sun of 2 × 10−15 km/s2 (multiply the values in kilometers per second squared by 6.7 × 1012 to express them in units of 15,000 kilometers per decade squared, where 15,000 is about 2½ Earth-radii, sufficient to provide a safety margin in missing Earth), while a 0.2-kilometer-diameter asteroid has 10 times this acceleration. Because only a fraction of this pressure can be tapped for useful, along-track accelerations, the time that it takes to shift the asteroid’s location enough to safely miss Earth becomes very long (centuries for an 0.2-kilometer-diameter NEO). The natural acceleration due to thermal effects on the NEO is a small fraction of this upper limit, but so is the likely efficiency in using enhancement.
Enhanced Evaporation of Surface Material
A different approach but related to that of the enhancement of natural effects is to concentrate solar energy on the surface of the NEO to cause vaporization, creating a jet of mixed vapor and rock debris from the NEO’s surface that will then accelerate the body by its reaction to the jet’s force. This process operates naturally in comets, and the orbits of very volatile comets change every time they approach the Sun owing to their reaction to gas venting from their surfaces. Because the time for heating surface rocks to evaporation can be short (tens of seconds), the NEO’s rotation is not an issue: the source of the jet simply tracks over the surface as the NEO rotates beneath the spot where sunlight is focused. No physical ties to the NEO are required, and because the acceleration is low, binary NEO systems will not disperse. The main requirement for the evaporation is a large, solar collector that will concentrate sunlight. This collector, for example could be lightweight and use an inflatable parabolic mirror and direct sunlight into a series of lenses or mirrors that eventually focus the light on the surface of the NEO. Insofar as the diameter of the solar collector can be scaled to the size of the NEO (the acceleration scales as the inverse of the NEO’s mass and the square of the collector diameter), orbits of NEOs up to several kilometers in diameter could, in theory, be sufficiently changed by very large collector systems. However, these systems have not yet been demonstrated. The Sun’s energy might also be collected by a large number of smaller parabolic mirrors
rather than by one large one. In this sense, a solar collector system can be considered modular and scalable. One major unknown of systems of this type is how to prevent evaporated rock material from condensing on and fouling parts of the optical system. This technique could potentially be the most powerful slow-push approach, but its dependence on the properties of the NEO and its controllability (e.g., the enhanced evaporation can change the NEO’s rotational state significantly) require much more study before it can be considered ready for use. A recent study (Kahle et al., 2006) shows that some optical elements, at least in some designs, would not last more than a few minutes due to extreme heating. Thus the technique might be limited to use on NEOs that require very small speed changes, <0.1 millimeter per second.
Application of Contact Force
In the approach involving contact force, a mechanical connection to the NEO is assumed, and by means of this connection a force is applied to the body. An early concept was for a “tugboat” spacecraft to physically push on the NEO, similar to a tugboat moving a much larger ship by applying a small but consistent force. Also in this vein are “mass drivers,” which require a mechanism to be placed on the surface to eject mass from the NEO as propellant. One complicating factor for such approaches is the need to deal with the NEO’s rotation; for the efficient delivery of force, the rotation state of the body must often be altered. These approaches are generally not considered viable given the current lack of mechanical and physical understanding of small-body surfaces and subsurfaces. When additional information is obtained on these aspects, it may be possible to design surface coupling devices robustly and to understand the levels of force that can be sustained through them. Until then, the uncertainties in applying these techniques—even if they had been developed—are too large to allow their use with any confidence.
Application of Gravitational Force
Using gravitational force is the only approach that is nearly independent of the physical properties of the NEO, except for its mass (Lu and Love, 2005; Fahnestock and Broschart, 2009; Fahnestock and Scheeres, 2008; Wie, 2008; Yeomans et al., 2008), and it is the slow-pull method with the highest technology readiness level. The physics is quite simple—a “gravity-tractor” spacecraft positions itself in close proximity to an NEO, which generates an appreciable gravitational attraction between the two bodies. The forces are equal and opposite, but due to the mass disparity the accelerations are quite different. The maximum acceleration that a 10-ton spacecraft could induce on a 1-kilometer-diameter NEO is exceptionally small, on the order of 7 × 10−16 km/s2, whereas it is 7 × 10−14 km/s2 for a 100-meter-diameter NEO of the same density, because, for the same NEO shape, the gravity tractor could be positioned tenfold closer to the smaller NEO. This force is somewhat larger than the maximum possible acceleration from asymmetry in the NEO’s thermal radiation (known as the Yarkovsky effect). It does indicate that small, natural forces must be understood. The spacecraft thrusts to maintain a fixed location relative to the asteroid, without any of its propellant landing on the NEO’s surface, as the gravitational force provides the connection to the NEO. In this way, there is a constant force acting on the NEO in the direction of the spacecraft; the center of mass of the system experiences a net acceleration equal to the acceleration induced on the NEO by the attraction of the spacecraft.
Detailed simulations of this approach have been carried out, considering the movement of both single asteroids and binary asteroids—both of which types seem feasible to control. One of the main advantages of the gravity-tractor approach is that there is no need to attach the spacecraft physically to the NEO’s surface. Also, the precision of the orbital change can be quite high, as spacecraft can be well instrumented and tracked with high accuracy. Finally, the technology for this approach is well understood and can be implemented without further scientific studies; thus a technology demonstration of this approach is feasible with current technology. The main caveat is the requirement for the spacecraft propulsion system to operate reliably for perhaps a decade or more.
The attainable accelerations are, however, quite low. The committee considers displacement by 15,000 kilometers (a bit more than one Earth-diameter) as sufficient margin with a well-determined orbit for the NEO. For long warning times (on the order of four decades), one could spend somewhat less than a decade to design, build, and launch the spacecraft and travel to the NEO, then spend a decade thrusting, followed by somewhat more than two decades of
monitoring, for all NEOs up to about 100 meters in diameter. If one launched successor gravity tractors (to overcome fuel and lifetime limitations), one could thrust for the full 30 years and raise the limiting size by a factor 1.5 to 2. Some NEOs, probably fewer than 10 percent, have trajectories that can pass through small regions of space near Earth, called keyholes, where Earth’s gravitational pull changes the NEO’s orbit just enough that the NEO hits Earth on a future approach. Changing the orbit of an NEO to miss one of these keyholes can be accomplished for larger objects, since the required orbital change is much smaller. Because of the wide range of keyhole sizes (hundreds of meters to hundreds of kilometers in diameter), it is unrealistic to estimate limiting the sizes of NEOs in this niche.
Applicability of Slow-Push-Pull Mitigation Techniques
Unless a very long warning time before impact is available, the practical application of slow-push-pull techniques is limited to NEOs that are predicted to pass through a keyhole and to small NEOs near the limit for which civil defense alone might be adequate. As with any attempt to divert an NEO, long warning times typically imply substantial uncertainty in whether the NEO is on a trajectory to impact, and on the one hand long warning times may lead to political indecision; on the other hand, slow-push techniques might be ideal for refining the result after a larger change in orbit by some other method, and they are well suited for preventing an NEO from passing through a keyhole. The well-known asteroid Apophis is one of the objects that does pass near a keyhole and might be an appropriate target for a slow push or pull—for example, with a gravity tractor. However, the probability that Apophis will impact Earth is now so low that mitigation does not appear to be needed at this time.
Finding: Slow-push-pull techniques are the most accurately controllable and are adequate for changing the orbits of small NEOs (tens of meters to roughly 100 meters in diameter) with decades of advance warning and for somewhat larger NEOs (hundreds of meters in diameter) in those few cases in which the NEO would pass through a keyhole that would put it onto an impact trajectory. Of the slow-push-pull techniques, the gravity tractor appears to be the most independent of variations in the properties of the NEO and by far the closest to technological readiness.
KINETIC IMPACT METHODS
Description of Kinetic Impact and Its Use
Kinetic impact mitigation uses one or more very-high-velocity (typically more than about 5 km/s) impacts of a large spacecraft (“impactor”) into a hazardous object. These impacts would change the velocity of the hazardous object by some small amount, which would result in a new orbit for the hazardous object that would cause it to miss Earth. The method is relatively simple and effective for NEOs with diameters up to about half a kilometer, and it is well within current capabilities given modest hardware and control developments. This method would likely be the method of choice for the mitigation of hazardous objects of the size range just indicated when there are years or more of warning time.
In this approach either the spacecraft can “run into” the hazardous object, or the hazardous object can run into the spacecraft; only the relative velocity of the impact is relevant. The achievable relative velocity varies significantly with the details of the NEO’s orbit, but, unlike the variability in other parameters that affect this and other methods, the orbit of any particular NEO will be known with sufficient accuracy that various spacecraft trajectories can be studied with a view to achieving the maximum relative velocity in the best direction at encounter (see also the later discussion of trajectories). NASA’s Deep Impact mission in 2006 demonstrated this principle, although with a smaller impactor on a larger body (6 kilometers in diameter). That impact was at 10 km/s and the committee will adopt that value for estimating effectiveness, but it is noted that for present capabilities the range of relative velocities due to different orbits of the NEOs is likely to be anywhere from a few to a few tens of kilometers per second.
There is one physical parameter that is important—the efficiency of transferring the spacecraft’s motion to the motion of the NEO, usually denoted by β. If the impactor is simply absorbed by the NEO, the momentum of
the impactor is transferred to the NEO, resulting in a change of velocity of the NEO that is the relative velocity of the two divided by the ratio of NEO mass to impactor mass. The effect is enhanced if material is ejected from the NEO, as will usually be the case with β likely to be between 1 and 10. (For material ejected forward, as in a “pathological” case, β could be less than unity.) The value of β is likely to increase with relative velocity, but this effect has not been studied in detail. The committee notes that the value of β is likely to be correlated with density of the NEO, being low (1-2) for very porous NEOs and high (5 or even higher) for hard, rocky NEOs, owing to the variation with materials mentioned above. The efficiency of changing an NEO’s trajectory depends not only on β but also on the shape of the NEO (which affects the direction of the ejecta) and on the direction of the spacecraft’s motion relative to the NEO’s motion. As shown later in this chapter, intercept trajectories are often such that the reduction in the effective change to the orbit is not large, but any given case must be analyzed in detail.
The instantaneous change in velocity of an NEO from a kinetic impact is thus given by
(Eq. 5.2)
where m and M are the masses of the impactor and the NEO, U is their relative velocity, and the factor β is greater than or equal to unity (Melosh et al., 1994). This equation can be used to determine the mass m of an impactor required to change the velocity of an NEO by 1 cm/s as a function of an NEO’s diameter and the relative velocity, as shown in Figure 5.1. This plot uses the estimates for β (1 to 5) as a function of impact velocity as given by Holsapple (2009). The required mass increases as the time to Earth intercept decreases.
As an extreme example, if the β factor were as much as 10, using a single 10-ton spacecraft impacting at 50 km/s, a 700-meter-diameter NEO of density 3 g/cm3 could be deflected by 1 cm/s. In that case, deflecting even a 1-kilometer-diameter body might be possible with 3 impacts. For comparison with slow-push-pull methods, an impulsive change of 1 cm/s is comparable to displacing the object by 15,000 kilometers 10 years in the future. But, for a more conservative example consistent with a more porous NEO body, if the β factor is only unity, the mass density is 1.5 g/cm3 and at a much lower impact velocity of 5 km/s, a 10-ton mass could change the orbit of only a 180-meter-diameter NEO sufficiently to avoid collision in all cases; 10 such impacts would be required for a 400-meter-diameter object. Different mission designs may trade spacecraft mass, impact velocity, and the time from intercept to the time of impact with Earth if no mitigation intervened.
To intercept any given NEO will require precise information about its orbit, which will set limits on mission designs. These limits are illustrated in Table 5.3, which shows the body sizes of NEOs whose orbit velocities could be changed by 1 cm/s. The table takes six representative cases by assuming a payload mass of 5 tons (now) or 50 tons (future) with three different intercept velocities: 5, 10, and 20 km/s. These cases are crossed with two types of NEO composition: (1) a somewhat porous body with a density of 1.9 g/cm3 and (2) a rocky body with a density of 3.0 g/cm3.
Summary
The kinetic impact method is relatively robust and would be feasible to use with moderate engineering developments. A major uncertainty is that the value of β is relatively unknown, although it has a firm lower limit of unity, applicable for highly porous NEOs from which little or no material would be ejected. A mission based on the European Space Agency’s (ESA’s) Don Quijote concept would reduce the uncertainties, especially for high-impact velocities and highly porous bodies, for which the uncertainties are largest.
In addition, important questions will have to be addressed about the ability to hit a small NEO at high relative velocity; those considerations may limit the intercept velocities at which kinetic impacts can be effective. The possibility of an inadvertent disruption of the NEO and the resulting consequences also need further study. This need is considered further in Chapter 6.
With the same warning time of 40 years as discussed for the gravity tractor, one could launch a series of perhaps ten 10-ton impactors to divert, 30 years before impact, NEOs with diameters on the order of ¾ kilometers, and with diameters even greater than 1 kilometer in the case of very-low-density NEOs. For a 10-year warning time and a crash program to launch 10 spacecraft in, say, 4 or 5 years, it might be possible to prevent a collision with
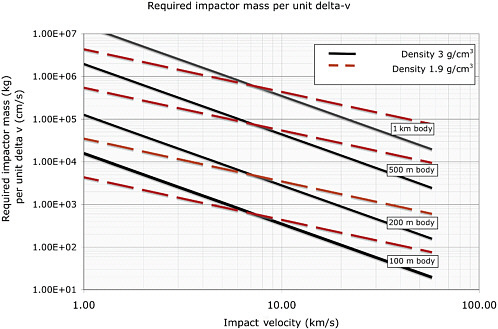
FIGURE 5.1 The estimated mass (kg) required to change the orbit of a near-Earth object (NEO) per unit of required velocity change (cm/s) by means of a direct impact, as a function of the impact velocity and for different-sized bodies. For example, a 1 cm/s velocity increment of a 200-meter-diameter body of density 3 g/cm3 impacted at 20 km/s requires an impactor mass of 103 kg, or 1 ton. A speed of change of 0.1 cm/s would require a 0.1 ton impactor. The reason that the lower-density porous body requires less impactor mass at low impact velocity is because it has less mass than that of a nonporous body of the same diameter. But at the higher impact velocities that porous body does not have the large momentum multiplication that the rocky body has, so the nonporous rocky body requires less impact mass. This plot uses the estimates for β (1 to 5) as a function of impact velocity as given by Holsapple (2009).
TABLE 5.3 Sizes of Near-Earth Objects (NEOs; diameter in meters) Whose Orbit Velocity Could Be Changed by 1 Centimeter per Second (cm/s) with a Single Impact
a ½-kilometer-diameter NEO with the gravity tractor; new, heavy-lift launchers such as the Ares cargo launcher might allow delivering 5 times more massive impactors. Multiple impactors provide robustness against random failures and the opportunity to fine-tune the results by varying the number of impacts. Even a single impactor that could be launched within 6 months of discovery might change the orbit of a 100-meter-diameter NEO, the size that is near the upper limit for the use only of civil defense mitigation, with a warning time of only 1 to 2 years.
Finding: Kinetic impactors are adequate to prevent impacts on Earth by moderate-sized NEOs (many hundreds of meters to 1 kilometer in diameter) with decades of advance warning. The concept has been demonstrated in space, but the result is sensitive to the properties of the NEO and requires further study.
NUCLEAR METHODS
Nuclear explosives constitute a mature technology, with well-characterized outputs. They represent by far the most mass-efficient method of energy transport and should be considered as an option for NEO mitigation. Nuclear explosives provide the only option for large NEOs (>500 meters in diameter) when the time to impact is short (years to months), or when other methods have failed and time is running out. The extensive test history of nuclear explosives demonstrates a proven ability to provide a tailored output (the desired mixture of x rays, neutrons, or gamma rays) and dependable yields from about 100 tons to many megatons of TNT-equivalent energy (see Appendix E). Coupled with this test history is an abundance of data on the effects of surface and subsurface blasts, including shock generation and cratering.
Various methods have been proposed for using nuclear explosions to reduce or eliminate an NEO threat; for a given mass of the NEO, the warning time is a primary criterion for choosing among them. With decades of warning, the required change in velocity (ΔV) from the explosion is millimeters to a centimeter per second and can be met for NEOs several kilometers in diameter. This range of values is much less than the 25 to 50 cm/s escape velocity from moderate to large (500- to 1,000-meter-diameter) bodies, so it is reasonable to assume that such a small ΔV would not lead to the target’s fragmentation or to excessive ejecta (i.e., debris thrown off the object). This expectation is met in hydrodynamic simulations presented here that show that nuclear explosions can provide ΔV from 0.7 to 2.4 cm/s, for payload masses less than 1 ton (including the nuclear device’s fuse and environmental cocoon). In models of NEOs with surface densities as in terrestrial environments, nearly 98 percent of a body remains bound as a single object through only its own weak gravity. The small amount of ejecta expands over the decades to form a large cloud of low-density debris, reducing its posed threat by another factor of 104 to 105. The amount of the ejecta depends on the surface porosity. As in the case of kinetic impacts, a dissipative, low-density surface will reduce the amount of ejecta, thus reducing the ΔV.
Alternatively, when the time to projected impact is short (i.e., years rather than decades), it may be impossible to apply a sufficient ΔV without fragmentation, but the limiting factor is assembly and launch. A nuclear package with a new fuse (i.e., a fuse that is not designed for terrestrial use) and a new container requires a cylinder about 1 meter in length and 35 centimeters in diameter, with a mass under 220 kilograms. The longest lead-time item for incorporating such a device in a rocket system is the development of a container to deliver the device and a fusing system capable of operating with the timing constraints required by the spacecraft velocities near impact with the NEO. Specifications for a nuclear bus could be the same as those for a kinetic-impactor mission, but it would be very challenging to construct and integrate with the booster rocket and the nuclear package in under a year. This “latency time” between the decision to act and the launch can be reduced dramatically (perhaps as much as 100-fold) by designing and testing these critical components in advance of discovering a hazardous NEO.
Models and Uncertainties
Nuclear outputs are well determined from tests. Just as with kinetic impactors, the greatest uncertainty in their use lies in the NEO response—the uncertainty relating particularly to current understanding of shock propagation through low-density material and of the large variety of NEO structures and behavior upon impact that could be encountered. Consider as examples: Asteroid Itokawa, like many asteroids, appears to consist of rubble weakly
bound together by gravity. It was found to have a bulk density of about 2 g/cm3 (Abe et al., 2006), that is, a porosity near 40 percent. Some asteroids, such as Eros, have densities near that of solids but are probably heavily fractured (Britt et al., 2002). However, “2001 0E84” is a large (approximately 1-kilometer-diameter) body rotating so rapidly that it must be very strong and is therefore not very porous; “(6187) 1986 DA” is essentially a solid iron NEO.1 All other known fast-spinning bodies are small (<200 meters in diameter). There are also low-density objects, like Asteroid Mathilde, on which observed craters suggest a very porous surface with larger efficient shock dissipation. The bulk density of cometary nuclei is likely less than 1 g/cm3.
NEOs have a wide range of shapes, sizes, and densities. The bulk density of those asteroids for which it is known is comparable with that of materials used in nuclear-effects simulations (e.g., gravel ≈ 1.5 g/cm3 and gravel with sand ≈ 1.9 g/cm3). The sophisticated computer simulations discussed here were used to model one of many possible structures, a 1-kilometer-diameter structure with a high-density core of 2.63 g/cm3 surrounded by a 250-meter-thick surface layer of 1.91 g/cm3.
Experimental results indicate that high porosity can significantly reduce the shock strength and rebound of shocked material (Holsapple, 2004). The impulse from a given energy coupled into a porous surface is lower than it would be for a nonporous solid, and the ejecta is reduced. A complete and adequate crushing model is necessary to determine the shock effects on a porous body. High-porosity dissipative surfaces lead to quantitatively similar uncertainties for both nuclear explosives and kinetic impactors, and an impactor mission to study asteroid structure would provide useful data for both approaches.
The limited set of conditions studied in the simulation described below begin to examine uncertainties in important physical properties in order to lead to an understanding of the application of nuclear explosions to NEO orbit change. They are not exhaustive, and there is much more to learn about the effects of shape, spin, and structure. Except for NEOs 10 kilometers in diameter or larger, it is generally likely that nuclear explosives can provide a more-than-large-enough ΔV, with little material loss and with essentially no danger of fragmentation.
Decades to Go—Standoff Burst
In the nuclear standoff scenario, the short burst of energy from a nuclear explosive is used to strongly heat a thin layer of an NEO’s surface. As this layer accelerates away from the NEO, the NEO’s main body recoils in the opposite direction and, if this “back reaction” of the NEO is large enough, the NEO’s path is altered to avoid collision with Earth. A nuclear explosion in space radiates most of its energy as x rays and gamma rays or as fast-moving neutrons. The proportion of x rays to neutrons is a function of the nuclear reactions that predominate in the explosion. For a given yield, fusion reactions produce more neutrons than do fission explosives. Neutrons offer an advantage for the standoff scenario because they penetrate about 1,000 times deeper into the NEO’s surface than do x rays and thus can heat a larger volume of material, giving a stronger impulse because more mass is ejected above escape speed. Neutron penetration is also nearly independent of the NEO’s composition for atoms between carbon and iron in the periodic table. Large amounts of hydrogen in the surface (such as in comets or asteroids with hydrated minerals) more strongly limit neutron penetration.
The area of the NEO’s surface that is heated by a standoff nuclear explosion depends on the distance between the asteroid and the point of detonation; the depth of penetration depends on the distance between the surface and the detonation point. Thus, detonation close to the surface heats only a small area close to the explosion, whereas more distant explosions spread their energy over a larger area of the asteroid. The neutrons penetrate most deeply vertically underneath the explosion and, because of the increased distance, penetrate less deeply at other places.
A detailed simulation of energetic neutrons incident on granite (Bedrossian, 2004) found that more than 70 percent of the incident energy was deposited in the granite (efficient deposition). More than 30 percent of the incident energy was deposited into a depth of about 15 centimeters. The energy required to convert rock into hot (more than 10,000 kelvin) plasma is high: 10 kilotons of TNT converts about 4,000 tons of surface material into plasma expanding at more than 2 km/s (Dearborn, 2004). The high efficiency of the deposition and relatively deep penetration of neutrons reduce the necessary neutron yield to near 100 kilotons of TNT-equivalent. High-fusion
devices were tested in the Plowshares program (an activity that explored the feasibility of using nuclear explosives for industrial applications), and the July 1962 Sedan nuclear test was more than 70 percent fusion (see DOE, 2000). If sufficient warning time is available, the largely fusion device can be chosen from tested designs and built with modern safety and security features.
To understand the action of a standoff nuclear explosion, and its ΔV capability, a member of the Mitigation Panel (David S.P. Dearborn, Lawrence Livermore National Laboratory) simulated the effect of a nuclear standoff detonation on homogeneous 1-kilometer-diameter NEOs with densities between 1.91 and 1.31 g/cm3. In these numerical models of a standoff burst about 150 meters above the NEO’s surface, about 40 seconds after the burst the NEO’s speed change ranged from 2.2 to 2.4 cm/s. Approximately 97.5 percent of each NEO remained intact (the NEO was held together by gravity only—it had no tensile strength), while about 2.5 percent of its mass was ejected at greater than escape speed by the rebound to the shock wave that passed through the body in reaction to the ejection of heated material. Higher porosity of the NEO will dissipate more energy, resulting in less ejecta and less speed change. The minimum speed change for a highly porous NEO is controlled by the amount of totally vaporized material. In these models this minimum ΔV is about 0.8 cm/s for an explosion with a strong neutron output. This work is preliminary, and the results provide only the scale of what can be done. NEOs come in many more sizes, shapes, and structures than what the committee could include in this simulation.
A standoff burst is usually considered the preferred approach among the nuclear options. One clear advantage is that there is no need to maneuver for a low approach speed as might be required for a surface or shallow sub-surface delivery. Neutron output associated with high fusion-to-fission ratios has many advantages including deeper neutron penetration (more impulse), high coupling efficiency, and an insensitivity to NEO composition.
Decades to Go—Small Surface Burst
Ahrens and Harris (1992, 1994) suggested using a surface or near-surface nuclear explosion. NASA’s 2006 study proposed the detonation of one or more subkiloton nuclear explosives on an NEO’s surface (NASA PA&E, 2006). In this approach the yield of the explosive must be stable and well determined. At 100 kilotons, the effect of 0.5-kiloton yield uncertainty is negligible, but not when the entire yield is 0.5 kiloton. The test base provides assurance of an effective yield with negligible uncertainty between 100 tons and 1 kiloton, but not for smaller yields. The committee notes that a rendezvous mission to implant explosives may be far more difficult than delivering a larger explosive package just above the surface.
As seen in Figure 5.2, yields between 100 and 500 tons provide significant speed increments to the body of an NEO with only modest amounts of ejecta (large amounts would be undesirable). Most of the ejected material has speeds in excess of 10 m/s, and should spread over many Earth-radii in only a year or two. The debris predicted from these models was not propagated along the sample orbits, but it is likely that the fraction of the ejecta that remains on a threatening orbit years later is no more than 10−4. As with the standoff simulations, future modeling of a more dissipative surface with very high porosity is likely to result in lower ΔV and less ejecta.
Delivering a nuclear explosive to the depth used in the simulation would be achievable with present earth-penetration technology, but it would require an approach speed equivalent to that of a rendezvous mission. Flyby speeds could be used with a fuse that fires on contact with the target and with a slightly higher-yield explosive than for rendezvous. The necessary calculations for this approach are straightforward, but current fuses would have to be upgraded to operate at the higher speeds.
Conclusions
Nuclear explosives can provide considerable protection against a potential NEO impact. This may be the only current means to prevent an impact by a large hazardous object (>500 meters in diameter) with a warning time under a decade or by a larger object (>1 kilometer in diameter) object with a warning time of several decades. With decades of warning for such large objects, the preferred approach uses a standoff detonation. Neutron output has certain advantages (Dearborn, 2004), as the energy coupling is relatively insensitive to the surface composition and density of the NEO. The simulations show that speed changes (ΔV) on the order of 2 cm/s are achievable with
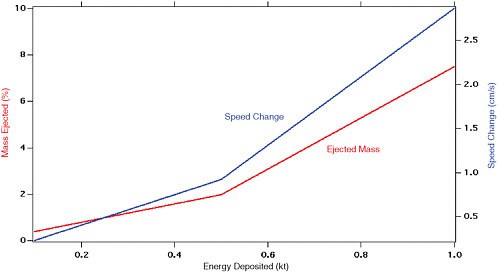
FIGURE 5.2 The speed change (blue) and ejected mass (red) for a 1-kilometer-diameter near-Earth object (NEO) versus energy deposited on the body, measured in kilotons of equivalent TNT.
gravitational binding mostly maintaining the NEO as a single body. About 2 percent of the body mass is ejected, evolving to such a low density that it would likely pose no threat to Earth. Very low yield surface explosives also showed great promise for speed changes on the order of 1 cm/s. As the NEO size decreases and the required yield of the nuclear explosive drops below the tested regime, which extends down to about 0.1 kilotons, the kinetic impact approach will have to be used.
Although the nuclear option provides considerable mitigation potential, for NEOs above some size the tested limits of nuclear explosives will become inadequate. Devices in the nuclear stockpile have equivalent energy releases of megatons of TNT, but NEOs larger in diameter than about 10 kilometers are likely to require larger explosive energies, a regime for which devices have not been tested or simulated. Modeling the shock dissipation of highly porous materials appears to be the primary uncertainty for both impactors and standoff bursts. This uncertainty holds particularly true for NEOs with very low density aggregates that can exist only in low-gravity environments. At present, the simulations have not examined the effects of the range of structures, shapes, and rotational states, but with Defense Threat Reduction Agency support to extend the present studies, these simulations could be done. Currently the United States and several other nations maintain nuclear stockpiles and the infrastructure to build them for purposes of national defense. Efforts to reduce those stockpiles continue, but it seems likely that they will exist for some decades. When defense concerns no longer apply, the governments involved may either accept the longer response time for a Manhattan Project-like effort or decide whether adequate safeguards can be developed so that some entity could maintain a small number of nuclear explosive packages to allow humanity to counter an NEO that could, for example, cause mass extinctions.
Finding: Other than a large flotilla (100 or more) of massive spacecraft being sent as impactors, nuclear explosions are the only current, practical means for changing the orbit of large NEOs (diameter greater than about 1 kilometer). Nuclear explosions also remain as a backup strategy for somewhat smaller objects if other methods have failed. They may be the only method for dealing with smaller objects when warning time is short, but additional research is necessary for such cases.
DELIVERING PAYLOADS TO NEAR-EARTH OBJECTS
A key element of any comprehensive mitigation strategy is the ability to deliver a payload to a hazardous NEO, either by means of a rendezvous (e.g., for characterization, for attaching an accurate tracking device, or for applying a slow-push-pull technique to the NEO) or a high-speed approach (e.g., to deliver a kinetic impactor or to deliver a nuclear explosive package to change the orbit). Once an NEO has been identified as hazardous and the time to impact has been determined, the question becomes: Is it technologically possible to act and succeed in preventing an impact on Earth within the time available? The committee notes that the time to design, build, and launch a mission is typically a large fraction (more than half) of a decade, but this time could be shortened with a necessarily expensive “crash program.” The part that is harder to control is the time from launch to arrival at the NEO, which depends on the NEO’s orbit. A second key element, equally important for mitigation either by a gravity tractor or by a kinetic impactor, is the amount of mass that can be delivered to the NEO. This section addresses the issues of mass deliverable to an NEO and the time to reach the NEO after launch. The discussion of developing crash programs is left to the arena of public policy.
NEOs as a group have a very wide range of orbital properties, from nearly circular orbits with orbital periods of about a year, to very elongated orbits with periods from less than a year to decades if the discussion ignores the long-period comets, and to much longer periods if they are included. A complete statistical description of the time to reach an NEO with an orbit anywhere within this distribution is beyond the scope of this study, so only a very small number of examples is considered here. The statistical distribution of the orbits of the NEOs has been studied by Chesley and Spahr (2004), while Perozzi et al. (2002) have considered trajectories to NEOs as well as the deliverable mass. Any optimization of the trajectory to a given NEO would depend on the goal, as well as on the details of the individual orbit. Prior statistical studies will provide a start on this problem, but a detailed study of possible trajectories to any specific NEO will be needed.
The warning time—the length of time from the decision to prevent an impact until the predicted time of impact—is a key parameter. For short warning times, of say a decade, high-speed intercepts may be the only possible choice. For longer warning times, of many decades, one could choose between a high-speed intercept and a rendezvous, depending on the size and physical nature of the NEO.
The key parameters of a launch are the mass that can be launched to escape Earth’s gravity and then the additional velocity that must be provided to put the spacecraft on a trajectory to the NEO of interest. The former is determined entirely by the available launch vehicles, whereas the latter is determined by the details of the orbit of the NEO. (Note, too, that the mass of the fuel required to provide the Earth-escape velocity and this additional velocity will come at the expense of payload mass.) The additional velocity that must be provided is usually characterized by a parameter called C3, which is a measure of this extra propulsion energy needed to change the spacecraft’s trajectory. This quantity can range from almost zero to very many tens of kilometers per second squared for realistic missions. Values of hundreds of kilometers per second squared may be required for some trajectories, but for traditional scientific missions these are not considered feasible. The use of in-space propulsion, such as the engines commonly called solar-electric propulsion or nuclear-electric propulsion, can significantly reduce the mass of fuel that the spacecraft needs at launch but with a cost in time for using in-space propulsion.
Table 5.4 lists the maximum payload in tons that can be carried by various launch vehicles currently available, as well as an estimate of the corresponding capability of the Ares V launcher, which is being developed and might be available for use in the near future. The capability of these launch vehicles is well above the capability assumed nearly a decade ago by Perozzi et al. (2002). The table includes in the first two rows data taken from published literature that provide a starting point, but which in themselves are not directly relevant. The values in the table are for the maximum payloads that can be delivered to a low-Earth orbit (LEO, such as the orbit of the International Space Station) and to a higher orbit that is commonly used as an intermediate step before going to interplanetary space, the geostationary transfer orbit (GTO). The third row lists the mass that can be launched to escape Earth’s gravity, and in the last row shows the mass that can be launched to a relatively easy-to-achieve but realistic orbit that intercepts an NEO.
The differences in Table 5.4 between the corresponding entries in the last two rows—a factor of two—show that even for the NEOs in orbits easiest to reach, the penalty on payload mass is severe. For orbits harder to reach,
TABLE 5.4 Payload Capability (in tons) of Current and Planned Launch Vehicles
|
|
Ariane V |
Atlas V |
Delta IV |
Proton |
Zenith |
Long March 5 |
Ares V |
|
LEO |
20 |
30 |
26 |
~22 |
~14 |
~25 |
~190 |
|
GTO |
11 |
14 |
11 |
~6 |
~5 |
~14 |
~70 |
|
Escape |
9 |
12 |
9 |
5 |
4 |
12 |
70 |
|
C3 = 10 (km/s)2 |
5 |
6 |
5 |
3 |
2 |
6 |
35 |
|
NOTE: LEO, low-Earth orbit; GTO, geostationary transfer orbit; C3, see Appendix E in this report. |
|||||||
the payload mass drops quickly to zero because of the mass needed for chemical propulsion. An alternative is to use so-called electric propulsion systems, which can be used in principle at any stage beyond LEO but in practice have been used primarily beyond escape from Earth. They substantially reduce the need for fuel and thus increase the payload that can be delivered. However, the available electric power, whether generated from solar or nuclear sources, is not large with current technology, so the electric propulsion systems take a long time to move the spacecraft to any desired velocity and thus significantly increase the time to reach an NEO. New technology that is under discussion and development may improve the situation, but there will always be a trade-off between transit time and launch mass. In practice electric propulsion has been used primarily for rendezvous missions, for which it can provide both initial acceleration and subsequent deceleration to the rendezvous.
The committee presents some sample trajectories to illustrate what is possible with today’s launch vehicles—that is, not including Ares V. Two different trajectories to reach each of two NEO orbits are considered. The first NEO orbit is like that of Apophis, but, for convenience, with the NEO starting from a different position in the orbit than Apophis is at now. The second NEO orbit (“NEO #2”) was chosen to be more elongated than the first. The two different trajectories for each orbit were chosen to approximately maximize the time between the encounter of the spacecraft with the NEO and the predicted impact of the NEO on Earth, for the two cases, one each of high- and low-speed arrival at the NEO. The high-speed arrival corresponds, for example, to maximizing the relative speed of the NEO and spacecraft at encounters for kinetic impact, and the low-speed arrival corresponds to minimizing this relative speed to allow rendezvous for the delivery of a subsurface nuclear device. (Formal optimization calculations were, however, not carried out.) The trajectories shown in Figure 5.3 and Table 5.5 imply launches about a decade before the predicted impact. The decision to act would of course need to be made much earlier in order to design, build, and launch the spacecraft. Note the far smaller mass that can be delivered for a rendezvous mission.
These trajectories, which are all feasible to achieve with current technology, assume launch on an Atlas V rocket with a single upper stage to place the spacecraft on the intercept trajectory. Clearly, much larger masses (“payloads”) can be delivered to a high-speed intercept than to a rendezvous, and the difficulty of getting to a target depends in detail not only on the shape of the NEO’s orbit but also on where the NEO is in its orbit at a specific time. The rendezvous trajectories require an additional propulsion system for rapid deceleration as the spacecraft nears the NEO. The intercept trajectories all make an angle of less than 30° to the orbit at interception, so that an impactor would deliver a large fraction of its momentum in the favorable direction, parallel to or exactly opposite to the NEO’s motion. The trajectories for rendezvous become very different if one uses in-space propulsion, allowing near-zero rendezvous speeds and allowing massive payloads but at the expense of much longer flight times than in the cases shown here. New in-space propulsion systems that have been considered and/or are under development can considerably improve the situation by shortening the flight time. Longer warning times offer several other possibilities, including gravity assists from planets.
The most challenging trajectories are those to long-period comets, largely because of the likely short time from discovery to their impact on Earth coupled with their very elongated orbits. In general, these comets would require a spacecraft that is ready to launch when the decision is made to act. Cometary impacts on Earth can occur either when the comet is inbound or when it is outbound. Figure 5.4 and Table 5.6 present intercept trajectories that assume launch on a Delta IV-heavy rocket with a single upper stage and a 0.5-ton payload. This payload is sufficient for a nuclear package but rather small for a kinetic impactor. The trajectories were designed to maximize the time between intercept and predicted NEO impact on Earth.
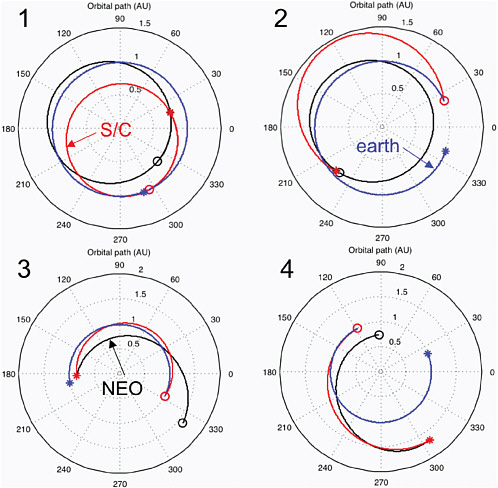
FIGURE 5.3 Sample trajectories of a spacecraft are shown in red. The Sun is at the center of each diagram, and the distance from the Sun increases to 1.5 AU at the edge of the upper panels and to 2 AU at the edge of the lower panels. Earth’s orbit is shown in blue, with the launch point shown by a small circle. The near-Earth object’s (NEO’s) orbit in each case is shown in black, with a small asterisk at the point of intercept. Each panel corresponds to the indicated column in Table 5.5: Panel 1, Apophis-Like HighSpeed; Panel 2, Apophis-Like Rendezvous; Panel 3, NEO #2, High-Speed; Panel 4, NEO #2, Rendezvous.
These trajectories to a comet are examples of a relatively easy case, as they assume that the comet’s orbit is in the same plane as Earth’s orbit. Other orbits are harder to reach. However, the key point is that intercept trajectories with reasonable flight times are feasible. A next-generation launch vehicle, such as Ares V, would make kinetic impacts feasible for some long-period comets.
In summary, current technology allows the delivery of payloads for purposes of mitigation to NEOs in a wide range of orbits. However, in cases of short warning (under, say, a decade), payloads are likely to be severely limited in mass but may often be sufficient to deliver a nuclear device. The development of the next generation of heavy-
TABLE 5.5 Values of Key Parameters for Sample Trajectories Using Chemical Propulsion
|
|
Apophis-Like High-Speed |
Apophis-Like Rendezvous |
NEO #2 High-Speed |
NEO #2 Rendezvous |
|
Launch to Earth impact (years) |
14 |
9.5 |
12 |
7.5 |
|
Launch to NEO (days) |
360 |
320 |
220 |
270 |
|
Intercept velocity (km/s) |
12 |
3.2 |
12 |
3.0 |
|
C3 (km/s)2 |
15 |
70a |
17 |
19 |
|
Payload mass (tons) |
6.5 |
0.6 |
5.9 |
4.0 |
|
NOTE: C3, see Appendix E in this report. aThe large difference in this entry and the others for C3 illustrates the great sensitivity of C3 requirements to spacecraft launch dates. |
||||
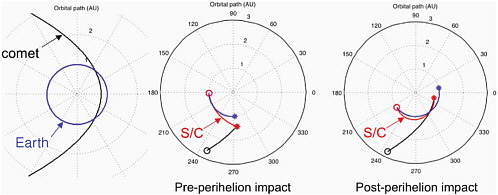
FIGURE 5.4 Intercept trajectories for a hazardous, long-period comet. The left panel shows the comet’s orbit and the two places at which it intercepts Earth’s orbit. The next two panels show the intercept trajectories corresponding to the two rows in Table 5.6. In other respects, the panels are similar to those in Figure 5.3.
TABLE 5.6 Parameter Values for Delivering a 500-Kilogram Payload to a Long-Period Comet
|
|
Intercept Speeda (km/s) |
Launch to Impactb (days) |
Flight Timec (days) |
Intercept to Impact Timed (days) |
|
Pre-perihelion impact |
37 |
130 |
95 |
34 |
|
Post-perihelion impact |
15 |
200 |
160 |
40 |
|
aRelative speed of spacecraft and comet at impact. bTime from spacecraft launch to predicted Earth impact of comet. cTime from spacecraft launch to its intercept of comet. dArrival time of spacecraft at comet prior to predicted impact of Earth by comet. |
||||
lift launch vehicles will considerably improve the situation. The development of advanced engines for in-space propulsion will considerably improve the capability of delivering rendezvous payloads (for characterization, to act as gravity tractors, or to emplace surface explosives) when the warning time is in decades.
Finding: For a wide range of impact scenarios, launch capability exists to deliver an appropriate payload to mitigate the effects of a NEO impact. For some scenarios, particularly short-warning scenarios, the capability is inadequate. The development of foreseen heavy-lift launch vehicles, such as the Ares cargo vehicle,
should enable the use of a variety of methods for NEOs up to two times larger than is possible with current launch vehicles.
DISRUPTION
Both the kinetic impact and the nuclear detonation mitigation methods are capable of including larger changes in the velocity of the NEO than those discussed above, particularly for smaller objects; in those cases, however, these methods deliver so much energy that there is a likelihood of totally disrupting the NEO (i.e., fragmenting it). Disruption has been widely proposed as a mitigation option, but disruption could make the situation worse. Specifically, if the hazardous object breaks into a small number of large fragments with only a very small spread in velocity, the multiple impacts on Earth might cause far more damage than a single, larger impact. Thus, disruption or fragmentation is a sensible strategy only if it can be shown that the hazard is truly diminished. In the case of a very large impactor (e.g., a 10-kilometer-diameter, civilization-destroying NEO) discovered without many years of warning, adequate orbital change may not be possible, leaving disruption as the only option for mitigation. This option would likely require a system on standby at all times and a decision to disrupt made long before the probability of impact was high. Even in this situation one would want assurance, from previous studies, that disruption would both succeed and reduce the hazard.
Numerous studies of the catastrophic disruption of asteroids, undertaken in order to increase the understanding of the evolution of the asteroid belt, have shown that the energy required for catastrophic disruption per unit of mass of an asteroid has a minimum for bodies with diameters of a few hundred meters (e.g., Holsapple, 2002). These calculations, of course, assume physical properties for the asteroids, and those properties are not well known in any particular case. Early laboratory experiments and subsequent basic physical and numerical simulations (Housen and Holsapple, 1990; Michel et al., 2004) show that when an asteroid is catastrophically disrupted, only one large fragment remains, and the size of that fragment shrinks with increasing energy of the impact. Furthermore, energy arguments imply that most of the other fragments disperse with velocities comparable to or greater than the escape velocity from the original body, that is, >1 meter per second for a kilometer-sized NEO. To the extent that these calculations and laboratory experiments are relevant, they suggest that disruption might leave one much smaller object on an impact trajectory, with most of the other pieces spreading out over a cross section much larger than Earth within less than a year.
Thus disruption might be a useful mitigation technique. However, the uncertainties in the structure of NEOs are sufficiently large that this committee does not now have high enough confidence in the disruption approach to recommend it as a valid technique for mitigation at this time. Additional research, including a suite of independent calculations and laboratory experiments, but particularly including experiments on real comets and asteroids, might show that disruption is well enough understood to use as a mitigation technique.
To avoid disruption, both kinetic impact and nuclear detonation approaches to orbit change benefit dramatically from using multiple events. (They also allow the effective orbit change of larger NEOs, but disruption is rarely an issue in that case.) This strategy also allows for the adjustment of the total effect when the hazardous object’s response to an event is not accurately predictable in advance.
SUMMARY
Figure 5.5 summarizes the range of parameter space in which each of the four types of mitigation could be considered primary, emphasizing the still-significant uncertainty in the boundaries between the various regimes. Other parameters (density of the NEO, details of the NEO’s orbit, probability of impact at a given warning time, etc.) all play a role in the uncertainty. Furthermore, civil defense should play a role in all of the regimes, and one might choose to apply multiple methods in a given case, thus further blurring the distinctions. Toward the left edge of the figure, representing short warning times, one would likely be able to carry out nothing but civil defense, unless disruption was shown to be reliable; toward the right edge of the figure, representing long warning times, the uncertainty in the prediction might discourage action. Toward the right half of the figure, there would often be time to design, build, and launch a mitigation mission. Toward the left half, one might need a mission ready to
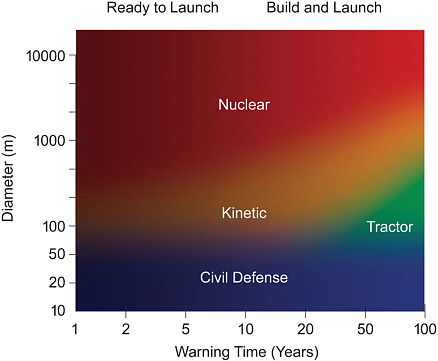
FIGURE 5.5 Approximate outline of the regimes of primary applicability of the four types of mitigation (see text for the many caveats associated with this figure). Image courtesy of Tim Warchocki.
launch on discovery of a hazardous NEO. Significant research efforts are needed to ensure success in large areas of the figure.
This chapter has considered both the range of likely mitigation measures available to society and the circumstances in which each might be appropriately used, albeit with fuzzy boundaries. However, there are also issues related to reliability and robustness that need to be considered. In particular, if mitigation is needed, the stakes are much higher than for a typical scientific mission to deep space, and assured success is crucial. The general principle of “Do no harm” is also crucial. Assured success includes being certain that the mitigation will not increase the hazard. This assurance is particularly important when one must initiate a mission to change the orbit of an NEO before the probability of impact approaches unity, which will often be the case, since an orbit change could then, in principle, divert a near-miss object onto an impact trajectory. The principle is equally important in the much-less-likely circumstance of a late-discovered, large NEO for which the energy needed for the required orbit change approaches the energy needed for disruption.
This need for assured success implies that, if time permits, a characterization mission prior to mitigation is highly desirable. The efficiency of orbit change in most approaches, the gravity tractor excepted, is very sensitive to some physical properties of the NEO, particularly the porosity and density in the outer tens of meters, that cannot be determined from remote sensing. An in situ characterization mission, if properly designed, can measure the key physical properties needed for reliable control of orbit change. Similarly, there is a need for verification of the orbit change. For most slow-push techniques the verification is straightforward, since there is a spacecraft near the NEO for the duration. If there were an advance characterization mission, that mission could also be configured for verification. Even if there were not time for a characterization mission, there might be time to launch
a verification mission that has a rendezvous with the NEO prior to the change in its orbit so as to measure this change; this approach should be implemented wherever possible.
The committee also notes that civil defense is likely needed in all mitigation scenarios, not just in those situations for which it is the most cost-effective approach. One aspect of civil defense is educating the public about the nature of the hazard and the manner in which individuals should respond. Public information about the hazard is crucial. For those impacts that cause very localized damage on the ground, there may nonetheless be peripheral effects on climate, probably small and of short duration but important enough that the public needs to understand them. There may also be effects on infrastructure, such as on communications, that extend well outside the area of direct damage. Dealing with these issues is all part of civil defense preparedness.
With the current uncertainty regarding both the properties of the NEOs themselves and the efficiency of an interaction with an NEO for kinetic and nuclear orbit change, and even from the general standpoint of confidence of success, functional redundancy is crucial. Instead of changing the orbit of an NEO with a single kinetic impactor, a series of impactors spread slightly in time provides much more reliability, and in some situations it might even allow assessment of the effect of the first impactor before the second arrived. Depending on the details of the specific orbit, it might be desirable and possible to divert later impactors, but the applicability of this concept needs further study. Alternatively, as long as there is a nuclear capability, one could consider readying a nuclear mission as a late-stage backup for a kinetic impactor that might, even with some very low probability, fail. Similarly, a kinetic impactor might be a backup for a gravity tractor on the chance that the gravity tractor might suddenly have a fuel leak or some other failure after a long but incomplete period of “pulling” the NEO.
A nuclear detonation approach, however implemented, is likely to raise significant public concern. If an NEO capable of massive death and destruction was discovered with certainty to be on a collision path with Earth and if there was no other way to stop it, presumably any concerns about the nuclear approach would be overridden. But in the early mitigation planning stages, public concern might inhibit development. This is primarily a public policy, rather than a technical question, and is therefore outside the scope of this committee’s task. Similarly, as noted above in the section on “Nuclear Methods,” the question of whether to maintain a nuclear stockpile for NEO mitigation purposes is not a technical question. In this report, the committee has assumed that a nuclear stockpile and nuclear development capability are on hand for other purposes.
Perhaps the most significant conclusion that can be drawn is the large uncertainty in the effectiveness of the mitigation techniques because of their dependence on the physical properties of NEOs that are not well known, and because of the difficulty of scaling any laboratory experiments to this regime. At this point it is not even possible to determine reliably the boundaries of applicability of the various approaches. In a later chapter the committee addresses organizational aspects of the decision-making process, but it still lacks information to guide that process. Any process must carry out a detailed study of where to draw the boundaries and what additional information would be needed. An applied research program, directed explicitly at the NEO hazard, could significantly reduce the uncertainties. At the lowest meaningful level of investigating the mitigation issues, this program would include both numerical simulations by multiple groups and laboratory experiments.
A much-larger-scale effort to address the mitigation of NEO hazards will likely include activities in space. The single most-significant step in this area appears to be a kinetic impact mission on a far larger scale than the Deep Impact mission, employing a much larger impactor on a much smaller target, with another spacecraft that has a rendezvous with the target well prior to impact to characterize the target and its orbit very precisely. This characterizing spacecraft would remain with the target until long after the impact in order to determine accurately the change in its orbit resulting from the impact. The Don Quijote mission that was studied by the ESA but is no longer under active consideration would have addressed most of these goals. Suggestions have been made to use the rendezvous spacecraft as a gravity tractor after the primary mission, but given the different design considerations it is not yet clear whether this is a good approach or not. A demonstration flight of a gravity tractor appears to be the second most significant step, since lesser knowledge of NEO behavior is needed for implementation. Both the kinetic impact and gravity-tractor approaches require significant engineering study, but more basic knowledge is needed for the kinetic impactor.
In cases of the late discovery of a hazardous NEO, the change in the NEO’s orbit that must be made for it to miss Earth can be so large that the required impact energy is comparable to or greater than the energy to disrupt
the body. Depending on how the body disrupts, the effect on Earth could, in some circumstances, be worse overall than if disruption were not attempted. Alternatively, disruption might lead to less total damage to Earth but more damage to, for example, a particular populated location. With the uncertainty in the present understanding of fragmentation and disruption, the committee does not now endorse disruption as a mitigation strategy, but it suggests that further study of this issue should be an important part of any research program into mitigation of the NEO hazard. (See Chapter 6.)
Finding: The mitigation of the threat from NEOs would benefit dramatically from their in situ characterization prior to mitigation if there is time.
Finding: Changing the orbit of an NEO given the current level of understanding is sufficiently uncertain that, in most cases, it requires an accompanying verification. This is easy to implement with many slow-push techniques, but it would require considerable additional effort for other techniques.
Recommendation: If Congress chooses to fund mitigation research at an appropriately high level, the first priority for a space mission in the mitigation area is an experimental test of a kinetic impactor along with a characterization, monitoring, and verification system, such as the Don Quijote mission that was previously considered, but not funded, by the European Space Agency. This mission would produce the most significant advances in understanding and provide an ideal chance for international collaboration in a realistic mitigation scenario.
BIBLIOGRAPHY
Abe, S., T. Mukai, N. Hirata, O.S. Barnouin-Jha, A.F. Cheng, H. Demura, R.W. Gaskell, T. Hashimoto, K. Hiraoka, T. Honda, T. Kubota, M. Matsuoka, T. Mizuno, R. Nakamura, D.J. Scheeres, and M. Yoshikawa. 2006. Mass and local topography measurements of Itokawa. Science 312:1344-1347.
Ahrens, T.J., and A.W. Harris. 1992. Deflection and fragmentation of near-Earth asteroids. Nature 360(6403):429-433.
Ahrens, T.J., and A.W. Harris. 1994. Deflection and fragmentation of near-Earth asteroids. In Hazards Due to Comets and Asteroids (T. Gehrels, ed.). University of Arizona Press, Tucson.
Bedrossian, P.J. 2004. Neutrons and Granite: Transport and Activation. UCRL-TR-203529. Lawrence Livermore National Laboratory, Livermore, Calif.
Britt, D.T., D. Yeomans, K. Housen, and G. Consolmagno. 2002. Asteroid density, porosity, and structure. In Asteroids III. University of Arizona Press, Tucson.
Chesley, S.R., and T.B. Spahr. 2004. Earth-impactors: Orbital characteristics and warning times. Pp. 22-37 in Mitigation of Hazardous Comets and Asteroids (M.J.S. Belton, T.H. Morgan, N.H. Samarashinha, and D.K. Yeomans, eds.). Cambridge University Press, Cambridge, Mass.
Dearborn, D.S. 2004. 21st century steam for asteroid mitigation. Planetary Defense Conference: Protecting Earth from Asteroids, Orange County, Calif. AIAA-2004-1413. American Institute of Aeronautics and Astronautics, Reston, Va.
DOE (Department of Energy). 2000. United States Nuclear Tests; July 1945 through September 1992. Report DOE/NV-209-REV 15. Department of Energy, Nevada Operations Office, Las Vegas, Nev. December. Available at http://www.nv.doe.gov/library/publications/historical/DOENV_209_REV15.pdf.
Fahnestock, E.G., and S.B. Broschart. 2009. Dynamical characterization, control, and performance analysis of gravity tractor operation at binary asteroids. First International Academy of Astronautics (IAA) Planetary Defense Conference: Protecting Earth from Asteroids, Granada, Spain, April 27-30, 2009.
Fahnestock, E.G., and D.J. Scheeres. 2008. Dynamical characterization and stabilization of large gravity tractor designs. AIAA Journal of Guidance, Control, and Dynamics 31(3):501-521.
Giorgini, J.D., L.A.M. Benner, S.J. Ostro, M.C. Nolan, and M.W. Busch. 2008. Predicting the Earth encounters of (99942) Apophis. Icarus 193(1):1-19.
Holsapple, K.A. 2002. The deflection of menacing rubble pile asteroids. Extended Abstracts Volume of the Workshop on Scientific Requirements for Mitigation of Hazardous Comets and Asteroids, Arlington, Virginia, on September 3-6, 2002. National Optical Astronomy Observatory, Tucson, Ariz. Available at http://www.noao.edu/meetings/mitigation/media/arlington.extended.pdf.
Holsapple, K.A. 2004. An assessment of our present ability to deflect asteroids and comets. Planetary Defense Conference: Protecting Earth from Asteroids, Orange County, Calif. AIAA-2004-1413. American Institute of Aeronautics and Astronautics, Reston, Va.
Holsapple, K.A. 2009. On the “strength” of the small bodies of the solar system: A review of strength theories and their implementation for analyses of impact disruptions. Planetary and Space Science 57(2):127-141.
Housen, K.R., and K.A. Holsapple 1990. On the fragmentation of asteroids and planetary satellites. Icarus 84:226-253.
Kahle, R., E. Kuhrt, G. Hahn, and J. Knollenberg. 2006. Physical limits of solar collectors in deflecting Earth-threatening asteroids. Aerospace Science and Technology 10(3):256-263.
Lu, E.T., and S.G. Love. 2005. Gravitational tractor for towing asteroids. Nature 483:177-178.
Melosh, H.J., I.V. Nemchinov, and Y.I. Zetzer. 1994. Non-nuclear strategies for deflecting comets and asteroids. Pp. 1111-1134 in Hazards from Comets and Asteroids (T. Geherls, ed.). University of Arizona Press, Tucson.
Michel, P., W. Benz, and D.C. Richardson. 2004. Catastrophic disruption of asteroids and family formation: A review of numerical simulations including both fragmentation and gravitational reaccumulation. Planetary and Space Science 52:1109-1117.
NASA PA&E (NASA Program Analysis and Evaluation). 2006. 2006 Near-Earth Object Survey and Deflection Study. NASA Headquarters, Washington, D.C.
Niven, L., and J. Pournelle. 1977. Lucifer’s Hammer. Playboy Press, Chicago.
Perozzi, E., L. Casalino, G. Colasurdo, A. Rossi, and G.B. Valsecchi. 2002. Resonant fly-by missions to near Earth asteroids. Celestial Mechanics and Dynamical Astronomy 83(1-4):49-62.
Shute, N. 1957. On The Beach. Ballantine Books, New York.
Wie, B. 2008. Dynamics and control of gravity tractor spacecraft for asteroid deflection. Journal of Guidance, Control, and Dynamics 31(5):1413-1423.
Yeomans, D., S. Bhaskaran, S. Broschart, S. Chesley, M. J. P.W. Chodas, and T. Sweetser. 2008. Near-Earth Object (NEO) Analysis of Transponder Tracking and Gravity Tractor Performance. Report submitted to the B612 Foundation per JPL Task Plan No. 82-120022. Jet Propulsion Laboratory, Pasadena, Calif., September.