8
Opportunities to Generate Evidence
|
KEY MESSAGES
|
The preceding chapter outlines a standard for assembling evidence that requires access to potentially useful sources of information; the blending of theory, expert opinion, experience, and local wisdom; the availability of scientifically trained staff or colleagues skilled in using these resources; a time window that allows for the process
of locating, evaluating, and assembling evidence; and, most important, the existence of relevant evidence. Use of the L.E.A.D. framework to broaden what is considered useful, high-quality evidence and to gradually increase the availability of such evidence will help in attaining this standard. Together with the importance of taking a systems approach and making the best possible use of diverse types of evidence that are relevant to the user’s perspective and the question being asked, a major emphasis of this report is the urgent need to generate more evidence to inform efforts to address obesity prevention and other complex public health problems. Much of what is called for in the framework will meet the expectations and needs of decision makers when sufficient evidence exists, although clearly such is not yet the case (see Chapter 3). On the other hand, failure to find relevant evidence may either (erroneously) reinforce the perception that effective interventions cannot be identified, or increase skepticism or resistance on the part of decision makers—who must proceed in the interim—with respect to the utility of incorporating evidence into their decision-making process. As described in Chapter 7, when decision makers face choices that must be made and actions that must be taken in the relative absence of evidence, or at least on the basis of inconclusive, inconsistent, or incomplete evidence, the L.E.A.D. framework calls for critical evaluation and systematic building on experience in a continuous translation, action, monitoring, surveillance, and feedback loop (i.e., matching, mapping, pooling, and patching; see Appendix E for more detail).
The purpose of this chapter is to motivate researchers and others whose primary role is to generate (i.e., support, fund, publish) evidence to adopt the L.E.A.D. framework as a guide to identifying and generating the types of evidence that are needed to support decision making on obesity prevention and other complex public health problems (see Figure 8-1). The focus is on evidence related to “What” and “How” questions, that is, evidence demonstrating the types of interventions that are effective in various contexts; what their impacts are; and which are relatively more or less effective, whether they are associated with unexpected benefits or problems, and what practical issues are involved in their implementation. As noted in Chapter 3 and defined in Chapter 5, these concerns point to areas in which a lack of evidence is most likely to be problematic. This chapter also anticipates a cycle that begins with planning from incomplete evidence, blended with theory, expert opinion, experience, and local wisdom (see Chapter 7), and ends with evaluating the consequences of interventions. Such a cycle, in turn, may produce the most credible evidence for other jurisdictions seeking practical models to emulate.
The chapter begins by briefly reviewing existing evidence needs and outlining the need for new directions in evidence generation and transdisciplinary exchange. It then addresses the limitations in the way evidence is reported in scientific journals and the need to take advantage of natural experiments and emerging and ongoing interventions as sources of practice-based evidence to fill the gaps in the best available evidence. The chapter concludes with a discussion of alternatives to randomized
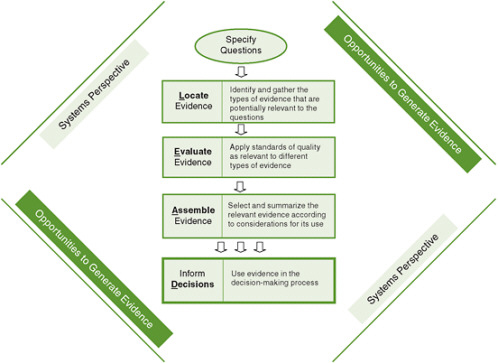
FIGURE 8-1 The Locate Evidence, Evaluate Evidence, Assemble Evidence, Inform Decisions (L.E.A.D.) framework for obesity prevention decision making.
NOTE: The element of the framework addressed in this chapter is highlighted.
experiments, with a focus on the level of certainty of the causal relationship between an intervention and the observed outcomes.
EXISTING EVIDENCE NEEDS
The generation of evidence related to interventions and their effectiveness can be approached through evaluation research, where evaluation is defined as “a systematic assessment of the quality and effectiveness of an initiative, program, or policy…” (IOM, 2007, p. 26). As explained in Chapter 1, the 2007 Institute of Medicine (IOM) report Progress in Preventing Childhood Obesity, which is current through 2006, strongly emphasizes the need for evaluation of ongoing and emerging initiatives. The committee that produced the report found that, in response to the urgency of the problem of childhood obesity with respect to prevalence and economic costs, numerous efforts were being undertaken on the basis of what was already known from theory or practice. Given the inherent relevance of implemented programs to natural settings, such spontaneous or endogenous interventions may be of most interest to
decision makers. However, many of these programs are not evaluated. Issues for consideration in increasing the use and appropriateness of such evaluation, taken from the 2007 IOM committee’s assessment, are shown in Box 8-1.
A working group convened by the National Heart, Lung, and Blood Institute of the National Institutes of Health (NIH) also has made several recommendations for research needs related to the prevention of child obesity, many of which are directly relevant to the types of population-based approaches addressed in this report (Pratt et al., 2008). Several of these recommendations are listed in Box 8-2. Consistent with the issues highlighted by the 2007 IOM committee, the NIH recommendations include the evaluation of existing promising programs, as well as the conduct of studies of multilevel and multicomponent interventions.
The examples in Box 8-2 relate specifically to child obesity. However, the need for more evidence relevant to decision making is also recognized with respect to obesity in adults and other complex public health problems. The Congressional Budget Office (CBO), for example, has identified several areas in which having more evidence would be helpful. CBO found some evidence on net cost reductions for certain disease management programs, but it was unclear whether these strategies could be replicated or applied in a broader population. In general, CBO found the availability of clinical and economic research assessing and comparing treatments for preventive services to be limited (CBO, 2008).
|
Box 8-1 Considerations for Increasing Evaluation of Obesity Prevention Initiatives
SOURCE: IOM, 2007, pp. 27-28. |
|
Box 8-2 Selected Recommendations for Research in Childhood Obesity Prevention Settings
Implementation, Dissemination, Translation, Evaluation
Methodology
High-Risk Populations
Other Recommendations
SOURCE: Adapted and reprinted from Pratt et al., Copyright © 2008, with permission from Elsevier. |
THE NEED FOR NEW DIRECTIONS AND TRANSDISCIPLINARY EXCHANGE
The two methodological recommendations in Box 8-2 highlight one of the major problems encountered by those who wish to generate policy- or program-relevant evidence regarding population health problems such as obesity. These recommendations refer to the need to identify optimal and appropriate study designs, including designs that will allow for timely assessment of initiatives that constitute “natural experiments” (detailed later in this chapter); quasi-experimental designs are mentioned in addition to randomized designs. One major question raised by these recommendations relates to the prevailing preference for randomized controlled trials (RCTs) in biomedical science because of their advantages for drawing causal inferences: Are there good alternatives to randomized designs that will accomplish the same thing but can be implemented more flexibly in natural or field settings? (West et al., 2008). A related question, also reflected in the considerations from the 2007 IOM report and the NIH recommendations, is the complexity of many interventions conducted in the community: To what degree do the multiple components of interventions need to be separated to isolate their causal effects? In some, perhaps many, cases, the separation may be artificial—the effectiveness of each component may be dependent on the others, and the full treatment package may be of primary interest (West and Aiken, 1997). In other cases, components may need to be deleted because of ineffectiveness or iatrogenic effects or for cost-effectiveness reasons. Chapter 4 provides a fuller discussion of these conceptual issues.
A more general issue is how experts who are trained in a particular research approach can expand their capabilities for addressing issues that can be well studied only with different, less familiar approaches. For example, how do biomedical researchers, who have traditionally conducted the research on obesity, become conversant with methods for evaluating evidence that may be available from other fields and with the experts, or expertise, in implementing those methods? How do researchers in fields other than biomedicine—for example, education, community design, or economics—become involved and expert in studying problems, such as obesity, some aspects of which do not lend themselves to their typical methods? And how can obesity researchers benefit from the scholarship of colleagues who have focused on different, similarly complex public health problems, such as tobacco control?
Transdisciplinary exchange refers to researchers’ use of a “shared conceptual framework drawing together disciplinary-specific theories, concepts, and approaches to address a common problem” (Rosenfield, 1992, p. 1351). Both the medical and social sciences are challenged to expand their notion of methods and study designs that can inform the study of obesity prevention and other population health problems by considering contextual concerns (social, economic, environmental, institutional, and political factors) that influence health outcomes. For example, NIH’s National Institute on Aging has supported a network or team approach to studying the “biological, psychological and social pathways to positive and not-so-positive health” (Kessel
and Rosenfield, 2008, p. S229); the result has been enhanced quality of published research that crosses disciplinary lines. Funding agencies such as NIH have therefore been encouraged to continue to support this type of research and urge researchers to value collaboration and partnerships in a variety of fields.
Stimulated by a 2006 National Cancer Institute conference that highlighted the need for transdisciplinary research in health, Kessel and Rosenfield (2008) describe a number of factors that have both facilitated and constrained transdisciplinary science (Table 8-1). The authors identified these factors from research programs that have successfully crossed disciplinary boundaries. Reflecting the type of transdisciplinary
TABLE 8-1 Factors Facilitating and Constraining Transdisciplinary Team Science
exchange that is needed among researchers, the final section of this chapter examines alternatives to randomized experiments from the perspective of evaluation experts in the behavioral sciences, economometrics, education, public health, and statistics and explains why these alternatives are particularly important for obesity prevention (a more detailed discussion of selected study designs is offered in Appendix E).
LIMITATIONS IN THE WAY EVIDENCE IS REPORTED IN SCIENTIFIC JOURNALS
Decision makers (e.g., policy makers, professional caregivers, public health officials, and advocates) have concerns beyond scientists’ certainty of causal relationships in judging the utility and persuasiveness of evidence (see Chapter 7). All of these concerns fall to some degree under the broad rubric of generalizability (Garfield et al., 2003; Glasgow et al., 2003, 2006; Green, 2001; Green and Glasgow, 2006; Green and Lewis, 1981; Green et al., 1980; Shadish et al., 2002, Chapters 11-13). As described in Chapter 5, the generalizability of a study refers to the degree to which its results can be expected to apply equally to other individuals, settings, contexts, and time frames. The generalizability of evidence-based practices is seldom considered in individual studies or systematic reviews of the evidence, but is often decisive in decision makers’ adoption of research evidence for practical purposes such as obesity prevention. Some authors have begun to make a regular practice of noting the “applicability” of findings, with caveats when the range of populations or settings in which the evidence from trials was derived is notably limited (Shepherd and Moore, 2008). Others have proposed combining reviews of clinical and community evidence in a more “ecologically comprehensive” (multimethod, multilevel) approach to the use of evidence in such areas as tobacco and obesity control (Ockene et al., 2007). And some journals have begun to make the generalizability of a study more of an issue in considering manuscripts (e.g., Eriksen, 2006; Steckler and McLeroy, 2008), on occasion with qualifications and noted constraints (Patrick et al., 2008).
The usual manner of reporting results of obesity prevention efforts in journals often adds to the problem of incomplete evidence because useful aspects of an intervention and research related to its generalizability are not discussed. At a meeting of the editors of 13 medical and health journals, several agreed to make individual and joint efforts to devote more attention to issues of a study’s generalizability and to press for more reporting of (1) recruitment and selection procedures, participation rates, and representativeness at the levels of individuals, intervention staff, and delivery settings; (2) the level of consistency with which the intervention being tested was implemented in the study; (3) the impact on a variety of outcomes, especially those important to patients, clinicians, program cost, and adverse consequences; and (4) in follow-up reports, attrition of subjects in the study at all levels, long-term effects on outcomes, and program institutionalization, modification, or discontinuation (Green et al., 2009; supported by Cook and Campbell, 1979, pp. 74-80; Glasgow et al., 2007; Shadish et al., 2002). These moves by journal editors relevant to obesity control
hold promise for the greater relevance and usefulness of the published scientific literature for other decision makers, responding to some of their major concerns.
Specifically in childhood obesity prevention, Klesges and colleagues (2008) examined studies published between 1980 and 2004 that were controlled, long-term research trials with a behavioral target of either physical activity or healthful eating or both, together with at least one anthropometric outcome. Using review criteria for a study’s generalizability to other individuals, settings, contexts, and time frames (external validity) developed by Green and Glasgow (2006), they found that all of the 19 publications that met their selection criteria lacked full reporting on the 24 dimensions of external validity expected in an optimal paper to enable users to judge potential generalizability (see Box 8-3). Median reporting over all elements was 34.5 percent; the mode was 0 percent with a range of 0 percent to 100 percent. Only four dimensions (descriptions of the target audience and target setting, inclusion–exclusion criteria, and attrition rate) were reported in at least 90 percent of the studies. Most infrequent were reports of setting-level selection criteria and representativeness, characteristics of intervention staff, implementation of intervention content, costs, and program sustainability. These limitations of individual studies are also seen and sometimes multiplied in systematic reviews, such as meta-analyses, of whole bodies of literature. The cumulative problems of inadequate reporting of sampling, settings, and interventions have been noted, for example, in meta-analyses of the patient education literature on preventive health interventions in clinical settings (Simons-Morton et al., 1992; Tabak et al., 1991).
These findings provide strong support for the conclusion of Klesges and colleagues (2008) that the aspects of generalizability that potential users need most to see reported more thoroughly in the published evidence are the “3 Rs”: the representativeness of participants, settings, and intervention staff; the robustness of the intervention across varied populations and staffing or delivery approaches; and the replicability of study results in other places. The specific questions most decision makers will have within these broad categories relate to cost (affordability); scalability; and acceptability in particular populations, times, and settings.
Even with more complete reporting on these issues of a study’s generalizability to other populations, gaps will inevitably remain. RCTs can never fill all of the cells in a matrix of potentially relevant evidence representing all combinations of a study’s dimensions of generalizability: population × setting × intervention × time × staffing × other resources. The empty cells in such a matrix require potential users of evidence to make inferential leaps or more studied extrapolations from the existing coverage of the evidence to their own population, setting, intervention, time, staffing, and other resources. In short, users should bring to bear on their decisions their own theories or assumptions about the fit of the evidence to their situation, which will vary along each of the above dimensions.
A particular challenge for obesity prevention, as in some other areas of chronic disease control, is the multiplicity and complexity of these dimensions. For each
|
Box 8-3 Percentage of 19 Studies Reporting External Validitya Dimensions, 1980-2004
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
intervention, for example, there will be a multiplicity of points of intervention, from individuals to families, social groups, organizations, whole communities, regions, or states, each calling for different sources or types of evidence. Complexity will further confound the translation of evidence with respect to the projected time frame, even across the lifespan, to account for variations in interventions that make them age-appropriate and account for such relevant background variables as media coverage of the issue, social discourse, and changing social norms.
WAYS TO FILL THE GAPS IN THE BEST AVAILABLE EVIDENCE
This section examines the need to take advantage of natural experiments and emerging and ongoing interventions as sources of practice-based evidence to compensate for the fundamental limitations of even the best available evidence.
Natural Experiments as Sources of Practice-Based Evidence
Rather than waiting for the funding, vetting, implementation, and publication of RCTs (and other forms of research) to answer practical and locally specific questions, one alternative is to treat the myriad programs and policies being implemented across the country as natural experiments (Ramanathan et al., 2008). Applying more systematic evaluation to interventions as they emerge, even with limited experimental control over their implementation, will yield more immediate and practice-based evidence for what is possible, acceptable, and effective in real-world settings and populations. What makes such evaluation of these natural experiments even more valuable is that it produces data from settings that decision makers in other jurisdictions can view as more like their own than the settings of the typical published trials. Seeing how other state and local jurisdictions are performing in a given sphere of public concern also may activate competitive instincts that spur state and local decision makers to take action.
The Centers for Disease Control and Prevention’s (CDC’s) Office on Smoking and Health used this strategy of making comparisons across jurisdictions when California and Massachusetts raised cigarette taxes and launched tax-based, comprehensive statewide tobacco control programs (see Chapter 4). Noting the accelerated rates of reduced tobacco consumption in those states compared with the other 48 states, CDC collaborated with the two states to evaluate these natural experiments and analyze their components (e.g., mass media, school programs) and the associated costs. CDC then offered the per capita costs of each component as a recommended basis for budgeting for other states wishing to emulate these successful programs (CDC, 1999). Many of the states used these budgetary allocations, at least temporarily before the tobacco settlement funds from the tobacco industry were diverted to general revenue or other purposes.
“Evaluability Assessment” of Emerging Innovations
As experience accumulates with local initiatives and innovative practices that have not yet been subjected to systematic evaluation, that experience can be disseminated to the larger community of public health officials. Funding should be directed at institutionalizing methods and resources that support a culture of local experimentation, evaluation, and continuous quality assessment and sharing. One such method that serves the broader community of decision makers is called “evaluability assessment” (Leviton et al., 2010a) or the systematic screening and assessment (Leviton et al., 2010b). This method was originally developed to assess whether a program had been sufficiently implemented before an outcome evaluation was undertaken (Wholey, 1977). It has been defined more recently as assessing the rationale, design, implementation, and characteristics of a program before a full-scale evaluation is undertaken to be sure the evaluation will be feasible and useful (Leviton et al., 1998; Wholey, 1994).
Recently, a Robert Wood Johnson Foundation/CDC partnership conducted a major evaluability assessment that involved taking an inventory of purported innovative programs and policies in childhood obesity control, assessing their potential for evaluation, and providing resources to assist in their evaluation (RWJF, 2006, 2009). The partners believed an evaluability assessment approach to the evidence in childhood obesity control was necessary because so many formally untested ideas, policies, and strategies were emerging across the country. Decision makers had taken seriously the public health warning signals of the obesity epidemic, but found little in the scientific literature on tested policies and methods for addressing the problem in their communities. They had no choice but to innovate, and the Foundation and CDC, also facing the paucity of evidence, had no choice but to seize upon the strands of practice-based evidence these innovations might offer. They conducted a national survey of experts and observers in the field, inviting nominations of innovative policies and programs. From the pool of hundreds, with the aid of a national panel of experts, they systematically assessed the characteristics of each that would qualify it as promising in its reach, effectiveness, adoption potential, and sustainability. They then conducted site visits to those deemed promising and from these site visits produced logic models of the mediating variables addressed by each and the evaluation capacity of the staff. From these assessments, they selected the interventions that were most worthy of formal evaluation.
This process of a centralized inventory of and evaluation assistance to the most promising interventions warrants particular attention when the urgency of action is great and the evidence for specific actions is thin. Local program staff will often need assistance with design, measurement, conduct, and analysis issues when carrying out an evaluation (Green, 2007). Without such assistance, many evaluations might respond to some local needs but would not provide the practice-based evidence of greatest use to others. The main lesson from experience with evaluability assessment is the advantage of the bottom-up, practice-driven approach over the top-down, science-
driven process for generating evidence for problem solving. Taking full advantage of this lesson will require building an infrastructure of surveillance capacity and tools for self-monitoring of the implementation and effects of interventions.
Continuous Quality Assessment of Ongoing Programs
Once interventions have been established as evidence-based (in the larger sense suggested in this chapter of a combination of evidence, theory, professional experience, and local participation), continuous assessment of the quality of implementation is necessary to ensure that the interventions do not slip into a pattern of compromised effort and attenuated resources and that they build on experience with changing circumstances, clientele, and personnel. Methods for continuous quality assessment have been borrowed from industry (e.g., Edwards and Schwarzenberg, 2009) and adapted to public health program assessment to support the development of practice-based evidence in real time with real programs (Green, 2007; Katz, 2009; Kottke et al., 2008).
Continuous quality assessments of individual interventions can be pooled and analyzed for their implications for the adjustment of programs and policies to changing circumstances. These findings, in turn, can be pooled and analyzed at the state and national levels to derive guidelines, manuals, and interactive online guides for a combination of best practices and best processes. What meta-analyses and other systematic reviews may be telling us, with their inconsistent results or variability of findings over time, is that there is nothing inherently superior about most intervention practices. Rather, social, epidemiological, behavioral, educational, environmental, and administrative diagnoses lead to the appropriate application of an intervention to suit a particular purpose, population, time, setting, and other contextual variables. Such was the conclusion of a comparative meta-analysis of patient education and counseling interventions (Mullen et al., 1985).
Similarly, in clinical practice, where the application of evidence-based medicine (EBM) is generally expected, “Physicians reported that when making clinical decisions, they more often rely on clinical experience, the opinions of colleagues, and EBM summarizing electronic clinical resources rather than refer directly to EBM literature” (Hay et al., 2008, p. 707). These alternatives to the direct and simple translation of EBM guidelines, as in other fields of practice, should not be surprising in the face of the limited representation of types of patients or populations and circumstances in EBM studies. The challenge, then, is how to use the experience and results from these combinations of explicit scientific evidence and tacit experiential evidence to enrich the evidence pool. Hay and colleagues (2008) suggest methods of “evidence farming” to systematize the collection of data from clinical experience to feed back into the evidence–practice–evidence cycle.
ALTERNATIVES TO RANDOMIZED EXPERIMENTS
As discussed in previous chapters, randomized experiments are generally viewed as the gold standard for research designs. A prototype is a RCT of a drug treatment compared with a placebo or other drug. In a prevention context, an RCT would be a study in a community or broader setting in which individuals or groups would be assigned by the researchers to experience or be exposed to different interventions. When a randomized experiment is properly implemented and its assumptions can be met, it produces results that are unrivaled in the certainty with which they support causal inferences in the specific research context in which the trial was conducted. According to Shadish and colleagues (2002), the advantages of RCTs are that they protect against threats to the level of certainty of the relationship between an intervention and the observed outcomes due to history, maturation, selection, testing and instrumentation biases, ambiguous temporal precedence, and the tendency of measurement to regress to the mean. As discussed here, however, the RCT has several limitations, some inherent and some associated with typical implementations, that can decrease its value as a tool for informing decision makers addressing complex public health problems. (See also Mercer and colleagues [2007], who summarize discussions at a symposium of experts that weighed the strengths, limitations, and trade-offs of alternative designs for studying the effectiveness and translation of complex, multilevel health interventions.)
RCTs require that a pool of subjects be identified who are willing to be randomized and that providers be available who are willing to deliver the identical treatment or control intervention to each subject according to the randomization protocol. Randomization has typically been conducted at the level of individual participants. It may also be conducted with interventions being delivered to groups or communities (termed “cluster randomization”; see Donner and Klar, 2000; Kriemler et al., 2010; Murray, 1998). Or it may be conducted at multiple sites, often in different geographic regions, using parallel RCTs in which individual participants or groups are assigned to the treatment or control intervention at each site, with the results being combined (see Raudenbush and Liu, 2000). Cluster randomization designs offer new possibilities to study new types of interventions, potentially with different interventions occurring at multiple levels (e.g., individual, group, small community). Multisite designs offer possibilities to study the effects of interventions with more diverse populations, settings, and even sets of treatment providers. At the same time, cluster and multisite randomized trials raise new challenges for design and implementation, as well as statistical analysis and interpretation (e.g., Varnell et al., 2004).
With all of these types of randomized trials, moreover, practical problems commonly arise when structural or policy interventions are being studied (Bonell et al., 2006). Subjects may not want to be randomized; randomization may not be accepted, or may not be ethical or practical in the research context; or only atypical participants may be willing to be randomized.
Consider, for example, the difficulty of using an RCT design to study the effects on health of secondhand tobacco smoke or the removal of physical education classes from schools. Both of these exposures are unlikely to be within the control of a researcher. In other cases, only atypical participants would be willing to participate. An example is an RCT of a faith-based or spiritually oriented wellness group compared with a non-faith-based group because people cannot be assigned to be or not be spiritually oriented. Highly religious participants might refuse to be assigned to a non-faith-based program, while nonreligious participants might be unable to participate sincerely in a faith-based program. Or the faith-based treatment providers might believe that all people desiring the intervention should receive it. A cardiovascular disease prevention study among African American faith-based organizations in Baltimore, Maryland, encountered both of these challenges in a randomized trial (Yanek et al., 2001). Many pastors of potentially participating churches were uncomfortable with randomization, wanting to know their intervention assignment before agreeing to participate. In addition, an intended comparison between a spiritually oriented and standard version of the program could not be implemented because those in the standard condition spontaneously incorporated spirituality. These issues decrease the likelihood that an RCT can be implemented successfully and potentially decrease the likelihood that its results can ultimately be generalized to important policy contexts (Green and Glasgow, 2006; Shadish and Cook, 2009; Weisz et al., 1992).
In addition, the need to identify a pool of subjects willing to be randomized subtley privileges certain types of interventions. RCTs involving interventions designed to influence individuals or small groups (cluster randomization) are far easier to implement than those involving larger units (e.g., cities, states), given political and cost issues and methodological concerns about both the comparability of units and the ability to study a sufficient number of units to achieve adequate statistical power. That is, when aggregate units rather than individuals are randomly assigned, sample size and statistical power are based on the number of units, even if measurements are taken from individuals within each unit.
Finally, given the length of time required to plan and carry out an RCT, a trial may yield results long after the time frame in which the information is needed by decision makers. Or the results may no longer be as relevant in the context in which they would be applied when the trial has been completed. In the Women’s Health Initiative Dietary Modification Trial, for example, the nature of the low-fat dietary intervention did not address important issues, related to the types of fat, that were identified while the trial was in progress and could have influenced the results (Anderson and Appel, 2006).
The above limitations can result in RCTs having less impact in research on public policy relative to other, nonrandomized designs. Consider the changes in policy that led to what is viewed as one of the major recent public health triumphs—the reduction of the amount and prevalence of tobacco smoking in the United States. None of the key large-scale interventions that were utilized—a ban on cigarette advertising,
increases in the cost of tobacco products, and bans on indoor smoking in public places—were supported by direct evidence from an RCT.
Perspectives on Causal Inference
Because RCTs frequently are not possible for multicomponent interventions that deal with determinants at multiple levels (e.g., individual, family, health plan), evidence should be sought (or generated) from other designs, and some of the advantages of RCTs must be sacrificed. For example, randomized encouragement designs, in which individuals are randomized to be encouraged to take up an intervention, may allow for recruitment of a more representative sample since participants are involved in the choice of their treatment, but the level of certainty may be reduced. Cluster randomization trials may avoid the difficulties of recruiting individuals in complex settings (e.g., schoolrooms, workplaces, medical clinics, or even whole communities) while retaining randomized assignment of an intervention, but the cost or feasibility of identifying a sufficient number of groups can be prohibitive. Nonrandomized designs, with or without controls (quasi-experimental designs), may be the only feasible approach in situations where randomization is difficult or impossible. These include pre–post designs, interrupted time series, and regression discontinuity designs (elaborated in Appendix E). Such designs, when implemented well, can produce valuable evidence for effectiveness but require trade-offs with the level of certainty of causality and control of bias.
Two perspectives provide useful, complementary approaches on which researchers can draw to strengthen causal inferences, including approaches that do not involve experimentation. In the behavioral sciences, Campbell and colleagues (Campbell, 1957; Campbell and Stanley, 1966; Cook and Campbell, 1979; Shadish and Cook, 2009; Shadish et al., 2002) have developed a practical theory providing guidelines for ruling out confounders that may yield alternative explanations of research results. In the field of statistics, Rubin and colleagues (Holland, 1986; Rubin, 1974, 1978, 2005, 2008) have developed the potential outcomes perspective, which provides a deductive, mathematical approach based on making explicit, ideally verifiable assumptions. Shadish (2010), West and colleagues (2000), and West and Thoemmes (2010) offer full discussions and comparisons of these two perspectives.
Campbell’s Perspective
Campbell and colleagues have considered the full range of experimental, quasi-experimental, and pre-experimental designs used by researchers in the behavioral sciences. They have identified an extensive list of threats to validity, which represent an accumulation of the various criticisms that have been made of research designs in the field of social sciences and are applicable to other fields as well (Campbell, 1988). Although Cook and Campbell (1979) describe four general types of threats to validity, the focus here is on potential confounders that undermine the level of certainty of
a causal link between an intervention and the observed outcomes (internal validity) and later in the chapter is on threats that may limit the generalizability of the results (external validity). With respect to the level of certainty of causal inference, Campbell and colleagues emphasize that researchers need consider only threats to validity that are plausible given their specific design and the prior empirical research in their particular research context (Campbell, 1957; Shadish et al., 2002). Table 8-2 presents common threats to the level of certainty of causal inference associated with several major quantitative designs.
After researchers have identified the plausible threats to the level of certainty in their research context, several approaches may be taken to rule out each identified threat. First, features may be added to the design to prevent the threat from occurring. For example, a key threat in many designs is participant attrition. Shadish and colleagues (2002) describe the importance of retaining participants in a study and point to extensive protocols developed to maximize retention (see Ribisl et al., 1996). Second, certain elements may be added to the basic design. Appendix E presents several examples in which elements are added to a variety of basic designs to address those specific threats to the level of certainty that are plausible in the context of the design and prior research in the area. Shadish and Cook (1999) offer an extensive list of elements that can be included in a wide variety of research designs (see Box 8-4).
To illustrate, in the pre-experimental design with only a pretest and posttest, discussed in Appendix E, one plausible threat to a study’s level of certainty is history: another event in addition to the treatment might have occurred between the pre- and posttests. Consider a year-long school-based intervention program that demonstrates a decrease in teenagers’ smoking from the beginning to the end of the school year. Suppose that during the same year and unrelated to the program, the community also removed all cigarette machines that allowed children to purchase cigarettes easily. Adding the design element of replicating the study at different times in different participant cohorts would help rule out the possibility that the removal of cigarette machines rather than the school-based program was responsible for the results. If the school-based program were effective, reductions in smoking would have occurred in each replication. In contrast, removal of the cigarette machines would be expected to lead to a decrease only in the first replication, a different expected pattern of results. Matching the pattern of results to that predicted by the theory of the intervention versus that predicted by the plausible confounders provides a powerful method of ruling out threats to a study’s level of certainty.
Campbell’s approach strongly prefers such design strategies over alternative statistical adjustment strategies to deal with threats to the level of certainty. It also emphasizes strategies for increasing researchers’ understanding of the particular conceptual aspects of the treatment that are responsible for the causal effects under the rubric of the construct validity of the independent variable. Shadish and colleagues (2002) present a general discussion of these issues, and West and Aiken (1997) and Collins and colleagues (2009) discuss experimental designs for studying the effective-
TABLE 8-2 Key Assumptions/Threats to Internal Validitya and Example Remedies for Randomized Controlled Trials and Alternatives
ness of individual components in multiple-component designs. West and Aiken (1997) and MacKinnon (2008) also consider the statistical method of mediational analysis that permits researchers to probe these issues, although in a less definitive manner.
Rubin’s Perspective
Rubin’s potential outcomes model takes a formal mathematical/statistical approach to causal inference. Building on earlier work by Splawa-Neyman (1990), it emphasizes precise definition of the desired causal effect and specification of explicit, ideally verifiable assumptions that are sufficient to draw causal inferences for each research design. Rubin defines a causal effect as the difference between the outcomes for a single unit (e.g., person, community) given two different well-defined treatments at the identical time and in the same context. This definition represents a conceptually useful ideal that cannot be realized in practice.
Holland (1986) notes that three approaches, each with its own assumptions, can be taken to approximate this ideal. First, a within-subjects design can be used in which the two treatments (e.g., intervention, control) are given to the same unit. This design assumes (1) temporal stability in which the same outcome will be observed regardless of when the treatment is delivered and (2) causal transience in which the administration of the first treatment has no effect on the outcome of the second treatment. These assumptions will frequently be violated in research on obesity. Second, homogeneous units can be selected or created so that each unit can be expected to have the same response to the treatment. This strategy is commonly used in engineering applications, but raises concern about the comparability of units in human research—even monozygotic twins raised in similar environments can differ in important ways in some research contexts. The matching procedures used in the potential outcomes approach discussed below rely on this approach; they assume that the units can indeed be made homogeneous on all potentially important background variables. Third, units can be randomly assigned to treatment and control conditions. This strategy creates groups that are, on average, equal on all possible background variables at pretest so that the difference between the means of the two groups now represents the average causal effect. This strategy makes several assumptions (see Table 8-2; Holland, 1986; West and Thoemmes, 2010), including full treatment adherence, independence of units, no attrition from posttest measurement, and the nondependence of the response of a unit to a treatment on the treatment received by other units (or SUTVA, the stable unit treatment value assumption). The SUTVA highlights the challenges in community research of considering possible dependence between units and possible variation in each treatment across sites (Rubin, 2010). Well-defined treatment (and no-treatment) conditions that are implemented identically across units are a key feature of strong causal inference in Rubin’s perspective. Hernan and Traubman (2008) discuss the importance of this assumption in the context of obesity research. Beyond requiring this set of foundational assumptions, randomization has another subtle effect: it shifts the focus from a causal effect defined at the level of the individual to an
|
Box 8-4 Design Elements Used in Constructing Quasi-Experiments Assignment (control of assignment strategies to increase group comparability)
Measurement (use of measures to learn whether threats to causal inference actually operate)
|
average causal effect that characterizes the difference between the treatment and control groups. The ability to make statements about individual causal effects, important in many clinical and health contexts, is diminished without additional assumptions being made (e.g., the causal effect is constant for all individuals).
A key idea in Rubin’s perspective is that of possible outcomes. The outcome of a single unit (participant) receiving a treatment is compared with the outcome that would have occurred if the same unit had received the alternative treatment. This idea has proven to be a remarkably generative way of thinking about how to obtain precise estimates of causal effects. It focuses the researcher on the precise nature of the comparison that needs to be made and clearly delineates the participants for whom the comparison is appropriate. It provides a basis for elegant solutions to such problems as treatment nonadherence and appropriate matching in nonrandomized studies (West and Thoemmes, 2010).
Comparison groups (selecting comparisons that are “less nonequivalent” or that bracket the treatment group at the pretest[s])
Treatment (manipulations of the treatment to demonstrate that treatment variability affects outcome variability)
SOURCE: Reprinted, with permission. Shadish and Cook, 1999. Copyright © 1999 by the Institute of Mathematical Statistics. |
Other Perspectives on Causality
Other perspectives on causal inference exist. In economics, Granger (1988; Granger and Newbold, 1977; see also Bollen, 1989, in sociology and Kenny, 1979, in psychology) argues that three conditions are necessary to infer that one variable X causes changes in another variable Y:
-
Association—The two variables X and Y must be associated (nonlinear association is permitted).
-
Temporal precedence—X must precede Y in time.
-
Nonspuriousness—X contains unique information about Y that is not available elsewhere. Otherwise stated, with all other causes partialed out, X still predicts Y.
This perspective can be particularly useful for thinking about causal inference when X cannot be manipulated (e.g., age), but is typically less useful for studying the effects of interventions. The primary challenge is how one can establish nonspuriousness, and Granger’s perspective provides few guidelines in this regard relative to the Campbell and Rubin perspectives.
A second class of perspectives, founded in philosophical and computer science, takes a graph theoretic approach. In this approach, a complex model of the process is specified and is compared with data. If the model and its underlying assumptions are true, the approach can discern whether causal inferences can be supported. Within this approach, a computer program known as Tetrad (Spirtes et al., 2000) can identify any other models involving the set of variables in the system that provide an equally good account of the data, if they exist. In separate work, Pearl (2009) has also utilized the graph theoretic approach, developing a mathematical calculus for problems of causal inference. This approach offers great promise as a source of understanding of causal effects in complex systems in the future. Compared with the Campbell and Rubin approaches, however, to date it has provided little practical guidance for researchers attempting to strengthen the inferences about the effectiveness of interventions that can be drawn from evaluation studies.
How Well Do Alternative Designs Work?
Early attempts to compare the magnitude of the causal effects estimated from RCTs and nonrandomized designs used one of two approaches. First, the results from an RCT and a separate observational study investigating the same question were compared. For example, LaLonde (1986) found that an RCT and nonrandomized evaluations of the effectiveness of job training programs led to completely different results. Second, the results of interventions in a research area evaluated using randomized and nonrandomized designs were compared in a meta-analytic review. For example, Sacks and colleagues (1983) compared results of RCTs of medical interventions with results of nonrandomized designs using historical controls, finding that the nonrandomized designs overestimated the effectiveness of the interventions. A number of studies showing the noncomparability of results of RCTs and nonrandomized designs exist, although many of the larger meta-analyses in medicine (Ioannidis et al., 2001) and the behavioral sciences (Lipsey and Wilson, 1993) find no evidence of consistent bias.
More recently, Cook and colleagues (2008) compared the small set of randomized and nonrandomized studies that shared the same treatment group and the same measurement of the outcome variable. All cases in which an RCT was compared with a regression discontinuity or interrupted time series study design (see Appendix E for discussion of these study designs) showed no differences in effect size. Observational studies produced more variable results, but the results did not differ from those of an RCT given that (1) a control group of similar participants was employed or (2) the mechanism for selection into treatment and control groups was known. Hernán
and colleagues (2008) considered the disparate results of an RCT (Women’s Health Initiative) and an observational study (Nurses’ Health Study) of the effectiveness of postmenopausal hormone replacement therapy. When the observational study was analyzed using propensity score methods with participants who met the same eligibility criteria and the same intention-to-treat causal effect was estimated, discrepancies were minimal. Finally, Shadish and colleagues (2008) randomly assigned student participants to an RCT or observational study (self-selection) of the effects of math or vocabulary training. They found little difference in the estimates of causal effects after adjusting for an extensive set of baseline covariates in the observational study.
The results of the small number of focused comparisons of randomized and nonrandomized designs to date are encouraging. Additional research comparing treatment effect estimates for randomized and nonrandomized designs using similar treatments, populations of participants, and effect size estimates is needed to determine the generality of this finding.
REFERENCES
Anderson, C. A., and L. J. Appel. 2006. Dietary modification and CVD prevention: A matter of fat. Journal of the American Medical Association 295(6):693-695.
Bollen, K. A. 1989. Structural equations with latent variables. New York: John Wiley and Sons, Inc.
Bonell, C., J. Hargreaves, V. Strange, P. Pronyk, and J. Porter. 2006. Should structural interventions be evaluated using RCTs? The case of HIV prevention. Social Science and Medicine 63(5):1135-1142.
Campbell, D. T. 1957. Factors relevant to the validity of experiments in social settings. Psychological Bulletin 54(4):297-312.
Campbell, D. T. 1988. Can we be scientific in applied social science? In Methodology and epistemology for social science: Selected papers of Donald T. Campbell, edited by E. S. Overman. Chicago, IL: University of Chicago Press. Pp. 315-334.
Campbell, D. T., and J. C. Stanley. 1966. Experimental and quasi-experimental designs for research. Chicago, IL: Rand McNally.
CBO (Congressional Budget Office). 2008. Key issues in analyzing major health insurance proposals. Publication No. 3102. Washington, DC: U.S. Congress.
CDC (Centers for Disease Control and Prevention). 1999. Best practices for comprehensive tobacco control programs—April 1999. Atlanta, GA: U.S. Department of Health and Human Services, National Center for Chronic Disease Prevention and Health Promotion, Office on Smoking and Health.
Collins, L. M., J. J. Dziak, and R. Li. 2009. Design of experiments with multiple independent variables: A resource management perspective on complete and reduced factorial designs. Psychological Methods 14(3):202-224.
Cook, T. D., and D. T. Campbell. 1979. Quasi-experimentation: Design and analysis issues for field settings. Chicago, IL: Rand McNally College Publishing Co.
Cook, T. D., W. R. Shadish, and V. C. Wong. 2008. Three conditions under which experiments and observational studies produce comparable causal estimates: New findings from within-study comparisons. Journal of Policy Analysis and Management 27(4):724-750.
Donner, A., and N. Klar. 2000. Design and analysis of cluster randomization trials in health research. London: Arnold.
Edwards, N. M., and S. J. Schwarzenberg. 2009. Designing and implementing an effective pediatric weight management program. Reviews in Endocrine and Metabolic Disorders 10(3):197-203.
Eriksen, M. 2006. Are there public health lessons that can be used to help prevent childhood obesity? Health Education Research 21(6):753-754.
Garfield, S. A., S. Malozowski, M. H. Chin, K. M. Narayan, R. E. Glasgow, L. W. Green, R. G. Hiss, and H. M. Krumholz. 2003. Considerations for diabetes translational research in real-world settings. Diabetes Care 26(9):2670-2674.
Glasgow, R. E., E. Lichtenstein, and A. C. Marcus. 2003. Why don’t we see more translation of health promotion research to practice? Rethinking the efficacy-to-effectiveness transition. American Journal of Public Health 93(8):1261-1267.
Glasgow, R., L. Green, L. Klesges, D. Abrams, E. Fisher, M. Goldstein, L. Hayman, J. Ockene, and C. Olrleans. 2006. External validity: We need to do more. Annals of Behavioral Medicine 31(2):105-108.
Glasgow, R. E., L. W. Green, and A. Ammerman. 2007. A focus on external validity. Evaluation and the Health Professions 30(2):115-117.
Granger, C. W. J. 1988. Some recent development in a concept of causality. Journal of Econometrics 39(1-2):199-211.
Granger, C. W. J., and P. Newbold. 1977. Forecasting economic time series. New York: Academic Press.
Green, L. W. 2001. From research to “best practices” in other settings and populations. American Journal of Health Behavior 25(3):165-178.
Green, L. W. 2007. The Prevention Research Centers as models of practice-based evidence: Two decades on. American Journal of Preventive Medicine 33(1, Supplement):S6-S8.
Green, L. W., and R. E. Glasgow. 2006. Evaluating the relevance, generalization, and applicability of research: Issues in external validation and translation methodology. Evaluation & the Health Professions 29(1):126-153.
Green, L. W., and F. M. Lewis. 1981. Issues in relating evaluation to theory, policy, and practice in continuing education and health education. Mobius 81(1):46-58.
Green, L. W., F. M. Lewis, and D. M. Levine. 1980. Balancing statistical data and clinician judgments in the diagnosis of patient educational needs. Journal of Community Health 6(2):79-91.
Green, L. W., R. E. Glasgow, D. Atkins, and K. Stange. 2009. Making evidence from research more relevant, useful, and actionable in policy, program planning, and practice: Slips “twixt cup and lip”. American Journal of Preventive Medicine 37(6, Supplement 1):S187-S191.
Hay, M. C., T. S. Weisner, S. Subramanian, N. Duan, E. J. Niedzinski, and R. L. Kravitz. 2008. Harnessing experience: Exploring the gap between evidence-based medicine and clinical practice. Journal of Evaluation in Clinical Practice 14(5):707-713.
Hernan, M. A., and S. L. Taubman. 2008. Does obesity shorten life? The importance of well-defined interventions to answer causal questions. International Journal of Obesity (London) 32(Supplement 3):S8-S14.
Hernan, M. A., A. Alonso, R. Logan, F. Grodstein, K. B. Michels, W. C. Willett, J. E. Manson, and J. M. Robins. 2008. Observational studies analyzed like randomized experiments: An application to postmenopausal hormone therapy and coronary heart disease. Epidemiology 19(6):766-779.
Holland, P. W. 1986. Statistics and causal inference (with discussion). Journal of the American Statistical Association 81(396):945-960.
Ioannidis, J. P. A., A. B. Haidich, M. Pappa, N. Pantazis, S. I. Kokori, M. G. Tektonidou, D. G. Contopoulos-Ioannidis, and J. Lau. 2001. Comparison of evidence of treatment effects in randomized and nonrandomized studies. Journal of the American Medical Association 286(7):821-830.
IOM (Institute of Medicine). 2007. Progress in preventing childhood obesity: How do we measure up? Edited by J. Koplan, C. T. Liverman, V. I. Kraak, and S. L. Wisham. Washington, DC: The National Academies Press.
Katz, R. J. 2009. Communities and academia working together: Report of the Association of Schools of Public Health Prevention Research Centers Blue Ribbon Panel. Public Health Reports 124(2):334-338.
Kenny, D. A. 1979. Correlation and causality. New York: John Wiley Interscience.
Kessel, F., and P. L. Rosenfield. 2003. Fostering interdisciplinary innovation: The way forward. In Expanding the boundaries of health and social science: Case studies of interdisciplinary innovation, edited by F. Kessel, P. L. Rosenfield and N. B. Anderson. New York: Oxford University Press, Inc. p. 401.
Kessel, F., and P. L. Rosenfield. 2008. Toward transdisciplinary research: Historical and contemporary perspectives. American Journal of Preventive Medicine 35(2 Supplement): S225-S234.
Klesges, L. M., D. A. Dzewaltowski, and R. E. Glasgow. 2008. Review of external validity reporting in childhood obesity prevention research. American Journal of Preventive Medicine 34(3):216-223.
Kottke, T. E., L. I. Solberg, A. F. Nelson, D. W. Belcher, W. Caplan, L. W. Green, E. Lydick, D. J. Magid, S. J. Rolnick, and S. H. Woolf. 2008. Optimizing practice through research: A new perspective to solve an old problem. Annals of Family Medicine 6(5):459-462.
Kriemler, S., L. Zahner, C. Schindler, U. Meyer, T. Hartmann, H. Hebestreit, H. P. Brunner-La Rocca, W. van Mechelen, and J. J. Puder. 2010. Effect of school based physical activity programme (KISS) on fitness and adiposity in primary schoolchildren: Cluster randomised controlled trial. British Medical Journal 340:c785.
LaLonde, R. J. 1986. Evaluating the econometric evaluations of training programs with experimental data. American Economic Review 76(4):604-620.
Leviton, L. 2001. External validity. In International encyclopedia of the behavioral and social sciences. Vol. 8, edited by N. J. Smelser and P. B. Baltes. Oxford: Elsevier. Pp. 5195-5200.
Leviton, L. C., C. B. Collins, B. L. Liard, and P. P. Kratt. 1998. Teaching evaluation using evaluability assessment. Evaluation 4(4):389-409.
Leviton, L., L. Kettel Khan, D. Rog, N. Dawkins, and D. Cotton. 2010a. Exploratory evaluation of public health policies, programs, and practices. Annual Review of Public Health 31:213-233.
Leviton, L. C., L. Kettel Khan, and N. Dawkins (editors). 2010b. The systematic screening and assessment method: Finding innovations worth evaluating. New directions in evaluation 2010(125):1-118.
Lipsey, M. W., and D. B. Wilson. 1993. The efficacy of psychological, educational, and behavioral treatment: Confirmation from meta-analysis. American Psychologist 48(12):1181-1209.
MacKinnon, D. P. 2008. An introduction to statistical meditation analysis. New York: Lawrence Erlbaum Associates.
Mercer, S. L., B. J. DeVinney, L. J. Fine, L. W. Green, and D. Dougherty. 2007. Study designs for effectiveness and translation research: Identifying trade-offs. American Journal of Preventive Medicine 33(2):139-154.
Mullen, P. D., L. W. Green, and G. S. Persinger. 1985. Clinical trials of patient education for chronic conditions: A comparative meta-analysis of intervention types. Preventive Medicine 14(6):753-781.
Murray, D. M. 1998. Design and analysis of group randomized trials. New York: Oxford.
Ockene, J. K., E. A. Edgerton, S. M. Teutsch, L. N. Marion, T. Miller, J. L. Genevro, C. J. Loveland-Cherry, J. E. Fielding, and P. A. Briss. 2007. Integrating evidence-based clinical and community strategies to improve health. American Journal of Preventive Medicine 32(3):244-252.
Patrick, K., F. D. Scutchfield, and S. H. Woolf. 2008. External validity reporting in prevention research. American Journal of Preventive Medicine 34(3):260-262.
Pearl, J. 2009. Causality: Models, reasoning, and interference. 2nd ed. New York: Cambridge.
Pratt, C. A., J. Stevens, and S. Daniels. 2008. Childhood obesity prevention and treatment: Recommendations for future research. American Journal of Preventive Medicine 35(3):249-252.
Ramanathan, S., K. R. Allison, G. Faulkner, and J. J. Dwyer. 2008. Challenges in assessing the implementation and effectiveness of physical activity and nutrition policy interventions as natural experiments. Health Promotion International 23(3):290-297.
Raudenbush, S. W., and X. Liu. 2000. Statistical power and optimal design for multisite randomized trials. Psychological Methods 5(2):199-213.
Ribisl, K. M., M. A. Walton, C. T. Mowbray, D. A. Luke, W. S. Davidson II, and B. J. Bootsmiller. 1996. Minimizing participant attrition in panel studies through the use of effective retention and tracking strategies: Review and recommendations. Evaluation and Program Planning 19(1):1-25.
Rosenfield, P. L. 1992. The potential of transdisciplinary research for sustaining and extending linkages between the health and social sciences. Social Science and Medicine 35(11):1343-1357.
Rubin, D. B. 1974. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology 66(5):688-701.
Rubin, D. B. 1978. Bayesian inference for causal effects: The role of randomization. Annals of Statistics 6(1):34-58.
Rubin, D. B. 2005. Causal inference using potential outcomes: Design, modeling, decisions. Journal of the American Statistical Association 100(469):322-331.
Rubin, D. B. 2008. Statistical inference for causal effects, with emphasis on applications in epidemiology and medical statistics. In Handbook of statistics 27: Epidemiology and medi-
cal statistics, edited by C. R. Rao, J. P. Miller and D. C. Rao. Amsterdam, the Netherlands: Elsevier. Pp. 28-63.
Rubin, D. B. 2010. Reflections stimulated by the comments of Shadish (2010) and West and Thoemmes (2010). Psychological Methods 15(1):38-46.
RWJF (Robert Wood Johnson Foundation). 2006. Early assessment of environmental interventions to prevent childhood obesity. meeting summary, January 19–20, 2006. http://www. rwjf.org/files/publications/other/EA%20Report%200612.pdf (accessed January 4, 2010).
RWJF. 2009. Early assessment of programs and policies on childhood obesity. http://www.rwjf. org/pr/product.jsp?id=37330 (accessed January 4, 2010).
Sacks, H. S., T. C. Chalmers, and H. Smith Jr. 1983. Sensitivity and specificity of clinical trials: Randomized v historical controls. Archives of Internal Medicine 143(4):753-755.
Shadish, W. R. 2010. Campbell and Rubin: A primer and comparison of their approaches to causal inference in field settings. Psychological Methods 15(1):3-17.
Shadish, W. R., and T. D. Cook. 1999. Design rules: More steps toward a complete theory of quasi-experimentation. Statistical Science 14:294-300.
Shadish, W. R., and T. D. Cook. 2009. The renaissance of field experimentation in evaluating interventions. Annual Review of Psychology 60:607-629.
Shadish, W. R., T. D. Cook, and D. T. Campbell. 2002. Experimental and quasi-experimental designs for generalized causal inference. Boston: Houghton Mifflin.
Shadish, W. R., M. H. Clark, and P. M. Streiner. 2008. Can nonrandomized experiments yield accurate answers? A randomized experiment comparing random and nonrandom assignments. Journal of the American Statistical Association 103:1334-1356.
Shepherd, W. L., and A. Moore. 2008. Task force recommendations: Application in the “real world” of community intervention. American Journal of Preventive Medicine 35(1, Supplement):S1-S2.
Simons-Morton, D. G., P. D. Mullen, D. A. Mains, E. R. Tabak, and L. W. Green. 1992. Characteristics of controlled studies of patient education and counseling for preventive health behaviors. Patient Education and Counseling 19(2):175-204.
Spirtes, P., C. Glymour, and R. Scheines. 2000. Causation, prediction, and search. 2nd ed. New York: MIT Press.
Splawa-Neyman, J., D. M. Dabrowska, and T. P. Speed. 1990. On the application of probability theory to agricultural experiments. Essay on principles. Section 9. Statistical Science 5(4):465-472.
Steckler, A., and K. R. McLeroy. 2008. The importance of external validity. American Journal of Public Health 98(1):9-10.
Tabak, E. R., P. D. Mullen, D. G. Simons-Morton, L. W. Green, D. A. Mains, S. EilatGreenberg, R. F. Frankowski, and M. C. Glenday. 1991. Definition and yield of inclusion criteria for a meta-analysis of patient education studies in clinical preventive services. Evaluation and the Health Professions 14(4):388-411.
Varnell, S. P., D. M. Murray, J. B. Janega, and J. L. Blitstein. 2004. Design and analysis of group-randomized trials: A review of recent practices. American Journal of Public Health 94(3):393-399.
Weisz, J. R., B. Weiss, and G. R. Donenberg. 1992. The lab versus the clinic: Effects of child and adolescent psychotherapy. American Psychologist 47(12):1578-1585.
West, S. G., and L. S. Aiken. 1997. Towards understanding individual effects in multiple component prevention programs: Design and analysis strategies. In Recent advances in prevention methodology: Alcohol and substance abuse research, edited by K. Bryant, M. Windle, and S. G. West. Washington, DC: American Psychological Association.
West, S. G., and F. Thoemmes. 2010. Campbell’s and Rubin’s perspectives on causal inference. Psychological Methods 15(1):18-37.
West, S., J. Biesanz, and S. Pitts. 2000. Causal inference and generalization in field settings: Experimental and quasi-experimental designs. In Handbook of research methods in social and personality psychology, edited by H. Reis and C. Judd. Cambridge: University Press. Pp. 40-84.
West, S., J. Duan, W. Pequegnat, P. Gaist, D. Des Jarlais, D. Holtgrave, J. Szapocznik, M. Fishbein, B. Rapkin, M. Clatts, and P. Mullen. 2008. Alternatives to the randomized controlled trial. American Journal of Public Health 98(8):1359-1366.
Wholey, J. 1977. Evaluability assessment. In Evaluation research methods: A basic guide, edited by L. Rutman. Beverly Hills, CA: Sage. Pp. 41-56.
Wholey, J. 1994. Assessing the feasibility and likely usefulness of evaluation. In The handbook of practical program evaluation, edited by J. S. Wholey, H. P. Hatry, and K. E. Newcomer. San Francisco, CA: Jossey-Bass.
Yanek, L. R., D. M. Becker, T. F. Moy, J. Gittelsohn, and D. M. Koffman. 2001. Project joy: Faith-based cardiovascular health promotion for African American women. Public Health Reports 116(Supplement 1):68-81.




























