4
Case Studies
The discussions in Chapter 3 above are general in nature, comprehensively addressing the building blocks of a full ISI forecast system. To provide a more concrete flavor for many of the issues involved in ISI prediction, the present chapter focuses on three cross-cutting examples—El Niño-Southern Oscillation (ENSO), the Madden-Julian Oscillation (MJO), and soil moisture. Knowledge of the state of each of these phenomena or quantities is known to contribute to ISI forecast quality. For each process, we address the scientific basis for expecting the process to contribute to the quality of ISI predictions, the manner in which forecast systems try to realize this potential (using the elements outlined in Chapter 3), their ability (or lack thereof) to do so, and the gaps in understanding and treatment of the process that have yet to be overcome.
EL NIÑO-SOUTHERN OSCILLATION (ENSO)
On interannual timescales, the variability in the tropical Pacific is dominated by the ENSO phenomenon (Rasmusson and Carpenter 1982; among others). During the transition to the warm phase of this oscillation, there is a dynamic adjustment of heat and mass between the western and eastern tropical Pacific, producing a positive sea surface temperature anomaly (SSTA) in the eastern Pacific. Associated with this dynamic adjustment, precipitation is displaced eastward from the climatological warm pool region toward the date line, and the normally easterly trade winds weaken or even become temporarily westerly. During the cold phase, the eastern tropical Pacific SSTA is negative, the trade winds are anomalously strong, and the precipitation is tightly confined to the warm pool region of the western Pacific. Typically, the time between warm events is around 2 to 7 years; however, there is also considerable modulation of the ENSO cycle on decadal timescales. Despite the quasi-periodicity, the predictability of ENSO is largely determined by the life cycle of individual events, which depends on the memory or inertia associated with upper ocean heat content and coupled ocean-atmosphere interactions. As the event evolves there are large spatial shifts in tropical Pacific rainfall leading to large-scale changes in global circulation and precipitation (Figure 4.1). It is these changes in circulation and precipitation that make ENSO a primary source for ISI predictability in remote regions and offer the potential for decision support and risk management.
Scientific Basis for Prediction
The advent of dynamic ENSO prediction can be traced back to Bjerknes’s conceptual model. While the phenomenon of the Southern Oscillation was discovered and applied to
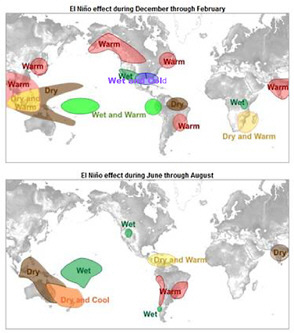
FIGURE 4.1 ENSO impacts on seasonal climate. SOURCE: Adapted from CPC/NCEP/NOAA.
seasonal prediction of the Indian monsoon in the early 1930s (Walker, 1932), the modern concept of ENSO was established three decades later by the pioneering work of Bjerknes (1966, 1969) who visualized the linkage between the atmospheric Southern Oscillation and oceanic warming in the eastern Pacific (El Niño) via tight coupling among the sea surface temperature, surface winds, and precipitation. Bjerknes’s work laid a physical basis and a conceptual framework for ENSO prediction (Neelin et al., 1998; Burgers et al., 2005). The coupled instability mechanism described by Bjerknes (1969) works as follows. If a positive eastern equatorial SSTA exists, the temperature gradient between the eastern Pacific and the western Pacific is reduced, which then produces a weakening of the easterly trade winds, augmenting the warming in the eastern Pacific. The additional warming in the east further weakens the trade winds, constituting a coupled ocean–atmosphere positive feedback. A reversal of the argument explains the growth of a cold event. This positive feedback between the SSTA and the atmospheric wind anomaly leads to a continually growing anomaly, although it does not provide an explanation for what causes the transition from one extreme state to the other.
About the same time, independent but related theoretical findings coincidently emerged, i.e., the equatorial wave theory in an unbounded equatorial atmosphere (Matsuno, 1966) and in a finite ocean basin (Moore, 1968). These theoretical findings stimulated rapid development of the equatorial oceanography. In the 1970s and 1980s, Bjerknes’s conceptual model was transformed and expanded into theoretical and simple dynamical models, which advanced understanding of
the basic ENSO dynamics, including coupled ocean-atmospheric instability, thermocline adjustment by oceanic waves, and mechanisms possibly sustaining ENSO and causing irregularity, non-stationarity, and skewness. The theoretical work has led to the understanding of destabilized equatorial waves (Philander et al., 1984) and a theory for the transition between warm and cold states (e.g., the so-called delayed or recharge oscillators, Suarez and Schopf, 1988; Battisti and Hirst, 1989; Jin, 1997; Kirtman, 1997). Moreover, this theoretical understanding clearly delineates the scientific basis for ENSO prediction, namely that sub-surface ocean thermal structure or thermocline displacements are pre-cursors for ENSO events and can be used to make forecasts.
Forecast System Methodologies
The pioneering El Niño forecast was made with an intermediate-complexity coupled ocean-atmosphere model (Cane et al., 1986). Since then, a variety of methods for ENSO prediction have flourished, including purely statistical techniques (e.g., Graham et al., 1987), combinations of dynamical and statistical models, and purely dynamic models (e.g., Ji et al., 1994; Kleeman et al., 1995; Rosati et al., 1997; Berhinger et al., 1998; Stockdale et al., 1998; Schneider et al.,1999; Kirtman, 2003; Keenlyside et al., 2005; DeWitt, 2005; Gualdi et al., 2005; Jin et al., 2008). All of these forecasting strategies rely on four well-defined basic ingredients of a state-of-the-art prediction system: (1) a dynamical model (i.e., coupled GCM) that consists of a series of mathematical expressions or statistical relationships that represent the physical laws that govern how the ocean and atmosphere behave and interact; (2) an observing system to provide input for initializing, developing, and verifying both dynamic and statistical forecast systems; (3) initial conditions or an estimate of the current state of the climate system, usually based on sophisticated data assimilation systems; and (4) a series of retrospective forecasts for calibration and assessing quality. The models used in these forecasting strategies have varying degrees of sophistication and diverse initialization schemes.
The importance of the observing system for the development of the statistical and dynamical prediction capability cannot be overstated. NOAA’s Equatorial Pacific Climate Study program deployed the earliest buoys along 110ºW and then along 140ºW, starting with the prototype Atlas moorings in 1984–85. This pioneering observational effort eventually led to the establishment of the mooring array along the entire equatorial Pacific basin. Development of the Tropical Atmosphere Ocean (TAO) array (Hayes et al., 1991) was further motivated by the 1982–1983 El Niño event, the strongest of the century up to that time, which was neither predicted nor detected until nearly at its peak. The event highlighted the need for real-time data from the tropical Pacific for monitoring, prediction, and improved understanding of El Niño. Eventually, the TOGA-TAO array (now renamed TAO/TRITON, see “Ocean Observations” section in Chapter 3) was completed in 1994 to include 70 moorings. The moorings provide winds, sea surface temperature, relative humidity, air temperature, and subsurface temperature at 10 depths in the upper 500 m. Five moorings along the equator also measure ocean velocity. These data remain key components of operational ENSO prediction and continue to provide critical data for understanding ENSO-related physical processes.
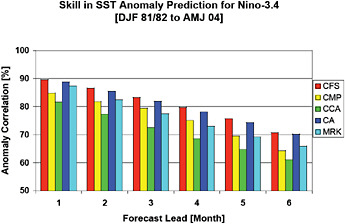
FIGURE 4.2 Nino3.4 correlation coefficient (predictions versus observations) for retrospective forecasts plotted as a function of lead time. The red and yellow bars correspond to dynamical models: the Climate Forecast System (CFS) is a state-of-the-art model developed in the mid-2000s (Saha et al. 2006), while the Coupled Model Project (CMP) prediction is older and was developed in the mid 1990s (Ji et al., 1995). CCA, CA, and MRK correspond to statistical models (Canonical Correlation Analysis, Constructed Analogues, Markov; see Appendix A). The figure highlights two points: (1) comparing the red and yellow bars indicates how coupled dynamical models have improved for this particular metric over the last two decades and (2) the statistical methods and the dynamical model methods are quite competitive with each other. Identical to Figure 3.14. SOURCE: Adapted from Saha et al. (2006)
Forecast Quality
ENSO forecast quality has clearly improved from initial attempts in the late 1980s. Undoubtedly, this improvement is due to better models, enhanced observing systems, and better use of observational estimates through improved data assimilation techniques. In the late 1980s and early 1990s the state-of-the-art dynamical model forecast quality for ENSO markedly lagged behind most statistical techniques (Anderson et al. 1999). During the mid to late 1990s dynamical models began to make much better use of observational estimates of the state of the sub-surface ocean in the tropical Pacific, which led to notable improvements in forecast quality. Most recently, the dynamical models have become quite competitive with the statistical models in predicting the state of ENSO in the tropical Pacific (see Figure 4.2) as seen by comparing the red and yellow bars (dynamic models) with the remaining bars (statistical models). The unprecedented 1997–1998 El Niño was perhaps the first real-time test of modern ENSO prediction systems and was fairly well predicted three to six months in advance using a number of different state-of-the-art coupled GCMs (e.g., Anderson et al., 2003), although the models failed to capture its large amplitude and its rapid onset (Barnston et al., 1999). Figure 4.3 underscores the point that multi-model combinations can improve ENSO prediction skill as measured by, for example Nino3.4 correlation skill. It indicates that combining
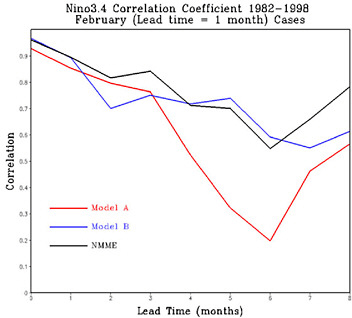
FIGURE 4.3 Nino3.4 correlation coefficient (predictions vs. observations) for two U.S. models (red and blue lines) and a multi-model ensemble (black line). The figure indicates that multimodel combinations improve this particular skill metric (black line is above the colored lines), that rapid progress on multi-model prediction in the United States can be made quickly (i.e., multi-model U.S. prediction systems are available today), and in comparison with Figures 2.11 and 3.13, that significant seasonal dependence exists in the correlation. The correlation shown here shows a rapid drop in boreal spring. This is commonly referred to as the “spring prediction barrier,” but it is unknown if it is due to model errors or is a fundamental property of the climate system. SOURCE: Kirtman and Min (2009).
two U.S. national models improves this particular skill metric and suggests that the United States is indeed well positioned to make multi-model operational ENSO predictions. Finally, this figure, consistent with Figures 2.11 and 3.13, indicates that there is significant seasonality in the correlation; this seasonality is not fully understood.
Most recently, the advances in ENSO prediction include: (1) the recognition that forecasts need to include quantitative information regarding uncertainty (i.e., probabilistic prediction) and that verification needs to include skill measures for probability forecasts (Kirtman, 2003); and (2) that a multi-model ensemble strategy (see Figures 2.9, 3.9, and 4.3) may be the best current approach for adequately quantifying forecast uncertainty. Although an MME strategy represents the “best current approach” for estimating uncertainty, it should be noted an MME forecast does not quantify the relationship between individual model errors and forecast uncertainty. The spread among the ensemble members can only provide a relative estimate of the forecast uncertainty.
How individual model errors contribute to forecast uncertainty is an active area of research. In terms of quantifying how model error contributes to forecast uncertainty, a number of international projects have been organized, among which the most comprehensive projects are the European Union-sponsored Development of a European Multi-model Ensemble System for Seasonal to Inter-Annual Prediction (DEMETER; Palmer, 2004), the Climate Prediction and its Application to Society (CliPAS) project, sponsored by the Asian-Pacific Economic Cooperation (APEC) Climate Center (APCC), and the Climate System Historical Forecast Project (CHFP, Kirtman and Pirani, 2009). These hindcast datasets provide a test-bed for assessing forecast quality and forecast uncertainty based upon uncertainty in model formulation. The multi-model approach has proven to be more skillful than any single model (Krishnamurti et al., 1999, 2000; Doblas-Reyes et al., 2000; Shukla et al. 2000; Palmer et al., 2000; Jin et al., 2008; Kirtman and Min, 2009). For example, the Mean Square Skill Score (MSSS) against climatology is a good way to assess the deterministic skill of ENSO forecasts. In particular, it gives a measure of error relative to the signal strength; in this case, the signal is the forcing on the atmosphere by the ocean. State-of-the-art MSSS for Nino 3.4 SST at 5 months lead-time is about 0.7 for the best single models, and 0.75 for multi-model combinations. Despite the improvements associated with the multi-model approach, the ad hoc nature of the strategy is troubling (Blanke et al., 1997; Kessler and Kleeman, 2000; Boulanger et al., 2001; Lengaigne et al., 2003; Eisenman et al., 2005; Vecchi et al., 2006; Gebbie et al., 2007; Jin et al., 2007; Kug et al., 2008; Kug et al., 2009; see “Multi-Model Ensembles section in Chapter 3).
Comparing the correlation skill (i.e., correlation between forecast and observations) of different forecasting systems on common sets of forecasts shows that there has been slow but steady progress over the last 10 years. Again, this is highlighted by comparing the red and yellow bars in Figure 4.2. Improvement in ENSO SST forecasts is expected to continue in the years ahead—the errors in today’s forecasting systems are still substantial and statistical post-processing and calibration improve forecast quality.
Consideration of a set of individual forecasts shows that today’s models provide good guidance as to the future evolution of SST, but relatively large errors can still occur. Some of the failures in the past might be related to an inadequately observed initial state, and certainly some of these errors are related to model fidelity.
The use of multi-model ensembles can give a definite boost to the quality compared to that obtained by a single model (e.g., Fedorov and Philander, 2001; Hagedorn et al., 2005; Codron et al., 2001; Guilyardi, 2006; Zhang et al., 2008; Jin et al., 2008; Kirtman and Min, 2009), and multi-model approaches to ENSO prediction are encouraged. Nonetheless, improvement of the individual models is strongly needed to improve the quality of future forecasts (single or multi-model). Typically, models are used to produce ensemble forecasts in order to quantify uncertainty and estimate higher moments. Forecast spread does vary according to season and ENSO phase in the models, but the relationship of forecast error to model spread is weak. For real applications, any model forecast needs to be post-processed in some way. Probabilistic verification of calibrated and post-processed forecasts is to be encouraged, but at the moment the information content of the forecasts is thought to be very largely dominated by the first moment, i.e. the ensemble mean.
Gaps in Understanding
Our ability to predict ENSO with dynamical models has dramatically improved from the mid-1980s to the beginning of the 21st century. Past improvements were due to the convergence of many factors, including a theoretical understanding of coupled ocean-atmosphere dynamics, improvement of the coupled model forecast systems, and international efforts to observe and monitor conditions in the tropical Pacific. However, basic questions regarding our knowledge of physical processes in the tropical Pacific remain open challenges in the forecast community. For instance, it is unclear how the MJO, westerly wind bursts (WWBs), intra-seasonal variability or atmospheric weather noise influence predictability of ENSO (e.g., Thompson and Battisti, 2001; Kleeman et al., 2003; Flugel et al., 2004; Kirtman et al., 2005). It has been suggested that enhanced MJO and WWB activity was related to the rapid onset and the relatively large amplitude of the 1997–1998 event (e.g., Vecchi and Harrison, 2000; Eisenman et al., 2005). However, more research is needed to fully understand the scale interactions between ENSO and the MJO and the degree that MJO/WWB representation is needed in ENSO prediction models to better resolve the range of possibilities for the evolution of ENSO (Wittenberg, 2004). Typically, prediction systems do not adequately capture the differences among different ENSO events (Goddard and DeWitt, 2005). In essence, the prediction systems do not have a sufficient number of degrees of freedom for ENSO as compared to nature. There are also apparent decadal variations in ENSO forecast quality (Balmaseda et al., 1995; Ji and Kousky, 1996; Kirtman and Schopf, 1998; Barnston and Tippett, 2009), and the sources of these variations are the subject of some debate. It is unclear whether these variations are just sampling issues or are due to some lower frequency changes in the background state (see Kirtman et al. 2005 for a detailed discussion). Chronic biases in the coupled models in their mean states and intrinsic ENSO modes remain, and it is believed that these biases have a deleterious effect on SSTA forecast quality and the associated teleconnections. Some of these errors are extremely well known throughout the coupled modeling community. Three classic examples, which are likely interdependent, are (1) the so-called double ITCZ problem, (2) the excessively strong equatorial cold tongue typical to most models, and (3) the eastern Pacific and Atlantic warm biases endemic to all models. Such biases may limit our ability to predict seasonal-to-interannual climate fluctuations and could be indicative of errors in the model formulations. Finally, it remains unclear how changes in the mean climate will ultimately affect ENSO predictability (Collins, 2000).
In addition, procedural issues remain when initializing, making, and verifying ENSO forecasts. Quantifying the relationship between model uncertainty and forecast uncertainty is an area of active research. For instance, in an individual model, it is possible to introduce stochastic physics schemes in order to approximate the uncertainty arising from the model parameterizations of unresolved sub-grid scale processes (Buizza et al., 1999; Shutts, 2005; Bowler et al., 2008). These approaches are operationally used by ECMWF and the United Kingdom Meteorological Office for medium-range forecasts and are being tested on the seasonal-to-interannual prediction problem.
Other advancements include using novel data sets to initialize forecasts, particularly involving ocean data (Alves et al., 2004); moreover, other research indicates that forecast initialization strategies that are implemented within the framework of the coupled system as opposed to the individual component models may also lead to substantial improvements in skill (Chen et al., 1995).
MADDEN-JULIAN OSCILLATION (MJO)
Scientific Basis for Prediction
The dominant form of intraseasonal atmospheric variability, particularly in terms of rainfall generation and global reach of influence, is most often referred to as the Madden-Julian Oscillation (MJO; also known as the 30–60 day, 40–50 day, and intraseasonal oscillation (ISO), after its discoverers, Madden and Julian, (1971, 1994, 2005)). The left panels of Figure 4.4 (see also Figure 2.6) illustrate the space-time structure of rainfall and low-level winds in the tropics associated with an MJO “event” during boreal winter, with the interval between maps being 12.5 days. These maps illustrate the eastward propagation of the MJO’s large-scale tropical rainfall anomalies. In conjunction with these rainfall anomalies are baroclinic wind anomalies, with upper tropospheric divergence (convergence) occurring in conjunction with positive (negative) rainfall anomalies and vice versa for the lower troposphere (see Waliser, 2006). In addition, it can be seen that there is a significant modulation by the relatively warmer (cooler) eastern (western) hemisphere background state, with the large rainfall anomalies developing and propagating (~5 m s-1) over the warm waters of the Indian and west Pacific Oceans. Once the disturbances reach the vicinity of the International Date Line and the cooler eastern Pacific Ocean equatorial waters, the convection tends to subside and propagate southeastward into the South Pacific Convergence Zone. Beyond the Date Line, the disturbance continues to propagate eastward (~15–20 m s-1) and tends to be evident only in the near-equatorial wind field. (Hendon and Salby, 1994).
The off-equatorial structure of the MJO is also important, especially in relation to its connections to mid-latitudes. For example, associated with the positive near-equatorial rainfall anomalies are upper-level cyclonic (anticyclonic) gyres to the northeast and southeast (northwest and southwest) centered at latitudes of about 20º (Rui and Wang, 1990; Hendon and Salby, 1994). These tropical heating and subtropical circulation anomalies act as Rossby wave sources for mid-latitude variability (e.g., Weickmann, 1983; Liebmann and Hartmann, 1984; Weickmann et al., 1985; Lau and Phillips, 1986; Sardeshmukh and Hoskins, 1988; Berbery and Nogues-Paegle, 1993). Such connections with the extra-tropics have important ramifications for mid-latitude weather variability, regime changes, and forecasting capabilities (e.g., Ferranti et al., 1990; Higgins et al., 2000; Jones et al., 2004b). For example, Figure 4.5 illustrates the MJO influence on the mid-latitude circulation and its relationship with rainfall anomalies in the Pacific Northwest.
The characteristics of the intraseasonal variability driven by the MJO tend to be most strongly exhibited during the boreal winter and spring when the Indo-Pacific warm pool is centered at or near the equator. In the boreal summer, the MJO is still present, although its spatial variability and propagation characteristics are modified by the changes associated with the annual cycle. The right panels of Figure 4.4 illustrate the space-time structure of the MJO in boreal summer (for more in-depth observational descriptions see recent reviews by Goswami, 2005; Hsu, 2005). Note that the summertime manifestation of the MJO is often referred to as the Intraseasonal Oscillation (ISO), the boreal summer ISO, or monsoon ISO (MISO). Examination of the boreal summer rainfall maps shows that positive rainfall anomalies in the western and central Indian Ocean occur in conjunction with negative rainfall anomalies over a region extending between India and the western equatorial Pacific. This system then appears to
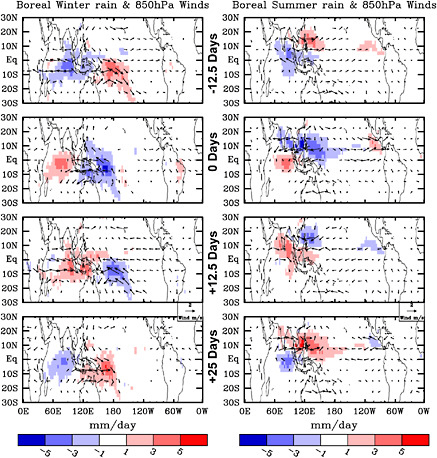
FIGURE 4.4 Characteristic circulation and precipitation patterns associated with an MJO event. Anomalous winds at 850 hPa (vectors) and precipitation anomalies (red: wet anomaly; blue: dry anomaly) are shown for the periods prior (top panels, 12.5 days preceding the event), during (second from top panels), and after an event (bottom two panels, 12.5 and 25 days following the event). Left panels show an event in the boreal winter (November–April); right panels are for the boreal summer (May–October). SOURCE: Waliser (2006).
propagate both eastward and northward (Yasunari, 1979; Lau and Chan, 1986; Lawrence and Webster, 2002; Hsu, 2005), similar to the boreal winter case. These large-scale rainfall variations have important implications for Asian monsoon onset and breaks.
While the diagrams in Figure 4.4 illustrate what might be considered typical winter and summer MJO events, it is important to recognize that these events have considerably more
complexity in reality and exhibit significant interannual variability. For example, the study by Wang and Rui (1990), and later by Jones et al. (2003), have further diagnosed the “synoptic climatology” of tropical MJO events, including their seasonal modulation. These studies show that boreal winter events display considerable variation in the longitudes at which the convection develops and dissipates. Moreover, it is well known that the convection associated with MJO events typically propagates further east during El Nino events (e.g., Kessler, 2001). Some of these features are illustrated in Figure 4.6. For the boreal summer case, Kemball-Cook and Wang (2001) show that there is a systematic intraseasonal change in the spatial structure and propagation characteristics of the MJO. In the early part of the summer (e.g., May-June), the
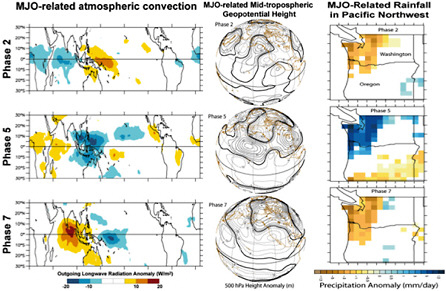
FIGURE 4.5 Example of the relationship among tropical outgoing long-wave radiation (OLR, left column), which is used to define the phase of the MJO, wintertime (JFM) 500-hPa geopotential height anomalies (middle column), and precipitation anomalies (right column). For example, Phase 5 (the middle row) of the MJO exhibits enhanced convection over the Maritime Continent that is accompanied by deep-troughing in the mid-troposphere over the North Pacific and enhanced precipitation in the Pacific Northwest. SOURCE: Adapted from Bond and Vecchi (2003).
off-equatorial variability is generally found west of Southeast Asia and the Maritime Continent, while in the later part of the summer, it expands to include much of the northwestern Tropical Pacific.
By the early 1990s, many physical characteristics of the MJO were documented and a number of reproducible features were recognized as occurring from one event to another as well as in events from one year to the next. In addition, theoretical and modeling studies suggested that the coupling observed between organized convection and low-frequency equatorial waves
(e.g., Kelvin, Rossby) were responsible for the slow, eastward propagation of the MJO and thus suggested an unexploited form of intraseasonal predictability (e.g., Wang et al., 2005). Given this and the emerging knowledge of the interactions of the MJO with other features of our weather and climate (e.g., Lau and Waliser, 2005; Waliser et al., 2005; Tian et al., 2007; 2008; Wong and Dessler, 2007), it was an obvious step to seriously consider MJO forecasting.
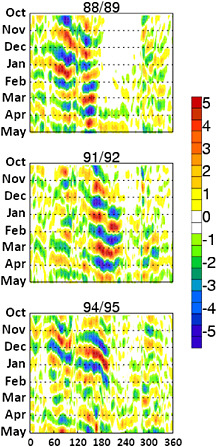
FIGURE 4.6 Precipitation anomalies (mm/day) observed for three winter periods (1988–1989, 1991–1992, and 1994–1995) illustrating the year-to-year differences in the location, magnitude, and rate of propagation of anomalies in convection near the Equator. The colors indicate OLR anomalies, with red corresponding to suppressed convection and blue corresponding to enhanced convection. Essentially, large differences can exist among MJO events in different years. SOURCE: Courtesy of D. Waliser and B. Tian.
Predictability Estimates and Forecast System Developments
Given that numerical weather and climate models typically have had, and still for the most part have, a relatively poor representation of the MJO (e.g., Slingo et al., 1996; Waliser et al., 2003a; Allen et al., 2005; Slingo et al., 2005; Kim et al., 2009), a natural avenue to consider for establishing an MJO forecasting capability was the development of empirical models. There were a number of different approaches and data sets used in these empirical studies, with most relying on linear approaches and quantities such as outgoing longwave radiation (OLR) and/or upper-level circulation quantities (von Storch and Xu, 1990; Waliser et al., 1999a; Jones et al., 2004a; Mo, 2001; Wheeler and Weickmann, 2001; Goswami and Xavier, 2003; Webster and Hoyas, 2004). The upshot of these studies is that empirical models demonstrate some accuracy in the prediction of the MJO on the order of 15–25 days or more, depending on the spatial scale and quantity being predicted. However, as with any empirical model, these models are limited in the totality of the weather and climate system they can predict, their ability to adapt to arbitrary conditions, and their ability to take advantage of known physical constraints.
To date, the majority of dynamical models still exhibit significant shortcomings in terms of their MJO simulation, particularly if pressed to do operational prediction. There have been a few models or versions of models that have demonstrated success at representing a number of the principal features of the MJO (Slingo et al., 1996; Sperber et al., 1997; Waliser et al., 1999b; Kemball-Cook et al., 2002; Maloney, 2002; Fu et al., 2003; Zheng et al., 2004; Kim et al., 2009). This level of model success was suggestive that better representation of the MJO in operational prediction models was likely to lead to improved quality of intraseasonal predictions (Waliser et al., 2003b; 2003d; Liess et al., 2004) with the additional indication that ocean coupling may yield further enhancements (Fu et al., 2006; Zheng et al., 2004; Zhang et al., 2006; Woolnough et al., 2007; Pegion and Kirtman, 2008).
Forecast Performance
Based on the results from empirical and dynamical modeling studies discussed above, there has been ample reason to push towards an operational MJO prediction capability. However, indications from early studies carried out in the context of operations showed little prediction quality due to the poor representation of the MJO in the models (Chen and Alpert, 1990; Lau and Chang, 1992; Jones et al., 2000; Hendon et al., 2000). In general these studies found reasonable accuracy only out to about 7–10 days for MJO-related variability, and were mainly hampered by MJO variability that was too weak and/or that propagated too fast. Probably the most optimistic set of demonstrative hindcast skill experiments for the MJO were a set of Asian monsoon MJO case studies performed by Krishnamurti et al. (1990; 1992; 1995). The novel approach in these cases was that an attempt was made to filter out the “weather” time and space scales from the initial conditions and leave only the “low-frequency modes.” The hindcast results demonstrated reasonable accuracy out to 3–4 weeks; however, there are some uncertainties associated with making such a technique operational and with the handling of the boundary-layer forcing (i.e. SST). More recent studies on this topic by Agudelo et al (2008) and Fu et al. (2009) raise questions as to the manner and degree that the fast time scales associated with processes such as
organized convection contribute to the overall forecast error, and suggest the need for further research in this area.
Given the need for forecast capability at the intraseasonal time scale, along with the poor representation of the MJO in dynamical models, a number of real-time efforts have been developed based on empirical methods. These include some of the schemes referenced above (Wheeler and Weickmann, 2001; Jones et al., 2004a; Wheeler and Hendon, 2004; Webster and Hoyas, 2004) as well as other novel techniques such as empirical wave propagation (EWP, van den Dool and Saha, 2002) and the use of a Linear Inverse Model (LIM, Winkler et al., 2001). Some of these techniques are being utilized in operational contexts, such as in forecast products at the Australian Bureau of Meteorology (ABOM; personal communication Matthew Wheeler) and the Global Tropics Benefits/Hazards Assessment at the National Centers for Environmental Prediction (NCEP, personal communication John Gottschalck). Given the developing reliance on the empirical forecast products mentioned above, it is important to note that many of them lie outside formal prediction centers and thus are only quasi-operational.
While dynamical models have not simulated the MJO in a particularly faithful manner, there have been improvements in their performance. An excellent example of improvement in forecast model quality is given in Figure 4.7, which shows the evolution of the ECMWF hindcast skill for the MJO during the Tropical Ocean Global Atmosphere Coupled Ocean Atmosphere Response Experiment (TOGA COARE) period (1992–1993). Notable improvements made to the model relative to the MJO had mostly to do with model parameterization changes including convection, clouds, radiation, and turbulent diffusion (Tompkins et al., 2007; Bechtold et al., 2008). These model improvements have resulted in a present-day ECMWF forecast skill, as measured by anomaly correlation, of about 0.6 at lead times extending out to about 20 days for the large-scale spatial patterns of the MJO (e.g., Figure 4.4). These values are competitive with if not better than the empirical models developed to date.
Since the MJO is largely an atmospheric phenomenon, most of the predictability is thought to come from the atmospheric structure of the mode itself that tends to be relatively well captured by conventional synoptic and satellite observations available today. However, there have been few studies that have addressed which aspects of the initial conditions of the atmospheric state are important to MJO forecasts. The study by Vintzileos and Pan (2007) is an exception, as it illustrated that the prediction quality of the MJO in the NCEP CFS model was significantly more sensitive to the choice of initial conditions (in this case Reanalysis-2 versus GDAS operational) than to model resolution (in this case T62, T126, T254). These types of issues for future work are discussed in the following section.
Gaps in Understanding
Based on the sorts of forecast activities and developments described above, there have been a number of efforts to take a more systematic and cross-community/center approach to MJO forecasting and model diagnosis. This has included a number of workshops held in recent years (Zhang et al., 2001; Schubert et al., 2002; Waliser et al., 2003c; ECMWF, 2004; ICTP, 2006; Sperber and Waliser, 2008) and efforts to develop cross-center/model experimental predictions (Waliser et al., 2005). These activities in turn helped to support and guide the formation of an MJO Working Group (MJOWG) under the auspices of U.S. CLIVAR. The objectives of this working group included the development of model diagnostics (CLIVAR
Madden-Julian Oscillation Working Group, 2009) to facilitate model development, assessments and comparison, and application of these diagnostics to a number of contemporary weather and climate models (Kim et al., 2009). Figure 4.8 shows wavenumber-frequency spectra for eight models (3 coupled and 5 uncoupled) and for observations/reanalysis. Although a couple of the models exhibit sizeable intraseasonal variability, none of these models provides a robust representation of the dominance of the variability at wavenumbers 1–3 and 30–80 days. Note the 30– and 80–day designations as vertical lines. In addition, common shortcomings among the
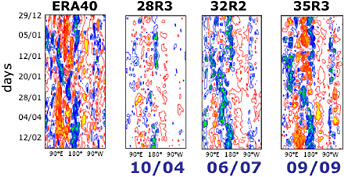
FIGURE 4.7 Improvements in forecasts of tropical outgoing long-wave radiation (OLR) from October 2004 to September 2009 over time. The time-longitude diagrams show the averaged outgoing long-wave radiation (OLR) near the Equator from observations and a series of forecasts for the period December 29, 1992 (top of panels) to February 15, 1993 (bottom of panels) with a lead time of 15-days from various versions of the ECWMF operational forecast model. The earlier version of the model performs poorly (labeled “10/04”), while the later version replicates (labeled “09/09”) more features of the observations. Cycle identification and the date it became operational are given at the top and bottom of each panel, respectively. Red shading represents positive OLR anomalies and blue shading represents negative OLR anomalies. SOURCE: ECMWF; Bechtold et al. (2008); updates courtesy of Frederic Vitart (ECMWF).
models include weak and/or incoherent eastward propagation, particularly across the Maritime Continent, and difficulties representing the vertical structure associated with water vapor, clouds, and convective processes.
To facilitate more substantial gains in the operational context, the MJOWG developed an MJO forecast metric (adapted from Wheeler and Hendon, 2004), and along with the Working Group on Numerical Experimentation (WGNE) facilitated its adoption by a number of operational forecast centers. In addition, MJOWG has worked with CPC/NOAA to aggregate, display, and disseminate its real-time forecasts in a uniform manner (Gottschalck et al., 2010). The motivation for having such a metric is that it allows for a more quantitative assessment of forecast quality, the ability to track model forecast quality over time, the capability to measure potential model improvements relative to the MJO, and the means to develop a multi-model ensemble forecast of the MJO. The motivation for improving MJO forecasts and the means to evaluate them involve not only the MJO itself but extend to other weather patterns it influences
and interacts with such as extratropical weather patterns (e.g., Ferranti et al. 1990; Bond and Vecchi 2003; Jones et al. 2004a, b; Vecchi and Bond, 2004) and tropical cyclones (e.g., Maloney and Hartmann, 2000; Vitart et al. 2010). Given the importance of the MJO in terms of its contribution to ISI predictability, the above programmatic research work started by the US CLIVAR Working Group has been extended through the recent formation of a WCRP-WWPR/THORPEX MJO Task Force (see http://www.ucar.edu/yotc/mjo.html).
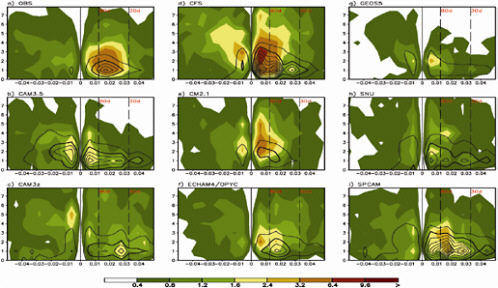
FIGURE 4.8 Precipitation and wind variability generated by dynamical models serve as a poor match to observations. The first panel (a) shows the observations of November–April wavenumber-frequency spectra (wavenumbers on the y-axis; temporal frequency on the x-axis) of averaged precipitation (shaded) and 850-hPa zonal wind (contoured), near the Equator. Very few of the models (b–i) exhibit rainfall or wind variability similar to that of the observations. The vertical lines indicate the spectral region where variability “should” be occurring. Units for the precipitation (zonal wind) spectrum are mm2 day-2 (m2 s-2) per frequency interval per wavenumber interval. SOURCE: Kim et al. (2009).
While the above efforts will facilitate continued development and improvements in operational MJO predictions, it is certain that capturing the forecast quality associated with the MJO is most strongly hampered by the systematic biases in the models, such as those illustrated in Figure 4.8. Rectifying these will likely require more examination and understanding of the vertical structure of clouds and associated diabatic heating (Lin et al., 2004; Jiang et al., 2009; Fu and Wang, 2009), cloud-radiative interactions (Lee et al., 2001; Lin and Mapes, 2004), microphysical processes (Tompkins et al., 2007; Waliser et al., 2009), interactions with the surface (Maloney and Sobel, 2004; Sobel et al., 2008) and the fine-scale structure embedded in
the MJO (Nakazawa, 1988; Lau et al., 1991; Chen et al., 1996; Moncrieff, 2004; Moncrieff and Liu, 2006; Majda and Stechmann, 2009).
In addition, there are a number of operational and implementation issues that need to be explored. For example, given that most of the predictability of the MJO is thought to reside in its large-scale atmospheric structure suggests that its state can be well captured by the conventional synoptic and satellite observations available today. However there have been few studies that identify which aspects of the initial conditions of the atmospheric state are important to MJO forecasts, as mentioned above (see Vintzileos and Pan, 2007). Apart from the prominence of the atmospheric state to the MJO, there are a host of theoretical and modeling studies that suggest the SST and mixed-layer heat content are important in the evolution of the MJO and thus are quantities that need to be represented accurately in the initial conditions and subsequent prediction model evolution (Fu et al., 2003; Zheng et al., 2004; Fu et al., 2006; Zhang et al., 2006; Woolnough et al., 2007; Pegion and Kirtman, 2008). Also, the initiation mechanism(s) associated with the MJO in the eastern/central Indian Ocean represents a significant outstanding question that impacts the development of MJO forecasting. A number of these issues will be explored through the analysis of the multi-model hindcast data set that was specifically designed for examination of the predictability and prediction sensitivities of the MJO and the development of multi-model ensemble strategies (see http://www.ucar.edu/yotc/iso.html). Moreover, field studies such as the upcoming DYNAMO/CINDY campaign in the Indian Ocean in late 2011 through early 2012 will be helpful to address the questions concerning MJO initiation. Additional discussion on the above issues and recommendations for ways forward can be found in numerous studies (Zhang, 2005; Waliser, 2006; Moncrieff et al., 2007; Sperber and Waliser, 2008; Waliser and Moncrieff, 2008; Gottschalck et al., 2010).
SOIL MOISTURE
The use of realistic soil moisture initialization can potentially improve precipitation and air temperature forecasts on ISI time scales. The mechanistic pathway can be described through a hypothetical situation. Consider a soil that is anomalously wet at the beginning of a forecast period. Due to the inherent memory associated with soil moisture, the anomaly would likely persist for several weeks, and during this time period, the evaporation rate from the land surface would likely be anomalously high. High evaporation, in turn, could lead to anomalously cool surface temperatures as a consequence of enhanced evaporative cooling. In addition, the anomalously high rate of evaporation could affect the atmosphere (e.g., changes to the boundary layer structure, humidity), which could increase the chance or amount of precipitation.
While easy to describe, many of the mechanisms involved are profoundly complex and are not yet fully understood, particularly those associated with the impacts of evaporation on rain generation. Understanding and quantifying the contribution of soil moisture initialization to climate forecast quality is the focus of many recent studies.
Scientific Basis for Prediction
Energy and water are naturally conserved at the land surface, and the energy balance and water balance equations share a common term: evaporation. Through the energy balance, higher
evaporation means a greater evaporative cooling of the land surface, which can translate to cooler air temperatures, as noted above. It can also, through both balances, affect precipitation—the lower sensible heat flux associated with higher evaporation can lead to shallower boundary layers and thus an easier build-up of the conditions that trigger convective rainfall (Betts et al. 1994), and the evaporation itself can serve as a moisture source. However, under certain (and probably rarer) conditions, higher evaporation rates may have the opposite effect—they may act to inhibit precipitation (Findell and Eltahir, 2003; Cook et al., 2006).
One of the chief controls over evaporation in many parts of the world is soil moisture. If the soil is not too wet to begin with, higher soil moisture tends to lead to higher evaporation; evaporation in many parts of the world is water-limited. (Soil moisture has an additional, secondary effect on the surface energy balance, and thus evaporation, through its impact on the surface albedo.) Thus, in a forecast system, if soil moisture could be accurately predicted, then evaporation could be better predicted, with potentially positive impacts on the prediction of precipitation and air temperature (see Figure 4.9) Soil moisture can in fact be predicted reasonably well at subseasonal timescales due to its inherent memory; observational studies (Vinnikov and Yeserkepova, 1991; Vinnikov et al., 1996; Entin et al., 2000) show that this memory is of the order of weeks to months, much longer than that of tropospheric variables. Note that the role of soil moisture in prediction is in some ways complementary to that of SSTs. While the timescale of soil moisture memory pales relative to that of ocean processes, the effects of soil moisture tend to be local and can help make up for a lack of teleconnection between forecasted SSTs and midlatitude continental weather during summer (Koster et al., 2000).
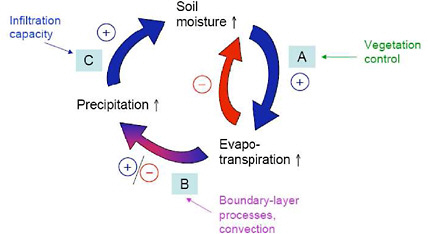
FIGURE 4.9 Simplified schematic showing how soil moisture anomalies can feed back on precipitation. In segment A of the cycle, a positive soil moisture anomaly leads to a positive evaporation anomaly (assuming evaporation is in a soil moisture-limited regime), and this in turn reduces the positive soil moisture anomaly. In segment B, a positive evaporation anomaly can lead to a positive precipitation anomaly, though in certain situations, it can instead lead to a negative precipitation anomaly. In segment C, a positive precipitation anomaly leads to a positive soil moisture anomaly. SOURCE: Seneviratne et al. (2010).
Naturally, given its potential, much research has focused on assessing the usefulness of soil moisture initialization in a forecast system. The first step is to examine how soil moisture variations help guide the evolution of atmospheric variables. The atmospheric general circulation model (AGCM) environment is a natural place to examine this, given the limitations of purely observation-based studies. Using observations, for example, to garner evidence of soil moisture impact on precipitation is difficult because the reverse direction of causality is overwhelmingly dominant—when rainfall is high, the soil gets wet. Some research has looked at lagged correlations between observed soil moisture and precipitation (does a wet soil tend to precede an anomalously high rainfall?), but even such lagged statistics cannot prove causality, given that the rainfall itself may have some long memory associated with it, as induced by remote SSTs, for example. With an AGCM, dominant directions of causality can be artificially disabled, allowing the lesser and potentially interesting ones to be isolated and quantified, at least for the biased AGCM climate.
Such AGCM studies can be segregated into two categories. The first involves assessing the response of the atmospheric variables to the prescription of soil moisture throughout the simulation period. In these studies, no thought is given to soil moisture prediction itself; soil moisture is in essence assumed to be “perfectly forecasted.” Shukla and Mintz (1982) demonstrated with an AGCM that a very dry land surface produces a substantially different climate response than a very wet surface. Numerous further studies have since shown that: (1) a suitably wet or dry soil moisture boundary condition can generate precipitation and runoff extremes (droughts and floods; e.g., Atlas et al., 1993; Hong and Kalnay, 2000), and (2) prescribed, more subtle variations in soil moisture lead to correspondingly subtle yet still measurable variations in precipitation and air temperature (e.g., Delworth and Manabe, 1989; Koster et al., 2000; Dirmeyer, 2000; Douville et al., 2001), if only in certain regions.
Such studies were formalized recently in GLACE (the Global Land-Atmosphere Coupling Experiment), a Global Energy and Water Cycle Experiment (GEWEX) and CLIVAR-sponsored international project (Koster et al., 2006; Guo et al., 2006). The GLACE project involved a dozen state-of-the-art AGCMs, each performing precisely the same numerical experiment, one designed specifically to quantify the degree to which the time evolution of simulated precipitation and air temperature can be guided through the specification of the (time and space-varying) soil moisture state. GLACE produced two main results: (1) AGCMs differ significantly in their estimates of how soil moisture variations affect precipitation and air temperature, and (2) they do nevertheless tend to agree that certain regions during certain times of year are more prone to soil moisture impacts on the atmosphere than others.
The regions for which the GLACE models show some consensus regarding impact are indicated in Figure 4.10. These areas are generally transition zones between wet and dry areas—regions like the U.S. Great Plains, which lies between the arid west and the humid east. Mechanistically, the relative importance of these transition zones for land-atmosphere coupling makes perfect sense; in regions that are too arid, evaporation variations are too small to affect the atmosphere, and in regions that are too wet, soil moisture availability does not limit evaporation (energy availability, through radiation, does instead), so that soil moisture variations are not translated into evaporation variations. These mechanistic controls have indeed been demonstrated outside of GLACE through various specially designed AGCM experiments. Fortuitously, satellite retrievals of soil moisture are generally reliable in these transition zones, where the vegetation is not too dense.
The second category of purely model-based studies focuses on the degree to which soil moisture initialization can affect the subsequent simulation of atmospheric variables. These studies do address the prediction of soil moisture since it is not prescribed throughout the forecast period—soil moisture and atmospheric variables are free to evolve together. Large initial soil moisture anomalies have been found to have a significant impact on subsequent precipitation (e.g., Rind, 1982; Oglesby and Erickson, 1999). Less extreme anomalies produce correspondingly more subtle impacts on the atmosphere, with some studies showing an almost
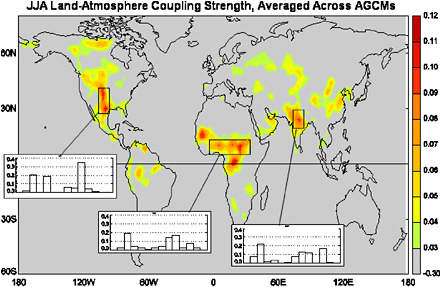
FIGURE 4.10. Areas for which the numerical models participating in the GLACE study tend to agree that variations in soil moisture exert some control on variations in precipitation. The variable plotted is the average across models of a land-atmosphere coupling strength diagnostic; the insets show how the magnitude of this diagnostic differs amongst the participating models. SOURCE: Koster et al. (2004).
negligible impact on (model-specific) precipitation predictions (though significant impact on air temperature predictions) associated with soil moisture initialization (e.g., Schlosser and Milly, 2002).
Forecast System Methodologies
Dynamical models used in forecasting rely on the initial state of soil moisture, which is provided by observations. As explained in Chapter 3 (“Land Observations” and “Data Assimilation” sections), analysis products provide the most useable data for forecasts, as they can provide information about soil moisture at broad spatial scales. In particular, the application of Land Data Assimilation Systems (LDAS) to raw meteorological observations (e.g.,
temperature, humidity, precipitation, winds) can greatly improve the initialization of soil moisture in dynamical models. The expected state-of-the-art for soil moisture initialization in coming years involves extending LDAS to include assimilated satellite information (soil moisture retrievals or the raw radiance measurements).
Statistical forecast models can also make use of such soil moisture information. For example, the Constructed Analogue technique (see “Constructed Analogs” section in Chapter 3) of van den Dool et al. (2003) makes use of historical soil moisture patterns to infer the evolution of soil moisture, temperature, and precipitation from present soil moisture patterns.
Forecast Performance
The obvious extensions to the idealized, model-based studies discussed in “Scientific Basis for Prediction” section are studies that use true forecast systems and observations of forecasted variables to examine the degree to which realistic soil moisture initialization improves forecast quality. Fennessy and Shukla (1999), for example, examined increases in accuracy derived from a proxy analysis-based soil moisture dataset. Douville and Chauvin (2000) initialized their model with soil moisture estimates derived from the Global Soil Wetness Project, and Viterbo and Betts (1999) examined the impact of soil moistures derived from the ERA-15 reanalysis on the simulation of the 1993 Mississippi flood. Koster et al. (2004) examined 15 years worth of forecasts (5 independent forecasts per year) to quantify forecast accuracy from a relatively sizeable set of forecasts. These studies, and others like them, strongly suggest that realistic soil moisture initialization can provide some increase in the quality of precipitation and air temperature prediction out to a month or more.
In an attempt to generate a multi-model “consensus” view of how realistic land initialization affects forecast quality, several modeling groups have recently embarked on the GLACE-2 project. In this project, the participants perform two parallel sets of forecasts: one in which land surface states, particularly soil moisture, are initialized realistically and one in which they are not. A comparison of the skill (square of correlation relative to observations) derived from these two sets allows a direct quantification of the impact of land initialization on forecast quality. The experiment is ongoing; first results show that across the models, land initialization does improve the correlation skill of temperature forecasts out to 60 days. The correlation skill increases substantially when conditioned on the size of the initial (local) soil moisture anomaly (see Figure 4.11).
The patterns in Figure 4.11 differ somewhat from those in Figure 4.10. These apparent discrepancies might be explained in several ways. First, the original GLACE examined the ability of imposed soil moisture variations to influence the atmosphere, whereas GLACE-2 examined the full prediction question, which also involves the ability of a model to retain an initial soil moisture anomaly through a forecast period. Analyses of model-generated soil moisture memory (e.g., Seneviratne et al. 2006a) suggest that the south central United States has a reduced soil moisture memory relative to the north central region, perhaps hindering the generation of skill there. Sampling error may also be a factor. In addition, results from the two GLACE experiments almost certainly differ because the first was purely synthetic—the patterns produced in the original GLACE experiment necessarily reflect the biased climatologies of the models, possibly shifting, for example, the area of high land-atmosphere coupling in the north central U.S. toward the west relative to that implied by the GLACE-2 results. The GLACE-2
experiment was not synthetic, and thus the patterns produced are controlled by both the climatology inherent in nature (through the realistic initialization) and by the ability of the models to perform realistically during the forecast.
Regarding precipitation, the consensus from GLACE-2 is less robust. The results do show, however, some small land-related increases in accuracy for precipitation out to at least 45 days, again especially when conditioned on the initial anomaly (Koster et al., 2010), and again especially in the north central United States.
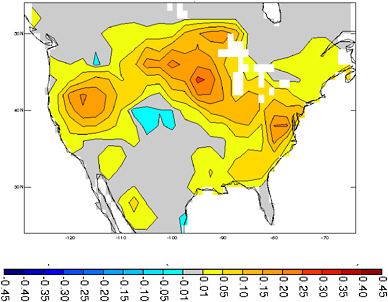
FIGURE 4.11. Conditional improvement in forecast accuracy for air temperature related to improved land initialization. “Warm” colors indicate areas where accuracy is gained when realistic land initialization is used. The metric plotted represents the square of the correlation coefficient (R2) obtained with realistic land initialization minus the R2 value obtained without it. The quantity predicted and compared to observations is the average air temperature over days 31–45 of the forecast. Forecasts at a given location are conditioned on the initial soil moisture at that location—only those start dates for which the initial soil moisture lies in the lowest or highest quintile of all realized values are used in the calculation. Adapted from Koster et al. (2010).
Some statistical analyses have addressed the potential impacts of soil moisture on skill (e.g., Karl, 1986; Huang et al., 1996b). These also point to the interior of North America as the place to find positive correlations between soil moisture and future temperature, though not always in the same locations.
Gaps in Understanding
While improvements to satellite retrievals and LDAS can improve the initialization of soil moisture, improving our understanding of the physical processes linking soil moisture to precipitation remains critical to exploiting the benefit of soil moisture to forecast quality, especially with respect to its impact on precipitation. The insets in Figure 4.10 above highlight the fact that models differ widely in their assessment of soil moisture’s ability to affect precipitation. This ability, the “land-atmosphere coupling strength”, underlies any contribution made by soil moisture initialization to precipitation prediction. (Similar inter-model variability is seen for the soil moisture—temperature connection.) As suggested above, we cannot even say which model performs best because the effective coupling strength operating in nature cannot be directly measured. Only indirect estimates are available, so only these can be used for model evaluation. The best way to do this is still unclear.
Presumably, an accurate simulation of land-atmosphere coupling relies on an accurate simulation of the complex and interacting model formulations that contribute to it. Work is needed to evaluate and improve model formulations of soil-moisture limited evaporation, turbulent transport from the land surface, atmospheric boundary layer generation, and moist convection, among other processes. The global distributions of the parameters (e.g., effective soil texture at large scale) that control some of these processes are often crudely estimated; work (possibly involving calibration) is needed to improve these fields. Additional work is needed to ensure that the simulated processes interact with each other in realistic ways.
Of course, even if all model formulations, and thus the simulated coupling strength, were perfect, prediction quality would still be limited by deficiencies in our ability to assign realistic global distributions of soil moisture initial conditions. As noted above, the expected state-of-the-art in the coming years is the production of soil moisture fields through data assimilation systems utilizing satellite data; even so, these estimates will be limited by errors in the meteorological forcing fields and retrieval estimates. The incremental improvement of satellite soil moisture retrievals (or the corresponding raw radiances) on the effectiveness of the soil moistures used in a forecast system is yet to be established.
Several facets of soil moisture’s impact on precipitation and temperature forecast quality are still largely unexplored. For example, soil moisture’s contribution to the accuracy of climate predictions may be larger for certain background climatic conditions. For a given region, can we expect the impact of soil moisture to be greater under certain SST and atmospheric circulation regimes, or for modified conditions associated with global climate change (Seneviratne et al., 2006b)? The time is ripe, and modeling systems are adequately advanced to address such questions.
Finally, in regard to ISI forecasting, we note that the value of soil moisture initialization is not necessarily limited to the prediction of meteorological variables. For example, water resource estimates in regions with significant snowpack are often made months in advance by estimating snow amounts—a greater amount of snow implies a greater amount of meltwater during the spring season and thus greater streamflow. However, the future streamflow can also depend on soil moisture. If the soil is dry below a melting snowpack, much of the meltwater may infiltrate the soil and then evaporate, and would not then be available to contribute to streamflow and thereby reservoir storage. On the other hand, if the soil is wet, a greater amount























