Appendix A
Background Information on Statistical Techniques
Throughout this report, various statistical techniques are mentioned. In some cases, these techniques are used in model validation efforts, as a way of measuring the performance of predictions or forecasts. Many of the forecast “metrics” involve some sort of statistical algorithm. If a forecast system is deemed to be of low quality, the statistical techniques may provide a first step in identifying opportunities for improvements to the forecast models. Alternatively, if bias is detected in the predictions or forecast, statistical techniques can also be used to devise methods of bias-correction. In other cases, statistical techniques have been used to identify and characterize “patterns of variability” within the climate system, and serve as the foundation for a forecast system.
The following sections provide some background material on several statistical techniques that are frequently mentioned in the report. First, a table listing 11 commonly used statistical techniques is provided, listing some of the advantages and disadvantages in their application to model validation efforts and forecasting. Then, five specific sets of techniques (correlation, multiple regression, composites, eigentechniques, and kernel methods) are discussed in more detail.
Table A.1. Commonly used statistical techniques and their advantages and disadvantages.
|
Technique |
Advantages |
Disadvantages |
|
Pearson’s Correlation |
Well understood. Intuitive scale. |
Linear, sensitive to outliers, not designed to find causal relationships. |
|
Spearman’s Correlation |
Well understood. Intuitive scale. Resistant to outliers. |
Linear in the ranks. EOF/PCA Well understood. Efficient compression of large datasets. Linear. Sensitive to sampling errors. In most applications, requires the estimation of the dimensionality of the signal. If modes identification is desired, may require post processing with additional linear transformation. |
|
Nonlinear (Complex) EOF/PCA |
Can result in very efficient compression of data. |
Sensitive to sampling errors. In most applications, requires the estimation of the dimensionality of the signal. |
|
CCA/SVD |
Well understood and applied often. |
Linear. No guarantee that the cross-correlation or covariances are larger than the correlations within each variable. Often pre-processed by extracting EOFs to avoid this problem. May need post-processing with linear transformations if more than one field is desired. |
|
Cluster Analysis |
Divides data into groups based on distance. |
Numerous cluster methods available that give different results when applied to a single data set using the same distance measure. Since it is an exploratory tool, does not contain rules for assigning membership to independent observations. |
|
Compositing |
Since it involves only averaging, it is well understood. |
Unless careful pre-screening of data has been performed, it is possible that multiple modes may be averaged and unrepresentative results can emerge. |
|
Discriminant Analysis |
Well suited to separation of a finite number of categories if linear separability is present. Numerous variations exist to allow or outliers and unequal variance in the groups. Rules learned to classify can be applied to independent data. |
Linear separability is not often present in large scale problems. Variable selection may be computationally intensive. |
|
Regression |
Well understood in basic form. Many variations exist for correlated predictors, nonlinear relationships, and when outliers are present. |
Traditional multiple linear regression makes numerous assumptions that are rarely met in climate analyses. |
|
Neural networks |
Allow for fitting nonlinear relationships |
Can be complicated to fit properly. Can be computationally intensive for large datasets. Does not give good guidance on the physics of a problem as there are no constant weights. |
|
Kernel methods |
Allow for fitting nonlinear relationships. |
Must test for an appropriate kernel to fit. Can be computationally intensive for large datasets. Unless a linear programming approach is used, does not give good guidance on the physics of a problem as there are no constant weights. |
1)
Correlation Patterns
The majority of analyses that seek to establish models’ teleconnections of atmospheric variability are covariance or correlation-based. Both of these statistics measure the linear relationship between a set of variables. The covariance is the cross-product of the anomalies from the mean. Owing to this definition, covariance is used to assess eddy transports in models, since the mean is used to represent climatology. This definition underscores an implicit assumption of stationarity of the mean, which is rarely present in the atmosphere. The Pearson’s correlation coefficient, commonly just referred to as the correlation coefficient, is a scaled version of the covariance, where the covariance is divided by the standard deviation of the fields. This provides a convenient range. Both these coefficients measure the property of two (or more) fields co-varying. It is also related to the mean squared error between two fields as the variance of one field multiplied by the correlation between the two fields times the anomaly of the second field. This gives rises to its popularity in the form of the “anomaly correlation”. However, such a relationship assumes both fields are bivariate normally distributed, which is rarely the case, and that there is a linear mapping between the fields, as both correlation and covariance measure the linear portion of the relationship between fields. Relationships that are nonlinear cannot be measured by these metrics, nor does a value of zero indicate statistical independence, despite such a statement in numerous research papers. As a rule, investigators need to insure that the distributions of the variables are valid and the relationships linear before making inferences from the correlation.
Nonlinear functional relationships that are linear in the ranks can be measured by Spearman’s correlation (Grantz et al., 2007). The distribution of the ranks should be approximately normally distributed. In both types of correlation coefficients, inference will require the use of the sample size. Any serial correlation will need to be accounted for by a degree of freedom calculation or a sampling strategy to remove serial correlation.
2)
Multiple Regression
A prediction model using multiple regression gives a mean of y (predictand) conditioned upon a linear combination of the various x’s (predictors). The model is linear in the parameters, although any parameter can be a nonlinear function of other variables. Interpretation of the model is similar to the simple regression model, except the variance accounted for by each predictor is examined as well as a multiple R2 statistic. The statistical significance of each model parameter can be tested with an F-test (a multivariate extension of a t-test). An additional model assumption is that each predictor is independent of the others. This assumption is rarely met in practice. Mild deviations from independence seem to have little effect on the model, whereas moderate to large correlations between predictors can lead to model instability. This can be assessed through use of a condition number statistic. If necessary, alternative models, such as ridge regression (Peña and van den Dool, 2008) or principal component regression (Tippett et al., 2008) have been shown to hold promise in additional skill and stability when applied to highly correlated predictors, although the tradeoff for the former technique is that the unbiased property of least squares is abandoned through the addition of constraints and for the latter technique, interpretation of the predictors is often difficult. Implicit in the discussion of multiple regression is model selection to obtain the m predictors. The principle of a compact model is important and there may be many more potential predictors than m. Stepwise regression is often used to reject additional predictors (Ohring, 1972; Mercer et al., 2008).
3)
Eigentechniques (EOF, PCA, SVD, CCA)
The use of eigentechniques was pioneered by Pearson in 1902 and formalized by Hotelling (1933) in a series of papers. In meteorology, the technique was named Empirical Orthogonal Functions (EOFs) by Lorenz (1956) who applied it to decompose a pressure data set. EOFs are unit length eigenvectors. The technique begins, implicitly or explicitly, with a correlation or covariance matrix that is decomposed into two new matrices, one of eigenvalues and one of eigenvectors. The use of these two matrices has played a central role in decomposing flows in the atmosphere into “modes of decomposition”. The key ideas behind eigentechniques are to take a high dimensional problem that has structure (often defined as a high degree of correlation) and establish a lower dimensional problem where a new set of variables (e.g., eigenvectors) can form a basis set to reconstruct a large amount of the variation in the original data set. The idea is to capture as much signal as possible and omit as much noise as possible. While that is not always possible, the low dimensional representation of a problem often leads to useful results. Assuming that the correlation or covariance matrix is positive semidefinite in the real domain, the eigenvalue of that matrix can be ordered in descending value to establish the relative importance of the associated eigenvectors. Sometimes the leading eigenvector is related to some important aspect of the flow or teleconnection (Ding and Wang, 2005). In cases where the data lie in a complex domain, eigenvectors can be extracted in “complex EOFs”. Such EOFs can give information on travelling waves, under certain circumstances, as can alternative EOF techniques that incorporate times lags to calculate the correlation matrix (Branstator, 1987). An alternative scaling of the eigenvectors leads to the principal component analysis (PCA) model. Both techniques are often used to filter correlated sets of times series arranged on a grid or array of stations into modes of variation. Such a decomposition requires the estimation of the number of modes that represent a geophysical signal. The techniques developed to accomplish this tend to be ad hoc (LEV test, Craddock and Flood, 1969) or based on white noise properties of the eigenvalues (North et al., 1982; Overland and Preisendorfer, 1982). Despite the widespread use of such tests, there has never been a formal linkage between the results of these tests and the true number of eigenvectors representing signal. Certain complications in such methods are the maximum variance property of the first eigenvector and the orthogonality of subsequent eigenvectors which tends to merge and smear known modes (Richman, 1986) as well as large sampling errors associated with those eigenvectors with closely spaced eigenvalues. In some cases, post-processing with an additional linear transformation of a reduced set of eigenvectors can help to draw out the modes that agree with correlation-based teleconnections. However, such analysis depends on correct determination of the number of signals in the data (Barnston and Livezey, 1987).
Canonical correlation analysis (CCA) is an extension of EOF/PCA for cases where pairs of fields are interrelated with the idea of finding couplings between the fields. The idea is to find a pair of patterns that maximize the correlation linear combinations of the eigenvectors of each field. A variation of CCA, known in meteorological research as singular value decomposition (SVD) maximizes the covariace between fields. Both techniques have been used routinely to generate medium range forecasts (Hwang et al, 2001; Shabbar and Barnston, 1996). Since CCA is an extension of PCA, the challenges of PCA, such as identification of the proper dimensionality and the effects of maximal variance and orthogonality are present in CCA (Cherry, 1996; Cheng and Dunkerton, 1995). Moreover, there is no guarantee that the desired cross correlation structure is large. In such cases, the correlations within each field may
dominate. To avoid this problem, CCA/SVD is often pre-processed with EOF to extract uncorrelated vectors. This does solve the problem but makes interpretation that much more difficult.
Discriminant analysis is used to divide data into a number of linearly separable groups with similar membership among the variables within each group. Hence it is a discrimination and classification methodology. The function that discriminates is essentially a linear combination of the variables that is an eigenfunction. Skillful forecasts of temperature have been identified using this approach (DelSole and Shukla, 2006). Variable selection is crucial for multiple discriminant analysis (Lehmiller et al., 1997).
Another technique that is used often to find patterns of variability is cluster analysis. There are two broad families of clustering, hierarchical and non-hierarchical. These techniques have been found useful to group members of forecast ensembles (Mo and Ghil, 1988; Tracton and Kalnay, 1993). Gong and Richman (1995) present modes of rainfall variability for numerous cluster methods and distance measures to illustrate the differences between the techniques.
4)
Composites
Modes of variability can be determined through composite analysis (averaging patterns with similar features). The technique is used often by synoptic meteorologists to determine dynamic fields of interest (Chen and Bosart, 1977). The idea of compositing has been extended to multivariate analyses for modes associated with the MJO (Weare, 2003). Climatological applications of composites would benefit from lessons learned from synoptic meteorology: all members of the composite pool need to be checked for consistency prior to averaging. This insures a unimodal distribution.
5)
Kernel Techniques
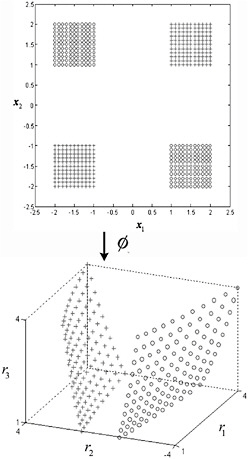
Kernel techniques use a process that replaces an inner product with a kernel and then the solution is made in high dimensional “feature” space. In comparing kernel techniques to traditional linear approaches, Lima et al. (2009) report that the kernel technique offers significant skill improvements over traditional linear methods.
One example of the use of a kernel technique is shown in Figure A.1 where two classes exist (+, 0) and cannot be separated in two-space. The kernel projects the data into three-space and a linear separation is possible. Kernel techniques have a high potential for mode identification where linear low level modes provide ambiguous separability (e.g., the Arctic Oscillation versus the North Atlantic Oscillation). The most challenging aspect of kernel methods is finding the appropriate kernel to fit. Most often experiments using linear, polynomial and radial basis functions are fit and the method that generalizes best (highest skill on independent data) is selected.