2
Climate Prediction
This part of the report begins by reviewing the concept of predictability, starting with a summary of the historical background for climate prediction. Lorenz’s work on weather prediction in the 1960s and 1970s is a foundation for present efforts. Progress in the 1980s extended prediction timescales, exploiting improved observational awareness of ENSO variability in the tropical Pacific and its associated teleconnections. Future improvements in prediction quality depend upon the ability to identify and understand patterns of variability and specific processes that operate on ISI timescales. Various processes in the atmosphere, ocean, and land offer sources of predictability; several are introduced in the following sections. Gaps in our present understanding of predictability are summarized to lay the foundation for discussion later in the report on how the future improvements are likely to be realized. In going forward, it will be necessary to assess the incremental skill gained from new sources of predictability. The methodologies to be used to quantitatively estimate prediction skill, validate models, and verify forecasts are discussed.
THE CONCEPT OF PREDICTABILITY
Lorenz in 1969 defined predictability as “a limit to the accuracy with which forecasting is possible” (Lorenz, 1969a). He later refined his view, providing two definitions of predictability (Lorenz, 2006): “intrinsic predictability—the extent to which the prediction is possible if an optimum procedure is used” and “practical predictability—the extent to which we ourselves are able to predict by the best-known procedures, either currently or in the foreseeable future.” The forecasting that interested Lorenz and others during the 1960s and 1970s, which focused on weather and the state of the mid-latitude troposphere, provided much of the framework regarding forecasting and predictability that remains applicable to longer-range forecasts of the climate system and is reviewed here. .
Atmospheric Predictability
Lorenz noted that practical predictability was a function of: (1) the physical system under investigation, (2) the available observations, and (3) the dynamical prediction models used to simulate the system. He noted in 2006 that the ability to predict could be limited by the lack of observations of the system and by the dynamical models’ shortcomings in their forward extrapolations. While estimates of the predictability of day-to-day weather have been made by investigating the physical system, analyzing observations, and experimenting with models (Table 2.1), no single approach provides a definitive and quantitative estimate of predictability.
TABLE 2.1 Historical methods for evaluating predictability and their advantages and disadvantages.
|
Method and References |
Description |
Analysis |
|
Physical System: Analytic closure (Leith, 1971) |
Assuming that the atmosphere is governed by the laws of two-dimensional turbulence, a predictability limit can be estimated from the rate of error growth implied by the energy spectrum. |
|
|
Model: (Lorenz, 1965; Tribbia and Baumhefner, 2004; Buizza, 1997; Kalnay, 2003) |
Using a dynamical model, experiments are designed to answer: How long is it expected to take for two random draws from the analysis distribution for this model and observing system to become practically indistinguishable from two random draws from the model’s climatological distribution? |
|
|
Observations: Observed Analogs (Lorenz, 1969a; Van den Dool, 1994; Van den Dool et al., 2003) |
The observed divergence in time of analogs (i.e., similar observed atmospheric states) provides an estimate of forecast divergence. |
|
The studies listed in Table 2.1 demonstrate that for practical purposes (i.e., using available atmospheric observations and dynamical models), the limit for making skillful forecasts of mid-latitude weather systems is estimated to be approximately two weeks5, largely due to the sensitivity of forecasts to the atmospheric initial conditions (see Box 2.1)6. However, their focus on weather and the state of the atmosphere excludes processes that are valuable for climate prediction. For instance, many factors external to the atmosphere were ignored, such as incoming solar radiation and the state of the ocean, land, and cryosphere. Single events, such as a volcanic eruption, that might influence predictability were not considered; nor were long-term trends in the climate system, such as global warming. In addition, the models were unable to replicate many features internal to the atmosphere, including tropical cyclones, the Quasi-Biennial Oscillation (QBO), the Madden Julian Oscillation (MJO), atmospheric tides, and low frequency atmospheric patterns of variability like the Arctic and Antarctic Oscillations. These additional features are important for the impacts that they may have on the estimates of weather predictability, as well as for their influence on predictability on longer climate timescales.
|
BOX 2.1 WEATHER AND CLIMATE FORECASTS AND THE IMPORTANCE OF INITIAL CONDITIONS Forecasts are computed as “initial value” problems: they require realistic models and accurate initial conditions of the system being simulated in order to generate accurate forecasts. Lorenz (1965) showed that even with a perfect model and essentially perfect initial conditions, the fact that the atmosphere is chaotic7 causes forecasts to lose all predictive information after a finite time. He estimated the “limit of predictability” for weather as about two weeks, an estimate that still stands: it is generally considered not possible to make detailed weather predictions beyond two weeks based on atmospheric initialization alone. Lorenz’s discovery was initially only of academic interest since, at that time, there was little quality in operational forecasts beyond two days, but in recent decades forecast quality has improved, especially since the introduction of ensemble forecasting. Useful forecasts now extend to the range of 5 to 10 days (see Figure 2.1). 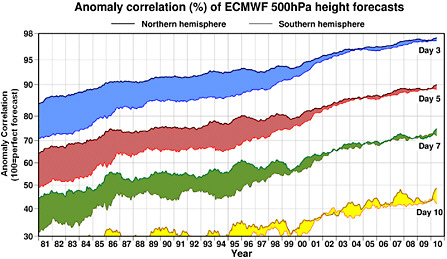 FIGURE 2.1. Evolution of ECMWF forecast skill for varying lead times (3 days in blue; 5 days in red; 7 days in green; 10 days in yellow) as measured by 500-hPa height anomaly correlation. Top line corresponds to the Northern Hemisphere; bottom line corresponds to the Southern hemisphere. Large improvements have been made, including a reduction in the gap in accuracy between the hemispheres. SOURCE: courtesy of ECMWF, adapted from Simmons and Hollingsworth (2002). |
|
The initial conditions for atmospheric forecasts are obtained through data assimilation, a way of combining short-range forecasts with observations to obtain an optimal estimate of the state of the atmosphere. Figure 2.2 shows the three factors on which the quality of the initial conditions depends: (1) good observations with good coverage, (2) a good model able to accurately reproduce the evolution of the atmosphere, and (3) an analysis scheme able to optimally combine the observations and the forecasts. The impressive improvement in 500-hPa geopotential height anomaly correlation in recent decades (Figure 2.1) has been due to improvements made in each of these three components. Since atmospheric predictability is highly dependent on the stability of the evolving atmosphere, ensemble forecasts made from slightly perturbed initial conditions have given forecasters an additional tool to estimate the reliability of the forecast. In other words, a minor error in an observation or in the model can lead to an abrupt loss of forecast quality if the atmospheric conditions are unstable. For climate prediction on ISI timescales, the initial conditions involve phenomena with much longer timescales than the dominant atmospheric instabilities. For example, the SST anomalies associated with an El Niño event need to be known when establishing the initial conditions. Essentially, the initial conditions extend beyond the atmosphere to include details on the states of the ocean and land surface. From these long-lived phenomena, predictability of atmospheric anomalies can theoretically be extended beyond approximately two weeks to at least a few seasons. 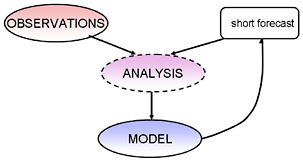 FIGURE 2.2 Schematic for data assimilation for an analysis cycle. The diagram shows the three factors that affect the initial conditions: observations, a model, and an analysis scheme. |
Predictability of the Ocean and Atmosphere
As better observations led to an improved understanding of the climate system in the 1970s and 1980s, predictions of the atmosphere beyond the limits of the “classical” predictability proliferated. Statistical forecast systems had already demonstrated that predictions for time averages of some mid-latitude atmospheric quantities could be made at well past two weeks (Charney and Shukla, 1981). Observations of ENSO made it clear that some aspects of the
tropical atmosphere could be predicted at longer lead-times as well. Observational, theoretical, and modeling studies (Horel and Wallace, 1981; Sarachik and Cane, 2010) demonstrated that there were relationships between variability observed in the tropical oceans and the variability of the extratropical atmosphere. It became clear that longer-range forecasts of atmospheric quantities could be made using predictions of the coupled ocean-atmosphere system.
Although operational, extended forecasts continued to focus on surface temperature and precipitation over continents, the atmospheric initial conditions were no longer considered important for making these forecasts; atmospheric ISI prediction was now considered a boundary value problem (Lorenz, 1975; Chen and Van den Dool, 1997; Shukla, 1998; Chu, 1999). Boundary forcing, initially from the ocean but later from the land and cryosphere (Brankovic et al., 1994), was used as the source of predictive information. This was appropriate because coupled models of the atmosphere, ocean, and land surface were still in their infancy and were not competitive with statistical prediction models (Anderson et al., 1999).
Given this context, researchers asked: if there exists a perfect prediction of ocean or land conditions, how well could the state of the mid-latitude atmosphere be predicted (Yang et al., 2004)? This question has been addressed observationally by estimating the signal-to-noise ratio. In this case the portion of the climate variance related to the lower boundary forcing is the signal, the portion of the climate variance related to atmospheric internal dynamics is the noise, and the ratio of the two represents one possible measure of predictability (e.g., Kang and Shukla, 2005). Such studies can lead to overly optimistic estimates of predictability because they assume that the boundary conditions are predicted perfectly.
There is an additional problem with this boundary-forced approach. These estimates assume that feedbacks between the atmosphere and the ocean do not contribute to the predictability. However, coupling between the atmosphere and the ocean can also be important in the evolution of SST anomalies (Wang et al., 2004; Zheng et al., 2004; Wu and Kirtman, 2005; Wang et al,. 2005; Kumar et al., 2005; Fu et al., 2003, 2006; Woolnough et al., 2007). Because the boundary-forced approach ignores this atmosphere-ocean co-variability (or any other climate system component couplings), these boundary-forced predictability estimates are of limited use.
Climate System Predictability
The techniques for estimating predictability shown in Table 2.1 can be applied to the coupled prediction problem (e.g., Goswami and Shukla, 1989; Kirtman and Schopf, 1998). However, each method is still subject to limitations similar to those mentioned in Table 2.1. Given the complexity of the climate system, estimates based on analytical closure are somewhat intractable (i.e., how can error growth rates from a simple system of equations relate to the real climate system?); approaches based on observations are limited by the relatively short length of the observational record, combined with the difficulty in identifying controlled analogs for a particular state of the climate. Non-stationarity in the climate system further reduces the chance that observed analogs would become useful in the foreseeable future, if ever. Model-based estimates are thus the most practical, but are still limited by the ability to measure the initial conditions for the climate and the mathematical representation of the physical processes.
As discussed in Chapter 1, most efforts to estimate prediction quality (or hindcast quality) are relatively recent, and involve analysis of numerous model-generated predictions for a similar
time period (Waliser, 2005; Waliser, 2006; Woolnaugh et al. 2007; Pegion and Kirtman, 2008; Kirtman and Pirani, 2008; Gottschalck et al. 2010). For example, Kirtman and Pirani (2008) reported on the WCRP Seasonal Prediction Workshop in Barcelona where the participants discussed validating and assessing the quality of seasonal predictions based on a number of international research projects on dynamical seasonal prediction (e.g., SMIP2/HFP, DEMETER, ENSEMBLES, APCC). This collection of international projects includes a variety of different experimental designs (i.e., coupled vs. uncoupled), different forecast periods, initial condition start dates, and levels of data availability. Despite these differences, there was an attempt to arrive at consensus regarding the current status of prediction quality. Several different deterministic and probabilistic skill metrics were proposed, and it was noted that no single metric is sufficiently comprehensive. This is particularly true in cases where forecasts are used for decision support. Nevertheless, the workshop report includes an evaluation of multi-model prediction for Nino3.4 SSTA, 2m-temperature and precipitation in 21 standard land regions (Giorgi and Francisco, 2000). While it was recognized that the various skill metrics used were incomplete8 and that there were difficulties related to the different experimental designs and protocols, the consensus was clear that multi-model skill scores were on average superior to any individual model (Kirtman and Pirani, 2008). Systematic efforts along the above lines for the intraseaosnal time scale have only recently begun with the development of an MJO forecast metric and a common approach to its application amongst a number of international forecast centers (Gottschalck et al. 2010) as well as the establishment of a multi-model MJO hindcast experiment (see www.ucar.edu/yotc/iso.html).
SOURCES OF PREDICTABILITY
Overview of Physical Foundations
Climate reflects a complex combination of behaviors of many interconnected physical and (often chaotic) dynamical processes operating at a variety of time scales in the atmosphere, ocean, and land. Its complexity is manifested in the varied forms of weather and climate variability and phenomena, and in turn, in their fundamental (if unmeasurable) limits of predictability, as defined above. Yet, embedded in the climate system are sources of predictability that can be utilized. Three categories can be used to characterize these sources of weather and climate predictability: inertia, patterns of variability, and external forcing. The actual predictability associated with an individual phenomenon typically involves interaction among these categories.
The first category is the “inertia” or “memory” of a climate variable when it is considered as a quantity stored in some reservoir of nonzero capacity, with fluxes (physical climate processes) that increase or decrease the amount of the variable within the reservoir over time, e.g., soil moisture near the land-atmosphere interface. Taking the top meter of soil as a control volume and the moisture within that volume as the climate variable of interest, the soil moisture increases with water infiltrated from the surface (rainfall or snowmelt), decreases with evaporation or transpiration, and changes further via within-soil fluxes of moisture through the sides and bottom of the volume. For a given soil moisture anomaly, the lifetime of the anomaly
(and thus our ability to predict soil moisture with time) will depend on these fluxes relative to the size of the control volume. Soil moisture anomalies at meter depth have inherent time scales of weeks to months. As panel (a) of Figure 2.3 shows, soil moisture anomalies exist considerably longer than the precipitation events that cause them.
Arguably, many variables related to the thermodynamic state of the climate system have some inertial memory that can be a source of predictability. Surface air temperature in a small regional control volume, for example, is a source of predictability that is very short given the efficiency of the processes (winds, radiation, surface turbulent fluxes, etc.) that affect it. If the air temperature at a given location is known at noon, its value at 12:05 PM that day can be predicted with a very high degree of certainty, whereas its predicted value days later is much more uncertain. In stark contrast, the inertial memory of ocean heat content can extend out to seasons and even years, depending on averaging depth. Examples of other variables with long memories include snowpack and trace gases (e.g., methane) stored in the soil or the ocean.
The second category involves patterns of variability—not variables describing the state of the climate and their underlying inertia, but rather interactions (e.g., feedbacks) between variables in coupled systems. These modes of variability are typically composed of amplification and decay mechanisms that result in dynamically growing and receding (and in some cases oscillating) patterns with definable and predictable characteristics and lifetimes. With modes of variability, predictability does not result from the decay of an initial anomaly associated with fluxes into and out of a reservoir, as in the first category, but rather with the prediction of the next stage(s) in the life cycle of the dynamic mode based on its current state and the equations or empirical relationships that determine its subsequent evolution. In many examples related to inertia or memory within the climate system, the atmosphere plays a “passive” and dissipative role in the evolution of the underlying anomaly. On the other hand, for the patterns of variability or feedbacks discussed here, the atmosphere plays a more active role in amplifying or maintaining an anomaly associated with processes occurring in the ocean or on land.
“Teleconnections” is a term used to describe certain patterns of variability, especially when they act over relatively large geographic distances. Teleconnections illustrate how interaction among the atmosphere, ocean, and land surface can “transmit” predictability in one region to another remote region. For example, during ENSO events, features of the planetary scale circulation (e.g., the strength and location of the mid-latitude jet stream) interact with anomalous convection in the tropical Pacific. These interactions can lead to anomalous temperature and precipitation patterns across the globe (panel b of figure 2.3). Thus, predictions of tropical Pacific sea surface temperature due to ENSO can be exploited to predict air temperature anomalies in some continental regions on the time scales of months to seasons. For air temperature, this teleconnection pattern offers enhanced predictability compared to memory alone, which would only be useful for minutes to hours. It should be noted that the predictability of teleconnection responses (in the above example, air temperature in a location outside of the tropical Pacific) will be lower than that of the source (in the above example, tropical Pacific SST) because of dynamical chaos that limits the transmission of predictability.
The third category involves the response of climatic variables to external forcing, and it includes some obvious examples. Naturally, many Earth system variables respond in very predictable ways to diurnal and annual cycles of solar forcing and even to the much longer cycles associated with orbital variations. Other examples of external forcing variations that can provide
predictability include human impacts—long-term changes in atmospheric aerosols, greenhouse gas concentrations, and land use change.
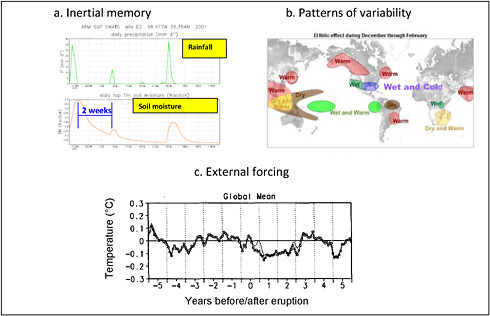
FIGURE 2.3 (a) Example of inertial memory. A positive soil moisture anomaly at the Atmospheric Radiation Measurement/Cloud and Radiation Testbed (ARM/CART) site in Oklahoma decreases with a time scale much longer than the atmospheric events that caused it. SOURCE: Greg Walker, personal communication. Soil moisture time scales measured at other sites are even longer than this (Vinnikov and Yeserkepova, 1991). (b) Example of teleconnections. Map of El Niño impacts on global climate, for December–February. SOURCE: Adapted from CPC/NCEP/NOAA (c) Example of external forcing. Global mean temperature anomaly prior (negative x-axis values) and following (positive x-axis values) volcanic eruptions, averaged for 6 events. Substantial cooling is observed for nearly 2 years following the date of eruption. The dark line has the ENSO events removed; the light line does not. SOURCE: Robock and Mao (1995).
Examples of Predictability Sources
Figure 2.4 provides a quick glimpse of various predictability sources in terms of their inherent time scales. This view, based on time scale, is an alternative or complement to the three-category framework (inertia, patterns of variability, and external forcing). Provided in the present section is a broad overview of predictability sources relevant to ISI time scales. Some of the examples will be discussed more comprehensively in later chapters.
It is important to realize that the timescales associated with sources of predictability often arise from a combination of inertia and feedback processes. Also, it should be noted that the
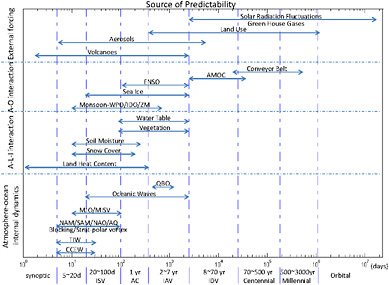
FIGURE 2.4 Processes that act as sources of ISI climate predictability extend over a wide range of timescales, and involve interactions among the atmosphere, ocean, and land. CCEW: convectively coupled equatorial waves (in the atmosphere); TIW: tropical instability wave (in the ocean); MJO/MISV: Madden-Julian Oscillation/Monsoon intraseasonal variability; NAM: Northern Hemisphere annular mode; SAM: Southern Hemisphere annular mode; AO: Arctic oscillation; NAO: North Atlantic oscillation; QBO: quasi-biennial oscillation, IOD/ZM: Indian Ocean dipole/zonal mode; AMOC: Atlantic meridional overturning circulation. For the y-axis, “A” indicates “atmosphere;” “L” indicates “land;” “I” indicates “ice;” and, “O” indicates “ocean.”
timescales in Figure 2.4 indicate the timescale of the variability associated with a particular process. This is distinct from the timescale associated with a prediction. For example, ENSO exhibits variability on the scale of years; however, information about the state of ENSO can be useful for making ISI predictions on weekly, monthly, and seasonal time scales.
As discussed in Chapter 1 (see Committee Approach to Predictability), it can be difficult to quantify the intrinsic predictability associated with any of the individual processes depicted in Figure 2.4 (i.e., for what lead-time is an ENSO prediction viable? And to what extent would that prediction contribute to skill for predicting temperature or precipitation in a particular region?). As mentioned earlier (see Climate System Predictability), prediction experiments form the foundation of our understanding. However, these experiments are rarely definitive in quantifying such limits of predictability. For example, for ENSO, there are three competing theories (inherently nonlinear; periodic, forced by weather noise; and the damped oscillator) that underlie various models of ENSO, each with its own estimate of predictability (see Kirtman et al., 2005 for a detailed discussion). At this time we are unable to resolve which theory is correct
since all yield results that are arguably “consistent” with observational estimates. To further complicate the understanding of the limits of predictability for ENSO, there are important interactions with other sources of predictability that may enhance or inhibit the predictability associated with ENSO (see Chapter 4). ENSO is just one example of how understanding what “sets” the predictability associated with a particular process is a critical challenge for the ISI prediction community. The challenge of improving forecast quality necessitates enhancing the individual building blocks (see Chapter 3) that make up our predictions systems, but it also requires a deeper understanding of the physical mechanisms and processes that are the sources of predictability.
Inertia
Upper ocean heat content
On seasonal-to-interannual time scales upper ocean heat content is a known source of predictability. The ocean can store a tremendous amount of heat. The heat capacity of 1 m3 of seawater is 4.2 x 106 joules m-3 K-1 or 3,500 times that of air and 1.8 times that of granite. Sunlight penetrates the upper ocean, and much of the energy associated with sunlight can be absorbed directly by the top few meters of the ocean. Mixing processes further distribute heat through the surface mixed layer, which can be tens to hundreds of meters thick. As Gill (1982) points out, with the difference in heat capacity and density, the upper 2.5 m of the ocean can, when cooling 1ºC, heat the entire column of air above it that same 1ºC. The ocean can also transport warm water from one location to another, so that warm tropical water is carried by the Gulf Stream off New England, where in winter during a cold-air outbreak, the ocean can heat the atmosphere at up to 1200 W m-2, a heating rate not that different from the solar constant. Stewart (2005) shows that a 100 m deep ocean mixed layer heated 10ºC seasonally stores 100 times more heat than 1 m thick layer of rock heated that same 10ºC; as a result the release of the heat from the ocean mixed layer can have a large impact on the atmosphere. Thus, the atmosphere acts as a “receiver” of any anomalies that have been stored in the ocean, and predictions of the evolution of air temperature over the ocean can be improved by consideration of the ocean state.
Soil moisture
Soil moisture memory spans intraseasonal time scales. Memory in soil moisture is translated to the atmosphere through the impact of soil moisture on the surface energy budget, mainly through its impact on evaporation. Soil moisture initialization in forecast systems is known to affect the evolution of forecasted precipitation and air temperature in certain areas during certain times of the year on intraseasonal time scales (e.g., Koster et al., 2010). Model studies (Fischer et al., 2007) suggest that the European heat wave of summer 2003 was exacerbated by dry soil moisture anomalies in the previous spring.
Snow cover
Snow acts to raise surface albedo and decouple the atmosphere from warmer underlying soil. Large snowpack anomalies during winter also imply large surface runoff and soil moisture
anomalies during and following the snowmelt season, anomalies that are of direct relevance to water resources management and that in turn could feed back on the atmosphere, potentially providing some predictability at the seasonal time scale. The impact of October Eurasian snow cover on atmospheric dynamics may improve the prediction quality of northern hemisphere wintertime temperature forecasts (Cohen and Fletcher, 2007). The autumn Siberian snow cover anomalies can be used for prediction of the East Asian winter monsoon strength (Jhun and Lee, 2004; Wang et al., 2009).
Vegetation
Vegetation structure and health respond slowly to climate anomalies, and anomalous vegetation properties may persist for some time (months to perhaps years) after the long-term climate anomaly that spawned them subsides. Vegetation properties such as species type, fractional cover, and leaf area index help control evaporation, radiation exchange, and momentum exchange at the land surface; thus, long-term memory in vegetation anomalies could be translated into the larger Earth system (e.g. Zeng et al., 1999).
Water table variations
Water table properties vary on much longer timescales (years or more for deep water tables) than surface soil moisture. Some useful predictability may stem from these variations, though the investigation of the connection of these variations to the overall climate system is still in its infancy, in part due to a paucity of relevant observations in time and space.
Land heat content
Thermal energy stored in land is released by molecular diffusion and thus over all time scales, but with a rate of release that decreases with the square root of the time scale. In practice, there is strong diurnal storage (up to 100 W m-2) of heat energy and a still significant amount over the annual cycle (up to 5 W m-2). This is particularly strong in relatively unvegetated regions where solar radiation is absorbed mostly by the soil, since vegetation has much less thermal inertia, or in higher latitudes where soil water seasonally freezes.
Polar sea ice
Sea ice is an active component of the climate system and is highly coupled with the atmosphere and ocean at time scales ranging from synoptic to decadal. When large anomalies are established in sea ice, they tend to persist due to inertial memory and to positive feedback in the atmosphere-ocean-sea ice system. These characteristics suggest that some aspects of sea ice may be predictable on ISI seasonal time scales. In the Southern Hemisphere, sea ice concentration anomalies can be predicted statistically by a linear Markov model on seasonal time scales (Chen and Yuan, 2004). The best cross-validated skill is at the large climate action centers in the southeast Pacific and Weddell Sea, reaching 0.5 correlation with observed estimates even at 12-month lead time, which is comparable to or even better than that for ENSO prediction. We have less understanding of how well sea ice impacts the predictability of the overlying atmosphere.
Patterns of Variability
Different components of the climate system, each with their own inertial memory, interact with each other in complex ways. The dynamics of the feedbacks and interactions can lead to the development of predictable modes, or patterns, of variability.
It should be noted that the descriptions for the patterns of variability provided in the following subsections describe their “typical” behavior, focusing on commonalities among observed events and the mechanisms that drive the phenomena. In reality, the manifestation or impact of a pattern may differ from these “typical” cases since the various patterns of variability can be affected by one another as well as by the unpredictable “noise” inherent to the climate system, especially in the atmosphere. For example, not all ENSO events have the same features, and in some cases, these differences among events can be understood from interactions between ENSO and the MJO (see the MJO case study in Chapter 4).
Low-frequency equatorial waves in the atmosphere and ocean
The equator provides an efficient wave guide by which tropical dynamical energy is organized, propagated, and dissipated. In the atmosphere, equatorial Kelvin and Rossby waves and mixed Rossby-Gravity waves (Matsuno, 1966) are observed. Due to the moist and vertically unstable nature of the tropics, these low-frequency waves are often associated with convection and are referred to as convectively-coupled equatorial waves (CCEWs) (Wheeler and Kiladis, 1999; Kiladis et al., 2009). The spatial scales of these disturbances can be quite large (on the order of thousands of kilometers), and their time scales for propagating across ocean basins can be of the order of days to weeks. Figure 2.5 shows a time-longitude plot of equatorial outgoing longwave radiation (OLR) anomalies, produced following a wavenumber-frequency analysis. OLR is a good proxy for deep tropical convection, and the colors in Figure 2.5 show areas of enhanced (hot colors) or suppressed (cool colors) convection. These patterns in OLR correspond to characteristic types of waves (green, blue, and black ovals), illustrating that variability in the tropical atmosphere is consistent with the simplified theory of Matsuno (Kiladis et al., 2009). Figure 2.5 also demonstrates the manner in which these waves are manifest in relation to the typical background variability. Although complicated by their coupling to atmospheric convection, the organization and propagation of these low-frequency waves provides an element of predictability for the tropical atmosphere and possibly the extra-tropics via teleconnections.
Analogous to the discussion of the atmosphere above, the equatorial ocean supports the presence of equatorial wave modes, such as the Kelvin, Rossby and mixed-Rossby gravity modes. One simplifying aspect for their presence in the ocean is that, in contrast to the atmosphere, no convection or phase changes are involved. Because the equivalent depth of the ocean is considerably smaller than that for the atmosphere, its propagation speeds are much slower, and thus the time scale (and the predictability that arises from it) is much longer (e.g., a Kelvin wave takes about 2–3 months to cross the Pacific Ocean). These waves play a crucial role in the ocean thermocline adjustment and ENSO turnaround, as discussed below.
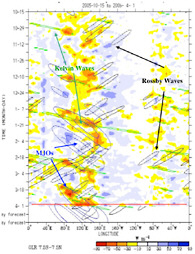
FIGURE 2.5 Some atmospheric waves offer an important source of predictability. The time-longitude diagram depicts the speed and direction of propagation that Kelvin waves (green ovals), Rossby waves (black ovals), and waves associated with the MJO (blue ovals) can exhibit in the tropics. The dense shading, which often overlaps with the position of the ovals, corresponds to anomalies in outgoing longwave-radiation (OLR); positive OLR anomalies indicate clear skies and suppressed convection; negative OLR anomalies indicate enhanced convection. SOURCE: Adapted from Wheeler and Weickmann (2001).
Madden-Julian Oscillation (MJO)
Another fundamental mode of tropical convectively-coupled wave-like variability is the Madden-Julian Oscillation (MJO; Madden and Julian, 1972, 1994). MJOs operate on the planetary scale, with most of the convective disturbance and variations occurring in the Indo-Pacific warm pool regions. The typical time scale of these quasi-periodic disturbances is of the order of 40–50 days. They tend to propagate eastward in boreal winter and north and/or northeastward in boreal summer. They strongly influence the onsets and breaks of the Australian and Asian monsoons and are sometimes referred to as monsoon intraseasonal variability (MISV) or oscillation (MISO). As with the CCEWs mentioned above, they are thought to be a source of both local predictability and predictability in the extra-tropics. The MJO and its associated predictability are discussed in more detail in Chapter 4 of this report. Figure 2.6 illustrates composite MJO events for boreal summer (May–October).
SST and mixed layer feedback on subseasonal time scales
The large/planetary spatial and subseasonal time scales of the CCEWs and MJO discussed above, along with the often strong impact of these phenomena on surface fluxes via wind speed and cloudiness, can result in significant modulation of the ocean surface mixed layer,
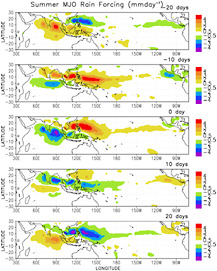
FIGURE 2.6 Characteristic rainfall patterns (mm per day) before, during, and following an MJO event during the boreal summer (May–October). Dry anomalies are indicated by “cool” colors (green, blue, purple) and wet anomalies are indicated by “hot” colors (yellow, orange, red). SOURCE: Waliser et al. (2005).
with variations in depth on the order of tens of meters and in temperature of the order of a degree. This process can impart a feedback onto the atmospheric wave processes which influences their subsequent evolution (e.g. amplitude, propagation speed).
Annular Modes (Northern or Southern, NAM or SAM)
The Annular Modes, also refereed to as the Arctic Oscillation (Figure 2.7) in the Northern Hemisphere, or the Antarctic Oscillation in the Southern Hemisphere, are dominant modes of variability outside the tropics. They are established on a weekly time scale due to atmospheric internal dynamics (such as mean flow-wave interaction or stratosphere-troposphere interaction). They offer some predictability on seasonal time scales through longer-timescale persistence of stratospheric winds (Baldwin and Dunkerton, 1999). The modes can influence surface temperature and precipitation, especially the frequency of extreme events (Thompson and Wallace, 2001).
The manifestation of the Arctic Oscillation in the Atlantic sector is commonly referred to at the North Atlantic Oscillation (NAO). An index for the NAO is typically formed from the difference in sea-level pressure between the Azores and Iceland. High index values correspond to stronger westerly flow across the North Atlantic, an intensification and northward shift of the storm track (Rogers, 1990) and warmer and wetter winters in northern Europe (Hurrell 1995). Covarying with the NAO there is an associated tripole pattern of sea surface temperature anomalies (Deser and Blackmon 1993).
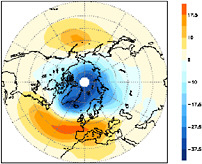
FIGURE 2.7 Characteristic pattern of anomalous sea level pressure (SLP; in hPa) associated with the positive polarity of the Arctic Oscillation (AO) in the winter. Blue indicates lower than normal SLP and red indicates higher than normal SLP; this phase of the AO exhibits an enhanced westerly jet over the Atlantic Ocean in the mid-latitudes. The North Atlantic Oscillation can be thought of as the portion of the AO pattern that resides in the Atlantic sector. SOURCE: Adapted from Thompson and Wallace (2000).
The NAO is the single largest contributing pattern to European interannual variability and plays an important role in predictions of European winter climate. However, the ability to predict the NAO on seasonal timescales is limited in current generation of models used for seasonal forecasting. There is some evidence that variability in the Atlantic Gulf Stream can influence the long-term variability of the NAO (Wu and Gordon, 2002). In addition, there is evidence of forcing of the NAO by ENSO (Bronniman et al., 2007; Ineson and Scaife 2009) and the stratospheric Quasi-Biennial Oscillation (Boer and Hamilton 2008).
Stratosphere-Troposphere Interaction, Quasi-Biennial Oscillation (QBO)
Since the stratosphere can interact with the troposphere, knowledge of the state of the stratosphere can serve almost as a boundary condition when attempting to simulate the troposphere. The stratospheric circulation can be highly variable, with a time scale much longer than that of the troposphere. The variability of the stratospheric circulation can be characterized mainly by the strength of the polar vortex, or equivalently the high latitude westerly winds. Stratospheric variability peaks during Northern winter and Southern late spring. When the flow just above the tropopause is anomalous, the tropospheric flow tends to be disturbed in the same manner, with the anomalous tropospheric flow lasting up to about two months (Baldwin et al., 2003a, 2003b). Generally, the surface pressure signature looks very much like the North Atlantic Oscillation or Northern Annular Mode. Surface temperature signals are also similar to those from the NAO and SAM and there are associated effects on extremes (Thompson et al., 2002). In sensitive areas such as Europe in winter, experiments suggest that the influence of stratospheric variability on land surface temperatures can exceed the local effect of sea surface temperature.
Sudden stratospheric warming events serve as an extreme example of how the stratosphere could serve as a source of predictability. During a sudden warming event the polar vortex abruptly (over the course of a few days) slows down, leading to an increase in polar stratospheric temperature of several tens of degrees Kelvin. Although attenuated, over the course
of the following weeks the warming signal migrates downward into the troposphere with signals that can be detected in the surface climate approximately a month following the warming event (Limpasuvan et al., 2004).
Additionally, the Quasi-Biennial Oscillation (QBO) of the stratospheric circulation offers a source of predictability for the tropospheric climate. The stratospheric QBO in the tropics arises from the interaction of the stratospheric mean flow with eddy fluxes of momentum carried upward by Rossby and gravity waves that are excited by tropical convection. The result is an oscillation in the stratospheric zonal winds having a period of about 26 months. While our weather and climate models do not often resolve or represent the QBO well, it is one of the more predictable features in the atmosphere, and it has been found to exhibit a signature in surface climate (Thompson et al., 2002).
Tropical Instability Waves (TIWs) in the ocean
TIWs are most prevalent in the eastern Pacific Ocean and are evident in SST and other quantities such as ocean surface chlorophyll and even boundary-layer cloudiness, particularly just north of the equator. They arise from shear-flow and baroclinic instabilities and result in westward propagating wave-like features having length scales on the order of 1000s of km and time scales of about 1–2 weeks. There is evidence that they may affect the overlying atmosphere. (Hoffman et al., 2009). That the strong SST gradients associated with the TIWs affect the surface winds has been documented by Chelton et al. (2001). Song et al. (2009) suggest that atmospheric models should improve the realism of their coupling between the atmosphere and ocean mesoscale variability in SST in order to correctly capture small scale variability in the wind field.
El Niño-Southern Oscillation (ENSO), involving subsurface ocean heat content
The evolution of ENSO can be predicted one to a few seasons in advance using coupled atmosphere-ocean models (e.g., Zebiak and Cane, 1987), and SST anomalies in the tropical Pacific Ocean can contribute to predictions of the global atmospheric circulation at seasonal leads (e.g., Shukla, 1998). Accurate prediction of ENSO is a key objective and benchmark of many operational seasonal forecasting efforts, as discussed in more detail in Chapter 4.
Rossby wave energy propagation in the atmosphere underlies important teleconnections involving ENSO, and can be understood by considering relatively basic climate dynamics. Rossby waves conserve absolute vorticity. Hence away from sources and sinks, north-south transport of the vorticity from the earth’s rotation is balanced by advective transport of wave disturbance vorticity. As a consequence, in the mid-latitudes where large scale winds are predominantly westerly, wavelike disturbances are possible in the wind, pressure, and temperature patterns, whereas in the tropics where easterly winds are dominant, forced disturbances remain localized. These waves provide teleconnections between the tropics and the midlatitudes.
The teleconnections associated with ENSO can be profoundly important because many populated areas would otherwise not be affected by this source of predictability. Figure 2.3 (panel b), for example, illustrates some of the teleconnections associated with the ENSO cycle. The positive phase of the ENSO cycle tends to promote warm conditions in the northeast United
States, even though this area is not involved in the dynamics underlying ENSO. In essence, the northeast United States is a passive recipient of ENSO predictability through a global-scale teleconnection process.
ENSO itself can be related to other patterns of variability. For example, westerly wind bursts associated with the MJO may help to trigger ENSO events (see the ENSO case study in Chapter 4). Also, Yuan (2004) describes a teleconnection process between ENSO and the Antarctic Dipole, a separate climate mode. ENSO forcing triggers the Antarctic Dipole, with implications for sea ice prediction at seasonal timescales.
Indian Ocean Dipole/Zonal Mode (IOD/IOZM)
A coupled mode of interannual variability has been found in the equatorial Indian Ocean in which the normally positive SST gradient is significantly weakened or reversed for a period on the order of a season (Saji et al., 1999; Webster et al., 1999). It can result in significant regional climate impacts, such as in east Africa and southern Asia. The independence of this mode and its connections to ENSO are still being investigated, but in any case the Indian Ocean Dipole/Zonal Mode (IOD/IOZM), like ENSO, appears to offer an intermittent source of interannual predictability. Similar to ENSO, the IOD/IOZM involves equatorial SST-wind-thermocline/upwelling feedback (Bjerknes, 1969); however, in contrast to ENSO, it also involves off-equatorial, SST-convection-atmospheric Rossby wave interaction (Li et al., 2003; Wang et al., 2003). The latter is strongly regulated by seasonal reversal of the monsoon circulation, hence the IOD/IOZM lasts only a season or two. The off-equatorial, SST-convection-Rossby wave interaction can maintain cooling of western North Pacific SST and anomalous anticyclonic circulation during the decaying phase of ENSO, providing a source of predictability for the East Asian summer monsoon (Wang et al., 2000).
External Forcing
Greenhouse gases (CO2, etc.)
Greenhouse gases have a direct impact on the radiation balance of the atmosphere: increases in greenhouse gases warm the global climate. The non-stationarity associated with this climate change is an important component of climate forecasts even on ISI timescales. For example, the NOAA Climate Prediction Center uses optimal climate normals and other empirical techniques to capture this non-stationarity in climate forecasts (Huang et al., 1996a; Livezey et al., 2007). However, regional details of this climate change are difficult to model numerically due to the myriad important feedbacks that need to be taken into account. These include feedbacks due to the enhancement of water vapor in the warming atmosphere and the associated changes in cloudiness and snow/ice amount, all of which can affect the radiation budget. In addition, there are feedbacks from the carbon cycle itself (including the release of additional greenhouse gases in northern latitudes as permafrost melts), the ocean thermohaline circulation, changes in the biosphere, and so on.
Anthropogenic Aerosols
Atmospheric aerosols, which affect the radiation budget of the Earth, include major human-related components that change with the nature of human activities, and thus which may be predictable. The human-related components include sulfate aerosols from fossil fuel combustion and organic aerosols from biomass burning and land use change.
The effect of changes in aerosols on precipitation at ISI timescales could be important. Bollasina and Nigam (2009) have shown that elevated aerosol concentrations over the Indian subcontinent can accompany periods of reduced cloudiness, increased downward shortwave radiation, and ultimately a delayed onset of the monsoon. However, the role of aerosols as the “cause” of a decrease or delay in precipitation is not yet confirmed—more research on sub-seasonal timescales is required to isolate the effect of aerosols from the influence of the large-scale synoptic flow and associated changes in precipitation.
Land use change
Humans have had a marked impact on the character of the land surface through deforestation, agricultural conversion, and urbanization. This change in surface character can have a long-term impact on surface energy and water budgets (e.g., deforested land may generate less evapotranspiration than forested land), which in turn can have a long-term impact on the rest of the climate system.
Fluctuations in solar output
The sun provides the energy that powers the Earth’s climate system. Its output varies slightly with an 11-year cycle that is highly predictable because it is nearly periodic. Larger changes may occur on longer time scales, but in the absence of measurements, these changes cannot be quantified beyond a statement that they appear to be small compared to the signal seen from greenhouse gases. As discussed by Haigh et al. (2005), it is likely that the mechanism that links solar fluctuations to surface climate involves the communication of anomalies between the stratosphere and troposphere, which is discussed in the “Gaps in Our Knowledge” section in this chapter.
Volcanoes and other high-impact modifications of atmospheric composition
There are a number of rare external forcing events that can cause a sudden drastic change to the atmospheric burden of aerosols, trace gases, and particulates. Volcanoes are one example. Major eruptions are relatively rare (less than one per decade) but can quickly inject large volumes of material high into the atmosphere. The effects on the climate system can be felt for years afterward, typically as a cooling of the global mean temperature (Robock and Mao, 1995). The impacts of major eruptions on temperature distributions over the continental United States can be larger than those from internal variations of the climate system discussed earlier in this section (Bradley, 1988). Shortened growing seasons caused by an overall reduction of solar radiation reaching the ground could have negative impacts on particular crops in some regions.
Forest fires provide another example of relatively rapid changes in atmospheric composition that can affect climate on ISI time scales. The Indonesian fires in 1997–98 helped to exacerbate the very strong El Niño drought. The aerosol loading altered regional radiative
balances (Davison et al., 2004), affecting precipitation in ways that were different from those predicted on the basis of the El Niño event (Graf et al., 2009; Rotsayn et al., 2010).
Other rare events that could significantly modify atmospheric composition include nuclear exchange (Robock et al., 2007) or impacts from space. While most of these high impact events cannot be predicted with any accuracy, intraseasonal to interannual climate predictions subsequent to the event would be affected by the changed atmospheric composition. Given a modern climate prediction system, it should be possible to observe and analyze the concentration of injected material in the atmosphere and produce ISI forecasts (Ramachandran et al., 2000).
Gaps in Our Knowledge
Our understanding of ISI climate predictability—both of its sources and extent—is still far from complete. Numerous gaps still exist in our observations of climate processes and variability, in our inclusion of the wide range of relevant processes in models, and in our knowledge of the sources of predictability:
-
We cannot yet claim to have identified all of the reservoirs, linkages, and teleconnection patterns associated with predictability in the Earth system. For many of the predictability sources we have identified, we cannot claim to understand fully the mechanisms that underlie them. The observational record contains many non-stationary trends that may relate to predictability but are not yet adequately explained. The science is proceeding but is encumbered by the overall complexity of the system.
-
The models that have been used to evaluate the known sources of predictability and to make forecasts are known to be deficient in many ways. Many key processes associated with predictability occur at spatial scales that cannot be resolved by current models. Examples in the atmosphere include cumulus convection, boundary-layer turbulence, and cloud-aerosol microphysics; examples in the ocean include horizontal transports associated with eddies and vertical mixing. In addition, processes associated with the coupling of the ocean or the land surface to the atmosphere through the exchanges of heat, fresh water, and other constituents can be difficult to resolve. The models thus rely on parameterizations, which are simple approximations that often have to be “tuned”, making them undependable in untested situations. A wealth of literature is available on the deficiencies of current, state-of-the-art climate models; it indicates that currently available dynamical models do not always outperform simple empirical models or persistence metrics.
-
Even if the models used were perfect—even if they included and represented accurately all physical and dynamical processes relevant to predictability at adequate spatial and temporal resolution—they would still be limited in their ability to make accurate forecasts by deficiencies in our ability to initialize prognostic fields.
The degree to which these gaps limit our ability to make forecasts—or, stated another way, the improvement we could make in forecasts if these gaps were fully addressed—is difficult to ascertain. Exploring sources of predictability, in particular addressing gaps in our understanding of these sources, might yield substantial improvements in forecast performance. Here we briefly outline several sources of predictability for which gaps in understanding can be clearly delineated.
Madden-Julian Oscillation
Gaps in our understanding of the MJO are discussed in detail in Chapter 4. Of primary importance, dynamical models exhibit systematic biases in representing the MJO. These biases could be a manifestation of many processes that are poorly represented and difficult to observe, including coupling between the ocean and atmosphere, shallow and deep convection, cloud microphysics, and cloud-radiation interactions. Additionally, it is still an open question as to how to best organize model experiments and pose model-observation comparisons for identifying model inadequacies. The MJO Working Group, formed under the auspices of U.S. CLIVAR, brought together representatives of the modeling community to address these gaps. This activity has since been extended through the formation of the WCRP-WWPR/THORPEX YOTC MJO Task Force (see http://www.ucar.edu/yotc).
Stratosphere
The stratospheric aspects of ISI prediction can only be captured by models that properly simulate stratospheric variability. Thus far, the stratosphere’s potential to improve ISI forecasts is largely untapped. To take advantage of this predictability source, it is essential that models used for seasonal forecasting simulate the intense, rapid shifts in the stratospheric circulation, as well as the downward propagation of circulation anomalies through the stratosphere. In addition, models need to be able to simulate the poorly understood connections between lower stratospheric and tropospheric circulations.
To maximize predictability from stratospheric processes, forecasting systems also need to predict stratospheric warmings and other variability at as long a lead time as possible. There are coordinated international experiments underway to examine how stratospheric processes impact ISI forecast quality.
Ocean-atmosphere feedbacks
The two-way interaction between the ocean and the atmosphere plays a very important role in ISI predictability. This interaction can manifest itself as decreased thermal damping, as in the case of the ocean mixed layer response to atmospheric forcing, or as quasi-periodic evolution of upper ocean heat content, as in the case of ENSO. Subgrid-scale processes, such as deep convection and stratus clouds in the atmosphere, or coastal upwelling in the ocean, are important components of this ocean-atmosphere interaction. Our current computational capabilities are insufficient to fully resolve these processes in numerical models, and gaps in our scientific knowledge of these processes limit our ability to parameterize them accurately.
Poor simulation of ocean-atmosphere feedbacks degrades the skill of ISI predictions though systematic as well as random errors. The systematic errors affect the ensemble-mean forecast and also manifest themselves as climate biases in ISI forecast models. Errors in the representation of low-level stratus in the vicinity of the coastal upwelling regions off the coasts of South America and Africa are a well-known example of the climate bias associated with ocean-atmosphere feedbacks. The random errors associated with the feedbacks can lead to incorrect estimation of the spread in an ensemble forecast. In the case of ENSO prediction,
random errors associated with the subgrid-scale parameterizations in the atmospheric model are believed to be responsible for the weak ensemble spread in ENSO forecasts.
Cryosphere
Generally, ISI prediction models use climatological sea ice or initialize a sea ice model with climatology. Despite the potential for prediction, the effects of sea ice are poorly included in ISI prediction models. From a simple energetic consistency perspective, active sea ice models that capture the relevant feedbacks need to be included in the ISI models. There is a clear need to identify the remote effects (and causes) of sea ice anomalies and understand associated processes and influence on forecast quality. Land ice (Antarctic and Greenland ice caps, glaciers) is similarly treated very simply, but it is considered to change on timescales too long to affect ISI variability.
Snow in the Northern Hemisphere is a highly variable surface condition in both space and time. Its impacts on the surface energy and water budgets make it a viable candidate for contributing to atmospheric anomalies and ISI predictability. The potential role for knowledge of snow cover anomalies to contribute to forecasts of the Northern Hemisphere winter temperature and East Asian winter monsoon has been mentioned in the Inertia subsection. However, operational models have yet to exploit this source of predictability. Models typically have some initialization and representation of snow cover effects, but the quality and impact of these effects are largely untested.
Soil Moisture
Soil moisture initialization as a source of subseasonal prediction quality is discussed in greater detail in Chapter 4. Although soil moisture can be initialized globally with current Land Data Assimilation System (LDAS, see Chapter 3) frameworks, the accuracy of the initialization could be improved with better measurements of (for example) rainfall and radiation, and it will presumably improve further with the advent of true and operational assimilation of land surface prognostic states. Improved estimates of land parameters (e.g., active soil depth, soil texture) would also help; accuracy in these estimates, which affect the simulation of surface hydrology and thus the surface energy balance, is currently limited by insufficient observational data. Statistical optimization of these parameter values may prove fruitful.
Arguably, in regard to ISI forecasting, the largest “gap” in the soil moisture realm is the degree of uncertainty in the strength of land-atmosphere coupling—our lack of knowledge of the degree to which soil moisture variations in nature affect variations in precipitation and air temperature. Such coupling strength cannot be measured directly with instruments (it can only be inferred indirectly at best), and the estimates of coupling strength quantified with modeling systems vary widely (Koster et al., 2006), indicating a substantial uncertainty in our knowledge of how best to model the relevant underlying physical processes such as evaporation, the structure of the boundary layer, and moist convection. Evaluating these individual components is thus important, but it is currently hindered by data availability. For example, direct joint measurements of evaporation and soil moisture at the hundred-kilometer scale are non-existent, making difficult the evaluation of whether model-generated evaporation fluxes respond realistically to soil moisture variations. Such gaps imply a need for joint model development and
observational analysis, focusing on all of the physical processes connecting soil moisture to atmospheric variables.
Non-stationarity
Many statistical models employ assumptions regarding stationarity in the data (i.e., the statistics associated with the predictand do not depend on the time of sampling). However, long term trends associated with global warming and other alterations to the climate system (e.g., changes in land cover) demonstrate that the requirements of stationarity are unlikely to be met for many time series of climate data. In addition to trends, examples of non-stationarity include alterations in the variability of sources of predictability by the annual cycle (i.e., the impact of the annual cycle on ENSO), or by interactions among sources of predictability. Although optimal climate normals (e.g. Lamb and Changnon, 1981; Huang et al., 1996a) offer a valuable statistical tool for dealing with non-stationarity, a better physical understanding is needed regarding the effect of trends on the sources of predictability as well as the ways in which the variability associated with a source may be non-stationary.
METHODOLOGIES USED TO QUANTITATIVELY ESTIMATE PREDICTION SKILL
Prediction skill has been studied in depth since the early 1900s when Finley claimed considerable skill in forecasting tornadoes. Nearly simultaneously, recognition of the limitations of measuring skill surfaced (Murphy, 1991; 1993) resulting in the modern definition of skill as the accuracy of a forecast relative to some known reference forecast, such as climatology or persistence. In Finley’s case, his claims of skill were relative to random forecasts.
The skill, or more generally the quality, of forecasts rests on all aspects of the forecast process: the assimilation of observed data for initialization, the completeness and accuracy of the observed data itself, the model(s), and the manner in which the models are employed and interpreted when producing the forecast. These elements and how they come together will be discussed in detail in Chapter 3. Here, the approaches and metrics commonly used to estimate the quality of a prediction or a model are described. In addition, discussion is offered for some newer and lesser-used metrics that could complement existing ones.
No single metric can provide a complete picture of prediction quality, even for a single variable. Thus, a suite of metrics needs to be considered (WMO SVS-LRF, 2002; Jolliffe and Stephenson, 2003), particularly when new models or forecast systems are compared with previous versions. Within any meaningful suite of metrics, one needs to consider the quality of the probabilistic information. The climate system is inherently chaotic, and our ability to measure its initial state is subject to uncertainty; thus any predicted or simulated representation of the climate needs to be probabilistic. While increased accuracy is often the goal of model or forecast improvements, the improved representation of some physical process in a model might not lead to increased accuracy, but it might better quantify the uncertainty in variables influenced by that process.
This section is broken into two subsections: model validation and forecast verification. The forecast verification section addresses the various metrics that are used to assess the quality of climate forecasts, typically for temperature and precipitation. As a good quality model is an
obvious prerequisite to a good quality forecast, the section on model validation is presented first. Model validation may incorporate some of the same metrics as used in forecast verification, but it involves more because the model contains the physical processes in addition to the desired prediction fields. Model validation is typically performed prior to using a model for real-time forecasting in order to design statistical corrections for systematic model biases and to better understand the model’s variability characteristics, such as accuracy of regional precipitation anomalies under El Niño conditions or the strength and timescale of the MJO.
Model Validation
Comparing a model environment to the observed conditions is a difficult task. Starting with the observed climate, there are numerous scales of variability that cannot be resolved, much less measured at regular intervals. As a result, any comparison would use an incomplete picture of the atmosphere or ocean. The “incompleteness” of the available observations constitutes sampling error. On a practical level, since measurement systems are not homogeneous in space and time, scientists select those variables that are considered most important. The problems become more complicated if a set of observations and model predictions are not available or valid over a common period. No numerical model is perfect, hence model errors are generated. Therefore, the observations and model predictions only can be collected to form two incomplete and imperfect probability density functions (PDFs), which provide a basis for comparison.
An example of several PDFs associated with predictions of SST in the tropical Pacific Ocean is shown in Figure 2.8. The initial prediction is shown in green. Relative to this PDF, the subsequent PDFs (red and blue) exhibit higher probabilities for warmer temperatures. This shift to warmer temperatures was in fact reflected by the verification: the observed temperature anomaly was just below 0.8ºC, in between the peaks of the two later PDFs. The standard deviation of the three PDFs is a function of lead-time, although the dependence is perhaps surprisingly small here. The relatively small dependence reflects the relatively large set of available tools and the fact the forecast uncertainty with these tools is large.
A realistic model strives to capture the full variability of the climate system. In particular, such a model needs to capture the full PDF and the temporal and spatial correlations of the observations, even if the forecast information to be disseminated is only a summarized version of that PDF. Additionally, PDFs allow for identification of multimodal distributions, whereas summary statistics (e.g., means, variances, skewnesses) cannot. Several goodness-of-fit tests exist that can check for a significant agreement between the observed and simulated PDFs. When such a test is not practical, the mean and variance should be compared between the observations and model, as a minimum, and the skewness, if possible. Skewness differences can point to processes not being captured, as well as to nonlinearities. Any statistical analysis of these PDFs, particularly ones that attempt to assess skill or significance, will hinge on specific assumptions of the tests applied. A sufficiently large sample size will show the models’ depiction of the atmosphere or ocean to differ from that of the observations. For those interested in comparing models to the observed world, this leaves us at an interesting juncture, one that may not have an answer without simplification (Oreskes et al., 1994). Can an experiment be designed to answer the question, “How good is a model or prediction?” Since we do not understand all of the processes and interactions that would lead to a perfect prediction, a strict validation is not possible. Additionally, it is possible that a model prediction can verify correctly
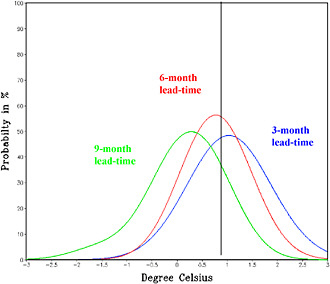
FIGURE 2.8 Examples of probabilistic predictions for Nino3.4 SST anomaly, represented by probability density functions (PDFs). The green curve is the prediction with the longest lead time (9 months), followed by the red (6 months) and blue (3 months) curves. With shorter lead times, the PDF for the prediction shifts to progressively warmer temperatures. The observed value for Nino3.4 SST anomaly is indicated by the vertical black line (0.78ºC). SOURCE: International Research Institute for Climate and Society (IRI).
for the incorrect reason. Although a perfect validation is not possible, obtaining a useful comparison is possible if one recognizes the level of uncertainty associated with the observations and model. Moreover, constructing specific hypothesis tests is a viable alternative. One might pose the question as “what aspect of the distribution of the observed atmosphere matches that of the atmosphere simulated by numerical models?”
Statistical Techniques for Identifying and Predicting Modes of Variability
The climate system is characterized by recurrent patterns of variability, sometimes referred to as modes of variability, which include ENSO, NAO, etc. Often, the identification of modes linking remote locations in the atmosphere or the ocean-atmosphere is useful for medium-to long-range prediction (Reynolds et al., 1996; Saravanan et al., 2000). Numerous methodologies have been applied to identify such modes, ranging from linear correlation to multivariate eigentechniques (Montroy et al., 1998) and nonlinear methods (Lu et al., 2009; Richman and Adrianto, 2010). Definitions of these techniques may be found in Wilks (2006) and a summary of their use for mode identification is contained in Appendix A. Often, as the time scale increases, the nonlinear contribution to the modes tends to be filtered. However,
Athanasiadis and Ambaum (2009) note that the maintenance and evolution of low frequency variability arise from inherently nonlinear processes, such as transient eddies, on the intraseasonal time scale. This suggests that linear techniques may not fully capture the predictability associated with the modes, and the use of nonlinear techniques needs to be explored (e.g., Kucharski et al., 2010).
Merits of Nonlinear Techniques
To date, nearly all mode identification has been limited to linear analyses. In fact, we have defined our concept of modes through linear correlations and empirical orthogonal functions (EOFs)/principal component analysis (PCA) as those were the techniques that were computationally feasible at the time. Recently, nonlinear mode identification has begun to emerge as efficient nonlinear classification techniques have developed and as computational power has increased. To assess the degree of nonlinearity, the skill of nonlinear techniques can be compared to that derived from traditional linear methods (Tang et al., 2000). Forecasters can investigate if extracting the linear part of the signal is sufficient for prediction. On the intraseasonal time scale, when monsoon variability has been probed by a nonlinear neural network technique (Cavazos et al., 2002), a picture emerges with nonlinear modes related to the nonlinear dynamics embedded in the observed systems (Cavazos et al., 2002) and model physics (Krasnopolsky et al., 2005). Nonlinear counterparts to PCA, such as neural network PCA, have been shown to identify the nonlinear part of the ENSO structure (Monahan and Dai, 2004). By using a nonlinear dimension reduction method that draws on the thermocline structure to predict the onset of ENSO events, Lima et al. (2009) have shown increased skill at longer lead times in when compared to traditional linear techniques, such as EOF and canonical correlation analysis (CCA). Techniques have also been applied to cloud classification (Lee et al., 2004), wind storm modeling (Mercer et al., 2008) and classification of tornado outbreaks (Mercer et al., 2009). Some nonlinear techniques, such as neural networks, are sensitive to noisy data and exhibit a propensity to overfit the data that they are trained on (Manzato, 2005), which can limit their utility in forecasting. Careful quality control of data is essential prior to the application of such methods. To assess the signal that is shared between the training and testing data, some form of cross-validation is typically required (Michaelson, 1987). Techniques include various forms of bootstrapping (Efron and Tibshirani, 1993), permutation tests (Mielke et al., 1981), jackknifing (Jarvis and Stuart, 2001) and n-fold cross validation (Cannon et al., 2002).
Kernel techniques, such as support vector machines, kernel principal components (Richman and Adrianto, 2010), and maximum variance unfolding, avoid the problem of finding a local minimum and overfitting. Kernel techniques have a high potential for mode identification where linear modes provide ambiguous separability (e.g., the overlapping patterns of the Arctic Oscillation and the North Atlantic Oscillation).
Forecast Verification
Finley’s tornado forecasts were more skillful than random forecasts, according to the metric he was using, which tabulated the percentage of correct forecasts. It credited forecasts of ‘no tornado’ on days with no tornadoes, and tornadoes were present on less than 2% of the days.
It turns out that if he had always predicted “no tornado” his skill would have been even greater (Jolliffe and Stephenson, 2003). This example illustrates the value in considering what aspect of forecast quality a metric should measure, and the baseline against which it is assessed. The particular assessment of forecast quality often depends on what characteristics of the forecast are of greatest interest to those who would use the information. No one verification measure can capture all aspects of forecast quality. Some measures are complementary, while others may provide redundant information. This section outlines several recommended (WMO SVS-LRF, 2002) and commonly-used metrics for verifying forecasts, and which aspects of forecast quality they address (see Jolliffe and Stephenson, 2003).
WMO’s Standard Verification System (SVS) for Long Range Forecasts (LRF) (2002) outlines specifications for long-range (monthly to seasonal) forecast evaluation and for exchange of verification scores. The SVS-LRF provides recommendations on scores for both deterministic and probabilistic forecasts. For deterministic forecasts, the recommended metrics are the mean square skill score and the relative operating characteristics (ROC; curve and area under the curve; Mason and Graham, 1999). For categorical forecasts the recommended metric is the Gerrity Score (Gerrity, 1992). For probabilistic forecasts, the recommended metrics are the ROC and reliability diagrams. While these metrics are the main ones advocated by the WMO, several others are in regular use by modeling and prediction centers, and still others are being promoted as potentially more interpretable, at least for forecast users. Below, a variety of metrics are discussed and evaluated.
Deterministic Measures
Correlation addresses the question: to what extent are the forecasts varying coherently with the observed variability? Correlation assessments are typically done with anomalies (Figure 2.9a), or deviations from the mean, and can be applied to spatial patterns of variability (pattern correlations) or to time series of variability (temporal correlations). The agreement of co-variability does not indicate if the forecast values are of the right magnitude, and so it is not strictly a measure of accuracy in the forecast.
The mean squared skill score (MSSS) addresses the question: How large are the typical errors in the forecast relative to those implied by the baseline? The baseline could be climatology, for example, assuming the next season’s temperature will be that of the average value from the previous 30 years. The MSSS is related to the mean squared error (MSE) and summarizes several contributions to forecast quality, namely correlation, bias, and variance error. The root mean squared error (RMSE; equal to the square root of MSE) is much more widely used than either MSE or MSSS. For a predicted variable whose magnitude is of particular interest, such as the SST index of ENSO, the RMSE may be a preferred metric of forecast quality given its straightforward interpretation. However, RMSE alone is of limited information to the forecast community that wishes to identify the source of the error (Figure 2.9b).
The relative operating characteristics (ROC) addresses the question: can the forecasts discriminate an event from a non-event? The ROC curve effectively plots the hit rate, which is the ratio of correct forecasts to the number of times an event occurred, against the false alarm
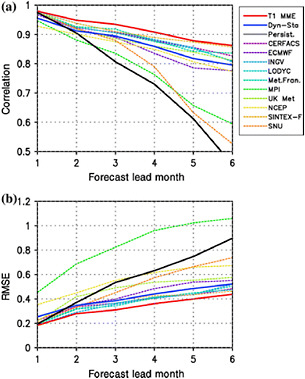
FIGURE 2.9 An example of a multi-model ensemble (MME) outperforming individual models in forecasting. (a) Anomaly correlation; the red line (MME) is above the individual models (colored lines), demonstrating that the pattern of anomalous temperature from the ensemble is a closer match to observations. (b) RMSE of NINO3.4; the red line is below the individual models, demonstrating that the magnitude of the errors associated with the ensemble is smaller. Black represents a persistence forecast. Names of the individual coupled models shown in the legend. SOURCE: Figure 7, Jin et al. (2008)
rate (probability of false detection), which is the ratio of false alarms to total number of non-occurrences. Therefore, one can assess the rate at which the forecast system correctly predicts the occurrence of a specific event (e.g. “above-normal temperature,” El Niño conditions, etc.), relative to the rate at which one predicts the occurrence of an event incorrectly (Figure 2.10). If the forecast system has no skill, then the hit rate and false alarm rates are similar and the curve lies along the diagonal in the graph (area = 0.5). Positive forecast skill exists when the curve lies above the diagonal (0.5 < area <= 1.0) and the skill can be measured by the “area under the ROC curve”.
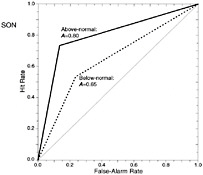
FIGURE 2.10 An example of a ROC curve that plots Hit Rates vs. False-Alarm Rates. In this case, the Hit Rate is the proportion of rainfall events (either above-normal, solid line, or below-normal, dotted-line) that were forecasted correctly; the False-Alarm Rate is the proportion of non-events (i.e., incidences of near normal rainfall) for which an event was forecasted. Since the curves are above the gray line, the forecast is considered skillful using this metric. The forecasts correspond to rainfall during September through November in a region in Africa during for the period 1950–1994 The areas beneath the curves, A, are indicated also. SOURCE: Figure 2, Mason and Graham (1999).
Probabilistic Measures
The key aspect of probabilistic forecasts is that they proffer quantitative uncertainty associated with the forecast. Thus, if a forecast includes uncertainty, it is important to assess the meaningfulness of that uncertainty; probabilistic forecasts need to be assessed probabilistically. Providing deterministic metrics as well, such as correlation or hit rate of the most likely outcome, may give additional information of use to decision makers, but provided alone, deterministic measures undermine the richness of the forecast information. For example, a deterministic measure such as a hit score based on collapsing the probabilistic forecasts to a deterministic forecast for the category with the largest probability, for purposes of verification, cannot then distinguish between a forecast of 100% likelihood and one of 40% likelihood of above-normal (e.g. for a 3-category system, with climatologically equal odds). However, the reaction of decision makers to such differing confidence in the predicted outcome would certainly be much different.
An important aspect of a quantitative probabilistic measure is that it is equitable. The term equitable means that a forecaster is not penalized for making a forecast that has a low climatological probability (e.g., forecasting a below normal temperature when the climatological probability of a below normal temperature is less than 10 percent).
The potential value of probabilistic assessment of forecasts is large for the model development, forecasting, and decision making communities. While users of the forecast information may stress the desire for “accurate” information, the climate system is inherently probabilistic. The most likely outcome, or equivalently the probabilistic median or the deterministic forecast, may give a general sense of expectations for the seasonal climate, but that
information needs to be accompanied by an estimate of the uncertainty. Commercial decisions are often made, not on the basis of events which are likely to occur, but on the basis of events which are unlikely to occur, but which if they did occur, would involve serious financial loss (Palmer, 2002).
The Heidke skill score (HSS), which is actually appropriate to binary forecasts rather than probabilistic forecasts, has been applied in the context of probabilistic categorical forecasts where they have been collapsed into binary categorical forecasts by retaining the category with highest probability. The HSS can be interpreted to addresses the question: did the forecast indicate the correct shift in the probability distribution more often than would be expected by chance? This score may be seen as desirable to some because it is convenient and easily interpreted (Livezey and Timofeyeva, 2008), indicating how often the forecast is “correct” or not (Figure 2.11). However, if it is applied to a probabilistic forecast the HSS degrades the information content as described above.
The Heidke Skill Score is considered biased and may not be equitable. Jolliffe and Stephenson (2003) claim it is equitable for applications involving binary predictions (e.g., yes or no; event or non-event). Wilks (2006) claims it is not equitable for higher-order designs, since the correct forecasts of less likely events do not properly receive more weight (personal communication, Wilks, 2009). Thus, the forecaster may be discouraged from forecasting rare events on the basis of their low climatological probability. The reason for the bias in the Heidke skill is that the reference hit rate in the denominator is not constrained to be unbiased. This means the imagined random reference forecasts in the denominator have a marginal distribution that is not necessarily equal to that of the sample climatology. Peirce Skill (Wilks, 2006) is unbiased and can be substituted for Heidke skill.
The probabilistic ROC is a variant of the ROC described previously that considers the hit rates and false alarm rates for events forecast at varying levels of probabilistic confidence.
The Brier skill score (BSS) is a summary score of forecast quality that encapsulates both reliability and resolution measures of forecast quality. Reliability, discussed more below, addresses the question: to what extent do the probabilities mean what they say? Resolution addresses the question: can the probabilistic forecasts discern changes in the frequency of observed events relative to the underlying climatological distribution? An example of good forecast resolution would be that when forecasts were issued with high probability for an El Niño event, El Niño events were much more likely to happen than would be estimated from their observed frequency over all years.
A reliability diagram shows the complete joint distribution of forecasts and observations for a probabilistic forecast of an event or forecast category (such as the above-normal tercile) (Figure 2.12). They indicate to what degree the probabilities assigned to an event are representative of the likely occurrence of that event. In a reliable forecast system, the probability assigned to a particular outcome should be the frequency with which—given the same forecast—that outcome should be observed. The information supplied by reliability diagrams includes calibration, or what is observed given a specific forecast (e.g., under and overforecasting), as well as resolution and refinement which is the frequency distribution of each of the possible forecasts giving information on the degree of aggregate forecaster confidence (small inset graph in Figure 2.12). Reliability diagrams can further indicate whether there are systematic biases in the forecasts, such as not predicting enough occurrences of above-normal temperatures. Such probabilistic verification, as ROC scores or reliability diagrams, also can be useful for estimating event-specific prediction skill, for example if El Niño events were better predicted than La Niña
FIGURE 2.11 Seasonal differences in forecast skill (contours) for temperature and how frequently (shading) forecasts differ from climatological odds (i.e., equal chances of normal, above-normal, and below-normal). Blue (tan) corresponds to areas where forecasts are often similar to (often different from) the climatological odds. The skill metric is a Heidke skill score, and is calculated by including only those forecasts that differ from climatological odds. Areas with high-valued contours indicate where deviations from climatology have frequently been forecasted correctly. The forecasts are from CPC and are valid ½ month from issuance. SOURCE: Figure14, O’Lenic et al. (2008).
FIGURE 2.12 An example of a reliability diagram, which indicates the skill of probabilistic forecasts. The diagram compares the forecasted probability of an event (in this case, above-normal winter rainfall in North America) to its observed frequency. A perfect forecast is represented by the dashed line, a horizontal line represents a forecast identical to climatology, and sloped lines are potentially skillful. The blue and red lines correspond to individual CGCMs and AGCMs, respectively, and are more horizontal than the black line, which represents the mean of these models. While the mean of the models is more reliable than any of the individual models, it tends to be underconfident for rare events (the black line lies above the perfect forecast line for low-probability events). Typically, a histogram accompanies a reliability diagram (inset), indicating the number of times that forecasts of various confidence levels were issued. SOURCE: Adapted from Goddard and Hoerling (2006).
events or if drought conditions were better predicted than very wet seasons. A distinction in prediction skill between the cases of high and low variability calls for further examination of the physical causes of the discrepancy, and whether it is inherent to the climate system dynamics or a shortcoming of the model(s).
Impacts of Non-Stationarity on Assessment of Skill
This section provides consideration of forecast verification in the context of a changing background climate. Many measures of prediction skill are sensitive to how much the prediction deviates from climatology; therefore, the assessment of seasonal predictions can be influenced by both changes in the drivers of climate predictability as well as trends or other slowly varying changes in the background state. ENSO exerts the greatest influence on seasonal-to-interannual climate variability globally (e.g. Glantz, 1996). As a result, climate predictions made during ENSO events yield much higher skill than those made during ENSO-neutral conditions (e.g. Goddard and Dilley, 2005; Livezey and Timofeyeva, 2008). Although an ENSO event typically occurs every 3–7 years, decadal modulation of the frequency and intensity of ENSO events is evident over the observational record of the 20th century (Zhang et al., 1997) and over the last millennium based on proxy coral data (Cobb et al., 2003). Therefore, there will be periods with higher prediction quality than others merely because there were more or stronger ENSO events during that period. Higher prediction skill will also appear in many metrics (e.g. correlation, Heidke skill score) when the background mean state climate is non-stationary, i.e. presence of trends; the non-stationarity could be due to anthropogenic climate change or natural variability
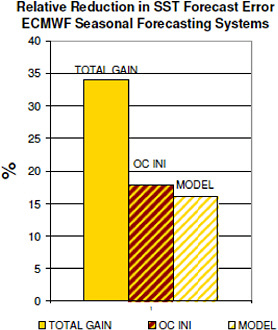
FIGURE 2.13 Progress in the seasonal forecast skill of the ECMWF operational system during the last decade. The solid bar shows the relative reduction in mean absolute error of forecast of SST in the Eastern Pacific (NINO3). The brown-striped bar shows the contribution from the ocean initialization, and the white-striped bar is the contribution from model improvement. SOURCE: Balmaseda et al. 2009.
on long multi-decadal timescales. Climate predictions are typically communicated as deviations from “climatology,” or the background mean-state. If the mean-state is changing over time, the magnitude of the seasonal deviation will depend on the period used to define the climatology. Equivalently, predictions of deviations in the same direction as the “trend” can be credited with relatively high quality that is derived more from the slowly evolving trend than the interannual variability. For example, under anthropogenic climate change, the temperatures over most land areas are increasing relative to the mean state, say 1971–2000 (Trenberth et al., 2007). That does not necessarily mean that each year will be warmer than the year preceding it. However, predicting temperatures to be “above-normal,” will appear skillful by many measures because temperatures in this decade are very likely to be warmer than those of 30 years prior.
A relevant question is then: can the forecast system discriminate between conditions in a pair of forecasts more often than not? For example, if year X is observed to be warmer than year Y, was that predicted to be so? Discrimination tests of forecast-observation pairs of cases addressing this type of question can be applied to deterministic or probabilistic forecasts. A generalization of such discrimination tests is outlined in Mason and Weigel (2009), and in many cases the metric becomes equivalent to those described above, such as generalized ROC areas for tercile probabilistic forecasts.
CHALLENGES TO IMPROVING PREDICTION SKILL
This chapter has provided the historical perspective on climate prediction, pointed to where there are opportunities to improve prediction quality by improving our understanding and representation in models of sources of predictability, and reviewed the methods available to quantify skill. From the 1980s to the 1990s, seasonal prediction quality improved dramatically, but then did not improve further (Kirtman and Pirani, 2008, 2009). The challenges in going forward are not only to determine where to gain further improvements but also to assess and understand the reasons for any incremental gains in prediction quality that have occurred.
In the following section we examine the building blocks of intraseasonal to interannual forecasting. Improvements may stem from better observations, better models, and improved assimilation. Recent analyses demonstrate how improvements in these components of forecast systems are the source for improvements in forecast quality (Stockdale et al., 2010; Balmaseda et al, 2009; Saha et al., 2006; Fig. 2.13), and thus predictability.
At the same time improvements may result from changes in the way in which the community works. Kirtman and Pirani’s (2008, 2009) summary of the first World Climate Research Program Workshop on Seasonal Prediction indicates that that workshop recommended adoption of best practices in seasonal forecasting, including the adoption of common approaches to the production, use, and assessment of seasonal forecasts.
Thus, the challenges to improving intraseasonal to interannual prediction skill lie not only in improvements of the building blocks but also in how the community works together. Experimental modeling and examination of the incremental skill to be gained from new sources of predictability are needed. The three case studies provide examples of physical processes being examined as sources of predictability. A further challenge is to develop the community framework to nurture ongoing improvements to dynamical models.

































