1
Where on Earth Am I Now?
To a sailor in the middle of the ocean or to a pilot above the clouds this question makes perfect sense, and a reliable answer to within a meter or so brings great comfort. With the development of intelligent transportation systems, passengers of vehicles on terra firma might pose the same question. It would seem that bridge builders or the operators of precise mining or agriculture machinery might not be so concerned, yet an answer accurate to a few centimeters is immensely valuable to them. It is rather less obvious why a geologist or a climate scientist would ask this very same question; but surprisingly, this is an even thornier issue for them, as they now require millimeter accuracy, both locally and globally. Only recently in human history has this age-old question become, on the one hand, an everyday practical issue and, on the other hand, a central scientific challenge. As our technologies have become more advanced, our need to know exactly where we are on Earth at any given moment has increased. As a result, innumerable activities of enormous economic and critical scientific value now depend directly or indirectly on the global, precise geodetic infrastructure.
The geodetic infrastructure in place today allows us to measure sea-level rise of a couple of millimeters a year; a shift in the center of the Earth by a tenth of a millimeter per year; changes in the length of the day of microseconds per day; and shifts in the position of the pole by fractions of a centimeter. Such highly precise measurements are critical to applications that monitor millimeter-scale deformation in the Earth’s crust in earthquake-prone or active volcano areas; real-time navigation systems that position vehicles, ships, and airplanes to an accuracy of a few centimeters; systems that enable farmers to reliably plant two different crop seeds centimeters apart on the same field; mining machinery that operates automatically to an accuracy of a few centimeters; and unmanned aircraft that can fly anywhere on the planet to survey natural disaster areas, erupting volcanoes, or combat theaters.
Remarkably, our ability to calculate location and time ever more precisely has kept pace with the demand, improving by almost an order of magnitude per decade since the advent of the space age (Chao, 2003). This is no small task, however. Instead of being a rigid ball upon which reference lines could be drawn once and for all, the Earth changes shape continuously. The ground in the
middle of continents moves up and down during the day by over 30 centimeters in response to lunar and solar tides; tectonic plates shift and collide; earthquakes and volcanoes disrupt the landscape by many meters; storms batter shorelines; ocean currents, hurricanes, and monsoons move enormous masses of air and water around the planet; and deep in the Earth’s mantle and core, convection cells move continents and power the geodynamo, which generates our protective magnetic field. Instead of spinning smoothly and steadily like a well-balanced top, the Earth wobbles in complex ways, and its spin rate (and, as a result, the length of day) changes over time scales as short as hours, while slowing down over long periods of time.1 To account for this continuous movement, we must continuously redraw the reference lines, and in turn continuously recalculate our position on Earth.
High-precision geodesy helps us to quantify and respond to local and regional problems by allowing us to “see” what we cannot sense directly. For example, the depletion of underground aquifers or oil and gas reserves can cause local subsidence, or sinking of the land, disrupting sewers and other underground utilities. On a much larger scale, geodesy enables us to monitor global climate change as it is reflected in ice sheet melting and sea level change. These trends, which only can be measured precisely with geodesy, ultimately may have significant—or potentially catastrophic—impacts, causing loss of life and billions of dollars of damage to homes, businesses, and the environment.
WHAT IS THE GLOBAL PRECISE GEODETIC INFRASTRUCTURE?
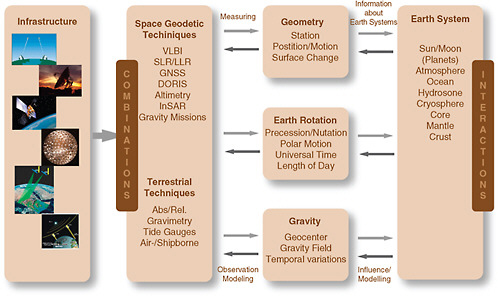
Geodesy is the science of measuring and understanding three fundamental parameters of the Earth—its shape, rotation and orientation, and gravity field—and their change over time. These parameters carry fundamental information about the planet and its workings. Today this is no longer a three-dimensional problem, but really a four-dimensional problem in which temporal changes in these quantities are tracked. Geodesists do this using an infrastructure based on precisely located positions of a set of reference (“fiducial”) points on the Earth’s surface. Using these reference points, geodesists create a terrestrial reference system (or spatial reference system)—a common coordinate framework for which scientists have determined, by calculation, all the reference points’ exact coordinates at a given time. The primary realization of the global spatial reference system is the International Terrestrial Reference Frame (ITRF). The ITRF and other terrestrial reference frames are established by equipping selected reference points with some combination of radio telescopes, laser ranging systems, Global Navigational Satellite Systems receivers (GNSS, a general term for systems like the Global Positioning System, or GPS) and radio beacons, and sometimes gravimeters. In addition, data from observations of Earth-orbiting satellites, the moon, and distant extragalactic objects known as quasars are incorporated. This combination of ground-based instruments and satellites constitutes the precise, global geodetic infrastructure.
A common spatial reference frame is both an important theoretical concept and a practical tool. Using geopositioning, one can locate a point or an object as it moves within a terrestrial reference frame. Beyond navigation, the ability to track the real-time location of mobile devices equipped with built-in GNSS/GPS receivers has sparked rapid growth in location-based services. Utility companies, for example, equip field crews with smart phones, enabling real-time access to dynamic maps of underground cables and pipes that can be updated “on the fly” as workers move around a field site. Developments in location-based services may drive revenues of more than $12.7 billion by 2014, according to a report published by Juniper Research (Wauters, 2010). The accuracy of geopositioning, and the scientific and societal applications that rely on it, depend on the continued existence of a reliable technological and scientific infrastructure.
THE VALUE OF PRECISE MEASUREMENTS
The power of modern geodesy is matched by the challenges it faces, namely, detecting minute changes in Earth’s system over time. Over the past 50 years, space-based geodetic technologies have revolutionized the way we look at our planet, allowing us to measure and monitor changes in the Earth’s system with unprecedented levels of accuracy and detail. Modern geodesy delivers precision to one part per billion, and precision of one part per trillion can be envisioned in the foreseeable future (see Box 1.1). The current level of precision enables us to track the shrinking distance between Los Angeles and San Francisco to an accuracy of 1 millimeter as we keep watch for the next California earthquake; or a millimeter shift of the pole associated with a large earthquake in Chile; or a microsecond change in the length of day associated with an Asian monsoon; or the slight change in the gravity field due to a drought-induced drop in the water table across the Mississippi drainage basin.
Such exquisitely precise measurements provide critical information for many areas of science with a tangible societal impact. One particularly complex example is sea level change. Over the past decade, the global sea level has increased by an average of 3.3 millimeters per year and has been predicted to rise by as much as one meter by the end of the 21st century. The shallow slope of some shorelines will exacerbate the impact of this vertical change in sea level, so that one meter of sea level rise would flood 2.2 million square kilometers of coastline, displace 145 million people worldwide, and result in the loss of $944 billion in combined global gross domestic product (Anthoff, 2006) (see Figure 1.1).
Geodetic technologies have been critical to measuring past sea level change over time, but predicting future changes can be exceedingly complex, underlining the need for precision infrastructure for global sea level monitoring. Global sea level change is largely caused by two factors: (1) changes in the thermal and salinity conditions of the ocean (which result from the expansion of the ocean’s volume due to heating), and (2) flow of water into the ocean from melting ice sheets and glaciers. The combined measurements obtained from three geodetic observing systems—altimetry and gravity satellite missions, and tide gauge networks—allow us to estimate the contributions of these sources. Recent measurements indicate that melting of glaciers and polar ice sheets contribute approximately 2 millimeters per year to sea level rise. In the year 2007 alone, the Greenland ice sheet lost nearly 300 billion tons of its mass, enough to bury the District of Columbia under a mountain of ice nearly 2,000 meters high (about 6,500 feet), or blanket the entire state of California with three-quarters of a meter (2.5 feet) of ice. The west Antarctic ice sheet is melting at a comparable rate, and the Antarctic continent as a whole is undergoing changes that we will not fully grasp until the comple-
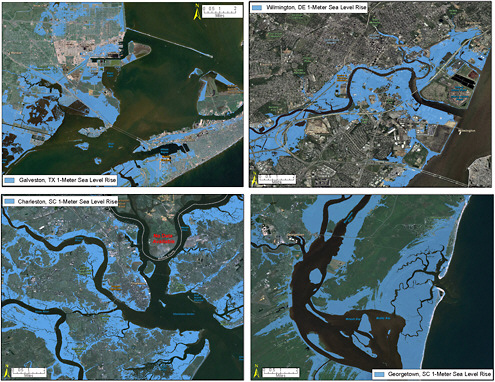
FIGURE 1.1 The potential flooding in coastal areas resulting from a potential sea level rise of one meter was mapped on either Mean High Water (MHW) or Mean Higher High Water (MHHW) depending on location (see Glossary for definitions). The sea level rise scenarios represent daily impacts at high tide, or the maximum extent of inundation. One meter of sea level rise by the year 2100 is a conservative estimate from the Intergovernmental Panel on Climate Change that is considered plausible (Rahmstorff et al., 2007). Geographic Information System (GIS) and spatial analyses were used to construct the projections; maps show the scale of potential flooding, but not the exact location, do not account for erosion or subsidence, and assume no wind, rainfall, or future construction. Model improvements for all these factors are possible, and would lead to improved forecasting and mitigation. All mapping was completed on the best available elevation data available to the Coastal Services Center. SOURCE: Courtesy of the NOAA Coastal Services Center.
tion of current and future satellite missions, part of the “decadal survey” list (NRC, 2007a). In this report, we examine the 0.6 millimeter per year error budget that the current geodetic infrastructure affords us. The combination of direct geometric measurements of sea-level, ice-sheet, and sea-ice changes (from ocean radar altimetry, ice-sheet laser altimetry, tide gauges, and other geodetic station elevations), and unprecedented mass change estimates (from satellite-based monthly gravity solutions) gives us unique and essential limits on climate dynamics models.
Although ice sheet melting causes global sea level rise—seven meters for a hypothetical total melting of Greenland and 3–5 meters for total collapse of West Antarctica—it also leads to significant regional variability. Counter-intuitively, the shedding of ice from a frozen continent can lead to a local lowering of sea level relative to the land near the disappearing ice sheet. This is because the removal of the ice load causes the ground to rebound upward, while at the same time the gravitational attraction of the ice mass that used to pile up ocean water around the ice sheet is
no longer there, so the water level drops locally. The detailed geographic pattern of relative sea level change is therefore a complex, but critical, piece of information in interpreting the causes—and preparing for the impacts—of climate change. Because of such complications, the geography of sea level rise caused by melting of the Antarctic and Greenland ice sheets is not accurately predicted. If the Greenland ice sheet should melt altogether, then the east coast of the United States would experience sea level rise, but England would initially see a sea level drop. If, on the other hand, the west Antarctic ice sheet melts, then Washington, DC, would have to contend with a local rise in sea-level of about 30 percent greater than the global average (Bamber et al. 2009; Mitrovica et al., 2009). This underscores how complex the impacts of an ice sheet collapse can be, and the need for precise monitoring of the Earth’s response to surface loads.
As this example illustrates, improvements in measurement precision have pushed geodesy beyond its traditional disciplinary boundaries and into research domains such as climate and atmospheric science, oceanography, hydrology, geology, seismology, geodynamics, geology, and glaciology. Geodetic observations of changes in the Earth’s shape, rotation, and gravity field offer new and unique insights into dynamic processes and mass transport in the Earth system, such as ice melting, sea level rise, land subsidence, and aquifer depletion. In addition, geodesy provides the foundation for most other Earth observations, and for a wide array of applications with broad societal and commercial impact—from early warning systems for hazards to location-based services. Unfortunately, the scientific infrastructure dedicated to geodetic observations has become fragile as a consequence of aging components, lack of redundancy with single-point-of-failure designs, and ongoing fiscal pressures on operations and maintenance budgets. Degradation of the geodetic infrastructure could lead to gaps in critical observations that are needed to test the validity of models for ice dynamics, sea level rise, and climate change. This report assesses the scientific and societal requirements for precise geodetic observations and offers options for the support of a sustainable national geodetic infrastructure capable of serving the full range of existing and future users.
COMMITTEE CHARGE AND APPROACH
This report is one of several undertaken by the National Research Council (NRC) examining the need for precise geodetic observations.2 The report Geodesy in the Year 2000 (NRC, 1990) identified many areas of science that would benefit from improvements in the accuracy of geodetic measurements and emphasized the need for continuity of geodetic measurements over many decades. The report International Global Network of Fiducial Stations: Scientific and Implementation Issues (NRC, 1991) assessed the scientific importance of and implementation strategies for a global network of fiducial sites to support both geodetic and geophysical measurements. It recommended the establishment of a core network of roughly 30 fiducial stations, later called the Fiducial Laboratories for an International Natural Science Network (FLINN) to locate and integrate GPS receivers and instruments used by other scientific disciplines at sites already occupied by equipment devoted to geodetic techniques, such as Very Long Baseline Interferometry (VLBI) and Satellite Laser Ranging (SLR). In addition, the report advocated for the establishment of data centers to ensure a
|
2 |
Other related NRC reports include: Geodesy in the Year 2000 (NRC, 1990); International Global Network of Fiducial Stations: Scientific and Implementation Issues (NRC, 1991); Forum on NOAA’s National Spatial Reference System (NRC, 1994); Airborne Geophysics and Precise Positioning: Scientific Issues and Future Directions (NRC, 1995a); The Global Positioning System: A Shared National Asset (NRC, 1995b); Satellite Gravity and the GeoSphere: Contributions to the Study of the Solid Earth and Its Fluid Envelope (NRC, 1997a); The Global Positioning System for the Geosciences: Summary and Proceedings of a Workshop on Improving the GPS Reference Station Infrastructure for Earth, Oceanic, and Atmospheric Science Applications (NRC, 1997b); Review of EarthScope Integrated Science (NRC, 2001a); Weaving a National Map: Review of the U.S. Geological Survey Concept of the National Map (NRC, 2003); Review of Goals and Plans for NASA’s Space and Earth Sciences (NRC, 2006); and Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond (commonly called “the Decadal Survey;” NRC, 2007a). |
smooth flow of data from the network operators to the user community and for the establishment of analysis centers to develop and test techniques that support part-per-billion, three-dimensional geodesy. Finally, the report Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond (commonly called “the Decadal Survey;” [NRC, 2007a]) warned that the nation’s geodetic infrastructure is now at a critical juncture:
“The geodetic infrastructure needed to enhance or even to maintain the terrestrial reference frame is in danger of collapse (cf. Chapter 1). Improvements in both accuracy and economic efficiency are needed. Investing resources to assure the improvement and the continued operation of this geodetic infrastructure is a requirement of virtually all the [satellite] missions of every Panel in this study.”
The terrestrial reference frame is realized through integration of the high-precision networks of the Global Positioning System (GPS), VLBI, and SLR. It provides the foundation for virtually all space-based and ground-based observations in Earth science and studies of global change, including remote monitoring of sea level, sea-surface topography, plate motions, crustal deformation, the geoid, and time-varying gravity from space. It is through this reference frame that all measurements can be interrelated for robust, long-term monitoring of global change. A precise reference frame is also essential for interplanetary navigation and diverse national strategic needs (NRC, 2007a, p. 223).
Other notable reports from which the committee has drawn include the “Williamstown Report” (Kaula, 1970), the “Erice Report” (Mueller and Zerbini, 1989), the “Coolfont Reports” (NASA, 1991a,b,c), the “Living on a Restless Planet” report of the Solid Earth Science Working Group of NASA (Solomon and the Solid Earth Science Working Group, 2002), the report on the InSAR Workshop (Zebker, 2005), and Global Geodetic Observing System: Meeting the Requirements of a Global Society on a Changing Planet in 2020 (Plag and Pearlman, 2009).3
Building on these prior studies, this report assesses the scientific and societal benefits of precise geodetic observations and networks to the nation, discusses the associated requirements, explores opportunities for technological innovation, and suggests ways to improve national coordination and implementation of the geodetic infrastructure (Box S.1). It was not within the committee’s charge, however, to consider budgets, to do a cost comparison, or to estimate the economic impacts of precision geodetic infrastructure, although such an evaluation would be useful.
Although the contributions of geodetic observations and infrastructure to modern science, commerce, and society are immense, they are mostly—with the notable exception of GNSS/GPS—hidden from the public eye. Because the responsibility for building and maintaining the geodetic infrastructure is distributed across a range of federal agencies, statements made by agency personnel concerning the importance of this infrastructure to the nation do not always resonate with policy makers and the public. It was in this context that the NRC was asked by several federal agencies—the National Aeronautics and Space Administration (NASA), the U.S. Naval Observatory (USNO), the National Geospatial-Intelligence Agency (NGA) of the Department of Defense (DoD), the National Science Foundation (NSF), the National Geodetic Survey (NGS) of the National Oceanic and Atmospheric Administration (NOAA), and the U.S. Geological Survey (USGS)—to provide an independent assessment of the benefits provided by the geodetic observations and networks, as well as a cohesive plan for the future development and support of the infrastructure as scientific and commercial users increasingly demand greater precision.
The committee addressed Tasks 1 through 5 of its charge (see Box S.1) by gathering information from the scientific literature, presentations, and discussions with representatives of the federal
agencies that requested the study. The committee also received briefings from representatives of the Department of Transportation, as well as academic, nonprofit, and industry researchers. All presenters, with their affiliations and presentation titles, are listed in Appendix B. The committee also relied on relevant technical documents, pertinent NRC reports, and the collective expertise of the committee members. These considerations led the committee to develop recommendations focused on maintaining capability and mitigating the risk of infrastructure degradation, and supporting a long-term, sustainable national infrastructure capable of serving the full range of existing and future users.
ORGANIZATION OF THE REPORT
This report examines the national need for high-precision geodetic infrastructure. The remaining sections of Chapter 1 review the fundamental geodetic parameters, define what is meant by geodetic infrastructure for the purposes of this report, and outline the respective roles and responsibilities of federal agencies and offices with respect to the nation’s precision geodetic infrastructure. Chapter 2 explores the potential of geodetic observations and networks to transform science and to promote broad societal applications. Chapter 3 describes the range of science and societal objectives that drive advances in geodetic observations and networks. Chapters 4 and 5 examine the requirements for maintaining a robust geodetic infrastructure, as well as the importance of the ITRF. Chapter 6 identifies key institutional and workforce issues and offers a plan for the long-term support of a national geodetic infrastructure capable of servicing the full range of existing and future users. Biographical sketches of the committee members (Appendix A), a list of presentations made to the committee (Appendix B), and a glossary of commonly used terms and acronyms (Appendixes C and D) appear at the end of the report.
FUNDAMENTAL GEODETIC PARAMETERS
The fundamental parameters of geodesy include the Earth’s shape (land and sea surface topography, bathymetry, and ice sheet thickness), rotation and orientation in space, and gravity field. These parameters all change with time as a consequence of the dynamic nature of the Earth’s system. Geophysical processes transform the Earth’s surface, modify the distribution of mass within the Earth’s interior and its oceans, and consequently alter its gravity field and rotation.
Geometric Shape of the Earth
The shape of the Earth’s solid surface is described by land surface elevation (topography), the underwater surface of lakes and ocean floors (bathymetry), and ice surface elevation. These three surfaces are most often measured with respect to mean sea level, which approximately defines the location of zero on the measurement scale. The global mean sea level is the measure of the average height of the ocean’s surface (the halfway point between the mean high tide and the mean low tide). In order to extend the definition of mean sea level to the land, we approximate it with a model of the Earth called the geoid (Figure 1.2). The geoid describes a surface to which the force of gravity is perpendicular everywhere (that is, a surface with uniform gravitational potential). If the oceans were undisturbed by currents, winds, and waves, then the mean sea level would correspond exactly with the surface of the geoid. In reality, external forces such as tides and weather cause the geoid and mean sea surface to differ; this difference is referred to as sea surface height (or sea surface topography).
Elevations—or more technically, orthometric heights (H)—are determined by calculating the height of the land surface above the geoid (Figure 1.2). The precise determination of elevation is
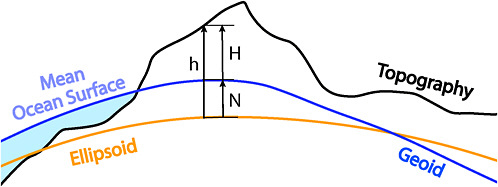
FIGURE 1.2 Schematic showing the approximate relationship between the geoid, based on the Earth’s gravity field (and coinciding with the mean sea level), and the surface of the Earth (topography). Surveys using spirit leveling measure height differences along the geoid. Water flows downhill as defined by the orthometric heights (H). On the other hand, geometric heights (h) are reckoned relative to a conventional ellipsoid and are calculated from coordinates relative to the center of the Earth. In order to use such heights for flood modeling, an independent knowledge of the orthometric height relative to the ellipsoid (N) is required, known as the geoid height. This calls for densely sampled maps of the gravity field, which can be greatly improved nowadays by airborne surveys using GPS/GNSS navigation. Source: Committee on the National Requirements for Precision Geodetic Infrastructure.
important for a wide range of applications, including floodplain mapping and storm surge modeling. Vertical positions determined from GNSS/GPS are not connected to the geoid but represent an absolute height—called the geometric height (or ellipsoid height) (h)—calculated from coordinates whose origin is at the center of the Earth. The vertical distance from the ellipsoid and the geoid at any location on Earth is called the geoid height (N). Independent knowledge of the geoid allows geodesists to relate geometric to orthometric heights and, for example, to infer land surface elevations from GNSS/GPS measurements.
Time and the Earth’s Rotation
The Earth spins and wobbles in complex ways, causing the positions of the poles to shift by millimeters over the course of a day and by meters over the course of a year. Day-to-day variations in the length of day (which measures the Earth’s rate of spin) are typically on the order of fractions of milliseconds per day. The length of day also gradually lengthens as energy is dissipated—primarily through tidal friction—requiring the occasional “leap second” that is applied by international convention.4
One of the primary roles of the global geodetic infrastructure is to determine the length of day and Earth orientation parameters and how they change with time relative to the Earth’s interior, as well as how they change relative to distant, “fixed” objects such as quasars. This requires the ability to synchronize distant clocks accurately, an operation commonly referred to as “time transfer.” Time synchronization is less stringent for such everyday functions such as bank transfers, transportation, television broadcasting, and power grid regulation (i.e., on the order of milliseconds or less). Even higher accuracy is needed for modern high-bandwidth digital networks. GNSS/GPS signals are the
|
4 |
The changes in Earth’s spin rate and the wobbles of its rotation axis also affect the evolution of a terrestrial reference frame over time. Motions of geodetic targets, either satellites or quasars, are modeled in a non-rotating system. To relate their instantaneous coordinates to Earth-fixed systems requires knowledge of the Earth orientation parameter with the same accuracy as the terrestrial coordinates. |
most popular and economical way to achieve clock synchronization for most of these commercial applications. Scientific applications, on the other hand, have yet more demanding time synchronization requirements, at the nanosecond level (10–9 seconds) or better. Thus, the high-accuracy methods at the heart of geodetic techniques enable precise measurements of time and frequency, as well as tests of fundamental physics, including the Theory of General Relativity. “Precise time-transfer” is typically only needed to synchronize clocks with comparable precisions (for example, atomic clocks). Because the international definitions of time (International Atomic Time and Coordinated Universal Time) are based on careful combinations of the records from approximately 300 atomic clocks, the precision of the time-transfer method is just as important as building the clocks themselves (Arias, 2005). The United States has demonstrated its long-standing commitment to the definition of International Atomic Time by contributing more than half of the clocks used to define the international timescale.
Gravity
Gravity, as measured on the Earth’s surface, depends on the distribution of mass within the entire Earth system. Therefore, spatial and temporal changes in mass (in density, volume, or both) in the Earth’s solid and fluid interior, atmosphere, oceans, hydrosphere, and cryosphere—such as seasonal snowpack and groundwater changes or post-glacial rebound—can be detected as corresponding variations in the Earth’s gravity. Gravity measurements also can distinguish the underlying mechanisms behind mass redistribution, such as thermal expansion of the ocean or the addition of water from the melting of continental ice sheets, which are both contributing to global sea level rise. Because these gravitational variations are one thousand to one billion times smaller than the mean value of gravity of the Earth (approximately 9.81 meters per second squared), precise geodetic observations are needed across regional and global scales and over long periods of time. The precision of gravity measurements has improved by roughly three orders of magnitude over the past 50 years, and is currently at one part per billion (Plag and Pearlman, 2009).5
Gravity measurements obtained from the GRACE (Gravity Recovery and Climate Experiment) satellite mission (discussed in Chapter 3), launched in 2002, have led to improvements in the accuracy of the geoid to the centimeter level (Tapley et al., 2004a,b), and consequently to improvements in the reliability of the National Spatial Reference System (NSRS). The NSRS, managed by NOAA’s NGS, is a consistent national coordinate system that specifies latitude, longitude, height, scale, gravity, and orientation throughout the nation, and tracks how these values change over time (NRC, 1994, 2003). Variations in the gravity field over time can be large enough to affect the NSRS.
Because variations in the gravity field perturb the orbits of satellites, an accurate model of the Earth’s gravity field is needed to correctly predict their positions. Similarly, an accurate gravity model improves the accuracy of other geodetic techniques, such as satellite altimetry and synthetic aperture radar interferometry, and aids the development of digital terrain models.
THE GEODETIC INFRASTRUCTURE
Geodetic observing systems provide a significant benefit to society in an astonishing array of commercial and scientific areas with a wide range of precision requirements. Underlying these observing networks is the precise geodetic infrastructure, made up of a variety of components. In this report, the committee distinguishes between geodetic observing systems and geodetic infrastructure.
|
5 |
Monthly global maps of the Earth’s gravity field derived from the GRACE mission verify the earlier NRC assessment (NRC, 1997a) that “the time-varying effects [of gravity] are three to four orders of magnitude smaller than the static field variations, so dense temporal and spatial coverage and highly accurate measurements are necessary” (see Reigber et al., 2005). |
Although these overlap, the two are distinguished by their primary purpose. When the committee refers to geodetic observing systems (or in some cases geodetic observing networks), it refers to systems that are designed to address specific goals (such as measuring sea level changes) and may be used for a finite period of time. Geodetic infrastructure, on the other hand, supports all observing systems and applications over time; its main function is to provide necessary information for the International Terrestrial Reference Frame (ITRF) that underpins many Earth observation missions and location-based applications. The strength of the infrastructure lies in its longevity, continuity, stability, robustness, accuracy, speed of accessibility, and its capability for supporting innovation through the development of new observing systems that exploit the accuracy of the infrastructure. Geodetic observing systems therefore rely on the existence of the geodetic infrastructure to achieve their goals.
In the broadest sense, the geodetic infrastructure includes the following:
-
Geodetic bench marks in the ground that define specific locations;
-
Ground-based geodetic system hardware that may range in size, cost, and complexity from GNSS/GPS receivers to large radio telescopes or satellite laser-ranging systems;
-
Ground and airborne systems for the measurement of gravity;
-
Tide gauges;
-
A host of satellite systems for radar, LiDAR (Light Detection and Ranging), and gravity measurements;
-
The data analysis that turns geodetic observations into geographic and other information, including the ITRF;
-
The systems that define procedures for data analysis and combination; and
-
Computer systems for archival of raw data and data products.
This report focuses on those components of the geodetic infrastructure that contribute globally, in particular the four geodetic hardware systems and associated services that form the backbone of the ITRF.
Very Long Baseline Interferometry (VLBI)
Based on a technique developed for astronomy, VLBI uses fairly large, ground-based, parabolic-dish radio telescopes to observe quasars (the most distant objects in the cosmos), thus providing a connection to the “outside universe.” A small network of VLBI sites provides critical information on the direction of the Earth’s spin axis against this background constellation of quasars and allows the Earth’s rotation to be connected to this stable background.
Satellite Laser Ranging (SLR) and Lunar Laser Ranging (LLR)
In this technique, a laser signal is transmitted from a ground-based station, reflects off specially designed mirrors (retro-reflectors) placed on artificial satellites (SLR) or on the moon (LLR), and is received back at the station. Satellites and the moon orbit the Earth due to the Earth’s gravitational pull. This technique therefore provides a unique connection between the Earth’s surface and its gravity field, which reflects the distribution of mass deep within the planet.
Global Navigational Satellite Systems (GNSS)
This is a generic term for satellite navigation systems that provide autonomous spatial positioning with global coverage. The U.S. NAVSTAR Global Positioning System (GPS) falls into this
category; other countries also have or are developing GNSS systems. Coded signals transmitted from multiple satellites and received by multiple GNSS receivers allow time delay, and indirectly distance, measurements between the satellites and GNSS receivers. Although GNSS/GPS is designed to be accurate to the meter level, geodesists have determined how to use these signals to achieve accuracies 1,000 times better. The strength of these systems lies in the low cost of the ground-based systems (the systems do not include satellites) compared to VLBI or SLR/LLR. GNSS, therefore, provides a geographic coverage unequaled by these other systems because they can be inexpensively deployed and have a wide range of applications.
Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS)
DORIS is a tracking system developed and operated by France. In some respects, it is an inversion of GNSS/GPS because the transmitters are on the ground and the receivers are on satellites. Many of the same principles that apply to GNSS/GPS also apply to DORIS. DORIS was designed for precise orbit determination required by ocean altimeter satellites and therefore helps connect sea-level measurements to the solid Earth.
These systems together provide some of the most important measurements of the Earth’s short-term (daily and shorter) and long-term (years and longer) motions, including deformation (Figure 1.3). To obtain these measurements, the information acquired by these infrastructure systems travels a long path. The data from each system (blue boxes in Figure S.2) are analyzed (red boxes) to provide intermediate data products, which are then combined to yield the information (green) that can then be easily incorporated into other observing systems by users (cyan). Thus, at the lowest levels, these systems must be coordinated to ensure that there is complete consistency. In fact, the global geodetic community has worked for decades to provide common standards for analysis and data formats for the precise global geodetic infrastructure, of which the United States’ geodetic infrastructure is a leading component.
Professional geodesists are as important to the field of geodesy as the infrastructure itself. The measurements gathered by the instruments have no value without being analyzed and incorporated into models of the physical world. Formal training in geodesy includes study across a broad range of topics that provide the analytical tools and the knowledge of the observational systems needed to carry out research in this field. A “geodesist,” therefore, might be defined as someone with formal training in the following areas, which can be thought of as the building blocks of a geodetic education:
-
Positioning and reference systems. The methods for describing the location of positions on the surface of a changing planet at ever-increasing levels of precision.
-
Gravity field theory. Mathematical approach for describing the gravitational field of a planet, including, in the case of the Earth, such geometric constructs as mean sea level.
-
Dynamics of the Earth’s rotation. Observations on the small variations in the rotation of the Earth, which provide unique probes into the structure of the planet and the mass variations within the planet and on its surface.
-
Crustal deformation due to mass load changes. Investigations on how the Earth’s crust deforms due to an increase (such as the extra weight of water at the land’s edge at high tide) or a decrease (such as loss of ice in a polar ice sheet) in the mass load. These investigations provide information about the planet’s crust and mantle composition, as well as the nature of the forcing of that deformation from loading due to ocean tides, atmospheric pressure, ice and water variations, and other changes.
-
Propagation of radio waves through the atmosphere. Study of how the atmosphere refracts radiometric signals. Signal delays provide a measure of air density, moisture content, and charged particles.
-
Satellite orbit determination. The science of determining an orbiting satellite’s position as a function of time, an essential component of accurate geodetic measurements. This involves complex mathematical modeling of the physics of spacecraft motion and ingesting the available tracking data into that model through various estimation techniques.
-
Techniques for estimating model parameters from observational data and error analysis of those estimates. The process of estimating unknown or poorly known parameters for a mathematical model. To be useful, an assessment of the accuracy of these estimates is also essential.
A geodesist combines these areas of knowledge to achieve the goals of his or her work. This work may be purely theoretical, it may use one or more of the geodetic observation techniques discussed in this report, or it may involve the development of new geodetic techniques and observing systems. Although some of the above topics may be part of a course of study in other disciplines, the combination of these topics is unique to the science of geodesy.
FEDERAL SUPPORT FOR THE GEODETIC INFRASTRUCTURE
Within the United States, support for precision geodetic infrastructure is provided by a number of agencies and offices, including, FAA, NASA, NGA, NOAA, NSF, PNT, USGS, and USNO. Other agencies, such as the U.S. Department of Agriculture (USDA) and the Environmental Protection Agency (EPA), assist with coordination and are users of precision geodetic information. The respective roles and responsibilities of these agencies are summarized in Table 1.1.
Federal Aviation Authority (FAA)
The FAA is focused on public safety and reliability, but uses relative positioning, rather than precision and absolute positioning. FAA has developed a separate infrastructure to meet its specific demands.
National Aeronautics and Space Administration (NASA)
Starting in the 1960s, NASA has been a leader in researching and developing geodetic techniques and coordinating the deployment of the associated global infrastructure (see Kaula, 1970). Initially, the primary technologies developed by NASA included VLBI, SLR, and LLR. These technologies came to fruition in the 1980s under the Crustal Dynamics Project, allowing geodesists to determine coordinates of sparse global networks with sufficient accuracy to measure directly the rates of motion (velocities) of these points at the centimeters per year level—and much better over time—and thus map truly “instantaneous” tectonic motions. In the 1990s, civilian networks of permanent GPS stations were developed and deployed, first in southern California and Japan, and later globally, thereby permitting the production of detailed, time-dependent deformation maps in seismic and volcanic areas. Further advances led to precise satellite orbits derived from onboard GPS receivers, and more recently ultra-precise (to an accuracy of 10 centimeters) navigation of manned and unmanned aircraft anywhere in the world.
Almost all space missions rely directly or indirectly on the precise, global geodetic infrastructure. This includes both U.S. and foreign missions. Of special note are:
-
LAGEOS and similar passive geodetic satellites (for example, Etalon and Starlette) that led to major advances in geoid determination
-
Radar imaging missions (for example, SeaSat , Geosat, SRTM, and Envisat)
-
Radar and LiDAR altimetry missions (for example, TOPEX-Poseidon, Jason, and ICESat)
TABLE 1.1 Main Government Stakeholders (Users of and Contributors to) the Precise, Global Geodetic Infrastructure
|
Organization |
Contributor |
User |
Notes |
|
NASA |
Yes |
Yes |
Provides primary support for critical U.S. geodetic infrastructure components of global ground-based networks; supports fundamental geodetic research; supports development of the Global Geodetic Observing System; supports geodetic infrastructure critical to many satellite missions. |
|
DoD |
Yes |
Yes |
Operates the Global Positioning System (GPS); supports heavy military usage of GNSS/GPS; supports geodetic infrastructure used to improve GNSS/GPS; USNO provides many GNSS/GPS-based products that rely on geodetic infrastructure. |
|
NGA |
Yes |
Yes |
Relies on geodetic infrastructure to provide geospatial intelligence; supports, and maintains WGS-84 (DoD Terrestrial Reference System) |
|
NGS |
Yes |
Yes |
Relies on geodetic infrastructure to provide CORS data products (used by surveyors) and for NSRS; performs analysis of global data for reference frames and orbits; proposed GRAV-D for redefinition of U.S. vertical reference datum. |
|
NOAA (non-NGS) |
No |
Yes |
Uses geodetic infrastructure to support ground-based water-vapor measurements for weather forecasts, climate observing system (COSMIC), tsunami warning, and sea-level change. |
|
NSF |
Yes |
Yes |
Relies on geodetic infrastructure for studies of tectonics, volcanoes, earthquakes, glaciology, and climate; supports infrastructure for U.S. observing systems that rely on geodetic infrastructure (for example, EarthScope/PBO). |
|
PNT |
No |
Yes |
Advises and coordinates federal departments and agencies on matters concerning GNSS/GPS. |
|
USGS |
No |
Yes |
Relies on geodetic infrastructure for analysis of USGS geodetic networks used to asses risks from earthquakes and volcanoes. |
|
DoT |
No |
Yes |
Uses GNSS/GPS, but uses do not require the highest precision; FAA operates independent networks for air traffic operations and WAAS. |
|
State and local governments |
No |
Yes |
Surveying for roads, highways, and property; primary government interface with civilian surveyors and engineers. |
-
Gravity measurement missions (for example, CHAMP and GRACE)
-
Atmospheric and ionospheric sounding (GPSMet, Champ, SAC-C, and COSMIC)
In addition to the infrastructure, NASA historically has supported fundamental research and development programs in space geodesy and continues to do so (with increased emphasis on real-time dynamic applications and high spatial and temporal resolution of climatic and tectonic forcings). It is, therefore, not surprising that there is a NASA influence in the treatment of many global scientific problems, including sea-level change, ice budget, ocean circulation, climate change, and geohazards.
National Geospatial-Intelligence Agency (NGA)
The mission of the NGA Office of GEOINT Sciences is to provide accurate and timely geodetic, geophysical, and geospatial analysis and intelligence information to support the DoD’s national security and intelligence objectives. The NGA supports satellite geodesy by maintaining its permanent GPS tracking network and implementing improvements to GPS orbit determination. The NGA also works to maintain and improve the World Geodetic System 1984 (WGS 84), the reference frame currently used by GPS and the Department of Defense. Further, NGA is responsible for collecting, processing, and evaluating geodetic data, which are used to compute the WGS 84 Earth Gravitational Model, geomagnetic models, and global digital terrain models.
National Oceanic and Atmospheric Administration (NOAA)
NOAA, through the National Geodetic Survey (NGS), has the federal mandate for defining, maintaining, and providing access to the National Spatial Reference System (NSRS). The NSRS allows consistent positioning to meet a wide range of needs, from delineating property lines and exclusive economic zones to determining the heights of levees and tide gauges relative to sea level. Historically, NGS installed thousands of survey monuments across the nation in support of the NSRS. By establishing a network of Continuously Operating Reference Stations (CORS) using GPS and by making the observational data available, NGS now allows users to connect directly to the NSRS without the need to place receivers at NGS survey monuments. Each CORS site provides GPS carrier phase and code range measurements to support three-dimensional positioning activities throughout the United States and its territories, with accuracies that approach a few centimeters, measured in the NSRS, both horizontally and vertically. The CORS system is operated in partnership with many local, state, and federal agencies, and contains CORS stations that are located at sites of varying positional stability and with various models of receivers, antennas, and documentation.
In cooperation with the USGS, NOAA also has responsibilities for supporting the geodetic infrastructure to provide ocean bathymetry, coastline and sea surface topography, which are critical for understanding tsunamis and predicting where they might come ashore, as well as for determining local or regional changes in sea level. NOAA further cooperates with NASA and USNO in the National Earth Orientation Service, or NEOS. NOAA’s National Geodetic Survey chairs the Federal Geodetic Control Subcommittee (FGCS) of the Federal Geographic Data Committee (FGDC), with membership drawn from all federal agencies involved in surveying, mapping and geospatial data, to promote a common standard of content, format and accuracy for geodetic data for the nation.
National Science Foundation (NSF)
The NSF supports a large number of scientific research projects that depend on the geodetic infrastructure. In addition, the NSF supports national geodetic infrastructure through financial support for the UNAVCO Facility (formerly known as the University NAVSTAR Consortium) and the
EarthScope program, which facilitate testing, adoption, and implementation of geodetic technologies to support fundamental geodynamic research, such as the study of earthquakes and volcanic eruptions. The Plate Boundary Observatory (PBO)—a component of EarthScope—provides geodetic imaging of plate boundary deformation.
National Space-Based Positioning, Navigation, and Timing (PNT) Executive Committee and Coordination Office
The National Executive Committee for Space-Based Positioning, Navigation, and Timing (PNT) coordinates policy activities relating to the Global Positioning System (GPS) and Global Navigation Satellite Systems (GNSS). It is chaired jointly by the Deputy Secretaries of Defense and Transportation. The Space-Based PNT National Coordination Office staffs the operational activities of the National Executive Committee. A formal Federal Advisory Board provides external advice and recommendations on PNT issues to the National Executive Committee.
U.S. Geological Survey (USGS)
Although data from some GPS stations operated by USGS are processed by the International GNSS Service, they are not used to to maintain the International Terrestrial Reference Frame. USGS depends on geodetic infrastructure to cary out its earthquake and volcano monitoring mission, and that infrastructure is crucial to development and production of data products, such as hazard maps and real-time ShakeMaps.
U.S. Naval Observatory (USNO)
The USNO is responsible for establishing, maintaining, and coordinating the astronomical reference frames for celestial navigation and orientation of space systems. Specifically, the USNO is the sole provider of the Earth Orientation Parameters (EOP) to the Department of Defense. USNO also serves as the official source of time for the Department of Defense and a standard of time for the entire United States.
International Services
Many international services have been established in response to the need for international cooperation to support geodetic activities. The most important of these services are the International Earth Rotation and Reference System Service (IERS) (Vondrák and Richter, 2004); the International GNSS Service (formerly the International GPS Service, or IGS) (Dow et al., 2005); the International VLBI Service (IVS) (Schlüter et al., 2002); the International Laser Ranging Service (ILRS) (Pearlman et al., 2002); and the International DORIS Service (IDS) (Tavernier et al., 2006). These services are described in more detail in Chapter 4. In general, the Central Bureau for each service is supported by the host country with volunteer contributions by the international scientific community. For example, the Central Bureaus for the IGS, IVS, and ILRS are all hosted in the United States and are supported by NASA.