Appendix A
Characterization of Uncertainty1
The characterization of uncertainty is recognized as a critical component of any risk assessment activity (Cullen and Small, 2004; NRC, 1983, 1994, 1996, 2008). Uncertainty is always present in our ability to predict what might occur in the future, and is present as well in our ability to reconstruct and understand what has happened in the past. This uncertainty arises from missing or incomplete observations and data; imperfect understanding of the physical and behavioral processes that determine the response of natural and built environments and the people within them; and our inability to synthesize data and knowledge into working models able to provide predictions where and when we need them.
A key element of effective treatments of uncertainty is the ability to clearly distinguish between the (inherent) variability of a system, often referred to aleatory or statistical uncertainty, and the (reducible) uncertainty due to lack of full knowledge about the system, referred to as epistemic or systematic uncertainty. The former applies to processes that vary randomly with time, or space, or from sample to sample (e.g., person to person, item to item). Even if a perfectly specified probability model is available to describe this variation, the inherent variability dictates that we are uncertain about what will occur during the next year or decade, at the next location, or for the next sample.
Models that consider only variability are typically formulated for well-characterized, well-understood systems such as those assumed to follow the rules of probability (flipping coins, tossing dice, choosing cards from a deck) or those for which a long period of observation has given us confidence that the probabilities are estimated with a high degree of precision, such as weather outcomes, common accident rates, or failure probabilities for manufactured parts that have been tested and used by the tens of thousands or more. Even in these cases, however, unrecognized nonstationarity (changes that occur over time)—for example, from climate change—can render historical estimates inaccurate and uncertain for future prediction. In these cases, uncertainty in our characterization of variability must also be considered.
To illustrate the combined effects of variability and uncertainty on future predictions, consider an event that has known probability of occurrence in a year of p*. Consider the simple case where a single event occurs during each year with probability p*, or no event occurs (with probability 1 - p*). The probability
|
1 |
References for this appendix A are included in the report’s “References.” |
distribution function for the number of events that might occur in the next N years is given by the well-known binomial distribution, with expected value p*N, but with some chance for more than this number of events occurring during the next N years, and some chance of less. For example, if p* = 0.15 (a 15 percent chance of an event occurring each year) and N = 20 years, the expected number of events over the 20-year period is 0.15 ×20 = 3 events. We can also calculate the standard deviation for this amount (= [p*(1- p*)N]1/2), which in this case is calculated to be 1.6 events. All this, however, assumes that we are certain that p* = 0.15. In most homeland security modeling, such certainty will not be possible because the assumptions here do not hold for terrorism events. A more sophisticated analysis is needed to show the implications of our uncertainty in p* in those cases.
A common model used to represent uncertainty in an event occurrence probability, p (e.g., a failure rate for a machine part), is the beta distribution. The beta distribution is characterized by two parameters that are directly related to the mean and standard deviation of the distribution of p; this distribution represents the uncertainty in p (i.e., the true value of p might be p*, but it might lower than p* or higher than p*). The event outcomes are then said to follow a beta-binomial model, where the “beta” part refers to the uncertainty and the “binomial” part refers to the variability. When the mean value of the beta distribution for p is equal to p*, the mean number of events in N years is the same as that calculated above for the simple binomial equation (with known p = p*). In our example, with mean p = p* = 0.15 and N = 20 years, the expected number of events in the 20-year period is still equal to 3. However, the standard deviation is larger. So, for example, if our uncertainty in p is characterized by a beta distribution with mean = 0.15 and standard deviation = 0.10 (a standard deviation nearly as great or greater than the mean is not uncommon for highly uncertain events such as those considered in homeland security applications), then the standard deviation of the number of events that could occur in the 20-year period is computed to be 2.5. This is 60 percent larger than the value computed above for the binomial case where p is assumed known (standard deviation of number of events in 20 years = 1.6), demonstrating the added uncertainty in future outcomes that can result from uncertainty in event probabilities. This added uncertainty is also illustrated in Figure A-1, comparing the assumed probability distribution functions for the uncertain p (top graph in Figure A-1) and the resulting probability distribution functions for the uncertain number of events occurring in a 20-year period (bottom graph in Figure A-1) for the simple binomial and the beta-binomial models. As indicated, the beta-binomial model results in a greater chance of 0 or 1 event occurring in 20 years, but also a greater chance of 7 or more events occurring, with significant probability up to and including 11 events. In this case, characterizing the uncertainty in the threat estimate is clearly critical when estimating the full uncertainty in future outcomes.
Proper recognition and characterization of both variability and uncertainty is important in all elements of a risk assessment, including effective interpreta-
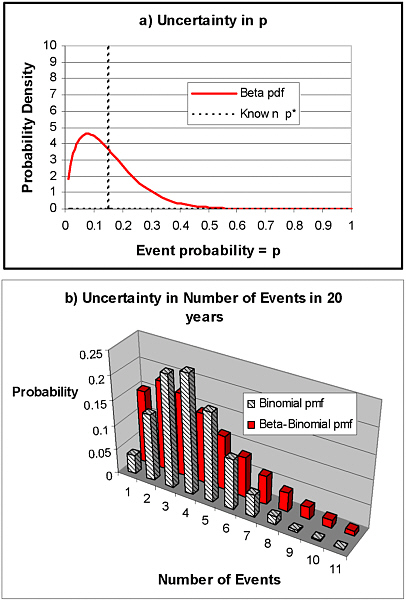
FIGURE A-1 Comparison of binomial model assuming known event probability p and beta-binomial model assuming that event probability is uncertain:(a) uncertainty distribution for p; mean of uncertain beta distribution is equal to the known value p* for the binomial case;((b) distribution of number of events in a future 20-year period; the binomial distribution considers only variability while the beta-binomial model reflects both variability and uncertainty.
tion of vulnerability, consequence, intelligence, and event occurrence data as they are collected over time. It also provides a basis for identifying which data are most critical to collect to reduce the uncertainties that matter for decision making, using a value-of-information approach as described below.
A range of analytical and numerical methods are available to estimate the uncertainty in model predictions resulting from uncertain model structure and inputs. A key objective in applying these methods is to evaluate which assumptions and inputs are most important in determining model output (through sensitivity analysis) and model uncertainty (through uncertainty analysis), especially those uncertainties that matter for (1) consistency with observed data and (2) the response and management decisions that are informed by the model. Studies to reduce the uncertainty in these assumptions and inputs then become prime targets in the value-of-information approach described below. Bayesian methods are especially useful for integrating new information as it becomes available, allowing iterative recalibration of model parameters and output uncertainty over time.
Learning and the Value of Information
A key element of risk-based management for homeland security and natural disasters is deciding which additional information collection efforts would be most beneficial to provide the key knowledge for more effective decisions. Effort invested in intelligence gathering is intrinsically viewed from this perspective; investments in more routine data collection and long-term research should be viewed similarly. When risk assessments include an explicit representation of uncertainty, the value of new information can be measured by its ability to reduce the uncertainties that matter in subsequent decisions derived from the risk analyses. A number of methods have been developed to quantify this, including scientific estimates based on variance reduction, decision-analytic methods based on the expected value of decisions made with and without the information, and a newer approach based on the potential for information to yield consensus among different stakeholders or decision makers involved in a risk management decision. These approaches are briefly reviewed.
Scientists and engineers often focus on the uncertainty variance of predicted outcomes from their assessments and how much this variance might be reduced by new or additional data (e.g., Abbaspour et al., 1996; Brand and Small, 1995; Chao and Hobbs, 1997; James and Gorelick, 1994; Patwardhan and Small, 1992; Smith and French, 1993; Sohn et al., 2000; Wagner, 1995, 1999). Although determining the uncertainty variance of model predictions and the potential to reduce them is very useful, this is in principle just the first step in characterizing the value of information. The key question is: In the context of pending risk management decisions, do the uncertainties matter? To address this question, the decision sciences have developed a decision analytic framework for the value of information (VOI) that considers: (1) whether the reduced uncertainty
could lead the decision maker to alter their decision and (2) what the expected increase in monetary value of the decision is as a result of the new information.
Decision analysis provides formal methods for choosing among alternatives under uncertainty, including options for collecting more information to reduce the uncertainty so that the outcomes associated with the alternatives are predicted with greater accuracy and precision (Chao and Hobbs, 1997; Clemen, 1996; Keeney, 1982; Raiffa, 1968; Winkler and Murphy, 1985). With no options for further study or data collection, the rational, fully informed decision maker will choose the option that maximizes the expected utility (or equivalently, minimizes the expected reduction in utility). Other decision rules may be considered as well, such as minimizing the maximum possible loss for a risk-averse decision maker.
When a possible program for further study or data collection is available, it should be chosen only if its results have the potential to influence the decision maker to change his or her preferred pre-information (prior) decision, and only if the increase in the expected value of the decision exceeds the program’s cost. Since information of different types and different quality can be considered, and these can affect the uncertainty of in the predicted outcomes associated with alternative decisions in different ways, a number of different measures of VOI can be considered (Hammitt and Shlyakhter, 1999; Hilton, 1981; Morgan and Henrion, 1990), including the following:
-
The Expected Value of Perfect Information (EVPI): how much higher is the expected value of the optimal decision when all uncertainty is removed?
-
The Expected Value of Perfect Information About X (EVPIX): how much higher is the expected value of the optimal decision when all of the uncertainty about a particular aspect of the problem, X (e.g., a particular input to an infrastructure simulation model), is removed?
-
The Expected Value of Sample Information (EVSI): how much higher is the expected value of the optimal decision made contingent upon the results of a sampling or research program that has less than perfect information, that is, with finite sample size and/or the presence of some measurement error?
Examples demonstrating the computation of these different measures of VOI have been developed for environmental decisions (Abbaspour, 1996; Freeze et al., 1990; James and Gorelick, 1994; Massmann and Freeze, 1987a,b; Wagner, 1999) and other elements of an integrated risk or economic assessment (Costello et al., 1998; Finkel and Evans, 1987; Taylor et al., 1993).
The basic decision-analytic approach described above assumes a single decision maker with a single set of valuations for the outcomes, a single set of prior probabilities for these outcomes under the different decision options, and a fixed and known mechanism for translating study results into posterior probabilities (i.e., a known and agreed-upon likelihood function for the proposed or ongoing research and data collection). However, for many decisions, multiple stakeholders with different values and beliefs must deliberate and come to some
consensus, informed by the science and the study results, but also affected by their differing valuations, prior probabilities and interpretation, and trust in scientific studies. This often leads to conflict in the decision process or, when one party has the authority or power to impose its will on others, dissatisfaction of the other parties with the decision outcome. What is needed then is a decision-analysis framework that identifies the sources of these differences and provides a rational basis for concrete steps that can overcome them. This leads to a broader and potentially more powerful notion of information value, based on the value of information for conflict resolution.
The idea that better information could help to facilitate conflict resolution is an intuitive one. If part of the failure to reach consensus is due to a different view of the science—a disagreement over the “facts”—then a reduction in the uncertainty concerning these facts should help to eliminate this source of conflict. Scientists often disagree on the facts (Cooke, 1991; Hammitt and Shlyakhter, 1999; Morgan and Keith, 1995). While the source of this disagreement may stem from (“legitimate”) disciplinary or systematic differences in culture, perspective, knowledge, and experience or (“less legitimate,” but just as real) motivational biases associated with research sponsorship and expectation, strong evidence that is collected, peer-reviewed, published, tested and replicated in the open scientific community and literature should lead eventually to a convergence of opinion. The Bayesian framework provides a good model for this process: even very different prior distributions should converge to the same posterior distribution when updated by a very large sample size with accurate and precise data.
Consider now a decision-analytic framework that must translate the implications of changes in assessments resulting from new information for scientists and the “decision support community” into new assessments for decision makers and interested and affected parties. Even were the science to be perfect and all scientists and stakeholders agree that the outcomes associated with each decision option are known with certainty, the different stakeholders to the problem are likely to value these outcomes differently, due to real or perceived differences in allocation of the benefits, costs, and risks associated with them. Measures of VOI for this situation must thus consider the likelihood that the information will convince conflicting participants to reach consensus, a situation of relevance to Department of Homeland Security (DHS). A VOI for conflict resolution has been proposed for this purpose (Small, 2004), and (Adams and Thompson, 2002; Douglas, 1987; Thompson et al., 1990; Verweij, 2006) addresses the underlying problem of policy analysis where stakeholder groups have very diverse worldviews. These differing ways of evaluating the VOI in a risk analysis should be considered by DHS in developing its research and data collections programs.






