7
PBPK Modeling White Paper: Addressing the Use of PBPK Models to Support Derivation of Acute Exposure Guideline Levels1
PREFACE
This White Paper describes the guidance that is proposed for use in the integration of physiologically based pharmacokinetic (PBPK) modeling in risk assessment in the EPA Acute Exposure Guideline Level (AEGL) program. After finalization, the guidance document will be added to the existing AEGL guidance for risk assessment activities. Therefore, the PBPK White Paper does not describe the entire methodology; rather, it describes the additional steps when PBPK modeling is undertaken within the existing risk assessment paradigm. As in any methodology, every facet of the method cannot be explicitly stated in a manner that is universally applicable to all chemicals. Where some details are not specified, the risk assessment process will be handled in accordance with the U.S. Environmental Protection Agency (EPA) document Approaches for the Application of Physiologically Based Pharmacokinetic (PBPK) Modeling and Supporting Data in Risk Assessment (EPA 2006).
1.
INTRODUCTION
AEGL values are developed in accordance with the Standing Operating Procedures for Developing Acute Exposure Guidelines Levels (AEGLs) for Hazardous Substances (NRC 2001). At the request of the AEGL/National Advisory Committee (NAC) and the AEGL Subcommittee of the Committee on Toxicology, National Academy of Sciences, this White Paper has been prepared to describe an approach for integrating the use of PBPK modeling into the development of AEGL values.
PBPK modeling serves as a useful adjunct to risk assessment of systemically acting chemicals by improving the basis of, or entirely allowing for, extrapolation of pharmacokinetics between animals and humans, extrapolation between various exposure scenarios (e.g., what exposure concentration for 10 minutes [min] results in the same internal dose produced from a 4-hour [h] exposure), and other types of extrapolation. As internal dose of a chemical agent is more closely associated with toxicity than is external exposure level of chemicals, extrapolating on the basis of internal dose is more reliable. In a sense, the use of PBPK models factors pharmacokinetic differences out of the extrapolation because they are handled by dose calculations instead of on the basis of an assumed equivalency followed by application of an uncertainty factor (UF) that is usually preset because of lack of knowledge about the true difference. As a result of using calculated doses, the overall uncertainty is reduced, and therefore the overall UFs may be reduced, allowing for more realistic exposure guidelines, which is the purpose in the advancement of the risk assessment process.
The risk assessment process includes identifying a point of departure (POD) from toxicity studies. The POD is usually the highest exposure concentration that did not result in the effect under consideration and may be a no-observed-adverse-effect level (NOAEL), a lowest-observed-adverse-effect level (LOAEL) if a NOAEL is not available, a level from a benchmark dose (BMD), or another value. The POD is then divided by UFs composed of estimated uncertainty in interspecies extrapolation, intraspecies variability, and other factors including weakness in the toxicologic database of information on a chemical.
Briefly, PBPK models are a description of the body and processes within the body (animal and human) that affect the disposition of a chemical. Disposition, or pharmacokinetics, includes the processes of absorption, distribution, metabolism, and excretion of chemicals. After development with necessary parameters and equations, the models calculate the concentration of the chemical (and metabolites, if necessary) in various parts of the body using exposure concentrations as the input.
The main function PBPK modeling serves in risk assessments is to provide a computational biology basis for some extrapolations that need to be made in the course of the risk assessment. This process is done by using PBPK models to determine the target tissue dose in humans or the test species (EPA 2006). Historically, in the AEGL program, types of extrapolations have included animal to human, within the human population, and for different periods of expo-
sure. Animal-to-human extrapolation occurs when human studies are not available or cannot be used to determine the POD; therefore, the animal POD is used to estimate human risk. If an animal study is used, an interspecies UF is applied to the POD to guard against the likelihood that humans are more sensitive than other animals at a given exposure. The human variability issue is an extrapolation in the sense that the POD for a set of experimental subjects is a projection of the values that should protect most of the population. This extrapolation is offset by applying the intraspecies UF, which is intended to protect individuals who are more sensitive than those represented by the experimental data. The temporal extrapolation is performed when a POD is based on studies with different exposure durations than the AEGL value. Thus, the value for one period is extrapolated to another exposure period. This extrapolation is currently performed using the ten Berge empirical formula, by holding the value constant for all exposure durations, or possibly other approaches.
When PBPK modeling is used as an alternative method of extrapolation, associated UFs can be eliminated or reduced and other approaches can be supplanted. The animal-to-human extrapolation is made directly on the basis of internal dose, so the pharmacokinetic portion of the interspecies UF can be reduced. Temporal extrapolations, currently made by using empirical approaches, can be done with explicit calculations of the internal dose. Finally, PBPK modeling can be used to examine some types of intraspecies uncertainty.
Many toxicity studies are performed with the human volunteer or animal effectively in a resting condition. However, humans may be stressed, working, or otherwise in an altered physiologic state during an emergency event or other scenarios where the AEGLs may be applied. Altered physiologic states significantly affect the pharmacokinetics of some chemicals. The consequent alterations in pharmacokinetics are not commonly addressed in a traditional risk assessment.
PBPK modeling can be used to reduce both inter- and intraspecies uncertainties in human health risk assessments for chemicals. Risk assessments traditionally have been performed by using the external exposure concentration, as opposed to an internal exposure concentration, as the basis for the dose-response assessment that results in the POD selection. In recent years, there has been a movement to use internal measures of exposure calculated with a PBPK model instead of external measures. Risk assessments that rely on this general concept have been performed for many chemicals, often in the cancer, chronic noncancer, and developmental risk assessment areas. The rationale for using PBPK modeling in these other types of risk assessments applies as well in the assessment of acute exposure risks.
The difference between a PBPK-based and a traditional dose-response assessment is that the PBPK method relies on an internal measure of exposure rather than an external one. An internal measure of exposure can be thought of as the exposure of the target tissue to the chemical, or “dose.” If the dose of chemical that reaches a target tissue can be determined with reasonable accuracy, then the pharmacokinetic issues described above can be dealt with by us-
ing known biology rather than UFs and empirical techniques. PBPK approaches are further empowered through the use of different methods for integrating the measure of dose. Depending on the chemical, the best predictor of toxicity may be the average tissue concentration of chemical, the peak concentration, the area under the curve (AUC) (concentration × time), or some other expression of concentration. The specific integrated measure of dose is referred to as the dose metric (DM) and is selected based on the mode of toxicologic action of the chemical. PBPK models are used to determine the DM at the POD. This concentration would become, in effect, a pharmacokinetic POD. If the critical study involves humans, this target DM is used to determine the equivalent concentration for different exposure durations or physiologic conditions. If the critical study involves animals, the pharmacokinetic POD would be determined in an animal version of the model and a human version of the model would then be used to determine the exposure concentration that results in the same DM value in human tissue. Thus, extrapolating from an animal to a human is performed with uncertainty limited to model error that is assessed during evaluation of the model.
PBPK modeling can be utilized in quantifying the effect of workload (exercise) on toxicity. Values for physiologic properties of the human in the model can be adjusted to account for exercise. Exposure concentrations that yield the same target tissue DM value could be determined under the exercise condition. Likewise, extrapolating to other exposure periods can be performed by determining the exposure concentration under a different exposure duration that yields the same target tissue DM value. Thus, the PBPK model minimizes some sources of uncertainty by basing the risk assessment on an appropriate internal DM, so that species, temporal, and physiologic differences are explicitly taken into account.
PBPK modeling is advocated and frequently used in modern risk assessments, but there are times when it is not appropriate. There are no set criteria, but in general PBPK models can be used for AEGL risk assessment when:
-
Existing PBPK models are available for a given chemical.
-
Existing models can be used in their current form or can be readily adapted for use.
-
Existing models can be adapted for the relevant species.
-
The ability of the model to simulate DMs (evaluation) within the context of their use in AEGLs is reasonable.
-
The PBPK models can calculate a DM that is appropriate, given the critical effect that is used in the risk assessment.
Different chemicals, exposure periods, and PODs may necessitate the use of different types of models. The criteria for deciding whether a model is acceptable for use in deriving AEGL values are provided in Section 4. When these criteria are not substantially met, PBPK models are not appropriate for use.
When they are not appropriate and available for use in deriving AEGL values, the AEGL values should be derived with existing methodologies.
A mode of toxicologic action consists of both pharmacokinetic and pharmacodynamic processes. Pharmacokinetics is what the body does with the chemical, and pharmacodynamics is what the chemical does to the body. For example, if a chemical enters a tissue, binds to a receptor protein, and interferes with signal transduction, the entry into the tissue is a pharmacokinetic process and the effects are pharmacodynamic. As the two processes are often conceptually separate, different models can sometimes be developed for each aspect, and the models can be linked to produce a biologically based dose-response model. While PBPK models describe the relationship between exposure and tissue dose, physiologically based pharmacodynamic (PBPD) models describe the relationship between tissue dose and response. The linked PBPK and PBPD models are often referred to as PBPK/PD models. In some cases, it may not be possible to develop separate PBPK and PBPD models. Some examples of PBPK/PD models include those developed for acetylcholinesterase inhibition for chlorpyrifos (Timchalk et al. 2002) and other organophosphate pesticides, glutathione depletion (Frederick et al. 1992), and cytotoxic responses due to intracellular acidification (Andersen et al. 2000). If such models exist for an AEGL chemical and can be incorporated into derivation of AEGLs, these models would serve to further reduce uncertainty and may reduce the pharmacodynamic portion of the UF.
The methodology for using PBPK modeling in risk assessments has been described (Clewell et al. 2002). The methodology provided in this White Paper is consistent with the guidance provided by the current EPA document on the use of PBPK modeling in risk assessment (EPA 2006). This document describes the process and explores specific issues that arise in the context of AEGL development. Although not often used in the risk assessment context, under specific circumstances classical (i.e., non-physiologically based) pharmacokinetic modeling may be useful for performing the temporal extrapolations when a PBPK model is not available.
2.
DESCRIPTION OF PBPK MODELING
In this section, PBPK models are described in a general manner. Additional detail may be found in various literature reviews of PBPK models (Krishnan and Andersen 1994; Leung and Paustenbach 1995; Bailer and Dankovic 1997; Reddy et al. 2005).
The pharmaceutical and medical sciences have studied and used pharmacokinetics for many years to determine appropriate doses of intentionally administered chemicals and drugs (pharmaceuticals) and, to a more limited extent, evaluate the effect of unintentional exposures (accidental overdoses, poisonings, narcotics usage). In these sciences, measures of dose such as the peak concentration (Cmax), time of peak concentration (Tmax), and AUC of concentration versus time have been of interest in determining the therapeutic dose. These
efforts were made after it was recognized that internal dose was a better predictor of therapy or toxicity than external exposures. Mathematically, measures of dose were usually determined by using curve-fitting regression methods that fit a simple empirical model to the concentration-versus-time data. The data were usually fit with formulas that replicated either a one- or a two-compartment system that represents either whole body or tissue and body water constructs.
This approach served the intended pharmaceutical needs because they were usually based on relatively rich data sets, including human data from clinical trials. Thus, extrapolations to other exposure scenarios were not a major factor in their use, as a range of doses could be studied in experimental trials. If extrapolation were needed, it could be performed in an empirical manner. PBPK models first received attention in the medical literature. As far back as the 1920s, they were described for ether, an anesthetic gas. Unfortunately, the computation burden in these models is such that the model could be solved only at steady state. In the 1950s and 1960s, PBPK models were described for additional drugs, including the chemotherapeutic methotrexate. Later work by Fiserova-Bergerova and others in the 1970s returned to a series of other anesthetic gases. Starting in the 1980s, PBPK models largely turned to considering environmental risk assessment, starting with work on methylene chloride and other chemicals.
The classical pharmacokinetic modeling approaches used in pharmaceutics did not serve the needs of environmental risk assessments nearly as well, where the data are relatively less abundant. In environmental risk assessment, intentional dosing studies that cover a range of exposures are often not available. High-dose studies could be associated with morbidity and are therefore not permissible. Experiments designed to evaluate effects of low-dose toxicity would require doses much lower than typical therapeutic doses and generally do not have large enough study populations to detect effects. Thus, risk assessments are enhanced when supported by estimates of internal tissue dose (EPA 2006). Extrapolating to low or high doses could be performed using proportional methods or classical pharmacokinetic methodologies. Proportional methods rely on the assumption that dose is proportional to exposure. This assumption is not the case for many exposures because of nonlinear physiologic processes such as saturable metabolism. This issue is also a limitation of classical pharmacokinetics; that is, Cmax at a dose of 3x is often not three times the Cmax at a dose of x. Tissue responses are more closely related to the internal target tissue dose versus the external chemical compound.
The PBPK model mitigates this dilemma and reduces the uncertainty in the dose-response assessment. The use of mathematical representation of the body based on first principles, meaning that the underlying construct of the body is true to life rather than entirely empirical, allows for full utilization of available data. Each compartment in the model represents an actual portion of the body, and the more important physiologic and biochemical processes are explicitly included in the mathematics of the model. However, there is simplification, such as considering major metabolic processes while ignoring minor ones. This sim-
plification is justified by the assumption, which can be tested, that the minor processes not included do not have a significant effect on model outcome. When all significant biologic processes are included in a model with equations that reflect the biology of the actual process, the outcome of the model will be a true representation of pharmacokinetics even when the doses are changed, so such models are a sounder basis for extrapolation. An example of the impact of using a PBPK model rather than empirical methods is provided in Figure 7-1. In this figure, the blood concentration is not directly proportional to exposure level. For example, at 8 h, the concentration of toluene in blood is about 1 milligram per liter (mg/L) after exposure to 100 parts per million (ppm); after a 1,000-ppm exposure, it exceeds 20 mg/L.
The internal concentration of a chemical or a chemical’s metabolite has been referred to as tissue dose, which is considered a more salient measure of dose (DM) for a POD than the external exposure. The ultimate tissue dose versus time profile is a composite event that results from all pharmacokinetic processes that occur, broadly divided into the processes of absorption, distribution, metabolism, and elimination. When a chemical such as an anesthetic gas is inhaled, it is taken up through the upper respiratory passages into the deep lung. More water-soluble chemicals may be absorbed into the upper respiratory tract and may even cause toxicity in those tissues. Chemicals that persist into the deep lung are presented to the lung cells, perhaps after absorption into mucous layers. In accordance with chemical equilibrium partitioning and diffusion characteristics, the chemical is absorbed into lung tissue cells several layers thick and eventually diffuses out of the tissue and into the blood, which perfuses that tissue. In the blood (and the lymph), the chemical may remain as a free compound or may bind with macromolecules and be transported to other parts of the body.
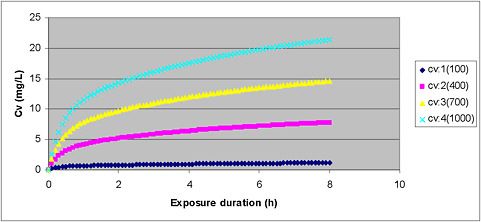
FIGURE 7-1 Plot of venous blood concentration (CV) of toluene (mg/L) versus time for four exposure levels (100, 400, 700, and 1,000 ppm) for up to 8 h. Based on PBPK model for toluene used for setting AEGL values for toluene.
When reaching other tissues of the body, chemicals again diffuse into cells in accordance with rates of diffusion and equilibrium partitioning. For chemicals that diffuse relatively rapidly, it is usually assumed that diffusion rates are unimportant and that the concentration of the chemical in the blood leaving the tissue will be in equilibrium with the concentration in the tissue. When this assumption has been tested for small molecular weight hydrophobic chemicals, it has been found to be reasonable. In other cases, the rate of diffusion must be explicitly incorporated in the model.
Metabolism may occur in various tissues. For some chemicals, the liver is the major metabolic organ, but a significant degree of metabolism may occur in other tissues as well. These processes are incorporated in a PBPK model by inserting the Michaelis-Menten equation into the rate expression for concentration of chemical in the tissue. At low concentrations, the rate expression compresses to the linear rate of metabolism with tissue concentration as the variable parameter; at high concentrations, a zero order rate of metabolism occurs. For example, many small molecular weight organic molecules that are substrates for low-affinity constant enzyme cytochrome P-450 (CYP) 2E1 can begin to saturate the enzyme at exposure levels that are relevant to the AEGL risk assessment process. As many parallel or sequential metabolic steps as needed can be included. If the toxic agent is the parent chemical, the models are usually not set up to trace the pharmacokinetics of metabolites. However, some models are constructed to evaluate the pharmacokinetics of metabolites by including a submodel with the necessary equations and parameter values for partitioning, absorption, metabolism, and other biologic processes for the metabolite. A chemical may be eliminated via exhalation, excretion through the kidney (urine) or liver (bile), or, in a sense, metabolized. Rate expressions for any significant elimination process would be included, such as in models that have successfully simulated the appearance of a metabolite in urine or feces (Gearhart et al. 1993).
While the body undergoes many thousands of simultaneous processes on a macro or molecular basis, when chemical concentrations are measured in tissues, their pharmacokinetics are often dominated by a selected few macroscale processes. Absorption of airborne chemicals is dominated by breathing rates and equilibrium between the lung air and lung tissue blood. Distribution is dominated by rates of blood flow to various tissues and equilibrium in those locations. Metabolism of inhaled chemicals occurs in metabolically active tissues such as the liver and can involve multiple CYP enzymes and others as well. In some cases, the data indicate that one enzyme in one principal tissue, often the liver, predominates and that an adequate model can be developed in which the contribution of other isoforms or enzymes in the principal tissue or the same or other enzymes in other tissues can reasonably be lumped with the activity of the major enzyme in the predominant tissue. In other cases, multiple enzymes and multiple metabolic tissues are sufficiently important that they should be incorporated in the PBPK model. The determination of how complex the model should be must be guided by the available data for each chemical during model development. For many chemicals, PBPK models can be constructed with only a few
rate expressions. Likewise, the anatomy of the body can be represented simply as well.
The use of PBPK modeling has been compared with results of using the ten Berge empirical equation for inhalation exposure to toluene. The specific results of this analysis are presented in Appendix A. The PBPK model was developed and then used to calculate the AEGL values at each exposure duration, based on achieving the same target tissue dose at all durations (toluene in brain or equivalently in blood). The target tissue dose was derived from the key study for that AEGL. In the toluene example, the PBPK model was able to determine the AEGL value for each duration that would yield the same expected tissue dose, while the ten Berge equation yielded tissue doses that varied from the target dose by a factor of 2-3.
The structure of a PBPK model has anatomic and kinetic elements. Anatomically, the body is represented as a system of compartments connected via blood flow. Typically, compartments are established for target tissue, a lung, blood, fat tissue, and the liver. Other tissues are usually grouped into rapidly perfused and slowly perfused tissues, and some tissues are combined when the processes that occur in them are relatively similar. For example, the gastrointestinal tract and kidney can be classified as rapidly perfused tissues, while muscle and bone can be considered slowly perfused tissues. Alternatively, any of the lumped-compartment tissues can be separated into its own compartment. Measured anatomic values for the size (volume or weight) of the tissue compartment are physiologic parameters. The sum of the tissue compartments is usually 80% to 90% of total body mass, as 10% to 20% of the body is not perfused with blood. A simple four-compartment model is shown in Figure 7-2.
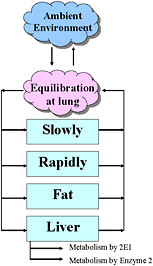
FIGURE 7-2 Four-compartment model.
Kinetic elements of the model structure include ventilation, blood flow, and biochemical expressions for metabolism, excretion, and other processes. Unless lymph, bile, or other fluids are included in the model, the only flow rates that need to be included are alveolar ventilation and blood flows. Alveolar ventilation is the fraction of pulmonary ventilation that reaches the gas-exchanging tissue in the deep lung. Total ventilation may be relevant for some types of models. Blood flows include cardiac output, arterial and venous blood flow, and blood flow to tissue compartments. Each of these values is taken from standard physiology literature (Brown et al. 1997) as model inputs.
Biochemical expressions depend on the chemical in question. If the metabolic rate is significant, equations are included representing metabolism as saturable (Michaelis-Menten), first order, or second order, as indicated by experimental data. Excretion of parent chemical or metabolites through the lung is handled by lung equilibration. The model does not need to compute the time course of metabolites if the DM relates to the parent compound, but if metabolites need to be included, excretion to feces or urine may be relevant and in some cases for the parent compound. These processes can be represented as first-order rates or by other appropriate kinetic mechanisms.
This description of a simple four-compartment model is often used for lipophilic chemicals. Many other model structures have been developed to describe various types of chemicals. For example, some models have more detailed descriptions of the lung or skin compartment (McDougal et al. 1986; Frederick et al. 1992) and some models have descriptions of biochemical processes such as protein binding, diffusion-limited kinetics, or enterohepatic recirculation. In practice, the concept of modeling parsimony should be exercised. This concept states that the model should be kept as simple as possible yet still provide the information needed for the analysis. In the AEGL program, PBPK models considered may often be more complex than the four-compartment model and should be used with due regard for the parsimony principle.
The PBPK model consists of a series of equations that include differential equations for the rate expressions and algebraic equations that compute other quantities. The equations were originally developed using the mass balance concept, which means that the amount of chemical entering a compartment equals the amount leaving or cleared from the same compartment plus the amount retained in the compartment. These values are expressed as a function of time. During acute exposure, the tissue concentrations are often not at steady state and therefore are significantly affected by the duration of exposure.
The typical mass balance equation for a compartment is
where
Qi = blood flow to tissue i,
CA = arterial blood concentration,
CVi = chemical concentration in the venous blood leaving tissue i, and
clearance is an additional rate expression describing clearance processes, such as metabolism in the tissue.
The equation determines the rate of change in amount of the chemical in the ith compartment. The mass of chemical in the compartment is determined by integrating the equation. This normally has to be done by using a numerical method for integration. In other words, the mass balance equation can be restated:
Rate of change in the chemical amount in the tissue (mg/h) = tissue blood flow rate (L/h) × (concentration in arterial blood [mg/L] – concentration in venous blood leaving the tissue [mg/L]) – rate of change in chemical amount due to metabolism in the tissue (mg/h).
Additional quantities are then calculated:
CT = AT/VT concentration in each tissue compartment and
CVi = CT/PT concentration in venous blood leaving tissue,
where
CT = chemical concentration in each tissue,
AT = amount in each tissue,
VT = volume of each tissue, and
PT = partition coefficient between the tissue and blood.
Metabolism is computed by another rate equation. For Michaelis-Menten kinetics in the liver,
where
Vmax = maximum rate of metabolism,
CVL = concentration in venous blood leaving the liver, and
Km = affinity constant for the chemical.
Other rate equations describe the uptake of chemical into lung blood by equilibration. Full versions of model codes have been provided for typical models in the literature (Clewell et al. 2000). Models developed for AEGLs should be scientifically supported and documented when possible.
3.
RECOMMENDATIONS FOR USE OF PBPK MODELS IN RISK ASSESSMENT
The EPA and other risk assessment organizations and practitioners have advocated the use of PBPK models to support risk assessment. These recom-
mendations go back to at least 1987, when the National Research Council (NRC) stated that “relevant PBPK data can be used to reduce uncertainty in extrapolation and risk assessment” (NRC 1987). In another recommendation specifically addressing community emergency exposure levels, the predecessor to AEGLs, the NRC stated “If PBPK models for calculating delivered dose and cross-species extrapolation have been developed, the pharmacokinetic information should be incorporated into the quantitative risk assessments” (NRC 1993).
The EPA has strongly endorsed the use of PBPK modeling in risk assessment. In 2002, the EPA stated “The optimal approach for extrapolating from one dose-duration response situation to another is the use of a physiologically based pharmacokinetic model (PBPK) model” (EPA 2002a). The EPA has made similar recommendations in its “Draft Final Guidelines for Carcinogen Risk Assessment” and in the context of cumulative risk assessment (EPA 2001, 2003) and reference concentration development methodology for Category 3 gases (EPA 1994). Moreover, the EPA has recently developed a report on the use of PBPK modeling in risk assessment (EPA 2006). The proposed methodology for use of PBPK in AEGL risk assessments has been informed by and is consistent with this EPA methodology.
The EPA has recently used PBPK modeling in risk assessments for perchlorate (EPA 2002b), vinyl chloride (EPA 2000), and other compounds. The most recent permissible exposure limit promulgated by the Occupational Safety and Health Administration (OSHA) for methylene chloride was derived with a PBPK model (OSHA 1997). Risk assessments based on PBPK modeling have also been developed by groups on a variety of chemicals, including trichloroethylene (Fisher and Allen 1993), vinyl acetate (Bogdanffy et al. 1999), formaldehyde (Schlosser et al. 2003), ethyl acrylate (Sweeney et al. 2004), and methylene chloride (Andersen et al. 1987a). Several authors as well as the National Academy of Sciences have advocated using PBPK modeling in AEGL development (Bruckner et al. 2004; Krewski et al. 2004). An initial example for trichloroethylene has been described (Boyes et al. 2000, 2002, 2003, 2005; Simmons et al. 2002, 2005). Thus, guidance from both the EPA and input from the scientific community have clearly established that PBPK models should be considered for use in supporting risk assessment when such models are available and capable of predicting tissue dose of the chemical under conditions similar to environmental exposure or experimental studies.
The specific types of risk assessment applications for which PBPK modeling can be useful in the AEGL context have been previously demonstrated in other risk assessment applications, often for cancer and chronic noncancer risks. Many papers have illustrated the value of PBPK modeling for interspecies scaling (Ramsey and Andersen 1984; Clewell et al. 2001; Timchalk et al. 2002).
PBPK models have been previously used to time-scale dose from exposure regimens in chronic bioassays (e.g., 6 h/day, 5 days/week) to 24 h/day, 7 days/week (Clewell et al. 1997). PBPK models have also been used to time-scale worker exposure levels for long and short exposures (Andersen et al. 1987b). Their use in AEGL derivation is an extension of these previous uses.
For each AEGL level, the critical study that determines the POD usually provides an estimate of the POD only at one time point—for example, a median lethal concentration (LC50) study for 4 h. Thus, one task in the AEGL development process is to extrapolate from one exposure duration to others. It may be necessary to extrapolate from longer to shorter durations or vice versa. It has been done in the past by using various approaches, including the ten Berge equation (k = Cn × t) where k = a constant, C = exposure concentration, n = an empirical constant, and t = time (ten Berge et al. 1986). The exponent n can be derived from available data; often, the default assumptions are used that n = 1 when extrapolating from shorter to longer periods and n = 3 when extrapolating from longer to shorter periods. However, as with any empirical approach, these assumptions do not always reflect the underlying pharmacokinetics in the animal and can lead to errors when extrapolating to humans.
PBPK models have also been used for workload physiology extrapolation ( Johanson 1986; Dankovic and Bailer 1994; Kumagai et al. 1998; Jonsson et al. 2001). Workload physiology extrapolation is important because the tissue DMs for some chemicals can be significantly affected by increased ventilation, and altered blood flow can affect the distribution of the chemical. Studies have demonstrated that the tissue dose of several organic solvents were found to be increased with increasing workload (Carlsson 1982; Pezzagno et al. 1988), particularly with chemicals that have a relatively high blood-air partition coefficient (PB). Csanady and Filser noted that workload was a significant factor in the pharmacokinetics of chemicals with a PB greater than 6 (Csanady and Filser 2001). Numerous chemicals on the target list of AEGLs have higher PB values. However, in a non-steady-state environment, this issue can be addressed only with a pharmacokinetic model.
PBPK modeling can be used to develop AEGL-1, AEGL-2, and AEGL-3 values. Depending on the availability of appropriate models and DMs, the PBPK models can be used for some or all of the AEGL level values, with other methods used for the values not derived by PBPK modeling.
4.
CRITERIA FOR USE OF PBPK MODELING IN AEGL DEVELOPMENT
Several issues must be addressed when PBPK models are being considered for use in AEGL development. Using PBPK modeling in AEGL development has three stages: initial determination of feasibility, in-depth determination of adequacy, and implementation. The initial determination of feasibility is a screening process in which the use of PBPK modeling for a particular chemical can be evaluated based on a priori criteria that are simple to evaluate. The in-depth determination of adequacy is a second required stage, because a number of problems that are not immediately obvious can appear during model development or evaluation. For example, a published model may be developed with one data set, but evaluation with additional data could indicate that the model
should not be used for AEGL value development because its overall performance is judged to be inadequate. Implementation involves using the models to determine AEGL values. These assessments should be conducted in a manner consistent with EPA guidance (EPA 2006).
4.1.
Initial Determination of PBPK Modeling Feasibility
When a chemical is being considered for the development of AEGLs or revisions to existing AEGLs are being made, the applicability of PBPK modeling should be considered. The AEGL development team should include someone with PBPK modeling experience to help in this evaluation. The determination should weigh the following factors:
-
Is there a basis to expect that PBPK modeling may yield more reliable and realistic AEGL values than other approaches?
-
Is there an existing PBPK model for the chemical? If the model is not in a strain or species of interest, it may still be viable, as modification of species may not be overly time-consuming if data are available. At times, development of a new PBPK model may be warranted. For example, if AEGLs are being developed for a chemical similar to another with an existing model, and data are available for adjusting the parameters, the model development process may be worthwhile.
-
Can the model provide data on appropriate DMs? A tentative DM should be determined early in the process, based on the mode of toxicologic action of the chemical.
4.2.
In-Depth Determination of Adequacy
This stage is a continuation of the screening analysis but denotes a more in-depth analysis of the models and data available and consequently is more time-consuming. PBPK model adequacy for use in AEGL value determination rests on a number of factors that relate to the ability of the model to calculate the DM.
During development and evaluation of the model, some factors that should be considered in determining whether the model is sufficient include the following:
-
Is an existing model established for humans? If not, can an animal model be reliably modified to apply to humans?
-
If animal models are required, are existing models available for the species of interest? If not, can existing models be adapted for the species?
-
If no existing models are available, can one be developed with a reasonable amount of effort?
-
How well do these data project to the conditions relevant to AEGLs? Do they include exposures at reasonably high concentrations and short durations? Do they include pharmacokinetic data for workload conditions (for human models where applicable)?
-
Are the existing models sufficiently well described in publication to be usable?
-
Are parameters available for all needed inputs?
-
Do the models calculate appropriate DMs or can they be modified to do so?
-
Are sufficient data available to evaluate the models? How well evaluated are the models?
4.3.
Model Selection
In some cases, more than one existing model is available for use. The possibility exists that modification of an existing model may improve it for use in AEGL development. Therefore, a model has to be selected during the development process. The following procedures should be used in this regard.
Published literature should be thoroughly reviewed to identify existing models. All available models should be reviewed for potential use in AEGL development. During the review, the following questions should be considered:
-
Was the model fully documented in terms of equations and parameter values?
-
How was the model evaluated? What kinds of data were used?
-
Was the model published in the peer-reviewed literature?
-
Is the model appropriate for AEGL development? Will it support computation of the DM relevant for AEGL end points?
In general, the use of existing models is preferable to revising models or developing new ones. The existing models should be reviewed by comparing model performance. This review is done by running each model against a group of data sets that are chosen a priori for the purpose of model evaluation. Data sets that are representative and relevant for the AEGL development process and that include data from laboratories other than those connected with the model’s developers should be used and justified. Other considerations for data set selection include the following:
-
Do the data involve exposures in the range of interest (likely range of AEGL values)?
-
Do the data provide multiple concentrations in one set of studies?
-
Are data from time-course studies rather than a single time point?
-
Are there data for more than one tissue?
-
Are the data collected from the species of interest?
-
Are there PBPK model parameters for the experimental species?
-
Were body weights reported?
-
Are exposure conditions clearly defined?
-
Is the route of exposure appropriate?
-
Do the data relate to the DM?
-
Are there data from more than one laboratory?
-
Are there data for exercising humans?
Selection of the most appropriate model depends on many of these factors as well as professional judgment. Evaluation of model performance depends heavily on the ability of the model to describe pharmacokinetic data, especially those data in the region of interest. This evaluation can be performed by visual observation of the plots of model predictions or by statistical analysis. Use of visual observation is consistent with EPA guidance at this time (EPA 2006), although implementation of statistical procedures to evaluate a particular model or to select from multiple models is also consistent with current guidance. If the results of the model performance indicate that model improvement is worthwhile, models can then be revised and compared with the existing models. The best overall model should then be selected for use based on considerations described by the EPA (EPA 2006).
4.4.
Considerations for Model Modifications
When modifications are being considered, sensitivity analysis should be used to guide the process. For new, modified, or existing models, sensitivity analysis should be performed and reported to help reviewers understand the relative importance of parameters.
Optimization, the statistical process of modifying a parameter’s value until the best fit to a calibration data set is achieved, should be performed numerically after a best visual fit is obtained. Optimized parameter values should be within the range of existing measurements or estimates and should be reasonable when compared with values for similar compounds.
Human parameter values for partition coefficients and metabolism are preferred to animal values when using the human versions of the models. Although these parameters are often similar, the differences that occur can have a significant impact on DMs. Parameters that were determined experimentally rather than through optimization are preferred. However, optimization is acceptable, particularly in the range of experimental results. All resulting parameter values should be reasonable and should be compared with parameter values reported in the literature.
Generally, models published in the peer-reviewed literature would be used in an unmodified manner for AEGLs. In some instances, modified models offer significant improvement to warrant the investment required to modify them. For
example, available models might have been developed for exposure levels far lower than the range from which AEGL values will be set. When a significant improvement can be made, these modified models may be used for setting AEGLs, but peer review of the modified model is required before such use.
4.5.
Model Evaluation and Verification
Model evaluation is one the most critical aspects in selection and use of a PBPK model. Evaluation of PBPK models has been discussed elsewhere (Clark et al. 2004) and pertinent points are discussed below. The evaluation should be performed using as much data as practicable. In particular, data in the strain and species for which the model is developed, for the exposure route of interest, in the concentration range of interest, and for the DM of interest should be used. Data from as many different laboratories as possible will strengthen the model. Data for pharmacokinetics during workload conditions should also be used if workload is an appropriate consideration. Data for more than one tissue, even for tissues that are not target tissues, will strengthen the model.
Models should be evaluated with the following considerations:
-
Are the deviations between simulations and experimental data large or small?
-
Do the deviations have a systematic component; for example, does the model consistently over- or underpredict portions of the data such as early time points or high exposures?
-
How does the magnitude of the deviations compare among the model undergoing evaluation and other models that have been used for risk assessment?
-
How well does the model perform in the exposure and duration range of interest?
-
How rich were the animal and particularly the human data?
Results of model evaluation should be reported, generally in graphic format.
4.6.
Model Quality Assurance and Documentation
As with other parts of the AEGL risk assessment, the PBPK model should be formulated into a report for inserting into a technical support document (TSD). Before issuance, it should go through a quality assurance review. This review would have two parts: editorial review and technical review that would include reproduction of some model output and calculations to check for accuracy.
To facilitate the review process, the model and all related calculations should be fully documented in the model report. This report should include true copies of all model codes, parameter lists, data sets, and outputs. They should also be made available electronically. Standardized software should be used so that model runs can be repeated with minimal effort. If any scripts are used, they should be designed to take the user through the steps required to reproduce all evaluations and calculation processes. For example, a statement could be provided such as “Fig. X is produced by running Script A, then B with a concentration of C.” Additional guidance on evaluation and documentation of PBPK models is available (Clark et al. 2004).
5.
APPLICATION OF PBPK MODELING TO THE AEGL DEVELOPMENT PROCESS
Figure 7-3 describes the process by which PBPK modeling can be used in AEGL development as a series of sequential steps.
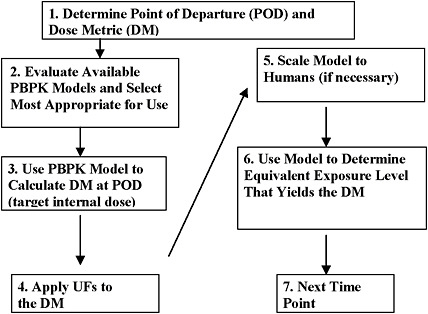
FIGURE 7-3 Use of PBPK models in AEGL development.
Step 1. Determine POD and DM. The key study and effect are determined through a review of all available literature. If the mode of toxicologic action is understood so that a DM can be determined through a PBPK (or PBPD) model, then modeling will be undertaken. For example, the AEGL-2 POD for toluene was based on a study in which the NOAEL for toluene exposure was 700 ppm for 20 min.
Step 2. Evaluate available PBPK models and select most appropriate for use. Available PBPK models will be evaluated. The most appropriate model will be selected for use, as described in Section 4. This step is often the most time-consuming step of the process, but it is critical. Returning to the example of the toluene AEGL PBPK model, existing models poorly described high-exposure-level data, so a modified model was selected for AEGL development.
Step 3. Use PBPK model to calculate DM @ POD (target internal dose). Use the selected model to calculate the DM at the POD. In the case of toluene, the AEGL-2 critical study involved an experimental design that made it difficult to determine the POD for two reasons. First, it required extrapolation from the very short exposure to longer exposure periods. Second, the 700-ppm exposure was preceded by exposures at 100, 300, and 500 ppm and a break, confounding the assessment of the POD. PBPK modeling was used to determine the internal DM for the exposure at the NOAEL. This yielded a DM of toluene in venous blood of 6.5 mg/L.
Step 4. Apply uncertainty factors to the DM. UFs for toluene consisted of a total of 3 for intraspecies. This DM would be applied to the internal DM but in some instances might be applied to final values instead (see discussion in Section 5.1). Thus, the final target dose of toluene in venous blood was 6.5/3, or 2.16 mg/L.
Step 5. Scale model to humans (if necessary). The model is scaled to humans if the original was an animal model. For example, in the toluene AEGL, no scaling was required because the human model was used to determine the internal DM level in the critical study, which involved human subjects. On the other hand, the AEGL-3 for toluene was based on animal data. In either case, the model selected for use had been evaluated against human data and accepted for use.
Step 6. Use model to determine equivalent exposure level that yields the DM. The model is then used to determine the human equivalent concentration for one exposure duration, such as 10 min. This method is referred to as “boot-strapping” because the model is iteratively run until the concentration input that leads to the targeted internal dose is found. For example, with toluene, the model was bootstrapped until the concentration was found that yielded a venous blood concentration of 2.16 mg/L after 10 min of exposure.
Step 7. Next time point. The bootstrapping method is repeated for each exposure period. The process is repeated for each AEGL level where modeling will be used.
5.1.
Application of UFs
In the AEGL process that does not generally incorporate modeling, two UFs are frequently applied to the POD: the interspecies UF when the POD is obtained from an animal study and the intraspecies UF that adjusts for human variability. The intraspecies UF may be reduced in some cases by PBPK modeling, although the methods for doing so are not as readily accepted by the scientific community. For instance, if data were available to allow modeling of the most sensitive human subpopulation, a reduction in the intraspecies UF may be justified. Other UFs can be considered but are used less often in the AEGL development process, including LOAEL to NOAEL and database UFs. PBPK modeling can be a useful tool in replacing some of these UFs, but its most frequent applications are in the interspecies context and in temporal extrapolation.
The interspecies UF default of 10 can be subdivided into a pharmacokinetic component and a pharmacodynamic component according to the existing standard operating procedures for AEGLs (NRC 2001). Typically, the practice is to split the interspecies UF into 3 for pharmacokinetics and 3 for pharmacodynamics (EPA 2006). When PBPK modeling is used to perform the internal dose calculations for extrapolation, the EPA supports an appropriate reduction in the pharmacokinetic portion of the interspecies UF (EPA 2006). Similar reductions in other UFs should be considered if PBPK (or PBPD) modeling can be used to reduce uncertainty in the extrapolation.
During AEGL development without PBPK modeling, the UFs are generally applied only to the POD. When PBPK modeling is used, the UFs can reasonably be applied in two places. First, they can be applied to the target DM level, the internal dose that corresponds to the POD. For example, if the POD corresponds to a tissue dose of 20 mg/L and the UF is 3, the target tissue dose would become 6.67 mg/L. The PBPK model would then be run again to determine the human exposure that yields that target dose level. The second option is to apply the UFs after the human equivalent concentration is determined via the model. Thus, for the example above, the model would determine the human equivalent concentration that yields an internal dose of 20 mg/L and that concentration would be divided by 3. Given that there often are UFs pertaining to inter- and intraspecies extrapolations, a third choice of application is also present: one of the UFs could be applied to the DM and the other to the final values.
Whether there is a difference in the final AEGL value when the UF is applied to the internal DM or the POD depends on the shape of the exposure-dose curves. The exposure-dose curve may be quite linear, depending on the chemical and the concentration range. In these cases, there is no difference in the resulting AEGL value determined by either method. However, when there are significant nonlinearities in the concentration-dose curve, differences can occur.
To assess the potential magnitude of these differences, AEGL values were calculated both ways for two chemicals: toluene and xylene. In the proposed AEGLs for toluene and xylene, under standard AEGL derivation the comparison was made with UFs of 3, 10, and 30. For these two chemicals, no appreciable
difference between the approaches was found when the total UF was assumed to be 3. More frequently, an appreciable difference was found when the total UF was 10 or 30, particularly the latter. The differences were greater for the 8-h AEGLs than for the shorter time periods. Either method could yield the larger AEGL value at different times. When a difference was found, most of the time the two values were within a factor of 2 and occasionally were as high as 2.5.
The argument for applying the UF to the DM is that this approach results in a more reliable reduction of risk as the internal dose is more closely correlated with risk than the external exposure level (Clewell and Jarnot 1994; Clewell et al. 1997, 2002). Stated another way, if the UF is applied to the final values, the reduction in internal dose will not exactly equal the intended UF reduction based on the net reduction in the internal dose, so applying the UF to the internal dose is more scientifically defensible. On the other hand, it has been observed that default UFs represent policy decisions rather than clear estimates of uncertainty and thus should be applied to final values. There is some consensus indicating that the interspecies UF (pharmacodynamics) is best applied to the DM, while there is less consensus indicating that the intraspecies UF should be applied to the DM. While the EPA position on this matter is being established, the AEGL program will need to implement one of the following options:
-
Option 1: Apply all UFs to the DM.
-
Option 2: Apply all UFs to the final values.
-
Option 3: If both intraspecies (PD) and interspecies (PD/PK) UFs are to be applied, apply the interspecies to the DM and the intraspecies to the final values.
As the best approach is undecided, another factor should be considered. In many cases in the AEGL program, human pharmacokinetic data are at lower levels than the POD, especially for AEGL-3, which is usually obtained from animal studies. When the UFs are applied to the DM, they reduce the target tissue dose before modeling is used to determine human equivalent concentrations , thereby reducing the extent of the high-dose extrapolation of the human model. For these reasons, Option 1 is the default choice of method. However, the NAC at its discretion may select one of the alternative methods on a case-by-case basis where indicated by scientific data.
5.2.
Use of Benchmark Dose Statistical Modeling
An alternative to using a NOAEL as the POD is the use of a BMD. If a BMD is to be calculated and a PBPK model is available, the model should be used to calculate the DM for each exposure level in the critical study. The DM values should be used as inputs into the BMD calculation rather than the exposure levels. For example, for the toluene AEGL-3, the BMD can be determined by using the PBPK model to determine the peak blood concentration of toluene
at each exposure level that goes into the BMD calculation, and these blood concentrations are used for the dose side of the BMD input. This approach is preferable because the closer relationship between the DM and toxicity subjects the statistical model to less confounding by the nonlinear relationship between exposure and internal dose (Clewell et al. 2002). Examples of the use of BMD and PBPK modeling were developed for acute and longer-term exposure guidelines at the Agency for Toxic Substances and Disease Registry (Clewell et al. 1997).
5.3.
Inclusion of Exercise Physiology
The current AEGL standard operating procedure does not recommend adjusting AEGL values based on activity levels. Therefore, the NAC has decided not to adjust values for activity levels even when possible by using the PBPK model.
REFERENCES
Andersen, M.E., H.J. Clewell III, M.L. Gargas, F.A. Smith, and R.H. Reitz. 1987a. Physiologically based pharmacokinetics and the risk assessment process for methylene chloride. Toxicol. Appl. Pharmacol. 87(2):185-205.
Andersen, M.E., M.G. MacNaughton, H.J. Clewell III, and D.J. Paustenbach. 1987b. Adjusting exposure limits for long and short exposure periods using a physiological pharmacokinetic model. Am. Ind. Hyg. Assoc. J. 48(4):335-343.
Andersen, M., R. Sarangapani, R. Gentry, H. Clewell, T. Covington, and C.B. Frederick. 2000. Application of a hybrid CFD-PBPK nasal dosimetry model in an inhalation risk assessment: An example with acrylic acid. Toxicol. Sci. 57(2):312-325.
Bailer, A.J., and D.A. Dankovic. 1997. An introduction to the use of physiologically based pharmacokinetic models in risk assessment. Stat. Methods Med. Res. 6(4):341-358.
Bogdanffy, M.S., R. Sarangapani, D.R. Plowchalk, A. Jarabek, and M.E. Andersen. 1999. A biologically based risk assessment for vinyl acetate-induced cancer and noncancer inhalation toxicity. Toxicol. Sci. 51(1):19-35.
Boyes, W.K., P.J. Bushnell, K.M. Crofton, M. Evans, and J.E. Simmons. 2000. Neurotoxic and pharmacokinetic responses to trichloroethylene as a function of exposure scenario. Environ. Health Perspect. 108(Suppl. 2):317-322.
Boyes, W.K., J.E. Simmons, C. Eklund, E. Kenyon, and M. Evans. 2002. Physiologically-Based Pharmacokinetic Modeling of Trichloroethylene. Letter to P. Janssen, Center of Substances and Risk Assessment, National Institute of Public Health and the Environment, Bilthoven, the Netherlands. February 14, 2002. Appendix A in Trichloroethylene (CAS Reg. No. 79-01-6) Proposed Acute Exposure Guideline Levels (AEGLs), Trichloroethylene TSD ND Proposed FR08 090704 OPPT-2004-0079-0090, draft July 23, 2002.
Boyes, W.K., M. Bercegeay, J.S. Ali, T. Krantz, J. McGee, M. Evans, J.H. Raymer, P.J. Bushnell, and J.E. Simmons. 2003. Dose-based duration adjustments for the effects of inhaled trichloroethylene on rat visual function. Toxicol. Sci. 76(1):121-130.
Boyes, W.K., M.V. Evans, C. Eklund, P. Janssen, and J.E. Simmons. 2005. Duration adjustment of acute exposure guideline level values for trichloroethylene using a physiologically-based pharmacokinetic model. Risk Anal. 25(3):677-686.
Brown, R.P., M.D. Delp, S.L. Lindstedt, L.R. Rhomberg, and R.P. Beliles. 1997. Physiological parameter values for physiologically based pharmacokinetic models. Toxicol. Ind. Health 13(4):407-484.
Bruckner, J.V., D.A. Keys, and J.W. Fisher. 2004. The Acute Exposure Guideline Level (AEGL) program: Applications of physiologically based pharmacokinetic modeling. J. Toxicol. Environ. Health A 67(8-10):621-634.
Carlsson, A. 1982. Exposure to toluene: Uptake, distribution and elimination in man. Scand. J. Work Environ. Health 8(1):43-55.
Clark, L.H., R.W. Setzer, and H.A. Barton. 2004. Framework for evaluation of physiologically-based pharmacokinetic models for use in safety or risk assessment. Risk Anal. 24(6):1697-1717.
Clewell, H.J., III, and B.M. Jarnot. 1994. Incorporation of pharmacokinetics in noncancer risk assessment: Example with chloropentafluorobenzene. Risk Anal. 14(3):265-276.
Clewell, H.J., III, P.R. Gentry, and J.M. Gearhart. 1997. Investigation of the potential impact of benchmark dose and pharmacokinetic modeling in noncancer risk assessment. J. Toxicol. Environ. Health 52(6):475-515.
Clewell, H.J., III, P.R. Gentry, T.R. Covington, and J.M. Gearhart. 2000. Development of a physiologically based pharmacokinetic model of trichloroethylene and its metabolites for use in risk assessment. Environ. Health Perspect. 108(Suppl. 2):283-305.
Clewell, H.J., P.R. Gentry, J.M. Gearhart, B.C. Allen, and M.E. Andersen. 2001. Comparison of cancer risk estimates for vinyl chloride using animal and human data with a PBPK model. Sci. Total Environ. 274(1-3):37-66.
Clewell, H.J., III, M.E. Andersen, and H.A. Barton. 2002. A consistent approach for the application of pharmacokinetic modeling in cancer and noncancer risk assessment. Environ. Health Perspect. 110(1):85-93.
Csanady, G.A., and J.G. Filser. 2001. The relevance of physical activity for the kinetics of inhaled gaseous substances. Arch. Toxicol. 74(11):663-672.
Dankovic, D.A., and A.J. Bailer. 1994. The impact of exercise and intersubject variability on dose estimates for dichloromethane derived from a physiologically based pharmacokinetic model. Fundam. Appl. Toxicol. 22(1):20-25.
EPA (U.S. Environmental Protection Agency). 1994. Methods of Derivation of Inhalation Reference Concentrations and Application of Inhalation Dosimetry. EPA/600/8-90/066F. Office of Research and Development, Office of Health and Environmental Assessment, U.S. Environmental Protection Agency, Washington, DC [online]. Available: http://www.epa.gov/raf/publications/pdfs/RFCMETHODOLOGY.PDF [accessed Apr. 22, 2010].
EPA (U.S. Environmental Protection Agency). 2000. Toxicological Review of Vinyl Chloride (CAS No. 75-01-4) In Support of Summary Information on the Integrated Risk Information System (IRIS). EPA/635R-00/004. U.S. Environmental Protection Agency, Washington, DC. May 2000 [online]. Available: http://www.epa.gov/iris/toxreviews/1001tr.pdf [accessed Apr. 22, 2010].
EPA (U.S. Environmental Protection Agency). 2001. Preliminary Cumulative Risk Assessment of the Organophosphorus Pesticides. Office of Pesticide Programs, U.S. Environmental Protection Agency, Washington, DC. December 3, 2001 [online]. Available: http://www.epa.gov/oppsrrd1/cumulative/pra-op/[accessed Apr. 22, 2010].
EPA (U.S. Environmental Protection Agency). 2002a. A Review of the Reference Dose and Reference Concentration Processes. EPA/630/P-02/002F. Risk Assessment Forum, U.S. Environmental Protection Agency, Washington, DC [online]. Available: http://cfpub.epa.gov/ncea/cfm/recordisplay.cfm?deid=55365 [accessed Apr. 22, 2010].
EPA (U.S. Environmental Protection Agency). 2002b. Perchlorate Environmental Contamination: Toxicological Review and Risk Characterization. External Review Draft. NCEA-1-0503. National Center for Environmental Assessment, Office of Research and Development, U.S. Environmental Protection Agency, Washington, DC. January 16, 2002 [online]. Available: http://cfpub.epa.gov/ncea/cfm/recordisplay.cfm?deid=24002 [accessed Apr. 22, 2010].
EPA (U.S. Environmental Protection Agency). 2003. Draft Final Guidelines for Carcinogen Risk Assessment. EPA/630/P-03/001A. NCEA-F-0644A. Risk Assessment Forum, U.S. Environmental Protection Agency, Washington, DC. February 2003 [online]. Available: oaspub.epa.gov/eims/eimscomm.getfile?p_download_id=36765 [accessed Apr. 22, 2010].
EPA (U.S. Environmental Protection Agency). 2006. Approaches for the Application of Physiologically Based Pharmacokinetic (PBPK) Models and Supporting Data in Risk Assessment. EPA/600/R-05/043F. National Center for Environmental Assessment, Office of Research and Development, U.S. Environmental Protection Agency, Washington, DC. August 2006 [0nline]. Available: http://cfpub.epa.gov/ncea/CFM/recordisplay.cfm?deid=157668 [accessed Apr. 26, 2010].
Fisher, J.W., and B.C. Allen. 1993. Evaluating the risk of liver cancer in humans exposed to trichloroethylene using physiological models. Risk Anal. 13(1):87-95.
Frederick, C.B., D.W. Potter, M.I. Chang-Mateu, and M.E. Andersen. 1992. A physiologically based pharmacokinetic and pharmacodynamic model to describe the oral dosing of rats with ethyl acrylate and its implications for risk assessment. Toxicol. Appl. Pharmacol. 114(2):246-260.
Gearhart, J.M., D.A. Mahle, R.J. Greene, C.S. Seckel, C.D. Flemming, J.W. Fisher, and Clewell, H.J., III. 1993. Variability of physiologically based pharmacokinetic (PBPK) model parameters and their effects on PBPK model predictions in a risk assessment for perchloroethylene (PCE). Toxicol. Lett. 68(1-2):131-144.
Johanson, G. 1986. Physiologically based pharmacokinetic modeling of inhaled 2-butoxyethanol in man. Toxicol. Lett. 34(1):23-31.
Jonsson, F., F. Bois, and G. Johanson. 2001. Physiologically based pharmacokinetic modeling of inhalation exposure of humans to dichloromethane during moderate to heavy exercise. Toxicol. Sci. 59(2):209-218.
Krewski, D., K. Bakshi, R. Garrett, E. Falke, G. Rusch, and D. Gaylor. 2004. Development of acute exposure guideline levels for airborne exposures to hazardous substances. Regul. Toxicol. Pharmacol. 39(2):184-201.
Krishnan, K., and M. Andersen. 1994. Physiologically based pharmacokinetic modeling in toxicology. Pp. 193-242 in Principals and Methods of Toxicology, 4th Ed., A.W. Hayes, ed. New York: Raven.
Kumagai, S., I. Matsunaga, and T. Tabuchi. 1998. Effects of variation in exposure to airborne acetone and difference in work load on acetone concentrations in blood, urine, and exhaled air. Am. Ind. Hyg. Assoc. J. 59(4):242-251.
Leung, H.W., and D.J. Paustenbach. 1995. Physiologically based pharmacokinetic and pharmacodynamic modeling in health risk assessment and characterization of hazardous substances. Toxicol. Lett. 79(1-3):55-65.
McDougal, J.N., G.W. Jepson, H.J. Clewell III, M.G. MacNaughton, and M.E. Andersen. 1986. A physiological pharmacokinetic model for dermal absorption of vapors in the rat. Toxicol. Appl. Pharmacol. 85(2):286-294.
NRC (National Research Council). 1987. Drinking Water and Health, Vol. 8. Pharmacokinetics in Risk Assessment. Washington, DC: National Academy Press.
NRC (National Research Council). 1993. Guidelines for Developing Community Emergency Exposure Levels for Hazardous Substances. Washington, DC: National Academy Press.
NRC (National Research Council). 2001. Standing Operating Procedures for Developing Acute Exposure Guidelines Levels for Hazardous Substances. Washington, DC: National Academy Press.
OSHA (Occupational Safety and Health Administration). 1997. Occupational Exposure to Methylene Chloride, Section 6. Quantitative Risk Assessment. U.S. Department of Labor, Occupational Safety and Health Administration, Washington, DC [online]. Available: http://www.osha.gov/pls/oshaweb/owadisp.show_document?p_id=1006&p_table=PREAMBLES [accessed Apr. 26, 2010].
Pezzagno, G., M. Imbriani, S. Ghittori, and E. Capodaglio. 1988. Urinary concentration, environmental concentration, and respiratory uptake of some solvents: Effect of the work load. Am. Ind. Hyg. Assoc. J. 49(11):546-552.
Powers, S.K., and E.T. Howley. 1997. Exercise Physiology: Theory and Application to Fitness and Performance, 3rd Ed. Madison: Brown and Benchmark Publishers.
Ramsey, J.C., and M.E. Andersen. 1984. A physiologically based description of the inhalation pharmacokinetics of styrene in rats and humans. Toxicol. Appl. Pharmacol. 73(1):159-175.
Reddy, M., R.S. Yang, M.E. Andersen, and H.J. Clewell III. 2005. Physiologically Based Pharmacokinetic Modeling: Science and Applications. New York: Wiley.
Schlosser, P.M., P.D. Lilly, R.B. Conolly, D.B. Janszen, and J.S. Kimbell. 2003. Benchmark dose risk assessment for formaldehyde using airflow modeling and a single-compartment, DNA-protein cross-link dosimetry model to estimate human equivalent doses. Risk Anal. 23(3):473-487.
Simmons, J.E., W.K. Boyes, P.J. Bushnell, J.H. Raymer, T. Limsakun, A. McDonald, Y.M. Sey, and M.V. Evans. 2002. A physiologically based pharmacokinetic model for trichloroethylene in the male Long-Evans rat. Toxicol. Sci. 69(1):3-15.
Simmons, J.E., M.V. Evans, and W.K. Boyes. 2005. Moving from external exposure concentration to internal dose: Duration extrapolation based on physiologically-based pharmacokinetic derived estimates of internal dose. J. Toxicol. Environ. Health A 68(11-12):927-950.
Sweeney, L.M., M.E. Andersen, and M.L. Gargas. 2004. Ethyl acrylate risk assessment with a hybrid computational fluid dynamics and physiologically based nasal dosimetry model. Toxicol. Sci. 79(2):394-403.
ten Berge, W.F., A. Zwart, and L.M. Appelman. 1986. Concentration-time mortality response relationship of irritant and systemically acting vapors and gases. J. Hazard. Mater. 13(3):301-309.
Timchalk, C., R.J. Nolan, A.L. Mendrala, D.A. Dittenber, K.A. Brzak, and J.L. Mattsson. 2002. A physiologically based pharmacokinetic and pharmacodynamic (PBPK/PD) model for the organophosphate insecticide chlorpyrifos in rats and humans. Toxicol. Sci. 66(1):34-53.
APPENDIX A
PBPK Modeling-Based Derivation of AEGL Values for Toluene
SUMMARY
The method used in this study to determine human equivalent AEGL values is similar to that previously reported (Bruckner et al. 2004; Krewski et al. 2004). The method reduces the uncertainty inherent in extrapolating rat toxicity data to humans and extrapolating toxicity data across time-scales by using validated PBPK models to perform the extrapolation based on an internal measure of dose. This reduces the uncertainty in the pharmacokinetic component of the extrapolation. Uncertainty in the pharmacodynamic component of the rat-to-human extrapolation is handled with standard UFs.
The end points found in the critical studies for all three AEGLs can be reasonably associated with the blood concentration of toluene. The blood concentration is superior to the applied concentration (exposure concentration) as a measure of dose because, as an internal measure of dose, pharmacokinetic alterations in tissue dosimetry are addressed in extrapolation by explicit quantification. In extrapolation, for example, of a 1-h AEGL to an 8-h AEGL, the increase in blood concentration over time is explicitly compensated for by reducing the 8-h AEGL to the point where blood concentrations are equivalent. This process obviates the need for algorithms such as the ten Berge (ten Berge et al. 1986) equation, which can result in corresponding errors when the empirical parameters are unknown.
Fundamentally, the PBPK-based AEGL values are based on the same critical studies as the AEGL values established in the TSD; only the method of extrapolating from rat to human (dosimetry replaces pharmacokinetic uncertainty factors) and over time (dosimetry replaces empirical formulas) differs. When the PBPK-based approach replaces pharmacokinetic UFs, the resulting AEGL value may be higher, potentially avoiding issues with AEGLs that are close to occupational exposure limits. Thus, this approach may avoid the problem of overconservatism in setting AEGLs caused by extrapolative uncertainty.
The PBPK risk assessment method involves the following specific steps:
Step 1. At the NOAEL found in the critical study for setting AEGL-1 (of X ppm in rats), the CV is determined. This CV is the target internal dose for any time period at that AEGL. If the AEGL is based on human data, the CV is computed directly in the human model (skip to Step 2).
Step 2. The human version of the model is used to determine the exposure level that yields the same internal dose for each exposure period (10 and 30 min and 1, 4, and 8 h). This value is then divided by applicable pharmacodynamic or intraspecies UFs to yield the final AEGL value.
As humans may be under exertion during emergency events, the human model has been run using physiologic parameters corresponding to each of four states: resting state, 50 watts (W) of workload, 75 W of workload, and 100 W of workload.
Step 3. Repeat for AEGL-2 and AEGL-3.
This appendix has three parts. First, the structure and parameterization of the toluene PBPK model are described. Second, the model is validated by showing model performance against rat and human data sets obtained from the literature. Third, recommended AEGL values are derived.
The AEGLs based on PBPK dosimetry are often quite different from those based on the ten Berge equation (as described in the TSD document). When extrapolated to shorter timeframes, the toluene PBPK-based AEGLs tend to be much higher than the ones derived with the ten Berge equation. Conversely, the PBPK-based AEGLs are much reduced if the exercise scenario is considered. From the 10-min to 8-h AEGLs, the PBPK-based approach yields values that decrease quickly, as toluene takes longer to reach steady state in this PBPK model than previously thought.
INTRODUCTION
The critical studies that provide the NOAEL used in this analysis are the same as those used in the TSD (Table A-1) to calculate AEGL values. As in the TSD, supporting studies were not used in any of the AEGL calculations.
Additional information and justification of these choices of critical studies are available in the TSD. The target tissue dose (CV) was determined from these studies.
Selection of Dose Metric
The DM used for the PBPK-based risk assessment is the CV of toluene. The critical effect of toluene for setting AEGLs is depression of the central nervous system (CNS), based on the analysis of toxicity studies presented in the TSD. It has been generally suggested that CNS depression caused by organic solvents such as toluene is mediated by the action of the parent chemical and not metabolites (Bruckner and Warren 2001). The concentration of toluene in the target tissue, such as brain, is proportional to the CV (van Asperen et al. 2003), so AEGL values determined using either DM should be equivalent. Furthermore, although substantial data are available to validate a model for blood toluene, only limited data for brain concentrations exist. Therefore, CV has been selected as the DM for the analysis. It has previously been used as a surrogate DM for CNS effects (Haddad et al. 1999a; Dobrev et al. 2001), although arterial concentrations (CA) have also been used (Benignus et al. 1998; Bruckner et al.
2004). The PBPK models have been optimized to provide CV as model output under the exposure conditions indicated for this assessment.
Model Selection
The current approach requires a validated PBPK model for rats and humans. Three options exist for developing or selecting a model to use: develop a new model, modify an existing model, or select an existing model and use it in its current form. If an existing model would serve the needs of this risk assessment, option 3 is the preferred choice and was the first approach to be used. Ultimately, an existing model was used with minor modifications for the current risk assessment.
An evaluation of all existing models can be performed in principle to determine the best available model. However, this process is time-consuming and can be arbitrary to some extent. Therefore, the method of selecting a model was to screen models for good candidates by using specific criteria and evaluate models one by one until an acceptable model was identified. The criteria used to screen models included the following: (1) the model should include the inhalation route of exposure (primarily), (2) development of the model should incorporate validation against venous blood data, (3) the model should be reported in the peer-reviewed literature, and (4) the model should have as a primary purpose the goal of rat-to-human extrapolation.
A number of PBPK models have been developed for inhalation of toluene (Purcell et al. 1990; Tardif et al. 1993; Pierce et al. 1996a; Tardif et al. 1997; Benignus et al. 1998; Pierce et al. 1998; Ali and Tardif 1999; Haddad et al. 1999a; Pierce et al. 1999; Vicini et al. 1999; Jonsson and Johanson 2001; Tardif et al. 2002; van Asperen et al. 2003). Several of them are quite similar. Some were developed for rats, others for humans, and some for both (with modification of appropriate parameter values). The purpose of some models was to evaluate mixture interactions, although in each case a model was first developed for toluene as a single chemical.
TABLE A-1 Critical Studies for Toluene AEGLs
|
AEGL |
Study |
Species |
NOAEL |
Duration |
|
AEGL-1 |
Weight-of-evidence |
Human |
200 ppm |
8 h |
|
AEGL-2 |
Gamberale and Hultengren 1972 |
Human |
700 ppma |
20 min |
|
AEGL3 |
Mullin and Krivanek 1982 |
Rat |
6,250 ppm |
2 h |
|
aAfter initial exposures at 100 to 500 ppm. |
||||
The first models of this group that generally met the criteria expressed above were the models published by Tardif et al. (Tardif et al. 1993, 1997; Haddad et al. 1999a). It is quite possible, although outside the scope of this work to determine, that other models may perform similarly or better.
The models described in these publications (Tardif et al. 1993, 1997; Haddad et al. 1999a) are “essentially equivalent” models with some minor changes from one to another. The Tardif et al. (1993, 1997) models were essentially the same. Haddad et al. (1999a) used a slightly different set of physiologic parameters, and that led to reoptimization of metabolic parameters, which then varied slightly from the earlier versions. The two models by Tardif et al. (1993, 1997) addressed rats and humans, while the Haddad et al. (1999a) model addressed only rats. However, the human version of the final model could be easily inferred from the earlier work. The final version of this model (Haddad et al. (1999a)) was therefore selected for initial validation studies.
Most experimental data in rats, and more so in humans, are at moderate exposures of less than 500 ppm, and often less than 100 ppm. However, the purpose of this PBPK model is to perform high-dose extrapolations. Therefore, special attention was paid to validating the model with all available data sets for high-level exposure. In addition, attention was paid to validating the model for work and exercise.
Model Structure
A four-compartment PBPK model was used in this analysis, similar to that used in the past (Figure A-1).
In this model, the four compartments (fat, liver, and slowly and rapidly perfused tissues) are linked by the arterial and venous blood supply. The CA is set equal to the concentration in a small volume of lung blood, which is assumed to be in equilibrium with the exhaled air concentration. All metabolism is assumed to occur in the liver, because only slight differences were noted when a proportion of the metabolism occurs in extrahepatic tissues (data not shown). In tissues, equilibrium is assumed to exist between the venous blood returning from the tissues and the tissue itself, according to the tissue-blood partition coefficient. This equilibrium requires that diffusional resistance to mass transfer of the chemical is insignificant, which has ordinarily been observed in PBPK models for small molecular weight organic solvents (Ramsey and Andersen 1984; Dennison et al. 2003). All structural model details are identical to those of Haddad et al. (1999a) except for (1) the lung blood compartment, the use of which is a slightly better approach than the use of a steady-state assumption, although differences are not noted for most chemicals; and (2) the incorporation of a second metabolic pathway, as described below.
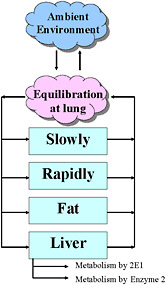
FIGURE A-1 Structure of the PBPK model used in this analysis. The four-compartment model includes fat, liver, and slowly and rapidly perfused tissue groups. A small lung blood compartment is present where equilibration occurs between the arterial blood and the exhaled air. All metabolism is assumed to occur in the liver.
PHYSIOLOGIC PARAMETER VALUES
Physiologic parameter values used in the current model for rats and for humans at different levels of exercise are listed in Tables A-2 and A-3.
In summary, all parameter values were set to be the same as those in the Haddad et al. (1999a) study except as noted here. The Haddad et al. (1999a) study did not include a PBPK model for humans. Therefore, the PBPK model parameters for human tissue volumes were taken from the earlier version of the model (Tardif et al. 1997). These parameter values are similar to values used in similar studies. The PB was also taken from another study, for reasons described below.
The body weight parameter depends on the context of the model. For validation studies, actual or assumed body weights are used. Validation studies include relevant studies in which venous blood and other data are provided. In some of these studies, actual body weight ranges are provided. In these cases, the arithmetic average of the weight range is used when simulating the blood data with the model. In some cases, the age and strain of the animal is provided without body weight. In these cases, the average weight of the species or closest species of rat was used, as provided by a laboratory animal supplier (Harlan 2004). In human studies, if no body weights are provided, 70 kg is assumed. It was further verified that model output was generally insensitive to the body
weight (see below). Therefore, this assumption was justifiable. When AEGL values were calculated, 70 kg was also used as the human body weight.
Several studies have shown that the blood concentrations of several small molecular weight organic solvents are highly dependent on physiologic parameters, which in turn are highly dependent on workload (Droz and Fernandez 1977; Johanson 1986; Kumagai et al. 1998; Jonsson et al. 2001). In an assessment of the effect of the PB on blood concentrations, modified by exercise level, Csanady et al. recommended that exercise be incorporated in risk assessments if the PB is greater than ~6 (Csanady and Filser 2001). As the PB of toluene is ~15, it is relevant for derivation of toluene AEGL values.
TABLE A-2 Summary of Parameter Values Used in Rat and Human PBPK Model
|
Variable |
Rat |
Human |
|
Body weight (BW) (kg) |
70b |
|
|
Tissue compartment weight (kg/(kg/BW)): |
|
|
|
Fraction fat tissue (VFC) |
0.07c |
0.19d |
|
Fraction liver tissue (VLC) |
0.04c |
0.026d |
|
Fraction rapidly perfused (VRC) |
0.05c |
0.05d |
|
Fraction slowly perfused (VSC) |
0.75c |
0.62d |
|
Fraction lung blood (VBC) |
0.0005e |
0.0005e |
|
Partition coefficients |
|
|
|
Blood-air (PB) |
18f |
13.9g |
|
Fat-air (PFA) |
1021f |
1021f |
|
Slowly perfused air (PSA) |
27.7f |
27.7f |
|
Rapidly perfused air (PRA) |
83.6f |
83.6f |
|
Liver-air (PLA)] |
83.6f |
83.6f |
|
Maximum velocity of metabolism (before scaling for body weight) (mg/h/kg0.75) VmaxC |
||
|
Affinity constant (mg/L) (Km) |
0.13c |
0.13c |
|
Linear metabolism rate constant (mg/L/kg0.3 (KFC) |
0.05e |
0.05e |
|
Note: Names of parameters are provided in the left column, followed by the units used, and acronym (if applicable). aBody weights were set equal to those reported or inferred from applicable studies. bHuman body weight is 70 kg in the AEGL analysis and was 70 kg in validation studies unless indicated otherwise in the study description. cHaddad et al. 1999a. dTardif et al. 1997. eThis study. fUsed by Haddad et al. (1999a) and Tardif et al. (1997), as originally determined by Gargas et al. (1989). gThrall et al. (2002). hScaled to L/h/kg0.75, as done previously (Haddad et al. 1999a). |
||
TABLE A-3 Summary of Blood Flow Parameter Values and Alveolar Ventilation at Rest and Workloads
|
Variable |
Rat |
Human |
||||
|
Rest |
Rest |
50 W |
75 W |
100 W |
150 W |
|
|
Alveolar ventilation (QPC) (L/h/kg0.75) |
15a |
18b |
53c |
70d |
87c |
100e |
|
Cardiac output (QCC) (L/h/kg0.75) |
15a |
18b |
50f |
59d |
68.5f |
79f |
|
Fraction of QCC to liver (QLC) (%) |
25a |
26b |
13f |
10d |
7.6f |
4.2f |
|
Fraction of QCC to Fat (QFC) (%) |
9a |
9 |
3.1f |
3d |
3.4f |
2.4f |
|
Fraction of QCC to Rapidly perfused (QRC) (%) |
51a |
55 |
60f |
59d |
58f |
58f |
|
Fraction of QCC to Slowly perfused (QSC) (%) |
15a |
10 |
23.9f |
28d |
31f |
35.4f |
|
c(Jonsson et al. 2001). fRecalculated from Johanson 1986. a(Haddad et al. 1999a). b(Tardif et al. 1997). dAverage of 50- and 100-W values. eThis study. |
||||||
The principal effects of exercise on an organic solvent’s pharmacokinetics involve alveolar ventilation, cardiac output, and blood flow to tissues. Data are incomplete on these rates in human exercise conditions. Therefore, the approach used should be improved in the future, when possible. For the current analysis, parameters were taken from the literature, as listed in Table A-3.
The model was coded into the ordinary differential equation solver, Berkeley Madonna, 8.0.2a8. The model code is included in Attachment A-1. Data sets were electronically read with Digimatic (Digimatic 2004). Numerical optimization was performed by visually estimating the best fit, as Berkeley Madonna is not capable of optimizing against multiple experiments at the same time.
RAT PBPK MODEL
Model Calibration
Two aspects of the Haddad et al. (1999a) model were reoptimized during the evaluation process: metabolism and the PB. These aspects of the model were selected after observation of the model’s performance versus data sets from other laboratories. The error structure in model deviations and other literature on toluene suggested that these parameters should be reconsidered.
The PB is an important parameter in this toluene PBPK model (see Sensitivity Analysis section below). However, there is uncertainty about the correct parameter value. Various studies have reported different values for the PB of toluene (Table A-4).
Many PBPK models have used a value of 18 for PB in rats (Purcell et al. 1990; Haddad et al. 1999a). van Asperen et al. (2003) used a PB of 13; however, it was based on optimization and not on in vitro data. The value selected for the rat PB in this model (18) has been used in numerous toluene PBPK models for rats and lies in the middle of three published values; it appears to allow a successful description of rat blood data (see below).
Human PB values tend to be lower than those of rats (Gargas et al. 1989). For example, Thrall et al. (2002) measured a toluene PB in humans of 13.9 and in rats of 21, although Sato and Nakajima (1979a,b) measured a toluene PB in humans of 15.6 and in rats of 15.2. Gargas et al. (1989) examined the relationship between human and rat (Fischer 344) PBs for 36 organic solvents. Their regression equation predicts a human PB for toluene of 11.0. The value of 13.9 published by Thrall et al. (2002) was used in this model because it is closest to the arithmetic average of the four published values (Table A-4), it is more consistent with the empirical relationship published by Gargas et al. (1989), and it permitted a reasonable description of the human blood data (see below). This value does not work well with the data from Tardif et al. (1997) (not shown), but this data set consisted of blood data after exposure of four male volunteers at a single low concentration. The concentration used by Tardif et al. (1997) (17 ppm) was much lower than concentrations of concern in this model, and additional verification at other exposure levels is not available. The value of 15.6 used by Tardif et al. (1997) was not substantially higher than the value used here.
TABLE A-4 Reported Blood-Air Partition Coefficients for Toluene in Rats and Humans
|
PB Value (unitless) |
Species |
Study |
|
18 |
F344 rats |
(Gargas et al. 1989) |
|
21 |
F344 rats |
(Thrall et al. 2002) |
|
15.2 |
Wistar rats |
(Sato and Nakajima 1979b) |
|
13 |
WAG/RijCrlBR rats |
(van Asperen et al. 2003) |
|
13.9 |
Human |
(Thrall et al. 2002) |
|
15.6 |
Human |
(Sato and Nakajima 1979b) |
|
10.0 |
Human |
(Fiserova-Bergerova and Diaz 1986) |
|
18.3 |
Human |
(Pierce et al. 1996b) |
|
11.0 |
Human |
(Gargas et al. 1989) |
|
Abbreviation: F344 rats, Fischer rats. |
||
At high exposure levels, previous models have sometimes incorporated a second metabolic pathway (Leavens and Bond 1996; Clewell et al. 2001). The initial step of toluene metabolism is oxidation by CYP. The primary isozyme responsible for toluene metabolism is CYP2E1 but other CYP isozymes are also involved, particularly at higher substrate concentrations (Kim et al. 1997; Nakajima et al. 1997). Thus, CYP2E1 is the high-affinity, low-capacity isozyme, and a second metabolic pathway can be used to represent the total metabolism by high-capacity, low-affinity isozymes. In this model, it is represented by saturable (Michaelis-Menten) metabolism (Vmax, Km) for CYP2E1 and by linear metabolism for the total metabolism by other CYPs.
The parameter value for the linear metabolic pathway rate constant (KFC) was determined by using data sets from Kishi et al. (1988). The Kishi et al. data (Figure A-2) were overpredicted by the Haddad et al. (1999a) model (data not shown) and the degree of overprediction increased at higher exposure concentrations, suggesting that a low-affinity enzyme was involved. Increasing the maximum rate of metabolism (Vmax) or decreasing the affinity constant (Km) improved the model at some exposure levels but did not achieve a reasonable fit at others. Adding the second metabolic pathway with a rate constant of 0.05/h to increase metabolism at the higher concentrations allowed a reasonable fit to the Kishi et al. data at all exposures (Figure A-2).
Tardif et al. (1993, 1997) and Haddad et al. (1999a) incorporated a single saturable enzyme in the model. The Tardif et al. (1993) gas uptake pharmacokinetic data (Figure A-3) were reasonably well represented with the single enzyme (upper curves). However, adding a second enzyme with a metabolic constant of 0.05/h (lower curves) improved the fit of the second and third exposure levels. At the highest exposure level, the model with the second enzyme tended to underpredict by a greater margin. Possible reasons for this underprediction include suppression of ventilation and blood flow (Dennison et al. 2003). In addition, including the second enzyme provided a better fit to other data sets. Therefore, the second metabolic pathway was retained.
Rat Model Validation
The following data sets were used to evaluate the model with parameters listed above. In other words, these data sets were not used to further optimize parameter values but served as model validation.
In two publications, Tardif and co-workers published blood data on Fischer 344 rats (Tardif et al. 1997; Haddad et al. 1999a). The data were collected for 2 h in the postexposure period after a 4-h exposure to toluene at 50, 100, and 200 ppm. A reasonable correspondence was obtained between the revised model and these data (see Figure A-4).
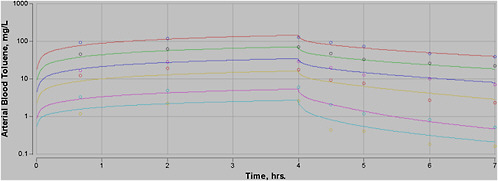
FIGURE A-2 PBPK model and Kishi et al. data. Output from the PBPK model with the second linear metabolic pathway included, based on six exposure levels (4 h and 3 h postexposure) in Wistar rats (7 weeks, estimated weight 200 g). Without the second pathway, the model consistently overpredicted the blood data (not shown). In all figures, symbols represent experimental data and curves are output of the model as described.
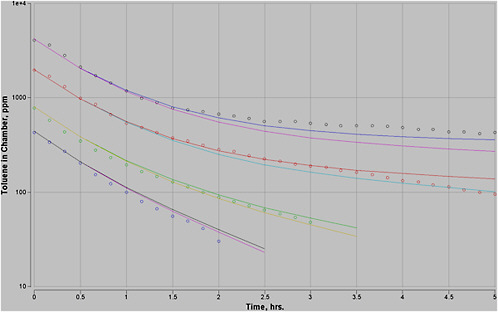
FIGURE A-3 PBPK model and Tardif et al. (1993) gas uptake data. Output from the PBPK model described above was plotted against data from Tardif et al. (1993) at four exposure concentrations. The upper curve in each group included a single enzyme and the lower curve also included a linear pathway representing other CYPs.
Another group conducted pharmacokinetic experiments with toluene (van Asperen et al. 2003). These studies used WAG/RijCrlBR rats, which are slowly growing rats produced in the Netherlands, derived from the Wistar strain. At an age of 14 weeks, this rat weighs only about 212 g (J.H. Lammers, TNO Nutrition and Food Research, personal commun., August 11, 2004), compared with Wistar and other strains, which weigh 300 to 400 g at that age.
In the model by van Asperen et al. (2003), the PB was set at 13 after the authors observed that the model overpredicted the data when a PB of 18 was used. This value is much lower than other published values and could imply that the human value would need to be lower yet. At the same time, with PB at 13, the data for the lower concentration were slightly underpredicted, suggesting that the PB may not be the only parameter that should be considered.
A reasonable fit between the present PBPK model with a rat PB of 18 and the van Asperen et al. (2003) experimental data from exposure at 2,667 ppm for 7.5 h was obtained (Figure A-5). Possible reasons why this model described the data without a reduction in the rat PB include the fact that the models differed structurally in some ways, and the current model included a second metabolic pathway. Interstrain differences in the rats are also possible. Given the reasonable fit with the existing model, the current value of PB appears to be justifiable.
Human Model Validation
After development and validation of the model using rat data and parameters, the model was scaled up to humans and revalidated against additional human data. The scaling was done by changing the values of anatomic and physiologic parameters to human values as listed in Tables A-2 and A-3. No equations in the model were altered.
After scaling to humans, the model was run in a manner corresponding to various experiments in which data were available for validation. On the basis of the reported information in each paper from which data were taken, the body weight was altered (or assumed to be 70 kg if not reported), and the concentration and duration of exposure were used in the model. Of the large number of potential data sets, key data sets were selected based on the following primary criteria: (1) exposure concentration and duration were clearly reported; (2) emphasis was placed on data sets that included exposure during exercise; (3) emphasis was placed on high exposure levels. Several of the data sets selected according to these criteria were unique in that exposure concentrations and workloads both varied or were varied several times during a single pharmacokinetic experiment, challenging the model from several perspectives. In the figures, when complex variations in exposure concentration or workload occurred, the model incorporated the changes as step functions that are displayed on the right axis to help clarify the experimental protocol.
Astrand et al. (1972) exposed a subject to toluene at 0, 95, or 175 ppm at rest or a workload of 50 W (Figure A-6). While the model somewhat underpredicted the CV, it closely predicted the exhaled air concentration except at the end of the experiment. During the final segment of the experiment, the volunteer ceased exercising at 50 W and rested. However, the relevant physiologic functions do not immediately step down to basal rates as specified in this model. The actual rate of the decrease to the basal state is unknown, but in principle it could be included in the model. Ultimately, if the increases were gradually relaxed to basal levels, both exhaled air and venous blood levels would be lower than the model currently predicts. Therefore, a model coded with a more realistic parameter set for the postexercise period would better simulate the last-stage data. This phenomenon could affect other model outputs at cessation of exercise.
Astrand et al. (1972) exposed a volunteer to toluene at 105 ppm for 1 h at 75 and 150 W of workload (Figure A-7). While the model predicted the uptake phase reasonably well, it grossly overpredicted the postexposure phase (data not shown). Because of the extreme change in physiologic parameters, the current model was recoded to extend the exercise (but not exposure) for 10 min after it was ceased in the experiment and then immediately decreased to a basal state. This revision resulted in better correspondence between the data and the model (Figure A-7). A closer fit might occur if the actual parameters were known.
This issue raises the question of whether the noninstantaneous rise in parameter values at the onset of exercise would have any effect. Most likely, the current approach of simulating work as an instantaneous rise overstates the uptake of chemical into the body by some amount. However, the error introduced at the onset of exercise should be smaller than at the cessation of exercise because physiologic function reaches the new steady state faster at the onset of a higher workload than at the onset of a lower workload.
Astrand et al. (1972) also exposed a volunteer to toluene at 200 ppm at rest and at 50 W of workload (Figure A-8). A reasonable correspondence was obtained between the model and data during uptake, although the venous blood prediction was high during the first segment. In the postexposure phase, the fit was not good. However, the venous blood data do not track well with the exhaled air data in the final stage of the experiment, so experimental issues may be present with this part of the data.
The model performs reasonably well against these three Astrand et al. (1972) data sets, although only a single volunteer was used in all three experiments.
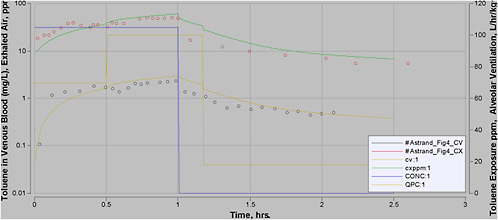
FIGURE A-7 PBPK model and data from Astrand et al. (1972, Figure 4). One subject was exposed to toluene at 105 ppm for 1 h. The first half hour was at 75 W and the second half hour was at 150 W of work. The upper curve is exhaled air and the lower curve is CV. The rapid decrease in toluene concentrations after exposure ended was not simulated well when the simulated work level decreased to resting levels immediately. Here, it was assumed that exercise continued for 10 min after exposure ended.
Carlsson (1982) exposed volunteers to toluene at about 80 ppm for 2 h at rest, 50 W of workload, and at workloads of rest, 50, 100, and 150 W in equal segments (Figures A-9 to A-11). A good correspondence between the data for venous blood and exhaled air was obtained at rest and at 50 W (Figures A-9 and A-10). In the third experiment, the workload was increased from resting to 150 W in four equal segments of 30 min each (Figure A-11). An excellent description of the blood data was obtained at all workloads and a good fit to the exhaled air data was obtained except during the resting period. Because of the cumulative nature of the error, the model performs well at all three levels of exercise but underpredicts at the end of the resting period.
To check the validity of the model against the data set with the highest available human exposures, the data of Gamberale and Hultengren (1972) were used. These investigators exposed a group of volunteers to variable concentrations of toluene. Twenty-minute sequential exposures to toluene at 100, 300, 500, and 700 ppm with a brief break in the middle were conducted (Figure A-12). The model with the resting parameter set (lower curve) provided an excellent description of the exhaled air data at all concentrations. The upper curve (modeled at 50 W) underscores the fact that exercise is an important determinant of the dosimetry.
Time to Steady State
The time it takes toluene to reach steady state in the blood can be easily calculated with the PBPK model. As the concentration of toluene in blood approaches the pharmacokinetic limit asymptotically, it is common to speak of benchmarks such as 95% of steady state or 99% of steady state. The time to steady state was plotted (Figure A-13) over time for exposures to 200 ppm at 50 W and at rest. The time to steady state for other exposure levels is almost identical (not shown). As shown in Figure A-13, the approach to steady state is governed in part by exercise conditions; as the workload increases, steady state is approached faster. The current model varies in its ability to describe different data sets in the approach to the steady-state period. For example, data from Carlsson (1982) and Gamberale and Hultengren (1972) are reasonably well predicted in the first few minutes of exposure, while data from Astrand et al. (1972) are not as well predicted. The reason for this discrepancy is not clear, but evidently the data sets are not consistent with each other. Which data better represent actual conditions is unknown. A possible explanation is that the subjects in the studies that exhibit higher initial blood concentration data were not fully at rest or were at a higher workload than reported (stress). If data such as those of Astrand et al. (1972) are more representative of normal conditions, then the current PBPK model will overstate the AEGL values for short timeframes, especially the 10-min values. A previous model explored this issue for a series of anesthetic gases (Vinegar et al. 1998). For these chemicals, it was shown that a
simple model of lung structure did not adequately describe data in the very early stages of uptake. However, the deviations for these chemicals were observed only in the period up to 2 min, and thereafter the simple model (similar to the one used here) performed adequately.
Sensitivity Analysis
A sensitivity analysis was conducted on the model with the parameter values listed in Tables A-2 and A-3. A sensitivity analysis is performed by assessing the relative impact of a small change in a parameter value on model output. The parameters that exhibit the most sensitivity are ones that should be given the most careful consideration. The sensitivity of a given parameter, however, varies with experimental settings, such as exposure concentration, exposure duration, and workload. Therefore, the sensitivity analysis was conducted on the human model at two exposures—one at rest and one at 50 W for an 8-h period. The output variable used for the analysis was venous blood concentration, as it is the DM used for the risk assessment.
The analysis results in a sensitivity coefficient (S) that is computed according to S = 100 × (CV1 – CV2)/CV1, where CV1 is the venous blood concentration predicted by the base model (no parameter change) and CV2 is the venous blood concentration predicted when one parameter was increased by 1% of its normal value in the model. The absolute values of the changes are plotted in Figure A-14a and b. Under both conditions, the model was sensitive to PB and the alveolar ventilation rate (QPC). These parameters were given careful consideration during model validation.
Overview of Validation Data
For the rat model validations, the model reasonably predicts blood data from three different labs at toluene exposures ranging from 50 to 4,000 ppm. The lower limit of this range is below the range of exposures considered in the AEGL extrapolations and the upper limit is close to the upper limit of the extrapolations. The gas uptake data are reasonably well predicted by the model. Therefore, the rat version of the model is deemed adequate for risk assessment extrapolation in or near these ranges.
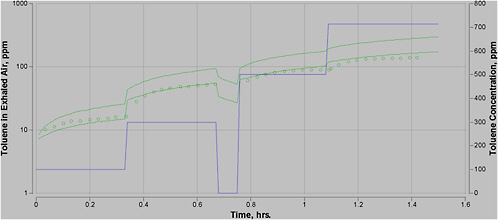
FIGURE A-12 PBPK model and data from Gamberale and Hultengren (1972, Figure 1). Mean values for toluene in exhaled air for 12 subjects exposed to different levels of toluene at rest. Toluene concentrations were approximately 100, 300, 0, 500, and 700 ppm as indicated on the right axis. Lower curve is simulation at rest and upper curve is simulation at 50 W.
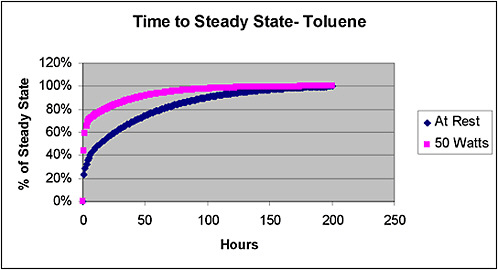
FIGURE A-13 Time to steady state as determined by the current PBPK model. Simulations were conducted for exposures to toluene at 200 ppm at rest and at 50 W of workload. At higher workloads, the approach to steady state is much faster. Results of the simulation for higher concentrations were identical.
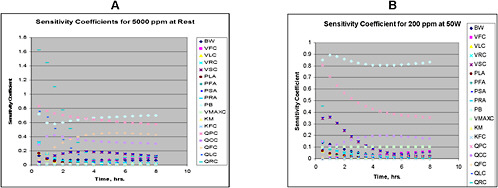
FIGURE A-14 a and b.Sensitivity coefficients for the toluene PBPK model. Sensitivity analysis at 5,000 ppm (rest) and 200 ppm (50 W) were calculated. At 50 W and 200 ppm, the model is primarily sensitive to PB and QPC. At rest and 5,000 ppm, the model is sensitive to these parameters and also moderately sensitive to QFC (percent of blood flow going to fat) and QCC (cardiac output). The model is also differentially sensitive to some other parameters in the period of initial uptake, especially to QRC (percent of blood flow going to rapidly perfused tissue) in a.
The human version of the model also reasonably represents the data sets used for validation. These data sets include data from seven experiments from three labs and include both venous blood and exhaled air data. Where available, modeling of arterial blood concentrations (CA) provided a similar fit to arterial data, although not shown because of overlap on the figures. The range of toluene exposures was 80 to 700 ppm. The lower bound of this range is less than the lower bound of the AEGL extrapolations, although the upper bound of validation is lower than some of the AEGL values. The quality of the fit in many cases was very close, and the deviations did not tend to show an overall low or high bias, so the model could be viewed as evening out differences from lab to lab.
The model appears to perform well at resting and exercise levels. The sensitivity of the model to the exercise parameters is shown by the upper curve in Figure A-12. The large differences between the exhaled air concentrations at rest and work support the observation that the model deals well with exercise, as the differences are large compared with the errors between the model and the validation data sets. Furthermore, the numerous changes in exposure levels and workload in some of the data sets provide a comparatively demanding test of the model’s validity. Therefore, the human version of the model is also deemed adequate for the AEGL risk assessment.
DERIVATION OF AEGLS WITH PBPK-BASED RISK APPROACH
For AEGL-1, no specific critical study was identified in the TSD. However, based on numerous studies (weight of evidence), a critical effect level of 200 ppm for 8 h was selected. This value is shown in parentheses in Table A-5. With the PBPK model, this value was time-scaled back to 10 min. Increasing the workload greatly increases the CV, thereby decreasing the exposure needed to produce the critical effect.
The AEGL-2 critical study was by Gamberale and Hultengren (1972), in which subjects were exposed to toluene vapor at 100, 300, 500, and 700 ppm for 20 min at each level and with a short break in the middle. The CV calculated by the PBPK model is much greater when the full exposure regimen was simulated, compared with the concentration after only a 20-min exposure (~6.5 versus 4.5 mg/L). The exposures were roughly equivalent to a 20-min exposure to ~1,000 ppm. Therefore, the CV determined for the actual experimental conditions was used to derive AEGL-2 values. Because of the prior exposure to lower levels of toluene, the 30-min AEGL (at rest) is actually more than 700 ppm. The 20-min value was time-scaled down to 10 min and up to 8 h and was extrapolated to higher workloads (Table A-6).
The AEGL-3 was based on a rat NOAEL for lethality. The CV of toluene during this experimental scenario (6,250 ppm for 2 h) was determined and served as the target concentration for setting the AEGLs. The human model was then used to determine the exposure levels in humans that yield the same con-
centrations. This exposure level (top section of Table A-7) was then divided by the same intraspecies UF that was used in the TSD (3).
TABLE A-5 AEGL-1 Values Determined with PBPK Model, ppm
TABLE A-6 AEGL-2 Values Determined with PBPK Model, ppm
TABLE A-7 AEGL-3 Values Determined with PBPK Model, ppm
Order of Application of Uncertainty Factors
The uncertainty factor for intraspecies (3) can be applied before or after the PBPK dosimetric adjustment is made. In a previous PBPK-based determination of AEGLs for xylene, the UF was applied after dosimetric adjustment (see the TSD for xylene). However, in a case example, the UF was applied first (Bruckner et al. 2004). The argument can be made that, as the dosimetric adjustment is being applied to “real data,” in a biologically plausible manner (using a PBPK model), and the UF is more loosely determined, dividing the final values is more appropriate. However, for toluene, the order of application was inconsequential. To evaluate this, the AEGL-3 at 50 W was also determined by dividing the rat NOAEL by 3 to obtain a target CV, and the human model was then used to determine the equivalent human concentration for the five time points (Table A-8). The results were quite similar, although not identical. For example, the 1-h AEGL determined above was 2,397 ppm, while applying the UF first led to an AEGL of 2,360.
Comparison of PBPK-Based AEGL Values with ten Berge Approach
A useful comparison can be made between the AEGL values determined using the ten Berge approach (ten Berge et al. 1986) and the PBPK model. In Figure A-15, the CV of toluene was calculated using the PBPK model for three scenarios: the AEGL values determined with the PBPK model, the AEGL values recommended with the ten Berge time-scaling equation assuming the subject is at rest during the emergency event, and the AEGL values recommended with the ten Berge time-scaling equation assuming the subject is at work, 50 W, during the emergency event. As the AEGL values were reverse-calculated with the PBPK model, the PBPK model predicted a consistent CV of 6.54 mg/L. The CVs based on the ten Berge approach were highly variable. If the subject is at rest during an emergency event, the ten Berge values may be below or above the target dose. However, if the subject is exercising, the ten Berge values are consistently above the target dose; in other words, the ten Berge AEGL values were underprotective.
Advantages of the PBPK Model Approach
The PBPK model has several distinct advantages that make the modeling effort worthwhile. First, the AEGL values for different timeframes determined by using the PBPK model are all equally protective, assuming that peak CV is an appropriate DM for a given AEGL level toxicity end point. The ten Berge-derived AEGL values can vary in protectiveness because peak CV can vary by a factor of 2 to 3. Whether the calculated target tissue dose is appropriate depends primarily on appropriate selection of the critical data and not on the validity of the PBPK model used.
TABLE A-8 AEGL-3 Based on Target CV of 53.8 (rat CV for NOAEL of 6,250 ppm divided by UF of 3), ppm
|
Workload |
10 min |
30 min |
1 h |
4 h |
8 h |
|
50 W |
6,540 |
3,430 |
2,360 |
1,520 |
1,410 |
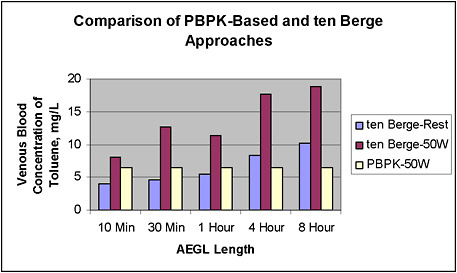
FIGURE A-15 Comparison of CVs of toluene resulting from exposure for each AEGL time period at the values resulting from the PBPK-based approach and the ten Berge equation. The CV for toluene was determined with the PBPK model for each AEGL-2 value determined by using the ten Berge equation (as listed in the TSD) or with the PBPK model. The PBPK model, for obvious reasons, predicts a constant CV of 6.54 mg/L. The CVs from the AEGLs derived using the ten Berge equation were determined both at rest and at a workload of 50 W. If the exposed subject is at rest, the CVs associated with the ten Berge-derived AEGLs are lower or higher than those derived by using the PBPK approach. At 50 W, the CVs associated with the ten Berge-derived AEGLs are consistently higher than those corresponding to the human NOAEL, by a factor of up to ~3.
Second, the existing ten Berge approach does not permit consideration of exertion, which has a pronounced impact on tissue dosimetry. Recent research has indicated that exercise is an important factor in determining internal dose related to toxicity for toluene and similar chemicals (Csanady and Filser 2001). Therefore, if exercise during emergency events is the probable physiologic mode for exposed persons, the ten Berge approach will not be adequately protective.
Third, the PBPK modeling approach is uniquely suited for use when a critical study had a complex exposure scenario, as in the case of the Gamberale and Hultengren (1972) model. The ten Berge approach used a DM of 700 ppm (the final experimental concentration). It was separately determined that the ex-
perimental concentration was equivalent to an exposure to 1,000 ppm (for 20 min), but this could not be accounted for without the PBPK model.
Fourth, the PBPK-based approach allows an improvement in the basis for the animal-to-human extrapolation. While this advantage was not relevant at all levels, the AEGL-3 for toluene was based on a rat-to-human extrapolation of lethality data.
Some concern may exist over setting AEGLs at less than the existing permissible exposure limits (PEL) from OSHA (200 ppm). However, the current PEL for toluene was derived from toxicologic assessment performed in the mid-1940s. The Threshold Limit Value (TLV) was 200 ppm until adoption as a PEL in 1970 by OSHA, but the TLV was reduced to 100 ppm in the early 1970s and to 50 ppm in 1991-1992. Thus, the studies that are the basis for the AEGLs had not even been conducted when the current PEL was established, the organization that set the value that eventually became the PEL has since lowered the value two times, and the current PEL is effectively a 60-year-old standard.
REFERENCES
Ali, N., and R. Tardif. 1999. Toxicokinetic modeling of the combined exposure to toluene and n-hexane in rats and humans. J. Occup. Health 41:95-103.
Astrand, I., H. Ehrner-Samuel, A. Kilbom, and P. Ovrum. 1972. Toluene exposure. I. Concentration in alveolar air and blood at rest and during exercise. Work Environ. Health 9:119-130.
Benignus, V.A., W.K. Boyes, and P.J. Bushnell. 1998. A dosimetric analysis of behavioral effects of acute toluene exposure in rats and humans. Toxicol. Sci. 43(2):186-195.
Brown, R.P., M.D. Delp, S.L. Lindstedt, L.R. Rhomberg, and R.P. Beliles. 1997. Physiological parameter values for physiologically based pharmacokinetic models. Toxicol. Ind. Health 13(4):407-484.
Bruckner, J.V., and D.A. Warren. 2001. Toxic effects of solvents and vapors. Pp. 869-916 in Casarett and Doull's Toxicology: The Basic Science of Poisons, 6th Ed., C.D. Klaassen, ed. New York: McGraw-Hill.
Bruckner, J.V., D.A. Keys, and J.W. Fisher. 2004. The Acute Exposure Guideline Level (AEGL) program: Applications of physiologically based pharmacokinetic modeling. J. Toxicol. Environ. Health A 67(8-10):621-634.
Carlsson, A. 1982. Exposure to toluene: Uptake, distribution and elimination in man. Scand. J. Work Environ. Health 8(1):43-55.
Clewell, H.J., P.R. Gentry, J.M. Gearhart, B.C. Allen, and M.E. Andersen. 2001. Comparison of cancer risk estimates for vinyl chloride using animal and human data with a PBPK model. Sci. Total Environ. 274(1-3):37-66.
Csanady, G.A., and J.G. Filser. 2001. The relevance of physical activity for the kinetics of inhaled gaseous substances. Arch. Toxicol. 74(11):663-672.
Dennison, J.E., M.E. Andersen, and R.S. Yang. 2003. Characterization of the pharmacokinetics of gasoline using PBPK modeling with a complex mixtures chemical lumping approach. Inhal. Toxicol. 15(10):961-986.
Digimatic. 2004. Digimatic, Version 2. FEBSoftware, Chesterfield, VA.
Dobrev, I.D., M.E. Andersen, and R.S. Yang. 2001. Assessing interaction thresholds for trichloroethylene in combination with tetrachloroethylene and 1,1,1-trichloroethane using gas uptake studies and PBPK modeling. Arch. Toxicol. 75(3):134-144.
Droz, P.O., and J.G. Fernandez. 1977. Effect of physical workload on retention and metabolism of inhaled organic solvents. A comparative theoretical approach and its applications with regards to exposure monitoring. Int. Arch. Occup. Environ. Health 38(4):231-246.
Fiserova-Bergerova, V., and M.L. Diaz. 1986. Determination and prediction of tissue-gas partition coefficients. Int. Arch. Occup. Environ. Health 58(1):75-87.
Gamberale, F., and M. Hultengren. 1972. Toluene exposure. II. Psychophysiological functions. Work Environ. Health 9:131-139.
Gargas, M.L., R.J. Burgess, D.E. Voisard, G.H. Cason, and M.E. Andersen. 1989. Partition coefficients of low-molecular-weight volatile chemicals in various liquids and tissues. Toxicol. Appl. Pharmacol. 98(1):87-99.
Haddad, S., R. Tardif, G. Charest-Tardif, and K. Krishnan. 1999a. Physiological modeling of the toxicokinetic interactions in a quaternary mixture of aromatic hydrocarbons. Toxicol. Appl. Pharmacol. 161(3):249-257.
Haddad, S., R. Tardif, C. Viau, and K. Krishnan. 1999a. A modeling approach to account for toxicokinetic interactions in the calculation of biological hazard index for chemical mixtures. Toxicol. Lett. 108(2-3):303-308.
Harlan 2004. Harlan Product Guide, 2003-2004. Harlan [online]. Available: http://www.harlan.com/library.html
Johanson, G. 1986. Physiologically based pharmacokinetic modeling of inhaled 2-butoxyethanol in man. Toxicol. Lett. 34(1):23-31.
Jonsson, F., and G. Johanson. 2001. Bayesian estimation of variability in adipose tissue blood flow in man by physiologically based pharmacokinetic modeling of inhalation exposure to toluene. Toxicology 157(3):177-193.
Jonsson, F., F. Bois, and G. Johanson. 2001. Physiologically based pharmacokinetic modeling of inhalation exposure of humans to dichloromethane during moderate to heavy exercise. Toxicol. Sci. 59(2):209-218.
Kim, H., R.S. Wang, E. Elovaara, H. Raunio, O. Pelkonen, T. Aoyama, H. Vainio, and T. Nakajima. 1997. Cytochrome P450 isozymes responsible for the metabolism of toluene and styrene in human liver microsomes. Xenobiotica 27(7):657-665.
Kishi, R., I. Harabuchi, T. Ikeda, H. Yokota, and H. Miyake. 1988. Neurobehavioral effects and pharmacokinetics of toluene in rats and their relevance to man. Br. J. Ind. Med. 45(6):396-408.
Krewski, D., K. Bakshi, R. Garrett, E. Falke, G. Rusch, and D. Gaylor. 2004. Development of acute exposure guideline levels for airborne exposures to hazardous substances. Regul. Toxicol. Pharmacol. 39(2):184-201.
Kumagai, S., I. Matsunaga, and T. Tabuchi. 1998. Effects of variation in exposure to airborne acetone and difference in work load on acetone concentrations in blood, urine, and exhaled air. Am. Ind. Hyg. Assoc. J. 59(4):242-251.
Leavens, T.L., and J.A. Bond. 1996. Pharmacokinetic model describing the disposition of butadiene and styrene in mice. Toxicology 113(1-3):310-313.
Mullin, L.S., and N.D. Krivanek. 1982. Comparison of unconditioned reflex and conditioned avoidance tests in rats exposure by inhalation to carbon monoxide, 1,1,1-trichloroethane, toluene or ethanol. Neurotoxicity 3(1):126-137.
Nakajima, T., R.S. Wang, E. Elovaara, F.J. Gonzalez, H.V. Gelboin, H. Raunio, O. Pelkonen, H. Vainio, and T. Aoyama. 1997. Toluene metabolism by cDNA-expressed human hepatic cytochrome P450. Biochem. Pharmacol. 53(3):271-277.
Pierce, C.H., R.L. Dills, M.S. Morgan, G.L. Nothstein, D.D. Shen, and D.A. Kalman. 1996a. Interindividual differences in 2H8-toluene toxicokinetics assessed by semiempirical physiologically based model. Toxicol. Appl. Pharmacol. 139(1): 49-61.
Pierce, C.H., R.L. Dills, G.W. Silvey, and D.A. Kalman. 1996b. Partition coefficients between human blood or adipose tissue and air for aromatic solvents. Scand. J. Work Environ. Health 22(2):112-118.
Pierce, C.H., R.L. Dills, M.S. Morgan, P. Vicini, and D.A. Kalman. 1998. Biological monitoring of controlled toluene exposure. Int. Arch. Occup. Environ. Health 71(7):433-444.
Pierce, C.H., T.A. Lewandowski, R.L. Dills, M.S. Morgan, M.A. Wessels, D.D. Shen, and D.A. Kalman. 1999. A comparison of 1H8- and 2H8-toluene toxicokinetics in men. Xenobiotica 29(1):93-108.
Purcell, K.J., G.H. Cason, M.L. Gargas, M.E. Andersen, and C.C. Travis. 1990. In vivo metabolic interactions of benzene and toluene. Toxicol. Lett. 52(2):141-152.
Ramsey, J.C., and M.E. Andersen. 1984. A physiologically based description of the inhalation pharmacokinetics of styrene in rats and humans. Toxicol. Appl. Pharmacol. 73(1):159-175.
Sato, A., and T. Nakajima. 1979a. Dose-dependent metabolic interaction between benzene and toluene in vivo and in vitro. Toxicol. Appl. Pharmacol. 48(2):249-256.
Sato, A., and T. Nakajima. 1979b. Partition coefficients of some aromatic hydrocarbons and ketones in water, blood and oil. Br. J. Ind. Med. 36(3):231-234.
Tardif, R., S. Lapare, K. Krishnan, and J. Brodeur. 1993. Physiologically based modeling of the toxicokinetic interaction between toluene and m-xylene in the rat. Toxicol. Appl. Pharmacol. 120(2):266-273.
Tardif, R., G. Charest-Tardif, J. Brodeur, and K. Krishnan. 1997. Physiologically based pharmacokinetic modeling of a ternary mixture of alkyl benzenes in rats and humans. Toxicol. Appl. Pharmacol. 144(1):120-134.
Tardif, R., P.O. Droz, G. Charest-Tardif, G. Pierrehumbert, and G. Truchon. 2002. Impact of human variability on the biological monitoring of exposure to toluene: I. Physiologically based toxicokinetic modelling. Toxicol. Lett. 134(1-3):155-163.
ten Berge, W.F., A. Zwart, and L.M. Appelman. 1986. Concentration-time mortality response relationship of irritant and systemically acting vapors and gases. J. Hazard. Mater. 13(3):301-309.
Thrall, K.D., R.A. Gies, J. Muniz, A.D. Woodstock, and G. Higgins. 2002. Route-of-entry and brain tissue partition coefficients for common superfund contaminants. J. Toxicol. Environ. Health A 65(24):2075-2086.
van Asperen, J., W.R. Rijcken, and J.H. Lammers. 2003. Application of physiologically based toxicokinetic modelling to study the impact of the exposure scenario on the toxicokinetics and the behavioural effects of toluene in rats. Toxicol. Lett. 138(1-2):51-62.
Vicini, P., C.H. Pierce, R.L. Dills, M.S. Morgan, and D.A. Kalman. 1999. Individual prior information in a physiological model of 2H8-toluene kinetics: An empirical Bayes estimation strategy. Risk Anal. 19(6):1127-1134.
Vinegar, A., G.W. Jepson, and J.H. Overton. 1998. PBPK modeling of the short-term (0 to 5 min) human inhalation exposures to halogenated hydrocarbons. Inhal. Toxicol. 10(5):411-429.
Abbreviations
AEGL acute exposure guideline level
AT amount of chemical in each tissue
AUC area under the curve
BMD benchmark dose
BW body weight
CA arterial blood concentration
Cmax maximum concentration
CNS central nervous system
CT chemical concentration in each tissue
CV venous blood concentration
CVi chemical concentration in the venous blood leaving tissue i
CVL concentration of chemical in venous blood leaving the liver
CYP cytochrome P-450
DM dose metric
EPA U.S. Environmental Protection Agency
h hour
KFC linear metabolism rate constant
Km affinity constant for the chemical
LC50 median lethal concentration
LOAEL lowest-observed-adverse-effect level
mg/L milligram per liter
min minute
NAC National Advisory Committee
NOAEL no-observed-adverse-effect level
NRC National Research Council
OSHA Occupational Safety and Health Administration
PB blood-air partition coefficient
PBPD physiologically based pharmacodynamic
PBPK physiologically based pharmacokinetic
PEL permissible exposure limits
PFA fat-air coefficient
PLA liver-air coefficient
POD point of departure
ppm parts per million
PRA rapidly perfused air coefficient
PSA slowly perfused air coefficient
PT partition coefficient between the tissue and blood
QCC cardiac output
QFC percentage of blood flow going to fat
Qi blood flow to tissue i
QLC fraction of QCC to liver
QPC alveolar ventilation rate
QRC percentage of blood flow going to rapidly perfused tissues
QSC percentage of blood flow going to slowly perfused tissues
S sensitivity coefficient
TLV Threshold Limit Value
Tmax time (of maximum concentration)
TSD technical support document
UF uncertainty factor
VBC fraction lung blood
VFC fraction fat tissue
VLC fraction liver tissue
Vmax maximum rate of metabolism
VmaxC maximum velocity of metabolism
VRC fraction rapidly perfused
VSC fraction slowly perfused
VT volume of each tissue
W watt
ATTACHMENT 1
PBPK MODEL EQUATIONS FOR TOLUENE AEGL MODEL2
This is a four-compartment model for toluene inhalation in the rat and human.
|
;Physiologic parameters |
|
|
BW = 70 |
;Body weight (kg) |
|
VFC = 0.19 |
;Fraction fat tissue (kg/(kg/BW)) |
|
VLC = 0.026 |
;Fraction liver tissue (kg/(kg/BW)) |
|
VRC= 0.05 |
;Fraction rapidly perfused (kg/(kg/BW)) |
|
VSC = 0.62 |
;Fraction slowly perfused (kg/(kg/BW)) |
|
SF = .75 |
;Scaling coefficient |
|
QPC = 18 |
;Alveolar ventilation rate (L/h/kg) |
|
QCC = 18 |
;Cardiac output (L/h/kg) |
|
QFC = 0.09 |
;Fractional blood flow to fat ((L/h)/QC) |
|
QLC = 0.26 |
;Fractional blood flow to liver ((L/h)/QC) |
|
QRC= 0.55 |
;Fractional blood flow to rapidly perfused ((L/h)/QC) |
|
;Chemical-specific parameters |
|
|
PLA = 83.6 |
;Liver-air partition coefficient |
|
PFA = 1021 |
;Fat-air partition coefficient |
|
PSA = 27.7 |
;Slowly perfused air partition coefficient |
|
PRA = 83.6 |
;Rapidly perfused air partition coefficient |
|
PB = 18 |
;Blood-air partition coefficient |
|
PL = PLA/PB |
;Liver-blood partition coefficient |
|
PF = PFA/PB |
;Fat-blood partition coefficient |
|
PS = PSA/PB |
;Slowly perfused blood partition coefficient |
|
PR = PRA/PB |
;Rapidly perfused blood partition coefficient |
|
MW = 92.13 |
;Molecular weight (g/mol) |
|
VMAXC = 3.44 |
;Maximum velocity of metabolism (mg/h/kg) |
|
KM = 0.13 |
;Michaelis-Menten (mg/L) |
|
KFC = 0.05 |
;First-order rate constant |
|
;Calculated parameters |
|
|
QC = QCC × BWSF |
;Cardiac output |
|
QP = QPC × BWSF |
;Alveolar vent |
|
VS = VSC × BW |
;Volume slowly perfused tissue (L) |
|
VF = VFC × BW |
;Volume fat tissue (L) |
|
VL = VLC × BW |
;Volume liver (L) |
|
VR= VRC × BW |
;Volume rapidly perfused (L) |
|
VB = 0.0005 × BW |
;Lung blood volume (L) |
|
QF = QFC × QC |
;Blood flow to fat (L/h) |
|
QL = QLC × QC |
;Blood flow to liver (L/h) |
|
QS = QC – QF – QL – QR |
;Blood flow to nonfat tissue (L/h) |
|
QR = QRC × QC |
;Blood flow to rapidly perfused (L/h) |
|
VMAX = VMAXC × BWSF |
;Maximum rate of metabolism (mg/h) |
|
KF = KFC/BW0.3 |
;Linear metabolic rate |
;Parameters for simulated experiment
|
CONC = 500 |
;Inhaled concentration (ppm) |
;Parameters for exercise (50 W, 75 W, 100 W, 150 W)
QPC50 = 53
QCC50 = 50
QLC50 = 0.13
QFC50 = 0.031
QRC50 = 0.60
QPC75 = 70
QCC75 = 59
QLC75 = 0.10
QFC75 = 0.030
QRC75 = 0.28
QPC100 = 87
QCC100 = 68.5
QLC100 = 0.076
QFC100 = 0.034
QRC100 = 0.58
QPC150 = 100
QCC150 = 79
QLC150 = 0.042
QFC150 = 0.024
QRC150 = 0.58
;The following IF THEN statements implement the Carlsson Stage 3 exercise scenario (rest, 50 W, 100 W, 150 W)
;QPC = IF TIME >= 1.5 THEN QPC150 ELSE IF TIME >= 1.0 THEN QPC100 ELSE IF TIME >= .5 THEN QPC50 ELSE 18
;QCC = IF TIME >= 1.5 THEN QCC150 ELSE IF TIME >= 1.0 THEN QCC100 ELSE IF TIME >= 0.5 THEN QCC50 ELSE 18
;QLC = IF TIME >= 1.5 THEN QLC150 ELSE IF TIME >= 1.0 THEN QLC100 ELSE IF TIME >= 0.5 THEN QLC50 ELSE 0.26
;QFC = IF TIME >= 1.5 THEN QFC150 ELSE IF TIME >= 1.0 THEN QFC100 ELSE IF TIME >= 0.5 THEN QFC50 ELSE 0.09
;QRC = IF TIME >= 1.5 THEN QRC150 ELSE IF TIME >= 1.0 THEN QRC100 ELSE IF TIME >= 0.5 THEN QRC50 ELSE 0.55
;The following IF THEN statements implement the Carlsson Stage 3 exercise scenario (rest, 50 W, 100 W, 150 W) with QPC and QCC from QCP2004 calculations
;QPC = IF TIME >= 1.5 THEN 129 ELSE IF TIME >= 1.0 THEN 88.4 ELSE IF TIME >= .5 THEN 45 ELSE 14.7
;QCC = IF TIME >= 1.5 THEN 46.6 ELSE IF TIME >= 1.0 THEN 37.1 ELSE IF TIME >= 0.5 THEN 26 ELSE 14.4
;QLC = IF TIME >= 1.5 THEN 0.05 ELSE IF TIME >= 1.0 THEN .076 ELSE IF TIME >= 0.5 THEN 0.13 ELSE 0.26
;QFC = IF TIME >= 1.5 THEN 0.03 ELSE IF TIME >= 1.0 THEN 0.03 ELSE IF TIME >= 0.5 THEN 0.03 ELSE 0.09
;QRC = IF TIME >= 1.5 THEN 0.58 ELSE IF TIME >= 1.0 THEN 0.58 ELSE IF TIME >= 0.5 THEN 0.60 ELSE 0.55
;The following IF THEN statements implement the Astrand et al. (1972) Figure 3, Steps 1 and 2, exercise scenario (rest, 50 W)
;QPC = IF TIME >= 0.5 THEN QPC50 ELSE 18
;QCC = IF TIME >= 0.5 THEN QCC50 ELSE 18
;QLC = IF TIME >= 0.5 THEN QLC50 ELSE 0.26
;QFC = IF TIME >= 0.5 THEN QFC50 ELSE 0.09
;QRC = IF TIME >= 0.5 THEN QRC50 ELSE 0.55
;The following IF THEN statements implement the Astrand et al. (1972) Figure 3, Steps 1 to 4, exercise scenario (rest, 50 W)
;QPC = IF TIME >= 1.08 THEN 18 ELSE IF TIME >= .55 THEN 53 ELSE 18
;QCC = IF TIME >= 1.08 THEN 18 ELSE IF TIME >= .55 THEN 50 ELSE 18
;QLC = IF TIME >= 1.08 THEN 0.26 ELSE IF TIME >= .55 THEN .13 ELSE 0.26
;QFC = IF TIME >= 1.08 THEN 0.09 ELSE IF TIME >= .55 THEN 0.03 ELSE 0.09
;QRC = IF TIME >= 1.08 THEN 0.55 ELSE IF TIME >= .55 THEN 0.6 ELSE 0.55
;CONC = IF TIME >= 1.37 THEN 175 ELSE IF TIME >= 1.08 THEN 0 ELSE 95
;The following IF THEN statements implement the Astrand et al. (1972) Figure 3, Steps 1 to 6, exercise scenario (rest, 50 W)
;QPC = IF TIME >= 2.4 THEN 18 ELSE IF TIME >= 1.9 THEN QPC50 ELSE IF TIME>= 1.08 THEN 18 ELSE IF TIME >= .55 THEN QPC50 ELSE 18
;QCC = IF TIME >= 2.4 THEN 18 ELSE IF TIME >= 1.9 THEN QCC50 ELSE IF TIME >= 1.08 THEN 18 ELSE IF TIME >= .55 THEN QCC50 ELSE 18
;QLC = IF TIME >= 2.4 THEN .26 ELSE IF TIME >= 1.9 THEN QLC50 ELSE IF TIME >= 1.08 THEN 0.26 ELSE IF TIME >= .55 THEN QLC50 ELSE 0.26
;QFC = IF TIME >= 2.4 THEN .09 ELSE IF TIME >= 1.9 THEN QFC50 ELSE IF TIME >= 1.08 THEN 0.09 ELSE IF TIME >= .55 THEN QFC50 ELSE 0.09
;QRC = IF TIME >= 2.4 THEN .55 ELSE IF TIME >= 1.9 THEN QRC50 ELSE IF TIME >= 1.08 THEN 0.55 ELSE IF TIME >= .55 THEN QRC50 ELSE 0.55
;CONC = IF TIME >= 2.4 THEN 0 ELSE IF TIME >= 1.37 THEN 175 ELSE IF TIME >= 1.08 THEN 0 ELSE 95
;The following IF THEN statements implement the Astrand et al. (1972) Figure 4 exercise scenario (75 W, 150 W, rest)
;QPC = IF TIME >= 1.17 THEN 18 ELSE IF TIME >= .5 THEN QPC150 ELSE QPC75
;QCC = IF TIME >= 1.17 THEN 18 ELSE IF TIME >= .5 THEN QCC150 ELSE QCC75
;QLC = IF TIME >= 1.17 THEN 0.26 ELSE IF TIME >= .5 THEN QLC150 ELSE QLC75
;QFC = IF TIME >= 1.17 THEN 0.09 ELSE IF TIME >= .5 THEN QFC150 ELSE QFC75
;QRC = IF TIME >= 1.17 THEN 0.55 ELSE IF TIME >= .5 THEN QRC150 ELSE QRC75
;CONC = IF TIME >= 1 THEN 0 ELSE 105
;The following IF THEN statements implement the Astrand et al. (1972) Figure 9 exercise scenario
;QPC = IF TIME >= 1.4 THEN 18 ELSE IF TIME >= 0.92 THEN 53 ELSE IF TIME >= .5 THEN 18 ELSE 18
;QCC = IF TIME >= 1.4 THEN 18 ELSE IF TIME >= 0.92 THEN 50 ELSE IF TIME >= 0.5 THEN 18 ELSE 18
;QLC = IF TIME >= 1.4 THEN 0.26 ELSE IF TIME >= 0.92 THEN .13 ELSE IF TIME >= 0.5 THEN 0.26 ELSE 0.26
;QFC = IF TIME >= 1.4 THEN 0.09 ELSE IF TIME >= 0.92 THEN 0.03 ELSE IF TIME >= 0.5 THEN 0.09 ELSE 0.09
;QRC = IF TIME >= 1.4 THEN 0.55 ELSE IF TIME >= 0.92 THEN 0.6 ELSE IF TIME >= 0.5 THEN 0.55 ELSE 0.55
;CONC = IF TIME >= 1.4 THEN 0 ELSE IF TIME >= .92 THEN 200 ELSE IF TIME >= .5 THEN 0 ELSE 200
;The following IF THEN statements implement the Gamberale and Hultengren (1972) experiment (Figure 1)
;CONC = IF TIME >= 1.08 THEN 714 ELSE IF TIME >= .75 THEN 501 ELSE IF TIME >= .67 THEN 0 ELSE IF TIME >= .33 THEN 300 ELSE 100
|
CIX = CONC × MW/24,450 |
;Exposure concentration (mg/L) |
|
LENGTH = 4 |
;Length of inhalation exposure (h) |
|
INTERVAL = 8 |
|
|
CI = CIX × (mod(time,interval)<=length) |
|
|
method RK4 |
;Rosenbrock stiff solver |
|
starttime = 0 |
;start integration |
|
stoptime = 8 |
;end integration |
|
dtmin = 0.0001 |
;minimum (and initial) step size |
|
dtmax = 1 |
;maximum step size |
|
tolerance = 0.0001 |
;error tolerance for stiff solver |
|
dtout = 0.1 |
;communication interval (optional) |
|
deltaT = stepsize |
;allows plotting step sizes used as deltaT (optional) |
|
display cv, ca, vlc, vrc, vfc, vsc, qfc, qlc, qrc, sf, dose, mass, massbal, pfa, pla, psa, pra display length, bw, qpc, qcc, pb, vfc, km, vmaxc, interval, kfc display cl, cr, cxppm, ci, conc, af, as, ar, al |
|
;INTEGRATIONS
;Chemical in blood
AB' = QP × (CI – CX) + QC × (CV– CA)
INIT AB = 0
CA = AB/VB
CV = (QF × CVF + QR × CVR + QL × CVL + QS × CVS)/QC
;Mixed venous (mg/L)
;Exhaled chemical
|
CX = CA/PB |
;Alveolar (mg/L) |
|
CXPPM = CX × 24,450/MW |
|
|
;Chemical in slowly perfused compartment |
|
|
AS' = QS × (CA – CVS) |
;(mg/h) |
|
init AS = 0. ;(mg) |
|
|
CS = AS/VS ;(mg/L) |
|
|
CVS = CS/PS |
;Venous blood (mg/L) |
|
Chemical in fat compartment |
|
|
AF' = QF × (CA – CVF) |
;(mg/h) |
|
init AF = 0 |
;(mg) |
|
CF = AF/VF |
;(mg/L) |
|
CVF = CF/PF |
;Venous blood (mg/L) |
|
;Chemical in rapidly perfused compartment |
|
|
AR' = QR × (CA – CVR) |
;(mg/h) |
|
init AR = 0 |
;(mg) |
|
CR = AR/VR |
;(mg/L) |
|
CVR = CR/PR |
;Venous blood (mg/L) |
|
;Chemical in liver compartment |
|
|
AL' = QL × (CA – CVL) – AM' |
;(mg/h) |
|
init AL = 0 |
;(mg) |
|
CL = AL/VL |
;(mg/L) |
|
CVL = CL/PL |
;Venous blood (mg/L) |
|
;Metabolism |
|
|
AMS' = VMAX × CVL/(KM + CVL) |
;Saturable metabolism (mg/h) |
|
init AMS = 0 |
|
|
AML' = KF × CVL |
;Linear metabolism (mg/h) |
|
init AML = 0 |
|
|
AM' = AMS' + AML' |
;Total metabolism |
|
init AM = 0 |
|
|
;Mass balance |
|
|
DOSE' = QP × (CI – CX) |
;Net absorption (mg/h) |
|
init DOSE = 0 |
;Net absorption (mg) |
|
MASS = AF + AS + AL + AM + AR + AB |
;In tissues + metabolized (mg) |
|
MASSBAL = DOSE – MASS + 1 |
|