Appendix B
Vicarious Calibration1
This appendix expands on the importance of a vicarious calibration. It provides the technical details associated with using Marine Optical Buoy (MOBY) for the ocean color vicarious calibration.
The following measurement equation is used to derive water-leaving radiance (Lw) (Franz et al., 2007):
Lt = [Lr + La + tdv(Lf + Lw)tgvtgs fp]
L: radiance;
t: transmittance;
Lt: spectral radiance at the satellite sensor;
Lr: Rayleigh contribution from the atmosphere;
La: aerosol contribution from the atmosphere (including Rayleigh-aerosol interactions);
Lf: sea-foam contribution;
tdv: diffuse transmittance along the satellite-to-surface path ;
tg: transmittance through gaseous absorption along the satellite-to-surface path;
ts: the transmittance along the sun-to-surface path; and
fp: accounts for the polarization dependence of the satellite sensor.
Sun glint is not included in the equation because these data would have been flagged under normal operations. All of these quantities depend on wavelength, and all but the Lw term can be determined from ancillary data (e.g., surface pressure is required to calculate Lr, wind speed for Lf, etc.) or, for La, through models combined with near-infrared measurements of the surface area that is being used for the vicarious calibration, in order to estimate the aerosol contribution at the blue-green spectral region of interest for the match-up dataset.
It is assumed that all quantities except Lw have zero uncertainty2 and propagate uncertainties according to the International Organization for Standardization’s (ISO) Guide to the Expression of Uncertainty in Measurement (GUM; ISO, 1993).
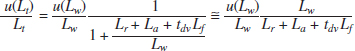
The approximation follows because Lw is small compared to Lt, e.g., about 5 percent, and no more than 15 percent. So to achieve a relative uncertainty of 5 percent in Lw we need the sensor to be producing Lt values with a relative uncertainty of » 0.3 percent (=5 percent × 5/95). However, this level of uncertainty on a satellite sensor in orbit is not possible at the present time. It requires pre-flight calibration of sufficient accuracy, complete and robust instrument characterizations, and the ability to monitor any change in the response upon launch. One limit is the uncertainty in the standards of spectral radiance supplied by National Institute of Standards and Technology (NIST), which typically have an uncertainty of 0.5 percent (k = 2) in the visible region of the spectrum.
A stringent vicarious calibration is required to overcome the inability to constrain the sensor’s uncertainty to 0.3 percent or less. To achieve this calibration, a natural source is selected as the surface reference site of Lw values, the site is instrumented with a robust, high-quality assured measurement facility, and the experiment is designed so as to
____________________________
1 Based on a white paper provided by C. Johnson, July 2010.
2 Uncertainty can be classified as arising from random or systematic effects. Uncertainty values from random effects can generally be reduced by increasing the number of measurements; they scale as 1/√N, where N is the number of measurements. For systematic effects, increasing the number of measurements has no impact whatsoever on the associated uncertainty values. Uncertainty values of either type are estimated as “standard uncertainties” corresponding to the estimated standard deviation (k = 1) and the combined uncertainty is the root-sum-square of the individual component values (assuming the values are uncorrelated). The GUM explains how to derive standard uncertainties for uncertainty estimates that can be evaluated statistically (Type A) and through other means (Type B).
minimize sources of bias and improve the data return (e.g., consideration of cloud cover probabilities).
The MOBY site has been used to calibrate ocean color sensors in the post-Coastal Zone Color Scanner (CZCS) era, and the requirements for ocean color vicarious calibration have been well documented (NASA, 2003). Here, we present the concept of random and systematic uncertainty and the measurement equation to support the role of a MOBY-like facility in ocean color research. First, in order to have acceptable values for the random components of uncertainty one can either have a broad distribution, or a narrow, well-defined distribution. The latter requires fewer samples to achieve the same uncertainty value. The well-defined, narrow distribution is found at the MOBY facility, with its stable marine atmosphere, central Pacific location, uniform oligotrophic waters, and robust instrument design that results in good measurement precision. An example of a broader distribution would be the BOUSSOLE or Aeronet-OC (Bailey et al., 2008). It can be argued that the best technical approach for vicariously calibrating a new satellite sensor such as VIIRS would be to have a precise, stable dataset so that the number of observations required to produce the asymptotic value of the random uncertainty component is as small as possible. The Ocean Biology Processing Group (OBPG) studied the effect of sample size on the uncertainty in the vicarious gain coefficient using MOBY for SeaWiFS; it concluded 45 to 60 samples would be required for reliable vicarious calibration of a stable sensor such as SeaWiFS (see Figure B.1).
Second, in order to have acceptable values for the systematic components of uncertainty, one needs a robust, well-characterized, high-quality assured dataset. Spectral biases cannot be tolerated at any level, because the bio-optical algorithms rely on band ratios. Unidentified or difficult to quantify bias introduced by the “atmospheric correction” (e.g., the process of estimating all the terms in the measurement equation except Lw) are mitigated by selecting sites where the atmospheric conditions and the marine environment are as simple as possible, the necessary ancillary data are available, and the models can be verified and improved upon. Likewise, the in situ instrument must be
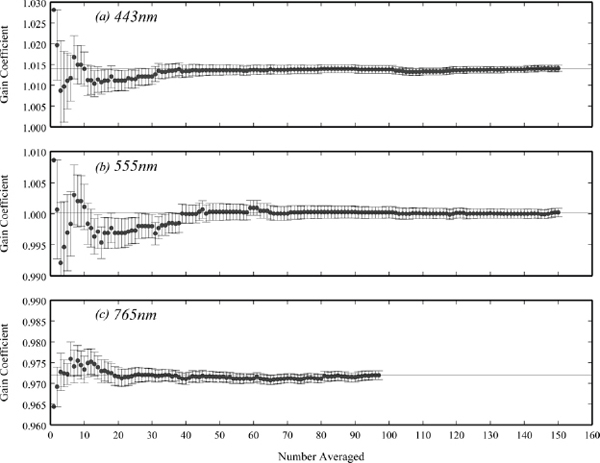
FIGURE B.1 Mean vicarious gains, g, derived for SeaWiFS bands at 443, 555, and 765 nm based on calibration samples between September 1997 and March 2006. Individual gains from the mission-long set of calibration match-ups were randomly sampled; growing the sample set one case at a time and averaging to show the effect of increasing sample size on g. Vertical error bars show the standard error on the mean at each sample size.
SOURCE: Franz et al., 2007; used with permission from the Optical Society.
fully characterized and supply values that are SI-traceable. The more robust this procedure, the more reliable is the final product. The MOBY project has gone to great effort to meet these objectives by incorporation of check standards, repeat calibrations, close linkage with NIST, expert and dedicated staff, good instrument design, and so forth. The evidence of the degree of the stability and precision of the MOBY products and the atmospheric correction procedures is demonstrated in Franz et al. (2007).
The MOBY site was selected to represent the majority of the observed natural sources—the open oceans. Coastal regions exhibit variations in Lw and the other terms in the measurement equation on many different temporal and spatial time scales compared to the MOBY site off Lanai, Hawaii. The sensor measures Lt, the proper interpretation of these data depend on thorough understanding of the sensor characterization (linearity, polarization, spectral out of band, etc.) and response to this top of the atmosphere radiant flux. A case could be made for additional sites, including coastal sites, with a MOBY-like site producing the basic calibration and the other equally robust sites, serving to explore the intricacies of the atmospheric correction methods, dark pixel assumptions, and the satellite sensor characterization functions themselves.
In conclusion, study of the measurement equation and robust experimental design establishes that the MOBY approach and its uncertainty values are necessary for productive ocean color research. An examination of the uncertainty in upwelling spectral radiance for MOBY is given in Brown et al. (2007), where the Type A random uncertainty was estimated to be 1 percent. Franz et al. (2007) state that without the vicarious calibration provided by MOBY, the bias in Lwn resulting from the errors in the pre-flight calibration for SeaWiFS would have been 25 percent at 490 nm and 75 percent at 412 nm and the mean Ca retrieval would be biased low by 25 percent.



