Social Evolution in
Multispecies Biofilms
![]()
SARA MITRI,*†§ÃO B. XAVIER,‡AND KEVIN R. FOSTER*†§
Microbial ecology is revealing the vast diversity of strains and species that coexist in many environments, ranging from free-living communities to the symbionts that compose the human microbiome. In parallel, there is growing evidence of the importance of cooperative phenotypes for the growth and behavior of microbial groups. Here we ask: How does the presence of multiple species affect the evolution of cooperative secretions? We use a computer simulation of spatially structured cellular groups that captures key features of their biology and physical environment. When nutrient competition is strong, we find that the addition of new species can inhibit cooperation by eradicating secreting strains before they can become established. When nutrients are abundant and many species mix in one environment, however, our model predicts that secretor strains of any one species will be surrounded by other species. This “social insulation” protects secretors from competition with non-secretors of the same species and can improve the prospects of within-species cooperation. We also observe constraints on the evolution of mutualistic interactions among species, because it is difficult to find conditions that simultaneously favor both within- and among-species cooperation. Although relatively simple, our model reveals the richness of interactions between the ecology and social evolution of multispecies microbial groups, which can be critical for the evolution of cooperation.
________________
*Department of Zoology, University of Oxford, Oxford OX1 3PS, United Kingdom; †Ox-ford Centre for Integrative Systems Biology, Oxford University, Oxford OX1 3QU, United Kingdom; and ‡Program in Computational Biology, Memorial Sloan-Kettering Cancer Center, New York, NY 10065. §To whom correspondence should be addressed. E-mail: sara.mitri@zoo.ox.ac.uk or kevin.foster@zoo.ox.ac.uk.
It would seem justified to assert that, so far, no revision of the Darwinian paradigm has become necessary as a consequence of the spectacular discoveries of molecular biology. But there is something else that has indeed affected our understanding of the living world: that is its immense diversity.
Ernst Mayr (2004)
DNA sequencing continues to reveal new species that could not be found with conventional methods. Nowhere is this more true than in the microbial world where the sequence-based estimates of species in a gram of soil commonly run into the thousands (Gans et al., 2005; Roesch et al., 2007). Only a fraction of these species would typically be identified by culture-based methods, revealing that the majority of microbial species will not grow in current laboratory conditions (Hugenholtz et al., 1998). This realization, along with the rapidly decreasing cost of DNA sequencing, has led to an impressive effort to identify and catalog microbial diversity across a wide range of environments. These environments include soil, which is often considered one of the most diverse environments, but also range out to marine environments including the open ocean (Yooseph et al., 2007), the massive microbial mats that form stromatolites (Baumgartner et al., 2009) (Fig. 7.1C), and hydrothermal vents where large numbers of rare species have been found (Sogin et al., 2006).
The survey of microbial life is also looking inward to the species that live in and on humans, as exemplified by the concept of the human micro-biome. Numerous projects are under way to catalog genetic diversity in areas including the skin, the oral cavity, and the intestine (Dethlefsen et al., 2006; Ley et al., 2006a). Whereas intestinal communities have been found to be quite similar across humans as compared with other mammals (Ley et al., 2008), different people often carry different sets of micro-bial species, underlining the complexity of intestinal ecology (Guarner and Malagelada, 2003; Eckburg et al., 2005; Dethlefsen et al., 2006). The composition of the gut microbiota has also been found to have important implications for health and has been linked to a range of diseases including obesity, inflammatory bowel disease, and colonic cancer (Guarner and Malagelada, 2003; McGarr et al., 2005; Dethlefsen et al., 2006; Ley et al., 2006b; Manichanh et al., 2006).
Recognition of the vast diversity within microbial communities has occurred alongside another realization about microbial life: the importance of social interactions. It is now accepted that many phenotypes of one cell influence the ability of surrounding cells to divide and survive, which are social traits in an evolutionary sense (Crespi, 2001; West et

FIGURE 7.1 Microbial diversity: examples of natural microbial communities. (A) A two-species bacterial biofilm cultivated in the laboratory in which one strain evolves to increase its exploitation of the other. Adapted by permission from Macmillian Publishers Ltd: Nature (Hansen et al., 2007), copyright 2007. (B) A two-strain bacterial aggregate detected on a bean leaf surface (magnification 500×) [Appl Environ Microbiol (2005) 71(9):5484–5493, 10.1128/AEM.71.9.5484–5493.2005. Reproduced with permission from the American Society for Microbiology] (Monier and Lindow, 2005). (C) Stromatolite fossil that is ~2 billion years old. Modern stromatolites consist of multilayered sheets of microorganisms, and are a good example of very diverse, yet spatially structured microbial communities (copyright Merv Feick, http://www.Indiana9Fossils.com). (D) The detection of two of the species present in a bacterial biofilm covering the intestinal mucosae of a self-limiting colitis patient, imaged using triple-color fluorescence in situ hybridization [J Clin Microbiol (2005) 43(7):3380–3389, 10.1128/JCM.43.7. 3380–3389.2005. Reproduced with permission from the American Society for Microbiology] (Swidsinski et al., 2005).
al., 2006; Foster, 2010). Social phenotypes in microbes include not only growth rate regulation (Kreft, 2004), which has the potential to affect the nutrients of surrounding cells, but also the widespread secretion of compounds that either promote or inhibit the growth of neighboring cells (Kerr et al., 2002; Griffin et al., 2004; Xavier et al., 2011).
In a bid to understand social phenotypes in microbes, theories of social evolution first developed for social animals have been used for the study of microbial groups (Brown, 1999; West et al., 2006; Nadell et al., 2010). A key prediction of this work is that the degree of mixing between different genotypes will be critical in determining the classes of social traits that evolve in microbial groups (Hamilton, 1964a). All else being equal, when cells of one genotype mix with many others, there is more potential for the evolution of competitive traits that harm neighboring cells than when strains are surrounded by clonemates. Clonal groups of cells are instead expected to display phenotypes that optimize the productivity of the group, like cells in a multicellular organism. For example, cells might display slow and efficient growth and secrete enzymes that harvest nutrients for all cells in the area. A growing body of empirical work has shown that genotypic mixing has the potential to limit cooperativity in a wide range of microbial traits (Greig and Travisano, 2004; Gore et al., 2009), including enzyme secretion (Griffin et al., 2004), iron scavenging (Diggle et al., 2007b), quorum sensing, and fruiting body formation (Foster et al., 2002; Buttery et al., 2009). Genetic mixing experiments also reveal the importance of the fitness costs and benefits for social phenotypes, with the potential for cooperation to be stabilized by either constraints on competitive traits (Foster et al., 2004; Harrison and Buckling 2009) or strategies that make cooperation carry little or no cost (Xavier et al., 2011).
Although our understanding of the evolution of social phenotypes in microbial populations in the laboratory is growing, we still understand little of how the theory and experiments relate to natural microbial communities (Little et al., 2008; Filoche et al., 2010; Foster, 2010). In particular, studies from social evolution typically consider well-mixed groups in liquid where local spatial structure is lacking (Griffin et al., 2004; Harrison et al., 2008). While shaking culture is an excellent technique with which to simplify and study interactions, microbes commonly form large surface-attached communities, known as biofilms. These biofilms carry spatial structure, and the potential for social interactions will typically be much greater than in liquid (O’Toole and Kolter, 1998; Hall-Stoodley et al., 2004; Monds and O’Toole, 2009; Nadell et al., 2009) (Fig. 7.1). In addition, the primary focus has been on mixing strains of a single species, which contrasts with the lesson from metagenomics that thousands of species are commonly present in any one environment. Natural microbial communities are thus often characterized by spatial structure and a multitude of species and environments, making it challenging to understand the links between social evolution and microbial ecology, not in the least because so many of the species involved cannot yet be cultured.
Our goal here is to develop models to explore the role of species diversity within biofilm-like microbial communities on the evolution of social phenotypes. In particular, we focus on the evolution of a growth-promoting secretion within a focal microbial species and ask: How does the presence and behavior of additional species affect the evolution of the growth-promoting secretion? This chapter is centered around a series of virtual experiments that use an individual-based simulation of microbial biofilms. The model captures many of the key biological and physical processes that affect cell groups, such as nutrient diffusion, secretion, cell division, and colony expansion. Although simulations are ultimately no substitute for experiments with real organisms, we can explore a much greater range of parameters than is possible with an empirical project. The analysis reveals a number of interdependencies between ecological competition among microbial species and the evolution of cooperation.
RESULTS
This chapter is centered on models of competition that investigate the evolutionary success of a strain that secretes a growth-promoting substance, such as an enzyme that diffuses outward and increases the availability of nutrients to all cells in proportion to its concentration. This focal strain is compared with a strain that does not secrete and by doing so saves energy that can be redirected into growth. The general question we ask is: What are the conditions that allow a cooperative secretor strain to outcompete the nonsecretor strain, or vice versa? Whereas we focus on a secretion phenotype, the general conclusions of the model should have relevance for any cooperative traits that affect the growth rate of neighboring cells (Kreft, 2004).
The framework used here is an agent-based model that employs mechanistic descriptions of solute diffusion and cell growth (Xavier et al., 2005; Xavier and Foster, 2007; Nadell et al., 2008) (Materials and Methods) and has been developed over the last decade for applications in the field of biochemical engineering. The underlying assumptions are described and justified in detail elsewhere (Matsushita and Fujikawa, 1990; Ben-Jacob et al., 1994; Kessler and Levine, 1998; Nadell et al., 2008), and empirical tests have demonstrated the framework’s ability to make accurate predictions for real biological systems (Xavier et al., 2004, 2007).
Briefly, the simulations consider a two-dimensional surface on which a number of microbial cells (of the different phenotypes or species) attach, grow, and divide, resulting in a biofilm-like structure. Other geometries, including radial expansions from a point and three-dimensional simulations, can also be implemented but do not appear to
affect evolutionary conclusions (Nadell et al., 2010). A constant concentration of nutrients is available at a fixed diffusion rate that cells take up, which leads to local gradients in nutrient concentrations. Cells may also secrete extracellular products, which become available to neighboring cells through diffusion. In the simulations presented, we assume that secretion carries an energetic cost of 30% of growth rate, in line with experimental results (Diggle et al., 2007b; Harcombe, 2010). However, we also investigate the effect of varying this cost (Figs. S1 and S6¶). In all experiments, cells are left to grow to a fixed total mass, at which point the fitness values of secretor and nonsecretor phenotypes (computed as the average number of cell divisions per unit time) (Materials and Methods) are compared to determine which of the two phenotypes would be expected to dominate in local competition. This cutoff point at which fitness is measured can be taken to model an environmental disturbance that occurs at a given frequency. The general effects of altering this parameter are discussed in Foster and Xavier (2007) and Brockhurst et al. (2007). Each cell is implemented as a circular agent, grows according to a Michaelis–Menten function of the substrate concentration in its local environment, and divides once it reaches a maximum radius (Materials and Methods). We do not consider active movement but cells can move passively due to the forces exerted between neighboring individuals as they grow and divide.
Single Species
In single-species simulations, Nadell et al. (2010) found that environmental nutrient concentration can determine whether a secretor or a nonsecretor strain is more evolutionarily successful. We begin this study by reproducing these results, which then serve as an experimental control with which to compare the effects of introducing additional species. In agreement with the previous study, our single-species simulations show that low nutrient concentrations result in tower-like clonal clusters of cells, whereas high nutrient concentrations result in the mixing of cell types as they grow (Fig. 7.2). Nadell et al. (2010) showed that this difference is due to changes in the depth of the growing front of the cell group, which depends on a multitude of factors in addition to nutrient concentration, such as the diffusion rates of nutrients into the cell groups, or on the growth rates of the cells. It should be kept in mind, therefore,
_________________
¶Figures S1 through S8 are available online as supporting information for the original PNAS article [108(Suppl 2):10839–10846] at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1100292108/-/DCSupplemental.
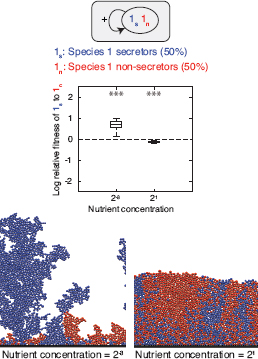
FIGURE 7.2 Secretors and nonsecretors of a single species. Equal proportions of two strains of the same species 1 are inoculated and left to grow to a fixed total biomass. Strain 1s secretes a product that benefits both strains. Strain 1n does not secrete the product. Product secretion incurs a cost of 30% of the cells’ growth rate. Boxplots show log relative fitness (Materials and Methods) of secreting to nonsecreting cells [log(w(1s):w(1n))] in 40 replicates with high and low nutrient concentrations. The dashed line shows the level at which the two phenotypes are equally fit. Asterisks indicate the significance of the difference between secretor and nonsecretor fitness, ***P < 0.001; **P < 0.01; *P < 0.05; ns, not significant. Below each boxplot is an image generated using the simulation from one of the 40 simulations that was closest to the median in the boxplot. It is shown that secretors can outcompete nonsecretors when the two phenotypes are well segregated, whereas they are at a disadvantage under conditions leading to high mixing.
that a change in nutrient levels in the simulations captures the effects of changing a number of factors.
When nutrients are low and growth results in clonal clusters, cells secreting a growth-promoting product (1s) are more likely to be surrounded by others that also secrete the product. Consequently, the growth benefits of the product are preferentially directed toward clonal
cells, whereas nonsecretors (1n) rarely benefit from the secretions. In agreement with this logic, at a low nutrient concentration, secretor cells have a significantly higher fitness than nonsecretors, regardless of whether product secretion incurred a cost (30% of their growth rate) or not (Mann–Whitney test, df = 38, both P < 0.001, Figs. 7.2 and S1A). In contrast, increasing nutrient concentration leads to more mixing between the two cell types, such that the benefit of the secreted product is now equally distributed among both cell types. Secretors therefore grow as well as nonsecretors when secretion is free (P = 0.39, Fig. S1A), but have a significantly lower fitness when secretion incurs a cost [P < 0.001, Fig. 7.2; see also Nadell et al. (2010)].
Ecological Competition Can Inhibit Cooperation
We next ask how the presence of additional species can affect the conclusions of the single-species model. We focus on how additional species will influence the competition between the two secretor phenotypes in our focal species. We do not analyze the competition playing out among the different species nor do we investigate mechanisms that can maintain species diversity in the face of the potential for competitive exclusion (Dethlefsen et al., 2006; Scheffer and van Nes, 2006; Gudelj et al., 2010; Robinson et al., 2010). Instead, we assume a simple model of species interaction that excludes the possibility for strong coevolutionary feedbacks among species (Box 7.1).
To investigate the effects of additional species, we introduce a new class of cells that can have different biological properties from the focal species. We assume that the second species uses the same nutrients as species 1 to grow so that it is an ecological competitor and can benefit from the secretions of species 1 (for results where species 2 does not benefit from the secreted product, see Fig. S2). As for the single-species model, we examine the outcome of competition between equal numbers of the secretor and nonsecretor phenotypes, with product secretion costing cells 30% of their growth rate. However, the total number of species 1 cells inoculated is now half that of the single-species case, with the other half being species 2 (results are qualitatively similar if density is doubled, Fig S.3).
The addition of species 2 led to a significant reduction in the relative fitness of secretors at low nutrient concentration (Mann–Whitney test, df = 38, P < 0.001), such that nonsecretors now have a significantly higher fitness than secretors (P < 0.001, Fig. 7.3A) and secretor cells are outcompeted. The poor performance of secretor cells is explained by an inability to compete when inoculated at low frequency (Fig. S4). In particular, adding a second species appears to interfere with the initial formation of
BOX 7.1 Species and Niche
In the various models presented throughout the chapter, the phenotype of the introduced species differs only minimally from the two phenotypes of the focal species. This similarity among the species poses the following question: How is the introduction of a second species different from simply increasing the frequency of one of the two phenotypes in the focal species? The key difference is that the focal species is mainly under selection in the focal environment, whereas the second species has its main selection component in different environments. A species in our model is thus functionally defined as a set of one or more phenotypes that share the same niche over evolutionary timescales. In this way, our “species 1” and “species 2” formally represent a dichotomous split between focal-niche and other-niche phenotypes. Each category could, in principle, contain multiple taxonomic species. In particular, species 2 is a proxy for multiple species that overlap only slightly (in space and/or time) with the focal species (see diagram). Whereas no one of these species interacts with the focal species enough for coevolution to be important, there is enough net overlap to influence selection on the focal species. Accordingly, we disregard changes in the fitness of the nonfocal species and concentrate solely on competition between the two focal phenotypes. A more realistic analysis would allow for a full range of niche overlaps rather than our binary division into complete niche overlap and minor overlap.
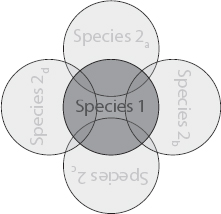
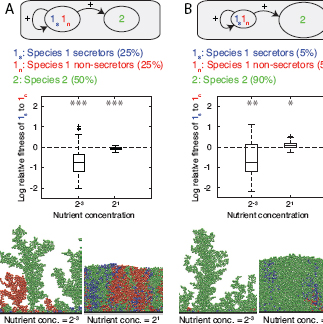
FIGURE 7.3 Ecological competition with a second species. A second species is added to the competition between secretors and nonsecretors (Fig. 7.2). This second species is intended to also approximate the effects of a mixture of many species (Box 7.1). Species 1 is equally divided into secretor and nonsecretor strains, whereas species 2 represents either (A) 50% or (B) 90% of the cells inoculated. All cells are then left to grow to a fixed total biomass. Strain 1s secretes a product that benefits both strains of its own species, as well as species 2. Strain 1n and species 2 do not secrete any products. Product secretion incurs a cost of 30% of the cells’ growth rate. See Fig. 7.2 legend for explanations on data representation. It is shown that when cells are highly segregated, secretor cells lose their advantage (compared with Fig. 7.2, Bottom Left), independently of the two proportions of species 2. At high levels of mixing, however, secretors can outcompete nonsecretors when there is a high proportion of species 2 cells. The image (B, Bottom Right) shows the social insulation effect discussed in the text.
cooperative clumps of secretors such that secretors are more often overgrown. Consistent with the importance of ecological competition with species 2, we observe that the advantage of secretors over nonsecretors is significantly negatively correlated with the maximum growth rate of species 2 (Spearman’s rank correlation test, p = -0.51, P < 0.001, Fig. S5A) and with the cost of secretions (p = -0.67, P < 0.001, Fig. S6A). In addition, decreasing the density of inoculated cells (by doubling the size of the growth area) results in a significant growth advantage for secretors over nonsecretors (Mann–Whitney test, df = 38, P < 0.001, Fig. S5C). The
data thus far show that under low nutrient conditions, competition with a second species for nutrients and space can eliminate the advantage of cooperation.
Abundance of Additional Species Insulates Secretors from Nonsecretors
At high nutrient concentrations, we were surprised to find that the relative fitness of the secretor phenotype was significantly higher in the presence of species 2 than in its absence (Mann–Whitney test, df = 38, P < 0.001), although secretors still had a significantly lower fitness than nonsecretors (P < 0.001). To confirm that this result depended on the presence of species 2, we repeated the simulation, but instead of using equal proportions of both species, we started the simulation with 90% of the cells being of species 2 (Fig. 7.3B). Our focal species 1 is again divided equally among the two phenotypes, secretor and nonsecretor. This model is analogous to a conglomerate of multiple ecologically similar species (e.g., the model can be thought of as a mixture of 10 equally common species), where any focal species may often be in a minority (Box 7.1).
The higher initial proportion of cells of species 2 had no effect on the relative fitness of secretors and nonsecretors at low nutrient concentration compared with equal proportions (P = 0.78, Fig. 7.3B). The ecological competition effect still dominated and secretor strains fared poorly. However, at a high nutrient concentration, secretors now had a significantly higher fitness than nonsecretors (P < 0.05) and a higher relative fitness than when the initial number of cells of the two species was equal (P < 0.001). Overall, the proportion of species 2 inoculated together with species 1 correlated positively with the relative fitness of secretor cells (Spearman’s rank correlation test, p = 0.67, P < 0.001, Fig. S7D). We hypothesized that this increase in the competitiveness of secretors was because species 2 was insulating the secretor strain 1s from the nonsecretor strain 1n, thereby reducing the access of the latter to the secretions of the former.
To examine this hypothesis further, we assessed the effect of species 2 on the spatiogenetic structure of species 1. In the high-nutrient case, increasing the proportion of inoculated cells of species 2 leads to an increase in the segregation index (Materials and Methods) between the two phenotypes of species 1 (Spearman’s rank correlation test, p = 0.94, P < 0.001, Fig. S7B), suggesting a causal relationship between segregation and the increase in the relative fitness of secretors. This pattern was not observed at low nutrient concentrations (Fig. S7A and C).
Increasing the proportion of species 2 also decreases the number of cells of species 1 inoculated in the system, which might explain the
increase in segregation among strains, independently of the presence of the additional species. To examine this idea, we repeated the simulation in the absence of species 2. This simulation was thus identical to that with species 1 alone (Fig. 7.2), except that the initial number of inoculated cells was 10 times lower. Secretors have a significantly lower fitness than nonsecretors (Mann–Whitney test, df = 38, P < 0.05) and the relative fitness of secretors is significantly lower than when species 2 was present (P < 0.001). However, the relative fitness of secretors is higher than in the original simulation with a higher number of inoculated cells (P < 0.001). This result suggests that reducing the inoculation density at high nutrient concentrations can increase segregation of the two phenotypes (see also Fig. S5D), but that species 2 was critical in acting as a social insulator that protects secretors from nonsecretors. Note that the insulation effect rests upon the assumption that the niches of the insulating species do not overlap perfectly with the focal species (Box 7.1). If the niches perfectly overlap, then the insulator species effectively become an excess of non-secretors, which will tend to disfavor secretion (Fig. S4B).
Constraint on Multispecies Mutualism
We have explored the effect of competing species on the evolution of cooperative secretions in a focal species. Some species also exchange products or services that are mutually beneficial (Shimoyama et al., 2009). To investigate this possibility, we ran new simulations with an equal proportion of the two species in which the product secreted by strain 1s provided benefits to both species 1 and 2, as in the simulations described above, but where species 2 additionally secreted a noncostly product that was beneficial to species 1. We assume that the trait of species 2 is not costly to focus upon the evolution of costly cooperation within species 1.
We found that the return benefit from species 2 slightly improves the prospects of the secretor cells of species 1. In particular, the fitness of nonsecretors is no longer significantly different from that of the secretors at low nutrient concentrations (Mann–Whitney test, df = 38, P = 0.22). However, this fitness improvement is rather small; that is, the relative fitness of secretors is not significantly different from the case where species 2 secretes nothing (P = 0.12). The beneficial product secreted by species 2 then does not strongly promote the fitness of secretor cells.
In the simulations described thus far, secreted products were always beneficial for cells of species 1. We next model a case involving the exchange of products that are only beneficial to the other species (Little et al., 2008) (Fig. 7.4B). Strikingly, secretors now have a significantly lower fitness than nonsecretors, independent of nutrient concentration (both P < 0.001). What explains the failure of secretors of species 1 to capitalize
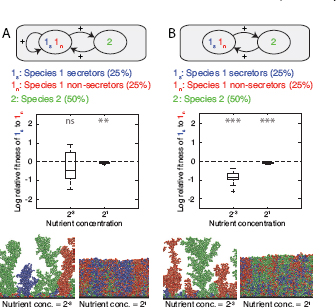
FIGURE 7.4 Multispecies mutualism. Species 2 now secretes a product that is beneficial to species 1, resulting in a mutualism between the two species. Species 1 is equally divided into secretor and nonsecretor strains, whereas species 1 and 2 are inoculated in equal proportions and left to grow to a fixed total biomass. Strain 1s secretes a product that either benefits both strains of its own species, as well as species 2 (A) or species 2 only (B). Product secretion by 1s incurs a cost of 30% of the cells’ growth rate. In turn, species 2 secretes a cost-free product that benefits species 1. Strain 1n does not secrete any products. See Fig. 7.2 legend for explanations on data representation. It is shown that secretor cells do not have a clear advantage over nonsecretors in any one of the four conditions considered here. This result is because mixing is important for the benefits of the two secreting strains to be shared, but is detrimental because it allows nonsecretors to grow faster than secretors, thereby undermining the mutualistic interaction.
on the return benefits from species 2? The answer is revealed by running simulations in which species 2 is mixed with either secretors or nonsecretors, but not both at the same time. At low nutrient concentration, nonsecretors perform better with species 2 than secretors with species 2 (P < 0.001, Fig. S8A) because spatial genetic segregation prevents secretors from interacting effectively with species 2. This explanation is further confirmed by the high-nutrient case where secretors with species 2 perform better than nonsecretors that are alone with species 2 (P < 0.001, Fig. S8B). However, the strain mixing that allows this positive effect is the same process in the full model that renders secretors vulnerable to
competition from nonsecretors. The result is that in three-way competitions, the secretors always perform poorly.
Competition Among Microbial Groups
The results presented above predict the evolutionary trajectory within a group of microbes and form a good first step to understand the effect of additional species on cooperation within a microbial group. However, when the total productivity of microbial groups is important for their ability to colonize new patches (“hard” selection at the group level), there is the potential for higher-level evolutionary competition among different microbial groups. This competition can strongly affect the outcome of natural selection (Wilson, 1975; Rousset, 2004). In particular, it can favor genotypes that result in the most productive groups, even if those genotypes tend to do poorly within their groups.
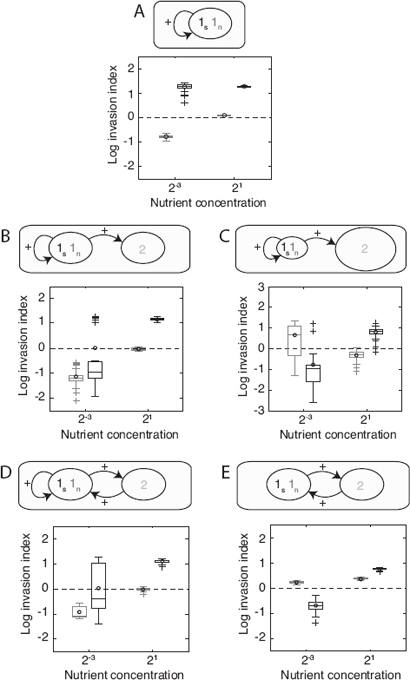
To investigate the effects of competition among groups, we model the extreme case of maximum dispersal whereby after growth, cell groups disperse and mix with the cells of the same species in all other groups, before reforming groups containing two randomly chosen strains from the population. These groups then grow again before dispersing, and so on. Under this simple demography, we can estimate the potential for a rare secretor genotype to invade a population dominated by nonsecretors. This estimation is done by comparing the fitness of secretors in mixed groups with nonsecretors (a rare secretor genotype will tend to meet a nonsecretor genotype) to that of nonsecretor cells in the presence of other nonsecretors (nonsecretors are the common genotype and will tend to meet each other) (Xavier and Foster, 2007; Nadell et al., 2010). If the secretors tend to produce more cells per unit time in their groups, they will increase in frequency in the population: They are capable of evolutionary invasion. We can then reverse the problem and ask: Could a rare nonsecretor genotype invade a population of secretors? Under the assumptions of our model, we predict that if only one strain can invade, there will be a single strain at equilibrium. If both can invade, the prediction is that both can persist over evolutionary time.
As expected, competition among microbial groups increases the likelihood of the maintenance of cooperative secretions (Fig. 7.5). This result occurs because even though secretors often lose to nonsecretors in a group, the group they are in tends to do better and produces cells more rapidly than groups containing only nonsecretors (a phenomenon related to Simpson’s paradox) (Sober and Wilson, 1999). Nevertheless, the overall effect of introducing a second species is similar to the within-group analyses of the previous sections: Under low-nutrient conditions, the addition of species 2 reduces the advantage of secretors. In the single-
species invasion model, nonsecretors are unable to invade at low nutrient concentration (Fig. 7.5A, Left). By contrast, in two of four multispecies simulations where nutrients are low (Fig. 7.5B–E, Left), the nonsecretors can invade while excluding secretors. Under high-nutrient conditions, the effect of social insulation that promotes cooperation is again seen. With a majority of species 2 and high nutrients, secretors not only can invade but also can do so to the exclusion of nonsecretor cells (Fig. 7.5C, Right). The most significant deviation from the within-group results occurs for the two-species mutualism under high-nutrient conditions. Here, competition among microbial groups allows some secretors to be maintained, providing a way in which the constraint on mutualism discussed in the preceding section might be overcome.
DISCUSSION
Ecological Competition
Our model suggests that among-species interactions can strongly influence the potential for cooperation within a species in spatially structured microbial groups. We find that ecological competition with other species can preferentially harm secretor cells over nonsecretors. This result arises because investment in secretion can slow the growth of cell lineages at critical stages and lead to their overgrowth by another species. This initial investment leaves secretor cells vulnerable to being out-competed by other lineages, particularly under low-nutrient conditions where resources are limiting and most lineages are eliminated through strong genetic bottlenecks (Fig. 7.3A, Bottom Left). The potential for such bottlenecks in growing microbial groups is empirically well documented (Gage, 2002; Hallatschek et al., 2007). Bottlenecks have been interpreted as being favorable for the evolution of cooperation because they promote genetic identity in the emerging clonal groups (Brockhurst, 2007; Nadell et al., 2010). Our study supports this interpretation in the single-species model (Fig. 7.2, Bottom Left), but suggests that this conclusion should be tempered by the fact that bottlenecks can also be indicative of strong ecological competition, which can eliminate cooperators before they have a chance to establish themselves.
The potential for ecological competition to preferentially harm cooperators was seen in a study that added Staphylococcus aureus to iron-limited cultures of Pseudomonas aeruginosa (Harrison et al., 2008). P. aeruginosa secretes iron-scavenging siderophores under iron-limiting conditions, and secreting strains are susceptible to the evolution of nonsecreting strains that use siderophores without producing them. The study is not a direct test of the results of our simulations, as it used shaking cultures
where spatial structure is lacking. Nevertheless, the addition of S. aureus promoted nonsecreting P. aeruginosa over secreting strains, thereby disfavoring cooperation. In contrast, other theory and experiments have highlighted the potential for ecological competition to favor cooperation within species. A model by Rankin et al. (2007) showed how ecological competition can strongly enrich for cooperation when noncooperative species compete poorly with other species. In support of this, a study on two termite species suggested that the species more affected by within-colony competition was more likely to be outcompeted by the other species (Korb and Foster, 2010).
What explains the difference between these results and our predictions? The key is whether within-species cooperation increases or decreases the ability to compete with other species. The model by Rankin et al. (2007) and the termite example concern competition among established social groups of each species where within-species cooperation improves the ability to compete with groups of the other species. By contrast, in our model, lone cooperator cells meet the other species before they have a chance to establish a clonal group, which can mean that cooperators are
FIGURE 7.5 Invasion analysis. The invasion index estimates the probability of a given minority phenotype to spread in a metapopulation consisting of many groups of the other phenotype (Materials and Methods). A–E correspond to Figs. 7.2–7.4. (A) Competition between secretors and nonsecretors of a single species (Fig. 7.2). (B and C) The invasion index of the two phenotypes is compared when an introduced species competes with the first species at (B) 1:1 inoculation (Fig. 7.3A) or (C) 1:9 inoculation densities of the two species (Fig. 7.3B). (D and E) The case of a mutualistic interaction with the second species (D) with self-benefit (Fig. 7.4A) or (E) without (Fig. 7.4B). See respective figure legends for details on simulations. Boxplots show log relative invasion index (Materials and Methods) of nonsecretor [log(I1n→1s), light gray] and secretor [log(I1s→1n), dark gray] cells separately in 40 replicates with high and low nutrient concentrations. Black circles show the mean of the distributions. The dashed line shows the level above which a phenotype can invade a metapopulation of the other. If the mean of only one of the two phenotypes is above the line, we predict that this phenotype would invade the other in a metapopulation. If both means are above the line, we expect the evolutionary equilibrium to consist of a mixture of both phenotypes. It is shown that under high nutrient conditions, secretors are expected to at least persist in the population, even though they were often at a disadvantage under local competition (Figs. 7.2–7.4). At low nutrient concentration, results are similar to the local competition simulations, where the presence of species 2 reduces the advantage of secretors over nonsecretors.
poor ecological competitors. It is interesting to speculate that this early-stage cost to cooperation may be important in both natural selection for quorum sensing regulation of secreted products (Diggle et al., 2007b) and the evolution of clumped dispersal (Gardner and West, 2006), which both limit the likelihood of being a solitary secreting cell. These mechanisms are not part of our simulations, but may help to restrict cooperation to established clonal groups in nature. If effective, there may be conditions under which microbial cooperation is favored rather than disfavored by ecological competition, as was seen in the termites (Korb and Foster, 2010).
Social Insulation
Under high-nutrient conditions, competitive effects are less severe and, accordingly, the impact of additional species upon within-species cooperation is reduced. Indeed, the model even predicts that interactions with other species can promote the evolution of secretor genotypes. Analysis of the spatiogenetic segregation in the simulations revealed that species 2 can act as a social insulator that keeps nonsecretor genotypes away from secretor genotypes. This insulation allows secretor cells to form patches in which they preferentially help their own genotype, in the same way that general spatial structuring can promote the evolution of cooperation (Hamilton, 1964a; Nowak and May, 1992; Rousset, 2004). Although the importance of social insulation effects in natural communities is not yet clear, our model suggests that it will be most important under relatively high nutrient conditions where many species meet and mix. One interesting candidate, therefore, is the human microbiome, and in particular the intestine, where cells can form dense biofilms containing multiple species (Fig. 7.1) (Macfarlane and Dillon, 2007).
Multispecies Mutualism
The conditions for the evolution of multispecies mutualism in the model were relatively restrictive. When the secretion of species 1 benefited cells of its own species as well as species 2 (Fig. 7.4A), the conditions for cooperation were similar to the case where there was no return benefit from species 2 (Fig. 7.3A). In the absence of within-species benefits, however, the evolution of costly secretions in the focal species was particularly unlikely (Fig. 7.4B). This result was due to an unexpected tension between the conditions that favor within- and among-species cooperation. One of the requirements for cooperation between groups of two species is cooperation within each species group (Foster and Wenseleers, 2006). However, within-species cooperation is favored by spatial segregation that keeps secretors away from nonsecretors, whereas among-species
cooperation is favored by mixing that allows efficient exchange of mutual benefits. The tension between the requirements for the two forms of cooperation makes costly cooperative exchanges among microbial species relatively difficult to evolve. We know of no direct tests of this idea to date but some support comes from an example of cross-feeding among Escherichia coli strains where increasing spatial structure inhibited the benefits of the interaction among mutualists (Saxer et al., 2009). When within- and among-species mixing is coupled, however, our model suggests that mutualism is less likely to be favored.
This tension between within- and between-species cooperation has not been observed in previous theory on multispecies cooperation. For example, Doebeli and Knowlton (1998) performed an on-lattice simulation of two positively interacting species, which readily found conditions under which cooperation could be maintained. In addition, a simple model by Foster and Wenseleers (2006) predicts that among-species mutualism can be favored as long as within-species genetic assortment is high and there are reliable feedback benefits from the other species. The difference between these models and the current simulation is that both previous studies assume that within- and among-species assortment can be decoupled [Doebeli and Knowlton (1998) placed the two species on separate lattices]. This is a reasonable assumption for many mutualisms where interacting species have different ecologies. For example, genetic assortment within symbiont populations can be entirely independent of their degree of interaction with their host (Foster and Wenseleers, 2006): A bobtail squid can select for and interact with a near-clonal population of light-producing Vibrio fischeri (Visick et al., 2000). When within- and among-species mixing is coupled, however, our model suggests that mutualism is less likely to be favored.
On the basis of this argument, we predict that mechanisms that decouple mixing within and among species will promote the evolution of costly cooperation among microbial species. Species growing on different nutrient sources is one candidate mechanism suggested by our simulations. With different nutrient requirements, the segregation index within species is significantly higher than between species under low nutrient concentrations (Mann–Whitney test, df = 38, P < 0.001, Fig. 7.6, Bottom Left). Growing on different nutrients also reduces competition among species. Together with the effects on mixing that we observe, this result predicts that species with different metabolic lifestyles are most likely to be mutualists, which is broadly compatible with current data (Little et al., 2008). Mechanisms to select mutualistic partners may drive similar effects. One example is seen in the bacterium Pelotomaculum thermopropionicum, which uses its flagella to physically attach itself to the methanogenic archaeon Methanothermobacter thermautotrophicus with which it
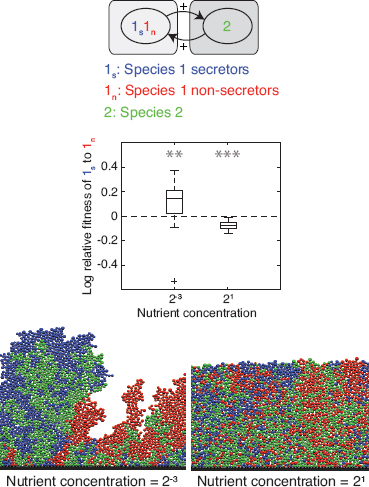
FIGURE 7.6 Mutualism when two species do not compete for nutrients: identical to Fig. 7.4B, but where species 1 and 2 consume different nutrients. See Fig. 7.4 legend for details on simulations and Fig. 7.2 legend for explanations on data representation. It is shown that reduced competition for nutrients between the two species can result in a significant advantage for mutualistic secretors under low nutrient conditions. It appears that this condition allows secretors of the two species to mix, while keeping the two phenotypes of species 1 separate. This result is not observed when nutrient concentration is high.
exchanges metabolic services (Shimoyama et al., 2009). Another candidate is chemotaxis by one species toward the secreting members of the other species, although additional mechanisms would presumably have to exist to ensure that the swimming species itself cooperates.
Mutualistic interactions have also been shown to persist between two engineered bacterial species under low inoculation density on agar
plates (Harcombe, 2010). These experiments suggest that low colonization densities provide yet another mechanism to separate within- and between-species interactions by creating subpopulation structures, in which mutualist pairs can thrive in the absence of noncooperator strains. Selection for mutualism in this system was extremely strong, however, in that cells could hardly grow in the absence of secretors of the other species (Harcombe, 2010). More generally, the potential for within- and among-species cooperation in microbial communities will be promoted when there is higher-level competition among communities (invasion analyses, Fig. 7.5). The potential for such higher-level selection to shape microbial communities was seen in a large-scale simulation of microbial species growing and dispersing among a series of 10 interconnected flasks (Williams and Lenton, 2008). Over time, sets of species that limited harm to their local environment—a form of cooperation—were favored over more rapacious species that limited group productivity, something also seen in experiments that artificially selected for group productivity in real microbial communities (Swenson et al., 2000). Ultimately, the importance of local versus global competition will depend on the ecology of each species and the relative importance of within-community evolution compared with dispersal and colonization events.
Finally, we have deliberately focused on mutualisms where the investment in another species is an adaptation that carries an energetic cost. The majority of positive interactions among strains in nature may come about from cross-feeding by two species that comes at no energetic cost to the species involved. Such byproduct mutualisms are expected to often be evolutionarily stable (Connor, 1986; Foster and Wenseleers, 2006) and may be widespread in natural systems. However, our simulations suggest that even this form of mutualism can often be selectively neutral (Fig. S1D and E).
CONCLUSIONS
Although studies of microbial ecology and microbial sociality are progressing rapidly, we understand relatively little of the intersection between these disciplines. Our models indicate that this intersection can be important, owing to the interconnectedness of within- and between-species interactions in microbial groups. Contrary to typical social evolution predictions, we find that environmental conditions that promote genetic bottlenecks (and raise relatedness) can also increase ecological competition, thus disfavoring cooperation. Bottlenecks are also associated with segregation between species, which limits the potential for among-species mutualistic cooperation. The potential for social insulation by other species and the occurrence of higher-level competition
among microbial groups, however, can counter these effects and favor cooperative phenotypes.
Ultimately, our simulations are simple and are able to capture only a small part of the complexity within real microbial communities. Nevertheless, we identify a number of familiar themes that can inform our understanding of microbial communities. A central theme is the importance of spatial structure for microbial interactions, which can simultaneously promote within-species cooperation and limit among-species interactions. Spatial structure in microbial groups can depend on a number of factors in addition to nutrient concentrations emphasized here. Motility will also influence spatial structures, where mixing may increase through undirected motility or decrease through chemotaxis. In addition, cell–cell adhesion can affect genetic mixing both within (Queller et al., 2003; Smu-kalla et al., 2008) and between species (Shimoyama et al., 2009). Related to this is the physical scale of social interactions. Strong spatial genetic structure may have no impact on the evolution of secretions that diffuse rapidly across strain and species boundaries.
The models also reemphasize the importance of the costs and benefits of social traits for the trajectories of their evolution (Hamilton, 1964a). The majority of the ecological barriers to cooperative evolution discussed here can be overcome by strategies that limit the cost of social traits, such as prudent regulation that produces a secretion only when it is cheap to do so (Xavier et al., 2011). The study of factors such as spatial structure and fitness costs promises a better understanding of when and why the members of microbial communities cooperate with one another.
MATERIALS AND METHODS
Model Framework
An individual-based model, described in detail previously (Xavier et al., 2005; Nadell et al., 2010), is used to simulate growing cell groups. Simulation parameter values (listed in Table 7.1) were taken from previous work (Nadell et al., 2010). At the beginning of each simulation, cells are placed at random positions on a surface and are left to grow to a fixed biomass. Most simulations are started with 120 cells but the effect of varying this number is discussed. Each cell grows according to the concentration of nutrients ([G]) and the concentration of extracellular secreted products ([E]) in its local microenvironment. The stoichiometry tables describing the metabolic model of cells (growth and secretion) can be found in Table 7.2. Cells whose radius exceeds a given value are divided into two new cells. Cells that overlap due to the growth and/ or division process are moved to eliminate the overlap, causing the cell
TABLE 7.1 List of Parameters and the Values Used in Our Simulation Models
| Symbol | Description | Dimension | Value |
| μmax1 | Maximum cell growth rate of species 1 | T-1 | 1 |
| μmax2 | Maximum cell growth rate of species 2 | T-1 | 1 |
| τ | Threshold for extracellular product concentration | MEL-3 | 4 × 10-3 |
| B1 | Growth factor increase of species 1 due to the presence of product secreted either by species 1 or by species 2 at or above threshold concentration τ | Dimensionless | 3 |
| B2 | Growth factor increase of species 2 due to the presence of product secreted by species 1 at or above threshold concentration τ | Dimensionless | 3 |
| C1s | Growth factor decrease in growth rate of strain 1s due to the secretion of extracellular products | Dimensionless | 0 or 0.3 |
| C2 | Growth factor decrease in growth rate of species 2 due to the secretion of extracellular products | Dimensionless | 0 |
| DG | Growth substrate (nutrient) diffusivity | L2T-1 | 4 × 104 |
| DE | Extracellular secreted product diffusivity | L2T-1 | 3 × 105 |
| [E1s] | Local concentration of extracellular product secreted by strain 1s | MEL-3 | NA |
| [E2] | Local concentration of extracellular product secreted by species 2 | MEL-3 | NA |
| Gbulk | Bulk concentration of growth substrate (nutrient) | MGL-3 | 2-3 or 2 |
| [G] | Local concentration of growth substrate (nutrient) | MGL-3 | NA |
| KG | Half saturation constant for growth substrate concentration | MGL-3 | 3.5 × 10-5 |
| Nx,t | Number of cells of strain or species x in a cell group at time t | Dimensionless | NA |
| RE1s | Rate of secretion of extracellular product by strain 1s | MEMX-1T-1 | 1 |
| RE2 | Rate of secretion of extracellular product by species 2 | MEMX-1T-1 | 0 or 1 |
| ωx | Fitness of strain or species x | T-1 | NA |
| X1s | Concentration of biomass of strain 1s (secretor cells) | MXL-3 | NA |
| X1n | Concentration of biomass of strain 1n (nonsecretor cells) | MXL-3 | NA |
| X2 | Concentration of biomass of species 2 | MXL-3 | NA |
| Y1 | Yield of biomass of species 1 on substrate | MXMG-1 | 0.5 |
| Y2 | Yield of biomass of species | MXMG-1 | 0.5 |
Notes: ME represents mass of extracellular enzyme, MG represents mass of growth substrate, MX represents cell biomass, L represents length, and T represents time. NA, not applicable.
TABLE 7.2 Stoichiometry of Cell Metabolism Used in the Simulation Models

group’s front to advance where there are no physical barriers (e.g., the inoculation surface).
Nutrients come from above and the concentration of the nutrient source (bulk concentration, Gbulk) in the region above the upper boundary of growing cells is held constant (see Table 7.1 for values used) throughout the simulations. Under the assumption that reaction–diffusion is much faster than cell growth and division (Xavier et al., 2005), we update solute (nutrient and extracellular product) concentration fields after each cellular growth and division step. The new spatial concentration fields of all solutes S (G and E) are determined by solving the reaction–diffusion equation
![]()
where t represents time, Ds is the diffusivity of solute S, ![]() 2[S] is the Laplacian of the local solute concentration [S], r is cell growth rate (computed using Table 7.2), and Y is the yield of biomass on substrate (see Table 7.1 for values used).
2[S] is the Laplacian of the local solute concentration [S], r is cell growth rate (computed using Table 7.2), and Y is the yield of biomass on substrate (see Table 7.1 for values used).
The individual-based simulation framework was written in the Java programming language. Numerical methods used in the model are detailed elsewhere (Xavier et al., 2005). Briefly, they include the Euler method to grow cells at each iteration, a hard-sphere collision detection method to identify pushing events between neighboring agents, and the FAS multigrid to solve reaction-diffusion equations to steady state (Rumbaugh et al., 2009; Press et al., 1997). All images were rendered using POV-Ray.
Calculating Fitness
Fitness w of a phenotype or species is calculated as the mean number of rounds of cell division per unit time that the cells of that phenotype achieve over the course of a simulation,
![]()
where Nx,t is the number of cells of phenotype or species x present within the cell group at time t, and tend is the time that cells have taken to grow to the maximum total biomass. The log relative fitness of phenotype 1s in local competition with phenotype 1n (Figs. 7.2–7.4) is defined as log(w1s/w1n).
Segregation Index
The segregation index used here is based on that used in previous work, with some minor differences (Nadell et al., 2010). To measure segregation in a population of M cells, we consider each cell ci, i = 1, …, M in the population and identify all other individuals within a distance of 10 cell lengths. The N cells in this neighborhood are indexed by cj, with j = 1, …, N. In this case, we consider only cells of species 1. Cells of species 2 are treated as empty space. We define a phenotypic identity function, p(ci, cj):
![]()
Segregation with respect to a focal cell, s(ci), was calculated as the mean of the p function for every cell in its neighborhood:
![]()
Finally, we define the segregation index σ for the entire cell group as the mean value of s(ci) across the population of cells:
![]()
The segregation index measures the degree to which colocalized cells are clonally related to each other. The index is related to, and expected to correlate with, the relatedness coefficient from social evolution theory. However, the exact relation will depend on both the relative benefits of secretions to neighboring cells (Nadell et al., 2010) and the patterns of dispersal among different groups of cells (Rousset, 2004). Here, it is intended to illustrate only that genetic relatedness will tend to increase through the process of social insulation by other species.
Invasion Analysis
Analyses of relative fitness indicate which strains would be most likely to outnumber the other locally. The invasion analysis [based on that in Nadell et al. (2010)], on the other hand, is conducted to determine whether a rare mutant with a particular phenotype would survive in a metapopulation of cell groups where dispersal and colonization of new patches or hosts are common. We assume the existence of a very large number of
cell groups where the great majority of groups are of a single dominant genotype and only a small minority will contain the mutant. Each group is seeded at random from the population with a particular number of strains. We focus here on groups seeded by two strains of species 1. We also assume that all subpopulations have identical conditions regarding the presence of the second species.
Under these conditions, a strain 1x (rare mutant) can invade a metapopulation of strain 1y (majority resident) if the fitness of 1x in local competition with 1y is greater than the average fitness of the whole metapopulation, denoted <w1y> (Maynard Smith, 1982). The fitness w1y was computed in 40 replicates of the simulations as in previous analyses in this chapter (with 1:1 inoculation frequencies of the two cell types). Because the great majority of cell groups in the metapopulation consist purely of the majority strain 1y, <w1y> is approximated by the mean fitness of the majority strain, 1y, when growing on its own (or with species 2). To calculate <w1y>, the mean of w1y over 40 simulations is computed, where the cells of strain 1x inoculated initially are replaced with 1y cells (a total of 120 or 60 cells of strain 1y together with 0 or 60 cells of species 2 are inoculated in the single- or multispecies simulations, respectively). The invasion index of a rare mutant 1x into a metapopulation with majority strain 1y was calculated for each of the 40 replicates as follows:
![]()
Under the assumptions of our model, we conclude that 1x can invade in a population of 1y when the mean of l1x →1 1>1.
Statistical Analysis
All simulations were repeated in 40 independent replicates. Boxplots are used to illustrate the distribution (medians, upper and lower quartiles, and outliers) of the 40 values. Because some of the data did not follow a normal distribution, nonparametric statistical methods were used to compare medians (Mann-Whitney tests) and to detect correlations (Spearman’s rank correlation test). All statistical tests were conducted using Matlab.
ACKNOWLEDGMENTS
We thank Angus Buckling, Dan Cronforth, Laurent Keller, Wook Kim, Jan-Ulrich Kreft, Daniel Marbach, Carey Nadell, Nuno Oliveira, Jonas Schluter, and two anonymous reviewers for useful discussions and
comments on the manuscript. S.M. is supported by the Swiss National Science Foundation; J.B.X. by a seed grant from the Lucille Castori Center for Microbes, Inflammation, and Cancer; and K.R.F. by European Research Council Grant 242670.




























