Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter. Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.

Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.

OCR for page 25
3 Practices That Support Effective STEM Education T he schools that deliver effective STEM education clearly vary in significant ways, as Adam Gamoran observed. Even within the four primary categories there are marked differences, he noted, and research has not yet provided clear answers as to what makes different approaches work. Thus, it is important to look inside schools at the effects of particular practices and conditions that make them successful. This chapter explores the characteristics of effective science and mathematics instruction, respectively, and then discusses assessment approaches that support STEM instruction. The STEM fields are interrelated in important ways, and the whole may be greater than the sum of its parts. As one participant noted, math - ematics is the language of science, and engineering and technology are both integral to science. Nevertheless, the STEM fields are often treated separately, and science and mathematics are the subject of the most research. Following that research, the workshop and this report focus separately on science and mathematics. SCIENCE Richard Duschl described recent approaches focused on treating sci - ence in the classroom as a practice, and Okhee Lee discussed ways science education can reach traditionally underserved students. 25

OCR for page 25
26 SUCCESSFUL STEM EDUCATION Teaching Science as a Practice Richard Duschl noted that the volume of recent reports on the reform of science education demonstrates the attention now focused on the topic. Improving science education has become a “cultural imperative, ” essen - tial to the nation’s future as a prosperous and democratic state, he said, but he observed that there are several pedagogical challenges. Students are generally not motivated by the economic arguments at the heart of such reports as Rising Above the Gathering Storm (National Academy of Sciences, National Academy of Engineering, and Institute of Medicine, 2007) or Tough Choices or Tough Times (National Center on Education and the Economy, 2006). Reaching students and helping them to develop as science learners depends instead on instruction that is rich in core knowl- edge and the practices that are essential to science, such as argument and critique, modeling and representation, and ways in which knowledge is applied. And science is a broad subject, encompassing physics, chemistry, life sciences, and geographic and earth system sciences. Although these subjects all require many of the same tools and technologies, identifying the most important skills and knowledge that students should acquire is not easy. A recent report offered a vision of science in the context of K-12 edu- cation. Taking Science to School (National Research Council, 2007) describes science as a social phenomenon, in which a community of peers pursues shared objectives and abides by shared conventions that shape their work, Duschl said. Specifically, science involves practices in which students must learn to engage, such as: • building and refining theories and models, • collecting and analyzing data from observations or experiments, • constructing and critiquing arguments, and • using specialized ways of talking, writing, and representing phenomena. Science has evolved, Duschl observed. Not only have technologies become more sophisticated, conceptions of the essential nature of science have also changed. During the first part of the 20th century, Duschl sug - gested, the focus of science was to test hypotheses and use deductive rea - soning to learn from such experiments. Beginning in the 1960s, the focus shifted to the building and revision of theories. In the past two decades, scientists have grown more interested in building and revising models, which are logical representations of the relationships among phenomena that are observed—as opposed to theoretical explanatory frameworks. Regardless of such conceptual distinctions, science has yielded major achievements with both theoretical and practical importance—such as

OCR for page 25
27 PRACTICES THAT SUPPORT EFFECTIVE STEM EDUCATION the theory of relativity, the atomic theory of matter, or the germ theory of disease—as well as failures such as crystalline sphere astronomy or theories of spontaneous generation. Science education does not always fully address the extent of change in science knowledge and practice, and this is one of the reasons why there are ongoing tensions between the way science is conducted and the way science is taught, in Duschl’s view. As is noted in Taking Science to School, for example, argument is central to science but rare in classrooms. Teaching tends to focus on what students will need to recall, rather than on model-based reasoning about observed phenomena. The norms of the K-12 classroom, where answers are typically provided by teachers and textbooks, are at odds with the way scientists conduct their work, which entails painstakingly building scientific models from accumulating evi - dence. Curricula and standards that are incoherent and unfocused, and that vary from state to state, work against the logical development of understanding, he said. The demands of the marketplace lead commercial textbook and curriculum developers to focus on stand-alone modules that can be useful in a variety of contexts, rather than on coherent progressions of learning. Still drawing on Taking Science to School, Duschl stressed the impor- tance of teaching the practices of science and engaging students in the kinds of activities in which scientists engage. Doing so means allow- ing students to design and conduct empirical investigations, linking the investigations to the core knowledge students are developing, working from a curriculum that is linked to meaningful problems, and providing frequent opportunities for students to engage in logical arguments as they learn to build and refine explanations for their observations. Table 3-1 illustrates the relationships among the categories of empirical reasoning students need to develop, scientific practices, and the actions involved in those practices. Currently, science education does not reflect this approach, Duschl said. Taking Science to School found that current curricula and standards: • contain too many disconnected topics of equal priority, • use declarative “what we know” language that does not make clear what it means to understand and use knowledge, • tend to divorce science content from practices, and • are not sequenced in ways that reflect what is known about the cumulative development of children’s scientific understandings. In contrast, the report advocates a move to the use of learning progres - sions (National Research Council, 2007). Learning progressions are descriptions of the way students’ understanding in a particular discipline

OCR for page 25
28 SUCCESSFUL STEM EDUCATION TABLE 3-1 Relationships Among Categories of Empirical Reasoning, Scientific Practices, and Actions Categories for Empirical Reasoninga Scientific Practicesb Verbsb Planning, Selection of observation tools Presents, asks, responds, Designing Data and schedule, selection of discusses, revises, expands, Acquisition measurement tools and units challenges, critiques, knows, of measurement, selection of uses, interprets questions(s), understanding interrelationships among central science concepts, use central science concepts to build and critique arguments Data Collection Observing systematically, Examines, reviews, measuring accurately, evaluates, modifies, structuring data, setting generates standards for quality control, posing controls, forming conventions Evidence Use results of measurement Extends, refines, revises, (data use) and observation, generating decides, categorizes evidence, structuring evidence, construct and defend arguments, mastering conceptual understanding Patterns (modeled Presenting evidence; Represents, evaluates, evidence) mathematical modeling; predicts, discovers, evidence-based model building; interprets, manipulates, masters use of mathematical, builds, refines, analyzes, physical, and computational models tools Explanation Posing theories, conceptual- Builds, refines, represents, based models building, interacts search for core explanation, considering alternatives, understands how evidence and arguments based on evidence are generated, revises predictions and explanations, generates new and productive questions aDuschl, and Grandy, (Eds.) (2008). bMichaels, Shouse, and Schweingruber (2008). SOURCE: Duschl (2011). Reprinted with permission.

OCR for page 25
29 PRACTICES THAT SUPPORT EFFECTIVE STEM EDUCATION develops over time from naïve to sophisticated conceptual understanding (Corcoran, Mosher, and Rogat, 2009). Based on research in neuroscience and other fields that have illuminated many aspects of the way people learn (see National Research Council, 1999, 2001), learning progressions are developed through empirical research on conceptual development related to a specific topic, such as the carbon cycle. They describe goals for the understanding and knowledge that students could be expected to develop by a defined time (e.g., high school graduation), the sorts of misconceptions and naïve understandings students generally begin with, and the intermediate learning steps that lead to the goal of more complete understanding. Learning progressions are used to coordinate the teaching of knowl- edge and practices across grades and in the development of assessments that teachers can use to guide students’ learning and target their instruc - tion. Standards and curricula that are based in learning progressions support the effective instruction that develops students’ understanding of science as a practice. However, the concept of learning progressions is relatively new, Duschl explained, and it is not widely understood. There is a need for more research on students’ learning pathways in different domains or subjects, as well as research on ways to use learning progres- sions effectively in teaching. Reaching Diverse and Underserved Students Persistent achievement gaps between student groups are a particular concern in science education because of the increasing economic impor- tance of science and technology, Okhee Lee noted. She described research showing that the gaps in outcomes between “mainstream” students (those who are white, from middle- to high-income families, and are native speakers of standard English) and “nonmainstream” students (students of color, who are from low-income families, and who are learning English as a new language) reflect the different learning opportunities available to these groups (Lee, 2011). Thus, it is critical, she said, to start with the premise that high achievement in science is attainable for most children. To understand science outcomes for the nonmainstream groups, Lee said, it is important to consider not only standardized test scores, course taking, and school retention or dropout rates, but also these students’ opportunities to learn with understanding, to develop an identity as a science learner while also developing their own cultural and linguistic identity, and to develop a sense of agency in their education. Thus, she defined equitable learning environments as those in which (1) the expe - riences that all students bring from their homes and communities are valued, (2) their cultural and linguistic knowledge is integrated with

OCR for page 25
30 SUCCESSFUL STEM EDUCATION the disciplinary learning they face at school, and (3) there are sufficient educational resources to support learning. Given these conditions, she explained, nonmainstream students are capable of attaining outcomes comparable to those of their mainstream peers. Lee described three different perspectives on ways of providing equi - table science learning opportunities for nonmainstream students. It is important to consider theoretical approaches, she suggested, because they illuminate underlying mechanisms that apply to different aspects of schooling and different groups, and they also provide a basis for develop- ing strategies to address different challenges. Cognitive science provides the basis for one approach to understand - ing how best to promote science learning among students with varying backgrounds. For example, one group of researchers used case studies to explore the ways low-income students from African American, Haitian, and Latino backgrounds in both bilingual and monolingual classrooms engaged in reasoning, problem solving, inquiry, and argument (Rosebery, Warren, and Conant, 1992). The researchers found that the students brought alternative linguistic, conceptual, and imaginative resources to their classrooms but were able to integrate these resources with standard scientific practices. Questioning, argumentation, and innovative uses of everyday words to construct meaning are all practices common in these nonmainstream cultures and also in the practice of science. For example, one aspect of a Haitian oral tradition called bay odyans is animated argu- ment about observed phenomena, and teachers can use it to engage their students in scientific discourse in English. The implication of this cognitive perspective for instruction, Lee observed, is that “when teachers identify and incorporate students’ cul - tural and linguistic experiences as intellectual resources for science learn - ing, they provide opportunities for students to learn to use language, think, and act as members of a science learning community.” Other researchers have explored the ways in which nonmainstream students’ cultural traditions may be at odds with Western science as it is practiced and taught, and Lee called this the cross-cultural perspec - tive because it is grounded in the literature on multicultural education. These researchers have examined varying world views and culturally specific patterns of communication and interaction (see, e.g., Snively and Corsiglia, 2001). For example, research on Yup’ik children in Alaska has shown that they learn science-related skills by engaging in activities (such as fishing or navigating by the stars) with adults that build their knowl - edge over time. In their schools, however, learning is organized around short and frequent lessons in which students are expected to listen, fol- low directions, and respond quickly to questions verbally and in writing. Though many of the children’s scientific ideas may be in harmony with

OCR for page 25
31 PRACTICES THAT SUPPORT EFFECTIVE STEM EDUCATION Western traditions, they need explicit guidance in the “rules of the game,” Lee explained. They need to learn to negotiate the boundaries between their own cultural traditions and the expectations of school science, which is described in the literature as “cultural border crossing.” When students have this opportunity, she said, they can achieve academically while maintaining their cultural and linguistic identities. The sociopolitical perspective, which is grounded in critical theory on issues of power, prestige, and privilege, provides another way of think- ing about nonmainstream students’ and science learning. Researchers working in this tradition, Lee explained, question the value of science as it is currently taught for students who have traditionally been poorly served by the school system (e.g., Calabrese-Barton, 1998; Rodriguez and Berryman, 2002; Seiler, Tobin, and Sokolic, 2001). They suggest that instead of bringing students’ world views more in line with science teach- ers might reconceptualize science to to be more relevant to members of non-mainstream groups. Studies in this tradition focus on settings in which teachers allow students to take the lead in formulating questions, planning activities, and documenting their explorations. The role of teachers, Lee explained, is to build trust with their students so they are viewed as allies, and the teaching environment is intended to foster the students’ cultural identities and sense of agency. Studies of informal science learning, in particular, she noted, suggest that students perform at high levels when they see science as personally meaningful and relevant to their current and future lives, and when they are able to actively engage in it. This research sug - gests that the mistrust that nonmainstream students bring to the typical classroom is a formidable challenge for their science learning, and that science teachers “must learn to take into account the historical, social, and cultural environments in which their students live,” Lee said. Lee noted that each of these perspectives stresses that finding connec- tions between students’ cultural and linguistic experiences and scientific practices is a key to developing equitable learning opportunities. At the same time, they point to a variety of instructional approaches to meeting the learning needs of nonmainstream students. First, teachers need to identify areas in which scientific practices are congruent with students’ everyday knowledge and build on them, as the cognitive perspective suggests. Second, teachers need to make the norms and practices of sci - ence explicit for students, especially when those norms are at odds with students’ experiences, as the cross-cultural perspective suggests. And, third, teachers need to build trusting and caring relationships with their students and engage with them in critical analysis of the purposes of schooling and of science, as the sociopolitical perspective suggests. Per-

OCR for page 25
32 SUCCESSFUL STEM EDUCATION haps most important, Lee said, is that “a one-size-fits-all instructional approach will surely fail.” MATHEMATICS The findings from the mathematics literature are similar to those for science, as Jere Confrey and Na’ila Suad Nasir discussed. Engineering for Effectiveness Calls to improve schools often focus on the search for “what works,” Jere Confrey noted, but a more useful question would be “what works, for whom, and under what conditions?” (Bryk, Gomez, and Grunow, 2011; Means and Penuel, 2005). Many researchers point out that broad scientific principles or guidelines about educational practice are of limited value because the precise conditions in which instruction takes place, the resources available, and other factors have a critical influence on results. Thus, in Confrey’s view, a better approach is “engineering for effective - ness,” where communities of practitioners and researchers conduct ongo- ing experiments in a particular context to collect real-time data and use it to tailor improvements, just as engineers might do in an industrial setting. A number of scholars have suggested variations on this approach, and from their work Confrey has developed an approach to the search for effectiveness that has four elements (Confrey and Maloney, 2011, p. 4): 1. Education must be viewed as a complex system with interlocking parts. 2. Bands and pockets of variability are expected, examined for causes and correlates, and used as sources of insight, rather than adjusted for, suppressed, or controlled. 3. Causal or covarying cycles with feedback and interaction are critical elements of educational systems, in which learning is a fundamental process. 4. Education should be treated as an organizational system that seeks, and is expected, to improve continuously. Confrey discussed the results from three recent studies of the effec- tiveness of curricula to illustrate the research approach she advocates. The first was a comparison of the effects of two mathematics curricula for high school students (Grouws et al., 2010). The researchers used a quasi- experimental design in which participants were matched according to their achievement prior to the study to examine and compare the imple- mentation of an integrated mathematics curriculum and a traditional

OCR for page 25
33 PRACTICES THAT SUPPORT EFFECTIVE STEM EDUCATION curriculum that treated mathematics subjects (e.g., algebra and geometry) in sequence. The study was conducted in 11 high schools in 6 districts around the country. The populations in the schools ranged from 19 to 23 percent eligible for free or reduced-price lunches. Participating students chose freely between the parallel courses (rather than being tracked) and were evaluated using three outcome measures: two assessments devel - oped for the study—one a test of content common to both curricula, based on a content analysis of the two curricula, and one of reasoning and problem solving. Researchers used multiple data sources—pertaining to factors such as professional development, familiarity with standards, distribution of classroom time among lesson development, noninstruc- tion, practice, and closure—to develop understanding of the relationship of student outcomes to teachers’ implementation of the curricula (see Confrey and Maloney, 2011). The researchers found that, on average, the teachers of the integrated curriculum covered 61 percent of the intended material, and teachers of the single-subject curriculum covered 76 percent. In both courses, teach- ers also augmented many of the lessons with supplemental material: 28 percent of the integrated course teachers and 33 percent of the single- subject course teachers did so. And what is critical, Confrey said, is not the intended curriculum, but what was actually taught. Thus, to assess this outcome, one needs to look at what was learned. The preliminary results indicate that the students in the integrated mathematics course made larger gains than the students in the tradi - tional course did, and that having greater opportunity to learn was sig - nificantly correlated with high performance. The researchers identified seven factors that influenced the impact of these curricula: • classroom environment (e.g., the degree of focus on mathematics reasoning and other mathematical thinking); • fidelity of implementation (e.g., how much of the curriculum was taught); • use of technology and collaborative learning; • opportunity to learn; • teachers’ knowledge of the classroom learning environment; • teachers’ experience; and • teachers’ professional development. Another study compared the results of four different curricula for 1st and 2nd grades (Agodini et al., 2010): “Investigations in Number, Data, and Space,” which was categorized as student centered; “Math Expressions,” which was categorized as a blend of student and teacher centered; “Saxon Math,” which was described as scripted; and the Scott

OCR for page 25
34 SUCCESSFUL STEM EDUCATION Foresman-Addison Wesley Mathematics, which is a basal textbook. This study also explored the influence of school and teacher characteristics on the implementation of mathematics curricula. The researchers looked at 109 1st grade classes and 70 2nd grade classes in disadvantaged schools that were randomly assigned to one of four curricula. Confrey noted that the study had an extremely low response rate— just 12 of 473 districts agreed to participate—so it is important to con - sider whether willingness to participate may be associated with other characteristics that might have an important influence on outcomes. Student results were measured using the Early Childhood Longitudinal Study Measure. The researchers found the highest scores for the students exposed to “Math Expressions” and “Saxon Math.” Confrey noted that teachers using “Math Expressions” received more professional devel - opment than did teachers using the other curricula, and those teachers also provided more supplements to the curriculum. “Saxon Math” was taught 1 more hour per week than the other curricula. Confrey also noted that both of these curricula were already familiar to the teachers when the study began. The researchers were careful in defining the elements of adherence to instructional practices consistent with the curriculum developers’ inten - tions, analyzing textbooks and interviewing publishers to make sure what was intended, and then surveying and interviewing teachers to understand what they actually did. Nevertheless, Confrey pointed out, with this study it is difficult to say whether the differences were related to the nature of the curricula or to the specific ways in which they were implemented. Although researchers work hard to maximize the internal validity of such studies, Confrey noted that practitioners will focus not on how results can be generalized but on how the approach might work in their own context. The third study compared the quality of the implementation of two reform-oriented curricula for grades K-5 in two districts (Stein and Kaufman, 2010). These researchers conducted more than 300 observations (on 3 consecutive days each in the fall and the spring) and were able to cover each of the six grades. They specifically hoped to explore the effects of aspects of high-quality implementation, such as ensuring that instruc - tion places a high-cognitive demand on students, drawing on students’ own thinking, and giving the students authority to find solutions. The researchers supplemented the observations with surveys and interviews. They found that teachers using the Investigations curriculum tended to maintain the cognitive demands better, have more emphasis on student thinking, and establish higher classroom norms. In contrast, teachers who used Everyday Math reported that frequent shifts of topic in that spiraling curriculum made it more difficult to identify and link the major mathematical concepts they wanted to build.

OCR for page 25
35 PRACTICES THAT SUPPORT EFFECTIVE STEM EDUCATION The study shows that implementation quality cannot be inferred only from content topic analysis but depends also on how the tasks are struc- tured, and appears to relate to the extent of professional development support, facilitated by the district and afforded by the materials, more than to teachers’ education, experience, and mathematical knowledge of teaching. The extent to which teachers use the materials to look for “big ideas” correlated with implementation quality across both curricula. Each of these studies has limitations, Confrey observed, and they do not necessarily support cause-and-effect conclusions. They provide com - plex results about complex systems, and highlight some critical points. It is very important to be clear about what outcomes the measures are cap- turing and what factors influence implementation in a particular context before drawing conclusions about a curriculum. Teachers’ capacities and the professional development they receive are critical, Confrey concluded. These are among the elements that define what she called the “instructional core”: “If we don’t have an effect on the instructional core, we are not going to improve instruction in math and science,” she added. Thus, her focus is on helping school systems design the technological capability to gather the information they need and analyze it to support continuous improvement. Noting the important opportunity that states’ adoption of the Common Core standards has pro- vided, she closed with a set of specific steps that would constitute a plan for “engineering for effectiveness”: • Construct databases of assessment items linked to the Common Core state standards that can support fair tests of what students are taught. • Use content analysis to analyze alignment of curricula. • Build a data system to monitor how curricula are implemented, the ways teachers supplement them, and their reasons for supple- menting them. • Collect data on curricular implementation factors. • Interconnect the data categories and outcome measures with demographic data for students, classrooms, schools, and districts, and with teacher demographic and survey data. • Collect teacher demographic and survey data. • Conduct valid classroom observations and triangulate those data with teacher self-reports. • Form “networked improvement communities” (see Bryk et al., 2011). • Define tractable problems. • Implement continuous improvement models.

OCR for page 25
36 SUCCESSFUL STEM EDUCATION Reaching Diverse and Underserved Students As with science, researchers have explored the mathematics learning of students from nonmainstream groups, including low-income, African American, and Latino students and those with limited English proficiency. Na’ilah Suad Nasir described some of this work (Nasir et al., 2011). She focused on the factors that open up or narrow learning pathways for students, looking particularly at research on the ways schools and society tend to structure lower-quality academic experiences for nonmainstream students. She noted that the majority of the research focuses on students of color and English learners and that the research base is very uneven. Nasir began by reminding participants of persistent disparities in mathematics achievement. Among 8th graders, for example, just 9 percent of African American and 13 percent of Latino students score at the pro- ficient level, compared with 39 percent of white students. This disparity may be partly explained by the fact that 47 percent of African American students and 49 percent of Latino students complete pre-algebra classes by grade 8, compared with 68 percent of white students. Black and Latino students are also severely underrepresented in honors and advanced placement courses, she added, and there are similar disparities for low- income students. The situation for English language learners is simi- lar, and they are frequently blocked from advanced mathematics tracks because of their lack of English language skills. Not only are these gaps large, Nasir added, they actually, in many cases, widened in the early 1990s, after a period of narrowing in the 1970s and 1980s. Nasir argued that there are political, economic, and social forces that tend to restrict opportunities for nonmainstream groups and thus to perpetuate the gaps. Schools that serve low-income and minority students tend to have fewer resources, in terms of well-prepared teachers, buildings, supplies, technology, and course offerings. Tracking systems that shuttle black, Latino, and less affluent students into less rigorous edu- cational experiences are both pervasive and rigid. “It is very difficult to jump tracks, Nasir noted, “especially as students move into high school.” Discipline systems also tend to disproportionately penalize male black and Latino students, she said, which affects their academic experiences. Lack of access to a high-quality curriculum and to advanced courses contributes specifically to the achievement gap in mathematics. Class - rooms that serve low-income and minority students are much more likely to focus on basics and emphasize instruction that focuses on repetition, practice, and mastering basic arithmetic, Nasir reported from her reading of the research. These conditions have been exacerbated by the recent focus on high-stakes testing, as districts serving nonmainstream students often follow curriculum and instructional practices that have been charac- terized as teaching to the test in an attempt to increase student scores on

OCR for page 25
37 PRACTICES THAT SUPPORT EFFECTIVE STEM EDUCATION state-mandated assessments. As a consequence, the students are provided with fewer opportunities to engage with complex mathematical ideas. Students with limited English proficiency may be compelled to repeat material they have already learned when they are placed in low-track classes because of their language skills. In addition, because English language learners often switch into their dominant language to engage with higher-level mathematics content, studying only in English before they are fluent may obstruct their access to rich mathematical content. Nasir’s own and other research also suggests that students’ mathematics learning is also influenced by positive and negative stereotypes and role models, which shape their expectations about who is likely to succeed in mathematics. The small body of research that compares more and less successful strategies for teaching mathematics to nonmainstream groups highlights two points, Nasir added. The first is that a high-quality curriculum that presents cognitively demanding tasks and builds conceptual understand- ing and reasoning skills helps students build their skills and become “facile with multiple mathematical representations and multiple solution strategies.” Second, classroom practices that foster student-centered dis - course and free exploration of mathematical ideas, while addressing mul- tiple kinds of abilities, also help marginalized students learn. “Teachers in successful classrooms find ways to disrupt traditional notions of math- ematical competence, such as speed,” Nasir explained, “and find ways to assign competence to students who have in the past been unsuccessful in mathematics—for example, by pointing out that particular students ask really good questions.” Additional descriptive research also suggests the importance of approaches in which teachers connect to students’ cultural and social backgrounds and focus on building strong relationships with students. This work indicates that when mathematics teachers view equity as a shared mission and work together to “disrupt” the achievement gaps, Nasir said, they are more likely to be successful than when they work on their own. Nasir used a case study of a California high school she called Railside (to protect students’ and faculty members’ privacy) that has developed very successful equity practices to illustrate some of the main points she found in the literature. Railside is a large, urban, comprehensive high school with a large nonmainstream student population: it is 80 percent nonwhite, 25 percent of the students are English language learners, and 30 percent qualify for free or reduced-price lunches. In the late 1990s, Railside abandoned tracking in mathematics. All incoming 9th graders were given the same algebra course, and the school adopted what the staff called a “multi-ability” curriculum, in which

OCR for page 25
38 SUCCESSFUL STEM EDUCATION TABLE 3-2 Results for Railside School and Two Comparison Schools (in percentage) Comparison Result or Factor Railside Schools Students scoring “basic” or better on 49 41 California Standards Test* Seniors in advanced mathematics classes 41 27 (calculus and precalculus) Students who “like mathematics” 74 54 Students interested in mathematics-related careers 39 5 *For information about the California Standards Test, see California Department of Educa- tion (2011). SOURCE: Nasir et al. (2011), data from Boaler and Staples (2008). Reprinted with permission. instruction in a single classroom could develop a range of mathematical skills. Interviews with Railside teachers showed that they see mathemat - ics teaching as a complex system, Nasir explained: “They work in iterative ways with one another to solve the teaching problems that come up in their classroom. It is not a static approach, but rather a fluid approach [in which] they adapt to the students that are in their classrooms.” Table 3-2 shows data from a study comparing Railside with two other schools in the same Northern California city, indicating that Railside performed well in a variety of outcomes measures (Boaler and Staples, 2008). The study also showed that gender- and race-based achievement gaps were eliminated by students’ senior year. Unfortunately, however, Nasir reported, the Railside mathematics department has recently been under pressure from the district to raise standardized test scores and to use textbooks as the core of their instruc - tion. This pressure has coincided with a district mandate to move from a block schedule, which allowed 90-minute periods, to a schedule with seven 45-minute periods every day and an increase in class sizes (the result of budget cuts in the district). Railside teachers had actually written their own textbook, Nasir explained, and had a system of continuing to rewrite and rework their assignments and activities to make them better, so this was a very frustrating period for them. At the end of the 2009-2010 school year, several of the teacher leaders and former math department heads left Railside because they believed they could no longer sustain their equity practices, Nasir reported: “The remaining teachers feel hope - less about their ability to continue to do the work that they have done together as a department for over 20 years. They say they are just biding time until retirement.” Despite the sobering situation at Railside, Nasir remains optimis-

OCR for page 25
39 PRACTICES THAT SUPPORT EFFECTIVE STEM EDUCATION tic about the potential for schools in which reducing achievement gaps becomes a collective focus for the staff. Yet, she conceded, the research base is not yet sufficient. Studies comparing outcomes for different instructional approaches are needed, as are longitudinal studies that can link classroom practices to equity outcomes. Also important, in her view, will be the development of improved learning measures that can better capture the most important knowledge and skills that students should acquire. ASSESSMENT Assessment can have a powerful influence on instruction, for good or ill. James Minstrell described an approach to formative assessment, building on learner thinking (BOLT), that treats assessment and instruc- tion as two facets of a single enterprise (Minstrell, Anderson, and Li, 2011). Formative assessment, he noted, has been defined as “a process used by teachers and students during instruction that provides feedback to adjust ongoing teaching and learning to improve students’ achieve - ment of intended instructional outcomes” (Council of Chief State School Officers, 2008). There are a variety of ways to do formative assessment, however, and Minstrell explained that BOLT is based on research on learning and cognition (see, e.g., National Research Council, 1999, 2001). A major finding from this literature is that students bring many kinds of preconceptions to the classroom that affect the way they think about new learning experiences. If instruction does not address the preconceptions that are problematic, students tend to leave the class with those precon - ceptions intact (National Research Council, 1999). Students also often struggle to transfer what they learn in school to real-world situations, a sign of the limits of their understanding. Research has shown, however, Minstrell explained, that student per- formance improves when the teachers and the curriculum purposefully elicit students’ thinking about the topic of instruction and address pos- sible misconceptions. Formative assessment is the key to doing so, but there are better and worse ways of using it. Sometimes, Minstrell and his colleagues have found, the focus is on the teacher, on what has been taught, and simply on whether the students “got it” or did not. The results are used to assess the quantity and pace of planned instruction and decide whether the teacher should go on or reteach. More effective, Minstrell said, but less frequently done, is using formative assessment to find out what understandings, including misconceptions or incomplete knowledge, students have, and then to adjust instruction to promote deeper understanding. The BOLT framework, which has several components, takes this sec-

OCR for page 25
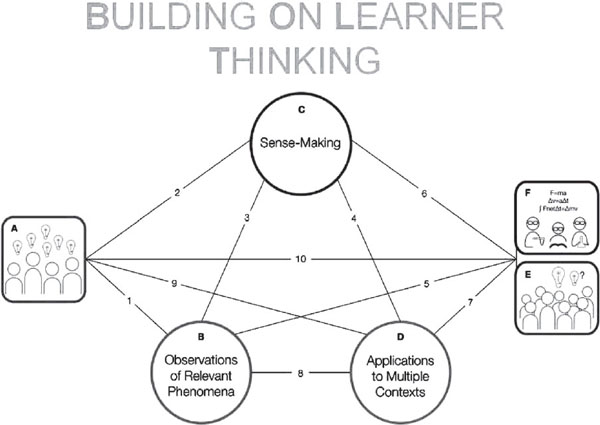
40 SUCCESSFUL STEM EDUCATION FIGURE 3-1 BOLT: An approach that uses formative assessment to drive instruction. SOURCE: Minstrell, Anderson, and Li (2011, p. 4). Reprinted with permission. ond approach: see Figure 3-1. Box A represents the students’ ideas prior to instruction on a topic, and boxes E and F represent, respectively, the consensus understanding that a successful class will collectively reach as the students attempt to understand a segment of their curriculum, and the formal ideas of professional scientists. Circle B represents the expe - riences students have as they learn, which may include observations, tasks, or experiments. Circle C represents another aspect of learning, which Minstrell calls sense-making. Simply doing hands-on activities, he explained, is not sufficient. Students must also mentally process their observations and findings, develop inferences about their meaning, and construct explanations. Finally, circle D represents the many other con - texts and representations that promote generalization and the transfer of ideas they produced through the learning experiences, for example, by exploring other hypotheses that may explain the phenomena they have observed. The lines connecting the circles and boxes represent the ways in which instruction develops the connections among these elements. For example, when a teacher has a clear understanding of the ideas students bring to the topic, he or she can choose or adapt activities and learning opportuni - ties that address those student ideas as well as the learning goals. Each

OCR for page 25
41 PRACTICES THAT SUPPORT EFFECTIVE STEM EDUCATION of these connections provides opportunities for “on-the-fly assessment,” he explained, using questions such as “how do you know?” or “how can you support that idea?” In contrast to this conceptual approach, however, many typical classroom activities follow a pattern in which the teacher skips students’ ideas and presents scientists’ ideas, following up with assignments to see whether students have gained procedural and factual knowledge. The activities may be problem sets or lab work in which students are guided to apply the ideas that have been presented and see them in action: these approaches do not typically get students thinking about how the knowledge in question was generated or come up with ideas of their own about how to solve a problem or explain phenomena. BOLT, instead, focuses on the process of “coming to know” science ideas, Minstrell explained, and the development of the classroom as a “community of science learning.” As a class works together to develop consensus in their understanding of the material they are studying, they operate as scientists do. In doing so, they take responsibility for their own learning. The teacher uses formative assessment to identify strengths on which to build and problem areas to address. Diagnostic assessments can be based on “facet clusters,” which are a framework for organizing the research on student knowledge and typical misconceptions: see Box 3-1. Facet clusters are derived from standards documents but they also draw 3-16 BOX 3-1 BOX 3-1 FACET Cluster—Forces as Interactions FACET Cluster—Forces as Interactions SOURCE: Minstrell (2011, slide 9). Reprinted with permission from FACET Innovations. Minstrell (2011). Reprinted with permission. SOURCE:

OCR for page 25
42 SUCCESSFUL STEM EDUCATION on research on problematic student conceptions to describe in detail both explicit learning goals and also difficulties in reasoning and understand - ing that students are likely to encounter as they progress toward scientifi - cally accurate understanding of the material. Minstrell acknowledged how difficult it can be for teachers to adopt this approach, noting that one teacher with whom he has worked for many years had explained: “[Y]ou are thinking on your feet constantly. It is draining because you become so intensely involved with your stu- dents.” Moreover, Minstrell added, “the devil is in the details.” Teachers need support not only in how to collect the formative data, but also in how to use it. In response to concerns about how to take the successes the program has had with small groups of teachers to a larger scale, Minstrell added, he and his colleagues have developed a web-based program, called Diagnoser Instructional Tools, which provides learning goals, ques- tions designed to elicit student thinking, developmental lessons, and tools for reporting data to students and teachers students. All the tools are based on the research-based facet clusters.1 There is also a need for much more research to support the develop- ment of such tools as the facet clusters, Minstrell explained. Much of the existing research on formative assessment has focused on the area of literacy. To reflect the practices of science, research in other kinds of skills will be needed. Moreover, relatively little has been done to explore the ways that formative assessments, such as the BOLT approach, can be used to elicit the cultural influences and perspectives that previous speakers discussed. 1 See http://www.diagnoser.com/diagnoser/ [July 2011].