Problem Solving, Spatial Thinking,
and the Use of Representations
in Science and Engineering
Chapter 4 explored students’ conceptual understanding in science and engineering, with the goal of helping students advance toward a more expert-like understanding. This chapter addresses how students use those understandings to solve problems, and how scientific representations, such as pictures, diagrams, graphs, maps, models, and simulations facilitate or impede students’ problem solving and understanding of science and engineering. Although we recognize that there are other important dimensions to promoting a deep understanding of science and engineering—including strong mathematical knowledge—we start with these topics because they are vital to acquiring greater expertise in the disciplines, and discipline-based education research (DBER) on them is relatively extensive and robust.
The discussion of each topic in this chapter begins with an introduction of that topic and its importance to undergraduate science and engineering education. Following these introductions, we provide an overview that summarizes the focus of DBER on the topic, the theoretical frames in which DBER is grounded, and the typical methods used. We then discuss the research from each discipline and summarize key findings across disciplines. The discussion of each topic concludes with an identification of directions for future research.
Problem solving may be the quintessential expression of human thinking. It is required whenever there is a goal to reach and attainment of that goal is not possible either by direct action or by retrieving a sequence of
previously learned steps from memory (Bassok and Novick, 2012; Martinez, 2010). That is, during problem solving the path to the intended goal is uncertain. This characterization describes much of what people do on a daily basis, from (a) mundane activities like deciding what to cook for dinner given the ingredients at hand or how to get from work to home given certain street closures, to (b) student activities such as interpreting laboratory results, figuring out how to organize a term paper on evidence for speciation, or designing a roller coaster for an engineering class, to (c) professional work such as curing illnesses or determining the best way to structure a class so that students will understand a key concept. Clearly, problem solving is central to science and engineering as well to everyday life.
Researchers in numerous disciplines have drawn a distinction between well-defined and ill-defined problems (Hsu et al., 2004; Reitman, 1965). Most of the problems students encounter in their science and engineering classes are well-defined, such as a mechanics word problem. In these problems, the initial conditions, the goal, the means for generating and evaluating the solution, and the constraints on the solution are all clearly specified for students. For other types of problems, however, such as a more open-ended laboratory or an authentic design problem in engineering, students have to define one or more of the problem components on their own (Fay et al., 2007; Whitson, Bretz, and Towns, 2008). In a laboratory, the means of generating the solution may be ill-defined. For an engineering problem, the goal may be ill-defined; as a result, it may not be clear how to determine whether the goal has been accomplished. For example, what constitutes a better coffee cup, and how does one decide that a new cup design represents a big enough improvement over the status quo to declare the design finished?
Society’s most important problems are usually ill-defined in some way. Consider two examples: (1) How can the rapid regrowth of human skin be promoted so that life-threatening infections in burn patients are prevented? (2) How can affordable, alternative energy to power cars be generated, thereby limiting reliance on fossil fuels? These are the kinds of problems students will have to solve after they graduate. Students who have scant experience with ill-defined problems during their undergraduate education may be poorly prepared to grapple with the most significant problems in their fields.
This discussion of problem solving is structured around important findings from DBER that are consistent with prominent themes from the cognitive science literature, namely problem representation and the nature of the solution process. In the cases for which the findings apply to only a small number of problem domains or disciplines, their broader applicability to problem solving within the disciplines of interest here is an open question. For example, as the following discussion will show, research has shown that
experts adopt a working forward strategy in certain situations (e.g., solving introductory mechanics problems from physics). That strategy may reflect the nature of the particular problem-solving tasks that have been investigated; other problems, from the same or other disciplines, may require different strategies or approaches for successful and/or efficient solution.
Where findings have been replicated in numerous disciplines within and outside the sciences, it is probably safe to presume that those findings generalize to new problem domains or disciplines yet to be investigated. A prime candidate for such a finding is the differential reliance of experts and novices on structural versus superficial features of problems, respectively.
A potential complication of generalizing from cognitive science research relates to the research setting and nature of the problems studied. DBER is typically conducted in classroom settings with discipline-specific problems, whereas much of the cognitive science research—especially early in that field’s history—has been conducted in laboratory settings with puzzle problems or brain teasers. However, cognitive science research on problem solving in more ecologically valid settings and in domains such as physics and mathematics has often yielded comparable results to studies of puzzle problems (Bassok and Novick, 2012). What changes from one problem to another in these situations is the specific knowledge students need to bring to bear on their solution attempts, rather than the underlying cognitive processes. This general pattern of consistent results across disparate types of problems lends support to the committee’s view that findings from cognitive science research on problem solving may be applicable in undergraduate science and engineering domains in which they have not yet been investigated. After all, humans have a single cognitive system, with specific operating parameters and constraints, that underlies their learning and problem solving regardless of the problem or discipline under investigation (Simon, 1978). At the same time, domain knowledge, which the general processes take as input, is important as well. In the inevitable cases where different patterns of results are found across problems or disciplines, these patterns will point to specific areas of science learning where disciplinary knowledge and perspectives are especially critical.
Overview of Discipline-Based Education
Research on Problem Solving
Problem solving is a significant focus of DBER in physics (see Docktor and Mestre, 2011, for a review), chemistry (for reviews, see Bodner and Herron, 2002; Gabel and Bunce, 1994), and engineering (see Svinicki, 2011, for a review), and an emerging area of study in biology and the geosciences. Because problem solving is not taught frequently enough in astronomy, the committee did not find peer-reviewed astronomy education
research on problem solving. As a result, this discussion does not include astronomy.
A significant body of research on problem solving also exists in cognitive science, and that research overlaps considerably with DBER. Cognitive science research corroborates some DBER findings, can help to explain or extend others, serves as the theoretical basis for some studies, and provides potential building blocks for future DBER on problem solving (Bassok and Novick, 2012). Because of these linkages, this section interweaves discussions of DBER and cognitive science.
Research Focus
DBER studies on problem solving range from investigations of general problem solving strategies, to behavioral differences between novices and experts, to measurements of the effectiveness of instructional strategies that teach problem solving. Most of these studies investigate how students solve quantitative, well-defined problems. Accordingly, unless otherwise noted, the bulk of the discussion in this chapter refers to well-defined problems.
The rich research base on problem solving in physics builds on many studies in cognitive science dating back more than 50 years. Many of these studies are based on the information-processing approach to understanding thinking, which comes from cognitive psychology (e.g., Simon, 1978). Key ideas from this framework include a step-by-step approach to problem solving, the importance of both internal knowledge representations and processes for understanding human thinking, the role of prior knowledge (which supports analogical transfer of knowledge gained from previously solved problems to solve new problems), and a limited capacity processing system.
In chemistry, the study of problem solving is muddied by disagreements over what constitutes a problem (Bodner, 2004). These debates notwithstanding, a large group of studies has examined problem solving strategies in a specific content area of chemistry, such as stoichiometry or equilibrium. Studies on these topics have used several models of problem solving as a framework for inquiry, including the Pólya model (1945)—originally developed in the context of mathematics—of understanding the problem, devising and carrying out a plan, and checking work; Wheatley’s (1984) model of the steps successful problems solvers take to solve novel problems in mathematics; and the expert novice paradigm described in this chapter. More recently, chemistry education research studies have drawn on knowledge space theory, which describes possible states of knowledge (Taagapera and Noori, 2000) and the ACT-R theory for understanding human cognition (Taatgen and Anderson, 2008).
Most research on student learning outcomes in engineering focuses on problem solving and engineering design (ABET accrediting criteria C and D; see Chapter 3). Early studies on this topic drew on information processing theory (Simon, 1978). More recent studies are grounded in constructivist (Piaget, 1978) or, less commonly, socioconstructivist (Lave and Wenger, 1991; Resnick, 1991) theories of learning.
Research on problem solving in biology and the geosciences is sparse. The six biology studies that the committee reviewed examined individual differences in problem-solving strategies and did not explicitly situate themselves in broader learning theory. In the geosciences, one emerging line of research draws on the cognitive science field of naturalistic decision making (Klein et al., 1993; Marshall, 1995) to investigate student problem solving in the field setting using global positioning satellites.
Methods
DBER scholars use a wide variety of qualitative and quantitative methods to study problem solving. Some data are gathered using think-aloud interviews, in which students are asked to solve problems and verbalize their thoughts while being video and/or audio taped.1 Many studies comparing expert and novice problem solvers have used categorization tasks, which require participants to group problems based on the similarity of the solution method. Other methods of tracking student problem-solving strategies include computer systems that use knowledge space theory (Taagepera and Noori, 2000), and artificial neural networks and Hidden Markov Models (Cooper et al., 2008).
Some studies use student-generated summaries of their problem-solving approaches, course exam scores, and final grades to measure proficiency with problem solving, rather than examining problem solving processes. In physics, students’ written solutions to problems that have been designed by the researcher(s) and/or adapted from existing problem sources such as textbook end-of-chapter problems are another common data source. These data are typically analyzed by scoring students’ solutions relative to rubrics that characterize expert problem solving.
Study populations range from high school students to community college students to graduate students, with the preponderance of studies focusing on students enrolled in introductory college courses. Sample sizes in these studies range from fewer than 20 to several hundred students. The research typically is conducted in classroom settings—although in physics, this research also involves students both in research settings.
__________________
1Ericsson and Simon (1980, 1993) have provided important theoretical and practical guidance for collecting and interpreting think-aloud protocols.
Many DBER studies of problem solving have compared undergraduate students (novices) to more expert problem solvers such as graduate students, faculty, or professionals outside academia (e.g., Larkin et al., 1980; Petcovic, Libarkin, and Baker, 2009). Similarly, a major focus of cognitive science research on problem solving has been to compare the performance of novices (usually, although not always, college students) with that of experts. The definition of expert varies across studies, ranging from graduate students in an academic discipline such as physics, to grandmaster chess players or practicing physicians with 20 years of experience in their field. In cognitive science research, the typical study has used an extreme groups design, comparing a group of novices to a single group of (relative) experts. Fewer studies have compared problem solving across multiple levels of expertise. Regardless of the number of groups included, these studies provide important information for discipline-based education researchers because they give insight into the nature of the transition that needs to occur and the goal toward which students should strive (Lajoie, 2003).
As discussed in Chapter 4, the committee recognizes that students are not expected to become experts within a single class, or even across the four years of their undergraduate education. They are, however, expected to progress along the path of increasing expertise. Thus, our frame of reference for this discussion is focused on helping students move toward the more expert end of the continuum.
The Nature of the Solution Process
A problem representation is an internal (i.e., existing in memory) or external (e.g., drawn on paper) model of the problem that is constructed by the solver to summarize his or her understanding of the problem. Ideally, this model includes information about the objects or elements in the problem, their interrelations, the goal, the types of operations that can be performed on the elements (e.g., algebraic operations for certain types of problems), and any constraints on the solution process. A student’s representation of the problem at hand is critical because the representation constructed affects the types of operations that can be applied (i.e., the steps that can be taken) to solve the problem (see “The Role of Visualization and Representation in Conceptual Understanding and Problem Solving” in this chapter).
According to a review of cognitive science research (Bassok and Novick, 2012), for some problems, getting the right representation is the key to solving the problem, or at least to solving it in a straightforward manner. Although problem representation is especially important for ill-defined problems, it can also be critical for solving well-defined problems. For other problems, determining the best representation is a relatively straightforward process,
and the primary work is to discover a (or the best) path connecting the situation as presented to the goal state. Representation and step-by-step solution are interactive processes, however, and both are important in most cases of problem solving. As noted, the solver’s representation of the problem guides the process of generating a possible solution. The step-by-step solution process, in turn, may change the solver’s representation of the problem, leading to corresponding changes in the solution method attempted. This iterative process of representation and step-by-step solution continues until the problem is solved or the solver abandons the goal.
One difference between relative experts and novices concerns how they allocate their problem solving time between creating a representation and working to find a solution. In some disciplines, experts spend relatively more of their time on understanding the problem, that is, on analyzing the structure of the problem, developing a coherent representation of the problem, and enriching that representation with relevant information retrieved from long-term memory (Simon and Simon, 1978; Voss, et al., 1983). Because experts construct better developed representations and have stored in memory effective procedures for responding in the face of familiar patterns (Gobet and Simon, 1996), they have been found to adopt a working-forward strategy for solving certain problems. Thus, in certain cases experts proceed from the information given, to inferences based on that information, to further inferences, and so on until the goal is reached. Novices, in contrast, often proceed backward from the goal to an equation to calculate that goal, to a second equation to calculate an unknown quantity in the first equation, etc., until an equation is found for which all the quantities needed are part of the given information of the problem. Such a difference between experts and novices has been observed repeatedly in physics, and one small-scale study involving genetics problems in biology adds to the support for this emerging consensus (Smith and Good, 1984).
Students’ working backward strategy (referred to as a means-ends analysis in the cognitive science literature), although often effective for solving problems, places a heavy load on working memory, leaving little capacity for learning more general information from the solution attempt, such as a general schema for solving such problems. Working memory refers to the information processing resource that allows a person to (a) hold information in mind temporarily while completing a task or solving a problem and (b) do the work of problem solving (reasoning, language comprehension, etc.). This information burden, known as the working memory load, can be taxing because the working memory system is limited in its capacity to store information and engage in cognitive work (Baddeley, 2007). Thus, it is easy to forget one or more crucial elements of a problem.
As noted by Sweller (1988), when using means-ends analysis, “a problem solver must simultaneously consider the current problem state, the goal
state, the relation between the current problem state and the goal state, the relations between problem-solving operators and lastly, if subgoals have been used, a goal stack must be maintained” (p. 261). Solving a problem with a nonspecific goal (e.g., to calculate the value of as many variables as possible) obviates the need to keep several of the aforementioned items in working memory. Indeed, computer simulation work by Sweller (1988) in kinematics, geometry, and trigonometry has demonstrated that problems with nonspecific goals (i.e., open-ended problems) reduce working memory load.
Physics
Research in physics provides support for the working forward/working backward finding. This research has shown that expert problem solvers typically begin by describing problem information qualitatively and using that information to decide on a solution strategy before writing down equations (Bagno and Eylon, 1997; Chi, Glaser, and Rees, 1982; Eylon and Reif, 1984; Larkin, 1979, 1981a, 1981b; Larkin et al., 1980). A successful solver’s strategy includes the appropriate physics concept or principle and, usually, a plan for applying the principle to the particular conditions in the stated problem (Finegold and Mass, 1985; Larkin et al., 1980). This plan leads experts to work forward from the given information to the desired solution. Experts also monitor their progress while solving problems and evaluate the reasonableness of the answer (Chi, 2006; Chi et al. 1989; Larkin, 1981b; Reif and Heller, 1982; Singh, Granville, and Dika, 2002; see Chapter 6 for a more detailed discussion of metacognition). In contrast, beginning physics students typically start by writing down equations that match given or desired quantities in the problem statement and then work backward, somewhat less efficiently, to find an equation for which the unknowns are given directly in the problem (Larkin et al., 1980). When beginning students get stuck using this approach, they lack strategies to go further (Reif and Heller, 1982).2
To illustrate the working forward/working backward contrast, consider a problem for which the goal is to determine the final velocity of a block when it reaches the bottom of an inclined plane. As discussed by Larkin, (1981b), expert physicists begin by noting that the motion of the block on the inclined plane depends on gravitational and frictional forces. This approach leads them to retrieve from memory the equation F = ma (force = mass × acceleration). That equation, in turn, leads to retrieval of an equation relating final velocity, the goal of the problem, to acceleration. Novices,
__________________
2This section draws heavily on a review of physics education research that the committee commissioned for this study (Docktor and Mestre, 2011).
in contrast, begin by focusing on the goal of determining the final velocity. This focus leads them to first find an equation that involves that unknown quantity, in this case the equation relating final velocity to acceleration. Acceleration is an unknown in that equation, so novices then look for a new equation that relates acceleration to information given in the problem, in this case F = ma.
Chemistry
Some scholars in chemistry focus not on expert-novice comparisons, but on general problem-solving approaches and on identifying the characteristics of successful problem solvers. According to Herron and Greenbowe (1986), successful problem solvers have a strong command of basic facts and principles; construct appropriate representations; have general reasoning strategies that permit logical connections among the different elements of the problem, and apply verification strategies at multiple points during the problem-solving process. However, similar to findings from physics and cognitive science, research on problem solving in stoichiometry and equilibrium indicates that students are sometimes able to solve a problem using algorithmic/algebraic strategies or analogous problems, with only a superficial understanding of the underlying concept (Camacho and Good, 1989; Chandrasegaran et al., 2009; Gabel and Bunce, 1994; Tingle and Good, 1990). Similarly, a limited amount of research on how students approach organic chemistry problems that involve the use of representations but no calculations suggests that many students memorize the relevant reaction and apply it to a novel task, rather than applying more general skills they have been taught to solve a novel problem (Bhattacharyya and Bodner, 2005).
Some research in chemistry has explored the dichotomy between algorithmic problem solving and problem solving that involves only conceptual understanding (e.g., a multiple-choice question measuring conceptual understanding of gases using no mathematics) (Nurrenbern and Pickering, 1987). A spate of papers in the 1990s probed this subject (e.g., Nakhleh and Mitchell, 1993; Sawrey, 1990), but much of that research used questions that centered on visualizations of the particulate nature of matter (PNOM) as alternatives to algorithmic problem solving. At that time, most textbooks did not contain PNOM problems; because such problems were unfamiliar to students (and many faculty), inferences cannot be readily drawn from those studies. Although PNOM problems are now more common, there is no clear evidence demonstrating whether the use of particulate representations leads to improvements in conceptual problem solving or in problem solving using algorithmic calculations.
Engineering
Similar to the cognitive science findings presented above, a limited amount of engineering education research shows that translating the problem into a visual representation and then into a mathematical representation is an important step in solving problems (Eastman, 2001). Even so, students often go straight to a mathematical formula without creating a visual representation of the problem. This approach usually results in failure or misapplication of a formula leading to a dead-end rather than a deeper understanding of the phenomenon under study. One obstacle is students’ lack of understanding of concepts that serve as gatekeepers to more sophisticated conceptions of a field (Baillie, Goodhew, and Skryabina, 2006; Meyer and Land, 2005). These concepts are difficult for most students, often abstract, and not recognized by students as keys to new ways of thinking about the discipline. For engineering students, the difficulty also can manifest itself as dependence on ritualistic algorithmic problem solving rather than true understanding, sometimes resulting in the inability of the student to even recognize the problem.3
Summary
Taken together, these findings suggest that it is important for science and engineering instructors to help students understand that both a good representation of the problem at hand and a good solution method are needed for successful problem solving. Moreover, when students encounter difficulty in solving problems, they need to learn to consider alternative procedures for figuring out the answer and alternative representations of the problem itself (or at least refinements to their current representation). Perhaps one component of an effective instructional strategy would be to provide a compelling example of how much difference a good representation can make for the ease of solution (Posner, 1973, provides one such example).
Problem Representation
Another consistent finding from DBER and cognitive science is that superficial characteristics of problems have an undue influence on novices’ problem solving. One source of cognitive science evidence for this claim is that isomorphic problems (problems that have the same underlying structure) may lead people to construct very different representations of their
__________________
3This section draws heavily from a review of the literature that the committee commissioned for this study (Svinicki, 2011).
(identical) underlying structure because of the different situations they present (e.g., discs of different sizes stacked on a peg versus acrobats of different sizes standing on one another’s shoulders), with clear consequences for solution time, accuracy, and method of solving (Bassok and Novick, 2012).
These findings mean that although experts in a domain may easily see that two apparently different problems are really the same kind of problem “deep down,” students are likely to assume these problems are of distinctly different types. This assumption impairs students’ ability to apply what they learned on one problem to new problems that have similar underlying structures despite superficial differences. Although the initial research in this area involved brain-teaser-type puzzle problems (Hayes and Simon, 1977; Kotovksy, Hayes, and Simon, 1985), similar results have been found more recently for problems from academic domains such as mathematical word problems (Bassok and Olseth, 1995; Bassok, Chase, and Martin, 1998; Martin and Bassok, 2005).
A second source of evidence comes from a large number of studies, in cognitive science and DBER, showing that (relative) experts and novices in a domain (or even good and poor students) differ with respect to the problem features they highlight in their representations. In particular, novices often focus on superficial features of problems, such as the specific objects and terms mentioned and the particular way the question happens to be phrased. Experts, in contrast, typically focus on underlying structural features concerning the relations among the elements in the problem. The structural features are critical for solving the problem and the surface features are not. The following sections on physics, chemistry, and biology education research present results from problem-solving studies that are consistent with this finding. Additional supporting evidence exists based on the results of memory tasks using stimuli from engineering (electric circuit diagrams: Egan and Schwartz, 1979) and biology (clinical cases in medicine: Coughlin and Patel, 1987). Indeed, using a variety of experimental tasks, this finding of expertise differences in problem representations has been replicated in numerous domains, including chess (Gobet and Simon, 1996), computer programming (McKeithen et al., 1981), mathematics (Schoenfeld and Herrmann, 1982), and sports such as basketball and field hockey (Allard and Starkes, 1991). Clearly, this difference is a fundamental aspect of human cognition, relevant to science and nonscience disciplines alike. Part of acquiring expertise in a domain involves learning to identify the important structural features of that domain, and part of being an expert means seeing problems through the lens of the domain’s principles (i.e., its deep structure).
Representational differences between experts and novices have implications for problem solving accuracy, solution time, and the ability to transfer analogous solutions across superficially dissimilar problems (Hardiman,
Dufresne, and Mestre, 1989; Novick, 1988; Novick and Sherman, 2008). This coupling of representation and solution occurs because the perceptual configurations and structural relationships that experts discern are often associated with stored plans in long-term memory concerning what to do in the presence of those configurations. Thus, experts often see solutions that novices have to laboriously compute (Chase and Simon, 1973).
Physics
Physics education research has revealed differences in how experts and novices represent problems. Novice representations include physical objects (e.g., a drawing of a car in a problem with acceleration), whereas scientific or expert representations add details based on the laws of physics and incorporate abstractions (e.g., a graph of the car’s motion) (Larkin, 1983). A common task used to investigate the nature of people’s problem representations involves having them categorize problems according to how they are solved. Physics education research has found that whereas experts categorize physics problems according to the major concepts or principles that can be applied to solve them (e.g., Newton’s second law), novices rely much more on the surface attributes of the problems—such as the specific objects mentioned (e.g., pulleys versus inclined planes versus springs)—as the basis for categorization (Chi, Feltovich, and Glaser, 1981; de Jong and Ferguson-Hessler, 1986). Nevertheless, depending on the problem description, even experts sometimes have difficulty focusing on the major principle in certain types of categorization tasks, and some novices are able to consistently rely on principles to make categorization decisions (Hardiman, Dufresne, and Mestre, 1989). Across different levels of expertise, physics principles play a key role in the organization of conceptual and procedural knowledge for those who are good problem solvers.
Expertise-related differences in problem representations have important implications for teaching and learning because naïve representations may incline novices to develop incorrect assumptions based on common sense (Anzai, 1991). On the other hand, an instructional intervention in which physics students were directed to attend to the underlying structure of problems in the way that experts do yielded more expert judgments of the extent to which problems were similar, which resulted in improved problem solving (Dufresne et al., 1992).
Chemistry
Problem representation has not been a significant focus of research on chemistry problem solving. However, a limited amount of small-scale research does support the finding that novices focus on superficial aspects of
problems. In a study of the mental models that organic chemistry students use when making predictions about the relative acid strength of different substances, 7 of 19 students interviewed had mental models that caused them to classify acids and bases by surface features and simple heuristics rather than using information about the structures themselves to predict and explain the properties of those structures (McClary and Talanquer, 2010). Another interview study of how students use their understanding of hydrogen bonding to characterize molecules revealed that after four semesters of chemistry, students were still unable to easily identify concepts that were relevant—or not relevant—to the problems they were solving (Henderleiter et al., 2001). In addition to documenting the intransigence of students’ difficulties in identifying the critical attributes of a problem, a few studies have linked these difficulties to challenges of transferring existing knowledge to a new concept (Kelley and Jones, 2008; Tien, Teichert, and Rickey, 2007; see Chapter 7 for a more detailed discussion).
Biology
Two small-scale interview studies from biology also illustrate expert-novice differences in problem representation. Smith (1992) found that undergraduate biology students grouped classical genetics problems based on superficial features (e.g., whether the problem concerned humans or fruit flies, how the question was worded), whereas biology professors grouped them according to key underlying concepts (e.g., the mechanism of inheritance). Genetics counselors showed an intermediate pattern of grouping. In another study, Kindfield (1993/1994) investigated the diagrams drawn by 15 participants with more versus less accurate knowledge of meiosis and chromosomes (three professors, two graduate students, and four undergraduate honors students in genetics compared with one honors student and four biology majors enrolled in an introductory genetics course) while solving problems involving meiosis. Kindfield found that less knowledgeable participants often drew chromosome representations that more literally resembled chromosome appearance under a light microscope, and included features that are irrelevant to solution (e.g., dimensionality and shape). In contrast, the drawings of more knowledgeable participants included chromosome features that are biologically relevant to the given problem.
Individual and Group Differences
Across DBER, individual and group differences are not a common focus of study. However, some research in chemistry and biology has investigated group differences in problem solving. Although some of this
research has been conducted on a relatively large scale (i.e., with more than 100 students), the committee has characterized the strength of conclusions that can be drawn from this research as limited because few studies exist.
Chemistry
Most chemistry education research on differences in problem solving has examined differences in cognitive abilities rather than demographic characteristics. One example relates to working memory capacity. By their very nature, complex problems contain a considerable amount of relevant information, which often must be held in students’ working memory. Some research on problem solving in chemistry indicates that as the working memory load of a problem increases, success rate decreases (Johnstone and El-Banna, 1986; Niaz, 1989). That research also has shown that chemistry students who have a larger working memory capacity (as measured by the Pascual-Leone FIT test) perform better on problem solving. This research has been conducted on a relatively large scale and the findings are consistent with a large body of research in cognitive psychology documenting enhanced performance (e.g., language comprehension, problem solving, etc.) when more working memory resources are available to complete the task at hand (e.g., Baddeley, 2007).
Other research on individual differences has examined the relationship between spatial thinking, or the ability to mentally manipulate two- and three-dimensional figures, and problem solving in chemistry. Here, the evidence is mixed. On the one hand, Bodner and McMillan (1986) have found that problem solving activities appear to be correlated with spatial skills. Stieff, Hegarty, and Dixon (2010) also have reported evidence for a correlation between spatial skills and molecular visualization (or interpreting visual representations of molecules), which may affect performance on some kinds of chemistry problems. On the other hand, Wu and Shah (2004) have postulated that other cognitive factors may be correlated with spatial skills, which may explain Bodner and McMillan’s results.
Biology
In contrast to chemistry, biology education research on group differences has concentrated on demographic characteristics. A series of studies used the Interactive MultiMedia Exercises (IMMEX), a multimedia software program that allows educators to track students’ progress as they solve problems (Stevens and Palacia-Cayetano, 2003). Comparisons of the performance of two-year college and university students on numerous IMMEX exercises revealed several differences between the two groups. In particular, community college students more frequently used simple
statements that repeated text from the exercise and asked fewer questions during decision making, which indicated a lower degree of analysis and hypothesis forming. On the other hand, community college students showed greater awareness of their progress (or lack thereof) toward the task goals than university students, who were more successful in problem solving overall.
Ill-Defined Problems
Relatively little DBER has been conducted on ill-defined, open-ended problems. Most of this research comes from chemistry. Some engineering education research also investigates ill-defined problems, typically in the context of instructional strategies (discussed under “Instructional Practices to Improve Problem Solving”). The committee has characterized the strength of the conclusions that can be drawn from this evidence as moderate because although relatively few studies exist, they have been conducted on a relatively large scale (i.e., across multiple courses or institutions, with several hundred students) and include quasi-experimental studies.
Chemistry
As mentioned, IMMEX is a problem-solving assessment system. Because many IMMEX assignments are case-based problems, some research in chemistry has used IMMEX to investigate students’ solving of ill-defined problems. Some research on a qualitative analysis problem requiring students to identify an unknown compound based on the results of the physical and chemical tests that they request in the context of the IMMEX problem has shown that after five attempts at solving a problem, students stabilize on a problem-solving strategy, even when that strategy is unsuccessful (Cooper et al., 2008).
Other studies on ill-defined problems have used the IMMEX system to measure the effects of group problem-solving sessions or an intervention designed to increase metacognitive activity (Sandi-Urena, Cooper, and Stevens, 2011). The results suggest that students working on ill-structured problems in collaborative groups are better able to describe their problem-solving strategies than students working alone. Also, when solving problems individually immediately after the grouping, students who had worked in a group retained the strategies that the group developed (Cooper et al., 2008).
Instructional Practices to Improve Problem Solving
Across all disciplines, instructional strategies to improve students’ conceptual understanding, problem solving, and overall academic performance
are the subject of considerable inquiry in DBER. In this section, we highlight research that specifically investigates strategies to improve problem solving (see Chapter 4 for a discussion of research on strategies for promoting conceptual change and Chapter 6 for a discussion of research on more general instructional strategies).
Physics
Whereas early research in physics identified problem-solving differences between experts and novices, current research on physics problem solving primarily investigates how to move students from novice toward expert problem solving within the domain. To this end, DBER has investigated the efficacy of various types of support for students (or scaffolding), including the following:
• using a specific problem-solving framework (Heller and Heller, 2000; Pólya, 1945; Reif, 1995; Van Heuvelen, 1991),
• elucidating different problem types (Mestre, 2002; Van Heuvelen, 1995; Van Heuvelen and Maloney, 1999),
• providing example solutions (Chi et al., 1989; Ward and Sweller, 1990), and
• altering the classroom format to provide more guidance and interaction (Cummings et al., 1999; Duch, 1997; Hoellwarth, Moelter, and Knight, 2005).
Other areas of inquiry include the efficacy and use of example problems (Cohen et al., 2008), nontraditional problem types (Ogilvie, 2009), computer coaches (Gertner and VanLehn, 2000; Hsu and Heller, 2009; Reif and Scott, 1999), and cooperative group interactions (Heller and Hollabaugh, 1992; Heller, Keith, and Anderson, 1992). This research is being conducted in a wide range of settings from small-scale research laboratory situations to large classroom studies, and the committee has characterized the strength of findings from the research on this topic as strong.
Overall, this research indicates that expert skills in physics problem solving can be taught and that carefully designed support appears to be beneficial for students. However, individual studies suggest that problem-solving gains from a given type of scaffolding are small and difficult to measure. Moreover, various types of scaffolding are interrelated, which makes individual effects difficult to determine.
Another line of physics education research has shown that making symbols more transparent to students helps them apply concepts and solve problems (Brookes and Etkina, 2007). For example, instead of writing forces as W (weight) or T (tension), students benefit when labeling each
force with two subscripts to identify two interacting objects, such as FEonO (force exerted by Earth on object) or FRonO (force exerted by rope on object). As another example, to help students understand that heat is a process of energy transfer and not energy itself, the term heat can be substituted with “heating.” Although some physics education research-based curriculum materials use this more descriptive language (Van Heuvelen and Etkina, 2006), research on the efficacy of those materials is scant.
These results suggest that a systematic approach to improving such a complex skill as problem solving, with multiple forms of supporting scaffolding, is indicated. Such approaches typically are consistent with the theoretical framework of cognitive apprenticeship (Brown, Collins, and Duguid, 1989; Yerushalmi et al., 2007), which proposes that complex skills depend on an interlocking set of experiences and instruction whose efficacy, in turn, depends on the learner and the community of practitioners with whom the learner interacts (see Box 5-1 for a discussion of cognitive apprenticeship).
Chemistry
Teaching general problem-solving methods is a significant emphasis of chemistry education research. Pólya (1945) recommended teaching an organized approach to solving problems in mathematics, and developed the strategy of (1) understanding the problem, (2) devising a plan, (3) carrying out the plan, and (4) looking back. Other scholars have modified that approach for chemistry and studied the effects of using those approaches on problem solving. A summary of this literature concluded that “when chemistry students are taught to solve problems in a systematic manner, they are more successful. Strategies based on Pólya’s heuristics or variations thereof appear to facilitate students’ ability to solve routine problems even though there is some evidence that students may be doing so using algorithms” (Gabel and Bunce, 1994, p. 318). Despite these benefits, some research suggests that many students do not continue using the strategies they were initially taught (Bunce and Heikkinen, 1986).
Engineering
Engineering education effectively has incorporated key elements of cognitive science into problem-solving and design4 experiences for engineering courses and curricula, and into the research about effects on learning (e.g.,
__________________
4“Design” has distinct meanings across engineering sub-disciplines. In mechanical and civil engineering, design typically has a physical connotation. In computer science and computer engineering, design can be different both in the scale of application and the use of simulation instead of actual construction (Dutson et al., 1997).
BOX 5-1
Cognitive Apprenticeship
A chemistry postdoctoral researcher shows an undergraduate how the gas chromatograph/mass spectrometer needs to be calibrated; a young astronomer watches her mentor give a research talk at a conference; an engineering student uses a computer-aided design program for the first time and follows step-by-step instructions prepared by his professor. In each of these cases, skills—and often cultural norms—are passed down from an expert to a novice. History recognizes this process as apprenticeship.
Traditional apprenticeship includes four dimensions:
1. Modeling, where the expert demonstrates how to do a task.
2. Scaffolding the various types of support that the expert provides as the novice proceeds.
3. Fading, or the gradual removal of scaffolding as the novice takes more responsibility.
4. Coaching by the expert to guide the novice toward success, for example by pointing out strengths and weaknesses in the novices’ product or performance.
Cognitive apprenticeship builds on the traditional apprenticeship model, but makes every aspect more explicit and relevant. Developed by Collins, Brown, and Newman (1989), cognitive apprenticeship has been shown to be successful in teaching mathematical problem solving, reading, and writing. Cognitive apprenticeship has been used as a framework to explore the affective side of undergraduate research experiences (Sadler et al., 2010; see Chapter 7), develop physics problem solving (Heller, Keith, and Anderson, 1992), and develop introductory engineering software skills (Hundhausen et al., 2011). Although cognitive apprenticeship is not useful for teaching rote knowledge, it is a robust and well-researched technique for teaching complex tasks in many disciplines.
Atman, Kilgore, and McKenna, 2008; Cordray, Harris, and Klein, 2009). The committee has characterized the strength of conclusions that can be drawn from this research as moderate because the body of research includes a review and a line of research with multiple studies that were conducted in multiple courses.
Particularly in design, it is important to use authentic problems and to sequence experiences within various courses to support the learning of core concepts. Strategies such as case analyses, model-eliciting activities,
worked-out problem examples, and heuristics provide opportunities for students to gain experience and confidence in solving open-ended problems (Sankar, Varma, and Raju, 2008; Svinicki, 2011). Indeed, a series of mixed-methods studies in engineering has shown that model-eliciting activities in which teams of students work with open-ended, real-world problems can improve students’ problem solving (Yildirim, Shuman, and Besterfield-Sacre, 2010). However, these activities must be implemented correctly to be effective. Some factors that contribute to effective implementation of model-eliciting activities include the nature and quality of guidance and feedback provided by the instructor, duration of the activity, size of student teams, and instructors’ level of experience with model-eliciting activities (Yildirim, Shuman, and Besterfield-Sacre, 2010). Incorporating reflection and self-explanation prompts into instruction also has been shown to improve student problem solving (Cheville, 2010; Cordray, Harris, and Klein, 2009; Litzinger et al., 2010; Svinicki, 2011) (see Chapter 6 for a more detailed discussion of metacognition).
Biology
The strength of conclusions that can be drawn from biology research on problem solving is limited because the research base consists of a few studies that have been conducted in the context of single courses. However, consistent with findings from physics and engineering, the results suggest that problem-solving skills can be enhanced through instruction. One quasi-experimental study examined the use of “invention activities” as a way to improve biology problem-solving strategies (Taylor et al., 2010). Invention activities are based on work that challenges students to solve problems that seem unrelated to current class material, which then helps students to construct a mental framework that promotes better understanding of the course content. Students in a first-year biology class who participated in an invention activity began working on problems much more quickly and generated more hypotheses (many of which were plausible) than students who did not participate in the invention activity (Taylor et al., 2010).
As discussed in Chapter 6, collaborative problem-solving activities are increasingly popular in physics, chemistry, and biology. Some recent work has been done to develop and validate tools for comparing collaborative and individual problem-solving strategies in large (60-100 students) biochemistry courses where students discuss ill-defined problems in small online groups (Anderson et al., 2008) and then work on individual exams based on similar, but not identical, problems (Anderson et al., 2011). Both of these assessment tools allow students to regularly practice their problem-solving skills, and, perhaps more importantly, allow instructors the opportunity to provide targeted intervention, as appropriate, to groups
and individual students in this critical area of student development. Studies using these instruments are ongoing and have not yet been published.
The Geosciences
Problem-solving skills in the geosciences are commonly taught in the context of problem-based learning (Macdonald et al., 2005), an instructional approach in which students are given complex, realistic problems to solve individually or in groups (Barrows, 1986). With instructional strategies and activities that are influenced by Bransford, Vye, and Bateman (2002) and Kolb (1984), problem-based learning in the geosciences often involves ill-defined problems that have applications to society, such as environmental issues, public policy, geology and human health, natural hazards, and Earth resources (see Ishikawa et al., 2011 for an example). The products of these learning activities typically are measured against professional norms of geoscience research projects, such as geologic maps and written reports (Carlson, 1999; Connor, 2009; de Wet et al., 2009; Fuller et al., 2006; Gonzales and Semken, 2009; Maskall and Stokes, 2008; May et al., 2009; Potter, Niemitz, and Sak, 2009).
For the most part, the geoscience education literature describes these activities and does not examine their efficacy. However, Ault (1994) made a notable early effort to formulate a research agenda on problem solving for Earth science education, laying out the difficulties that confront students. These difficulties included incomplete observations, systems that are “complex beyond complete prediction” (Ault, 1994, p. 275), systems with contingent histories in which extrapolation is unreliable, and value-laden contexts surrounding socially critical problems. In addition, as discussed in Chapter 6, technologies such as GPS tracking devices are being used to monitor student navigation and yield insight into problem-solving skills (Riggs, Balliet, and Lieder, 2009; Riggs, Lieder, and Balliet, 2009). That research reported an optimum amount of relocation and backtracking in field geology: too much retracing indicates confusion, and too little reoccupation of key areas appears to accompany a failure to recognize important geologic features.
Summary of Key Findings on Problem Solving
• The different fields of discipline-based education research have studied somewhat different aspects of problem solving, consistent with disciplinary differences in what problem solving entails. Early research in physics emphasized expert-novice differences in various aspects of the solution process, whereas chemistry education research and later research in physics has examined the
nature of the solution process and strategies for successful problem solving more broadly. Most of the research in engineering has addressed instructional strategies, particularly around authentic problems; instruction is also an important area of inquiry for physics. Research on problem solving in biology and the geosciences examines individuals’ problem-solving processes, rather than expert-novice differences.
• With the exception of engineering and chemistry, discipline-based education research on problem solving typically focuses on well-defined, quantitative problems. In most disciplines, considerably less research exists on problems that are more characteristic of what scientists and engineers encounter in their professional lives.
• Part of acquiring expertise in a domain involves learning to identify the important structural features of that domain, and part of being an expert means seeing problems through the lens of the domain’s principles. Students (novices) have difficulty with all aspects of problem solving and approach well-defined problem solving in ways that are consistently and identifiably different from those of experts. Specifically, experts often preferentially focus on creating a representation of the problem at the outset. In addition, experts and undergraduate students represent problems in very different ways, with experts attending to the underlying principles required for solution and students focusing on superficial features such as the particular objects mentioned in the problems. These differences have important implications for problem solving success and, in turn, instruction.
• As cognitive science research has shown more broadly, insufficient spatial skills and working memory capacity may impede performance on some forms of problem solving.
• Several conditions and strategies appear to improve problem-solving skills, including socially mediated learning environments, the use of open-ended and authentic problems, and interventions that promote metacognitive activity. Nonetheless, some research shows that students often do not persist in using effective strategies over the long term.
Directions for Future Research on Problem Solving
Problem solving has been a significant focus of DBER in many disciplines, and DBER has generated important insights into the nature of the problem-solving process, differences between experts and novices, and strategies for improving problem solving. However, some areas remain ripe for exploration. For example, little DBER has investigated individual and
group differences in problem solving. A better understanding of similarities and differences in problem solving among subpopulations of students is needed, along with careful studies investigating the effects of various individual differences (spatial skills, working memory capacity, logical thinking ability) and their implications for instruction.
In all disciplines, DBER scholars have a pressing need for measurement tools that will assess student problem-solving skills for large numbers of students in an authentic classroom setting. Some of these tools have been developed in physics (Docktor and Heller, 2009), and in chemistry (Cooper et al., 2008; Sandi-Urena and Cooper, 2009), but they have yet to be applied widely enough to gauge their utility.
The committee’s analysis revealed that most DBER on problem solving is aimed at identifying, categorizing, and clarifying what students do wrong. Although this is an important first step, more resources should now be devoted to investigating the effect of instructional interventions on students’ problem-solving skills (similar to Mestre and Ross, 2011, for example, or Sandi-Urena and Cooper, 2011). Many research papers offer implications for teaching, but relatively few actually investigate the effect of an intervention designed to improve problem solving in some context (most of these studies come from physics, chemistry, and engineering). A productive approach might be to identify trajectories that can lead to greater problem-solving expertise (Lajoie, 2003). Further research on attributes that might characterize trajectories toward problem-solving competence could include data on interpersonal interactions when discussing problems, and the use of methodologies such as eye tracking (Smith, Mestre, and Ross, 2010).
Systematic explorations also are needed of the effects of changing problem features (e.g., format of the problem statement; familiarity with the problem context; whether the values provided are numeric or symbolic) and the effects of different types of worked examples on problem-solving performance. In addition, strategies should be developed for effectively reducing working memory load while still highlighting important aspects of problem solving. Sweller and colleagues (Owen and Sweller, 1985; Sweller and Levine, 1982; Sweller, Mawer, and Ward, 1983) in psychology have shown that one effective way to accomplish this goal is to have students engage in open-ended problem solving rather than attempt to reach a particular goal (e.g., “Calculate the value of as many variables as you can” versus “What is the final velocity of the car?”). As discussed, the open-ended approach reduces the number of variables and problem conditions that students must keep in their working memory. This research has used problems in kinematics, geometry, and trigonometry, which suggests that the technique may be widely applicable to the science and engineering domains that are the purview of this report.
Real-world problems are often considerably different from the types of problems students typically solve in the laboratory or class, because they are ill-defined, messy, and knowledge intensive (Novick and Bassok, 2005). Most DBER on problem solving addresses well-defined problems. Substantial work remains to be done to understand how students approach less well-defined problems and how to improve their ability to tackle these problems. Moreover, discipline-based education researchers must investigate the extent to which instructional strategies for improving students’ problem solving for well-defined and real-world problems transfer to ill-defined problems as well. Although well-defined numerical problems are typical in traditional science and engineering courses, most practicing scientists and engineers typically solve conceptual problems, such as deducing structure with spectroscopic tools and designing experiments or approaches to target molecules. One strategy to address this complex issue would be to compare students’ performance on problems at differing levels of approximation to real-world problem solving.
The consideration of well-defined versus ill-defined problems naturally leads to the distinction between problem solving and problem finding (or problem discovery). Before professionals engage in problem solving, they must confront the critical initial step of choosing which problem(s) to solve. Not all problems are equally worthy of extended effort, and not all are equally likely to result in significant insights or breakthroughs. For scientists and engineers, therefore, problem finding is crucial. In most educational situations, however, students are simply provided problems by their teachers. Instructors and discipline-based education researchers may under-emphasize the importance of problem finding because, traditionally at least, it is not a task in which students are expected to engage. Thus, research is needed on factors that affect students’ ability to engage in problem finding.
In biology and the geosciences, rich opportunities exist to conduct research on ill-defined or open-ended problems. As physics education research and chemistry education research have done, this work can readily extend the more general research on the development of problem-solving skills in cognitive science. In the geosciences, it would be productive to build on emerging research on cognitive apprenticeship and related work on metacognition in which geoscientists reveal their thought processes in a mentoring capacity to students (Manduca and Kastens, 2012; Petcovic and Libarkin, 2007).
Visual/spatial, mathematical, logical, and verbal representations are central to human thinking, as well as to learning and instruction in virtually
all disciplines. Considering only visual/spatial representations, McKim (1980, p. 142) noted that “…you will find graphic-language expressions on the blackboards of almost every department of a university, from aeronautics to zoology.”
Representations like diagrams, graphs, and mathematical equations are important in science and engineering because they facilitate communication, aid in the discovery of scientific facts, assist in problem solving, serve as memory aids, and generally function as tools for thinking (Dufour-Janvier, Bednarz, and Belanger, 1987; Kindfield, 1993/1994; Larkin and Simon, 1987; Lynch, 1990; Novick, 2001). In addition, abstract spatial representations can actually modify, and in some cases simplify, the nature of a task (Larkin and Simon, 1987). For example, people can usually estimate proportions more easily from a pie chart than from a table of numeric data. In addition to interpreting representations produced by experts, students can construct their own representations to enhance learning and engagement (Ainsworth, Prain, and Tytler, 2011).
Because a wide variety of visual/spatial representations play a central role in science and engineering, students need to develop skills in constructing, interpreting, transforming, and coordinating these representations (see Box 5-2 for a description of the obligatory components of representations that students must understand). This suite of skills has been termed representational competence (Hegarty, 2011).
Developing representational competence requires the ability to mentally manipulate two- and three-dimensional objects, a skill that is called visuospatial thinking or spatial ability. Given the importance of spatial representations and thinking processes in science, it seems logical that spatial ability is correlated with participation in science generally (Shea, Lubinski, and Benbow, 2001; Wai, Lubinski, and Benbow, 2009; Webb, Lubinski, and Benbow, 2007). However, as the following discussion illustrates, evidence from DBER on the role of spatial ability is mixed.
Overview of Discipline-Based Education Research on
the Use of Representations and Spatial Thinking
Spatial thinking and the use of representations are important areas of inquiry for DBER because representational competence is so vital to acquiring expertise within a discipline. For example, the visualization and representation of the unseen molecular level is central to a robust understanding of chemistry. Chemistry students must learn how to create novel, discipline-specific representations, how to translate those representations into the more familiar equation format, and how and when to apply each representational format for solving problems. As another example, the ability to visualize a three-dimensional image from a two-dimensional graphical representation,
BOX 5-2
The Four Components of Representations
Representations have four obligatory components, described by Markman (1999):
1. The situation that is being represented (called the “represented world”). In the science and engineering disciplines, the represented world might be a problem to be solved or a device to be designed.
2. The elements used to construct the representation (called the “representing world”). These elements could be any of the following:
(a) physical objects, such as when balls and sticks are used to model the structure of a chemical compound;
(b) diagrammatic elements such as lines and geometric figures that can be used, for example, to create a sketch of the internal structure of a cell or a graph showing the acceleration of an object over time;
(c) mental elements, such as components of a mental model of a pulley system that students may attempt to animate mentally to reason about the behavior of the system.
3. Rules for mapping elements of one world to those of the other world, or a set of conventions for constructing a particular type of representation (Hegarty, Carpenter, and Just, 1991), which students must learn if they are to successfully use appropriate representations to solve problems and reason about scientific phenomena.
4. Processes that operate on the representing world. One set of processes uses the mapping rules to create the representation. Other processes then extract information from the representation to reason about the represented world.
and the ability to mentally rotate three-dimensional objects, are important to success in engineering, and especially so in engineering design (Sorby, 2009; see Box 5-3 for a description of representations used in design).
DBER on representations and spatial ability is particularly valuable in understanding the many disciplinary differences that pertain to thinking visually and understanding visual representations. For example, in some disciplines (e.g., geology, anatomy), penetrative thinking, or the ability to represent and reason about the hidden internal structure of a multilayered three-dimensional object, is critically important (Hegarty, 2011; see “The Role of Spatial Ability in Visualization and Mental Model Formation” in
BOX 5-3
Representations in Engineering: The Languages of Design
Representations are an essential component of engineering design, and the following representations constitute a major part of the “languages of design” (Dym et al., 2005, p. 108):
verbal or textual statements used to articulate design projects, describe objects, describe constraints or limitations, communicate between different members of design and manufacturing teams, and document completed designs;
graphical representations used to provide pictorial descriptions of designed artifacts such as sketches, renderings, and engineering drawings;
shape grammars (a computational approach to the generation of designs) used to provide formal rules of syntax for combining simpler shapes into more complex shapes;
features used to aggregate and specialize given geometrical shapes that are often identified with particular functions;
mathematical or analytical models used to express some aspect of an artifact’s function or behavior, where this behavior is in turn often derived from some physical principle(s); and
numbers used to represent discrete-valued design information (e.g., part dimensions) and parameters in design calculations or within algorithms representing a mathematical model.
in this chapter). Mental animation ability may be more important in disciplines for which motion is a central concern (e.g., mechanics, meteorology, oceanography).
Disciplines may also differ in the extent to which they use graphical versus mathematical representations as the means of conveying critical insights. In a comparison of representations in scientific papers across several scientific fields, authors of geoscience and chemistry papers were found to use the most figures whereas authors of physics papers inclined more toward equations and psychology authors toward tables (Kastens and Manduca, 2012). Biology is increasingly coming to rely on mathematical representations, especially to interpret large genomic databases. In chemistry, spatial and mathematical representations are both important.
Different science and engineering disciplines also may differ in the extent to which they call upon large-scale versus small-scale spatial ability (Hegarty et al., 2010). Small-scale spatial ability refers to one’s skill at perceiving and imagining transformations of objects that can be manipulated. In contrast, large-scale (or environmental) spatial ability refers to one’s success in tasks
such as learning the layout of a new environment, retracing a previously traveled route, and pointing to unseen locations in a familiar environment. The two kinds of spatial information may be processed separately by the human visual system (Previc, 1998). Hegarty et al.’s (2010) self-report data from scientists, engineers, and others suggest that large-scale spatial ability may be particularly important in the geosciences, whereas small-scale spatial ability may be particularly important in engineering. It should be noted, however, that tools for assessing small-scale spatial abilities are far more advanced than those for assessing large-scale spatial abilities (Hegarty, 2011).
This section discusses DBER on how students develop, use, and interpret representations, and the role of spatial thinking in visualization and mental model formation. Because representations are so important to human thinking and learning, a large literature in cognitive science addresses students’ understanding of visual/spatial, mathematical, logical, and verbal representations (see, for example, Glasgow, Narayanan, and Chandrasekaran, 1995; Thagard, 2005). A critical theme in this research is the importance of general cognitive and perceptual factors for understanding and reasoning with representations in science and engineering, as well as features related to the diagrams themselves. Because the breadth of cognitive science research in this area reflects the cross-disciplinary importance of representations, much of this research has used materials and tasks from various science disciplines. Given this interdependence between DBER and cognitive science, we use findings and principles from cognitive science to frame the findings of DBER.
Research Focus
Many of the disciplinary differences just described are reflected in the focus of DBER. In physics and chemistry, the research base on spatial ability and the use of representations is strong because multiple studies exist—many of relatively large scale—with high convergence of findings. As characterized by Docktor and Mestre (2011, p. 20), physics education research explores the use of external representations for describing information during problem solving, such as pictures, physics-specific descriptions (e.g., free-body diagrams, field line diagrams, or energy bar charts), concept maps, graphs, and equations. Some studies investigate the representations students construct during problem solving and how they use those representations (Heller and Reif, 1984; Larkin, 1983; Rosengrant, Etkina, and Van Heuvelen, 2005; Van Heuvelen and Zou, 2001), whereas other studies explore the facility with which students or experts can translate across multiple representations (Kohl and Finkelstein, 2005; Meltzer, 2005). Still other studies in physics focus on student difficulties with particular representations
like graphs or mathematical formulae (Beichner, 1994; Ferrini-Mundy and Graham, 1994; Goldberg and Anderson, 1989; McDermott, Rosenquist, and van Zee, 1987; Orton, 1983).
More than 100 studies exist on spatial thinking and representations in chemistry, including books (Gilbert and Treagust, 2009) and reviews (Taber, 2009). These studies examine difficulties translating between representations (Gilbert and Treagust, 2009; Johnstone, 1991), the role of spatial ability in visualization and mental model formation (Abraham, Varghese, and Tang, 2010; Bodner and McMillan, 1986; Pribyl and Bodner, 1987; Stieff, 2011), and the influence of animated and static visualizations on conceptual understanding (Abraham, Varghese, and Tang, 2010; Aldahmash and Abraham, 2009; Sanger and Bader, 2001).
Spatial ability and the use of representations are emerging areas of study in engineering (Sorby, 2009), biology (Dirks, 2011) and the geosciences (Piburn, van der Hoeven Kraft, and Pacheco, 2011). In engineering, much of this research addresses instructional approaches to improve spatial ability; these approaches typically are grounded in constructivist theories of learning (Gerson et al., 2001). Most of the biology studies investigate the role of different representations in improving understanding, promoting conceptual change, and stimulating interest in biology. Many are grounded in constructivism and dual-coding theory. The latter theoretical approach was refined in the model of Schönborn and Anderson (2009), which suggested that three factors may affect learners’ ability to interpret external representations in biology and biochemistry: students’ prior knowledge of the concepts underlying the external representation, students’ reasoning ability, and the mode or nature of the diagram. In the geosciences, research in this area has concentrated on the relationship between spatial ability and success in the geosciences (Liben, Kastens, and Christensen, 2011) and on instructional strategies to improve spatial ability (Piburn et al., 2005).
Methods
DBER scholars employ a wide range of methods to study spatial thinking and representations, including case studies on how students construct and use representations, think-aloud interviews, student-generated diagrams, surveys of students’ confidence and knowledge, pre- and post-tests of content knowledge, quasi-experimental studies, large-scale assessments, and mixed methods studies using technology to record and aggregate the data. Study populations range from nonmajors in introductory courses to graduate students, and some studies include high school students (Beichner, 1994; Swenson and Kastens, 2011). Research conducted in the context of physics problem solving typically involves qualitative investigations into the thinking of individual students in introductory physics courses. In many
cases, problem solvers are carefully observed while they do their work, and their written solutions are examined to see how they make use of different representations.
Indepth studies of the use of graphical representations in science and engineering necessarily include specific representations and tasks. This focus raises questions about the generalizability of these studies within their disciplines. Moreover, although research from the sciences and engineering is broadly concerned with spatial structures, the disciplines engage with dramatically different scales of time and space, which raises important questions of how spatial representations differ across the various science disciplines and whether students face common challenges across the disciplines.
How Students Develop, Use, and Interpret Representations
A critical step in helping students acquire greater disciplinary expertise is to understand how they develop, use, and interpret the representations that are central to a given discipline. As this discussion shows, research from physics, chemistry, biology, and the geosciences consistently indicates that students have difficulties interpreting representations, and that they struggle to see similarities among different representations that describe the same set of relationships.
More specifically, research in cognitive science has shown that across disciplines, students have (a) a preference for representations that have a high degree of visual similarity to their referents; (b) a bias to view representations as truthful depictions of reality; and (c) particular difficulty understanding the abstract nature of representations (similar to findings under “Problem Solving” that experts are more able than novices to see beyond the surface of what things look like to capture the essential nature of situations within their domain of expertise) (Hegarty, 2011). Knowing the conventions for how diagrams represent reality is not sufficient to ensure good comprehension or successful inference with these representations. Experts see patterns in representations that novices miss, even when novices know the conventions, because novices are distracted by salient but irrelevant surface features of the displays (see “Problem Solving” for more details).
Physics
A variety of studies in physics supports the finding that students have serious difficulties simply interpreting the representations commonly encountered in introductory physics courses. These studies often involve microcomputer and video-based labs and simulations on vectors, electric field lines, electric and magnetic fields, or waves (see Rosengrant, Etkina,
and Van Heuvelen, 2007 for a summary of the research). Some research indicates that students do not use diagrams because they misunderstand the quantities and concepts being represented, and because they are given few chances to specifically practice the skills needed to construct diagrams (Van Heuvelen, 1991). However, some research—including a quasi-experimental study with approximately 600 students at two universities (Kohl, Rosengrant, and Finkelstein, 2007)—shows that learning via more than one representation can help to build understanding (Van Heuvelen and Zou, 2001; see Box 5-4 for an example).
Chemistry
The relationship between structure and properties is central to chemistry, and students are expected to understand this relationship by the time students take organic chemistry and biochemistry. However, as we discussed in Chapter 4, an abundance of research on the macroscopic, symbolic, and particulate domains—three essential domains of chemistry learning that are depicted in Johnstone’s triangle (1991, see Box 5-5 and Chapter 4)—has revealed students’ difficulties in understanding the particulate nature of matter (the fact that matter is made of discrete particles). Specifically, students have difficulty constructing Lewis structures, commonly used particulate-level diagrams of chemical and physical phenomena that demonstrate molecular shape and bonding (Cooper et al., 2010; Nicoll, 2003). In a study of 166 undergraduate students in general and organic chemistry, the accuracy of students’ representations fell precipitously when the number of atoms on the Lewis structure increased from six to seven (Cooper et al., 2010). The increase from six to seven molecules represents a shift to an atomic structure where the bonds are not evident unless students recognize the molecule. That study, along with another study investigating students’ understanding of the Lewis structure of the molecule CH2O, also demonstrated that students’ understanding of these representations does not improve over time (Cooper et al., 2010; Nicoll, 2003).
Students also have difficulty translating among representations at the other two corners of Johnstone’s triangle (Gilbert and Treagust, 2009; Johnstone, 1991; Linenberger and Bretz, 2012). More generally, students have difficulty translating among alternative representations that describe the same set of relationships, such as videos, graphs, animations, equations, and verbal descriptions (Kozma and Russell, 1997). However, as with physics, the use of multiple representations appears to be beneficial. For example, in one quasi-experimental study, female students’ performance on problems improved more than males’ when students were taught particulate representations in addition to symbolic representations (Bunce and Gabel, 2002).
BOX 5-4
Visualization/Representation in Physics
The common free-body diagram helps students move from a physical view of concrete objects to the more abstract idea of vector forces. This is a major component of a multirepresentational teaching methodology developed by Alan Van Heuvelen (1991). Van Heuvelen and Zou (2001) found this approach to be more effective than traditional instruction.
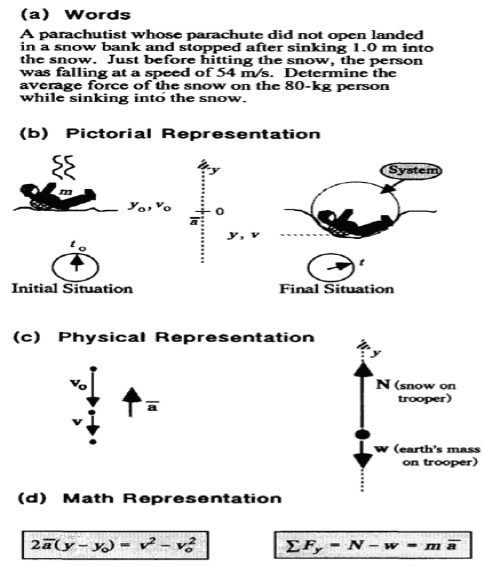
Reprinted with permission from Overview Case Study Physics, 1991, American Association of Physics Teachers.
BOX 5-5
Visualization/Representation in Chemistry
Johnstone’s 1991 paper entitled “Why Is Science Difficult to Learn?” challenged teachers of chemistry to reexamine their teaching. Chemistry is often taught as a foreign language of sorts, with numbers, letters, and grammatical rules for combining them. Yet chemistry is much more than just balanced equations and molecular formulas. Consider the equation 2Na(s) + Cl2(g) → 2NaCl(s). For a chemist, this equation represents the combination of a silvery metal that catches fire in water and a poisonous green gas to create white crystals eaten on french fries. It is the epitome of what excites chemists: the transformation of properties when atoms and molecules form an ordered lattice in which each Na cation is surrounded by six chlorides and vice versa. This equation also encompasses the corners of what is now known as “Johnstone’s Triangle:” symbolic, macroscopic, and particulate domains, which are essential to chemistry knowledge (see Chapter 4).
Students, however, typically restrict their efforts to memorizing the symbols for the elements Na and Cl2, balancing the charges of Na+ and Cl–, and balancing the equation. Johnstone noted that to teach chemistry is to help students explore the dyads of the triangle: the relationship between symbols and their corresponding features in particles of molecules and atoms, the connections between the particles and the properties that can be seen and smelled with the human senses, and the language of symbols used to represent elements and compounds.
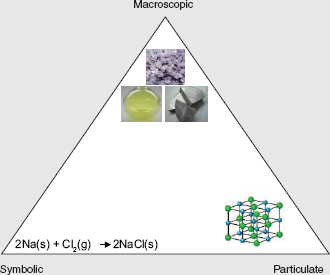
Biology
Similar to chemistry, some studies suggest that biology students have difficulty translating between alternative abstract diagrammatic representations of the same set of relationships (Novick and Catley, 2007; Novick, Catley, and Funk, 2010; Novick, Stull, and Catley, in press; see Box 5-6). In these studies, students’ understanding of the structure of hierarchical diagrams in evolutionary biology appears to be affected by knowledge of biology, by a general perceptual principle from Gestalt psychology called the principle of good continuation, and by a bias to process diagrams in the highly practiced left-to-right reading order.
The principle of good continuation states that a continuous line is perceived as a single entity. Good continuation has been shown to interfere with college students’ understanding of the hierarchical structure of cladograms (diagrammatic depictions of descent), and with their ability to reason about the evolutionary relationships depicted when the cladograms were drawn in a way that is commonly found in undergraduate biology textbooks (Catley and Novick, 2008; Novick and Catley, 2007, in press). In follow-up work, a manipulation that broke good continuation at exactly the points in the diagram that mark a new hierarchical level was associated with greatly improved performance (Novick, Catley, and Funk, 2010).
The Geosciences
Students’ use of representations is an emerging area of inquiry in the geosciences. Because relatively few studies exist and most were conducted on a relatively small scale (i.e., in the context of a single course), the strength of the conclusions that can be drawn from geosciences education research on the use of representations is limited. However, taken together, this research lends support to the finding from physics, chemistry, and biology that students have difficulty with specialized representations, and do not reliably interpret them as the maker of the representation had intended (Ishikawa et al., 2005; Swenson and Kastens, 2011). These findings resemble the body of research on students’ misconceptions, except that the misunderstandings pertain to a representation rather than a concept. Also similar to the findings from other fields, students have difficulty inferring comparable structures across different geologic representations, such as imagining the internal structure of a block of the earth’s crust when given a depiction of external surfaces (Kali and Orion, 1996; Orion et al., 1997).
Because maps are a primary form of representation in the geosciences, methods used in developmental psychology studies of children’s understanding of maps (Liben, 1997) provide a potentially useful framework for geoscience education research on the understanding of representations.
BOX 5-6
Visualization/Representation in Biology
Cladograms, or diagrams that depict evolutionary relationships among a set of taxa, are typically depicted in either a tree or ladder format. Trees are much more common in the evolutionary biology literature, while ladders are slightly more common in high school and college biology textbooks (Catley and Novick, 2008; Novick and Catley, 2007). Novick and Catley (2007) asked college students who had taken at least the first semester of the introductory biology class for majors to translate hierarchical relationships from the nested circles format to the tree and ladder formats and from the tree format to the ladder format and vice versa. The figure in this box shows an example cladogram of each type (the experiment used Latin names of real taxa rather than letters). The figure also shows that students’ translation accuracy was reduced whenever the ladder format was involved. Common errors when translating between the tree and ladder formats are consistent with students’ interpretation of the long, slanted “backbone” line of ladders as a single entity (i.e., hierarchical level), consistent with the Gestalt principle of good continuation (Kellman, 2000).
Some geoscience education research has focused on production tasks, which are posed in the context of the real world and require students to make or modify a representation. Studies in which participants produce a geological map by direct observation of rocks and structures in nature exemplify this category (Petcovic, Libarkin, and Baker, 2009; Riggs, Balliet, and Lieder, 2009; Riggs, Lieder, and Balliet, 2009). Those studies have revealed variation in the levels of sophistication of advanced geology students’ maps, and suggest that more effective traverses of the territory lead to better representations.
Representational correspondence tasks provide information in one representation and require the student to transfer or translate that information to another form of representation. A pioneering example is Kali and Orion’s (1996) study in which students were shown a block diagram of a three-dimensional geological structure and asked to sketch a vertical profile down through the center of the block. Most of Titus and Horsman’s (2009) tasks also fall in this category (see Box 5-7 for a more detailed discussion of this research).
A very limited amount of geoscience education research has been conducted on metarepresentational tasks, which require students to explain how a representation works. The work of Liben, Kastens, and Christensen (2011) in which students explain dip and strike (i.e. how to measure the orientation of a sloping planar surface) falls in this category (see “The Role of Spatial Ability in Visualization and Mental Model Formation”).
No research yet exists on comprehension tasks, which are posed in the context of the representation and require students to respond by performing an action in the real world. An example of this task from the geosciences would be to present students with an interpretive model from the published literature, and ask them to find evidence in an outcrop to support or refute this model (Mogk and Goodwin, 2012).
The Role of Spatial Ability in Visualization
and Mental Model Formation
In many science and engineering disciplines, spatial thinking is a vital component of expertise in the discipline. Some evidence suggests that spatial ability is correlated with learning and reasoning in specific science disciplines, although the strength and importance of the relationship may vary across disciplines (see Hegarty, 2011, for a review). Although these studies have limitations, most importantly concerning causation and causal direction, they do provide evidence for the importance of further investigating the role of spatial abilities in understanding science concepts across disciplines. They also raise issues about how spatial thinking should be promoted, a topic that is considered in some depth by Hegarty (2011).
BOX 5-7
Visualization/Representation in the Geosciences
In a study of visual penetrative ability, high school students were asked to sketch a specific plan view or profile slice through a three-dimensional volume, using information about the outside of the volume in the form of a block diagram (Kali and Orion, 1996; see the figures in this box). In general, students found this task difficult. Careful examination of incorrect responses and follow-up interviews revealed that partially successful students used specific strategies to “penetrate” the volume, such as continuing a pattern vertically or horizontally (such as depicted in panel 5.a of the figure in this box). Other students, however, gave completely “nonpenetrative” answers, in which they merely copied patterns from the outside of the volume (such as in panel 5.b of the figure in this box) (Kali and Orion, 1996).
Figure 5. Examples of incorrect answers which indicate an attempt to present interior properties of the structure. Students were required to draw a vertical cross-section through A and B.
Titus and Horsman (2009) extended this line of inquiry to college students, using more spatially challenging structures and tasks, such as drawing structural contours. Titus and Horsman (2009) and Murphy et al. (2011) show that college students’ performance on tasks that require visual penetrative ability can be improved by instruction and practice, and that such improvements can be accomplished within the time constraints of standard laboratory instruction.
Physics
The role of spatial ability in problem solving in mechanics has been an active area of research in physics education. These studies typically focus on the mental processes students use when imagining how the components of a mechanical system (e.g., a spring, gear, or pulley system) move and interact when the system is moving (e.g., Clement, 2009; Hegarty, 1992; Hegarty and Sims, 1994; Schwartz and Black, 1996). This task is referred to as mental animation. The findings from this research suggest that students use both mental images and mathematical analysis to understand how the system is moving and answer the question asked. Other studies on relating force and motion events, interpreting graphs of force and acceleration, extrapolating motion, and inferring the motion of machine components using mental animation have found positive correlations between spatial visualization ability and mechanics problem solving (Hegarty and Sims, 1994; Isaak and Just, 1995; Kozhevnikov, Hegarty, and Mayer, 2002; Kozhevnikov and Thornton, 2006).
Chemistry
In contrast to physics, research on the relationship between spatial ability and success in chemistry is mixed. Some researchers find spatial ability is a predictor of success on spatial organic chemistry tasks such as assigning configurations and understanding the mechanisms of some reactions (Bodner and McMillian, 1986; Pribyl and Bodner, 1987). Others do not find such correlations, and provide evidence that students of lower spatial ability can successfully use heuristics that do not rely on spatial ability (Abraham, Varghese, and Tang, 2010; Stieff, 2011).
Engineering
Despite the importance of spatial thinking to engineering, a relatively limited amount of engineering education research exists on this topic. This research reveals some differences related to gender: A 1993 study of 535 first-year Michigan Technological University engineering students showed that females were three times more likely than males to fail the Purdue Spatial Visualization Test on Rotations (PSVT:R) (Sorby, 2009). In addition, engineering education research suggests that spatial skills are correlated with the ability to use computer interfaces to perform database manipulations (Sorby, 2009).
The Geosciences
The relationship between spatial ability and understanding of geoscience concepts are of great interest to geoscience education researchers
(Liben, Kastens, and Christensen, 2011; Orion, Ben-Chaim, and Kali, 1997). Across many fields of the geosciences, the ability to envision a three-dimensional volume from information that is available in one or two dimensions is essential. This task involves mentally extending the available information into the dimension that is unrepresented, using a combination of spatial thinking ability and knowledge of plausible earth processes. Geologists engage in this activity when they envision what lies behind or between rock outcrops; geophysicists when they infer structures from images of seismic reflections; and oceanographers when they interpolate between stations where seawater temperature and salinity were measured. Kali and Orion (1996) called this ability “visual penetrative ability,” and developed a test for it in the context of working with geological structures. As described in Box 5-7, this research provides evidence of students’ difficulties with tasks involving visual penetrative ability, reveals variation in high-school students’ visual penetrative ability, and shows that the visual penetrative ability of college students can be improved with instruction.
Across the disciplines, very little DBER on spatial ability and representations attends to individual differences (e.g., ability levels) or group differences (e.g., race/ethnicity). A notable exception is a study of dip and strike in the geosciences (Liben, Kastens, and Christensen, 2011). In that study, the researchers purposefully selected participants so as to populate six bins of 20 students each: high-, medium, and low-spatial ability, by male and female. Low-spatial ability (as assessed on the water-level task) and being female were associated with worse performance on the strike and dip tasks (Liben, Kastens, and Christensen, 2011).
Astronomy
Considering that astronomy requires learners to imagine a three-dimensional dynamic universe of galaxies and orbiting planets by looking up at a flat sky, it would be reasonable to assume that spatial thinking is an active area of inquiry in astronomy education research. However, systematic research on spatial thinking in astronomy is very limited. Studies are under way to examine the relationships between spatial thinking and astronomy knowledge, but their results have not yet been published in peer-reviewed journals.
Instructional Strategies and Tools to Improve Students’
Spatial Ability and Use of Representations
Given the difficulties students have with spatial thinking and the use of representations, improving these skills is an important part of moving
students along the path toward greater expertise, and, in turn, an important focus of DBER. Related research in cognitive science has yielded insights into the reasons for students’ difficulties, which also have implications for instruction. Here we discuss these bodies of research as they relate to improving the use of diagrammatic displays, enhancing students’ spatial ability, and identifying the role of animations in these tasks.
Improving the Comprehension of Diagrammatic Displays
In addition to being important tools of discipline, diagrammatic displays—e.g., general-purpose abstract diagrams such as hierarchies and matrices, domain-specific diagrams such as free body diagrams in physics or a drawing of the components of a cell in biology, and graphs of data—are important tools in instruction. These displays can enhance reasoning and problem solving (Larkin and Simon, 1987; Lynch, 1990; Winn, 1989), whether in the sciences or in other disciplines. By storing information externally, diagrams free up working memory that can be used for other cognitive processes. Moreover, the spatial organization of information helps viewers to integrate related information (Hegarty, 2011). These displays can also enable viewers to offload more complex cognitive processes onto simpler perceptual processes. For example, a linear relationship between variables is immediately apparent in a graph but must be laboriously computed from a table of numbers. Similarly, when a display is interactive, people can manipulate the display itself instead of conducting their own computations of the values.
These benefits of graphical displays do not mean that their use is easy or transparent, however, as the previous sections clearly illustrate. One reason diagrams do not automatically facilitate reasoning and problem solving is that their successful use requires knowledge of the conventions underlying their construction (Hegarty et al., 1991). College science is taught by experts who are very familiar with the representations used in their field and may not realize how difficult these representations are for students to master. Instructors may need to provide students with more detailed introductions to the various graphical displays used in science. Such instruction may include the following (Hegarty, 2011):
• explicitly highlighting the relationships between alternative displays of the same or related information,
• explaining how different representations at different levels of abstraction are optimized for various tasks, and
• providing opportunities for extensive practice interpreting and producing appropriate types of representations.
Instruction and practice in making representations might include making “first inscriptions,” or representations that are made directly from the represented world or from the raw material of nature (Goodwin, 1994, Mogk and Goodwin, 2012).
A second reason diagrams are not always beneficial is because the relationship between perception and cognition affects how students process diagrams to draw inferences about the represented world. For example, circles and lines seem naturally suited to imply physical objects or locations rather than relationships or motion, respectively (Tversky et al., 2000). When diagrammatic representations are constructed in accordance with these conventions, college students are faster and more accurate at drawing appropriate inferences (Hurley and Novick, 2010). In addition, students often import their highly practiced left-to-right processing strategy from reading printed text to nonlinguistic visual tasks (Fuhrman and Boroditsky, 2010; Nachshon, 1985). In situations where left-to-right processing makes it difficult to interpret relationships in a scientific diagram, simply reflecting the diagram 180 degrees above the vertical axis can improve comprehension (Novick et al., in press). These results suggest that when instructors construct diagrammatic representations to illustrate scientific concepts or principles, they should attend to how people naturally interpret the components from which the representations are constructed.
The Gestalt psychologists identified many other perceptual features that have psychological importance, including two that have particular implications for DBER. The first is good continuation, which states that a continuous line is interpreted as a single entity (discussed in the biology education research section on the role of visualization and spatial ability). The second is spatial proximity, which states that items that are closer together tend to be processed together. This principle has been shown to play an important role in students’ understanding of cladograms (Novick and Catley, in press) and mathematical equations (Landy and Goldstone, 2007). Whether spatial proximity facilitates or hinders students’ performance depends on whether the conclusion based on proximity supports or conflicts with the correct response. In some situations, visual representations may be constructed in such a way that spatial proximity is a useful clue rather than a conflicting signal, as when a flow chart or network diagram is constructed with functionally related subsystem elements clustered together within a larger depicted system. In other cases, however, instructors probably need to tackle the issue directly, such as through the use of refutational instructional strategies (Hynd et al., 1994; Kowalski and Taylor, 2009), explaining why spatial proximity is not relevant and what structural features of the diagram instead provide the critical information needed for responding (Novick, Catley, and Schreiber, 2010).
Improving Spatial Ability
Research from engineering and the geosciences suggests that spatial ability can be improved through instruction. One review article (Sorby, 2009) summarizes more than a decade of applied research—including several longitudinal studies—aimed at identifying practical methods for improving three-dimensional spatial skills, especially for female engineering students. That article identifies strategies that appear to be effective in developing spatial skills. In the longitudinal studies, first-year engineering majors of low spatial ability (as measured by the PSVT:R) who took a specially designed, multimedia training course improved their spatial skills, earned higher grades, and persisted in the university at greater rates than students of similar spatial ability who did not take the course. The multimedia software and workbook that were part of the course materials were shown to improve students’ spatial skills. In addition, sketching was consistently identified as an important component of spatial skill development (Sorby, 2009).
Some research indicates that geoscience education involving visually rich materials can improve students’ spatial visualization skills on domain-specific tasks and general spatial tasks in ways that are practical to incorporate into instructional practices (Ozdemir et al., 2004; Piburn et al., 2005; Sawada et al., 2002; Titus and Horsman, 2009) (see Box 5-7 for an example). In some of those studies, including a quasi-experimental study (Piburn et al., 2005), an initial gap between males and females in spatial visualization ability (as measured by the surface development task) diminished after visualization-rich instruction in physical geology (Piburn et al., 2005; Sawada et al., 2002).
The Influence of Animated and Static Visualizations
on Conceptual Understanding
In addition to using specialized representations, expert scientists and engineers use technologies such as animations, interactive computer visualizations and virtual models to aid their work. These technologies have enormous potential for promoting representational competence and spatial thinking in science (Hegarty, 2011). Indeed, several quasi-experimental studies comparing the efficacy of static visuals with two- and three-dimensional animations of molecular structures and processes appear to improve student learning of stereochemistry, which concerns the spatial arrangement of atoms within molecules (Abraham, Varghese, and Tang, 2010; Aldahmash and Abraham, 2009; Sanger and Badger, 2001). These studies suggest that three-dimensional animations improve learning more than two-dimensional animations, which, in turn, are better than static
representations. The use of animations in biology classes also has been shown to increase retention of content knowledge in the short and long-term (Harris et al., 2009; McLean et al., 2005; O’Day, 2007). The animations in those studies included a three-dimensional animation of protein synthesis (McLean et al., 2005), a narrated animation related to a complex signal transduction pathway (O’Day, 2007), and a combination of a molecular imaging program and handheld physical models related to molecular structure and function (Harris et al., 2009). Although this research shows that students can learn more from animations than from static images, McLean et al. (2005) caution that “learning is best achieved when an animation is coupled with a lecture, because this combination provides a reference from which students can appreciate the knowledge presented in the animation” (p. 170).
The recommendation of McLean et al. (2005) might reflect the fact that visual technologies are typically more complex than static visualizations. Thus, these technologies may require greater spatial ability and other aspects of representational competence for their successful use. It is not a foregone conclusion, therefore, that all animations will necessarily be beneficial for learning. In this regard, some cognitive science research comparing static and animated displays of dynamic biological and mechanical processes has found no benefit in performance when animations were used (Tversky, Morrison, and Betrancourt, 2002).
Sometimes, animations present information too quickly for students to accurately perceive and comprehend. Although the pace of animations can easily be slowed, other problems are not so readily fixed. For example, animations of a mechanical system can give students the illusion that they understand the information being presented and may even cause them to “see” what they believe is true rather than what is actually presented (Kriz and Hegarty, 2007). Some research has found that animations showing how a mechanical system works were more effective in promoting learning when students had to predict how they thought the machine works before viewing the animation (Hegarty, Kriz, and Cate, 2003). The authors hypothesize that the prediction task improves the effectiveness of the animation by making students aware of what they do not understand, thus cueing them to the type of information to extract from the animation. This finding is consistent with those discussed in Chapter 6 about the benefits of interactive lecture demonstrations. One conclusion to draw is that although animated, three-dimensional, and interactive visualizations might seem to rely less on visualization skills, research to date has suggested that they actually require visualization skills for their use (Hegarty, 2011).
Summary of Key Findings on Spatial Thinking
and the Use of Representations
• How students create, use, interpret, and translate between graphical and mathematical representations provides insight into their understanding of important concepts in a discipline. DBER highlights discipline-specific challenges that students face when using such representations.
• Although equations, graphical displays, and other representations may seem easy to understand for undergraduate faculty who are domain experts, college students have difficulty extracting information from these representations, and constructing appropriate representations from existing information. College students also have difficulty relating and translating among different representations of the same entity or phenomenon.
• There is contradictory evidence about the relationship between spatial ability and performance in science. Consistent with findings from cognitive science that students with low-spatial ability especially have difficulty relating two- and three-dimensional representations, some DBER studies show a relationship between measures of spatial ability and success on specific science or engineering tasks. Other studies do not provide evidence of that relationship.
• The evidence on the effectiveness of animations is mixed: The use of animations has been shown to enhance learning in some circumstances, and to be ineffective or even detrimental to student learning in other situations.
Directions for Future Research on Spatial
Thinking and the Use of Representations
DBER and cognitive science have yielded many useful insights into how students use mathematical and graphical representations, but important gaps remain. For example, the research community, instructors, and those who develop representations would benefit from a deeper understanding of students’ use of representations as tools to enhance their learning, and studies along these lines should leverage what is already known about the basic cognitive and perceptual processes that students use to comprehend graphical representations.
The role of spatial ability also needs clarification. Spatial ability may be measured in many different ways, any one of which may be more or less relevant to any specific science or engineering task. Although several authors have proposed that many tasks (e.g., rotation tasks of three-dimensional models) require mental imagistic models, others have shown that many
students use heuristics and other strategies that do not employ visualization skills and are able to move flexibly between such strategies as needed. In addition to clarifying the overall role of spatial ability, it would be useful to evaluate the contributions of large-scale and small-scale spatial ability to learning in physics, chemistry, engineering, biology, the geosciences, and astronomy. DBER has not yet examined these different spatial abilities.
The research base on promoting students’ understanding of and facility with domain-specific representations is less robust. DBER does not provide conclusive evidence about how instructors, illustrators, and authors should design representations for maximum effect, or what the optimal representations are for a given situation. Moreover, additional research is needed to identify the range of instructional approaches that help students use mathematical and graphical representations to enhance their knowledge and understanding. For example, does designing and constructing representations affect students’ understanding differently than merely interpreting existing representations, and if so, how? Given the increasing use of technology, more research is needed on the educational efficacy of computer animations, simulations, and other technology-enhanced techniques that aid with visualization and representations, and the conditions under which those techniques are effective.
Representations vary within and across disciplines. As one example, the nature of the representations used in geoscience education varies enormously on multiple important dimensions, including the use of spatial representations to represent nonspatial data (Dutrow, 2007; Kastens, 2009, 2010; Libarkin and Brick, 2002). This variation presents a challenge to developing a research agenda for the use of visualizations and representations in undergraduate science and engineering education, because research using any specific representation may not be generalizable to other representations.












































