Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 11
/
Mathematical Simulations
When the Lab
Isn’t Big Enough
C
omputer simulations, which are built on mathematical modeling, are used daily
in scientific research of all types, for informing decision making in business and
government, including national defense, and for designing and controlling
complex systems such as those for transportation, utilities, and supply chains, and so on.
Simulations are used to gain insight into the expected quality and operation of those
systems and to carry out what-if evaluations of systems that may not yet exist or are not
amenable to experimentation.
As an example, one of the most important and spectacular events in the universe
is the explosion of a star into a supernova. Such explosions seeded our own solar
system with all of its heavier elements; they also have taught us, indirectly, a great deal
about the size, age, and composition of our universe. But within our galaxy, the Milky
Way, supernovas are exceedingly rare. How can you study something that cannot be
duplicated in a laboratory, would fry you if you got close to it, and rarely even occurs?
That is where mathematical sciences enter the story, via computer simulation. In
scores of applications, from physics to biology to chemistry to engineering, scientists use
computer models—whose construction requires the formulation of mathematical and
statistical models, the development of algorithms, and the creation of software—to study
phenomena that are too big, too small, too fast, too slow, too rare, or too dangerous to
study in a laboratory.
While scientists and engineers have long been able to write down equations to
describe physical systems, before the computer age they could only solve the equations
in certain highly simplified cases, literally using a pen and paper or chalk and a
blackboard. For example, they might assume the solutions were symmetric, or simplify a
problem to two or three variables, or operate at only one size scale or time scale.
in the 21st Century
The Mathematical Sciences
11
OCR for page 12
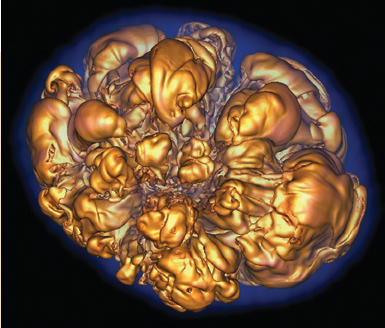
3 / Image from a three-dimensional simulation of an exploding superno-
va. Reprinted with permission from Professor Adam Burrows, Princeton
University. /
FUELING
innovation and discovery
12
OCR for page 13
Now, however, the scientific universe has changed. The study of supernovas is
a perfect case in point. It is possible to create a rudimentary theory of supernovas
by assuming that the star is perfectly symmetrical. Astrophysicists call this a one-
dimensional theory because all of the quantities depend on one parameter, the distance
from the center of the star. Unfortunately, it doesn’t work: You can’t get a one-
dimensional star to explode, and so simulations based on that simplified model cannot
represent all of the important aspects of this complex system. Of course, real stars are
Scholarly studies
not so symmetric; they bulge at the equator, due to rotation. So astrophysicists began
have estimated that
to simulate stars with a shape parameter as well as a size parameter, and they called
these two-dimensional simulations. However, such simulations still cannot capture the
at least half of the
behaviors of interest: Some fail to explode, while others explode but with less energy
improvement in
than a real supernova.
high-performance
Only with fully three-dimensional simulations have astrophysicists started to
produce supernovas with realistic energy outputs. And this tells us something computing
important: The energy of the supernova must be coming from convection, a process
capabilities over the
that cannot be properly modeled in two dimensions. In a supernova, the core of a
past 50 years can be
star collapses and then rebounds outward, forming an expanding shock wave. The
traced to advances
shock wave then stalls as it runs into matter falling in from the outside the star. That’s
the hurdle that two-dimensional simulations have trouble getting over. But in three
in mathematical
dimensions, the matter inside the shock wave starts to churn as it is irradiated by
sciences algorithms
neutrinos, like soup being heated in a microwave oven. This convection reenergizes
and numerical
the shock wave over a period of several seconds, and the star’s contents explode out
into the universe (see Figure 3). methods rather
While many are aware of the amazing gains in raw speed from Moore’s law—the
than to hardware
approximate doubling of computer hardware capabilities every 2 years—successful
developments alone.
simulation on this scale also depends to an equal degree on new algorithms that perform
the needed computations. For example, the transition from two to three dimensions
invariably increases (usually by an enormous factor) the difficulty of a problem, requiring
mathematical advances in representing reality as well as problem solving. Three-
dimensional simulations on this scale are possible only through a combination of massive
computing power and smart mathematical algorithms. The transition from a two- to
a three-dimensional model requires more than simply running the same code with
more data points. Often, new mathematical representations must be incorporated to
capture new phenomenology, and new comparisons against theory must be made to
assess the validity of the resulting three-dimensional model. More generally, advances
in mathematics and statistics and improved algorithms provide leapfrog advances in
computational capabilities. Scholarly studies have estimated that at least half of the
improvement in high-performance computing capabilities over the past 50 years can be
traced to advances in mathematical sciences algorithms and numerical methods rather
than to hardware developments alone.
in the 21st Century
The Mathematical Sciences
13
OCR for page 14
4 / Anton, a special-purpose supercomputer, is capable of performing atomically detailed simula-
tions of protein motions over periods 100 times longer than the longest such simulations previously
reported. These simulations are now allowing the examination of biologically important processes
that were previously inaccessible to both computational and experimental study. Printed with per-
mission from D.E. Shaw Research. /
The value of simulation is not limited to real-world problems of huge scale: It is just
as useful for tiny problems such as understanding processes within our cells. Many of
the cell’s functions are carried out by proteins—large molecules that fold into a precise
shape to accomplish a particular task. For example, the proteins in an ion channel,
which regulates the flow of ions across a cell membrane, need to fold autonomously
into a pore that will admit a potassium atom into the cell but not a sodium atom. A
mistake at the subcellular level can have implications that affect the whole body. In
cystic fibrosis the channels that are supposed to transport chlorine ions don’t work
correctly, possibly resulting in a buildup of fluid in the lungs; in certain kinds of heart
arrhythmias, the potassium channels do not properly regulate the movement of
potassium ions, which can interfere with the normal muscle contractions that create
each heartbeat.
At present, nobody knows how to take the chemical formula for a protein and
predict the shape it will fold into. The shape is determined by the forces between
the many atoms within the protein and between those atoms and their surroundings.
FUELING
innovation and discovery
14
OCR for page 15
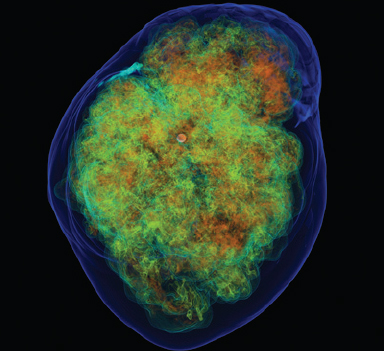
5 / Snapshots of the folding and unfolding
of a protein, obtained from a simulation
of unprecedented length performed on the
special-purpose supercomputer Anton. Mul-
tiple transitions are observed between a dis-
ordered “unfolded state” (red and gray) and
an ordered “folded” state (blue). Printed
with permission from D.E. Shaw Research. /
Calculating the net result of all those forces is a daunting computational challenge, but
simulations are getting close to that goal. Recently a special-purpose supercomputer
managed to simulate the motion of a relatively small protein called FiP35 over a period
of 200 microseconds (one five-thousandth of a second), during which time it folded and
unfolded 15 times (see Figures 4 and 5). Again, while part of this capability was made
possible by the special-purpose hardware, it also depends on mathematical advances.
First, the precise but computationally intractable force field must be replaced by a good
approximation based on empirical data and on simpler systems, and mathematical
analysis is necessary to characterize the adequacy of the approximation. Second,
computational algorithms have been developed to speed the computation of the
interactions between atoms. For the story of one such algorithm, see a later section,
“Fast Multipole Method: A Long-Term Payoff.”
These success stories illustrate the kinds of problems that scientists now routinely ask
computer simulations to solve. For decades, biology had only two modes of research—in
vivo (experiments with living organisms) and in vitro (experiments with chemicals in a
in the 21st Century
The Mathematical Sciences
15
OCR for page 16
test tube). Now, there is a third paradigm, in silico (experiments on a computer). And
the results of this kind of experiment are taken just as seriously.
Nevertheless, simulations face major challenges, which will be the focus of ongoing
research over the next 20 years.
First, real-world processes often require simulation over a wide range of scales, both
in space and in time. For instance, the core collapse of a supernova takes milliseconds,
while the crucial convection step takes place over a span of seconds and the aftermath
of the explosion lasts for centuries. Spatially, the thermonuclear flame of the supernova
varies from millimeters to hundreds of meters during the explosion.
In biology, the range of scales is just as daunting. Subcellular processes, like the
opening and closing of ion channels, are linked to events at the scale of a cell. These
effects cascade upward, affecting heart tissues, then the heart, and finally (in the
event of a heart attack) the health of the whole body. Likewise, the timescales also
span a vast range: microseconds for the folding of a protein, fractions of a second for
At the cutting the choreography of a single heartbeat, minutes for a heart attack, weeks or months
edge of research, for the body’s recovery. It is very difficult to incorporate all these scales into a single
mathematical model.
the importance
Related to the multiscale problem is the multiphysics problem. Often the types of
of new and better models used at different scales are incompatible with one another. Events at a subcellular
algorithms cannot level are often chemical and random, influenced by the presence or absence of a few
molecules. In the heart, these events translate into electrical currents and mechanical
be overstated.
motions that are governed by differential equations, which are usually deterministic.
Multiphysics can also characterize a single scale: The heart is simultaneously an electric
circuit and a hydraulic pump. It’s not easy to reconcile and simultaneously model those
two identities. Progress in such cases often depends on a combination of insights from
the domain science and the mathematical sciences.
Given the complexity of simulations, model validation also becomes an important
challenge. First the modeler has to make sure that the individual parts of the program are
working as expected; for a complex simulation, this can be very difficult. Then he or she
will test it to see if it reproduces the behavior of simple real-world systems and matches
existing data. Finally, the model will be used to make predictions about genuinely new
phenomena. But there is no universal procedure for deciding when a model is good
enough to use, so to some extent model validation is still more art than science.
Another major challenge for simulations in the near future has to do with hardware
and software. It goes without saying that any scientist who does simulations would like
more computing power. That is the main bottleneck in the supernova and protein-
folding simulations. Three-dimensional simulations are just barely feasible today, but
astrophysicists would really like to go up to six dimensions! That would allow more
accurate simulation of the velocity as well as the location of each particle.
But raw computing power is not the only solution. At the cutting edge of research,
FUELING
innovation and discovery
16
OCR for page 17
the importance of new and better algorithms cannot be overstated. To put it simply,
you can wait 2 years for Moore’s law to hand you a computer that is twice as fast—or
you can get the same speedup today by developing better algorithms.
Apparent advances in raw computation speed do not translate directly, and
perhaps not even indirectly, to simulations that are faster or more accurate. Today’s
expectation is that the high-end computers of the future will have huge numbers of
very fast “cores”—processing units operating individually at extremely high speed—but
that communication between cores will be relatively slow. Hence, software written
for computers with a single core (or a small number of cores) will not be efficient, and
standard computations, such as those for linear algebra, will need serious reworking by
mathematical and computer scientists.
in the 21st Century
The Mathematical Sciences
17
OCR for page 18
Mathematical Sciences Inside...
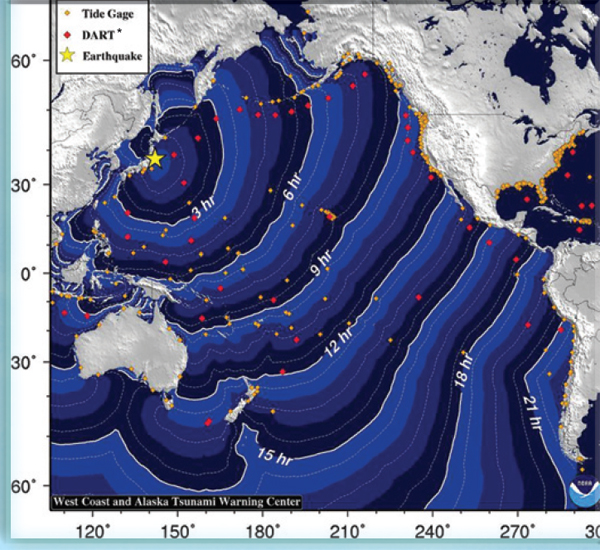
The mathematical sciences help to predict the path and strength of a tsunami
following an earthquake or other oceanic event (such as a massive landslide or
volcano eruption). Mathematical models underpin tsunami warning systems by
estimating where a tsunami will make landfall, how high the waves will be, and
how fast the waves will be traveling. More fundamentally, the mathematical
sciences help to map the topography of the ocean floor and infer large-scale wave
behavior from independent ocean tide gauges that are irregularly spaced and can
be hundreds of miles apart. This knowledge is behind emergency warnings and
evacuations, which help to avoid potentially devastating consequences.
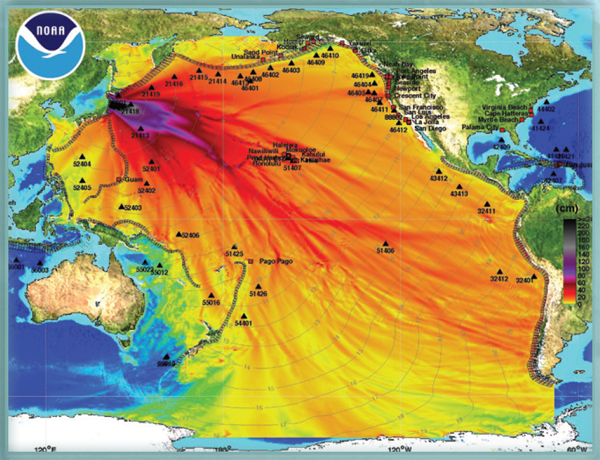
Numerical models are used to simulate the earthquake, transoceanic propagation, and
inundation of dry land. To save time in the event of an emergency, these simulations
are run for a variety of possible earthquake sizes and locations, and these scenarios are
then combined with ocean tide readings as they become available. This figure shows
the predicted sea level increase (in cm) resulting from the deadly 9.0 magnitude earth-
quake off the coast of Japan in March 2011.
18
OCR for page 19
*
Tsunamis
Mathematical science models help predict the timing and trajectory
of tsunami waves based on ocean floor mappings and ocean tide
gauge readings. This information is used to predict when tsunami
waves will hit different coasts. *Deep Ocean Assessment and Reporting of Tsunamis
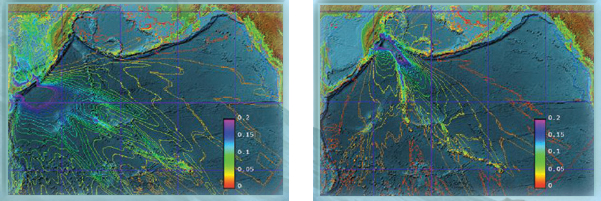
High-resolution computational models are used to simulate wave-heights for a traveling tsunami,
shown here for two different earthquakes. These estimates help to identify evacuation zones and
routes. The impacts of tsunamis vary widely, due to local topography, long-term sea level rise,
annual climate variability, monthly tidal cycles, and short-term meteorological events.
19
