During World War II, the German army, navy, and air force transmitted thousands of messages using an encrypting machine called Enigma. Little did they realize that British mathematicians were eavesdropping on them. (In fact, the secret did not fully come out until the 1970s.) The battle of Enigma was, in its way, just as important as any military engagement. It was won in part by a statistical method called Bayesian inference, which allowed code breakers to determine probabilistically which settings of the Enigma machine (which changed daily) were more likely than others (see Figure 6).
In the years after the war, Bayesian analysis continued to enjoy remarkable success. From 1960 to 1978, NBC forecast the results of elections using similar techniques. The U.S. Navy used Bayesian analysis to search for a lost hydrogen bomb and a wrecked U.S. submarine. Yet these successes were not shared, for security or proprietary reasons. In academic circles Bayesian inference was rarely espoused, for both historical and philosophical reasons (as explained below).

6 / The World War II-era Enigma is one of the most well-known examples of cryptography machines and was used to encrypt and decrypt secret messages. Photo by Karsten Sperling. /
Over the last 30 years, however, Bayesian analysis has become a central tool in statistics and science. Its primary advantage is that it answers the types of questions that scientists are most likely to ask, in a direct and intuitive
way. And it may be the best technique for extracting information out of very large and heterogeneous databases.
For example, in medical applications, classical statistics treats all patients as if they were the same at some level. In fact, classical statistics is fundamentally based on the notion of repetition; if one cannot embed the situation in a series of like events, classical statistics cannot be applied. Bayesian statistics, on the other hand, can better deal with uniqueness and can use information about the whole population to make inferences about individuals. In an era of individualized medicine, Bayesian analysis may become the tool of choice.
Bayesian and classical statistics begin with different answers to the philosophical question “What is probability?” To a classical statistician, a probability is a frequency. To say that the probability of a coin landing heads up is 50 percent means that in many tosses of the coin, it will come up heads about half the time.
By contrast, a Bayesian views probability as a degree of belief. Thus, if you say that football team A has a 75 percent chance of beating football team B, you are expressing your degree of belief in that outcome. The football game will certainly not be played many times, so your statement makes no sense from the frequency perspective. But to a Bayesian, it makes perfect sense; it means that you are willing to give 3-1 odds in a bet on team A.
The key ingredient in Bayesian statistics is Bayes’s rule (named after the Reverend Thomas Bayes, whose monograph on the subject was published posthumously in 1763). It is a simple formula that tells you how to assess new evidence. You start with a prior degree of belief in a hypothesis, which may be expressed as an odds ratio. Then you perform an experiment, or a number of them, which gives you new data. In the light of those data, your hypothesis may become either more or less likely. The change in odds is objective and quantifiable. Bayes’s rule yields a likelihood ratio or “Bayes factor,” which is multiplied by your prior odds (or degree of belief) to give you the new, posterior odds (see Figure 7 on page 22).
Classical statistics is good at providing answers to questions like this: If a certain drug is no better than a placebo, what is the probability that it will cure 10 percent more patients in a clinical trial just due to chance variation? Bayesian statistics answers the inverse question: If the drug cures 10 percent more patients in a clinical trial, what is the probability that it is better than a placebo?
Usually it is the latter probability that people really want to know. Yet classical statistics provides something called a p-value or a statistical significance level, neither of which is actually the probability that the drug is effective. Both of them relate to this probability only indirectly. In Bayesian statistics, however, you can directly compute the odds that the drug is better than a placebo.
So why did Bayesian analysis not become the norm? The main philosophical reason is that Bayes’s rule requires as input a prior degree of belief in the hypothesis you are testing, before you conduct any experiments.
The main philosophical reason is that Bayes’s rule requires as input a prior degree of belief in the hypothesis you are testing, before you conduct any experiments.
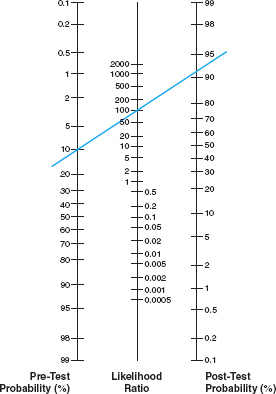
7 / Bayes’s rule can be visualized using a nomogram, a graphical device that assists in calculations. Suppose, for example, a drug test is 100 times more likely (the “likelihood ratio”) to give a true positive than a false positive. Also, you believe that 10 percent of the athletes participating in a particular sport (the “pre-test probability”) use the drug. Now Athlete A tests positive. If you draw a line from 10 percent on the first scale through 100 on the second scale, it intersects the third scale of the nomogram at 91.7. This means that the “post-test probability” that Athlete A is using the drug is 91.7 percent. Adapted from the Center for Evidence Based Medicine, www.cebm.net. /
testing, before you conduct any experiments. To many statisticians and other scientists this seemed to be an unacceptable incursion of subjectivity into science. But in reality, statisticians have known ways of choosing “objective” priors almost since Bayes’s rule was discovered. It is possible to do Bayesian statistics with subjective priors reflecting personal (or group) beliefs, but it is not necessary.
A second, and more practical, objection to Bayesian statistics was its computational difficulty. Classical statistics leads to a small number of well-understood, well-studied probability distributions. (The most important of these is the normal distribution, or bell-shaped curve, but there are others.) In Bayesian statistics you may start with a simple prior distribution, but in any sufficiently complicated real-world problem, the posterior probability distribution will be highly idiosyncratic—unique to that problem and that data set—and may in fact be impossible to compute directly.
However, two developments in the last 20 years have made the practical objections melt away. The more important one is theoretical. In the late 1980s, statisticians realized that a technique called Markov chain Monte Carlo provided a very efficient and general way to empirically sample a random distribution that is too complex to be expressed in a formula. Markov chain Monte Carlo had been developed in the 1950s by physicists who wanted to simulate random processes like the chain reactions of neutrons in a hydrogen bomb.
The second development for Bayesian statistics was the advent of reliable and fast numerical methods. Bayesian statistics, with its complicated posterior distributions, really had to wait for the computer age before Markov chain Monte Carlo could be practical.
The number of applications of Bayesian inference has been growing rapidly and will probably continue so over the next 20 years. For example, it is now widely used in astrophysics. Certain theories of cosmology contain fundamental parameters—the curvature of space, density of visible matter, density of dark matter, and dark energy—that are constrained by experiments. Bayesian inference can pin down these quantities in several different ways. If you subscribe to a particular model, you can work out the most likely parameter values given your prior belief. If you are not sure which model to believe, Bayes’s rule allows you to compute odds ratios on which one is more likely. Finally, if you don’t think the evidence is conclusive for any one model, you can average the probability distributions over all the candidate models and estimate the parameters that way.
Bayesian inference is also becoming popular in biology. For instance, genes in a cell interact in complicated networks called pathways. Using microarrays, biologists can see which pathways are active in a breast cancer cell. Many pathways are known already, but the databases are far from perfect. Bayesian inference gives biologists a way to move from prior hypotheses (this set of genes is likely to work together) to posterior ones (that set of genes is likely to be involved in breast cancer).
Bayesian inference is also becoming popular in biology. For instance, genes in a cell interact in complicated networks called pathways. Using microarrays, biologists can see which pathways are active in a breast cancer cell.
In economics, a Bayesian analysis of consumer surveys may allow companies to better predict the response to a new product offering. Bayesian methods can burrow into survey data and figure out what makes customers different (for instance, some like anchovies on their pizza, while others hate them).
Bayesian inference has proved to be effective in machine learning—for example, to teach spam filters to recognize junk e-mail. The probability distribution of all e-mail messages is so vast as to be unknowable; yet Bayesian inference can take the filter automatically from a prior state of not knowing anything about spam, to a posterior state where it recognizes that a message about “V1agra” is very likely to be spam.
While Bayesian inference has a variety of real-world applications, many of the advances in Bayesian statistics have depended and will depend on research that is not application-specific. Markov chain Monte Carlo, for example, arose out of a completely different field of science. One important area of research is the old problem of prior distributions. In many cases there is a unique prior distribution that allows an experimenter to avoid making an initial estimate of the values of the parameters that enter into a statistical model, while making full use of his or her knowledge of the geometry of the parameter space. For example, an experimenter might know that a parameter will be negative without knowing anything about the specific value of the parameter.
Basic research in these areas will complement the application-specific research on problems like finding breast cancer genes or building robots and will therefore ensure that Bayesian inference continues to find a wealth of new applications.




