Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 29
/
Fast Multipole Method
A Long-Term Payoff
I
n school, we all learn that the problem precedes the solution. But in the mathematical
sciences, it is sometimes the case that existing solutions suddenly become relevant to a
new problem.
In the early 1990s, Vladimir Rokhlin of Yale University and Leslie Greengard of
New York University had a solution. They had devised an algorithm called the Fast
Multipole Method to speed up the solution of certain kinds of integral equations. Later,
the American Institute of Physics and the IEEE Computer Society would name the Fast
Multipole Method as one of the top ten algorithms of the century.
Louis Auslander, on the other hand, was a man with problems—lots of them. As
the applied mathematics program manager at the Defense Advanced Research Projects
Agency, his job was to match up defense-related problems with people who could solve
them. When he heard about the Fast Multipole Method, he suspected that it could
resolve an issue that had long bothered the Air Force, the problem of automatic target
recognition.
The question is this: When you see an airplane on a radar screen, how can you tell
what kind of airplane it is? Ideally, the radar should be able to recognize both friendly and
enemy aircraft and determine which of the two kinds of plane it is. While this may appear
to be a simple problem, it is in fact very difficult. Even if the plane is doing nothing to
evade detection, every rivet on it, every bomb carried under its wings can change its radar
profile. For an everyday analogue, compare a disco ball to a perfectly round, polished
sphere. Even though their shapes are very similar, they reflect light very differently.
For years, the Air Force dreamed of having a library containing all the possible ways
that a plane’s radar signature could look. But to compile such a library, you would have
in the 21st Century
The Mathematical Sciences
29
OCR for page 30
to fly the plane past a radar detector thousands of times, from every possible angle and
with every possible configuration of bombs or fuel tanks or other attachments. This
would be prohibitively expensive and might be impossible for many enemy aircraft.
Alternatively, you could try to compute mathematically what the plane’s radar
signature should look like. If you could do that reliably, then it would be an easy matter
to tweak the configuration to take into account bombs, fuel tanks, etc.
The problem of directly computing a radar reflection boils down to solving a system
of differential equations called Maxwell’s equations, which describe the way that electric
and magnetic fields propagate through space. (A radar pulse is nothing more than an
electromagnetic wave.) There was nothing new about the physics; the Maxwell equations
have been known since the 19th century. The difficulty was all in the mathematics. Before
the Fast Multipole Method, it took a prohibitively large number of calculations to compute
the radar signature of something as complicated as an airplane. In fact, scientists could
not compute the radar reflection of anything other than simple shapes.
It was known in principle that Maxwell’s equations could be formulated as an
integral equation, which is more tolerant of facets, corners, and discontinuities. To solve
these, one must be able to calculate something called a Green’s function, which treats
the skin of the plane as if it were made up of many point emitters of radar waves, adding
. . . the difference up the contribution of each source. This approach reduces Maxwell’s equations from a
between computing three-dimensional problem to a two-dimensional one (the two dimensions of the plane’s
the radar signature surface). However, that reduction is still not enough to make the computation feasible.
Using Green’s function to evaluate the signal produced by N pulses from N points on the
of a coarse
target would seem to require N2 computations. Such a strategy does not work well for
approximation to large planes because the larger the plane is, the more data one needs to include and this
an airplane and approach requires an impractically large computational effort.
The Fast Multipole Method builds on the insight that the problem becomes more
computing the
manageable if the source points and target points are widely separated from one
radar signature of a another. In that case, the radar waves produced by the sources can be approximated
particular model of by a single “multipole” field. Although it still takes N computations to compute the
aircraft. multipole field the first time, after that you can reuse the same multipole function over
and over. Thus, instead of doing 1 million computations 1 million times (a trillion
computations), you do 1 million computations once, and then you do one computation
1 million times (2 million computations in total). Thus, Fast Multipole Method makes the
more efficient Green’s function approach computationally feasible.
A second ingenious idea behind the Fast Multipole Method is that it can be applied
even when the source points and target points are not widely separated. You simply
divide up space into a hierarchical arrangement of cubes. When sources and targets lie in
adjacent cubes, you compute their interaction directly (not with a multipole expansion).
That part of the Fast Multipole Method is slow. But the great majority of source-target
pairs are not in adjacent cubes. Thus their contributions to the Green’s function can be
FUELING
innovation and discovery
30
OCR for page 31
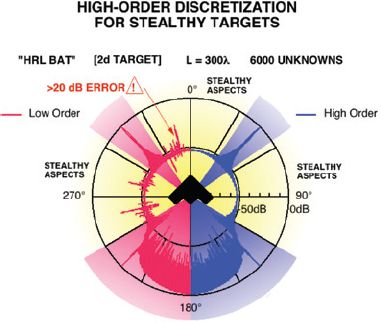
11 / Simulation of two-dimensional radar scat-
tering from a stealthy airplane, similar in shape
to the B-2 bomber. The front of the plane is at
the top; two simulated radar signals are plotted
in red and purple. On the left (red) is a com-
putation using a low-order discretization. It
incorrectly shows a considerable radar signal to
the front and side of the airplane. On the right
(purple) is a more accurate reconstruction of the
radar signal, which would in practice be com-
puted with the Fast Multipole Method. Note
the near absence of a radar signal to the front
and side of the airplane. (Actual three-dimen-
sional data for the B-2 bomber are classified.)
Reprinted with permission from Mark Stalzer,
California Institute of Technology. /
computed quickly, using the multipole approximation. Because most of the calculation is
accelerated and only a tiny part is slow, the overall effect is a great speedup.
In practice, the Fast Multipole Method has meant the difference between computing
the radar signature of a coarse approximation to an airplane and computing the radar
signature of a particular model of aircraft. While it would be tempting to say that it has
saved the Air Force millions of dollars, it would be more accurate to say that it has enabled
them to do something they could not previously do at any price (see Figure 11).
The applications of the Fast Multipole Method have not been limited to the military.
In fact, its most important application from a business perspective is for the fabrication
of computer chips and electronic components. Integrated circuits now pack 10 billion
transistors into a few square centimeters, and this makes their electromagnetic behavior
hard to predict. The electrons don’t just go through the wires they are supposed to, as
they would in a normal-sized circuit. A charge in one wire can induce a parasitic charge
in other wires that are only a few microns away.
Predicting the actual behavior of a chip means solving Maxwell’s equations, and the
Fast Multipole Method has proved to be the perfect tool. For example, most cell phones
now contain components that were tested with the Fast Multipole Method before they
were ever manufactured.
At present the semiconductor companies use a slightly simpler version of the
Fast Multipole Method than the original algorithm developed for Defense Advanced
Research Projects Agency. The simpler version is applicable to static electric fields or
in the 21st Century
The Mathematical Sciences
31
OCR for page 32
(a) (b) (c) (d)
(e) (f)
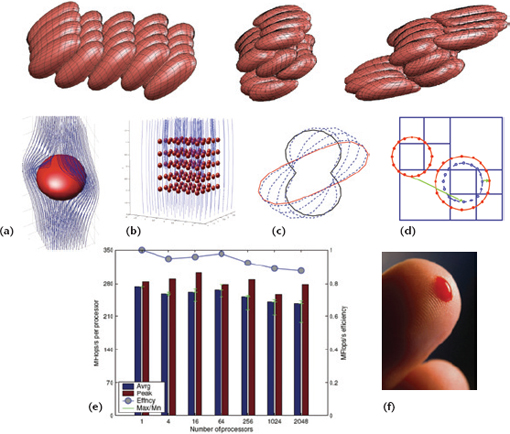
12 / A simulation of red blood cells, performed on the Jaguar computer at Oak Ridge National Labo-
ratory, won the Gordon Bell Prize for best use of supercomputing in 2010. The Fast Multipole Method
was used to accelerate the computation of long-range interactions between red blood cells and
plasma. A single-cell computation is shown in (a) and multicell interactions are shown in (b). Each
cell’s boundary is discretized (c). The hierarchical structure of the Fast Multipole Method computation
is shown schematically in (d) and (e). The volume of blood simulated is shown in (f). This was 10,000
times the volume of any previous computer simulation of blood flow that accurately represented cel-
lular interactions. Reprinted from A. Rahimian, I. Lashuk, S.K. Veerapaneni, C. Aparna, D. Malhotra,
L. Moon, R. Sampath, A. Shringarpure, J. Vetter, R. Vuduc, D. Zorin, and G. Biros, 2010, Petascale
direct numerical simulation of blood flow on 200K cores and heterogeneous architectures. ACM/IEEE
Supercomputing (SCxy) Conference Series: 1-11, Figure 1 with permission from IEEE. /
low-frequency electromagnetic waves. Believe it or not, even a 1-gigahertz chip—which
operates at 1 billion cycles per second—operates at low frequency from the point of view
of the Fast Multipole Method! That is because a 1-GHz electromagnetic wave still has a
wavelength that is much longer than the width of a chip.
However, it is quite possible that the computer industry will one day graduate to optical
chips, which will use light waves instead of electricity to communicate. A wavelength of
light is much shorter than the width of a chip. So for an integrated optical chip, the high-
frequency version of the Fast Multipole Method will become an essential part of the product
FUELING
innovation and discovery
32
OCR for page 33
development cycle. If so, the small investment in mathematical sciences that Auslander
made in 1990 will pay off in an even bigger way three or four decades later.
Finally, it is worth noting that variants of the Fast Multipole Method are applicable
to problems that have nothing to do with electromagnetism. The method is relevant to
any situation where a large number of objects interact with one another, such as stars
in a galaxy or red blood cells in an artery. Each red blood cell affects many nearby red
blood cells, because they are packed quite densely inside a viscous fluid (the plasma). In
addition, blood cells are squishy: they bend around curves or around each other. To
take this into account, a good computer simulation needs to track dozens of points on
the surface of each blood cell, and those points interact strongly with one another as the
cell maintains its structural integrity.
In 2010, a simulation of blood flow based on the Fast Multipole Method won the
prestigious Gordon Bell Prize for peak performance on a genuine (i.e., not a toy) problem
of supercomputing (Figure 12). Researchers at the Georgia Institute of Technology and
New York University used the Oak Ridge National Laboratory’s Jaguar supercomputer
to simulate the flow of 260 million deformable red blood cells (about the number from
one finger prick). This smashed the previous record of only 14,000 cells and allowed the
simulation to approximate the real fluid properties of blood. Although media attention
focused on the supercomputer, the calculation would not have been possible without
the Fast Multipole Method, implemented in a new way that was adapted to parallel
computing. Ultimately, such simulations will help doctors understand blood clotting
better and perhaps improve anticoagulation therapy for people with heart disease.
in the 21st Century
The Mathematical Sciences
33
OCR for page 34
Mathematical Sciences Inside...
The mathematical sciences underpin many of the technologies on which national defense
depends. Cutting-edge mathematics and statistics lie behind smart sensors and ad-
vanced control and communications. They are used
throughout the research, development, engineering,
and test and evaluation process. They are embed-
ded in simulation systems for planning and for war-
fighter training. Since World War II, the mathemati-
cal sciences have been key contributors to national
defense, and their utility continues to expand. This
graphic illustrates some of those impacts.
The mathematical sciences are used in planning
logistics, deployments, and scenario evaluations
for complex operations.
Mathematical simulations allow
predictions of the spread of smoke and
chemical and biological agents in urban
terrain.
Mathematics is used to design
Mathematics and statistics advanced armor.
underpin tools for control
and communications in
tactical operations.
34
OCR for page 35
The Battlefield
Signal analysis and control
theory are essential for drones.
Large-scale computational codes are
used to design aircraft, simulate flight
paths, and train personnel.
Signal processing facilitates
communication capabilities.
Mobile translation systems employ voice
Satellite-guided weapons utilize GPS
recognition software to reduce language
for highly-precise targeting, while
barriers when human linguists are not
mathematical methods improve
available More generally, math-based
ballistics.
simulations are used in mission and
specialty training.
Modeling and simulation facilitates
trade-off analysis during vehicle
design, while statistics underpins
test and evaluation.
35
