Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 36
/
Cellular Automata
Sublimely Complex
A
sandpile grows in an hourglass, one grain at a time. Occasionally the impact of
one sand grain will create a minicascade of grains. Even less often, a minicascade
will trigger a macrocascade that changes the shape of the whole sand pile. How
often do these cascades occur, and do they follow a predictable pattern?
A snowflake grows by attaching one molecule of water at a time. How does that
process lead to the lacy, frilly shapes that we see in real snowflakes? What do we get if
we grow the snowflake in different ways, using different attachment rules?
A city has two directions of traffic, east and north. At each intersection a car can
proceed only if there is no other car already in the intersection. How many cars do you
need to have in the city before gridlock ensues? Can the traffic self-organize into moving
patterns?
These are three examples of a stylized mathematical model called a cellular
automaton. Often inspired by real physical objects (such as sandpiles, snowflakes, and
traffic), cellular automata demonstrate that amazingly complicated large-scale effects
can arise from very simple local rules. They have been applied to other phenomena as
diverse as avalanches and wildfires.
There is a widespread belief that highly complex systems can only be understood
through computer simulation. However, mathematicians have found that simulation is
far from the only way to discern patterns and phenomenology.
“Packard snowflakes,” invented by Norman Packard in 1984, begin with a hexagonal
lattice, like a honeycomb, in which one cell is filled by an ice crystal. One particularly
interesting snowflake grows by the following rule: If an open cell is adjacent to 1, 4, 5, or
6 cells that are already filled, then at the next time step that cell fills and freezes. However,
nodes that are adjacent to 0, 2, or 3 “frozen” nodes remain unfrozen at the next step.
FUELING
innovation and discovery
36
OCR for page 37
After many steps, a shape emerges that bears a striking resemblance to a real
snowflake (Figure 13). What if we let the Packard snowflake grow for as long as we
want? Will all of the gaps in the snowflake eventually be filled?
In computer simulations, every gap seemed to fill eventually. But in 2006, it was
shown that unfillable gaps do exist. The closest unfillable gap to the center is at least
a billion cells away! Because a billion billion cells have to be filled before you can even
get to this gap, it’s no wonder that simulations never saw it. However, a billion billion is
not an unrealistic number. It is less than the number of molecules in a milligram of ice.
This example demonstrates the value of mathematical analysis and mathematical proof,
which can provide insights that may be otherwise unavailable.
The cellular version of a sandpile starts with a rectangular grid and a distribution
of sand grains on the grid that may be highly unstable. For instance, a thousand or a
million grains could be stacked up into a tower (something quite unachievable with real
sand). Like the Packard snowflake, the sandpile evolves by discrete steps. At each step
in this simulation, a rule requires that any cell that is occupied by a stack of four or more
grains of sand will redistribute one grain to each of its four neighbors. Of course, this
may cause one of the neighbors to have four or more grains, so that the cell topples at
the next time step. A cascade of toppling grains is thereby produced that can continue
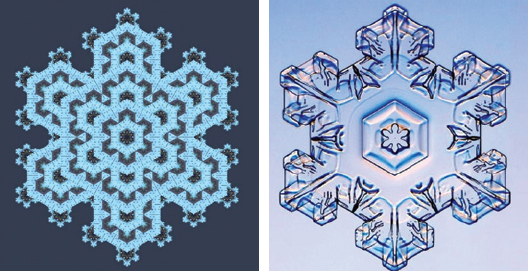
13 / A “snowfake” grows on a hexagonal grid by using simple attachment rules that model the ad-
hesion of water molecules to a growing ice crystal. The resulting model (left, reprinted with permis-
sion from Janko Gravner, UC Davis, and David Griffeath, University of Wisconsin) looks remarkably
similar to a real snowflake (right, reprinted with permission from Ken Libbrecht, California Institute
of Technology.). The final macroscopic shape depends in very subtle ways on the local attachment
rules on the molecular scale. /
in the 21st Century
The Mathematical Sciences
37
OCR for page 38
14 / In a cellular automaton model of a sandpile, a billion 15 / The rotor-router model is a deterministic version of
grains of sand form complex patterns whose existence and a random process called internal diffusion-limited ag-
shape can be confirmed from the mathematical theory of gregation. The boundary has been proven to be circu-
free-boundary problems. Colors denote the number of grains lar; the “puckers” are still unexplained. Reprinted with
of sand in each cell (0, 1, 2, or 3). Reprinted with permis- permission from Tobias Friedrich (Max Planck Institute)
sion from David B. Wilson, Microsoft Research. / and Lionel Levine (Cornell University). /
for a very long time but ultimately settles down into a final configuration that looks like
Figure 14. Note that in this figure, every cell contains 0, 1, 2, or 3 grains of sand and the
cells are color-coded accordingly.
What is the shape of this final configuration? Does it depend on the number of grains
of sand? What about the mysterious pattern of triangles that is so apparent in Figure 14?
In 2011, it was proved that at a large scale, the final shape is independent of the size.
Thus a sandpile with a billion grains looks about the same as a sandpile with a million
grains (only larger). Likewise, the pattern of colors stabilizes, so that every sufficiently
large sandpile will look the same as the others (only larger or smaller).
The proof involves a mathematical model known as a free-boundary problem. Such
problems arise, for example, in the study of combustion, glaciers, and stalactites, when
a scientist is solving for not just an unknown function (say, the temperature in a moving
flame) but also an unknown domain on which the function is defined. The theory of this
particular free-boundary problem is less than 20 years old. Thus the sandpile problem,
which might at first seem like an amusing game, is in fact intimately tied both to physics
and to new developments in the mathematical sciences.
Another beautiful and conceptually important cellular automaton is called the “rotor-
router.” One version was designed to mimic internal diffusion-limited aggregation,
which is more or less the flip side of snowflake growth. Imagine a crystal that instead of
growing by attachment of particles from outside, grows by attachment of new particles
from within. Each new particle wanders around the inside of the crystal at random until
it hits a cell that has not been occupied yet and stops there.
FUELING
innovation and discovery
38
OCR for page 39
Unlike the previous two examples, internal diffusion-limited aggregation involves
randomness. A rotor-router model was designed to be essentially a derandomized
version of internal diffusion-limited aggregation, where each new particle follows a
prescribed sequence of turns that is designed to distribute its motion equally in each
direction. In 2005, it was shown that the shape of a crystal grown by the deterministic
Though much
rotor-router model is the same as the shape of one grown by internal diffusion-
remains unknown
limited aggregation: a circle (see Figure 15). This result may appear specialized, but
the principle it illustrates is much more general: Sometimes the average behavior of about cellular
a random system can be well captured by a deterministic system. In such cases the
automata, it is
randomness may not actually be an essential feature of the process.
exactly at such
The theory of cellular automata remains a very lively area of research, awash in
wild and untamed
examples, with many unexplored territories and relatively few guiding or unifying principles
to join them. Cellular automata have been used to study avalanches, forest fires, landslides,
frontiers that the
and earthquakes, among others. The traffic model in Figure 16 shows that a traffic jam
mathematical
must happen before the city streets are 100 percent occupied. Simulations suggest that
sciences grow.
the onset of traffic jams happens when the density is between 30 and 40 percent, and no
one yet has been able to close the gap between the theory and the experiments to really
understand the dynamics of traffic. And there seems to be an intermediate and remarkably
structured regime between freely moving streets and gridlock that could be described as a
moving traffic jam whose existence has not yet been confirmed.
Though much remains unknown about cellular automata, it is exactly at such wild
and untamed frontiers that the mathematical sciences grow. The connections between
cellular automata and more classical mathematics, such as those mentioned above, bode
well for the future development of the subject. These connections are like wires bringing
electricity to the frontier.
16 / Biham-Levine-Middleton traffic model
(right, reprinted with permission from
Alexander Holroyd, Microsoft Research): In
this idealized version of a grid of one-way
streets, eastbound traffic (red) interacts
with northbound traffic (blue). Jammed
regions are solid, and flowing traffic forms
dashed lines. /
in the 21st Century
The Mathematical Sciences
39
