Probability and Statistical Physics
Connecting Microscopic and Macroscopic
In 1827, a botanist named Robert Brown noticed that grains of pollen suspended in water did a strange sort of dance when examined under a microscope. At first he thought the pollen was alive. But in 1905, Albert Einstein explained the real cause of “Brownian motion,” which had nothing to do with biology. The grains are constantly buffeted by collisions with water molecules, which cause them to jiggle in random directions.
It is surprisingly common for random microscopic events to produce predictable effects at a macroscopic level. The Brownian motion of any single particle of smoke is highly unpredictable, yet smoke spreads in a room at a predictable rate. Iron atoms make innumerable random choices on which way to spin, but at a predictable temperature their spins spontaneously line up and the iron becomes magnetized. The voids in a porous material may be distributed randomly, but at a certain density, which is predictable, they connect up and the material becomes permeable. There are three kinds of “random path” here: the meanderings of a smoke particle, the boundary between spin-up and spin-down atoms in a magnet, and the path of water through a rock. But remarkably, all these disparate phenomena (or at least a simplified mathematical model of each one) can be brought under one roof.
In 2000, a universal mechanism was discovered that shows how microscopic disorder can lead to macroscopic order for two-dimensional systems. This discovery is now called Schramm-Loewner evolution, which allows precise calculations of macroscale phenomena that could until then only be predicted nonrigorously. Not only that, the mechanism applies to the random processes mentioned above as well as to others. A single parameter, κ (the Greek letter kappa), distinguishes Brownian motion (κ = 8)
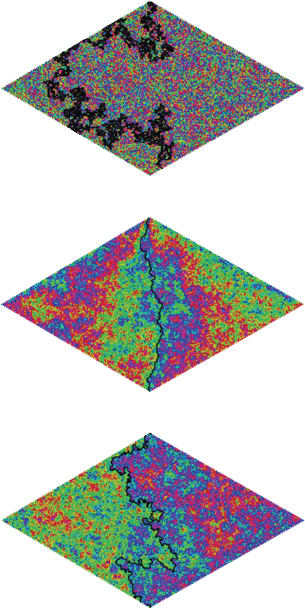
25 / Schramm-Loewner evolution for different values of k. For example, critical percolation (top) gives trajectories with κ = 6. The middle image shows κ = 0.5, and the bottom image κ = 8/3. Reprinted with permission from Scott Sheffield, Massachusetts Institute of Technology. /
from measures of the boundaries between small regions of materials (“magnetic grains”) that are aligned magnetically (κ = 3) or paths for water percolation (κ = 6) (Figure 25). Schramm-Loewner evolution is a wonderful unified description of all these separate phenomena, illuminating how disorder can create order.
The most essential feature of Schramm-Loewner evolution is a symmetry property called conformal invariance. Conformal invariance has two components: scale invariance and rotation invariance. The first means that a Brownian trajectory will look just the same at any level of magnification. If you blow it up by a factor of 10, it will look just as jiggly as before. The formerly small bounces will become big bounces—but you will see new, even smaller bounces that you couldn’t make out before. Rotation invariance means that Brownian motion has no preferred direction. For example, in a closed room, smoke will go everywhere.
Consider a crack that grows randomly inward from the edge of an infinite pane of glass. According to the idea on which Schramm-Loewner evolution is based, the pane of glass can always be “healed” by a conformal transformation, deforming the glass in a way that pushes the crack back out to the boundary. If the crack grows, the glass can be healed again. In this never-ending process of cracking and healing, the attachment point of the crack moves around. In fact, it jiggles very erratically along the edge of the glass. Does this sound familiar? The attachment point is actually undergoing one-dimensional Brownian motion. The intensity of the jiggling is described by the parameter κ larger values of κ correspond to more intense jiggling and to more jagged cracks. The basic idea of Schramm-Loewner evolution converts any two-dimensional, conformally invariant random process into a one-dimensional Brownian motion. Many questions become simpler after they are restated as a Schramm-Loewner evolution. What is the probability that the trajectories of two pollen grains in a petri dish will intersect before the grains reach the edge of the dish? What is the probability that water will percolate from one side of a

26 / Critical percolation model. When each cell has an equal probability of being red or white, the red and white cells connect up into very long networks, and the interface between them is a curve described by Schramm-Loewner evolution. Reprinted with permission from Michael Kozdron, University of Regina, Saskatchewan. /
rectangle to the other before it escapes out the top or bottom? What is the fractional dimension (or roughness) of the outside of a cloud of smoke? All of these questions have precise answers now.
Schramm-Loewner evolution is a purely mathematical construct. There is no known physical mechanism that can duplicate the cracking-and-healing process described above. It’s “mathemagic” in the best sense.
Conformally invariant processes are particularly relevant to the physics of phase transitions, such as the freezing of water or the magnetization of iron. (Just as there is a freezing point for water, above a certain temperature, iron will not magnetize; below that temperature, it will.) These processes are scale-invariant because it is precisely at a phase transition that, when the temperature is dropping, small-scale, local correlations become large-scale as the ice crystals or iron crystals lock into place.
Though Schramm-Loewner evolution is a key to understanding such random processes in two dimensions, it has two caveats. First, it is anything but routine to prove that a given random process corresponds to a particular value of κ. There are some processes, such as the growth of polymers (which are like self-avoiding random walks), where the appropriate value of κ is strongly suspected but not rigorously established.
Second, Schramm-Loewner evolution is—unfortunately—limited to two dimensions. It seems very likely that three-dimensional random processes cannot be classified by a single parameter such as κ. It is likely also that the critical exponents describing the correlation of nearby molecules are not as simple as they are in the two-dimensional case. So 21st century mathematical scientists still have their work cut out for them as they try to explain phase transitions in our three-dimensional world.
So 21st century mathematical scientists still have their work cut out for them as they try to explain phase transitions in our three-dimensional world.
However, Schramm-Loewner evolution provides a model for how a theory of phase transitions might look. Research based on Schramm-Loewner evolution has twice won the Fields Medal, one of the highest honors in the mathematical sciences. An award like this shows the remarkable amount of esteem among mathematical scientists for a discovery that is scarcely a decade old.
Remember how magical it seemed when CD players started to appear in automobiles? How could a precision instrument, which has to detect pits less than a micron across, possibly function in an environment where it is routinely jolted distances that are tens of thousands of times larger than that? The magic is not in the shock absorbers, it’s in the mathematical sciences. A method called maximum likelihood sequence estimation, based on the statistical technique called maximum likelihood, works out the most likely sequence of 1s and 0s recorded on the disk and compensates for the noise and errors created by the bumpy car ride.
Many other technologies that we now take for granted are based on mathematical ideas. Other inventions that seem visionary today but might be commonplace 20 years from now, likewise depend on math. To illustrate that point, the table below lists 10 inventions whose patents cite a method from the mathematical sciences. The data are from the Google patent database at www.google.com/patents, accessed on August 3, 2011. The terms are ordered roughly by their frequency of occurrence in the Google database.
![]() Fast Fourier Transform (FFT)
Fast Fourier Transform (FFT)
The industry standard way of decomposing an electronic signal into its constituent frequencies, based on samples taken at regular time intervals.
This patent is for a “monolithic” silicon chip that can compute FFT’s; such chips are used in digital image processing, speech recognition, and transmission as in cell phones.
Patent No. 4547862 (1985) TRW, Inc.
![]() Correlation coefficient
Correlation coefficient
A basic statistical method for determining how closely related two paired sets of data are.
An optical scanner locates a “bull’s-eye” on a label by finding the correlation between scanned pixel sequences and the expected sequence for a cross section of the bull’s-eye.
Patent No. 6122310 (2000) United Parcel Service

![]() Viterbi algorithm
Viterbi algorithm
Algorithm used in cell phones and CD and DVD players to decode noisy signals. Its key idea is to use “soft,” probabilistic decision procedures.
This patent is one of hundreds that tweaks the original version, here by speeding up the “traceback” part of the algorithm.
Patent No. 6904105 (2005) Intel

![]() Elliptic curve
Elliptic curve
Algebraic structure used in public-key cryptography—for example, to authenticate the user of a smart card.
In this patent, users can pick their own elliptic curve instead of selecting one from a centrally managed registry.
Patent No. 6446205 (2002) Citibank

![]() B-spline
B-spline
The industry standard method of representing smooth surfaces, used in computer-aided design and manufacturing.
B-splines have become popular in recent years with video game manufacturers; in this patent, they are used to generate smooth motions of three-dimensional figures under user control.
Patent No. 5982389 (1999) Microsoft
![]() Conjugate gradient method
Conjugate gradient method
An iterative method for solving linear equations (Ax = b) or energy minimization problems involving many variables.
Used in this patent to compute the electronic structure of simple molecules like glass. The energy depends on thousands of variables, each representing a possible electron orbit.
Patent No. 6106562 (2000) Corning
![]() Complex number
Complex number
Numbers of the form a + bi (where i = ![]() ).
).
Applications such as FFT require integrated circuits capable of adding and multiplying complex numbers, as described in this patent.
Patent No. 4858164 (1989) United Technologies
![]() Minimal surface
Minimal surface
Surfaces, such as soap films, that have the least area spanning a given boundary.
This patent proposes the Schwarz triply periodic minimal surface as a scaffold for regenerating human bone and organ tissue.
Patent No. 7718109 (2010) Mayo Foundation
![]() Support vector machine (SVM)
Support vector machine (SVM)
Recently discovered (1995) method for partitioning data into classes.
SVMs are used in an implantable “brain pacemaker” for Parkinson’s disease patients, to determine when the patient is having a seizure or movement disorder.
Patent No. 12/694035 (applied 2010) Medtronic, Inc.
![]() Quaternion
Quaternion

Hypercomplex numbers used primarily for composing spatial rotations.
This patent is for a toothbrush that will automatically track its location relative to the user’s teeth. Quaternions are used to compensate for motion of the user’s head.
Patent No. 12/866,381 (applied 2010) Philips
This page intentionally left blank.






