Determining the Necessary Level of Precision for Body Armor Testing
The new body armor testing protocol assesses body armor performance via two metrics, the probability of no penetration and backface deformation (BFD). Assessing the probability of no penetration is relatively straightforward in the sense that the outcome is binary (either a plate is penetrated or it is not), and the determination of that binary outcome is fairly clear-cut. Measuring and assessing BFD is less clear-cut because, as described in Chapter 4, the test methodology, particularly the use of Roma Plastilina #1 as a recording medium, introduces variability into the BFD measurement process. In this appendix the committee focuses on BFD measurement.
INTRODUCTION
As discussed in Chapter 7, there are two types of mistakes that are possible when interpreting the results of live-fire armor testing. The first is grievous—the inadvertent acceptance of armor from a manufacturer that should have been rejected. The second is the nonacceptance (failing) of armor from a manufacturer that should have been accepted. Both errors are theoretically possible in any type of statistically based test, though as will be discussed, for all practical purposes the existing armor testing protocol prevents the first type of mistake. This is true as long as the mean is accurate independent of the level of precision in the test.
For BFD, the protocol involves subjecting a set of 60 samples from a lot to live-fire testing. If on the first shot the 90 percent upper tolerance limit calculated with 90 percent confidence is in excess of 44 mm, the manufacturer fails the first article test (FAT). In the hypothetical case of armor with no variance and a test with no variance, the armor is accepted as long as the sample mean of the BFD calculated from the 60 samples is less than 44 mm. An increase in variance from any source (the armor itself, backing material behavior, or measurement) causes a spread in the data. If these effects are normally distributed, and if we assume that the distribution is perfectly estimated from the 60 shots (i.e., there is no sampling error), then a manufacturer will pass the FAT if the 90th percentile of the distribution is less than 44 mm and will fail if it is greater than 44 mm.
Under these conditions, if we assume that the variability of the armor, measured in terms of standard deviations, is 1 mm, then body armor designs with
a true mean BFD (µpop) less than 42.7 mm will pass FAT. Furthermore, under these conditions a design that just passes FAT with µpop = 42.7 mm will cause 10 percent of the individual body armor plates to experience BFDs ![]() 44 mm. In fact, 5 percent of the plates will have BFDs
44 mm. In fact, 5 percent of the plates will have BFDs ![]() 44.3 mm and 1 percent will have BFDs 45 mm.
44.3 mm and 1 percent will have BFDs 45 mm.
This effect can be illustrated as follows. First consider a hypothetical armor system that has negligibly small variance in true performance. If the backing material exhibits a variance characterized by a standard deviation σbckmatl, then the true population of BFDs will be
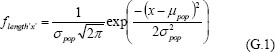
where µpop is the mean BFD for that particular armor system (which depends on the mechanical response of the armor and the elastic recovery in the backing material) and σpop= σbckmtl. For µpop = 42.7 mm and with σpop = 1 mm, Figure G-1 shows the distribution of BFDs for the hypothetical population of body armor.
The impact of employing a measurement technique that adds significant variability is illustrated in Figure G-2. In this illustration, we assume the
measurement technique adds 2 mm to the standard deviation, so that σpop= 3 mm . To pass the FAT, again assuming no sampling error, the manufacturer must now have a design in which µpop ![]() 40.15 mm. The dotted line curve represents a population of body armor that, with σpop= 3 mm, can just pass FAT with µpop= 40.15 mm. Comparing the two curves, we see that to decrease the likelihood of failing FAT, the manufacturer must shift the entire distribution to the left so that the area under the curve falling to the right of the 44 mm is less than 10 percent. If the additional variance reflected in the curve is due to the performance of the backing material during testing rather than variance in the armor, then it is proper to refer to this as a “design penalty.” In other words, armor that would appropriately prevent injury can be inadvertently rejected during testing due to variance associated with the test (i.e., variance in the backing material and, in addition, in the measurement methods).
40.15 mm. The dotted line curve represents a population of body armor that, with σpop= 3 mm, can just pass FAT with µpop= 40.15 mm. Comparing the two curves, we see that to decrease the likelihood of failing FAT, the manufacturer must shift the entire distribution to the left so that the area under the curve falling to the right of the 44 mm is less than 10 percent. If the additional variance reflected in the curve is due to the performance of the backing material during testing rather than variance in the armor, then it is proper to refer to this as a “design penalty.” In other words, armor that would appropriately prevent injury can be inadvertently rejected during testing due to variance associated with the test (i.e., variance in the backing material and, in addition, in the measurement methods).
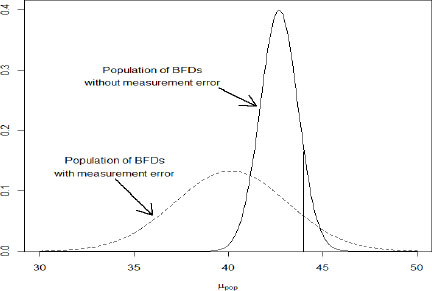
FIGURE G-2 The consequence of measurement error on the apparent depths of BFDs. The normal distribution given in Figure G-1 is convoluted with a Gaussian spreading function to represent measurement error. The result is another normal distribution with a larger standard deviation, given by the dotted line. Both populations are just able to pass the FAT (assuming no sampling error) as their 90th percentiles are just below 44 mm.
This means the test is more conservative, in the sense that, if anything, armor that might have been adequate is rejected. Measurement error will not increase the chance of armor with a given mean BFD, µpop, being accepted. Various people have referred to this as, for instance, erring on the safe side or taking the soldiers’ perspective.
This inadvertent rejection of adequate armor, however, also is a problem. It decreases the availability of armor directly due to its rejection; concomitantly it increases cost and produces a degree of randomness in the testing that can diminish vendor confidence, because indistinguishable lots of armor will sometimes pass and sometimes fail.
The relative contribution of variance in the clay and finite precision in the measurement technique is therefore important and can be assessed quantitatively. In particular, it is possible to identify the relative importance of the precision of the measurement.
RELATIONSHIP BETWEEN BACKING MATERIAL VARIANCE AND MEASUREMENT PRECISION
The process of characterizing the cavities produced in the plastic backing material during live-fire ballistic testing of hard body armor is the same as measuring critical dimensions of manufactured articles. In all such problems there exists a trade-off between cost (capital equipment, operating costs, and throughput rate, and so on) and precision. Therefore the field of engineering economics has long employed rigorous methods for making decisions about the value of precision relative to its cost. Development efforts frequently have the goal of achieving high precision at low cost. In deployment the decision is one of selecting amongst available techniques to achieve maximum utility.
That is, with a few substitutions (in square brackets in following extract), an expression of the principles employed in specifying metrology tools in the context of manufacturing can be generalized to apply to measurement deformation results (Besfamil’naya, 1974, pp. 458-460):
If a planned level [of dimensional reproducibility] is to be justified economically, it is not only necessary to select, or focus upon, the measurable variables suitable for evaluating [dimensions], but also to assign the appropriate precision, and consequently also the cost of measurements and inspection. That explains why one of the central aspects of … quality assurance … is optimized selection of monitoring and measuring equipment, as well as the characteristics set forth in technical specifications for new instruments and gages as to precision, reliability, cost, etc.
One advantage of employing a rigorous decision-making process is that it permits a meaningful choice to be made under current circumstance and creates a framework to identify how precision requirements must evolve as specifications and capabilities change.
Three ideas are developed below. The first is a general discussion of stacked errors—that is, how variability of backing material deformation and variability in the results of the measurement tools combine to give the general result. Secondly, the available data associated with the use of RP #1 is considered in the context of justifiable precision. Finally, the need for precision in the context of improving the backing material or shifting to an alternative technology is discussed.
As described in Chapter 3, the cavities produced in the backing medium during both low-velocity calibration drop tests and high-velocity tests of stingballs and soft armor are all characterized by substantial variance. Thus, the problem to be considered is how much the variance of the measurement technique adds to an already recognized noisy signal (i.e., the depth of the cavities in the backing medium).
The initial portion of the following analysis assumes a normal distribution for both the population of cavity depths under identical conditions and for the error associated with the measurement techniques (calipers, laser scanner, or the like). Subsequently, it is shown that the same result obtains without the assumption of normality.
If we have a population of lengths that follow a normal distribution, the frequency of lengths is given by
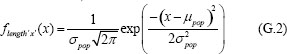
where µpop is the mean length in the population and σ pop is the standard deviation of the population. When integrated over a particular range, this function gives the probability that any given element in the population is in that range.
If the lengths are measured with a tool that yields an instrumental spreading function of the form
![]()
then the function for the apparent length z (z = x + y) that will be recorded is the convolution of these two functions. One of the properties of the Gaussian distribution function is that when convoluted with another Gaussian function the result also is a Gaussian. Assuming there is no systematic error in the measurement tool (i.e., that it is not biased) the mean remains the same and the standard deviations are added in quadrature:
![]()
This is equivalent to the result obtained when there are independent sources of error. Of course we can rewrite this as
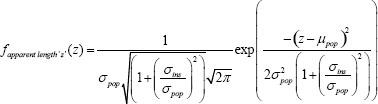
and defining ![]() once again yields the simple Gaussian form back:
once again yields the simple Gaussian form back:
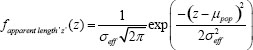
So, one way to assess the effect of high or low precision of the instrument on a signal that has noise is to compare the standard deviation of the “apparent length” distribution to that of the native population.
The fractional change is given by
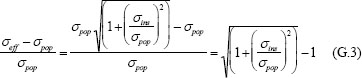
These results can be illustrated graphically (Figure G-3). The purpose of this is to emphasize the contribution of the measurement error relative to variation in cavity formation, given by σins and σpop, respectively. Therefore, the fractional increase in standard deviation, ![]() , is plotted as a function of
, is plotted as a function of ![]() that is, the inverse of the ratio on the right-hand side of equation G.3. When this ratio is 1, the variance associated with the production of the cavity and that of the measurement technique are the same. If the standard deviation of the population (in our case determined by RP #1) is held constant, larger values for this ratio indicate progressively more precise measurement techniques. As Figure G-3 makes evident, there is little practical benefit to improving the measurement technique past the point of σins =0.1xσpop.
that is, the inverse of the ratio on the right-hand side of equation G.3. When this ratio is 1, the variance associated with the production of the cavity and that of the measurement technique are the same. If the standard deviation of the population (in our case determined by RP #1) is held constant, larger values for this ratio indicate progressively more precise measurement techniques. As Figure G-3 makes evident, there is little practical benefit to improving the measurement technique past the point of σins =0.1xσpop.
Specifically, if we assume σpop = 3 mm, all BFD measuring devices with standard deviations of less than 0.3 mm are equivalently precise from a practical perspective in terms of yielding useful data for decision making.
The above analysis assumes that the distributions of both depths and measurements are normal, largely for purposes of clarity. It is not necessary to make this assumption to reach this conclusion. However, this result is more general and holds whenever the length X is probabilistically independent of the measurement error Y. That is, equation G.3 follows from the fact that the variance of the sum of two independent random variables is equal to the sum of their variances (see Appendix M). Thus, the result described here is not dependent on the assumption of normality.
KEY POINT 1: The useful precision of a device used to measure BFD is fundamentally related to the variance in the signal due to the performance of the armor itself and the variance in the medium recording the BFD. Increased precision adds cost without adding benefit if it exceeds a well defined value, i.e., σpop/σins![]() 10.
10.
Based on information briefed to the committee, 3 mm ![]() σ pop
σ pop![]() 4 mm Therefore there is no advantage for the current system to have a measurement tool with precision σins
4 mm Therefore there is no advantage for the current system to have a measurement tool with precision σins ![]() 0.3 to 0 4 mm.
0.3 to 0 4 mm.
Variance in the recording medium in particular, and from the entire test methodology in general, is parasitic and tends to cloud the data, preventing the variance in the armor from being manifest in the test. It also creates a condition that either leads to adequate armor being rejected, overdesign of the armor itself, or both.
As recommended in this report, the main path to improvement of armor testing is to replace RP #1 with a material(s) of lower variance. When this is done, it is crucial that the precision of the BFD be commensurate with that of the improved simulant materials. That is, when the simulant material indents are more reproducibly created, the precision of their measurement becomes more important.
ESTIMATION OF THE RELATIVE PRECISION OF MEASUREMENT TECHNIQUES
With the aggregate set of data provided to the committee, it is possible to make a quantitative assessment for the techniques employed in cavity measurement in RP #1 on the range. First, the data provided in Figure 4-7a in Chapter 4 indicate the standard deviation of drop test results is between 2 and 3 mm depending on the particular clay box.
For illustration, we can use the calculated measurement standard deviations on RP #1 from Walton (2008): 0.82 mm and 0.10 mm for the digital caliper and the Faro laser scanner, respectively.69
Thus, for the Faro arm the ratio of σins/σpop is 0.03, whereas for the digital caliper the same ratio is 0.27. In practical terms, the Faro results in an essentially perfect measurement that is, the variation in recorded measurements of cavity depth will be indistinguishable from the variation observed in the modeling clay.
The digital caliper yields a population of measurements that has a standard deviation that is 3.5 percent larger than that of the BFD population. Thus the variability of the BFDs is dominated by the inherent properties of the RP #1,
________________________
69Appendix M describes possible issues with the methods of Walton et al. (2008).
although this dominance does not mean the precision of the measuring tool is not without cost.
The significance of the limited precision of the caliper is dependent on the design strategy of the armor manufacturer. A worked example helps to illustrate this. Consider the DOT&E BFD protocol requirement: For the first shot test of 60 plates, the 90 percent upper tolerance limit must be less than 44 mm with a 90 percent confidence to pass FAT.
The one-sided upper confidence limit is
![]()
where
![]()
The k1 factor, assuming the data are normally distributed, is
![]()
where
![]()
For the case under consideration, N = 60 and z1-p = zH= z1-0.9 = 1.281552, so a = 0.986 and b = 1.615. Thus, the upper tolerance limit is ![]() , and a manufacturer will pass FAT if YU
, and a manufacturer will pass FAT if YU![]() 44 mm and fail otherwise.
44 mm and fail otherwise.
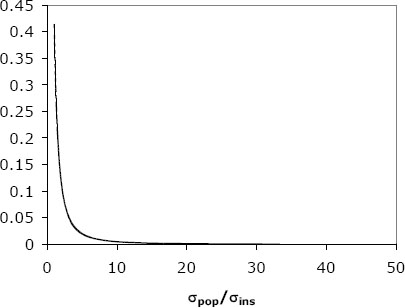
The question, then, is What is the effect on the probability a manufacturer passes or fails FAT for Y ~ N(µ,9), that is, σeff = 3 mm (perfect Faro measurement) versus Y ~ N(µ,9.64), σeff = 3 × 1.035 = 3.105 mm (caliper measurement)?
Because both the sample mean and sample standard deviation are stochastic, rather than derive an analytical expression to calculate the probability a manufacturer passes or fails, we simulate it. That is, we simulate sets of 60 random Y values from the appropriate distribution, from them calculate many YU values, and from those YU values estimate the probability of failing (by calculating the fraction of YU values greater than or equal to 44 mm) for various values of µ 35 ![]() µ
µ ![]() 46.
46.
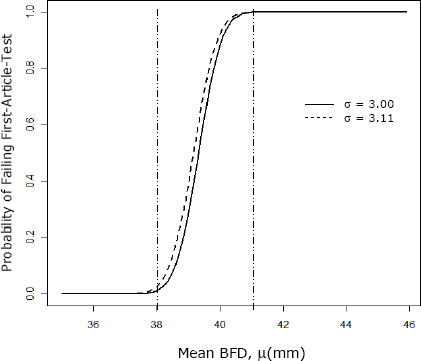
Figure G-4 shows the result, where we see the probability of failure for the hypothetical perfect measurement σ = 3.00 mm, compared to that calculated taking into account the measurement error of the digital caliper a = 3.11 mm.
Before contrasting the two curves it is helpful to consider the general shape of the curve. The form is essentially two plateaus. When the mean value for the BFD is less than 1σ below the critical value, that armor will essentially always be rejected, whereas when the average is a bit more than 2σ below the critical value the armor will be virtually always be accepted.
KEY POINT 2: The variance in the system determines whether or not armor is accepted, where the “system” consists of both the testing methodology, including the BFD measurement tool used in the test, and the armor being tested. If the overall system variance is dominated by the armor, this is correct, as the accept-or-reject decision appropriately prevents highly variable armor (meaning some will be underperforming) from being accepted. However, if the system variance is dominated by the variance in the tissue simulant material (as is the case when RP #1 is used) and/or some other aspect of the testing methodology, including the measurement tool, then Figure G-4 represents a design penalty in units of length.
In other words, even though an armor design gives a BFD 90 percent upper tolerance level ![]() 44 mm in theory, to be certain of passing the test the manufacturer will seek a design with a mean BFD
44 mm in theory, to be certain of passing the test the manufacturer will seek a design with a mean BFD ![]() (44 - 2σ). To the extent that a, the standard deviation observed in the test, is mainly the result of the testing methodology (e.g., Roma Plastilina #1), the manufacturer is forced to overdesign the armor. Conversely, to the extent that the variation induced by the testing methodology can be decreased, the manufacturer has more design space for the armor while still being able to pass FAT.
(44 - 2σ). To the extent that a, the standard deviation observed in the test, is mainly the result of the testing methodology (e.g., Roma Plastilina #1), the manufacturer is forced to overdesign the armor. Conversely, to the extent that the variation induced by the testing methodology can be decreased, the manufacturer has more design space for the armor while still being able to pass FAT.
And, in fact, the available data indicate that the variance in the system is significantly influenced by the behavior of RP #1. The data presented in Figures 4-7 and 4-8 give the standard deviation for the drop tests in the clay of somewhere between 1 and 3 mm. The observed standard deviation reported by Ceradyne for an armor FAT or LAT ranges between 2.93 and 3.82 mm, with most results clustered around 3 mm.70
There are perhaps two complementary ways to view the difference between the two curves. Firstly, the digital caliper always has a higher chance of rejection—that is, the same armor tested with a less precise measuring device is more likely to be rejected.
In looking at Figure G-4, the difference in the probabilities of failure seem small, and, in fact, if the armor designers have as a design target armor with a mean value that is less than 2σ below the cutoff, there is no practical difference. However, if the armor manufacturers are seeking to be on the low end of the rising portion of the curve, there will be a significant difference.
Figure G-5 shows the difference between the two curves (i.e., the probability of failing using the caliper minus the probability of failing using the Faro for each value of µ). This figure shows that for a range of µ values, the increase in the
________________________
70David Reed, President, North American Operations, Ceradyne, Inc., “Pragmatics of Body Armor Testing Manufacturer’s View,” presentation to the committee, August 9, 2010.
probability of failure is significant. For µ ≒ 39 mm, the difference is somewhere around 11 percent; for 38.5 ![]() µ
µ ![]() 40 or so, the difference is at least 5 percent.
40 or so, the difference is at least 5 percent.
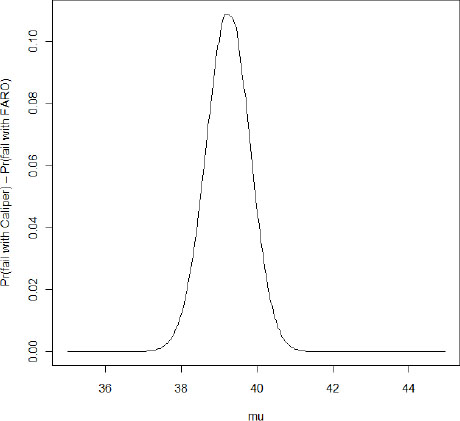
FIGURE G-5 Plot of the difference between the two FAT failure curves given in Figure G-4. This confirms that the maximum distinction occurs for -2σsys![]() (µlot - zcrit)
(µlot - zcrit) ![]() -1σsys. In that range, the probability of rejection can be as much as 11 percent higher.
-1σsys. In that range, the probability of rejection can be as much as 11 percent higher.
There are data available to check whether or not the order-of-magnitude effect expected by this analysis is consistent. The presentation by Ceradyne gives the average BFD and standard deviations for data sets from ESAPI and XSAPI plates
measured by the Aberdeen Test Center (ATC) and H.P. White Laboratory with both caliper and laser scanner.71
First, the standard deviations are between 2.93 and 3.82 mm. Therefore the assumption of a baseline standard deviation of roughly 3 mm in order to estimate the significance of effects is a reasonable choice.
Second, the standard deviations of the populations obtained using laser scanning are roughly 10 percent lower than that using the caliper (for the XSAPI plates, one set is 15 percent lower with laser scanning, the other 4 percent; for the ESAPI plates, the standard deviation is unchanged). This is consistent with the estimates from adding, in quadrature, the standard deviation associated with clay behavior and that of the digital caliper—that is, ![]()
Now, there is another way to view the data presented in Figure G-3. The plateau is a design penalty. For typical results, it is about 4 to 6 mm (twice the standard deviation). The shift between the two curves indicates that the measurement error of the caliper is about 0.2 mm (or 200 µm). Thus, the design penalty associated with the error inherent in the caliper is well over an order of magnitude smaller (3-5 percent) than the design penalty associated with other aggregate sources of variance.
The equivalence of an increased variance to an offset is shown in Figure G-6. This formalism allows comparison to other sources of offset in the data such as are developed in the next section.
KEY POINT 3: A more precise and therefore more expensive measurement device leads to a net reduction in the design penalty of no more than 5 percent.
________________________
71Ibid.
INTRODUCTION OF BIAS OR OFFSET DUE TO HIGH SPATIAL RESOLUTION LASER SCANNING
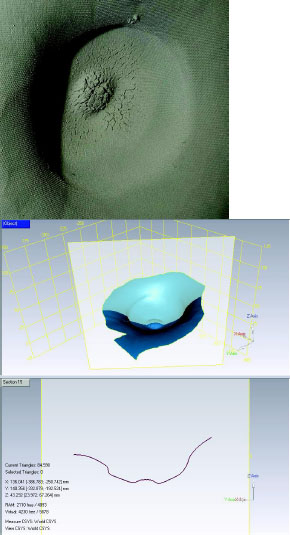
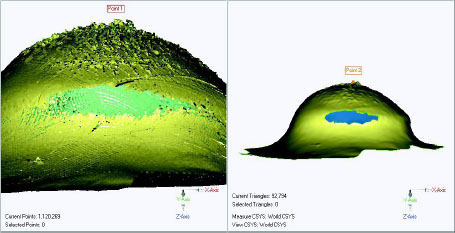
The surfaces of the craters produced during live-fire testing are rough (see Figure G-6). Much of this roughness is not going to be sensed by either the roughly 3 mm (1/8 in.) probe tip used by ATC or, certainly, the roughly 19 mm used by some commercial labs (see Figure G-7).
However, much of the roughness is imaged by the laser scanner, which not only has greater depth resolution (in what is usually called the z-direction), but also has much greater spatial resolution (nominally in the plane perpendicular to the z-direction).

Figure G-8 shows two images provided by the ATC. The image on the left shows the roughness detected at the maximum resolution of the scanner raw data. The data on the right represent the same data set after digital filtering (the point set appears to have been tessellated with triangles to create a surface). The maximum depression in the first case is 42.841 mm whereas in the second it is reported as 41.819 mm. That is, there is a difference between the two in excess of 1 full millimeter. Significantly, the smoothed surface still appears to reflect significant surface roughness that would not be taken into account by the digital caliper probe tip. This roughness of the scanner data is a function of the smoothing algorithm employed.
This estimate of a systematic shift of roughly 1 mm or so in apparent depths is consistent with the assertion in the D. Reed presentation and the data therein on the XSAPI plates.72 Ceradyne calculated average BFDs from the H.P. White Laboratory data: 37.84 mm for the digital caliper and 38.78 mm for the laser scanner. From the ATC data the respective averages were 38.16 mm and 39.41 mm. That is, a net offset is seen between the digital caliper and the laser scanner of approximately 1 mm in tests carried out by a commercial lab and by the Army.
Thus, the apparent offset associated with the way the laser scanner is currently operated appears to be an effective design penalty on the order of 1 mm, or five times larger than that produced by the lower measurement precision of the digital caliper.
KEY POINT 4 When one measurement technique is substituted for another it is necessary to analyze fully how the two techniques differ. In this case, it appears the lower spatial resolution of the digital caliper leads to a lower average indent depth measurement relative to the laser scanner. Thus, there is a design advantage for the manufacturer because it is easier to pass the test, while the higher spatial resolution of the laser as it is currently operated creates a design penalty that is roughly five times larger. In short, the digital caliper is biased toward making it easier for a manufacturer to pass the test while the laser, as it is currently being operated, is biased toward making it harder to pass the test. As discussed in Chapter 5, a best-utility measurement tool should not introduce bias into the measurement.
TOLERANCE INTERVAL REQUIREMENTS
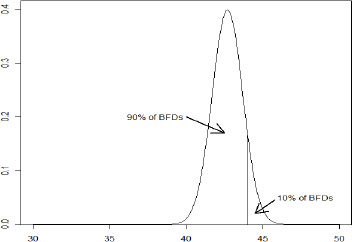
A common mistake is to interpret the tolerance interval test criterion as meaning that each individual body armor BFD (either in the tested sample or the larger population) must be less than 44 mm. Rather, the requirement is, roughly speaking, that one will be very sure that the 90th percentile of all BFDs in the population is less than 44 mm.
Consider, for example, a manufacturer that passes the first article test and whose armor population has a mean BFD performance of 40 mm with a standard deviation of 3 mm. Then the probability that any individual plate produced by this manufacturer will have a BFD greater than 50 mm is 0.000429. While seemingly small, such a probability means that one plate in about 2,300 will have a BFD greater than 50 mm. Given all the plates the Department of Defense procures, that translates into a not insignificant number of plates that will perform in this region. Thus under the current DOT&E protocol it is possible to see BFDs at or above 50 mm.
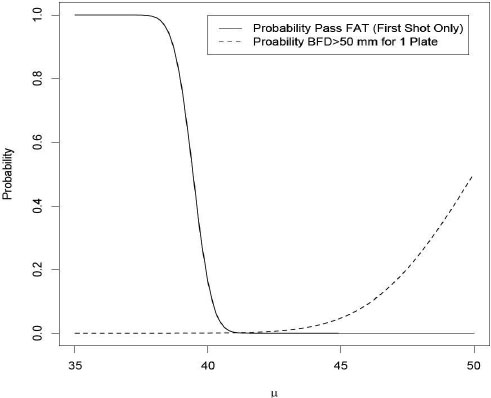
Figure G-9 compares the probability a manufacturer will pass the first article, first shot BFD test (90 percent upper tolerance limit less than 44 mm with 90 percent confidence) for various true BFD levels, µ, against the probability that
________________________
72Ibid.
a plate from the same population will have a BFD greater than 50 mm. The plot shows that the probability a manufacturer can pass FAT recedes virtually to zero before the probability a plate has a BFD ![]() 50 mm becomes large. This is appropriate assuming that 50 mm is the threshold at which serious injury may start to occur. That said, note that at µ = 40 mm there is still some chance that a manufacturer would pass FAT (roughly one chance in 10 or so). If such a manufacturer were to pass FAT then, as previously described, the probability that any one plate could have a BFD
50 mm becomes large. This is appropriate assuming that 50 mm is the threshold at which serious injury may start to occur. That said, note that at µ = 40 mm there is still some chance that a manufacturer would pass FAT (roughly one chance in 10 or so). If such a manufacturer were to pass FAT then, as previously described, the probability that any one plate could have a BFD ![]() 50 mm is 0.000429.
50 mm is 0.000429.
KEY POINT 5: The 44 mm tolerance interval requirement does not mean that all plates will have BFDs less than 44 mm. Rather, the 44 mm tolerance interval requirement in the DOT&E protocol is designed to ensure that the vast majority of plates will have BFDs less than 50 mm, but some small number may exceed 50 mm.
REFERENCES
Besfamil’naya, L.V. 1974. How precision of monitoring and measuring instruments and gages affects cost utilization factors. Measurement Techniques 17(3):458-460.
Rice, K., M. Riley, A. Forster, S.D. Phillips, C.M. Shakarji, D. Sawyer, C. Blackburn, B. Borchardt, and J. Filliben. 2010. Dimensional metrology issues of Army body armor testing. National Institute of Standards and Technology, Final report: February 17.
Walton, S., A. Fournier, B. Gillich, J. Hosto, W. Boughers, C. Andres, C. Miser, J. Huber, and M. Swearingen. 2008. Summary Report of Laser Scanning Method Certification Study for Body Armor Backface Deformation Measurements. Aberdeen Proving Ground, MD: U.S. Army Aberdeen Test Center.