Suppose that a manufacturer must demonstrate that a high percentage of units (say, 100p percent) meet a particular specification with some level of confidence—say, 100(1 - α) percent. Since every unit cannot be tested, any statement must be based on a sample of units (say, n).
The statistical tool to make this demonstration is called a “tolerance bound.” An easy way to think about a tolerance bound is as follows. (The result is stated for upper confidence bounds, as those are the most relevant for the assessment of body armor.)
An upper 100(1 - α) percent tolerance bound for 100p percent of a population is the same as an upper 100(1 - α) percent confidence bound for the 100p percentile of the population distribution.
More formally, the interpretation of an upper tolerance bound is as follows: “If we calculated an upper tolerance bound from many independent groups of random samples, 100(1 - α) % of the bounds would, in the long run, correctly include 100p percent of the population.”
The procedure and/or formula for calculating the one-sided tolerance bound varies depending on the underlying population distribution. This distribution is unknown, and it must be estimated from historical data. If the underlying distribution is normal, then the tolerance bound is calculated as
![]()
where ![]() is the sample mean, s is the sample standard deviation of n data points, and g’ is a factor to adjust the width of the interval. It is available in many software packages, in Odeh and Owen (1980) or in less extensive tabulations in Hahn and Meeker (1991). Notice that the value of g’ depends on the desired confidence, the desired percentage of units, and the sample size.
is the sample mean, s is the sample standard deviation of n data points, and g’ is a factor to adjust the width of the interval. It is available in many software packages, in Odeh and Owen (1980) or in less extensive tabulations in Hahn and Meeker (1991). Notice that the value of g’ depends on the desired confidence, the desired percentage of units, and the sample size.
If the data are not normal, the formulas for tolerance bound calculations are worked out for a number of distributions: see, for example, Krishnamoorthy and Mathew (2009) and Young (2010).
Another option for constructing the tolerance bound is to use a “nonparametric tolerance interval.” The nonparametric tolerance intervals do not make assumptions about the underlying population distribution. However, the cost of not making distributional assumptions is that the nonparametric methods
require larger sample sizes to achieve the same length of bound. In other words, for the same sample size, an upper nonparametric tolerance bound will tend to be higher.
The procedure for calculating a nonparametric tolerance bound is as follows:
• Order the sample data x1, . ., xn from smallest to largest. Denote the ordered set of data as x(1), …, x(n). One of the sample data points will be chosen as the nonparametric bound.
• Find the smallest integer k so that ![]()
![]() , where X is a binomial( n, p) random variable. If k = n + 1, then use the x(n) as the order statistic. Otherwise, x(n) is the upper tolerance bound.
, where X is a binomial( n, p) random variable. If k = n + 1, then use the x(n) as the order statistic. Otherwise, x(n) is the upper tolerance bound.
• The actual confidence level is ![]() . Note that it may not be possible to find a tolerance bound with the values of p and a that are desired. In particular, the smallest sample size needed to have 100(1 - a) percent confidence that the largest observation in the sample will exceed at least 100p percent of the population is n = log(α)/log(p).
. Note that it may not be possible to find a tolerance bound with the values of p and a that are desired. In particular, the smallest sample size needed to have 100(1 - a) percent confidence that the largest observation in the sample will exceed at least 100p percent of the population is n = log(α)/log(p).
In Figure H-1, the bell curve represents the population distribution and the solid vertical line is the 95th quantile of the population distribution. In practice, both of these are unknown. The dotted vertical line is the specification. Since the population distribution is unknown, we test a sample from the population. The small circles are 50-sample observations.
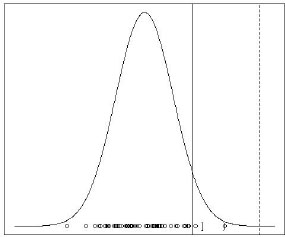
The right bracket (]) shown in the figure is the calculated 90 percent normal tolerance bound for 95 percent of the population. To calculate this bound, we have to assume that the sample data are from a normal distribution. We make this assumption based on the 50 samples and any previous data that we have collected.
The right parenthesis) in the figure is the calculated 90 percent one-sided nonparametric tolerance bound for 95 percent of the population. Notice that the nonparametric tolerance bound is equal to the maximum observation.
In practice, one would calculate only one tolerance bound. If the tolerance bound is lower than the specification (as it is in this case), the test is “passed.” More formally, we are 90 percent confident that 95 percent of the population is below the specification.
As another example, suppose that we have 15 observations: 1.57, -0.57, -1.19, 0.08, 0.83, -1.55, 1.14, 0.63, -0.11, 1.64, 0.79, -0.44, 0.27, 1.18, -0.47. We want to calculate a 90 percent confidence bound for 95 percent of the population. We have x = 0.2533333 and s = 0.9725935.
Using the equation for the normal one-sided tolerance bound, we have g’ = 2.063 and Tp= 0.2533333 + 2.068(0.9725935) = 2.264657.
Using the nonparametric tolerance interval, we order the observations from smallest to largest: -1.55, -1.19, -0.57, -0.47, -0.44, -0.11, 0.08, 0.27, 0.63, 0.79, 0.83, 1.14, 1.18, 1.57, 1.64.
We find that k = 16, so our one-sided tolerance bound is 1.64. However, our confidence level is P(X ![]() 14|5,0.95) = 0.5397, or 54 percent. We require at least n = log(0.1)/log(0.95) = 45 samples to achieve a 90 percent confidence level using the largest sample value as our upper tolerance bound.
14|5,0.95) = 0.5397, or 54 percent. We require at least n = log(0.1)/log(0.95) = 45 samples to achieve a 90 percent confidence level using the largest sample value as our upper tolerance bound.
REFERENCES
Hahn, G.J., and W.Q. Meeker. 1991. Statistical Intervals: A Guide for Practitioners. New York, N.Y.: John Wiley & Sons.
Krishnamoorthy, K., and T. Mahew. 2009. Statistical Tolerance Regions: Theory, Applications, and Computation. New York, N.Y.: John Wiley & Sons.
Odeh, R.E., and D.B. Owen. 1980. Tables for Normal Tolerance Limits, Sampling Plans, and Screening. New York, N.Y.: Marcel Dekker, Inc.
Young, D. 2010. tolerance: An R package for estimating tolerance intervals. Journal of Statistical Software 36(5).



