Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 19
2
Sources of Uncertainty and Error
2.1 INTRODUCTION
The development of a computational model to predict the behavior of a physical system requires a number of
choices from both the analyst, who develops the computational model, and the decision maker, who uses model
results to inform decisions.1 These choices, informed by expert judgment, mathematical and computational con -
siderations, and budget constraints, as well as aspects of the application at hand, all impact how well the computa -
tional model represents reality. Each of these choices has the potential to push the computational model away from
reality, impacting the validation assessment and contributing to the resulting prediction uncertainty of the model.
In approaching a system whose performance requires a quantitative prediction, the analyst will typically need
to make (or at least consider) a series of choices before the analysis can get under way. In particular, thought needs
to be given to the following:
• Relevant or interesting measures of the quantity of interest (QOI) from the point of view of any proposed
application or decision;
• The underlying quantitative model or theory to use for representing the physical system;
• The adequacy of that underlying model or theory for the proposed application;
• The degree to which the simulation code, as implemented, approximates the results of the underlying
model or theory; and
• The fidelity with which the system is represented in the code.
The last four choices in this list are prime sources of analytic uncertainty. In broad terms, the analyst will be
uncertain about (1) the choice of theoretical model to use for predicting the QOI, (2) the inherent adequacy of the
theoretical model(s) chosen to predict the QOI, and (3) the degree to which any finite computational implementa -
tion of a given model for a given problem approximates the actual model solution for that problem. To proceed
to a more fine-grained understanding and taxonomy of sources of analytic uncertainty and error, it will be helpful
to consider a specific situation—one that is simplified sufficiently to be tractable and yet complex enough to be
1 The terms analyst and decision maker refer to the roles that the two parties fulfill. Someone who is a decision maker in one context may
well be an analyst in another. For example, scientists are often asked to recommend courses of action with regard to funding research projects.
In that role, those scientists will be consumers, rather than producers, of simulation-based information.
19
OCR for page 20
20 ASSESSING THE RELIABILITY OF COMPLEX MODELS
relevant to the purposes of this study. Tracing the series of analytic choices above in the context of a particular
example should help illustrate where potential areas of analytic uncertainty and error can enter into a representa -
tive application of simulation-based prediction.
2.2 PROJECTILE-IMPACT EXAMPLE PROBLEM
Consider the situation depicted in Figure 2.1, which is an example adapted from Thompson (1972). The system
under consideration consists of a cylindrical aluminum rod impacting the center of a cylindrical aluminum plate
at high speed. This kind of system could be informative when trying to understand the behavior of a projectile
impacting armor.
At the start of the problem, the cylindrical rod is moving downward at high velocity and is just touching the
thick plate (Figure 2.1, left). The image on the right in Figure 2.1 represents a “slice” through the center of the
system and uses color to represent density.
Assume that interest centers on the problem of predicting the behavior of the rod and plate system. First, it
must be decided which aspects of the system behavior are required to be predicted—the QOIs. There are several
possibilities: the depth of penetration of the plate as a function of impactor velocity, the extent of gross damage
to the plate, the fine-scale metallographic structure of the plate after impact, the amount of plate material ejected
backward after the rod impact, the time-dependent structure of loading and unloading waves during the impact, and
so on. In general, the number of possible QOIs that could be considered as reasonable candidates for prediction
is large. Which aspects are important is application-dependent—depending, for example, on whether application
focus is on improving the performance of the projectile or of the armor plate—and will influence to a large degree
the simulation approach taken by the analyst.
A question that emerges at this stage is the degree of accuracy to which the prediction needs to be made. This
also depends on the application under consideration. In this rod and plate example, it may be that the primary QOI
Density at 0.00e+00 seconds
g/cm3
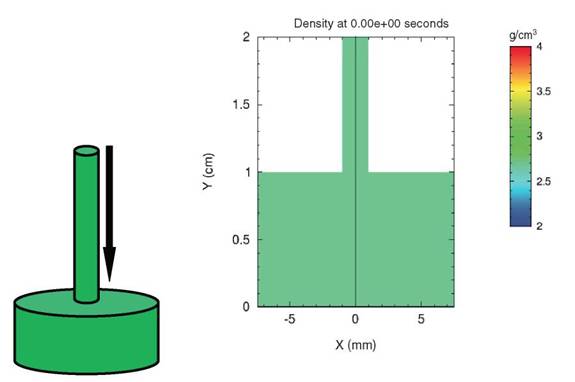
FIGURE 2.1 Aluminum rod impacting a cylindrical aluminum plate.
Figure 2.1a and b.eps
bitmap on right, vector on left
OCR for page 21
21
SOURCES OF UNCERTAINTY AND ERROR
that is important is the depth of penetration of the rod as a function of impactor velocity, and that the depth only
to within a couple of millimeters is the only QOI needed. Having specified the system under consideration, the
QOI(s) that require prediction, and the accuracy requirements on that prediction, the analyst can proceed to survey
the possible theories or models that are available to estimate the behavior of the system. This aspect of the problem
usually requires judgment informed by subject-matter expertise. In this example, the analyst is starting with the
equations of solid mechanics. Further, the analyst is assuming that typical impactor velocities are sufficiently large,
and the resulting pressures sufficiently high, that the metal rod and plate system can be modeled as a compressible
fluid, neglecting considerations of elastic and plastic deformation, material strength, and so on. This is the kind of
assumption that draws on relevant background information. Most moderately complex applications rely on such
background assumptions (whether or not they are explicitly stated). The specification of the conservation (“gov -
erning”) equations is given in Box 2.1. The thermodynamic development is not described in any detail, but the
problem of specifying thermodynamic properties requires assumptions about model forms—in this example, shown
in Box 2.1. The governing equations and other assumptions combine to determine the mathematical model that will
be employed, and the specific assumptions made influence the predicted deformation behavior at a fundamental
level. The range of validity of any particular set of assumptions is often far more limited than the range of validity
of the governing equations. The subsequent predicted results are bounded by the most limiting range of validity.
At this point, strategies for simulating these equations numerically have to be considered—that is, the com -
putational model must be specified. Accomplishing this is far from obvious, and it is greatly complicated by the
existence of nonlinear wave solutions (particularly shock waves) to the equations of fluid mechanics. The details of
numerical hydrodynamics will not be explored here, but the important point is that the specification of a well-posed
mathematical model to represent the physical system is usually just the beginning of any realistic analysis. Strate -
gies for numerically solving the mathematical model on a computer involve significant approximations affecting
the computed QOI. The errors resulting from these approximations may be quantified as part of verification activi -
ties. Even after a strategy for solving the nonlinear governing equations numerically is chosen, the thermodynamic
relations mentioned above have to be computed somehow. This introduces additional approximations as well as
uncertain input parameters, and these introduce further uncertainty into the analysis.
Suppose that both a numerical hydrodynamics code (for addressing the governing equations) and the relevant
thermodynamic tables (for addressing the thermodynamic assumptions) are readily available. The next issue to
consider is the resolution of the spatial grid to use for discretizing the problem. Finite grid resolution introduces
numerical error into the computed solution, which is yet another source of error that contributes to the predic -
tion uncertainty for the QOIs. The uncertainty in the QOIs due to numerical error is studied and quantified in the
solution verification phase of the verification, validation, and uncertainty quantification (VVUQ) process. After
having made all these choices, the simulation can (finally) be run. The computed result is shown in Figure 2.2.
The code predicts that the rod penetrates to a depth of about 0.7 cm in the plate at the time shown in the
simulation. The result also shows strong shock compression of the plate that depends in complicated ways on the
location within the plate. Finally, there is evidence of interesting fine-scale structure (due to complex interactions
of loading and unloading waves) on the surface of the plate.
Any, or all, of these results may be of interest to both the analyst and the decision maker. The exact solu -
tion of the mathematical model cannot be obtained for this problem because the propagation of nonlinear waves
through real materials in realistic geometries is generally not solvable analytically. Had the analyst been unable
to run the code, he or she might still have been able to give an estimate of the QOI, but that estimate would, most
likely, have been vastly more uncertain—and less quantifiable—than an estimate based on a reasonably accurate
simulation. A primary goal of a VVUQ effort is to estimate the prediction uncertainty for the QOI, given that some
computational tools are available and some experimental measurements of related systems are also available. The
experimental measurements permit an assessment of the difference between the computational model and reality,
at least under the conditions of the available experiments, a topic that is discussed throughout Chapter 5, “Model
Validation and Prediction.” Note that uncertainties in experimental measurements also impact this validation
assessment. An important point to realize, for the purposes of this discussion, is that the computational model
results all depend on the many choices made in developing the computational model, each potentially pushing the
computed QOI away from its counterpart from the true, physical system. Different choices at any of the stages
OCR for page 22
22 ASSESSING THE RELIABILITY OF COMPLEX MODELS
Box 2.1
Equations for Conservation of Mass, Momentum, and Energy
To be explicit about the form that the rod and plate analysis might take, it is useful to write the govern-
ing equations of continuum mechanics. These are laws of conservation of mass, momentum, and energy:1
dρ
= –ρ∇kuk
dt
duk
= ∇l τkl
ρ
dt
dE ·
= τkl εkl
ρ
dt
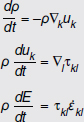
In these equations, ρ denotes the mass density, E the internal energy per unit volume, uk is the velocity
vector written in Cartesian coordinates, and τkl is the stress tensor, again written in Cartesian coordinates.
∇k denotes the differentiation with respect to the kth spatial direction.
The strain-rate tensor in the energy equation is given by:
1
·
εkl = (∇kul + ∇l uk)
2
and the stress tensor in the momentum and energy equations by:
τkl = P δkl + τ diss
kl
These equations are quite general and do not depend on assumptions about elastic or plastic de-
formation, material strength, and the like. They are simply conservation laws, and their introduction is
accompanied by very little uncertainty, at least for this application.
However, the specific form taken by the dissipative component of the stress tensor, tdiss, relies on ap-
proximations, particularly involving the thermodynamic specification of the system. If, following the analysis
mentioned above, it is decided that the rod and plate system will be modeled as a viscous fluid, then the
viscous component of the stress tensor can be expressed as a function of the shear and bulk viscosities,
hs and hn:
2
· ·
τ diss = τ NS = 2ηsεkl + (2ηv – η )ε δ
3 s rr kl
kl kl
These viscosities (and the internal energy) must be expressed in terms of independent thermodynamic
variables, which require approximations that introduce still more uncertainty into the predicted quantities
of interest.
1 For these equations and notable conventions, see Wallace (1982).
OCR for page 23
23
SOURCES OF UNCERTAINTY AND ERROR
Density at 7.51e-07 seconds
g/cm3
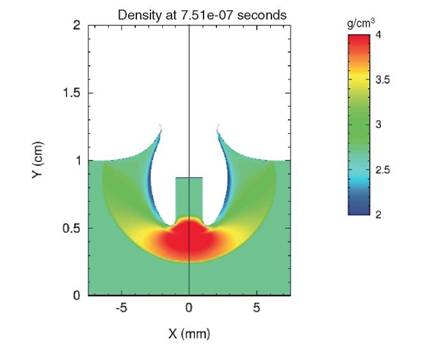
FIGURE 2.2 Aluminum rod at the end of simulation. The figure shows a slice through the system (which began as two cylin -
ders). Color represents density.
Figure 2.2.eps
bitmap
discussed above would produce different results from those pictured in Figure 2.2. The results, however, are not
equally sensitive to every choice—some choices have greater influence than others on the computational results.
A major goal of any uncertainty quantification (UQ) effort is to disentangle these sensitivities for the problem at
hand. The problem discussed here exhibits many of the sources of uncertainty that are likely to be present in most
computational analyses of physical or engineered systems. It is worthwhile to extract some of the salient themes
from this cursory overview.
2.3 INITIAL CONDITIONS
One uncertainty that the discussion of this example problem did not emphasize is uncertainty in the initial
data for the problem. It was simply assumed that the initial dimensions, velocities, densities, and so forth for the
combined rod and plate system were known arbitrarily well. Many problems that are commonly simulated do not
enjoy this luxury. For example, hydrodynamic simulations of incompressible turbulent flows often suffer from large
uncertainties in the initial conditions of the physical system. In principle, these uncertainties must be parameterized
in some way and then processed through the simulation code so that different parameter settings describe different
initial conditions. If the rest of the modeling process is perfect—something that the above discussion indicates
is far from likely—uncertainty in the initial conditions will be the dominant contributor to prediction uncertainty
in the QOI. In this case, methods mentioned in Chapter 4, “Emulation, Reduced-Order Modeling, and Forward
Propagation,” for the propagation of input uncertainty would describe the prediction uncertainty. The main thrust
of the preceding discussion of the example problem has been to point out the many possible additional sources of
uncertainty over and above uncertainty in the initial conditions.
Finding: Common practice in uncertainty quantification has been to focus on the propagation of input uncertainties
through the computational model in order to quantify the resulting uncertainties in output quantities of interest,
with substantially less attention given to other sources of uncertainty.
OCR for page 24
24 ASSESSING THE RELIABILITY OF COMPLEX MODELS
There is a need for improved theory, methods, and tools for identifying and quantifying uncertainties from
sources other than uncertain computational inputs and for aggregating the uncertainties that arise from all sources.
2.4 LEVEL OF FIDELITY
Fidelity of the numerical representation of a complex system is another aspect of many simulation-based
predictions that is not well exemplified by the preceding example problem. The geometry of a cylindrical rod
impacting a plate is not a particularly difficult geometry to capture in modern computer codes. Many other
problems of interest, however, have significant difficulties in capturing all the geometric intricacies of the real
system. In many cases, rather complex three-dimensional geometries are simplified to two-, one-, or even zero-
dimensional numerical representations.2 But even if the full dimensionality of the problem is retained, it is often
the case—especially for intricate systems like a car engine—that many of the pieces of a complex system have to
be either ignored or greatly simplified in the code just to get the problem generated or for the code to run stably
in a reasonable amount of time.
These decisions are present in most simulation analyses. They are typically made on the basis of expert
judgment. One method of determining the effect of a judgment regarding what to neglect or simplify is to try to
include a more complete representation and see if it affects the answer significantly. However, if every aspect
of the real world could be accurately represented, that is generally what the analyst would do; so in some cases,
more detailed modeling is not feasible. An alternative method is to simplify the representation sufficiently that
it can be accommodated by the code and computer that are available and accept the impact that the approximate
representation has on the simulation output. This is often the only reasonably available strategy for getting an
answer and so is frequently the one taken. However, this method also leaves a great deal of latitude to the analyst
in making choices on how to represent the system numerically and on judging whether or not the simplifications
compromise the simulation results or provide information of utility to the decision maker.
2.5 NUMERICAL ACCURACY
As mentioned briefly in the discussion of the example problem, every analyst confronts the issues of uncer-
tainty in the numerical solution of the equations embodied in the code. Three different broad, but potentially
overlapping, categories of uncertainty can be distinguished:
• Inadequate algorithms,
• Inadequate resolution, and
• Code bugs.
Algorithmic inadequacies and resolution inadequacies stem from a common cause: most mathematical models
in computational science and engineering are formulated using continuous variables and so have the cardinality
of the real numbers; but all computers are finite. In most cases, derivatives are finite differences and integrals are
finite sums. Different algorithms for approximating, say, a differential equation on a computer will have different
convergence properties as the spatial and temporal resolution are increased. Because the spatial and temporal reso -
lutions or number of Monte Carlo samples of a probability distribution are generally fixed by the computational
hardware available, certain algorithms will usually be more appropriate than others. There may be additional
factors that also favor one algorithm over another. It is a time-honored warning, though, that every algorithm, no
matter how well it performs generally, may have an Achilles’ heel—some weakness that will cause it to stumble
when faced with a certain problem. Unfortunately, these weaknesses are usually found in one of two ways: first,
by comparing the code against a problem with a known solution; second, by comparing the code against reality. In
either case, checks are made to see where the code is found wanting. The problem with checking against a known
solution—while undoubtedly a useful and important procedure—is that it is very difficult to determine whether
2 An example of a much-used zero-dimensional code is the ORIGEN2 nuclear reactor isotope depletion code. See Croff (1980).
OCR for page 25
25
SOURCES OF UNCERTAINTY AND ERROR
or not the weakness thus revealed in the simple problem will play an important role in the true application. Again,
one should note that any judgments made by the analyst on how to factor in algorithmic issues are typically both
complex and somewhat subjective.
Resolution inadequacies are slightly different in that they can be checked, at least in principle, by increas -
ing (or decreasing) the spatial and temporal resolutions to estimate the impact of resolution on the simulation
result. Notice, again, that here the analyst will be restricted by computational expense and, perhaps, by intrinsic
algorithmic limitations.
Finally, code bugs are the rule, not the exception, in all codes of any complexity. Software quality engineer-
ing and code verification are finely developed fields in their own right. Nightly regression suites (software to test
whether software changes have introduced new errors), manufactured solutions, 3 and extensive testing are all
attempts to ensure that as many of the lines of code as possible are error-free. It may be trite but is certainly true
to say that a single bug may be sufficient to ensure that the best computational model in the world, run on the most
capable computing platform, produces results that are utterly worthless.
Finding: The VVUQ process would be enhanced if the methods and tools used for VVUQ and the methods and
algorithms in the computer model were designed to work together. To facilitate this, it is important that code
developers and model developers learn the basics of VVUQ methodologies and that VVUQ method developers
learn the basics of computational science and engineering. The fundamentals of VVUQ, including strengths, weak -
nesses, and underlying assumptions, are important components in the education of analysts who are responsible
for making predictions with quantified uncertainties.
2.6 MULTISCALE PHENOMENA
Systems that require computational simulation to predict their evolution in time and space are most fre -
quently intrinsically nonlinear. Fluid dynamics is a paradigmatic example. The hallmark of a nonlinear system
is that the dynamics of the system couple many different degrees of freedom. This phenomenon is seen in the
example problem of a rod impacting a plate. Steady nonlinear waves, such as shocks, critically depend on the
nonlinearity of the dynamical equations. A shock couples the large-scale motions of the solid or fluid system
to the small-scale regions where the work done by the viscous stresses is dissipated. Multiscale phenomena
always complicate a simulation. As was seen very briefly above, the net effect of the nonlinearity is to present
the modeler with a choice of options:
• Option 1: Directly model all the scales of interest, or
• Option 2: Choose a cutoff scale—that is, a scale below which the phenomena will not be represented
directly in the simulation, replacing the physical model with another model that is cutoff-dependent.
Each alternative has associated advantages and disadvantages. Option 1 is initially appealing, but it usually
dramatically increases the computational expense of even a simple problem, and the time spent in setting up
such a simulation might be unwarranted for the task at hand. Moreover, it often introduces additional parameters,
governing system behavior at different scales, that need to be calibrated beforehand, frequently in regimes where
those parameters are poorly known. The uncertainties induced by these uncertain parameters might exceed the
additional fidelity that one could expect from a more complete model. Option 2, on the other hand, reduces the
computational expense by limiting the degrees of freedom that the simulation resolves, but it usually involves the
construction of physically artificial numerical models whose form is, to some extent, unconstrained and which
usually have their own adjustable parameters. In practice, such effective models are almost always tuned, or cali -
brated, to reproduce the behavior of selected problems for which the correct large-scale behavior is known. The
3 Manufactured solutions refers to the process of postulating a solution in the form of a function, followed by substituting it into the operator
characterizing the mathematical model in order to obtain (domain and boundary) source terms for the model equations. This process then
provides an exact solution for a model that is driven by these source terms (Knupp and Salari, 2003; Oden, 1994).
OCR for page 26
26 ASSESSING THE RELIABILITY OF COMPLEX MODELS
example problem presents the analyst with this choice. In keeping with the usual practice in compressible-fluid
numerical hydrodynamics, Option 2 was followed. The dynamics were modeled with an effective numerical model,
an artificial viscosity. Each of these options presents its own type of uncertainty.
2.7 PARAMETRIC SETTINGS
If it is assumed that the form of the small-scale physics is known (Option 1), then the main residual uncer-
tainty of Option 1 is parametric, that is, due to uncertainty about the correct values to assign to the parameters in
the correct physics model. The fortunate aspect of parametric uncertainty is that many methods (e.g., Bayesian,
maximum-likelihood) of parameter calibration are available for estimating parameters from experimental data,
if such data are available. Again, however, one has to compare the computational expense involved in the direct
simulation of many different length scales with the expense of obtaining additional data.
2.8 CHOOSING A MODEL FORM
Option 2, choosing a cutoff scale, introduces a potentially important contributor to model discrepancy: model-
form uncertainty. When an effective model is created to mimic the physics of the length scales that are deleted
from the simulation, the form of the model—the types of terms that enter into the equations—is usually not fully
determined by the requirement that the effective model reproduce the physics of a selected subset of large-scale
motions. For example, the Von Neumann-Richtmyer artificial viscosity method (Von Neumann and Richtmyer,
1950) (and its descendants) is a way of introducing some effects of viscosity into simulations based on equations
that do not otherwise represent the root causes of viscosity. These methods are a good illustration of potential
model-form error in that they can accurately propagate planar shocks in a single material—the physics that they
are designed to replicate—while failing (in different ways) to model higher-dimensional, or multimaterial, hydro -
dynamic situations.
A typical strategy to use in constructing effective models is to require that the effective model obey whatever
symmetries happen to be present in the full model. In fluid dynamics, for example, one would prefer to have a
subgrid model possess the symmetries of the full Navier-Stokes equations.4 Often, however, retaining the full
symmetry group is not practicable. Even when it is, however, the symmetry group still usually permits an infinite
number of possible terms that may satisfy the symmetry requirements. Which of these terms need to be retained
is, unfortunately, often problem-dependent, a fact that can create difficulties for general-purpose codes. Moreover,
methods for expressing model-form error, and assessing its impact on prediction uncertainty, are in their infancy
compared to methods for addressing parametric uncertainty. Sometimes, however, it is possible to parameterize a
model-form uncertainty, allowing it to be treated as a parametric uncertainty. This type of reduction can occur by
using parameters to control the appearance of the terms in an effective model after the imposition of symmetry
requirements.
2.9 SUMMARY
The simplified, but still representative, simulation problem discussed here is presented in the hope of identify -
ing at least some sources of error and uncertainty in model-based predictions. It should be clear that the impact of
including these different effects is to, on the whole, push a computed QOI away from its counterpart in the physical
system, increasing the resulting prediction uncertainty. However, the manner in which this increase occurs will
depend considerably on the details of the simulation and uncertainty models under consideration. Some uncertain -
ties will add in an independent manner; others may have strong positive or negative correlations. It is important to
realize that some uncertainties may be limited by the availability of relevant experimental data. The most straight -
forward example occurs when one has data that constrain the possible values of one or more input parameters to
the simulation code being used in the analysis. Clearly, the details of such interactions and constraints and the
4 These symmetries are discussed in Frisch (1995, Chapter 2).
OCR for page 27
27
SOURCES OF UNCERTAINTY AND ERROR
structure of the analysis are closely interrelated. The sources of uncertainty and error identified here, while almost
certainly not an exhaustive list, will likely be present in most simulation-based analyses. Developing quantitative
methods to address such a wide variety of uncertainty and error also presents difficult challenges, and exciting
research opportunities, to the verification and validation (V&V) and UQ communities.
2.10 CLIMATE-MODELING CASE STUDY
The previous discussion noted that uncertainty is pervasive in models of real-world phenomena, and climate
models are no exception. In this case study, the committee is not judging the validity or results of any of the existing
climate models, nor is it minimizing the successes of climate modeling. The intent is only to discuss how VVUQ
methods in these models can be used to improve the reliability of the predictions that they yield and provide a
much more complete picture of this crucial scientific arena.
Climate change is at the forefront of much scientific study and debate today, and UQ should be central to the
discussion. To set the stage, one of the early efforts at UQ analysis for a climate model is described (from Stainforth
et al., 2005). This study considered two types of input uncertainties for climate models: uncertainty in the initial
conditions for the climate model (i.e., the posited initial state of climate on Earth, which is very imprecisely known,
particularly with respect to the state of the ocean) and uncertainty in the climate model parameters (i.e., uncertainty
in coefficients of equations defining the climate model, related to unknown or incompletely represented physics). It
is standard in weather forecasting, and relatively common in climate modeling, to deal with uncertainty in the initial
conditions by starting with an ensemble (or set) of possible initial states and propagating this ensemble through
the model. It is less common to attempt to deal with the uncertainty in the model parameters, although this has
been considered in Forest et al. (2002) and Murphy et al. (2004), for example. The climate model studied was a
version of a general circulation model from the United Kingdom Met Office5 consisting of the atmospheric model
HadAM36 coupled to a mixed-layer ocean. Out of the many parameters in the model, six parameters—relating to
the way clouds and precipitation are represented in the model—were varied over three plausible values (chosen
by scientific experts). For emphasis, note that the standard output that one would see from runs of this climate
model would be from the run that uses the central value of each of the three possible parameters. Figure 2.3(b)
(from Stainforth et al., 2005) indicates the effect of this parameter uncertainty in the prediction of the effect of
CO2-doubling on global mean temperature change over a 15-year period. This discussion does not consider the
calibration and control phases of the analyses, but note the considerable uncertainty in the final prediction of global
mean temperature change at the end of the final CO2-doubling phase. If the climate model were simply run at its
usual setting for the parameters, one would obtain only one result, corresponding to an increase of 3.4 degrees.
Note also that the initial state of the climate is unknown; to reflect this, a total of 2,578 runs of the climate model
were made, varying both the model parameters and the initial conditions. The uncertainty in the final prediction
of global mean temperature is then indicated by the larger final spread in Figure 2.3(a).
This discussion only scratches the surface of UQ analysis for climate change. The variation allowed in this
study in the model parameters was modest, and only six of the many model parameters were varied. Uncertainty
caused by model resolution and incorrect or incomplete structural physics (e.g., the form of the equations) also
needs to be considered. The former could be partially addressed by studying models at differing resolutions, and
the latter might be approached by comparing different climate models (see, e.g., Smith et al., 2009); it is quite
likely, however, that differing climate models make many of the same modeling approximations, and, because of
the finite resolution inherent in today’s computers, can only imperfectly resolve difficult topological features. The
extent of the effect of chaotic behavior is also poorly understood in climate change (the dust bowl of the 1930s
may well have been a chaotic event that would not appear in climate models—see Seager et al., 2009), regional
effects are likely to be even more variable, and uncertainty as to future significant changes in forcing parameters
(e.g., the actual level of CO2 increase) should also be taken into account. Of course, future CO2 levels depend on
human action, which adds more difficulties to an already complex problem.
5 See www.metoffice.gov.uk. Accessed August 19, 2011.
6 See Pope et al. (2000).
OCR for page 28
28 ASSESSING THE RELIABILITY OF COMPLEX MODELS
(a) Frequency Distribution of All Independent Simulations
Change in Global Mean Temperature (K) Global Mean Temperature (Celsius)
22
20
18
16
14
12
10
.
(b) Frequency Distribution of Perturbed-Physics Ensemble
8
6
4
2
0
-2
2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44
Calibration Phase Center Phase Double CO2 Phase
Year of Simulation
0.0 1.5 3.0 4.5 6.0
Percent of simulations per 0.1 degrees C
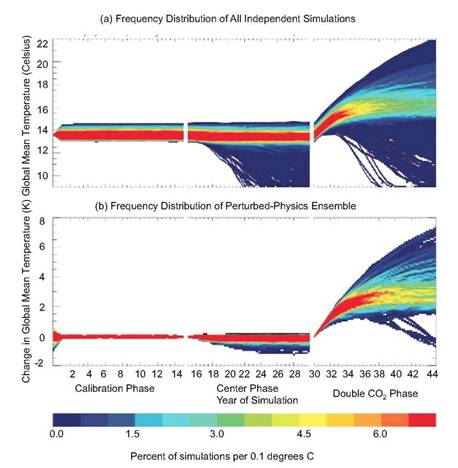
FIGURE 2.3 After calibration and control phases, the effect on global mean temperature of 15 years of doubling of CO2 forcing
is considered (a) when both initial conditions and model parameters are varied and (b) when only model parameters are varied.
SOURCE: Stainforth et al. (2005).
2.10.1 Is Formal UQ Possible for Truly Complex Models?
The preceding case study provides a useful venue for elaboration on a more general issue concerning UQ that
was raised by committee discussions with James McWilliams (University of California, Los Angeles), Leonard
Smith (London School of Economics), and Michael Stein (University of Chicago). The general issue is whether
formal validation of models of complex systems is actually feasible. This issue is both philosophical and practical
and is discussed in greater depth in, for example, McWilliams (2007), Oreskes et al. (1994), and Stainforth et al.
(2007). As discussed in this report, carrying out the validation process is feasible for complex systems. It depends
on clear definitions of the intended use of the model, the domain of applicability, and specific QOIs. This is dis -
cussed further in Chapter 5, “Model Validation and Prediction.”
Several factors make uncertainty quantification for climate models difficult. These include:
1. If the system is hugely complex, the model is, by necessity, only a rough approximation to reality. That
this is the case for climate models is indicated by the difficulty of simultaneously tuning climate models
to fit numerous outputs; global climate predictions can often be tuned to match various statistics from
OCR for page 29
29
SOURCES OF UNCERTAINTY AND ERROR
nature, but then will be skewed for others. Formally quantifying the uncertainty caused by all of the sim -
plifying assumptions needed to construct a climate model is daunting and involves the participation of
people—not just the use of software—because one has to vary the model structure in meaningful ways.
One must understand which simplifying assumptions that were made in model construction were rather
arbitrary and have plausible alternatives.
Another fundamental challenge is that the resulting variations in model predictions do not naturally
arise probabilistically, so that it is unclear how to describe the uncertainty formally and to combine it with
the other uncertainties in the problem. For the latter, it might be practically necessary to use a probabilistic
representation, but an understanding of the limitations or biases in such an approach is needed.
2. Simultaneously combining all of the sources of uncertainty relating to climate models in order to assess
the uncertainty of model predictions is highly challenging, both at the formulation level and in technical
implementation.7
3. There is a need to make decisions regarding climate change before a complete UQ analysis will be avail -
able. This, of course, is not unique to climate modeling, but is a feature of other problems like stewardship
of the nuclear stockpile. This does not mean that UQ can be ignored but rather that decisions need to be
made in the face of only partial knowledge of the uncertainties involved. The “science” of these kinds of
decisions is still evolving, and the various versions of decision analysis are certainly relevant.
2.10.2 Future Directions for Research and Teaching Involving UQ for Climate Models
In spite of the challenges in the formal implementation of UQ in climate modeling, the committee agrees that
understanding uncertainties and trying to assess their impact is a crucial undertaking. Some future directions for
research and teaching that the committee views as highly promising are the following:
1. It is important to instill an appreciation that modeling truly complex systems is a lengthy process that
cannot proceed without exploring mathematical and computational alternatives. Instead, it is a process of
learning the behavior of the system being modeled and understanding limitations in the ability to predict
such systems.
2. One must recognize that it is often possible to perform formally UQ only on part of a complex system
and that one should develop ways in which this partial UQ can be used. For instance, one might state
bounds on the predictive uncertainty arising from the partial UQ and then list the other sources of uncer -
tainty that have not been analyzed. And, as always, the domain of applicability of the UQ analysis must
be stated—for example, it may be that the assessment is only valid for predictions on a continental scale
and for a horizon of 20 years. This recognition is even more important when one realizes that even a
complex system such as a climate model is ultimately itself just a component of a more complex system,
involving paleoclimate models, space-time hierarchical models, and so on.
3. There is a tendency among modelers to always use the most complex model available, but such a model
can be too expensive to run to allow for UQ analysis. It would be beneficial to instill an appreciation that
use of a smaller model, together with UQ analysis, is often superior to a single analysis with the most
complex model. In weather forecasting, for instance, it was discovered that running a smaller model
with ensembles of initial conditions gave better forecasts than those from a single run of a bigger model.
This discovery has carried over to some extent in climate modeling—climate models are kept at a level
of complexity wherein an ensemble of initial conditions can be considered, but allowance for UQ with
other uncertainties is also needed.
7 See,for example, R. Knutti, R. Furer, C. Tebaldi, J. Cermak, and G.A. Mehl. 2010. Challenges in Combining Projections in Multiple
Climate Models. Journal of Climate 23(10):2739-2758.
OCR for page 30
30 ASSESSING THE RELIABILITY OF COMPLEX MODELS
2.11 REFERENCES
Croff, A.G. 1980. ORIGEN2—A Revised and Updated Version of the Oak Ridge Isotope Generation and Depletion Code. Oak Ridge National
Laboratory Report ORNL-5621. Oak Ridge, Tenn.: Oak Ridge National Laboratory.
Forest, C.E., P.H. Stone, A.P. Sokolov, M.R. Allen, and M.D. Webster. 2002. Quantifying Uncertainties in Climate System Properties with the
Use of Recent Climate Observations. Science 295(5552):113-117.
Frisch, U. 1995. Turbulence. Cambridge, U.K.: Cambridge University Press.
Knupp, P., and K. Salari. 2003. Verification of Computer Codes in Computational Science and Engineering. Boca Raton, Fla.: Chapman and
Hall/CRC.
McWilliams, J.C. 2007. Irreducible Imprecision in Atmospheric and Oceanic Simulations. Proceedings of the National Academy of Sciences
104:8709-8713.
Murphy, J.M., D.M.H. Sexton, D.N. Barnett, G.S. Jones, M.J. Webb, M. Collins, and D.A. Stainforth. 2004. Quantification of Modelling Un-
certainties in a Large Ensemble of Climate Change Simulations. Nature 430(7001)768-772.
Oden, J.T. 1994. Error Estimation and Control in Computational Fluid Dynamics. Pp. 1-23 in The Mathematics of Finite Elements and Applica-
tions. J.R. Whiteman (Ed.). New York: Wiley.
Oreskes N., K. Shrader-Frechette, and K. Belitz. 1994. Verification, Validation, and Confirmation of Numerical Models in the Earth Sciences.
Science 263:641-646.
Pope, V.D., M.L. Gallani, P.R. Rowntree, and R.A. Stratton. 2000. The Impact of New Physical Parameterizations in the Hadley Centre Climate
Model: HadAM3. Climate Dynamics 16(2-3):123-146.
Seager, R., Y. Kushnir, M.F. Ting, M. Cane, N. Naik, and J. Miller. 2009. Would Advance Knowledge of 1930s SSTs Have Allowed Prediction
of the Dust Bowl Drought? Journal of Climate 22:193-199.
Smith, R., C. Tebaldi, D. Nychka, and L. Mearns. 2009. Bayesian Modeling of Uncertainty in Ensembles of Climate Models. Journal of the
American Statistical Association 104:97-116.
Stainforth, D.A., T. Aina, C. Christensen, M. Collins, N. Faull, D.J. Fram, J.A. Kettleborough, S. Knight, A. Martin, J.M. Murphy, C. Piani, D.
Sexton, L.A. Smith, R.A. Spicer, A.J. Thorpe, and M.R. Allen. 2005. Uncertainty in Predictions of the Climate Response to Rising Levels
of Greenhouse Gases. Nature 433:403-406.
Stainforth, D.A., M.R. Allen, E. Tredger, and L.A. Smith. 2007. Confidence, Uncertainty and Decision-Support Relevance in Climate Predic-
tions. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 365(1857):2145-2161.
Thompson, P. 1972. Compressible-Fluid Dynamics. New York: McGraw-Hill.
Von Neumann, J., and R.D. Richtmyer. 1950. A Method for the Numerical Calculation of Hydrodynamic Shocks. Journal of Applied Physics
21(3):232-237.
Wallace, D.C. 1982. Theory of the Shock Process in Dense Fluids. Physical Review A 25(6):3290-3301.
