5
Model Validation and Prediction
From a mathematical perspective, validation is the process of assessing whether or not the quantity of interest (QOI) for a physical system is within some tolerance—determined by the intended use of the model—of the model prediction. Although “prediction” sometimes refers to situations where no data exist, in this report it refers to the output of the model in general.
In simple settings validation could be accomplished by directly comparing model results to physical measurements for the QOI and computing a confidence interval for the difference, or carrying out a hypothesis test of whether or not the difference is greater than the tolerance (see Oberkampf and Roy, 2010, Chapter 12). In other settings, a more complicated statistical modeling formulation may be required to combine simulation output, various kinds of physical observations, and expert judgment to produce a prediction with accompanying prediction uncertainty, which can then be used for the assessment. This more complicated formulation can also produce predictions for system behavior in new domains where no physical observations are available (see Bayarri et al., 2007a; Wang et al., 2009; or the case studies of this chapter).
Assessing prediction uncertainty is crucial for both validation (which involves comparison with measured data) and prediction of yet-unmeasured QOIs. This uncertainty typically comes from a number of sources, including:
• Input uncertainty—lack of knowledge about parameters and other model inputs (initial conditions, forcings, boundary values, and so on);
• Model discrepancy—the difference between model and reality (even at the best, or most correct, model input settings);
• Limited evaluations of the computational model; and
• Solution and coding errors.
In some cases, the verification effort can effectively eliminate the uncertainty due to solution and coding errors, leaving only the first three sources of uncertainty. Likewise, if the computational model runs very quickly, one could evaluate the model at any required input setting, eliminating the need to estimate what the model would have produced at an untried input setting.
The process of validation and prediction, explored in previous publications (e.g., Klein et al., 2006; NRC, 2007, Chapter 4), is described in this chapter from a more mathematical perspective. The basic
process includes identifying and representing key sources of uncertainty; identifying physical observations; experiments, or other information sources for the assessment; assessing prediction uncertainty; assessing the reliability or quality of the prediction; supplying information on how to improve the assessment; and communicating results.
Identifying and representing uncertainties typically involves sensitivity analysis to determine which features or inputs of the model affect key model outputs. Once they are identified, one must determine how best to represent these important contributors to uncertainty—parametric representations of input conditions, forcings, or physical modeling schemes (e.g., turbulent mixing of fluids). In addition to parametric forms, some analyses might assess the impact of alternative physical representations/schemes within the model. If solution errors or other sources of model discrepancy are likely to be important contributors to prediction uncertainty, their impact must also be captured in some way.
The available physical observations are key to any validation assessment. In some cases these data are observational, provided by nature (e.g., meteorological measurements, supernova luminosities); in other cases, data come from a carefully planned hierarchy of controlled experiments—e.g., the Predictive Engineering and Computational Sciences (PECOS) case study in Section 5.9. In addition to physical observations, information may come from the literature or expert judgment that may incorporate historical data or known physical behavior.
Estimating prediction uncertainty requires the combination of computational models, physical observations, and possibly other information sources. Exactly how this estimation is carried out can range from very direct, as in the weather forecasting example in Figure 5.1, to quite complicated, as described in the case studies in this chapter. In these examples, some physical observations are used to refine or constrain uncertainties that contribute to prediction uncertainty. Estimating prediction uncertainty is a vibrant research topic whose methods vary depending on the features of the problem at hand.
For any prediction, assessing the quality, or reliability, of the prediction is crucial. This concept of prediction reliability is more qualitative than is prediction uncertainty. It includes verifying the assumptions on which an estimate is based, examining the available physical measurements and the features of the computational model, and applying expert judgment. For example, well-designed sets of experiments can lead to stronger statements regarding the quality and reliability of more extrapolative predictions, as compared to observational data from a single source. Here the concept of “nearness” of the physical observations to the predictions of the intended use of the model becomes relevant, as does the notion of the domain of applicability for the prediction. However,
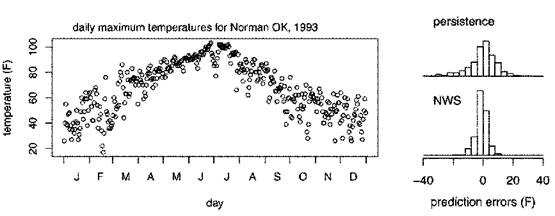
FIGURE 5.1 Daily maximum temperatures for Norman, Oklahoma (left), and histograms of next-day prediction errors (right) using two prediction models. The top histogram shows residuals from the persistence model, predicting tomorrow’s high temperature with today’s high temperature. The bottom histogram shows residuals from the National Weather Service (NWS) forecast. Ninety percent of the actual temperatures are within ±14°F for the persistence-model forecasts and within ±6°F for the NWS forecasts. The greater accuracy of the NWS forecasts is due to NWS’s use of computational models and additional meteorological information. The assessment of these two forecast methods is relatively straightforward because of the large number of comparisons of model forecast to measurement. SOURCE: Data from Brooks and Doswell (1996).
while most practitioners recognize that this concept and notion are important, rigorous mathematical definitions and quantifications remain an unsolved problem.
In some validation applications, an opportunity exists to carry out additional experiments to improve the prediction uncertainty and/or the reliability of the prediction. Estimating how different forms of additional information would improve predictions or the validation assessment can be an important component of the validation effort, guiding decisions about where to invest resources in order to maximize the reduction of uncertainty and/ or an increase in reliability.
Communicating the results of the prediction or validation assessment includes both quantitative aspects (the predicted QOI and its uncertainty) and qualitative aspects (the strength of the assumptions on which the assessment is based). While the communication component is not fundamentally mathematical, effective communication may depend on mathematical aspects of the assessment.
The various tasks mentioned in the preceding paragraphs give a broad outline of validation and prediction. Exactly how these tasks are carried out depends on features of the specific application. The list below covers a number of important considerations that will have an impact on the methods and approaches for carrying out validation and prediction:
• The amount and relevance of the available physical observations for the assessment,
• The accuracy and uncertainty accompanying the physical observations,
• The complexity of the physical system being modeled,
• The degree of extrapolation required for the prediction relative to the available physical observations and the level of empiricism encoded in the model,
• The computational demands (run time, computing infrastructure) of the computational model,
• The accuracy of the computational model’s solution relative to that of the mathematical model (numerical error),
• The accuracy of the computational model’s solution relative to that of the true, physical system (model discrepancy),
• The existence of model parameters that require calibration using the available physical observations, and
• The availability of alternative computational models to assess the impact of different modeling schemes or physics implementations on the prediction.
These considerations are discussed throughout this chapter, which describes key mathematical issues associated with validation and prediction, surveying approaches for constraining and estimating different sources of prediction uncertainty. Specifically, the chapter briefly describes issues regarding measurement uncertainty (Section 5.2), model calibration and parameter estimation (Section 5.3), model discrepancy (Section 5.4), and the quality of predictions (Section 5.5), focusing on their impact on prediction uncertainty. These concepts are illuminated by two simple examples (Boxes 5.1 and 5.2) that extend the ball-drop example in Chapter 1, and by two case studies (Sections 5.6 and 5.9). Leveraging multiple computational models (Section 5.7) and multiple sources of physical observations (Section 5.8) is also covered, as is the use of computational models for aid in dealing with rare, high-consequence events (Section 5.10). The chapter concludes with a discussion of promising research directions to help address open problems.
5.1.1 Note Regarding Methodology
Most of the examples and case studies presented in this chapter use Bayesian methods (Gelman et al., 1996) to incorporate the various forms of uncertainty that contribute to the prediction uncertainty. Bayesian methods require a prior description of uncertainty for the uncertain components in a formulation. The resulting estimates of uncertainty—for parameters, model discrepancy, and predictions—will depend on the physical observations and the details of the model formulation, including the prior specification. This report does not go into such details but points to references on modeling and model checking from a Bayesian perspective (Gelman et al., 1996; Gelfand and Ghosh, 1998). While the Bayesian approach is prevalent in the VVUQ literature, effectively dealing with many
Box 5.1
The Ball-Drop Experiment Using a Variety of Balls
In addition to the measurements of drop times for the bowling ball, we now have measurements for a basketball and baseball as well. The measured drop times are normally distributed about the true time, with a standard deviation of 0.1 seconds. The QOI is the drop time for the softball—an untested ball—at a height of 100 m. This QOI is an extrapolation in two ways: no drops over 60 m have been carried out; no measurements have been obtained for a softball.
The conceptual/mathematical model (Figure 5.1.1(b)) accounts for acceleration due to gravity g and air resistance using a standard model. Air resistance depends on the radius and density of the ball (Rball, ρball), as well as the density of the air (ρair). Figure 5.1.1(a) shows various balls and their position in radius-density space. It is assumed that air density is known. In addition to depending on the descriptors of the ball (Rball, ρball), the model also depends on two parameters—the acceleration of gravity g and a dimensionless friction coefficient CD—which need to be constrained with measurements. Initial ranges of 8 ≤ g ≤ 12 and 0.2 ≤ CD ≤ 2.0 are specified for the two model parameters. Measured drop times from heights of 20, 40, and 60 m are obtained for the basketball and baseball; measured drop times from heights of 10, 20,…, 60 m are obtained for the bowling ball. These measurements constrain the uncertainty of the parameters to the ellipsoidal region shown in Figure 5.1.1(c).
Figure 5.1.1(d) shows initial and constrained prediction uncertainties for the four different balls using the mathematical model in Figure 5.1.1(b). The light lines correspond to the parameter settings depicted by the points in Figure 5.1.1(c). The dark region shows prediction uncertainty induced by the constrained uncertainty for the parameters. A prediction (with uncertainty) for the softball is given by the spread of the dark region of the rightmost frame.
However, the model has never been tested against drops higher than 60 m. It has also never been directly compared to any softball drops. From Figure 5.1.1(a), one could argue that the softball is at the interior of the (Rball, ρball)-space spanned by the basketball, baseball, and bowling ball, leading one to trust the prediction (and uncertainty) for the softball at 40 m, or even 100 m. However, the softball differs from these other balls in more ways than just radius and density (e.g., surface smoothness). How should one modify predictions and uncertainties to account for these flavors of extrapolation? This is an open question in V&V and UQ research.
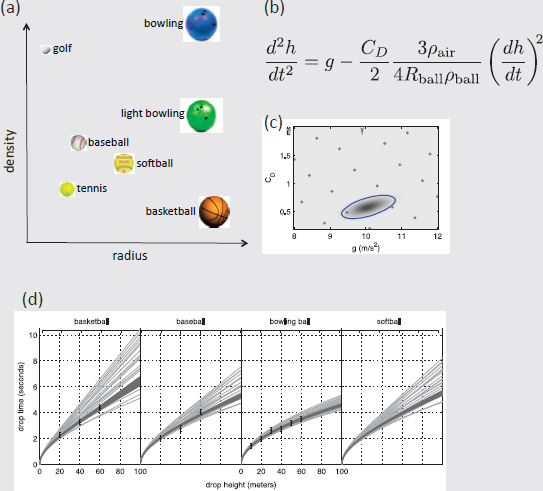
FIGURE 5.1.1
Box 5.2
Using an Emulator for Calibration and Prediction with Limited Model Runs
Physical measurements (black dots) and prior prediction uncertainty (green lines) for the bowling ball drop time as a function of height (as shown in Box 1.1). The experimentally measured drop times for drops of 10, 20,…, 50 m are shown in Figure 5.2.1(a); the uncertainty due to prior uncertainty for gravity g is also shown in the inset figure.
If the number of computer model runs were limited—perhaps due to computational constraints— then an ensemble of runs could be carried out at different (x, θ) input settings. Figure 5.2.1(b) shows model runs carried out over a statistical design of 20 input settings. Here x denotes height and θ denotes the model parameter g. The modeled drop times at these input settings are given by the height of the circle plotting symbols in Figures 5.2.1(a) and (b).
With these 20 computer model runs, a Gaussian process is used to produce a probabilistic prediction of the model output at untried input settings (x, θ), as shown in Figure 5.2.1(c). This emulator is used to facilitate the computations required to estimate the posterior distribution for θ, which is constrained by the physical observations.
The Bayesian model formulation, with an emulator to assist with limited model runs, produces a posterior distribution for the unknown parameter θ (g, given by the blue lines of the inset in Figure 5.2.1(d)), which then can be propagated through the emulator to produce constrained, posterior prediction uncertainties (blue lines).
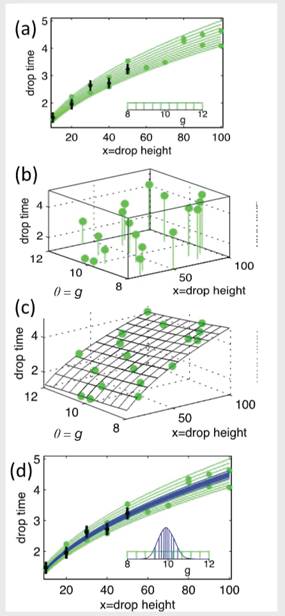
FIGURE 5.2.1
issues discussed here, the use of these methods in the examples and case studies in this chapter should not be seen as an exclusive endorsement of Bayesian methods over other approaches for calculating with and representing uncertainty, such as likelihood (Berger and Wolpert, 1988), Dempster-Shafer theory (Shafer, 1976), possibility theory (Dubois et al., 1988), fuzzy logic (Klir and Yuan, 1995), probability bounds analysis (Ferson et al., 2003), and so on. The committee believes that relevance of the main issues discussed in this chapter is not specific to the details of how uncertainty is represented.
5.1.2 The Ball-Drop Example Revisited
To elaborate these ideas, an extension of the simple ball-drop example from Box 1.1 in Chapter 1 is used; the experiment here includes multiple types of balls (Box 5.1). Drop times for balls of various radii and densities are considered. The basic model that assumes only acceleration due to gravity is clearly insufficient when considering balls of various sizes and densities, suggesting the need for a model that explicitly accounts for drag due to air friction. This new model describes initial conditions for a single experiment, with the radius of the ball Rball and the density of the ball ρball. The model also has two parameters—the acceleration due to gravity, g, and a friction constant, CD—that can be further constrained, or calibrated, using experimental measurements. Of course, treating the acceleration due to gravity g as something uncertain may not be appropriate in a serious application, since this quantity has been determined experimentally with very high accuracy. The motivation for treating g as uncertain is to illustrate issues regarding uncertain physical constants, which are common in many applications.
Using measured drop times for three balls—a bowling ball, baseball, and basketball—the object is to predict the drop time for a softball at 100 meters (m). Hence the QOI is the drop time for a softball dropped from a height of 100 m. Drops are conducted from a 60 m tower. The required prediction is an extrapolation in two ways: no drops over 60 m have been carried out, and no drop-time measurements have been obtained for the softball. Section 5.5 looks more closely at how validation and UQ approaches depend on the availability of measurements and the degree of extrapolation associated with the prediction.
Initially, the uncertainty about the uncertain model parameters is that 8 < g < 12, and 0.2 < CD < 2, which is given by the equation in Figure 5.1.1(b). Model predictions can be made using various (g, CD) values over this region (the dots in Figure 5.1.1(c)); the resulting drop-time predictions are given by the light lines in Figure 5.1.1(d). This uncertainty is obtained by simple forward propagation of the uncertainty in g and CD, as described in Section 4.2 in Chapter 4. If the validation assessment were a question of whether or not the model can predict the 100 m softball drop time to within ± 2 seconds, or whether the drop time will be larger than 10 seconds, this preliminary assessment might be sufficient. If more accuracy is required, the uncertainty in the parameters (g, CD) can be further constrained using the observed drop times for the different balls, as given by the ellipse in Figure 5.1.1(c), showing a 95 percent probability range for (g, CD). This process of constraining parameter uncertainties using experimental measurements is called model calibration, or parameter estimation, and is discussed in more detail in Section 5.3. Physical measurements are uncertain, each giving an imperfect interrogation of the physical system, and this uncertainty affects how tightly these measurements constrain parameter uncertainty. Measurement uncertainty also plays an important role in the comparison of model prediction to reality. This topic is discussed briefly in Section 5.2.
Although the ball-drop example used here does not show any evidence of a systematic discrepancy between model and reality, such discrepancies are common in practice. Once identified and quantified, systematic model discrepancy can be accounted for to improve the model-based predictions (e.g., a computational-model prediction that is systematically 10 percent too low for a given QOI can simply be adjusted up by 10 percent to predict reality more accurately). Section 5.4 discusses the related idea of making the best predictions that one can with an imperfect model (and quantifying their uncertainties), embedded within a statistical framework aided by subject-matter knowledge and available measurements.
The relevant body of knowledge in the ball-drop example consists of measurements from three basketball drops, three baseball drops, and six bowling-ball drops, along with the mathematical and computational models. The friction term in the model is an effective physics model, slowing the ball as it drops and attempting to capture small-scale effects of airflow around the ball. Experience suggests that the friction constant depends on the velocity and smoothness of the ball, as well as on properties of the air. Ideally, part of the assessment of the uncertainty
about the QOI (softball drop time from 100 m) will include at least a qualitative assessment of the appropriateness of using this form of friction model, with a single value for CD, for these drops. This notion of assessing the reliability, or quality, of a model-based prediction is discussed in Section 5.5.
More generally, the body of knowledge could include a variety of information sources, ranging from experimental measurements to expert judgment, to results from related studies. Some of these information sources may be used explicitly, constraining parameter uncertainties, estimating variances, or describing prediction uncertainties. Other information sources might lend evidence to support assumptions used in the analysis, such as the adequacy of the model for predictions that move away from the conditions in which experimental measurements are available.
Ideally, the domain of applicability for this model in predicting drop times of various balls will also be specified. For example, given the current body of knowledge, a conservative domain of applicability might include only basketballs, baseballs, and bowling balls dropped from heights between 10 m and 60 m. In this case, one would not be willing to use the model-based uncertainty given in Box 5.1 to characterize the drop time for a softball at 40 m, let alone 100 m. A more liberal definition of the domain of applicability might be any ball with a radius-density combination in the interior of the basketball-baseball-bowling ball triangle in Figure 5.1.1(a).
Alternatively, one might also consider what perturbations of a basketball, say, would be included in this domain of applicability. Should predictions and uncertainties for a slightly smaller basketball be trusted? What about a slightly less dense basketball? At what density should the predictions and uncertainties no longer be trusted? Put differently, can we assess what perturbations of a basketball are sufficiently “near” to the tested basketball to result in accurate predictions and uncertainty estimates? Often, a sensitivity analysis (SA) can help address the question—this example informing trust in model-based predictions and uncertainties for balls as density decreases. One might also consider conditions that are not accounted for in the model. For example, should the drop times of a rubber basketball differ from those of a leather one? Does ball texture affect drop time? Without additional experiments, such model-applicability issues must necessarily be addressed with expert judgment or other information sources. Quantifying the impact of such issues remains an unsolved problem.
In general, the domain of applicability describes the conditions over which the predictions and uncertainties derived from a computational model are reliable. This should include descriptors of the initial conditions that are accounted for in the model, as well as those that are not. It might also include descriptors of the geometric and/ or physical complexity of the system for which the prediction is being made. Such considerations are crucial for designing a series of validation experiments to help map out this domain of applicability. Defining this domain of applicability depends on the available body of knowledge, including subject-matter expertise, and involves a number of qualitative features about the inference being made.
5.1.3 Model Validation Statement
In summary, validation is a process, involving measurements, computational modeling, and subject-matter expertise, for assessing how well a model represents reality for a specified QOI and domain of applicability. Although it is often possible to demonstrate that a model does not adequately reproduce reality, the generic term validated model does not make sense. There is at most a body of evidence that can be presented to suggest that the model will produce results that are consistent with reality (with a given uncertainty).
Finding: A simple declaration that a model is “validated” cannot be justified. Rather, a validation statement should specify the QOIs, accuracy, and domain of applicability for which it applies.
The body of knowledge that supports the appropriateness of a given model and its ability to predict the QOI in question, as well as the key assumptions used to make the prediction, is important information to include in the reporting of model results. Such information will allow decision makers to better understand the adequacy of the model, as well as the key assumptions and data sources on which the reported prediction and uncertainty rely.
The degree to which available physical data are relevant to the prediction of interest is a key concept in the V&V literature (Easterling, 2001; Oberkampf et al., 2004; Klein et al., 2006). How one uses the available body of
knowledge to help define this domain of validity is part of how the argument for trust in model-based prediction is constructed. This topic is explored further in Section 5.5.
5.2 UNCERTAINTIES IN PHYSICAL MEASUREMENTS
Throughout this chapter, reference is continually made to learning about the computational model and its uncertainties through comparing the predictions of the computational model to available physical data relevant to the QOI. A complication that typically arises is that the physical measurements are themselves subject to uncertainties and possibly bias. In the ball-drop example in Box 5.1, for instance, there were three multiple observations for each type of ball drop, and these were believed to be normally distributed, centered at the true drop time and with standard deviation of 0.1 seconds. The uncertainty in the physical measurements was part of the reason that the parameters in the example were constrained only to the ellipse in Figure 5.1.1(c) and not to a smaller area.
Although the characterization of such measurement uncertainty is often a crucial part of a VVUQ analysis, the issue is not highlighted in this report because such characterization is the standard domain of statistics, and vast methodology and experience exist for characterizing such uncertainty (Youden, 1961, 1972; Rabinovich, 1995; Box et al., 2005). However, there are several issues that must be kept in mind when obtaining physical data for use in VVUQ analyses.
For experiments that have not yet been performed, the design of the experiment for collecting the physical data should be developed in cooperation with the VVUQ analyst and the decision maker to provide maximum VVUQ benefit when practical. Experimental data are often expensive (as when each data point arises from crashing a prototype vehicle, for instance) and should be chosen to provide optimal information from the perspective of the desired calibration, VVUQ analysis, and/or the prediction for the computational model.
One particularly relevant consideration in the context of VVUQ is the desirability of replications1 of the physical measurements—that is, of obtaining repeat measurements under the same conditions (same model-input values). This might seem counterintuitive from the perspective of the computational model; if the analyst is trying to judge how well the model predicts reality, observing reality at as many input values as possible would seem logical. When the physical data are subject to measurement error, however, the picture changes, because it is first crucial to learn how well the physical data represent reality. If the physical data do not constrain reality significantly at any input values, little has been learned that will help in judging the fidelity of the computational model with respect to reality.
If the measurement error of the physical data and variability of the physical system are known (e.g., the data has a known standard deviation) and are judged to be small enough to adequately constrain reality, then replicate observations are perhaps not needed. However, it is wise to view the presumption of known standard deviation with healthy skepticism. When the magnitude of the measurement error is derived from the properties of measurement apparatus and theoretical considerations, it is common to miss important sources of variation and bias that are present in the measurement process. Hence, resources may be better spent obtaining replicate observations, rather than attempting to account for every possible source of uncertainty present in a single measurement/experiment. One may be able to afford only enough physical data with replications to adequately constrain reality at a few input values, but knowing reality, with accurately quantified uncertainty, at a few input values is often better than having a vague idea about reality at many input values.
One does not always have control over the process of obtaining physical measurements. They may have been based on historical experiments or observations, for which important details may be unknown. They may have arisen from auxiliary inverse-problem analyses (e.g., inferring a quantity such as temperature or contaminant concentration from remotely sensed signals). This inexactness can be problematic from a number of perspectives, including the possibility that uncertainties in the physical data may have been estimated poorly, or not given at
_____________________
1 Here we mean genuine replicates as described in Box and Draper (1987, p. 71): “Replicate runs must be subject to all the usual setup errors, sampling errors, and analytical errors which affect runs made at different conditions. Failure to achieve this will typically cause underestimation of the error and will invalidate the analysis.”
all. In such cases it may be fruitful to include this auxiliary inverse problem as part of the validation and prediction process.
A significant issue that can arise is possible bias in the physical data, wherein a common error induces a similar effect on all of the measurements. In the ball-drop example, for instance, a bias in the physical observations would be present if the stopwatch used to time all of the drops were systematically slow. Similarly, if each ball were released with a slight downward velocity, then measured drop times would be systematically too short.
The methodological issue of how to incorporate uncertainty in the physical data into the UQ analysis is also important. Standard statistical techniques can allow one to summarize the physical data in terms of the constraints that they place on reality, but a VVUQ analysis requires interfacing this uncertainty with the computational model, especially if calibration is also being done based on the physical data. Bayesian analysis (discussed in Section 5.3) has the appeal of providing a direct methodology for such incorporation of uncertainty.
5.3 MODEL CALIBRATION AND INVERSE PROBLEMS
Many applications in VVUQ use physical measurements to constrain uncertain parameters in the computational model. A simple example is given in Figure 5.1.1(c), in which measured drop times are used to reduce the uncertainty in the two model parameters—g and CD. This basic task of model calibration is a standard problem in statistical inference. Model calibration applications may involve parameters ranging from one or two, as in Box 5.1, to thousands or millions, as is often the case when one is inferring heterogeneous fields (material properties, initial conditions, or source terms—e.g., Akçelik et al., 2005).
The problem of estimating from observations the uncertain parameters in a simulation model is fundamentally an inverse problem. The forward problem seeks to predict output observables (such as seismic ground motion at seismometer locations) given the parameters (such as the heterogeneous elastic-wave speeds and density throughout a region of interest) by solving the governing equations (such as the elastic-wave equations). The forward problem is usually well posed (the solution exists, is unique, and is stable to perturbations in inputs), causal (later-time solutions depend only on earlier-time solutions), and local (the forward operator includes derivatives that couple nearby solutions in space and time).
The inverse problem reverses this relationship, however, by seeking to determine parameter values that are consistent with particular measurements. Solving inverse problems can be very challenging for the following reasons: (1) the mapping from observations (i.e., measurements) to parameters may not be one to one, particularly when the number of parameters is large and the number of measurements is small; (2) small changes in the measurement value may lead to changes in many or all parameters, particularly when the forward model is nonlinear; and (3) typically, all that is available to the analyst is a computational model that approximately solves the forward problem.
In simple model calibration, or inverse problems, post-calibration parameter uncertainty can be described by a “best estimate” of uncertainty determined by a covariance matrix, characterizing variance and correlations in the parameter uncertainties. When the solution to the inverse problem is not unique, and/or when the measurement errors have a nonstandard form, determining even a best estimate can be problematic. The popular approach to obtaining a unique “solution” to the inverse problem in these circumstances is to formulate it as an optimization problem—minimize the sum of two terms: the first is a combination of the misfit between observed and predicted outputs in an appropriate norm, and the second is a regularization term that penalizes unwanted features of the parameters. This is often called Occam’s approach—find the “simplest” set of parameters that is consistent with the measured data. The inverse problem thus leads to a nonlinear optimization problem in which the forward simulation model is embedded in the misfit term. When the forward model takes the form of partial differential equations (PDEs) or some other expensive model, the result is an optimization problem that may be extremely large scale in the state variables (displacements, temperatures, pressure, and so on), even when the number of inversion parameters is small. More generally, uncertain parameters can be taken from numbers on a continuum (such as initial or boundary conditions, heterogeneous material parameters, or heterogeneous sources) that, when discretized, result in an inverse problem that is very large scale in the inversion parameters as well.
An estimation of parameters using the regularization approach to inverse problems as described above will yield an estimate of the “best” parameter values that minimize the combined misfit and penalty function.
However, in UQ, the analyst is interested not just in point estimates of the best-fit parameters but also in a complete statistical description of all parameter values that are consistent with the data. The Bayesian approach does this by reformulating the inverse problem as a problem in statistical inference, incorporating uncertainties in the measurements, the forward model, and any prior information about the parameters. The solution of this inverse problem is the set of so-called posterior probability densities of the parameters, describing updated uncertainty in the model parameters (Kaipio and Somersalo, 2005; Tarantola, 2005). Thus the resulting uncertainty in the model parameters can be quantified, taking into account uncertainties in the data, uncertainties in the model, and prior information. The term parameter is used here in the broadest sense and includes initial and boundary conditions, sources, material properties and other coefficients of the model, and so on; indeed, Bayesian methods have been developed to infer uncertainties in the form of the model as well (so-called structural uncertainties or model inadequacy are discussed in Section 5.4).
The Bayesian solution of the inverse problem proceeds as follows. Let the relationship between model predictions of observable outputs y and uncertain input parameters![]() be denoted by
be denoted by
![]()
where e represents noise due to measurement and/or modeling errors. In other words, given the parameters θ, the function f(θ) invokes the solution of the forward problem to yield y, the predictions of the observables. Suppose that the analyst has a prior probability density![]() , which encodes the prior information about the unknown parameters (i.e., independent of information from the present observations). Suppose further that the analyst can build—using the computational model—the likelihood function
, which encodes the prior information about the unknown parameters (i.e., independent of information from the present observations). Suppose further that the analyst can build—using the computational model—the likelihood function![]() , which describes the conditional probability that the parameters θ gave rise to the actual measurements yobs. Then Bayes’s theorem expresses the posterior probability density of the parameters,
, which describes the conditional probability that the parameters θ gave rise to the actual measurements yobs. Then Bayes’s theorem expresses the posterior probability density of the parameters,![]() , given the data
, given the data![]() , as the conditional probability
, as the conditional probability
![]() (5.1)
(5.1)
The expression (5.1) provides the statistical solution of the inverse problem as a probability density for the model parameters θ.
Although it is easy to write down expressions for the posterior probability density such as expression 5.1, making use of these expressions poses a challenge owing to the high dimensionality of posterior probability density (which is a surface of dimension equal to the number of parameters), and because the solution of the forward problem is required at each point on this surface. Straightforward grid-based sampling is out of the question for anything other than a few parameters and inexpensive forward simulations. Special sampling techniques, such as Markov chain Monte Carlo (MCMC) methods, have been developed to generate sample ensembles that typically require many fewer points than are required for grid-based sampling (Kaipio and Somersalo, 2005; Tarantola, 2005). Even so, MCMC approaches become intractable as the complexity of the forward simulations and the dimension of the parameter spaces increase. The combination of a high-dimensional parameter space and a forward model that takes hours to solve makes standard MCMC approaches computationally infeasible.
As discussed in Chapter 4, one of the keys to overcoming this computational bottleneck lies in examining the details of the forward model and effectively exploiting its structure in order to reduce implicitly or explicitly the dimension of both the parameter space and the state space. The motivation for doing so is that the data are often informative about just a fraction of the “modes” of the parameter field, because the inverse problem is ill-posed. Another way of saying this is that the Jacobian of the parameter-to-observable map is typically a compact operator and thus can be represented effectively using a low-rank approximation—that is, it is often sparse with respect to some basis (Flath et al., 2011). The remaining dimensions of parameter space, which cannot be inferred from the data, are typically informed by the prior; however, the prior does not require the solution of expensive forward problems and is thus usually much cheaper to compute. Compactness of the parameter-to-observable map suggests that the state space of the forward problem can be reduced as well. Note that although generic, regularizing priors (e.g., Besag et al., 1995; Kaipio et al., 2000; Oliver et al., 1997) make posterior exploration possible, giving useful point estimates, they may not adequately describe the uncertainty in the actual field. This is common when the
physical field exhibits roughness or discontinuities that are not allowed under the prior model used in the analysis. In such cases, the uncertainties produced from such an analysis will not be appropriate at small spatial scales. Such difficulties can be overcome by specifying more realistic priors.
A number of current approaches to model reduction for inverse problems show promise. These range from Gaussian process (GP) response-surface approximation of the parameter-to-observable map (Kennedy and O’Hagen, 2001); to projection-type forward-model reductions (Galbally et al., 2010; Lieberman et al., 2010); to polynomial chaos (PC) approximations of the stochastic forward problem (Badri Narayanan and Zabaras, 2004; Ghanem and Doostan, 2006; Marzouk and Najm, 2009); to low-rank approximation of the Hessian of the log-posterior (Flath et al., 2011; Martin et al., in preparation2). Approaches that exploit multiple model resolutions have also proven effective for speeding up MCMC in the presence of a computationally demanding forward model (Efendiev et al., 2009; Christen and Fox, 2005).
An alternative to using the standard MCMC methods on the computer model directly is to use an emulator (see Section 4.1.1, Computer Model Emulation) in its place. In many cases, this approach alleviates the computational bottleneck caused by solving the inverse problem by applying MCMC to the computer model directly. Box 5.2 shows how an emulator can reduce the number of computer model runs for the bowling ball drop application in Box 5.1.
Here the measured drop times are governed by the unknown parameters, q (the acceleration due to gravity g, for this example), and also quantities, x, that can be measured or adjusted in the physical system. For this example x denotes drop height, but more generally x might describe system geometry, initial conditions, or boundary conditions. The relationship between observable outputs and uncertain input parameters q, at a particular x, is now denoted by
![]() (5.2)
(5.2)
where e denotes the measurement error. The computer model is exercised at a limited number of input configurations (x,θ), shown by the dots in Figures 5.2.1(a), (b), and (c). Next, an emulator of the computational model can be constructed and used in place of the simulator (Figure 5.2.1(b)). Alternately, the construction of the emulator and estimation of θ can be done jointly using a hierarchical model that specifies, say, a GP model for η( ) and treats the estimation of θ as a missing-data problem. Inferences about the parameter θ, for example, can be made using its posterior probability distribution, usually sampled by means of MCMC (Higdon et al., 2005; Bayarri et al., 2007a).
The physical observations and the computational model can be combined to estimate the parameter θ, thereby constraining the predictions of the computational model. Looking again at Figure 5.2.1(c), the probability density function (PDF) (shown by the solid curve in the center) shows the updated uncertainty for θ after combining the computational model with the physical observations. Clearly, the physical observations have greatly improved the knowledge of the unknown parameter, reducing the prediction uncertainty in the drop time for a bowling-ball drop of 100 m.
Finding: Bayesian methods can be used to estimate parameters and provide companion measures of uncertainty in a broad spectrum of model calibration and inverse problems. Methodological challenges remain in settings that include high-dimensional parameter spaces, expensive forward models, highly nonlinear or even discontinuous forward models, and high-dimensional observables, or in which small probabilities need to be estimated.
Recommendation: Researchers should understand both VVUQ methods and computational modeling to more effectively exploit synergies at their interface. Educational programs, including research programs with graduate-education components, should be designed to foster this understanding.
_____________________
2 Martin, J., L.C. Wilcox, C. Burstedde, and O. Ghattas, A Stochastic Newton MCMC Method for Large Scale Statistical Inverse Problems with Application to Seismic Inversion. SIAM Journal on Scientific Computing, to appear.
Computer models of processes are rarely perfect representations of the real process being modeled; there is usually some discrepancy between model and reality. Although few would disagree with this near tautology, reactions are bounded between two positions: (1) “If it is the best model we can construct at the current time and with the current resources, we cannot do better than to simply use the model as a surrogate for reality” and (2) “Use of a model is never justifiable unless it has been ‘proven’ to be an accurate representation of reality.”
The first position may appear attractive in certain applications in which one must do something (e.g., decide whether or not to evacuate because of a potential tsunami), but it often leaves much to be desired from a scientific standpoint. The second position is harder to criticize because it seems to have the ring of scientific veracity, but it can result in doing nothing when something should be done. For instance, it is unlikely that, in the near future, any climate model will be proven to be an accurate representation of reality, in a detailed absolute sense, yet the consequences of ignoring what the climate models suggest could be significant.
Dealing with model inadequacy is the most difficult part of VVUQ. Although one may be able to list the possible sources of model inadequacy, understanding their impact on the model’s predictions of QOIs is exceedingly difficult. Furthermore, dealing with model inadequacy is arguably the most important part of VVUQ: if the model is grossly wrong because of limited capability in incorporating the physics, chemistry, biology, or mathematics, the fact that the other uncertainties in the analysis have been accounted for may be meaningless.
Formal approaches to dealing with model inadequacy can be characterized as being in one of two camps, depending on the information available. In one camp, evaluation is performed by comparing model output to physical data from the real process being modeled. The common rationale for this philosophy is that the only way to see if a model actually works is to see if its predictions are correct. This report refers to this approach as the predictive approach to evaluation. The other camp focuses on the model itself and tries to assess the accuracy or uncertainty corresponding to each constructed element of the model. The common rationale for this philosophy is that if the model contains all of the elements of the system it represents, if all of these elements (including computational elements) can be shown to be correct, and if they are correctly coupled, then logically the model must give accurate predictions. This report refers to this as the logical approach to model evaluation. Of course, any evaluation of a given model’s adequacy could involve elements from each camp.
Before discussing these formal approaches, it is important to consider the metric and tolerance by which model adequacy should be measured. The obvious metric is simply accuracy in the prediction of the desired feature of the real process—the quantity of interest. The point is that no model is likely to predict every aspect of a real process accurately, but a model may accurately predict a key feature of interest of the real process, to within an acceptable tolerance for the intended application. Furthermore, because uncertainties abound, prediction inevitably has an uncertainty range attached. Thus the prediction may be in the form of a statement such as this: “The real QOI will be 5 ± 2 (with probability 0.9).” There are many advantages of viewing model adequacy through such statements. They include the following:
• Models rarely give highly accurate predictions over the entire range of inputs of possible interest, and it is difficult to characterize regions of accuracy and inaccuracy in advance. The type of statement given above indicates the accuracy of the predicted quantity of interest, and the user can decide whether the accuracy is sufficient or not.
• The degree of accuracy in the prediction (both the 2 and the 0.9 in the statement above) will typically vary from one application of the computer model to another and from one QOI to another. The degree of accuracy that is required may also differ for different intended applications and different QOIs.
• The uncertainty statements can simultaneously incorporate probabilistic uncertainty and structural uncertainty (also known as model bias or discrepancy).
Note, in particular, that the blanket statements “The model is valid” (i.e., always valid) or “The model is invalid” (i.e., always invalid) are almost always devoid of useful information (although in some cases the latter may not be). Keeping this metric of model validity in mind, there is then a formal approach to modeling inadequacy when
data from the real process are available (Kennedy and O’Hagan, 2001; Higdon et al., 2005; Bayarri et al., 2007a). The automobile-suspension case study described below makes use of this approach, which is now briefly outlined.
The failure to model the system perfectly, even given the correct inputs, is due to model discrepancy, which often varies with the experimental conditions x. Let us denote the relationship between observable outputs, y, and the parameters governing the system, (x, θ), by
![]()
where e represents noise. One formal approach for combining data from the real process with computer model runs (Kennedy and O’Hagan, 2001; Higdon et al., 2005; Bayarri et al., 2007a) views the physical observations as the sum of the computer-model output, a model inadequacy function, and noise. Mathematically this is stated as
![]()
where ![]() is the computer-model output with inputs
is the computer-model output with inputs ![]() and
and ![]() is the discrepancy between the computer-model output and the true, physical mean QOI at a particular value of x (the observable or adjustable system variables).
is the discrepancy between the computer-model output and the true, physical mean QOI at a particular value of x (the observable or adjustable system variables).
The aim is to use realizations from the computer model and the physical observations to (1) solve the inverse problem, thereby estimating θ, (2) assess the model adequacy; and (3) build a predictive model for the system. These goals are most frequently achieved using a Bayesian hierarchical model that specifies, for example, Gaussain process (GP) models for![]() and treats the estimation of θ as a missing-data problem. Prior distributions must be specified for the GP parameters and also for θ. Sampling from the joint posterior distribution of these parameters is typically carried out using an MCMC algorithm, leading to estimates of all unknowns, including the discrepancy
and treats the estimation of θ as a missing-data problem. Prior distributions must be specified for the GP parameters and also for θ. Sampling from the joint posterior distribution of these parameters is typically carried out using an MCMC algorithm, leading to estimates of all unknowns, including the discrepancy![]() , together with error bands quantifying the uncertainties in the estimates. For alternative but related formulations for combining computational models with physical measurements for calibration and prediction, see Fuentes and Raftery (2004), Goldstein and Rougier (2004), and Tonkin and Doherty (2009).
, together with error bands quantifying the uncertainties in the estimates. For alternative but related formulations for combining computational models with physical measurements for calibration and prediction, see Fuentes and Raftery (2004), Goldstein and Rougier (2004), and Tonkin and Doherty (2009).
To make these extensions more concrete, consider the reduced version of the ball-drop experiments in Box 5.3. In this illustration, the computational model is the simple model outlined in Box 5.1, and the unknown parameter in the model, θ, is the acceleration due to gravity g. This simple model fails to take into account the ball properties and the effect of air friction. Suppose for the moment that the experiments are performed only with the bowling ball (i.e., see Box 1.1 in Chapter 1, or Box 5.2) and the inverse problem is solved as outlined in Section 5.3, Model Calibration and Inverse Problems. Notice that the constrained prediction of the bowling-ball drop times performs quite well. However, the first two plots in Figure 5.3.1(a) show that the model does not accurately predict the drop times for the basketball and baseball. This would also indicate that predictions for the untested softball are problematic.
If all of the observations for the basketball, baseball, and bowling ball are available, then a model discrepancy (i.e., model inadequacy) term that accounts for each ball’s radius and density can be estimated. The particular discrepancy is estimated in Figure 5.3.1(c). A glance at Figure 5.3.1(d) shows that the discrepancy-adjusted model does a much better job of predicting the physical responses. Also notice that the 95 percent probability interval for each ball is wider than those illustrated in Box 5.1. This is because the statistical model is estimating g as well as parameters for the discrepancy model (the parameters that describe the function ![]()
Continuing with this illustration, suppose that interest also lies in predicting the drop times for the softball, but there are no observations available. Since the discrepancy is modeled as a function of the ball’s radius and density, then discrepancy-adjusted predictions can be made for the softball (see Figure 5.3.1(d)). The 95 percent probability intervals are wider than the intervals for the other balls because there are no observations of the softball, and the inadequacy for this setting is informed through the estimated discrepancy model.
One might be tempted to use this approach to estimate drop times for the golf ball. Notice that the golf ball is not in the interior of the radius and density ranges explored in the experiments. Such a scenario constitutes an extrapolation of the discrepancy function where one is not likely to know its functional form. In any case, extrapolating beyond the experimental region should be done with great caution.
Box 5.3
Using a Model Discrepancy Term to Predict Drop Times
After the calibration of the model, which accounts only for acceleration due to gravity (Box 5.2), we find that the model does not accurately predict drop times for the basketball and baseball (Figure 5.3.1(a)). Thus the model is not considered to be adequate for predicting the drop time for a softball at 40 m or 100 m.
The conceptual and mathematical model accounts for acceleration due to gravity g only. A discrepancy-adjusted prediction is produced by adjusting the simulated drop times according to the equation:
Drop time = simulated drop time + α × drop height,
where α depends on the radius and density of the ball![]() . The model produces an estimate for α that increases as ball density decreases (Figure 5.3.1(c)).
. The model produces an estimate for α that increases as ball density decreases (Figure 5.3.1(c)).
Figure 5.3.1(d) shows predictions using the discrepancy-adjusted model described above. The added uncertainty is due to uncertainty in both g and α in this model.
The resulting predictions and uncertainty use a model that more accurately fits known data but does not accurately reproduce reality in general. Furthermore, the discrepancy term is not physically derived. For example, this discrepancy-adjusted model does not produce a constant terminal velocity for an object that falls for a long time. This suggests that the quality of these predictions is less than those produced from the drag model used in Box 5.1. In particular, predictions for drops from greater heights, resulting in greater velocities, are suspect for this discrepancy-adjusted model. A key question is at what height (for a softball, say) this prediction (with uncertainty) becomes unreliable.
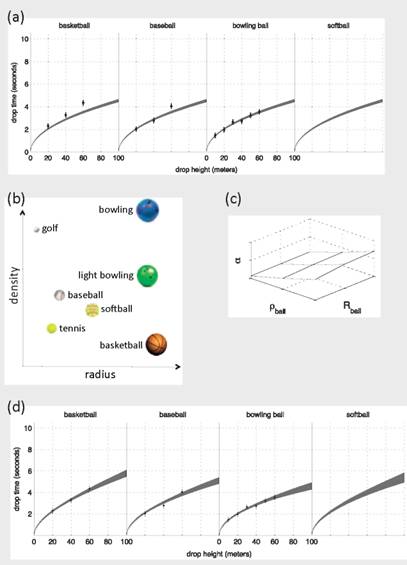
FIGURE 5.3.1
The additive discrepancy term described in this chapter—which in many published applications has been modeled as a Gaussian process—could be replaced by other, more physically motivated forms. It is also common to embed discrepancy terms within the computational-model specification. For example, the air friction term in the ordinary differential equation (ODE) in Figure 5.1.1(b) could be considered a physically motivated, embedded discrepancy term. Such terms are more commonly called parameterized, or effective, physics terms. Generally, the more physically motivated a discrepancy term is, the broader the prediction’s domain of applicability. This broader perspective of constructing general approaches for adjusting basic, inadequate models to give useful predictions is likely to be a productive field for future VVUQ research.
The approach of embedding discrepancy terms within the computational-model specification is not a panacea, however, and thus it comes with a few notes of caution. For example, the approach can suffer from serious confounding between the estimates of the parameters, θ, and the estimated discrepancy function. Broadly speaking, the discrepancy can account for both good and bad choices of θ (Loeppky et al., 2011). Indeed, in cases where model inadequacy exists (i.e., the discrepancy cannot be safely estimated as zero), one should not view the estimates of the unknown parameters, θ, as solutions to the inverse problem but instead should view them more as tuning parameters to allow the sum of the computer model and discrepancy to best match the observations. Furthermore, the estimated discrepancy does not necessarily extrapolate well to new situations (although it can if one is lucky), because the “model bias or discrepancy correction” can claim to be accurate only in regions close to where there are real-process data. In spite of these issues, formally exploring the discrepancy surface can be of considerable value, exposing the regions of the input space for which the computational model is inadequate, potentially leading to opportunities for improvement in the model.
Finding: A discrepancy function can help adjust the computational model to give better interpolative predictions. A discrepancy function can also be beneficial in reducing the overtuning of parameters used to adjust or calibrate the model that can otherwise result.
If no data on the real process are available (e.g., as in the PECOS case study of Section 5.9, or for parts of the problem of determining the condition of the nuclear stockpile), there is no alternative to the “logical” approach to assessing model adequacy (although the adequacy of subcomponents of the model could be partly assessed through real-process data relevant to the subcomponents). Care is needed in analyzing the uncertainties from each possible source. It is tempting to do “worst-case” analyses, but these will often not result in useful policy guidelines because the “worst cases” are too extreme, especially if the system has a large number of components and the “worst cases” of each are combined.
For example, suppose we have a 15-component system and the probability of failure of each component is known quite accurately to be between 0.002 and 0.007. Then a worst-case analysis shows only that the probability of failure of the system (assuming it fails if any component fails) is between 0.03 and 0.10, which may be an overly wide interval for decision purposes. In contrast, if one were willing to assume that the failure probabilities of the components were (independently) uniformly distributed between 0.002 and 0.007, the resulting 95 percent confidence interval for system failure would be the interval from 0.060 to 0.070, a much smaller interval. Although one could certainly argue against the assumptions made in the latter analysis, from the decision standpoint, it might be preferable to accept such assumptions in lieu of the large uncertainties produced by the worst-case analysis.
Research and educational issues abound in the areas of accounting for model discrepancy. Below, a few main issues are summarized.
• The predictive approach to evaluating model adequacy has implementation problems: it leads to identifiability issues because of trade-offs between the model parameters and the discrepancy term, and it is difficult to implement in high-dimensional problems.
• The use of physically motivated forms for the discrepancy term, using insight from the application and from an understanding of the model’s shortcomings, is an open problem that can be advanced by researchers who are versed in VVUQ methods, computational modeling, and the application at hand.
• One motivation for using multimodel ensembles (Section 5.7) is to estimate physical reality using a collection of models, each with its own discrepancy. Can ensembles of models help in estimating model discrepancy? Can one construct an ensemble of models, perhaps using bounding ideas, that allows one to quantify the difference between model predictions and reality?
• Typically, VVUQ will ultimately be tied into decision making. If model discrepancy is an important contributor to prediction uncertainty, this will need to be reflected in decision-making problems that use the model. The VVUQ analysis must produce results that can be incorporated into the encompassing decision problem.
• Assessing model adequacy should be viewed as an evolutionary process with the accumulation of evidence enhancing or degrading confidence in the model outputs and their use for an intended application. Therefore, the formal methodology must accommodate the updating of current conclusions as more information arrives.
As an alternative to the Bayesian approach, one might formally perform a hypothesis test to decide if it can be assumed that the discrepancy is zero in the tested regimes (Hills and Trucano, 2002). Two problems can arise with this approach, however. The first is that the test may suffer from a lack of statistical power. For instance, if one has physical data that are very uncertain and provide almost no constraint on reality, then the null hypothesis of zero discrepancy will not be statistically rejected, even if the computational model is extremely biased. At the opposite extreme, one might have a quite good computational model with discrepancy that is close enough to zero to make the model very useful, and yet have so much physical data that one would resoundingly reject the null hypothesis of zero discrepancy with any formal statistical test. (For an example of the latter, see Bayarri et al., 2009a.) Accordingly, the committee believes that the approach of estimating the discrepancy, together with associated error bands and specified tolerance, is the more fruitful approach.
5.5 ASSESSING THE QUALITY OF PREDICTIONS
Predictions with uncertainty are necessary for decision makers to assess risks and take actions to mitigate potential adverse events with limited resources. In addition to providing an estimate of the uncertainty, it is also crucial to assess the quality of the prediction (and accompanying uncertainty), describing and assessing the appropriateness of key assumptions on which the estimates are based, as well as the ability of the modeling process to make such a prediction. The way that one assesses the quality, or reliability, of a prediction and describes its uncertainty depends on a variety of factors, including the availability of relevant physical measurements, the complexity of the system being modeled, and the ability of the computational model to reproduce the important features of the physical system on which the QOI depends.
This section surveys issues related to assessing the quality of predictions, their prediction uncertainty, and their dependence on features of the application—including the physical measurements, the computational model, and the degree of extrapolation required to make inferences about the QOI.
For repeatable events, a computational model’s predictive uncertainty can often be reliably assessed empirically, without a detailed understanding of how the model works and without a detailed understanding of how the model differs from reality. For example, consider two models for predicting tomorrow’s high temperature (Figure 5.1)— one model uses today’s high temperature as the prediction, and the other is the prediction provided by the National Weather Service (NWS) using state-of-the-art computational models and data feeds from ground stations and satellites. By comparing predictions to physical observations over the past year, one can infer that although both models are unbiased, the prediction from the NWS model is more accurate. A 90 percent prediction interval for the NWS predictions is ±6°F, whereas the same prediction interval for the empirical persistence model is ±14°F
This combination of computational model with physical observations is a classic example of data assimilation. This is a mature field, with substantial literature and research focused on such filtering, or data-assimilation problems (Evensen, 2009; Welch and Bishop, 1995; Wan and Van Der Merwe, 2000; Lorenc, 2003; Naevdal et al., 2005), in which the model is repeatedly updated given new physical observations. In these applications the
prediction and its uncertainty are reliably estimated, the data are relatively plentiful, and data are directly comparable to model output.
In many model-based prediction problems, a purely empirical, or statistical, approach is not feasible because there are insufficient measurement data in the domain of interest with which to assess the computational model’s prediction accuracy directly. For example, consider the ball-drop experiment described in Boxes 5.1 and 5.2. The prediction as to how long it takes a softball to fall 100 m is based on a computational model and experiments involving various balls—none of which are softballs—and various drop heights, none of which are above 60 m. The automobile suspension system case study discussed in Section 5.6 is another example, as is the thermal problem described in Hills et al. (2008). In each of these examples there are limited data available that can be combined with a computational model to produce predictions and accompanying uncertainty estimates. This means that there is some degree of extrapolation involved in these predictions. Assessing the quality of the prediction and uncertainty estimate in these cases requires an understanding of the physical process and the computational model in addition to the VVUQ methodology being used.
The combination of measurement data and computational model(s) can be more intricate, as described in the PECOS Center’s application on assessing the thermal protection layer of a reentry vehicle (Section 5.9), or in the cruise-missile assessment described in Oberkampf and Trucano (2000), or in the validation work of the Department of Energy (DOE) National Nuclear Security Administration (NNSA) laboratories’ stockpile stewardship program (Thornton, 2011). In these applications, a hierarchy of different experiments explores different features of the physical system. Some experiments probe a single phenomenon, such as material strength or equation of state, whereas others produce measurements from processes that involve multiple physical phenomena, requiring multiphysics models. Typically, experimental measurements are more readily available for simpler experiments, involving a single effect. Highly integrated experiments are more expensive and less common. In such applications, a model to predict the QOI typically requires a multiphysics code, and the QOI is often difficult, or even impossible, to observe directly in experiments. One needs to combine measurements from these various experiments with the computational model to produce predictions with uncertainty for the QOI. Ideally, one should also assess the quality of resulting predictions and of their estimated uncertainties.
The above applications have limited data in the domain of interest, and others are even more extrapolative. The climate-modeling case study discussed in Section 2.10 of Chapter 2 is a good example of extrapolation. The QOI is global mean temperature after 15 years of doubled CO2 forcing. In addition to extrapolations in time and forcing conditions, the predictions are based on models that do not contain all of the physical processes present in the actual climate system. The many issues in such an investigation are detailed in that case study. Other examples, such as assessing the risk of groundwater contamination from transport over the span of hundreds or thousands of years, can also be highly extrapolative. A danger in such applications is that the model may be missing key physical phenomena that are not important to the processes controlling the calibration and/or validation phase of the assessment but that are important in the system for the extrapolative prediction. Although it is quite difficult to account for potential missing processes and to quantify their effects on predicted QOIs, their existence is likely to push the model predictions away from reality in highly extrapolative settings. See Kersting et al. (1999) for a notable example in subsurface contaminant transport.
Although there does not appear to be any common, agreed-upon mathematical framework to assess the quality of validation and UQ in extrapolative situations, nearly all such applications invoke some notion of a domain space, describing key features of the physical and modeling processes relevant to the QOI. A very simple example is given in Box 5.2, where each experiment is described by its initial conditions—drop height, ball radius, and ball density.
This notion of the domain space is also present in the hierarchical validation scenario described in Figure 5.7, in Section 5.9.5, with the space accounting for different basic processes in the system, as well as the integration of these different processes. Figure 5.2 shows a number of domain space concepts from the VVUQ literature, ranging from specific descriptions of initial conditions to vaguer descriptors of system complexity.
This notion of domain space enables one to estimate prediction uncertainty, or quality, as a function of position in this space. In Box 5.3, the domain space, describing initial conditions, is used as the support on which the model discrepancy term is defined, enabling a quantitative description of prediction uncertainty as a function of drop height, ball radius, and ball density. Clearly, this domain space can incorporate more than just
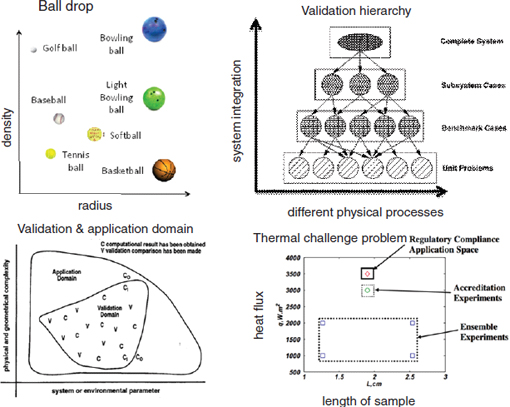
FIGURE 5.2 Domain spaces from four different VVUQ sources. The domain space describes the conditions relevant to assessing the accuracy with which a model reproduces an experiment. In some cases this domain space is very specific, describing initial conditions; in others this space is more generically specified. SOURCE: The validation hierarchy is taken from AIAA (1998); the validation and application domains are from Oberkampf et al. (2004); the thermal challenge example is from Hills et al. (2008).
model-input terms. For example, Higdon et al. (2008) uses a discrepancy term defined over two-dimensional features present in the experimental observations that cannot be incorporated into the one-dimensional model that was employed.
As Figure 5.2 suggests, it may also be fruitful to define a domain space that describes the important physical phenomena/regimes that control or affect the true physical QOI. Examples might include quantitative dimensions such as temperature and pressure visited by the physical system, as well as qualitative ones such as whether or not the QOI is affected by a phase change, turbulence, or boundary effects. By constructing such a domain space, more direct diagnoses of model shortcomings could be made. For example, if the system undergoes a phase change, then the computed QOI is not reliable since the model does not address this phenomenon. Such a phenomenon-based description of a domain space may be difficult to obtain since such features are often difficult to access experimentally. Models may help, but they may not faithfully reproduce these features of the physical system.
Mapping out such a domain space can help build understanding regarding the situations for which a computational model is expected to give sufficiently accurate predictions. It also may facilitate judgments of the nearness of available physical observations to conditions for which a model-based prediction is required. For example, subject-matter and modeling experts might agree that the model will still give reliable prediction results as certain dimensions of this space are varied, whereas with changes in other dimensions it will not. Sensitivity analysis is likely involved in specifying this domain, but it must go beyond simply exploring the model. Understanding the
strengths and weakness of both the mathematical and the computational models, as they compare to reality for this application, is key. This understanding must rely heavily on subject-matter expertise.
5.6 AUTOMOBILE SUSPENSION SYSTEMS CASE STUDY
The use of computer models of processes has enormous potential in industry for replacing costly prototype design and experimentation with much less costly computational simulations of processes. In the automotive industry, for instance, each prototype vehicle can cost hundreds of thousands of dollars to construct, and the physical testing of the vehicles is expensive. Great savings can be achieved if computer models of the vehicles, or components thereof, are used instead of prototype vehicles for design and testing. Of course, a computer model can be trusted for this only if it can be shown to provide a successful representation of the real process.
This section discusses a study that was made of a computer model of an automotive suspension system (Bayarri et al., 2007b). Of primary interest was the ability of the computer model to predict loads resulting from events stressful to the suspension system—for example, hitting a pothole. The case study provides an illustration of much of the range of needed inference in uncertainty quantification, covering the following:
• Uncertainty in model inputs,
• The need for calibration or tuning of model parameters,
• Assessment of the discrepancy between the model and the real process,
• Provision of uncertainty bounds for predictions of the model, and
• The allowing of model prediction improvements through a discrepancy adjustment.
The approach taken in the study was based on Bayesian probability analysis, which has the singular feature of allowing all of the above issues to be dealt with simultaneously and which also provided final uncertainty bounds on model predictions that account for all of the uncertainties in the inputs and model. In particular, model predictions were always presented with 90 percent confidence bands, allowing direct and intuitive assessment of whether the model predictions are accurate enough for the intended use. However, commercial software was used in the study, and so verification was not carried out, since it was assumed to be the responsibility of the software developer.
An ADAMS3 computer model (a commercially available, widely used finite-element-based code that analyzes the dynamic behavior of mechanical assemblies) was implemented (Bayarri et al., 2007b) to re-create the loads resulting from stresses on a vehicular suspension system.
In addition to the finite-element model itself (which must be constructed for each vehicle type), the computer model has several inputs:
• Two calibration parameters, u1 and u2, which quantify two types of damping (energy dissipation) that need to be estimated for (or tuned to) the physical process under study; and
• Seven unmeasured parameters of the system corresponding to characteristics of parts of the suspension system (tires, bushings, and bumpers) as well as vehicle mass; these have known nominal values but are subject to manufacturing variations and hence are treated as randomly varying around their nominal value.
5.6.3 The Process Being Modeled and Data
The initially envisaged use of the computer model was to replace (or massively reduce) the need for the field-testing of actual vehicles on a test track that included several stressors (potholes). The result of a vehicle test is a
_____________________
3 See http://www.mscsoftware.com/Products/CAE-Tools/Adams.aspx. Accessed September 1, 2011.
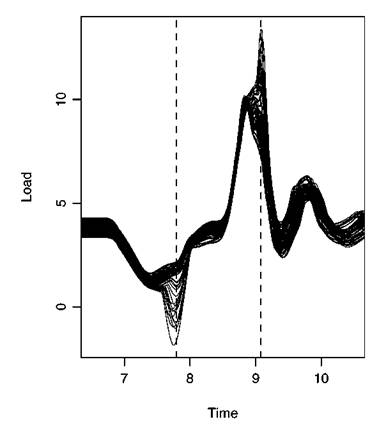
FIGURE 5.3 Computer model predictions of force on the suspension system at 65 inputs. SOURCE: Bayarri et al. (2007a).
time trace of the load on the suspension system as the vehicle drives down the test track. Figure 5.3 presents the computer model prediction of these time traces for 65 different combinations of values for the nine input parameters described above. These 65 input value sets were chosen, using a Latin hypercube design, so as to “cover” the design space of possible input values in a representative fashion. (For simplicity, only part of the time traces are given in Figure 5.3—as the vehicle runs over a single pothole and a span of about 3 m—and only analyses for this region are discussed here.)
This was a context in which the predictive approach to model validation could be entertained; the validation process would center on field data obtained from actual physical runs of a vehicle over the test track. A test vehicle was outfitted with sensors at various locations on the suspension system and was physically driven seven times over the test track. This resulted in seven “real” independent time series of road loads, measured subject to random error but not to bias.
5.6.4 Modeling the Uncertainties
To understand the uncertainties in predictions of the computer model, it is first necessary to model the uncertainties in model inputs, the real-process data, and the model itself. For the nine model input parameters, these uncertainties were given in the form of prior probability distributions, obtained by consultation with the engineers involved with the project. Many of these were simply the known distributions of suspension system parts arising from manufacturing variability. The measurement errors in the data were modeled using a wavelet decomposition process.
There were two sources of uncertainty concerning the computer model itself. The model discrepancy issue discussed in Section 5.3, “Model Calibration and Inverse Problems,” was handled by allowing a functional deviation of the computer model from reality and a Gaussian process prior to this discrepancy (following Kennedy and O’Hagan, 2001). The second source of uncertainty in the model was in the use of an emulator (an approximation to the computer model) because of the expense of running the computer model. Since a Gaussian process was used to construct the emulator, the uncertainty in its approximation can be readily incorporated into the overall assessment of uncertainty.
The collection of probability distributions representing the uncertain model inputs, uncertain real-process data, and uncertain model was processed through Bayesian analysis involving MCMC computation (Bayarri et al., 2007b). The results of the analysis are expressed as posterior distributions of QOIs, summarized by a posterior expected values (the “prediction” of the quantity) and confidence intervals to indicate the uncertainty in the prediction.
Figure 5.4 presents the estimated model discrepancy—that is, the estimated difference between the computer-model prediction and the real process. The dashed line is the mean discrepancy, and the solid lines are 90 percent
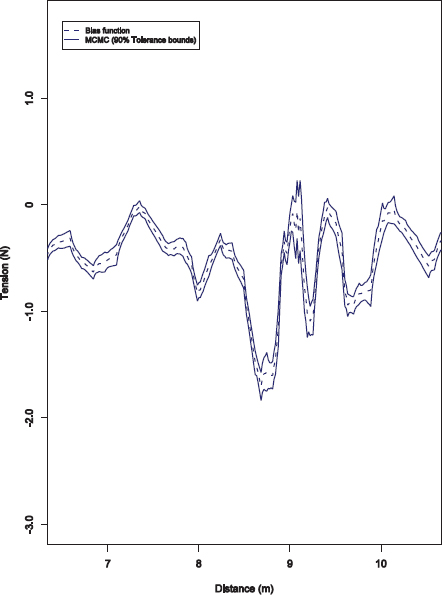
FIGURE 5.4 Estimated discrepancy of the computer model from reality. SOURCE: Bayarri et al. (2007b).
uncertainty bands for this discrepancy. As can be seen, the computer model provided a reasonable approximation to the real process; a constant value of zero for the discrepancy would indicate a perfect validation.
The shown deviation from zero was not deemed by the engineers to be excessive, except for the spike (which occurred at the pothole). An effort was made to incorporate the discrepancy assessment into improved predictions of reality from the computer model. Note that this incorporation is not a matter of simply “adding” the discrepancy to the model prediction because the uncertainties in the discrepancy and damping parameters are highly dependent, so that their joint posterior distribution must be utilized to determine the adjustment.
Various prediction scenarios can be considered. The most challenging of these was the prediction for a new vehicle type having different nominal values of the input parameters. The most valuable engineering use of computer models is, indeed, to extrapolate to such a system having new input values, since then the expense of obtaining real-process data can be avoided. Such extrapolation requires strong assumptions concerning the discrepancy. The simplest assumption is that the new system has the same discrepancy function (or distribution) as the old system, and that was assumed here. Because of physical understanding of the system, the discrepancy was viewed as being multiplicative rather than additive.
To predict the road-load time trace for the new vehicle type, the computer model (in which the new vehicle type was close enough in design to allow the use of the same finite-element representation as for the previous vehicle type) was run at 65 values of the uncertain inputs. These were now centered around nominal input values assessed for the new vehicle. A Bayesian analysis was subsequently performed, utilizing these 65 computer-model runs, the prior distributions for the seven suspension characteristics, and the joint posterior distribution of the discrepancy and damping parameters obtained from the original vehicle.
Figure 5.5 summarizes the results of this analysis. Clearly there is a significant difference between the predictions of the computer model alone and the predictions that incorporated the discrepancy of the model that was determined by using previous experimental data. Eventually, the new vehicle was driven over the test track, with the actual road-load traces being measured—the heavy black band in Figure 5.5. While not perfect, the Bayesian predictions are considerably more accurate than predictions from the computer model alone.
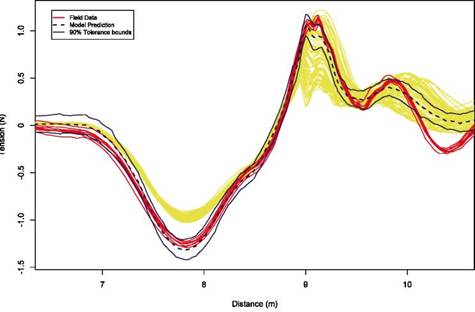
FIGURE 5.5 Results of analysis. The green curves show the 65 computer-model runs. The Bayesian posterior mean of the road-load trace is the dashed line, the 90 percent uncertainty bands are the solid blue lines, and the heavy red line is the field data. SOURCE: Bayarri et al. (2007b).
This example shows a successful use of discrepancy-adjusted prediction; such adjustment will not always be acceptable, however, because extrapolation beyond the range of relevant data is always a challenge, depending as it does on assumptions about continuity in the underlying model validity and about conditions under which extrapolating estimates of parameter values can be assumed to be smooth. However, since the computer model itself is used to do the computational “heavy lifting” in the extrapolation, with the discrepancy adjustment playing a lesser role, concerns about extrapolation can be somewhat mitigated.
More important, the Bayesian approach implicitly incorporates all uncertainties in the analysis and folds these into assessment of the overall uncertainty in the posterior distributions of all QOI. The main limitation of the approach is the need for MCMC computation, which could sometimes require either extensive computational effort or the development of a good emulator for the more computationally challenging components of the computer model.
5.7 INFERENCE FROM MULTIPLE COMPUTER MODELS
In applications such as climate change, uncertainties in 20- or 100-year forecasts are likely dominated by structural uncertainty—uncertainty due to the discrepancy between model and reality. Since there are few or no physical observations from which to estimate model discrepancy directly, predictions from a number of different climate models are often used to help quantify prediction uncertainty.
Some forecasting applications have made successful use of combining predictions from different models (e.g., Gneiting and Raftery, 2005). These approaches incorporate multiple model-based predictions within a statistical modeling framework, often producing predictions more accurate those of than any single model, with more-reliable estimated uncertainties. Although climate and weather are the main examples discussed in this section, these basic approaches have been applied in a wider variety of applications.
The Intergovernmental Panel on Climate Change (IPCC) uses predictions of the future climate state from multiple computational global climate models, developed under various research efforts from around the world, to make assessments about climate change under different future emission scenarios (Meehl et al., 2007). The resulting multimodel ensemble (MME) of climate model runs, carried out largely for the IPCC assessment, has been used by a variety of researchers to produce predictions of future climate along with estimates of prediction uncertainty. The most common approach for using such an MME to make predictions about future climate is the use of a hierarchical modeling framework, effectively treating the output from different models as noisy versions of the actual climate system (Tebaldi et al., 2005; Buser et al., 2009; Smith et al., 2010). Researchers readily admit that such hierarchical modeling approaches are far from ideal—the ensemble of models is a sample of convenience, and dependencies between different computational models are typically not accounted for in the statistical modeling. Interestingly, the estimated prediction uncertainty typically decreases as the ensemble size increases. It is not at all clear that this should be the case. One can argue that even if infinitely many models could be sampled, future climate would still not be perfectly understood because of our limited knowledge of climate physics. However, the hierarchical modeling approach is a first step for developing more realistic prediction uncertainties using MMEs. Research is needed to establish the connection between model-to-model differences and model-to-reality differences.
In forecasting applications, where repeated relevant physical observations are abundant, the combination of multiple computational models has led to improved predictions and improved prediction uncertainties. The probcast (web page: http://probcast.washington.edu/) methodology of Gneiting and Raftery (2005) is a notable example. This approach, like many others, uses Bayesian model averaging (Hoeting et al., 1999), which models the physical observations as coming from one of the models in the ensemble—but which model is chosen is uncertain. The resulting analysis produces a posterior distribution for the forecast that is a weighted average of the individual model predictions (with uncertainty). The resulting predictions from the Bayesian model averaging approach are generally more accurate than any single prediction, and the resulting prediction uncertainty better describes the variation of the prediction about the observed value than does the raw ensemble.
So far, the success of such model-averaging approaches in forecasting has not been translated to more extrapolative, data-poor settings such as climate change where predictions and their uncertainty cannot be calibrated with an abundant supply of relevant physical observations. The hierarchical model-based approaches for assessing prediction
uncertainty using multimodel ensembles can deal with the relative paucity of physical observations and can capture key sources of uncertainty that may be missed using more traditional parametric variations within a single computational model, but are justified only under assumptions that are often not met in practice. Additional research will likely improve the state of the art in combining predictions from multimodel ensembles. Such research includes improved methods for constructing ensembles of models, analysis of interdependence among models, assessment of confidence in particular models and their predictive power, and use of information-theoretic and statistical means for developing robust and reliable methods for model comparison, selection, and averaging/pooling.
5.8 EXPLOITING MULTIPLE SOURCES OF PHYSICAL OBSERVATIONS
In many applications, multiple sources of physical observations may be available for the validation/prediction assessment. In engineering applications, the data sources might conform to a validation hierarchy (see Figure 5.7 in Section 5.9.5), whereas in other applications these different data sources might include different sensing modalities (e.g., infrared, visible, seismic) or different data sources (e.g., pressure measurements or well cores). It may also be appropriate to use output from high-quality simulations as surrogates for physical observations (e.g., direct numerical simulation of turbulent flow using resolved Navier-Stokes equations may inform about predictions using coarser, Reynolds-averaged, Navier-Stokes simulations). There is the opportunity to make use of these various sources of physical observations to address key issues such as model calibration, model discrepancy, prediction uncertainty, and assessing the quality of the prediction. There is also opportunity to use what is learned from such analyses to inform how to select additional observations or to design additional experiments.
For a given collection of physical observations, there is the question of how best to use these sources for validation and prediction. For example, should low-level experiments in a validation hierarchy be used for calibration, saving the more integrated experiments for assessing the model? Or should both calibration and assessment be done together? Different strategies will require different approaches, which may affect the quality of the predictions.
Multiple sources of physical observations provide an opportunity to assess a prediction and the accompanying prediction uncertainty. One way to exploit this opportunity is to identify collections of experiments, or observation sources, that can be used to assess the quality of a “surrogate” prediction that has important commonalities with the QOI prediction. The characteristics that define an appropriate surrogate, if they exist, will depend on features of the domain space. Does a candidate surrogate prediction depend on the physical process in a way similar to the QOI prediction? Does the surrogate have similar sensitivities to model inputs? Does the model discrepancy function (if there is one) adequately capture uncertainty for these predictions? Should the same model discrepancy function transfer to the QOI? Exactly how best to use multiple sources of physical data to improve the quality and accuracy of predictions is an active VVUQ research area.
In cases where the validation effort will call for additional experiments, the methodologies of validation and prediction can be used to help assess the value of additional experiments and might also suggest new types of experiments to address weaknesses in the assessment. Ideas from the design of experiments from statistics (Wu and Hamada, 2009) are relevant here, but the design of validation experiments involves additional complications that make this an open research topic. The computational demands of the computational model are a complicating factor, as is the issue of dealing with model discrepancies. Also, some of the key requirements for additional experiments—such as improving the reliability of the assessment or improving communication to stakeholders or decision makers—are not easily quantified. The experimental planning enterprise is considered from a broader perspective in Chapter 6.
The Center for Predictive Engineering and Computational Sciences, called the PECOS Center, at the University of Texas at Austin is part of the Predictive Science Academic Alliance Program (PSAAP) of the Department of Energy’s National Nuclear Security Administration. The PECOS Center is engaged in developing VVUQ processes
to gain an understanding of the reentry of a space capsule (e.g., NASA’s proposed Orion vehicle) into Earth’s atmosphere. Of primary interest is the performance of the thermal protection system (TPS), which protects the vehicle from the extreme thermal environment arising from travel through the atmosphere at speeds of Mach 20 or higher, depending on the trajectory. Vehicles that use ablative heat shields (e.g., Orion and Apollo) are being simulated to predict the rate at which the ablator is being consumed.
TPS consumption is a critical issue in the design and operation of a reentry vehicle—if the entire heat shield is consumed, the vehicle will burn up. TPS consumption is governed by a range of physical phenomena, including high speed and turbulent fluid flow, high-temperature aero-thermo-chemistry, radiative heating, and the response of complex materials (the ablator). Thus, a numerical simulation of reentry vehicles requires models of these phenomena.
The reentry vehicle simulations share a number of complicating characteristics with many other high-consequence computational science applications. These complicating characteristics include the following:
• The QOIs are not accessible for direct measurement under the conditions in which the predictions are to be made;
• The predictions involve multiple interacting physical models;
• Experimental data available for calibrating and validating models are difficult to obtain, include significant uncertainty, are sparse, and often describe physical conditions not directly related to the predictions; and
• The best-available models for some of the physical phenomena are known to include sizable errors.
These characteristics greatly complicate the assessment of prediction reliability and the application of VVUQ techniques.
As described above, there are two components of the verification of computer simulation: (1) ensuring that the computer code used in the simulation correctly implements the intended numerical discretization of the model (code verification) and (2) ensuring that the errors introduced by the numerical discretization are sufficiently small (solution verification).
There are many aspects of ensuring the correct implementation of a mathematical model in a computer code. Many of these are just good software engineering practices, such as exhaustive model development and user documentation, modern software design, configuration control, and continuous unit and regression testing. Commonly understood to be important but less commonly practiced, these processes are an integral part of the PECOS software environment.
To ensure that an implementation is actually producing correct solutions, one wants to compare results to known, preferably analytic, solutions. Unfortunately, analytic solutions are not generally available, which is the reason for the use of the method of manufactured solutions (MMS), in which source terms are added to the equations to make a prespecified “solution” exact (Steinberg and Roache, 1985; Roache, 1998; Knupp and Salari, 2003; Long et al., 2010; and Oberkampf and Roy, 2010). Although MMS is a widely recognized approach, it is not commonly used. One reason is that it is much more difficult to implement for complex problems than it appears. First, even for systems of moderate complexity (e.g., three-dimensional compressible Navier-Stokes) there can be many hundreds of source terms, and it is clearly necessary that the evaluation of these terms be done with high reliability. Thus, constructing analytic solutions is itself a software engineering and reliability challenge. Second, the introduction of the source terms into the code being tested must be done with minimal (preferably no) changes to the code, so that the tests are relevant to the code as it will be used. Unfortunately, this introduction of the source terms may not be possible in codes that have not been designed for it. Finally, it is necessary that manufactured solutions have characteristics similar to those of the problems that the codes will be used to solve. This is important so that bugs are not masked by the fact that the terms in which they occur may be insignificant in a manufactured solution that is too simple.
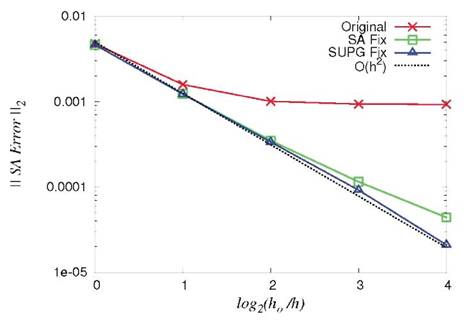
FIGURE 5.6 Dependence of the L2 error in the Spalart-Allmaras (SA) turbulence model manufactured solution on the grid size, under uniform refinement. Shown are the original test, the test after the correction of a bug in the SA equations, and that after subsequent correction of a bug in streamline-upwind/Petrov Galerkin regularization. The theoretical convergence is second order.
At the PECOS Center, to make MMS useful for the verification of reentry vehicle codes, a highly reliable software library for implementing manufactured solutions (the Manufactured Analytic Solution Abstraction, or MASA) and a library of manufactured solutions, using symbolic manipulation software (e.g., Maple), have been developed. These manufactured solutions have been imported into MASA. MASA and associated solutions have been publicly released.4 Further, part of the PECOS Center software development process involves developing and documenting a verification plan (usually involving MMS) before development begins, so that codes are designed to enable MMS. These efforts have paid off by exposing a number of subtle but important bugs in PECOS software. An example is shown in Figure 5.6, in which the convergence with grid refinement of the Spalart-Allmaras (SA) turbulence model5 equations to a manufactured solution is shown. In the initial test, the solution error did not converge to zero with uniform grid refinement, which led to the discovery of a bug in the implementation of the SA equations. When this bug was fixed, the error did reduce with refinement, but not at the theoretically expected rate of h2. The slower rate was caused by a long-standing bug in the implementation of streamline-upwind/Petrov-Galerkin (SUPG) stabilization in the LibMesh finite-element infrastructure in which the model was implemented.
The question in solution verification is whether a numerical solution to a set of model equations is “close enough” to the exact solution. A “close enough” standard is necessary because, although discretization errors can generally be made arbitrarily small through refinement of the discretization, it is neither practical nor necessary to drive these errors to the level of round-off error. Generally, the models are used to predict certain output QOIs, and one wants to ensure that these quantities are within some tolerance of those from the exact solution of the models.
_____________________
4 See https://red.ices.utexas.edu/projects/software/wiki/MASA. Accessed March 19, 2012.
5 For a definition and details of this model, see http://turbmodels.larc.nasa.gov/spalart.html. Accessed March 24, 2012.
An acceptable numerical error tolerance depends on the circumstances. At the PECOS Center, since the numerical discretization errors are under the control of the analyst, the view is taken that they should be made sufficiently small to be negligible compared to other sources of uncertainty. This avoids the need to model the uncertainty arising from such errors. It is important to identify the QOIs for which predictions are being made because the numerical discretization requirements for predicting some quantities (e.g., high-order derivatives) are much more stringent than for other quantities.
Solution verification, then, requires that the discretization error in the QOIs be estimated. The common practice of comparing solutions on two grids to check how much they differ is not sufficient. In simple situations it is possible to refine the discretization uniformly (e.g., half the grid spacing everywhere) and then to apply Richardson extrapolation to develop an error estimate. A more general technique, and the one used at the PECOS Center, is adjoint-based a posteriori error estimation (Bangerth and Rannacher, 2003). Once one has an estimate of the errors in the QOIs, it may be necessary to refine the discretization to reduce this error. Adjoint-based error estimators also provide an indicator of where (in space and/or time) the discretization errors are contributing most to errors in the QOIs. Goal-oriented adaptivity (Bangerth and Rannacher, 2003; Oden and Prudhomme, 1998; Prudhomme and Oden, 1999; Strouboules et al., 2000) uses this adjoint information to drive adaptive refinement of the discretization.
At the PECOS Center, the simulation codes used to make predictions of the ablator consumption rate (the QOI) have been developed to perform adjoint-based error estimation and goal-oriented refinement. For example, a hypersonic flow code (FIN-S) supporting goal-oriented refinement was built on the LibMesh infrastructure (Kirk et al., 2006). Adaptivity is used to reduced the estimated error in the QOIs to below specified tolerances, thereby accomplishing solution verification.
Data and associated models of data uncertainty are critical to predictive simulation. They are needed for the calibration of physical models and inadequacy models and for the validation of these models. At the PECOS Center, the calibration, validation, and prediction processes are closely related, interdependent, and at the heart of uncertainty quantification in computational modeling.
A number of complications arise from the need to pursue validation in the context of a QOI. First, note that in most situations the QOI in the prediction scenario is not accessible for observation, since otherwise, a prediction would generally not be needed. This inability to observe the QOI can arise for many reasons, such as legal or ethical restrictions, lack of instrumentation, limitations of laboratory facilities to reproduce the prediction scenario, cost, or that the prediction is about the future. At the PECOS Center, the QOI is the consumption rate of an ablative heat shield at peak heating for a particular trajectory of a reentry vehicle. It is experimentally unobservable because the conditions are not accessible in the laboratory and because flight tests are expensive, making it impractical to test every trajectory of interest.
Validation tests are of course posed by comparing to observations the outputs of the model for some observable quantity. The central challenge is to determine what the mismatch between observations and the model, and the relevant prediction uncertainties, imply about predictions of unobserved QOIs. Because the QOIs cannot be observed, the only access that one has to them is through the model, and so this assessment can be done only in the context of the model.
Another complication arises when the system being modeled is complicated with many parts or encompasses many interacting physical phenomena. In this case, the validation process is commonly hierarchical, with validation tests of models for subcomponents or individual physical phenomena based on relatively simple (inexpensive) experiments. As an example, in the reentry vehicle problem being pursued at the PECOS Center, the individual physical phenomena include aero-chemistry, turbulence, thermal radiation, surface chemistry, and ablator material response.
Combinations of subcomponents or physical phenomena are then tested against more complicated, less-abundant multiphysics experiments. Finally, in the best circumstances, one has some experimental observations available for the complete system, allowing a validation test for the complete model. The hierarchical validation process can be envisioned as a validation pyramid shown in Figure 5.7.
FIGURE 5.7 The prediction pyramid depicting the increasing complexity of the physical scenarios (Sc, Sv, and Sp) accompanied by the decreasing availability of data (dc and dv) for calibration and validation of complex multiphysics models, with the prediction quantity of interest (Qp) residing at the highest level of the pyramid.
The hierarchical nature of multiphysics validation poses further challenges. First, the QOIs are generally accessible only through the model of the full system, so that single-physics models do not have access to the QOI, making QOI-aware validation difficult. Generally, surrogate QOIs are devised for single-physics models— a surrogate QOI being as closely related to the full system QOI as possible. For example, in the validation of boundary-layer turbulence models for the reentry vehicle simulations pursued at the PECOS Center, the turbulent wall heat flux is identified as a surrogate QOI, since it is directly related to, and is a driver for, the ablation rate. Multiphysics validation tests performed at higher levels of the pyramid are important because they generally test the models for the coupling between the single-physics models. But the fact that data are generally scarce at these higher levels means that these coupling models are commonly not as rigorously tested as the simpler models are, affecting the overall quality of the final prediction.
5.10 RARE, HIGH-CONSEQUENCE EVENTS
Large-scale computational models play a role in the assessment and mitigation of rare, high-consequence events. By definition, such events occur very infrequently, which means that there is little measured data from them. Thus, the issues that complicate extrapolative predictions are almost always present in predictions involving rare events. Still, computational models play a key role in safety assessments for nuclear reactors by the Nuclear Regulatory Commission (Mosleh et al., 1998) and in assessing safety risks in subsurface contaminant transport at Department of Energy facilities (Neuman and Wierenga, 2003). Computational models also play a role in characterizing the causes and consequences of potential natural disasters such as earthquakes, tsumanis, severe storms, avalanches, fires, or even meteor impacts. The behavior of engineered systems (e.g., bridges, buildings) under extreme conditions, or simply as a result of aging and normal wear and tear, can also fall under this heading of rare, high-consequence events.
In many cases, such as probabilistic risk assessment (Kumamoto and Henley, 1996) applied to nuclear reactor safety, computational models are used to evaluate the consequences of identified scenarios, helping to quantify the
risk—the product of the chance of an event and its consequences. This is also true of assessments of the risks from large meteor impacts, for which computer models simulate the consequences of impacts under different conditions (Furnish et al., 1995). Although it is difficult to assess confidence in such extrapolative predictions, their results can be integrated into a larger risk analysis to prioritize threats. In such analyses, it may be a more efficient use of resources to further scrutinize the model results only for the threats with highest priority.
Computational models can also be used to seek out combinations of initial conditions, forcings, and even parameter settings that give rise to extreme, or high-consequence, events. Assessing the chances of such events comes after their discovery. Many of the methods described in Chapters 3 and 4 are relevant to this task, but now with a focus on finding aberrant behavior rather than inferring settings that match measurements. This may involve exploring how a physical system can be “stretched” to produce (as yet) unseen, extreme behavior, perhaps induced by interactions among different processes. This is the opposite of designing, or engineering, a system to ensure that interactions among the various processes are minimized. Calculating such extreme behavior may tax a model to the point that its ability to reproduce reality is questionable. Methods for assessing and improving confidence in such model predictions are challenging and largely open problems, as they are for extrapolative predictions.
Once a high-consequence event is identified, computational models can be viable tools for assessing its probability. Such events are rare, and so standard approaches such as Monte Carlo simulation are infeasible because large numbers of model runs would be required to estimate these small probabilities. There are rich lines of current research in this area. Oakley and O’Hagan (2004) use a combination of emulation and importance sampling for assessing small probabilities in infrastructure management. Picard (2005) biases a particle-based code to produce more extreme events, statistically adjusting for this bias in producing estimates. In addition to response-surface approaches, one might also use a combination of high- and low-fidelity models to seek out and estimate rare-event probabilities. Another possible multifidelity strategy would be to use a low-fidelity model to seed promising boundary conditions to a high-fidelity, localized model (Sain et al., 2011). Embedding computational models in standard statistical approaches is another promising direction. For example, Cooley (2009) combines computer model output and extreme value theory from statistics to estimate the frequency of extreme rainfall events. Bayarri et al. (2009b) utilize a computer model to identify the catastrophic region in input space for extreme pyroclastic volcanic flows and statistical modeling of the input distributions to compute the probability of the extreme events.
A better understanding of complex dynamical systems could help in the search for precursors to extreme events or important changes in system dynamics (Scheffer et al., 2009). Computational models will likely have a role in such searches—even when the models are known to have shortcomings in their representation of such complex systems. Currently, computational models are being used to help inform monitoring efforts, helping to provide early warnings of events ranging from groundwater contamination to a terrorist attack.
Finally, bounding and “worst-case” approaches, if not too conservative, can provide actionable information about rare, high-consequence events. Recent work by Lucas et al. (2009) uses concentration-of-measure inequalities to bound the probability of extreme outcomes, without having to specify fully the distribution of the input uncertainties. Also, more traditional decision-theoretic approaches (e.g., minimax decision rules [Berger, 1985]; worst-case priors [Evans and Stark, 2002]) may be useful for dealing with rare, high-consequence events. One could imagine embedding these ideas into a computational model, using a worst-case value for a reaction coefficient, a permeability field, a boundary condition, or even how a physical process is represented in the computational model.
This chapter discusses numerous tasks that contribute to validation and prediction from the perspective of mathematical foundations, pointing out areas of potential fruitful research. As noted, details of these tasks depend substantially on the features of the application—the maturity, quality, and speed of the computational model; the available physical observations; and their relation to the QOI. The concept of embedding the computational model within a mathematical/statistical framework that can account for and model relevant uncertainties, including those caused by initial and boundary conditions, input parameters, and model discrepancy is also described.
Some applications involve making predictions and uncertainty estimates in settings for which physical observations are plentiful. In even mildly extrapolative settings, obtaining these estimates and assessing their reliability remains an open problem. The NRC (2007) report on the use of models in environmental regulatory decision
making states, “When model results are to be extrapolated outside of conditions for which they have been evaluated, it is important that they have the strongest possible theoretical basis, explicitly representing the processes that will most affect outcomes in the new conditions to be modeled, and embodying the best possible parameter estimates” (p. 129). The findings and recommendation below relate to making extrapolative predictions.
Finding: Mathematical considerations alone cannot address the appropriateness of a model prediction in a new, untested setting. Quantifying uncertainties and assessing their reliability for a prediction require both statistical and subject-matter reasoning.
Finding: The idea of a domain of applicability is helpful for communicating the conditions for which predictions (with uncertainty) can be trusted. However, the mathematical foundations have not been established for defining such a domain or its boundaries.
Finding: Research and development on methods for assessing uncertainties of model-based predictions in new, untested conditions (i.e., “extrapolations”) will likely require expertise from mathematics, statistics, computational modeling, and the science and engineering areas relevant to a given application. Specific needs in assessing uncertainties in prediction include:
• Approaches for specifying and estimating model discrepancy terms that leverage physical understanding, features of the application, and known strengths and deficiencies of the computational model for the application;
• Computational models developed with VVUQ in mind, which might include the need for availability of derivative information; a faster, lower-fidelity representation of the model (perhaps with specified discrepancy); or embedding physically motivated discrepancy terms within the model that can produce more reliable prediction uncertainties for the QOI and that can be calibrated with available physical observations;
• A framework for efficiently exploiting a hierarchy of available experiments—allocating experiments for calibration, assessing prediction accuracy, assessing the reliability of predictions, and suggesting new experiments within the hierarchy that would improve the quality of estimated prediction uncertainties;
• Guidelines for reporting predictions and accompanying prediction uncertainties, including disclosure of which sources of uncertainty are accounted for, which are not, what assumptions these estimates rely on, and the reliability or quality of these assumptions; and
• Compelling examples of VVUQ done well in problems with different degrees of complexity.
A similar conclusion was reached by the National Science Foundation (NSF) Division of Mathematics and Physical Sciences (MPS), which in its May 2010 advisory committee report recommended as follows:
MPS should encourage interdisciplinary interaction between domain scientists and mathematicians on the topic of uncertainty quantification, verification and validation, risk assessment, and decision making. (NSF, 2010)
The above ideas are particularly relevant to the modeling of complex systems where even a slight deviation from physically tested conditions may change features of the system in many ways, some of which are incorporated in the model and some of which are not.
The field of VVUQ is still developing, making it too soon to offer any specific recommendations regarding particular methods and approaches. However, a number of principles and accompanying best practices are listed below regarding validation and prediction from the perspective of mathematical foundations.
• Principle: A validation assessment is well-defined only in terms of specified QOIs and the accuracy needed for the intended use of the model.
—Best practice: Early in the validation process, specify the QOIs that will be addressed and the required accuracy.
—Best practice: Tailor the level of effort in assessment and estimation of prediction uncertainties to the needs of the application.
• Principle: A validation assessment provides direct information about model accuracy only in the domain of applicability that is “covered” by the physical observations employed in the assessment.
—Best practice: When quantifying or bounding model error for a QOI in the problem at hand, systematically assess the relevance of supporting data and validation assessments (which were based on data from different problems, often with different QOIs). Subject-matter expertise should inform this assessment of relevance (as discussed above and in Chapter 7).
—Best practice: If possible, use a broad range of physical observation sources so that the accuracy of a model can be checked under different conditions and at multiple levels of integration.
—Best practice: Use “holdout tests” to test validation and prediction methodologies. In such a test some validation data are withheld from the validation process, the prediction machinery is employed to “predict” the withheld QOIs, with quantified uncertainties, and finally the predictions are compared to the withheld data.
—Best practice: If the desired QOI was not observed for the physical systems used in the validation process, compare sensitivities of the available physical observations with those of the QOI.
—Best practice: Consider multiple metrics for comparing model outputs against physical observations.
• Principle: The efficiency and effectiveness of validation and prediction assessments are often improved by exploiting the hierarchical composition of computational and mathematical models, with assessments beginning on the lowest-level building blocks and proceeding to successively more complex levels.
—Best practice: Identify hierarchies in computational and mathematical models, seek measured data that facilitate hierarchical validation assessments, and exploit the hierarchical composition to the extent possible.
—Best practice: If possible, use physical observations, especially at more basic levels of the hierarchy, to constrain uncertainties in model inputs and parameters.
• Principle: Validation and prediction often involve specifying or calibrating model parameters.
—Best practice: Be explicit about what data/information sources are used to fix or constrain model parameters.
—Best practice: If possible, use a broad range of observations over carefully chosen conditions to produce more reliable parameter estimates and uncertainties, with less “trade-off” between different model parameters.
• Principle: The uncertainty in the prediction of a physical QOI must be aggregated from uncertainties and errors introduced by many sources, including discrepancies in the mathematical model, numerical and code errors in the computational model, and uncertainties in model inputs and parameters.
—Best practice: Document assumptions that go into the assessment of uncertainty in the predicted QOI, and also document any omitted factors. Record the justification for each assumption and omission.
—Best practice: Assess the sensitivity of the predicted QOI and its associated uncertainties to each source of uncertainty as well as to key assumptions and omissions.
—Best practice: Document key judgments—including those regarding the relevance of validation studies to the problem at hand—and assess the sensitivity of the predicted QOI and its associated uncertainties to reasonable variations in these judgments.
—Best practice: The methodology used to estimate uncertainty in the prediction of a physical QOI should also be equipped to identify paths for reducing uncertainty.
• Principle: Validation assessments must take into account the uncertainties and errors in physical observations (measured data).
—Best practice: Identify all important sources of uncertainty/error in validation data—including instrument calibration, uncontrolled variation in initial conditions, variability in measurement setup, and so on—and quantify the impact of each.
—Best practice: If possible, use replications to help estimate variability and measurement uncertainty.
—Remark: Assessing measurement uncertainties can be difficult when the “measured” quantity is actually the product of an auxiliary inverse problem—that is, when it is not measured directly but is inferred from other measured quantities.
Finally, it is worth pointing out that there is a fairly extensive literature in statistics focused on model assessment that may be helpful if adapted to the model validation process. Basic principles such as model diagnostics (Gelman et al., 1996; Cook and Weisberg, 1999), visualization and graphical methods (Cleveland, 1984; Anselin, 1999), hypothesis testing and model selection (Raftery, 1996; Bayarri and Berger, 2000; Robins et al., 2000; Lehmann and Romano, 2005), cross-validation and the use of holdout tests (Hastie et al., 2009) could play central roles in validation and prediction, as they do for statistical model checking.
Akçelik, V., G. Biros, A. Draganescu, O. Ghattas, J. Hill, and B. Van Bloeman Waanders. 2005. Dynamic Data-Driven Inversion for Terascale Simulations: Real-Time Identification of Airborne Contaminants, in Proceedings of SC2005.
AIAA (American Institute for Aeronautics and Astronautics). 1998. Guide for the Verification and Validation of Computational Fluid Dynamics Simulations. Reston, Va.: AIAA.
Anselin, L., 1999. Interactive Techniques and Exploratory Spatial Data Analysis. Geographical Information Systems: Principles, Techniques, Management and Applications 1:251-264.
Badri Narayanan, V.A., and N. Zabaras. 2004. Stochastic Inverse Heat Conduction Using a Spectral Approach. International Journal for Numerical Methods Engineering 60:1569-1593.
Bangerth, W., and R. Rannacher. 2003. Adaptive Finite Element Methods for Differential Equations. Basil, Switzerland: Birkhauser Verlag.
Bayarri, M.J., and J.O. Berger. 2000. P Values for Composite Null Models. Journal of the American Statistical Association 95(452):1269-1276.
Bayarri, M.J., J.O. Berger, M.C. Kennedy, A. Kottas, R. Paulo, J. Sacks, J.A. Cafeo, C.H. Lin, and J. Tu. 2005. Bayesian Validation of a Computer Model for Vehicle Crashworthiness. Technical Report 163. Research Triangle Park, N.C: National Institute of Statistical Sciences.
Bayarri, M.J., J. Berger, R. Paulo, J. Sacks, J. Cafeo, J. Cavendish, C. Lin, and J. Tu. 2007a. A Framework for Validation of Computer Models. Technometrics 49:138-154.
Bayarri, M.J., J. Berger, G. Garcia-Donato, F. Liu, J. Palomo, R. Paulo, J. Sacks, D. Walsh, J. Cafeo, and R. Parthasarathy. 2007b. Computer Model Validation with Functional Output. Annals of Statistics 35:1874-1906.
Bayarri, M.J., J.O. Berger, M.C. Kennedy, A. Kottas, R. Paulo, J. Sacks, J.A. Cafeo, C.H. Lin, and J. Tu. 2009a. Predicting Vehicle Crashworthiness: Validation of Computer Models for Functional and Hierarchical Data. Journal of the American Statistical Association 104:929-943.
Bayarri, M.J., J.O. Berger, E.S. Calder, K. Dalbey, S. Lunagomez, A.K. Patra, E.B. Pitman, E.T. Spiller, and R.L. Wolpert. 2009b. Using Statistical and Computer Models to Quantify Volcanic Hazards. Technometrics 5:402-413.
Berger, J.O. 1985. Statistical Decision Theory and Bayesian Analysis. New York: Springer.
Berger, J.L., and R.L. Wolpert. 1988. The Liklihood Principle. Lecture notes available at http://books.google.com/books?hl=en&lr=&id=7fz8JGLmWbgC&oi=fnd&pg=PA1&dq=berger+and+wolpert+the+likelihood+principle&ots=iTkq2Ekz_Z&sig=qKnLby2avTKEP_unAWSJ_BUI#v=onepage&q=berger%20and%20wolpert%20the%20likelihood%20principle&f=false. Accessed March 20, 2012.
Besag, J., P.J. Green, D.M. Higdon, and K. Mengerson. 1995. Bayesian Computation and Stochastic Systems. Statistical Science 10:3-66.
Box, G., and N. Draper. 1987. Empirical Model Building and Response Surfaces. New York: Wiley.
Box, G.E.P., J.S. Hunter, and W.G. Hunter. 2005. Statistics for Experimenters: Design Innovation, and Discovery, Volume 2. New York: Wiley Online Library.
Brooks, H.E., and C.A. Doswell III. 1996. A Comparison of Measures-Oriented and Distributions-Oriented Approaches to Forecast Verification. Weather Forecasting 11:288-303.
Buser, C.M., H.R. Kunsch, D. Luth, M. Wild, and C. Schar. 2009. Bayesian Multi-Model Projection of Climate: Bias Assumptions and Interannual Variability. Climate Dynamics 33(6):849-868.
Christen, J.A., and C. Fox. 2005. Markov Chain Monte Carlo Using an Approximation. Journal of Computational and Graphical Statistics 14(4):795-810.
Cleveland, W.S. 1984. Elements of Graphing Data. Belmont, Calif.: Wadsworth.
Cook, R.D., and S. Weisberg. 1999. Applied Regression Including Computing and Graphics. New York: Wiley Online Library.
Cooley, D. 2009. Extreme Value Analysis and the Study of Climate Change. Climatic Change 97(1):77-83.
Dubois, D., H. Prade, and E.F. Harding. 1988. Possibility Theory: An Approach to Computerized Processing of Uncertainty. New York: Plenum Press.
Easterling, R.G. 2001. Measuring the Predictive Capability of Computational Models: Principles and Methods, Issues and Illustrations. SAND2001-0243. Albuquerque, N.Mex.: Sandia National Laboratories.
Efendiev, Y., A. Datta-Gupta, X. Ma, and B. Mallick. 2009. Efficient Sampling Techniques for Uncertainty Quantification. In History Matching Using Nonlinear Error Models and Ensemble Level Upscaling Techniques. Washington, D.C.: Water Resources Research and American Geophysical Union.
Evans, S.N., and P.B. Stark. 2002. Inverse Problems as Statistics. Inverse Problems 18:R55.
Evensen, G. 2009. Data Assimilation: The Ensemble Kalman Filter. New York: Springer Verlag.
Ferson, S., V. Kreinovich, L. Ginzburg, D.S. Myers, and K. Sentz. 2003. Constructing Probability Boxes and Dempster-Shafer Structures. Albuquerque, N.M.: Sandia National Laboratories.
Flath, H.P., L.C. Filcox, V. Akçelik, J. Hill, B. Van Bloeman Waanders, and O. Glattas. 2011. Fast Algorithms for Bayesian Uncertainty Quantification in Large-Scale Linear Inverse Problems Based on Low-Rank Partial Hessian Approximations. SIAM Journal on Scientific Computing 33(1):407-432.
Fuentes, M., and A.E. Raftery. 2004. Model Validation and Spatial Interpolation by Combining Observations with Outputs from Numerical Models via Bayesian Melding. Journal of the American Statistical Association, Biometrics 6:36-45.
Furnish, M.D., M.B Boslough, and G.T. Gray. 1995. Dynamical Properties Measurements for Asteroid, Comet and Meteorite Material Applicable to Impact Modeling and Mitigation Calculations. International Journal of Impact Engineering 17(3):53-59.
Galbally, D.K., K. Fidkowski, K. Willcox, and O. Ghattas. 2010. Nonlinear Model Reduction for Uncertainty Quantification in Large-Scale Inverse Problems. International Journal for Numerical Methods in Engineering 81:1581-1608.
Gelfand, A.E., and S.K. Ghosh. 1998. Model Choice: A Minimum Posterior Predictive Loss Approach. Biometrica 85(1):1-11.
Gelman, A., X.L. Meng, and H. Stern. 1996. Posterior Predictive Assessment of Model Fitness via Realized Discrepancies. Statistica Sinica 6:733-769.
Ghanem, R., and A. Doostan. 2006. On the Construction and Analysis of Stochastic Predictive Models: Characterization and Propagation of the Errors Associated with Limited Data. Journal of Computational Physics 217(1):63-81.
Gneiting, T., and A.E. Raftery. 2005. Weather Forecasting with Ensemble Methods. Science 310(5746):248-249.
Goldstein, M., and J.C. Rougier. 2004. Probabilistic Formulations for Transferring Inferences from Mathematical Models to Physical Systems. SIAM Journal on Scientific Computing 26(2):467-487.
Hastie, T., R. Tibshirani, and J.H. Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer.
Higdon, D., M. Kennedy, J.C. Cavendish, J.A. Cafeo, and R.D. Ryne. 2005. Combining Field Data and Computer Simulations for Calibration and Prediction. SIAM Journal on Scientific Computing 26(2):448-466.
Higdon, D., J. Gattiker, B.Williams, and M. Rightley. 2008. Computer Model Calibration Using High-Dimensional Output. Journal of the American Statistical Association 103(482):570-583.
Hills, R., and T. Trucano. 2002. Statistical Validation of Engineering and Scientific Models: A Maximum Likelihood Based Metric. SAND2001-1789. Albuequerque, N. Mex.: Sandia National Laboratories.
Hills, R.G., K.J. Dowding, and L. Swiler. 2008. Thermal Challenge Problem: Summary. Computer Methods in Applied Mechanics and Engineering 197:2490-2495.
Hoeting, J.A., D. Madilgan, A.E. Raftery, and C.T. Volinsky. 1999. Bayesian Model Averaging: A Tutorial. Statistical Science 15:382-401.
Kaipio, J.P., and E. Somersalo. 2005. Statistical and Computational Inverse Problems. New York: Springer.
Kaipio, J.P., V. Kolehmainen, I. Somersalo, and M. Vauhkonen. 2000. Statistical Inversion and Monte Carlo Sampling Methods in Electrical Impedance Tomography. Inverse Problems 16:1487.
Kennedy, M.C., and A. O’Hagan. 2001. Bayesian Calibration of Computer Models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 63:425-464.
Kersting, A.B., D.W. Efurd, D.L. Finnegan, D.J. Rokop, D.K. Smith, and J.L.Thompson. 1999. Migration of Plutonium in Ground Water at the Nevada Test Site. Nature 397(6714):56-59.
Kirk, B., J. Peterson, R. Stogner, and G. Carey. 2006. A C++ Library for Parallel Adaptive Mesh Refinement/Coarsening Simulations. Engineering with Computers 22(3-4):237-254.
Klein, R., S. Doebling, F. Graziani, M. Pilch, and T. Trucano. 2006. ASC Predictive Science Academic Alliance Program Verification and Validation Whitepaper. UCRL-TR-220711. Livermore, Calif.: Lawrence Livermore National Laboratory.
Klir, G.J., and B. Yuan. 1995. Fuzzy Sets and Fuzzy Logic. Upper Saddle River, N.J.: Prentice Hall.
Knupp, P., and K. Salari. 2003. Verification of Computer Codes in Computational Science and Engineering. Boca Raton, Fla.: Chapman and Hall/CRC.
Knutti, R., R. Furer, C. Tebaldi, J. Cermak, and G.A. Mehl. 2010. Challenges in Combining Projections in Multiple Climate Models. Journal of Climate 23(10):2739-2758.
Kumamoto, H., and E.J. Henley. 1996. Probabalistic Risk Assessment and Management for Engineers and Scientists. New York: IEEE Press.
Lehmann, E.L., and J.P. Romano. 2005. Testing Statistical Hypotheses. New York: Springer.
Lieberman, C., K. Willcox, and O. Ghattas. 2010. Parameter and State Model Reduction for Large-Scale Statistical Inverse Problems. SIAM Journal on Scientific Computing 32:2523-2542.
Loeppky, J., D. Bingham, and W.J. Welch. 2011. Computer Model Calibration or Tuning in Practice. Technometrics. Submitted for publication.
Long, K., R. Kirty, and B. Van Bloemen Waanders. 2010. Unified Embedded Parallel Finite Element Computations via Software-Based Frechet Differentiation. SIAM Journal on Scientific Computing 32(6):3323-3351.
Lorenc, A.C. 2003. The Potential of the Ensemble Kalman Filter for NWP—A Comparison with 4D-Var. Quarterly Journal of the Royal Meteorological Society 129:3183-3203.
Lucas, L.J., H. Owhadi, and M. Ortiz. 2009. Rigorous Verification, Validation, Uncertainty Quantification and Certification Through Concentration-of-Measure Inequalities. Computer Methods in Applied Mechanics and Engineering 57(51-52):4591-4609.
Marzouk, Y.M., and H.N. Najm. 2009. Dimensionality Reduction and Polynomial Chaos Acceleration of Bayesian Inference in Inverse Problems. Journal of Computational Physics 228:1862-1902.
Meehl, G.A., C. Covey, T. Delworth, M. Latif, B. McAvaney, J.F.B. Mitchell, B. Stouffer, and K.E. Taylor. 2007. The WCRP CMIP3 Multi-model Dataset. Bulletin of the American Meteorological Society 88:1388-1394.
Mosleh, A., D.M. Rasmuson, F.M. Marshall, and U.S. Nuclear Regulatory Commission. 1998. Guidelines on Modeling Common-Cause Failures in Probabilistic Risk Assessment. Washington, D.C.: Safety Programs Division, Office for Analysis and Evaluation of Operational Data, U.S. Nuclear Regulatory Commission.
Naevdal, G., L. Johnsen, S. Aanonsen, and D. E. Vefring. 2005. Reservoir Monitoring and Continuous Model Updating Using Ensemble Kalman Filter. Society of Petroleum Engineers Journal 10(1):66-74.
NRC (National Research Council). 2007. Models in Environmental Regulatory Decision Making, Washington, D.C.: National Academies Press.
NSF (National Science Foundation). 2010. Minutes of the Advisory Committee Meeting. April 1-2, 2010. Available at http://www.nsf.gov/attachments/117978/public/MPSAC_April_1-2_2010_Minutes_Final.pdf. Accessed March 20, 2012.
Neuman, S.P. and J.W. Wierenga. 2003. A Comprehensive Strategy of Hydrogeologic Modeling and Uncertainty Analysis for Nuclear Facilities and Sites. Washington, D.C.: U.S. Nuclear Regulatory Commission.
Oakley, J.E., and A. O’Hagan. 2004. Probabilistic Sensitivity Analysis of Complex Models: A Bayesian Approach. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 66(3):751-769.
Oberkampf, W.L., and C. Roy. 2010. Verification and Validation in Scientific Computing. Cambridge, U.K.: Cambridge University Press.
Oberkampf, W.L., and T.G. Trucano. 2000. Validation Methodology in Computational Fluid Dynamics. American Institute of Aeronautics and Astronautics, AIAA 200-2549, Fluids 2000 Conference, Denver, Colo.
Oberkampf, W.L., T.G. Trucano, and C. Hirsch. 2004. Verification, Validation, and Predictive Capability in Computational Engineering and Physics. Applied Mechanical Reviews 57:345.
Oden, J.T., and S. Prudhomme. 1998. A Technique for A Posteriori Error Estimation of h-p Approximations of the Stokes Equations. Advances in Adaptive Computational Methods in Mechanics 47:43-63.
Oliver, D.S., B.C. Luciane, and A.C. Reynolds. 1997. Markov Chain Monte Carlo Methods for Conditioning a Permeability Field to Pressure Data. Mathematical Geology 29:61-91.
Picard, R.R. 2005. Importance Sampling for Simulation of Markovian Physical Processes. Technometrics 47(2):202-211.
Prudhomme, S., and J.T. Oden. 1999. On Goal-Oriented Error Estimation for Elliptic Problems: Application to Pointwise Errors. Computation Methods in Applied Mechanics and Engineering 176:313-331.
Rabinovich, S. 1995. Measurement Errors, Theory and Practice. New York: The American Institute of Physics.
Raftery, A.E. 1996. Hypothesis Testing and Model Selection via Posterior Simulation. Pp. 163-168 in Practical Markov Chain Monte Carlo. London, U.K.: Chapman and Hall.
Roache, P. 1998. Verification and Validation in Computational Science and Engineering. Socorro, N.Mex.: Hermosa Publishers.
Robins, J.M., A. van der Vaart, and V. Ventura. 2000. Asymptotic Distribution of P Values in Composite Null Models. Journal of the American Statistical Association 95(452):1143-1156.
Rougier, J., M. Goldstein, and L. House. 2010. Assessing Model Discrepancy Using a Multi-Model Ensemble. University of Bristol Statistics Department Technical Report #08:17. Bristol, U.K.: University of Bristol.
Sain, S.R., R. Furrer, and N. Cressie. 2011. A Spatial Analysis of Multivariate Output from Regional Climate Models. Annals of Applied Statistics 5(1):150-175.
Scheffer, M., J. Bascompte, W.A. Brock, V. Brovkin, S.R. Carpenter, V. Dakos, H. Held, H.E.H. Van Nes, M. Rietkerk, and G. Sugihara. 2009. Early-Warning Signals for Critical Transitions. Nature 461(7260):53-59.
Shafer, G. 1976. A Mathematical Theory of Evidence. Princeton, N.J.: Princeton University Press.
Smith, R.L., C. Tebaldi, D. Nychka, and L.O. Mearns. 2010. Bayesian Modeling of Uncertainty in Ensembles of Climate Models. Journal of the American Statistical Association 104(485):97-116.
Steinberg, S., and P. Roache. 1985. Symbolic Manipulation and Computational Fluid Dynamics. Journal of Computational Physics 57(2):251-284.
Strouboules, F., I. Babuska, D.K. Dalta, K. Copps, and S.K. Gangarai. 2000. A Posteriori Estimation and Adaptive Control of the Error in the Quantity of Interest. Part 1: A Posterioric Estimations of the Error in the Von Mises Stress and the Stress Intensity Factor. Computational Methods in Applied Mechanics and Engineering 181:261-294.
Tarantola, A. 2005. Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia, Pa.: SIAM.
Tebaldi, C., and R. Knutti. 2007. The Use of the Multi-Model Ensemble in Probabilistic Climate Projections. Philosophical Transactions of the Royal Society, Series A 365:2053-2075.
Tebaldi, C., R.L. Smith, D. Nychka, and L.O. Mearns. 2005. Quantifying Uncertainty in Projections of Regional Climate: A Bayesian Approach to the Analysis of Multimodel Ensembles. Journal of Climate 18:1524-1540.
Thornton, J. 2011. No Testing Allowed: Nuclear Stockpile Stewardship Is a Simulation Challenge. Mechanical Engineering-CIME 133(5):38-41.
Tonkin, M., and J. Doherty. 2009. Calibration-Constrained Monte Carlo Analysis of Highly Parameterized Models Using Subspace Techniques. Water Resources Research 45(12):w00b10.
Wan, E.A., and R. Van Der Merwe. 2000. The Unscented Kalman Filter for Nonlinear Estimation. Pp.153-158 in Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000. AS-SPCC/IEEE, Lake Louise, Alta., Canada.
Wang, S., W. Chen, and K.L. Tsui. 2009. Bayesian Validation of Computer Models. Technometrics 51(4):439-451.
Welch, G., and G. Bishop. 1995. An Introduction to the Kalman Filter. Technical Report 95-041. Chapel Hill: University of North Carolina.
Wu, C.F.J., and M. Hamada. 2009. Experiments: Planning, Analysis, and Optimization. New York: Wiley.
Youden, W.J. 1961. Uncertainties in Calibration. Precision Measurement and Calibration: Statistical Concepts and Procedures 1:63.
Youden, W.J. 1972. Enduring Values. Technometrics 14(1)1-15.


































