The ultimate goal of verification, validation, and uncertainty quantification (VVUQ) activities is to assist decision makers in reaching informed decisions about an intended application. As such, VVUQ activities are part of a larger group of decision-support tools that include modeling, simulation, and experimentation. The role of VVUQ could be as simple as providing uncertainty bounds or a worst-case analysis for a particular risk metric, or it could be as complex as using more rigorous methods (such as the design of validation experiments or other applications requiring optimization under uncertainty) to compare various options.
This chapter discusses decisions that have to be made during VVUQ activities and presents two examples describing how VVUQ activities enhance the eventual decision about the intended application. The incorporation of models and simulations within a complete decision-making system is a deep and complex question. The report Models in Environmental Regulatory Decision Making (NRC, 2007) provides a good discussion of this broader topic, which is beyond the scope of the current report. The types of decision discussed here can be grouped into two broad categories: (1) decisions that arise as part of the planning and conduct of the VVUQ activities themselves and (2) decisions made with the use of VVUQ results about an application at hand. Sections 6.4 and 6.5 present detailed examples of VVUQ applications.
6.2 DECISIONS WITHIN VVUQ ACTIVITIES
The nature of VVUQ activities depends fundamentally on how the results will be used in the eventual decision concerning an application. For example, an effort to obtain conservative bounds for a risk metric will be quite different from a study to obtain a comprehensive uncertainty quantification (UQ) analysis that informs a strategy for reducing uncertainty over time.
Finding: It is important that, before VVUQ activities begin, decision makers and practitioners of VVUQ discuss and arrive at an agreement on how the results of VVUQ analyses will be used.
As discussed throughout this report, VVUQ involves a large number of activities, each requiring many decisions. For example, verification studies deal with the implementation of numerical algorithms, encompassing the choice and allocation of resources to different types of algorithm testing (analytical solutions for simplified
physics, the method of manufactured solutions, and so on), among other issues. Similarly, software quality assurance involves decisions about the different types and the extent of software testing, coverage analysis, and so on. Validation studies also involve many activities, ranging from the choice of input space, to the design and fielding of experiments, to the selection of emulators, to the analysis of output data, and so on. Again, there are many important choices to be made within each of these activities and many important decisions to be made on how to trade off resources and time among them.
The results of a UQ study can help to inform the decision maker on the relative priorities among a broad set of choices. These choices can be viewed as a large set of possible trade-offs through which the uncertainty is managed (an uncertainty management trade space). Components of this trade space include the following:
• Fundamental improvements to physics models,
• Improvements to the integrated simulation and modeling capability,
• The design and conduct of computer experiments,
• The design and conduct of relevant constraining physical experiments, and
• The engineering and design of the system to tolerate the predicted uncertainty.
The first four of these activities are typically (although not exclusively) considered as decisions within VVUQ. The final activity is typically considered to occur after the completion of the VVUQ study (treated in more detail in Section 6.3). All of these activities require resources, which include employing domain experts, accessing computational and experimental facilities, and influencing engineering design decisions. Decision makers must allocate resources throughout the VVUQ process, keeping in mind the goal of the study. For example, decision makers must weigh the relative benefit of investing in improvements to the fidelity of a given physics model against the benefit of conducting relevant physical experiments for calibration. Computing resources must be allocated across studies investigating detailed convergence, model fidelity, and completeness of UQ ensembles. Physical experiments must be selected from choices ranging from experiments involving components to fully integrated experiments. In industrial contexts, it is not uncommon for there to be a single budget for the entire process of modeling, simulator development, and UQ analysis—and the trade-offs are then even more critical. Ideally, the VVUQ framework helps to inform decisions on the relative impact of these activities and can be used to prioritize the allocation of resources.
Regardless of how carefully and efficiently the activities are carried out, difficult decisions will have to be made during the course of VVUQ. These decisions will have to withstand subsequent scrutiny and review by independent third parties.
Adequate documentation and transparency about the VVUQ process will facilitate peer review and provide archival information for future studies. It is important that peer reviewers be given access to all relevant information, data, and computational models (including codes, where appropriate) used in the VVUQ process.
Finding: It is important to include in any presentation of VVUQ results the assumptions as well as the sources of uncertainty that were considered. Appropriate documentation and transparency about the process and body of knowledge that were used to assess and quantify uncertainties in the relevant quantities of interest are also crucial for a complete understanding of the results of the VVUQ analysis.
6.3 DECISIONS BASED ON VVUQ INFORMATION
Ultimately, decision makers are faced with a set of choices, each one of which will have certain advantages and disadvantages. Within this framework, decision makers must make trade-offs based on the analyses and the probabilities of the various scenarios. For example, someone in environmental management may have to choose between two remediation strategies for cleaning up a contaminated site. The decision maker could choose an option for monitored natural attenuation—in other words, leaving the site as is but closely monitoring it to make sure that the contamination does not spread to high-risk areas. Or the decision maker could choose a more active, but also more costly, procedure that might clean up the site. The choice of option will be based on several underlying computational models, each with its own set of uncertainties that need to be compared against one another.
In the case of the Stockpile Stewardship Program (SSP) described in Section 6.4, similar types of decisions must be made. The SSP has developed its own framework, known as Quantification of Margins and Uncertainty (QMU), that produces a quantity known as the margin-to-uncertainty (M/U) ratio (Goodwin and Juzaitis, 2006). If the M/U ratio is “large,” diligence is required, but the safety, security, and reliability of the weapon system are assured. If the M/U ratio approaches unity, decision makers are presented with a variety of options that involve trade-offs between two broad categories: increasing the margin or reducing the uncertainty. Each of these choices involves decisions that must take into account computational models and uncertainties as well as stochastic variables.
In many cases (and in the two examples referred to above), there is a close analogy to several areas of optimization that can play an important role in the mathematical foundation for decision making based on VVUQ. For example, the field of multiobjective optimization (Miettinen, 1999) is focused on the development of methods and algorithms for the solution of problems that involve multiple objectives that must be simultaneously minimized. This leads to approaches that can be used to trade off among different options. Stochastic optimization (Ermoliev, 1988; Heyman and Sobol, 2003) is another relevant area, in which some of the design parameters or constraints are described by random variables. The theory for these types of problems could be used to develop better bounds on the uncertainties associated with each decision. The simulation optimization field has other approaches. One alternative approach is that of robust optimization. Here, one seeks to find optimal solutions over a broad range of nonstochastic but uncertain input parameters (Ben-Tal and Nemirovski, 2002). In this case, a robust solution is one that remains “optimal” under the entire range given for the uncertain input parameters (Taguchi et al., 1987). These types of solutions are desirable if available, because decision makers can be assured that whatever option they choose, the consequences of uncertain input parameters will not generate large changes from the optimal solutions. All of these examples indicate that optimization will be a central component of the mathematical foundation for decision making under uncertainty.
A summary of the body of information that enables an assessment of the appropriateness of a model and its ability to predict the relevant quantities of interest (QOIs), as well as inclusion of the key assumptions used to make the prediction, is a necessary part of reporting model results. This information will allow decision makers to understand better the adequacy of the model as well as the key assumptions and data sources on which the reported prediction and uncertainty rely. In addition, the finding regarding transparency and documentation stated in Section 6.2 should be made available to decision makers and peer reviewers.
It is important to recognize that a UQ study will often be an ongoing effort, with decision making happening throughout the study, with respect to both the study itself and the external applications. The climate-modeling case study discussed in Section 2.10 in Chapter 2 is an example of such an ongoing effort—only limited UQ information is currently available for use in policy decisions. This example highlights the need for the development of decision-making platforms that can be based on only partial or very limited UQ information. It also highlights the need to identify situations for which more detailed UQ characterization would give additional clarity for decision making.
6.4 DECISION MAKING INFORMED BY VVUQ IN THE STOCKPILE STEWARDSHIP PROGRAM
When the moratorium on nuclear testing was begun in 1992, the Department of Energy (DOE) established alternative means for maintaining and assessing the nation’s nuclear weapons stockpile. The SSP was created to “ensure the preservation of the core intellectual and technical competencies of the United States in nuclear weapons” (U.S. Congress, 1994). The SSP must assess, on an annual basis, the safety, security, and reliability of the nuclear weapons stockpile in the absence of nuclear testing. A key product of the annual assessment process is a report on the state of the stockpile, issued by the directors of the three national security laboratories—Lawrence Livermore National Laboratory, Los Alamos National Laboratory, and Sandia National Laboratories1—to the Secretary of Energy, the Secretary of Defense, and the Nuclear Weapons Council. With this report in hand, the Secretary of Energy, the Secretary of Defense, and the Commander of the U.S. Strategic Command each write a letter to
_____________________
1 Sandia National Laboratories is a multiprogram laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000.
the President of the United States providing their individual views on the health of the stockpile and on whether nuclear-explosive testing should resume. The SSP assessment thus provides the technical basis for the President’s decision on whether or not to resume nuclear testing.
QMU, a component in the assessment framework, is a decision-support process. This case study illustrates the importance of UQ to reducing uncertainties in the QMU process and, thus, enhancing the decision-making process. By quantifying the largest sources of uncertainty, UQ, in this case, is essential to inform resource allocation for reducing error in inputs to the models. It provides a means of quantifying and then communicating the confidence in the performance and operation of a nuclear weapon. QMU provides a framework for systematically including the results of modeling and simulation, ongoing nonnuclear experiments, legacy nuclear testing, and informed judgment from nuclear weapons design physicists. A summary of the QMU methodology and current state of practice can be found in a study conducted by the National Research Council (NRC, 2009). The key concepts in QMU are quantification of the margin, the threshold for acceptable performance, and quantification of the uncertainty, representing imperfect knowledge of the physics and manufacturing of the weapon system. UQ is fundamental to the QMU framework.
QMU is the assessment methodology for focusing the SSP on risks to the stockpile and for delivering and communicating UQ-informed recommendations. As stewards of its nuclear deterrence capability, decision makers responsible for the nation’s nuclear weapons stockpile have a range of options to consider if an issue arises:
• Do nothing (accepting the risks identified through QMU);
• Reduce the uncertainty in the relevant QOIs by employing theory, simulation, and/or experiments;
• Modify the weapon system;
• Engage the military to alter the characteristics of and/or requirements for the weapon system;
• Modify operations within the nuclear weapons complex and/or Department of Defense; or
• Cease certification of the weapon system.
This decision space has high consequences because of its impact on the nation’s nuclear deterrence. The options under consideration may have an impact on the deterrence posture or require significant expenditures or both. Given the consequences of these decisions, the SSP uses QMU as a common language in all interactions (internally, in peer review, and with stakeholders), demonstrating the rational basis for decisions relating to the U.S. stockpile. QMU, being quantitative, provides transparency to the decision-making process.
The QMU framework, as it pertains to the SSP, requires highly trained design and computational physicists; it does not deliver a mathematical procedure that can be executed independent of informed judgment. Design judgment, informed by quantitative input, is at the heart of the SSP and is an essential part of the decision-making process. Judgment is based on technical rigor, tempered by experience, and demonstrated by performance. It requires quantitative inputs from simulation models with a finite domain of validity, experiments, and theory. In essence, judgment is knowing what questions to ask and an ability to draw conclusions from inputs, which are often limited and sometimes conflicting. Judgment is not simply assertion, nor is it independent of hard technical assessment.
Working with the QMU framework involves several key activities:
• Determining key performance metrics against which margins will be assessed;
• Establishing the verification and validation bases for simulation models;
• Performing uncertainty quantification; incorporating uncertainty owing to input data, manufacturing variations, and model-form uncertainty (where possible); and model calibration (where necessary);
• Establishing thresholds in performance metrics and quantifying margins and uncertainties; and
• Delivering a documentation basis including both the margin and the uncertainty and subjecting those results to internal and external peer review.
Each of these activities is identified in the present report, although perhaps with slightly different language. The key performance metrics are analogous to the quantities of interest identified in a UQ study; establishing thresholds in those metrics is a key contribution from experienced design staff; and VVUQ and documentation
are important here as they are in other VVUQ activities. Ultimately, the product is summarized as a margin with an associated uncertainty in the key performance metrics.
Establishing thresholds, margins, and uncertainties must accommodate the use of calibrated models. Simulation tools employed in the SSP use the best physics modeling achieved to date. However, even with the vast computing resources available to the National Nuclear Security Administration, fully first-principles models for nuclear weapon performance are not practicable. Given that, the UQ methodology must help inform how calibrated models diverge as simulation models are extrapolated away from the calibration point. This concept, discussed above, is an essential aspect of the application of UQ within the SSP.
An increase in margin can be achieved by altering the required characteristics of the weapon system, modifying operations across the complex, or modifying the weapon system itself. Altering the required characteristics of the weapon system must be decided in partnership with the Department of Defense and may not be an available option. Modifying operations or the weapon system itself may require significant financial expenditures. Further, these modifications may move the system away from the established calibration basis, an action that, by definition, introduces additional uncertainty. The increase in margin must compensate for this increase in uncertainty in order to deliver a net increase in the M/U ratio.
Reducing uncertainties can be achieved through the application of a breadth of capabilities available to the SSP. A UQ-informed recommendation is a key component in this decision-making process. QMU quantifies uncertainties compared to the assessed margins, focusing on margins that need to be increased or uncertainties that need to be reduced or better quantified. A main-effects analysis, which can quantify the largest sources of uncertainty, is essential in order to inform resource allocation for reducing input errors. Improvements may be obtained by improving the theory for the relevant physics model, which will constrain the model-form error and possibly eliminate the need for calibration. Improvements can also be achieved by conducting an experimental campaign to improve the calibration basis for simulation models, which constrains the error introduced by the calibration process. Similarly, experiments may be performed to expand the domain of validity of the simulation models, which could reduce prediction uncertainty for QOI or other key metrics. Finally, improvements can be achieved by reducing the errors associated with the model inputs, through improved input characterization, improved experimental data, or improved theory. Importantly, UQ-informed decisions help identify when, in a particular focus area, “enough is enough” and continued investment is unlikely to improve the overall confidence in system performance.
QMU provides a credible, quantifiable, and scientifically defensible basis for making programmatic decisions that impact planning, prioritizing, integrating, and communicating across various elements of the SSP. A strategy to fulfill the nation’s stockpile decision-making responsibilities must provide a balance of capabilities—informed by QMU—across experimentation, physics models, simulation tools, theory, and analysis methods. UQ-informed simulation capabilities enable the use of high-fidelity design studies to provide U.S. policy makers with options for the future, including options that affect the stockpile, the weapons manufacturing complex, and experimental facilities.
6.5 DECISION MAKING INFORMED BY VVUQ AT THE NEVADA NATIONAL SECURITY SITE
The context of this case study involving the Nevada National Security Site is Yucca Flat, Nevada Test Site (Figure 6.1), where a total of 659 underground nuclear tests were conducted between 1951 and 1992 (Fenelon, 2005). Most of the deep, large tests at Yucca Flat were conducted beneath the water table in complex layers of volcanic rocks dissected by numerous faults. Numerical models are being developed to predict the migration of radionuclides in the groundwater system away from the test cavities over the next 1,000 years. Of particular concern is a regionally extensive carbonate aquifer just below the volcanic layers. Predictions such as the size and extent of the plume as it evolves over time, the total volume of water exceeding the Safe Water Drinking Act standards, and the mass flux of radionuclides to the lower aquifer must be placed in a probabilistic framework. For the purpose of the study discussed in this report, which does not yet consider contaminant transport, the QOI is the increase in water volume flowing from the study site into the lower aquifer over the next 1,000 years. This case study also
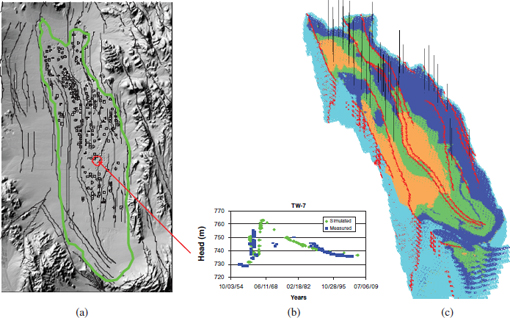
FIGURE 6.1 Yucca Flat, Nevada Test Site. (a) Study site locations of nuclear tests are denoted by black circles. The green outline depicts the region being modeled. The red circle indicates the location of the test well whose data are plotted in (c). (b) Hydraulic area level data over time for the test well identified by the red circle in (a). (c) Computation model grid for the high-fidelity model includes aquifers (light and dark blue), aquitards (orange and green), and faults (red) lines. The black lines denote well locations. SOURCE: Keating et al. (2010).
illustrated the use of UQ to quantify uncertainty in the decision-making process. In this case, however, the QOI under study accumulates over 1000 years and, so, cannot be observed. The DOE and the Nevada Division of Environmental Protection will be making key decisions concerning remediation, monitoring, and future hydrogeologic data collection on the basis of the results of this larger investigation. Although verification and validation play crucial roles in this larger effort, this case study focuses on the UQ aspects, showing how results are obtained and how they affect communication and decision making.
This case study has two main phases: (1) a calibration phase, in which available measurements are used to constrain uncertain parameters in the model, and (2) a prediction phase, in which prediction uncertainty is estimated for the QOI.
There are many important processes to be considered in this example, some focusing heavily on the source term (underground nuclear tests) and others focusing on flow and transport processes in the groundwater. In the former category are processes that cause drastic alteration in rock properties and pore water pressures near the working point and processes that distribute radionuclides in the cavity and beyond. All of these processes occurred in the area surrounding each test site within the first few seconds after a blast. In the latter category were processes such as advection, diffusion, dispersion, mass transfer between fractures and rock matrix, ground-surface subsidence due to long-term depressurization of the aquifer, sorption to mineral surfaces, and radioactive decay.
6.5.3 Computational Modeling of the Physical System
The study models the system using two iterative-coupled codes. The first is a phenomenological testing-effects model that simulates the instantaneous rock and fluid pressure changes that are due to underground testing. The second is a finite-volume heat- and mass- transfer code (Zyvoloski et al., 1997) used to simulate the transient flow of groundwater and the transport of radionuclides. The coupled model requires approximately 7 hours to run on a 3.6- GHz processor on a finely resolved numerical mesh (Figure 6.1(c)). Only the testing-effects and groundwater flow (not the radionuclide transport) portion of the simulations are considered in this report. An understanding of how testing effects groundwater flow is key to addressing the eventual question of radionuclide transport.
Several hundred parameters are used in this model. Many of these are related to the (possibly) unique characteristics of each underground nuclear test. Others are related to the permeability, porosity, and storage characteristics of the various rock layers and fault zones. Many (if not most) of the parameters are associated with essentially irreducible uncertainty. However, it is important to constrain as many parameters as possible. Transient hydraulic head data, basically measuring pressure at the monitoring wells (black lines in Figure 6.1(c)), were collected during the period of testing at approximately 60 wells; these data were used for the parameter estimation.
The model-calibration process uses the hydraulic head measurements, capturing pressure at the monitoring wells, collected at various times for the approximately 60 wells. Measurements at various times are shown for one of the wells in Figure 6.1(b). The goal is to use these calibration data to constrain parameter uncertainty, which can then be used to produce uncertainties for the prediction of the QOI. This prediction with its associated uncertainty can then be used to help make decisions regarding additional monitoring or mitigation.
It is important that uncertainty be adequately captured in applications such as this one, in which no direct measurements of the QOI are available. This UQ analysis was designed with the goal that it not only would produce a reasonably well-calibrated model but at the same time would establish the framework for the following uncertainty-assessment phase for the QOI. These two goals can sometimes be in conflict in the following sense: traditional calibration methods fail when parameter dimensionality is large compared to data availability (the ill-posed inverse problem), a frequent occurrence in hydrogeologic inverse problems. A common strategy for dealing with this ill-posedness is to “fix” most model parameters at a nominal setting, allowing only those that are sensitive to the calibration data to vary. Unfortunately, although this parsimony-based strategy can be successful in producing a set of parameters that are close to the measurements, it can vastly underrepresent parameter uncertainty, producing inappropriately certain estimates of the QOI (Hunt et al., 2007). Here the QOI is the increase in water volume flowing from the study area to the lower aquifer over the next 1,000 years.
A Bayesian formulation of the inverse problem was used to describe the uncertainty in the 200+ parameters induced by conditioning on the calibration data. This requires the specification of a distribution and range for each of the input parameters, as well as the specification of a likelihood for the hydraulic head measurements given the model parameters. An approach called null-space Monte Carlo (Tonkin and Doherty, 2009) was used to produce samples from the resulting posterior distribution, which is available in the PEST2 software suite (Doherty, 2009). This approach uses derivative-based searching as well as Monte Carlo sampling of the posterior density. A key feature of this analysis is that the large number of parameters not constrained by calibration data can be freely varied in the uncertainty analysis, producing a wider range of outcomes for the QOI.
This forward model is highly nonlinear and computationally demanding, which makes it difficult to tune and assess UQ methods for this application. To facilitate the development and testing of a suitable parameter-estimation and uncertainty-analysis strategy for this application, a fast-running reduced model was constructed. This reduced model (Keating et al., 2010) has a number of parameters similar to that of the process model and could be calibrated against the same data set described above. The null-space Monte Carlo approach, after tuning and testing using this reduced model, is ported over to and used for the calibration of the high-fidelity CPU-intensive process model.
_____________________
2 See pesthomepage.org. Accessed September 7, 2011.
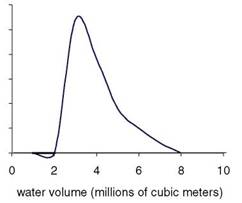
FIGURE 6.2 An ensemble of predictions of the quantity of interest—the additional water volume expected to move to the lower aquifer owing to nuclear testing effects, integrated over the study region and over the time span of 1,000 years at the Yucca Flat, Nevada Test Site. Even the highest values of this prediction are less than 1 percent of the total volume of water moving into the lower aquifer over this 1,000-year time span. SOURCE Keating et al. (2010).
6.5.5 Making (Extrapolative) Predictions and Describing Uncertainty
The posterior sample of parameter settings given the calibration data (which were found in the previous section) was then propagated forward through the computationally intensive process model, generating an ensemble of predictions for the QOI—the additional water volume attributable to the effects of nuclear testing, integrated over the study region (outlined in Figure 6.1(a)), and integrated over the span of 1,000 years. A probability density function for the QOI estimated from this ensemble is shown in Figure 6.2. The size of the ensemble was fairly small due to computational resource constraints.
To help assess the reliability of the prediction for the QOI, an ensemble of predictions was generated for a quantity that had not been used in model calibration—ground-surface subsidence (Keating et al., 2010). It was found that for nearly 90 percent of the model domain, measured subsidence fell within the bounds of the ensemble of predictions, giving some indication that this model can extrapolate from well-head measurements to other important model outputs (Keating et al., 2010).
Additionally, a number of discrete alternative conceptual models were created, primarily addressing key issues concerning the coupling of testing phenomenology and rock mechanics. These are essentially irreducible uncertainties. The alternative models were equally well calibrated to measured field data and could be considered to be equally plausible. The range of predictions generated using these discrete models was low, however, providing confidence in the robustness of results based on any single model.
6.5.6 Reporting Results to Decision Makers and Stakeholders
During the model development, analysis, and predictive phases, frequent briefings with the stakeholders (DOE and Nevada Division of Environment Protection) were held. The briefings provided the opportunity for stakeholders to give input and feedback and to gain confidence with the transparency of the process. It was particularly important to ensure that any and every credible conceptual model be included in the uncertainty analysis.
As detailed in this chapter, a decision can be made regarding the allocation of resources during a VVUQ study, as well as after the VVUQ analyses are completed, the results serving as a key input to the decision-making process. Clearly, the information that goes into such a decision is likely to be both qualitative and quantitative. Also, decisions within the VVUQ process can be made to improve both qualitative and quantitative aspects of the information, just as might be done for designing validation experiments.
In cases where quantitative results are needed, optimality criteria will likely involve a mathematical summary of information or prediction uncertainty. The computations required to carry out such optimization searches are typically quite demanding, making the discussion in Chapter 4 on emulation and reduced-order models relevant here. Also, even when qualitative information is desired, it is often obtained through a quantitative analysis. This was the case in the case study presented in Section 6.5, in which quantitative information about ground surface subsistence was used to produce qualitative information regarding the prediction uncertainty for the QOI.
Finding: High-consequence decisions have been and continue to be informed by UQ assessments.
Ben-Tal, A., and A. Nemirovski. 2002. Robust Optimization—Methodology and Applications. Mathematical Programming, Series B 92, pp. 453-480.
Doherty, J. 2009. Addendum to the PEST Manual. Corinda, Australia: Watermark Numerical Computing.
Ermoliev, Y. 1988. Nonlinear Multiobjective Optimization. New York: Springer.
Fenelon, J.M. 2005. Analysis of Ground-Water Levels and Associated Trends in Yucca Flat, Nevada Test Site, Nye County, Nevada, 1951-2003. U.S. Geological Survey Scientific Investigations Report 2005-5175. Washington, D.C.: U.S. Department of the Interior.
Goodwin, B.T., and R.J. Juzaitis. 2006. National Certification Methodology for the Nuclear Weapon Stockpile. UCRL-TR-223486. Available at http://www.osti.gov/bridge/product.biblio.jsp?_id=929177. Accessed March 19, 2011.
Heyman, D.P., and M.J. Sobel. 2003. Stochastic Models in Operations Research, Vol. II: Stochastic Optimization. Mineola, N.Y.: Dover Publications.
Hunt, R.J., J. Doherty, and M.J. Tonkin. 2007. Are Models Too Simple? Arguments for Increased Parameterization. Ground Water 45(3):254-262.
Keating, E.H., J. Doherty, J.A.Vrugt, and Q. Kang. 2010. Optimization and Uncertainty Assessment of Strongly Nonlinear Groundwater Models with High Parameter Dimensionality. Water Resources Research 46(10):W10517.
Miettinen, K. 1999. Nonlinear Multiobjective Optimization. New York: Springer.
NRC (National Research Council). 2007. Models in Environmental Regulatory Decision Making. Washington, D.C.: National Academies Press.
NRC. 2009. Evaluation of Quantification of Margins and Uncertainties Methodology for Assessing and Certifying the Reliability of the Nuclear Stockpile. Washington, D.C.: The National Academies Press.
Oldenburg, C.M., B.M. Freifeld, K. Pruess, L. Pan, S. Finsterle, and G.J. Moridis. 2011. Numerical Simulations of the Macondo Well Blowout Reveal Strong Control of Oil Flow by Reservoir Permeability and Exsolution of Gas. Proceedings of the National Academy of Sciences: July.
Taguchi, G., L.W. Tung, and D. Clausing. 1987. System of Experimental Design: Engineering Methods to Optimize Quality and Minimize Costs. New York: Unipub.
Tonkin, M., and J. Doherty. 2009. Calibration-Constrained Monte Carlo Analysis of Highly Parameterized Models Using Subspace Techniques. Water Resources Research 45(12):w00b10.
U.S. Congress. 1994. Section 3138, National Defense Authorization Act for the Year 1994. Public Law 103-160; 42 U.S.C. 2121 Note.
Zyvoloski, G.A., B.A. Robinson, Z.V. Dash, and L.L. Trease. 1997. User’s Manual for the FEHM Application—A Finite-Element Heat- and Mass-Transfer Code. Los Alamos, N.Mex.: Los Alamos National Laboratory.









