Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 81
Appendix C
Two-Year College Mathematics
and Student Progression in
STEM Programs of Study
Debra D. Bragg
Professor and Director,
Office of Community College Research and Leadership
University of Illinois at Urbana-Champaign
EXECUTIVE SUMMARY
In spite of the strident pursuit of standards-based reform of two-
year college mathematics, implementation of reform has been slow and
uneven. National studies show student enrollment in two-year college
mathematics is growing in proportion to overall enrollment growth in
higher education, but a substantial portion of these students are taking
pre-college mathematics courses. Research suggests many of these stu -
dents never reach college-level mathematics. Improvements need to be
made to two-year college mathematics to prepare more students for sci -
ence, technology, engineering, and mathematics (STEM)-related careers.
Specific recommendations to support this goal are
Take a P-20 approach to reforming the entire mathematics curricu-
lum. Without a strategic, collaborative endeavor, it will be difficult for
two-year colleges that are caught between K-12 education and higher
education to implement and sustain meaningful change.
Conduct more research on the teaching and learning of two-year
college mathematics. Finding ways to support two-year college faculty
to engage in professional development that reinforces innovative peda-
gogies is important. Included in this list are topics linked to quantitative
literacy, accelerated and contextualized instruction, and college placement
and related assessments that need to be better linked closely to student
learning.
Investigate more fully the characteristics, experiences, and aspira -
81
OCR for page 82
82 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
tions of students who enroll in two-year college mathematics. More
information is needed about how diverse learners, especially women and
minorities, experience their two-year mathematics courses (pre-college
and college level) and how these experiences influence their subsequent
enrollment, completion, and career decisions related to STEM.
Engage practitioners in action research on mathematics education
to facilitate the adoption and scale-up of innovation. Two-year faculty
would benefit from opportunities to engage in action research that helps
them to understand how various pedagogical and assessment strategies
impact the learning of diverse students, and then employ these strategies
in their classrooms.
INTRODUCTION
There is wide consensus that mastery of mathematics is essential to
progressing into and through STEM programs of study, yet many stu-
dents are unsuccessful at navigating the normative mathematics course
sequence (Cullinane and Treisman, 2010) that is fundamental to their
advancement into STEM-related careers. Recent concerns about inter-
national competition and the struggling economy have focused atten -
tion on this important issue and renewed concerns about the challenges
that many students, particularly women and minorities, face succeeding
in mathematics coursework (National Academy of Sciences, National
Academy of Engineering, and Institute of Medicine, 2010). Resolving this
problem is an urgent priority if the nation is to see growth in student
enrollment and success in STEM programs of study, placement of gradu -
ates in STEM-related careers, and rejuvenation of the nation’s economy.
This paper examines the influence of the two-year mathematics cur-
riculum on students’ progression into and through STEM programs by
drawing upon extant literature, materials on the Internet, and personal
communication with two-year college mathematics experts and practitio -
ners. It acknowledges the expansive developmental mathematics curricu-
lum offered by two-year colleges, but even more importantly, provides
insights into college-level mathematics that has been overshadowed by
a preoccupation with developmental education. The paper begins with
a brief historical perspective and then proceeds to address such ques -
tions as: what is the status of two-year mathematics courses, who teaches
them, and how are they taught? What standards-based reforms are associ-
ated with two-year college mathematics, what curricular and pedagogical
innovations are capturing the attention of mathematics reformers, and
what do we know about the impact of these reforms on student success?
This paper concludes with recommendations for future research, policy,
and practice on two-year college mathematics that is intended to enhance
OCR for page 83
83
APPENDIX C
student progression through STEM programs of study and into STEM-
related careers.
PERSPECTIVES ON MATHEMATICS CURRICULUM
IN THE TWO-YEAR COLLEGE
A useful framework for understanding two-year mathematics cur-
riculum comes from Cullinane and Treisman (2010), who label the math-
ematics curriculum in the United States the “normative mathematics
course sequence” (pp. 7-8), which they claim is ubiquitous to the P-20
(primary through grade 20) education system. The normative mathemat -
ics course sequence extends from basic arithmetic, to pre-algebra, algebra,
and intermediate algebra on to trigonometry, pre-calculus, calculus, and
other calculus-based courses, with a fuzzy demarcation between pre-
college and college-level mathematics that starts with college algebra.
Geometry may be part of the sequential mathematics continuum, or it
may be omitted, to the detriment of students’ advancement into calculus
and calculus-based sciences such as physics. Because this framework
represents the dominant schema for which mathematics is taught and for
which student competence is assessed at the secondary and postsecond -
ary levels, I use this framework as the basis for discussing the literature.
Later, in my discussion of reforms of the two-year college mathematics
curriculum, I again cite Cullinane and Treisman (2010) who are studying
alternatives to the normative mathematics course sequence. First, how -
ever, I provide a brief historical foundation and then move to contempo -
rary developments in two-year college mathematics.
Liberal arts and sciences courses, including mathematics courses,
have been part of the two-year college curriculum since creation of junior
colleges in the early 1900s. Cohen and Brawer (1982) observed that, by
the time two-year colleges arrived on the U.S. higher education scene, the
academic disciplines were already “codified” (p. 284) by the rest of the
educational system. Junior colleges that emerged to fill the void between
high schools and universities adopted the prevailing curriculum structure
advocated by the mathematics discipline and were therefore caught in
between the K-12 sector and the four-year college sector from the start.
To this end, Cohen and Brawer observed that, “the liberal arts [courses of
two-year colleges] were captives of the disciplines; the disciplines dictated
the structure of the courses; [and] the courses encompassed the collegiate
function” (1982, p. 285). To facilitate the acceptance of college credits at
the university level, two-year colleges reproduced the curriculum as well
as the pedagogical methods used by universities to which their students
sought entry.
Transfer was born from these early replication efforts. A landmark
OCR for page 84
84 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
study of junior colleges conducted at mid-20th century by Medsker (1960)
confirmed the lengths to which two-year colleges mimicked university
curriculum to enhance students’ ability to transfer. He noted, “the junior
college forfeits its identity and its opportunity to experiment in the devel -
opment of a program most appropriate for it” (p. 53). Looking back to the
start of the comprehensive curriculum of the two-year college, Cohen and
Brawer (1982) cited findings from a very early study of 58 junior colleges
conducted in 1921 and 1922 by Koos (1924, p. 29) that showed liberal arts,
sciences, and humanities courses dominated the early junior college cur-
riculum, with three-fourths of all courses representing these disciplines.
Across a broad array of the liberal arts and sciences, mathematics repre -
sented about 8% of all course offerings. Whereas mathematics was not
as dominant as English, communications, and the sciences, it was nearly
universally offered in the two-year college. By the late-1950s, a national
survey conducted by Medsker (1960) of 230 two-year colleges in 15 states
confirmed mathematics courses were ubiquitous to the two-year college
curriculum, but still, only a relatively modest proportion of students
enrolled in them. In fact, only about one-quarter of two-year colleges
required their students to take at least one mathematics course to meet
general education requirements. Medsker’s study was also important
because it was one of the first to document the prevalence of pre-college
courses in reading, writing, and mathematics, foreshadowing a phenom-
enon that would continue to grow to the present day.
Several decades subsequent to Medsker’s study, Cohen and Brawer
(1987) studied the two-year college curriculum and found remarkably
similar findings about mathematics course-taking. Their analysis showed
9 percent of total course enrollments in the liberal arts, sciences, and
humanities curriculum were in mathematics, and again reflective of
Medsker’s results, the survey revealed a high proportion of mathematics
courses were at the pre-college1 level. Subsequent studies conducted by
Cohen, Brawer, and colleagues included a curriculum mapping study
conducted by Cohen and Ignash (1992) about two decades ago. This study
examined courses offered by a national sample of two-year colleges by
scouring the spring 1991 catalogs and course schedules of 164 commu -
nity colleges, balanced by small (less than 1,500 students), medium, and
large (over 6,000 students) institution size. Cohen and Ignash mapped
the liberal arts and nonliberal arts curriculum into broad subject areas of
which mathematics and computer science were combined into one area.
Their study showed the preponderance of mathematics enrollments were
1Consistent with other literature on two-year college mathematics (see, for example, Blair,
2006), I use the term pre-college to refer to mathematics courses offered below the college
level, including courses often referred to as developmental and remedial education courses.
OCR for page 85
85
APPENDIX C
in classes offered at the introductory and intermediate course levels, with
enrollments at the introductory or intermediate level being nearly 9 times
larger than enrollments at the advanced level (about 766,000 enrollments
in the former and approximately 87,000 enrollments in the latter). Though
enrollments were substantially lower in advanced mathematics courses,
this study confirmed that two-year colleges offered a substantial array
of mathematics courses, including courses extending from the develop-
mental level to calculus, as well as statistics. The number of sections of
mathematics accounted for 10.7 percent of the total liberal arts curricu -
lum, which ranked mathematics just behind humanities at 13.4 percent
and English at 12.8 percent.
Another important aspect of two-year college mathematics curricu -
lum that is evident in the curriculum mapping study of Cohen and Ignash
(1992), and that also has relevance to this discussion, pertains to the rise
of nonliberal arts curriculum, a trend that began in the 1970s (Cohen and
Brawer, 1987). Since much of mathematics course-taking in the two-year
colleges relates to the majors that students choose in nonmathematics
subjects, it is important to understand the ways mathematics is used to
fulfill general education requirements. Cohen and Ignash (1994) identi-
fied the emergence of occupational-technical fields of study (many hav -
ing a technical focus and having some STEM-related content) beginning
in the 1970s, and they documented the growth of technical education,
trades and industrial education, and other programs of study offered
by two-year colleges that require various levels and forms of mathemat -
ics. Whereas the offering of liberal arts and sciences courses has been
relatively robust over the years, by the 1990s nonliberal arts and sciences
courses accounted for about 45 percent of the two-year college curricu -
lum and occupational-technical education course were prominent among
them. Technical mathematics and courses tailored for other majors such as
elementary education were apparent in the curriculum as well. One impli-
cation of this trend is that the teaching of mathematics, which had been
the purview of the mathematics discipline, spread to other instructional
units and efforts to integrate mathematics with other subjects emerged as
a strategy to increase learners’ abilities to apply mathematics in diverse
occupational settings (Grubb, 1999).
Concerns about students’ lack of preparation for college-level math-
ematics were also growing during the latter decades of the 20th century,
as noted by an American Mathematical Association of Two-Year Col-
leges (AMATYC) report that showed developmental mathematics courses
were offered by 91 percent of two-year colleges (Baldwin and the Devel-
opmental Mathematics Committee, 1975). Literature documenting the
growth in remedial enrollments in two-year colleges observed pre-college
mathematics courses were necessary for “marginally literate students
OCR for page 86
86 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
emanating from the secondary schools” (Cohen, 1984, p. 1). In a national
survey conducted in the early 2000s, Greene and Forster (2003) found
only 32 percent of all high school graduates demonstrated the level of
competence needed to enter college mathematics coursework. Among all
learners, Greene and Forster identified Hispanics and African Americans
as “seriously underrepresented in the pool of minimally qualified col -
lege applicants” (p. 3), and they attributed their lack of preparation to
inadequate K-12 education rather than “financial aid or affirmative action
policies” (p. 3). Their research points to the uniquely important role that
community colleges play in transferring underserved students to the uni -
versity level in STEM-related careers (Arbona and Nora, 2009). However,
transfer is not possible if students are unable to navigate the mathematics
curriculum that begins at the pre-college level. Attewell et al. (2006) found
60 percent of community college entrants are required to take one or more
developmental courses, usually mathematics, and numerous studies by
Bailey and colleagues at the Community College Research Center (CCRC)
(see, for example, Bailey, Jeong, and Cho, 2010) reveal the dismal success
rates of students whose placement test scores prescribe multiple devel -
opmental mathematics courses. Beyond the developmental level, Adel -
man (2004) noted failure and withdrawal rates of 50 percent or higher in
college algebra and pre-calculus courses, demonstrating problems with
student success extend beyond to the gatekeeper course level. This trend
and other critical aspects of the two-year mathematics curriculum, includ-
ing documenting enrollment in mathematics course sequences extending
from pre-college to college level, are examined in the next section.
CONTEMPORARY TWO-YEAR COLLEGE MATHEMATICS
Most of what we know about two-year college mathematics in the
United States comes from a few large-scale national surveys. The fullest
depiction of the curricular landscape about two-year college mathematics
is the national inventory of the mathematics curriculum in U.S. higher
education that has been conducted every five years starting in 1965 by
the Conference Board of Mathematical Sciences (CBMS) with support
from the National Science Foundation (NSF). The CBMS2005: Fall 2005
Statistical Abstract of Undergraduate Programs in the Mathematical Sciences
in the United States is the last published installment of the national survey
results on the two-year college mathematics curriculum (Lutzer et al.,
2007). However, preliminary results of the 2010 CBMS national inventory
on two-year college mathematics were shared with me by Ellen Kirkman
and Rikki Blair (personal communication, December 4, 2011) to update
OCR for page 87
87
APPENDIX C
this paper.2 Taken together, the 2005 and 2010 reports (as well as selective
use of earlier CBMS surveys) provide the most detailed description of
two-year college mathematics curriculum offered by public community
colleges in the United States, including trends in student enrollments,
courses, faculty, and instructional practices.
The CBMS survey used a stratified, simple random sampling design,
with strata based on the three variables of curriculum, highest degree
level offered, and total institutional enrollments to address three distinct
universes: two-year college mathematics programs, mathematics depart -
ments in four-year colleges and universities, and statistics departments
in four-year colleges and universities. The stratum specifications used
in the 2005 CBMS administration exactly replicated the ones used in the
CBMS 2000, and closely emulates the specifications of previous CBMS
surveys that were adjusted over time to improve national estimates. With
respect to the 2005 CBMS administration, the most recent date for which
a full report of methodology is available, a total of 600 public two- and
four-year colleges and universities were surveyed during the period of
September 2005 to May 2006. Minor adjustments are made to the CBMS
at each administration, but the core of items included on the survey
remains constant to address enrollments, instructional strategies, faculty
demographics, and so forth.
Figure C-1 reveals fall enrollments in mathematics and statistics at a
5-year interval from 1975 to 2005 (Lutzer et al., 2007), compared to total
enrollments in public four-year and two-year colleges obtained from the
Community Colleges, Special Supplement to the Condition of Education, 2008
report (Provasnik and Planty, 2008). Results suggest the enrollments in
mathematics and statistics are growing commensurate with the increase
in enrollments in public four-year and two-year colleges over the last
25-year period. Total enrollment growth in public two-year college is
highly correlated (r = .96) with mathematics and statistics enrollment
over this time span. More recent enrollment figures for Fall 2010 for
mathematics and statistics show enrollment climbed to an all-time high
of 2,096,000 (E. Kirkman and R. Blair, personal communication), mirroring
the enrollment growth in public two-year colleges to an unprecedented
high of 7,101,000 for 2009, the latest year statistics are available from the
U.S. Census Bureau (2012). With respect to the growth in mathematics
enrollment, the CBMS 2010 survey showed a 26 percent increase from
2005, which is about the same percentage increase that was observed
between 2000 and 2005.
2Iwant to express my sincere appreciation to Ellen Kirkman and Rikki Blair for their gen -
erosity in sharing preliminary tables from the forthcoming CBMS2010: Fall 2010 Statistical
Abstract of Undergraduate Programs in the Mathematical Sciences in the United States .
OCR for page 88
88 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
8,000
7,000
6,000
5,000
Thousands
4,000
3,000
2,000
1,000
0
Fall 1975 Fall 1980 Fall 1985 Fall 1990 Fall 1995 Fall 2000 Fall 2005
Public Four-Year College Enrollment Public Two-Year College Enrollment
Two-Year Math and Stats Enrollment
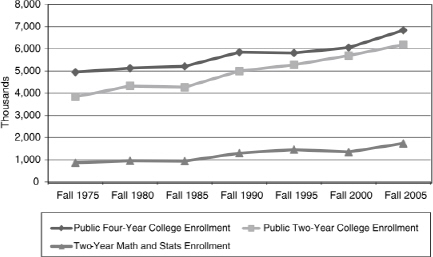
FIGURE C-1 Total public enrollment in two-year and four-year colleges and two-
year mathematics and statistics enrollment (Fall 1975–Fall 2005).
Figure C-2 shows two-year college mathematics enrollments are criti-
cal to the overall U.S. postsecondary education system. Whereas two-year
mathematics enrollment has seen some fluctuation over the 15-year period
from 1990 to 2005, the 2005 mathematics enrollment figure confirms sub-
stantial growth from earlier years to the point where there were only mod-
estly fewer enrollments in mathematics at the public two-year colleges ( n
= 1,580,000) than four-year public and private colleges (n = 1,607,000) by
Fall 2005, based on 2005 CBMS results (Lutzer et al., 2007). These totals
take into account dual enrollment, which has grown substantially over
the last decade (Waits, Setzer, and Lewis, 2005); however, they do not
take into account mathematics courses taught outside of mathematics
disciplinary units, including centralized pre-college education units that
are responsible for teaching pre-college mathematics classes. Therefore,
these figures almost certainly underestimate enrollments in pre-college
mathematics (arithmetic, pre-algebra, elementary algebra, intermediate
algebra, and geometry) and possibly other mathematics-related courses
taught on two-year college campuses, suggesting the actual enrollment in
two-year college mathematics may be higher still.
Figure C-3 shows the percentage enrollment in two-year college
mathematics courses by type of course and by the year the survey data
were collected, based on the most recent CBMS 2010 data supplied by
Kirkman and Blair (personal communication). Looking at the overall cur-
riculum delivered by two-year college mathematics units, the preponder-
OCR for page 89
89
APPENDIX C
2,000
1,500
Thousands
1,000
500
-
Fall 1990 Fall 1995 Fall 2000 Fall 2005
Four-Year Math Enrollment Two-Year Math Enrollment
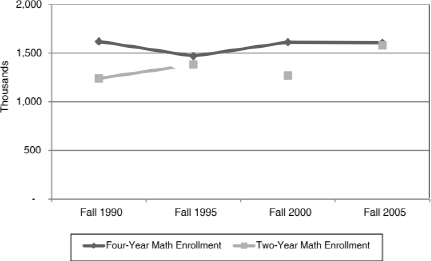
FIGURE C-2 Total enrollment in four-year college mathematics and two-year col -
lege mathematics (Fall 1990–Fall 2005).
2,500
2,016
2,000
1,696
1,425
Thousands
1,500
1,347
1,271
57.0%
56.8%
1,000
56.1% 56.6%
57%
500
-
Fall 1990 Fall 1995 Fall 2000 Fall 2005 Fall 2010
Pre-College Math Enrollment College Math Enrollment
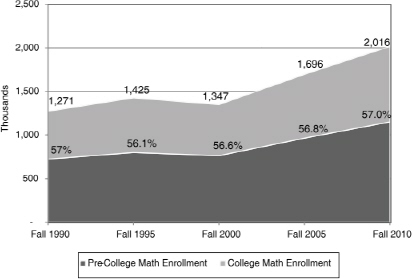
FIGURE C-3 Total two-year college enrollment in mathematics and percentage
of total enrollment at the pre-college level (Fall 1990–Fall 2010).
OCR for page 90
90 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
ance of enrollment is at the pre-college level, with a persistent percentage
of about 57 percent of all enrollments in mathematics units over the last
two decades. Other survey results reveal only modest changes in the
distribution of enrollment across the mathematics curriculum since 1990
(not shown in tabular form), with a small but persistent decline in enroll -
ment in pre-calculus (college algebra and trigonometry) courses since
1995, a slight drop but also fluctuation in calculus enrollment from 1990 to
2010, and a modest increase in enrollment in statistics courses since 1990
and in other mathematics courses since 1995, including classes for non-
mathematics majors (e.g., mathematics for liberal arts and mathematics
for elementary school teachers).
The CBMS also examined faculty and instruction, which is an impor-
tant issue for two-year colleges where part-time faculty are well docu-
mented and an important part of the teaching workforce (Townsend and
Twombly, 2008). The Fall 2005 survey reveals the extent to which part-time
faculty are engaged in mathematics instruction (Lutzer et al., 2007), with
the percentage of two-year college mathematics sections taught by part-
time faculty being 44 percent. (Although a percentage was not apparent
in preliminary results from the Fall 2010 survey, it is clear that part-time
faculty numbers remain high in the 2010 CBMS survey.) Part-time faculty
members are most evident at the pre-college level, with 56 percent of these
sections being taught by part-time faculty, and part-time faculty are least
involved in teaching of mainstream calculus and advanced mathematics
compared to other courses in the two-year mathematics curriculum, with
only 12 percent and 9 percent, respectively.
These results suggest students taking the advanced college-level
mathematics curriculum are most likely to be taught by a full-time fac -
ulty, a finding that seems to recognize the importance of advanced math -
ematics curriculum being taught by professionally trained mathematics
specialists as well as the need to align standards with disciplinary require-
ments that support student progression (transfer) to the university. Not -
ing this advantage, there is little evidence to suggest students who take
even the most advanced two-year college mathematics courses intend
to continue their study of mathematics at the university level as math -
ematics or STEM majors. Looking at all the CBMS data for 2005, Lutzer
et al. (2007) suggested relatively few two-year college students intend to
transfer to the university and major in mathematics at the four-year col-
lege level, although community college science and engineering (S&E)
students do transfer to the baccalaureate level to pursue S&E and engi -
neering technology baccalaureate degrees. Indeed, associates’ degrees
in S&E and engineering technology constitute about 11 percent of all
associate’s degrees awarded in 2007 (National Science Board, 2010), and
presumably most of these students are interested in transferring. Looking
OCR for page 91
91
APPENDIX C
retrospectively, about 44 percent of S&E graduates attended community
colleges (Tsapogas, 2004). The proportion of associate’s degree holders
who are racial-ethnic minorities is higher among associate’s degree than
bachelor’s degree holders in S&E fields, making these programs a rich
ground for recruiting of STEM majors at the baccalaureate level (Handel,
2011). From 1995 to 2007, the number of S&E associate’s degrees earned by
racial-ethnic minority students more than doubled from 7,836 to 19,435.
The Fall 2005 CBMS survey data report on instructional approaches
that provide insights into how two-year mathematics curriculum courses
are taught (Lutzer et al., 2007). These data show over three-quarters of
on-campus sections of college algebra and trigonometry, two courses core
to the mathematics curriculum for many transfer students, are taught
using the standard lecture method. The standard lecture method was less
evident in pre-college course sections such as arithmetic (64%) and more
evident in mainstream and nonmainstream calculus, elementary statis-
tics, differential equations and technical mathematics (calculus), ranging
from 81 percent to 93 percent. Given that calls for reform of mathematical
pedagogy have been made for many years (see, for example, Wubbels and
Girgus, 1997, and the authors of two-year college standards-based reform
mentioned in the next section), it is perplexing that so little change has
occurred in the teaching of such important two-year college mathematics
courses.
Looking at both instructional and outreach methods in the Fall 2005
and Fall 2010 CBMS surveys (E. Kirkman and R. Blair, personal com-
munication, December 4, 2011; Lutzer et al., 2007), results show college
placement testing in mathematics is nearly universal in two-year colleges,
although the preliminary finding from CBMS 2010 shows a 7 percent drop
from 2005 to 2010 that deserves further study. Blair indicated she and her
colleagues are still exploring the reason for this drop, but point out that
all of the 90 percent of two-year colleges that report diagnostic testing
report requiring mathematics placement testing for all incoming students.
These results also show an increase in K-12 outreach opportunities and
undergraduate research, but a decline in honors sections and special
programs to encourage women and minorities to enroll in two-year col-
lege mathematics. In terms of the use of distance and online learning, the
CBMS 2010 surveys show relatively modest use of online instruction, with
most courses showing less than 10 percent of the sections using online
learning systems. These results are consistent with previous results from
CBMS 2000 and CBMS 2005.
Given the dearth of information about student enrollments and out-
comes in two-year college mathematics, results of a national study by
Horn and Li (2009) on postsecondary awards (credentials) below the
baccalaureate level provide some insights into the scope and status of
OCR for page 96
96 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
mathematics courses have been immensely important to understanding
student success (or lack thereof) in mathematics courses and the larger
STEM pipeline. Researchers such as Bailey, Jeong, and Cho (2009); Perry
et al. (2010); and many others have laid a foundation for understanding
complex issues associated with pre-college mathematics. Despite a grow -
ing body of research, more rigorous research is needed on pre-college
as well as college-level mathematics curriculum at the two-year college
level. Research on mathematics teaching and learning at the classroom
level is needed to provide a fuller and more nuanced understanding
of content-based and pedagogically oriented reforms that may promote
mathematics competency and positive student outcomes at the two-year
level, including mastery of pre-college competencies, matriculating to
and mastering advanced competencies, and advancing to and through
the STEM pipeline.
An important recommendation that emerged from the AMATYC
standards-based reform reports, particularly the 2006 Beyond Crossroads
report, is consistent with the wider national and international conversa -
tions to emphasize quantitative literacy and quantitative reasoning as an
element of or, in some cases, alternative to the normative mathematics
course sequence. A leader in the dialogue about quantitative literacy,
Steen (2001) argues that enabling students to use mathematics to solve
real-world problems that are complex, ambiguous, and incomplete is the
most important thing that college mathematics courses can do. She notes
that “rarely will high school graduates be faced with problems that pres-
ent themselves in the language of algebra” (Steen, 1992, n.p.), but just
because students don’t appreciate algebra in its traditional forms does not
mean that it is not applicable or useful to them. Steen notes that quantita -
tive literacy is rooted in real data that are part of life’s diverse contexts
and situations. She believes pedagogy should change to encourage quan -
titative thought that can help learners “to understand the meaning of
numbers, to see the benefits (and risks) of thinking quantitatively about
commonplace issues, and to approach complex problems with confidence
in the value of careful reasoning” (Steen, 2001, p. 58). Students who
experience quantitative literacy are empowered to think independently,
to ask smart questions, and to confront complexities and challenges with
confidence, and, as Steen concludes, “these are the skills required to thrive
in the modern world” (p. 58).
Given the importance of this topic, it is unfortunate that the litera -
ture on quantitative literacy and quantitative reasoning is disconnected
from literature on contextualized teaching and learning, integrated aca -
demic and technical curriculum, and problem-based learning. Referring
to this collection of curricular and instructional approaches, Perin (2011)
described contextualization as the “practice of systematically connect -
OCR for page 97
97
APPENDIX C
ing basic skills instruction [in fields of study such as mathematics] to
a specific content that is meaningful and useful to students” (p. 3). Her
recent review of the literature includes findings of various types of con-
textualization employed in postsecondary settings, especially pre-college
mathematics courses. Baker, Hope, and Karandjeff (2009) have explored
the wide range of definitions that are used for contextualized instruction,
and, to their credit, they link practices associated with contextualization
to theories of learning and pedagogical strategies. Among the recommen -
dations made by Baker et al. is the importance of exploring alternative
formats for delivering the normative mathematics curriculum. Whereas
rigorous research has not been performed on contextualized math at the
two-year college level, an experimental study that examined the effect of
training of high school math and career and technical education (CTE)
teachers to work cooperatively to make math explicit in CTE classrooms
produced statistically significant outcomes, including higher scores on
standardized and college placement tests without negatively impacting
technical skill attainment (Stone, Alfeld, and Pearson, 2008). This study
has not been replicated in the two-year college context, but it would be
very helpful to do so.
Examples of other innovative mathematics curriculum formats that are
being studied include modularization, which involves delivering instruc -
tion in manageable segments or “chunks” (Rutschow and Schneider, 2011,
p. 25), rather than traditional, semester-long courses. Mostly applied to
pre-college mathematics, this strategy of chunking the curriculum could
be extended to college-level mathematics. When implemented properly,
students can achieve success in shorter time periods than traditional
courses, which also motivates them to persist to the next shortened seg -
ment. Bailey et al. (2003) evaluated modularization in six NSF Advanced
Technological Education (ATE) projects and four centers, and they noted
that instructors praised the method for its flexibility and adaptability.
The National Center for Academic Transformation Mathematics Empo -
rium model, which Twigg (2011) described as a “silver bullet,” combines
modularization with technology-supported instruction (G. Reese and C.
Kirby, personal communication, October 18, 2011).
Another innovation that is being attempted in mathematics, particu-
larly pre-college mathematics, involves compression of the curriculum,
meaning compressing the amount of time it takes for students to complete
mathematics course sequences, and accelerating them toward their next
course or completion. Compression often requires scheduling courses
more hours a day for shorter amounts of time, and pairing courses that
complement one another, including pairing mathematics and science
courses or pairing multiple mathematics courses (including pre-college
and college level) to create an intensive learning experience. Though
OCR for page 98
98 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
most of the research on compression and acceleration is focused on the
pre-college level curriculum, this strategy may be useful to attempt with
college-level mathematics courses (e.g., college algebra and statistics). For
example, two forms of acceleration were used by the FastStart Program
at the Community College of Denver, wherein FastStart accelerated stu-
dents through the mathematics course sequence by allowing students to
enroll in a developmental course concurrently with a college-level course.
Results from 11 student cohorts who began developmental mathematics
at various levels revealed encouraging outcomes on retention and credit
accumulation (Bragg, Baker, and Puryear, 2010). Synthesizing the litera -
ture on acceleration, Edgecombe (2011) noted evidence of the impact of
acceleration on developmental education is limited but promising based
on evaluations of FastStart and other similar programs.
Change of not only how mathematics is taught but also what is taught
is also important for mathematics reformers. One of the most notable
efforts in this regard are the Carnegie Foundation for Learning and the
Dana Center’s Quantway™ and Statway™ projects (Carnegie Foundation
for the Advancement of Teaching, 2011a, 2001b) that are attempting to
replace the normative pre-college mathematics courses with mathematics
courses focused on quantitative literacy and statistics. Using an acceler-
ated timeframe, the Quantway and Statway projects seek to prepare stu-
dents for college level mathematics instruction. Quantway and Statway
“enable developmental mathematics students in community colleges to
complete a[n accelerated] credit-bearing, transferable mathematics course
in one academic year while simultaneously building skills for long-term
college success” (Cullinane and Treisman, 2010, p. 4). The Statway course
sequence assists students to develop statistical literacy and engages them
in mathematical reasoning using data, and it provides them with college
credit in statistics. Cullinane and Treisman hypothesize that the adoption
of a statistics sequence such as Statway will support many more students
to engage in mathematical reasoning, especially when the curriculum is
institutionalized from K-12 education and extended to the postsecond -
ary level. Quantway is similarly focused on increasing the mathematical
literacy of students who need to take pre-college mathematics by replac-
ing traditional textbook-based, procedural instruction with numerical
reasoning that is necessary to solve real-world problems. The Quantway
pathway promotes an accelerated format, allowing students who place
into elementary algebra to gain access to and move through a college-level
quantitative reasoning course in one year.
Reform of instructional materials such as those associated with Stat -
way and Quantway address a disconcerting problem that Kays (2004),
Mesa (2010), and others have noted in the literature: the reliance on
textbooks to structure and guide classroom instruction of mathematics.
OCR for page 99
99
APPENDIX C
These studies demonstrate the ways classroom teaching that relies on
procedural-based textbooks reinforce the memorization of procedural
knowledge at the expense of quantitative reasoning. Many mathemat -
ics texts are also tied to the normative math course sequence, and tra -
ditional pedagogies associated with teaching the mainstay courses in
that sequence (e.g., algebra, geometry, trigonometry, and calculus) pro -
vide a valuable backdrop for a discussion of the critical needs that lay
ahead as two-year college mathematics educators delve more deeply
into reform. These studies suggest that systemic reforms, including cur-
riculum, instruction, and instructional materials, are need to be pursued
if mathematics education is to be responsive to the diversity of learners
who seek the opportunity to pursue STEM-related programs of study in
the two-year college.
RECOMMENDATIONS FOR FURTHER
RESEARCH, POLICY, AND PRACTICE
In spite of strident pursuit of standards-based reform of two-year
college mathematics, implementation of reform of the mathematics cur-
riculum has been slow and uneven. National studies show more students
are enrolling in two-year college mathematics, but a substantial portion of
these enrollments are at the pre-college level, and many of these students
never reach college-level mathematics. Thus, the STEM pipeline appears
to be widening at the start, which is encouraging, but it also seems to nar-
row rapidly as students attempt to advance to college-level mathematics,
a prerequisite to pursuing STEM programs of study and STEM-related
careers.
To facilitate the role that two-year mathematics can play in providing
access to the STEM pipeline and preparing larger numbers of postsecond-
ary students, mathematics instruction needs to be sufficiently engaging
and useful to support their interests and to assist them to make the com-
mitment necessary to pursue a STEM program of study. A whole host of
issues need to be addressed with respect to two-year college mathematics
and the preparation of students who seek subbaccalaureate credentials
and who desire to transfer to universities in STEM fields. Specific rec -
ommendations for research, policy, and practice to support this goal are
described below.
A systemic, P-20 approach is needed to reform mathematics cur-
riculum. Recommendations offered by a plethora of professional groups,
including AMATYC and the Mathematics Association of American
(MAA), and at different levels of the educational system are logical, rea-
sonable, and substantive, and equally importantly, they consistently argue
OCR for page 100
100 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
for a multi-level yet coordinated P-20 approach. Without such a strategic,
collaborative endeavor, it will be difficult for two-year colleges that are
caught between K-12 education and higher education to engage in reform,
except in isolated ways. Given the national imperative to enhance the
STEM pipeline, and the critical role that mathematics needs to play in that
work, this recommendation may be the most important of all to emerge
from the Summit on Realizing the Potential of Community Colleges as
Pathways to STEM Education and Careers.
More research is needed to improve two-year college mathemat-
ics instruction. Although numerous pedagogical strategies are emerging
that offer promise to change the way mathematics is taught at the two-
year college level, CBMS survey data confirm the prevalence of lecture-
led, teacher-centered instruction rather than the sorts of contextualized,
problem- and project-based approaches that support quantitative literacy.
Finding ways to support two-year college faculty to engage in profes-
sional development that reinforces innovative instructional reforms is
important. Included in this list is the importance of helping faculty to
adopt curriculum and instruction that draws upon students’ everyday
life experiences in the workforce, their communities, and other aspects
of their lives. Mathematics instructors also need to understand how to
integrate technologies to deliver instruction in the classroom or from a
distance. Moreover, mathematics instructors need to understand how col-
lege placement tests can either impede or advance students through the
mathematics curriculum. Involving faculty in decisions about assessment
may help them to understand how college placement testing impacts stu -
dent learning and ultimately, improves student outcomes.
More research is needed on the students who enroll in two-year col-
lege mathematics, especially college-level mathematics (college algebra
and beyond), and how their experiences and performance in college-level
mathematics courses influences subsequent enrollment, completion, and
career decisions. Because two-year colleges are the gateway to postsecond-
ary education for diverse learners, these schools have an important role
to creating pathways that prepare students to advance to higher levels of
postsecondary education. More research is needed to support the study of
mathematics pathways, other than the normative mathematics sequence,
and to understand how students “develop the ‘habits of the mathematical
mind’ that are required to be successful in mathematics and science and
engineering and technology courses” (R. Blair, personal communication,
December 8, 2011). Students need to know what these new mathematical
pathways look like and how they lead to STEM careers, and they can-
not be expected to understand or navigate them on their own, without
encouragement and support. Systemic change is needed to ensure that all
students who have aspirations for STEM careers get the chance to learn
OCR for page 101
101
APPENDIX C
mathematics in ways that fully and respectfully support their goals. If
the nation expects more women and minorities to participate in STEM
programs of study, fulfilling this recommendation is essential.
More and better data are needed to support practitioner engagement
in active research on mathematics education at the local level, where
two-year college mathematics faculty and other stakeholders engage in
the teaching and learning process. Beyond participating in training, many
two-year faculty would appreciate and benefit from opportunities to
engage in active research that encourages them to try out new pedagogi-
cal strategies in the classroom and determine how they impact student
learning. The Equity Scorecard™ and Benchmarking projects of the Center
for Urban Education at the University of Southern California provide
valuable examples of ways that professional development of two-year
college faculty can be integrated with action research to address equity
issues for minority students who seek to participate in STEM programs
(Baldwin et al., 2011). The Achieving the Dream initiative has established
a strong track record of engaging practitioners in using data to improve
pre-college mathematics (Rutschow et al., 2011). Lessons learned from this
initiative and other newer ones, such as Pathways to Results in Illinois
(Bragg and Bennett, 2011), offer the potential to improve two-year college
mathematics and support student success in STEM programs of study.
SUPPLEMENTAL INFORMATION
Methods
This paper relies on existing literature available from a number of
sources. Most importantly, academic databases were queried to identify
peer-refereed articles as well as books, monographs, reports, papers, and
conference presentations on two-year college mathematics. Databases
included in this review were ERIC, EBSCO, Education Full-Text, JSTOR,
Dissertation Abstracts, and Sociological Abstracts. In addition, Google and
Google Scholar were queried to identify relevant documents and materi -
als that appear outside of the traditional scholarly databases. Searches of
websites maintained by organizations known to research and publish on
the topic of two-year college mathematics were conducted, including the
National Center for Education Statistics, the National Science Foundation,
the Community College Research Center at Teachers College, and Charles
A. Dana Center at the University of Texas at Austin, the AMATYC web-
site, and others. Keywords used in these searches included the following
words singularly and in combination with one another: math, mathemat -
ics, mathematics education, developmental, remedial, pre-college, alge -
bra, calculus, advanced mathematics, statistics, etc.
OCR for page 102
102 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
Keywords used to understand how the scholarly literature situates
two-year mathematics curriculum in the broader liberal arts and sciences
context included the following: liberal arts and sciences, liberal arts, sci -
ence, STEM, STEM education, technology, technology education, engi-
neering, engineering education, technician education, etc. Also, to ensure
that the full spectrum of literature on two-year colleges was included in
this literature review, I used an extensive set of keywords to capture the
institutional context, including the following: two-year college, commu -
nity college, technical college, and junior college. I also entered keywords
related to four-year college and university, transfer, and articulation to
determine whether literature was available to compare the two-year con -
text to the four-year context, including transfer.
In addition to the above methods, I reached out to several two-year
college mathematics experts, including David Lutzer, Ellen Kirkman,
and Rikki Blair, all authors of the Fall 2005 and/or Fall 2010 CBMS
surveys. Rikki Blair also served as editor of the 2006 Beyond Crossroads
report of AMATYC and was an especially thoughtful and gracious con -
tributor. I also sought guidance from several two-year college mathemat -
ics practitioners and colleagues at the University of Illinois, including
George Reese, director of the Office of Mathematics, Science and Tech-
nology Education, and Catherine Kirby, assistant director of the Office of
Community College Research and Leadership, who collaborated recently
on a literature review on this same topic and brought numerous sources
on two-year college mathematics to my attention. Finally, I offer my grati-
tude to Dr. Julia Makala, research specialist at the Office of Community
College Research and Leadership, who offered a critical review that was
invaluable to the final draft of this paper.
REFERENCES
Adelman, C. (2004). Principal indicators of student academic histories in postsecondary educa -
tion, 1972-2000. Washington, DC: U.S. Department of Education, Institute of Educa -
tion Sciences. Available: http://www2.ed.gov/rschstat/research/pubs/prinindicat/
prinindicat.pdf [June 25, 2012].
Albers, D.J., Loftsgaarden, D., Rung, D., and Watkins, A. (1992). Statistical abstracts of under-
graduate programs in the mathematical sciences and computer science in the United States,
1990-1991 CBMS Survey. (MAA Notes Number 23). Washington, DC: Mathematical
Association of America.
American Mathematics Association for Two-Year Colleges. (n.d.). The right stuff: Appropriate
mathematics for all students. Memphis, TN: Author. Available: http://www.therightstuff.
amatyc.org/ [June 25, 2012].
Arbona, C., and Nora, A. (2009). The influence of academic and environmental factors on
Hispanic college degree attainment. The Review of Higher Education, 30(3), 247-269.
Arnold, R. (2010). Contextualization toolkit: A tool for helping low-skilled adults gain postsecondary
certificates and degrees. Boston, MA: Jobs for the Future. Available: http://www.jff.org/
sites/default/files/BT_toolkit_June7.pdf [June 25, 2012].
OCR for page 103
103
APPENDIX C
Attewell, P., Lavin, D., Domina, T., and Levey, T. (2006). New evidence on college remedia -
tion. The Journal of Higher Education, 77(5), 887-924.
Bailey, T., Matsuzuka, Y., Jacobs, J., Morest, V.S., and Hughes, K. (2003). Institutionalization
and sustainability of the National Science Foundation’s Advanced Technological Education
Program. New York: Community College Research Center, Teachers College, Columbia
University.
Bailey, T., Jeong, D.W., and Cho, S. (2010). Referral, enrollment, and completion in devel -
opmental education sequences in community college. Economics of Education Review,
29(2), 255-270.
Baker, E., Hope, L., and Karandjeff, K. (2009). Contextualized teaching and learning: A faculty
primer. Sacramento, CA: The Chancellor’s Office of the California Community Col-
leges. Available: http://www.cccbsi.org/Websites/basicskills/Images/CTL.pdf [June
25, 2012].
Baldwin, J., and the Developmental Mathematics Committee. (1975). Survey of developmental
mathematics courses at colleges in the United States. Garden City, NY: American Math-
ematical Association of Two-Year Colleges. Available: http://www.eric.ed.gov/PDFS/
ED125688.pdf [June 25, 2012].
Baldwin, C., Bensimon, E.M., Dowd, A.C., and Kleiman, L. (2011). Measuring student suc -
cess. New Directions for Community Colleges, 153(spring), 75-88.
Blair, R. (Ed.). (2006). Beyond Crossroads: Implementing mathematics standards in the first two
years of college. Memphis, TN: American Mathematical Association of Two-Year Col-
leges. Available: http://www.amatyc.org/Crossroads/CRRV6/BC_V6_home.htm
[June 25, 2012].
Bragg, D.D., and Bennett, S. (2011). Introduction to pathways to results. Champaign, IL: Uni-
versity of Illinois, Office of Community College Research and Leadership. Available:
http://occrl.illinois.edu/files/Projects/ptr/Modules/PTR%20Intro%20Module.pdf
[June 25, 2012].
Bragg, D.D., Baker, E.D., and Puryear, M. (2010). 2010 Follow-up of Community College Den-
ver FastStart Program. Champaign, IL: University of Illinois, Office of Community
College Research and Leadership. Available: http://occrl.illinois.edu/files/Projects/
breaking_through/FastStart_Final.pdf [June 25, 2012].
Carnegie Foundation for the Advancement of Teaching. (2011a). Quantway. Available:
http://www.carnegiefoundation.org/quantway [June 25, 2012].
Carnegie Foundation for the Advancement of Teaching. (2011b). Statway. Available: http://
www.carnegiefoundation.org/statway [June 25, 2012].
Cohen, A. (1984, July). Mathematics in today’s community college. Paper presentation at the
Sloan Foundation Conference on New Directions in Two-Year College Mathematics in
Atherton, CA. ERIC Reproduction no. Ed 244 656. Available: http://www.eric.ed.gov/
PDFS/ED244656.pdf [June 25, 2012].
Cohen, A., and Brawer, F. (1982). The American community college, 1st ed. San Francisco:
Jossey-Bass.
Cohen, A., and Brawer, F. (1987). The collegiate function of community colleges. San Francisco:
Jossey-Bass.
Cohen, A., and Ignash, J. (1992). Trends in the liberal arts curriculum. Community College
Review, 20(2), 50-60.
Cohen, A., and Ignash, J. (1994). An overview of the total college curriculum. New Directions
for Community Colleges, 86 (Summer), 13-29.
Cohen, D. (Ed.) (1995). Crossroads in mathematics: Standards for introductory college mathematics
before calculus. Memphis, TN: American Mathematical Association of Two-Year Col-
leges. Available: http://beyondcrossroads.amatyc.org/doc/CH1.html [June 25, 2012].
Contemporary College Mathematics. (n.d.) Available: http://www.contemporarycollege
algebra.org/index.html [June 25, 2012].
OCR for page 104
104 COMMUNITY COLLEGES IN THE EVOLVING STEM EDUCATION LANDSCAPE
Cullinane, J., and Treisman, P.U. (2010). Improving developmental mathematics education in
community colleges: A prospectus and early progress report on the Statway Initiative . Paper
presentation at the National Center for Postsecondary Research (NCPR) Developmen -
tal Education Conference: What Policies and Practices Work for Students? Available:
http://www.utdanacenter.org/downloads/spotlights/CullinaneTreismanStatway
Paper.pdf [June 25, 2012].
Dowd, A.C., Malcom, L.E., and Bensimon, E.M. (2009, December). Benchmarking the success
of latina and latino students in STEM to achieve national graduation goals. Los Angeles:
University of Southern California, Center for Urban Education.
Edgecombe, N. (2011, May). Accelerating the academic achievement of students referred to de -
velopmental education. CCRC Brief No. 55. New York: Community College Research
Center, Teachers College, Columbia University. Available: http://ccrc.tc.columbia.edu/
Publication.asp?UID=920 [June 25, 2012].
Ganter, S.L., and Barker, W. (Eds.). (2004). Curriculum foundations project: Voices of the partner
disciplines. Washington, DC: Mathematical Association of America. Available: http://
www.maa.org/cupm/crafty/Chapt1.pdf [June 25, 2012].
Greene, J., and Forster, G. (2003). Public high school graduation and college readiness rates in the
United States. New York: Manhattan Institute, Center for Civic Information. Available:
http://www3.northern.edu/rc/pages/Reading_Clinic/highschool_graduation.pdf
[June 25, 2012].
Grubb, W.N. (1999). Honored but invisible: An inside look at teaching in community colleges. New
York: Routledge.
Handel, S. (2011, July). Improving student transfer from community colleges to four-year in-
stitutions—The perspective of leaders from baccalaureate-granting institutions . New York:
The College Board. Available: http://advocacy.collegeboard.org/sites/default/
files/11b3193transpartweb110712.pdf [June 25, 2012].
Hillyard, C., Korey, J., Leoni, D., and Hartzler, R. (2010, February). Math across the com-
munity college curriculum: A successful path to quantitative literacy. MathAMATYC
Educator, 1(2), 4-9.
Horn, L., and Li, X. (2009, November). Changes in postsecondary awards below the bachelor’s
degree: 1997 to 2007. Washington, DC: National Center for Education Statistics, Institute
of Education Sciences, U.S. Department of Education. Available: http://nces.ed.gov/
pubs2010/2010167.pdf [June 25, 2012].
Kays, V. (2004). National standards, foundation mathematics and Illinois community colleges:
Textbooks and faculty as the keepers of content. (Doctoral Dissertation). Office of Commu-
nity College Research and Leadership, University of Illinois at Urbana–Champaign.
Available: http://occrl.illinois.edu/publications/dissertation/2004/3 [June 25, 2012].
Koos, L. (1924). The junior college. Minneapolis, MN: University of Minnesota Press.
Lutzer, D., Rodi, S., Kirkman, E., and Maxwell, J. (2007). Statistical abstract of undergraduate
programs in mathematical science in the United States, Fall 2005 CBMS Survey. Providence,
RI: American Mathematical Society. Available: http://www.ams.org/profession/data/
cbms-survey/full-report.pdf [June 25, 2012].
Medsker, L. (1960). The junior college: Progress and prospect. New York: McGraw-Hill.
Mesa, V. (2010). Examples in textbooks: Examining their potential for developing metacogni-
tive knowledge. MathAMATYC Educator, 2(1), 50-55.
National Academy of Sciences, National Academy of Engineering, and Institute of Medicine.
(2006). Rising above the gathering storm: Energizing and employing America for a brighter
economic future. Committee on Science, Engineering, and Public Policy. Washington,
DC: The National Academies Press.
National Council of Teachers of Mathematics. (2000). Principles and standards for school
mathematics. Reston, VA: Author. Available: http://www.nctm.org/standards/[June
25, 2012].
OCR for page 105
105
APPENDIX C
National Science Board. (2010). Science and engineering indicators 2010. Arlington, VA: Na-
tional Science Foundation. Available: http://www.nsf.gov/statistics/seind10/pdf/
front.pdf [June 25, 2012].
Perin, D. (2011). Facilitating student learning through contextualization: A review of evidence. Co-
lumbia University, Teachers College, Community College Research Center. Available:
http://ccrc.tc.columbia.edu/Publication.asp?UID=954 [June 25, 2012].
Perry, M., Bahr, P.R., Rosin, M., and Woodward, K.M. (2010). Course-taking patterns, policies,
and practices in developmental education in the California Community Colleges . Mountain
View, CA: EdSource.
Provasnik, S., and Planty, M. (2008). Community colleges, Special supplement to The Condition
of Education, 2008. (NCES 2008-033). Washington, DC: U.S. Department of Education,
National Center for Education Statistics.
Rutschow, E.Z., and Schneider, E. (2011). Unlocking the gate: What we know about improving
developmental education. New York: MDRC. Available: http://www.mdrc.org/staff_
publications_386.html [June 25, 2012].
Rutschow, E. Z., Richburg-Hayes, L., Brock, T., Orr, G. Cerna, O., Cullinan, D., Kerrigan, M.
R., Jenkins, D., Gooden, S., and Martin, K. (2011, February). Turning the tide: Five years
of Achieving the Dream in community colleges. New York: MDRC. Available: http://www.
mdrc.org/publications/578/overview.html [June 25, 2012].
Small, D. (2002). An urgent call to improve traditional college algebra programs. Available:
http://www.contemporarycollegealgebra.org/national_movement/an_urgent_call.
html [June 25, 2012].
Steen, L.A. (1992). Does everybody need to study algebra. Mathematics Teacher, 85(4), 258-
260. Available: http://www.stolaf.edu/people/steen/Papers/everybody.html [June
25, 2012].
Steen, L.A. (2001). Quantitative literacy. Education Week on the Web, 21(1), 58.
Stone, J., Alfeld, C., and Pearson, D. (2008). Rigor and relevance: Enhancing high school
students’ math skills through career and technical education. American Educational
Research Journal, 45(3), 767-795.
Townsend, B., and Twombly, S. (2008). Community college faculty: What we know and need
to know. Community College Review, 36, 5-24.
Tsapogas, J. (2004, April). The role of community colleges in the education of recent science and en -
gineering graduates. InfoBrief (NSF 04-315). Arlington, VA: National Science Foundation.
Twigg, C.A. (2011, May/June). The math emporium: Higher education’s silver bullet.
Change Magazine (online). Available: http://www.changemag.org/Archives/Back%20
Issues/2011/May-June%202011/math-emporium-full.html [June 25, 2012].
U.S. Census Bureau. (2012). The 2012 statistical abstract: The national data book. Washington,
DC: Author.
Waits, T., Setzer, J.C., and Lewis, L. (2005). Dual credit and exam-based courses in U.S. public
high schools, 2002-03. Washington, DC: U.S. Department of Education, National Center
for Education Statistics. Available: http://nces.ed.gov/pubs2005/2005009.pdf [June
25, 2012].
Wubbels, G., and Girgus, J. (1997). The natural sciences and mathematics. In J. Gaff and R.
Ratcliff and Associates (Eds.), Handbook of the undergraduate curriculum (pp. 280-300).
San Francisco: Jossey-Bass.
OCR for page 106
