Appendix E
Sampling Variability and Uncertainty Analyses
In Appendix D, uncertainty in the analytical measurement process was considered and confidence intervals that reflect that uncertainty in an unknown true concentration x were developed. However, if one obtains a series of n measurements of a given piece of equipment, or of an area of potential contamination such as a room, or n soil samples in an area where contamination may have occured, then inferences about the potential area of concern must incorporate the sampling variability associated with the n measured concentrations. In a perfect world, one would compute a (1 -α)100 percent normal upper confidence limit (UCL), and if the UCL was less than the regulatory standard, one could conclude with (1 - α)100 percent certainty that the true concentration mean for the piece of equipment or spatial area was less than the regulatory standard of interest. Note that this does not require all measurements to be below the regulatory standard. Of course, the converse is also true—namely, that all of the individual measurements can be below the regulatory standard but the UCL may still exceed the standard. It should be noted that there is considerable EPA guidance supporting this approach, including but not limited to SW846 (EPA, 2007) guidance and the EPA unified statistical guidance document (EPA, 2009). In addition, this general approach is also clearly recommended in the ASTM consensus standard (D7048) (ASTM, 2010).
Factors that complicate the simple use of a normal UCL are these: (1) the distribution of measured concentrations is rarely normal and generally has a long right tail, which is characteristic of a lognormal or gamma distribution; (2) the analyte is often not detected in a substantial proportion of the samples; and (3) the large number of statistical comparisons that are made leads to a large number of positive results, consistent with chance expectations but likely to be false positives. In the following sections, a general statistical methodology that can be followed to address such factors is outlined.
NORMAL CONFIDENCE LIMITS FOR THE MEAN1
For a normally distributed constituent that is detected in all cases the (1 -α)100 percent normal lower confidence level (LCL) (assessment sampling and monitoring) for the mean of n measurements is computed as
![]()
1The remainder of this appendix is largely an adaptation from Gibbons, 2009.
![]()
The (1 - α)100 percent normal UCL (corrective action) for the mean of n measurements is computed as
![]()
When nondetects are present, several reasonable options are possible. If n < 8, nondetects are replaced by one-half of the detection limit (DL) since with fewer than eight measurements, more sophisticated statistical adjustments are typically not appropriate. Similarly, a normal UCL is typically used because seven or fewer samples are insufficient to confidently determine distributional form of the data. Because of a lognormal limit with small samples can result in extreme limit estimates, it is reasonable and conservative to default to normality for cases in which n < 8.
If n ≥ 8, a good choice is to use the method of Aitchison (1955) to adjust for nondetects and test for normality and lognormality of the data using the Shapiro-Wilk test. However, the ability of the Shapiro-Wilk test (and other distributional tests) to detect nonnormality is highly dependent on sample size. For most applications, 95 percent confidence is a reasonable choice. Note that alternatives such as the method of Cohen (1961) can be used; however, the DL must be constant.
LOGNORMAL CONFIDENCE LIMITS FOR THE MEDIAN
For a lognormally distributed constituent—that is, ![]() (x) is distributed
(x) is distributed ![]() —the (1 -α)100 percent LCL for the median or 50th percentile of the distribution is given by
—the (1 -α)100 percent LCL for the median or 50th percentile of the distribution is given by
![]()
where ![]() and sy are the mean and standard deviation of the natural log transformed concentrations. Note that the exponentiated limit is, in fact, an LCL for the median and not the mean concentration. In general, the median and corresponding LCL will be low than the mean and its corresponding LCL. The (1 - α)100 percent UCL for the median 50th percentile of the distribution is given by
and sy are the mean and standard deviation of the natural log transformed concentrations. Note that the exponentiated limit is, in fact, an LCL for the median and not the mean concentration. In general, the median and corresponding LCL will be low than the mean and its corresponding LCL. The (1 - α)100 percent UCL for the median 50th percentile of the distribution is given by
![]()
LOGNORMAL CONFIDENCE LIMITS FOR THE MEAN
The Exact Method
Land (1971) developed an exact method for computing confidence limits for linear functions of the normal mean and variance. The classic example is the normalization of a lognormally distributed random variable x through the transformation ![]() , where, as noted previously, y is distributed normal with mean μ and variance σ2, or
, where, as noted previously, y is distributed normal with mean μ and variance σ2, or ![]() . Using Land’s (1975) tabled coefficients Hα, the one-sided (1 -α)100 percent lognormal LCL for the mean is
. Using Land’s (1975) tabled coefficients Hα, the one-sided (1 -α)100 percent lognormal LCL for the mean is

Alternatively, using H1-α, the one-sided (1 -α)100 percent lognormal UCL for the mean is
![]()
The factors H are given by Land (1975) and ![]() and sy are the mean and standard deviation of the natural log transformed data (i.e.,
and sy are the mean and standard deviation of the natural log transformed data (i.e., ![]() ). Gilbert (1987) has a small subset of these extensive tables for n = 3 through 101, sy = .1 through 10.0, and α = .05 and .10 (i.e., upper and lower 90 percent and 95 percent confidence limit factors). Because these tables had historically been difficult to find, Gibbons and Coleman (2001) reproduced the complete set of Land’s (1975) tables and have also included computing approximations that can be used for automated applications. Land (1975) suggests that cubic interpolation (i.e., four-point Lagrangian interpolation) be used when working with these tables (Abramawitz and Stegun, 1964). A much easier and quite reasonable alternative is to use logarithmic interpolation.
). Gilbert (1987) has a small subset of these extensive tables for n = 3 through 101, sy = .1 through 10.0, and α = .05 and .10 (i.e., upper and lower 90 percent and 95 percent confidence limit factors). Because these tables had historically been difficult to find, Gibbons and Coleman (2001) reproduced the complete set of Land’s (1975) tables and have also included computing approximations that can be used for automated applications. Land (1975) suggests that cubic interpolation (i.e., four-point Lagrangian interpolation) be used when working with these tables (Abramawitz and Stegun, 1964). A much easier and quite reasonable alternative is to use logarithmic interpolation.
Approximate Lognormal Confidence Limit Methods
There are also several approximations to lognormal confidence limits for the mean that have been proposed. These have been conveniently classified as either transformation methods or direct methods (Land, 1970). A transformation method is one in which the confidence limit is obtained for the expected value of some function of x and then transformed by some appropriate function to give an approximate limit for the
expectation of x (i.e., E(x)), which in the lognormal case is ![]() . This estimate is assumed to be normally distributed and approximate confidence limits are computed accordingly.
. This estimate is assumed to be normally distributed and approximate confidence limits are computed accordingly.
The simplest transformation method is the naive transformation, which simply involves taking a log transformation of the data, computing the confidence limit on a log scale, and then exponentiating the limit. As previously noted, this is, in fact, a confidence limit for the median and not the mean. The method provides somewhat reasonable results as a confidence limit for the mean when σy is very small but deteriorates quickly as σy increases (Land, 1970).
Patterson (1966) proposed use of the transformation
![]()
to remove the obvious bias of the naive method. Patterson’s transformation would be exact if ![]() were known; however, when the variance is unknown, it too behaves poorly when σy increases (Land, 1970). More complicated alternatives described by Finney (1941) and Hoyle (1968) provide results similar to those of Patterson’s transformation and are therefore not presented.
were known; however, when the variance is unknown, it too behaves poorly when σy increases (Land, 1970). More complicated alternatives described by Finney (1941) and Hoyle (1968) provide results similar to those of Patterson’s transformation and are therefore not presented.
Direct methods offer an advantage over transformation methods in that they obtain confidence intervals directly for E(x) or some function of E(x) . In light of this, these methods do not suffer from the bias introduced by failing to take into account the dependence of E(x) on both μ and σ2. However, by applying normality assumptions to E(x), direct estimates can produce inadmissible confidence limits for E(x). To this end, Aitchison and Brown (1957) have suggested computing the usual normal confidence limit, which under the Central Limit theorem should converge to exact limits as n becomes large. Hoyle (1968) suggested replacing ![]() and
and ![]() by their minimum variance unbiased estimates (MVUE). Finney (1941) derived the MVUE of E(x) as follows
by their minimum variance unbiased estimates (MVUE). Finney (1941) derived the MVUE of E(x) as follows
![]()
and Hoyle (1968) derived the MVUE for the variance of E(x) as
![]()
where
![]()
is a Bessel function with argument g. In this method, the normal quantile zα replaces tn-1,σ since there is no reason to believe that ![]() is chi-squared and independent of
is chi-squared and independent of ![]() . Unfortunately, Land (1970) has shown that these methods are only useful for large n (i.e., n > 100) and even there only for small values of sy.
. Unfortunately, Land (1970) has shown that these methods are only useful for large n (i.e., n > 100) and even there only for small values of sy.
The final direct method, which is attributed to D.R. Cox, has been shown to give the best overall results of any of the approximate methods (Land, 1970). The MVUE of ![]() , and the MVUE of the variance γ2 of
, and the MVUE of the variance γ2 of ![]() is
is
![]()
Assuming approximate normality for ![]() , one may obtain approximate confidence limits for E(x) of the form
, one may obtain approximate confidence limits for E(x) of the form
![]()
and
![]()
NONPARAMETRIC CONFIDENCE LIMITS FOR THE MEDIAN
When data are neither normally or lognormally distributed or the detection frequency is too low (e.g., < 50 %) for a meaningful distributional analysis, nonparametric confidence limits become the method of choice. The nonparametric confidence limit is defined by an order statistic (i.e., a ranked observation) of the n measurements. Note that in the nonparametric case, one is restricted to computing confidence limits on percentiles of the distribution, for example, the 50th percentile or median of the on-site/downgradient distribution. Unless the distribution is symmetric (i.e., the mean and median are equivalent), there is no direct nonparametric way of constructing a confidence limit for the mean concentration.
To construct a confidence limit for the median concentration, one uses the fact that the number of samples falling below the p(100)th percentile of the distribution (e.g., p = .5, where p is between 0 and 1) out of a set on n samples will follow a binomial distribution with parameters n and success probability p, where success is defined as the event that a sample measurement is below the p(100)th percentile. The cumulative binomial distribution, Bin(x;n, p), represents the probability of getting x or fewer successes in n trials with success probability p, and can be evaluated as
![]()
The notation ![]() denotes the number of combinations of n things taken i at a time, where
denotes the number of combinations of n things taken i at a time, where

and k! = 1.2.3 … k for any counting number k. For example, the number of ways in which two things can be selected from three things is
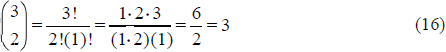
To compute a nonparametric confidence limit for the median, begin by rank ordering the n measurements from smallest to largest as x(1), x(2), …, x(n). Denote the candidate end points selected to bracket the 50th percentile (i.e., (n +1)*.5) as L* and U* for lower and upper bound, respectively. For the LCL, compute the probability
![]()
If the probability is less than the desired confidence level, 1—α, select a new value of L* = L* — 1 and repeat the process until the desired confidence level is achieved. For the UCL, compute the probability
![]()
If the probability is less than the desired confidence level, —α, select a new value of U* = U* +1 and repeat the process until the desired confidence level is achieved. If the desired confidence level cannot be achieved, set the LCL to the smallest value or the UCL to the largest value and report the achieved confidence level.
Another distribution that is often used for skewed data is the gamma distribution. Suppose x follows a gamma distribution with the shape parameter k and scale parameter ![]() . Then the gamma density is given by
. Then the gamma density is given by
![]()
Let x(1), x(2), …, x(n) be a random sample of size n drawn from this population to estimate the unknown parameters. Denote the arithmetic and geometric means based on this random sample by ![]() and
and ![]() , respectively. The maximum likelihood estimators of
, respectively. The maximum likelihood estimators of ![]() and K, denoted by
and K, denoted by ![]() and
and ![]() , are solutions to the following equations:
, are solutions to the following equations:
![]()
where Ψ denotes a digamma or Euler’s psi function. The mean and variance of x are:
![]()
To construct the UCL for this type of data, Aryal et al. (2009) constructed the following statistic:
![]()
where Rn is the logarithm of the ratio of the arithmetic mean to the geometric mean and μ is the mean of the population. X is the sum of all the observations. The UCL of μ is obtained by solving the following equation and taking the largest root:
![]()
where F1-α is the (1 - α) 100th percentile of the F distribution with degrees of freedom 1 and n - 1. To compute the (1 -α)100 percent UCL, invert the test statistic T, from which one obtains
![]()
where
![]()
REFERENCES
Abramawitz, M. and I. Stegun. 1964. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Washington, D.C.: National Bureau of Standards.
Aitchison, J. 1955. On the distribution of a positive random variable having a discrete probability mass at the origin. Journal of American Statistical Association 50: 901-908.
Aitchison, J. and J. Brown. 1957. The Log-normal Distribution. Cambridge, UK: Cambridge University Press.
Aryal, S., D. Bhaumik, S. Santra, and R. Gibbons. 2009. Confidence interval for random- effects calibration curves with left-censored data. Environmetrics 20(2): 181-189.
ASTM (American Society for Testing and Materials). 2010. ASTM D7048-04 Standard Guide for Applying Statistical Methods for Assessment and Corrective Action Environmental Monitoring Programs. West Conshohocken, Pa.: ASTM International.
Cohen, A. 1961. Tables for maximum likelihood estimates: singly truncated and singly censored samples. Technometrics 3: 535-541.
U.S. Environmental Protection Agency (EPA). 2007. SW-846 Test Methods for Evaluating Solid Waste, Physical/Chemical Methods. Washington, D.C.: Environmental Protection Agency.
EPA. 2009. Statistical Analysis of Groundwater Monitoring Data at RCRA Facilities Unified Guidance. EPA 530/R-09-007. Washington, D.C.: Environmental Protection Agency Office of Resource Conservation and Recovery.
Finney, D. 1941. On the distribution of a variate whose logarithm is normally distributed. Journal of the Royal Statistical Society, Series B 7: 155-161.
Gibbons, R. 2009. Assessment and corrective action monitoring. Pp. 317-335 in Statistical Methods for Groundwater Monitoring, edited by R. Gibbons, D. Bhaumik, and S. Aryal. Hoboken, N.J.: John Wiley & Sons, Inc.
Gibbons, R. and D. Coleman. 2001. Statistical Methods for Detection and Quantification of Environmental Contamination. New York, N.Y.: John Wiley & Sons, Inc.
Gilbert, R. 1987. Statistical Methods for Environmental Pollution Monitoring. New York, N.Y.: John Wiley and Sons, Inc.
Hoyle, M. 1968. The estimation of variances after using a gaussianating transformation. Annals of Mathematical Statistics 39: 1125-1143.
Land, L. 1970. Phreatic Versus Vadose Meteoric Diagenesis of Limestones: Evidence from a Fossil Water Table.
Land, C. 1971. Confidence intervals for linear functions of the normal mean and variance. Annals of Mathematical Statistics 42:1187-1205.
Land, C. 1975. Tables of confidence limits for linear functions of the normal mean and variance. Selected Tables in Mathematical Statistics 3: 385-419.
Patterson, C. and D. Settle. 1966. 7th Materials Research Symposium. National Bureau of Standards Special Publication 422. Washington, D.C.: U.S. Government Printing Office.
This page is blank










