The committee was tasked with assessing Air Force Space Command (AFSPC) orbit determination and prediction models, and with comparing these algorithms with leading alternatives. Although the committee was approved to review these algorithms in detail, it determined that it did not have to review the actual codes. Because leading alternatives are proprietary data, the committee could not access them. However, the features of the algorithms are public information, and the committee found these data satisfactory for its purposes. Table 2.1 summarizes the major features of these algorithms. The standardized algorithms listed in Box 1.1 include basic routines that involve geometry and variable transformations. In contrast, Table 2.1 and this report in general focus on the more challenging orbit determination and propagation functions.
The current algorithms are not positioned to be effectively responsive to future challenges in space situational awareness. Monitoring the growing population of objects in Earth orbit will require improved algorithms including fundamentals such as force model evaluation and statistical orbit determination, and critical tasks such as conjunction analysis and sensor resource management. The evolving sensor sets will also enable expanded characterization capabilities that the current system cannot accommodate.
The committee reviewed alternative algorithms from several governmental and commercial organizations.1,2,3 The briefings showed the growing community interest in astrodynamics algorithms and the products they produce. While these alternative algorithms demonstrate innovative solutions to particular issues in the current AFSPC algorithms and products, the committee believes that none of the alternatives addresses the full requirements set. In addition, the current architecture, both hardware and software, makes it difficult to incorporate additional alternatives into the system even when the alternative algorithms could improve performance for some subset of requirements. Finally, and importantly, the current system must address the needs of a wide range of customers/clients—some who need improved products and have the resources to adapt and others who are satisfied with the legacy products and may not have the resources to adapt.
The current concept of the new Joint Space Operations Center (JSpOC) Mission System under development
![]()
1 C. Acton, Jet Propulsion Laboratory, Navigation and Ancillary Information Facility, “The SPICE System,” presentation to the Committee for the Assessment of the U.S. Air Force’s Astrodynamic Standards on December 13, 2011.
2 F. Hoots and T. Cerven, Aerospace Corporation Systems Engineering Division/Systems Analysis and Simulation, “Covariance Realism,” presentation to the Committee for the Assessment of the U.S. Air Force’s Astrodynamic Standards, February 7, 2012.
3 J. Woodburn, AGI, “User Requirements Analysis and COTS Status,” presentation to the Committee for the Assessment of the U.S. Air Force’s Astrodynamic Standards, February 7, 2012.
TABLE 2.1 Summary of Current AFSPC Standardized Astrodynamics Algorithms
| AFSPC Algorithm | ||
| Astrodynamics Task | Special Perturbations | General Perturbations |
| Atmosphere model | J70 plus HASDM | Simple atmosphere |
| Force models | ||
| Drag | Piecewise-constant ballistic coefficient | Constant ballistic coefficient |
| Solar radiation pressure (SRP) | Piecewise-constant reflectivity coefficient | None |
| Earth gravity | High-order geopotential (Earth Gravitational Model 1996) truncated to medium degree and order plus Earth and ocean tides (from U.S. Naval Observatory) | Low-degree zonals only geopotential |
| Third-body gravity | Sun and Moon (option for analytic or JPL ephemerides model) | Semi-analytic Sun and Moon |
| Trajectory propagation | Gauss-Jackson eighth order | SGP4 |
| Orbit determination | Weighted batch least-squares, with drag/SRP segmentation | Weighted batch least-squares, sequential differential correction |
| Error estimation | Covariance propagation | Covariance computed but not distributed |
should address many of these issues—and opportunities. A modern service-oriented architecture and well-engineered software can provide a platform to encourage innovation throughout the community, ease integration of alternative algorithms that offer improvements for all or a subset of customers/clients, and address the interface requirements of users who need legacy products and those who need more technically advanced products.
In this chapter, the committee surveys state-of-the-art and historical approaches to AFSPC astrodynamics tasks and provides an outlook and general recommendations for future advances and applications. In particular, a number of specific technical areas are discussed in which the space situational awareness enterprise is likely to expand, many of them requiring the development of standardized astrodynamics algorithms beyond the current set. These representative technical areas are perceived by the committee as critical to meeting future needs of AFSPC, the JSpOC, the warfighter, and the broader space situational awareness community. Potential areas for improvement are considered in the context of fundamental tasks currently in practice as well as new methods and applications that respond to the changing mission and computing environments. Included are case studies and discussions of new and future possible advances in algorithms, theory, and modeling. The content of this chapter is not exhaustive, but it is representative of the committee’s vision of how the needs and capabilities of space situational awareness within AFSPC are likely to expand in the future. Any of these areas can serve as motivation for the future expansion of the astrodynamics algorithms toward more diverse capabilities.
The chapter is organized according to a logical flow of astrodynamics information: atmosphere models (needed to compute drag forces), force models (needed to propagate orbits), trajectory propagation (including numerical integration techniques), and orbit determination. A section is then devoted to uncertainty representation and computation, which, as discussed in Chapter 1, is an area that needs improvement in order to meet user needs for conjunction assessments. The chapter concludes with a section examining the important future drivers and directions for space situational awareness research. The section ordering is not indicative of perceived priority or importance. Important subtopics include data association methods, analytic techniques, modern dynamical systems, nonlinear filtering, and characterization of objects in orbit.
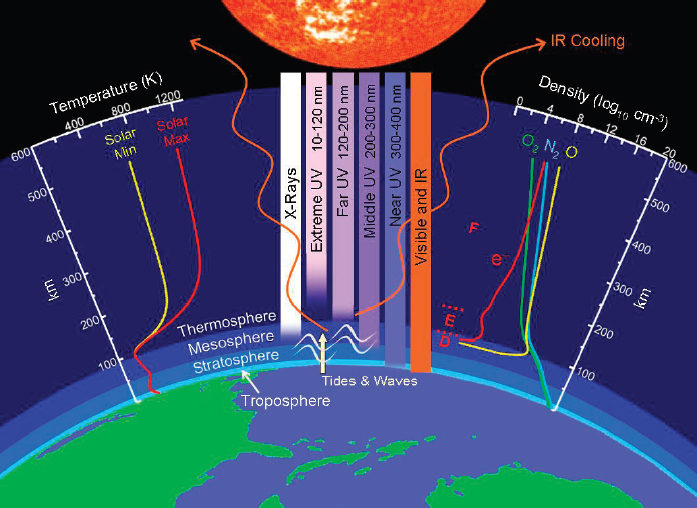
FIGURE 2.1 Atmospheric structure and processes. SOURCE: Adapted from J.T. Emmert, A physicist’s tour of the upper atmosphere, Physics Today 61(12):70-71, 2008.
Atmospheric drag is the largest source of uncertainty in orbit determination and prediction for low-perigee objects. Most of the uncertainty stems from inaccurate knowledge of atmospheric density (the remainder is due to inaccurate modeling, discussed in the next section, of the interaction between the atmosphere and an object).4 On global scales, for example, the root-mean-square relative error of density models generally decreases with decreasing altitude (from 20-25 percent at 600 km to 5-10 percent at 200 km). However, the drag force increases exponentially with decreasing altitude, and atmospheric variations on smaller spatial scales become increasingly important, which presents enormous challenges for accurate reentry predictions.
Earth’s thermosphere (~90-600 km altitude) and exosphere (>600 km) are a hot, partially ionized gas. This region is heated primarily by absorption of solar ultraviolet radiation, by electromagnetic energy and energetic particles from the solar wind, and by dissipation of waves propagating upward from the underlying atmosphere (see Figure 2.1). The heating is balanced by cooling from infrared emissions in the lower thermosphere, primarily by the trace species CO2 and NO. Cooling is very inefficient in the upper thermosphere, which sheds its heat via thermal conduction to the cooler lower thermosphere. Below ~100 km, the atmosphere is well mixed (~78 percent
![]()
4 M.F. Storz, B.R. Bowman, M.J.I. Branson, S.J. Casali, W.K. Tobiska, High accuracy satellite drag model (HASDM), Advances in Space Research 36:2497-2505, 2005.
N2, 21 percent O2, etc.). Above 100 km, diffusive separation of species begins to occur, and the density of the heavier species falls off more rapidly than that of the lighter species. Atomic oxygen (O), which is produced primarily by photodissociation of O2, is the dominant species between ~200 and 600 km and is responsible for most of the drag on objects in low Earth orbit (LEO). Part of the difficulty of accurately modeling thermospheric mass density can be traced to the complex photochemical origins of O and the highly variable transition layer between the fully mixed (homosphere) and diffusively separated (heterosphere) portions of the atmosphere.
The thermosphere may be modeled as being in hydrostatic equilibrium to a high degree of accuracy, particularly on the time scales and large spatial scales most relevant to routine orbit prediction; most empirical and physical models employ this constraint. The more restrictive constraint of diffusive equilibrium is well established above ~160 km. Although fluid equations provide a poorer description of the exosphere (>600 km), where the mean free path exceeds the scale height, hydrostatic equilibrium is still a reasonable assumption up to ~1000 km. Given a temperature profile, the number density of each species can thus be computed by vertical integration of the hydrostatic equilibrium equation, and the mass density is then calculated by summing the contribution from each species. This connection between the temperature profile and the density profile provides a powerful method for modeling density with a small number of parameters, and allows assimilation of both density and temperature data to estimate those parameters.
Atmosphere models may be broadly divided into two classes: empirical models, which represent the average behavior of past data under specified conditions, and physical models, which solve the time-dependent fluid and photochemical equations that govern the atmosphere. In practice, however, empirical models usually include some physics (especially the hydrostatic constraint), and physical models rely on empirical parameterizations for energy inputs, boundary conditions, and subgrid-scale processes. Figure 2.2 illustrates selected atmospheric models in terms of the number of physical processes they include and the amount, diversity, and timeliness of the data they assimilate.
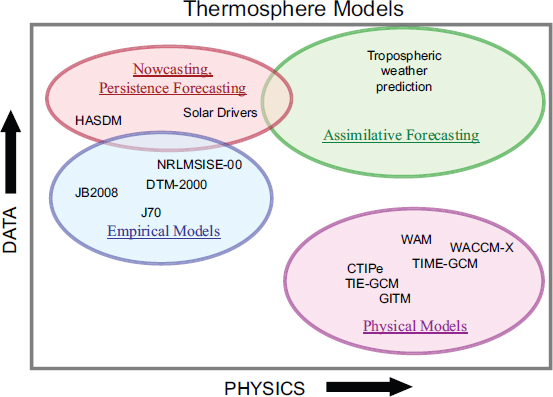
FIGURE 2.2 Fidelity levels of existing thermospheric models.
The Jacchia 70 model5 (J70) is an early empirical model developed from total mass densities derived from orbit analysis, as well as published analyses of composition from rocket experiments. J70 begins at an altitude of 90 km with fixed (temporally invariant and spatially uniform) density and temperature, with composition essentially the same as that of the sea-level atmosphere.
In the late 1970s, the mass spectrometer-incoherent scatter (MSIS) series of atmospheric empirical models was initiated at NASA/Goddard Space Flight Center. The first model assimilated in situ mass spectrometer measurements of temperature and composition, and temperatures inferred from incoherent scatter radar data.6,7 The latest version of the model, NRLMSISE-00, used, in addition, orbit- and accelerometer-derived mass densities, ultraviolet occultation measurements of lower thermospheric composition, and sounding rocket data.8 The model represents temperature and seven-species composition from the ground to the exosphere.
The Drag-Temperature Model (DTM) was initially developed in Europe in 1978 using orbit-derived mass densities.9 The latest version, DTM-2000, also incorporates mass spectrometer and incoherent scatter radar data, as well as optical spectrometer measurements.10 The model represents temperature and five-species composition from 120 km to the exosphere.
J70, MSIS, and DTM are in hydrostatic equilibrium, but the models use different representations of the vertical temperature profile, which affects how density is computed. MSIS and DTM use the Bates-Walker temperature profile.11,12 This formulation is analytically integrable and produces a closed-form solution for density, whereas J70 uses a temperature profile that must be numerically integrated to obtain density.
Because J70, MSIS, and DTM are climate models based on historical data, they are not able to capture day-to-day density variability during a specific period. Furthermore, imperfect representation of solar drivers (all three models use the solar radio flux at a wavelength of 10.7 cm, F10.7, as a proxy for extreme ultraviolet [EUV] heating) can result in additional errors when the models are used to predict density for a specific epoch. The High Accuracy Satellite Drag Model (HASDM) was developed by AFSPC to provide dynamic corrections to the J70 model. HASDM is based on tracking observations from ~75 calibration objects and is currently the operational standardized astrodynamics algorithm used in the astrodynamics support workstation.13 Other dynamic correction
![]()
5 L.G. Jacchia, New Static Models of the Thermosphere and Exosphere with Empirical Temperature Profiles, SAO Special Report 313, Smithsonian Astrophysical Observatory, Cambridge, Mass., 1970.
6 A.E. Hedin, J.E. Salah, J.V. Evans, C.A. Reber, G.P. Newton, N.W. Spencer, D.C. Kayser, D. Alcaydé, P. Bauer, L. Cogger, and J.P. McClure, A global thermospheric model based on mass spectrometer and incoherent scatter data MSIS, 1, N2 density and temperature, Journal of Geophysical Research 82:2139-2147, 1977.
7 A.E. Hedin, C.A. Reber, G.P. Newton, N.W. Spencer, H.C. Brinton, H.G. Mayr, and W.E. Potter, A global thermospheric model based on mass spectrometer and incoherent scatter data MSIS, 2, Composition, Journal of Geophysical Research 82:2148-2156, 1977.
8 J.M. Picone, A.E. Hedin, D.P. Drob, and A.C. Aikin, NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues, Journal of Geophysical Research 107:1468, doi:10.1029/2002JA009430, 2002.
9 F. Barlier, C. Berger, J.L. Falin, G. Kockarts, and G. Thuillier, A thermospheric model based on satellite drag data, Annals of Geophysics, 34:9–24, 1978.
10 S. Bruinsma, G. Thuillier, and F. Barlier, The DTM-2000 empirical thermosphere model with new data assimilation and constraints at lower boundary: Accuracy and properties, Journal of Atmospheric and Solar-Terrestrial Physics 65:1053–1070, 2003.
11 D.R. Bates, Some problems concerning the terrestrial atmosphere above about the 100 km level, Proceedings of the Royal Society of London, Series A 253:451–462, 1959.
12 J.C.G. Walker, Analytic representation of upper atmosphere densities based on Jacchia’s static diffusion models, Journal of Atmospheric Sciences 22:462–463, 1965.
13 M.F. Storz, B.R. Bowman, M.J.I. Branson, S.J. Casali, W.K. Tobiska, High accuracy satellite drag model (HASDM), Advances in Space Research 36, 2497–2505, 2005.
schemes, using two-line elements (TLEs), have been developed independently of HASDM.14,15,16,17,18 The use of TLEs produces densities with accuracy similar to that of HASDM’s SP assimilation, but with lower temporal resolution.
The “nowcast” (i.e., a description of present conditions) that HASDM and other dynamic corrections provide is a significant advance over the use of climate models for specifying the thermosphere. HASDM also empirically extrapolates the J70 corrections into the future to produce a 72-hour prediction; this extrapolation may be regarded as a sophisticated form of persistence forecasting. The advantage of dynamic corrections over climate models decreases with increasing forecast time. The current dynamic correction approaches could be improved, for example by incorporating other types of data besides mass densities; lower-thermosphere temperature and composition data are likely to be particularly valuable.
The Jacchia-Bowman 2008 (JB2008) model was developed by AFSPC and is slated to replace J70 as the baseline density model in HASDM.19 It is a climate model that builds on the J70 formulation, by either replacing or correcting the various components of J70, based on 1997-2007 orbit-derived density data. JB2008 significantly improves on the performance of J70 with its use of the MgII index of solar EUV irradiance, which is a more precise indicator of short-term (~1 day to 1 year) variations in EUV irradiance than F10.7 (however, it has not been established that JB2008’s use of four different irradiance indices robustly improves performance). JB2008 is also based on density data more recent than that in any other climate model. Unexplained density variability occurs on interannual, decadal, and longer time scales, and so a model that is optimized for the most recent solar cycle is likely to outperform models that rely on decades-old data.20 One disadvantage of JB2008 is that it overrides J70’s physical constraint of hydrostatic equilibrium, rendering the model less suitable as a basis for assimilating data types other than mass density data or for extrapolating assimilated mass density data.
Several physical models of the thermosphere have been developed over the past three decades and are currently used primarily for research purposes. The Thermosphere Ionosphere Electrodynamics General Circulation Model (TIE-GCM) was developed at the National Center for Atmospheric Research (NCAR).21 TIE-GCM represents the thermosphere and ionosphere between 97 km and ~500 km altitude. A subsequent model, TIME-GCM, extended TIE-GCM down to 30 km, encompassing the mesosphere and upper stratosphere and the chemical processes therein.22 The Coupled Thermosphere Ionosphere Plasmasphere Electrodynamics model (CTIPe) is the most recent version of another line of thermosphere-ionosphere models; its construction is similar to that of TIE-GCM.23 The Global Ionosphere-Thermosphere Model (GITM) has a lower boundary of 95 km and, unlike other
![]()
14 V. Yurasov, A. Nazarenko, P. Cefola, and K. Alfriend, Density corrections for the NRLMSIS-00 atmosphere model (AAS 05-168), Advances in the Astronautical Sciences 120(Part 2):1079–1108, 2005.
15 E. Doornbos, H. Klinkrad, and P. Visser, Use of two-line element data for thermosphere neutral density model calibration, Advances in Space Research 41:1115–1122, 2008.
16 J.T. Emmert, A long-term data set of globally averaged thermospheric total mass density, Journal of Geophysical Research 114:A06315, doi:10.1029/2009JA014102, 2009.
17 E. Doornbos, Thermospheric density and wind determination from satellite dynamics, Ph.D. dissertation, Delft University of Technology, 2011.
18 Aerospace Corporation, Calibration/Validation Final Report for the Special Sensor Ultraviolet Limb Imager (SSULI) and the Special Sensor Ultraviolet Spectrographic Imager (SSUSI) on the Defense Meteorological Satellite Program (DMPS) F18 Spacecraft, Report No. TOR-2012(1550)-5.
19 B.R. Bowman, W.K. Tobiska, F.A. Marcos, and C. Valladares, The JB2006 empirical thermospheric density model, Journal of Atmospheric and Solar-Terrestrial Physics 70:774–793, 2008.
20 J.T. Emmert and J.M. Picone, Statistical uncertainty of 1967-2005 thermospheric density trends derived from orbital drag, Journal of Geophysical Research 116:A00H09, doi:10.1029/2010JA016382, 2011.
21 A.D. Richmond, E.C. Ridley, and R.G. Roble, A thermosphere/ionosphere general circulation model with coupled electrodynamics, Geophysical Research Letters 19:601–604, 1992.
22 R.G. Roble, and E.C. Ridley, A thermosphere-ionosphere-mesosphere-electrodynamics general circulation model (time-GCM): Equinox solar cycle minimum simulations (30-500 km), Geophysical Research Letters 21:417–420, 1994.
23 T.J. Fuller-Rowell, D. Rees, S. Quegan, R.J. Moffett, M.V. Codrescu, and G.H. Milward, A coupled thermosphere-ionosphere model (CTIM), pp. 217-238 in STEP Handbook of Ionospheric Models (R.W. Schunk, ed.), Utah State University, Logan, Utah, 1996.
physical models, does not assume hydrostatic equilibrium, allowing it to capture the rapid, localized changes to the thermosphere that occur at high latitudes.24
Recent research has shed new light on the importance of lower-atmosphere meteorology and climate on the thermosphere, and these results have motivated the development of models that describe the atmosphere from the ground to the exosphere. The Whole Atmosphere Model (WAM), developed at NOAA, is an upward extension of the National Weather Service’s operational Global Forecast System.25 WACCM-X, developed at NCAR, is an extension of the Whole Atmosphere Community Climate Model (WACCM), which previously had an upper boundary at ~145 km, into the upper thermosphere.26 Whereas WAM is primarily a dynamical model, WACCM-X additionally includes detailed chemistry.
Because the atmosphere is a chaotic system (a short discussion of chaotic systems is given below in the section “Insights from Modern Dynamical Systems”), improved forecasts of thermospheric density will ultimately require accurate specification of initial conditions, along with physical models to reliably propagate the system forward in time.27 Lower-atmosphere meteorological forecast systems are often held up as a model to which space weather efforts should aspire. The sophisticated physical models and enormous amount of data on which such forecast systems rely place them in the upper-right corner of Figure 2.2. However, achieving this position for thermospheric forecasting presents unique challenges. The space weather system is currently monitored much more sparsely than meteorological forecast systems, but the volume of space that must be specified is larger by several orders of magnitude. Obtaining data from the upper atmosphere is much more expensive than from the lower atmosphere, particularly in the key region between 100 and 200 km. For this reason, this sparse database characteristic is not likely to change for many years. The problem, then, is to assimilate sparse data into a physics-based assimilation/forecast system, and efforts toward this goal are in the nascent stages. The lack of data must be compensated by comprehensive, fundamental theoretical (physics and chemistry) understanding and modeling of the medium, which has not yet been achieved. There has been recent progress in assimilating sparse data up to ~90 km; such specifications of the thermosphere’s lower boundary may facilitate improved density forecasts, but advances in modeling the turbulent processes in the lower thermosphere will likely also be required.28
Another major challenge for improving thermospheric forecasts is the prediction of the solar drivers: spectral irradiance, solar wind, and the interaction of the latter with Earth’s magnetosphere and high-latitude thermosphere. Some progress has been made in this area by exploiting solar rotation to predict the recurrence of active regions and high-speed solar wind streams, and several research spacecraft now monitor the Sun in unprecedented detail.29,30 However, considerable additional research is needed to accurately predict the evolution of active regions and the occurrence and propagation of coronal mass ejections, and operational monitoring of the Sun from the L5 libration point is needed, in conjunction with better models, to produce a transformative advance in solar forecasting. Several efforts have been initiated to model the entire Sun-Earth system in an integrated framework.31
![]()
24 A.J. Ridley, Y. Deng, and G. Toth, The global ionosphere-thermosphere model, Journal of Atmospheric and Solar-Terrestrial Physics 68:839-864, 2006.
25 R.A. Akmaev, Whole atmosphere modeling: Connecting terrestrial and space weather, Reviews of Geophysics 49:RG4004, doi: 10.1029/2011RG000364, 2011.
26 H.-L. Liu, B.T. Foster, M.E. Hagan, J.M. McInerney, A. Maute, L. Qian, A.D. Richmond, R.G. Roble, S.C. Solomon, R.R. Garcia, D. Kinnison, D.R. Marsh, A.K. Smith, J. Richter, F. Sassi, and J. Oberheide, Thermosphere extension of the Whole Atmosphere Community Climate Model, Journal of Geophysical Research 115:A12302, doi:10.1029/2010JA015586, 2010.
27 E.N. Lorenz, The Essence of Chaos, University of Washington Press, Seattle, Wash., 1993.
28 S.D. Eckermann, K.W. Hoppel, L. Coy, J.P. McCormack, D.E. Siskind, K. Nielsen, A. Kochenash, M.H. Stevens, C.R. Englert, W. Singer, and M. Hervig, High-altitude data assimilation system experiments for the northern summer mesosphere season of 2007, Journal of Atmospheric and Solar-Terrestrial Physics 71:531–551, 2009.
29 J.L. Lean, T.N. Woods, F.G. Eparvier, R.R. Meier, D.J. Strickland, J.T. Correira, and J.S. Evans, Solar extreme ultraviolet irradiance: Present, past, and future, Journal of Geophysical Research 116:A01102, doi:10.1029/2010JA015901, 2011.
30 J. Lei, J.P. Thayer, J.M. Forbes, E.K. Sutton, R.S. Nerem, M. Temmer, and A.M. Veronig, Global thermospheric density variations caused by high-speed solar wind streams during the declining phase of solar cycle 23, Journal of Geophysical Research 113:A11303, doi:10.1029/2008JA013433, 2008.
31 J.J. Lean, J.D. Huba, S.E. McDonald, S. Slinker, D.P. Drob, J.T. Emmert, R.R. Meier, J.M. Picone, G. Joyce, J. Krall, A. Stephan, et al., Integrating the Sun-Earth System for the Operational Environment (ISES-OE), pp. 244-245 in NRL Review 2010, Naval Research Laboratory, Washington, D.C., 2011.
Physical models are much more computationally intensive than empirical models, and they utilize discrete grids to solve the fluid equations. Therefore, their use in orbit propagation will require interpolation of the gridded density predictions to each object’s trajectory.32 This difference in the application of physical and empirical models does not constitute a significant advantage for either approach; after all, astrodynamics implementations of the J70 empirical model originally interpolated among pre-computed lookup tables.33
Although physics-based forecasting systems will likely outperform empirical models in the future, physical models currently predict neutral density with accuracy similar to that of empirical models.34 Even after physical modeling systems improve, empirical models will still play important roles in thermospheric specification. There is considerable room for improvement of empirical models; for example, several climatological features associated with ion-neutral interactions and atmospheric tides are currently not captured by empirical models.35 The development of both physical and empirical models would be facilitated if the input data to HASDM were made available to the scientific community.
Mass density is the atmospheric variable most relevant to orbit prediction, but winds may also need to be considered, particularly for precision orbit and reentry applications. Winds are currently neglected in operational orbit prediction; a co-rotating atmosphere (i.e., zero winds in the rotating reference frame) is instead assumed. Average global wind patterns are now fairly well understood, and their inclusion in drag force models may improve performance. Wind speeds are typically 100-200 m/s, and can reach up to 800 m/s during severe geomagnetic storms. Such speeds are a non-negligible fraction of LEO orbital velocities.
Finally, accurate characterization of unmodeled density variance will likely be needed to obtain realistic position covariance in the high-drag regime. This is particularly true for suborbital and reentry altitudes, where strong vertical variability in density and wind (typically 50 percent and 150 m/s, respectively) contribute to large uncertainties in reentry predictions.36,37 To date, density covariance has received little research attention. Development and application of reliable density covariance estimates may prove challenging, given the complicated temporal and spatial coherence of density model errors.
Finding: AFSPC has made some key improvements in density modeling, but there is a need for continued research to more accurately model the atmosphere to improve the orbit predictions for satellites experiencing drag. Progress will likely require advances in both empirical and physics-based modeling.
Although many forces are important when considering high-precision orbit applications, all perturbations combined are generally less than 1 part in 1,000 compared to the dominant spherical Earth term. However, accurately modeling these perturbations is critical to the JSpOC mission. Among the most important perturbations are nonspherical gravity, luni-solar gravitational perturbations, atmospheric drag, solar radiation pressure, and propulsion. AFSPC astrodynamics algorithms deal effectively with most of these forces in the context of current space catalog operations, but the future environment will require improved force models. In some cases, faster and more accurate force models could enable operational solutions to previously intractable problems. However, all terms in the spacecraft equations of motion should be considered when seeking improvements in accuracy, computational speed, or both. Examples of small but well-known forces that are considered less relevant include Earth radia-
![]()
32 T.J. Fuller-Rowell, “Thermosphere Modeling Challenges,” presentation to the Committee for the Assessment of the U.S. Air Force’s Astrodynamic Standards on February 7, 2012.
33 L.G. Jacchia, New Static Models of the Thermosphere and Exosphere with Empirical Temperature Profiles, SAO Special Report 313, Smithsonian Astrophysical Observatory, Cambridge, Mass., 1970.
34 T.J. Fuller-Rowell, “Thermosphere Modeling Challenges,” presentation to the Committee for the Assessment of the U.S. Air Force’s Astrodynamic Standards on February 7, 2012.
35 T.J. Fuller-Rowell, “Thermosphere Modeling Challenges,” presentation to the Committee for the Assessment of the U.S. Air Force’s Astrodynamic Standards on February 7, 2012.
36 T.J. Fuller-Rowell, “Thermosphere Modeling Challenges,” presentation to the Committee for the Assessment of the U.S. Air Force’s Astrodynamic Standards on February 7, 2012.
37 Omitron, Inc., Fiery Dragon Final Report, September 30, 2008, Beltsville, Md.
tion and third-body gravity due to bodies other than the Sun and Moon. The section is organized according to the general distinction of nongravitational versus gravitational models.
A limiting factor for catalog maintenance is the modeling and estimation of nongravitational forces acting on objects in orbit. There are two main nongravitational effects that impact orbital motion: atmospheric drag and solar radiation pressure (SRP). Computation of atmospheric drag requires knowledge of atmospheric density, composition, and wind (see previous section), as well as the shape, mass, and external composition of the object. Although the drag force is typically small compared to other perturbations, it is a nonconservative force whose orbital effects accrue over time. Drag and SRP have significantly different physical representations and attendant models, although they are loosely linked through the object’s average area to mass ratio. Current practice in the general perturbation (GP) catalog is to use a single ballistic parameter to account for nongravitational forces, not only ignoring the different physics that may be acting on these bodies but also using one parameter to capture multiple perturbations. Although the special perturbations catalog has parameters that distinguish between drag and SRP, the models used for capturing these effects are simple and do not take into account the satellite attitude, shape, or other properties. Simple additions to the models used in orbit determination and propagation could improve and impact the overall quality of orbit fits and predictions.
The research community has been pursuing alternative modeling and estimation techniques for objects’ nongravitational forces across a range of different approaches. These include, for example, incorporation of dynamic fit spans and time series methods that have been developed within AFSPC, use of extended Kalman filters with imposed stochastic accelerations,38,39 development of multi-dimensional nongravitational models that more accurately capture the interaction of an object with the environment (including the effects of atmospheric composition and winds), and the inclusion of coupling between estimates of an object’s attitude and its orbit estimation process.40,41,42
To a significant degree, improvement of nongravitational drag force models in the catalog is a limiting factor for ephemeris improvement. Although there have been significant advances in modeling the upper atmospheric density, these improved density models are ultimately only as good as the nongravitational models used to predict their interaction with objects. Thus, improvements in estimation accuracy will require modeling improvements to both the specific object and the environment. Rigorous evaluation of different approaches for improving the existing simple nongravitational drag models, and their eventual incorporation into the catalog model and the object database, will yield significant improvements in orbit precision.
For satellites at higher altitudes, and especially at geostationary orbit (GEO), the solar radiation pressure effects become the dominant nongravitational force. For example, the estimation and prediction accuracy of GPS satellites is currently limited by the fidelity of their SRP models.43,44 In the GEO realm, the recently discovered high area-to-mass ratio objects are thought to have SRP forces that vary significantly because of their changing spin
![]()
38 J. Wright and J. Woodburn, “Simultaneous real-time estimation of atmospheric density and ballistic coefficient,” Paper AAS 04-175, AAS/AIAA Spaceflight Mechanics Meeting, 2004.
39 J. Wright, “Nonlinear variable lag smoother,” Paper AAS 08-303, 2008/01 AAS/AIAA Spaceflight Mechanics Meeting, Galveston, Tex., 2008, available at http://www.agi.com/resources/user-resources/downloads/white-paper.aspx?id=64.
40 M. Ziebart, Generalized analytical solar radiation pressure modeling algorithm for spacecraft of complex shape, Journal of Spacecraft and Rockets 41(5):840-484, 2004.
41 J. McMahon and D.J. Scheeres, New radiation pressure force model for navigation, Journal of Guidance, Control and Dynamics 33(5):1418-1428, 2010.
42 M.D. Pilinski, B.M. Argrow, and S.E. Palo, Drag coefficients of satellites with concave geometries: Comparing models and observations, Journal of Spacecraft and Rockets 48(2):312-325, 2011.
43 T. Springer, G. Beutler, and M. Rothacher, A new solar radiation pressure model for GPS satellites, GPS Solutions 2(3):50-62, 1999.
44 Y.E. Bar-Sever, New and Improved Solar Radiation Pressure Models for GPS Satellites Based on Flight Data, Technical Report, Jet Propulsion Laboratory, Pasadena, Calif., 1997.
|
TABLE 2.2 Gravity Perturbation Terms in Descending Order of General Importance |
|||
| Terms | SGP4 | SP | Future Considerations |
| 1. Low-order nonspherical Earth perturbations | x | x | x |
| 2. Third-body perturbations due to Sun and Moon | x | x | x |
| 3. Low-order solid and ocean tides | x | x | |
| 4. High-order nonspherical Earth perturbations | xa | x | |
| 5. High-order solid and ocean tides | x | ||
| 6. General relativity perturbations | x | ||
| aCurrent operational SP uses a “medium”-order level of fidelity. | |||
dynamics or shape deformations. Long-term prediction of these objects is a significant challenge for developing a robust and accurate catalog of all objects in GEO.45,46
Gravity is the dominant force in astrodynamics. Aside from drag, SRP, and propulsion, all major perturbations relevant to the space catalog are gravitational. The primary gravity-related terms are separated according to approximate importance in Table 2.2. Although the specifics are considered beyond the scope of the current study, detailed analyses regarding perturbations and their relative importance in the context of the Earth environment are provided in the literature.47
Gravity perturbation terms are well understood and can be modeled with extreme precision for any object. Practical limitations on fidelity are imposed by (1) computational burdens and (2) effective saturation (i.e., diminishing returns compared to uncertainty in nongravitational forces). While the latter limitation can be remedied in part with improved nongravitational force models, the former can be remedied with modern computational strategies such as parallel computing and flexible hardware and software implementations.
First-generation software for space catalog applications relied primarily on analytic theories for averaged spacecraft motion, due to computational limitations. At the time, significant efforts were required to include the averaged effects of low-order zonal coefficients and luni-solar perturbations (as well as drag) into the analytic theories that are encapsulated in SGP4.48,49 As computer speeds advanced and full numerical integration (SP) became feasible, it also allowed for more sophisticated and higher-order perturbation models. The current SP catalog utilizes a “medium” level of geopotential fidelity, with spherical harmonics typically truncated to degree and order 36 × 36. Low-order dynamic adjustments are also included to account for solid and ocean tides.
As computational capabilities and strategies continue to progress, future generations of SP models may benefit from a more complete treatment of gravitational modeling, including high-order geopotentials, high-order dynamic
![]()
45 T. Schildknecht, R. Musci, M. Ploner, G. Beutler, W. Flury, J. Kuusela, J. de Leon Cruz, and L. de Fatima Dominguez Palmero, Optical observations of space debris in GEO and in highly-eccentric orbits, Advances in Space Research 34(5):901-911, 2004.
46 L. Anselmo and C. Pardini, Long-term dynamical evolution of high area-to-mass ratio debris released into high earth orbits, Acta Astronautica 67(1-2):204-216, 2010.
47 In particular, interested readers are pointed to the following: Astrodynamics—Propagation Specifications, Technical Definitions, and Recommended Practices (American National Standard and American Institute of Aeronautics and Astronautics, ANSI/AIAA S-131-2010, 2010) and Figure 3.1 on p. 55 of O. Montenbruck and G. Gill, Satellite Orbits, Springer, New York, 2005; J.R. Vetter, Fifty years of orbit determination: Development of modern astrodynamics methods, Johns Hopkins APL Technical Digest 27(3), 2007; A. Rossi, The Earth orbital environment, in Encyclopedia of Aerospace Engineering, John Wiley & Sons, Ltd., Chichester, U.K., doi:10.1002/9780470686652.eae289, 2010.
48 F.R. Hoots, P.W. Schumacher, and T. DeVere, 50 years of satellite tracking and cataloging in the US, Advances in the Astronautical Sciences 129(Part 2):1251-1278, 2008.
49 F.R. Hoots, P.W. Schumacher, Jr., and R.A. Glover, History of analytical orbit modeling in the U.S. Space Surveillance System, Journal of Guidance Control, and Dynamics 27(2):174-185, doi:10.2514/1.9161, 2004.
adjustments due to solid and ocean tides, and possibly even general relativity terms, which are known to have nontrivial effects on long-term propagations.50,51
As an example, consider the batch least-squares orbit determination process, in which, by definition, all of the solve-for parameters are adjusted to minimize residuals. Like any least-squares problem, the parameters are only sensitive to the model provided and are transparent to the real physics of the problem. Any errors in the models are absorbed to the extent possible by all of the free parameters. The segmented ballistic coefficient, for instance, is loosely constrained and has a high degree of uncertainty, and is therefore particularly vulnerable to absorbing any types of modeling errors. Therefore in the current orbital determination process, any errors caused by the omission of high-degree and high-order gravity terms will be nonphysically absorbed into terms such as the ballistic coefficient, even though they minimize the residuals and result in state estimations that are satisfactory to current requirements. Therefore, in order to maximize the physics-based accuracy of critical solve-for parameters such as the ballistic coefficient, all of the well-understood gravity models in Table 2.2 should be considered with higher fidelity, subject to computational limitations. Note that the absorption of errors due to poor modeling may result in state estimations that meet current accuracy requirements for positions within the fit span. However, because of the incorrect solution, the accuracy may degrade rapidly upon propagation outside the fit span of the observations. Naturally, as computational strategies and capabilities advance and the nongravitiational force models mature, the argument supporting higher-fidelity gravity models (referring to all terms in Table 2.2) grows stronger.
Recent innovations in high-fidelity gravity modeling have demonstrated computational speeds up to two orders of magnitude faster than conventional methods, through the use of sophisticated interpolation methods and new formulations amenable to parallel evaluation.52,53,54,55,56,57,58 It is noted and applauded that some of these efforts have been and are currently being funded by the Air Force Office of Scientific Research for space situational awareness and future catalog maintenance purposes.
Finding: The development and use of higher-fidelity force models, both nongravitational and gravitational, will yield significant improvements to the current catalog accuracy. Incorporation of these new models will require fundamental changes within the existing trajectory propagation, orbit determination, and force evaluation algorithms.
DATA ASSOCIATION, TRAJECTORY PROPAGATION, AND ORBIT DETERMINATION
Two key problems in tracking multiple space objects are those of data association and fusion of information. Given a collection of reports (measurements, sensor tracks), the data association problem is that of determining which sequence of reports emanate from a common object and which are false reports or uncorrelated tracks. Said in another way, the data association problem is that of partitioning a collection of reports into (1) tracks or orbits and (2) false reports or uncorrelated tracks. Given the solution of the association problem, the information fusion
![]()
50 American National Standard, American Institute of Aeronautics and Astronautics, Astrodynamics—Propagation Specifications, Technical Definitions, and Recommended Practices, ANSI/AIAA S-131-2010, 2010.
51 International Earth Rotation and Reference Systems Service, IERS Conventions (2010) (G. Petit and B. Luzum, eds.), IERS Technical Note 36, Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt am Main, 2010.
52 J.L. Junkins, Investigation of finite-element representations of the geopotential, AIAA Journal 14(6):803-808, 1976.
53 G. Beylkin and R. Cramer, Toward multiresolution estimation and efficient representation of gravitational fields, Celestial Mechanics and Dynamical Astronomy 84(1):87-104, 2002.
54 B.A. Jones, G.H. Born, and G. Beylkin, Comparisons of the Cubed-Sphere Gravity Model with the spherical harmonics, Journal of Guidance, Control, and Dynamics 33(2):415-425, 2010.
55 A. Colombi, A.H. Hirani, and B.F. Villac, Adaptive gravitational force representation for fast trajectory propagation near small bodies, Journal of Guidance, Control, and Dynamics 31(4):1041-1051, 2008.
56 R.P. Russell and N. Arora, Global point mascon models for simple, accurate and parallel geopotential computation, Journal of Guidance, Control, and Dynamics, accepted February 2012.
57 N. Arora and R.P. Russell, A fast, accurate, and smooth planetary ephemeris retrieval system, Celestial Mechanics and Dynamical Astronomy 108(2):107-124, doi:10.1007/s10569-010-9296-0, 2010.
58 N. Arora and R.P. Russell, “Fast, efficient and adaptive interpolation of the geopotential,” Paper AAS 11-501, AAS/AIAA Astrodynamics Specialist Conference, Girdwood, Ark., August 2011.
problem is that of combining information associated with a common object from one or more sources to improve the state or understanding of the object.
While the current algorithms were sufficient to handle past needs, future demands will require new association and nonlinear estimation algorithms to aid in decision making by operators of the system. In addition to advanced computer architectures, the achievement of a robust system will require possible advances in data association methods, orbit propagation, orbit determination, bias estimation and mitigation, batch and nonlinear filtering methods, and report-to-orbit updates.
The data association method currently used in AFSPC algorithms is a nonstatistical fixed gated association method called ROTAS (Report Observation Association). ROTAS has worked well in the past for widely spaced objects in the space catalog and against a benign background. LEO breakups and GEO clusters require new classes of algorithms because objects can be closely spaced and the association can be ambiguous. Outside of the space catalog, the problem of associating uncorrelated tracks from one sensor to that of another or to the same sensor after multiple orbits is the problem of data association, which is considered to be the central problem in the general subject of multiple target tracking.59,60 Misassociation or cross-tagging also contributes to the degradation of covariance realism.61
Radar produces a short burst of measurements that are smoothed or filtered using a dynamic model. A sequence of (range, azimuth, elevation) measurements is then determined from the smoothed sensor track, resulting in statistically cross-correlated measurements. Right ascension and declination measurements are produced from the electro-optical sensors from which one can develop a sensor track consisting of two angles and angle rates. In addition to kinematic data, the association process should make use of features (e.g., radar cross section, intensity, brightness) and nontraditional data (multi-band photometry, radiometry), given the data-starved environment of space. The data association problem for space surveillance, then, is that of partitioning these measurements (or sensor tracks) into states and false reports or uncorrelated tracks (UCTs). Algorithms for solving the data association problem generally divide into two broad classes: single-frame and multiple-frame methods. Examples of single-frame methods include nearest neighbor and global nearest neighbor. The global nearest neighbor formulation is posed as a two-dimensional assignment problem and works well in light clutter and for reasonably spaced targets. The most successful of the multiple-frame methods are track-oriented multiple hypothesis tracking (MHT) including multiple-frame assignments and hypothesis-oriented MHT such as Reid’s original algorithm implemented as a sequential k-best, two-dimensional assignment algorithm.62,63,64,65 The survey by Blackman discusses several of the MHT algorithms currently in use.66 MHT methods mitigate misassociation or cross-tagging by holding difficult association decisions in abeyance until additional information is available, i.e., by providing the ability to improve current decisions by changing past ones.
While MHT methods have been in use over the past 30 years, they have begun to appear in actual systems only in the past 5 to 10 years. The development of advanced association methods such as MHT for space could address several challenges. MHT methods could be adapted to advanced computer architectures, e.g., paralleliza-
![]()
59 S. Blackman and R. Popoli, Design and Analysis of Modern Tracking Systems, Artech House, Boston, London, 1999.
60 A.B. Poore, Multidimensional assignment formulation of data association problems arising from multitarget tracking and multisensor data fusion, Computational Optimization and Applications 3:27-57, 1994.
61 O.E. Drummond, T.L. Ogle, and S. Waugh, Metrics for evaluating track covariance consistency, in SPIE Proceedings: Signal and Data Processing of Small Targets 2007, Volume 6699, SPIE, Bellingham, Wash., 2007.
62 S. Blackman and R. Popoli, Design and Analysis of Modern Tracking Systems, Artech House, Boston, London, 1999.
63 S.S. Blackman, Multiple hypothesis tracking for multiple target tracking, IEEE A & E Systems Magazine 19(1):5-18, 2004.
64 A.B. Poore, Multidimensional assignment formulation of data association problems arising from multitarget tracking and multisensor data fusion, Computational Optimization and Applications 3:27-57, 1994.
65 I. Cox and S. Hingorani, An efficient implementation and evaluation of Reid’s multiple hypothesis tracking algorithm for visual tracking, pp. 437-442 in Proceedings of the International Conference on Pattern Recognition, Institute of Electrical and Electronics Engineers, Inc., New York, 1994.
66 S.S. Blackman, Multiple hypothesis tracking for multiple target tracking, IEEE A & E Systems Magazine 19(1):5-18, 2004.
tion, with a focus on control of the computational costs for these architectures. The use of all available data including kinematic, feature, and nontraditional data is essential to disambiguate the association process when needed. Finally, the association methods themselves should be adapted to the complexity of the problem. For widely spaced objects, simple methods such as nearest neighbor should be used whereas for LEO breakups and GEO clusters, a full MHT algorithm may be required.
Finding: Advanced data association methods such as multiple hypothesis tracking will produce a significant improvement in the automation of the space surveillance system, including the sensor processing. The algorithms should be adapted to high-performance computing and advanced computer architectures and should make use of kinematic, feature, and nontraditional data.
Efficient orbital propagators are critical for space situational awareness because they drive uncertainty propagation, which is necessary for tracking, conjunction analysis, and anomaly detection. The current AFSPC SP orbital propagator utilizes a Gauss-Jackson method.67 Many comparisons have been made over the years between such explicit schemes as Dormand-Prince (8/7), Runge-Kutta-Nystrom (12/10), Adams-Bashforth-Moulton, and Gauss-Jackson.68 Considerable experience with the Gauss-Jackson method on different types of orbits has led to a good balance between performance and accuracy. (For example, the classic Sundman transformation in which the independent variable is changed to ![]() can lead to good performance across a broad range of eccentricities.) While there are differences in these methods, the differences in accuracy and performance have not warranted a change in the orbital propagator, primarily because more significant improvements in accuracy have come from improvements in the force models.
can lead to good performance across a broad range of eccentricities.) While there are differences in these methods, the differences in accuracy and performance have not warranted a change in the orbital propagator, primarily because more significant improvements in accuracy have come from improvements in the force models.
Looking to the future in which advanced computer architectures (parallelized processing, multiple cores, GPUs; see details in a later section) will play a dominant role and in which the propagation of realistic uncertainty (e.g., covariance) will receive greater emphasis, new methods for orbit propagation may prove especially beneficial and even necessary. For example, certain subsets of implicit Runge-Kutta (IRK) methods (1) are highly parallelizable, (2) have variants that are symplectic (i.e., a special class of integrators for Hamiltonian systems that can also be used for nonconservative dynamical systems), (3) can be used with or without error step-size control, (4) have strong stability properties, (5) can provide extreme accuracy even for large step sizes such as a quarter of an orbit, and (6) can be more efficient than the above explicit methods, especially for orbital propagation. Another promising and parallelizable method for orbit propagation is that of modified Chebyshev-Picard iteration (MCPI).69,70,71,72,73 Implicit methods are also appealing because they can use analytic and perturbation techniques such as Keplerian dynamics, J2 gravity, and possibly even GP or SGP4 to warm-start the required iterations, thereby further reducing the computational cost of orbit propagation. (Analytic methods are further discussed below.) Although these are all good reasons to consider such a new class of orbital propagators, the real benefit may lie in the future need to propagate uncertainty using nonlinear transformations from, for example, unscented Kalman filters, higher-order
![]()
67 M.M. Berry and L.M. Healy, Implementation of Gauss-Jackson integration for orbit propagation, Journal of the Astronautical Sciences 52(3):331-357, 2004.
68 O. Montenbruck and E. Gill, Satellite Orbits, Springer, New York, 2005.
69 X. Bai (Advisor John L. Junkins), “Modified Chebyshev-Picard iteration methods for solution of initial and boundary value problems,” Dissertation, Texas A&M University, August 2010, available at http://repository.tamu.edu/bitstream/handle/1969.1/ETD-TAMU-2010-08-8240/BAI-DISSERTATION.pdf.
70 J.C. Butcher, Numerical Methods for Ordinary Differential Equations, 2nd. ed., John Wiley & Sons, Inc., New York, 2008.
71 G. Beylkin and K. Sandberg, “ODE Solvers Using Bandlimited Approximations,” preprint, 2012; available from B.K. Bradley, University of Colorado, Boulder.
72 B.K. Bradley, B.A. Jones, G. Beylkin, and P. Axelrad, “A New Numerical Integration Technique in Astrodynamics,” Paper 12-216, 22nd Annual AAS/AIAA Space Flight Mechanics Meeting, Charleston, S.C., January 29-February 2, 2012, available at http://ccar.colorado.edu/geryon/papers/Conference/bradley_2012a.pdf.
73 E. Hairer, C. Lubich, and G. Wanner, Geometric Numerical Integration: Structure-preserving Algorithms for Ordinary Differential Equations, Volume 31, Springer Series in Computational Mathematics, Springer, New York, 2006, Chapter 6.
Gauss-Hermite filters, polynomial chaos expansions, or possibly even the particle filter for special cases.74 Owing to their implicit formulation, IRK and MCPI methods have the potential to significantly improve the accuracy and efficiency of these nonlinear transformations for the propagation of uncertainty.
Finding: Future computational demands such as the characterization of uncertainty and use of high-fidelity models may require the development and use of fast and accurate ordinary differential equation propagators that take advantage of advanced computer architectures and parallel formulations.
Statistical Initial Orbit Determination
Currently, initial orbits (sensor tracks) are generated by starting from an initial approximation such as Gooding’s method for electro-optical and the Lambert-Gauss method for radar followed by a Batch Differential Correction (BATCHDC) optimization procedure to recover sensor track states from a small number of sensor measurements. The smoothed state and its (osculating) covariance are used to estimate the initial orbit. The covariance is sometimes inflated a posteriori to address the uncertainty in the measurement noise by a factor that is proportional to the square of the residual of the weighted least-squares estimate.75 Achieving covariance realism at this stage is difficult, but is fundamentally important because the covariance is used in updating the tracks, achieving the correct association of report to tracks, conjunction analysis, and maneuver detection.76 Indeed, the user community is trying to improve the covariance using inflation where appropriate. If achieving covariance realism is not possible, a measure of confidence or uncertainty in the covariance is highly desirable.
The problem of determining an estimate of the state of an object given a few measurements is generally posed as that of a weighted nonlinear least-squares problem.77 (Such procedures often ignore process noise in the batch formulation, but it can be included as demonstrated in the book by Jazwinski.78) Since a limited number of measurements is used in the state estimation, the estimates of the state can sometimes be of low accuracy, and the estimates of the covariance matrix can sometimes be misrepresented. (The process of estimating the covariance can also be numerically unstable because of observability of the state, which in turn can arise from the lack of time and geometric diversity in the measurements.) Other algorithms for batch estimation such as a full Newton method or hybrid methods along with a globalization technique, e.g., line search or trust region method, might improve the convergence or the covariance matrix. As part of these procedures, numerical linear algebra methods can be used to identify observability issues.
Finding: Current methods such as BATCHDC already provide reasonable estimates of the state. In addition to the state estimate, improvements in the batch estimation formulation and algorithms may improve the overall system-level uncertainty (e.g., covariance) realism.
It is worth noting that, despite the clear direction of the community toward high-fidelity special perturbations methods, the committee sees value in continued support, research, and development of analytic and semi-analytic methods. After all, the analytic methods and their innovators bootstrapped the catalog maintenance problem “out of whole cloth,” thereby setting precedence for, enabling the solution to, and still influencing most of the processes
![]()
74 B.A. Jones, A. Doostan, and G.H. Born, Nonlinear propagation of orbit uncertainty using non-intrusive polynomial chaos, Journal of Guidance, Control, and Dynamics, accepted April 2012.
75 D.M. Bates and D.G. Watts, Nonlinear Regression Analysis and Its Applications, John Wiley & Sons, Inc., New York, 1988.
76 D.A. Vallado and J.H. Seago, “Covariance realism,” Paper AAS 09-304, presented at the AAS/AIAA Astrodynamics Specialist Conference, Pittsburgh, Pa., August 9-13, 2009.
77 B.D. Tapley, B.E. Schutz, and G.H. Born, Statistical Orbit Determination, Elsevier Academic Press, Burlington, Mass., 2004.
78 A.H. Jazwinski, Stochastic Processes and Filtering Theory, Academic Press, New York, 1970.
still in place today.79 Aside from organizational inertia and the associated need for users to maintain backwards compatibility, analytic (GP) methods provide significant insight into the dynamics of the spacecraft problem that are simply unavailable to pure numerical (SP) methods.
GP methods use transformation methods (e.g., variable transformations and averaging theories) to produce solutions that are qualitatively accurate over long time spans, while SP models use full dynamics to produce solutions that are quantitatively accurate over short time spans.80 Accordingly, very long term predictions are not usually done with conventional SP methods, because their errors accumulate with propagation time (although certain classes of symplectic integrators can, under certain conditions, preserve important quantities such as the Hamiltonian).81 The GP methods rely on averaged dynamics, for which the individual effects of perturbations (nongravitational and gravitational) can be isolated and understood, providing dynamical insight into the secular, short-period and long-period variations.82,83,84,85,86,87,88 The spacecraft equations of motion are formed in orbit element space where the generating potentials can be averaged over the fast-moving variables (such as mean anomaly) in order to isolate the more important secular components. The averaged potentials can in some cases lead to a complete reduction of the system to quadratures, revealing equilibrium points as saddles and extrema in the middle of circulating flows in the reduced space. Vital information about both local and global stability of the design space can be gleaned using analytic techniques. Furthermore, the use of modern algebraic manipulation tools can provide high-order analytic theories that were impossible to produce in decades past. Such high-order methods and other analytic innovations can provide insight and benefit to a variety of future astrodynamics space situational awareness tasks.89,90,91,92,93,94 It is therefore imperative that the astrodynamics community and AFSPC maintain their expertise, familiarity with, and continued support for analytic theories (in the context of both operations and theoretical development) in order to meet future needs.
![]()
79 F.R. Hoots, P.W. Schumacher, and T. DeVere, 50 years of satellite tracking and cataloging in the US, Advances in the Astronautical Sciences 129(Part 2):1251-1278, 2008.
80 M.M. Berry and L.M. Healy, Implementation of Gauss-Jackson integration for orbit propagation, Journal of the Astronautical Sciences 52(3):331-357, 2004.
81 J. Wisdom and M. Holman, Symplectic maps for the n-body problem, The Astronomical Journal 102(4):1528, 1991.
82 M. Ziebart, Generalized analytical solar radiation pressure modeling algorithm for spacecraft of complex shape, Journal of Spacecraft and Rockets 41(5):840-484, 2004.
83 J. McMahon and D.J. Scheeres, New radiation pressure force model for navigation, Journal of Guidance, Control and Dynamics 33(5):1418-1428, 2010.
84 R. Broucke, Long-term third-body effects via double averaging, Journal of Guidance, Control, and Dynamics 26(1):27-32, doi:10.2514/2.5041, 2003.
85 J.F. Palacian, M. Lara, R.P. Russell, Averaging and mission design: The paradigm of Enceladus, Celestial Mechanics and Dynamical Astronomy 108(1):1-22, doi:10.1007/s10569-010-9286-2, 2010.
86 M. Paskowitz Possner and D.J. Scheeres, Control of science orbits about planetary satellites, Journal of Guidance, Control and Dynamics 32(1):223-231, 2009.
87 S. Coffey, A. Deprit, É. Deprit, and L. Healy, Painting the phase space portrait of an integrable dynamical system, Science 247:833-836, 1990.
88 S. Coffey, A. Deprit, and É. Deprit, Frozen orbits for satellites close to an Earth-like planet, Celestial Mechanics and Dynamical Astronomy 59(1):37-72, 1994.
89 R.H. Battin, An Introduction to the Mathematics and Methods of Astrodynamics, American Institute of Aeronautics and Astronautics, New York, 1987, p. 483.
90 R.S. Park and D.J. Scheeres, Nonlinear semi-analytic methods for trajectory estimation, Journal of Guidance, Control and Dynamics 30(6):1668-1676, 2007.
91 K. Fujimoto, D.J. Scheeres, K.T. Alfriend, Analytical nonlinear propagation of uncertainty in the two-body problem, Journal of Guidance, Control and Dynamics 35(2):497-509, doi:10.2514/1.54385, 2012.
92 D.W. Gim and K.T. Alfriend, State transition matrix of relative motion for the perturbed noncircular reference orbit, Journal of Guidance, Control, and Dynamics 26(6):956-971, 2003.
93 D.A. Danielson, C.P. Sagovac, B. Neta, and L.W. Early, Semianalytic Satellite Theory, Research Report, Mathematics Department, Naval Postgraduate School, 1995, available at http://www.dtic.mil/cgi-bin/GetTRDoc?Location=U2&doc=GetTRDoc.pdf&AD=ADA531136.
94 B. Weeden and P. Cefola, “Computer systems and algorithms for space situational awareness: History and future development,” paper presented at the 12th International Space Conference of Pacific-basin Societies (ISCOPS), July 27-30, 2010, Montreal, Quebec, Canada, 2010, available at http://swfound.org/resource-library/space-situational-awareness.
Finding: Analytic theories will continue to be important for both operations and theoretical development in order to meet future needs.
Insights from Modern Dynamical Systems
While advances coming from several disciplines, such as physics, programming, computer technology, and others, have been incorporated into determining the dynamics of orbits, a striking omission is that this study of the dynamics of objects does not employ the significant progress that has been made in dynamical systems. Instead, the level of the analysis of the dynamics is essentially the same as known during the formative years of the 1960s. All of this earlier work predates the breakthroughs (starting in the late 1970s) that have completely changed how nonlinear dynamics and chaotic systems are treated and analyzed. That the advantages of these new approaches have not even been explored by AFSPC was supported by responses when people testifying were queried; without exception, the answer was no. Furthermore, there is a clear lack of awareness of the experts at AFSPC even of the existence of this literature and the advantages it could provide.
Other areas of astrodynamics have benefited tremendously from the incorporation of dynamical systems theory and principles. A recent highlight includes space mission design to the Earth-Sun and Earth-Moon libration points. The connections between the abstract theory of dynamical systems and practical and applied spaceflight have yielded an expansive growth in the ability to design (previously undiscovered) efficient and practical transfers within a highly perturbed, multi-body environment.95,96,97
There are excellent reasons to accept that the dynamics of satellite systems experience chaotic effects. Evidence comes from the fact that observed behavior strongly mimics standard and expected predictions of chaotic dynamical systems. As illustrations, orbits starting from very similar settings can experience dissimilar dynamical futures, predicted and actual orbits can diverge, and covariance and other means of predicting the likelihood of conjunction can vary in unexpected ways. These traits are expected from nonlinear systems, and are observed in satellite systems.
Adding support to the expectation that these orbits have chaotic behavior is that chaotic systems typically are characterized by dynamics that experience:
• Expansion (i.e., nearby orbits can separate) and
• Recurrence effects (i.e., they repeat).
That satellite systems have a dynamic recurrence is obvious. The expansion can be caused by drag, the nonspherical shape of objects, inhomogeneous gravitational forces (e.g., the oblateness of the Earth), and practically all effects that affect satellite behavior. These features—expansion and recurrence—are common in essentially all N-body systems, and so most of these systems must be expected to exhibit these chaotic behaviors; moreover, celestial mechanics is precisely the area where the discovery of chaotic behavior was first made in the late 19th century.
Value added by incorporating the newly developed ways to analyze dynamical systems can be expected to create new insights leading to different ways to understand and predict the structure of these orbits. As just one example, characteristics of nonlinear systems, which permit orbits to spread in unexpected ways, suggest that the standard covariance approach used to determine the likelihood of conjunction must be reexamined.
An unfortunate fact, which reflects a shortcoming in STEM education, is that courses and appropriate books needed to learn the fundamentals of modern dynamical systems are not readily available. Until and unless a program is developed to solve this issue, such as AFSPC creating such courses, or placing pressure on university systems to do so, it is unrealistic to expect current AFSPC personnel to adopt these mathematical approaches.
![]()
95 R.W. Farquhar, D.P. Muhonen, D.L. Richardson, Mission design for a halo orbiter of the Earth, Journal of Spacecraft and Rockets 14(3):183-188, 1977.
96 G. Gomez, J. Llibre, R. Martinez, and C. Simo, Dynamics and Mission Design Near Libration Points, Volumes 1-4, World Scientific Monograph Series in Mathematics, World Scientific Publishing Co., Singapore, 2001.
97 K.C. Howell, B.T Barden, M.W. Lo, Application of dynamical systems theory to trajectory design for a libration point mission, Journal of the Astronautical Sciences 45(2):161-178, 1997.
Until then, and because something must be done to handle the escalating nature of these problems, one approach toward achieving longer-term advances would be to encourage collaboration between experts in astrodynamics and academic experts in dynamical systems.98
Finding: While advances coming from a variety of disciplines, such as physics, programming, computer technology, and others, have been incorporated into the dynamics of orbit determination, a notable omission involves a use of advances that have been made in the area of dynamical systems. One challenge in the use of these techniques is to develop more efficient algorithms, e.g., to perform data association and state estimation.
UNCERTAINTY REPRESENTATION AND COMPUTATION
Knowledge of the state (e.g., position and velocity) of a resident space object always contains a degree of uncertainty. As described in the section on modern dynamics, a portion of this uncertainty can be attributed to features of the underlying dynamical system. The goal of providing an accurate and truthful representation of the state uncertainty is the objective of uncertainty characterization and management and is essential in the problems of data association (correlation), especially in LEO breakups and GEO clusters, conjunction analysis, maneuver/anomaly detection, and sensor management. If the uncertainty is properly characterized, one can then attempt to manage the uncertainty by tasking which sensors to view which objects within the field of view of the sensors up to the limits of the information and availability of sensor coverage.
For Gaussian or nearly Gaussian processes, uncertainty is represented through a covariance matrix. The term “covariance realism” is then used to express the accurate representation of the uncertainty, i.e., that the covariance matrix has the right size and shape, in a statistical sense.99 For many objects in the space catalog that receive periodic updates, a Gaussian random variable can properly represent the state and uncertainty in such an object over many orbits. In these cases, achieving covariance realism is the goal. For other objects, especially UCTs or objects for which few updates have been received due to the data-starved environment of space, a more complete description of the uncertainty in the form of the true probability density function may be needed for the non-Gaussian processes. Drummond has identified seven reasons why covariances degrade in tracking systems.100 Based on this list, here is a brief summary of the issues that should be addressed when trying to achieve uncertainty (e.g., covariance) realism for space surveillance:
1. Proper characterization of the uncertainty of the input data for measurements, including the lack of whiteness, features, and nontraditional data;
2. Compensation for residual biases, bias drift between sensor calibrations, and time tags plus the correct representation of their covariances or uncertainty;
3. Compensation for missing data and for misassociations or cross-tagging;
4. Correct characterization of non-Gaussian probability density functions arising from nonlinear transformations such as nonlinear dynamics and coordinate transformations;
5. Correct characterization of errors in the model dynamics (e.g., atmospheric drag and solar radiation) and their uncertainty including process noise (sometimes called stochastic acceleration);
6. Well-designed numerical procedures that achieve robustness, thereby avoiding numerical round-off errors in the presence of simplified or incorrectly designed computations or ill-conditioned transformations; and
7. Hardware or software faults.
![]()
98 A large number of references can be found with a search of “chaos, satellites.” Also, there currently are a large number of introductory textbooks on nonlinear dynamics. Other references to provide a flavor are the following: J. Laskar, Large-scale chaos in the solar system, Astronomy and Astrophysics 287(1):L9-L12, 1994; and D.G. Saari and Z. Xia, Off to infinity in finite time, Notices of the AMS 42(5):538-546, 1995.
99 D.A. Vallado and J.H. Seago, “Covariance realism,” Paper AAS 09-304 presented at the AAS/AIAA Astrodynamics Specialist Conference, Pittsburgh, Pa., August 9-13, 2009, available at http://www.centerforspace.com/downloads/files/pubs/AAS%2009-304final.pdf.
100 O.E. Drummond, T.L. Ogle, and S. Waugh, Metrics for evaluating track covariance consistency, Signal and Data Processing of Small Targets 2007 6699:669916, 2007.
BOX 2.1
Illustration of the Uncertainty Characterization During Orbit Propagation
To provide an example of covariance degradation due to nonlinearity and to explain the difference between the extended Kalman filter (EKF), unscented Kalman filter (UKF), and an exact nonlinear transformation, consider the representation of uncertainty in Figure 2.1.1.
Figure 2.1.1(top) is a representation of an initial Gaussian in equinoctial orbital element space but plotted here on the semi-major axis–mean longitude plane. (The 1,000 particles are dispersed according to the level curves ranging from 0.5 to 3 sigmas in half sigma increments.) The initial orbit is circular and non-inclined with a semi-major axis of 7136.635 km, so that the instantaneous orbital period corresponds to exactly 1 hour and 40 minutes. The errors for the initial Gaussian are σa = 20 km, σh = σk = σp = σq = 10-3, σl = 36 arc-seconds. Although the range error of 20 km is extreme, it is not inconsistent with some cases seen in real data. Figure 2.1.1(bottom) illustrates the propagation of the three uncertainty representations through eight orbital periods using AFSPC’s Special Perturbations (SP) propagator. The true distribution, represented by the particles propagated through the eight orbital periods (13 hours and 20 minutes), is presented in the bottom portion of Figure 2.1.1, as are the propagated mean and covariances using the EKF and UKF transformations. The mean and covariance of the UKF were obtained by propagating the 13 sigma points but agree with those computed from the probability density function (PDF) represented by the particles. The covariance from the UKF is consistent or realistic in the sense that it agrees with that computed from the definition of the true PDF. The same is true of the mean; however, the mean is displaced from the mode of the PDF, and the covariance does not represent the uncertainty in the true PDF. The EKF, on the other hand, provides a good representation of the mode, but the covariance tends to collapse, making inflation necessary to begin to cover the uncertainty. In neither case does the covariance accurately model the uncertainty. One can argue, and rightly so, that the example presented is an extreme one with the standard deviation σa = 20 km. On the other hand, similar results occur after 7 days and 100 orbital periods when the semi-major axis standard deviation is reduced to a more realistic 1 km. In this case, the covariance remains valid over 50 orbits or so; however, it also degrades in due course. This example illustrates the problem of using covariances to represent the uncertainty and suggests that a better representation of the probability density function is needed if one is to achieve statistically robust characterization of uncertainty, which again is fundamental to achieving a robust capability across the Space Surveillance Network.
FIGURE 2.1.1 Top: Initial Gaussian representation of uncertainty with 1,000 particles. Bottom: Propagated uncertainty using an extended Kalman filter (EKF), an unscented Kalman filter (UKF), and an exact filter. SOURCE: Courtesy of Numerica Corporation.
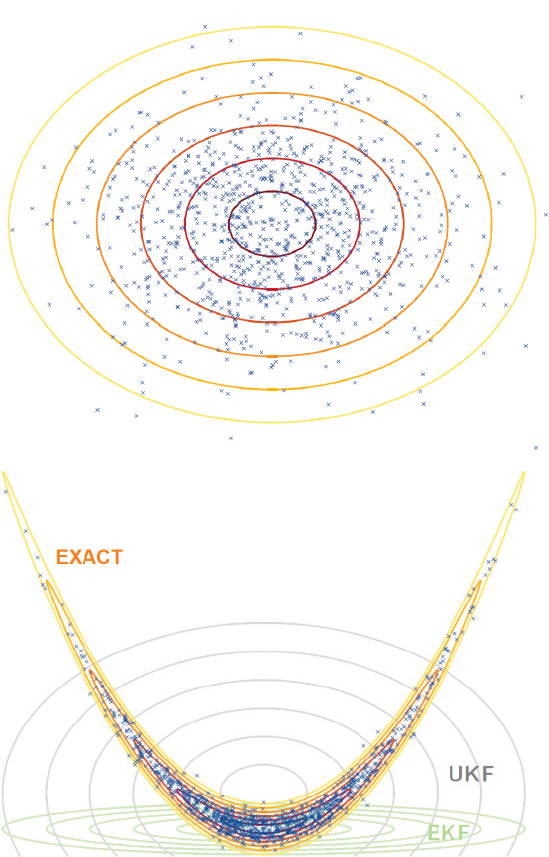
As noted above, the covariance matrix may be sufficient to characterize the uncertainty for some objects in the space catalog, whereas a more complete approximation to the true probability density function may be needed in other cases such as during orbital propagation. An example that demonstrates the need to think beyond standard Gaussian distributions and covariance matrices in the representation of uncertainty is provided in Box 2.1. This example also demonstrates the deficiencies in the extended Kalman filter and the unscented Kalman filter for space surveillance. Similar examples can be found in the literature.101,102,103,104 The case for improved understanding and treatment of the sensor error characterization (random and bias errors) with the goal of improving covariance realism in the orbit determination is made below. While uncertainty in some of the parameters in the nonlinear dynamic models is often addressed statistically through a consider analysis and process noise as stressed in issue number five (5) above, nonstatistical errors in the modeling of the dynamic forces on a body also play a part in the uncertainty characterization of space objects.
Nonlinear Estimation and Filtering
Given the correct association of sensor measurements to a track, the problem of fusing this information with the track to obtain an updated estimate of the track is generally posed as either (1) a general Bayesian nonlinear filtering problem augmented by smoothing or (2) a batch estimation in the form of a weighted nonlinear least-squares problem discussed above. Batch estimation methods are robust if they converge, but are more computationally intensive than filtering methods. The various options for potential improvement are listed above. As indicated below, filtering methods require a complete and realistic probability density function of the state to start the sequential process, while batch estimation can be used even when the state probability density function is ill-conditioned. Indeed, the observability of the state can be determined as part of the solution. The connection between these two approaches, namely, differential corrections (or the Gauss Newton method) and filtering and smoothing, is provided in the paper by Bell.105
For the propagation of uncertainty, the extended Kalman filter is often used; however, the unscented Kalman filter should also be considered.106,107 As illustrated in Figure 2.1.1, more general nonlinear filtering methods are needed that can more closely approximate the evolution of the true probability density function. (The example in Box 2.1 illustrates the pros and cons of the extended Kalman, unscented Kalman, and an exact filter in an orbital propagation scenario.) Ultimately, the Fokker-Planck equation is the correct formulation; however, its computational cost is too high, except in special cases. The use of coordinate systems, such as the equinoctial orbital elements in which the dynamics are less nonlinear than Earth-centered inertial (ECI) coordinates, can extend the time that “covariance realism” can be maintained under orbital propagation.108,109,110 Alternately, Gaussian sum filters, higher order extended and unscented Kalman filters, higher-order Gauss-Hermite filters, and possibly even
![]()
101 J. Junkins, M. Akella, and K. Alfriend, Non-Gaussian error propagation in orbital mechanics, Journal of the Astronautical Sciences 44(4):541-563, 1996.
102 D. Giza, P. Singla, and M. Jah, “An approach for nonlinear uncertainty propagation: Application to orbital mechanics,” Paper AIAA-2009-6082, AIAA Guidance, Navigation, and Control Conference, Chicago, Ill., August 10-13, 2009, American Institute of Aeronautics and Astronautics, Reston, Va.
103 R.S. Park and D.J. Scheeres, Nonlinear mapping of Gaussian statistics: Theory and applications to spacecraft trajectory design, Journal of Guidance, Control, and Dynamics 29(6):1367-1375, 2006.
104 B.M. Bell, The iterated Kalman smoother as a Gauss-Newton method, SIAM Journal of Optimization 4(3):626-636, 1994.
105 B.M. Bell, The iterated Kalman smoother as a Gauss-Newton method, SIAM Journal of Optimization 4(3):626-636, 1994.
106 S.J. Julier, J.K. Uhlmann, and H.F. Durant-Whyte, A new method for the nonlinear transformation of means and covariances in filters and estimators, IEEE Transactions on Automatic Control 55:477-482, 2000.
107 S. Särkkä, On unscented Kalman filtering for state estimation of continuous-time nonlinear systems, IEEE Transactions on Automatic Control 52(9):1631-1641, 2007.
108 J. Junkins, M. Akella, and K. Alfriend, Non-Gaussian error propagation in orbital mechanics, Journal of the Astronautical Sciences 44(4):541-563, 1996.
109 F.R. Hoots, “Satellite location uncertainty prediction,” Paper AAS 11-579, 2011 Astrodynamics Specialist Conference, Girdwood, Ala., July 31-August 3, 2011, available at http://www.univelt.com/AASPapers.
110 J.T. Horwood, N.D. Aragon, and A.B. Poore, Gaussian sum filters for space surveillance: Theory and simulations, Journal of Guidance, Control and Dynamics 34(6):1839-1851, 2011.
particle filters may prove to be useful in future applications.111,112,113,114,115,116,117,118,119 Corresponding smoothing techniques are used to improve the quality of the estimates. In addition to the large number of traditional estimators,120 Lp-norm and polynomial chaos estimators are also applicable to problems in astrodynamics. In the applied mathematics and statistics community the subject of uncertainty quantification and stochastic differential equations is an active area of research, both in modeling and in the development of numerical algorithms, and may impact the approaches to nonlinear estimation and modeling in astrodynamics. Given the data-starved environment of space, parameters in the dynamics may be part of the state and need to be estimated. Because it can take some time for a filter to settle down, such “state augmented” or “multiple model” filtering techniques can be particularly valuable for converging sooner with limited data.121,122 Multiple model filters have been particularly successful for detecting and tracking aircraft and missiles during maneuvers, especially when sensor measurements are available during maneuvers. In space surveillance, a maneuver may not be observed; however, multiple model filtering may still be successful in detecting maneuvers. Such maneuvers may then be confirmed using optimal control.
Finding: The proper characterization of uncertainty in a state estimate of a space object requires advanced nonlinear estimation techniques for the measurement models and stochastic differential equations arising in astrodynamics. Such characterizations must address Gaussian and non-Gaussian random processes beyond the Gaussian processes in the extended or unscented Kalman filters.
In the process of determining the orbit, the uncertainty (covariance) of the orbit estimate is also determined. Only in the past few years has the accuracy of this covariance become important. The first major use of the covariance started in the late 1990s when NASA needed the covariance to compute the probability of collision of objects that were going to pass close to the International Space Station or the space shuttle. A factor-of-two error in the covariance can change the probability of collision by three to four orders of magnitude near the threshold where the decision is made to make a collision avoidance maneuver. A covariance that is optimistic, or too small, could result in a decision to not make a maneuver when one should be made, and a covariance that is too large could result in the opposite, making an unnecessary maneuver and wasting fuel. As noted earlier, the user community is trying to improve the covariance using inflation where appropriate. Thus, having a covariance that represents the real uncertainty is critical to the space community as a whole. Other uses of the covariance include correlating uncorrelated tracks, maneuver detection, and sensor resource management. Obviously these uses also require an
![]()
111 D.L. Alspach and H.W. Sorenson, Nonlinear Bayesian estimation using Gaussian sum approximations, IEEE Transactions on Automatic Control AC-17(4):439-448, 1972.
112 K.J. DeMars, “Nonlinear Orbit Uncertainty Prediction and Rectification for Space Situational Awareness,” Ph.D. thesis, The University of Texas at Austin, 2010.
113 J.T. Horwood, N.D. Aragon, and A.B. Poore, Gaussian sum filters for space surveillance: Theory and simulations, Journal of Guidance, Control and Dynamics 34(6):1839-1851, 2011.
114 A. Gelb, Applied Optimal Estimation, MIT Press, Cambridge, Mass., 1974.
115 J.H. Kotecha and P.M. Djuric, Gaussian particle filtering, IEEE Transactions on Signal Processing 51(10):2592-2601, 2003.
116 M. Norgaard, N.K. Poulsen, and O. Ravn, New developments in state estimation for nonlinear systems, Automatica 36(11):1627-1638, 2000.
117 B. Ristic, S. Arulampalam, and N. Gordon, Beyond the Kalman Filter: Particle Filters for Tracking Applications, Artech House, Boston, Mass., 2004.
118 A.H. Jazwinski, Stochastic Processes and Filtering Theory, Academic Press, New York, 1970.
119 H. Tanizaki, Nonlinear Filters: Estimation and Applications, Springer-Verlag, Berlin, 1993.
120 J. Shao, Mathematical Statistics, Second Edition, Springer, New York, 2003.
121 R. Linares, J. Crassidis, M. Jah, and H. Kim, “Astrometric and photometric data fusion for resident space object orbit, attitude, and shape determination via multiple-model adaptive estimation,” Paper AIAA-2010-8341, 2010 AIAA Guidance, Navigation, and Control Conference, Toronto, Canada, August 2-5, 2010.
122 Y. Bar-Shalom, X. Rong Li, and T. Kirubarajan, Estimation with Applications to Tracking and Navigation, John Wiley & Sons, Inc., New York, 2001.
accurate covariance. The primary factors that cause the covariance to not represent the real uncertainty in this case include three of the seven reasons (by Drummond) presented previously, namely:
• Incorrect representation of the sensor errors, biases, residual bases, and noise;
• Misrepresentation of the uncertainty in the forces on the space object, the primary ones being atmospheric drag and solar radiation; and
• The nonlinearities neglected in the orbit determination method becoming large.
The nonlinear effects tend to be small when updating the orbit of objects in the catalog, but they can become dominant when (1) correlating uncorrelated tracks to obtain the initial orbits of space objects or (2) predicting uncertainty for long time periods without additional measurments. For objects not affected by atmospheric drag the primary factor causing the covariance to not be realistic is the mischaracterization of the sensor errors. The radars are calibrated by tracking objects for which the orbits already are very accurate as a result of being tracked by lasers. Each day, each of the sensors track these objects. From the residuals, the mean and the standard deviation are computed for each sensor for each measurement type, e.g., range, azimuth, and elevation. One of the major factors that cause measurement errors is the ionosphere, but the ionospheric effect is a function of the elevation. Using a model of the ionosphere, its effect on the measurement is estimated and this is taken into account, but the model is not perfect and there are residual errors. Consequently, the errors increase at lower elevations, but this effect is not taken into account in the error estimate. In addition, the ionospheric effects are a function of the time of day, and this effect is not taken into account in the sensor error estimate. Thus, the measurement errors are a function of the time of day and the elevation angle, but just one value of the sensor measurement error is used for all elevations and all day. This is just one example of how the sensor errors are not correctly estimated in the current JSpOC calibration process.
Finding: A major factor in the uncertainty (e.g., covariance) not being representative of the true orbit error is the mischaracterization of the sensor errors. (Nonstatistical errors such as the approximation of nonlinear dynamics are also contributing factors to uncertainty.) A program to better characterize these errors will improve the uncertainty, which will improve the accuracy of the probability of collision and improve space safety.
As the number and the sophistication of space-faring nations increase, it is imperative that the operational and analytical capabilities of the JSpOC and AFSPC have the capacity to grow and evolve to provide adequate and necessary monitoring of the space object population. Although it is possible to provide a notional list of what activities and capabilities should exist to better manage these activities, such a prescriptive approach cannot be complete and may neglect important capabilities that are still over the horizon. Instead, in this section the committee provides a brief overview of recent space situational awareness research, and then focuses on a key framework perceived by the committee to be particularly impactful in terms of meeting future JSpOC space situational awareness needs.
Broad Research in Space Situational Awareness
Recent research in the realm of space situational awareness has cast a wide net: a survey of recent conference presentations at the yearly Advanced Maui Optical and Space Surveillance Technologies (AMOS) Conference (available at www.amostech.com) indicates a capacious range of topics, in a number of different arenas. Representative areas of interest include:
1. Analytical capabilities such as maneuver detection, satellite orbit reachability predictions, and strategic analysis of an object’s changing characteristics;
2. Data correlation, association, and initial orbit determination to build and maintain a catalog, both in quiescent operations and in the presence of a debris-generating event;
3. Sensor resource management based on potential object covariance improvements;
4. Satellite formation identification and tracking; and
5. Alternative object states and their characterization, such as attitude, color, and shape.
Although these areas of interest will all benefit from the expanded capabilities and models discussed above, they are topics of research in their own right. Any advances in these areas should be able to be integrated into the activities of the JSpOC given the more flexible architecture of the JMS system.
For example, consider maneuver detection, the automatic detection and estimation of maneuvers and the computation of bounds on these maneuvers.123,124,125,126 Detection capabilities currently exist in a basic form within the JSpOC, but these detected maneuvers cannot be easily estimated within the catalog using tracking data. This necessitates that the state of the maneuvering satellite be estimated “from scratch” after a maneuver is detected, making immediate future prediction difficult. A more robust way to deal with maneuvers is to add an “estimated maneuver” into the orbit determination filter, which allows the maneuver to be precisely estimated based on pre- and post-maneuver tracking and enabling an accurate prediction to be immediately generated. Incorporation of such capabilities could play an essential role in and enable the effective analysis of an object’s activities. Systematic inclusion of these capabilities into the space situational awareness catalog process will motivate the development of more flexible filtering methods with the ability to vary what is considered in the estimated state of the object. These capabilities will also motivate additional computations associated with an object related to characterizing the apparent thrust capability (including electric propulsion and other low-level continuous thrusting) of an object and its propellant usage, which could be essential for making strategic decisions.
Likewise, the other areas of research listed above also provide motivation for a flexible approach that the proposed JMS will enable. However, more fundamental than any specific advancement is the need for a systematic approach to the characterization and categorization of the object population, the topic of the next subsection.
Object Characterization and a More Complete Catalog
Space objects have traditionally been characterized in the catalog by their orbit and, at most, an additional parameter representing the ballistic coefficient of the body. This approach is only acceptable for tracking the trajectory motion of an object over short time periods, but does not provide for the incorporation of any additional information that may be used or available to represent the object and its state, writ large, more accurately. The development and acquisition of such additional information on objects has been a subject of active research, including uniquely characterizing an object based on information that supplements and is different from orbital data. The spectral signature, including both color and reflectivity, of an object can be an important component of the object and can be used for identification. The shape and size of an object can be inferred from high-resolution imagers or from radar range-Doppler imaging of objects and confer unique information about a given object. Even with lower-resolution imaging it is possible to estimate the rotational dynamics and relative attitude of an object using light curves. Finally, significant improvements to the legacy nongravitational parameters currently used in the catalog are being developed and may have significantly better accuracy and utility as estimated parameters for both fitting orbit data and performing more effective extrapolation of these estimates to yield more precise predictions of satellite motion. When appropriately fused together, these characterization techniques can provide a much richer picture of an object. If appropriately stored over time they can also be used to detect an evolving
![]()
123 M.J. Holzinger and D.J. Scheeres, “Object correlation, maneuver detection, and maneuver characterization using control effort metrics with uncertain boundary conditions and measurements,” AIAA Conference on Guidance, Navigation, and Control, Toronto, 2010.
124 T. Kelecy, D. Hall, K. Hamada, and M.D. Stocker, “Satellite maneuver detection using two-line element (TLE) data,” AMOS Technical Conference Proceedings, Wailea, Hawaii, 2007.
125 T. Kelecy and M. Jah, Detection and orbit determination of a satellite executing low thrust maneuvers, Acta Astronautica 66(5):798-809, 2010.
126 N. Singh, J.T. Horwood, and A.B. Poore, “Space object maneuver detection via a joint optimal control and multiple hypothesis tracking approach,” Paper AAS-12-159, 22nd AAS/AIAA Space Flight Mechanics Meeting, Charleston, S.C., January 2012.
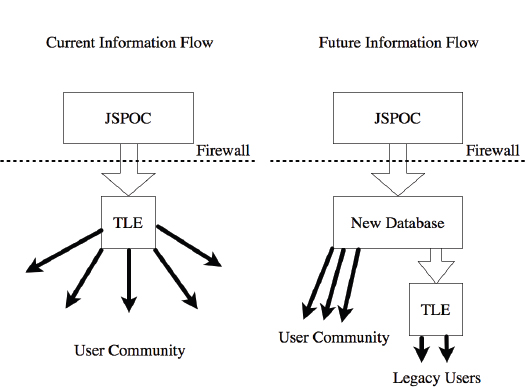
FIGURE 2.3 Proposed new information dissemination model for two-line elements.
mission for a specific object by identifying fundamental changes in an object’s shape or mass due to deployments, or even enable estimates for the pointing of an object and its attendant imaging targets.
To enable such a richer catalog to become real, however, requires that the current limited catalog be enhanced to enable multiple object properties to be tied to each other across a distributed database. To be effective such a database must be flexible enough to enable inclusion of new properties without disrupting existing structures. Such relational databases have been developed to support the storage and retrieval of dynamical and contextual information for scientific missions, and have become a worldwide standard.127,128 In those applications, each object is provided with an identification number, which then can be used to uniquely associate many different aspects of that body, including ephemeris, attitude, and estimated constants. For complex bodies, these ID numbers can be further nested, allowing for a detailed and high-dimensional model to be tracked, thereby providing a framework for tracking satellite clusters and formations in the space situational awareness population. For active bodies, a history of events, maneuvers, and deployments can also be automatically accessed and evaluated.
Such existing products provide a direction for capturing the future potential of expanding object characterization beyond the currently limited approach. Because the storage of this information is not necessarily within a single file, but can be distributed across several files, it is also feasible for sensitive information about an object to be effectively segregated by omitting sensitive files from the distribution. Examples of such sensitive information may include attitude tracking, covariance information, and observed shape changes. The mere act of withholding that information would prevent it from being correlated with more common information such as ephemeris predictions.
Adoption of such a relational database approach could also help resolve the existing issues related to the dis-
![]()
127 C.H. Acton, Jr., Ancillary data services of NASA’s Navigation and Ancillary Information Facility, Planetary and Space Science 44(1):65-70, 1996.
128 C. Acton, N. Bachman, L. Elson, B. Semenov, F. Turner, and E. Wright, “Extending NASA’s SPICE ancillary information system to meet future mission needs,” SpaceOps 2002 Conference, Houston, Tex., October 9, 2002.
semination of orbit and catalog information. For example, the low-accuracy GP catalog is currently locked into the decades-old and inflexible two-line element (TLE) format that does not allow for various levels of accuracy or the inclusion of ancillary information. This legacy format also makes any updates extremely difficult, if not impossible, because of the extent to which these formats are embedded in the user community. The database solutions mentioned here can resolve this problem by placing an additional layer before the TLE dissemination, thereby enabling non-TLE ephemeris inputs to be transformed automatically into a TLE format for those organizations that want only this information, yet allowing a pathway for greatly improved ephemeris predictions and additional information for organizations that have found the TLEs to be inadequate for their needs (see Figure 2.3).
Recommendation: Air Force Space Command should work with Air Force Materiel Command, the National Aeronautics and Space Administration, the National Oceanic and Atmospheric Administration, and other community members to create and expand research programs in the astrodynamics research and development community through the Air Force Research Laboratory to:
• Measure, model, and forecast conditions in the upper atmosphere;
• Develop and implement improved nongravitational models for solar radiation pressure and atmospheric drag;
• Develop and implement continued improvements to gravitational modeling;
• Investigate new data association methods, especially for breakups in low Earth orbit and geostationary Earth orbit clusters;
• Develop a program to better characterize sensor-level errors including biases to improve the input to orbit determination;
• Improve nonlinear estimation and the representation of uncertainty to ensure realism in estimations of uncertainty (covariance);
• Investigate modern methods of dynamical systems to develop new ways to analyze and handle astrodynamics challenges;
• Continue to develop and improve classical analytical techniques for the efficient description and prediction of satellite motion; and
• Explore new techniques to meet community needs.

























