Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 106
6
Aging, Productivity, and Innovation
BACKGROUND
One of the important issues raised by the aging society is its impact
on productivity, adaptation, and innovation. Improvements in productiv-
ity play a central role in the growth of long-run living standards, and an
important aspect of a society is its ability to innovate and adapt to chang-
ing conditions. It is worth remembering that small changes in productivity
growth will lead to large improvements in living standards over time.
There has been relatively little research on the impact of a changing
age structure on overall economic productivity. There are many ways in
which changes in the age distribution can affect productivity. For example,
the performance of certain tasks may differ over the life cycle. There is sub-
stantial research on different ages in the psychology literature. But actual
productivity is more complicated than the undertaking of simple tasks, and
experience, work skills, health status, job turnover, and other more subtle
factors also have a major impact on productivity. The net effect, as best as
the committee can judge from the literature, is that there is likely to be little
net effect of changes in the age distribution on productivity in the United
States over the next two decades.
Productivity growth is commonly measured as the growth of output
per unit of input, either per unit of labor input or per unit of all factors
combined. Analyses of productivity growth generally separate the determi-
nants of labor productivity growth into those generated by (1) increases
in the quantity and quality of inputs combined with labor and (2) techno-
106
OCR for page 107
AGING, PRODUCTIVITY, AND INNOVATION 107
logical change, either new or improved products or improved processes of
production.
The first factor--increases in productivity due to higher inputs--would
include the improved education, training, and skill acquisition of labor as
well as higher quality and quantity of complementary factors such as capital
and resources. For example, increased levels of education of the workforce
improve the quality of labor inputs and thereby increase output per hour
worked. Changes in the quantity of inputs would be the first important
channel through which an aging population could change productivity. As
the workforce ages, it becomes more experienced, and greater experience
is generally associated with higher earnings and productivity. But an aging
workforce might also experience deterioration in the relevant skills if job
requirements change over time or if people's skills decline. Some believe,
for example, that increased penetration of information technologies into the
workplace might place older workers at a disadvantage. This chapter will
review below the evidence on how these factors interact in the workplace.
The second factor in productivity growth involves ingredients other
than increases of inputs. Called "technological advance," it also includes
advances in knowledge and organization and has a completely different
mechanism. Over the long run, technological advance arises from several
channels: the generation and diffusion of new scientific, technological, and
engineering knowledge and improvements in production processes and
social overhead capital. For example, the vast improvements in productiv-
ity in computation arose from a long line of technological developments,
from transistors to improved communications to programmable software.
Innovations in organizational structure and management practices and
improved political and legal environments have also fostered significant
productivity gains. While technological advance and other changes have
played a key role in productivity growth, their rate and direction have
varied greatly from decade to decade, and the pattern of change is not well
understood.
Studies of productivity growth and technological change emphasize
that progress does not typically occur through a grand leap by a single
ingenious inventor. Rather, improvements in products and processes are
typically the result of many small and unspectacular steps. They result from
the application of basic research and engineering, from learning by doing,
and from suggestions by workers on the production line.
Clearly, the processes involved in increasing productivity involve both
very local forces, such as the skills of individual workers, and more global
trends in new and improved technologies and processes. Moreover, eco-
nomic studies indicate that the second factor--technological advance--is
the major contributor to long-run growth in productivity. Depending on
OCR for page 108
108 AGING AND THE MACROECONOMY
the time, place, and approach, studies indicate that anywhere from half to
virtually all of the growth in output per hour worked or per capita income
is due to advances in knowledge, and that the balance is due to increases
in capital and other inputs per unit of labor.
RESEARCH ON THE IMPACTS OF AGING
AT THE INDIVIDUAL LEVEL
There is a substantial literature on behavioral measures of productiv-
ity or proxies for it over the life cycle. Studies include psychometric ones
(such as ones that measure verbal or quantitative reasoning), ratings (such
as those of supervisors), productivity measures (such as in piece rates or
baseball scores), and statistical studies at the company level. Useful surveys
are those by Prskawetz and Lindh (2006) and Skirbekk (2004).
On the whole, the literature on individual productivity measures shows
great diversity across age, individuals, and measures. As one of the pioneers
in the field, Salthouse (1991) found that the relationship between age and
cognition varies considerably across different cognitive tests.
Many psychometric measures show a clear relationship to age. Verhaegen
and Salthouse (1997) provide a meta-analysis of cognitive s tudies (p. 246).
They compare the performance of individuals over and under 50 years of age
and conclude as follows:
[M]eta-analyses of correlations between age and different measures of
cognition revealed that the age relations in this literature are somewhat
stronger with measures of speed than with measures of reasoning, spatial
abilities, and working and episodic memory and that primary memory has
a smaller age relation than do the latter variables.
Avolio and Waldman (1994) examine a series of studies that measure
work-related skills using the General Aptitude Test Battery (GATB) for
more than 25,000 workers from 16 to 74 years old. They conclude that
age accounted for a relatively small percentage of the variance in ability test
scores once experience, education, and occupational type were controlled.
Differences in performance across age groups were relatively small until at
least age 65. However, unlike the earnings data reviewed below, job experi-
ence has little value in predicting the maintenance of abilities over the long
run except for complex jobs.
Literature using other metrics for individual productivity also shows
divergent results by age and metric. One survey concludes that supervisors'
ratings typically do not find any clear systematic relationship between age
and productivity. The evidence on productivity as measured by piece rates
is mixed.
An important new approach is cross-sectional employer-employee
OCR for page 109
AGING, PRODUCTIVITY, AND INNOVATION 109
matched data. These studies also show a mixed pattern, with many stud-
ies estimating peak productivity at around 40 years of age, while a few
find peak productivity at older ages. Case studies in the United States and
Germany shed more light on the age-productivity relation. Kotlikoff and
Wise (1989) found that the productivity of salespeople in a large insurance
company, measured by the value of contracts sold, increases with age.
Boersch-Supan, Duezguen, and Weiss (2008) and Boersch-Supan and Weiss
(2011) assembled a large data set on production workers in a German car
manufacturing company over many years and show a similar effect. They
measure productivity by the absence of errors in a well-defined production
process. They find that, while the number of small errors is larger among
older workers, major errors are more frequent among younger ones. Their
measure of productivity finds that older workers have higher productivity.
Although the literature on productivity and behavior at the individual
level provides weighty evidence on the impact of aging on many individual
attributes, we need to be cautious about the application of those attributes
to aggregate productivity. Many of the studies are cross-sectional and do
not take into account changes in occupation or, in labor market studies,
attrition.
Additionally, the determinants of individual productivity are extremely
complex and are unlikely to be captured in most metrics. For example, a
typical cross-sectional study of earnings can explain a small fraction of the
dispersion on the basis of personal attributes such as intelligence. Moreover,
while it is true in a few areas that reasonable output metrics have been
developed (such as for athletes), we know that in other areas the measures
have often proven highly unreliable and even systemically dangerous (such
as the compensation metrics used in many financial firms).
Furthermore, the important skill sets, and the difficulties in accurately
measuring them, will change over the life cycle as workers move from being
unskilled workers at fast food stores in summer jobs, to entry-level techni-
cians, to middle and upper management positions. Given the multitude of
attributes and vast number of different jobs, it has proven very difficult to
make an accurate measure of the economic value of an individual's attri-
butes and the changes in those over time due to aging.
A final reason to discount metrics on individual attributes is that work
increasingly takes place in teams. Teams are often composed of individuals
with different backgrounds and experiences, and it is difficult to separate
the contribution of individuals. So while we might focus on the hitting
scores of star baseball players, it is worth considering how well nine play-
ers would perform in the absence of (generally older) coaches, trainers,
surgeons, and owners. In an economy, it is generally the bundle or teams
that are productive, not the individuals.
For this reason, the committee tends to prefer market-based measures
OCR for page 110
110 AGING AND THE MACROECONOMY
to estimate the impact of aging on productivity, either measures based on
market earnings or ones based on aggregate measures of productivity.
AGING AND THE ECONOMICS OF
INNOVATION AND INVENTION
The first important question involves the impact of changes in the age
distribution of the population on a society's innovation and invention. An
important aspect of new knowledge is that it is a public good, a process in
which new technologies generated anywhere can potentially spread and be
used by all, young and old, rich and poor, at home and abroad. Hence the
stock of useful and productive knowledge should be seen in the context of
the global stock rather than that of an individual person or country. If other
countries take up more of the innovational activities that were over the last
century led by the United States and other current high-income countries,
the overall trend in income and productivity growth might well continue
to grow rapidly. So a first important point is that it is global inventive and
innovative activity that over the coming decades will influence long-run U.S.
productivity and income growth. Countries are not technological islands
in an increasingly globalized world. As countries grow and increase their
inventive activity in an increasingly networked world, the United States will
benefit from the inventiveness outside its borders (Jones and Romer, 2010).
While long-run productivity growth is likely to be largely determined
by global trends in frontier technologies, national characteristics are critical
for diffusion and adoption of best-practice technologies and for actual lev-
els of productivity. Studies of diffusion show that best-practice knowledge
and techniques diffuse more slowly across national borders than within na-
tions. The rate of adoption depends on many non-age-related factors, such
as openness to trade and capital flows; competitiveness of domestic market
structures; profitability; and regulatory structures. The major impacts of
age-related factors reflect the composition of demand. For example, an ag-
ing population or one with strong demand for health services is likely not
only to generate but also to adopt technologies that are in great domestic
demand in this sector.
There is a substantial literature on the age distribution of producers of
inventions, patents, publications, and other creative material. Historians of
science have generally concluded that scientific output tends to rise steeply
in the twenties and thirties, peak in the late thirties or early forties, and
then trail off slowly through later years. There is some variation among
disciplines, but most studies find that peak scientific productivity tends to
be in the interval between ages 30 and 40 (Lehman, 1953; Simonton, 1988
and 1991).
Benjamin Jones (2010) has investigated the question of age and "great
OCR for page 111
AGING, PRODUCTIVITY, AND INNOVATION 111
achievement" in a statistical framework using data covering more than a
century. His sample is of Nobel prize winners in physics, chemistry, medi-
cine, and economics (N = 544) and great technological inventors (N = 286).
Figure 6-1 shows the age distribution for each group from his sample. In
each case, the average age was 39.1 There is considerable dispersion in the
distribution.
Another important finding of Jones's study is that the average age at
which invention occurred increased over the twentieth century. For recipi-
ents of Nobel prizes in physics, chemistry, and medicine, the increase in
the median age has been around 2 years per century, while the increase
in the mean has been 8 years. The increase has resulted from an increase in
the starting age (the age at which the youngest inventors did their prize-
winning work) as well as the ending age (the age at which oldest inventors
did their prize-winning work). In part, the increase in the ending age is due
to the longer life span over which invention occurs that comes from longer
life expectancy.
From a policy perspective, one of the most important findings is a delay
in the start of the creative period. Jones finds a significant delay in the onset
of scientific creativity. He points to two potential factors in the delay: the
increased complexity of acquiring knowledge because of the greater depth
of accumulated knowledge and the longer time to a final degree (see also
National Research Council, 1990 and 1998).
There is genuine concern on the part of the scientific establishment in
universities as well as federal scientific agencies that the longer time for
young researchers to enter their careers as productive scientists is due to
institutional impediments.
Patents and Other Areas
Another measure of innovative output, and one that is generally closer
to economic activity, is patents. Patents have been the subject of study as
indicators of inventive output for many years (see the overview in Griliches,
1990). They have the advantage of passing some threshold of importance
and nonobviousness. Their shortcoming is that they have highly variable
importance and commercial value. Jones (2009) examined the characteris-
tics of patent awardees over the twentieth century and found increases in
three important measures: (1) the age at which an inventor makes the first
invention; (2) a measure of specialization in patents; and (3) the size of
teams. He concludes that the nature of the scientific and inventive process
is becoming more complicated as more knowledge is accumulated. Addi-
tionally, the age at which applied knowledge was crystallized in the form
1Age refers to the age at which a discovery was made, as best as could be determined.
OCR for page 112
112 AGING AND THE MACROECONOMY
0.05
0.04
Frequency
0.03
0.02
0.01
0
20 30 40 50 60 70 80
Age
Nobel Prize Winners Great Inventors
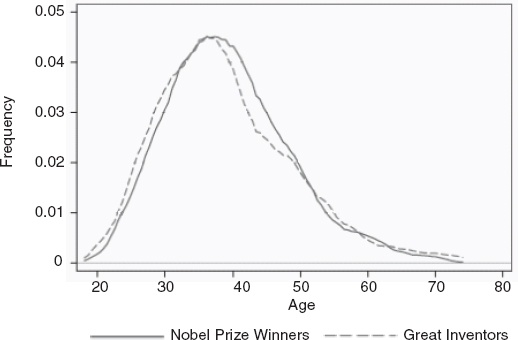
FIGURE 6-1 Age distribution of great inventors and Nobel prize winners. SOURCE:
Jones (2010). Reprinted by permission.
6-1.eps
3 bitmaps with vector type
of patents tends to be about a decade later than transformational science
or great inventions.
Other studies have examined the age of artistic creation, such as for
works of fine art (Galenson 2004a and 2004b). There appears to be greater
dispersion in the ages of creative works than of scientific achievements.
Galenson also distinguishes between conceptual innovations (done at an
early age) and experimental creativity (often performed at a later age). But
the basic idea about the distinctive role of the early years (from 25 to 45
years of age) emerges from these other studies as well.
Determinants Other Than Age
While age is an important determinant of invention and innovation, it
explains very little about actual performance across societies. Other factors,
such as education, support institutions, economic and social rewards, and
religious institutions, tend to dominate the actual distribution of scientific
output.
This can be illustrated by examining the distribution of Nobel prize
awards in chemistry and physics over the last century. If we assume that
the distribution of awards should be proportional to that of raw talent, and
that raw talent should be equally distributed around the world, then we
would expect that the number of prize winners should be distributed pro-
portionally to the population (or young population) of different countries.
OCR for page 113
AGING, PRODUCTIVITY, AND INNOVATION 113
In reality, the proportion of prize winners born in Africa or India is lower
by a factor of more than 100 than that of those born in Western Europe and
North America. Moreover, the least developed countries, with 10 percent of
the world's population, have not produced a single prize winner in physics
or chemistry during the entire history of those prizes.
Put differently, over two-thirds of Nobel prizewinning research done
since 1960 has occurred in the United States, even though the United States
averaged only 5 percent of the world's population. The fact that 30 percent
of U.S.-based Nobel prize winners were foreign born indicates the impor-
tance of the research environment for successful invention.
Looking forward, the key to continuing strong advances in knowledge
for the United States and other countries is to increase investments in young
scientists and other creative talent. The importance of the support environ-
ment is an emphatic reminder of the key role of educational and other social
institutions in nurturing innovation. The United States has performed rela-
tively poorly in recent years in K-12 education compared to other countries,
according to the Organisation for Economic Co-Operation and Develop-
ment (OECD) Programme for International Student Assessment. Also, most
urban school districts in the United States see high school graduation rates
of only 50 percent. These indicators are a reminder of the vast potential
supply of scientific and innovational talents that remains untapped in the
United States and the rest of the world, and of the important determinants
of technological advance other than age.
PRODUCTIVITY AND THE AGE STRUCTURE
OF THE POPULATION
The second important factor in the productivity of the population in-
volves the interaction of the quality of the workforce and the distribution
of the population with a given technology. As noted above, this influence
would include the impact of improved education, training, skill acquisition
of labor as well as higher quality and quantity of complementary factors
such as capital and resources. In its discussion, the committee focuses on the
impact of a workforce whose composition is changing; the reason for this
focus is that the impact of the age distribution on complementary factors
such as capital and resources appears to be less significant.
The basic idea is that workers have different productivities as a result
of evolving skills, experience, formal and informal education, training,
and personal attributes over their life cycles. In the human capital model,
productivity is a function of the amount of accumulated human capital.
Human capital will vary over the life span. Generally, we expect produc-
tivity to be relatively low for unskilled and inexperienced workers; to rise
with education and experience and as workers find a good match between
OCR for page 114
114 AGING AND THE MACROECONOMY
their skills and the opportunities in the workplace; and eventually to de-
cline either as (or if) their skills decline or their specific human capital and
experience depreciate.
A central issue in this context is the age distribution of productivity
for the workforce. Changes in aggregate productivity arise from the inter
action of the age distribution of productivity and the changing age dis
tribution of the labor force. This can be called the "age composition effect."
A plot of this effect would be analogous to the productivity curve shown in
Figure 6-1, although it would look quite different. There are two alternative
approaches to estimating the age composition effect. The first examines the
age distribution of earnings and assumes that earnings are proportional to
productivity. The second looks directly at the impact of the age distribution
on aggregate productivity.
Earnings and the Changing Distribution of the Workforce
There is a vast literature on the distribution of earnings by different
attributes, including age, experience, and education. A recent survey of this
approach summarized the results as follows:
Perhaps the most widely estimated regression equation in economics is
Mincer's log-earnings function that relates the log of individual earnings or
wages to observed measures of schooling and potential work experience.
The regression has been estimated in numerous studies, employing various
data sets from almost every historical period and country for which micro
data are available, with remarkably robust regularities. First, workers'
wage profiles are well ranked by education level; at any experience level,
workers earn more, on average, as their schooling increases. Second, aver-
age wages grow at a decreasing rate until late in one's working lifetime.
(Rubinstein and Weiss, 2006, p. 3)
In the simplest approach, with perfectly competitive markets, a work-
er's hourly earnings are equal to the value of the marginal product of an
hour worked. This relationship would hold even if the worker is investing
in general (non-firm-specific) human capital. Labor economists have reser-
vations about this theory. The link between current earnings and current
marginal productivity may be decoupled if there are long-term relations or
contracts between the worker and the company. In some areas, for example,
compensation is back-loaded to provide incentives for workers to stay with
companies. Additionally, most earnings estimates exclude fringe benefits
such as health care, which are an increasingly important fraction of total
compensation. While labor economists generally believe that fringe benefits
are a dollar-for-dollar substitute for wages, this may hold for the company
and is unlikely to hold for individual workers in large companies, so ex-
OCR for page 115
AGING, PRODUCTIVITY, AND INNOVATION 115
amination of earnings without fringe benefits is an appropriate approach.
While the earnings-marginal productivity theory has many shortcomings,
it does provide a useful benchmark for purposes of estimating the impact
of a changing age structure.
The examples provided here take the simplest case in which earnings
are assumed to be proportional to marginal productivities.2 This specifica-
tion initially assumes no impact of changes in the distribution of the labor
force on relative earnings or productivity, and this assumption will be
relaxed below.
The standard earnings-age-experience model assumes that earnings
are a quadratic function of age or experience. A careful review of the data
indicates that this introduces inaccurate estimates in the tails of the dis-
tribution. It underestimates the growth of earnings in the early years and
overestimates the decline in the later years. Since these are exactly the years
that are important for present purposes, estimation of distributional effects
is accordingly uncertain.
For the present purpose, the committee took estimates of the age-
earnings profile for college graduates and high school graduates. The esti-
mates are drawn from a study by Lemieux (2006) based on earlier work
of Murphy and Welch (1990) and are very similar to those made by
Rubinstein and Weiss (2006). The Lemieux estimates rely on 1999-2001
Current Population Survey data on hourly earnings with a dummy for edu-
cation and for year. Estimates of the earnings-experience curve are shown
in Figure 6-2. The shaded line is the unconstrained curve, while the other
two show the results using quadratic and quartic functions of experience.
To generate estimates of the impact of a changing age distribution
on productivity, the committee used the 1999-2001 age-experience curve
as its age-productivity relationship in conjunction with the committee's
estimates and projections of the distribution of the labor force by age (see
Appendix A) for three different years, 2010, 2020, and 2030, and applied
the estimates for males to all workers. This yields three different experi-
ence curves: the quadratic fits the standard quadratic function to the actual
data; the quartic fit is the result of Lemieux's equation; and the actual is the
unconstrained age-experience curve. These results are shown in Table 6-1
separately for college and high school graduates.
2The procedure for estimating the age composition effect assumes that the workforce has
a distribution given by {1,t,..., n,t}, where i,t is the share of the labor force, employment,
or population in age group i and time period t. We assume that productivity is a separable
function of the share of workers in each age group and of other factors. Then we can write
the aggregate production function as
Yt = AtF [Ht,Kt], Ht = [(i,t Lt) wi,t]
where Lt is total labor inputs in year t, Ht is an index of aggregate labor input, Kt is capital
and other inputs, wi,t is average earnings of group i, and At is an index of technology.
OCR for page 116
116 AGING AND THE MACROECONOMY
1.0
0.9
0.8 Confidence band on
unrestricted profile
0.7
Log Wage Differential
0.6
0.5
0.4
0.3
0.2
Quadratic fit:
0.1
Quartic fit:
0
-0.1
0 5 10 15 20 25 30 35 40
Years of Potential Experience
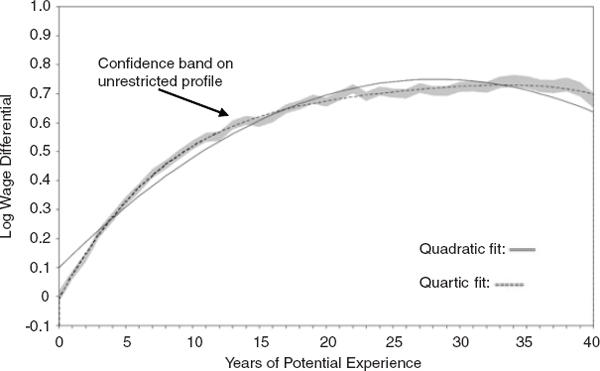
FIGURE 6-2 Distribution of earnings, by age. This figure shows the unrestricted
(shaded band) as well as quadratic and quartic fit to the ln wage data for males us-
ing data from the 1999-2001 Current Population Survey. The series are estimated
6-2.eps
with a full set of education, experience, and year dummies. SOURCE: Lemieux
(2006). Reprinted by permission.
bitmap with vector type and arrow
Note that the earnings functions usually do not go beyond 40 years of
experience (taken to be 62 years of age for college graduates and 58 years
for high school graduates). Therefore, this analysis takes the distribution
only through 40 years of experience, which covers between 87 and 91 per-
cent of the distribution depending upon the year. There is some truncation
bias, but this appears to make little difference to the estimates.3
Table 6-1 shows the calculated impact of the changing age distribution
on the rate of growth of productivity over the 2010-2020 and 2020-2030
periods. The estimates suggest that the age composition effect is likely to be
very small for all specifications and both periods. The largest positive num-
ber is 0.024 percentage points per year and the largest negative estimate
is -0.013 percentage points per year. For reference purposes, multifactor
productivity growth over the 1987-2010 period has averaged 1.1 percent
per year according to the Bureau of Labor Statistics (2011a).
3The
sensitivity of these estimates can be determined by extrapolating the experience curve
through labor force projections to age 90. The impact is around -0.008 percentage point
using specifications for college graduates. Another adjustment would be to take into account
unemployment rates by age, but the committee did not undertake this estimate.
OCR for page 117
AGING, PRODUCTIVITY, AND INNOVATION 117
TABLE 6-1 Projected Impact of Changing Age Distribution on
Productivity for Two Education Groups, 2010-2020 and 2020-2030
Impact of Changing Age Distribution on Productivity
(percentage points per year)
Education Group 2010-2020 2020-2030
High school
Quartic fit 0.020 0.005
Actual 0.023 0.004
Quadratic specification -0.013 0.006
College
Quartic fit 0.006 0.011
Actual -0.003 0.009
Quadratic specification -0.010 0.024
Research indicates that changes in the age distribution of workers may
impact relative wages. Card and Lemieux (2001) estimate that a 1 percent
increase in the share of workers in a cohort relative to other workers will
lower their earnings by approximately 0.2 percent for a given education and
cohort, while Carneiro and Lee (2011) estimate an impact that is approxi-
mately one-half of that. The committee examined the impact of allowing
imperfect substitutability on the age-productivity relationship. Dividing the
workforce into six subgroups, it estimates that assuming perfect substitu-
tion among different age groups raises calculated productivity growth by
0.01 to 0.02 percentage points per year over the 2010-2030 period, depend-
ing upon which of the two estimates is used. In the context of all the factors
at work, the substitution impact is very small.
The committee concludes that, taking earnings as a proxy for produc-
tivity, the impact of the changing age distribution on the level of productiv-
ity is negligible. The intuition behind these results can be explained using
the quadratic specification of the earnings function for college graduates.
According to the committee's projections, the average age of the labor
force in the age range examined here is expected to increase by 2.0 years
from 2010 to 2030. It estimates the slope of the log experience curve at the
average experience for this period for college graduates is 1.2 percent per
year of experience. Over the 20-year period, this averages 1.2 × (2.0)/20
= 0.12 percentage points per year. The estimates in Table 6-1 are slightly
lower than this estimate because of asymmetries in the age distribution,
but from an economic point of view the estimates are virtually identical.
The impact of the changing age distribution on productivity is small fun-
damentally because the slope of the earnings curve at the current average
age of the labor force is close to zero. In other words, if the average age of
the workforce were to increase by a single year (and ignoring for simplicity
OCR for page 118
118 AGING AND THE MACROECONOMY
the dispersion of worker ages), the impact of estimated productivity would
be essentially nil.
Productivity and the Changing Distribution of the Workforce
In contrast to the vast enterprise engaged in estimating earnings-
experience functions, there is very little research on the question of the
impact of changes in the age distribution on overall productivity. An early
study by Cutler et al. (1990) looked at the impact of changes in the growth
rate of the labor force on labor productivity using a panel of countries over
the period 1960-1985 and subperiods. After conducting a battery of tests,
they conclude, "Because the annual labor force growth rate is predicted
to fall by about 1 percentage point between 1990 and 2050, with most
of the change occurring between 1990 and 2010, our estimates imply an
increase of about 0.6 percentage point in annual productivity growth" (p.
43). When they correct for the average age of the labor force (similar to
below), they find a slightly smaller impact. Their net results are that slower
labor force growth accompanied by a higher average age leads to higher
labor productivity.
More recent work by Feyrer (2007 and 2008) uses more detailed
demographic data. His approach takes measures of productivity growth
in major countries and combines them with estimates of the shares of the
labor force in different age groups, using output data from the Penn World
Table 6.0 and worker data from the International Labor Organization
for decadal observations, the latter interpolated for 5-year intervals using
population data from the United Nations. The total sample is 87 countries,
while a more appropriate sample of countries for our purpose is limited to
21 OECD countries.
The Feyrer work shows an implausible pattern of coefficients when all
six age groups are included. The ordinary least squares estimates for the
OECD countries indicate that there is a logarithmic productivity bonus for
workers in the 40-49 age group of 2.3 (a factor of 10) relative to work-
ers aged 30-39 and of 2.0 (a factor of 8) relative to workers 50-59. These
estimates likely reflect sampling error that arises from an excessive number
of estimated parameters (i.e., equations that include all share variables).
The committee therefore reestimated the productivity equations using lin-
ear, quadratic, and cubic functions of the average age.4 This reestimation
4This analysis examines OECD countries only (total observations N = 126) because the
other countries not only have poorer quality data but also seem less relevant to understanding
productivity patterns in an aging society. If the equations for all countries are used, the esti-
mated impact on productivity growth is a larger positive number than that shown in Table 6-2.
OCR for page 119
AGING, PRODUCTIVITY, AND INNOVATION 119
produced reasonable estimates, with a hump-shaped function of age that
reaches a maximum at approximately 40 years.
For the sample of OECD countries, the United States lies pretty much in
the mean of the sample of average ages. For the latest year (2000), the mean
age of the U.S. workforce in the Feyrer data set is 40.1, while the range for
OECD countries is 37.7 to 45.0 years. The average age of the workforce
is estimated to increase from 41.1 years in 2010 to 43.2 years in 2030, so
the mean value is within the range of estimates in the data used to estimate
the productivity function.
Table 6-2 shows calculations analogous to those shown in Table 6-1 for
the aggregate productivity equations. These equations estimate the impact
of polynomial functions of the change in mean age on the change in the
logarithm of total factor productivity using the Feyrer data set. For all three
specifications, the committee has taken the mean age of the labor force from
its estimated and projected age distributions for the years 2010, 2020, and
2030. If the equations are nested, the cubic term is statistically insignificant
when the linear and quadratic terms are included (p = 0.46). The quadratic
term is statistically significant when the linear term is included (p = 0.034).
On a statistical basis, therefore, the committee prefers the quadratic speci-
fication in Table 6-2.
In the preferred equation, the change in the age distribution subtracts
approximately 0.1 percent per year from aggregate productivity over
the next two decades. However, this finding is sensitive to alternative
specifications.
Conclusion on Productivity
The impact of changes in the composition of the labor force on pro-
ductivity shows consistent results in all the committee's tests. Even though
the numbers vary slightly depending on the technique, estimation period,
and group, the estimates all indicate that the age composition effect on
TABLE 6-2 Projected Impact of Changing Age Distribution on
Productivity Using Three Aggregate Productivity Estimates, 2010-2020
and 2020-2030
Impact of Changing Age Distribution on Productivity
(% change per year)
Productivity Estimates 2010-2020 2020-2030
Linear 0.60 0.25
Quadratic -0.06 -0.14
Cubic 0.09 0.04
OCR for page 120
120 AGING AND THE MACROECONOMY
productivity for the U.S. labor force over the next two decades is very
small. The only exception is the linear productivity equation in Table 6-2,
but this estimate should be discounted both because it is inconsistent with
the earnings approach and because the quadratic approach has superior
statistical qualities.
Therefore, the bottom line is that the committee's estimates indicate
that there is likely to be a negligible effect of the age composition of the
labor force on aggregate productivity over the next two decades. The sum-
mary judgment is that the age composition effect is between -0.1 and +0.1
percentage point per year.
However, these estimates are subject to some remaining uncertainty.
For the earnings estimates, the uncertainties arise because of the concern
that earnings do not reflect marginal productivities. If that relationship were
clearly established, then the estimates in Table 6-1 indicate that the impact
of the changing age distribution is close to zero. From a conceptual point
of view, the productivity approach is superior because it would capture
the substitution and complementarities among different groups as well as
any externalities (at least in the sample period). However, at present, the
empirical results are quite fragile and subject to specification concerns, so
the results shown in Table 6-2 must be taken as very tentative.
IMPLICATIONS
The committee has considered the implications of its review of the
relationship between the aging of the workforce and productivity and in-
novation. There are multiple pathways from a changing age distribution to
the growth of productivity and income and their eventual magnitude. The
most important in the long run is the rate of total factor productivity. The
United States has been a major contributor to technological change, so it
is important to ensure that policies are well-designed for innovation in an
aging society.
One of the major policy levers on productivity and innovation is im-
migration. This is particularly important for scientists and innovators,
where the United States has proven to be fertile soil for nurturing inventive
talent, as was seen in the preceding discussion of the greatest scientists.
Immigration has been a major source of scientific and innovative gains in
this country over the last century. Immigration, and particularly the skill
characteristics of immigration, is perhaps the most important way to affect
innovativeness. Immigration policies must therefore be very sensitive to
the potential for retarding the flow of the best talent to the United States.
Another factor that can play a particularly important role is the pattern
of support for young scientists and engineers. This is an area where small
changes in public policy and funding might have a large effect on creative
OCR for page 121
AGING, PRODUCTIVITY, AND INNOVATION 121
outputs. While there has been attention paid to the lengthening time to the
doctorate and the increased age at which scientists win their first grants, it
appears that this is a particularly critical question for creative life spans.
Earlier NRC studies discussed issues in this area, and the present committee
would note two measures that are particularly important. First, it is impor-
tant to ensure that young researchers have access to federal grants. This
will be especially critical in an environment in which the federal budget is
constrained and federal funds for science and engineering are likely to be
under severe pressure. Additionally, it is important to ensure that the time
to degree for young researchers be kept at the minimum so that they can
progress to productive and independent scientific careers. This emphasizes
the need for strong support for doctoral and postdoctoral scientists and
engineers as well as measures that shorten the time during which young
people are dependent on older researchers for support.
An important area for innovational structure is retirement policy. Fiscal
concerns suggest that the country should support measures that encour-
age people to work longer. This is particularly true of incentives to retire
early that have been discussed in Chapter 5 and elsewhere in this report.
However, the committee would issue cautions about the potential squeeze
on young scientists in a period in which universities and other institutions
of innovation are under pressure. There has been aging in our innovational
institutions over recent years, and this is of concern for a sector where the
most innovative work is done early in the life cycle, as seen above. Atten-
tion to the needs of young scientists will help advance the early stages of
scientific careers. Innovational institutions should pay increased attention
to the need to ensure that there is ample room for young scientists and
scholars in their ranks.
Finally, some federal spending and tax structures are more likely to
promote innovation than others. Programs to support education, science
programs, and scholarships for college and postgraduate students are better
at creating an innovative society than many existing federal programs. It
is important that fiscal decisions in a constrained budget environment be
mindful of the impact of policies on innovation and adaptiveness.
